Einige Fragen aus den Elementen der Darstellenden Geometrie,
|
|
|
- Bärbel Tiedeman
- vor 7 Jahren
- Abrufe
Transkript
1 Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und Aufriss des Punktes P sind, und man diese Punkte vertauscht, also P' mit Q" und P" mit Q' bezeichnet, so kann man fragen, welche Lage die Punkte P, Q im Raume zueinander haben. Die Punkte P, Q haben in verkehrtem Sinne gleiche Abstände von den zwei Bildebenen ; der Punkt P liegt so weit oberhalb oder unterhalb der ersten Bildebene als der Punkt Q hinter oder vor der zweiten Bildebene liegt. Daher liegen die zwei Punkte P, Q symmetrisch zur Deckebene oder hintern Halbierungsebene 1), d. i. die Ebene, welche diejenigen zwei Quadranten halbiert, durch welche die zweite Bildebene gedreht wird, bis sie mit der ersten Bildebene zusammenfällt. Die Mitte M' " von P' P" ist die vereinigte Projektion der Mitte von PQ in der Deckebene. Die vereinigten Spurpunkte S 1. 9 der Geraden PQ liegen so, dass OS,., = 2 OM'. " ist, wenn 0 der Schnittpunkt der sogenannten Ordnungslinie P' P" mit der Achse ist, d. i. die Schnittlinie der beiden Bildebenen. II. Wenn g', g" in dem System der vereinigten Bildebenen der Grund und Aufriss der Geraden g sind, so kann man g', g" miteinander vertauschen, d. h. g' mit 1" bezeichnen und g" mit l' ; dann entsteht die Frage nach der Lage der Geraden g, l im Raum. Wählt man auf der Geraden g den Punkt P und vertauscht seine Projektionen, so entsteht der symmetrische Punkt Q zum Punkt P in bezug auf die Deckebene. Durchläuft der Punkt P die Gerade g, so beschreibt der Punkt Q die symmetrische Gerade b zur Geraden g in bezug auf die I) Dieses Resultat ergibt sich auch durch folgende Überlegung. Die Strecken P' Q', P" Q" fallen in verkehrtem Sinne aufeinander. Daher hat die Mitte M von PQ zusammenfallende Projektionen und liegt in der Deckebene. Die Strecke PQ stebt auf der Deckebene senkrecht, weil die Projektionen in verkehrtem Sinne zusammenfallen,
2 Jahrg. 74. A. KIEFER. Fragen aus den Elementen der Darstellenden Geometrie. 165 Deckebene. Die gegebene Gerade g und die durch Vertauschen ihrer Projektionen entstehende Gerade l liegen symmetrisch zur Deckebene. Die Spurpunkte der beiden Geraden g, l fallen verkehrt aufeinander. Man erhält also zu einer Geraden die symmetrische Gerade in bezug auf die Deckebene, indem man die Spurpunkte der Geraden vertauscht. Die Verbindungsgerade der beiden Spurpunkte von g ist die vereinigte Spur der Ebene (g, 1). Der Schnittpunkt G', G" von, g" ist der gemeinsame Schnittpunkt der Deckebene mit der Geraden g und mit der Geraden d. Die Verbindungslinie des Punktes G'" mit dem Punkt, wo die vereinigten Spuren die Achse treffen, ist die Halbierungslinie des Winkels (g, l) und zugleich die Affinitätsachse der Ebene (g, l). Die beiden Geraden g, l haben noch eine andere Ialbierungslinie; sie steht senkrecht auf der Deckebene, zu welcher g, l symmetrisch liegen. Die Projektionen der Halbiernngslinie gehen durch G' " und laufen senkrecht zur Achse, das ist die Schnittlinie der beiden Bildebenen ; die Spurpunkte der Halbierungslinie liegen auf den vereinigten Spuren der Ebene (g, l). Liegt g in einer Bildebene, so fällt die entsprechende Gerade l in die andere Bild ebene. Durch einen Punkt R', R" des Raumes geht ein Strahlenbündel; vertauscht man die Projektionen der einzelnen Strahlen, so entsteht das symmetrische Strahlenbündel in bezug auf die Deckebene, dessen Scheitelpunkt der symmetrische Pnnkt von R in bezug auf die Deckebene ist. Die Projektionen der einzelnen Strahlen des Bündels auf die Deckebene bilden ein Strahlenbüschel, dessen Grund und Aufriss zusammenfallen ; der Scheitelpunkt ist der Fusspunkt des Lotes von R auf die Deckebene, cl. h. die Mitte von R', R". III. Die Symmetrieebene, d. i. die Ebene, welche den ersten und dritten Quadranten halbiert und die Deckebene stehen mit mancherlei Aufgahen im Zusammenhang. Jede Gerade, die zur Symmetrieebene oder zur Deckebene parallel ist, bildet mit beiden Bildebenen gleich grosse Winkel; im ersten Fall bilden die Projektionen der Geraden mit der Achse in verkehrtem Sinne gleiche Winkel und im zweiten Falle sind die Projektionen der Geraden zueinander parallel. Alle Geraden des Raumes, welche mit beiden Bildebenen gleich grosse Neigungswinkel besitzen und zwei gegebene windschiefe Geraden des Raumes schneiden, erfüllen ein hyperbolisches Paraboloid, für welches die zwei Geraden Leitlinien sind, während die dritte Leitlinie im ersten Falle die unendlich ferne Gerade der Symmetrieebene und im zweiten Falle die unendlich
3 166 Vierteijahrsschnift der Naturf. Gesellschaft in Zürich ferne Gerade der Deckehene ist. Wenn eine Ebene zur Symmetrieebene oder zur Deckebene parallel ist und man legt in die Ebene irgendein Polygon oder eine Figur, so sind die zwei Projektionen kongruent, und zwar im ersten Falle in verkehrtem Sinne und im zweiten Falle im gleichen Sinne. Wenn eine Ebene zur Symmetrieebene oder zur Deckebene senkrecht steht, so bildet die Ebene mit beiden Bildebenen gleiche Winkel; legt man in die Ebene ein Polygon oder eine Figur, so sind Grund und Aufriss von gleichem Inhalt. IV. Wenn e,, e ^ in dem System der vereinigten Bildebenen die erste und zweite Spur der Ebene E sind, so kann man e l, e 2 miteinander vertauschen, d. h. e, mit f 2 und e 2 mit f 1 bezeichnen; dann entsteht die Frage nach der Lage der zwei Ebenen E, F im Raum. Legt man in die Ebene E zwei beliebige Geraden g, l, und vertauscht man. die Spuren der Ebene, so vertauschen sich die Spurpunkte von g und auch von 1; man erhält die symmetrischen Geraden zu g, l in bezug auf die Deckebene. Durch Vertauschen der Spuren einer Ebene entsteht die zur Ehene in bezug auf die Deckebene symmetrisch gele géne Ebene.') Wenn die Spuren einer Ebene zusammenfallen, so muss sie mit ihrer zur Deckebene symmetrisch gelegenen Ebene zusammenfallen; in der Tat ist die Ebene senkrecht zur Deckebene. Irgendein Punkt der Ebene und sein symmetrischer in bezug.auf die Deckebene liegen so, dass die Strecke zwischen den Projektionen der zwei Punkte von der Affinitätsachse der Ebene halbiert wird. Wenn zwei Ebenen zur Deckebene symmetrisch liegen, so entstehen durch Vertauschen der Projektionen der Punkte der einen Ebene die Punkte der andern Ebene; die zwei Ehenen haben eine gemeinsame Affinitätsachse. Hat man durch die Gerade g ein Ebenenbüschel und vertauscht man g' mit g" und auch die Spuren der Ebenen, so entsteht das zur Deckebene symmetrisch gelegene Ebenenbüschel. Die Ebenen schneiden die Deckebene in Geraden, die durch den Schnittpunkt von g', g" nach den Schnittpunkten der Spuren mit der Achse gehen, d. i. die Schnittlinie der beiden Bildebenen. V. Wenn in dem System der vereinigten Bildebenen die Spuren e l, e2 einer Ebene E aufeinander senkrecht stehen, so kann man nach der 1) Man kann dieses Ergebnis auch anders finden. Man vertauscht die Projektionen vo n e, untereinander und ebenso diejenigen von e 2 ; das gibt die Spuren f2, f, der neuen Ebene, die also zu e 1, e 2 in bezug auf die Deckebene symmetrisch liegt.
4 Jahrg. 74. A. KIEFER. Fragen aus den Elementen der Darstellenden Geometrie. 167 besonderen Lage aller solchen Ebenen E im Raume fragen. Hält man den Schnittpunkt 0 der beiden Spuren auf der Achse fest und dreht die eine Spur um diesen Punkt, so beschreibt sie ein Strahlenbüschel und die andere Spur beschreibt ebenfalls ein Strahlenbüschel ; die beiden Strahlenbüschel sind projektivisch. Dreht man die zweite Bildebene mit dem in ihr gelegenen Strahlenbüschel auf, bis sie auf der ersten Bildebene senkrecht steht, so bleibt das Büschel der ersten Spuren zum Büschel der zweiten Spuren projektivisch. Denkt man sich immer durch entsprechende Strahlen eine Ebene gelegt, so umhüllt die Ebene eine Kegelfläche zweiter Klasse mit dem Punkt 0 als Spitze. Die Kegelfläche berührt jede der zwei Bildebenen, und zwar längs der Geraden, die in der einen oder anderen Bildebene in dem festen Punkte 0 auf der Achse senkrecht steht. Die Kegelfläche wird von jeder Parallelebene zu einer Bildebene in einer Parabel geschnitten nnd jede zur Achse senkrechte Ebene schneidet eine gleichseitige Hyperbel heraus. Die Gesamtheit aller Ebenen, deren Spuren im vereinigten System der beiden Bildebenen aufeinander senkrecht stehen, besteht aus den Parallelebenen zu den Tangentialebenen einer Kegelfläche zweiter Klasse, welche die angegebene Lage hat. VI. Man kann die Frage im vorigen Abschnitt dadurch verallgemeinern, dass man verlangt, dass die beiden Spuren e I, e 2 einer Ebene im System der vereinigten Bildebenen nicht aufeinander senkrecht stehen, sondern einen Winkel von konstanter Grösse cp einschliessen. Hält man wieder den Schnittpunkt 0 der Spuren auf der Achse fest, so gehören zu einer ersten Spur zwei Lagen der zweiten Spur, von denen jede mit der ersten Spur den Winkel cp einschliesst. Wählt man eine zweite Spur, so gehören zu ihr ebenfalls zwei Lagen der ersten Spur, von denen jede mit der zweiten Spur den Winkel 99 einschliesst. Die beiden Büschel der ersten und zweiten Spuren sind also zwei-zweidentig aufeinander bezogen. Bringt man die Aufrissebene mit dem Büschel der zweiten Spuren in senkrechte Lage zur Grundrissebene, so bleiben die beiden Strahlenbüschel zwei-zweideutig aufeinander bezogen. Daher umhüllen die Verbindungsebenen von entsprechenden Strahlen eine Kegelfläche vierter Klasse. Sie berührt jede der zwei Bildebenen längs der zwei Geraden, die der Achse entsprechen, d.- h. durch 0 gehen und mit der Achse den Winkel cp einschliessen. Die Gesamtheit der Ebenen im Raum, deren Spuren im System der vereinigten Bildebenen den konstanten Winkel ry ein-
5 168 Viertetj:ahrsschnift der Naturf. Gesellschaft in Zürich schliessen, besteht aus den Parallelebenen zu den Tangentialehenen einer Kegelfläche vierter Klasse, welche die angegebene Lage hat. VII. Wenn in dem System der vereinigten Bildebenen die Projektionen g', g" der Geraden g aufeinander senkrecht stehen, so kann man nach der besonderen Lage von allen solchen Geraden g im Raume fragen. Wählt man den Schnittpunkt 0 von g', g" auf der Achse und hält ihn fest, so gehört zu jeder Geraden g' eine Lage von g" und umgekehrt. Entsprechende Geraden stehen immer aufeinander senkrecht und bilden zwei projektivische Strahlenbüschel. Dreht man die Aufrissebene mit den zweiten Projektionen der Geraden, bis sie auf der Grundrissebene senkrecht steht, so bleibt die Projektivität der beiden Strahlenbüschel bestehen. Legt man jetzt durch das Büschel der Geraden g' die ersten projizierenden Ebenen und durch das Büschel der Geraden g" die zweiten projizierenden Ebenen, so entstehen zwei projektivische Ebenenbüschel. Ihr Erzeugnis ist eine Kegelfläche zweiten Grades, welche jede Bildebene längs der Geraden berührt, die im Punkte 0 auf der Achse senkrecht steht. Die Gesamtheit aller Geraden des Raumes, deren Projektionen in dem System der vereinigten Bildebenen aufeinander senkrecht stehen, besteht aus allen parallelen Geraden zu den Erzeugenden dieser Kegelfläche zweiten Grades. VIII. Man kann die Frage im vorigen Abschnitt dadurch verallgemeinern, dass man verlangt, dass die Projektionen g', g" einer Geraden g im vereinigten System der beiden Bildebenen nicht aufeinander senkrecht stehen, sondern einen Winkel von konstanter Grösse cp einschliessen. Wählt man wieder den Schnittpunkt 0 von g', g" auf der Achse und hält ihn fest, so gehören zu jeder Lage von g' zwei Lagen von g", die ebenfalls durch 0 gehen und mit g' den Winkel cp einschliessen; umgekehrt entsprechen irgendeiner Lage von g" durch 0 zwei Lagen von g', die ebenfalls durch 0 gehen und mit g" den Winkel cp einschliessen. Die beiden Büschel der Strahlen g' und g" sind also zwei-zweideutig aufeinander bezogen. Bringt man die Aufrissebene mit dem Büschel der Geraden g" in senkrechte Lage zur Grundrissebene, so kann man durch die Geraden des Büschels g" die zweiten projizierenden Ebenen legen und durch das Büschel der Geraden g' kann man die ersten projizierenden Ebenen legen. Diese zwei Büschel von projizierenden Ebenen entsprechen sich ebenfalls zwei-zweideutig. Sie
6 Jahrg. 74. A. KIEFER. Fragen aus den Elementen der Darstellenden Geometrie. 169 erzeugen daher durch das Schneiden entsprechender Ebenen eine Kegelfläche vierten Grades. Jede Gerade des Raumes, die zu einer Erzeugenden der Kegelfläche vierten Grades parallel ist, hat im System der vereinigten Bildebenen zwei Projektionen, die einen Winkel von gegebener Grösse cp einschliessen. B e m e r k u n g. Der Verfasser dieses Artikels überlegte die verschiedenen Fragen, die vermutlich bekannt sind, vor vielen Jahren. Damals untersuchte sein früherer Schüler Herr HENDRIK DE VRIES (jetzt Professor in Amsterdam) die Frage nach den Geraden, die entstehen, wenn man im vereinigten System von drei paarweise aufeinander senkrecht stehenden Bildebenen den Grundriss einer Geraden mit dem Seitenriss zusammenfallen lässt. Die bezügliche Publikation findet sich innieuw Arch. von Wisk. 2 e Reeks. Deel I
Über Regelflächen zweiten Grades. Von. (Als Manuskript eingegangen ans 14. Oktober 1922.)
 Über Regelflächen zweiten Grades. Von A. KIEFER (Zürich). (Als Manuskript eingegangen ans 14. Oktober 1922.) I. Welches ist der Ort des Durchschnittspunktes derjenigen Erzeugenden eines Hyperboloids, welche
Über Regelflächen zweiten Grades. Von A. KIEFER (Zürich). (Als Manuskript eingegangen ans 14. Oktober 1922.) I. Welches ist der Ort des Durchschnittspunktes derjenigen Erzeugenden eines Hyperboloids, welche
Liber Kegelflächen. A. KIEFER (Zürich),
 Liber Kegelflächen. Von A. KIEFER (Zürich), (Als Manuskript eingegangen am 13. November 1923.) Die Durchdringungskurve vierten Grades von zwei Kegelflächen zweiten Grades bekommt bekanntlich einen Doppelpunkt,
Liber Kegelflächen. Von A. KIEFER (Zürich), (Als Manuskript eingegangen am 13. November 1923.) Die Durchdringungskurve vierten Grades von zwei Kegelflächen zweiten Grades bekommt bekanntlich einen Doppelpunkt,
Eine Projektionsaufgabe und eine Kugelaufgabe.
 Eine Projektionsaufgabe und eine Kugelaufgabe. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 1. September 1921.) I. Gesucht im Raum der Ort eines Punktes 0, von dem aus die Zentralprojektion eines
Eine Projektionsaufgabe und eine Kugelaufgabe. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 1. September 1921.) I. Gesucht im Raum der Ort eines Punktes 0, von dem aus die Zentralprojektion eines
Einige Aufgaben über extreme Werte.
 Einige Aufgaben über extreme Werte. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 5. August 1926.) I. Gesucht auf einer Regelfläche zweiten Grades von der einen Regelschar diejenigen Erzeugenden,
Einige Aufgaben über extreme Werte. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 5. August 1926.) I. Gesucht auf einer Regelfläche zweiten Grades von der einen Regelschar diejenigen Erzeugenden,
Zwei Aufgaben, die auf windschiefe Regelflächen führen,
 Zwei Aufgaben, die auf windschiefe Regelflächen führen, von À. KIEFER (Zürich). (Als Manuskript eingegangen am 25. Januar 1926.) I. Gesucht im Raum der Ort des Punktes, von dem aus die Zentralprojektionen
Zwei Aufgaben, die auf windschiefe Regelflächen führen, von À. KIEFER (Zürich). (Als Manuskript eingegangen am 25. Januar 1926.) I. Gesucht im Raum der Ort des Punktes, von dem aus die Zentralprojektionen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Elemente der Zweitafelprojektion
 Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Über gewisse Parabelreihen. 593
 592 A. Kiefer. Kreis geht dnrch den Halbierungspunkt C' der Höhe CF, weil FC' eine Lage von t ist; weil FA = 2 C' N, so läuft der von C' ausgehende Durchmesser C' CI des Kreises nach der Mitte von FA und
592 A. Kiefer. Kreis geht dnrch den Halbierungspunkt C' der Höhe CF, weil FC' eine Lage von t ist; weil FA = 2 C' N, so läuft der von C' ausgehende Durchmesser C' CI des Kreises nach der Mitte von FA und
Grundrissebene und Aufrissebene
 Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
. 18. Polarsystem in der Ebene und im Strahlenbünde!.
 131 zugeordnete Punkte durcfh eine Linie, so bildet diese mit der ihr zugeordneten Linie eine geschlossene Linie, welche ganz in dem Körper liegt und also von parer Ordnung ist. Da nun ein involutorisches
131 zugeordnete Punkte durcfh eine Linie, so bildet diese mit der ihr zugeordneten Linie eine geschlossene Linie, welche ganz in dem Körper liegt und also von parer Ordnung ist. Da nun ein involutorisches
Strophoiden. Eckart Schmidt
 Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
5. Gegenseitige Lage von Geraden und Ebenen. 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene
 5 5. Gegenseitige Lage von Geraden und Ebenen 5. Gegenseitige Lage zweier Geraden (siehe Kap..) 5.: Schnittpunkt einer Geraden mit einer Ebene Beispiel: : x + y + 4z - 4 = g = P(6, -, )Q(, 6, 4) geometrisch:
5 5. Gegenseitige Lage von Geraden und Ebenen 5. Gegenseitige Lage zweier Geraden (siehe Kap..) 5.: Schnittpunkt einer Geraden mit einer Ebene Beispiel: : x + y + 4z - 4 = g = P(6, -, )Q(, 6, 4) geometrisch:
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
SCHRIFTLICHE ABITURPRÜFUNG Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten
 Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten L 1, L 2 und L 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten L 1, L 2 und L 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Spezielle Kurven vierter Ordnung.
 Spezielle Kurven vierter Ordnung. Von G. STINDR (Winterthur). (Mit 2 Figuren.) (Als Manuskript eingegangen am B. September 1925.) Im Verlauf einer Untersuchung über die typischen Formen der Durchschnittskurven
Spezielle Kurven vierter Ordnung. Von G. STINDR (Winterthur). (Mit 2 Figuren.) (Als Manuskript eingegangen am B. September 1925.) Im Verlauf einer Untersuchung über die typischen Formen der Durchschnittskurven
eingesetzt in die Ebenengleichung
 25 5. Gegenseitige Lage von Geraden und Ebenen 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene Beispiel: ε: 2x + 3y + 4z - 24 = 0 g = P(6, -2, 2)Q(0,
25 5. Gegenseitige Lage von Geraden und Ebenen 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene Beispiel: ε: 2x + 3y + 4z - 24 = 0 g = P(6, -2, 2)Q(0,
. 2. Die Ebene. Der Strahlenbüschel und der Ebenenbüschel.
 7 die Fläche getrennt ist. Ein Halbstrahlenbündel wird durch eine Fläche der erwähnten Art in ein Paar Scheitelräume getheilt, welche einen gemeinschaftlichen Mantel haben, daher die beiden Hälften eines
7 die Fläche getrennt ist. Ein Halbstrahlenbündel wird durch eine Fläche der erwähnten Art in ein Paar Scheitelräume getheilt, welche einen gemeinschaftlichen Mantel haben, daher die beiden Hälften eines
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
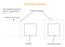 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Achsen- und punktsymmetrische Figuren
 Achsensymmetrie Der Punkt P und sein Bildpunkt P sind symmetrisch bzgl. der Achse s, wenn ihre Verbindungsstrecke [PP ] senkrecht auf der Achse a steht und von dieser halbiert wird. Zueinander symmetrische......strecken
Achsensymmetrie Der Punkt P und sein Bildpunkt P sind symmetrisch bzgl. der Achse s, wenn ihre Verbindungsstrecke [PP ] senkrecht auf der Achse a steht und von dieser halbiert wird. Zueinander symmetrische......strecken
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Geraden und Ebenen. 1 Geraden. 2 Ebenen. Thérèse Tomiska 2. Oktober Parameterdarstellung (R 2 und R 3 )
 Geraden und Ebenen Thérèse Tomiska 2. Oktober 2008 1 Geraden 1.1 Parameterdarstellung (R 2 und R 3 ) a... Richtungsvektor der Geraden g t... Parameter X = P + t P Q P Q... Richtungsvektor der Geraden g
Geraden und Ebenen Thérèse Tomiska 2. Oktober 2008 1 Geraden 1.1 Parameterdarstellung (R 2 und R 3 ) a... Richtungsvektor der Geraden g t... Parameter X = P + t P Q P Q... Richtungsvektor der Geraden g
 I. II. I. II. III. IV. I. II. III. I. II. III. IV. I. II. III. IV. V. I. II. III. IV. V. VI. I. II. I. II. III. I. II. I. II. I. II. I. II. III. I. II. III. IV. V. VI. VII. VIII.
I. II. I. II. III. IV. I. II. III. I. II. III. IV. I. II. III. IV. V. I. II. III. IV. V. VI. I. II. I. II. III. I. II. I. II. I. II. I. II. III. I. II. III. IV. V. VI. VII. VIII.
Zwei spezielle Tetraeder.
 Zwei spezielle Tetraeder. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 18. ApriI 195.) Eine gerade Kreiszylinderfläche vom Radins null kann als das System der zwei Ebenen anfgefasst werden, welche
Zwei spezielle Tetraeder. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 18. ApriI 195.) Eine gerade Kreiszylinderfläche vom Radins null kann als das System der zwei Ebenen anfgefasst werden, welche
A Vektorrechnung. B Geraden und Ebenen
 A Vektorrechnung Seite 1 Lineare Gleichungssysteme... 4 2 Gauß-Algorithmus... 6 3 Vektoren... 10 4 Vektorberechnungen und Vektorlängen... 12 5 Linearkombination und Einheitsvektor... 16 6 Lineare Abhängigkeit
A Vektorrechnung Seite 1 Lineare Gleichungssysteme... 4 2 Gauß-Algorithmus... 6 3 Vektoren... 10 4 Vektorberechnungen und Vektorlängen... 12 5 Linearkombination und Einheitsvektor... 16 6 Lineare Abhängigkeit
Lage zweier Ebenen. Suche alle Punkte von E 1 die in E 2 enthalten sind. Setze also die Parameterform von E 1 in die Koordinatenform von E 2.
 LAGE Lage zweier Ebenen Suche alle Punkte von E die in E 2 enthalten sind. Setze also die Parameterform von E in die Koordinatenform von E 2. B = E : X E 2 : x + x 2 + x 3 = Parameterform (PF) in Koordinatenform
LAGE Lage zweier Ebenen Suche alle Punkte von E die in E 2 enthalten sind. Setze also die Parameterform von E in die Koordinatenform von E 2. B = E : X E 2 : x + x 2 + x 3 = Parameterform (PF) in Koordinatenform
1 Dreiecke. 1.6 Ähnliche Dreiecke. Mathematische Probleme, SS 2019 Donnerstag 2.5. $Id: dreieck.tex,v /05/03 14:05:29 hk Exp $
 $Id: dreieck.tex,v 1.60 2019/05/03 14:05:29 hk Exp $ 1 Dreiecke 1.6 Ähnliche Dreiecke Wir hatten zwei Dreiecke kongruent genannt wenn in ihnen entsprechende Seiten jeweils dieselbe Länge haben und dann
$Id: dreieck.tex,v 1.60 2019/05/03 14:05:29 hk Exp $ 1 Dreiecke 1.6 Ähnliche Dreiecke Wir hatten zwei Dreiecke kongruent genannt wenn in ihnen entsprechende Seiten jeweils dieselbe Länge haben und dann
Beweis von Pohlke's Fundamentalsatz der Axonometrie,
 Beweis von Pohlke's Fundamentalsatz der Axonometrie, von Dr. ' Th. Reye. Wird ein Körper durch parallele Strahlen auf eine beliebige Ebene projicirt, so kann die Projektion desselben auf folgende Art axonometrisch
Beweis von Pohlke's Fundamentalsatz der Axonometrie, von Dr. ' Th. Reye. Wird ein Körper durch parallele Strahlen auf eine beliebige Ebene projicirt, so kann die Projektion desselben auf folgende Art axonometrisch
Abitur 2011 G8 Musterabitur Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Euklid ( v. Chr.) Markus Wurster
 Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
4.22 Buch XI der Elemente
 4.22 Buch XI der Elemente In Buch XI werden die Grundbegriffe der räumlichen Geometrie eingeführt und für viele Propositionen aus den Büchern I und VI die entsprechende dreidimensionale Aussagen bewiesen.
4.22 Buch XI der Elemente In Buch XI werden die Grundbegriffe der räumlichen Geometrie eingeführt und für viele Propositionen aus den Büchern I und VI die entsprechende dreidimensionale Aussagen bewiesen.
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Termin: 9. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Abstände und Zwischenwinkel
 Abstände und Zwischenwinkel Die folgenden Grundaufgaben wurden von Oliver Riesen, KS Zug, erstellt und von Stefan Gubser, KS Zug, überarbeitet. Aufgabe 1: Bestimme den Abstand der beiden Punkte P( 3 /
Abstände und Zwischenwinkel Die folgenden Grundaufgaben wurden von Oliver Riesen, KS Zug, erstellt und von Stefan Gubser, KS Zug, überarbeitet. Aufgabe 1: Bestimme den Abstand der beiden Punkte P( 3 /
Seite 1 Einleitung Elemente der Darstellenden Geometrie 13. Lernkontrolle A 1 15
 Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Das Wichtigste auf einen Blick
 Das Wichtigste auf einen Blick Zusammenfassung Geometrie.Parameterform einer Geraden Eine Gerade ist wie auch in der Analysis durch zwei Punkte A, B im Raum eindeutig bestimmt einer der beiden Punkte,
Das Wichtigste auf einen Blick Zusammenfassung Geometrie.Parameterform einer Geraden Eine Gerade ist wie auch in der Analysis durch zwei Punkte A, B im Raum eindeutig bestimmt einer der beiden Punkte,
Hans Walser. Raumgeometrie. Modul 4 Die Ebene Lernumgebung Teil 2
 Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Termin: 8. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Trainingslager der bayerischen Olympiamannschaft in Altdorf vom 20. bis 23. März 1996
 altdorf Trainingslager der bayerischen Olympiamannschaft in Altdorf vom 0. bis 3. März 996 Aufgaben Die Aufgaben sind entnommen Eric F. Müller []: Trainingsaufgaben für die Internationale Mathematikolympiade,
altdorf Trainingslager der bayerischen Olympiamannschaft in Altdorf vom 0. bis 3. März 996 Aufgaben Die Aufgaben sind entnommen Eric F. Müller []: Trainingsaufgaben für die Internationale Mathematikolympiade,
D C. Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
 V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler Problem
 Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler roblem von Reimund Albers, Bremen Im Baseler roblem geht es um die Summe der reziproken Quadrate, also + + 2 3 + 2 4 + +..., und ein exaktes
Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler roblem von Reimund Albers, Bremen Im Baseler roblem geht es um die Summe der reziproken Quadrate, also + + 2 3 + 2 4 + +..., und ein exaktes
Geometrie Winkel und Vierecke PRÜFUNG 02. Ohne Formelsammlung! Name: Klasse: Datum: Punkte: Note: Klassenschnitt/ Maximalnote : Ausgabe: 2.
 GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
Name und des Einsenders
 Titel der Einheit Stoffgebiet Name und Email des Einsenders Ziel der Einheit Inhalt Voraussetzungen Konstruktion von Kegelschnitten Geometrie Andreas Ulovec Andreas.Ulovec@univie.ac.at Verwenden von Dynamischer
Titel der Einheit Stoffgebiet Name und Email des Einsenders Ziel der Einheit Inhalt Voraussetzungen Konstruktion von Kegelschnitten Geometrie Andreas Ulovec Andreas.Ulovec@univie.ac.at Verwenden von Dynamischer
Analytische Geometrie II
 Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Lk Mathematik 12 Analytische Geometrie Arbeitsblatt A.1
 Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Abbildung eines Punkts
 x 3 (bzw. z) - Höhe Abbildung eines Punkts Höhenmaßstab A A x 2 (bzw. y) - Breite 1 B 0 C A B (-5) C=C B C=C (0) A (3,5) B x 1 (bzw. x) - Tiefe In Klammern erfolgt jeweils die Angabe der Kote. Zusammenhang
x 3 (bzw. z) - Höhe Abbildung eines Punkts Höhenmaßstab A A x 2 (bzw. y) - Breite 1 B 0 C A B (-5) C=C B C=C (0) A (3,5) B x 1 (bzw. x) - Tiefe In Klammern erfolgt jeweils die Angabe der Kote. Zusammenhang
7 Geraden mit der Funktion f 2 (x) in den Punkten P 1 und f1. 7 verläuft eine zweite Gerade mit der Funktion f 3 (x)
 R. Brinkmann http://brinkmann-du.de Seite.. Lösungen Parabel und Gerade II und ausführliche Lösungen: E Eine Parabel mit der Funktion f () wird von einer Geraden mit der Funktion f () in den Punkten P
R. Brinkmann http://brinkmann-du.de Seite.. Lösungen Parabel und Gerade II und ausführliche Lösungen: E Eine Parabel mit der Funktion f () wird von einer Geraden mit der Funktion f () in den Punkten P
Inhalt. Erster Abschnitt. Parallelprojektion und Zentralprojektion ebener Mguren.
 Inhalt. Erster Abschnitt. Parallelprojektion und Zentralprojektion ebener Mguren. 1 6. Die Affinität. Definition und Eigenschaften. 1 7. Die Ellipse als affines Bild (Parallelprojektion) des Kreises. 5
Inhalt. Erster Abschnitt. Parallelprojektion und Zentralprojektion ebener Mguren. 1 6. Die Affinität. Definition und Eigenschaften. 1 7. Die Ellipse als affines Bild (Parallelprojektion) des Kreises. 5
Ein Problem der Dreiecksspiegelung
 Ein Problem der Dreiecksspiegelung Tobias Schoel 10. Februar 2008 1 Die Dreiecksspiegelung 1.1 Spiegelung eines Punktes Es sei ein Dreieck ABC mit den Seiten BC = a, AC = b und AB = c gegeben und P sei
Ein Problem der Dreiecksspiegelung Tobias Schoel 10. Februar 2008 1 Die Dreiecksspiegelung 1.1 Spiegelung eines Punktes Es sei ein Dreieck ABC mit den Seiten BC = a, AC = b und AB = c gegeben und P sei
Ebene Geometrie; Kreis
 Testen und Fördern Lösungen Name: Klasse: Datum: 1) Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm Raumhöhe
Testen und Fördern Lösungen Name: Klasse: Datum: 1) Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm Raumhöhe
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
EINFÜHRUNG IN DIE GEOMETRIE
 Dr. Michael Gieding www.ph-heidelberg.de/wp/gieding EINFÜHRUNG IN DIE GEOMETRIE SKRIT ZUR GLEICHNAMIGEN VORLESUNG IM WINTERSEMESTER 2007/2008 KAITEL 1 AXIOMATIK 1 Die zwei Aspekte des Kongruenzbegriffs
Dr. Michael Gieding www.ph-heidelberg.de/wp/gieding EINFÜHRUNG IN DIE GEOMETRIE SKRIT ZUR GLEICHNAMIGEN VORLESUNG IM WINTERSEMESTER 2007/2008 KAITEL 1 AXIOMATIK 1 Die zwei Aspekte des Kongruenzbegriffs
Die Abbildung (x 1 ;x 2 ) 7! (x 1 ;x 2 ; 1) ist eine Einbettung von R 2 in P 2 (als Mengen). Punkte mit z 6= 0 sind endliche" Punkte mit inhomogenen K
 Kapitel IV Projektive Geometrie In diesem Kapitel wird eine kurze Einführung in die projektive Geometrie gegeben. Es sollen unendlich ferne Punkte mit Hilfe von homogene Koordinaten eingeführt werden und
Kapitel IV Projektive Geometrie In diesem Kapitel wird eine kurze Einführung in die projektive Geometrie gegeben. Es sollen unendlich ferne Punkte mit Hilfe von homogene Koordinaten eingeführt werden und
Lineare Funktionen und Funktionenscharen
 . Erkläre folgende Begriffe: a) Ursprungsgerade b) Steigung bzw. Steigungsdreieck c) Steigende u. fallende Gerade d) Geradenbüschel, Parallelenschar e) y- Achsenabschnitt f) Lineare Funktion g) Normalform
. Erkläre folgende Begriffe: a) Ursprungsgerade b) Steigung bzw. Steigungsdreieck c) Steigende u. fallende Gerade d) Geradenbüschel, Parallelenschar e) y- Achsenabschnitt f) Lineare Funktion g) Normalform
. 4. Von den necken, nkanten und Polyedern.
 18 ebenenbüschel projicirt. Jedes begrenzte Stück der Geraden wird im erstem Falle durch einen Parallelstreifen, im letztern aber durch einen Parallelraum projicirt, welchen dasselbe spannt. Ein ebenes
18 ebenenbüschel projicirt. Jedes begrenzte Stück der Geraden wird im erstem Falle durch einen Parallelstreifen, im letztern aber durch einen Parallelraum projicirt, welchen dasselbe spannt. Ein ebenes
r a t u Parametergleichung der Geraden durch den Punkt A mit dem Richtungsvektor u t R heisst Parameter
 8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
Gundlagen Klasse 5/6 Geometrie. nach oben. Inhaltsverzeichnis
 Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
3 Die Theorie des Spiegelbuches
 3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
Übungsblatt 3 (Vektorgeometrie)
 Fachhochschule Nordwestschweiz (FHNW Hochschule für Technik Institut für Mathematik- und Naturwissenschaft Übungsblatt (Vektorgeometrie Roger Burkhardt 08 Mathematik. Aufgabe Gegeben seien die Vektoren
Fachhochschule Nordwestschweiz (FHNW Hochschule für Technik Institut für Mathematik- und Naturwissenschaft Übungsblatt (Vektorgeometrie Roger Burkhardt 08 Mathematik. Aufgabe Gegeben seien die Vektoren
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Zum Einstieg. Mittelsenkrechte
 Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Lineare Funktion. Wolfgang Kippels 21. März 2011
 Lineare Funktion Wolfgang Kippels. März 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Lineare Funktion Wolfgang Kippels. März 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel.
 1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Viel Glück und Erfolg!
 Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2014/15 Prüfer: Mag. Helgrid Müller Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle Computerbeispiele
Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2014/15 Prüfer: Mag. Helgrid Müller Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle Computerbeispiele
Abitur 2010 Mathematik LK Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Abb.1. Falls die Spitze des Kegels (bzw. Doppelkegels) nicht in der jeweiligen Schnittebene liegt, können die folgende Kurven entstehen:
 Kegelschnitte Ein Kegelschnitt ist eine ebene Kurve, die entsteht, wenn man die Oberfläche eines Kreiskegels bzw. Doppelkreiskegels mit einer Ebene schneidet (vgl.abb.1). Der Doppelkreiskegel seinerseits
Kegelschnitte Ein Kegelschnitt ist eine ebene Kurve, die entsteht, wenn man die Oberfläche eines Kreiskegels bzw. Doppelkreiskegels mit einer Ebene schneidet (vgl.abb.1). Der Doppelkreiskegel seinerseits
Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans
 Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans josef.coenen@web.de Abitour Analytische Geometrie Leistungskurs Aufgaben 1. Welche Lagebeziehungen zwischen
Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans josef.coenen@web.de Abitour Analytische Geometrie Leistungskurs Aufgaben 1. Welche Lagebeziehungen zwischen
Ebene Geometrie; Kreis Lösungen
 1) Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm Raumhöhe 47 cm Länge eines Schulbuches 2) Kreuze jeweils
1) Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm Raumhöhe 47 cm Länge eines Schulbuches 2) Kreuze jeweils
Abitur 2017 Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur 7 Mathematik Geometrie VI Gegeben sind die beiden bezüglich der x x 3 -Ebene symmetrisch liegenden Punkte A( 3 ) und B( 3 ) sowie der Punkt C( ). Teilaufgabe
Seite http://www.abiturloesung.de/ Seite Abitur 7 Mathematik Geometrie VI Gegeben sind die beiden bezüglich der x x 3 -Ebene symmetrisch liegenden Punkte A( 3 ) und B( 3 ) sowie der Punkt C( ). Teilaufgabe
Euklid: Elemente. die. Stoicheia
 Euklid: Elemente die Stoicheia Die Lehrsätze Bücher I bis IV: Geometrie ohne Zahlen und Messwerte Buch I. Dreiecke, Parallele, Parallelogramm Buch II. Strecken und Rechtecke Buch III. Kreise, Ähnliche
Euklid: Elemente die Stoicheia Die Lehrsätze Bücher I bis IV: Geometrie ohne Zahlen und Messwerte Buch I. Dreiecke, Parallele, Parallelogramm Buch II. Strecken und Rechtecke Buch III. Kreise, Ähnliche
Waben-Sudoku. Günter Aumann und Klaus Spitzmüller. Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen.
 Waben-Sudoku Günter Aumann und Klaus Spitzmüller Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen. Eine Vorüberlegung Reguläre Vierecke und Sechsecke zeichnen sich vor allen anderen
Waben-Sudoku Günter Aumann und Klaus Spitzmüller Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen. Eine Vorüberlegung Reguläre Vierecke und Sechsecke zeichnen sich vor allen anderen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Lernkarten. Analytische Geometrie. 6 Seiten
 Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Übungsaufgaben Geometrie und lineare Algebra - Serie 1
 Übungsaufgaben Geometrie und lineare Algebra - Serie. Bei einer geraden Pyramide mit einer quadratischen Grundfläche von 00 cm beträgt die Seitenkante 3 cm. a) Welche Höhe hat die Pyramide? b) Wie groß
Übungsaufgaben Geometrie und lineare Algebra - Serie. Bei einer geraden Pyramide mit einer quadratischen Grundfläche von 00 cm beträgt die Seitenkante 3 cm. a) Welche Höhe hat die Pyramide? b) Wie groß
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
Graph der linearen Funktion
 Graph der linearen Funktion Im unten stehenden Diagramm sind die Grafen der Funktionen f und g gezeichnet (a) Stelle die Gleichungen von f und g auf und berechne die Nullstellen der beiden Funktionen (b)
Graph der linearen Funktion Im unten stehenden Diagramm sind die Grafen der Funktionen f und g gezeichnet (a) Stelle die Gleichungen von f und g auf und berechne die Nullstellen der beiden Funktionen (b)
Euklid von Alexandria
 Euklid von Alexandria lebte ca. 360 v. Chr. bis ca. 280 v. Chr. systematisierte in 13 Büchern ( Elemente ) das mathematische Wissen der Antike - bis ins 19. Jahrhundert nach Bibel das am meisten verbreitete
Euklid von Alexandria lebte ca. 360 v. Chr. bis ca. 280 v. Chr. systematisierte in 13 Büchern ( Elemente ) das mathematische Wissen der Antike - bis ins 19. Jahrhundert nach Bibel das am meisten verbreitete
Hans Walser. Raumgeometrie. Modul 3 Rissebenen. Punkt und Gerade
 Hans Walser Raumgeometrie Modul 3 Rissebenen. Punkt und Gerade Hans Walser: Modul 3, Rissebenen. Punkt und Gerade ii Modul 3 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002
Hans Walser Raumgeometrie Modul 3 Rissebenen. Punkt und Gerade Hans Walser: Modul 3, Rissebenen. Punkt und Gerade ii Modul 3 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002
Abituraufgaben Analytische Geometrie Wahlteil 2016 BW
 Abituraufgaben Analytische Geometrie Wahlteil 216 BW Aufgabe B1.1 In einem Koordinatensystem be-schreiben die Punkte 15, 15 2 und 2 6 Eckpunkte der rechteckigen Nutzfläche einer Tribüne (alle Koordinatenangaben
Abituraufgaben Analytische Geometrie Wahlteil 216 BW Aufgabe B1.1 In einem Koordinatensystem be-schreiben die Punkte 15, 15 2 und 2 6 Eckpunkte der rechteckigen Nutzfläche einer Tribüne (alle Koordinatenangaben
Abitur 2010 Mathematik GK Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik GK Geometrie VI In einem kartesischen Koordinatensystem mit Ursprung O sind die Punkte A( ), B( ) und die Gerade g : x = O A + λ, λ R, gegeben.
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik GK Geometrie VI In einem kartesischen Koordinatensystem mit Ursprung O sind die Punkte A( ), B( ) und die Gerade g : x = O A + λ, λ R, gegeben.
ANALYTISCHEN GEOMETRIE DER EBENE.
 DIE ELEMENTE DEB ANALYTISCHEN GEOMETRIE DER EBENE. ZUM GEBRAUCH AN HÖHEREN LEHRANSTALTEN SOWIE ZUM SELBSTSTUDIUM DARGESTELLT UND MIT ZAHLREICHEN ÜBUNGSBEISPIELEN VERSEHEN VON DR. H. GANTER UND DE. F. RUDIO
DIE ELEMENTE DEB ANALYTISCHEN GEOMETRIE DER EBENE. ZUM GEBRAUCH AN HÖHEREN LEHRANSTALTEN SOWIE ZUM SELBSTSTUDIUM DARGESTELLT UND MIT ZAHLREICHEN ÜBUNGSBEISPIELEN VERSEHEN VON DR. H. GANTER UND DE. F. RUDIO
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 3 Der Axiator Eigenschaften des Axiators Bestimmung des Kegelschnitts Geometrische Betrachtungen Dualer Kegelschnitt Pol-Polare
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 3 Der Axiator Eigenschaften des Axiators Bestimmung des Kegelschnitts Geometrische Betrachtungen Dualer Kegelschnitt Pol-Polare
1993 III Aufgabe. In einem kartesischen Koordinatensystem sind die Gerade
 993 III Aufgabe In einem kartesischen Koordinatensystem sind die Gerade = g : X mit R sowie die beiden Punkte A( -) und C(- 2 ) gegeben. A und C bestimmen die Gerade h..a) Begründen Sie, dass der Mittelpunkt
993 III Aufgabe In einem kartesischen Koordinatensystem sind die Gerade = g : X mit R sowie die beiden Punkte A( -) und C(- 2 ) gegeben. A und C bestimmen die Gerade h..a) Begründen Sie, dass der Mittelpunkt
9. ANALYTISCHE GEOMETRIE MIT EBENEN
 ANALYTISCHE GEOMETRIE MIT EBENEN 9. ANALYTISCHE GEOMETRIE MIT EBENEN Die Bilder zeigen: Verschiebt man ein Geradenstück parallel entlang eines anderen Geradenstücks, so entsteht ein ebenes Flächenstück.
ANALYTISCHE GEOMETRIE MIT EBENEN 9. ANALYTISCHE GEOMETRIE MIT EBENEN Die Bilder zeigen: Verschiebt man ein Geradenstück parallel entlang eines anderen Geradenstücks, so entsteht ein ebenes Flächenstück.
3 Die Theorie des Spiegelbuches
 3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
Beispiellösungen zu Blatt 96
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 96 Gegeben sei ein Oktaeder. Auf dessen Kanten suchen wir Wege von einer
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 96 Gegeben sei ein Oktaeder. Auf dessen Kanten suchen wir Wege von einer
