Elemente der Zweitafelprojektion
|
|
|
- Karin Egger
- vor 5 Jahren
- Abrufe
Transkript
1 Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss exakt(längen, Winkel) und übersichtlich(farben, Beschriftung Prioritäten) sein Material: 2 gespitzte Bleistifte 8 Farben (dünne Filzstifte oder gespitzte Farbstifte) Spitzer, Gummi grosses Geodreick, Massstab gespitzter Zirkel genügend A4-Blätter (4 mm) Die Zweitafelprojektion arbeitet mit zwei Projektionsebenen: Grundrissebene π 1 (xy-ebene) Aufrissebene π 2 (yz-ebene) Diese Ebenen schneiden sich in der Rissachse (y-achse) Für die Darstellung auf dem Zeichenblatt wird π 1 so um die Rissachse gedreht, bis π 1 mit +π 2 und +π 1 mit π 2 zusammenfallen. 1
2 2 Darstellung von Punkten 2.1 Allgemeine Lagen eines Punktes Die Projektionen des Punktes P auf π 1 und π 2 heissen P und P. Grund und Aufriss eines Punktes liegen (in DG-Darstellung) auf einer Normalen zur Rissachse, genannt Ordner. Beispiel 1: Lies die Koordinaten der Punkte P, Q, R und S ab. (Einheit 1H) P S S Q 0 R R P Q Beispiel 2: Stelle folgende Punkte in der Zweitafelprojektion dar. (Einheit 1 H) A(4 9 1) B( 5 3 4) C( 2 4 3) D(4 4 1) 0 2
3 2.2 Spezielle Lagen eines Punktes Punkt in der Symmetrieebene Punkt in der Koinzidenzebene Punkt auf π 1 bzw. π 2 3
4 3 Darstellung von Geraden Eine Gerade ist durch ihre Risse bestimmt, insbesondere durch die Risse zweier auf der Geraden liegender Punkte. Beispiel 1: Stelle die Gerade g = (AB) in der Zweitafelprojektion dar. A( ), B( ) (Einheit 1 H) 0 Für Punkte auf der Geraden gilt: P g P g und P g Beispiel 2: Überprüfe, ob C(6 8 6) und D(4 5 6) auf g liegen. Beispiel 3: Konstruiere auf der Geraden g den Punkt E mit der z-koordinate 8. Welche Koordinaten hat E? 4
5 Definition: Die Spurpunkte S 1, S 2 einer Geraden sind die Schnittpunkte der Geraden mit den Projektionsebenen π 1, π Die erste Standardaufgabe (Spurpunkte einer Geraden) 1. Gegeben: Gerade g 2. Gesucht: Spurpunkte S 1, S 2 3. Lösungsidee: Die Grundrissebene sieht man im Aufriss nur als Gerade (Rissachse) 4. Konstruktion: g g 5. Konstruktionsbericht: (a) (b) (c) (d) Beispiel 4: Stelle die Gerade g = (AB) in der Zweitalfelprojektion dar. Konstruiere die Spurpunkte S 1 und S 2 und lies deren Koordinaten ab. A( 1 6 8), B(4 4 2) 0 5
6 3.2 Geraden in spezieller Lage Geraden in den Koordinatenebenen Projizierende Geraden Definition: Eine Normale zu π 1 heisst erstprojizierende Gerade. Eine Normale zu π 2 heisst zweitprojizierende Gerade Hauptgeraden Definition: Eine Gerade parallel zu π 1 heisst erste Hauptgerade. Eine Gerade parallel zu π 2 heisst zweite Hauptgerade. 6
7 3.3 Gegenseitige Lage zweier Geraden Sich schneidende Geraden Zwei Geraden schneiden sich genau dann, wenn der Schnittpunkt ihrer Grundrisse und der Schnittpunkt ihrer Aufrisse auf einem Ordner liegen. h g 0 h g Parallele Geraden Zwei Geraden sind genau dann parallel, wenn sowohl ihre Grund als auch ihre Aufrisse je parallel sind. e f 0 e f 7
8 3.3.3 Windschiefe Geraden Definition: Zwei Geraden heissen windschief, wenn sie sich weder schneiden noch parallel sind. e f 0 e f Windschiefe Geraden mit parallelen Grundrissen und sich schneidenden Aufrissen. e f 0 f e Windschiefe Geraden mit sich schneidenden Rissen. 8
9 4 Die Darstellung der Ebene Eine Ebene in R 3 wird definiert durch zwei sich schneidende Geraden zwei parallele Geraden drei Punkte einen Punkt und eine Gerade Besonders anschaulich ist die Darstellung der Ebene im DG-Bild durch zwei Spuren. Zur Vereinfachung lässt man die Projektionsbezeichnungen e 1 und e 2 weg und schreibt e 1 für den Grundriss der ersten Spur und e 2 für den Aufriss der zweiten Spur. Beachte: e 1 und e 2 sind zwei verschiedene Geraden! e 1 ist der Grundriss; der zu e 1 gehörende Aufriss ist die Rissachse. e 2 ist der Aufriss; der zu e 2 gehörende Grundriss ist die Rissachse. e 1 und e 2 schneiden sich auf der Rissachse. 9
10 4.1 Die zweite Standardaufgabe 1. Gegeben: Ebene ε durch A, B und C 2. Gesucht: Spuren e 1, e 2 3. Lösungsidee: Spurpunkte von Geraden in ε liegen auf den Spuren 4. Konstruktion: C A B C B A 5. Konstruktionsbericht: (a) (b) (c) (d) (e) (f) 10
11 4.2 Ebenen in spezieller Lage Hauptebenen Definition: Verläuft eine Ebene parallel zu einer der Projektionsebenen π 1, π 2 oder π 3, so nennt man sie eine erste, eine zweite oder eine dritte Hauptebene (HE). Erste Hauptebene α Zweite Hauptebene β Dritte Hauptebene γ 11
12 4.2.2 Projizierende Ebenen Definition: Steht eine Ebene normal zu einer der Projektionsebenen π 1, π 2 oder π 3, so nennt man sie eine erst-, eine zweit- oder eine drittprojizierende Ebene (PE). Erstprojizierende Ebene δ Zweitprojizierende Ebene ε Drittprojizierende Ebene ϕ 12
13 Teil II Lageaufgaben 5 Punkt Gerade Ebene 5.1 Die Gerade in der Ebene Die 3. Standardaufgabe Gegeben: Ebene ε durch e 1, e 2 ; Grundriss g einer Geraden g Gesucht: Aufriss g von g, so dass g ε Lösungsidee: Wegen g ε, müssen S 1 e 1 und S 2 e 2 sein Konstruktion: e 2 e 1 Konstruktionsbericht: g 13
14 5.1.2 Spezialfälle zur 3. Standardaufgabe Beispiel 1 Gegeben: Drittprojizierende Ebene ε und g Gesucht: Aufriss g von g so dass g ε e 2 g e 1 Konstruktionsbericht: 14
15 Beispiel 2 Gegeben: Ebene ε durch e 1, e 2 und Grundriss g einer Geraden g Gesucht: Aufriss g von g so dass g ε g e 1 e 2 Problem: Lösungsidee: 15
16 Beispiel 3 Gegeben: Erstprojizierende Ebene ϕ = (f 1,f 2 ) und Aufriss g einer Geraden g Gesucht: Grundriss g von g so dass g ϕ f 2 g f 1 Beispiel 4 Gegeben: Drittprojizierende Ebene α = (a 1,a 2 ) und Grundriss g einer Geraden g Gesucht: Aufriss g von g so dass g α a 2 g a 1 16
17 5.2 Spezielle Lagen von Geraden in einer Ebene Die Spurparallele Definition: Eine Gerade, welche in einer Ebene liegt und parallel zu einer Spur derselben verläuft, nennt man Spurparallele; sie ist zugleich auch Hauptgerade. Darstellung einer ersten Spurparallelen: Bei einer ersten Spurparallelen ist der Aufriss parallel zur Rissachse und der Grundriss parallel zur ersten Spur der Ebene. π 2 π 1 Darstellung einer zweiten Spurparallelen: Bei einer zweiten Spurparallelen ist der Aufriss parallel zur zweiten Spur der Ebene und der Grundriss parallel zur Rissachse. π 2 π 1 Eine Spurparallele nennt man auch Niveaugerade oder Höhengerade. Dieser Name stammt daher, weil eine erste Spurparallele überall dieselbe Höhe hat. 17
18 5.2.2 Die Spurnormale Definition: Eine Gerade, welche in einer Ebene liegt und senkrecht zu einer Spur derselben ist, nennt man eine Spurnormale oder Fallgerade. Eine erste Spurnormale gibt die Richtung der grössten Steigung bzw. des grössten Gefälles der Ebene an. Daher auch der Name Fallgerade. π 2 π 1 Der Grundriss einer Spurnormalen bezüglich e 1 steht senkrecht auf e 1. π 2 π 1 Der Aufriss einer Spurnormalen bezüglich e 2 steht senkrecht auf e 2. 18
19 5.2.3 Erhaltungssätze für rechte Winkel Liegt ein Schenkel eines rechten Winkels auf einer ersten Hauptgeraden, so bleibt der rechte Winkel im Grundriss erhalten. π 2 π 1 Liegt ein Schenkel eines rechten Winkels auf einer zweiten Hauptgeraden, so bleibt der rechte Winkel im Aufriss erhalten. π 2 π 1 19
20 5.3 Der Punkt in der Ebene Die 4. Standardaufgabe Lösung mittels beliebiger Hilfsgerade Gegeben: Ebene ε durch e 1, e 2 ; Aufriss P von P Gesucht: Grundriss P von P, so dass P ε Lösungsidee: Hilfsgerade m durch P 3. Standardaufgabe Konstruktion: e 2 P e 1 Konstruktionsbericht: 20
21 Lösung der 4. Standardaufgabe mittels erster Spurparallelen (1. HG) Gegeben: Ebene ε durch e 1, e 2 ; Aufriss P von P Gesucht: Grundriss P von P, so dass P ε Lösungsidee: Man verwendet eine Hauptgerade in ε als Hilfsgerade e 2 π 2 h 1 P e 1 π 1 e 2 P e 1 Konstruktionsbericht: 21
22 Lösung der 4. Standardaufgabe mittels zweiter Spurparallelen (2. HG) Gegeben: Ebene ε durch e 1, e 2 ; Aufriss P von P Gesucht: Grundriss P von P, so dass P ε e 2 π 2 h 2 P e 1 π 1 e 2 P e 1 Konstruktionsbericht: 22
23 Lösung der 4. Standardaufgabe mittels einer Spurnormalen Gegeben: Ebene ε durch e 1, e 2 ; Aufriss P von P Gesucht: Grundriss P von P, so dass P ε e 2 π 2 n 2 P e 1 π 1 e 2 P e 1 Konstruktionsbericht: 23
24 5.4 Parallele Ebenen π 2 π 1 Satz: Parallele Ebenen haben parallele Spuren. Beispiel Gegeben: Ebene ε durch ihre Spuren e 1, e 2 und ein Punkt P Gesucht: Ebene ϕ parallel zu ε mit P ϕ Erste Lösung mit h 1 : Erste Spurparallele durch P e 2 P P e 1 Konstruktionsbericht: 24
25 Zweite Lösung mit h 2 : Zweite Spurparallele durch P e 2 P P e 1 Konstruktionsbericht: 25
26 6 Schnittgerade und Durchstosspunkt 6.1 Die 5. Standardaufgabe Gegeben: Zwei Ebenen α und β Gesucht: Schnittgerade α β s Lösungsidee: Die Schnittpunkte entsprechender Spuren (S 1, S 2 ) sind Punkte der Schnittgeraden. π 2 π 1 Konstruktion: b 2 a 2 b 1 a 1 Konstruktionsbericht: 26
27 6.2 Spezialfälle zur 5. Standardaufgabe Beispiel 1 Schnitt mit einer ersten Hauptebene e 2 h 2 e 1 Beispiel 2 Schnitt mit einer zweitprojizierenden Ebene p 2 e 2 e 1 p 1 27
28 Beispiel 3 Die Spuren schneiden sich nicht auf dem Blatt. Lösungsidee: Wir verwenden eine Hauptebene als Hilfsebene. Schneiden wir diese Hauptebene mit den gegebenen Ebenen, so erhalten wir die Spurparallelen m und n. Der Schnitt von m und n ergibt einen weiteren Punkt P der gesuchten Schnittgeraden. a 2 b 2 b 1 a 1 28
29 6.3 Die 6. Standardaufgabe Gegeben: Eine Ebene ε = ab (bzw. ε = e 1 e 2 ) und eine Gerade g (g ε). Gesucht: Schnittpunkt S = ε g Lösungsidee: Wir konstruieren eine erstprojizierende Hilfsebenebene δ mit gleichen Grundriss wie g. Dann schneiden wir δ und ε und erhalten eine Schnittgerade d. Diese Schnittgerade schneiden wir schliesslich mit g und erhalten S (siehe Bild). Eine analoge Idee gilt für eine zweitprojizierende Hilfsebene mit gleichem Aufriss wie g. d 2 π 2 ε g S d π 1 δ g = d 1 29
30 Beispiel 1 Die Ebene ε ist durch zwei schneidende Geraden a, b gegeben g b a b g a Konstruktionsbericht 30
31 Beispiel 2 Die Ebene ε ist durch ihre Spuren e 1, e 2 gegeben e 2 g g e 1 Konstruktionsbericht
32 Beispiel 3 Schnitt von zwei Ebenen ε = ab und δ = gh h b a g b h g a Konstruktionsbericht 32
33 Beispiel 4 Gegeben: Dreiecke ABC und KLM Gesucht: Teilstrecke der Schnittgeraden s = ε(abc) ϕ(klm), die innerhalb der beiden Dreiecke ABC und KLM liegt K C M A L B L C A B M K Konstruktionsbericht 33
34 6.4 Sichtbarkeit a A 1 a b B 1 2 = A 2 = B 2 b 2 a a 1 = A 1 = B 1 A 2 1 B 2 b b Bei zueinander windschiefen Geraden a, b liegt im Punkt... 1 = a b entweder a über b oder b über a 2 = a b entweder a vor b oder b vor a Kriterium zur Entscheidung der Sichtbarkeit im Grundriss bzw. Aufriss: a sichtbar bezüglich b (in 1 = A 1 = B 1) a über b A 1 > B 1 b sichtbar bezüglich a (in 2 = A 2 = B 2) b vor a B 2 > A 2 Ob man von einer Ebene im Grundriss und im Aufriss dieselbe Seite oder verschiedene Seiten sieht, stellt man mit Hilfe eines in der Ebene liegenden Dreiecks fest: je nachdem erscheint es in den beiden Rissen mit gleichem oder mit entgegengesetztem Umlaufssinn. π 2 C π 2 C A A C C B B A A A C B B B π 1 A B π 1 C 34
Hans Walser. Raumgeometrie. Modul 4 Die Ebene
 Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Grundrissebene und Aufrissebene
 Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
eingesetzt in die Ebenengleichung
 25 5. Gegenseitige Lage von Geraden und Ebenen 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene Beispiel: ε: 2x + 3y + 4z - 24 = 0 g = P(6, -2, 2)Q(0,
25 5. Gegenseitige Lage von Geraden und Ebenen 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene Beispiel: ε: 2x + 3y + 4z - 24 = 0 g = P(6, -2, 2)Q(0,
5. Gegenseitige Lage von Geraden und Ebenen. 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene
 5 5. Gegenseitige Lage von Geraden und Ebenen 5. Gegenseitige Lage zweier Geraden (siehe Kap..) 5.: Schnittpunkt einer Geraden mit einer Ebene Beispiel: : x + y + 4z - 4 = g = P(6, -, )Q(, 6, 4) geometrisch:
5 5. Gegenseitige Lage von Geraden und Ebenen 5. Gegenseitige Lage zweier Geraden (siehe Kap..) 5.: Schnittpunkt einer Geraden mit einer Ebene Beispiel: : x + y + 4z - 4 = g = P(6, -, )Q(, 6, 4) geometrisch:
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Durchstoßpunkt Gerade Ebene. Vorkurs Darstellende Geometrie. Erstprojizierende Hilfsebene ν durch g. Teil I. Lösung mit erstprojizierender Hilfsebene
 Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Termin: 9. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Hans Walser. Raumgeometrie. Modul 4 Die Ebene Lernumgebung Teil 2
 Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C /07
 Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C - 6/7. Gegenseitige Lage von Geraden Gesucht ist die gegenseitige Lage der Geraden g durch die beiden Punkte A( ) und B( 5 9 ) und der Geraden
Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C - 6/7. Gegenseitige Lage von Geraden Gesucht ist die gegenseitige Lage der Geraden g durch die beiden Punkte A( ) und B( 5 9 ) und der Geraden
Termin: 8. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Seite 1 Einleitung Elemente der Darstellenden Geometrie 13. Lernkontrolle A 1 15
 Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Abbildung eines Punkts
 x 3 (bzw. z) - Höhe Abbildung eines Punkts Höhenmaßstab A A x 2 (bzw. y) - Breite 1 B 0 C A B (-5) C=C B C=C (0) A (3,5) B x 1 (bzw. x) - Tiefe In Klammern erfolgt jeweils die Angabe der Kote. Zusammenhang
x 3 (bzw. z) - Höhe Abbildung eines Punkts Höhenmaßstab A A x 2 (bzw. y) - Breite 1 B 0 C A B (-5) C=C B C=C (0) A (3,5) B x 1 (bzw. x) - Tiefe In Klammern erfolgt jeweils die Angabe der Kote. Zusammenhang
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT
 Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Viel Glück und Erfolg!
 Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2016/17 Prüfer: Mag. Helgrid Müller Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle Computerbeispiele
Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2016/17 Prüfer: Mag. Helgrid Müller Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle Computerbeispiele
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
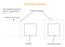 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Die Konstruktion der Schnittgeraden zweier Ebenen ist auf unterschiedliche Art und Weise möglich:
 Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Zweidimensionale Vektorrechnung:
 Zweidimensionale Vektorrechnung: Gib jeweils den Vektor AB und seine Länge an! (a A(, B(6 5 (b A(, B( 4 (c A(, B( 0 (d A(0 0, B(4 (e A(0, B( 0 (f A(, B( Gib jeweils die Summe a + b und die Differenz a
Zweidimensionale Vektorrechnung: Gib jeweils den Vektor AB und seine Länge an! (a A(, B(6 5 (b A(, B( 4 (c A(, B( 0 (d A(0 0, B(4 (e A(0, B( 0 (f A(, B( Gib jeweils die Summe a + b und die Differenz a
Grundsätzliche Konstruktionshilfen:
 Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Einige Fragen aus den Elementen der Darstellenden Geometrie,
 Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Schulübung zur Wiederholung. für die 4. Schulaufgabe
 Schulübung zur Wiederholung für die 4. Schulaufgabe Aufgabe 1 Bestimmung der Burggrabenweite Man beginnt mit der Seite ST. Vorgehensweise: Man beginnt mit der Seite ST. Aufgabe 1 Bestimmung der Burggrabenweite
Schulübung zur Wiederholung für die 4. Schulaufgabe Aufgabe 1 Bestimmung der Burggrabenweite Man beginnt mit der Seite ST. Vorgehensweise: Man beginnt mit der Seite ST. Aufgabe 1 Bestimmung der Burggrabenweite
Analytische Geometrie - Das Lotfußpunktverfahren - Gerade/Gerade (R 3 )
 Analytische Geometrie - Das Lotfußpunktverfahren - Gerade/Gerade R 3 ) Gerade - Gerade in R 3 ) Der Fall sich schneidender Geraden ist uninteressant. Es existiert dann ein beliebiger Abstand je nach der
Analytische Geometrie - Das Lotfußpunktverfahren - Gerade/Gerade R 3 ) Gerade - Gerade in R 3 ) Der Fall sich schneidender Geraden ist uninteressant. Es existiert dann ein beliebiger Abstand je nach der
1 lineare Gleichungssysteme
 Hinweise und Lösungen: http://mathemathemathe.de/lineare-algebra-grundlagen 1 lineare Gleichungssysteme Übung 1.1: Löse das lineare Gleichungssystem: I 3x + 3y + 7z = 13 II 1x 2y + 2, 5z = 1, 5 III 4x
Hinweise und Lösungen: http://mathemathemathe.de/lineare-algebra-grundlagen 1 lineare Gleichungssysteme Übung 1.1: Löse das lineare Gleichungssystem: I 3x + 3y + 7z = 13 II 1x 2y + 2, 5z = 1, 5 III 4x
Analytische Geometrie II
 Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Gegenseitige Lage von Geraden und Ebenen
 Gegenseitige Lage von Geraden und Ebenen. Gegeben sind die Ebene E : x + = und die Gerade g : x = +λ Lösung: (a) E : (a) Berechne die Koordinaten der Achsenpunkte A, A und A von E sowie der Durchstoßpunkte
Gegenseitige Lage von Geraden und Ebenen. Gegeben sind die Ebene E : x + = und die Gerade g : x = +λ Lösung: (a) E : (a) Berechne die Koordinaten der Achsenpunkte A, A und A von E sowie der Durchstoßpunkte
7) Normale Axonometrie
 7) In der 7.Klasse haben wir (allgemeine) axonometrische Risse technischer Objekte hergestellt; dabei haben wir die Eigenschaften von Parallelrissen ausgenützt. Nun wollen wir axonometrische Angaben so
7) In der 7.Klasse haben wir (allgemeine) axonometrische Risse technischer Objekte hergestellt; dabei haben wir die Eigenschaften von Parallelrissen ausgenützt. Nun wollen wir axonometrische Angaben so
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO
 1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Viel Glück und Erfolg!
 Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2016/17 Prüfer: Mag. Helgrid Müller Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle Computerbeispiele
Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2016/17 Prüfer: Mag. Helgrid Müller Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle Computerbeispiele
Modul 1 Der Würfel! 1
 Modul 1 Der Würfel! 1 2 3 4 Der 2-1-1-Würfel 5 Der 2-1-1-Würfel 6 Der 5-3-2-Würfel 7 Der 5-3-2-Würfel 8 Der 5-3-2-Würfel 9 Der 5-3-2-Würfel 10 10-2-2-Würfel und 10-3-2-Würfel 11 10-2-2-Würfel und 10-3-2-Würfel
Modul 1 Der Würfel! 1 2 3 4 Der 2-1-1-Würfel 5 Der 2-1-1-Würfel 6 Der 5-3-2-Würfel 7 Der 5-3-2-Würfel 8 Der 5-3-2-Würfel 9 Der 5-3-2-Würfel 10 10-2-2-Würfel und 10-3-2-Würfel 11 10-2-2-Würfel und 10-3-2-Würfel
Lösungen zum Thema Geometrie. Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt.
 Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
(x 1. Vektoren. g: x = p + r u. p r (u1. x 2. u 2. p 2
 Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
1 Kartesische Normalkoordinatensysteme 5
 Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Projektionskurve Abiturprüfung LK Bayern 2003
 Projektionskurve Abiturprüfung LK Bayern 03 In einem kartesischen Koordinatensystem des R 3 ist die Ebene H: x 1 + x 2 + x 3 8 = 0 sowie die Schar von Geraden ( a 2 ) ( ) 3a g a : x = 0 a 2 + λ 3a 8, λ
Projektionskurve Abiturprüfung LK Bayern 03 In einem kartesischen Koordinatensystem des R 3 ist die Ebene H: x 1 + x 2 + x 3 8 = 0 sowie die Schar von Geraden ( a 2 ) ( ) 3a g a : x = 0 a 2 + λ 3a 8, λ
b 1 b 2 b 3 a 1 b 1 a 2 b 2 a 2 b 2 a b a b a 1 b 1 a 2 b 2 a 3 b 3
 1. Rechnen mit Vektoren Skalarprodukt a b a b cos a 1 a 2 a 3 b 1 b 2 b 3 a 1 b 1 a 2 b 2 a 2 b 2 b a 1. Betrag Länge eines Vektors: a a a a 2 1 a 2 2 a 2 3 2. Winkel zwischen 2 Vektoren: cos a b a b a
1. Rechnen mit Vektoren Skalarprodukt a b a b cos a 1 a 2 a 3 b 1 b 2 b 3 a 1 b 1 a 2 b 2 a 2 b 2 b a 1. Betrag Länge eines Vektors: a a a a 2 1 a 2 2 a 2 3 2. Winkel zwischen 2 Vektoren: cos a b a b a
Ein Exkurs in analytischer Geometrie des Raumes anhand Euklidischer Lehrsätze
 Ein Exkurs in analytischer Geometrie des Raumes anhand Euklidischer Lehrsätze Im Koordinatenkreuz mit 3 Koordinatenachsen gilt: Ein Punkt P hat die Koordinaten P: (x; y; z). Die Größe OP ist die Entfernung
Ein Exkurs in analytischer Geometrie des Raumes anhand Euklidischer Lehrsätze Im Koordinatenkreuz mit 3 Koordinatenachsen gilt: Ein Punkt P hat die Koordinaten P: (x; y; z). Die Größe OP ist die Entfernung
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Abstände und Zwischenwinkel
 Abstände und Zwischenwinkel Die folgenden Grundaufgaben wurden von Oliver Riesen, KS Zug, erstellt und von Stefan Gubser, KS Zug, überarbeitet. Aufgabe 1: Bestimme den Abstand der beiden Punkte P( 3 /
Abstände und Zwischenwinkel Die folgenden Grundaufgaben wurden von Oliver Riesen, KS Zug, erstellt und von Stefan Gubser, KS Zug, überarbeitet. Aufgabe 1: Bestimme den Abstand der beiden Punkte P( 3 /
Grundwissen Abitur Geometrie 15. Juli 2012
 Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Grundlagen. y P(4;3;2) Schrägbild 1. Punkte im Raum. Ein Punkt ist im Raum durch drei Koordinaten (x,y,z) festgelegt.
 Grundlagen Schrägbild 1 Punkte im Raum z y P(4;3;2) 2 3 4 x Ein Punkt ist im Raum durch drei Koordinaten (x,y,z) festgelegt. ufgabe Versuche die Punkte (0;0;0), (1;1;1) und (3;2;-2) in einem Schrägbild
Grundlagen Schrägbild 1 Punkte im Raum z y P(4;3;2) 2 3 4 x Ein Punkt ist im Raum durch drei Koordinaten (x,y,z) festgelegt. ufgabe Versuche die Punkte (0;0;0), (1;1;1) und (3;2;-2) in einem Schrägbild
Übungen 4 Gerade, Ebene - Kurze Aufgaben Ebene: Spurpunkte, Spurgerade, Achsenabschnittsform Gerade, Ebene U04 Übungen 4 - Seite 1 (von 5)
 Übungen Gerade, Ebene - Kurze Aufgaben ) Gesucht ist Normalenform einer Ebene, die den Punkt P( ) enthält und auf der x- Achse senkrecht steht. ) Gegeben ist die Ebene E: x ( Gesucht ist der Winkel zwischen
Übungen Gerade, Ebene - Kurze Aufgaben ) Gesucht ist Normalenform einer Ebene, die den Punkt P( ) enthält und auf der x- Achse senkrecht steht. ) Gegeben ist die Ebene E: x ( Gesucht ist der Winkel zwischen
einführendes Beispiel: In der Skizze ist die durch die Punkte A(2, 4, 3) B(2, 6, 2) C(4, 4, 2) festgelegte Ebene ε dargestellt.
 6 4. Darstellung der Ebene 4. Die Parametergleichung der Ebene einführendes Beispiel: In der Skizze ist die durch die Punkte A(2, 4, 3) B(2, 6, 2) C(4, 4, 2) festgelegte Ebene ε dargestellt. 0 2 r uuur
6 4. Darstellung der Ebene 4. Die Parametergleichung der Ebene einführendes Beispiel: In der Skizze ist die durch die Punkte A(2, 4, 3) B(2, 6, 2) C(4, 4, 2) festgelegte Ebene ε dargestellt. 0 2 r uuur
b 1 b 2 b 3 = a 1 b 1 + a 2 b 2 + a 3 b 3 a b = a 1 b 1 + a 2 b 2 + a 3 b 3
 1. Rechnen mit Vektoren Skalarprodukt a b = a b cosα = a 1 a 2 a 3 b 1 b 2 b 3 = a 1 b 1 + a 2 b 2 + a 3 b 3 b a 1. Betrag = Länge eines Vektors: a = a a = a 2 1 + a 2 2 + a 2 3 2. Winkel zwischen 2 Vektoren:
1. Rechnen mit Vektoren Skalarprodukt a b = a b cosα = a 1 a 2 a 3 b 1 b 2 b 3 = a 1 b 1 + a 2 b 2 + a 3 b 3 b a 1. Betrag = Länge eines Vektors: a = a a = a 2 1 + a 2 2 + a 2 3 2. Winkel zwischen 2 Vektoren:
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Lösungen der Übungsaufgaben III
 Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
D C. Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
 V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
3 Brüche Bildungsstandards
 Brüche Bildungsstandards B B Sind die folgenden Aussagen richtig oder falsch? Kreuze an und begründe deine Entscheidung! Aussage richtig falsch Begründung, Beispiel a) Die Hälfte der Schüler einer Klasse
Brüche Bildungsstandards B B Sind die folgenden Aussagen richtig oder falsch? Kreuze an und begründe deine Entscheidung! Aussage richtig falsch Begründung, Beispiel a) Die Hälfte der Schüler einer Klasse
Achsen- und punktsymmetrische Figuren
 Achsensymmetrie Der Punkt P und sein Bildpunkt P sind symmetrisch bzgl. der Achse s, wenn ihre Verbindungsstrecke [PP ] senkrecht auf der Achse a steht und von dieser halbiert wird. Zueinander symmetrische......strecken
Achsensymmetrie Der Punkt P und sein Bildpunkt P sind symmetrisch bzgl. der Achse s, wenn ihre Verbindungsstrecke [PP ] senkrecht auf der Achse a steht und von dieser halbiert wird. Zueinander symmetrische......strecken
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Lösungen IV ) β = 54,8 ; γ = 70,4 106) a) 65 b) 65 (115?) d) 57,5
 (Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
(Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
KOP1_1_28. Lüftungsschacht
 Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
x 3 Genau dann liegt ein Punkt X mit dem Ortsvektor x auf g, wenn es ein λ R gib,t so dass
 V. Geradengleichungen in Parameterform 5. Definition ---------------------------------------------------------------------------------------------------------------- x 3 v a x x x Definition und Satz :
V. Geradengleichungen in Parameterform 5. Definition ---------------------------------------------------------------------------------------------------------------- x 3 v a x x x Definition und Satz :
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Universität Bielefeld. Elementare Geometrie. Sommersemester Elemente, Buch I. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Elemente, Buch I Stefan Witzel Vierecke Vier Punkte P, Q, R, S bilden ein Viereck PQRS, wenn sich weder die Segmente PQ und RS noch die Segmente
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Elemente, Buch I Stefan Witzel Vierecke Vier Punkte P, Q, R, S bilden ein Viereck PQRS, wenn sich weder die Segmente PQ und RS noch die Segmente
Lernkarten. Analytische Geometrie. 6 Seiten
 Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
r a t u Parametergleichung der Geraden durch den Punkt A mit dem Richtungsvektor u t R heisst Parameter
 8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
S Gegenseitige Lage von Ebeben. 2 Schnitt von Ebenen. a) E : x 1 2x 2 + 3x 3 6 = 0 und F : x 1 + 2x 2 + x 3 4 = 0. E + F : 2x 1 + 4x 3 10 = 0
 S. 8 7 Gegenseitige Lage von Ebeben Schnitt von Ebenen a) E : x x + x 6 = und F : x + x + x = E + F : x + x = Parametrisierung: x = λ x = λ In F eingesetzt: λ + x + λ = x = + λ Schnittgerade: X =,, b)
S. 8 7 Gegenseitige Lage von Ebeben Schnitt von Ebenen a) E : x x + x 6 = und F : x + x + x = E + F : x + x = Parametrisierung: x = λ x = λ In F eingesetzt: λ + x + λ = x = + λ Schnittgerade: X =,, b)
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Grundbegriffe Geraden Kreis Winkel Kreis. Rund um den Kreis. Dr. Elke Warmuth. Sommersemester / 20
 Rund um den Kreis Dr. Elke Warmuth Sommersemester 2018 1 / 20 Grundbegriffe Geraden Kreis Winkel Kreis 2 / 20 Kreis Kreisfläche oder Kreislinie Definition Die Kreislinie um M mit dem Radius r ist die Menge
Rund um den Kreis Dr. Elke Warmuth Sommersemester 2018 1 / 20 Grundbegriffe Geraden Kreis Winkel Kreis 2 / 20 Kreis Kreisfläche oder Kreislinie Definition Die Kreislinie um M mit dem Radius r ist die Menge
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
1 aus allen 3 Zeilen folgt t = 1, also liegt A auf g. Orsvektor und Richtungsvektor der Geraden werden übernommen, den zweiten Spannvektor bekommt
 Lösungsskizzen Klassische Aufgaben Lösung zu Abi - PTV Punktprobe: = + t aus allen Zeilen folgt t =, also liegt A auf g. Richtungsvektor von g: u = ; Normalenvektor von E: n = Da die n und u Vielfache
Lösungsskizzen Klassische Aufgaben Lösung zu Abi - PTV Punktprobe: = + t aus allen Zeilen folgt t =, also liegt A auf g. Richtungsvektor von g: u = ; Normalenvektor von E: n = Da die n und u Vielfache
Wie lautet die Gleichung der Geraden, durch die beiden Punkte A(4/1) und B(-5/8)?
 Übungsbeispiel / 2 Gerade durch 2 Punkte Wie lautet die Gleichung der Geraden, durch die beiden Punkte A(4/) und B(-5/8)? Maturavorbereitung 8. Klasse ACDCA 999 Vektorrechnung Übungsbeispiel 2 / 2 Gerade
Übungsbeispiel / 2 Gerade durch 2 Punkte Wie lautet die Gleichung der Geraden, durch die beiden Punkte A(4/) und B(-5/8)? Maturavorbereitung 8. Klasse ACDCA 999 Vektorrechnung Übungsbeispiel 2 / 2 Gerade
HTW MST Mathematik 1. Vektorrechnung. Zu Aufgabe 1. Zu Aufgabe Lösungen zu Übungsblatt 5. Lösung: Lösung: = 39
 Vektorrechnung Zu Aufgabe 1 Berechnen Sie den Flächeninhalt des Dreiecks, das durch die Vektoren 1 a =, b =, 3 1 c = 6 1 aufgespannt wird! Zu Aufgabe Berechnen Sie das Volumen des durch folgende 3 Vektoren
Vektorrechnung Zu Aufgabe 1 Berechnen Sie den Flächeninhalt des Dreiecks, das durch die Vektoren 1 a =, b =, 3 1 c = 6 1 aufgespannt wird! Zu Aufgabe Berechnen Sie das Volumen des durch folgende 3 Vektoren
Dipl, ng (FH) Darstellende
 Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Anwendungen der Vektorrechnung in R 3 mit GeoGebra
 Anwendungen der Vektorrechnung in R 3 mit GeoGebra 1. Parallelogramm Die Punkte A = ( 2, 1,0), B = (3, 2,2), C = (5,4,3) sind Eckpunkte eines Parallelogramms. Gesucht ist der fehlende Eckpunkt D sowie
Anwendungen der Vektorrechnung in R 3 mit GeoGebra 1. Parallelogramm Die Punkte A = ( 2, 1,0), B = (3, 2,2), C = (5,4,3) sind Eckpunkte eines Parallelogramms. Gesucht ist der fehlende Eckpunkt D sowie
Mathematik I für MB/ME
 Mathematik I für MB/ME Fachbereich Grundlagenwissenschaften Prof Dr Viola Weiÿ Wintersemester 25/26 Übungsaufgaben Serie 4: Lineare Unabhängigkeit, Matrizen, Determinanten, LGS Prüfen Sie, ob die folgenden
Mathematik I für MB/ME Fachbereich Grundlagenwissenschaften Prof Dr Viola Weiÿ Wintersemester 25/26 Übungsaufgaben Serie 4: Lineare Unabhängigkeit, Matrizen, Determinanten, LGS Prüfen Sie, ob die folgenden
SEMESTERPRÜFUNG MATHEMATIK. 1. Klassen KSR. Dienstag, 29. Mai :10-14:40 Uhr
 KLASSE: NAME: VORNAME: Mögliche Punktzahl: 75 68 Pte. = Note 6 Erreichte Punktzahl: Note: SEMESTERPRÜFUNG MATHEMATIK 1. Klassen KSR Dienstag, 9. Mai 01 1:10-14:40 Uhr Allgemeines Diese Prüfung hat 14 Seiten
KLASSE: NAME: VORNAME: Mögliche Punktzahl: 75 68 Pte. = Note 6 Erreichte Punktzahl: Note: SEMESTERPRÜFUNG MATHEMATIK 1. Klassen KSR Dienstag, 9. Mai 01 1:10-14:40 Uhr Allgemeines Diese Prüfung hat 14 Seiten
Klausur Nr. 2. Ebenen und Geraden untersuchen. keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt.
 Klausur Nr. 2 Ebenen und Geraden untersuchen Göttge-Piller, Höger Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche
Klausur Nr. 2 Ebenen und Geraden untersuchen Göttge-Piller, Höger Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche
SEMESTERPRÜFUNG MATHEMATIK. 1. Klassen KSR. Dienstag, 29. Mai :10-14:40 Uhr
 KLASSE: NAME: VORNAME: Mögliche Punktzahl: 75 68 Pte. = Note 6 Erreichte Punktzahl: Note: SEMESTERPRÜFUNG MATHEMATIK 1. Klassen KSR Dienstag, 9. Mai 01 1:10-14:40 Uhr Allgemeines Diese Prüfung hat 14 Seiten
KLASSE: NAME: VORNAME: Mögliche Punktzahl: 75 68 Pte. = Note 6 Erreichte Punktzahl: Note: SEMESTERPRÜFUNG MATHEMATIK 1. Klassen KSR Dienstag, 9. Mai 01 1:10-14:40 Uhr Allgemeines Diese Prüfung hat 14 Seiten
Josef Vogelmann Darstellende Geometrie
 Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
Winkel zeichnen. Hilfe. ACHTUNG! Achte immer genau darauf
 Hilfe Winkel zeichnen 1. Zeichne einen Schenkel (die rote Linie) S 2. Lege das Geodreieck mit der Null am Scheitelpunkt an. (Dort wo der Winkel hinkommen soll) S 3. Möchtest du zum Beispiel einen Winkel
Hilfe Winkel zeichnen 1. Zeichne einen Schenkel (die rote Linie) S 2. Lege das Geodreieck mit der Null am Scheitelpunkt an. (Dort wo der Winkel hinkommen soll) S 3. Möchtest du zum Beispiel einen Winkel
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Unterrichtsreihe zur Parabel
 Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: m (ausgesprochen: T von t und m)
 Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Hans Walser. Raumgeometrie. Modul 3 Rissebenen. Punkt und Gerade
 Hans Walser Raumgeometrie Modul 3 Rissebenen. Punkt und Gerade Hans Walser: Modul 3, Rissebenen. Punkt und Gerade ii Modul 3 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002
Hans Walser Raumgeometrie Modul 3 Rissebenen. Punkt und Gerade Hans Walser: Modul 3, Rissebenen. Punkt und Gerade ii Modul 3 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002
