6. Adaptive Finite-Element-Methoden
|
|
|
- Stefan Hochberg
- vor 7 Jahren
- Abrufe
Transkript
1 6. Adaptive Finite-Element-Methoden Adaptive Finite-Element-Methoden werden eingesetzt, um die FE-Lösung lokal oder global zu verbessern. Dieses Thema ist Gegenstand der heutigen Vorlesung. 6.1 Herleitung des FE-Lastfalls für die Scheibe Im Kapitel 3 dieser Vorlesungsreihe hatten wir den Finite-Element-Lastfall p h eingeführt. Bei der Scheibe besteht er je nach Polynomgrad der Ansatzfunktionen aus veränderlichen Elementlasten und veränderlichen Randlasten auf den Kanten der Elemente. Für die lineare Elastizitätstheorie erhält man den Gebietsanteil des FE- Lastfalls durch elementweises Einsetzen der Spannungen in das statische Gleichgewicht, div S hi = p hi auf Ω i. (1) Die Randlasten ergeben sich auf den lokalen Elementkanten aus dem Cauchy- Theorem, S hi n i = t hi auf Γ i Γ, (2) welche an den globalen Kanten folgendermaßen zusammengefasst werden: t hi := t + h i + t h i auf Γ i Γ, (3) t hi := S hi n i auf Γ i Γ. (4) Hierbei bezeichne t + h i und t h i jeweils die lokalen Randlasten zweier benachbarter Elemente auf Γ i. Der Finite-Element-Lastfall für die Scheibe wird nun definiert mit der Summe aller Elementlasten p hi über sämtliche Elemente Ω i sowie der Summe aller Kantenlasten t hi über alle globalen Kanten Γ i des Gebiets, { m } k p h := p hi, t hi. (5) i=1 i=1
2 6.2 Fehlerlasten und Fehlerindikatoren Eine naheliegende Idee ist es, die Lösung lokal dort zu verbessern, wo die Fehlerlasten besonders groß sind. Dies führt uns zu den adaptiven Methoden, welche auf diese Weise vorgehen. Bei den Fehlerschätzern für die Energienorm werden Fehlerlasten als Differenz aus dem Originallastfall und dem Finite-Element-Lastfall als Fehlerindikatoren zur Lokalisierung des Fehlers in den einzelnen Elementen verwendet. Das Ziel derartiger Fehlerschätzer ist es, ein optimales Netz zu erzeugen, bei welchem der Fehler in jedem Element etwa gleich groß ist und der globale Energienormfehler eine vorgegebene Schranke bei minimaler Anzahl von Freiheitsgraden nicht überschreitet. Den wohl anschaulichsten Fehlerschätzer stellt der residuale Fehlerschätzer von Babuška, Rheinboldt und Miller dar. Bei diesem Fehlerschätzer werden zunächst die Fehlerlasten in jedem Element aus einem Anteil der Gebietslasten (engl.: residuum) und einem Anteil der Kantenlasten (engl.: jumps) berechnet: R i := p p hi auf Ω i, (6a) J i := 1 2 (t t h i ) auf Γ i Γ, (6b) J i := (t t hi ) auf Γ i Γ N J i := 0 auf Γ i Γ D (6c) Weil an jeder globalen Innenkante zwei Elemente angrenzen, wird der Kantenfehler J i je zur Hälfte auf die angrenzenden Elemente verteilt, so dass auf den Innenkanten in Gl. (6b) der Faktor 1/2 eingeführt worden ist. Als nächstes werden lokale Fehlerindikatoren η i eingeführt, welche auf Elementebene den Beitrag eines einzelnen Elements zum Gesamtfehler beschreiben und aus der gewichteten L 2 Norm der Fehlerlasten berechnet werden, η 2 i = h 2 k R i 2 + h k J i 2. (7) Der Fehlerschätzer η wird schließlich aus der Summe der Fehlerindikatoren angegeben, η 2 = η 2 i. (8)
3 6.3 Visualisierung der Fehlerindikatoren Die größten Unsicherheiten bei der Bemessung von Tragwerken herrschen mit Sicherheit an den singulären Stellen. Unsere Idee war es daher, ein Fehlerbild zu entwickeln, welches die kritischen Bereiche optisch anzeigt, und somit dem Anwender ein vollautomatisches Verfahren zur Lokalisierung des Fehlers bietet. Die Entwicklung dieses Fehlerbildes und die Implementierung in WINFEM basiert auf der Beobachtung, dass die Fehlerlasten an den kritischen Stellen besonders groß sind. Das Fehlerbild selbst basiert nun darauf, die Fehlerindikatoren in Relation zueinander als Graustufenplot zu visualisieren. Dunkle Elemente signalisieren in diesem Fall Bereiche mit einem großen Fehler, während helle Elemente auf Gebiete mit entsprechend kleineren Fehlern hinweisen. Zur Anwendung des Fehlerbildes bei der Schnittgrößenermittlung mit finiten Elementen werden die folgenden Empfehlungen gegeben: Tendenziell sollten zur Bemessung eines Tragwerks nur Spannungswerte aus den hellen Bereichen des Fehlerbildes verwendet werden. Zur Bemessung in den dunklen Bereichen des Fehlerbildes sollte auf die Bildung integraler Schnittgrößen zurückgegriffen werden. In vorwiegend dunklen Bereichen sollte eine manuelle Netzverfeinerung vorgenommen werden, wobei sich die Güte der Nachvernetzung anhand eines neuen Fehlerbildes sofort überprüfen ließe.
4 6.4 Adaptionsstrategien Nach Berechnung der Fehlerindikatoren wird die Verbesserung der Lösung durch eine lokale Betrachtung anhand der folgenden Adaptionsstrategien vorgenommen: h Adaption: Verfeinerung des FE-Netzes p Adaption: Erhöhung der lokalen Ansatzordnung hp Adaption: Verfeinerung und Erhöhung der Ansatzordnung zugleich r Adaption: Neuvernetzung bei gleich bleibender Anzahl der Freiheitsgrade Bei der h Adaption wird ausgehend von einem provisorischen Netz eine sukzessive Verfeinerung der Elemente mit einem hohen Fehlerbeitrag vorgenommen. Bei der p Adaption wird im Gegensatz dazu die polynomiale Ordnung der Ansatzfunktion im Element erhöht. Theoretisch am günstigsten ist ein hp Adaption, bei welcher eine h und p Adaption gleichzeitig ablaufen. Bei der r Adaption wird eine Neuvernetzung der Struktur ohne Änderung der Anzahl der Freiheitsgrade vorgenommen. Eine Schwierigkeit bei dieser Strategie besteht allerdings in der Entstehung von stark verzerrten Elementgeometrien, wodurch unerwünschte Locking-Effekte auftreten können.
5 6.5 Einige technische Details Da es sich bei dem (gewichteten) Energienormfehler η und den lokalen Fehlerindikatoren η i um absolute Größen handelt, müssen zunächst aus η rel = η 100 % und η rel i = η i 100 % (9) u E u i E die relativen Fehler η rel und η rel i berechnet werden. Weil die exakte Lösung u unbekannt ist, werden die relativen Fehler in Anlehnung an Kelly aus η rel = η uh 2 E + η2 100 % und ηrel i = η i uhi 2 E % η2 i (10) berechnet. Die relativen Fehler geben dabei näherungsweise den Fehler einer FE-Lösung in der Energienorm an. In der praktischen Umsetzung gibt der Anwender zunächst einen angestrebten relativen Energiefehler η = e E u E (11) an, für welchen er z.b. η = 5 % wählt. Bei einer optimalen Fehlerverteilung wird davon ausgegangen, dass der Fehlerbeitrag jedes einzelnen Elementes zum Gesamtfehler in etwa gleich sein muss. Hierzu wird ein geforderter Elementfehler e m eingeführt: uh 2 E e m = η m m = Anzahl der Elemente. (12) Das Verhältnis ξ i = η i e m (13) gibt an, ob Elemente zu verfeinern sind oder nicht: ξ i = η i = e m > 1, Netz verfeinern < 1, Netz vergröbern = 1, keine Netzänderung (14) Das gesamte Verfahren wird effektiver, wenn nicht in jedem Schritt alle Elemente mit ξ i > 1 verfeinert werden. Gerade bei Tragwerken mit Singularitäten ist es oftmals sinnvoller, nur % der Elemente mit ξ > 1 zu verfeinern. Die Prozentzahl der zu verfeinernden Elemente bezeichnen wir in dieser Arbeit als γ Wert.
6 6.6 Beispiel: Eingespannte Zugscheibe Abb. 1 zeigt den Adaptionsprozeß für eine eingespannte Zugscheibe mit Einkerbungen. Man erkennt an dem Adaptionsprozeß, dass die größten Energienormfehler im Bereich der einspringenden Ecken beobachtet werden. Der Energienormfehler kann wie dargestellt aus anfänglich % auf 6.68 % verringert werden. Das Verfahren erweist sich als effektiv und stabil. Energienormfehler: % Energienormfehler: % Energienormfehler: % Energienormfehler: 8.80 % Energienormfehler: % Energienormfehler: 6.68 % Abb. 1: Adaptive Netzverfeinerung für eine Zugscheibe mit Einkerbungen
7 6.7 Einfluss des γ Wertes Im nächsten Beispiel ist der Einfluss des Verfeinerungsgrades (γ Wert) auf das Konvergenzverhalten für eine eingespannte Scheibe mit Öffnungen untersucht worden. Hierzu wird jeweils ein γ Wert von 30 %, 50 % und 70 % angenommen. An den Netzen in Abb. 2 lässt sich erkennen, dass mit kleinerem γ Wert die Netzdichte im Bereich der Ecken ansteigt, wobei der Energienormfehler für den γ Wert von 30 % in Relation zur Freiheitsgradanzahl am günstigsten ist. a) Energienormfehler % (98 Fhg.) b) Energienormfehler: 7.49 % (2014 Fhg.) c) Energienormfehler: 7.16 % (2644 Fhg.) d) Energienormfehler: 9.00 % (2096 Fhg.) Abb. 2: Adaptive Netzverfeinerung für eine gelochte Zugscheibe in Abhängigkeit des γ Werts: a) Startnetz, b) γ = 30 %, c) γ = 50 %, d) γ = 70 %
8 6.8 Eine neue Entwicklung: Lokale Fehlerschätzer In der Vorlesung vom wurde darauf hingewiesen, dass die Güte einzelner lokaler Werte direkt von der Güte der auf einem Netz darstellbaren Greenschen Funktionen abhängt. Eine bestimmte Variante adaptiver Methoden hat in jüngerer Zeit diese Erkenntnis aufgegriffen und lokale Fehlerschätzer vorgestellt, die eine Abschätzung beliebiger lokaler Größen anhand des Fehlers in den zugehörigen Greenschen Funktionen vornehmen. Ausgangspunkt der lokalen Fehlerschätzer ist die Variationsgleichung a(g i, v) = (δ j i, v) = i u j (x) v V. (15) Aus der Linearität des Skalarprodukts folgt a(g i, u u h ) = (δ j i, u u h) = i u j (x) i u h j (x) u h V h. (16) Mit der Galerkin-Orthogonalität kann die folgende Erweiterung vorgenommen werden, a(g i g h i, u u h ) = (δ j i, u u h) := i u j (x) i u h j (x). (17) Die Anwendung der Cauchy-Schwarzschen Ungleichung liefert schließlich i u j (x) i u h j (x) = a(g i g h i, u u h ) Die Grunderkenntnis aus Gl. (18) lautet damit: g i g h i E u u h E. (18) Zur Abschätzung des Fehlers beliebiger lokaler Größen dient der Energienormfehler des dualen Problems g i g h i E als Wichtung des Energienormfehlers e E des ursprünglichen Problems. Die konkrete Berechnung des Fehlers kann wieder mit adaptiven Standardtechniken vorgenommen werden. Dazu wird der Gesamtfehler aus den Beiträgen der einzelnen Elemente berechnet, i u j (x) i u h j (x) m i=1 { g i g hi E,Ωi u u h E,Ωi }. (19)
9 6.9 Ein Beispiel zur lokalen Fehlerschätzung In Abb. 3 soll für eine gelagerte Wandscheibe unter Winddruckbelastung von rechts (10 kn/m) die lokale Spannung σ h yy im angegebenen Aufpunkt mit Hilfe eines lokalen Fehlerschätzers kontrolliert werden. Es ergaben sich die folgenden Werte: Netz a) Netz b) Netz c) Netz d) REM Fhg σ h yy [kn/m 2 ] Die erzielten Ergebnisse dokumentieren die besondere Wirtschaftlichkeit der lokalen Fehlerschätzung. Die Spannung für die lokale Schätzung entspricht zwar etwa der des Netzes für die Energienorm, allerdings wird dieser Wert mit einer deutlich geringeren Anzahl von Freiheitsgraden erreicht. a) b) Aufpunkt c) d) Abb. 3: Wandscheibe unter Windbelastung: a) Startnetz, b) gleichmäßige Verfeinerung, c) Fehlerschätzung in der Energienorm, d) lokale Fehlerschätzung
Finite Elemente I Konvergenzaussagen
 Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Finite Elemente am Beispiel der Poissongleichung
 am Beispiel der Poissongleichung Roland Tomasi 11.12.2013 Inhalt 1 2 3 Poissongleichung Sei R n ein Gebiet mit abschnittsweise glattem Rand und f L 2 (). Wir suchen u : R, so dass u = f in, u = 0 Physikalische
am Beispiel der Poissongleichung Roland Tomasi 11.12.2013 Inhalt 1 2 3 Poissongleichung Sei R n ein Gebiet mit abschnittsweise glattem Rand und f L 2 (). Wir suchen u : R, so dass u = f in, u = 0 Physikalische
Entwicklung einer hp-fast-multipole-
 Entwicklung einer hp-fast-multipole- Boundary-Elemente-Methode Übersicht: 1. Motivation 2. Theoretische Grundlagen a) Boundary-Elemente-Methode b) Fast-Multipole-Methode 3. Erweiterungen a) Elementordnung
Entwicklung einer hp-fast-multipole- Boundary-Elemente-Methode Übersicht: 1. Motivation 2. Theoretische Grundlagen a) Boundary-Elemente-Methode b) Fast-Multipole-Methode 3. Erweiterungen a) Elementordnung
Finite Elemente Methoden (aus der Sicht des Mathematikers)
 Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht: Partielle Differentialgleichungen, Approximation der Lösung, Finite Elemente, lineare und höhere Ansatzfunktionen, Dünn
Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht: Partielle Differentialgleichungen, Approximation der Lösung, Finite Elemente, lineare und höhere Ansatzfunktionen, Dünn
Einführung FEM 1D - Beispiel
 p. 1/28 Einführung FEM 1D - Beispiel /home/lehre/vl-mhs-1/folien/vorlesung/4_fem_intro/deckblatt.tex Seite 1 von 28 p. 2/28 Inhaltsverzeichnis 1D Beispiel - Finite Elemente Methode 1. 1D Aufbau Geometrie
p. 1/28 Einführung FEM 1D - Beispiel /home/lehre/vl-mhs-1/folien/vorlesung/4_fem_intro/deckblatt.tex Seite 1 von 28 p. 2/28 Inhaltsverzeichnis 1D Beispiel - Finite Elemente Methode 1. 1D Aufbau Geometrie
Numerische Mathematik
 Michael Knorrenschild Mathematik-Studienhilfen Numerische Mathematik Eine beispielorientierte Einführung 6., aktualisierte und erweiterte Auflage 1.1 Grundbegriffe und Gleitpunktarithmetik 15 second, also
Michael Knorrenschild Mathematik-Studienhilfen Numerische Mathematik Eine beispielorientierte Einführung 6., aktualisierte und erweiterte Auflage 1.1 Grundbegriffe und Gleitpunktarithmetik 15 second, also
4. Das Verfahren von Galerkin
 4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Adaptivität II - Theorie
 Adaptivität II - Theorie Hubertus Bromberger, Manuel Nesensohn, Johannes Reinhardt, Johannes Schnur 8. November 2007 Fazit des ersten Vortrages Ein geeignet verfeinertes Gitter ermöglicht massive Einsparung
Adaptivität II - Theorie Hubertus Bromberger, Manuel Nesensohn, Johannes Reinhardt, Johannes Schnur 8. November 2007 Fazit des ersten Vortrages Ein geeignet verfeinertes Gitter ermöglicht massive Einsparung
Partielle Differenzialgleichungen FE-Methode. Finite Elemente. Fakultät Grundlagen. April 2011
 Finite Elemente Fakultät Grundlagen April 2011 Fakultät Grundlagen Finite Elemente Übersicht 1 Lösungsmethoden Balkenbiegung Wärmeleitung 2 Fakultät Grundlagen Finite Elemente Folie: 2 Lösungsmethoden
Finite Elemente Fakultät Grundlagen April 2011 Fakultät Grundlagen Finite Elemente Übersicht 1 Lösungsmethoden Balkenbiegung Wärmeleitung 2 Fakultät Grundlagen Finite Elemente Folie: 2 Lösungsmethoden
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Numerische Methoden I FEM/REM
 Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 06.0.206 Zusammenfassung 8. Vorlesung. Schiefwinklige Scheibenelemente Numerischer
Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 06.0.206 Zusammenfassung 8. Vorlesung. Schiefwinklige Scheibenelemente Numerischer
Entwicklung von p-mehrgitter-verfahren für turbulente Strömungen
 Entwicklung von p-mehrgitter-verfahren für turbulente Strömungen Institut für Aerodynamik und Strömungstechnik DLR 10.11.2011 1 / 24 Übersicht Motivation DG-Verfahren Gleichungen p-mehrgitter Voraussetzungen
Entwicklung von p-mehrgitter-verfahren für turbulente Strömungen Institut für Aerodynamik und Strömungstechnik DLR 10.11.2011 1 / 24 Übersicht Motivation DG-Verfahren Gleichungen p-mehrgitter Voraussetzungen
WS 2014/15 FINITE-ELEMENT-METHODE JUN.-PROF. D. JUHRE
 2.5 ANFANGSRANDWERTPROBLEM DER ELASTOMECHANIK Charakterisierung Die Zusammenfassung der in den vorangehenden Folien entwickelten Grundgleichungen des dreidimensionalen Kontinuums bildet das Anfangsrandwertproblem
2.5 ANFANGSRANDWERTPROBLEM DER ELASTOMECHANIK Charakterisierung Die Zusammenfassung der in den vorangehenden Folien entwickelten Grundgleichungen des dreidimensionalen Kontinuums bildet das Anfangsrandwertproblem
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 1 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 1 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig (IMNG)
Vororientierung zur Kurseinheit 7
 92 4 Berechnung linearer Netzwerke Vororientierung zur urseinheit 7 In diesem apitel wird Ihnen gezeigt, wie man aus linearen Zweipolen aufgebaute Netzwerke in systematischer Weise analysieren kann. Dazu
92 4 Berechnung linearer Netzwerke Vororientierung zur urseinheit 7 In diesem apitel wird Ihnen gezeigt, wie man aus linearen Zweipolen aufgebaute Netzwerke in systematischer Weise analysieren kann. Dazu
1. EINFLUSSLINIEN FÜR KRAFTGRÖßEN
 Arbeitsblätter 1 Hinweise zur Konstruktion und Berechnung von Einflusslinien Definition: Eine Einflusslinie (EL) liefert den Einfluss einer Wanderlast P = 1 von festgelegter Wirkungsrichtung. längs des
Arbeitsblätter 1 Hinweise zur Konstruktion und Berechnung von Einflusslinien Definition: Eine Einflusslinie (EL) liefert den Einfluss einer Wanderlast P = 1 von festgelegter Wirkungsrichtung. längs des
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
3. Prinzip der virtuellen Arbeit
 3. Prinzip der virtuellen rbeit Mit dem Satz von Castigliano können erschiebungen für Freiheitsgrade berechnet werden, an denen Lasten angreifen. Dabei werden nicht immer alle Terme der Formänderungsenergie
3. Prinzip der virtuellen rbeit Mit dem Satz von Castigliano können erschiebungen für Freiheitsgrade berechnet werden, an denen Lasten angreifen. Dabei werden nicht immer alle Terme der Formänderungsenergie
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Dipl.-Ing. Christoph Erath 10. November FVM-BEM Kopplung. Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln?
 Dipl.-Ing. Christoph Erath 10. November 2007 FVM-BEM Kopplung Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln? Seite 2 FVM-BEM Kopplung 10. November 2007 Dipl.-Ing. Christoph Erath
Dipl.-Ing. Christoph Erath 10. November 2007 FVM-BEM Kopplung Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln? Seite 2 FVM-BEM Kopplung 10. November 2007 Dipl.-Ing. Christoph Erath
Projektionen auf abgeschlossene konvexe Mengen
 Projektionen auf abgeschlossene konvexe Mengen Seminarvortrag von Veronika Pick Seminar Optimierung bei Herrn Prof. Dr. F. Jarre Heinrich-Heine-Universität Düsseldorf SS 2006 1 Vorbemerkung Das Seminarthema
Projektionen auf abgeschlossene konvexe Mengen Seminarvortrag von Veronika Pick Seminar Optimierung bei Herrn Prof. Dr. F. Jarre Heinrich-Heine-Universität Düsseldorf SS 2006 1 Vorbemerkung Das Seminarthema
Singularitäten in der FEM und deren Bewertung
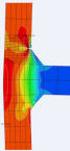 Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Elemente der Analysis II
 Elemente der Analysis II Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 8. Mai 2009 1 / 29 Bemerkung In der Vorlesung Elemente der Analysis I wurden Funktionen
Elemente der Analysis II Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 8. Mai 2009 1 / 29 Bemerkung In der Vorlesung Elemente der Analysis I wurden Funktionen
Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode
 Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode Dr. Stefan Reul, PRETECH GmbH 2. Norddeutsches Simulationsforum 27. Mai 2010 All rights reserved Copyright per DIN 34 Seite 1 Diskussionspunkte»
Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode Dr. Stefan Reul, PRETECH GmbH 2. Norddeutsches Simulationsforum 27. Mai 2010 All rights reserved Copyright per DIN 34 Seite 1 Diskussionspunkte»
Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof. Dr. Ulrich Reif
 14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
42 Orthogonalität Motivation Definition: Orthogonalität Beispiel
 4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
Inhaltsverzeichnis. Vorwort... v Vorwort zur ersten Auflage... vi Bezeichnungen... xiii
 Inhaltsverzeichnis Vorwort... v Vorwort zur ersten Auflage... vi Bezeichnungen... xiii Kapitel I Einführung 1 1. Beispiele und Typeneinteilung... 2 Beispiele 2 Typeneinteilung 7 Sachgemäß gestellte Probleme
Inhaltsverzeichnis Vorwort... v Vorwort zur ersten Auflage... vi Bezeichnungen... xiii Kapitel I Einführung 1 1. Beispiele und Typeneinteilung... 2 Beispiele 2 Typeneinteilung 7 Sachgemäß gestellte Probleme
Bedingte nichtlineare Regression Worum geht es in diesem Modul? Beispiel: Das Verhältnismodell für geometrisch-optische Täuschungen III
 Bedingte nichtlineare Regression 1 Worum geht es in diesem Modul? Beispiel: Das Verhältnismodell für geometrisch-optische Täuschungen III Bedingte lineare Quasi-Regression Eigenschaften des Residuums Parametrisierungen
Bedingte nichtlineare Regression 1 Worum geht es in diesem Modul? Beispiel: Das Verhältnismodell für geometrisch-optische Täuschungen III Bedingte lineare Quasi-Regression Eigenschaften des Residuums Parametrisierungen
Kapitel 4: Nichtlineare Nullstellenprobleme
 Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Die Funktion f wird als Regressionsfunktion bezeichnet.
 Regressionsanalyse Mit Hilfe der Techniken der klassischen Regressionsanalyse kann die Abhängigkeit metrischer (intervallskalierter) Zielgrößen von metrischen (intervallskalierten) Einflussgrößen untersucht
Regressionsanalyse Mit Hilfe der Techniken der klassischen Regressionsanalyse kann die Abhängigkeit metrischer (intervallskalierter) Zielgrößen von metrischen (intervallskalierten) Einflussgrößen untersucht
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Probeklausur zu Mathematik 3 für Informatik Lösungshinweise (ohne Garantie auf Fehlefreiheit)
 Gunter Ochs 9. Juni 05 Probeklausur zu Mathematik für Informatik Lösungshinweise ohne Garantie auf Fehlefreiheit. Sei fx x x. a Bestimmen Sie den Grenzwert lim x fx. Da an der Stelle x Zähler Nenner Null
Gunter Ochs 9. Juni 05 Probeklausur zu Mathematik für Informatik Lösungshinweise ohne Garantie auf Fehlefreiheit. Sei fx x x. a Bestimmen Sie den Grenzwert lim x fx. Da an der Stelle x Zähler Nenner Null
4. Verzerrungen. Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich
 4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
mit. Wir definieren (Skalarprodukt = Winkel).
 1 Grundidee des Simplexverfahrens (von George Dantzig): Man bestimmt eine beliebige Ecke (Extremalpunkt) einer Lösungsmenge eines Ungleichungssystems. Nun geht man an den Kanten vom Punkt entlang und kontrolliert
1 Grundidee des Simplexverfahrens (von George Dantzig): Man bestimmt eine beliebige Ecke (Extremalpunkt) einer Lösungsmenge eines Ungleichungssystems. Nun geht man an den Kanten vom Punkt entlang und kontrolliert
31 Die Potentialgleichung
 3 Die Potentialgleichung Die Potentialgleichung oder auch Poisson-Gleichung ist die lineare Gleichung zweiter Ordnung u = f in einem Gebiet R n. Im homogenen Fall f = 0 spricht man auch von der Laplace-
3 Die Potentialgleichung Die Potentialgleichung oder auch Poisson-Gleichung ist die lineare Gleichung zweiter Ordnung u = f in einem Gebiet R n. Im homogenen Fall f = 0 spricht man auch von der Laplace-
4.5 Schranken an die Dichte von Kugelpackungen
 Gitter und Codes c Rudolf Scharlau 19. Juli 2009 341 4.5 Schranken an die Dichte von Kugelpackungen Schon in Abschnitt 1.4 hatten wir die Dichte einer Kugelpackung, speziell eines Gitters bzw. einer quadratischen
Gitter und Codes c Rudolf Scharlau 19. Juli 2009 341 4.5 Schranken an die Dichte von Kugelpackungen Schon in Abschnitt 1.4 hatten wir die Dichte einer Kugelpackung, speziell eines Gitters bzw. einer quadratischen
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Stahlbau 1. Name:... Matr. Nr.:...
 1/10 Name:... Matr. Nr.:... A. Rechnerischer steil 1. Stabilitätsnachweis Der in Abb.1 dargestellte Rahmen, bestehend aus zwei Stützen [rechteckige Hohlprofile, a= 260mm,b= 140mm, s= 8mm] und einem Riegel
1/10 Name:... Matr. Nr.:... A. Rechnerischer steil 1. Stabilitätsnachweis Der in Abb.1 dargestellte Rahmen, bestehend aus zwei Stützen [rechteckige Hohlprofile, a= 260mm,b= 140mm, s= 8mm] und einem Riegel
Aufgaben / Lösungen der Klausur Nr. 4 vom Juni 2002 im LK 12. nx ln(x)dx
 Aufgaben / Lösungen der Klausur Nr. 4 vom Juni 2002 im LK 2 Aufgabe ) a) Berechne für alle natürlichen Zahlen n N das Integral e nx ln(x)dx. Mit Hilfe der partiellen Integration für f (x) = nx, somit f(x)
Aufgaben / Lösungen der Klausur Nr. 4 vom Juni 2002 im LK 2 Aufgabe ) a) Berechne für alle natürlichen Zahlen n N das Integral e nx ln(x)dx. Mit Hilfe der partiellen Integration für f (x) = nx, somit f(x)
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Beugung am Gitter. Beugung tritt immer dann auf, wenn Hindernisse die Ausbreitung des Lichtes
 PeP Vom Kerzenlicht zum Laser Versuchsanleitung Versuch 2: Beugung am Gitter Beugung am Gitter Theoretische Grundlagen Beugung tritt immer dann auf, wenn Hindernisse die Ausbreitung des Lichtes beeinträchtigen.
PeP Vom Kerzenlicht zum Laser Versuchsanleitung Versuch 2: Beugung am Gitter Beugung am Gitter Theoretische Grundlagen Beugung tritt immer dann auf, wenn Hindernisse die Ausbreitung des Lichtes beeinträchtigen.
Potentielle Energie, P.d.v.K. und P.d.v.V.
 IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Potentielle Energie, P.d.v.K. und P.d.v.V. Fachgebiet Baustatik 2. Februar 26 Inhaltsverzeichnis 1 Die potentielle Energie 1 1.1
IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Potentielle Energie, P.d.v.K. und P.d.v.V. Fachgebiet Baustatik 2. Februar 26 Inhaltsverzeichnis 1 Die potentielle Energie 1 1.1
Finite Elemente Methode für elliptische Differentialgleichungen
 Finite Elemente Methode für elliptische Differentialgleichungen Michael Pokojovy 8. Oktober 2007 Das Ritzsche Verfahren Sei R n ein beschränktes offenes Gebiet mit abschnittsweise glattem Rand S. Betrachte
Finite Elemente Methode für elliptische Differentialgleichungen Michael Pokojovy 8. Oktober 2007 Das Ritzsche Verfahren Sei R n ein beschränktes offenes Gebiet mit abschnittsweise glattem Rand S. Betrachte
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
72 Orthonormalbasen und Konvergenz im quadratischen Mittel
 72 Orthonormalbasen und Konvergenz im quadratischen Mittel 30 72 Orthonormalbasen und Konvergenz im quadratischen Mittel Wir untersuchen nun die Konvergenz von Fourier-Reihen im quadratischen Mittel in
72 Orthonormalbasen und Konvergenz im quadratischen Mittel 30 72 Orthonormalbasen und Konvergenz im quadratischen Mittel Wir untersuchen nun die Konvergenz von Fourier-Reihen im quadratischen Mittel in
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Analysis II - 1. Klausur
 Analysis II -. Klausur Sommersemester 25 Vorname: Name: Aufgabe Aufgabe 2 Aufgabe 3 Aufgabe 4 Aufgabe 5 Aufgabe 6 Aufgabe 7 Aufgabe 8 Aufgabe 9 Summe Analysis II -. Klausur 2.5.25 Aufgabe 2 Punkte Berechnen
Analysis II -. Klausur Sommersemester 25 Vorname: Name: Aufgabe Aufgabe 2 Aufgabe 3 Aufgabe 4 Aufgabe 5 Aufgabe 6 Aufgabe 7 Aufgabe 8 Aufgabe 9 Summe Analysis II -. Klausur 2.5.25 Aufgabe 2 Punkte Berechnen
Punktschätzer Optimalitätskonzepte
 Kapitel 1 Punktschätzer Optimalitätskonzepte Sei ein statistisches Modell gegeben: M, A, P ϑ Sei eine Funktion des Parameters ϑ gegeben, γ : Θ G, mit irgendeiner Menge G, und sei noch eine Sigma-Algebra
Kapitel 1 Punktschätzer Optimalitätskonzepte Sei ein statistisches Modell gegeben: M, A, P ϑ Sei eine Funktion des Parameters ϑ gegeben, γ : Θ G, mit irgendeiner Menge G, und sei noch eine Sigma-Algebra
Vorlesung: Mechanische Verfahrenstechnik Seminar - Siebklassierung
 Vorlesung: Mechanische Verfahrenstechnik Seminar - Siebklassierung Aufgabe 1: Auslegung eines Kreiswuchtschwingsiebes Aufgabenstellung: Für die Klassierung eines trockenen Kieses der Schüttgutdichte ρ
Vorlesung: Mechanische Verfahrenstechnik Seminar - Siebklassierung Aufgabe 1: Auslegung eines Kreiswuchtschwingsiebes Aufgabenstellung: Für die Klassierung eines trockenen Kieses der Schüttgutdichte ρ
Fehler- und Ausgleichsrechnung
 Fehler- und Ausgleichsrechnung Daniel Gerth Daniel Gerth (JKU) Fehler- und Ausgleichsrechnung 1 / 12 Überblick Fehler- und Ausgleichsrechnung Dieses Kapitel erklärt: Wie man Ausgleichsrechnung betreibt
Fehler- und Ausgleichsrechnung Daniel Gerth Daniel Gerth (JKU) Fehler- und Ausgleichsrechnung 1 / 12 Überblick Fehler- und Ausgleichsrechnung Dieses Kapitel erklärt: Wie man Ausgleichsrechnung betreibt
Protokoll Grundpraktikum: O1 Dünne Linsen
 Protokoll Grundpraktikum: O1 Dünne Linsen Sebastian Pfitzner 22. Januar 2013 Durchführung: Sebastian Pfitzner (553983), Jannis Schürmer (552892) Arbeitsplatz: 3 Betreuer: A. Ahlrichs Versuchsdatum: 16.01.2013
Protokoll Grundpraktikum: O1 Dünne Linsen Sebastian Pfitzner 22. Januar 2013 Durchführung: Sebastian Pfitzner (553983), Jannis Schürmer (552892) Arbeitsplatz: 3 Betreuer: A. Ahlrichs Versuchsdatum: 16.01.2013
Lineare Algebra und Numerische Mathematik für D-BAUG
 P. Grohs T. Welti F. Weber Herbstsemester 5 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe. Skalarprodukt und Orthogonalität.a) Bezüglich des euklidischen
P. Grohs T. Welti F. Weber Herbstsemester 5 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe. Skalarprodukt und Orthogonalität.a) Bezüglich des euklidischen
Ingenieurmathematik I Lernstandserhebung 2 24./
 Ingenieurmathematik I Lernstandserhebung 4./5..7 Bitte Namen, Vornamen und Matrikel-Nr. einsetzen. Name:............................................................................ Vorname:.........................................................................
Ingenieurmathematik I Lernstandserhebung 4./5..7 Bitte Namen, Vornamen und Matrikel-Nr. einsetzen. Name:............................................................................ Vorname:.........................................................................
Outline. 1 Funktionen von mehreren Veränderlichen. 2 Grenzwert und Stetigkeit. 3 Partielle Ableitungen. 4 Die verallgemeinerte Kettenregel
 Outline 1 Funktionen von mehreren Veränderlichen 2 Grenzwert und Stetigkeit 3 Partielle Ableitungen 4 Die verallgemeinerte Kettenregel 5 Das totale Differential 6 Extremstellen Roman Wienands (Universität
Outline 1 Funktionen von mehreren Veränderlichen 2 Grenzwert und Stetigkeit 3 Partielle Ableitungen 4 Die verallgemeinerte Kettenregel 5 Das totale Differential 6 Extremstellen Roman Wienands (Universität
3.4 Kondition eines Problems
 38 KAPITEL 3. FEHLERANALYSE Beispiel 3.18 Betrachte M(10, 5, 1). Dann sind x 4.2832, y 4.2821, z 5.7632 darstellare Zahlen und (x y)z 0.00633952. Das korrekte Ergenis in M ist daher 0.0063395. Der Ausdruck
38 KAPITEL 3. FEHLERANALYSE Beispiel 3.18 Betrachte M(10, 5, 1). Dann sind x 4.2832, y 4.2821, z 5.7632 darstellare Zahlen und (x y)z 0.00633952. Das korrekte Ergenis in M ist daher 0.0063395. Der Ausdruck
ERLÄUTERUNGEN ZUM KRAFTGRÖßENVERFAHREN An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.
 FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
Modellieren in der Angewandten Geologie II. Sebastian Bauer
 Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Iterationsverfahren und Stabilitätsuntersuchung
 1 FÜR INTERESSIERTE! NICHT TESTRELEVANT 1! Iterationsverfahren und Stabilitätsuntersuchung Unter Iterationsverfahren versteht man rekursive numerische Methoden mit welchen auch analytisch nicht lösbare
1 FÜR INTERESSIERTE! NICHT TESTRELEVANT 1! Iterationsverfahren und Stabilitätsuntersuchung Unter Iterationsverfahren versteht man rekursive numerische Methoden mit welchen auch analytisch nicht lösbare
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Maschinelles Lernen: Symbolische Ansätze
 Maschinelles Lernen: Symbolische Ansätze Wintersemester 2008/2009 Musterlösung für das 5. Übungsblatt Aufgabe 1: Covering-Algorithmus und Coverage-Space Visualisieren Sie den Ablauf des Covering-Algorithmus
Maschinelles Lernen: Symbolische Ansätze Wintersemester 2008/2009 Musterlösung für das 5. Übungsblatt Aufgabe 1: Covering-Algorithmus und Coverage-Space Visualisieren Sie den Ablauf des Covering-Algorithmus
7. Grenzwertsätze. Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012
 7. Grenzwertsätze Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Mittelwerte von Zufallsvariablen Wir betrachten die arithmetischen Mittelwerte X n = 1 n (X 1 + X 2 + + X n ) von unabhängigen
7. Grenzwertsätze Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Mittelwerte von Zufallsvariablen Wir betrachten die arithmetischen Mittelwerte X n = 1 n (X 1 + X 2 + + X n ) von unabhängigen
Simulation eines Geburtstagsproblems
 Simulation eines Geburtstagsproblems Jürgen Appel Kurzfassung des Inhalts: Bei der Aufgabe handelt es sich um eine einfache Variante eines Geburtstagsproblems mit drei Personen. Die Wahrscheinlichkeit
Simulation eines Geburtstagsproblems Jürgen Appel Kurzfassung des Inhalts: Bei der Aufgabe handelt es sich um eine einfache Variante eines Geburtstagsproblems mit drei Personen. Die Wahrscheinlichkeit
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
FEM isoparametrisches Konzept
 FEM isoparametrisches Konzept /home/lehre/vl-mhs-/folien/vorlesung/5_fem_isopara/deckblatt.tex Seite von 25. p./25 Inhaltsverzeichnis. Interpolationsfunktion für die finiten Elemente 2. Finite-Element-Typen
FEM isoparametrisches Konzept /home/lehre/vl-mhs-/folien/vorlesung/5_fem_isopara/deckblatt.tex Seite von 25. p./25 Inhaltsverzeichnis. Interpolationsfunktion für die finiten Elemente 2. Finite-Element-Typen
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Prof. Dr. H. Brenner Osnabrück SS Analysis II. Vorlesung 50. Hinreichende Kriterien für lokale Extrema
 Prof. Dr. H. Brenner Osnabrück SS 205 Analysis II Vorlesung 50 Hinreichende Kriterien für lokale Extrema Wir kommen jetzt zu hinreichenden Kriterien für die Existenz von lokalen Extrema einer Funktion
Prof. Dr. H. Brenner Osnabrück SS 205 Analysis II Vorlesung 50 Hinreichende Kriterien für lokale Extrema Wir kommen jetzt zu hinreichenden Kriterien für die Existenz von lokalen Extrema einer Funktion
Auswertung und Lösung
 Körperkraft [Nm] 0 50 100 150 200 250 0 20 40 60 80 Lean Body Mass [kg] Dieses Quiz soll Ihnen helfen, den R Output einer einfachen linearen Regression besser zu verstehen (s. Kapitel 5.4.1) Es wurden
Körperkraft [Nm] 0 50 100 150 200 250 0 20 40 60 80 Lean Body Mass [kg] Dieses Quiz soll Ihnen helfen, den R Output einer einfachen linearen Regression besser zu verstehen (s. Kapitel 5.4.1) Es wurden
Hypothesen: Fehler 1. und 2. Art, Power eines statistischen Tests
 ue biostatistik: hypothesen, fehler 1. und. art, power 1/8 h. lettner / physik Hypothesen: Fehler 1. und. Art, Power eines statistischen Tests Die äußerst wichtige Tabelle über die Zusammenhänge zwischen
ue biostatistik: hypothesen, fehler 1. und. art, power 1/8 h. lettner / physik Hypothesen: Fehler 1. und. Art, Power eines statistischen Tests Die äußerst wichtige Tabelle über die Zusammenhänge zwischen
RUHR-UNIVERSITÄT BOCHUM FAKULTÄT FÜR BAUINGENIEURWESEN STATIK UND DYNAMIK. Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Fehlerfortpflanzung & Extremwertbestimmung. Folie 1
 Fehlerfortpflanzung & Etremwertbestimmung Folie 1 Fehlerfortpflanzung Einführung In vielen technischen Zusammenhängen sind die Werte bestimmter Größen nicht genau bekannt sondern mit einer Unsicherheit
Fehlerfortpflanzung & Etremwertbestimmung Folie 1 Fehlerfortpflanzung Einführung In vielen technischen Zusammenhängen sind die Werte bestimmter Größen nicht genau bekannt sondern mit einer Unsicherheit
[ 1 ] Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
![[ 1 ] Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an. [ 1 ] Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.](/thumbs/52/30312207.jpg) 13 Zeitreihenanalyse 1 Kapitel 13: Zeitreihenanalyse A: Übungsaufgaben: [ 1 ] 1 a a) Nach der Formel x t+i berechnet man einen ein f achen gleitenden Durchschnitt. 2a + 1 i= a b) Die Residuale berechnet
13 Zeitreihenanalyse 1 Kapitel 13: Zeitreihenanalyse A: Übungsaufgaben: [ 1 ] 1 a a) Nach der Formel x t+i berechnet man einen ein f achen gleitenden Durchschnitt. 2a + 1 i= a b) Die Residuale berechnet
Über die Dialogleiste wird nun der Mittelpunkt 5 4 der Stütze eingegeben. Danach können wir die Breite der Stütze in x und y Richtung eingeben.
 Übung 3.1: Plattensystem, Modellierung einer Stütze STATISCHES SYSTEM 10m 8m Stb. Decke: C20/25 Pfeiler/Wände: MW 8/MG IIa Einspannungsfreie Lagerung am Rand. Plattendicke h = 0,2 m, = 0,2 Flächenlast
Übung 3.1: Plattensystem, Modellierung einer Stütze STATISCHES SYSTEM 10m 8m Stb. Decke: C20/25 Pfeiler/Wände: MW 8/MG IIa Einspannungsfreie Lagerung am Rand. Plattendicke h = 0,2 m, = 0,2 Flächenlast
Kapitel 1 Parallele Modelle Wie rechnet man parallel?
 PRAM- PRAM- DAG- R UND R Coles und Kapitel 1 Wie rechnet man parallel? Vorlesung Theorie Paralleler und Verteilter Systeme vom 11. April 2008 der Das DAG- Das PRAM- Das werkmodell Institut für Theoretische
PRAM- PRAM- DAG- R UND R Coles und Kapitel 1 Wie rechnet man parallel? Vorlesung Theorie Paralleler und Verteilter Systeme vom 11. April 2008 der Das DAG- Das PRAM- Das werkmodell Institut für Theoretische
Inhaltsverzeichnis. Vorwort zur ersten Auflage. Bezeichnungen
 Inhaltsverzeichnis Vorwort zur vierten Auflage Vorwort zur ersten Auflage Bezeichnungen v vi xv Kapitel I Einführung 1 1. Beispiele und Typeneinteilung 2 Beispiele 2 Typeneinteilung 7 Sachgemäß gestellte
Inhaltsverzeichnis Vorwort zur vierten Auflage Vorwort zur ersten Auflage Bezeichnungen v vi xv Kapitel I Einführung 1 1. Beispiele und Typeneinteilung 2 Beispiele 2 Typeneinteilung 7 Sachgemäß gestellte
Bemessung von Stützbauwerken
 Bemessung von Stützbauwerken II/2.ppt 1 1 2 2 Erddruck 3 3 4 4 Aktiver Erddruck 5 5 6 6 Passiver Erddruck 7 7 8 8 Standsicherheitsnachweise für Stützmauern (a) Nachweis der äußeren Standsicherheit Grenzzustände:
Bemessung von Stützbauwerken II/2.ppt 1 1 2 2 Erddruck 3 3 4 4 Aktiver Erddruck 5 5 6 6 Passiver Erddruck 7 7 8 8 Standsicherheitsnachweise für Stützmauern (a) Nachweis der äußeren Standsicherheit Grenzzustände:
3. Kraftgrößenverfahren
 .Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
.Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
KAPITEL 1. Einleitung
 KAPITEL 1 Einleitung Wir beschäftigen uns in dieser Vorlesung mit Verfahren aus der Numerischen linearen Algebra und insbesondere dem sogenannten Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
KAPITEL 1 Einleitung Wir beschäftigen uns in dieser Vorlesung mit Verfahren aus der Numerischen linearen Algebra und insbesondere dem sogenannten Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
5. Die eindimensionale Wellengleichung
 H.J. Oberle Differentialgleichungen II SoSe 2013 5. Die eindimensionale Wellengleichung Wir suchen Lösungen u(x, t) der eindimensionale Wellengleichung u t t c 2 u xx = 0, x R, t 0, (5.1) wobei die Wellengeschwindigkeit
H.J. Oberle Differentialgleichungen II SoSe 2013 5. Die eindimensionale Wellengleichung Wir suchen Lösungen u(x, t) der eindimensionale Wellengleichung u t t c 2 u xx = 0, x R, t 0, (5.1) wobei die Wellengeschwindigkeit
Statistik II. Regressionsanalyse. Statistik II
 Statistik II Regressionsanalyse Statistik II - 23.06.2006 1 Einfachregression Annahmen an die Störterme : 1. sind unabhängige Realisationen der Zufallsvariable, d.h. i.i.d. (unabh.-identisch verteilt)
Statistik II Regressionsanalyse Statistik II - 23.06.2006 1 Einfachregression Annahmen an die Störterme : 1. sind unabhängige Realisationen der Zufallsvariable, d.h. i.i.d. (unabh.-identisch verteilt)
Spherical Maps. 1 Selbst gestellte Aufgabe. 2 Umsetzung. 2.1 Programmstruktur
 1 Selbst gestellte Aufgabe 1 Spherical Maps Bearbeitet von Andreas Petermann MNr.: 162586 Danilo Gulamhussene MNr.: 162795 Sascha Baldt MNr.: 162773 als Bildinformationstechik-Praktikum im Wintersemester
1 Selbst gestellte Aufgabe 1 Spherical Maps Bearbeitet von Andreas Petermann MNr.: 162586 Danilo Gulamhussene MNr.: 162795 Sascha Baldt MNr.: 162773 als Bildinformationstechik-Praktikum im Wintersemester
Probeklausur Optimierung
 Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Die Familie der χ 2 (n)-verteilungen
 Die Familie der χ (n)-verteilungen Sind Z 1,..., Z m für m 1 unabhängig identisch standardnormalverteilte Zufallsvariablen, so genügt die Summe der quadrierten Zufallsvariablen χ := m Z i = Z 1 +... +
Die Familie der χ (n)-verteilungen Sind Z 1,..., Z m für m 1 unabhängig identisch standardnormalverteilte Zufallsvariablen, so genügt die Summe der quadrierten Zufallsvariablen χ := m Z i = Z 1 +... +
Numerik I. Aufgaben und Lösungen
 Universität zu Köln SS 2009 Mathematisches Institut Prof Dr C Tischendorf Dr M Selva, mselva@mathuni-koelnde Numerik I Musterlösung Übungsblatt 4, Kondition (5 Punkte) Aufgaben Lösungen (4 Punkte) Zeigen
Universität zu Köln SS 2009 Mathematisches Institut Prof Dr C Tischendorf Dr M Selva, mselva@mathuni-koelnde Numerik I Musterlösung Übungsblatt 4, Kondition (5 Punkte) Aufgaben Lösungen (4 Punkte) Zeigen
Über die Summation der Reihen, die in dieser Form enthalten sind
 Über die Summation der Reihen, die in dieser Form enthalten sind a + a 4 + a3 9 + a4 + a5 5 + a 3 + etc Leonhard Euler Aus diesen Dingen, welche ich einst als erster über die Summation der Potenzen der
Über die Summation der Reihen, die in dieser Form enthalten sind a + a 4 + a3 9 + a4 + a5 5 + a 3 + etc Leonhard Euler Aus diesen Dingen, welche ich einst als erster über die Summation der Potenzen der
Quasi-Monte-Carlo-Algorithmen
 Quasi-Monte-Carlo-Algorithmen Peter Kritzer Institut für Finanzmathematik/Institut für Didaktik der Mathematik Johannes Kepler Universität Linz peter.kritzer@jku.at Tag der Mathematik, April 2011 P. Kritzer
Quasi-Monte-Carlo-Algorithmen Peter Kritzer Institut für Finanzmathematik/Institut für Didaktik der Mathematik Johannes Kepler Universität Linz peter.kritzer@jku.at Tag der Mathematik, April 2011 P. Kritzer
2 für 1: Subventionieren Fahrgäste der 2. Klasse bei der Deutschen Bahn die 1. Klasse?
 2 für 1: Subventionieren Fahrgäste der 2. Klasse bei der Deutschen Bahn die 1. Klasse? Felix Zesch November 5, 2016 Abstract Eine kürzlich veröffentlichte These lautet, dass bei der Deutschen Bahn die
2 für 1: Subventionieren Fahrgäste der 2. Klasse bei der Deutschen Bahn die 1. Klasse? Felix Zesch November 5, 2016 Abstract Eine kürzlich veröffentlichte These lautet, dass bei der Deutschen Bahn die
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Der Begriff der konvexen Menge ist bereits aus Definition 1.4, Teil I, bekannt.
 Kapitel 3 Konvexität 3.1 Konvexe Mengen Der Begriff der konvexen Menge ist bereits aus Definition 1.4, Teil I, bekannt. Definition 3.1 Konvexer Kegel. Eine Menge Ω R n heißt konvexer Kegel, wenn mit x
Kapitel 3 Konvexität 3.1 Konvexe Mengen Der Begriff der konvexen Menge ist bereits aus Definition 1.4, Teil I, bekannt. Definition 3.1 Konvexer Kegel. Eine Menge Ω R n heißt konvexer Kegel, wenn mit x
5. Mathematik Olympiade 1. Stufe (Schulolympiade) Klasse 8 Saison 1965/1966 Aufgaben und Lösungen
 5. Mathematik Olympiade Saison 1965/1966 Aufgaben und Lösungen 1 OJM 5. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
5. Mathematik Olympiade Saison 1965/1966 Aufgaben und Lösungen 1 OJM 5. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen Safe
Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen Safe
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 25. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 25.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 25. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 25.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Online Algorithmen. Online Kürzeste Wege Probleme. Online Algorithmen Kompetitivität
 Online Algorithmen Wiederholung Eigenschaften von Online Algorithmen Unvollständige (Vorab-)Information Sequentielle Anfragen Abarbeitung der aktuellen Anfragen ohne Information über zukünftige Anfragen
Online Algorithmen Wiederholung Eigenschaften von Online Algorithmen Unvollständige (Vorab-)Information Sequentielle Anfragen Abarbeitung der aktuellen Anfragen ohne Information über zukünftige Anfragen
Übungsblatt 1: Lösungswege und Lösungen
 Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
