KAPITEL 9 Splinefunktionen
|
|
|
- Hanna Fleischer
- vor 5 Jahren
- Abrufe
Transkript
1 KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge τ = {τ 0,..., τ l+1 } mit a = τ 0 < τ 1 <... < τ l < τ l+1 = b und k 1 definieren wir den Splineraum der Splines der Ordnung k durch P 1,τ = { f : [a, b) R f [τi,τ i+1 ) Π 0, 0 i l }, P k,τ = {f C k 2 ([a, b]) f [τi,τ i+1 ) Π k 1, 0 i l }, k 2. Für k = 4 ergibt sich gerade der Raum der kubischen Splines. Dahmen-Reusken Kapitel 9 1
2 Lemma 9.1. Es gilt: dim P k,τ = k + l. Bemerkung 9.2. Fehlerschranke für eine beste Näherung im Splineraum P k,τ. Sei h = max j=0,...,l (τ j+1 τ j ) und g = max g(x) ( g C([a, b])). x [a,b] Für jedes k 2 existiert eine positive Konstante c <, so daß für jedes m k und jede Funktion f C m ([a, b]) gilt min f S k ch m f (m). S k P k,τ Dieses Resultat kann für den Fall m = 0 verbessert werden: Sei f C([a, b]) und k 1 beliebig, dann existiert für jedes ε > 0 ein h > 0, so daß min S k P k,τ f S k ε. Dahmen-Reusken Kapitel 9 2
3 Bemerkung 9.3. Da jedes Polynom insbesondere ein stückweises Polynom ist, das zudem sogar unendlich oft differenzierbar ist, gilt natürlich Außerdem sieht man leicht, daß Π k 1 P k,τ. wobei, für m 0, (τ i x) k 1 + P k,τ, i = 1,..., l, x m + = { x m für x > 0, 0 für x 0, die sogenannten abgebrochenen Potenzen sind. Die k + l Funktionen x i, i = 0,..., k 1, (τ i x) + k 1, i = 1,..., l, sind linear unabhängig. Diese Funktionen bilden also eine Basis für P k,τ. Dahmen-Reusken Kapitel 9 3
4 9.1.1 B-Splines Eine viel bessere Basis für P k,τ bilden die sogenannten B-Splines. Wir betrachten erst den Fall k = 1. Die charakteristischen Funktionen N j,1 (x) := χ [τj,τ j+1 ) (x) := { 1 für x [τj, τ j+1 ), 0 sonst, j = 0,..., l, bilden eine Basis für P 1,τ. Der Träger ( support ) der Funktion N j,1 wird durch supp N j,1 := {x R N j,1 (x) 0} definiert. Die Basis N j,1, 0 j l, ist lokal. S(x) = l j=0 c j N j,1 (x) läßt sich mit dem Koeffizientenvektor c = (c j ) l j=0 identifizieren. Es gilt c = l j=0 Die Basis ist in diesem Sinne stabil. c j N j,1. Dahmen-Reusken Kapitel 9 4
5 Der Fall k = 2. Es werden zwei Hilfsknoten τ 1 < τ 0 = a, τ l+2 > τ l+1 = b und zugehörige Hilfsfunktionen N 1,1, N l+1,1 eingeführt: Die Funktion N 1,1 := χ [τ 1,τ 0 ), N l+1,1 := χ [τl+1,τ l+2 ). N j,2 (x) := x τ j τ j+1 τ j N j,1 (x) + τ j+2 x τ j+2 τ j+1 N j+1,1 (x), j = 1,..., l, hat folgende Eigenschaften: 1) sie nimmt von Null verschiedene Werte nach Definition von N j,1 (x) und N j+1,1 (x) nur auf dem Intervall [τ j, τ j+2 ] an; 2) auf jedem der Intervalle [τ j, τ j+1 ], [τ j+1, τ j+2 ] ist N j,2 (x) linear; 3) N j,2 (x) ist stetig. Dahmen-Reusken Kapitel 9 5
6 Hutfunktionen N j,2 1 N 1,2 (x) N 0,2 (x) N 1,2 (x) N 2,2 (x) a = τ 0 τ 1 τ 2 τ 3 = b x Dahmen-Reusken Kapitel 9 6
7 Definition 9.4 (B-Splines). Sei t 1 < t 2 <... < t n eine beliebige Folge von paarweise verschiedenen Knoten. Dann werden die B-Splines N j,k der Ordnung k (1 k < n) rekursiv definiert durch N j,1 (x) := χ [tj,t j+1 ) für j = 1,..., n 1, N j,k (x) := x t j N j,k 1 (x) + t j+k x N j+1,k 1 (x), t j+k 1 t j t j+k t j+1 für k = 2,..., n 1, und j = 1,..., n k. Lemma 9.5. Für diese B-Splines N j,k gilt: (i) supp N j,k [t j, t j+k ], (ii) N j,k (x) > 0 für alle x (t j, t j+k ), (iii) (N j,k ) [ti,t i+1 ) Π k 1, (iv) N j,k C k 2 ([t 1, t n ]). Dahmen-Reusken Kapitel 9 7
8 Für 1 j n k: die dividierte Differenz [t j,..., t j+k ]( x) k 1 + ist als führender Koeffizient des Lagrange-Interpolations-Polynoms der Funktion f k 1 (s) := (s x) k 1 + an den Stützstellen t j,..., t j+k definiert. Explizite Darstellung für die B-Splines: Satz 9.6. Die B-Splines N j,k haben folgende Darstellung: N j,k (x) = (t j+k t j )[t j,..., t j+k ]( x) k 1 +, für 1 k < n, 1 j n k. Die dividierte Differenz wirkt auf das Argument. Zum Beispiel: [t j, t j+1 ]( x) m + = [t j+1]( x) m + [t j]( x) m + t j+1 t j = (t j+1 x) m + (t j x) m + t j+1 t j. Dahmen-Reusken Kapitel 9 8
9 Folgerung 9.8. Für k 3 gilt { N j,k Nj,k 1 (x) = (k 1) (x) N } j+1,k 1(x), t j+k 1 t j t j+k t j+1 d.h., die Ableitungen von B-Splines sind gewichtete Differenzen von B-Splines niedrigerer Ordnung. Dahmen-Reusken Kapitel 9 9
10 9.1.2 B-Splines als Basis für den Splineraum Ziel der bisherigen Überlegungen war, eine stabile Basis für P k,τ zu gewinnen. Sei P k,τ der Splineraum wie in (9.1). Zur Knotenmenge τ = {τ 0,..., τ l+1 } mit a = τ 0 < τ 1 <... < τ l < τ l+1 = b definieren wir eine erweiterte Knotenmenge T: T = {t 1,..., t n } mit n := 2k + l, t 1 <... < t k = τ 0, t k+j = τ j für j = 1,..., l, τ l+1 = t k+l+1 <... < t 2k+l. Zu dieser erweiterten Knotenmenge T werden die B-Splines N j,k, 1 j n k = k + l, wie in Definition 9.4 definiert. Dahmen-Reusken Kapitel 9 10
11 Die Funktionswerte N j,k (x) sind für alle x R definiert. Im Splineraum P k,τ sind nur die Werte N j,k (x) mit x [a, b] von Interesse. Wir definieren nun S k,t = span{ N j,k [a,b] 1 j k + l }. Folgendes Hauptresultat zeigt, daß die (auf [a, b] restringierten) B-Splines N j,k eine Basis für den Splineraum P k,τ bilden. Satz 9.9. Es gilt P k,τ = S k,t. Bemerkung Die Definition von S k,t ist unabhängig von der Wahl der Hilfsknoten t 1,..., t k 1 < a und t k+l+2,..., t 2k+l > b. Man läßt sie deshalb oft auf den jeweiligen Intervallenden a bzw. b zusammenfallen. Dahmen-Reusken Kapitel 9 11
12 Beispiel Wir betrachten [a, b] = [0,1], k = 4, l = 5, t 1 = t 2 = t 3 = t 4 = 0, t 5 = 0.1, t 6 = 0.3, t 7 = 0.45, t 8 = 0.65, t 9 = 0.8, t 10 = t 11 = t 12 = t 13 = 1. Für j = 2,3,4,5 werden die kubische B-Splines N j,4 unten abgebildet j=2 j=4 j=5 0.6 j= Dahmen-Reusken Kapitel 9 12
13 9.1.3 Rechnen mit Linearkombinationen von B-Splines Jeder Spline S P k,τ hat eine eindeutige Darstellung S(x) = k+l j=1 c j N j,k (x), x [a, b]. Seien c 1,..., c k+l bekannt. Hilfsgrößen für eine effiziente Auswertung von S: c [p] j (x) = c j, p = 0 x t j c [p 1] t j+k p t j (x) + t j+k p x c [p 1] j t j+k p t j 1 (x) j sonst. Dahmen-Reusken Kapitel 9 13
14 Algorithmus 9.12 (Auswertung von S). Gegeben: x [a, b] und c 1,..., c k+l aus der obigen Darstellung. Bestimme m mit x [t m, t m+1 ). (Es ist k m k + l.) Setze Für p = 1,..., k 1 berechne c [0] j (x) = c j, j = 1,..., k + l. c [p] j (x), j = m k p,..., m. S(x) = c [k 1] m (x). Dahmen-Reusken Kapitel 9 14
15 In analoger Weise kann man Ableitungen von Splinefunktionen behandeln. Es ergibt sich folgende Darstellung der p-ten Ableitung: S (p) (x) = k+l j=1+p c (p) j N j,k p (x) als Linearkombination von B-Splines der Ordnung k p. Die neuen Koeffizienten c (p) j sind p-te Differenzen der ursprünglichen Koeffizienten: c (p) j = c j, p = 0, c (p 1) (k p) c(p 1) j j 1 t j+k p t, 0 < p k 2. j Dahmen-Reusken Kapitel 9 15
16 9.1.4 Stabilität der B-Spline-Basis Einer der Hauptgründe für die Wichtigkeit der B-Splines: Für jedes k N existiert eine positive Konstante c, so daß für alle Knotenmengen T = {t j } n j=1 wie in (9.10) und alle {c j} k+l j=1 gilt c max j=1,...,k+l c j max x [a,b] k+l j=1 c j N j,k (x) max j=1,...,k+l c j. Das heißt kleine Änderungen in den Koeffizienten bewirken nur kleine Änderungen in der entsprechenden Splinefunktion und umgekehrt und zwar unabhängig von der Lage der Knoten. Dahmen-Reusken Kapitel 9 16
17 9.2. Splineinterpolation Der folgende Satz (von Schoenberg und Whitney) charakterisiert, wann ein Interpolationsproblem eindeutig für alle Daten lösbar ist. Satz 9.15 Sei T = {t j } n j=1 wie in (9.10). Seien x 1,..., x k+l [a, b] Stützstellen und f 1,..., f k+l die zugehörigen Daten. Das Problem der Bestimmung eines S S k,t, so daß S(x j ) = f j, j = 1,..., k + l gilt, hat genau dann eine eindeutig bestimmte Lösung, wenn x j (t j, t j+k ), j = 1,..., k + l, d.h., wenn in den Träger jedes B-Splines mindestens eine Stützstelle fällt. Man kann sogar zeigen, daß die Aussage für Hermite- Interpolation gültig bleibt. Dahmen-Reusken Kapitel 9 17
18 Kubische Splineinterpolation Wir gehen nun auf den wichtigen Spezialfall der kubischen Splineinterpolation nochmals ein. Dies betrifft den Fall, daß k = 4 ist und Stützstellen und Knoten übereinstimmen: x j := t j+3 = τ j 1 für j = 1,..., l + 2. Dies liefert allerdings nur l + 2 Bedingungen. Mögliche weitere Bedingungen (dim S 4,T = 4 + l): (a) Vollständige kubische Splineinterpolation: S(t j ) = f(t j ), j = 4,..., l + 5, S (a) = f (a), S (b) = f (b). (b) Natürliche kubische Splineinterpolation: S(t j ) = f(t j ), j = 4,..., l + 5, S (a) = S (b) = 0. Dahmen-Reusken Kapitel 9 18
19 Lemma Sei g C 2 ([a, b]) und S S 4,T, so daß g(t i ) = S(t i ) für i = 4,..., l + 5, S (b) ( g (b) S (b) ) = S (a) ( g (a) S (a) ). Dann gilt b a S (x) 2 dx b a g (x) 2 dx. Dahmen-Reusken Kapitel 9 19
20 Für die vollständige kubische Splineinterpolation ergibt sich folgendes Resultat: Satz Zu jedem f C 1 ([a, b]) existiert ein eindeutiger Spline I 4 f S 4,T, so daß (I 4 f)(t j ) = f(t j ), j = 4,..., l + 5, (I 4 f) (a) = f (a), (I 4 f) (b) = f (b). Ferner erfüllt I 4 f die Extremaleigenschaft b a (I 4f) (x) 2 dx b a g (x) 2 dx für alle Funktionen g C 2 ([a, b]), die die gleichen Interpolationsund Randbedingungen wie I 4 f erfüllen. Dahmen-Reusken Kapitel 9 20
21 Völlig analog kann man folgendes Resultat für die natürliche kubische Splineinterpolation beweisen: Satz Zu jedem f C 2 [(a, b]) existiert ein eindeutiger Spline Î 4 f S 4,T, so daß (Î 4 f)(t j ) = f(t j ), j = 4,..., l + 5, (Î 4 f) (a) = (Î 4 f) (b) = 0. Ferner erfüllt Î 4 f die Extremaleigenschaft b a (Î 4 f) (x) 2 dx b a g (x) 2 dx für alle Funktionen g C 2 ([a, b]) die die gleichen Interpolationsund Randbedingungen wie Î 4 f erfüllen. Dahmen-Reusken Kapitel 9 21
22 Bemerkung Sei und f C 4 ([a, b]). Man kann beweisen, daß h = max j=1,...,l (τ j+1 τ j ) f I 4 f h4 16 f(4) gilt, wobei die Maximumnorm auf [a, b] ist. Der Vergleich mit Bemerkung 9.2 zeigt, daß die kubische Interpolation (unabhängig von der Lage der Knoten!) die bestmögliche Approximationsordnung realisiert. Dahmen-Reusken Kapitel 9 22
23 Berechnung der vollständigen kubischen Splineinterpolation Sei I 4 f die vollständige Splineinterpolation einer Funktion f C 1 ([a, b]). Wegen Satz 9.9 hat I 4 f die Form (I 4 f)(x) = l+4 j=1 c j N j,4 (x). Die Lösung des Interpolationsproblems verlangt nun, die Koeffizienten c j über die Interpolationsbedingungen (9.25) zu bestimmen. Es gilt c 1 = f(t 4 ), c l+4 = f(t l+5 ), c 2 = f (a) f(a)n 1,4 (a) N 2,4 (a), c l+3 = f (b) f(b)n l+4,4 (b) N l+3,4 (b). Dahmen-Reusken Kapitel 9 23
24 Es sind lediglich noch die Koeffizienten (c 3,..., c l+2 ) T = c zu bestimmen sind. Dafür ergibt sich das Gleichungssystem A T c = f, wobei f = (f 3,..., f l+2 ) T mit f 3 = f(t 5 ) c 2 N 2,4 (t 5 ), f l+2 = f(t l+4 ) c l+3 N l+3,4 (t l+4 ), f j = f(t j+2 ), j = 4,..., l + 1, und A T = N 3,4 (t 5 ) N 4,4 (t 5 ) N 3,4 (t 6 ) N 4,4 (t 6 ) N 5,4 (t 6 ) N 4,4 (t 7 ) N 5,4 (t 7 ) N l+2,4 (t l+3 ) N l+1,4 (t l+4 ) N l+2,4 (t l+4 ). Dahmen-Reusken Kapitel 9 24
25 Seien Beispiel τ j = j 0.1, j = 0,...,14, f j = 1, j = 0,...,5, f j = 0.5, j = 6,...,14. Die entsprechende natürliche kubische-splineinterpolation ist in Abb. 9.4 dargestellt. Man stellt fest, daß wegen des Sprunges in den Daten Oszillationen auftreten Dahmen-Reusken Kapitel 9 25
26 9.3 Datenfit-Smoothing Splines Gegeben seien Messungen f j, j = 1,..., m, die gewissen Abszissen x j, j = 1,..., m, in einem Intervall [a, b] zugeordnet werden. Eine Approximation S S k,t läßt sich dann folgendermaßen bestimmen: Finde c = (c 1,..., c k+l ) T, so daß S(x) = k+l j=1 c jn j,k (x) m j=1 ( S(xj ) f j ) 2 = min c R k+l m j=1 ( k+l l=1 c l N l,k (x j ) f j ) 2 erfüllt. Hierbei ist i.a. m k + l, und die x j müssen natürlich nicht mit den Knoten t j übereinstimmen. Diese Aufgabe ist ein lineares Ausgleichsproblem der Form A T c f 2 = min, wobei hier A T = ( N j,k (x i ) ) m,k+l i=1,j=1 Rm (k+l), f = (f 1,..., f m ) T R m. Dahmen-Reusken Kapitel 9 26
27 Auch beim obigen Ausgleichsansatz können stark fehlerbehaftete Datensätze und starke Datenausreißer ein Überfitten mit entsprechenden Oszillationen bewirken. Das Konzept des Smoothing-Splines schafft da Abhilfe. Ein Strafterm soll starke Ausschläge unterdrücken und die Daten glätten. Für ein θ 0 sucht man dasjenige S S k,t, das m j=1 erfüllt. (S(x j ) f j ) 2 + θ 2 S 2 2 = min S S k,t m j=1 ( S(x j ) f j ) 2 + θ 2 S 2 2 Wegen (9.17) und (9.20) für p = 2 gilt für S(x) = k+l j=1 c jn j,k (x) c 2 k+l j=3 ( ) (2) 2 c j N j,k 2 2 S 2 2 k+l C2 j=3 ( c (2) j N j,k 2 2 ) 2. Dahmen-Reusken Kapitel 9 27
28 Man erhält also im Wesentlichen das qualitativ selbe Funktional, wenn man S 2 2 durch k+l j=3 ĉ2 j, mit ĉ j := c (2) N j,k 2 2, ersetzt. Dies führt zu folgendem Minimierungsproblem: Finde S(x) = k+l j=1 c jn j,k (x) so daß, j Hierbei gilt m j=1 ( k+l i=1 = min c R k+l c (2) (k 1)(k 2) j = ) 2 c i N i,k (x j ) f j + θ 2 k+l m j=1 [ t j+k 2 t j ( 1 + t j+k 1 t j ( k+l i=1 ĉ 2 j j=3 ) 2 c i N i,k (x j ) f j + θ 2 k+l 1 t j+k 2 t j 1 c j 2 1 t j+k 2 t j 1 ) cj 1 + j=3 ĉ 2 j. ] 1 c j t j+k 1 t j, für j = 3,..., k + l. Dahmen-Reusken Kapitel 9 28
29 Mit ĉ := (ĉ 3,..., ĉ k+l ) T ergibt sich ĉ = B T c, B T := b 3,1 b 3,2 b 3,3 b 4,2 b 4,3 b 4, b k+l,k+l 2 b k+l,k+l 1 b k+l,k+l d j := (k 1)(k 2) N j,k 2 2 t j+k 2 t j, b j,j 2 := b j,j := d j t j+k 1 t j, b j,j 1 := ( ) b j,j 2 + b j,j. Das Minimierungsproblem erhält dann die Form d j, t j+k 2 t j 1, A T c f θ2 B T c 2 2 = min c R k+l A T c f θ2 B T c 2 2, was wiederum gleichbedeutend mit ( ) ( AT f c θb T 0 ) 2 min und somit ein Standard-Ausgleichsproblem ist. Dahmen-Reusken Kapitel 9 29
30 Beispiel Messungen (x j, f j ), j = 1,...,20 ( in Abbildung). Zur Approximation (und Glättung) dieser Daten benutzen wir kubische Splines mit äquidistanten Knoten τ j = j 0.1, j = 0,...,10. Für drei Parameterwerte θ = 0, 10 3, 10 2 werden die Splinefunktionen S(x) = 13 j=1 c jn j,4 (x) gezeigt Dahmen-Reusken Kapitel 9 30
KAPITEL 8. Interpolation
 KAPITEL 8. Interpolation 8.2 Lagrange-Interpolationsaufgabe für Polynome Wir beschränken uns auf die Lagrange-Interpolation mit Polynomen. Der Raum der Polynome vom Grad n: Stützstellen: Π n = { n j=0
KAPITEL 8. Interpolation 8.2 Lagrange-Interpolationsaufgabe für Polynome Wir beschränken uns auf die Lagrange-Interpolation mit Polynomen. Der Raum der Polynome vom Grad n: Stützstellen: Π n = { n j=0
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Spline-Interpolation
 Spline-Interpolation Tim Schmölzer 20 November 2009 Tim Schmölzer Spline-Interpolation 20 November 2009 1 / 38 Übersicht 1 Vorbemerkungen 2 Lösbarkeit des Interpolationsproblems 3 Stabilität der Interpolation
Spline-Interpolation Tim Schmölzer 20 November 2009 Tim Schmölzer Spline-Interpolation 20 November 2009 1 / 38 Übersicht 1 Vorbemerkungen 2 Lösbarkeit des Interpolationsproblems 3 Stabilität der Interpolation
Spline-Räume - B-Spline-Basen
 Spline-Räume - B-Spline-Basen René Janssens 4. November 2009 René Janssens () Spline-Räume - B-Spline-Basen 4. November 2009 1 / 56 Übersicht 1 Erster Abschnitt: Räume von Splinefunktionen Grundlegende
Spline-Räume - B-Spline-Basen René Janssens 4. November 2009 René Janssens () Spline-Räume - B-Spline-Basen 4. November 2009 1 / 56 Übersicht 1 Erster Abschnitt: Räume von Splinefunktionen Grundlegende
H.J. Oberle Analysis II SoSe Interpolation
 HJ Oberle Analysis II SoSe 2012 7 Interpolation 71 Allgemeine Problemstellung Interpolation ist die Kunst, zwischen den Zeilen einer Tabelle zu lesen (Rutishauser) Von f : R R seien Funktionswerte (x j,
HJ Oberle Analysis II SoSe 2012 7 Interpolation 71 Allgemeine Problemstellung Interpolation ist die Kunst, zwischen den Zeilen einer Tabelle zu lesen (Rutishauser) Von f : R R seien Funktionswerte (x j,
6. Polynom-Interpolation
 6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
8 Interpolation. 8.1 Problemstellung. Gegeben: Diskrete Werte einer Funktion f : R R an n + 1 Stützstellen. x 0 < x 1 <... < x n.
 8 Interpolation 81 Problemstellung Gegeben: Diskrete Werte einer Funktion f : R R an n + 1 Stützstellen x 0 < x 1 < < x n Eingabedaten: (x 0, f 0 ),(x 1, f 1 ),,(x n, f n ) Gegebene Daten (x j, f j ) Analysis
8 Interpolation 81 Problemstellung Gegeben: Diskrete Werte einer Funktion f : R R an n + 1 Stützstellen x 0 < x 1 < < x n Eingabedaten: (x 0, f 0 ),(x 1, f 1 ),,(x n, f n ) Gegebene Daten (x j, f j ) Analysis
Kapitel 7. Interpolation und Approximation II. Inhalt: 7.1 Spline-Interpolation 7.2 Trigonometrische Interpolation 7.3 Tschebyscheff-Approximation
 Kapitel 7. Interpolation und Approximation II Inhalt: 7.1 Spline-Interpolation 7.2 Trigonometrische Interpolation 7.3 Tschebyscheff-Approximation Numerische Mathematik I 275 Interpolation als lineares
Kapitel 7. Interpolation und Approximation II Inhalt: 7.1 Spline-Interpolation 7.2 Trigonometrische Interpolation 7.3 Tschebyscheff-Approximation Numerische Mathematik I 275 Interpolation als lineares
1 2 x x x x x x2 + 83
 Polynominterpolation Aufgabe 1 Gegeben sei die Wertetabelle i 0 1 2 3 x i 0 1 2 4 f i 3 1 2 7 a) Bestimmen Sie das Interpolationspolynom von Lagrange durch die obigen Wertepaare. b) Interpolieren Sie die
Polynominterpolation Aufgabe 1 Gegeben sei die Wertetabelle i 0 1 2 3 x i 0 1 2 4 f i 3 1 2 7 a) Bestimmen Sie das Interpolationspolynom von Lagrange durch die obigen Wertepaare. b) Interpolieren Sie die
Übungen zu Splines Lösungen zu Übung 20
 Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
3.1.3 Newtonsche Interpolationsformel / Dividierte Differenzen
 KAPITEL 3 INTERPOLATION UND APPROXIMATION 4 33 Newtonsche Interpolationsformel / Dividierte Differenzen Das Verfahren von Neville ist unpraktisch, wenn man das Polynom selbst sucht oder das Polynom an
KAPITEL 3 INTERPOLATION UND APPROXIMATION 4 33 Newtonsche Interpolationsformel / Dividierte Differenzen Das Verfahren von Neville ist unpraktisch, wenn man das Polynom selbst sucht oder das Polynom an
Numerisches Programmieren, Übungen
 Technische Universität München SoSe 20 Institut für Informatik Prof Dr Thomas Huckle Dipl-Inf Christoph Riesinger Dipl-Math Jürgen Bräckle Numerisches Programmieren, Übungen Musterlösung 6 Übungsblatt:
Technische Universität München SoSe 20 Institut für Informatik Prof Dr Thomas Huckle Dipl-Inf Christoph Riesinger Dipl-Math Jürgen Bräckle Numerisches Programmieren, Übungen Musterlösung 6 Übungsblatt:
Gitterfreie Methoden. Florian Hewener. 29. Oktober 2013
 Gitterfreie Methoden 1D 2D Florian Hewener 29. Oktober 2013 Gliederung 1 Interpolationsprobleme Problemstellung Haar-Räume 2 Mehrdimensionale Polynominterpolation 3 Splines Kubische Splines und natürliche
Gitterfreie Methoden 1D 2D Florian Hewener 29. Oktober 2013 Gliederung 1 Interpolationsprobleme Problemstellung Haar-Räume 2 Mehrdimensionale Polynominterpolation 3 Splines Kubische Splines und natürliche
(c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 =
![(c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 = (c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 =](/thumbs/88/117470920.jpg) 1. (a) i. Wann besitzt A R n n eine eindeutige LR-Zerlegung mit R invertierbar? ii. Definieren Sie die Konditionszahl κ(a) einer Matrix A bzgl. einer Norm.! iii. Welche Eigenschaften benötigt eine Matrix
1. (a) i. Wann besitzt A R n n eine eindeutige LR-Zerlegung mit R invertierbar? ii. Definieren Sie die Konditionszahl κ(a) einer Matrix A bzgl. einer Norm.! iii. Welche Eigenschaften benötigt eine Matrix
8 Polynominterpolation
 8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
Polynominterpolation. Allgemeines Problem: Beispiel 1 (Teil 1):
 . Großübung Polynominterpolation Allgemeines Problem: Aufgrund gegebener Messwerte (Paare aus Werten i und Funktionswerten f( i )) soll ein Funktionsverlauf rekonstruiert bzw. zumeist angenähert werden.
. Großübung Polynominterpolation Allgemeines Problem: Aufgrund gegebener Messwerte (Paare aus Werten i und Funktionswerten f( i )) soll ein Funktionsverlauf rekonstruiert bzw. zumeist angenähert werden.
Interpolation. Heinrich Voss. TUHH Heinrich Voss Kapitel / 49.
 Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation TUHH Heinrich Voss Kapitel 2 2010 1 / 49 Interpolationsproblem Gegeben seien eine Funktion Φ (x; a 1,...,
Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation TUHH Heinrich Voss Kapitel 2 2010 1 / 49 Interpolationsproblem Gegeben seien eine Funktion Φ (x; a 1,...,
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Interpolation und Approximation von Funktionen
 Kapitel 6 Interpolation und Approximation von Funktionen Bei ökonomischen Anwendungen tritt oft das Problem auf, dass eine analytisch nicht verwendbare (oder auch unbekannte) Funktion f durch eine numerisch
Kapitel 6 Interpolation und Approximation von Funktionen Bei ökonomischen Anwendungen tritt oft das Problem auf, dass eine analytisch nicht verwendbare (oder auch unbekannte) Funktion f durch eine numerisch
Polynominterpolation mit Matlab.
 Polynominterpolation mit Matlab. Die Matlab-Funktion polyfit a = polyfit(x,f,n-1); berechnet die Koeffizienten a = (a(1),a(2),...,a(n)); des Interpolationspolynoms p(x) = a(1)*x^(n-1) + a(2)*x^(n-2) +...
Polynominterpolation mit Matlab. Die Matlab-Funktion polyfit a = polyfit(x,f,n-1); berechnet die Koeffizienten a = (a(1),a(2),...,a(n)); des Interpolationspolynoms p(x) = a(1)*x^(n-1) + a(2)*x^(n-2) +...
Kapitel 4: Interpolation Sei U eine Klasse von einfach strukturierten Funktionen, z.b.
 Kapitel 4: Interpolation Sei U eine Klasse von einfach strukturierten Funktionen, z.b. - Polynome, - rationale Funktionen, - trigonometrische Polynome, - Splines. Interpolationsproblem 4: Sei f : [a,b]
Kapitel 4: Interpolation Sei U eine Klasse von einfach strukturierten Funktionen, z.b. - Polynome, - rationale Funktionen, - trigonometrische Polynome, - Splines. Interpolationsproblem 4: Sei f : [a,b]
NUMERISCHE MATHEMATIK II 1. (Studiengang Mathematik) Prof. Dr. Hans Babovsky. Institut für Mathematik. Technische Universität Ilmenau WS 2001/2002
 NUMERISCHE MATHEMATIK II 1 (Studiengang Mathematik) Prof Dr Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2001/2002 1 Korrekturen, Kommentare und Verbesserungsvorschläge bitte
NUMERISCHE MATHEMATIK II 1 (Studiengang Mathematik) Prof Dr Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2001/2002 1 Korrekturen, Kommentare und Verbesserungsvorschläge bitte
1. Anhang: Spline-Funktionen
 C:\D\DOKU\NUM KURS\SPLINE.TEX C:\UG\.AI 20. Juli 1998 Vorbemerkung: Wenn der Satz stimmt, daß jede Formel eines Textes die Leserzahl halbiert, dann brauche ich bei grob geschätzt 40 Formeln etwa 2 40 =
C:\D\DOKU\NUM KURS\SPLINE.TEX C:\UG\.AI 20. Juli 1998 Vorbemerkung: Wenn der Satz stimmt, daß jede Formel eines Textes die Leserzahl halbiert, dann brauche ich bei grob geschätzt 40 Formeln etwa 2 40 =
Approximation durch Polynome
 durch n Anwendungen: zur Vereinfachung einer gegebenen Funktion durch einen Polynomausdruck. Dann sind übliche Rechenoperation +,,, / möglich. zur Interpolation von Daten einer Tabelle n Beispiel Trotz
durch n Anwendungen: zur Vereinfachung einer gegebenen Funktion durch einen Polynomausdruck. Dann sind übliche Rechenoperation +,,, / möglich. zur Interpolation von Daten einer Tabelle n Beispiel Trotz
T n (1) = 1 T n (cos π n )= 1. deg T n q n 1.
 KAPITEL 3. INTERPOLATION UND APPROXIMATION 47 Beweis: Wir nehmen an qx) für alle x [, ] und führen diese Annahme zu einem Widerspruch. Es gilt nach Folgerung ii) T n ) T n cos π n ). Wir betrachten die
KAPITEL 3. INTERPOLATION UND APPROXIMATION 47 Beweis: Wir nehmen an qx) für alle x [, ] und führen diese Annahme zu einem Widerspruch. Es gilt nach Folgerung ii) T n ) T n cos π n ). Wir betrachten die
Nachklausur am Donnerstag, den 7. August 2008
 Nachklausur zur Vorlesung Numerische Mathematik (V2E2) Sommersemester 2008 Prof. Dr. Martin Rumpf Dr. Martin Lenz Dipl.-Math. Nadine Olischläger Nachklausur am Donnerstag, den 7. August 2008 Bearbeitungszeit:
Nachklausur zur Vorlesung Numerische Mathematik (V2E2) Sommersemester 2008 Prof. Dr. Martin Rumpf Dr. Martin Lenz Dipl.-Math. Nadine Olischläger Nachklausur am Donnerstag, den 7. August 2008 Bearbeitungszeit:
Übungsblatt 1 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
19. Januar Universität Erlangen-Nürnberg Department Mathematik PD Dr. Markus Bause. . Danach liefert die Gauss-Elinination. .
 Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
6 Polynominterpolation
 Vorlesungsskript HM-Numerik (SS 2014): Kapitel 6 Version: 1 Juli 2014 6 Polynominterpolation Gegeben: Wertepaare { (x i,f i ) R 2 i = 0,,n } Gesucht: Einfache Funktion g : R R mit g(x i ) = f i i {0,1,,n}
Vorlesungsskript HM-Numerik (SS 2014): Kapitel 6 Version: 1 Juli 2014 6 Polynominterpolation Gegeben: Wertepaare { (x i,f i ) R 2 i = 0,,n } Gesucht: Einfache Funktion g : R R mit g(x i ) = f i i {0,1,,n}
0.1 Modellierung von Kurven und Flächen mittels B-Splines
 Vorlesung vom 28.04.06 Skript erstellt von Antonia Wittmers und Maria Gensel 0.1 Modellierung von Kurven und Flächen mittels B-Splines Das Wort Spline, übersetzt mit längliches, dünnes Stück Holz oder
Vorlesung vom 28.04.06 Skript erstellt von Antonia Wittmers und Maria Gensel 0.1 Modellierung von Kurven und Flächen mittels B-Splines Das Wort Spline, übersetzt mit längliches, dünnes Stück Holz oder
HTL Kapfenberg SPLINE Interpolation Seite 1 von 7.
 HTL Kapfenberg SPLINE Interpolation Seite von 7 Roland Pichler roland.pichler@htl-kapfenberg.ac.at SPLINE Interpolation Mathematische / Fachliche Inhalte in Stichworten: Polynome, Gleichungssysteme, Differenzialrechnung
HTL Kapfenberg SPLINE Interpolation Seite von 7 Roland Pichler roland.pichler@htl-kapfenberg.ac.at SPLINE Interpolation Mathematische / Fachliche Inhalte in Stichworten: Polynome, Gleichungssysteme, Differenzialrechnung
Diplom VP Informatik / Numerik 2. September 2002
 Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen
 Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Numerik für Ingenieure I Wintersemester 2008
 1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
9. Parametrische Kurven und Flächen
 9. Parametrische Kurven und Flächen Polylinien bzw. Polygone sind stückweise lineare Approximationen für Kurven bzw. Flächen Nachteile: hohe Zahl von Eckpunkten für genaue Repräsentation erforderlich interaktive
9. Parametrische Kurven und Flächen Polylinien bzw. Polygone sind stückweise lineare Approximationen für Kurven bzw. Flächen Nachteile: hohe Zahl von Eckpunkten für genaue Repräsentation erforderlich interaktive
19.2 Mittelwertsatz der Differentialrechnung
 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
Lineare Differentialgleichungen höherer Ordnung
 Lineare Differentialgleichungen höherer Ordnung I. Grundlegendes Eine homogene lineare Differentialgleichung n-ter Ordnung besitzt die Form y (n) + a n 1 (x)y (n 1) +... + a 1 (x)y + a 0 (x)y = 0 Eine
Lineare Differentialgleichungen höherer Ordnung I. Grundlegendes Eine homogene lineare Differentialgleichung n-ter Ordnung besitzt die Form y (n) + a n 1 (x)y (n 1) +... + a 1 (x)y + a 0 (x)y = 0 Eine
Interpolation. Kapitel 3
 Kapitel 3 Interpolation Die Interpolation von Funktionen oder Daten ist ein häufig auftretendes Problem sowohl in der Mathematik als auch in vielen Anwendungen Das allgemeine Problem, die sogenannte Dateninterpolation,
Kapitel 3 Interpolation Die Interpolation von Funktionen oder Daten ist ein häufig auftretendes Problem sowohl in der Mathematik als auch in vielen Anwendungen Das allgemeine Problem, die sogenannte Dateninterpolation,
c) Realisierung des Gauß Algorithmus in Gleitpunktarithmetik: Fehlerschranke hängt linear ab von max i,k l ik. 8n 3 max i,j,k a (k) ij ε.
 Matrix unverändert: A = QR cond 2 (R) = cond 2 (A). c) Realisierung des Gauß Algorithmus in Gleitpunktarithmetik: Fehlerschranke hängt linear ab von max i,k l ik. Spaltenpivotisierung: l ik 1 kleine Fehlerschranke
Matrix unverändert: A = QR cond 2 (R) = cond 2 (A). c) Realisierung des Gauß Algorithmus in Gleitpunktarithmetik: Fehlerschranke hängt linear ab von max i,k l ik. Spaltenpivotisierung: l ik 1 kleine Fehlerschranke
Die Interpolationsaufgabe besteht darin, eine (einfache) Funktion u n U n zu finden,
 Kapitel 3 Interpolation 31 Einführung Bemerkung 31 Motivation, Aufgabenstellung Gegeben seien eine Funktion f C([a,b]) und x i [a,b], i = 0,n, mit a x 0 < x 1 < < x n b (31) Die Interpolationsaufgabe besteht
Kapitel 3 Interpolation 31 Einführung Bemerkung 31 Motivation, Aufgabenstellung Gegeben seien eine Funktion f C([a,b]) und x i [a,b], i = 0,n, mit a x 0 < x 1 < < x n b (31) Die Interpolationsaufgabe besteht
Themen Lagrange-Interpolation Hermite-Interpolation. Splines. Bézier-Kurven. 5 Interpolation. Interpolation Die Lagrangesche Interpolationsaufgabe
 5 Themen Lagrange- Bézier-Kurven saufgabe sformel Der sfehler 5.1 saufgabe È n = Raum der reellen Polynome vom Grad n. saufgabe sformel Der sfehler 5.1 saufgabe È n = Raum der reellen Polynome vom Grad
5 Themen Lagrange- Bézier-Kurven saufgabe sformel Der sfehler 5.1 saufgabe È n = Raum der reellen Polynome vom Grad n. saufgabe sformel Der sfehler 5.1 saufgabe È n = Raum der reellen Polynome vom Grad
9 Höhere partielle Ableitungen und die Taylorformel
 Vorlesung SS 29 Analsis 2 Prof Dr Siegfried Echterhoff 9 Höhere partielle Ableitungen und die Talorformel Definition 91 Sei U R n offen, f : U R m eine Funktion Dann heißt f 2-mal partiell differenzierbar,
Vorlesung SS 29 Analsis 2 Prof Dr Siegfried Echterhoff 9 Höhere partielle Ableitungen und die Talorformel Definition 91 Sei U R n offen, f : U R m eine Funktion Dann heißt f 2-mal partiell differenzierbar,
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Interpolationsproblem. Interpolation. Interpolationsproblem. Interpolationsproblem. Gegeben seien eine Funktion. Φ (x; a 1,...
 sproblem Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation Gegeben seien eine Funktion Φ (x; a 1,..., a n ) : R I R, die auf einem Intervall I erklärt
sproblem Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation Gegeben seien eine Funktion Φ (x; a 1,..., a n ) : R I R, die auf einem Intervall I erklärt
Übungen zu Einführung in die Numerische Mathematik (V2E2) Sommersemester 2016
 Übungen zu Einführung in die Numerische Mathematik (VE) Sommersemester 6 Prof. Dr. Martin Rumpf Pascal Huber Sascha Tölkes Übungsblatt 8 Abgabe:.6.6 Aufgabe 5 (Elliptisches Randwertproblem auf einem Ring)
Übungen zu Einführung in die Numerische Mathematik (VE) Sommersemester 6 Prof. Dr. Martin Rumpf Pascal Huber Sascha Tölkes Übungsblatt 8 Abgabe:.6.6 Aufgabe 5 (Elliptisches Randwertproblem auf einem Ring)
Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) = sin(πx) und geben die folgenden Stützstellen und Stützwerte vor:
 5 Splineinterpolation Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) sin(πx) und geben die folgenden Stützstellen und Stützwerte vor: x i 3 f i Damit ist n 5, h Forderung
5 Splineinterpolation Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) sin(πx) und geben die folgenden Stützstellen und Stützwerte vor: x i 3 f i Damit ist n 5, h Forderung
5 Lineare Algebra (Teil 3): Skalarprodukt
 5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
Numerische Mathematik Sommersemester 2013
 TU Chemnitz 5. Februr 2014 Professur Numerische Mthemtik Prof. Dr. Oliver Ernst Dipl.-Mth. Ingolf Busch Dipl.-Mth. techn. Tommy Etling Numerische Mthemtik Sommersemester 2013 Musterlösungen zu nicht behndelten
TU Chemnitz 5. Februr 2014 Professur Numerische Mthemtik Prof. Dr. Oliver Ernst Dipl.-Mth. Ingolf Busch Dipl.-Mth. techn. Tommy Etling Numerische Mthemtik Sommersemester 2013 Musterlösungen zu nicht behndelten
Numerische Verfahren
 Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 08.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren 1 / 68 Übersicht
Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 08.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren 1 / 68 Übersicht
GMA. Grundlagen Mathematik und Analysis. Nullstellen und Fixpunkte Reelle Funktionen 3. Christian Cenker Gabriele Uchida
 GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
 Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 6.8.005 1 Aufgabe N1 Gegeben seien A = 5-10 -5-10 8-10 -5-10 13 R 3 3 und b = a) Überprüfen Sie, ob die Matrix A positiv definit ist. b) Bestimmen
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 6.8.005 1 Aufgabe N1 Gegeben seien A = 5-10 -5-10 8-10 -5-10 13 R 3 3 und b = a) Überprüfen Sie, ob die Matrix A positiv definit ist. b) Bestimmen
a i x i, (1) Ein Teil der folgenden Betrachtungen gilt auch, wenn man den Körper durch einen Ring ersetzt.
 Polynome Definition 1. Ein Polynom f über einem Körper K mit der Unbestimmten x ist eine formale Summe f(x) = i 0 a i x i, (1) wobei nur endlich viele der Koeffizienten a i K von Null verschieden sind.
Polynome Definition 1. Ein Polynom f über einem Körper K mit der Unbestimmten x ist eine formale Summe f(x) = i 0 a i x i, (1) wobei nur endlich viele der Koeffizienten a i K von Null verschieden sind.
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Inhalt Kapitel IV: Interpolation
 Inhalt Kapitel IV: Interpolation IV Interpolation IV. Polynom-Interpolation IV. Spline-Interpolation Kapitel IV (InhaltIV) Die Interpolationsformel von Lagrange Zentrale Aussage: Zu beliebigen n + Stützpunkten
Inhalt Kapitel IV: Interpolation IV Interpolation IV. Polynom-Interpolation IV. Spline-Interpolation Kapitel IV (InhaltIV) Die Interpolationsformel von Lagrange Zentrale Aussage: Zu beliebigen n + Stützpunkten
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Stetige Funktionen. Definition. Seien (X, d) und (Y, D) metrische Räume und f : X Y eine Abbildung. i) f heißt stetig in x 0 (x 0 D(f)), wenn
 Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
GRUNDLAGEN MATHEMATIK
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 4. Differentialrechnung Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 4. Differentialrechnung Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies
Übungsblatt 3 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA4 - SS6 Übungsblatt Musterlösung Sei M,N N und f C M+N+ (B) eine komplexe Funktion, B eine kompakte Menge. Die Padé Approximation PN M (f)(x) ist die rationale
Numerik gewöhnlicher Differentialgleichungen MA4 - SS6 Übungsblatt Musterlösung Sei M,N N und f C M+N+ (B) eine komplexe Funktion, B eine kompakte Menge. Die Padé Approximation PN M (f)(x) ist die rationale
Interpolation, numerische Integration
 Interpolation, numerische Integration 8. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 8. Mai 2014 Gliederung 1 Interpolation polynomial Spline 2 Numerische
Interpolation, numerische Integration 8. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 8. Mai 2014 Gliederung 1 Interpolation polynomial Spline 2 Numerische
Approximationstheorie und Approximationspraxis
 Approximationstheorie und Approximationspraxis Martin Wagner Bergische Universität Wuppertal Fachbereich C - Mathematik und Naturwissenschaften AG Optmierung und Approximation 3. Februar 2010 1 / 20 Motivation
Approximationstheorie und Approximationspraxis Martin Wagner Bergische Universität Wuppertal Fachbereich C - Mathematik und Naturwissenschaften AG Optmierung und Approximation 3. Februar 2010 1 / 20 Motivation
4 Matrizenrechnung. Beide Operationen geschehen also koeffizientenweise. Daher übertragen sich die Rechenregeln von K(m n, k).
 4 Matrizenrechnung Der Vektorraum der m n Matrizen über K Sei K ein Körper und m, n N\{0} A sei eine m n Matrix über K: a a 2 a n a 2 a 22 a 2n A = = (a ij) mit a ij K a m a m2 a mn Die a ij heißen die
4 Matrizenrechnung Der Vektorraum der m n Matrizen über K Sei K ein Körper und m, n N\{0} A sei eine m n Matrix über K: a a 2 a n a 2 a 22 a 2n A = = (a ij) mit a ij K a m a m2 a mn Die a ij heißen die
Irrationale Zahlen. Ausarbeitung zum Proseminar Modul 4c Unendlichkeit. angefertigt von. Felix Schultes. Dozentin: Fr.
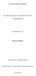 Irrationale Zahlen Ausarbeitung zum Proseminar Modul 4c Unendlichkeit angefertigt von Felix Schultes Dozentin: Fr. Regula Krapf Fachbereich 3 Universität Koblenz-Landau 24..207 INHALTSVERZEICHNIS Inhaltsverzeichnis
Irrationale Zahlen Ausarbeitung zum Proseminar Modul 4c Unendlichkeit angefertigt von Felix Schultes Dozentin: Fr. Regula Krapf Fachbereich 3 Universität Koblenz-Landau 24..207 INHALTSVERZEICHNIS Inhaltsverzeichnis
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
(Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
NUMERIK 1. Sommersemester 2016
 NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Kapitel 15 Lineare Gleichungssysteme
 Kapitel 15 Lineare Gleichungssysteme Kapitel 15 Lineare Gleichungssysteme Mathematischer Vorkurs TU Dortmund Seite 1 / 27 Kapitel 15 Lineare Gleichungssysteme Definition 15.1 (Lineares Gleichungssystem
Kapitel 15 Lineare Gleichungssysteme Kapitel 15 Lineare Gleichungssysteme Mathematischer Vorkurs TU Dortmund Seite 1 / 27 Kapitel 15 Lineare Gleichungssysteme Definition 15.1 (Lineares Gleichungssystem
bekannt: Eliminationsverfahren von Gauß Verfahren führt zu einer Zerlegung der Koeffizientenmatrix: A = LR A = LR
 LR-Zerlegung bekannt: Eliminationsverfahren von Gauß Verfahren führt zu einer Zerlegung der Koeffizientenmatrix: A = LR Definition 2.17 Unter einer LR-Zerlegung einer Matrix A R n n verstehen wir eine
LR-Zerlegung bekannt: Eliminationsverfahren von Gauß Verfahren führt zu einer Zerlegung der Koeffizientenmatrix: A = LR Definition 2.17 Unter einer LR-Zerlegung einer Matrix A R n n verstehen wir eine
Ausgleichsprobleme. 3 Nichtlineare Ausgleichsprobleme
 1 Normalengleichung Ausgleichsprobleme A T A T = AA 2 Orthogonalisierungsverfahren A = Q R 3 Nichtlineare Ausgleichsprobleme Typeset by FoilTEX 1 Motivation Ausgleichsprobleme treten meist dann auf, wenn
1 Normalengleichung Ausgleichsprobleme A T A T = AA 2 Orthogonalisierungsverfahren A = Q R 3 Nichtlineare Ausgleichsprobleme Typeset by FoilTEX 1 Motivation Ausgleichsprobleme treten meist dann auf, wenn
4.1. Vektorräume und lineare Abbildungen
 4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV Aufgabe N1 (LR-Zerlegung mit Pivotisierung) Gegeben seien R 3.
 Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Approximationsverfahren für die Kurvendarstellung
 Approximationsverfahren für die Kurvendarstellung (a) Bézier-Kurven spezielle Form polynomialer Kurven spezifiziert durch n+1 Kontrollpunkte P 0, P 1,..., P n Kurve läuft nicht durch alle Kontrollpunkte,
Approximationsverfahren für die Kurvendarstellung (a) Bézier-Kurven spezielle Form polynomialer Kurven spezifiziert durch n+1 Kontrollpunkte P 0, P 1,..., P n Kurve läuft nicht durch alle Kontrollpunkte,
Analysis 2, Woche 9. Mehrdimensionale Differentialrechnung I. 9.1 Differenzierbarkeit
 A Analysis, Woche 9 Mehrdimensionale Differentialrechnung I A 9. Differenzierbarkeit A3 =. (9.) Definition 9. Sei U R m offen, f : U R n eine Funktion und a R m. Die Funktion f heißt differenzierbar in
A Analysis, Woche 9 Mehrdimensionale Differentialrechnung I A 9. Differenzierbarkeit A3 =. (9.) Definition 9. Sei U R m offen, f : U R n eine Funktion und a R m. Die Funktion f heißt differenzierbar in
2 Vektorräume und Gleichungssysteme
 2 Vektorräume und Gleichungssysteme 21 Der n-dimensionale K-Vektorraum 2 Vektorräume und Gleichungssysteme 21 Der n-dimensionale K-Vektorraum Definition 21 Seien K = (K, +, ) ein Körper, V eine Menge und
2 Vektorräume und Gleichungssysteme 21 Der n-dimensionale K-Vektorraum 2 Vektorräume und Gleichungssysteme 21 Der n-dimensionale K-Vektorraum Definition 21 Seien K = (K, +, ) ein Körper, V eine Menge und
11. Darstellung von Kurven und Flächen
 H.J. Oberle Approximation WS 23/4. Darstellung von Kurven und Flächen Bézier Kurven. Unser Ziel ist es, polynomiale Kurven auf dem Rechner möglichst effizient darzustellen. Hierzu nutzen wir die Basisdarstellung
H.J. Oberle Approximation WS 23/4. Darstellung von Kurven und Flächen Bézier Kurven. Unser Ziel ist es, polynomiale Kurven auf dem Rechner möglichst effizient darzustellen. Hierzu nutzen wir die Basisdarstellung
9 Differentialrechnung für Funktionen in n Variablen
 $Id: diff.tex,v.7 29/7/2 3:4:3 hk Exp $ $Id: ntaylor.tex,v.2 29/7/2 3:26:42 hk Exp $ 9 Differentialrechnung für Funktionen in n Variablen 9.6 Lagrange Multiplikatoren Die Berechnung von Maxima und Minima
$Id: diff.tex,v.7 29/7/2 3:4:3 hk Exp $ $Id: ntaylor.tex,v.2 29/7/2 3:26:42 hk Exp $ 9 Differentialrechnung für Funktionen in n Variablen 9.6 Lagrange Multiplikatoren Die Berechnung von Maxima und Minima
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
1 Umkehrfunktionen und implizite Funktionen
 Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 20 Wiederholung: Fehlerbetrachtung.
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 20 Wiederholung: Fehlerbetrachtung.
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Michael Karow Thema: Satz von Taylor Die Taylor-Entwicklung I Satz von Taylor. Sei f : R D R an der Stelle x n-mal differenzierbar. Dann gilt für x D, n f (k) (x )
Vorlesung: Analysis I für Ingenieure Michael Karow Thema: Satz von Taylor Die Taylor-Entwicklung I Satz von Taylor. Sei f : R D R an der Stelle x n-mal differenzierbar. Dann gilt für x D, n f (k) (x )
Die duale Simplexmethode
 Kapitel 0 Die duale Simplexmethode Bei der dualen Simplexmethode ist eine Startlösung oftmals leichter angebbar als bei der Simplexmethode für das ursprüngliche lineare Programm, da man keine Nichtnegativitätsanforderungen
Kapitel 0 Die duale Simplexmethode Bei der dualen Simplexmethode ist eine Startlösung oftmals leichter angebbar als bei der Simplexmethode für das ursprüngliche lineare Programm, da man keine Nichtnegativitätsanforderungen
Differentiation und Taylorentwicklung. Thomas Fehm
 Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Lineare Abbildungen und Orthonormalsysteme
 KAPITEL Lineare Abbildungen und Orthonormalsysteme. Lineare Abbildungen und Koordinatendarstellungen.. Lineare Abbildungen und ihre Basisdarstellung. Seien V, W Vektorraume uber R. Mit einer Abbildung
KAPITEL Lineare Abbildungen und Orthonormalsysteme. Lineare Abbildungen und Koordinatendarstellungen.. Lineare Abbildungen und ihre Basisdarstellung. Seien V, W Vektorraume uber R. Mit einer Abbildung
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
