Maß- und Integrationstheorie
|
|
|
- Waltraud Maus
- vor 5 Jahren
- Abrufe
Transkript
1 Prof. H.C. Grunau E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn ich nur und kenne, kann ich A B und A \ B als Kombination von und schreiben? Stellen Sie die jeweils anderen mit Hilfe der beiden folgenden dar: 2 und 3 und \ 4 und \ 1.2 Aufgabe Sei X beliebige Menge, für A X bezeichne c A = X \ A. Man zeige für beliebige Teilmengen A, A i, B, B i X A \ B = A ( ) c B c A i = c A i ( ) i i c A i = ( ) ( ) c A i A i B i = (A i Bj ) i i i i,j i 1.3 Aufgabe Gegeben sei eine Abbildung f : X Y und A i X. Man ( beweise: ) f A i = ( ) f (A i ), f A i f (A i ) i i i i 1.4 Aufgabe Gegeben sei eine Folge a n,k Ist es wahr, daß lim n Und sup n sup k a n.k = sup k lim a n,k = lim k k sup a n,k? n lim a n,k? n 1
2 1.5 Aufgabe Gegeben seien die Folgen a n und b n mit lim sup a n = A lim inf a n = a lim sup b n = B lim inf b n = b Man beweise die folgenden Ungleichungen lim sup (a n + b n ) A + B lim inf (a n + b n ) a + b [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 2
3 Maß- und Integrationstheorie WS 2002/03 Prof. H.C. Grunau E. Sassone Aufgabe Gegeben sei X = {x R 2 : x < 1}. Seien A 1 = {A X : A hat eine zentrale Symmetrie bzgl. eines Punkts x 0 X} A 2 = {A X : A ist punktsymmetrisch in Bezug auf (0, 0) } A 3 = {A X : A hat einen glatten Rand }. Sind A 1, A 2, A 3 Algebren? Und σ-algebren? 2.2 Aufgabe Gegeben seien der Einheitwürfel in R 2 X = (0, 1] (0, 1] {1, 0} und die Mengenfamilie A = {A X : A eine Menge mit jeder Seite parallel zu einer von X und x A : x A (1, 0) oder (0, 1) sind die äußere Normale an A in der Punkt x oder wenn x Ecke einer Seite mit äußeren Normale (1,0) ist }. Ist A eine Algebra? Und eine σ-algebra? 2.3 Aufgabe Sei A = {A Q : A oder c A sind endlich }. Ist A eine Algebra? Und eine σ-algebra? 2.4 Aufgabe Gegeben seien eine Menge X und die Familien P(X) = {A : A Teilmenge von X}, A = {X, }. Man beweise, daß (X, P) und (X, A) σ-algebren sind. 2.5 Aufgabe a) Sei X = R n, A = P(X); x 0 R n sei fest. as irac-maß δ x0 in x 0 wird definiert durch { 1 falls x0 M δ x0 = 0 falls x 0 / M Ist (X, A, δ x0 ) ein Maßraum? b) Seien X = Q, A = P(Q) und µ das Zählmaß. Ist (X, A, µ) ein Maßraum? 3
4 2.6 Aufgabe Gegeben seien zwei offene Intervalle A = n i=1 (m i, n i ) ; B = n i=1 (p i, q i ), man schreibe die Menge A B als Intervall. [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 4
5 Prof. H.C. Grunau E. Sassone Maß- und Integrationstheorie WS 2002/ Aufgabe Man beweise, daß jede unendliche σ Algebra sogar überabzählbar unendlich ist. 3.2 Aufgabe Gegeben sei (A j ) j J eine beliebige Familie von σ-algebren; so ist A = A j ebenfalls eine σ Algebra. j J 3.3 Aufgabe Gegeben seien die Maßräume (X, A, µ k ) k N, ist auch ( k N µ k) ein Maß auf (X, A)? efinition Sei X eine beliebige nichtleere Menge. Wir nennen eine Funktion eine äußeres Maß auf X, falls gilt: 1. µ( ) = 0; 2. stets gilt: M N µ(m) µ(n); 3. stets gilt: µ ( k N M ) k k N µ (M k). µ : P(X) R 3.4 Aufgabe Wir definieren die folgende Abbildung µ : P(R n ) [0, ], so daß µ ( ) = 0 und für M : µ (M) = sup{ x i y i, i = 1,..., n, x, y M}. Ist µ ein äußeres Maß? 3.5 Aufgabe Es sei (µ j ) j J eine Familie von äußeren Maßen über P(X). a) Zeigen Sie: µ(m) = sup{µ j (M); j J} ist ein äußeres Maß. b) Ist ψ(m) = inf{µ j (M); j J} ein äußeres Maß? c) Zeigen Sie: es gibt ein eindeutig bestimmtes äußeres Maß µ mit 1) µ µ j für alle j J. 2) Ist λ ein weiteres äußeres Maß mit λ µ j für alle j J, so folgt λ µ. 5
6 3.6 Aufgabe Nehmen Sie ohne Beweis an, daß es eine offene beschränkte Menge G R n gibt mit G a > 0. iese offene Menge ist also insbesondere nicht Jordan-meßbar. Man beweise: Ist eine beschränkte offene Jordan meßbare Menge mit Ḡ Rn, so ist A = {M : M ist Jordan-meßbar } keine σ Algebra. 3.7 Aufgabe (Lebesguesches Lemma) Man beweise die folgende Behauptung. Sei K R n eine kompakte Menge, (G i ) i I eine offene Überdeckung von K. ann existiert ein λ > 0, so daß man für jedes M K mit diam(m) λ ein i finden kann mit M G i. [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 6
7 Prof. H.C. Grunau E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Sei G = [0, 1]; man schneide das offene Stück der Länge 1/q in der Mitte heraus; man entferne jeweils ein (1/q) 2 langes offenes Stück aus der Mitte der zwei neuen Intervalle. Wenn man unendlich oft dieselbe Prozedur mit offenen Stücken der Länge (1/q) n in allen neuen Intervallen wiederholt, bekommt man die sogenannte Cantormenge. Man beweise, daß die Cantormenge mit q = 3 eine überabzählbare (Lebesguesche) Nullmenge ist. 4.2 Aufgabe Sei C die Cantormenge mit q 4; man beweise daß C = C = ([0, 1] \ C). 4.3 Aufgabe Ist K R n kompakt, so gilt: K ist eine Lebesguesche Nullmenge genau dann, wenn K auch eine Jordansche Nullmenge ist. 4.4 Aufgabe Es sei X eine beliebige Menge, A ein System von Teilmengen von X und m : A [0, ] eine beliebige Funktion. ie Funktion µ : P(X) [0, ] sei definiert durch µ( ) = 0 µ(e) = inf { m(a i ) : A i A, E A i } für E X mit endlichen oder abzählbaren Überdeckungen (A i ) von E und µ(e) = falls es keine abzählbare Überdeckung von E in A gibt. Man beweise, daß µ ein äußeres Maß auf X ist. 4.5 Aufgabe Sei X ein metrischer Raum, A ε = {A X : diam(a) < ε} und m(a) = h(diam(a)) wo h eine stetige monoton wachsende Funktion ist, mit h(0) = 0. Wir wissen nach Aufgabe 4.4, daß A ε ein äußeres Maß µ ε induziert. Wir definieren jetzt µ(e) = lim ε 0+ µ ɛ (E) für E X. Man beweise, daß µ ein äußeres Maß mit der folgenden Eigenschaft ist: µ(a B) = µ(a) + µ(b), falls der Abstand der beiden Mengen A und B größer als Null ist. Sei h(s) = s α (α reell und positiv); wir nennen µ = µ (α) das α-dimensionale Hausdorff-Maß. as eindimensionale Hausdorff-Maß ist also durch µ (1) (E) = lim ε 0 + inf { diam (Ai ) : E A i, diam (A i ) < ε} definiert. Man beweise, daß das eindimensionale Hausdorff-Maß µ (1) für stetig differenzierbare Kurven in R n gerade die Kurvenlänge ist. 7
8 [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 8
9 Prof. H.C. Grunau E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien eine Cantorsche Menge G (für die efinition siehe man die Aufgabe 4.1) und eine beschränkte offene Menge mit Ḡ R; man berechne das Maß von G. Man beweise: A = {M : M ist Jordan-meßbar } ist keine σ Algebra. efinition Gegeben sei eine Menge M, wir definieren eine Relation auf den Elementen von M. Sie wird genau dann eine Äquivalenzrelation genannt, wenn gilt: a) Für jedes a M : a a. b) Für alle a, b M : a b b a c) Für alle a, b, c M mit a b und b c folgt stets a c. Wir nennen [a] = {b M : b a} die Äquivalenzklasse von a, Klasseneinteilung die Einteilung von M in Äquivalenzklassen. M ist paarweise disjunkte Vereinigung dieser Äquivalenzklassen. 5.2 Aufgabe Sei n Z fest. Wir definieren die Äquivalenzrelation Modulo n auf den Elementen von Z so, daß a b genau dann, wenn a b = kn für ein k Z. Man beweise, daß dieses eine Äquivalenzrelation ist. 5.3 Aufgabe Sei die folgende Äquivalenzrelation in R definiert : x y x y Q. ie zugehörigen Klassen sind die Mengen a + Q mit a R, und es ist a + Q = b + Q a b Q. Man wähle aus jeder Klasse einen Vertreter vom Betrag kleiner als 1. Es sei A ( 1, 1) die Menge dieser Vertreter (hier wird das Auswahlaxiom benutzt). In folgenden sind r, s rationale Zahlen. Man zeige: a) (r + A) (s + A) = für r s. b) (r + A) = R. r c) Für die Menge S = (r + A) ist ( 1, 1) S ( 3, 3). r <2 Man zeige, daß A nicht meßbar ist. [Hinweis: Mit Hilfe von a) und c) leite man aus der Meßbarkeit der Mengen r + A einen Widerspruch ab; dabei sind die Fälle λ(a) = 0 und λ(a) > 0 zu unterscheiden.] 9
10 5.4 Aufgabe Es sei µ ein äußeres Maß in R n mit der folgenden Additivitätseigenschaft: µ(a B) = µ(a) + µ(b) falls dist (A, B) > 0, (1) wobei dist (A, B) den Abstand der beiden Mengen bezeichnet. ie Menge A R n wird analog zur Vorlesung µ meßbar genannt, wenn µ(e) = µ(e A) + µ(e c A) für alle E R n. (2) ie µ meßbaren Mengen bilden eine σ Algebra S, auf der µ σ additiv ist. Man beweise die folgenden Sätze: (a) Seien G R n eine offene Menge und G k die Menge aller Punkte x G mit dist (x, c G) > 1 k, k = 1, 2,... Zeigen Sie: Hat µ die Eigenschaft (1), so gilt für jede beliebige Menge E G: µ(e) = lim k µ(e G k). Man kann G k annehmen. Es sei R k = G k+1 \ G k, E k = E G k und F k = E R k. Man zeige nacheinander: dist(g k, c G k+1 ) > 0, dist(r k, c G k+2 ) > 0 also dist(e k, E\E k+1 ) > 0, dist(f k, F k+2 ) dist((f k, E \ E k+2 ) > 0 (falls keine leere Menge auftritt). Aus µ(f k ) = folgt µ(f 2k ) = oder µ(f 2k+1 ) =, und hieraus ergibt sich mit (1), angewandt auf endliche Teilsummen, lim µ(e k ) = µ(e) =. Sind die beiden Summen konvergent, so strebt µ(e \ E k ) 0 und aus µ(e) µ(e k ) + µ(e \ E k ) folgt die Behauptung. (b) Wenn µ die Eigenschaft (1) hat, dann sind alle Borelschen Mengen µ meßbar. Hinweis: Zeigen Sie zunächst, daß Bedingung (2) für offene Mengen erfüllt ist. Natürlich dürfen Sie (a) und frühere Aufgaben verwenden. (c) Folgern Sie daraus, daß das Hausdorff Maß in der Tat ein Maß auf der Borel σ Algebra des R n ist. 5.5 Aufgabe Man definiert die Hausdorff-imension für eine beschränkte Menge M R n : (M) = inf{α : α dimensionales Hausdorffsches Maß von A ist Null } Bestimmen Sie dann die Hausdorff imension von k-dimensionalen Untervektorräumen des R n (geschnitten mit einer beliebigen Kugel). [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 10
11 Prof. H.C. Grunau E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Man beweise, daß jede abgeschlossene Menge H R n eine G δ Menge ist. 6.2 Aufgabe Sei R n meßbar. Seien f : R R stetig und g : R meßbar. Man beweise: f g ist auch meßbar. 6.3 Aufgabe Sei R n meßbar. Seien g, h : R meßbar. Man beweise die Äquivalenz von (a) - (d) von Satz 4.5 für die Funktion h d.h: h ist meßbar genau dann, wenn eine der folgenden gleichwertigen Bedingungen erfüllt ist: (a) Für jedes α R ist {h > α} L() (b) Für jedes α R ist {h α} L() (c) Für jedes α R ist {h < α} L() (d) Für jedes α R ist {h α} L() g +, g n (n N), 1 g ( falls g 0 in ), g h sind meßbar. 6.4 Aufgabe Seien f : E 1 E 2 eine Abbildung, E 1 eine σ Algebra auf E 1. Man zeige, daß {A E 2 : f 1 (A) E 1 } eine σ Algebra ist auf E 2 ist. 6.5 Aufgabe Seien (a k ) k K, K N, die paarweise verschiedenen Werte der Treppenfunktion f, so daß die Mengen k = {x : f(x) = a k } disjunkt sind, und f(x) = a k 1 k. k Man beweise, daß die Treppenfunktion genau dann meßbar ist, wenn alle k meßbar sind. 6.6 Aufgabe Sei R n meßbar. Gegeben seien zwei Funktionen f, g : [, ], meßbar. Man beweise, daß die Menge P = {x : f(x) < g(x)} meßbar ist. [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 11
12 Maß- und Integrationstheorie WS 2002/03 Prof. H. Ch. Grunau, E. Sassone Aufgabe Man beweise, daß die Menge der Punkte, wo eine Folge von reellen, meßbaren Funktionen (punktweise) konvergiert, eine meßbare Menge ist. ie folgenden Aufgaben beziehen sich (noch) auf das (uneigentliche) Riemann Integral und dienen dazu, Ihnen Hilfsmittel für praktische Rechnungen an die Hand zu geben. 7.2 Aufgabe Gegeben sei eine stetige Funktion f : R R, man beweise die folgende Formel für radialsymmetrische Integration: R F (R) := f( x ) dx = ne n r n 1 f(r) dr, x R wobei e n = vol n (B 1 (0)) = B 1 (0) 1 dx ist. 7.3 Aufgabe Berechnen Sie R 2 exp( x 2 y 2 ) d(x, y) und stellen Sie eine Verbindung mit dem (Gaußschen Fehler ) Integral exp( x 2 ) dx her. 7.4 Aufgabe Zeigen Sie, daß für das Volumen der Einheitskugel e n = vol n (B 1 (0)) = B 1 (0) 1 dx gilt: R e n = πn/2 Γ ( n 2 + 1), dabei ist Γ(x) = 0 t x 1 e t dt die Gamma-Funktion. Hinweis: Mittels des Satzes von Fubini und Aufgabe 7.2 können Sie eine Rekursionsformel für e n herleiten. Bei der Bestimmung von Γ ( 1 2) hilft Aufgabe 7.3. Bemerkung. In einer korrekt normierten efinition des α dimensionalen Hausdorffmaßes ist noch der Faktor e α 2 α mit aufzunehmen. ie vorhergehende Aufgabe gibt uns die Möglichkeit, e α für reelles positives α zu betrachten. 0 [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 12
13 Prof. H. Ch. Grunau E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Man benutze die efinition, um das Integral 1 0 xα dx mit α R zu berechnen. 8.2 Aufgabe Man beweise den folgenden Fortsetzungssatz (von Tietze): Jede auf einer abgeschlossenen Menge A R n stetige und reellwertige Funktion g besitzt eine stetige Fortsetzung h auf den ganzen Raum. Hinweise: man nimmt eine Folge von Punkten {a k } n N so daß die Folge dicht in A ist. ann, für x A sei ρ(x, a) = max(2 x a dist(x,a), 0) und man baue die Funktion g(x) falls x A 2 h(x) = k ρ(x,a k )g(a k ) k=1 falls x A 2 k ρ(x,a k ) k=1 8.3 Aufgabe Seien R n, meßbar, λ() <, f : R n R meßbar und ε > 0. Man beweise, daß ein kompaktes K existiert, mit λ(\k) < ε, und eine stetige Funktion f : R n R, sodaß f = f auf K. 8.4 Aufgabe Analog zur Vorlesung formuliere und diskutiere man das Integral auf (N 0, P(N 0 ),Zählmaß). 8.5 Aufgabe Sei R n meßbar, λ() <. Sei f k f punktweise fast überall in. Außerdem existiere ein Zahl M so daß für jedes k gilt: f k (x) M fast überall in. Man zeige, daß lim f h (x)dx = f(x)dx h 13
14 8.6 Aufgabe Man kontrolliere, falls man den lim mit dem Integral wechseln kann: n lim n 0 (1 x n )n e x 2 dx { k lim f k(x) := 2 x(1 kx) falls 0 x 1 k ; n 0 falls x > 1 k. [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 14
15 Prof. H.C. Grunau E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Man beweise den Hilfsatz 5.4: Seien R n eine Lebesgue meßbare Menge und f : R eine beliebige Funktion. Es gebe eine Partition π 0 von, so daß S ( f, π 0 ) <, d.h. (AK) gelte. ann gilt (a) π 2 π 1 π 0 : < S (f, π 1 ) S (f, π 2 ) S (f, π 2 ) S (f, π 1 ) < (b) Sind π 1, π 2 π 0, so ist S (f, π 1 ) S (f, π 2 ) (c) Für alle π π 0 und alle entsprechenden Stützstellenauswahlen gilt: S ( f, π 0 ) S (f, π) σ(f, π, ξ) S (f, π) S ( f, π 0 ) 9.2 Aufgabe Seien R n eine meßbare Menge, f : R eine beliebige Funktion und es gebe eine Partition π 0 von, so daß S ( f, π 0 ) <, d.h. (AK) gelte. Man beweise, daß die efinition von (Lebesgueschem) Ober- und Unterintegral keine Abhängigkeit von der Wahl der Partition π 0 hat. 9.3 Aufgabe Sei f L 1 (). Falls m f n und λ() <, dann existiert ein c, m c n, so daß f(x) dx = c λ(). 9.4 Aufgabe Seien L(R n ), ( k ) k N L(R n ), = k=1 k, k j = falls k j und f L 1 (). Man beweise, daß f auf integrierbar ist genau dann, wenn für alle k f auf k integrierbar ist und k k f dx <. In diesem Falle gilt f(x) dx = k=1 k f(x) dx 15
16 9.5 Aufgabe Sei f L 1 (R n ). Man zeige: (a) Zu jedem ε > 0 gibt es ein K > 0, so daß mit := {x R n : f(x) > K} gilt: f(x) dx ε. (b) Zu jedem ε > 0 gibt es eine beschränkte meßbare Menge R n, so daß f(x) dx ε. R n \ Hinweis: Sie dürfen bereits benutzen, daß jede integrierbare Funktion auch meßbar ist. 9.6 Aufgabe Sei f L 1 (R n ). Man zeige: Zu jedem ε > 0 gibt es ein δ > 0 derart, daß für jede meßbare Menge R n gilt: λ() < δ f(x) dx ε. Hinweis: ie vorhergehende Aufgabe. [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 16
17 Prof. H.C. Grunau, E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Man benutze den Satz von Beppo Levi, um zu beweisen 10.2 Aufgabe Seien 4 lim k 2 7k k(x 2) dx = 2 lim k 7k + 3 k(x 2) dx. k = {(x, y) : x 0, y 0, x 2 + y 2 k} f k = e kx2 k+2 e x2 +(y(k+1)) 2 k 2 Was können wir über lim k k f k (x, y)d(x, y) sagen? 10.3 Aufgabe Sei f : R R so, daß sogar f auf R uneigentlich Riemann-integrierbar ist. Man zeige: ann ist f L 1 (R). Gilt dieselbe Behauptung auch, wenn man nur f als uneigentlich Riemann-integrierbar voraussetzt? 10.4 Aufgabe { 1 falls n x < n + 1, Sei f n (x) = 0 sonst. a) Man finde die Funktion f(x) = lim f n(x). n b) Man beweise, daß lim n R f n(x)dx R f(x)dx. c) Welche Eigenschaft des Satzes von majorisierten Konvergenz von Lebesgue ist nicht erfüllt? 10.5 Aufgabe Sei f : [0, 1] R eine stetige Funktion. Man beweise, daß 1 lim k 0 f(x k )dx = f(0). 17
18 10.6 Aufgabe Sei f L 1 ([a, b]). Man beweise, daß die Integralfunktion F (x) = x a f(t) dt stetig in [a, b] ist. Hinweis: man benutze die Aufgabe Aufgabe Es seien R n meßbar und beschränkt und f k (k N), g : R meßbare Funktionen mit den Eigenschaften: Es gibt eine Konstante C > 0 derart, daß für alle k N gilt: f k (x) 2 dx C. Für fast alle x gilt: lim f k(x) = 0. k as folgende Integral ist endlich: Man zeige, daß dann gilt: g(x) 2 dx <. lim (f k (x) g(x)) dx = 0. k Hinweis: Für beliebiges δ > 0 und a, b R hat man ab δa δ b2. Absolutstetigkeit des Integrals. [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 18
19 Prof. H.C. Grunau, E. Sassone Aufgabe Maß- und Integrationstheorie WS 2002/03 Man beweise den folgenden Satz über die Stetigkeit parameterabhängiger Integrale: Sei G R m offen, R n meßbar und f : G R eine Funktion, so daß gilt: Für fast alle y ist G x f(x, y) stetig. Für alle x G ist y f(x, y) integrierbar. Es gibt eine integrierbare Funktion F L 1 (), so daß für alle (x, y) G gilt: f(x, y) F (y). ann gilt: ist stetig. G x f(x, y) dy 11.2 Aufgabe Man beweise den folgenden Satz über die ifferenzierbarkeit parameterabhängiger Integrale: Sei G R m offen, R n meßbar und f : G R eine Funktion, so daß gilt: Für fast alle y existieren die partiellen Ableitungen G x sind stetig. Für alle x G ist y f(x, y) integrierbar. x j f(x, y) (j = 1,..., m) und Es gibt eine integrierbare Funktion F L 1 (), so daß für alle (x, y) G und alle j = 1,..., m gilt: f(x, y) x j F (y). ann ist G x stetig partiell differenzierbar und es gilt: f(x, y) dy = x j f(x, y) dy x j f(x, y) dy. 19
20 11.3 Aufgabe Gegeben seien eine Funktion f L 1 (R n ), die Abbildung { ϕ(x) = c n e 1 1 x 2 x < 1 0 x 1 wo c n so ist, daß R n ϕ(x)dx = 1, und ein reeller Wert h > 0; man beweise, daß die Abbildung (f) h (x) = 1 h n ϕ R n ( x y in C (R n ) L 1 (R n ) liegt. Hinweis: Parameterabhängige Integrale, Satz von Fubini. h ) f(y)dy 11.4 Aufgabe Man beweise, daß die Gamma-Funktion beliebig oft stetig differenzierbar ist. Γ(x) = 0 t x 1 e t dt 11.5 Aufgabe Gegeben sei eine beliebige positive meßbare Funktion f : R n [0, ]. Man prüfe, daß diese Funktion durch L M µ(m) := f(x) dx auf R n ein bzgl. des Lebesgueschen Maßes λ absolutstetiges Maß µ induziert. Hinweis: Satz von Beppo Levi. Man folgere daraus: as Tragheitmoment eines (meßbaren) Körpers K R 3 bzgl. einer rehachse G kann als Maß interpretiert werden. Hinweis: as Tragheitsmoment eines Körpers K bzgl. einer rehachse G ist Γ = K d2 (x)µ(x)dx, wo d(x) der Abstand zwischen x und G und µ(x) die meßbare ichte des Körpers K ist. M [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 20
21 Prof. H.C. Grunau E. Sassone Maß- und Integrationstheorie WS 2002/03 Termin für die Scheinklausur: , 9-11 Uhr, Gebäude 2, Raum Aufgabe Seien f, g : R n R meßbar. Man zeige daß auch die Faltung in R 2n meßbar ist. Hinweis: Transformationsformel in R 2n Aufgabe (x, y) f(x y)g(y) Gegeben seien das Lebesguesche Maß λ auf R n, die Menge B = {x R n : x 1} und die Abbildung µ : L(R n ) [0, ], so daß für jedes M L gilt: µ(m) = λ(m B). Ist µ ein Maß? arf man den Satz von Radon-Nikodym benutzen? Falls ja, welches ist die Funktion f, so daß µ(m) = M f(x)dx? 12.3 Aufgabe Gegeben sei die Funktion h(x, y, z) = { 1 x 2 y 4 falls (x, y, z) B 1 (0), 0 falls (x, y, z) B 1 (0). Kann man das Integral nur bezüglich x auf dem ganzen Gebiet R als reelle Zahl berechnen? und bezüglich z? Kann man das Integral G() = h(x, y, z)d(x, y, z) für jede Menge L(R3 ) (wiederum als reelle Zahl) berechnen? 12.4 Aufgabe Gegeben sei die Abbildung G : L(R 3 ) [0, ], definiert wie oben. a) Ist G ein Maß? b) Kann man den Satz von Radon-Nikodym benutzen? Falls ja, finde man auch die erzeugende Funktion! 21
22 12.5 Aufgabe Gegeben seien das Gebiet G = {(x, y, z) : 3 < x < 3, 3 x 2 y 3} und die Funktion f(x, y, z) = man berechne das Integral mit der Transformationsformel in R 3. y xz 2, 12.6 Aufgabe Man berechne das Integral x 2 +y 2 π 2 cos(x 2 + y 2 )d(x, y) Aufgabe Sei B = B 1 (0) R 3 die Kugel vom Radius 1 mit Zentrum in dem Nullpunkt. Seien f L 1 (B), = (0, 1) (0, π) (0, 2π), φ : R 3, φ(r, θ, ψ) = Man bestimme das Bild φ(). Man beweise, daß (f φ)(r, θ, ψ)r 2 sin(θ) d(r, θ, ψ) = r sin(θ) cos(ψ) r sin(θ) sin(ψ) r cos(θ) B. f(x, y, z) d(x, y, z). [ ie mit gekennzeichneten Aufgaben sind Hausaufgaben. ie Lösungen geben Sie bitte am in der Vorlesung ab.] 22
23 Prof. H.C. Grunau, E. Sassone Maß- und Integrationstheorie WS 2002/03 Klausur, , Ohne Hilfsmittel Jede Aufgabe wird mit 5 Punkten bewertet. Ab 14 erreichten Punkten betrachten wir die Teilnahme an dieser Klausur als erfolgreich. Viel Erfolg! 1 Aufgabe Gegeben seien die Menge A = [0, 1] und die Familie A = {B A : B = oder B ist endliche Vereinigung von Intervallen mit rationalen Endpunkten }. Man beweise, daß A eine Algebra, aber keine σ Algebra ist. 2 Aufgabe Ist die Funktion f : R n R, f(x) = n x=1 x i auf R n messbar? Und integrierbar? 3 Aufgabe Man formuliere die Sätze von Beppo Levi und Lebesgue. 4 Aufgabe { x falls x 2 + y 2 1 Gegeben sei die Funktion f : R 2 R, f(x, y) = (x 2 +y 2 ) falls x 2 + y 2 < 1, Man entscheide begründet, für welche y das Integral R f(x, y)dx existiert. In diesem Fall berechne man es. 5 Aufgabe Gegeben sei die Funktion f(x, y) = {(x, y) : x 0, 1 (x 2 + y 2 ) e}. x (x 2 +y 2 ) 5 2, man berechne das Integral von f auf dem Gebiet G = 6 Aufgabe Gegeben sei die Folge von Funktionen { f k (x) = x k+5 2k+( 1) k + 5x, falls 0 < x < 10, x N, ( 1) k k, falls x [0, 10] N. 10 Kann man lim k 0 f k (x) dx berechnen? Welchen Wert erhält man? 23
24 7 Aufgabe Sei R n messbar, es seien f k : R messbar. ie Folge sei monoton wachsend: f k+1 (x) f k (x); f(x) := lim k f k (x). Außerdem sei f 1 L 1 (). ann gilt: f(x) dx = oder f(x) dx = lim f k (x) dx. k 24
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
2 Allgemeine Integrationstheorie
 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
Musterlösung Analysis 3 - Maßtherorie
 Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Wintersemester 2013/2014 Prof. Dr. Benjamin Schlein Inhaltsverzeichnis 1 Masstheorie 2 1.1 σ-algebren.................................. 6 1.2 Masse.....................................
Skript zur Vorlesung Analysis 3 Wintersemester 2013/2014 Prof. Dr. Benjamin Schlein Inhaltsverzeichnis 1 Masstheorie 2 1.1 σ-algebren.................................. 6 1.2 Masse.....................................
9. Übung zur Maß- und Integrationstheorie, Lösungsskizze Aufgaben
 9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
Analysis 2. Vorlesungsausarbeitung zum SS von Prof. Dr. Klaus Fritzsche. Inhaltsverzeichnis
 Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
ANALYSIS 3. Carsten Schütt WS 2008/9
 1. Es sei f : R 3 R 3 durch f 1 (r, φ 1,φ 2 ) = r cos φ 1 f 2 (r, φ 1,φ 2 ) = r sin φ 1 cos φ 2 f 3 (r, φ 1,φ 2 ) = r sin φ 1 sin φ 2 gegeben. Für welche (r, φ 1,φ 2 ) ist f lokal invertierbar? Ist f global
1. Es sei f : R 3 R 3 durch f 1 (r, φ 1,φ 2 ) = r cos φ 1 f 2 (r, φ 1,φ 2 ) = r sin φ 1 cos φ 2 f 3 (r, φ 1,φ 2 ) = r sin φ 1 sin φ 2 gegeben. Für welche (r, φ 1,φ 2 ) ist f lokal invertierbar? Ist f global
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit
 2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
Serie 2 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
Lebesgue-Integral und L p -Räume
 Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
2. Integration. {x : f(x) <a+ 1 n }
 9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
3. Übungsblatt - Lösungsskizzen. so, dass f tatsächlich eine Wahrscheinlichkeitsdichte
 Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Liste wichtiger Stammfunktionen
 Liste wichtiger Stammfunktionen Funktion Stammfunktion x n, x ln(x) n R \ { } n + xn+ ln( x ) x ln(x) x a x, a > sin(x) cos(x) sin 2 (x) cos 2 (x) x 2 x 2 a x ln(a) cos(x) sin(x) (x sin(x) cos(x)) 2 (x
Liste wichtiger Stammfunktionen Funktion Stammfunktion x n, x ln(x) n R \ { } n + xn+ ln( x ) x ln(x) x a x, a > sin(x) cos(x) sin 2 (x) cos 2 (x) x 2 x 2 a x ln(a) cos(x) sin(x) (x sin(x) cos(x)) 2 (x
Analysis 3. Weihnachtsblatt Prof. Dr. H. Koch Dr. F. Gmeineder Besprechung: TBC, Januar Aufgabe 1: (Besonders prüfungsrelevant)
 Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
1 Verbandstheorie. Aufgabensammlung. Höhere Mathematik für Physiker III Wintersemester 2014
 Aufgabensammlung Höhere Mathematik für Physiker III Wintersemester 2014 1 Verbandstheorie 1. Aufgabe: (a) Sei f C(R) eine stetige Funktion. Wenn Rf(x)φ(x)dx = 0 für alle Testfunktionen φ Cc (R) gilt, dann
Aufgabensammlung Höhere Mathematik für Physiker III Wintersemester 2014 1 Verbandstheorie 1. Aufgabe: (a) Sei f C(R) eine stetige Funktion. Wenn Rf(x)φ(x)dx = 0 für alle Testfunktionen φ Cc (R) gilt, dann
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Symmetrische Ableitungen von Massen
 Symmetrische Ableitungen von Massen Hyuksung Kwon 5. Juni 203 Inhaltsverzeichnis Einführung 2 Hardy-Littlewood Maximaloperator 2 3 Symmetrische Ableitung vom positiven Maß 7 Einführung Definition. (Borelmaß
Symmetrische Ableitungen von Massen Hyuksung Kwon 5. Juni 203 Inhaltsverzeichnis Einführung 2 Hardy-Littlewood Maximaloperator 2 3 Symmetrische Ableitung vom positiven Maß 7 Einführung Definition. (Borelmaß
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
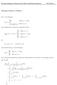 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Vorlesung Der Satz von Fubini. 6.2 Der Satz von Beppo Levi 6.1. DER SATZ VON FUBINI 33
 6.1. DER SATZ VON FUBINI 33 Vorlesung 6 6.1 Der Satz von Fubini Das Lebesgue-Integralkann natürlichauchüber mehrdimensionale Gebiete definiert werden. Wir haben uns hier auf den eindimenionalen Fallbeschränkt.
6.1. DER SATZ VON FUBINI 33 Vorlesung 6 6.1 Der Satz von Fubini Das Lebesgue-Integralkann natürlichauchüber mehrdimensionale Gebiete definiert werden. Wir haben uns hier auf den eindimenionalen Fallbeschränkt.
Rückblick auf die letzte Vorlesung
 Rückblick auf die letzte Vorlesung 1. Integration (Fortsetzung) 2. Existenz von Integralen auf Quadern und allgemeineren Mengen 3. Satz von Fubini 4. Berechnung von Integralen 5. Volumina 6. Normalgebiete
Rückblick auf die letzte Vorlesung 1. Integration (Fortsetzung) 2. Existenz von Integralen auf Quadern und allgemeineren Mengen 3. Satz von Fubini 4. Berechnung von Integralen 5. Volumina 6. Normalgebiete
Zusammenfassung Analysis 2
 Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
Integration (handgestrickt)
 Integration (handgestrickt) C c (R n ) :={f : R n R; f stetig, Träger(f) beschränkt}. B + b (Rn ) := { f : R n R; abei bedeutet f m konvergiert. J (R n ) := {f; a) f beschränkt, b) Träger(f) beschränkt,
Integration (handgestrickt) C c (R n ) :={f : R n R; f stetig, Träger(f) beschränkt}. B + b (Rn ) := { f : R n R; abei bedeutet f m konvergiert. J (R n ) := {f; a) f beschränkt, b) Träger(f) beschränkt,
1 Endlich additive Volumen auf R n
 Endlich additive Volumen auf R n In Satz. im Skript haben wir gezeigt, dass kein σ-additives Volumen auf der Potenzmenge P (R n ) definiert werden kann. Man könnte sich vorstellen, das Problem ist aus
Endlich additive Volumen auf R n In Satz. im Skript haben wir gezeigt, dass kein σ-additives Volumen auf der Potenzmenge P (R n ) definiert werden kann. Man könnte sich vorstellen, das Problem ist aus
Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie
 Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Analysis III - Bachelorversion
 Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
1 Das Lebesgue-Maß. 1.1 Etwas Maßtheorie. Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}.
 1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
3 Das n-dimensionale Integral
 3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Mathematik III für Physiker
 Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Berechnen Sie Mathematik III für Physiker WS 2002/03 1 0 1 y 2 0 1 0 1 1 x 2 dx 1 (1 x 2 )(1 y 2 ) dxdy 1.2 Aufgabe Gegeben sei das Gebiet D = {(x,
Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Berechnen Sie Mathematik III für Physiker WS 2002/03 1 0 1 y 2 0 1 0 1 1 x 2 dx 1 (1 x 2 )(1 y 2 ) dxdy 1.2 Aufgabe Gegeben sei das Gebiet D = {(x,
Klausur zu Maß- und Integrationstheorie
 Mathematisches Institut Universität Leipzig Prof. Dr. Bernd Kirchheim WS 2017/18 6.Februar 2018 Klausur zu Maß- und Integrationstheorie Erlaubte Hilfsmittel: Schreibmaterialien (ohne Kommunikations- oder
Mathematisches Institut Universität Leipzig Prof. Dr. Bernd Kirchheim WS 2017/18 6.Februar 2018 Klausur zu Maß- und Integrationstheorie Erlaubte Hilfsmittel: Schreibmaterialien (ohne Kommunikations- oder
Analysis III. Vorlesungsskriptum WS 2006/07. Fakultät für Mathematik, Ruhr-Universität Bochum
 Analysis III Vorlesungsskriptum WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel IX. Integralrechnung mehrerer Veränderlicher 5 IX.1. Nullmengen 5 IX.2.
Analysis III Vorlesungsskriptum WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel IX. Integralrechnung mehrerer Veränderlicher 5 IX.1. Nullmengen 5 IX.2.
Hausdorff-Maß und Hausdorff-Dimension. Jens Krüger
 Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Konversatorium zu Lineare Algebra und Analysis Analysis - Übungsbeispiele
 Univ.-Prof. Dr. Radu Ioan Boţ, Axel Böhm Konversatorium zu Lineare Algebra und Analysis Analysis - Übungsbeispiele SS18 A1. Sei f : [, + ) R so, dass und dass ein M existiert mit Zeigen Sie, dass f(s +
Univ.-Prof. Dr. Radu Ioan Boţ, Axel Böhm Konversatorium zu Lineare Algebra und Analysis Analysis - Übungsbeispiele SS18 A1. Sei f : [, + ) R so, dass und dass ein M existiert mit Zeigen Sie, dass f(s +
Studienbegleitende Prüfung Stochastik 2
 Universität Karlsruhe (TH) Institut für Stochastik Prof. Dr. N. Bäuerle Name: Vorname: Matr.-Nr.: Studienbegleitende Prüfung Stochastik 2 27. März 2007 Diese Klausur hat bestanden, wer mindestens 20 Punkte
Universität Karlsruhe (TH) Institut für Stochastik Prof. Dr. N. Bäuerle Name: Vorname: Matr.-Nr.: Studienbegleitende Prüfung Stochastik 2 27. März 2007 Diese Klausur hat bestanden, wer mindestens 20 Punkte
Klausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 003/004 Universität Karlsruhe 05. 04. 004 Prof. Dr. G. Last Klausur zur Vorlesung Stochastik II Dauer: 90 Minuten Name: Vorname: Matrikelnummer: Diese Klausur hat
Institut für Mathematische Stochastik WS 003/004 Universität Karlsruhe 05. 04. 004 Prof. Dr. G. Last Klausur zur Vorlesung Stochastik II Dauer: 90 Minuten Name: Vorname: Matrikelnummer: Diese Klausur hat
(y ) 2 0 bis t, so erhalten wir 1 y (t) (t t 0). L sen wir diese Ungleichung nun nach y (t) auf, so folgt
 0.. Lösung der Aufgabe. Wir nehmen an, es existiere eine nicht-triviale globale L sung y. Dann lesen wir direkt von der Gleichung ab, dass y 0 gilt auf ganz R, das heisst, die Funktion ist konvex. Da wir
0.. Lösung der Aufgabe. Wir nehmen an, es existiere eine nicht-triviale globale L sung y. Dann lesen wir direkt von der Gleichung ab, dass y 0 gilt auf ganz R, das heisst, die Funktion ist konvex. Da wir
Lemma (Eigenschaften elementarer Mengen) 1. Jede elementare Menge lässt sich als disjunkte Vereinigung halboffener Intervalle schreiben.
 12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
Existenz des Lebesgue-Borel-Maßes
 A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
Integration über allgemeine Integrationsbereiche.
 Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
Kapitel I. Maßtheorie
 Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
Skript zur Vorlesung. Maßtheorie WS 2017/2018. Peter Junghanns
 Skript zur Vorlesung Maßtheorie WS 2017/2018 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Gerüst zu den Inhalten der Vorlesung dar. Die Vorlesung selbst bietet weiterführende rläuterungen,
Skript zur Vorlesung Maßtheorie WS 2017/2018 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Gerüst zu den Inhalten der Vorlesung dar. Die Vorlesung selbst bietet weiterführende rläuterungen,
Lösungsvorschlag zu den Hausaufgaben der 3. Übung
 FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
Formelsammlung Analysis I & II
 Formelsammlung Analysis I & II Wichtige eindimensionale Integrale: { x s dx = s+ xs+ + C falls s log x + C falls s = exp(x dx = exp(x + C cos(x dx = sin(x + C sin(x dx = cos(x + C sinh(x dx = cosh(x +
Formelsammlung Analysis I & II Wichtige eindimensionale Integrale: { x s dx = s+ xs+ + C falls s log x + C falls s = exp(x dx = exp(x + C cos(x dx = sin(x + C sin(x dx = cos(x + C sinh(x dx = cosh(x +
Kapitel 8 Absolutstetige Verteilungen
 Kapitel 8 Absolutstetige Verteilungen Vorlesung Wahrscheinlichkeitsrechnung I vom 27. Mai 2009 Lehrstuhl für Angewandte Mathematik FAU 8. Absolutstetige Verteilungen Charakterisierung von Verteilungen
Kapitel 8 Absolutstetige Verteilungen Vorlesung Wahrscheinlichkeitsrechnung I vom 27. Mai 2009 Lehrstuhl für Angewandte Mathematik FAU 8. Absolutstetige Verteilungen Charakterisierung von Verteilungen
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
Nachklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
Skript zur Vorlesung. Mass und Integral. Urs Lang. Sommersemester 2005 ETH Zürich
 Skript zur Vorlesung Mass und Integral Urs Lang Sommersemester 2005 ETH Zürich Version vom 12. September 2006 Literatur [Rudin] W. Rudin, Real and Complex Analysis, Third Edition. McGraw-Hill Book Co.,
Skript zur Vorlesung Mass und Integral Urs Lang Sommersemester 2005 ETH Zürich Version vom 12. September 2006 Literatur [Rudin] W. Rudin, Real and Complex Analysis, Third Edition. McGraw-Hill Book Co.,
Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung. Lösungen zur Probeklausur 2.
 Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
6 Räume integrierbarer Funktionen
 $Id: L.tex,v 1.5 2012/01/19 15:07:43 hk Ex $ $Id: green.tex,v 1.3 2012/01/19 15:18:26 hk Ex hk $ 6 Räume integrierbarer Funktionen In der letzten Sitzung hatten wir die sogenannte L -Norm ( 1/ f := f(x)
$Id: L.tex,v 1.5 2012/01/19 15:07:43 hk Ex $ $Id: green.tex,v 1.3 2012/01/19 15:18:26 hk Ex hk $ 6 Räume integrierbarer Funktionen In der letzten Sitzung hatten wir die sogenannte L -Norm ( 1/ f := f(x)
Maße und Integrale. begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller. Berlin, den 26.
 Maße und Integrale begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller Berlin, den 26. April 2008 Inhaltsverzeichnis 1 Konstruktion von Maßen 3 2 Konstruktion von Integralen
Maße und Integrale begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller Berlin, den 26. April 2008 Inhaltsverzeichnis 1 Konstruktion von Maßen 3 2 Konstruktion von Integralen
Lösungen zur Klausur zur Analysis 1, WiSe 2016/17
 BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
Maß- und Integrationstheorie
 Maß- und Integrationstheorie Manuskript zur Vorlesung in SS26 Bálint Farkas farkas@mathematik.tu-darmstadt.de Inhaltsverzeichnis Einführung...................................................................
Maß- und Integrationstheorie Manuskript zur Vorlesung in SS26 Bálint Farkas farkas@mathematik.tu-darmstadt.de Inhaltsverzeichnis Einführung...................................................................
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
{ Anzahl Elemente in A wenn endlich, sonst,
 Analysis 3, Woche 3 Maße II 3.1 Äußeres Maß Man könnte hoffen, nachdem man durch die Erweiterung von X, A, µ zu X, A, µ einen vollständigen Maßraum konstruiert hat, dass auch alle Mengen messbar sein sollten.
Analysis 3, Woche 3 Maße II 3.1 Äußeres Maß Man könnte hoffen, nachdem man durch die Erweiterung von X, A, µ zu X, A, µ einen vollständigen Maßraum konstruiert hat, dass auch alle Mengen messbar sein sollten.
10 Der Satz von Radon-Nikodym
 uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
Klausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 24/25 Universität Karlsruhe 7. März 25 Priv-Doz. Dr. D. Kadelka Klausur zur Vorlesung Stochastik II Dauer: 9 Minuten Name: Vorname: Matrikelnummer: Diese Klausur
Institut für Mathematische Stochastik WS 24/25 Universität Karlsruhe 7. März 25 Priv-Doz. Dr. D. Kadelka Klausur zur Vorlesung Stochastik II Dauer: 9 Minuten Name: Vorname: Matrikelnummer: Diese Klausur
Serie 5 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
Das Lebesgue-Integral
 Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Kapitel 19. Das Lebesgue Maß σ Algebren und Maße
 Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Analysis III Wintersemester 2003/2004. W. Ebeling
 Analysis III Wintersemester 2003/2004 W. Ebeling 1 c Wolfgang Ebeling Institut für Algebraische Geometrie Leibniz Universität Hannover Postfach 6009 30060 Hannover E-mail: ebeling@math.uni-hannover.de
Analysis III Wintersemester 2003/2004 W. Ebeling 1 c Wolfgang Ebeling Institut für Algebraische Geometrie Leibniz Universität Hannover Postfach 6009 30060 Hannover E-mail: ebeling@math.uni-hannover.de
Darstellungssatz von Riesz in vollständig regulären Räumen. Carina Pöll Wintersemester 2012
 Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Maß- und Integrationstheorie
 Prof. Dr. László Székelyhidi Maß- und Integrationstheorie Vorlesungsskript WS2013/14 4. Februar 2014 Inhaltsverzeichnis 1 Maße und σ-algebren.......................................... 1 1.1 Einführung:
Prof. Dr. László Székelyhidi Maß- und Integrationstheorie Vorlesungsskript WS2013/14 4. Februar 2014 Inhaltsverzeichnis 1 Maße und σ-algebren.......................................... 1 1.1 Einführung:
Bálint Farkas. Analysis 3. Skript zur Vorlesung in WS2014/ Mai c by B. Farkas. compiled: 21-May-2015/11:13
 Bálint Farkas Analysis 3 Skript zur Vorlesung in WS2014/2015 21. Mai 2015 c by B. Farkas V O R B E M E R K U N G E N Dieses Skript beinhaltet das Material der Vorlesung Analysis 3 gehalten an der Bergischen
Bálint Farkas Analysis 3 Skript zur Vorlesung in WS2014/2015 21. Mai 2015 c by B. Farkas V O R B E M E R K U N G E N Dieses Skript beinhaltet das Material der Vorlesung Analysis 3 gehalten an der Bergischen
Kapitel 1. Übung 1. Bestimmen Sie die Mengen: [ n 0, 1 ) [0,r)
 Kapitel 1 Übungen Übung 1. Bestimmen Sie die Mengen: [ 1.,1 1 ] n 2. 3. 4. 5. n N n N [, 1 n r Q (,1 n N n N [,r [ 1 n+1, 1 n [ 1 n,1+ 1 n Übung 2. Sei X eine Menge und (A i i I eine abzählbare Partition
Kapitel 1 Übungen Übung 1. Bestimmen Sie die Mengen: [ 1.,1 1 ] n 2. 3. 4. 5. n N n N [, 1 n r Q (,1 n N n N [,r [ 1 n+1, 1 n [ 1 n,1+ 1 n Übung 2. Sei X eine Menge und (A i i I eine abzählbare Partition
Das mehrdimensionale Riemann-Integral. 1. Volumenintegrale
 Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Funktionalanalysis und Integrationstheorie
 Funktionalanalysis und Integrationstheorie Vorlesungsnotizen Johannes Kepler Universität Linz Technisch-Naturwissenschaftliche Fakultät Institut für Analysis Prof. Dr. Aicke Hinrichs Wintersemester 2015/16
Funktionalanalysis und Integrationstheorie Vorlesungsnotizen Johannes Kepler Universität Linz Technisch-Naturwissenschaftliche Fakultät Institut für Analysis Prof. Dr. Aicke Hinrichs Wintersemester 2015/16
Die Topologie von R, C und R n
 Die Topologie von R, C und R n Für R haben wir bereits eine Reihe von Strukturen kennengelernt: eine algebraische Struktur (Körper), eine Ordnungsstruktur und eine metrische Struktur (Absolutbetrag, Abstand).
Die Topologie von R, C und R n Für R haben wir bereits eine Reihe von Strukturen kennengelernt: eine algebraische Struktur (Körper), eine Ordnungsstruktur und eine metrische Struktur (Absolutbetrag, Abstand).
L 2 -Theorie und Plancherel-Theorem
 L -Theorie und Plancherel-Theorem Seminar Grundideen der Harmonischen Analysis bei Porf Dr Michael Struwe HS 007 Vortrag von Manuela Dübendorfer 1 Wiederholung aus der L 1 -Theorie Um die Fourier-Transformation
L -Theorie und Plancherel-Theorem Seminar Grundideen der Harmonischen Analysis bei Porf Dr Michael Struwe HS 007 Vortrag von Manuela Dübendorfer 1 Wiederholung aus der L 1 -Theorie Um die Fourier-Transformation
Analysis I - Stetige Funktionen
 Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Maßtheorie. Skript zur Vorlesung von Prof. Dr. Michael Kohler. Sommersemester 2005 und Wintersemester 2005/2006
 Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Probeklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 21717 Fakultät 4 - Mathematik und Naturwissenschaften Prof N V Shcherbina Dr T P Pawlaschyk wwwkanauni-wuppertalde Probeklausur zur Analysis 2, SoSe 217 Hinweis Die Lösungen
BERGISCHE UNIVERSITÄT WUPPERTAL 21717 Fakultät 4 - Mathematik und Naturwissenschaften Prof N V Shcherbina Dr T P Pawlaschyk wwwkanauni-wuppertalde Probeklausur zur Analysis 2, SoSe 217 Hinweis Die Lösungen
Definitionen und Aussagen zur Maßtheorie
 Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
12 Biholomorphe Abbildungen
 12 Biholomorphe Abbildungen 2 Funktionenräume Wir erinnern zunächst an den Weierstraßschen Konvergenzsatz : 2.1 Satz. Sei G C ein Gebiet, (f n ) eine Folge holomorpher Funktionen auf G, die auf G kompakt
12 Biholomorphe Abbildungen 2 Funktionenräume Wir erinnern zunächst an den Weierstraßschen Konvergenzsatz : 2.1 Satz. Sei G C ein Gebiet, (f n ) eine Folge holomorpher Funktionen auf G, die auf G kompakt
Lösungsvorschlag Klausur MA9802
 Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Merkblatt zur Funktionalanalysis
 Merkblatt zur Funktionalanalysis Literatur: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Merkblatt zur Funktionalanalysis Literatur: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Mehrdimensionale Integration
 Kapitel C Mehrdimensionale Integration h s r h h r h r Inhalt dieses Kapitels C000 1 Der Satz von Fubini 3 Aufgaben und Anwendungen 1 Vertauschen von Integral und Reihe Mehrdimensionale Integration #Der
Kapitel C Mehrdimensionale Integration h s r h h r h r Inhalt dieses Kapitels C000 1 Der Satz von Fubini 3 Aufgaben und Anwendungen 1 Vertauschen von Integral und Reihe Mehrdimensionale Integration #Der
Analysis III. Walter Bergweiler. Wintersemester 2013/14 Fassung vom 3. Februar 2014
 Analysis III Walter Bergweiler Wintersemester 2013/14 Fassung vom 3. Februar 2014 Inhaltsverzeichnis I Das Lebesgue-Integral 1 1 Treppenfunktionen und Hüllreihen................ 1 2 Definition und Eigenschaften
Analysis III Walter Bergweiler Wintersemester 2013/14 Fassung vom 3. Februar 2014 Inhaltsverzeichnis I Das Lebesgue-Integral 1 1 Treppenfunktionen und Hüllreihen................ 1 2 Definition und Eigenschaften
1. Masstheorie Mengensysteme 1. MASSTHEORIE 1
 1. MASSTHEORIE 1 1. Masstheorie In der Wahrscheinlichkeitstheorie betrachten wir Situationen, die wir nicht exakt vorhersagen können. Zum einen kann dies sein, da der Ausgang zufällig ist. Zum anderen
1. MASSTHEORIE 1 1. Masstheorie In der Wahrscheinlichkeitstheorie betrachten wir Situationen, die wir nicht exakt vorhersagen können. Zum einen kann dies sein, da der Ausgang zufällig ist. Zum anderen
