Zentralprojektion im virtuellen Raum eine Einführung mit Cabri 3D
|
|
|
- Jutta Pfaff
- vor 7 Jahren
- Abrufe
Transkript
1 Heinz Schumann Zentralprojektion im virtuellen Raum eine Einführung mit Cabri 3D 1. Einleitung Traditionelle Aufgabe der darstellenden Geometrie ist die Entwicklung und Anwendung zweckgebundener Abbildungsverfahren des Raumes auf die Ebene. Neben dem Informationsverlust, den die Verebnung räumlicher Konfigurationen mit sich bringt, konkurrieren zwei wesentliche Forderungen: die Anschaulichkeit und die Maßtreue der betreffende Abbildungen. Die Anschaulichkeit kann man so beschreiben: ein Betrachter der Abbildung der räumlichen Konfiguration soll deutlich erkennen, was sie räumlich darstellt. Während von einer maßtreuen Abbildung auf Kosten der Anschaulichkeit die wahren Abmessungen bzw. Maßverhältnisse abgelesen werden können. Abbildungsverfahren wie die der Zentralprojektion (auch Zentralperspektive genannt), die das einäugige Sehen, das Fotografieren und den von einer punktförmigen Lichtquelle, z. B. einer Glühbirne, hervorgerufenen Schattenwurf modellieren, vermitteln einen anschaulichen Raumeindruck. Aus den zentralprojektiven Abbildungen sind aber im allgemeinen nur auf komplizierte Weise die wahren Maße der abgebildeten räumlichen Objekte rekonstruierbar. Die Kugel kann beispielsweise auf die Ebene durch stereografische Projektion, die eine besondere Zentralprojektion ist, nur winkeltreu abgebildet werden. Aus parallelprojetiven Abbildern lassen sich auf einfache Weise die (maßstäblichen) Abmessungen der räumlichen Objekte ermitteln. Die Anwendung der Zentralprojektion ist das Metier von Künstlern, Grafikern und Architekten. Parallelprojektive Bilder finden bei vielen Produktplanungen, -herstellungen und -darstellungen Verwendung. Im folgenden nutzen wir die durch das computergrafische Werkzeug Cabri 3D in der Version 1.0 gegebenen interaktiven Möglichkeiten der raumgeometrischen Konstruktion, Visualisierung und Variation (vgl. Schumann 2005a/d), um auf neue Weise in die Zentralprojektion einzuführen. Im Gegensatz zur bisherigen zweidimensionalen Behandlung der Zentralprojektion können wir im virtuellen Raum sowohl die abzubildenden räumlichen Objekte als auch ihre zentralprojektiven Abbilder konstruieren. Wir arbeiten dabei in einer natürlichen Zentralprojektion des systeminternen dreidimensionalen geometrischen Raummodells auf die Bildschirmebene und entwickeln in dieser Art des virtuellen Raumes, der entsprechende räumliche Wahrnehmungsqualität hat, die Zentralprojektion als Abbildungsverfahren. Um in die Zentralprojektion einzuführen, benutzen wir also die im System implementierte Zentralprojektion. So können wir auch die anderen unter der Oberfläche des Systems versteckten Methoden der Darstellenden Geometrie, die optional verwendet werden können, verstehen lernen. 2. Zentralprojektion im virtuellen Raum Im folgenden skizzieren wir einen Einführungskurs in die Zentralprojektion, in dem wir nur relativ einfache geometrische Kenntnisse voraussetzen und den Sachverhalt durch entsprechende Abbildungen illustrieren. 2.1 Zur Begriffsbildung der Zentralprojektion Die Objekte einer Ebene (Originalebene) können auf eine zweite Ebene (Bildebene), die mit der ersteren eine Gerade (Achse) gemein hat, wie folgt abgebildet werden (Abb. 1): Der Durchstoßpunkt der Verbindungsgeraden durch einen festgewählten
2 26 Punkt Z (Zentrum), der nicht in beiden Ebenen liegt, und dem Originalpunkt mit der Bildebene ist der Bildpunkt. Die Abbildung bildet die Originalebene auf die Bildebene umkehrbar eindeutig ab. Eine solche Abbildung ist die Zentralprojektion der Originalebene auf die Bildebene. Sie ist geradentreu und lässt das Doppelverhältnis: DV(P, Q, R, S) = ( PR : PS ) : ( QR : QS ) invariant. Die Achse ist Fixpunktgerade. Solche Abbildungen werden auch perspektive Kollineationen (perspektive geradentreue Abbildungen) genannt. Die Bilder von Kegelschnitten sind Kegelschnitte und umgekehrt, haben Kegelschnitte als Originale wiederum Kegelschnitte (Kegelschnittstreue der Abbildung). Falls die Bildebene und die Originalebene parallel sind, so liegt eine zentrische Streckung mit dem Zentrum Z vor. Wandert das Zentrum Z etwa lotrecht zur Bildebeben in s Unendliche, d. h. Z wird zu einem unendlich fernen Punkt, so geht die Zentralprojektion in eine Parallelprojektion beider Ebenen aufeinander über. Abb. 1 Erweitert man den Definitionsbereich der Abbildung auf den Raum, so erhalten wir eine Zentralprojektion des Raumes auf eine Ebene (Abb. 2). Alle dreidimensionalen Objekte haben zweidimensionale Bilder; entsprechend ist der Informationsverlust! Derartige Abbildungen dreidimensionaler Objekte sind uns auch als Schattenbilder aus dem Alltag bekannt, die modellhaft durch eine punktförmige Lichtquelle Z erzeugt werden (Abb. 3, Schattenbild eines Kantenwürfels; wenn die Position von Z variiert wird, so verändert sich auch der Schatten; die Standebene ist zugleich die Bildebene). Die Abbildung 4 zeigt das Schattenbild eines Würfel-Flächenmodells. Bei der Konstruktion des Schatten und der unbeleuchteten Seitenflächen sind bei Variation der Lage von Z entsprechende Fallunterscheidungen zu treffen.
3 27 Abb. 2 Abb. 3 Abb. 4 Bezüglich eines auf einer Grundebene stehenden Objekts, hier eines stilisiertes Haus mit Satteldach, kann das Zentrum Z zusammen mit der Bildebene beliebig bewegt werden; die Bildebene ist dabei Tangentialebene an eine Kugel, die das Objekt umschließt (Abb. 5, mit Durchstoßpunkten der Sehstrahlen in der schrffierten Bildebene für die Konstruktion des zentralprojektiven Bildes). Variiert man die Position von Z bzw. die der Bildebene, so verändert sich das zentralperspektive Bild (Abb. 6-8 mit transparenter Bildebene). Man könnte auch so konstruieren, dass das Zentrum und die Bildebene fest bleibt und das Objekt mit einer es umschließenden Kugel beliebig bewegt wird, indem man die Kugel entsprechend rotiert. Das kommt einer Simulation des Virtual Sphere Device gleich.
4 28 Abb. 5 Abb. 6 Abb. 7 Abb. 8 In der Geschichte der Zentralprojektion wurde aber die Lagebeziehung von Standebene, Bildebene und Zentrum zur sogenannten Malerperspektive kanonisiert, wie wir der skizzenhaften Kopie eines Stichs von Albrecht Dürer entnehmen (Abb. 9, ein Glastafelverfahren von Dürer: Der Zeichner der Kanne, Dresdner Skizzenbuch 1525): Die Bildebene steht senkrecht auf der nicht eingezeichneten Gegenstandsebene. Ein Bildpunkt P des Objekts wird quasi als Durchstoßpunkt auf der Glastafel markiert, indem der Zeichner den Originalpunkt mittels einer gespannten Schnur anpeilt, die im Zentrum Z befestigt ist. Abb. 9
5 29 Abb. 10 In Abbildung 10 sind die heute üblichen Bezeichnungen des zentralprojektiven Abbildungsapparates zu sehen. Die Bildebene steht senkrecht zur Standebene und schneidet diese in der Achse a. Die parallele Ebene durch Z zur Bildebene ist die sog. Verschwindungsebene; ihre Punkte haben keine Bildpunkte. Die Schnittgerade der Verschwindungsebene mit der Gegenstandsebene ist die Verschwindungsgerade v. Das Lot vom Zentrum Z auf die Bildebene hat als Fußpunkt den Hauptpunkt H. Die Parallele zur Achse a durch H ist der Horizont h. Die Fußpunkte der Lote von H und Z sind H 0 und Z 0. Der Lotabstand des Zentrums bzw. Augpunkts, von der Bildebene ist die Aughöhe; ihre Größe entscheidet, ob der Gegenstand bezüglich des Horizonts mehr von oben oder mehr von unten gesehen wird. Der Abstand des Zentrums Z von der Bildebene, die Distanz, regelt die Größe des planaren Bildes. Die Blickrichtung auf das abzubildende Objekt kann durch seitliche Lageänderungen von Z variiert werden. Anmerkung: Das Sehen ist normalerweise zweiäugig (binokular); erst durch die Kombination der beiden zentralprojektiven Netzhautbilder entsteht das visuelle Abbild eines Objekts. Indem wir den zentralprojektiven Apparat durch einen zweiten Augpunkt ergänzen (Abb. 11, abzubildendes Objekt: Würfel mit dualem Oktaeder hinter der durchsichtigen Bildebene), können wir sozusagen simulativ zweiäugige zentralperspektive Bilder gewinnen (Abb. 12).
6 30 Abb. 11 Abb Parameter der Zentralprojektion Wir zeigen nun, wie sich die Variation der Größe der Parameter Aughöhe, Blickrichtung und Distanz auf die visuelle Wahrnehmung des zentralperspektiven Bildes eines Objekts auswirkt. Da das aktive Gesichtsfeld vom Augpunkt Z aus nicht beliebig groß ist, konstruieren wir noch einen Sichtkegel, der an der Spitze Z den empirisch belegten Öffnungswinkel von 60 hat. Objekte bzw. Teilobjekte innerhalb des entsprechenden Sichtkreises auf der Bildebene werden von Z aus auf einen Blick erfasst (Abb. 13). Abb. 13 In Abbildung 14 ist das Objekt in Vogelperspektive zu sehen, der Horizont h liegt o- berhalb des Objekts; man blickt auf das Objekt von vorn oben.
7 31 Abb. 14 In Abbildung 15 erscheint das Objekt sogenannter Normalprojektion ; der Horizont h liegt mittig zum Objekt, dessen Bild innerhalb des Sichtkreises liegt. Abb. 15 Die Abbildung 16 zeigt eine Froschperspektive; man blickt von vorn unten nach oben auf das Objekt, welches vor dem Betrachter aufragt. Abb. 16 Die Abbildung 17 zeigt das Objekt in Blickrichtung von links, Abbildung 18 mehr mit Blickrichtung von der Mitte aus usw.
8 32 Abb. 17 Abb. 18 Schließlich variieren wir die Distanz. Verringern wir die Distanz, so wird das Bild bzw. der Sichtkreis immer kleiner (Abb. 19); vergrößern wir die Distanz, so wird das Bild bzw. der Sichtkreis größer (Abb. 20). Abb. 19
9 33 Abb Zentralprojektives Abbilden einfacher Objekte Wir beginnen mit dem Abbilden von Geraden. Zuerst sollen Lotgeraden der Standebene abgebildet werden (Abb. 21). Die Lotgeraden sind parallel zur Bildebene, deshalb schneiden die Ebenen, jeweils gebildet aus Lotgerade und dem Zentrum Z, die Bildebene in parallelen Geraden, die die betreffenden Bildgeraden sind. Die Bildgeraden stehen auch senkrecht auf der Standebene und somit senkrecht auf der Achse. Abb. 21 Generell gilt für Geraden, die parallel zur Bildebene verlaufen, dass ihre Bildgeraden zu ihnen parallel sind (Abb. 22).
10 34 Abb. 22 Betrachten wir nun eine Gerade g, die nicht parallel zur Bildgeraden liegt und nicht durch Z geht (Abb. 23). Sie schneidet die Bildebene im Durchstoßpunkt D, der zugleich Bild- und Originalpunkt ist. Die Bildgerade g erhält man als Verbindungsgerade von D mit einem Bildpunkt P eines von D verschiedenen Geradenpunktes P. Wir verziehen nun auf der Geraden g den auf ihr beweglichen Punkt P. P geht in den Punkt F über, wenn P zum unendlich fernen Punkt der Geraden flüchtet ; die Gerade durch Z und P geht dabei in die Parallele zu g durch Z über. F heißt Fluchtpunkt der Geraden g; die Parallele zu g durch Z wird Fluchtgerade (f) der Geraden g genannt. F ist der Durchstoßpunkt der Fluchtgeraden f von g mit der Bildebene. Da F auf g liegt, kann man die Bildgerade auch aus D und F konstruieren. Alle Punkte der Fluchtgeraden werden auf ihren Durchstoßpunkt mit der Bildebene abgebildet; das gilt natürlich auch für alle durch Z verlaufenden Geraden. Abb. 23
11 35 Alle einander parallelen Geraden, die die Bildebene schneiden, haben dieselbe Fluchtgerade, denn es gibt nur eine Parallele zu ihnen durch Z (Abb. 24). Ihre Bildgeraden gehen durch den gemeinsamen Fluchtpunkt. Insbesondere haben die Lotgeraden auf die Bildebene dieselbe Fluchtgerade, die mit der Geraden durch den Hauptpunkt H und Z zusammenfällt; ihre Bildgeraden gehen durch H (Abb. 25). Abb. 24 Abb. 25 Die Fluchtgeraden zweier einander schneidender Originalgeraden schließen den selben Winkel des Maßes α ein, wie ihre zugehörige Fluchtgeraden, denn jede Fluchtgerade ist parallel zu ihrer Originalgeraden und die Winkelgleichheit folgt mit Stufenwinkelsatz an Parallelen (Abb. 26). Bildet man zum Beispiel ein Rechteck zentralprojektiv ab, so liegt Z auf dem Thaleskreis um den Mittelpunkt von F 1 F 2, wobei F 1, F 2 die Fluchtpunkte der im rechten
12 36 Winkel stehenden Trägergeraden der Rechteckseiten sind. Der Thaleskreis liegt in der zur Rechteckebene parallelen Ebene durch Z (Abb. 27). Abb. 26 Abb. 27 Einen Kreis bildet man ab, indem sein Sichtkegel mit der Bildebene geschnitten wird (Abb. 28). Die Schnittfigur ist ein Kegelschnitt. Liegt der Kreis nicht parallel zur Bildebene so geht der Kreismittelpunkt nicht in den Mittelpunkt des Kegelschnitts über. Das Bild eines Kreises ist eine Ellipse bzw. eine Parabel bzw. eine Hyperbel, falls der Originalkreis die Verschwindungsgerade meidet bzw. berührt bzw. schneidet. Interessant sind Umkehraufgaben, die bei gegebenem Bildobjekt nach dem (den) Originalobjekt(en) fragen. Beispielsweise: Wie muss ein Objekt (z. B. ein Buchstabe oder ein Verkehrszeichen auf die Originalebene (z. B. Straße) aufgezeichnet werden, damit man es auch gut erkennen kann. (Abb. 29).
13 37 Abb. 28 Abb Ein-, Zwei- und Drei-Fluchtpunktperspektive Die Bedeutung dieser klassischen Fluchtpunktperspektiven liegt in ihrer Anwendung zur einfachen Konstruktion von zentralprojektiven Bildern räumlicher Objekte. Wir erläutern sie am Beispiel des Würfels. Ein-Fluchtpunktperspektive: Liegen zwei der drei einen Würfel erzeugenden Kanten parallel zur Bildebene, so gehen die Fluchtgerade der dritten Bildkanten durch den Hauptpunkt H; dieser Punkt ist ihr Fluchtpunkt. (Abb. 30, Ein-Fluchtpunktperspektive eines Würfels in besonderer Lage).
14 38 Abb. 30 Zwei-Fluchtpunktperspektive: Hier ist nur noch eine der drei erzeugenden Würfelkante parallel zur Bildebene. Die Fluchtgeraden, die zu den restlichen Bildkanten gehören, schneiden einander in zwei Fluchtpunkten (Abb. 31, Zwei-Fluchtpunktperspektive eines Würfels in besonderer Lage). Abb. 31 Drei-Fluchtpunktperspektive: Liegen keine der den Würfel erzeugenden Kanten mehr parallel zur Bildebene, so treffen sich die Bildgeraden der Würfelkanten in drei Fluchtpunkten (Abb. 32 mit transparenter Bildebene).
15 39 Abb. 32 Da in jeder Würfelecke die Kanten im rechten Winkel stehen, so stehen auch ihre Fluchtgeraden in Z im rechten Winkel (Abb. 33, ZF 1, ZF 2, ZF 3 stehen paarweise senkrecht). Im Rechtwinkeltetraeder ZF 1 F 2 F 3 gilt für seine Seitenflächen: ZF 1 F 2 F 3 ²= ZF 1 F 2 ² + ZF 2 F 3 ² + Z F 3 F 2 ² (räumlicher Verallgemeinerung des Pythagoras-Satzes). Außerdem ist der Hauptpunkt H Höhenschnittpunkt im Dreieck F 1 F 2 F 3 und ZH ist Höhe in diesem Rechtwinkeltetraeder. Abb. 33
16 Anwendungsbeispiele In den folgenden Beispielen, die nicht über die Darstellung in Drei-Fluchtpunktperspektive hinausgehen, ist jeweils zuerst das abzubildende Objekt in der Gegenstandsebene konstruiert worden. Bei der Beschreibung der Beispiele meinen wir mit Ansicht von vorn, wenn wir den Abbildungsapparat von Z aus betrachten; eine Betrachtung von der Gegenseite wird mit Ansicht von hinten beschrieben. Die Abbildung 34 zeigt ein Portal, dessen Dach von zwei quadratischen Säulen getragen wird. Das ein-fluchtpunktperspektive Bild bietet eine Ansicht in Normalperspektive (Abb. 35). In Abbildung 36 ist das abzubildende Objekt durch eine gefüllte Bildebene verdeckt worden, um sein perspektives Bild besser betrachten zu können. Abb. 34 Abb. 35
17 41 Abb. 36 Ein quaderförmiger Innenraum ist in Abbildung 37 konstruiert; sein zentralperspektives Bild zeigt die Abbildung 38. Abb. 37
18 42 Abb. 38 Das abzubildende Objekt in Abbildung 39, ein achteckiges Prisma mit aufgesetzter Pyramide, ist dem Baptisterium in Florenz nachempfunden. Die Abbildung 40 zeigt ein zwei-fluchtpunktperspektives Bild wie bei Brunelleschi (Florentinischer Baumeister des 15. Jahrhunderts). Die zwei-fluchtpunktperspektive Ansicht einer Wand mit Fenster und parallelperspektivem Schattenwurf ist in Abbildung 41 (Ansicht von hinten) und in Abbildung 42 (Ansicht von vorn) zu sehen. Abb. 39
19 43 Abb. 40 Abb. 41 Abb. 42
20 44 Beim Fotografieren eines Objekts, z. B. eines Turms von unten, entsteht oft ein drei-fluchtpunktperspektives Bild. Beim Anvisieren durch den Kamerasucher liegt der Augpunkt in der Linse des Betrachterauges und die Bildebene ist die Ebene des Suchers. Die Bildebene steht dann nicht mehr senkrecht auf der Standebene des Objekts und es kommt je nach Neigung der Bildebene zu mehr oder weniger perspektiv verzerrten Darstellungen (Abb. 43/44). Abb. 43 Abb Verebnung der Zentralprojektion Wir klären jetzt die Schnittstelle zwischen der Konstruktion zentralprojektiver Bilder im virtuellen Raum und der Konstruktion solcher Bilder in der Zeichenebene. Durch Eindrehen bzw. Umklappen der Bildebene zusammen mit dem Zentrum in die Gegenstandsebene gewinnen wir aus der räumlichen Konstruktion eine Konstruktion in der Ebene. Räumlich erhalten wir die Bilder von Punkten als Durchstoßpunkte des Sehstrahls mit der Bildebene (Abb. 45). Man kann aber auch die Bildpunkte folgendermaßen konstruieren: Fällt man vom Originalpunkt das Lot auf die Bildebene so liegt der Bildpunkt auch auf Bildgeraden dieses Lotes, die durch H geht (vgl. Abschnitt 2.3). Der Sehstrahl zum Originalpunkt schneidet also die Bildgerade in seinem Bildpunkt. Dreht man nun die Bildebene zusammen mit dem Gelenkviereck ZHH 0 Z 0 in die Standebene (Abb. 46, das Rechteck ZHH 0 Z 0 wird zu einem Parallelogramm), so ergibt sich die entsprechende Konstruktion von zentralperspektiven Bildpunkten in der Ebene (Abb. 47).
21 45 Abb. 45 Abb. 46 Abb. 47
22 46 Jetzt können sich die üblichen planaren Konstruktionsverfahren der Zentralprojektion anschließen (vgl. u. a. Graf/Barner 1964). Die zentralprojektiv in der Zeichenebene darzustellenden räumlichen Objekte müssen dabei in maßtreuen parallelprojektiven Darstellungen verfügbar sein. 3 Schlußbemerkungen 3.2 Das Printmedium kann die Möglichkeiten der interaktiven Visualisierung und Variation nicht adäquat wiedergeben. Durch die Gestaltung des einführenden Kurses als ein Online-Dokument mit voll funktionsfähigen Applets, ist sein dynamischer Informationsgehalt besser vermittelbar. Ideal wäre eine Online-Gestaltung, bei der auch das konstruktive Werkzeug Cabri 3D im selben Dokument verfügbar wären. Zur Zeit müssen Kurs und Computerwerkzeug noch parallel in zwei Fenstern benutzt werden. 3.3 Die Frage, ob und in welchem Umfang die herkömmlichen zentralprojektiven Abbildungsverfahren noch behandelt werden sollen, wird hier nicht diskutiert. Wir betrachten die in diesem Beitrag skizzierten phänomenologische Einführung als ein Minimalprogramm, um mit dem Thema vertraut zu werden.u. E. sollte die interaktive Behandlung der Zentralprojektion im virtuellen Raum im Rahmen eines fächerübergreifenden bzw. anwendungsorientierten Geometrieunterrichts wegen ihrer Bedeutung für die anschauliche Darstellung des Raumes einen angemessenen Platz beanspruchen. 3.4 Cabri 3D ermöglicht im Vergleich mit bisherigen Raumgeometrie-Werkzeugen einen verbesserten Zugang zur synthetischen Raumgeometrie. Nicht nur die Darstellende Geometrie sondern auch die folgenden traditionellen raumgeometrischen Themen erfahren eine neue adäquate Behandlung bzw. Bewertung im Kontext des Geometrie-Unterrichts: - Körpergeometrie, insbesondere die Geometrie der Polyeder (z. B. der Platonischen Körper und ihrer Derivate) - Konzept und Lagebeziehungen geometrischer Objekte (z. B. von Punkten, Geraden, Ebenen) - Räumliche Konstruktionsaufgaben (z. B. mit Ebenenlineal und Kugelzirkel oder mit räumlichen Kongruenzabbildungen) - Räumliche Analogisierung von Begriffen und Sätzen der ebenen Geometrie (z. B. die Analogisierung der Dreiecksgeometrie zur Tetraedergeometrie) - Räumliche Behandlung der Kegelschnitte (z. B. als zentralprojektive Kreisbilder) - Kugelgeometrie (z. B. Kreisvieleck-Lehre) - anwendungsorientierte Modellierung. 4. Literatur Bainville, E., Laborde, J.-M. (2004): Cabri 3D 1.0. (Software). Grenoble: Cabrilog. Deutsche Version (Bearbeitung von H. Schumann) zu beziehen von Edgerton, S. Y. (2002): Die Entdeckung der Perspektive. München: Wilhelm Fink Graf, U. (1961): Darstellende Geometrie. Bearbeitet von M. Barner. Heidelberg: Quelle & Meyer Schumann, H. (2004): Entdeckung von Analogien mit Cabri 3D am Beispiel Dreieck Tetraeder. In: math. did. 27 (2004) Bd. 1, S Schumann, H. (2005 a): Dynamische Raumgeometrie. In: Beiträge zum Mathematikunterricht Hildesheim: Franzbecker
23 47 Schumann, H. (2005b): Interaktives geometrisches Modellieren im virtuellen Raum mit Cabri 3D. In: LOG IN Informatische Bildung und Computer in der Schule, Heft 133, S Schumann, H. (2005c): Dynamische Einführung der Kegelschnitte. Materialien Mathematik M 70. Stuttgart: Landesinstitut für Schulentwicklung Schumann, H. (2005d): Interaktives geometrisches Konstruieren im virtuellen Raum mit Cabri 3D. Erscheint in: LOG IN Informatische Bildung und Computer in der Schule, Heft 136/137
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D
 Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
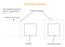 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Sätze über Kreise raumgeometrisch beweisen
 Sätze über Kreise raumgeometrisch beweisen Heinz Schumann Erschienen als Online-Ergänzung zu Praxis der Mathematik in der Schule 47 (2005) 6 Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet. Das
Sätze über Kreise raumgeometrisch beweisen Heinz Schumann Erschienen als Online-Ergänzung zu Praxis der Mathematik in der Schule 47 (2005) 6 Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet. Das
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Behandlung der Kegelschnitte im virtuellen Raum mit Cabri 3D
 Heinz Schumann mit Cabri 3D Zusammenfassung: In diesem Artikel wird eine Einführung in die Kegelschnitte dem dynamischen Raumgeometriesystem Cabri 3D gegeben, die traditionelle Inhalte auf neue Art und
Heinz Schumann mit Cabri 3D Zusammenfassung: In diesem Artikel wird eine Einführung in die Kegelschnitte dem dynamischen Raumgeometriesystem Cabri 3D gegeben, die traditionelle Inhalte auf neue Art und
Grundregeln der Perspektive und ihre elementargeometrische Herleitung
 Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien. Tutorial 02. Zentralperspektive Rekonstruktion
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial 02 Zentralperspektive Rekonstruktion Um ein perspektives Bild zu rekonstruieren, dh. die realen Abmessungen eines dreidimensionalen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial 02 Zentralperspektive Rekonstruktion Um ein perspektives Bild zu rekonstruieren, dh. die realen Abmessungen eines dreidimensionalen
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum (2)
 Heinz Schumann Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum (2) Analoge Dinge stimmen in gewissen Beziehungen zwischen ihren entsprechenden Teilen miteinander überein.
Heinz Schumann Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum (2) Analoge Dinge stimmen in gewissen Beziehungen zwischen ihren entsprechenden Teilen miteinander überein.
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Darstellende Geometrie Übungen. Tutorial 06. Übungsblatt: Schatten - Perspektive 04. Wohnhaus
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
DG für Kunstpädagogik
 DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung
 Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Schriftliche Reifeprüfung Darstellende Geometrie
 SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
Polyedrische Approximation von Körpern mit Cabri 3D
 Heinz Schumann Polyedrische Approximation von Körpern mit Cabri 3D Die Approximation von konvexen Körpern, deren Oberfläche nicht aus Polygonen besteht, mittels einbeschriebener konvexer Polyeder ist notwendig,
Heinz Schumann Polyedrische Approximation von Körpern mit Cabri 3D Die Approximation von konvexen Körpern, deren Oberfläche nicht aus Polygonen besteht, mittels einbeschriebener konvexer Polyeder ist notwendig,
Raum.Stationen.zu.linearen.
 Raum.Stationen.zu.linearen. Perspektiven Bearbeite die Stationen A bis K und mache dir Notizen im Hefter. Für die Übungen benutze bitte Zeichenpapier. Bsp.: (F) kannst du nur besuchen, wenn du (E) erledigt
Raum.Stationen.zu.linearen. Perspektiven Bearbeite die Stationen A bis K und mache dir Notizen im Hefter. Für die Übungen benutze bitte Zeichenpapier. Bsp.: (F) kannst du nur besuchen, wenn du (E) erledigt
Unmögliche Figuren perspektivisches Zeichnen:
 Unmögliche Figuren perspektivisches Zeichnen: Kompetenzen: Die Schüler/innen sollen Ein quaderförmiges Werkstück in der Schrägbildperspektive darstellen und bemaßen können. Ein Werkstück mit veränderter
Unmögliche Figuren perspektivisches Zeichnen: Kompetenzen: Die Schüler/innen sollen Ein quaderförmiges Werkstück in der Schrägbildperspektive darstellen und bemaßen können. Ein Werkstück mit veränderter
5A. Von der Perspektive zu den projektiven Ebenen.
 5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Josef Vogelmann Darstellende Geometrie
 Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Einige Fragen aus den Elementen der Darstellenden Geometrie,
 Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Zeichnen und Skizzieren von Szenarien
 Zeichnen und Skizzieren von Szenarien 2. Anatomie 3. Komposition 4. Struktur und Kontraste 5. Abstraktion 6. Abgabe Körper im Raum. Perspektivisches Umdenken. Räumlichkeit & Perspektive. Räumlichkeit
Zeichnen und Skizzieren von Szenarien 2. Anatomie 3. Komposition 4. Struktur und Kontraste 5. Abstraktion 6. Abgabe Körper im Raum. Perspektivisches Umdenken. Räumlichkeit & Perspektive. Räumlichkeit
Elementare Tetraedergeometrie Eine Einführung in die Raumgeometrie
 Heinz Schumann Elementare Tetraedergeometrie Eine Einführung in die Raumgeometrie Zum Inhalt des Buches und der Hypertext-CD Interaktive Dynamische Raumgeometrie-Systeme eröffnen heute einen direkten Zugang
Heinz Schumann Elementare Tetraedergeometrie Eine Einführung in die Raumgeometrie Zum Inhalt des Buches und der Hypertext-CD Interaktive Dynamische Raumgeometrie-Systeme eröffnen heute einen direkten Zugang
Sekundarschulabschluss für Erwachsene. Geometrie A b) Strecken Sie das Dreieck ABC (Streckfaktor: -1/ Streckzentrum Z) (3 Punkte)
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16. Prüfer: Mag.
 Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Name und des Einsenders
 Titel der Einheit Stoffgebiet Name und Email des Einsenders Ziel der Einheit Inhalt Voraussetzungen Konstruktion von Kegelschnitten Geometrie Andreas Ulovec Andreas.Ulovec@univie.ac.at Verwenden von Dynamischer
Titel der Einheit Stoffgebiet Name und Email des Einsenders Ziel der Einheit Inhalt Voraussetzungen Konstruktion von Kegelschnitten Geometrie Andreas Ulovec Andreas.Ulovec@univie.ac.at Verwenden von Dynamischer
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
m2l 60.odt Klausur 12/I B 1. Gegeben seien zwei Geraden. Wie gehen Sie vor, um über deren Lagebeziehung eine Aussage zu treffen.
 2. Klausur 12/I B Thema: Lagebeziehung Gerade, Ebene 1. Gegeben seien zwei Geraden. Wie gehen Sie vor, um über deren Lagebeziehung eine Aussage zu treffen. 5 6 s 3 0 11 10, g BC : x = 3 u 5 1 2. Gegeben
2. Klausur 12/I B Thema: Lagebeziehung Gerade, Ebene 1. Gegeben seien zwei Geraden. Wie gehen Sie vor, um über deren Lagebeziehung eine Aussage zu treffen. 5 6 s 3 0 11 10, g BC : x = 3 u 5 1 2. Gegeben
Bestimme ferner die Koordinaten des Bildpunktes von B bei der Spiegelung
 Vektoren - Skalar- und Vektorprodukt ================================================================== 1. Gegeben sind die Punkte A 1 2 3 und B 3 4 1 bzgl. eines kartesischen Koordina- tensystems mit
Vektoren - Skalar- und Vektorprodukt ================================================================== 1. Gegeben sind die Punkte A 1 2 3 und B 3 4 1 bzgl. eines kartesischen Koordina- tensystems mit
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.2 Projektionen und Kameramodelle
 Graphikprog. GRUNDLEGENDE VERFAHREN UND TECHNIKEN. Projektionen und Kameramodelle Nachdem alle Objekte einer Szenerie mittels der besprochenen Transformationen im D-Weltkoordinatensystem platziert sind,
Graphikprog. GRUNDLEGENDE VERFAHREN UND TECHNIKEN. Projektionen und Kameramodelle Nachdem alle Objekte einer Szenerie mittels der besprochenen Transformationen im D-Weltkoordinatensystem platziert sind,
Die Konstruktion der Schnittgeraden zweier Ebenen ist auf unterschiedliche Art und Weise möglich:
 Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Komplexe Zahlenmengen und ihre Abbildungen
 VERSTÄNDLICHE MATHEMATIK Ilse Rapsch Komplexe Zahlenmengen und ihre Abbildungen Der Versuch, ein Kapitel der höherervmathematik anschaulich zu machen franzbecker Inhaltsübersicht VORWORT 9 EINFÜHRUNG 11
VERSTÄNDLICHE MATHEMATIK Ilse Rapsch Komplexe Zahlenmengen und ihre Abbildungen Der Versuch, ein Kapitel der höherervmathematik anschaulich zu machen franzbecker Inhaltsübersicht VORWORT 9 EINFÜHRUNG 11
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive - Rekonstruktion
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial Übungsblatt: Perspektive - Rekonstruktion Gegeben sind ein Foto von einem quaderförmigen Objekt sowie die Abmessungen des Basisrechteckes.
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial Übungsblatt: Perspektive - Rekonstruktion Gegeben sind ein Foto von einem quaderförmigen Objekt sowie die Abmessungen des Basisrechteckes.
Polyeder und Platonische Körper
 Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
mentor Lernhilfe: Mathematik 7. Klasse Baumann
 mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
Konstruktionen am Dreieck
 Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
SINUS Saarland Geometrie beziehungshaltig entdecken Module für den Geometrieunterricht. Kurs 7: Module 13 und :00-18:00 Uhr
 SINUS Saarland Geometrie beziehungshaltig entdecken Module für den Geometrieunterricht Kurs 7: Module 13 und 14 08.01.2015 15:00-18:00 Uhr 1 Modul 13: Vielecke (Vielecke; regelmäßige Vielecke; Orientierungsfigur:
SINUS Saarland Geometrie beziehungshaltig entdecken Module für den Geometrieunterricht Kurs 7: Module 13 und 14 08.01.2015 15:00-18:00 Uhr 1 Modul 13: Vielecke (Vielecke; regelmäßige Vielecke; Orientierungsfigur:
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
Stereometrie. Rainer Hauser. Dezember 2010
 Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 Aufgabe 50. Projektivspiegelung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern Projektive Geometrie WS 2010/11 Lösungen zu Aufgabenblatt 12 (24.
Aufgabe 50. Projektivspiegelung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern Projektive Geometrie WS 2010/11 Lösungen zu Aufgabenblatt 12 (24.
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Interaktives geometrisches Konstruieren im virtuellen Raum mit Cabri 3D
 Heinz Schumann Interaktives geometrisches Konstruieren im virtuellen Raum mit Cabri 3D Das Beherrschen der mit den entsprechenden analogen bzw. digitalen Werkzeugen ausführbaren geometrischen Konstruktionen
Heinz Schumann Interaktives geometrisches Konstruieren im virtuellen Raum mit Cabri 3D Das Beherrschen der mit den entsprechenden analogen bzw. digitalen Werkzeugen ausführbaren geometrischen Konstruktionen
Einige Aufgaben über extreme Werte.
 Einige Aufgaben über extreme Werte. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 5. August 1926.) I. Gesucht auf einer Regelfläche zweiten Grades von der einen Regelschar diejenigen Erzeugenden,
Einige Aufgaben über extreme Werte. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 5. August 1926.) I. Gesucht auf einer Regelfläche zweiten Grades von der einen Regelschar diejenigen Erzeugenden,
Perspektive Vertiefung
 Arbeitsbereich Geometrie und CAD Universität Innsbruck Arbeitsblätter Perspektive Vertiefung Hans-Peter Schröcker Wintersemester 2007/08 Felder schraffieren Schraffieren Sie die angegebenen Felder mit
Arbeitsbereich Geometrie und CAD Universität Innsbruck Arbeitsblätter Perspektive Vertiefung Hans-Peter Schröcker Wintersemester 2007/08 Felder schraffieren Schraffieren Sie die angegebenen Felder mit
Übersicht zu den Textinhalten
 Abbildungen Übersicht zu den Textinhalten Zum Thema Abbildungen gibt es mehrere Texte. Hier wird aufgelistet, wo man was findet. Datei Nr. 11050 Stand 3. Oktober 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK
Abbildungen Übersicht zu den Textinhalten Zum Thema Abbildungen gibt es mehrere Texte. Hier wird aufgelistet, wo man was findet. Datei Nr. 11050 Stand 3. Oktober 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK
7.6. Prüfungsaufgaben zu Normalenformen
 7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
Jahresplanung Vorschlag 1
 Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
2 Das Bild In Schulbüchern und Arbeitsblättern sieht man oft Würfel -Darstellungen wie etwa in der Abbildung 1. Abb. 1: Was ist denn das?
 Hans Walser, [20131013], [20160331], [20160401] Quetschwürfel 1 Worum geht es? Es wird auf die Problematik der in Schulen weitverbreiteten Schrägbilder eingegangen. 2 Das Bild In Schulbüchern und Arbeitsblättern
Hans Walser, [20131013], [20160331], [20160401] Quetschwürfel 1 Worum geht es? Es wird auf die Problematik der in Schulen weitverbreiteten Schrägbilder eingegangen. 2 Das Bild In Schulbüchern und Arbeitsblättern
Einleitung. Aufgaben: Vergrössern / Verkleinern. 1. Die Geo-Maus
 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch
Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch
Gundlagen Klasse 5/6 Geometrie. nach oben. Inhaltsverzeichnis
 Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Ziel bei der Darstellung von räumlichen Figuren (Körpern): Startseite
 Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
AB1: Ähnliche Figuren untersuchen und zeichnen Was heißt Vergrößern und Verkleinern? Was ist eine zentrische Streckung?
 AB1: Ähnliche Figuren untersuchen und zeichnen Was heißt Vergrößern und Verkleinern? Was ist eine zentrische Streckung? 1 Finde möglichst viele Gemeinsamkeiten und Unterschiede der folgenden Abbildungen.
AB1: Ähnliche Figuren untersuchen und zeichnen Was heißt Vergrößern und Verkleinern? Was ist eine zentrische Streckung? 1 Finde möglichst viele Gemeinsamkeiten und Unterschiede der folgenden Abbildungen.
Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV)
 Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV) 1. Schülerleistungen 2. Darstellenden Geometrie und RVV im MU 3. Fachliche und begriffliche Probleme 4. Ergebnisse
Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV) 1. Schülerleistungen 2. Darstellenden Geometrie und RVV im MU 3. Fachliche und begriffliche Probleme 4. Ergebnisse
Weitere geometrische Abbildungen
 Weitere geometrische Abbildungen Anna Wegener, Matthias Wegen, Daniel Kretschmer 15.01.2015 1 / 38 Affinitätsabbildungen - Motivation Kongruenzabbildungen Ähnlichkeitsabbildungen Affinitätsabbildungen
Weitere geometrische Abbildungen Anna Wegener, Matthias Wegen, Daniel Kretschmer 15.01.2015 1 / 38 Affinitätsabbildungen - Motivation Kongruenzabbildungen Ähnlichkeitsabbildungen Affinitätsabbildungen
Kompetenzmodell. Geometrisches Zeichnen. Arbeitsblätter
 Kompetenzmodell Geometrisches Zeichnen Arbeitsblätter 4.10.2012 Inhaltsdimension Arbeitsblätter Risse Lesen und Skizzieren Bausteine Länge von Strecken Flächenmodelle Bedienung eines CAD-Programms 3D-CAD-Software:
Kompetenzmodell Geometrisches Zeichnen Arbeitsblätter 4.10.2012 Inhaltsdimension Arbeitsblätter Risse Lesen und Skizzieren Bausteine Länge von Strecken Flächenmodelle Bedienung eines CAD-Programms 3D-CAD-Software:
2.6. Aufgaben zu Kongruenzabbildungen
 Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Abiturprüfung 2000 LK Mathematik Baden-Württemberg
 Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Drei Kreise im Dreieck
 Ein Problem von, 171-1807 9. Juli 006 Gegeben sei das Dreieck ABC. Zeichne drei Kreise k 1, k, k im nneren von ABC, von denen jeder zwei Dreieckseiten und mindestens einen der übrigen zwei Kreise berührt
Ein Problem von, 171-1807 9. Juli 006 Gegeben sei das Dreieck ABC. Zeichne drei Kreise k 1, k, k im nneren von ABC, von denen jeder zwei Dreieckseiten und mindestens einen der übrigen zwei Kreise berührt
SCHRIFTLICHE ABITURPRÜFUNG Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten
 Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten L 1, L 2 und L 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten L 1, L 2 und L 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
geschlossene Schachtel mit einem kleinen Loch
 Kameramodellierung Lochkamera Kamerakonstante Kamerazentrum geschlossene Schachtel mit einem kleinen Loch ideale Kamera: Loch hat keine Ausdehnung die Strahlen sind ein Büschel von Geraden Abbildung erfolgt
Kameramodellierung Lochkamera Kamerakonstante Kamerazentrum geschlossene Schachtel mit einem kleinen Loch ideale Kamera: Loch hat keine Ausdehnung die Strahlen sind ein Büschel von Geraden Abbildung erfolgt
Zeichne einen Würfel unter Parallelprojektion
 Ulrich Schoenwaelder GEONExT-Fortbildung 15. April 2005 Lst. D für Mathematik Zeichne einen Würfel unter Parallelprojektion Klassenstufe: 9-10. Methodische Ziele: Raumvorstellung stärken. Genaues Beobachten,
Ulrich Schoenwaelder GEONExT-Fortbildung 15. April 2005 Lst. D für Mathematik Zeichne einen Würfel unter Parallelprojektion Klassenstufe: 9-10. Methodische Ziele: Raumvorstellung stärken. Genaues Beobachten,
Aufgabe 1 Erstelle mit Hilfe von GEOGEBRA ein dynamisches Geometrie-Programm, das die Mittelsenkrechte
 AB Mathematik Experimentieren mit GeoGebra Merke Alle folgenden Aufgaben sind mit dem Programm GEOGEBRA auszuführen! Eine ausführliche Einführung in die Bedienung des Programmes erfolgt im Unterricht.
AB Mathematik Experimentieren mit GeoGebra Merke Alle folgenden Aufgaben sind mit dem Programm GEOGEBRA auszuführen! Eine ausführliche Einführung in die Bedienung des Programmes erfolgt im Unterricht.
Die Strahlensätze. Ben Hambrecht. 1 Zentrische Streckungen 2. 2 Der 1. Strahlensatz 7. 3 Der Streckfaktor Der 2.
 Die Strahlensätze Ben Hambrecht Inhaltsverzeichnis 1 Zentrische Streckungen 2 2 Der 1. Strahlensatz 7 3 Der Streckfaktor 11 4 Der 2. Strahlensatz 14 5 Der 3. Strahlensatz 18 6 Die Umkehrungen der Strahlensätze
Die Strahlensätze Ben Hambrecht Inhaltsverzeichnis 1 Zentrische Streckungen 2 2 Der 1. Strahlensatz 7 3 Der Streckfaktor 11 4 Der 2. Strahlensatz 14 5 Der 3. Strahlensatz 18 6 Die Umkehrungen der Strahlensätze
. Wo liegt das Zentrum S? d) E ist das Bild von I mit
 Zentrische Streckung, Ähnlichkeit 1. Eine gegebene Strecke ist durch Konstruktion im Verhältnis 5 3 harmonisch zu teilen. 1 U und V teilen die Strecke mit der Länge 24 cm harmonisch im Verhältnis 5 3.
Zentrische Streckung, Ähnlichkeit 1. Eine gegebene Strecke ist durch Konstruktion im Verhältnis 5 3 harmonisch zu teilen. 1 U und V teilen die Strecke mit der Länge 24 cm harmonisch im Verhältnis 5 3.
Spiegeln an einem Punkt
 Spiegeln an einem Punkt D IE S PIEGELVORSCHRIFT Nach den Erfahrungen mit Makros beim Geradenspiegeln und Drehen können wir uns jetzt eine zusammenfassende Strategie für das Definieren von Makros bei Abbildungsvorschriften
Spiegeln an einem Punkt D IE S PIEGELVORSCHRIFT Nach den Erfahrungen mit Makros beim Geradenspiegeln und Drehen können wir uns jetzt eine zusammenfassende Strategie für das Definieren von Makros bei Abbildungsvorschriften
Hauscurriculum Q2 Lineare Algebra/Analytische Geometrie Grundkurs März 2017
 Hauscurriculum Q2 Lineare Algebra/Analytische Geometrie Grundkurs März 2017 Übersicht: Q2.3 im Raum Q2.4 Matrizen zur Beschreibung von Q2.6 Vertiefung der Analytischen Geometrie (nur Grundkurs) verbindlich:
Hauscurriculum Q2 Lineare Algebra/Analytische Geometrie Grundkurs März 2017 Übersicht: Q2.3 im Raum Q2.4 Matrizen zur Beschreibung von Q2.6 Vertiefung der Analytischen Geometrie (nur Grundkurs) verbindlich:
Landesabitur 2007 Beispielaufgaben 2005_M-LK_A 7. Eine quadratische Pyramide (Grundkante 4 und Höhe 6) steht neben einer Stufe. 1.
 I. Thema und Aufgabenstellung Lineare Algebra / Analytische Geometrie Aufgaben Eine quadratische Pyramide (Grundkante 4 und Höhe 6) steht neben einer Stufe. 3. Achse 2. Achse 1. Achse Die Sonne scheint
I. Thema und Aufgabenstellung Lineare Algebra / Analytische Geometrie Aufgaben Eine quadratische Pyramide (Grundkante 4 und Höhe 6) steht neben einer Stufe. 3. Achse 2. Achse 1. Achse Die Sonne scheint
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Konstruktion von Kreistangenten
 Konstruktion von Kreistangenten 1 Gegeben sind die Punkte A und B mit AB = 5cm Konstruiere die Geraden durch B, die von A den Abstand 3cm haben! 2 Eine Ecke einer Rasenfläche, an der die geraden Ränder
Konstruktion von Kreistangenten 1 Gegeben sind die Punkte A und B mit AB = 5cm Konstruiere die Geraden durch B, die von A den Abstand 3cm haben! 2 Eine Ecke einer Rasenfläche, an der die geraden Ränder
Die Hyperbel als Kreis
 Kapitel 6 Die Hyperbel als Kreis Wir haben uns im vorigen Kapitel mit der von der Wellenausbreitung nahegelegten Spiegelungskonstruktion und dem Lichteck (Abb. 4.8, 5.1) auseinandergesetzt. Diese Konstruktion
Kapitel 6 Die Hyperbel als Kreis Wir haben uns im vorigen Kapitel mit der von der Wellenausbreitung nahegelegten Spiegelungskonstruktion und dem Lichteck (Abb. 4.8, 5.1) auseinandergesetzt. Diese Konstruktion
