SIMULINK. Lineare und nichtlineare. Systeme
|
|
|
- Hilko Meyer
- vor 8 Jahren
- Abrufe
Transkript
1 SIMULINK Lineare und nichtlineare Systeme Dipl.-Ing. U. Wohlfarth
2 Inhalt SIMULINK Bibliothek Continuous Linearisierung, Ermittlung eines Gleichgewichtspunkts SIMULINK Bibliothek Nonlinear SIMULINK Bibliothek Functions&Tables Algebraische Schleifen S Funktionen Dipl.-Ing. U. Wohlfarth
3 SIMULINK Bibliothek Continuous Elemente zur Modellierung zeitkontinuierlicher Systeme Totzeiten 1 s Integrator x = Ax+Bu y = Cx+Du (s 1) s(s+1) Zero Pole Transport Delay du/dt State Space 1 Memory Derivative s+1 Transfer Fcn Variable Transport Delay Dipl.-Ing. U. Wohlfarth 1
4 Von der DGL zum Continuous Block Beispiel: Feder Masse Schwinger DGL: m ẍ(t) + k x(t) = 0 Lösung im Zeitbereich: x(t) = x 0 cos (ω 0 t) + v 0 ω 0 sin (ω 0 t) L 0 k Übergang in den Frequenzbereich: Übertragungsfunktion X(s) = 1 s 2 + ω 2 0 x m in SIMULINK: 0 Constant 1 s 2+2 Transfer Fcn (with initial outputs) Scope1 Dipl.-Ing. U. Wohlfarth 2
5 Beispiel zu Continuous Rücksetzen des Simulink Integrator-Blocks: 0.5 Constant 1 s xo Integrator 2 >= Relational Operator Scope Anfangswert Constant1 Dipl.-Ing. U. Wohlfarth 3
6 Linearisierung Linearisierung von Simulationsmodellen an beliebigem Arbeitspunkt Befehlsaufruf: [A,B,C,D] = linmod( sys, x, u, para, xpert, upert) [Ad,Bd,Cd,Dd] = dlinmod( sys, T s, x, u) Weitere Matlab Befehle aus der Control System Toolbox zur Analyse anwendbar (ss, tf, zpk, bode, lsim) Dipl.-Ing. U. Wohlfarth 4
7 Bestimmung eines Gleichgewichtspunkts Gleichgewichtspunkt entspricht dem eingeschwungenem Zustand des Systems, d.h. ẋ = 0 Befehlsaufruf: [x,u,y] = trim( sys, x0, u0, y0) weitere Optionen help trim Dipl.-Ing. U. Wohlfarth 5
8 SIMULINK Bibliothek Nonlinear Elemente zur Modellierung physikalischer Nichtlinearitäten Schalter Manual Switch Rate Limiter Quantizer Dead Zone Saturation Backlash Relay Coulomb & Viscous Friction Switch Multiport Switch Dipl.-Ing. U. Wohlfarth 6
9 Beispiele zu Nonlinear Beispiel zu Quantizer Clock f(u) (u(1) 5)^2 + 3 Quantizer Parabel quantisierte Parabel ausgabe To Workspace Beispiel zu Backlash Signal Generator 1 Constant u y Rate LimiterBacklash ausgabe To Workspace Dipl.-Ing. U. Wohlfarth 7
10 SIMULINK Bibliothek Functions&Tables Nachschlagetabellen programmierbare Funktionen Look Up Table Look Up Table (2 D) f(u) Fcn MATLAB Function MATLAB Fcn system S Function uvm. Dipl.-Ing. U. Wohlfarth 8
11 Beispiel zu Function&Tables Beispiel zu Look Up Table auslese Ramp Look Up Table To Workspace Dipl.-Ing. U. Wohlfarth 9
12 Algebraische Schleifen direct f eedthrough: Ausgang hängt vom Eingang zum gleichen Zeitpunkt ab u Sum y Blöcke mit direct f eedthrough: Sum, Gain, Product (State Space, Integrator, Transfer Function, Zero Pole) Lösung mit Algebraic Constraint: f(z) Solve f(z) = 0 Algebraic Constraint z Dipl.-Ing. U. Wohlfarth 10
13 Beispiel zu algebraischen Schleifen f(z) = 1 7 z sin z z 5 = 0 (1/7)* u^3 Fcn (1/28)* sin(u) Fcn1 f(z) Solve f(z) = 0 z z Algebraic Constraint Display Constant z Sum Dipl.-Ing. U. Wohlfarth 11
14 S Funktionen selbst programmierbare Funktionen Ausführung innerhalb eines SIMULINK Modells durch S Function Block programmierbar in Matlab (M Files) C, C ++, Fortran, Ada (MEX Files) Einbringen bereits vorhandenen Programm Codes Dipl.-Ing. U. Wohlfarth 12
15 Beispiel zu S Funktionen P T 1 : Übertragungsfunktion: Y (s) = st U(s) oder Zustandsdarstellung: ẋ = 1 T x + 1 T u y = x Step pt1sfun S Function y To Workspace Dipl.-Ing. U. Wohlfarth 13
16 Beispiel zu S Funktionen function [sys,x0,str,ts] = pt1sfun(t,x,u,flag,t) A = [-1/T]; % Zustandsmatrix % Unexpected flags % B = [ 1/T]; % Eingangsmatrix otherwise % Fehlerbehandlung C = [ 1 ]; % Ausgangsmatrix error([ Unhandled flag =,num2str(flag)]); D = [ 0 ]; % Durchschaltmatrix=0 end switch flag, % end pt1sfun % Initialization % case 0, %===================== [sys,x0,str,ts]=mdlinitializesizes(a,b,c,d); % mdlinitializesizes %===================== % Derivatives % % case 1, function [sys,x0,str,ts]=... sys=mdlderivatives(t,x,u,a,b,c,d); mdlinitializesizes(a,b,c,d) % Outputs % sizes = simsizes; case 3, sys=mdloutputs(t,x,u,a,b,c,d); sizes.numcontstates = size(a,1); sizes.numdiscstates = 0; % Nicht verwendete Flags sizes.numoutputs = size(c,1); case {2, 4, 9}, sys=[]; sizes.numinputs = size(b,1); Dipl.-Ing. U. Wohlfarth 14
17 Beispiel zu S Funktionen sizes.dirfeedthrough = 0; sizes.numsampletimes = 1; sys = simsizes(sizes); %==================== % mdloutputs %==================== x0 = zeros(size(a,1),1); % function sys=mdloutputs(t,x,u,a,b,c,d) str = []; sys = C*x + D*u; ts = [0 0]; % end mdlinitializesizes % end mdloutputs %=================== % mdlderivatives %=================== % function sys=mdlderivatives(t,x,u,a,b,c,d) sys = A*x + B*u; % end mdlderivatives Dipl.-Ing. U. Wohlfarth 15
SIMULINK. Grundlagen
 SIMULINK Grundlagen Dipl.-Ing. U. Wohlfarth Inhalt Was ist SIMULINK? SIMULINK Bibliotheken Sources, Sinks und Math Simulationsparameter Algorithmen zur numerischen Integration SIMULINK Bibliotheken Signals&Systems,
SIMULINK Grundlagen Dipl.-Ing. U. Wohlfarth Inhalt Was ist SIMULINK? SIMULINK Bibliotheken Sources, Sinks und Math Simulationsparameter Algorithmen zur numerischen Integration SIMULINK Bibliotheken Signals&Systems,
4. Simulink. Zweck und grundlegende Eigenschaften Mit Simulink werden Modelle mathematischer, physikalischer Systeme berechnet (simuliert)
 4. Simulink Simulink ist eine s.g. Toolbox von Matlab Zweck und grundlegende Eigenschaften Mit Simulink werden Modelle mathematischer, physikalischer Systeme berechnet (simuliert) Modell basiert auf Blöcken,
4. Simulink Simulink ist eine s.g. Toolbox von Matlab Zweck und grundlegende Eigenschaften Mit Simulink werden Modelle mathematischer, physikalischer Systeme berechnet (simuliert) Modell basiert auf Blöcken,
Umwelt-Campus Birkenfeld Numerik. der Fachhochschule Trier. Prof. Dr.-Ing. T. Preußler. MATLAB-Simulink
 MATLAB- 1. Einführung in ist eine MATLAB-Toolbox zur Simulation Dynamischer Systeme mit Hilfe einer grafischen Benutzeroberfläche. Insbesondere eignet sich zur Behandlung linearer und nichtlinerarer zeitabhängiger
MATLAB- 1. Einführung in ist eine MATLAB-Toolbox zur Simulation Dynamischer Systeme mit Hilfe einer grafischen Benutzeroberfläche. Insbesondere eignet sich zur Behandlung linearer und nichtlinerarer zeitabhängiger
Simulink: Einführende Beispiele
 Simulink: Einführende Beispiele Simulink ist eine grafische Oberfläche zur Ergänzung von Matlab, mit der Modelle mathematischer, physikalischer bzw. technischer Systeme aus Blöcken mittels plug-and-play
Simulink: Einführende Beispiele Simulink ist eine grafische Oberfläche zur Ergänzung von Matlab, mit der Modelle mathematischer, physikalischer bzw. technischer Systeme aus Blöcken mittels plug-and-play
Einführung in Simulink
 Einführung in Simulink Inhalt 1 Grundlegendes... 2 2 Simulink starten... 2 3 Erstellen von Simulinkmodellen... 3 3.1 Platzieren und Verbinden der Simulinkblöcke... 3 3.2 Eintragen der Block-Parameter...
Einführung in Simulink Inhalt 1 Grundlegendes... 2 2 Simulink starten... 2 3 Erstellen von Simulinkmodellen... 3 3.1 Platzieren und Verbinden der Simulinkblöcke... 3 3.2 Eintragen der Block-Parameter...
MATLAB -Simulink - Stateflow
 MATLAB -Simulink - Stateflow Grundlagen,Toolboxen, Beispiele von Dr.-lng. Anne Angermann, Dr.-lng. Michael Beuschel, Dr.-lng. Martin Rau, Dipl.-lng. Ulrich Wohlfarth 6., aktualisierte Auflage Oldenbourg
MATLAB -Simulink - Stateflow Grundlagen,Toolboxen, Beispiele von Dr.-lng. Anne Angermann, Dr.-lng. Michael Beuschel, Dr.-lng. Martin Rau, Dipl.-lng. Ulrich Wohlfarth 6., aktualisierte Auflage Oldenbourg
Einführung in MATLAB und SIMULINK 1 MATLAB. Institut für Prozess- und Verfahrenstechnik Fachgebiet Mess- und Regelungstechnik
 Institut für Prozess- und Verfahrenstechnik Fachgebiet Mess- und Regelungstechnik Prof. Dr.-Ing. R. King Seite 1 Einführung in MATLAB und SIMULINK (7. Dezember 2007) MATLAB und der graphische Aufsatz SIMULINK
Institut für Prozess- und Verfahrenstechnik Fachgebiet Mess- und Regelungstechnik Prof. Dr.-Ing. R. King Seite 1 Einführung in MATLAB und SIMULINK (7. Dezember 2007) MATLAB und der graphische Aufsatz SIMULINK
2 Systemanalyse mit Matlab/Simulink
 2 Systemanalyse mit Matlab/Simulink Ziel dieser Übung ist es, das Computerprogramm Matlab/Simulink für die Systemanalyse einzusetzen. Alle Aufgabenstellungen dieser Übungseinheit sind mit diesem Softwarepaket
2 Systemanalyse mit Matlab/Simulink Ziel dieser Übung ist es, das Computerprogramm Matlab/Simulink für die Systemanalyse einzusetzen. Alle Aufgabenstellungen dieser Übungseinheit sind mit diesem Softwarepaket
Funktionen in Matlab. Lehrstuhl für Angewandte Mathematik Sommersemester und 29. Mai 2008
 Funktionen in Matlab Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Sommersemester 2008 15. und 29. Mai 2008 Funktionen in Matlab Wir kennen schon diverse
Funktionen in Matlab Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Sommersemester 2008 15. und 29. Mai 2008 Funktionen in Matlab Wir kennen schon diverse
Einführung in moderne Simulationstechniken Kursteil: Matlab und Simulink. Felix Goßmann, Gunther Reißig
 Einführung in moderne Simulationstechniken Kursteil: Matlab und Simulink Felix Goßmann, Gunther Reißig Institut für Steuer- und Regelungstechnik Fakultät für Luft- und Raumfahrttechnik Universität der
Einführung in moderne Simulationstechniken Kursteil: Matlab und Simulink Felix Goßmann, Gunther Reißig Institut für Steuer- und Regelungstechnik Fakultät für Luft- und Raumfahrttechnik Universität der
MATLAB und Simulink. Eine kursorientierte Einführung. Ottmar Beucher
 MATLAB und Simulink Eine kursorientierte Einführung Ottmar Beucher 5 Einführung in Simulink Bei dem Simulationswerkzeug Simulink handelt es sich um ein Programm zur Simulation dynamischer Systeme mit einer
MATLAB und Simulink Eine kursorientierte Einführung Ottmar Beucher 5 Einführung in Simulink Bei dem Simulationswerkzeug Simulink handelt es sich um ein Programm zur Simulation dynamischer Systeme mit einer
Matlab Übersicht. Matlab steht für MATrix LABoratory, die Fa. The Mathworks wurde 1984 gegründet
 Matlab Übersicht Ziel: einfacher Zugang zu numerischen (FORTRAN)Bibliotheken [Freeware] Linpack (LINear Algebra Solution PACKage) und Eispack (EIgenvalue Solution PACKage) => aktuelle Version: Lapack (Linear
Matlab Übersicht Ziel: einfacher Zugang zu numerischen (FORTRAN)Bibliotheken [Freeware] Linpack (LINear Algebra Solution PACKage) und Eispack (EIgenvalue Solution PACKage) => aktuelle Version: Lapack (Linear
Regelungstechnik I (WS 15/16) Übung 2
 Regelungstechnik I (WS 5/6) Übung Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Aufgabe. (Linearität, Zeitinvarianz). Überprüfen Sie die folgenden dynamischen Systeme auf Linearität
Regelungstechnik I (WS 5/6) Übung Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Aufgabe. (Linearität, Zeitinvarianz). Überprüfen Sie die folgenden dynamischen Systeme auf Linearität
Simulink: Softwareentwurf für eingebettete Systeme ROS-Arduino-Interface. von Christian Schildwächter
 Simulink: Softwareentwurf für eingebettete Systeme ROS-Arduino-Interface von Christian Schildwächter Simulink Simulink S-Functions Softwareprojekt ROS-Arduino-Interface Simulink 3 LIVE DEMO 4 External
Simulink: Softwareentwurf für eingebettete Systeme ROS-Arduino-Interface von Christian Schildwächter Simulink Simulink S-Functions Softwareprojekt ROS-Arduino-Interface Simulink 3 LIVE DEMO 4 External
PRAKTIKUMSVERSUCH M/S 2
 Fakultät Informatik, Institut für Angewandte Informatik, Professur Technische Informationssysteme PRAKTIKUMSVERSUCH M/S 2 Betreuer: Dipl.-Ing. Burkhard Hensel Dr.-Ing. Alexander Dementjev ALLGEMEINE BEMERKUNGEN
Fakultät Informatik, Institut für Angewandte Informatik, Professur Technische Informationssysteme PRAKTIKUMSVERSUCH M/S 2 Betreuer: Dipl.-Ing. Burkhard Hensel Dr.-Ing. Alexander Dementjev ALLGEMEINE BEMERKUNGEN
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Treffpunkt MATLAB Einführung 1. Agenda. Begrüßung. Wie bekomme ich MATLAB? MATLAB im Studium. Vorstellung des Treffpunkt MATLAB. Vortrag von MathWorks
 Treffpunkt MATLAB Einführung 1 Agenda Begrüßung Wie bekomme ich MATLAB? MATLAB im Studium Vorstellung des Treffpunkt MATLAB Vortrag von MathWorks 1 Wie bekomme ich MATLAB 2015b Daniel Zöller Institut für
Treffpunkt MATLAB Einführung 1 Agenda Begrüßung Wie bekomme ich MATLAB? MATLAB im Studium Vorstellung des Treffpunkt MATLAB Vortrag von MathWorks 1 Wie bekomme ich MATLAB 2015b Daniel Zöller Institut für
Inversion dynamischer Systeme mit Matlab
 Inversion dynamischer Systeme mit Matlab Jörg J. Buchholz (Hochschule Bremen) Wolfgang v. Grünhagen (DLR Braunschweig) 7. Dezember 2007 Einleitung Eine Aufgabe im Rahmen des US/German Memorandum of Understanding
Inversion dynamischer Systeme mit Matlab Jörg J. Buchholz (Hochschule Bremen) Wolfgang v. Grünhagen (DLR Braunschweig) 7. Dezember 2007 Einleitung Eine Aufgabe im Rahmen des US/German Memorandum of Understanding
SIMULINK. Grundlagen
 SIMULINK Grundlagen Simulation mit Simulink/Matlab WS13/14 Inhalt SIMULINK Allgemeines SIMULINK Bibliotheken Sources, Sinks, Math Operations und Logic and Bit Operations Simulationsparameter Algorithmen
SIMULINK Grundlagen Simulation mit Simulink/Matlab WS13/14 Inhalt SIMULINK Allgemeines SIMULINK Bibliotheken Sources, Sinks, Math Operations und Logic and Bit Operations Simulationsparameter Algorithmen
Inhalt. 8. Simulink Grundlagen 9. Simulink Übungen. Daniel Schrammel - BA Stuttgart -
 Inhalt 8. Simulink Grundlagen 9. Simulink Übungen 8. Simulink-Grundlagen Was ist Simulink? SIMULINK ist Teil der Matlab Programmgruppe zur Simulation und Analyse von diskreter und kontinuierlicher dynamischer
Inhalt 8. Simulink Grundlagen 9. Simulink Übungen 8. Simulink-Grundlagen Was ist Simulink? SIMULINK ist Teil der Matlab Programmgruppe zur Simulation und Analyse von diskreter und kontinuierlicher dynamischer
Johannes Kepler Universität Linz. Automatisierungstechnik Praktikum SS 2016. Institut für Regelungstechnik und Prozessautomatisierung
 Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Automatisierungstechnik Praktikum SS 2016 Anastasiia Galkina Bernd Kolar Markus Schöberl Stand: 29. Februar 2016
Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Automatisierungstechnik Praktikum SS 2016 Anastasiia Galkina Bernd Kolar Markus Schöberl Stand: 29. Februar 2016
MATLAB Grundlagen MATLAB. Grundlagen. Vorlesung Matlab/Simulink Dipl.-Ing. U. Wohlfarth
 MATLAB Grundlagen Dipl.-Ing. U. Wohlfarth Was ist MATLAB? Softwarepaket zur numerischen Mathematik Speziell für Vektoren & Matrizen: MATrix LABoratory Basismodul für allgemeine Mathematik, Ein/Ausgabe,
MATLAB Grundlagen Dipl.-Ing. U. Wohlfarth Was ist MATLAB? Softwarepaket zur numerischen Mathematik Speziell für Vektoren & Matrizen: MATrix LABoratory Basismodul für allgemeine Mathematik, Ein/Ausgabe,
4.2 Selbstdefinierte Matlab-Funktionen 1. Teil
 4.2 Selbstdefinierte Matlab-Funktionen 1. Teil 37 Ein m-file mit Namen Funktionsname.m und einer ersten Zeile der folgen Form: function Funktionsname(input1,input2,...,inputn) oder function output1=funktionsname(input1,input2,...,inputn)
4.2 Selbstdefinierte Matlab-Funktionen 1. Teil 37 Ein m-file mit Namen Funktionsname.m und einer ersten Zeile der folgen Form: function Funktionsname(input1,input2,...,inputn) oder function output1=funktionsname(input1,input2,...,inputn)
Vordiplomprüfung Grundlagen der Elektrotechnik III
 Vordiplomprüfung Grundlagen der Elektrotechnik III 16. Februar 2007 Name:... Vorname:... Mat.Nr.:... Studienfach:... Abgegebene Arbeitsblätter:... Bitte unterschreiben Sie, wenn Sie mit der Veröffentlichung
Vordiplomprüfung Grundlagen der Elektrotechnik III 16. Februar 2007 Name:... Vorname:... Mat.Nr.:... Studienfach:... Abgegebene Arbeitsblätter:... Bitte unterschreiben Sie, wenn Sie mit der Veröffentlichung
Labor Informationstechnik FSK
 Labor Informationstechnik Prof. Dr. Ing. Lilia Lajmi Dipl. Ing. Irina Ikkert FSK Gruppennummer: eilnehmer: Name Vorname Matrikelnummer 1 2 Ostfalia Hochschule für angewandte Wissenschaften Hochschule Braunschweig/Wolfenbüttel
Labor Informationstechnik Prof. Dr. Ing. Lilia Lajmi Dipl. Ing. Irina Ikkert FSK Gruppennummer: eilnehmer: Name Vorname Matrikelnummer 1 2 Ostfalia Hochschule für angewandte Wissenschaften Hochschule Braunschweig/Wolfenbüttel
Eine Kurzanleitung zu Mathematica
 MOSES Projekt, GL, Juni 2003 Eine Kurzanleitung zu Mathematica Wir geben im Folgenden eine sehr kurze Einführung in die Möglichkeiten, die das Computer Algebra System Mathematica bietet. Diese Datei selbst
MOSES Projekt, GL, Juni 2003 Eine Kurzanleitung zu Mathematica Wir geben im Folgenden eine sehr kurze Einführung in die Möglichkeiten, die das Computer Algebra System Mathematica bietet. Diese Datei selbst
Praktikum zur Vorlesung Energienetze und Netzoptimierung
 Praktikum zur Vorlesung Energienetze und Netzoptimierung TU Bergakademie Freiberg Institut für Automatisierungstechnik Prof. Dr.-Ing. A. Rehkopf. Februar Anleitung Aufbau und Wirkungsweise eines Blockheizkraftwerks
Praktikum zur Vorlesung Energienetze und Netzoptimierung TU Bergakademie Freiberg Institut für Automatisierungstechnik Prof. Dr.-Ing. A. Rehkopf. Februar Anleitung Aufbau und Wirkungsweise eines Blockheizkraftwerks
Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder
 DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
Einführung in SIMULINK
 CIC Lab Computational Intelligence and Control Laboratory Einführung in SIMULINK Prof. Dipl.-Ing. Dipl.-Ing. Ulrich Lehmann Dipl.-Ing. Udo Reitz 22 Inhaltsverzeichnis Inhaltsverzeichnis 1 Grundsätzliches
CIC Lab Computational Intelligence and Control Laboratory Einführung in SIMULINK Prof. Dipl.-Ing. Dipl.-Ing. Ulrich Lehmann Dipl.-Ing. Udo Reitz 22 Inhaltsverzeichnis Inhaltsverzeichnis 1 Grundsätzliches
Matlab Einführung. Tobias Wunner
 Matlab Einführung Tobias Wunner 16. Oktober 2006 Vorteile Interpreter und interaktive Befehlseingabe Schnelles Implementieren von wissenschaftlichen Methoden Gutes Hilfesystem >> lookfor 'sum' TRACE Sum
Matlab Einführung Tobias Wunner 16. Oktober 2006 Vorteile Interpreter und interaktive Befehlseingabe Schnelles Implementieren von wissenschaftlichen Methoden Gutes Hilfesystem >> lookfor 'sum' TRACE Sum
R a i n e r N i e u w e n h u i z e n K a p e l l e n s t r G r e v e n T e l / F a x / e
 R a i n e r N i e u w e n h u i z e n K a p e l l e n s t r. 5 4 8 6 2 8 G r e v e n T e l. 0 2 5 7 1 / 9 5 2 6 1 0 F a x. 0 2 5 7 1 / 9 5 2 6 1 2 e - m a i l r a i n e r. n i e u w e n h u i z e n @ c
R a i n e r N i e u w e n h u i z e n K a p e l l e n s t r. 5 4 8 6 2 8 G r e v e n T e l. 0 2 5 7 1 / 9 5 2 6 1 0 F a x. 0 2 5 7 1 / 9 5 2 6 1 2 e - m a i l r a i n e r. n i e u w e n h u i z e n @ c
SSYLB2 SS06 Daniel Schrenk, Andreas Unterweger Übung 8. Laborprotokoll SSY. Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort
 SSYLB SS6 Daniel Schrenk, Andreas Unterweger Übung 8 Laborprotokoll SSY Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort Daniel Schrenk, Andreas Unterweger, ITS 4 SSYLB SS6 Daniel Schrenk,
SSYLB SS6 Daniel Schrenk, Andreas Unterweger Übung 8 Laborprotokoll SSY Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort Daniel Schrenk, Andreas Unterweger, ITS 4 SSYLB SS6 Daniel Schrenk,
Exascale Computing. = Exascale braucht Manycore-Hardware...und was für Software??? 46/58
 Exascale Computing Die FLOP/s-Tabelle: Name Faktor erreicht heute Giga 10 9 1976 CPU-Kern Tera 10 12 1997 Graphikkarte (GPU) Peta 10 15 2009 Supercomputer Exa 10 18 2020(?) Der gegenwärtig schnellste Rechner
Exascale Computing Die FLOP/s-Tabelle: Name Faktor erreicht heute Giga 10 9 1976 CPU-Kern Tera 10 12 1997 Graphikkarte (GPU) Peta 10 15 2009 Supercomputer Exa 10 18 2020(?) Der gegenwärtig schnellste Rechner
SIMULINK-iFBSpro-Compiler V3.2. zur Integration von Simulink- Modellen in das Funktionsblocksystem ifbspro. Bedienhandbuch
 SIMULINK-iFBSpro-Compiler V3.2 zur Integration von Simulink- Modellen in das Funktionsblocksystem ifbspro Bedienhandbuch Bearbeiter: und Dr. J. Alex Dr. T. B. To, ifak, Institut für Automation und Kommunikation
SIMULINK-iFBSpro-Compiler V3.2 zur Integration von Simulink- Modellen in das Funktionsblocksystem ifbspro Bedienhandbuch Bearbeiter: und Dr. J. Alex Dr. T. B. To, ifak, Institut für Automation und Kommunikation
AU-D21. Digital Audio Optical Switcher OPERATION MANUAL
 AU-D21 Digital Audio Optical Switcher OPERATION MANUAL Table of Contents 1. Introduction 1 2. Features 1 3. Operation Controls and Functions 2 3.1 Front Panel Diagram 2 3.2 Rear Panel Diagram 2 3.3 Side
AU-D21 Digital Audio Optical Switcher OPERATION MANUAL Table of Contents 1. Introduction 1 2. Features 1 3. Operation Controls and Functions 2 3.1 Front Panel Diagram 2 3.2 Rear Panel Diagram 2 3.3 Side
Matlab bis. zum Limit. Hier klicken, um Master-Titelformat zu bearbeiten. Hier klicken, um Master-Textformat zu bearbeiten. Zweite Ebene Dritte Ebene
 Matlab bis zum Limit Praxiserfahrungen mit komplexen Simulationen und Analysen unter Matlab / Simulink Dr.-Ing. Gordon Strickert Hier klicken, Matlab um Master-Titelformat? Was ist Matlab Matrix Laboratory
Matlab bis zum Limit Praxiserfahrungen mit komplexen Simulationen und Analysen unter Matlab / Simulink Dr.-Ing. Gordon Strickert Hier klicken, Matlab um Master-Titelformat? Was ist Matlab Matrix Laboratory
PRAKTIKUM SIMULATIONSTECHNIK
 FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM SIMULATIONSTECHNIK 1 Versuch1: Atmungsregulation 1.1 Einleitung Bei Säugetieren gewinnt jede Zelle ihre Energie hauptsächlich
FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM SIMULATIONSTECHNIK 1 Versuch1: Atmungsregulation 1.1 Einleitung Bei Säugetieren gewinnt jede Zelle ihre Energie hauptsächlich
Klimaregler Air-Conditioning Controllers
 1 limaregler Air-Conditioning Controllers anspruchsvolles Design/ attractive design hohe Präzision/ high precision robuste Zuverlässigkeit/ robust reliability 2 Invensys LR-E 7004 LR-E 7006 Anzeigelampen
1 limaregler Air-Conditioning Controllers anspruchsvolles Design/ attractive design hohe Präzision/ high precision robuste Zuverlässigkeit/ robust reliability 2 Invensys LR-E 7004 LR-E 7006 Anzeigelampen
All Digital Transceiver
 All Digital Transceiver Prinzip Digital-Empfänger ADC, Analog Digital Converter ( Analog-Digital-Wandler ) DDC, Digital Down Converter ( Digitaler Abwärtsmischer ) DSP, Digital Signal Processor SDR-14
All Digital Transceiver Prinzip Digital-Empfänger ADC, Analog Digital Converter ( Analog-Digital-Wandler ) DDC, Digital Down Converter ( Digitaler Abwärtsmischer ) DSP, Digital Signal Processor SDR-14
6. Erzwungene Schwingungen
 6. Erzwungene Schwingungen Ein durch zeitveränderliche äußere Einwirkung zum Schwingen angeregtes (gezwungenes) System führt erzwungene Schwingungen durch. Bedeutsam sind vor allem periodische Erregungen
6. Erzwungene Schwingungen Ein durch zeitveränderliche äußere Einwirkung zum Schwingen angeregtes (gezwungenes) System führt erzwungene Schwingungen durch. Bedeutsam sind vor allem periodische Erregungen
Zusicherungen und Laufzeit Überwachungen in der modellbasierten Software Entwicklung
 Zusicherungen und Laufzeit Überwachungen in der modellbasierten Software Entwicklung Methoden Design Integration STZ Softwaretechnik Andreas Rau STZ Softwaretechnik Im Gaugenmaier 20 73730 Esslingen Email:
Zusicherungen und Laufzeit Überwachungen in der modellbasierten Software Entwicklung Methoden Design Integration STZ Softwaretechnik Andreas Rau STZ Softwaretechnik Im Gaugenmaier 20 73730 Esslingen Email:
Optimal Control in Air Traffic Management
 Optimal Control in Air Traffic Management DGLR Workshop Bestimmung optimaler Trajektorien im Air Traffic Management 23.04.2013 Deutsche Flugsicherung GmbH, Langen 23.04.2013 1 Inhalt. Hintergrund und Motivation.
Optimal Control in Air Traffic Management DGLR Workshop Bestimmung optimaler Trajektorien im Air Traffic Management 23.04.2013 Deutsche Flugsicherung GmbH, Langen 23.04.2013 1 Inhalt. Hintergrund und Motivation.
Effekte einer negativen Rückführung
 Effekte einer negativen Rückführung Reduziert den Effekt von Störungen und Parameteränderungen. Reduziert den Einfluß von Nichtlinearitäten. Sorgt für eine konstante Verstärkung. Verändert die Systemeigenschaften.
Effekte einer negativen Rückführung Reduziert den Effekt von Störungen und Parameteränderungen. Reduziert den Einfluß von Nichtlinearitäten. Sorgt für eine konstante Verstärkung. Verändert die Systemeigenschaften.
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. 4. Dämpfungsmodelle. Elastodynamik 1 3.
 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
Eingebettete Systeme
 Einführung in Eingebettete Systeme Vorlesung 5 Bernd Finkbeiner 19/11/2014 [email protected] Prof. Bernd Finkbeiner, Ph.D. [email protected] 1 Hardware in a loop actuators 2 Sensorsysteme
Einführung in Eingebettete Systeme Vorlesung 5 Bernd Finkbeiner 19/11/2014 [email protected] Prof. Bernd Finkbeiner, Ph.D. [email protected] 1 Hardware in a loop actuators 2 Sensorsysteme
Dämpfung. . Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung. Elastodynamik 2 SS
 Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Einführung in MATLAB
 Kapitel 4 Einführung in MATLAB 41 Allgemeines MATLAB ist eine kommerzielle mathematische Software zur Lösung mathematischer Probleme und zur graphischen Darstellung der Ergebnisse Die Verfahren in MATLAB
Kapitel 4 Einführung in MATLAB 41 Allgemeines MATLAB ist eine kommerzielle mathematische Software zur Lösung mathematischer Probleme und zur graphischen Darstellung der Ergebnisse Die Verfahren in MATLAB
Musterlösung zur Klausur. Grundlagen der Mechatronik
 26.3.212 Musterlösung zur Klausur Grundlagen der Mechatronik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die Bearbeitungszeit
26.3.212 Musterlösung zur Klausur Grundlagen der Mechatronik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die Bearbeitungszeit
 - - CodE 11 CodE 0 0 0 0 0 0 0 0 2.o C 1 10.0 C 2 off 3 3.0 4 2.0 5 off 6 1 8 20.0 9 60 C 7 4.0 10 80 C 1 38 C 12 8 k 13 on 14 30.0 15 10 16 - - CodE 11 CodE 0 0 0 0 0 0 0 0 2.o C 1 10.0 C 2
- - CodE 11 CodE 0 0 0 0 0 0 0 0 2.o C 1 10.0 C 2 off 3 3.0 4 2.0 5 off 6 1 8 20.0 9 60 C 7 4.0 10 80 C 1 38 C 12 8 k 13 on 14 30.0 15 10 16 - - CodE 11 CodE 0 0 0 0 0 0 0 0 2.o C 1 10.0 C 2
Grundlagen der Regelungstechnik
 Grundlagen der Regelungstechnik Dr.-Ing. Georg von Wichert Siemens AG, Corporate Technology, München Wiederholung vom letzten Mal Einführung Regelungstechnik: Lehre von der gezielten Beeinflussung dynamischer
Grundlagen der Regelungstechnik Dr.-Ing. Georg von Wichert Siemens AG, Corporate Technology, München Wiederholung vom letzten Mal Einführung Regelungstechnik: Lehre von der gezielten Beeinflussung dynamischer
1 Konsole öffnen. 2 matlab & und return eingeben. 3 Konsole dauerhaft geöffnet lassen. 1 Menüpunkt File - Exit MATLAB oder. 2 quit (und return) oder
 Grundleges Einführung in Matlab Christof Eck, Monika Schulz und Jan Mayer Matlab starten: 1 Konsole öffnen 2 matlab & und return eingeben 3 Konsole dauerhaft geöffnet lassen Matlab been: 1 Menüpunkt File
Grundleges Einführung in Matlab Christof Eck, Monika Schulz und Jan Mayer Matlab starten: 1 Konsole öffnen 2 matlab & und return eingeben 3 Konsole dauerhaft geöffnet lassen Matlab been: 1 Menüpunkt File
Laplace-Transformation
 Laplace-Transformation Gegeben: Funktion mit beschränktem Wachstum: x(t) Ke ct t [, ) Definition: Laplace-Transformation: X(s) = e st x(t) dt = L{x(t)} s C Re(s) >c Definition: Inverse Laplace-Transformation:
Laplace-Transformation Gegeben: Funktion mit beschränktem Wachstum: x(t) Ke ct t [, ) Definition: Laplace-Transformation: X(s) = e st x(t) dt = L{x(t)} s C Re(s) >c Definition: Inverse Laplace-Transformation:
14 Übungen zu Regelung im Zustandsraum Teil 2
 Zoltán Zomotor Versionsstand: 9. März 25, :32 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3. Germany License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3./de/
Zoltán Zomotor Versionsstand: 9. März 25, :32 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3. Germany License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3./de/
Termin 4: Programmieren in MATLAB
 Termin 4: Programmieren in MATLAB Währ dieses Termins werden Sie die Gelegenheit haben, sich am PC in die Grundlagen der Programmierung in MATLAB einzuarbeiten. Sie werden zwei mögliche Programmformen
Termin 4: Programmieren in MATLAB Währ dieses Termins werden Sie die Gelegenheit haben, sich am PC in die Grundlagen der Programmierung in MATLAB einzuarbeiten. Sie werden zwei mögliche Programmformen
Description of version PASO MD2
 Deutscher Text folgt nach dem englischen Text ----------------------------------------------------------------------- English text Description of version PASO MD2 Version 2.1.0.2 (25.11.2015) - Error with
Deutscher Text folgt nach dem englischen Text ----------------------------------------------------------------------- English text Description of version PASO MD2 Version 2.1.0.2 (25.11.2015) - Error with
Ersatzschaltbild eines Operationsverstärkers für den Betrieb bei niederen Frequenzen
 Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Ersatzschaltbild eines Operationsverstärkers für den Betrieb bei niederen Frequenzen Unterlagen zur Vorlesung Regelungstechnik
Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Ersatzschaltbild eines Operationsverstärkers für den Betrieb bei niederen Frequenzen Unterlagen zur Vorlesung Regelungstechnik
PRAKTIKUM REGELUNGSTECHNIK 2
 FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM REGELUNGSTECHNIK 2 1 Versuch 2: Übertragungsfunktion und Polvorgabe 1.1 Einleitung Die Laplace Transformation ist ein äußerst
FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM REGELUNGSTECHNIK 2 1 Versuch 2: Übertragungsfunktion und Polvorgabe 1.1 Einleitung Die Laplace Transformation ist ein äußerst
4.2 Der Harmonische Oszillator
 Dieter Suter - 208 - Physik B3, SS03 4.2 Der Harmonische Oszillator 4.2.1 Harmonische Schwingungen Die Zeitabhängigkeit einer allgemeinen Schwingung ist beliebig, abgesehen von der Periodizität. Die mathematische
Dieter Suter - 208 - Physik B3, SS03 4.2 Der Harmonische Oszillator 4.2.1 Harmonische Schwingungen Die Zeitabhängigkeit einer allgemeinen Schwingung ist beliebig, abgesehen von der Periodizität. Die mathematische
Anwendungssoftware III (MATLAB)
 Anwendungssoftware III (MATLAB) VII - Spezielle Themen Michael Liedlgruber Fachbereich Computerwissenschaften Universität Salzburg Sommersemester 2014 M. Liedlgruber Anwendungssoftware III (MATLAB) SS
Anwendungssoftware III (MATLAB) VII - Spezielle Themen Michael Liedlgruber Fachbereich Computerwissenschaften Universität Salzburg Sommersemester 2014 M. Liedlgruber Anwendungssoftware III (MATLAB) SS
3 Kurzeinführung in Matlab
 3 Kurzeinführung in Matlab Matlab ist ein sehr leistungsfähiges interaktives Programmpaket für numerische Berechnungen. Nutzen Sie dies parallel zu den Vorlesungen. Sie können damit persönlich erfahren,
3 Kurzeinführung in Matlab Matlab ist ein sehr leistungsfähiges interaktives Programmpaket für numerische Berechnungen. Nutzen Sie dies parallel zu den Vorlesungen. Sie können damit persönlich erfahren,
 =!'04 #>4 )-:!- / )) $!# & $ % # %)6 ) + # 6 0 %% )90 % 1% $ 9116 69)" %" :"6. 1-0 &6 -% ' 0' )%1 0(,"'% #6 0 )90 1-11 ) 9 #,0. 1 #% 0 9 & %) ) '' #' ) 0 # %6 ;+'' 0 6%((&0 6?9 ;+'' 0 9)&6? #' 1 0 +& $
=!'04 #>4 )-:!- / )) $!# & $ % # %)6 ) + # 6 0 %% )90 % 1% $ 9116 69)" %" :"6. 1-0 &6 -% ' 0' )%1 0(,"'% #6 0 )90 1-11 ) 9 #,0. 1 #% 0 9 & %) ) '' #' ) 0 # %6 ;+'' 0 6%((&0 6?9 ;+'' 0 9)&6? #' 1 0 +& $
MATLAB. Control System Toolbox
 MATLAB Control System Toolbox Dipl.-Ing. U. Wohlfarth 1 Umfang Beschreibung linearer, zeitinvarianter Systeme (LTI): zeitkontinuierlich und zeitdiskret Single Input/Single Output (SISO) und Multiple Input/Multiple
MATLAB Control System Toolbox Dipl.-Ing. U. Wohlfarth 1 Umfang Beschreibung linearer, zeitinvarianter Systeme (LTI): zeitkontinuierlich und zeitdiskret Single Input/Single Output (SISO) und Multiple Input/Multiple
Determining Vibro-Acoustic Effects in Multidomain Systems using a Custom Simscape Gear Library
 Determining Vibro-Acoustic Effects in Multidomain Systems using a Custom Simscape Gear Library Tim Dackermann, Rolando Dölling Robert Bosch GmbH Lars Hedrich Goethe-University Ffm 1 Power Noise transmission
Determining Vibro-Acoustic Effects in Multidomain Systems using a Custom Simscape Gear Library Tim Dackermann, Rolando Dölling Robert Bosch GmbH Lars Hedrich Goethe-University Ffm 1 Power Noise transmission
Zustandsraum: Historische Einordnung
 Zustandsraum: Historische Einordnung Die Grundlagen der Zustandsraummethoden wurden im Zeitraum 1955 1965 von Kalman und seinen Kollegen in dem Research Institute for Advanced Studies in Baltimore entwickelt.
Zustandsraum: Historische Einordnung Die Grundlagen der Zustandsraummethoden wurden im Zeitraum 1955 1965 von Kalman und seinen Kollegen in dem Research Institute for Advanced Studies in Baltimore entwickelt.
Zugänge zur Kontinuierlichen Simulation
 Zugänge zur Kontinuierlichen Simulation R. Hohmann [email protected] Institut für Simulation und Graphik Universität Magdeburg, PF 4120, 39016 Magdeburg Kurzfassung Im folgenden werden drei
Zugänge zur Kontinuierlichen Simulation R. Hohmann [email protected] Institut für Simulation und Graphik Universität Magdeburg, PF 4120, 39016 Magdeburg Kurzfassung Im folgenden werden drei
IEMS Regelungstechnik Abschlussklausur
 IEMS Regelungstechnik Abschlussklausur Prof. Dr. Moritz Diehl, IMTEK, Universität Freiburg, und ESAT-STADIUS, KU Leuven 30. August, 0:5-3:5, Freiburg, Georges-Koehler-Allee 06, Raum 00-007 page 0 2 3 4
IEMS Regelungstechnik Abschlussklausur Prof. Dr. Moritz Diehl, IMTEK, Universität Freiburg, und ESAT-STADIUS, KU Leuven 30. August, 0:5-3:5, Freiburg, Georges-Koehler-Allee 06, Raum 00-007 page 0 2 3 4
TIn 1: Feedback Laboratories. Lecture 4 Data transfer. Question: What is the IP? Institut für Embedded Systems. Institut für Embedded Systems
 Mitglied der Zürcher Fachhochschule TIn 1: Lecture 4 Data transfer Feedback Laboratories Question: What is the IP? Why do we NEED an IP? Lecture 3: Lernziele Moving data, the why s and wherefores Moving
Mitglied der Zürcher Fachhochschule TIn 1: Lecture 4 Data transfer Feedback Laboratories Question: What is the IP? Why do we NEED an IP? Lecture 3: Lernziele Moving data, the why s and wherefores Moving
Selber Programmieren
 Selber Programmieren Wenn es für ein Problem keine fertige Lösung gibt, oder wenn man keine fertige Lösung finden kann, dann muss man sich das benötigte Werkzeug selbst herstellen: Ein eigenes Programm
Selber Programmieren Wenn es für ein Problem keine fertige Lösung gibt, oder wenn man keine fertige Lösung finden kann, dann muss man sich das benötigte Werkzeug selbst herstellen: Ein eigenes Programm
Automatisierungstechnik nach internationaler Norm programmieren (3) Folge 3: Einführung in die Handhabung von POE s und Bibliotheken
 Automatisierungstechnik nach internationaler Norm programmieren (3) Autor: Dr. Ulrich Becker Fachzentrum Automatisierungstechnik und vernetzte Systeme im BTZ Rohr-Kloster Mail: [email protected]
Automatisierungstechnik nach internationaler Norm programmieren (3) Autor: Dr. Ulrich Becker Fachzentrum Automatisierungstechnik und vernetzte Systeme im BTZ Rohr-Kloster Mail: [email protected]
Fakultät Grundlagen. Februar 2016
 Schwingungsdifferenzialgleichung Fakultät Grundlagen Hochschule Esslingen Februar 016 Fakultät Grundlagen Schwingungsdifferenzialgleichung Übersicht 1 Schwingungsdifferenzialgleichung Fakultät Grundlagen
Schwingungsdifferenzialgleichung Fakultät Grundlagen Hochschule Esslingen Februar 016 Fakultät Grundlagen Schwingungsdifferenzialgleichung Übersicht 1 Schwingungsdifferenzialgleichung Fakultät Grundlagen
SIMATIC HMI Mobile Panels 2nd Generation Wichtige Hinweise zu Ihrem Gerät Produktinformation
 SIMATIC HMI Mobile Panels 2nd Generation Wichtige e zu Ihrem Gerät Produktinformation A5E35655148 Gültigkeit Diese Produktinformation gilt für folgende Bediengeräte vom Typ "Mobile Panels 2nd Generation":
SIMATIC HMI Mobile Panels 2nd Generation Wichtige e zu Ihrem Gerät Produktinformation A5E35655148 Gültigkeit Diese Produktinformation gilt für folgende Bediengeräte vom Typ "Mobile Panels 2nd Generation":
PLC-5- und SLC-Prozessoren im DH+ Verbund (SLC 5/04 -Prozessoren)
 Schnellinformation PLC-5- und SLC-Prozessoren im DH+ Verbund (SLC 5/04 -Prozessoren) In dieser Publikation sind Informationen aus verfügbaren PLC - und SLC -Dokumentationen zusammengestellt, um die Kommunikation
Schnellinformation PLC-5- und SLC-Prozessoren im DH+ Verbund (SLC 5/04 -Prozessoren) In dieser Publikation sind Informationen aus verfügbaren PLC - und SLC -Dokumentationen zusammengestellt, um die Kommunikation
Einstieg in das Programmieren mit MATLAB
 Ulrich Stein Einstieg in das Programmieren mit MATLAB ISBN-10: 3-446-41009-0 ISBN-13: 978-3-446-41009-1 Inhaltsverzeichnis Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-41009-1
Ulrich Stein Einstieg in das Programmieren mit MATLAB ISBN-10: 3-446-41009-0 ISBN-13: 978-3-446-41009-1 Inhaltsverzeichnis Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-41009-1
Kontrollstrukturen MySQL Funktionen. MySQL 4, 5. Kapitel 20a: PHP Teil 2. Marcel Noe
 MySQL 4, 5 Kapitel 20a: PHP Teil 2 Gliederung 1 2 Gliederung 1 2 Die ermöglicht ein Bedingtes Ausführen von Code-Abschnitten. Nur wenn die Bedingung erfüllt ist wird der Block hinter if ausgeführt. Ist
MySQL 4, 5 Kapitel 20a: PHP Teil 2 Gliederung 1 2 Gliederung 1 2 Die ermöglicht ein Bedingtes Ausführen von Code-Abschnitten. Nur wenn die Bedingung erfüllt ist wird der Block hinter if ausgeführt. Ist
Signal Processing LWL-Sender/Empfänger mit Outdoor-Box für die störsichere Übertragung von Rechtecksignalen
 LWL-Sender/Empfänger mit Outdoor-Box für die störsichere Übertragung von Rechtecksignalen LWL Sender/Empfänger mit Outdoor-Box Merkmale LWL-SBR, Übertragungsweiten bis zu 1500 m Wandlung üblicher Rechtecksignale
LWL-Sender/Empfänger mit Outdoor-Box für die störsichere Übertragung von Rechtecksignalen LWL Sender/Empfänger mit Outdoor-Box Merkmale LWL-SBR, Übertragungsweiten bis zu 1500 m Wandlung üblicher Rechtecksignale
Typische Prüfungsaufgaben
 Fragenkatalog zur Prüfung, Stand: 18. Dez. 2014 Seite 1 Die schriftliche Prüfung für die Vorlesung Objektorientierte Modellierung mechatronischer Systeme (als Teil des Moduls Simulation von mechatronischen
Fragenkatalog zur Prüfung, Stand: 18. Dez. 2014 Seite 1 Die schriftliche Prüfung für die Vorlesung Objektorientierte Modellierung mechatronischer Systeme (als Teil des Moduls Simulation von mechatronischen
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
3 Schnellkurs in MATLAB
 3 Schnellkurs in MATLAB 3.1 Einführung MATLAB (= Matrix laboratory) Softwarepaket für numerische Berechnungen und Visualisierungen 1980 ( Cleve Moler; www.mathworks.com ) Ursprung in LINPACK und EISPACK
3 Schnellkurs in MATLAB 3.1 Einführung MATLAB (= Matrix laboratory) Softwarepaket für numerische Berechnungen und Visualisierungen 1980 ( Cleve Moler; www.mathworks.com ) Ursprung in LINPACK und EISPACK
Weiterbildung für Ingenieure Numerische Methoden für Differentialgleichungen Prinzipien und Praxis Taubert, Heitmann Universität Hamburg WS03/04
 Weiterbildung für Ingenieure Numerische Methoden für Differentialgleichungen Prinzipien und Praxis Taubert, Heitmann Universität Hamburg WS03/04 Linearisierung 1 K. Taubert LINEARISIERUNG und das VERHALTEN
Weiterbildung für Ingenieure Numerische Methoden für Differentialgleichungen Prinzipien und Praxis Taubert, Heitmann Universität Hamburg WS03/04 Linearisierung 1 K. Taubert LINEARISIERUNG und das VERHALTEN
Simulation of Longitudinal Beam Dynamics
 Fachgebiet Theoretische Elektrotechnik und Numerische Feldberechnung PD Dr. Markus Clemens DESY Beam Dynamics Meeting Simulation of Longitudinal Beam Dynamics, Markus Clemens Chair for Theory in Electrical
Fachgebiet Theoretische Elektrotechnik und Numerische Feldberechnung PD Dr. Markus Clemens DESY Beam Dynamics Meeting Simulation of Longitudinal Beam Dynamics, Markus Clemens Chair for Theory in Electrical
Test integrierter Schaltungen
 1. CAE Link und IC Qualifizierung 1.1 Ziel 1.1.1 CAE Link Bei der letzten Übung wurden die Zeitdefinitionen und die Test Pattern manuell eingegeben. Aber bei hochintegrierten Schaltkreise muß ein anderer
1. CAE Link und IC Qualifizierung 1.1 Ziel 1.1.1 CAE Link Bei der letzten Übung wurden die Zeitdefinitionen und die Test Pattern manuell eingegeben. Aber bei hochintegrierten Schaltkreise muß ein anderer
Gefesselte Masse. Jörg J. Buchholz 23. März 2014
 Gefesselte Masse Jörg J. Buchholz 23. März 204 Einleitung In Abbildung ist eine Punktmasse m dargestellt, die sich, von einem masselosen starren tab der Länge l gefesselt, auf einer Kreisbahn bewegt. Dabei
Gefesselte Masse Jörg J. Buchholz 23. März 204 Einleitung In Abbildung ist eine Punktmasse m dargestellt, die sich, von einem masselosen starren tab der Länge l gefesselt, auf einer Kreisbahn bewegt. Dabei
AU-D2. Coaxial/Optical Audio Converter OPERATION MANUAL
 AU-D2 Coaxial/Optical Audio Converter OPERATION MANUAL Table of Contents 1. Introduction 1 2. Features 1 3. Operation Controls and Functions 2 3.1 Input Panel Diagram 2 3.2 Output Panel Diagram 2 3.3 Switcher
AU-D2 Coaxial/Optical Audio Converter OPERATION MANUAL Table of Contents 1. Introduction 1 2. Features 1 3. Operation Controls and Functions 2 3.1 Input Panel Diagram 2 3.2 Output Panel Diagram 2 3.3 Switcher
Computersimulation physikalischer Phänomene mit der Finite- Elemente-Methode
 K.Bräuer: Computersimulation physikalischer Phänomene mit der Finiten-Elemente-Methode 1 Computersimulation physikalischer Phänomene mit der Finite- Elemente-Methode Kurt Bräuer Privatdozent am Institut
K.Bräuer: Computersimulation physikalischer Phänomene mit der Finiten-Elemente-Methode 1 Computersimulation physikalischer Phänomene mit der Finite- Elemente-Methode Kurt Bräuer Privatdozent am Institut
2. Übungsblatt zur Mathematik III für MB/MPE, LaB/WFM, VI, WI/MB
 Fachbereich Mathematik Prof. Dr. J. Lang Dipl.-Math. C. Schönberger Dipl.-Math. L. Kamenski WS 007/08 6.Oktober 007. Übungsblatt zur Mathematik III für MB/MPE, LaB/WFM, VI, WI/MB Gruppenübung Aufgabe G4
Fachbereich Mathematik Prof. Dr. J. Lang Dipl.-Math. C. Schönberger Dipl.-Math. L. Kamenski WS 007/08 6.Oktober 007. Übungsblatt zur Mathematik III für MB/MPE, LaB/WFM, VI, WI/MB Gruppenübung Aufgabe G4
Einführung in die C-Programmierung
 Einführung in die C-Programmierung Warum C? Sehr stark verbreitet (Praxisnähe) Höhere Programmiersprache Objektorientierte Erweiterung: C++ Aber auch hardwarenahe Programmierung möglich (z.b. Mikrokontroller).
Einführung in die C-Programmierung Warum C? Sehr stark verbreitet (Praxisnähe) Höhere Programmiersprache Objektorientierte Erweiterung: C++ Aber auch hardwarenahe Programmierung möglich (z.b. Mikrokontroller).
Modellbasierte Simula0on und experimentelle Anwendung von mechatronischen Systemen in der Lehre mit MATLAB, Simulink und Raspberry Pi.
 Modellbasierte Simula0on und experimentelle Anwendung von mechatronischen Systemen in der Lehre mit MATLAB, Simulink und Raspberry Pi. Dipl.- Ing., M.Sc. Jochen Theis Fachbereich LuO- und RaumfahrRechnik
Modellbasierte Simula0on und experimentelle Anwendung von mechatronischen Systemen in der Lehre mit MATLAB, Simulink und Raspberry Pi. Dipl.- Ing., M.Sc. Jochen Theis Fachbereich LuO- und RaumfahrRechnik
Einführung in Python Teil I Grundlagen
 Einführung in Python Teil I Grundlagen Valentin Flunkert Institut für Theoretische Physik Technische Universität Berlin Do. 27.5.2010 Nichtlineare Dynamik und Kontrolle SS2010 1 of 22 Diese Einführung
Einführung in Python Teil I Grundlagen Valentin Flunkert Institut für Theoretische Physik Technische Universität Berlin Do. 27.5.2010 Nichtlineare Dynamik und Kontrolle SS2010 1 of 22 Diese Einführung
Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik
![Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik](/thumbs/48/24765147.jpg) Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 4 Fourier-Transformation 3
Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 4 Fourier-Transformation 3
f = T φ ist negative für nacheilende Funktionen φ ist positive für voreilende Funktionen 2 Signale im Zeitbereich 2.1 Harmonische Funktionen
 2 Signale im Zeitbereich 2.1 Harmonische Funktionen = Xˆ sin( ω t) 1 f = T Einheiten: [ f ] = Hz ω = 2 π -1 [ ω] = s f mit Phasenverschiebung (hier: nacheilend) : = Xˆ sin( ω t - ϕ) φ ist negative für
2 Signale im Zeitbereich 2.1 Harmonische Funktionen = Xˆ sin( ω t) 1 f = T Einheiten: [ f ] = Hz ω = 2 π -1 [ ω] = s f mit Phasenverschiebung (hier: nacheilend) : = Xˆ sin( ω t - ϕ) φ ist negative für
Projekt 8: Terz-Band-Equalizer
 Institut für Eletronische Musik und Akustik Algorithmen in Akustik und Computermusik1, UE Projekt 8: Terz-Band-Equalizer Name: Michael Neffe Matr.Nr.: 9730540 Studienkennzahl: F-750 Betreuer: Piotr Majdak
Institut für Eletronische Musik und Akustik Algorithmen in Akustik und Computermusik1, UE Projekt 8: Terz-Band-Equalizer Name: Michael Neffe Matr.Nr.: 9730540 Studienkennzahl: F-750 Betreuer: Piotr Majdak
Hazards and measures against hazards by implementation of safe pneumatic circuits
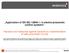 Application of EN ISO 13849-1 in electro-pneumatic control systems Hazards and measures against hazards by implementation of safe pneumatic circuits These examples of switching circuits are offered free
Application of EN ISO 13849-1 in electro-pneumatic control systems Hazards and measures against hazards by implementation of safe pneumatic circuits These examples of switching circuits are offered free
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Die CUTEr Testbibliothek
 Die CUTEr Testbibliothek Slide 1 Motivation Softwarepakete mit vollkommen verschiedenen Anwendungsschwerpunkten Optimierung entweder nur einer von vielen Schwerpunkten oder sogar nur Nebenprodukt zur Lösung
Die CUTEr Testbibliothek Slide 1 Motivation Softwarepakete mit vollkommen verschiedenen Anwendungsschwerpunkten Optimierung entweder nur einer von vielen Schwerpunkten oder sogar nur Nebenprodukt zur Lösung

