Inhaltsverzeichnis. 4 Rasterung
|
|
|
- Beate Wagner
- vor 6 Jahren
- Abrufe
Transkript
1 Inhaltsverzeichnis Hardwaregrundlagen Transformationen und Projektionen Repräsentation und Modellierung von Objekten. Rasterung von Linien. Rasterung von Geraden. Rasterung von Kreisen. Polygone & Füllalgorithmen.5 Rasterartefakte und Aliasing 5 Visibilität und Verdeckung 6 Rendering 7 Abbildungsverfahren 8 Freiformmodellierung Anhang: Graphiksprachen und Graphikstandards Anhang: Einführung in OpenGL
2 . Rasterung Darstellungsmöglichkeiten Vektordarstellung Plotter, Elektronenstrahl (Oszilloskop) Einzelne Linien (Vektoren) werden gezeichnet Bild setzt sich aus Linien zusammen Eingeschränkte Darstellungsmöglichkeiten
3 . Rasterung Darstellungsmöglichkeiten Vektordarstellung Rasterdisplays Bild wird in Bildpunkte diskretisiert Erfordert Framebuffer (Bildspeicher)
4 . Rasterung Die dominierenden Rasterbildschirmtechnologien erfordern die Zerlegung aller darzustellenden geometrischen Objekte in Bildschirmpunkte. Dieser Prozess wird auch als Rasterung bezeichnet. Dies ist die Aufgabe der Bilderzeugungseinheit DPU (Display Processing Unit) des Bildrechners: Rastereinheit/Rasterprozessor Wir beschäftigen uns näher mit: Rasterung von Geraden, Kreisen, Ellipsen, Polygonen Antialiasing von Linien und Polygonen
5 . Rasterung von Linien Problemstellung: Darstellung einer Linie auf einem Rasterbildschirm erfordert die Bestimmung der am besten passenden Punkte im Raster bzw. Gitter (geeignete ganzzahlige Rundung). P =(x,y ) P =(x,y ) Abb..: Mögliche Rasterkandidaten 5
6 . Rasterung von Linien Linien sollen gerade erscheinen Linien sollen gleichmäßig hell erscheinen Linien sollen schnell gezeichnet werden Algorithmus soll leicht in Hardware implementierbar sein Fallunterscheidung in Oktanten (nach Steigung) 5.. y.. P Oktant P 8. x Hier: Ursprung des zugeordneten Koordinatensystems in P. Oktant P und P auf Rastergitter 6
7 . Rasterung von Linien DDA-Algorithmus für Geraden [965] Digital Differential Analyzer / Digitaler Integrierer Ein DDA-Algorithmus generiert eine Kurve (nicht nur eine Gerade) aus einer beschreibenden Differentialgleichung x = x - x (= x i+ - x i ) y = y - y (= y i+ - y i ); - x / y y i+ = y / x * x i+ + b; x i+ = x +i, i=,..., x- P = (x,y) Plot(x i,round(y i )) = plot(x i,floor(/ + y i ) Dezimalbrüche erhöhen Rechenaufwand Fließkomma-Multiplikation Addition Rundung P = (x,y) 7
8 . Rasterung von Linien DDA-Algorithmus für Geraden Digital Differential Analyzer / Digitaler Integrierer Verbesserung: Inkrementeller Algorithmus y i+ = y / x * x i+ + b = y / x * (x i+ + (x i - x i )) + b = y / x * x i + b + y / x * (x i+ - x i ) = y i + y / x * P = (x,y) x = x; y = y; m=dy/dx; For (x=x; x<=x; x++) { Plot(x,y) y = round(y+m); } P = (x,y) 8
9 . Rasterung von Geraden Bresenham-Algorithmus für Geraden [965] Idee: Abhängig von der Steigung der Geraden wird die x- oder y- Koordinate immer um eine Einheit geändert. Die andere Koordinate wird entweder nicht oder ebenfalls um eine Einheit geändert Fallunterscheidung nach der kleineren Abweichung der Geraden zum nächsten Gitterpunkt in Koordinatenrichtung. 9
10 . Rasterung von Geraden y i+ =y i + y i+ =y i zu zeichnende Gerade Entweder Punkt oder Punkt wird gezeichnet, je nachdem, welcher näher zur Geraden liegt. y(x) = m x +c = m x y ' (x) = m = y x d Wenn d> /, d<=/ 0
11 . Rasterung von Geraden y(x) = m x +c = m x y ' (x) = m = y x d d,d E y x Zur Realisierung wird eine Entscheidungsgröße E eingeführt, welche die Abweichung zwischen dem exakten Punkt und der Mitte zwischen den beiden möglichen Rasterpunkten angibt. Das Vorzeichen von E dient dann als Kriterium für die Rundung auf den nächsten Rasterpunkt: E>0: x++; y++; E + y/ x - E 0: x++; E + y/ x
12 . Rasterung von Geraden Nur lineare Operationen, aber Dezimalbrüche (/) Skalieren um x, um Dezimalbrüche zu vermeiden E = y/ x -/ E = x( y/ x -/) = y - x E 0: x++; E := E + y E >0: x++; y++; E := E + y - x
13 . Rasterung von Geraden Bresenham-Algorithmus für den ersten Oktanten, der ausschließlich ganzzahlige Operanden verwendet, mit e:=e, dx := x, dy := y: // (x, y), (x, y) Ganzzahlig, x < x x = x; y = y; dx = x-x; dy = y-y; e = *dy-dx; // Initialisierung for(i=; i<=dx; i++) // Schleife fuer x { plot(x, y); } if(e >= 0) // oberen Punkt Zeichnen (y erhoehen) { y = y+; } e = e-*dx; x = x+; e = e+*dy; plot(x, y);
14 . Rasterung von Geraden Beispiel: P=(0, 0), P=(5, ) dx dy x y e i plot (0,0) -7 5 (,) (,) (,) 5 5 (,) (5,)
15 . Rasterung von Kreisen Darstellung eines Kreises mit Mittelpunkt (x M, y M ) und Radius r (i) implizit: f(x,y) = (x-x M ) + (y-y M ) - r = 0 (ii) Parameter: x( ) = x M + r cos( ), y( ) = y M + r sin( ), [0, [ Nachteil: Beide Methoden zur Kreisdarstellung sind rechenaufwändig und erfordern höhere Rechenoperationen. 5
16 . Rasterung von Kreisen Bemerkungen Mit der Berechung eines Kreispunktes sind durch Symmetrie 7 weitere Kreispunkte gegeben. Für eine gleichmäßige Rasterung müssen die Pixel entlang des Kreises möglichst gleichmäßig verteilt sein. (-x,y) (-x,-y) (-y,x) (y,x) (-y,-x) (y,-x) (x,y) (x,-y) von jedem Rasterquadrant dürfen nur Eckpunkte gesetzt werden Die Bewertung der Kreisapproximation im Raster ist subjektiv. Ein häufig verwendetes Kriterium ist die Minimierung des Residuums x i + y i - r. 6
17 . Rasterung von Kreisen Bresenham-Algorithmus für Kreise Beste Approximation über Entscheidungsgröße d i mittels minimalem Residuum. Hier: (x M, y M ) = (0, 0) Startpunkt ist Rasterpunkt r IN. Oktant D(S i ) = (x i- +) + y i- - r D(T i ) = (x i- +) + (y i- -) - r 7
18 . Rasterung von Kreisen Die Entscheidungsgröße d i = D(S i )-D(T i ) misst die Abstände zum oberen und unteren Rasterpunkt Für d i > 0: wähle P i = T i als nächsten Punkt, also x i = x i- +, y i = y i- - Für d i <= 0: wähle P i = S i als nächsten Punkt, also x i = x i- +, y i = y i- Innerhalb des. Oktanten (Kreisfunktion monoton fallend, Steigung zwischen 0 und -) gilt speziell: D(S i ) unter dem Betrag > 0, dh. S i liegt immer außerhalb der Kreislinie D(T i ) unter dem Betrag < 0, dh. T i liegt immer innerhalb der Kreislinie d i = (x i- +) + y i- - r + (x i- +) + (y i- -) - r 8
19 . Rasterung von Kreisen und damit rekursiv: (berechne d i+ aus d i ) d i+ = d i + (x i - y i ) + für di>0 d i+ = d i + x i + für d i <=0 d x y mit Startwert d = -r (x 0 =0, y 0 =r) Beispiel: r=
20 . Rasterung von Kreisen Ellipsendarstellung Zur Rasterung betrachtet man die Ellipsen in Normalform, und mit zu den Koordinatenachsen parallelen Hauptachsen. => Algorithmus von Kappel 0
21 . Polygonen & Füllalgorithmen Ziel: Füllen bzw. Einfärben eines begrenzten Bereiches oder Gebietes mit einer Füllfarbe oder einem Muster bzw. einer Schraffur Beispiele: Balkendiagramme, Flächen, Körper etc. Beschreibung der zu füllenden Gebiete erfolgt geometrisch, zb. durch Ecken, Strecken, Polygone, Kreise, etc. oder durch Pixel (inhalts- oder randdefiniert)
22 . Polygonen & Füllalgorithmen Wichtig: Zusammenhang von Gebieten Man unterscheidet -fach zusammenhängend (nur Horizontal- und Vertikalbewegung) 8-fach zusammenhängend (zusätzlich Diagonalbewegung möglich) -fach zusammenhängend 8-fach zusammenhängend
23 . Polygonen & Füllalgorithmen Bemerkungen Füllalgorithmen mit 8 Freiheitsgraden (Bewegungsrichtungen) können auch -fach zusammenhängende Gebiete füllen. Füllalgorithmen mit Freiheitsgraden können keine 8-fach zusammenhängenden Gebiete füllen Problem: -fach zusammenhängende Gebiete mit gemeinsamen Ecken Techniken zum Rastern eines Polygons / Füllen eines Gebietes Scan-Line-Methode Saatkorn-Methode Hybrid-Methoden
24 . Polygonen & Füllalgorithmen Scan-Line-Methode Auch Rasterzeilen-Methode oder Scan-Conversion genannt Arbeitet zeilenweise von oben nach unten Ein Pixel der aktuellen Zeile (Scan-Line) wird nur dann gezeichnet, wenn es innerhalb des Polygons liegt // einfachster Ansatz: for(y=y min ; y<=y max ; y++) for(x=x min ; x<=x max ; x++) if(inside(polygon, x, y) SetPixel(x,y); // row, Zeile // column, Spalte - für geometrisch als auch für pixelweise definierte Gebiete - sehr langsam => Verbesserung durch Ausnutzung von Kohärenz
25 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Verfahren basiert auf dem Prinzip der Zeilenkohärenz Benachbarte Pixel auf einer Zeile besitzen höchstwahrscheinlich die gleichen Intensitätswerte Pixelcharakteristik (Intensität) ändert sich nur dort, wo ein Schnittpunkt einer Polygonkante mit einer Scan Line vorliegt, d.h. der Bereich zwischen zwei Schnittpunkten gehört zum Polygon oder nicht y=: Schnitt mit Polygon für x =, 8 y=: Schnitt mit Polygon für x =,, 6, 8 5
26 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Scan-Line y=, Unterteilung der Scan-Line in Bereiche: x<: außerhalb des Polygons <=x<=8: innerhalb des Polygons x>8: außerhalb des Polygons 6
27 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Scan Line y=, Unterteilung der Scan Line in 5 Bereiche: x<: außerhalb des Polygons <=x<=: innerhalb des Polygons <x<6: außerhalb des Polygons 6<=x<=8: innerhalb des Polygons x>8: außerhalb des Polygons 7
28 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Günstige Wahl der Scan Lines Scan-Lines verlaufen durch die Pixelmitte Pixelaktivierung erfolgt, falls die Pixelmitte des Pixels rechts (>=) vom Schnittpunkt mit dem Polygon (Innenbereich) liegt. Vorsicht: hier sind die Pixelzeilen und -spalten nummeriert, nicht die Koordinaten der Achsen! 5 Scan-Lines 5 6 8
29 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Probleme treten bei Singularitäten auf, dh. die Scan-Line schneidet das Polygon in einer Ecke. => Betrachte lokale Extrema Lokales Extrema: y-werte der Endpunkte der in dieser Ecke beginnenden Polygonseiten sind beide größer, oder beide kleiner als der y-wert der Schnittecke => Fallunterscheidung: ist die Ecke ein lokales Extrema, so zählt der Schnitt zweifach ist die Ecke kein lokales Extrema, so zählt der Schnitt nur einfach 9
30 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Einfacher Kanten-Listen-Algorithmus: Ordered Edge List Algorithm Funktionsweise: Preprocessing + Scan Conversion Preprocessing Ermittle (zb. mit Bresenham- / DDA-Algorithmus) für jede Polygonkante die Schnittpunkte mit den Scan-Lines in der Pixelmitte. Ignoriere dabei horizontale Kanten. Speichere jeden Schnittpunkt (x, y) in einer Liste. Sortiere die Liste dann von oben nach unten und von links nach rechts. 0
31 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Scan-Conversion Betrachte jeweils zwei direkt aufeinander folgende Schnittpunkte (x, y ) und (x, y ) der Liste. (dh. Listenelemente und, Listenelemente und, usw.) Aufgrund des Preprocessing gilt für die Scan-Line y: y = y = y und x <= x Zeichne alle Pixel auf der Scan-Line y, für die gilt: x <= x < x mit ganzzahligem x
32 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Beispiel: Preprocessing (,7), (,7) (,6), (,6), (8,6), (8,6) (,5), (,5), (7,5), (8,5) (,), (,), (6,), (8,) (,), (5,), (5,), (8,) (,), (8,) (,), (8,) (,7),(,7),(,6),(,6),(8,6),(8,6),(,5),(,5),(7,5),(8,5),(,),(,),(6,),(8,), (,),(5,),(5,),(8,),(,),(8,),(,),(8,)
33 . Polygonen & Füllalgorithmen Scan-Line-Methode (Fortsetzung) Beispiel: Scan-Conversion (,7),(,7) (,6),(,6); (8,6),(8,6) (,5),(,5); (7,5),(8,5) (,),(,); (6,),(8,) (,),(5,); (5,),(8,) (,),(8,) (,),(8,) Bem.: Ein exakt rechts anschließendes Polygon würde die Pixel in Spalte 8 färben!
34 . Polygonen & Füllalgorithmen Saatpunkt-Methode / Seed-Fill Seed-Fill-Methoden füllen das Gebiet ausgehend von einem Ausgangspixel (Saatpunkt, Seed) und Eignet sich für pixelweise definierte Gebiete, also für Rastergeräte. Man unterscheidet nach der Art der Gebietsdefinition: (i) Boundary-Fill-Algorithmus für randdefinierte Gebiete Input: Algo.: Startpunkt (Saatpunkt), Farbe der Begrenzungskurve, Füllfarbe oder Muster Wiederhole Vom Startpixel ausgehend werden rekursiv Nachbarpixel umgefärbt, bis Pixel mit der Farbe der Begrenzungskurve oder bereits umgefärbte Pixel erreicht werden
35 . Polygonen & Füllalgorithmen Saatpunkt-Methode / Seed-Fill (Fortsetzung) (ii) Flood/Interior-Fill-Algorithmus für inhaltsdefinierte Gebiete Input: Algo.: Startpunkt (Saatkorn), Farbe der umzufärbenden Pixel, Füllfarbe oder Muster Wiederhole Vom Startpixel ausgehend werden rekursiv Nachbarpixel gleicher Farbe umgefärbt, bis Pixel mit abweichender Farbe erreicht werden 5
36 . Polygonen & Füllalgorithmen Saatpunkt-Methode / Seed-Fill (Fortsetzung) Einfacher Saatkorn-Algorithmus ( Bewegungsrichtungen, randdefiniertes Gebiet, FILO/LIFO-Prinzip) Empty(stack); Push(stack, seed-pixel); hier zb. while(stack not empty) { pixel = Pop(stack); setcolor(pixel, FillColor); for each of the -connected pixels p i { if(! ((p i == boundary_pixel) (colorof(p i ) == FillColor))) Push(stack, p i ); } } Bemerkung: Eventuell werden Pixel mehrfach im Stack abgelegt (und gefärbt)! 6
37 . Polygonen & Füllalgorithmen Saatpunkt-Methode / Seed-Fill (Fortsetzung) Beispiel: (die Zahlen geben die Position der Pixel im Stack an) 7 6,6 6 6,8,5 5 5,,5,5,7 7 7, 0 0,,,5,9 9,, 9 8,9,5 5,7,5,0 0,, ,,
38 . Polygonen & Füllalgorithmen Saatpunkt-Methode / Seed-Fill (Fortsetzung) Beispiel: Gebiet mit Loch 7 6 9,9,9,9 9 9, 5 5,9,0 0 0, 6,9 6, 7,9 7, 9 8 8,
39 . Polygonen & Füllalgorithmen Hybrid-Methoden Hybrid-Methoden verwenden die Ideen der Scan-Lineund Saatpunkt-Methoden gemeinsam. => Scan-Line-Seed-Fill-Algorithmus 9
40 .5 Rasterartefakte & Aliasing Aliasing (Begriff aus der Signaltheorie) Allgemein versteht man unter Aliasing-Effekten die fehlerhafte Rekonstruktion eines (kontinuierlichen) Ausgangssignals durch eine Abtastung mit zu geringer Frequenz. (vgl. Nyquist-Theorem) (Im Frequenzbereich bandbegrenzte Signale müssen mit mehr als der doppelten Grenzfrequenz abgetastet werden, um eine exakte Rekonstruktion zu ermöglichen) Der Begriff Aliasing in der Computergraphik Visuelle Artefakte durch Unterabtastung, (z.b. Aliasing bei einem Schachbrettmuster) Visuelle Artefakte durch Rasterkonvertierungseffekte zurückgehen (z.b. Treppeneffekte bei schrägen Linien). Örtliches und zeitliches Aliasing (z.b. scheinbar rückwärts drehende Wagenräder im Western). 0
41 .5 Rasterartefakte & Aliasing Aliasing (Fortsetzung) Anti-Aliasing-Verfahren: Methoden um Aliasing-Effekten entgegenzuwirken (z.b. Überabtastung, Filterung), Ein echtes Beseitigen ist oft (schon theoretisch) nicht möglich. (z.b. wenn die Signale einfach nicht bandbegrenzt sind; hier hilft zwar eine höhere Abtastfrequenz - also Überabtastung - aber es beseitigt nicht die Probleme) Bei Artefakten der Rasterkonvertierung spricht man bei Anti- Aliasing-Verfahren auch von Verfahren zur (Bild-)Kantenglättung.
42 .5 Rasterartefakte & Aliasing Aliasing (Fortsetzung) Aliasing-Artefakte in der Computergraphik Textur-Artefakte (z.b. Schachbrettmuster) Treppeneffekte beim Rastern von Kurven: Jagged Edges Verschwinden von Objekten, die kleiner als ein Pixel sind Verschwinden von langen, dünnen Objekten Detailverlust bei komplexen Bildern Aufblinken kleiner Objekte bei Bewegungen / Animationen: Popping
43 .5 Rasterartefakte & Aliasing Beispiel: Textur-Artefakte, unendliches Schachbrettmuster Üblicherweise treten visuelle Artefakte auf, wenn die Periodizität (hier die Kachelmuster) in der Textur die Größenordnung von Pixel erreicht. Linkes Bild: Am oberen Ende werden die Quadrate immer kleiner, plötzlich aber wieder größer (Aliasing). Dies ist ein Ergebnis zu grober Abtastung
44 .5 Rasterartefakte & Aliasing Beispiel (Fortsetzung): Rechtes Bild: Mittels zweifacher Überabtastung (Abtastung mit doppelter Frequenz, dh. vierfacher Rechenaufwand) können die Artefakte verringert werden Sie treten aber immer noch auf (bei höheren Frequenzen) Es gilt: Echtes Aliasing kann in Computergraphikbildern mittels Überabtastung nicht entfernt, sondern nur verbessert werden (nicht bandbegrenzt)
45 .5 Rasterartefakte & Aliasing Beispiel: Treppeneffekte, Jagged Edges, Jaggies Die bisher beschriebenen Verfahren zur Rasterung von Geraden und Kurven erzeugen Treppeneffekte (linkes Bild) Zeichnen von Punkten nur an Rasterpositionen möglich, Entsprechen i. a. nicht den tatsächlichen Positionen (Sollpositionen) 5
46 .5 Rasterartefakte & Aliasing Beispiel (Fortsetzung): Um solchen Aliasing-Effekten entgegenzuwirken, werden mehrere Intensitäten zur Erhöhung der visuellen Auflösung benutzt. Zum Beispiel verwendet eine Variante des Bresenham-Algorithmus für Geraden (im ersten Oktanten) für jeden x-wert zwei Pixel mit Grautönen entsprechend eines Abstandmaßes zur zu zeichnenden Strecke (rechtes Bild). 6
47 .5 Rasterartefakte & Aliasing Beispiel: Aliasing bei Polygonen 7
48 .5 Rasterartefakte & Aliasing Anti-Aliasing Ein einfaches globales (d. h. das gesamte Bild betreffende) Anti- Aliasing-Verfahren stellt die Überabtastung, auch als Oversampling oder Supersampling bezeichnet, dar. Jedes Pixel wird mit einer höheren Auflösung berechnet, als es schließlich dargestellt wird. Das Pixel erhält als eigentliche Grauwertintensität bzw. Farbwert einen gewichteten Durchschnitt der an ihm beteiligten Subpixelwerte. Dieses Vorgehen entspricht allgemein einem Filterprozess, dessen theoretische Grundlagen in der Digitalen Signalverarbeitung begründet liegen. Folgende Filterkerne (Crow, 98) werden i. d. R. verwendet: 8
49 x 5 x 5 7 x 7 Pixel Subpixel Abtastpunkt.5 Rasterartefakte & Aliasing Anti-Aliasing (Fortsetzung)
50 .5 Rasterartefakte & Aliasing Anti-Aliasing (Fortsetzung) Bei Linien und spitzen Dreiecken (dünnen Polygonen) kann es trotz Supersamplings zu überraschenden Effekten kommen: Linie verschwindet stellenweise, da keine Subpixel getroffen werden! dito für Dreieck! Bemerkung: Gesetzte Subpixel sind schwarz. Die Schraffur zeigt den Grauwert abhängig von der Anzahl der gesetzten Subpixel. 50
51 .5 Rasterartefakte & Aliasing Anti-Aliasing (Fortsetzung) Abhilfe für dieses Problem schafft erst eine (korrekte) Berechnung der überdeckten Fläche im Pixel Die praktische Anwendung dieser Methode schließt allerdings eine exakte analytische Berechnung der wirklich im Pixel überdeckten Fläche aus. Es existieren hierzu verschiedenste Näherungsverfahren. (Die überdeckte Fläche lässt sich auch durch eine Anzahl entsprechend gesetzter Subpixel angenähert darstellen.) 5
52 .5 Rasterartefakte & Aliasing Anti-Aliasing (Fortsetzung) Die folgenden Abbildungen zeigen die resultierenden Ergebnisse in den zuvor gezeigten Problemfällen Linie und spitzes Dreieck: 5
53 .5 Rasterartefakte & Aliasing Anti-Aliasing (Fortsetzung) Leistungsfähigkeit der vorgestellten Verfahren: Spitzes Dreieck ohne Glättung Spitzes Dreieck mit Oversampling Spitzes Dreieck mit korrekter Berechnung der überdeckten Fläche 5
54 .5 Rasterartefakte & Aliasing Anti-Aliasing (Fortsetzung) Bemerkung: Stochastische Methoden Beim stochastischen Abtasten wird das Oversampling mittels Monte-Carlo-Methoden durchgeführt, d.h. die Grauwerte (Intensität) werden an einigen zufälligen Punkten im Pixel ermittelt und das Ergebnis gemittelt. Auch bei der Berechnung der vom Polygon im Pixel überdeckten Fläche können Monte-Carlo-Methoden eingesetzt werden. Stochastische Methoden erhöhen die Effizienz, (schnellere Berechnung), neigen aber z.b. zu Problemen bei Animationen, da Objekte flimmern können. 5
55 Quellen Computergraphik, Universität Leipzig (Prof. D. Bartz) Graphische Datenverarbeitung I, Universität Tübingen (Prof. W. Straßer) Graphische Datenverarbeitung I, TU Darmstadt (Prof. M. Alexa) 55
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
Inhaltsverzeichnis. 1 Hardwaregrundlagen
 Inhaltsverzeichnis 1 Hardwaregrundlagen 2.4 2.5 Perspektivische 2.6 Parallele 2.7 Umsetzung der Zentralprojektion 2.8 Weitere 2.9 Koordinatensysteme, Frts. 2.10 Window to Viewport 2.11 Clipping 3 Repräsentation
Inhaltsverzeichnis 1 Hardwaregrundlagen 2.4 2.5 Perspektivische 2.6 Parallele 2.7 Umsetzung der Zentralprojektion 2.8 Weitere 2.9 Koordinatensysteme, Frts. 2.10 Window to Viewport 2.11 Clipping 3 Repräsentation
Welche Teilgebiete der Informatik beschäftigen sich mit der computergestützten Verarbeitung und Speicherung von Bildinformationen?
 . Begriffe Welche Teilgebiete der Informatik beschäftigen sich mit der computergestützten Verarbeitung und Speicherung von Bildinformationen? Bildverarbeitung (image processing) - Analyse von Bildern mit
. Begriffe Welche Teilgebiete der Informatik beschäftigen sich mit der computergestützten Verarbeitung und Speicherung von Bildinformationen? Bildverarbeitung (image processing) - Analyse von Bildern mit
Computergraphik I. Scan Conversion: Lines & Co. Einordnung in die Pipeline. G. Zachmann Clausthal University, Germany zach@tu-clausthal.
 11/4/10 lausthal omputergraphik I Scan onversion of Lines. Zachmann lausthal University, ermany zach@tu-clausthal.de Einordnung in die Pipeline Rasterisierung der Objekte in Pixel Ecken-Werte interpolieren
11/4/10 lausthal omputergraphik I Scan onversion of Lines. Zachmann lausthal University, ermany zach@tu-clausthal.de Einordnung in die Pipeline Rasterisierung der Objekte in Pixel Ecken-Werte interpolieren
1 Begriffe und Grundlagen. Achim Ebert CG.1.1
 1 Begriffe und Grundlagen Achim Ebert CG.1.1 1.1 Begriffe Computergrafik, Graphische Datenverarbeitung (computer graphics) Grobe Einordnung: Synthese von Bildern mit Hilfe des Rechners Erzeugung eines
1 Begriffe und Grundlagen Achim Ebert CG.1.1 1.1 Begriffe Computergrafik, Graphische Datenverarbeitung (computer graphics) Grobe Einordnung: Synthese von Bildern mit Hilfe des Rechners Erzeugung eines
0 Einführung. Computergrafik. Computergrafik. Abteilung für Bild- und Signalverarbeitung
 F1 Inhaltsverzeichnis 1 Hardwaregrundlagen 2 Transformationen und Projektionen 3 Repräsentation und Modellierung von Objekten 4 Rasterung 5 Visibilität und Verdeckung 6 Rendering 7 Abbildungsverfahren
F1 Inhaltsverzeichnis 1 Hardwaregrundlagen 2 Transformationen und Projektionen 3 Repräsentation und Modellierung von Objekten 4 Rasterung 5 Visibilität und Verdeckung 6 Rendering 7 Abbildungsverfahren
Rastergrafikalgorithmen
 Rastergrafikalgorithmen Vortrag über Rastergrafikalgorithmen im Rahmen des Proseminars Computergrafik Vortragender: Christian Vonsien Dienstag, 18. Mai 2010 Proseminar Computergrafik SS2010 - Rastergrafikalgorithmen
Rastergrafikalgorithmen Vortrag über Rastergrafikalgorithmen im Rahmen des Proseminars Computergrafik Vortragender: Christian Vonsien Dienstag, 18. Mai 2010 Proseminar Computergrafik SS2010 - Rastergrafikalgorithmen
3.6 Einführung in die Vektorrechnung
 3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
Aufgabe E 1 (8 Punkte)
 Aufgabe E (8 Punkte) Auf einem Billardtisch (bei dem die Koordinatenachsen x = 0 und y = 0 als Banden dienen) liegen zwei Kugeln P( ) und Q(3 ) Die Kugel P soll so angestoßen werden, dass sie nach Reflexion
Aufgabe E (8 Punkte) Auf einem Billardtisch (bei dem die Koordinatenachsen x = 0 und y = 0 als Banden dienen) liegen zwei Kugeln P( ) und Q(3 ) Die Kugel P soll so angestoßen werden, dass sie nach Reflexion
32. Algorithmus der Woche Kreise zeichnen mit Turbo Programmoptimierung: Wie kann man die Zahl der Rechenoperationen minimieren?
 32. Algorithmus der Woche Kreise zeichnen mit Turbo Programmoptimierung: Wie kann man die Zahl der Rechenoperationen minimieren? Autor Leif Kobbelt, RWTH Aachen Dominik Sibbing, RWTH Aachen Hast Du schon
32. Algorithmus der Woche Kreise zeichnen mit Turbo Programmoptimierung: Wie kann man die Zahl der Rechenoperationen minimieren? Autor Leif Kobbelt, RWTH Aachen Dominik Sibbing, RWTH Aachen Hast Du schon
Featurebasierte 3D Modellierung
 1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
10.6. Implizite ebene Kurven und Tangenten
 0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Zielbild B. all. Oft verwendet: kubische B-Splines. Bestimmung der Koeffizienten Vorlesung BV&ME
 2.2) geometrische Transformationen (CG/BV) 2.2.c) Resamplingproblem ( ) = A(x, y) 1 ( ) = A h { k,l} B k,l Qellbild A Zielbild B y x AT 1 Methodischer Ansatz 2 für das Resampling: Statt der gewichteten
2.2) geometrische Transformationen (CG/BV) 2.2.c) Resamplingproblem ( ) = A(x, y) 1 ( ) = A h { k,l} B k,l Qellbild A Zielbild B y x AT 1 Methodischer Ansatz 2 für das Resampling: Statt der gewichteten
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Übungen mit dem Applet Kurven in Polarkoordinaten
 Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
1.1. Geradengleichung aus Steigung und y-achsenabschnitt
 Version vom 4. Januar 2007 Gleichungen von Geraden in der Ebene 1999 Peter Senn * 1.1. Geradengleichung aus Steigung und y-achsenabschnitt In dieser Form lautet die Gleichung der Geraden wie folgt: g:
Version vom 4. Januar 2007 Gleichungen von Geraden in der Ebene 1999 Peter Senn * 1.1. Geradengleichung aus Steigung und y-achsenabschnitt In dieser Form lautet die Gleichung der Geraden wie folgt: g:
computer graphics & visualization
 Entwicklung und Implementierung echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs Motivation
Entwicklung und Implementierung echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs Motivation
Analytische Geometrie des Raumes
 Analytische Geometrie des Raumes Als Begründer der analytischen Geometrie gilt René Descartes (Discours de la méthode). Seine grundliegende Idee bestand darin, geometrische Gebilde (Gerade, Kreis, Ellipse
Analytische Geometrie des Raumes Als Begründer der analytischen Geometrie gilt René Descartes (Discours de la méthode). Seine grundliegende Idee bestand darin, geometrische Gebilde (Gerade, Kreis, Ellipse
:= Modellabbildung. Bildsynthese (Rendering) Bildsynthese
 Geometrisches Modell bestehend aus Datenstrukturen zur Verknüpfung geometrischer Primitive, welche eine Gesamtszene beschreiben Bildsynthese := Modellabbildung Pixelbasiertes Modell zur Darstellung eines
Geometrisches Modell bestehend aus Datenstrukturen zur Verknüpfung geometrischer Primitive, welche eine Gesamtszene beschreiben Bildsynthese := Modellabbildung Pixelbasiertes Modell zur Darstellung eines
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Skalarprodukte (Teschl/Teschl Kap. 13)
 Skalarprodukte (Teschl/Teschl Kap. ) Sei V Vektorraum über R. Ein Skalarprodukt auf V ist eine Abbildung V V R, (x, y) x, y mit den Eigenschaften () x, y = y, x (symmetrisch), () ax, y = a x, y und x +
Skalarprodukte (Teschl/Teschl Kap. ) Sei V Vektorraum über R. Ein Skalarprodukt auf V ist eine Abbildung V V R, (x, y) x, y mit den Eigenschaften () x, y = y, x (symmetrisch), () ax, y = a x, y und x +
Der Algorithmus von Bresenham
 Der Algorithmus von Bresenham Das Bresenham-Verfahren beruht im wesentlichen auf zwei grundsätzliche Beobachtungen: - Es reicht ein Verfahren aus um Geraden mit einer Steigung im Bereich von null bis eins
Der Algorithmus von Bresenham Das Bresenham-Verfahren beruht im wesentlichen auf zwei grundsätzliche Beobachtungen: - Es reicht ein Verfahren aus um Geraden mit einer Steigung im Bereich von null bis eins
Rastergrafikalgorithmen
 Rastergrafikalgorithmen Sebastian Kurfürst Proseminar Computergrafik Institut für Software-und Multimediatechnik TU Dresden 10. Juli 2008 Zusammenfassung Es wird eine Einführung in Basisalgorithmen der
Rastergrafikalgorithmen Sebastian Kurfürst Proseminar Computergrafik Institut für Software-und Multimediatechnik TU Dresden 10. Juli 2008 Zusammenfassung Es wird eine Einführung in Basisalgorithmen der
Nichtrealistische Darstellung von Gebirgen mit OpenGL
 Nichtrealistische Darstellung von Gebirgen mit OpenGL Großer Beleg Torsten Keil Betreuer: Prof. Deussen Zielstellung Entwicklung eines Algorithmus, der die 3D- Daten einer Geometrie in eine nichtrealistische
Nichtrealistische Darstellung von Gebirgen mit OpenGL Großer Beleg Torsten Keil Betreuer: Prof. Deussen Zielstellung Entwicklung eines Algorithmus, der die 3D- Daten einer Geometrie in eine nichtrealistische
Geometrie 1. Roman Sommer. Informatik 2 Programmiersysteme Martensstraße Erlangen
 Geometrie 1 Roman Sommer Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Grundlagen Punkte, Vektoren Schreibweise: Skalar: Vektor: Komponente: Punkt: (spitzer) Winkel zw. zwei Vektoren:
Geometrie 1 Roman Sommer Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Grundlagen Punkte, Vektoren Schreibweise: Skalar: Vektor: Komponente: Punkt: (spitzer) Winkel zw. zwei Vektoren:
6. Triangulation von Polygonen
 1 6. Triangulation von Polygonen 2 Problemstellung 3 Problemstellung 4 Problemstellung 5 Problemstellung 6 Jedes Polygon lässt sich triangulieren. Wir führen einen Induktionsbeweis nach der Anzahl der
1 6. Triangulation von Polygonen 2 Problemstellung 3 Problemstellung 4 Problemstellung 5 Problemstellung 6 Jedes Polygon lässt sich triangulieren. Wir führen einen Induktionsbeweis nach der Anzahl der
Plotten von Linien ( nach Jack Bresenham, 1962 )
 Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Aufgabe 4 (Musterlösung) Corel Draw
 Aufgabe 4 (Musterlösung; Zahnrad) Corel Draw Seite 1 von 8 Aufgabe 4 (Musterlösung) Corel Draw Inhaltsverzeichnis Vorbemerkung... 2 Musterlösung... 2 Zusatz... 8 Abbildungsverzeichnis Abb. 1: Die 3 Hilfslinien
Aufgabe 4 (Musterlösung; Zahnrad) Corel Draw Seite 1 von 8 Aufgabe 4 (Musterlösung) Corel Draw Inhaltsverzeichnis Vorbemerkung... 2 Musterlösung... 2 Zusatz... 8 Abbildungsverzeichnis Abb. 1: Die 3 Hilfslinien
Formelsammlung Mathematik Grundkurs Inhalt
 Formelsammlung Mathematik Grundkurs Inhalt Inhalt...1 Trigonometrie Grundlagen... Vektoren...3 Skalarprodukt...4 Geraden...5 Abstandsberechnungen...6 Ebenen...7 Lineare Gleichungssysteme (LGS)...8 Gauß'sches
Formelsammlung Mathematik Grundkurs Inhalt Inhalt...1 Trigonometrie Grundlagen... Vektoren...3 Skalarprodukt...4 Geraden...5 Abstandsberechnungen...6 Ebenen...7 Lineare Gleichungssysteme (LGS)...8 Gauß'sches
2. Digitale Codierung und Übertragung
 2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
Dynamische Geometrie
 Dynamische Geometrie 1) Die Mittelsenkrechten, die Seitenhalbierenden, die Höhen und die Winkelhalbierenden eines beliebigen Dreiecks schneiden sich jeweils in einem Punkt. a) Untersuchen Sie die Lage
Dynamische Geometrie 1) Die Mittelsenkrechten, die Seitenhalbierenden, die Höhen und die Winkelhalbierenden eines beliebigen Dreiecks schneiden sich jeweils in einem Punkt. a) Untersuchen Sie die Lage
Kurs zur Ergänzungsprüfung Darstellende Geometrie CAD. Ebenes Zeichnen (2D-CAD) und die ersten Befehle
 CAD Ebenes Zeichnen (2D-CAD) und die ersten Befehle Schnellzugriff-Werkzeugkasten (Quick Access Toolbar) Registerkarten (Tabs) Gruppenfenster (Panels) Zeichenfläche Befehlszeile: für schriftl. Eingabe
CAD Ebenes Zeichnen (2D-CAD) und die ersten Befehle Schnellzugriff-Werkzeugkasten (Quick Access Toolbar) Registerkarten (Tabs) Gruppenfenster (Panels) Zeichenfläche Befehlszeile: für schriftl. Eingabe
Geometrie 1. Christian Bay Christian Bay Geometrie / 46
 Geometrie 1 Christian Bay 02.07.2013 Christian Bay Geometrie 1 02.07.2013 1 / 46 Inhaltsverzeichnis Grundlagen CCW Polygone Picks Theorem Konvexe Hülle Christian Bay Geometrie 1 02.07.2013 2 / 46 Geometrie
Geometrie 1 Christian Bay 02.07.2013 Christian Bay Geometrie 1 02.07.2013 1 / 46 Inhaltsverzeichnis Grundlagen CCW Polygone Picks Theorem Konvexe Hülle Christian Bay Geometrie 1 02.07.2013 2 / 46 Geometrie
Motivation. Diskretisierung. Überblick. Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen. Diskretisierung und Quantisierung
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Flächeninhalt, Volumen und Integral
 Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 %
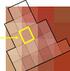
![A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 % A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 %](/thumbs/55/35914069.jpg) 5 Prozentrechnen Übung 50 Der ganze Streifen entspricht 100 % = 1 000 = 1. Welche Prozent- und Promillesätze stellen die unterschiedlich getönten Flächen dar? Abb. 27 1. 2. 3. Übung 51 Der volle Winkel
5 Prozentrechnen Übung 50 Der ganze Streifen entspricht 100 % = 1 000 = 1. Welche Prozent- und Promillesätze stellen die unterschiedlich getönten Flächen dar? Abb. 27 1. 2. 3. Übung 51 Der volle Winkel
Geometrie I. Sebastian Redinger Informatik 2 Programmiersysteme Martensstraße Erlangen
 Geometrie I Sebastian Redinger 01.07.2015 Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Gliederung Grundlagen CCW Polygone Picks Theorem Konvexe Hülle - Graham Scan - Jarvis March 2 Gliederung
Geometrie I Sebastian Redinger 01.07.2015 Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Gliederung Grundlagen CCW Polygone Picks Theorem Konvexe Hülle - Graham Scan - Jarvis March 2 Gliederung
EVC Repetitorium Blender
 EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
Abb. 5-5 Gegenüberstellung von Flat-Shading und Gouraud-Shading. Beleuchtungsberechnung mit nur einer Flächennormale pro Polygon
 Direkte Schattierungsverfahren (Gouraud) 5.1.5 Kontinuierliche Schattierung von Polygonen (Gouraud-Shading) bisher: Zerlegung gekrümmter Flächen (Zylinder, Kugeln, B-Spline-Flächen etc.) in Polygone (meist
Direkte Schattierungsverfahren (Gouraud) 5.1.5 Kontinuierliche Schattierung von Polygonen (Gouraud-Shading) bisher: Zerlegung gekrümmter Flächen (Zylinder, Kugeln, B-Spline-Flächen etc.) in Polygone (meist
Kapitel 4: Schattenberechnung
 Kapitel 4: Schattenberechnung 1 Überblick: Schattenberechnung Motivation Schattenvolumen Shadow Maps Projektive Schatten 2 Motivation Wesentlich für die Wahrnehmung einer 3D-Szene Eigentlich ein globaler
Kapitel 4: Schattenberechnung 1 Überblick: Schattenberechnung Motivation Schattenvolumen Shadow Maps Projektive Schatten 2 Motivation Wesentlich für die Wahrnehmung einer 3D-Szene Eigentlich ein globaler
Geometrie. 1 Vektorielle analytische Geometrie der Ebene, Kegelschnitte
 Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Geometrische Algorithmen
 Geometrische Algorithmen Thomas Röfer Motivation Scan-line-Prinzip Konvexe Hülle Distanzprobleme Voronoi-Diagramm Rückblick Manipulation von Mengen Vorrangwarteschlange Heap HeapSort swap(a, 0, 4) 1 5
Geometrische Algorithmen Thomas Röfer Motivation Scan-line-Prinzip Konvexe Hülle Distanzprobleme Voronoi-Diagramm Rückblick Manipulation von Mengen Vorrangwarteschlange Heap HeapSort swap(a, 0, 4) 1 5
Urs Wyder, 4057 Basel Funktionen. f x x x x 2
 Urs Wyder, 4057 Basel Urs.Wyder@edubs.ch Funktionen f 3 ( ) = + f ( ) = sin(4 ) Inhaltsverzeichnis DEFINITION DES FUNKTIONSBEGRIFFS...3. NOTATION...3. STETIGKEIT...3.3 ABSCHNITTSWEISE DEFINIERTE FUNKTIONEN...4
Urs Wyder, 4057 Basel Urs.Wyder@edubs.ch Funktionen f 3 ( ) = + f ( ) = sin(4 ) Inhaltsverzeichnis DEFINITION DES FUNKTIONSBEGRIFFS...3. NOTATION...3. STETIGKEIT...3.3 ABSCHNITTSWEISE DEFINIERTE FUNKTIONEN...4
3D-Computergrafik. Rastergrafik
 3D-Computergrafik Rastergrafik Notation von Polygonen Polygone werden nach 2D abgebildet Für weitere Betrachtungen reicht also zunächst: Betrachtung 2D-Prmitiven Erörtern der Aufgaben der Computergrafik
3D-Computergrafik Rastergrafik Notation von Polygonen Polygone werden nach 2D abgebildet Für weitere Betrachtungen reicht also zunächst: Betrachtung 2D-Prmitiven Erörtern der Aufgaben der Computergrafik
8 Blockbild und Hohenlinien
 Mathematik fur Ingenieure Institut fur Algebra, Zahlentheorie und Diskrete Mathematik Dr. Dirk Windelberg Universitat Hannover Stand: 18. August 008 http://www.iazd.uni-hannover.de/windelberg/teach/ing
Mathematik fur Ingenieure Institut fur Algebra, Zahlentheorie und Diskrete Mathematik Dr. Dirk Windelberg Universitat Hannover Stand: 18. August 008 http://www.iazd.uni-hannover.de/windelberg/teach/ing
Höhere Mathematik III WS 05/06 Lösungshinweis Aufgabe G 11 Blatt 2
 Höhere Mathematik III WS 5/6 Lösungshinweis Aufgabe G 11 Blatt Die zu optimierende Zielfunktion ist der Abstand zum Ursprung. Ein bekannter Trick (Vereinfachung der Rechnung) besteht darin, das Quadrat
Höhere Mathematik III WS 5/6 Lösungshinweis Aufgabe G 11 Blatt Die zu optimierende Zielfunktion ist der Abstand zum Ursprung. Ein bekannter Trick (Vereinfachung der Rechnung) besteht darin, das Quadrat
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II. x 2
 Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Krümmungsapproximation auf 3D-Modellen
 Krümmungsapproximation auf 3D-Modellen Mathematische Grundlagen und Approximation Christian Cyrus Matrikelnummer 157707 Fakultät für Informatik Otto-von-Guericke-Universität Magdeburg Diese Ausarbeitung
Krümmungsapproximation auf 3D-Modellen Mathematische Grundlagen und Approximation Christian Cyrus Matrikelnummer 157707 Fakultät für Informatik Otto-von-Guericke-Universität Magdeburg Diese Ausarbeitung
Lineare Algebra: Theorie und Anwendungen
 Lineare Algebra: Theorie und Anwendungen Sommersemester 2012 Bernhard Burgeth Universität des Saarlandes c 2010 2012, Bernhard Burgeth 1 VEKTOREN IN DER EBENE UND IM RAUM 2 1 Vektoren in der Ebene und
Lineare Algebra: Theorie und Anwendungen Sommersemester 2012 Bernhard Burgeth Universität des Saarlandes c 2010 2012, Bernhard Burgeth 1 VEKTOREN IN DER EBENE UND IM RAUM 2 1 Vektoren in der Ebene und
Computer Graphik I Polygon Scan Conversion
 11/23/09 lausthal omputer raphik I Polygon Scan onversion. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Klassifikation der Polygone Konvex Für jedes Punktepaar in einem konvexen Polygon
11/23/09 lausthal omputer raphik I Polygon Scan onversion. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Klassifikation der Polygone Konvex Für jedes Punktepaar in einem konvexen Polygon
5.5. Abituraufgaben zu ganzrationalen Funktionen
 .. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
.. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
Passerelle. Beschrieb der Fach-Module. von der Berufsmaturität. zu den universitären Hochschulen
 Passerelle von der Berufsmaturität zu den universitären Hochschulen Beschrieb der Fach-Module Fachbereich Mathematik Teilmodule Teilmodul 1: Analysis (Differential- und Integralrechnung) Teilmodul 2: Vektorgeometrie
Passerelle von der Berufsmaturität zu den universitären Hochschulen Beschrieb der Fach-Module Fachbereich Mathematik Teilmodule Teilmodul 1: Analysis (Differential- und Integralrechnung) Teilmodul 2: Vektorgeometrie
III. Integralrechnung 7. Übungen für die Klausur Teil 1 - Integralrechnung
 III. Integralrechnung 7. Übungen für die Klausur Teil - Integralrechnung Beachten Sie auch die Materialien aus dem Unterricht. Hier finden Sie viele Übungen, die Sie entweder noch nicht gemacht haben oder
III. Integralrechnung 7. Übungen für die Klausur Teil - Integralrechnung Beachten Sie auch die Materialien aus dem Unterricht. Hier finden Sie viele Übungen, die Sie entweder noch nicht gemacht haben oder
Wurzelfunktionen Aufgaben
 Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Klausurlösung Einführung in Numerische Methoden und FEM Universität Siegen, Department Maschinenbau,
 Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Morphologische Bildverarbeitung II
 FAKULTÄT FÜR MATHEMATIK UNIVERSITÄT ULM ABT. STOCHASTIK ABT. ANGEWANDTE INFORMATIONSVERARBEITUNG Seminar Simulation und Bildanalyse mit Java Morphologische Bildverarbeitung II BETREUER: JOHANNES MAYER
FAKULTÄT FÜR MATHEMATIK UNIVERSITÄT ULM ABT. STOCHASTIK ABT. ANGEWANDTE INFORMATIONSVERARBEITUNG Seminar Simulation und Bildanalyse mit Java Morphologische Bildverarbeitung II BETREUER: JOHANNES MAYER
Abiturprüfung 2000 LK Mathematik Baden-Württemberg
 Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Vektorrechnung Raumgeometrie
 Vektorrechnung Raumgeometrie Sofja Kowalewskaja (*1850, 1891) Hypatia of Alexandria (ca. *360, 415) Maria Gaetana Agnesi (*1718, 1799) Emmy Noether (*1882 1935) Émilie du Châtelet (*1706, 1749) Cathleen
Vektorrechnung Raumgeometrie Sofja Kowalewskaja (*1850, 1891) Hypatia of Alexandria (ca. *360, 415) Maria Gaetana Agnesi (*1718, 1799) Emmy Noether (*1882 1935) Émilie du Châtelet (*1706, 1749) Cathleen
1. Definition der trigonometrischen Funktionen für beliebige Winkel
 1 Trigonometrie 2 1. Definition der trigonometrischen Funktionen für beliebige Winkel In einem Kreis mit Mittelpunkt M(0,0) und Radius r ist der zunächst spitze Winkel α gezeichnet. α legt auf dem Kreis
1 Trigonometrie 2 1. Definition der trigonometrischen Funktionen für beliebige Winkel In einem Kreis mit Mittelpunkt M(0,0) und Radius r ist der zunächst spitze Winkel α gezeichnet. α legt auf dem Kreis
Grundlagen der Algorithmen und Datenstrukturen
 Grundlagen der Algorithmen und Datenstrukturen Christian Scheideler + Helmut Seidl SS 2009 01.04.09 Kapitel 0 1 Vorlesung: Organisatorisches Di 12:00 13:30 MI HS 1 Do 12:00 12:45 MI HS 1 Übungen: 34 Alternativen
Grundlagen der Algorithmen und Datenstrukturen Christian Scheideler + Helmut Seidl SS 2009 01.04.09 Kapitel 0 1 Vorlesung: Organisatorisches Di 12:00 13:30 MI HS 1 Do 12:00 12:45 MI HS 1 Übungen: 34 Alternativen
Triangulierung von einfachen Polygonen
 Triangulierung von einfachen Polygonen - Seminarvortrag von Tobias Kyrion - Inhalt: 1.1 Die Problemstellung Quellenangabe 1.1 Die Problemstellung Definition Polygon: endlich viele paarweise verschiedene
Triangulierung von einfachen Polygonen - Seminarvortrag von Tobias Kyrion - Inhalt: 1.1 Die Problemstellung Quellenangabe 1.1 Die Problemstellung Definition Polygon: endlich viele paarweise verschiedene
P 0 f (0) schneidet die Gerade mit der Gleichung x Ermitteln Sie die Koordinaten von S.
 Zentralabitur 015 im Fach Mathematik Analysis 1 Im nebenstehenden Bild sind die Graphen dreier Funktionen f, g und h dargestellt Geben Sie an, bei welcher der drei Funktionen es sich um eine Stammfunktion
Zentralabitur 015 im Fach Mathematik Analysis 1 Im nebenstehenden Bild sind die Graphen dreier Funktionen f, g und h dargestellt Geben Sie an, bei welcher der drei Funktionen es sich um eine Stammfunktion
Technische Universität München Zentrum Mathematik. Übungsblatt 11
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 11 Hausaufgaben Aufgabe 11.1 Berechnen Sie jeweils die Jacobi-Matrix folgender
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 11 Hausaufgaben Aufgabe 11.1 Berechnen Sie jeweils die Jacobi-Matrix folgender
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Inhaltsverzeichnis - Themen
 Inhaltsverzeichnis - Themen 1 Hardwaregrundlagen 2 Transformationen und Projektionen 3 Repräsentation und Modellierung von Objekten 4 Visibilität und Verdeckung 5 Rasterung 6 Rendering 7 Abbildungsverfahren
Inhaltsverzeichnis - Themen 1 Hardwaregrundlagen 2 Transformationen und Projektionen 3 Repräsentation und Modellierung von Objekten 4 Visibilität und Verdeckung 5 Rasterung 6 Rendering 7 Abbildungsverfahren
Kollisionserkennung
 1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
Aufgaben zur Übung der Anwendung von GeoGebra
 Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
11.3. Variablentrennung, Ähnlichkeit und Trajektorien
 3 Variablentrennung, Ähnlichkeit und Trajektorien Trennung der Veränderlichen (TdV) Es seien zwei stetige Funktionen a (der Variablen ) und b (der Variablen ) gegeben Die Dgl a( ) b( ) b( ) d d läßt sich
3 Variablentrennung, Ähnlichkeit und Trajektorien Trennung der Veränderlichen (TdV) Es seien zwei stetige Funktionen a (der Variablen ) und b (der Variablen ) gegeben Die Dgl a( ) b( ) b( ) d d läßt sich
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
11 Grafikprogrammierung
 11 Grafikprogrammierung Die Umsetzung quantitativer Information in eine grafische Darstellung ist nicht erst seit der Erfindung des Computers üblich geworden. Ein Bild sagt mehr als 1000 Worte und erst
11 Grafikprogrammierung Die Umsetzung quantitativer Information in eine grafische Darstellung ist nicht erst seit der Erfindung des Computers üblich geworden. Ein Bild sagt mehr als 1000 Worte und erst
Vektorgeometrie. 1. Vektoren eingeben, Norm, Skalarprodukt. 2 In einem kartesischen Koordinatensystem sind die Vektoren. , v. und. gegeben.
 Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Normalengleichungen. Für eine beliebige m n Matrix A erfüllt jede Lösung x des Ausgleichsproblems Ax b min die Normalengleichungen A t Ax = A t b,
 Normalengleichungen Für eine beliebige m n Matrix A erfüllt jede Lösung x des Ausgleichsproblems Ax b min die Normalengleichungen A t Ax = A t b, Normalengleichungen 1-1 Normalengleichungen Für eine beliebige
Normalengleichungen Für eine beliebige m n Matrix A erfüllt jede Lösung x des Ausgleichsproblems Ax b min die Normalengleichungen A t Ax = A t b, Normalengleichungen 1-1 Normalengleichungen Für eine beliebige
5 5 5 Abbildung : Raumkurve Abbildung 5: Tangente t existiert nur dann, wenn _ ~x(t ) = ist. Ein Punkt mit f _x; _y; _zg = f; ; g heißt ein regulärer
 3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
Analytische Geometrie - Schnittwinkel. u 1, u 2 Richtungsvektoren der Geraden
 Analytische Geometrie - Schnittwinkel. Möglichkeiten und Formeln Gerade / Gerade: cos( ) = u u 2 u u 2 Gerade / Ebene: sin( ) = n u n u Ebene / Ebene: cos( ) = n n 2 n n 2 u, u 2 Richtungsvektoren der
Analytische Geometrie - Schnittwinkel. Möglichkeiten und Formeln Gerade / Gerade: cos( ) = u u 2 u u 2 Gerade / Ebene: sin( ) = n u n u Ebene / Ebene: cos( ) = n n 2 n n 2 u, u 2 Richtungsvektoren der
Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B
 Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg
 Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Gymnasium Muttenz Maturitätsprüfung 2014 Mathematik Profile A und B
 Gymnasium Muttenz Maturitätsprüfung 2014 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Gymnasium Muttenz Maturitätsprüfung 2014 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Christina Nell. 3D-Computergrafik
 Christina Nell 3D-Computergrafik Was ist 3D-Computergrafik? 3D graphics is the art of cheating without getting caught. (unbekannte Quelle) Folie 2/52 Inhalt Beleuchtung Shading Texturierung Texturfilterung
Christina Nell 3D-Computergrafik Was ist 3D-Computergrafik? 3D graphics is the art of cheating without getting caught. (unbekannte Quelle) Folie 2/52 Inhalt Beleuchtung Shading Texturierung Texturfilterung
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Die Quadratur des Kreises
 Die Quadratur des Kreises Häufig hört man Leute sagen, vor allem wenn sie vor großen Schwierigkeiten stehen, so was wie hier wird die Quadratur des Kreises versucht. Was ist mit dieser Redewendung gemeint?
Die Quadratur des Kreises Häufig hört man Leute sagen, vor allem wenn sie vor großen Schwierigkeiten stehen, so was wie hier wird die Quadratur des Kreises versucht. Was ist mit dieser Redewendung gemeint?
Mathematik für das Ingenieurstudium
 Mathematik für das Ingenieurstudium von Martin Stämpfle, Jürgen Koch 2., aktual. Aufl. Hanser München 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 43232 1 Zu Inhaltsverzeichnis schnell
Mathematik für das Ingenieurstudium von Martin Stämpfle, Jürgen Koch 2., aktual. Aufl. Hanser München 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 43232 1 Zu Inhaltsverzeichnis schnell
Übersicht der Vorlesung
 Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Reconstruction and simplification of surfaces from contoures
 CG Seminar Reconstruction and simplification of surfaces from contoures Nach Klein, Schilling und Straßer Referent Thomas Kowalski Anfangssituation - Punktdaten Das zu rekonstruierende Objekt besteht aus
CG Seminar Reconstruction and simplification of surfaces from contoures Nach Klein, Schilling und Straßer Referent Thomas Kowalski Anfangssituation - Punktdaten Das zu rekonstruierende Objekt besteht aus
Plotten von Kreisen ( nach Jack Bresenham ) (C) Ac bis
 Plotten von Kreisen ( nach Jack Bresenham ) (C) Ac 3-1990 bis 2-2017 Wie zeichnet der Computer Kreise? Natürlich mithilfe von Pixels, picture elements, also kleinen Bildpunkten. Die beste Approximation
Plotten von Kreisen ( nach Jack Bresenham ) (C) Ac 3-1990 bis 2-2017 Wie zeichnet der Computer Kreise? Natürlich mithilfe von Pixels, picture elements, also kleinen Bildpunkten. Die beste Approximation
1.3. Beträge, Gleichungen und Ungleichungen
 1.3. Beträge, Gleichungen und Ungleichungen Das Maximum zweier Zahlen a, b wird mit max(a,b) bezeichnet, ihr Minimum mit min(a,b). Der Absolutbetrag einer reellen Zahl a ist a = max ( a, a ) oder auch
1.3. Beträge, Gleichungen und Ungleichungen Das Maximum zweier Zahlen a, b wird mit max(a,b) bezeichnet, ihr Minimum mit min(a,b). Der Absolutbetrag einer reellen Zahl a ist a = max ( a, a ) oder auch
Lk Mathematik 12 Analytische Geometrie Arbeitsblatt A.1
 Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen dx+ey+f = 0 1.1
 Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
Detektion von Eckpunkten und einfachen Kurven
 Detektion von Eckpunkten und einfachen Kurven Industrielle Bildverarbeitung, Vorlesung No. 7 1 M. O. Franz 21.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005.
Detektion von Eckpunkten und einfachen Kurven Industrielle Bildverarbeitung, Vorlesung No. 7 1 M. O. Franz 21.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005.
Berechnung von Formfaktoren
 Berechnung von Formfaktoren Oliver Deussen Formfaktorberechnung 1 Formfaktor ist eine Funktion in Abhängigkeit der Geometrie ist unabhängig von reflektierenden oder emittierenden Eigenschaften (ρ) der
Berechnung von Formfaktoren Oliver Deussen Formfaktorberechnung 1 Formfaktor ist eine Funktion in Abhängigkeit der Geometrie ist unabhängig von reflektierenden oder emittierenden Eigenschaften (ρ) der
Aufgabe 1. Zunächst wird die allgemeine Tangentengleichung in Abhängigkeit von a aufgestellt:
 Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
Lösungen der Übungsaufgaben III
 Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Konvexe Hülle. Konvexe Hülle. Mathematik. Konvexe Hülle: Definition. Mathematik. Konvexe Hülle: Eigenschaften. AK der Algorithmik 5, SS 2005 Hu Bin
 Konvexe Hülle Konvexe Hülle AK der Algorithmik 5, SS 2005 Hu Bin Anwendung: Computergraphik Boundary Kalkulationen Geometrische Optimierungsaufgaben Konvexe Hülle: Definition Mathematik Konvex: Linie zwischen
Konvexe Hülle Konvexe Hülle AK der Algorithmik 5, SS 2005 Hu Bin Anwendung: Computergraphik Boundary Kalkulationen Geometrische Optimierungsaufgaben Konvexe Hülle: Definition Mathematik Konvex: Linie zwischen
Ü bung GIT- Teil Nachrichtentechnik, 17.11.2015
 Ü bung GIT- Teil Nachrichtentechnik, 17.11.2015 1 OSI Schichtenmodell Systeme der Nachrichtentechnik werden häufig mittels des OSI-Referenzmodells charakterisiert. a) Benennen Sie die Schichten des OSI-Referenzmodells!
Ü bung GIT- Teil Nachrichtentechnik, 17.11.2015 1 OSI Schichtenmodell Systeme der Nachrichtentechnik werden häufig mittels des OSI-Referenzmodells charakterisiert. a) Benennen Sie die Schichten des OSI-Referenzmodells!
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
