1 Näherung quasistatische Temperaturverteilung
|
|
|
- Kristin Klein
- vor 6 Jahren
- Abrufe
Transkript
1 1 Näherung quasistatische Temperaturverteilung Behandelt wird das Braten von Fleisch, insbesondere das Braten einer Gans Die Gans wird als kugelförmig mit dem Radius r a angenommen Im Anfangszustand habe die Gans die einheitliche Anfangstemperatur T i gleich der Gartemperatur Die Oberfläche der Gans wird durch das Backrohr auf die Temperatur T a erwärmt Beim Garvorgang handelt es sich um einen Phasenübergang von ursprünglich rohem Zustand in den Zustand gebratenen Fleisches Rohes und gegartes Fleisch sind durch eine kugelflächenförmige Trennfläche mit dem Radius r i (t) - die Garfront - voneinander separiert Innerhalb der Garfront herrscht ungeändert die Temperatur T i Durch Wärmeleitung wird der Garfront die für das Garen notwendige Wärme zugeführt Dadurch bewegt sich diese Garfront beginnend von der Oberfläche ins Innere der Gans hinein Beendet ist der Garvorgang, wenn die Garfront das Zentrum der Gans erreicht Mit der Wärmestromdichte q i an der Garfront und der Garwärme pro Masseneinheit ergibt sich folgende Energiebilanz: 4 r i π q i dt = 4 r i π dr Wie üblich bezeichnet ρ die Dichte des Fleisches, von der angenommen wird, dass sie unabhängig vom Zustand des Fleisches - roh oder gar - ist Bei bekannter Wärmestromdichte q i gestattet diese Energiebilanz die Berechnung der Geschwindigkeit der Garfront: dt = 1 q i Unter der Annahme, dass im Bereich r i r r a eine näherungsweise stationäre Temperaturverteilung T = r ir a r Ta T i + T ar a T i r i
2 vorliegt, ergibt sich für die Wärmestromdichte q i = λ r a r i Ta T i Für die Geschwindigkeit der Garfront gilt dann die gewöhnliche Differentialgleichung dt = λ r a (T a T i ) 1 r i ( ) Das Integral r i r a r3 i 3 = λ r a (T a T i ) t + B dieser Differentialgleichung enthält eine Integrationskonstante B, die sich aus der Bedingung ermitteln lässt, dass die Garfront zum Zeitpnkt t = 0 mit der Oberfläche der Gans zusammenfällt: Man erhält r i (t = 0) = r a B = r3 a 3 Für die Position der Garfront in Abhängigkeit von der Zeit ergibt sich damit schließlich λ r a (T a T i ) t = r3 a 6 + r3 i 3 r i r a Der Garvorgang ist nun genau zu der Zeit t = τ beendet, zu der die Garfront das Zentrum der Gans r i (τ) = 0 erreicht Man erhält τ = r a 6 λ (T a T i) Drückt man den Radius r a der Gans durch ihre Masse m aus ergibt sich endlich die gesuchte Endformel für die Garzeit einer Gans: τ = 1 6 ( 3 4 π )/3 ρ1/3 m /3 λ (T a T i ) Im Unterschied zur Formel für die Garzeit im Buch Die Gourmetformel von DrWerner Gruber tritt die Differenz ΔT max = (T a T i ) von Backrohrtemperatur und Innentemperatur der Gans nicht im Quadrat, sondern nur linear auf
3 Dimensionsanalytische Überlegungen zur Garzeit Ohne die Annahme einer quasistatischen Temperaturverteilung und unter Verwendung der im vorigen Abschnitt eingeführten Größen zuzüglich der spezifischen Wärmekapazität c des gegarten Fleisches gilt für die gesuchte Garzeit ganz allgemein: τ = f(r a, ΔT max,, λ,, c) Die konkrete Gestalt der Funktion ist dabei unbekannt Da die Wahl des konkreten Einheitensystems keinen Einfluss auf die funktionale Abhängigkeit haben kann, muss sich diese Beziehung als Beziehung zwischen dimensionslosen Größen schreiben lassen Mittels dimensionsanalytischer Methoden lässt sich zeigen, dass es genau drei qualitativ verschiedene, dimensionslose Größen Π 1, Π und Π 3 gibt Ein möglicher Satz solcher Größen lautet: Π 1 = τ λ ΔT max r a, Π = c ΔT max und Π 3 = r a c λ Bei der Größe Π handelt es sich um das Verhältns der Wärmemenge, die pro Masseneinheit für eine Temperaturerhöhung ΔT erforderlich ist, zur Garwärme Unter Verwendung dieser drei dimensionslosen Größen, nimmt die Beziehung für die Garzeit die allgemeine Form Π 1 = f(π, Π 3 ) an Da Missverständnisse nicht zu befürchten sind, wurde wieder derselbe Funktionsname verwendet In den ursprünglichen physikalischen Größen bedeutet dies τ λ ΔT max r a = f( c ΔT max, ra c ) λ Nimmt man an, dass die Garwärme wesentlich größer ist, als die Wärmemenge c ΔT max - die Größe Π ist dann näherungsweise gleich Null - vereinfacht sich die Beziehung für die Garzeit zu τ = r a λ ΔT max f( r a c λ ) Wieder ergibt sich - im Einklang mit Abschnitt 1 - eine lineare Abhängigkeit der Garzeit vom Kehrwert der Temperaturdifferenz ΔT max 3 Überlegungen zum instationären Fall Für den allgemeineren Fall nicht quasistatischer Verhältnisse gilt es, die im gegarten Bereich gültige partielle Differentialgleichung ΔT t = a ΔT r (r r r ) mit a = λ ρ c für die Temperaturdifferenz ΔT (r)) = T (r) T i, zu lösen Zu dieser Gleichung gehören noch die Randbedingungen
4 ΔT (r = r a ) = ΔT max = T a T i ΔT (r = r i ) = 0 und die Anfangsbedingung ΔT (r < r a ) 0 Für den Radius r i der Garfront ergibt sich, wieder mit Hilfe der schon angeführten Energiebilanz, dt = λ ρ [ T r ] r=ri Durch die Einführung folgender Größen kann das Problem in dimensionslose Form gebracht werden: ˆT = ΔT ΔT max ˆr = r r a ˆt = t τ Dabei ist τ wieder die gesuchte Garzeit Das obige Gleichungssystem nimmt dann folgende Form an: ˆT ˆt = â ˆT ˆr (ˆr ˆr ˆr ) mit â = a τ ra ˆT (ˆr = 1) = 1 Tˆ(ˆr = ˆr i ) = 0 ˆT (r < 1) 0 dˆr i dˆt = ˆk[ ˆT ˆr ]ˆr=ˆri mit ˆk = λ ΔT max τ r a Wie man sieht, hängt die Lösung dieser partiellen Differentialgleichung neben ˆr und ˆt noch von genau zwei dimensionslosen Parametern â und ˆk ab: ˆT = ˆT (ˆr, ˆt, â, ˆk) und ˆr i = r i (â, ˆk, ˆt) Die Garfront erreicht das Zentrum ˆr i = 0 zur Zeit ˆt = 1 Es gilt also ˆr i (ˆt = 1, â, ˆk) = f(â, ˆk) = 0 Wegen
5 f(â, ˆk) = f(â ˆk ˆk, ˆk) = g( â ˆk, ˆk) = 0 folgt daraus ˆk = h(â ˆk ) mit der durch Lösung der Differentialgleichung zu bestimmenden Funktion h( â ) In physikalischen Größen ˆk ausgedrückt bedeutet das: τ = r a λ ΔT max h( c ΔT max ) In der Grenze c ΔTmax 1 ergibt sich wieder die quasistationäre Lösung des ersten Abschnittes
1. Die Wellengleichung
 1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
Mitschrift zu Wärmetransportphänomene bei Prof. Polifke SoSe 2010
 Inhalt 1. Einführung... 3 2. Grundbegriffe der Wärmeleitung... 3 2.1. Fourier sches Gesetz... 3 2.2. Fourier sche DGL... 3 3. Stationäre Wärmeleitung... 4 3.1. Wärmeleitung in einfachen Geometrien... 4
Inhalt 1. Einführung... 3 2. Grundbegriffe der Wärmeleitung... 3 2.1. Fourier sches Gesetz... 3 2.2. Fourier sche DGL... 3 3. Stationäre Wärmeleitung... 4 3.1. Wärmeleitung in einfachen Geometrien... 4
- 1 - angeführt. Die Beschleunigung ist die zweite Ableitung des Ortes x nach der Zeit, und das Gesetz lässt sich damit als 2.
 - 1 - Gewöhnliche Differentialgleichungen Teil I: Überblick Ein großer Teil der Grundgesetze der Phsik ist in Form von Gleichungen formuliert, in denen Ableitungen phsikalischer Größen vorkommen. Als Beispiel
- 1 - Gewöhnliche Differentialgleichungen Teil I: Überblick Ein großer Teil der Grundgesetze der Phsik ist in Form von Gleichungen formuliert, in denen Ableitungen phsikalischer Größen vorkommen. Als Beispiel
Numerische Integration
 A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
Überlegungen zur Leistung und zum Wirkungsgrad von Solarkochern
 Überlegungen zur Leistung und zum Wirkungsgrad von Solarkochern (Dr. Hartmut Ehmler) Einführung Die folgenden Überlegungen gelten ganz allgemein für Solarkocher, unabhängig ob es sich um einen Parabolkocher,
Überlegungen zur Leistung und zum Wirkungsgrad von Solarkochern (Dr. Hartmut Ehmler) Einführung Die folgenden Überlegungen gelten ganz allgemein für Solarkocher, unabhängig ob es sich um einen Parabolkocher,
Lineare Differentialgleichungen 1. Ordnung
 Lineare Differentialgleichungen 1. Ordnung Eine lineare Differentialgleichung 1. Ordnung hat folgende Gestalt: +f() = r(). Dabei sind f() und r() gewisse, nur von abhängige Funktionen. Wichtig: sowohl
Lineare Differentialgleichungen 1. Ordnung Eine lineare Differentialgleichung 1. Ordnung hat folgende Gestalt: +f() = r(). Dabei sind f() und r() gewisse, nur von abhängige Funktionen. Wichtig: sowohl
Klausur zur Vorlesung. Wärme- und Stoffübertragung
 Institut für Thermodynamik 27. Juli 202 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Wärme- und Stoffübertragung Für alle Aufgaben gilt: Der Rechen- und Gedankengang
Institut für Thermodynamik 27. Juli 202 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Wärme- und Stoffübertragung Für alle Aufgaben gilt: Der Rechen- und Gedankengang
Kontinuierliche Systeme und diskrete Systeme
 Kontinuierliche Systeme und diskrete Systeme home/lehre/vl-mhs-1/inhalt/folien/vorlesung/1_disk_kont_sys/deckblatt.tex Seite 1 von 24. p.1/24 Inhaltsverzeichnis Grundbegriffe ingenieurwissenschaftlicher
Kontinuierliche Systeme und diskrete Systeme home/lehre/vl-mhs-1/inhalt/folien/vorlesung/1_disk_kont_sys/deckblatt.tex Seite 1 von 24. p.1/24 Inhaltsverzeichnis Grundbegriffe ingenieurwissenschaftlicher
Technische Mathe: Problem-Lösungen: Wärmemenge in einer Flüssigkeit Seite 1 von 7
 Technische Mathe: Problem-Lösungen: Wärmemenge in einer Flüssigkeit Seite 1 von 7 Diese Lerneinheit ist besonders den Schülern gewidmet, für die jede Rechenaufgabe ein Problem darstellt. Ich versuche hier
Technische Mathe: Problem-Lösungen: Wärmemenge in einer Flüssigkeit Seite 1 von 7 Diese Lerneinheit ist besonders den Schülern gewidmet, für die jede Rechenaufgabe ein Problem darstellt. Ich versuche hier
Klausur Strömungslehre a) Beschreiben Sie kurz in Worten das Prinzip des hydrostatischen Auftriebs nach Archimedes.
 ......... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 20. 08. 2004 1. Aufgabe (11 Punkte) a) Beschreiben Sie kurz in Worten das Prinzip des hydrostatischen Auftriebs nach Archimedes. b) Nennen
......... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 20. 08. 2004 1. Aufgabe (11 Punkte) a) Beschreiben Sie kurz in Worten das Prinzip des hydrostatischen Auftriebs nach Archimedes. b) Nennen
SC-PROJEKT EISWÜRFEL: HÖHE = 21MM. Patrick Kurer & Marcel Meschenmoser
 SC-PROJEKT EISWÜRFEL: HÖHE = 21MM Patrick Kurer & Marcel Meschenmoser 2.1.2013 INHALTSVERZEICHNIS Inhaltsverzeichnis... 1 Allgemeine Parameter... 2 Aufgabe A Allgemeine Berechnung des Eiswürfels... 2 Aufgabe
SC-PROJEKT EISWÜRFEL: HÖHE = 21MM Patrick Kurer & Marcel Meschenmoser 2.1.2013 INHALTSVERZEICHNIS Inhaltsverzeichnis... 1 Allgemeine Parameter... 2 Aufgabe A Allgemeine Berechnung des Eiswürfels... 2 Aufgabe
! #!! % & ( )! ! +, +,# # !.. +, ) + + /) # %
 ! #! #!! % & ( )!! +, +,# #!.. +, ) + + /)!!.0. #+,)!## 2 +, ) + + 3 4 # )!#!! ), 5 # 6! # &!). ) # )!#! #, () # # ) #!# #. # ) 6 # ) )0 4 )) #, 7) 6!!. )0 +,!# +, 4 / 4, )!#!! ))# 0.(! & ( )!! 8 # ) #+,
! #! #!! % & ( )!! +, +,# #!.. +, ) + + /)!!.0. #+,)!## 2 +, ) + + 3 4 # )!#!! ), 5 # 6! # &!). ) # )!#! #, () # # ) #!# #. # ) 6 # ) )0 4 )) #, 7) 6!!. )0 +,!# +, 4 / 4, )!#!! ))# 0.(! & ( )!! 8 # ) #+,
c ) Wie verhält sich die Enthalpieänderung, wenn das Wasser in einer Düse beschleunigt wird?
 Aufgabe 4 An einer Drosselstelle wird ein kontinuierlich fließender Strom von Wasser von p 8 bar auf p 2 2 bar entspannt. Die Geschwindigkeiten vor und nach der Drosselung sollen gleich sein. Beim des
Aufgabe 4 An einer Drosselstelle wird ein kontinuierlich fließender Strom von Wasser von p 8 bar auf p 2 2 bar entspannt. Die Geschwindigkeiten vor und nach der Drosselung sollen gleich sein. Beim des
Differentialgleichungen II für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg SoSe 2006 Prof. Dr. R. Lauterbach Dr. K. Rothe Differentialgleichungen II für Studierende der Ingenieurwissenschaften Lösungen zu Blatt 4 Aufgabe 13: Gegeben
Fachbereich Mathematik der Universität Hamburg SoSe 2006 Prof. Dr. R. Lauterbach Dr. K. Rothe Differentialgleichungen II für Studierende der Ingenieurwissenschaften Lösungen zu Blatt 4 Aufgabe 13: Gegeben
Thermodynamische Prozesse in Untergrundspeichern für Gase
 Thermodynamische Prozesse in Untergrundspeichern für Gase Prof. Dr.-Ing. Reinhard Scholz, TU Clausthal Prof. Dr.-Ing. Michael Beckmann, TU Dresden Prof. Dr.-Ing. Uwe Gampe, TU Dresden Prof. Dr.-Ing. Hans
Thermodynamische Prozesse in Untergrundspeichern für Gase Prof. Dr.-Ing. Reinhard Scholz, TU Clausthal Prof. Dr.-Ing. Michael Beckmann, TU Dresden Prof. Dr.-Ing. Uwe Gampe, TU Dresden Prof. Dr.-Ing. Hans
Lösungen zu den Aufgaben Besuch aus dem Weltall ein kleiner Asteroid tritt ein in die Erdatmosphäre
 Lösungen zu den Aufgaben Besuch aus dem Weltall ein kleiner Asteroid tritt ein in die Erdatmosphäre Achtung Fehler: Die Werte für die spezifische Gaskonstante R s haben als Einheit J/kg/K, nicht, wie angegeben,
Lösungen zu den Aufgaben Besuch aus dem Weltall ein kleiner Asteroid tritt ein in die Erdatmosphäre Achtung Fehler: Die Werte für die spezifische Gaskonstante R s haben als Einheit J/kg/K, nicht, wie angegeben,
Gewöhnliche Autokorrelationsfunktion (ACF) eines stationären Prozesses {X t } t Z zum Lag h
 5. Die partielle Autokorrelationsfunktion 5.1 Definition, Berechnung, Schätzung Bisher: Gewöhnliche Autokorrelationsfunktion (ACF) eines stationären Prozesses {X t } t Z zum Lag h ρ X (h) = Corr(X t, X
5. Die partielle Autokorrelationsfunktion 5.1 Definition, Berechnung, Schätzung Bisher: Gewöhnliche Autokorrelationsfunktion (ACF) eines stationären Prozesses {X t } t Z zum Lag h ρ X (h) = Corr(X t, X
6 Gewöhnliche Differentialgleichungen
 6 Gewöhnliche Differentialgleichungen Differentialgleichungen sind Gleichungen in denen nicht nur eine Funktion selbst sondern auch ihre Ableitungen vorkommen. Im einfachsten Fall gibt es eine unabhängige
6 Gewöhnliche Differentialgleichungen Differentialgleichungen sind Gleichungen in denen nicht nur eine Funktion selbst sondern auch ihre Ableitungen vorkommen. Im einfachsten Fall gibt es eine unabhängige
Maßeinheiten der Wärmelehre
 Maßeinheiten der Wärmelehre Temperatur (thermodynamisch) Benennung der Einheit: Einheitenzeichen: T für Temp.-punkte, ΔT für Temp.-differenzen Kelvin K 1 K ist der 273,16te Teil der (thermodynamischen)
Maßeinheiten der Wärmelehre Temperatur (thermodynamisch) Benennung der Einheit: Einheitenzeichen: T für Temp.-punkte, ΔT für Temp.-differenzen Kelvin K 1 K ist der 273,16te Teil der (thermodynamischen)
9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts
 9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes Element
9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes Element
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 23 (5.8.23). Gegeben seien die Matrizen A = 2 3 3 und B = 5 2 5 (a) Bestimmen Sie die Eigenwerte von A und B sowie die
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 23 (5.8.23). Gegeben seien die Matrizen A = 2 3 3 und B = 5 2 5 (a) Bestimmen Sie die Eigenwerte von A und B sowie die
Gewöhnliche Differentialgleichungen Aufgaben, Teil 1
 Gewöhnliche Differentialgleichungen Aufgaben, Teil 1 4-E1 4-E2 4-E3 Gewöhnliche Differentialgleichung: Aufgaben Bestimmen Sie allgemeine und spezielle Lösungen der folgenden Differentialgleichungen Aufgabe
Gewöhnliche Differentialgleichungen Aufgaben, Teil 1 4-E1 4-E2 4-E3 Gewöhnliche Differentialgleichung: Aufgaben Bestimmen Sie allgemeine und spezielle Lösungen der folgenden Differentialgleichungen Aufgabe
oder 10 = 1bar = = 10 Pa Für viele Zwecke wird die Umrechnung 1bar = 10 verwendet.
 R. Brinkmann http://brinkmann-du.de Seite 1 5.11.013 HF14S Arbeitsblatt Wärme als Energieform Die Celsius-Skala ist durch folgende Fixpunkte definiert: 0 0 C: Schmelzpunkt des Eises bei einem Druck von
R. Brinkmann http://brinkmann-du.de Seite 1 5.11.013 HF14S Arbeitsblatt Wärme als Energieform Die Celsius-Skala ist durch folgende Fixpunkte definiert: 0 0 C: Schmelzpunkt des Eises bei einem Druck von
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
 Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Hydrodynamik: bewegte Flüssigkeiten
 Hydrodynamik: bewegte Flüssigkeiten Wir betrachten eine stationäre Strömung, d.h. die Geschwindigkeit der Strömung an einem gegebenen Punkt bleibt konstant im Laufe der Zeit. Außerdem betrachten wir zunächst
Hydrodynamik: bewegte Flüssigkeiten Wir betrachten eine stationäre Strömung, d.h. die Geschwindigkeit der Strömung an einem gegebenen Punkt bleibt konstant im Laufe der Zeit. Außerdem betrachten wir zunächst
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Regelungstechnik I (WS 13/14) Klausur ( )
 Regelungstechnik I (WS 13/14) Klausur (13.03.2014) Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Name: Matrikelnummer: Bitte beachten Sie: a) Diese Klausur enthält 4 Aufgaben auf den
Regelungstechnik I (WS 13/14) Klausur (13.03.2014) Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Name: Matrikelnummer: Bitte beachten Sie: a) Diese Klausur enthält 4 Aufgaben auf den
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Physikalisches Pendel
 Physikalisches Pendel Nach einer kurzen Einführung in die Theorie des physikalisch korrekten Pendels (ausgedehnte Masse) wurden die aus der Theorie gewonnenen Formeln in praktischen Messungen überprüft.
Physikalisches Pendel Nach einer kurzen Einführung in die Theorie des physikalisch korrekten Pendels (ausgedehnte Masse) wurden die aus der Theorie gewonnenen Formeln in praktischen Messungen überprüft.
Stickstoff kann als ideales Gas betrachtet werden mit einer spezifischen Gaskonstante von R N2 = 0,297 kj
 Aufgabe 4 Zylinder nach oben offen Der dargestellte Zylinder A und der zugehörige bis zum Ventil reichende Leitungsabschnitt enthalten Stickstoff. Dieser nimmt im Ausgangszustand ein Volumen V 5,0 dm 3
Aufgabe 4 Zylinder nach oben offen Der dargestellte Zylinder A und der zugehörige bis zum Ventil reichende Leitungsabschnitt enthalten Stickstoff. Dieser nimmt im Ausgangszustand ein Volumen V 5,0 dm 3
Bei der Wärmeübertragung kann man drei Transportvorgänge voneinander unterscheiden:
 6 ärmeübertragung Bei der ärmeübertragung kann man drei Transportvorgänge voneinander unterscheiden: ärmeleitung ärmeübergang / onvektion ärmestrahlung Der ärmetransport durch Leitung oder onvektion benötigt
6 ärmeübertragung Bei der ärmeübertragung kann man drei Transportvorgänge voneinander unterscheiden: ärmeleitung ärmeübergang / onvektion ärmestrahlung Der ärmetransport durch Leitung oder onvektion benötigt
Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen
 Kapitel 8 Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen Wir hatten im Beispiel 5. gesehen, dass die Wärmeleitungsgleichung t u u = f auf Ω (0, ) (8.1) eine parabolische Differentialgleichung
Kapitel 8 Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen Wir hatten im Beispiel 5. gesehen, dass die Wärmeleitungsgleichung t u u = f auf Ω (0, ) (8.1) eine parabolische Differentialgleichung
Ausblick. 1. Lineare dynamische Analysen 2. Nichtlineare Analysen 3. Weitere Anwendungen. Prof. Dr. Wandinger 5. Ausblick FEM 5-1
 Ausblick 1. Lineare dynamische Analysen 2. Nichtlineare Analysen 3. Weitere Anwendungen Prof. Dr. Wandinger 5. Ausblick FEM 5-1 1. Lineare dynamische Analysen Beschleunigungen: Bei linearen dynamischen
Ausblick 1. Lineare dynamische Analysen 2. Nichtlineare Analysen 3. Weitere Anwendungen Prof. Dr. Wandinger 5. Ausblick FEM 5-1 1. Lineare dynamische Analysen Beschleunigungen: Bei linearen dynamischen
4. Wellenausbreitung
 Motivation: Beim Stab konnten Lösungen der Form gefunden werden. u x,t = f 1 x ct f 2 x ct Diese Lösungen beschreiben die Ausbreitung von Wellen im Stab. Die Funktionen f 1 x und f 2 x werden durch die
Motivation: Beim Stab konnten Lösungen der Form gefunden werden. u x,t = f 1 x ct f 2 x ct Diese Lösungen beschreiben die Ausbreitung von Wellen im Stab. Die Funktionen f 1 x und f 2 x werden durch die
3 Anwendungen der Differentialrechnung. (x 1, x 2,..., x n 1, x n ) f xn (x 1, x 2,..., x n 1, x n ), 1 i n 1. y + cos z
 R Es sei f : R n D R eine einmal stetig differenzierbare Funktion, für die in einer Umgebung eines Punkte a = a 1, a,, a n D gilt: fa 1, a,, a n = 0, f xn a 1, a,, a n 0 Dann gibt es eines Umgebung U des
R Es sei f : R n D R eine einmal stetig differenzierbare Funktion, für die in einer Umgebung eines Punkte a = a 1, a,, a n D gilt: fa 1, a,, a n = 0, f xn a 1, a,, a n 0 Dann gibt es eines Umgebung U des
Angewandte Geometrie
 Technische Universität München SS 215 Zentrum Mathematik Blatt 4 Prof. Dr. J. Hartl Angewandte Geometrie 1. Ein Kind läuft einen geradlinigen Weg entlang und zieht an einer Schnur ein (seitlich des Weges
Technische Universität München SS 215 Zentrum Mathematik Blatt 4 Prof. Dr. J. Hartl Angewandte Geometrie 1. Ein Kind läuft einen geradlinigen Weg entlang und zieht an einer Schnur ein (seitlich des Weges
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
2 Extrema unter Nebenbedingungen
 $Id: lagrange.tex,v 1.6 2012/11/06 14:26:21 hk Exp hk $ 2 Extrema unter Nebenbedingungen 2.1 Restringierte Optimierungsaufgaben Nachdem wir jetzt die bereits bekannten Techniken zur Bestimmung der lokalen
$Id: lagrange.tex,v 1.6 2012/11/06 14:26:21 hk Exp hk $ 2 Extrema unter Nebenbedingungen 2.1 Restringierte Optimierungsaufgaben Nachdem wir jetzt die bereits bekannten Techniken zur Bestimmung der lokalen
(a) Lösen Sie die Differentialgleichung unter Verwendung der Mathematica-Funktion DSolve.
 Institut für Physikalische Chemie Methodenkurs Anwendungen von Mathematica und Matlab in der Physikalischen Chemie im WS 205/206 Prof Dr Stefan Weber, Dr Till Biskup Aufgabenblatt zum Teil (Mathematica)
Institut für Physikalische Chemie Methodenkurs Anwendungen von Mathematica und Matlab in der Physikalischen Chemie im WS 205/206 Prof Dr Stefan Weber, Dr Till Biskup Aufgabenblatt zum Teil (Mathematica)
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie
 Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Transport Einführung
 Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
DISPOSITION
 ABKÜHLUNGSPROZESSE DISPOSITION 2 Abkühlung von Wasser Newton sches Abkühlungsgesetz Abkühlung von Kaffee/Milch Bestimmung des Todeszeitpunktes Mpemba - Effekt Abkühlung eines Metallstabs Anwendungen von
ABKÜHLUNGSPROZESSE DISPOSITION 2 Abkühlung von Wasser Newton sches Abkühlungsgesetz Abkühlung von Kaffee/Milch Bestimmung des Todeszeitpunktes Mpemba - Effekt Abkühlung eines Metallstabs Anwendungen von
Institut für Analysis SS 2015 PD Dr. Peer Christian Kunstmann Dipl.-Math. Leonid Chaichenets
 Institut für Analysis SS 25 PD Dr. Peer Christian Kunstmann 7.9.25 Dipl.-Math. Leonid Chaichenets Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zur Bachelor-Modulprüfung Aufgabe :
Institut für Analysis SS 25 PD Dr. Peer Christian Kunstmann 7.9.25 Dipl.-Math. Leonid Chaichenets Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zur Bachelor-Modulprüfung Aufgabe :
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Quantenmechanische Probleme in drei Raumdimensionen
 KAPITEL VI Quantenmechanische Probleme in drei Raumdimensionen VI. Dreidimensionaler Kastenpotential Der Vollständigkeit halber... VI. Teilchen in einem Zentralpotential In diesem Abschnitt werden die
KAPITEL VI Quantenmechanische Probleme in drei Raumdimensionen VI. Dreidimensionaler Kastenpotential Der Vollständigkeit halber... VI. Teilchen in einem Zentralpotential In diesem Abschnitt werden die
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Die Differentialgleichung :
 Die Differentialgleichung : Erstellt von Judith Ackermann 1.) Definition, Zweck 1.1) verschiedene Arten von Differentialgleichungen 2.) Beispiele und Lösungswege 2.1) gewöhnliche Differentialgleichungen
Die Differentialgleichung : Erstellt von Judith Ackermann 1.) Definition, Zweck 1.1) verschiedene Arten von Differentialgleichungen 2.) Beispiele und Lösungswege 2.1) gewöhnliche Differentialgleichungen
3. Prozesse mit kontinuierlicher Zeit
 3. Prozesse mit kontinuierlicher Zeit 3.1 Einführung Wir betrachten nun Markov-Ketten (X(t)) t R +. 0 Wie beim Übergang von der geometrischen zur Exponentialverteilung können wir uns auch hier einen Grenzprozess
3. Prozesse mit kontinuierlicher Zeit 3.1 Einführung Wir betrachten nun Markov-Ketten (X(t)) t R +. 0 Wie beim Übergang von der geometrischen zur Exponentialverteilung können wir uns auch hier einen Grenzprozess
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
3. Diffusion und Brechungsindex
 3. Diffusion und Brechungsinde Die Diffusion in und aus einer Schicht ist die Grundlage vieler Sensoreffekte, wobei sich die einzelnen Sensoren dann nur noch in der Art der Übersetzung in ein meßbares
3. Diffusion und Brechungsinde Die Diffusion in und aus einer Schicht ist die Grundlage vieler Sensoreffekte, wobei sich die einzelnen Sensoren dann nur noch in der Art der Übersetzung in ein meßbares
Klausur zur Vorlesung
 Institut für Thermodynamik 9. März 20 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Wärme- und Stoffübertragung Für alle Aufgaben gilt: Der Rechen- und Gedankengang
Institut für Thermodynamik 9. März 20 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Wärme- und Stoffübertragung Für alle Aufgaben gilt: Der Rechen- und Gedankengang
Ferienkurs Theoretische Mechanik 2010 Lagrange Formalismus
 Fakultät für Physik Michael Schrapp Technische Universität München Vorlesung Ferienkurs Theoretische Mechanik 2010 Lagrange Formalismus Inhaltsverzeichnis 1 Motivation 2 2 Generalisierte Koordinaten und
Fakultät für Physik Michael Schrapp Technische Universität München Vorlesung Ferienkurs Theoretische Mechanik 2010 Lagrange Formalismus Inhaltsverzeichnis 1 Motivation 2 2 Generalisierte Koordinaten und
4. Dämpfungsmodelle. 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. Elastodynamik 3.
 4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
Aufgabe 2 Auf dem Bildschirm eines Oszillographen durchlaufe ein Elektronenstrahl eine Bahn mit dem zeitabhängigen Ortsvektor
 Thema: Vektoranalysis PT/LOT WS 13/14 Analysis III Serie 3 www.fh-jena.de/~puhl Aufgabe 1 Ein Massepunkt bewegt sich mit der Winkelgeschwindigkeit ω 1 auf einer Kreisbahn mit dem Radius R 1 und dem Mittelpunkt
Thema: Vektoranalysis PT/LOT WS 13/14 Analysis III Serie 3 www.fh-jena.de/~puhl Aufgabe 1 Ein Massepunkt bewegt sich mit der Winkelgeschwindigkeit ω 1 auf einer Kreisbahn mit dem Radius R 1 und dem Mittelpunkt
3. Berechnen Sie auch die Beschleunigung a als Funktion der Zeit t. 4. Erstellen Sie ein SIMULINK Modell, das x(t) numerisch berechnet.
 unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
Projektbericht Kondensation an einem Fenster
 Projektbericht Kondensation an einem Fenster Florian Hanzer Ruth Kalthaus Sommersemester 2009 Einleitung Da Glas ein relativ guter Wärmeleiter ist, sind Fenster einer der größten Schwachpunkte in Bezug
Projektbericht Kondensation an einem Fenster Florian Hanzer Ruth Kalthaus Sommersemester 2009 Einleitung Da Glas ein relativ guter Wärmeleiter ist, sind Fenster einer der größten Schwachpunkte in Bezug
Gibt es ein Maxima des polaren Trägheitsmoments eines Kreisrings?
 Gibt es ein Maxima des polaren Trägheitsmoments eines Kreisrings? Dipl.- Ing. Björnstjerne Zindler, M.Sc. Erstellt: 12. Mai 2012 Letzte Revision: 4. April 2015 Inhaltsverzeichnis 1 Berechnung des polaren
Gibt es ein Maxima des polaren Trägheitsmoments eines Kreisrings? Dipl.- Ing. Björnstjerne Zindler, M.Sc. Erstellt: 12. Mai 2012 Letzte Revision: 4. April 2015 Inhaltsverzeichnis 1 Berechnung des polaren
8 Euklidische Vektorräume und Fourierreihen
 Mathematik für Ingenieure II, SS 9 Dienstag 7.7 $Id: fourier.te,v 1.6 9/7/7 13:: hk Ep $ $Id: diff.te,v 1. 9/7/7 16:13:53 hk Ep $ 8 Euklidische Vektorräume und Fourierreihen 8.4 Anwendungen auf Differentialgleichungen
Mathematik für Ingenieure II, SS 9 Dienstag 7.7 $Id: fourier.te,v 1.6 9/7/7 13:: hk Ep $ $Id: diff.te,v 1. 9/7/7 16:13:53 hk Ep $ 8 Euklidische Vektorräume und Fourierreihen 8.4 Anwendungen auf Differentialgleichungen
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Technische Universität München Zentrum Mathematik. Übungsblatt 5
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 5 Hausaufgaben Aufgabe 5. Bestimmen Sie folgende Grenzwerte. Benutzen
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 5 Hausaufgaben Aufgabe 5. Bestimmen Sie folgende Grenzwerte. Benutzen
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge
 Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Blatt 4. Stoß und Streuung - Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 211 Blatt 4. Stoß und Streuung - Lösungsvorschlag Aufgabe 4.1. Stoß Zwei
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 211 Blatt 4. Stoß und Streuung - Lösungsvorschlag Aufgabe 4.1. Stoß Zwei
Höhere Mathematik II für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 4 Höhere Mathematik II für die Fachrichtung Informatik Lösungsvorschläge zum. Übungsblatt Aufgabe 37
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 4 Höhere Mathematik II für die Fachrichtung Informatik Lösungsvorschläge zum. Übungsblatt Aufgabe 37
Dispersion, nicht-lineare Effekte, Solitonen
 Dispersion, nicht-lineare Effekte, Solitonen Als Beispiel für Dispersion und Effekte aufgrund von Nichtlinearität verwenden wir Oberflächenwellen auf Wasser. An der Wasseroberfläche wirken Kräfte aufgrund
Dispersion, nicht-lineare Effekte, Solitonen Als Beispiel für Dispersion und Effekte aufgrund von Nichtlinearität verwenden wir Oberflächenwellen auf Wasser. An der Wasseroberfläche wirken Kräfte aufgrund
Computer und Software 1
 omputer und oftware 1. Köhler 6. aple Differentialgleichungen Folien: alint Aradi Differentialgleichungen Gewöhnliche Differentialgleichungen: f t, x t, x 1 t, x 2 t,..., x n t =0 x i t = d i x t dt i
omputer und oftware 1. Köhler 6. aple Differentialgleichungen Folien: alint Aradi Differentialgleichungen Gewöhnliche Differentialgleichungen: f t, x t, x 1 t, x 2 t,..., x n t =0 x i t = d i x t dt i
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik. SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am
 Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik Name: Vorname(n): Matrikelnummer: Bitte... SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am 16.03.018 Arbeitszeit: 150 min Aufgabe
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik Name: Vorname(n): Matrikelnummer: Bitte... SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am 16.03.018 Arbeitszeit: 150 min Aufgabe
Vergleich von experimentellen Ergebnissen mit realen Konfigurationen
 Ähnlichkeitstheorie Vergleich von experimentellen Ergebnissen mit realen Konfigurationen Verringerung der Anzahl der physikalischen Größen ( Anzahl der Experimente) Experimentelle Ergebnisse sind unabhängig
Ähnlichkeitstheorie Vergleich von experimentellen Ergebnissen mit realen Konfigurationen Verringerung der Anzahl der physikalischen Größen ( Anzahl der Experimente) Experimentelle Ergebnisse sind unabhängig
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
4. Stoßvorgänge. Stoßvorgänge sind Vorgänge von sehr kurzer Dauer, bei denen zwischen den beteiligten Körpern große Kräfte auftreten.
 4. Stoßvorgänge Stoßvorgänge sind Vorgänge von sehr kurzer Dauer, bei denen zwischen den beteiligten Körpern große Kräfte auftreten. Gesucht wird ein Zusammenhang zwischen den Geschwindigkeiten vor dem
4. Stoßvorgänge Stoßvorgänge sind Vorgänge von sehr kurzer Dauer, bei denen zwischen den beteiligten Körpern große Kräfte auftreten. Gesucht wird ein Zusammenhang zwischen den Geschwindigkeiten vor dem
Verbesserung des Wärmetransports:
 7. Wärmeübertragung durch berippte Flächen A b ϑ ϑ ) ( a Grundgleichung i Verbesserung des Wärmetransports: k zeigt 3 Möglichkeiten für 1.) Vergrößerung der Temperaturdifferenz: Durchführbarkeit: Meist
7. Wärmeübertragung durch berippte Flächen A b ϑ ϑ ) ( a Grundgleichung i Verbesserung des Wärmetransports: k zeigt 3 Möglichkeiten für 1.) Vergrößerung der Temperaturdifferenz: Durchführbarkeit: Meist
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 11. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 11. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 11. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 11. 06.
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 Vladimir Dyakonov #4 am 3.0.007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 Vladimir Dyakonov #4 am 3.0.007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Aufgabe 2 (5 Punkte) y = 1 x. y + 3e 3x+2 x. von f. (ii) Für welches u in R 2 gilt f(u) = [3, 3, 4] T? x 2 + a x 3 x 1 4x 2 + a x 3 2x 4
![Aufgabe 2 (5 Punkte) y = 1 x. y + 3e 3x+2 x. von f. (ii) Für welches u in R 2 gilt f(u) = [3, 3, 4] T? x 2 + a x 3 x 1 4x 2 + a x 3 2x 4 Aufgabe 2 (5 Punkte) y = 1 x. y + 3e 3x+2 x. von f. (ii) Für welches u in R 2 gilt f(u) = [3, 3, 4] T? x 2 + a x 3 x 1 4x 2 + a x 3 2x 4](/thumbs/65/53300283.jpg) Prof. Dr. B. Billhardt Wintersemester 4/5 Klausur zur Vorlesung Höhere Mathematik II (BNUW) 4.3.5 Aufgabe (a) Ermitteln Sie die Nullstellen des Polynoms p(z) = z 4 4z 3 + 3z + 8z. Tipp: p( + i) =. (b)
Prof. Dr. B. Billhardt Wintersemester 4/5 Klausur zur Vorlesung Höhere Mathematik II (BNUW) 4.3.5 Aufgabe (a) Ermitteln Sie die Nullstellen des Polynoms p(z) = z 4 4z 3 + 3z + 8z. Tipp: p( + i) =. (b)
10. Übung zur Linearen Algebra I -
 . Übung zur Linearen Algebra I - en Kommentare an Hannes.Klarner@FU-Berlin.de FU Berlin. WS 29-. Aufgabe 37 i Für welche α R besitzt das lineare Gleichungssystem 4 αx + αx 2 = 4x + α + 2x 2 = α genau eine,
. Übung zur Linearen Algebra I - en Kommentare an Hannes.Klarner@FU-Berlin.de FU Berlin. WS 29-. Aufgabe 37 i Für welche α R besitzt das lineare Gleichungssystem 4 αx + αx 2 = 4x + α + 2x 2 = α genau eine,
Vektoren, Tensoren, Operatoren Tensoren Rang 0 Skalar p,ρ,t,... Rang 1 Vektor F, v, I,... Spannungstensor
 Vektoren, Tensoren, Operatoren Tensoren Rang 0 Skalar p,ρ,t,... Rang 1 Vektor F, v, I,... Rang 2 Dyade }{{} σ, τ,... Spannungstensor Differential-Operatoren Nabla- / x Operator / y in kartesischen / Koordinaten
Vektoren, Tensoren, Operatoren Tensoren Rang 0 Skalar p,ρ,t,... Rang 1 Vektor F, v, I,... Rang 2 Dyade }{{} σ, τ,... Spannungstensor Differential-Operatoren Nabla- / x Operator / y in kartesischen / Koordinaten
Fehlerfortpflanzung. M. Schlup. 27. Mai 2011
 Fehlerfortpflanzung M. Schlup 7. Mai 0 Wird eine nicht direkt messbare physikalische Grösse durch das Messen anderer Grössen ermittelt, so stellt sich die Frage, wie die Unsicherheitsschranke dieser nicht-messbaren
Fehlerfortpflanzung M. Schlup 7. Mai 0 Wird eine nicht direkt messbare physikalische Grösse durch das Messen anderer Grössen ermittelt, so stellt sich die Frage, wie die Unsicherheitsschranke dieser nicht-messbaren
Physikalische Chemie Praktikum. Gase: Wärmeleitfähigkeit
 Hochschule Emden / Leer Physikalische Chemie Praktikum Gase: Wärmeleitfähigkeit Vers.Nr. 20 Mai 2017 Allgemeine Grundlagen Kinetische Gastheorie, Abhängigkeit der Wärmeleitfähigkeit von Druck (Gasdichte),
Hochschule Emden / Leer Physikalische Chemie Praktikum Gase: Wärmeleitfähigkeit Vers.Nr. 20 Mai 2017 Allgemeine Grundlagen Kinetische Gastheorie, Abhängigkeit der Wärmeleitfähigkeit von Druck (Gasdichte),
4.1.2 Quantitative Definition durch Wärmekapazitäten
 4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
E 3. Ergänzungen zu Kapitel 3
 E 3. Ergänzungen zu Kapitel 3 1 E 3.1 Kritisches Verhalten des van der Waals Gases 2 E 3.2 Kritisches Verhalten des Ising Spin-1/2 Modells 3 E 3.3 Theorie von Lee und Yang 4 E 3.4 Skalenhypothese nach
E 3. Ergänzungen zu Kapitel 3 1 E 3.1 Kritisches Verhalten des van der Waals Gases 2 E 3.2 Kritisches Verhalten des Ising Spin-1/2 Modells 3 E 3.3 Theorie von Lee und Yang 4 E 3.4 Skalenhypothese nach
Erste Schularbeit Mathematik Klasse 7A G am
 Erste Schularbeit Mathematik Klasse 7A G am 12.11.2015 SCHÜLERNAME: Punkte im ersten Teil: Punkte im zweiten Teil: Davon Kompensationspunkte: Note: Notenschlüssel: Falls die Summe der erzielten Kompensationspunkte
Erste Schularbeit Mathematik Klasse 7A G am 12.11.2015 SCHÜLERNAME: Punkte im ersten Teil: Punkte im zweiten Teil: Davon Kompensationspunkte: Note: Notenschlüssel: Falls die Summe der erzielten Kompensationspunkte
Das Volumen und die Oberfläche einer n-dimensionalen Kugel
 Das Volumen und die Oberfläche einer n-dimensionalen Kugel Alois Temmel 6. Februar 14 c 14, A. Temmel Inhaltsverzeichnis 1 Die Volumenformel 3 1.1 Die n-dimensionale Kugel.................... 3 1.1.1 Die
Das Volumen und die Oberfläche einer n-dimensionalen Kugel Alois Temmel 6. Februar 14 c 14, A. Temmel Inhaltsverzeichnis 1 Die Volumenformel 3 1.1 Die n-dimensionale Kugel.................... 3 1.1.1 Die
Herbst Gesundheitswissenschaften und Technologie Bachelor Mathematik DZ und Mathematik Lehrdiplom. Prof. Dr. Erich Walter Farkas
 Herbst 213 Gesundheitswissenschaften und Technologie Bachelor Mathematik DZ und Mathematik Lehrdiplom 5.3 Lösung von Prof. Dr. Erich Walter Farkas ETH Zürich Kapitel 5. Partielle Differentialgleichungen
Herbst 213 Gesundheitswissenschaften und Technologie Bachelor Mathematik DZ und Mathematik Lehrdiplom 5.3 Lösung von Prof. Dr. Erich Walter Farkas ETH Zürich Kapitel 5. Partielle Differentialgleichungen
4. Stoßvorgänge. Stoßvorgänge sind Vorgänge von sehr kurzer Dauer, bei denen zwischen den beteiligten Körpern große Kräfte auftreten.
 4. Stoßvorgänge Stoßvorgänge sind Vorgänge von sehr kurzer Dauer, bei denen zwischen den beteiligten Körpern große Kräfte auftreten. Gesucht wird ein Zusammenhang zwischen den Geschwindigkeiten vor dem
4. Stoßvorgänge Stoßvorgänge sind Vorgänge von sehr kurzer Dauer, bei denen zwischen den beteiligten Körpern große Kräfte auftreten. Gesucht wird ein Zusammenhang zwischen den Geschwindigkeiten vor dem
Kosmologie für die Schule
 Kosmologie für die Schule Matthias Bartelmann 1 & Tobias Kühnel 1 Max-Planck-Institut für Astrophysik Kosmologie für die Schule p.1/0 Ein symmetrisches Universum Die moderne Kosmologie beruht auf Einsteins
Kosmologie für die Schule Matthias Bartelmann 1 & Tobias Kühnel 1 Max-Planck-Institut für Astrophysik Kosmologie für die Schule p.1/0 Ein symmetrisches Universum Die moderne Kosmologie beruht auf Einsteins
MATHEMATIK III für Bauingenieure (Fernstudium und Wiederholer)
 TU DRESDEN Dresden, 16. Februar 4 Fachrichtung Mathematik / Institut für Analysis Doz.Dr.rer.nat.habil. N. Koksch Prüfungs-Klausur MATHEMATIK III für Bauingenieure (Fernstudium und Wiederholer) Name: Matrikel-Nr.:
TU DRESDEN Dresden, 16. Februar 4 Fachrichtung Mathematik / Institut für Analysis Doz.Dr.rer.nat.habil. N. Koksch Prüfungs-Klausur MATHEMATIK III für Bauingenieure (Fernstudium und Wiederholer) Name: Matrikel-Nr.:
Chaos im getriebenen nicht-linearen Pendel
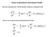 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
1. Aufgabe Auf dem Bildschirm eines Oszillographen durchlaufe ein Elektronenstrahl eine Bahn mit dem zeitabhängigen Ortsvektor
 Thema: Vektoranalysis Studiengang: PT/LOT Analysis III Serie 3 Semester: WS 1/11 1. Aufgabe Auf dem Bildschirm eines Oszillographen durchlaufe ein Elektronenstrahl eine Bahn mit dem zeitabhängigen Ortsvektor
Thema: Vektoranalysis Studiengang: PT/LOT Analysis III Serie 3 Semester: WS 1/11 1. Aufgabe Auf dem Bildschirm eines Oszillographen durchlaufe ein Elektronenstrahl eine Bahn mit dem zeitabhängigen Ortsvektor
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators
 Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Lösung zu Aufgabe 3.1
 Lösung zu Aufgabe 3.1 (a) Die an der Anordnung anliegende Spannung ist groß im Vergleich zur Schleusenspannung der Diode. Für eine Abschätzung des Diodenstroms wird zunächst die Näherung V = 0.7 V verwendet,
Lösung zu Aufgabe 3.1 (a) Die an der Anordnung anliegende Spannung ist groß im Vergleich zur Schleusenspannung der Diode. Für eine Abschätzung des Diodenstroms wird zunächst die Näherung V = 0.7 V verwendet,
11.4. Lineare Differentialgleichungen höherer Ordnung
 4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
Lagrange-Formalismus
 KAPITEL II Lagrange-Formalismus Die im letzten Kapitel dargelegte Formulierung der Mechanik nach Newton ist zwar sehr intuitiv: man zählt alle auf das zu studierende System wirkenden Kräfte auf, schreibt
KAPITEL II Lagrange-Formalismus Die im letzten Kapitel dargelegte Formulierung der Mechanik nach Newton ist zwar sehr intuitiv: man zählt alle auf das zu studierende System wirkenden Kräfte auf, schreibt
Übungen Theoretische Physik I (Mechanik) Blatt 5 ( )
 TU München Prof. P. Vogl Beispiel 1: Übungen Theoretische Physik I (Mechanik) Blatt 5 (26.08.11) Nach Gompertz (1825) wird die Ausbreitung von Rostfraß auf einem Werkstück aus Stahl durch eine lineare
TU München Prof. P. Vogl Beispiel 1: Übungen Theoretische Physik I (Mechanik) Blatt 5 (26.08.11) Nach Gompertz (1825) wird die Ausbreitung von Rostfraß auf einem Werkstück aus Stahl durch eine lineare
4. Gleichungen im Frequenzbereich
 Stationäre Geräusche: In der technischen Akustik werden überwiegend stationäre Geräusche untersucht. Stationäre Geräusche sind zusammengesetzt aus harmonischen Schallfeldern p x,t = p x cos t x Im Folgenden
Stationäre Geräusche: In der technischen Akustik werden überwiegend stationäre Geräusche untersucht. Stationäre Geräusche sind zusammengesetzt aus harmonischen Schallfeldern p x,t = p x cos t x Im Folgenden
Technische Universität München Zentrum Mathematik. Übungsblatt 13
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof Dr Anusch Taraz Dr Michael Ritter Übungsblatt 3 Hausaufgaben Aufgabe 3 Bestimmen Sie alle stationären Punkte der folgenden
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof Dr Anusch Taraz Dr Michael Ritter Übungsblatt 3 Hausaufgaben Aufgabe 3 Bestimmen Sie alle stationären Punkte der folgenden
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. 4. Dämpfungsmodelle. Elastodynamik 1 3.
 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
NTB Druckdatum: SC. typische Zeitkonstante für die Wärmeleitungsgleichung Beispiel
 SCIENTIFIC COMPUTING Die eindimensionale Wärmeleitungsgleichung (WLG) Begriffe Temperatur Spezifische Wärmekapazität Wärmefluss Wärmeleitkoeffizient Fourier'sche Gesetz Spezifische Wärmeleistung Mass für
SCIENTIFIC COMPUTING Die eindimensionale Wärmeleitungsgleichung (WLG) Begriffe Temperatur Spezifische Wärmekapazität Wärmefluss Wärmeleitkoeffizient Fourier'sche Gesetz Spezifische Wärmeleistung Mass für
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 29. 05. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 29. 05.
Elektrizitätslehre und Magnetismus Othmar Marti 29. 05. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 29. 05.
