Daraus ergibt sich: Eine Steigerung der Lokal-Magnitude um 1 entspricht einer Verzehnfachung des Ausschlags (denn 10 + M
|
|
|
- Edmund Weiß
- vor 7 Jahren
- Abrufe
Transkript
1 Erdbeben Außermathematische Anwendungen im Mathematikunterricht WS 2012/13 Franz Embacher, Universität Wien Entstehung von Erdbeben Siehe Das Magnituden-System Das bekannteste System zur Angabe der Stärke eines Erdbebens ist die Richter-Skala, entwickelt in den 1930er Jahren von Charles Francis Richter ( ) am California Institute of Technology Sie benutzt die so genannte Lokal-Magnitude, die folgendermaßen definiert ist: In einer Entfernung von 100 km vom Epizentrum wird der durch das Beben verursachte Maximalausschlag A eines Seismometers nach Wood und Anderson 1 gemessen und in Mikrometer (1 µm = 10-6 m) angegeben Dann ist 2 M = lg A, wobei lg der Logarithmus zur Basis 10 ist Ist die Lokal-Magnitude bekannt, so bestimmt sich der Ausschlag in 100 km Entfernung (in µm) zu A = 10 M Daraus ergibt sich: Eine Steigerung der Lokal-Magnitude um 1 entspricht einer M 1 Verzehnfachung des Ausschlags (denn 10 + M = ) Nicht nur der Ausschlag, sondern praktisch alle physikalisch interessanten Größen hängen exponentiell von M ab So ist die bei einem Beben freigesetzte Energie näherungsweise proportional zu 3 M /2 3/2 M M 10 (10 ) 32 = 3/2 A und daher zu 3 Eine Steigerung der Magnitude um 1 entspricht ungefähr einer Verzweiunddreißigfachung der Energie! Die Magnitude wird daher als logarithmisches Maß bezeichnet 1 Dieses Gerät wird heute nicht mehr verwendet Die Lokal-Magnitude wird auf der Basis von Messwerten modernerer Geräte ermittelt bzw hochgerechnet 2 In der Literatur wird diese Größe mit M L bezeichnet 3 Etwas genauer: Die freigesetzte Energie ist E k 10 M 3 /2, wobei k 6 10 Joule
2 Die Lokal-Magnitude wird üblicherweise mit einer Nachkommastelle angegeben und dient bis zu Werten von M 6 als Maß für die Stärke eines Erdbebens Das Magnituden-System nach Richter illustriert sehr schön die Nützlichkeit des Logarithmus: Würde man etwa den Ausschlag A (in µm) als Maß für die Stärke eines Erdbebens verwenden, so ergäben sich Werte, die viele Größenordnungen überstreichen Zudem können einfache Aufgaben die Grundlagen des Rechnens mit Logarithmen und Potenzen anhand einer für viele Menschen relevanten Anwendung veranschaulichen Frage: Welche Magnitude hat ein Beben, das einen (in 100 km Entfernung gemessenen) Ausschlag von 01 mm (= 100 µm) verursacht? M = lg100 = 2 (Idee des Logarithmus als Zahl der Nullen ) Frage: Welche Magnitude hat ein Beben, das einen (in 100 km Entfernung gemessenen) Ausschlag von 05 mm (= 500 µm) verursacht? M = lg Frage: Welchen Ausschlag verursacht ein Beben der Stärke 3 in 100 km Entfernung? 10 3 µm =1000 µm = 1 mm Frage: Welchen Ausschlag verursacht ein Beben der Stärke 35 in 100 km Entfernung? µm =3161 µm 32 mm Frage: Gibt es Beben mit negativer Magnitude? Theoretisch ja, das sind die Beben, die einen kleineren Ausschlag als 1 µm verursachen Man kann aber sprachlich die Konvention treffen, eine derart kleine Erschütterung nicht als Erdbeben zu bezeichnen Da sich selten in genau 100 km Entfernung ein Seismometer befindet, muss die Lokal- Magnitude in der Regel aus dem (ebenfalls in µm angegebenem) Ausschlag Ad ( ) in einer Entfernung d bestimmt werden, die man sich nicht aussuchen kann Da erfahrungsgemäß für Beben verschiedener Stärke die Abhängigkeiten der Ausschläge von der Entfernung zueinander proportional sind (dh ABeben 2 = CABeben 1, wobei C von den Stärken der beiden Beben, aber nicht von d abhängt), wird die Lokal-Magnitude üblicherweise in der Form M Ad ( ) = lg A0 definiert, wobei Ad ( ) der Ausschlag eines Wood-Anderson-Seismometers 5 in der Entfernung d vom Epizentrum und A ( ) 0 d der von einem Beben der Magnitude 0 in Die höchste gemessene Lokal-Magnitude war M = 86, und viel größer kann M aus physikalischen Gründen nicht werden Aufgrund dieser Sättigung werden oberhalb von M 6 andere Systeme verwendet (siehe weiter unten)
3 Entfernung d verursachte Ausschlag ist Die Funktion A ( ) 0 d wird vorab für eine Region (zb Südkalifornien) bestimmt und steht dann, wenn ein neuerliches Beben auftritt, zur Verfügung Damit ergeben sich weitere Aufgabenstellungen, die ein bisschen Rechnen mit Logarithmen und Potenzen erfordern Frage: Wie groß ist A 0 (100 km)? 1 (dh der Ausschlag beträgt 1 µm) Frage: Für eine bestimmte Region sei d ( ) A 100 km 0 d = (Das ist ein für Entfernungen bis zu einigen Hundert Kilometern einigermaßen realistisches Modell) Nun ereignet sich ein Beben, das in 300 km Entfernung zu einem Ausschlag von 1 cm (= 10 µm) führt Bestimme die Magnitude! A(300 km) 10 M = lg = lg 6 03 ( 1 3) = A0 (300 km) 10 Frage: Für eine bestimmte Region sei d ( ) A 100 km 0 d = Nun ereignet sich ein Beben der Magnitude 52 Wie groß ist der Seismometer-Ausschlag in 200 km Entfernung vom Epizentrum? Aus Daher ist Ad ( ) M M = lg folgt Ad ( ) = 10 A0 A0 ( ) A(200 km) = 10 A (200 km) = = Der Ausschlag beträgt 8 10 µ m = 8 cm Frage: Zwei Erdbeben ereignen sich mit dem gleichen Epizentrum In 250 km Entfernung ist der vom ersten Beben verursachte Ausschlag doppelt so groß wie der vom zweiten verursachte Ausschlag (i) In welchem Verhältnis stehen die Ausschläge der beiden Beben in einer Entfernung von 500 km? (ii) Was lässt sich über die Magnituden der beiden Beben sagen? M1 M 2 (i) im gleichen! (ii) Mit A1 = 10 A0 und A2 = 10 A0 folgt, und zwar ganz unabhängig von d, M1 A1 10 A0 M1 M2 2 = = = 10, M 2 A2 10 A0 daher M1 M2 = lg 2 03 Die Magnitude des ersten Bebens ist um 03 größer als jene des ersten (Diese Aufgabe zeigt: Ist ein Beben in einer bestimmten Entfernung gemessen am verursachten Ausschlag um einen bestimmten Faktor stärker als ein anderes mit dem gleichen Epizentrum, so gilt dies für jede Entfernung) 5 Vgl Fußnote 1
4 Neben der Richter-Skala gibt es noch andere Maße für die Stärke eines Erdbebens, die jeweils in verschiedenen Stärkebereichen verwendet und als die Magnitude eines Erdbebens zusammengefasst werden (siehe etwa Die größte jemals gemessene Magnitude betrug 96 (Chile 1960) Wir wollen hier zwischen diesen Systemen nicht unterscheiden und ab nun einfach von der Magnitude sprechen Häufigkeit von Erdbeben Im Jahr 195 fanden Beno Gutenberg ( ) und Charles Francis Richter durch statistische Auswertung von Erdbeben in Kalifornien einen Zusammenhang zwischen der Häufigkeit und der Stärke von Erdbeben, das sich später als sehr allgemeine Beziehung herausstellte: das Gutenberg-Richter-Gesetz: Ist NM ( ) die Zahl der in einer bestimmten Region pro Jahr stattfindenden Erdbeben mit einer Magnitude von mindestens M, so gilt näherungsweise lg N( M) = a bm, wobei a und b Konstanten sind Die Konstante b liegt nahe bei 1, die Konstante a hängt von der Region ab und kennzeichnet deren Seismizität Das Gesetz gilt auch weltweit, mit a 82 und b Plot der Funktion M NM ( ) für weltweite Erdbeben Er zeigt, einerseits, dass große Beben sehr selten auftreten ist, illustriert aber auch, dass der Verzicht auf den Logarithmus seine Nachteile besitzt: Für M > 25 kann man praktisch nichts mehr ablesen
5 8 6 2 Einige Rechenbeispiele: Plot der Funktion M lg NM ( ) für weltweite Erdbeben Frage: Wie viele Erdbeben (positiver Magnitude) finden weltweit pro Jahr statt? a 82 8 N (0) = Dabei überwiegen allerdings die ganz schwachen Beben, die nicht immer registriert werden Frage: Wie viele Erdbeben mit Magnitude mindestens 6 finden weltweit pro Jahr statt? N a 6 b (8) = Beben der Magnitude 6 finden etwa alle 3 Tage statt Frage: Wie viele Erdbeben mit Magnitude mindestens 8 finden weltweit pro Jahr statt? N = a 8 b (8) Es ist also weltweit ca einmal pro Jahr mit einem sehr starken Beben zu rechnen Die Zahl der Beben mit Magnitude zwischen M und M + dm ist durch a bm a b( M+ dm) d a bm dn = N( M ) N( M + dm ) = dm 10 = dm d = = ln10 ln10 10 dm ( a bm)ln10 ( a bm)ln10 a bm dm e b e dm b dm gegeben 6 Damit ergibt sich die Häufigkeitsverteilung zu dn b e b dm ( a bm)ln10 a bm = ln10 ln Dabei wurde die für alle a 0 und für alle reellen x geltende Beziehung a = e verwendet x xln a
6 Für M (sehr schwache Beben) wird dies beliebig groß Werden Beben negativer Magnitude außer Acht gelassen, so ist die entsprechende, nun auf [0, ) definierte die Wahrscheinlichkeitsdichte durch ρ b ln10 M bm ( M) = b ln10 e b ln10 10 gegeben Die Magnituden von Erdbeben sind exponentialverteilt Plot der Wahrscheinlichkeitsdichte M ρ( M) für weltweite Erdbeben Einige Rechenbeispiele: Frage: Wie groß ist die Wahrscheinlichkeit, dass das nächste irgendwo auf der Erde stattfindende Erdbeben eine Magnitude zwischen 1 und 2 hat? b ln10 M 232 M dm ρ( M ) = b ln10 dm e 232 dm e Frage: Wie groß ist die Wahrscheinlichkeit, dass das nächste irgendwo auf der Erde stattfindende Erdbeben eine Magnitude zwischen 3 und hat? b ln10 M 232 M dm ρ( M ) = b ln10 dm e 232 dm e Schwache Beben sind bei Weitem die häufigsten Mit jeder Steigerung der Magnitude um 1 nimmt die Wahrscheinlichkeit (und daher die Häufigkeit) um den Faktor 10 ab (Eigenschaft der Exponentialverteilung)
Daraus ergibt sich: Eine Steigerung der Lokal-Magnitude um 1 entspricht einer Verzehnfachung des Ausschlags (denn 10 + M
 Erdbeben Außermathematische Anwendungen im Mathematikunterricht WS 201/15 Franz Embacher, Universität Wien Entstehung von Erdbeben Wird in der Vorlesung besprochen Das Magnituden-System Das bekannteste
Erdbeben Außermathematische Anwendungen im Mathematikunterricht WS 201/15 Franz Embacher, Universität Wien Entstehung von Erdbeben Wird in der Vorlesung besprochen Das Magnituden-System Das bekannteste
Erdbeben, Erdbebenstärke und Opferzahlen. Quelle: Wikipedia Commons
 Erdbeben, Erdbebenstärke und Opferzahlen Quelle: Wikipedia Commons Lernziele 1. Wichtige Fachbegriffe im Zusammenhang mit Erdbeben korrekt verwenden und erklären können. 2. Zwei Erdbebenskalen unterscheiden
Erdbeben, Erdbebenstärke und Opferzahlen Quelle: Wikipedia Commons Lernziele 1. Wichtige Fachbegriffe im Zusammenhang mit Erdbeben korrekt verwenden und erklären können. 2. Zwei Erdbebenskalen unterscheiden
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 8. Dezember 2010 Teil V Schließende Statistik 1 Parameterschätzung Erwartungstreue und Konsistenz Maximum-Likelihood
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 8. Dezember 2010 Teil V Schließende Statistik 1 Parameterschätzung Erwartungstreue und Konsistenz Maximum-Likelihood
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Propädeutikum 3: Funktionen und Ableitungen, Vektoren Dr. Daniel Bick 27. Oktober 2017 Daniel Bick Physik für Biologen und Zahnmediziner 27. Oktober 2017 1 / 35 Inhalt
Physik für Biologen und Zahnmediziner Propädeutikum 3: Funktionen und Ableitungen, Vektoren Dr. Daniel Bick 27. Oktober 2017 Daniel Bick Physik für Biologen und Zahnmediziner 27. Oktober 2017 1 / 35 Inhalt
Potenzen, Wurzeln, Logarithmen
 KAPITEL 3 Potenzen, Wurzeln, Logarithmen 3.1 Funktionen und Umkehrfunktionen.............. 70 3.2 Wurzeln............................ 72 3.3 Warum ist a 2 + b 2 a + b?................. 73 3.4 Potenzfunktion........................
KAPITEL 3 Potenzen, Wurzeln, Logarithmen 3.1 Funktionen und Umkehrfunktionen.............. 70 3.2 Wurzeln............................ 72 3.3 Warum ist a 2 + b 2 a + b?................. 73 3.4 Potenzfunktion........................
Erdbebengefährdung Schweiz. Wann, wo und wie oft ereignen sich bestimmte Erschütterungen in der Schweiz?
 Erdbebengefährdung Schweiz Wann, wo und wie oft ereignen sich bestimmte Erschütterungen in der Schweiz? Gefährdung Die Gefährdungskarte bildet ab, wo wie häufig gewisse horizontale Beschleunigungen zu
Erdbebengefährdung Schweiz Wann, wo und wie oft ereignen sich bestimmte Erschütterungen in der Schweiz? Gefährdung Die Gefährdungskarte bildet ab, wo wie häufig gewisse horizontale Beschleunigungen zu
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION
 Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Exponentialfunktionen, Eulersche Zahl, Logarithmen
 Exponentialfunktionen, Eulersche Zahl, Logarithmen Jörn Loviscach Versionsstand: 16. November 2009, 19:01 1 Exponentialfunktionen Eine Funktion der Art x 7 3 x heißt Exponentialfunktion [exponential function].
Exponentialfunktionen, Eulersche Zahl, Logarithmen Jörn Loviscach Versionsstand: 16. November 2009, 19:01 1 Exponentialfunktionen Eine Funktion der Art x 7 3 x heißt Exponentialfunktion [exponential function].
lässt sich relativ einfach nach b auflösen, indem man a mit dem Kehrwert von c Potenziert: b=a 1/ c
 Logarithmen Die Gleichung a=b c lässt sich relativ einfach nach b auflösen, indem man a mit dem Kehrwert von c Potenziert: b=a 1/ c. Für das Auflösen nach c hingegen braucht es eine neue Funktion, den
Logarithmen Die Gleichung a=b c lässt sich relativ einfach nach b auflösen, indem man a mit dem Kehrwert von c Potenziert: b=a 1/ c. Für das Auflösen nach c hingegen braucht es eine neue Funktion, den
Aufbau der Erde und Plattentektonik Vulkane. Erdbeben und Tsunamis Erdrutsche Halbe Probe
 23.11. Aufbau der Erde und Plattentektonik 30.11. Vulkane 7.12. Erdbeben und Tsunamis 14.12. Erdrutsche 21.12. Halbe Probe Erdbeben Wo Gesteinsblöcke sich in unterschiedlichen Richtungen bewegen baut
23.11. Aufbau der Erde und Plattentektonik 30.11. Vulkane 7.12. Erdbeben und Tsunamis 14.12. Erdrutsche 21.12. Halbe Probe Erdbeben Wo Gesteinsblöcke sich in unterschiedlichen Richtungen bewegen baut
= T 2. Lösungsmenge ist die Menge aller Elemente des Definitionsbereiches D G, die die Gleichung zu einer Wahre Aussage machen.
 Gleichungen Eine Gleichung ist eine Aussage, in der die Gleichheit zweier Terme durch Mathematische Symbol ausgedrückt wird. Dies wird durch das Gleichheitssymbol = symbolisiert G : = T 2 Definitionsmenge
Gleichungen Eine Gleichung ist eine Aussage, in der die Gleichheit zweier Terme durch Mathematische Symbol ausgedrückt wird. Dies wird durch das Gleichheitssymbol = symbolisiert G : = T 2 Definitionsmenge
Exponentialfunktionen, Eulersche Zahl, Logarithmen
 Exponentialfunktionen, Eulersche Zahl, Logarithmen Jörn Loviscach Versionsstand: 22. Oktober 2010, 23:29 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.youtube.com/joernloviscach
Exponentialfunktionen, Eulersche Zahl, Logarithmen Jörn Loviscach Versionsstand: 22. Oktober 2010, 23:29 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.youtube.com/joernloviscach
Physikalisches Anfängerpraktikum Teil 2 Versuch PII 22: Lichtstreuung Auswertung
 Physikalisches Anfängerpraktikum Teil 2 Versuch PII 22: Lichtstreuung Auswertung Gruppe Mi-14: Marc A. Donges , 1060028 Tanja Pfister, 14846 05 07 12 1 1 Versuchsaufbau Der Versuch wurde
Physikalisches Anfängerpraktikum Teil 2 Versuch PII 22: Lichtstreuung Auswertung Gruppe Mi-14: Marc A. Donges , 1060028 Tanja Pfister, 14846 05 07 12 1 1 Versuchsaufbau Der Versuch wurde
1 Das Problem, welches zum Logarithmus führt
 1 Das Problem, welches zum Logarithmus führt Gegeben sei die folgende Gleichung: a = x n Um nun die Basis hier x) auszurechnen, muss man die n-te Wurzel aus a ziehen: a = x n n ) n a = x Soweit sollte
1 Das Problem, welches zum Logarithmus führt Gegeben sei die folgende Gleichung: a = x n Um nun die Basis hier x) auszurechnen, muss man die n-te Wurzel aus a ziehen: a = x n n ) n a = x Soweit sollte
1 Lambert-Beersches Gesetz
 Physikalische Chemie II Lösung 6 23. Oktober 205 Lambert-Beersches Gesetz Anhand des idealen Gasgesetzes lässt sich die Teilchenkonzentration C wie folgt ausrechnen: C = N V = n N A V pv =nrt = N A p R
Physikalische Chemie II Lösung 6 23. Oktober 205 Lambert-Beersches Gesetz Anhand des idealen Gasgesetzes lässt sich die Teilchenkonzentration C wie folgt ausrechnen: C = N V = n N A V pv =nrt = N A p R
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Erdbeben untersuchen - 9 auf der Richterskala
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Erdbeben untersuchen - 9 auf der Richterskala Das komplette Material finden Sie hier: School-Scout.de 15. Erdbeben untersuchen 1 von
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Erdbeben untersuchen - 9 auf der Richterskala Das komplette Material finden Sie hier: School-Scout.de 15. Erdbeben untersuchen 1 von
Computertomographie. Die Idee
 Computertomographie Außermathematische Anwendungen im Mathematikunterricht WS 202/3 Franz Embacher, Universität Wien Die Idee Die Idee der Computertomographie besteht darin, aus der Abschwächung (Absorption)
Computertomographie Außermathematische Anwendungen im Mathematikunterricht WS 202/3 Franz Embacher, Universität Wien Die Idee Die Idee der Computertomographie besteht darin, aus der Abschwächung (Absorption)
Exponentialgleichungen und Logarithmen
 . Exponentialgleichungen und Logarithmen. Logarithmen Ergänzung 3. Logarithmenregeln Seiten 4. Aufgaben Exponentialgleichungen 5. Didaktisches 6. Was sind Logarithmen? 7. Exponentialgleichungen Kurzfassung
. Exponentialgleichungen und Logarithmen. Logarithmen Ergänzung 3. Logarithmenregeln Seiten 4. Aufgaben Exponentialgleichungen 5. Didaktisches 6. Was sind Logarithmen? 7. Exponentialgleichungen Kurzfassung
Einstiegstext: Erdbeben können zerstören...
 Einstiegstext: Erdbeben können zerstören... Lies die Texte 1 und 2 für dich durch und diskutiere zusammen mit deiner Nachbarin oder deinem Nachbarn das Gelesene. Zu welchem Schluss kommt ihr? Text 1: Am
Einstiegstext: Erdbeben können zerstören... Lies die Texte 1 und 2 für dich durch und diskutiere zusammen mit deiner Nachbarin oder deinem Nachbarn das Gelesene. Zu welchem Schluss kommt ihr? Text 1: Am
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Vertretungsstunden in Klassen Das komplette Material finden Sie hier:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Vertretungsstunden in Klassen 5-10 Das komplette Material finden Sie hier: Download bei School-Scout.de II Naturfaktoren Beitrag 11
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Vertretungsstunden in Klassen 5-10 Das komplette Material finden Sie hier: Download bei School-Scout.de II Naturfaktoren Beitrag 11
2.4 Exponential - und Logarithmus - Funktionen
 25.05.20 2.4 Eponential - und Logarithmus - Funktionen Mit Hilfe der Potenz a t definiert man eine weitere Funktionsart, indem man statt der Basis den Eponenten durch die Variable ersetzt: Für a ε R >
25.05.20 2.4 Eponential - und Logarithmus - Funktionen Mit Hilfe der Potenz a t definiert man eine weitere Funktionsart, indem man statt der Basis den Eponenten durch die Variable ersetzt: Für a ε R >
Versuch: D07 - Fotoeffekt Auswertung
 Physikalisches Anfängerpraktikum Universität Hannover - Wintersemester 2008/2009 Kais Abdelkhalek - Vitali Müller Versuch: D07 - Fotoeffekt Auswertung 1 Vorbereitung 1.1 Fragen Wie ist die Einheit 1 ev
Physikalisches Anfängerpraktikum Universität Hannover - Wintersemester 2008/2009 Kais Abdelkhalek - Vitali Müller Versuch: D07 - Fotoeffekt Auswertung 1 Vorbereitung 1.1 Fragen Wie ist die Einheit 1 ev
Definition: Unter der n-ten Potenz einer beliebigen reellen Zahl a versteht man das n-fache Produkt von a mit sich selbst
 Potenzen mit ganzzahligen Exponenten Definition: Unter der n-ten Potenz einer beliebigen reellen Zahl a versteht man das n-fache Produkt von a mit sich selbst Man schreibt a n = b Dabei heißt a die Basis,
Potenzen mit ganzzahligen Exponenten Definition: Unter der n-ten Potenz einer beliebigen reellen Zahl a versteht man das n-fache Produkt von a mit sich selbst Man schreibt a n = b Dabei heißt a die Basis,
Praktikum Physikalische Chemie I 30. Januar Aktivierungsenergie. Guido Petri Anastasiya Knoch PC111/112, Gruppe 11
 Praktikum Physikalische Chemie I 30. Januar 2016 Aktivierungsenergie Guido Petri Anastasiya Knoch PC111/112, Gruppe 11 1 Aufgabenstellung Für die Reaktion von Saccharose mit Wasser zu Glucose und Fructose
Praktikum Physikalische Chemie I 30. Januar 2016 Aktivierungsenergie Guido Petri Anastasiya Knoch PC111/112, Gruppe 11 1 Aufgabenstellung Für die Reaktion von Saccharose mit Wasser zu Glucose und Fructose
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
= 4 = x + 3. y(x) = x
 Ü Aufgabenblatt Inhalt Brüche. Gleichungen. Summen. Potenzen. Logarithmen. Ebener Winkel (Definition und Einheiten). Trigonometrische Funktionen. Basisgrößen und Basiseinheiten des SI. Bequemes Rechnen
Ü Aufgabenblatt Inhalt Brüche. Gleichungen. Summen. Potenzen. Logarithmen. Ebener Winkel (Definition und Einheiten). Trigonometrische Funktionen. Basisgrößen und Basiseinheiten des SI. Bequemes Rechnen
Seebeben. Ablauf eines Seebebens:
 Seebeben Ablauf eines Seebebens Wie entstehen See- und Erdbeben? Wann und wo gab es Seebeben? Welche Gebiete der Erde sind seebebengefährdet? Messmethoden Ablauf eines Seebebens: Ein Seebeben ist ein unterseeisches
Seebeben Ablauf eines Seebebens Wie entstehen See- und Erdbeben? Wann und wo gab es Seebeben? Welche Gebiete der Erde sind seebebengefährdet? Messmethoden Ablauf eines Seebebens: Ein Seebeben ist ein unterseeisches
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Statistik für Ingenieure Vorlesung 5
 Statistik für Ingenieure Vorlesung 5 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 28. November 2017 3.4 Wichtige stetige Verteilungen 3.4.1 Exponentialverteilung Parameter:
Statistik für Ingenieure Vorlesung 5 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 28. November 2017 3.4 Wichtige stetige Verteilungen 3.4.1 Exponentialverteilung Parameter:
Die Höhenenergie. Nach diesen Überlegungen wird die Höhenenergie wie folgt festgelegt: Die Bewegungsenergie
 Die Höhenenergie Fallbeispiel: Fall 1: Ein Kran hebt einen Eisenträger ( G = 50.000 N ) in den 1. Stock eines Hauses. Dabei verbraucht er eine bestimmte Menge Treibstoff. Fall 2: Hebt der Kran die Last
Die Höhenenergie Fallbeispiel: Fall 1: Ein Kran hebt einen Eisenträger ( G = 50.000 N ) in den 1. Stock eines Hauses. Dabei verbraucht er eine bestimmte Menge Treibstoff. Fall 2: Hebt der Kran die Last
Übungen zu Physik 1 für Maschinenwesen
 Physikdepartment E13 WS 2011/12 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peter Müller-Buschbaum, Dr. Eva M. Herzig, Dr. Volker Körstgens, David Magerl, Markus Schindler, Moritz v. Sivers Vorlesung
Physikdepartment E13 WS 2011/12 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peter Müller-Buschbaum, Dr. Eva M. Herzig, Dr. Volker Körstgens, David Magerl, Markus Schindler, Moritz v. Sivers Vorlesung
Exponentialgleichungen und Logarithmen
 Exponentialgleichungen und Logarithmen 1. Löse die Gleichungen: a) 2 x = 16 b) 3 4x = 9 Tipp: Exponentialgleichungen (die Variable x steht im Exponenten) lassen sich durch Zurückführen auf die gleiche
Exponentialgleichungen und Logarithmen 1. Löse die Gleichungen: a) 2 x = 16 b) 3 4x = 9 Tipp: Exponentialgleichungen (die Variable x steht im Exponenten) lassen sich durch Zurückführen auf die gleiche
Potenzen mit ganzzahligen Exponenten
 Lüneburg, Fragment Potenzen mit ganzzahligen Exponenten -E -E2 Was sollen wir kennen? die Eigenschaften von Exponenten, die Wissenschaftliche Notation der reellen Zahlen, die Potenzenregeln. -E3 Wozu sind
Lüneburg, Fragment Potenzen mit ganzzahligen Exponenten -E -E2 Was sollen wir kennen? die Eigenschaften von Exponenten, die Wissenschaftliche Notation der reellen Zahlen, die Potenzenregeln. -E3 Wozu sind
2. Mathematische Grundlagen
 2. Mathematische Grundlagen Erforderliche mathematische Hilfsmittel: Summen und Produkte Exponential- und Logarithmusfunktionen 21 2.1 Endliche Summen und Produkte Betrachte n reelle Zahlen a 1, a 2,...,
2. Mathematische Grundlagen Erforderliche mathematische Hilfsmittel: Summen und Produkte Exponential- und Logarithmusfunktionen 21 2.1 Endliche Summen und Produkte Betrachte n reelle Zahlen a 1, a 2,...,
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Propädeutikum 3: Funktionen und Ableitungen Dr. Daniel Bick 21. Oktober 2015 Daniel Bick Physik für Biologen und Zahnmediziner 21. Oktober 2015 1 / 48 Hinweise zur
Physik für Biologen und Zahnmediziner Propädeutikum 3: Funktionen und Ableitungen Dr. Daniel Bick 21. Oktober 2015 Daniel Bick Physik für Biologen und Zahnmediziner 21. Oktober 2015 1 / 48 Hinweise zur
Klausur für die Teilnehmer des Physikalischen Praktikums für Mediziner und Zahnmediziner im Sommersemester 2008
 Name: Gruppennummer: Nummer: Aufgabe 1 2 3 4 5 6 7 8 9 10 insgesamt erreichte Punkte erreichte Punkte Aufgabe 11 12 13 14 15 16 erreichte Punkte Klausur für die Teilnehmer des Physikalischen Praktikums
Name: Gruppennummer: Nummer: Aufgabe 1 2 3 4 5 6 7 8 9 10 insgesamt erreichte Punkte erreichte Punkte Aufgabe 11 12 13 14 15 16 erreichte Punkte Klausur für die Teilnehmer des Physikalischen Praktikums
3. DER NATÜRLICHE LOGARITHMUS
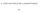 3. DER NATÜRLICHE LOGARITHMUS ln Der natürliche Logarithmus ln(x) betrachtet als Funktion in x, ist die Umkehrfunktion der Exponentialfunktion exp(x). Das bedeutet, für reelle Zahlen a und b gilt b = ln(a)
3. DER NATÜRLICHE LOGARITHMUS ln Der natürliche Logarithmus ln(x) betrachtet als Funktion in x, ist die Umkehrfunktion der Exponentialfunktion exp(x). Das bedeutet, für reelle Zahlen a und b gilt b = ln(a)
, = = 5* * *10 + 2*1 + 3*1/10 + 4*1/ *1/1000 = = /10 + 4/ /1000 =
 1 Das Zehner-Zahlensystem 5 7 0 2, 3 4 1 = = 5*1000 + 7*100 + 0*10 + 2*1 + 3*1/10 + 4*1/100 + 1*1/1000 = = 5000 + 700 + 0 + 2 + 3/10 + 4/100 + 1/1000 = = 5000 + 700 + 0 + 2 + 0,3 + 0,04 + 0,001 Teilt man
1 Das Zehner-Zahlensystem 5 7 0 2, 3 4 1 = = 5*1000 + 7*100 + 0*10 + 2*1 + 3*1/10 + 4*1/100 + 1*1/1000 = = 5000 + 700 + 0 + 2 + 3/10 + 4/100 + 1/1000 = = 5000 + 700 + 0 + 2 + 0,3 + 0,04 + 0,001 Teilt man
6.7 Isolierte Singularitäten
 6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
Grundwissen Physik 8. Klasse II
 Grundwissen Physik 8. Klasse II Größen in der Physik Physikalische Größen sind alle messbare Eigenschaften eines Körpers. Dabei gibt es Grundgrößen, deren Einheit der Mensch willkürlich, also beliebig
Grundwissen Physik 8. Klasse II Größen in der Physik Physikalische Größen sind alle messbare Eigenschaften eines Körpers. Dabei gibt es Grundgrößen, deren Einheit der Mensch willkürlich, also beliebig
Zahlen und elementares Rechnen
 und elementares Rechnen Christian Serpé Universität Münster 7. September 2011 Christian Serpé (Universität Münster) und elementares Rechnen 7. September 2011 1 / 51 Gliederung 1 2 Elementares Rechnen 3
und elementares Rechnen Christian Serpé Universität Münster 7. September 2011 Christian Serpé (Universität Münster) und elementares Rechnen 7. September 2011 1 / 51 Gliederung 1 2 Elementares Rechnen 3
1 Beschreibung der Grundlagen
 Westsächsische Hochschule Zwickau Fachgruppe Mathematik Grundlagen Inhaltsverzeichnis Aufgaben zu den Grundlagen findet man über den folgenden Link: Aufgaben zu den Grundlagen 01 1 Beschreibung der Grundlagen
Westsächsische Hochschule Zwickau Fachgruppe Mathematik Grundlagen Inhaltsverzeichnis Aufgaben zu den Grundlagen findet man über den folgenden Link: Aufgaben zu den Grundlagen 01 1 Beschreibung der Grundlagen
Praktikum Physik Radioaktivität 13GE RADIOAKTIVITÄT VERSUCHSAUSWERTUNG
 RADIOAKIVIÄ VERSUCHSAUSWERUNG I. VERSUCHSZIEL Die Zerfallskurve einer radioaktiven Substanz soll aufgenommen werden. Aus dieser Zerfallskurve soll das Gesetz des radioaktiven Zerfalls hergeleitet werden.
RADIOAKIVIÄ VERSUCHSAUSWERUNG I. VERSUCHSZIEL Die Zerfallskurve einer radioaktiven Substanz soll aufgenommen werden. Aus dieser Zerfallskurve soll das Gesetz des radioaktiven Zerfalls hergeleitet werden.
Widerstände. Schulversuchspraktikum WS 2000/2001 Redl Günther und 7.Klasse. Inhaltsverzeichnis:
 Schulversuchspraktikum WS 2000/2001 Redl Günther 9655337 Widerstände 3. und 7.Klasse Inhaltsverzeichnis: 1) Vorraussetzungen 2) Lernziele 3) Verwendete Quellen 4) Ohmsches Gesetz 5) Spezifischer Widerstand
Schulversuchspraktikum WS 2000/2001 Redl Günther 9655337 Widerstände 3. und 7.Klasse Inhaltsverzeichnis: 1) Vorraussetzungen 2) Lernziele 3) Verwendete Quellen 4) Ohmsches Gesetz 5) Spezifischer Widerstand
Physikalisches Grundpraktikum I
 INSTITUT FÜR PHYSIK DER HUMBOLDT-UNIVERSITÄT ZU BERLIN Physikalisches Grundpraktikum I Versuchsprotokoll P2 : F7 Statistik und Radioaktivität Versuchsort: Raum 217-2 Versuchsbetreuer: E. von Seggern, D.
INSTITUT FÜR PHYSIK DER HUMBOLDT-UNIVERSITÄT ZU BERLIN Physikalisches Grundpraktikum I Versuchsprotokoll P2 : F7 Statistik und Radioaktivität Versuchsort: Raum 217-2 Versuchsbetreuer: E. von Seggern, D.
Logarithmische Skalen
 Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Versuchsprotokoll. Mathematisch-Naturwissenschaftliche Fakultät I Institut für Physik. Versuch O8: Fraunhofersche Beugung Arbeitsplatz Nr.
 Mathematisch-Naturwissenschaftliche Fakultät I Institut für Physik Physikalisches Grundpraktikum I Versuchsprotokoll Versuch O8: Fraunhofersche Beugung Arbeitsplatz Nr. 1 0. Inhaltsverzeichnis 1. Einleitung.
Mathematisch-Naturwissenschaftliche Fakultät I Institut für Physik Physikalisches Grundpraktikum I Versuchsprotokoll Versuch O8: Fraunhofersche Beugung Arbeitsplatz Nr. 1 0. Inhaltsverzeichnis 1. Einleitung.
Logarithmen. Gesetzmäßigkeiten
 Logarithmen Gesetzmäßigkeiten Einführung Als erstes muss geklärt werden, für was ein Logarithmus gebraucht wird. Dazu sollte folgendes einführendes Beispiel gemacht werden. Beispiel 1: 2 x = 8 Wie an diesem
Logarithmen Gesetzmäßigkeiten Einführung Als erstes muss geklärt werden, für was ein Logarithmus gebraucht wird. Dazu sollte folgendes einführendes Beispiel gemacht werden. Beispiel 1: 2 x = 8 Wie an diesem
1 Lineare Gleichungssysteme und Matrizen
 1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
Exponentialfunktionen - Eigenschaften und Graphen
 Exponentialfunktionen - Eigenschaften und Graphen 1 Taschengeld Peter startet in wenigen Tagen zu einer zweiwöchigen Klassenfahrt Seine Eltern möchten ihm nach folgendem Plan Taschengeld mitgeben: Für
Exponentialfunktionen - Eigenschaften und Graphen 1 Taschengeld Peter startet in wenigen Tagen zu einer zweiwöchigen Klassenfahrt Seine Eltern möchten ihm nach folgendem Plan Taschengeld mitgeben: Für
Übungen zu Experimentalphysik 1 für MSE
 Physik-Department LS für Funktionelle Materialien WS 201/15 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Daniel Moseguí González, Pascal Neibecker, Nitin
Physik-Department LS für Funktionelle Materialien WS 201/15 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Daniel Moseguí González, Pascal Neibecker, Nitin
Wachstum und Zerfall / Exponentialfunktionen. a x = e (lna) x = e k x
 Wachstum und Zerfall / Exponentialfunktionen Mit Exponentialfunktionen können alle Wachstums- und Zerfalls- oder Abnahmeprozesse beschrieben werden. Im Allgemeinen geht es dabei um die Exponentialfunktionen
Wachstum und Zerfall / Exponentialfunktionen Mit Exponentialfunktionen können alle Wachstums- und Zerfalls- oder Abnahmeprozesse beschrieben werden. Im Allgemeinen geht es dabei um die Exponentialfunktionen
Was ist geschehen? Mit ShakeMaps und Schütter karten schnell über die Auswirkungen eines Erdbebens informiert
 Was ist geschehen? Mit ShakeMaps und Schütter karten schnell über die Auswirkungen eines Erdbebens informiert ShakeMap des Erdbebens bei Zug am 11. Februar 2012 um 23:45 Uhr mit einer Magnitude von 4.2.
Was ist geschehen? Mit ShakeMaps und Schütter karten schnell über die Auswirkungen eines Erdbebens informiert ShakeMap des Erdbebens bei Zug am 11. Februar 2012 um 23:45 Uhr mit einer Magnitude von 4.2.
49 Mathematik für Biologen, Biotechnologen und Biochemiker
 49 Mathematik für Biologen, Biotechnologen und Biochemiker 43 Momentane Wachstumsrate, Zuwachsrate pro Zeiteinheit und die Verdoppelungszeit Jede Exponentialfunktion f(t) = c exp(t) ist durch die beiden
49 Mathematik für Biologen, Biotechnologen und Biochemiker 43 Momentane Wachstumsrate, Zuwachsrate pro Zeiteinheit und die Verdoppelungszeit Jede Exponentialfunktion f(t) = c exp(t) ist durch die beiden
5.1 Exponentialgleichung und Logarithmus
 5 Logarithmen Henry riggs Das Auffinden des unbekannten Exponenten einer Potenz nennt man Logarithmieren. Der Erfinder und Namensgeber der Logarithmen ist der im Kapitel Potenzen mit rationalen Exponenten
5 Logarithmen Henry riggs Das Auffinden des unbekannten Exponenten einer Potenz nennt man Logarithmieren. Der Erfinder und Namensgeber der Logarithmen ist der im Kapitel Potenzen mit rationalen Exponenten
2. Freie gedämpfte Schwingungen
 2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
Wärmeleitung und thermoelektrische Effekte Versuchsauswertung
 Versuch P2-32 Wärmeleitung und thermoelektrische Effekte Versuchsauswertung Marco A., Gruppe: Mo-3 Karlsruhe Institut für Technologie, Bachelor Physik Versuchstag: 30.05.2011 1 Inhaltsverzeichnis 1 Bestimmung
Versuch P2-32 Wärmeleitung und thermoelektrische Effekte Versuchsauswertung Marco A., Gruppe: Mo-3 Karlsruhe Institut für Technologie, Bachelor Physik Versuchstag: 30.05.2011 1 Inhaltsverzeichnis 1 Bestimmung
1. Stationarität Definition: Ein stochastischer Prozess. heißt streng oder stark stationär, falls für
 " " " Beschreibung stochastischer Prozesse Wir betrachten diskrete Zeitpunkte und die zugehörigen Zufallsvariablen!. ann sind die Zufallsvariablen durch ihre gemeinsame ichte " #%$&#'$)(*#'$,+- charakterisiert.
" " " Beschreibung stochastischer Prozesse Wir betrachten diskrete Zeitpunkte und die zugehörigen Zufallsvariablen!. ann sind die Zufallsvariablen durch ihre gemeinsame ichte " #%$&#'$)(*#'$,+- charakterisiert.
Bremsweg von PKW und Geländewagen
 BspNr: E0012 Ziele Interpretation der Koeffizienten einer quadratischen Funktion Veranschaulichung des Begriffes mit Hilfe physikalischer Anwendungen Analoge Aufgabenstellungen Übungsbeispiele Lehrplanbezug
BspNr: E0012 Ziele Interpretation der Koeffizienten einer quadratischen Funktion Veranschaulichung des Begriffes mit Hilfe physikalischer Anwendungen Analoge Aufgabenstellungen Übungsbeispiele Lehrplanbezug
V. Claus, Juli 2005 Einführung in die Informatik II 45
 Um die Größenordnung einer reellwertigen oder ganzzahligen Funktion zu beschreiben, verwenden wir die so genannten Landau-Symbole (nach dem deutschen Mathematiker Edmund Landau, 1877-1938). Hierbei werden
Um die Größenordnung einer reellwertigen oder ganzzahligen Funktion zu beschreiben, verwenden wir die so genannten Landau-Symbole (nach dem deutschen Mathematiker Edmund Landau, 1877-1938). Hierbei werden
Analyse kategorialer Variablen Schriftliche Ausarbeitung des Referats vom 23. Mai 2002
 Universität Tübingen Tübingen, im Mai 2002 Geographisches Institut Sommersemester 2002 Seminar Verarbeitung Geographischer Daten Dozent: Dr. H.-J. Rosner Referenten: Katrin Oehlkers, Helke Neuendorff,
Universität Tübingen Tübingen, im Mai 2002 Geographisches Institut Sommersemester 2002 Seminar Verarbeitung Geographischer Daten Dozent: Dr. H.-J. Rosner Referenten: Katrin Oehlkers, Helke Neuendorff,
Mathematik Name: Klausur Nr.6 K1 Punkte: /30 Note: Schnitt:
 K1 Punkte: /30 Note: Schnitt: 0.1.18 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet
K1 Punkte: /30 Note: Schnitt: 0.1.18 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
Die Umkehrung des Potenzierens ist das Logarithmieren.
 Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a x = b, a,b > 0, a 1, so heißt x der Logarithmus von b zur Basis a. Bezeichnung: x = log a (b). Manchmal lassen wir die Angabe der Basis auch
Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a x = b, a,b > 0, a 1, so heißt x der Logarithmus von b zur Basis a. Bezeichnung: x = log a (b). Manchmal lassen wir die Angabe der Basis auch
Umgang mit Formeln Was kann ich?
 Umgang mit ormeln Was kann ich? ufgabe 1 (Quelle: DV Ph 010 5) In der Grafik werden einige Messpunkte der I-U- Kennlinie einer elektrischen Energiequelle dargestellt. a) Bei welchem der Messpunkte, B,
Umgang mit ormeln Was kann ich? ufgabe 1 (Quelle: DV Ph 010 5) In der Grafik werden einige Messpunkte der I-U- Kennlinie einer elektrischen Energiequelle dargestellt. a) Bei welchem der Messpunkte, B,
Protokoll Grundpraktikum I: T6 Thermoelement und newtonsches Abkühlungsgesetz
 Protokoll Grundpraktikum I: T6 Thermoelement und newtonsches Abkühlungsgesetz Sebastian Pfitzner 5. Juni 03 Durchführung: Sebastian Pfitzner (553983), Anna Andrle (55077) Arbeitsplatz: Platz 3 Betreuer:
Protokoll Grundpraktikum I: T6 Thermoelement und newtonsches Abkühlungsgesetz Sebastian Pfitzner 5. Juni 03 Durchführung: Sebastian Pfitzner (553983), Anna Andrle (55077) Arbeitsplatz: Platz 3 Betreuer:
1 Zahlen... 1 1.1 Anzahlen... 1 1.2 Reelle Zahlen... 10 1.3 Dokumentation von Messwerten... 12 1.4 Ausgewählte Übungsaufgaben...
 Inhaltsverzeichnis 1 Zahlen... 1 1.1 Anzahlen... 1 1.2 Reelle Zahlen... 10 1.3 Dokumentation von Messwerten... 12 1.4 Ausgewählte Übungsaufgaben... 14 2 Beschreibende Statistik... 15 2.1 Merkmale und ihre
Inhaltsverzeichnis 1 Zahlen... 1 1.1 Anzahlen... 1 1.2 Reelle Zahlen... 10 1.3 Dokumentation von Messwerten... 12 1.4 Ausgewählte Übungsaufgaben... 14 2 Beschreibende Statistik... 15 2.1 Merkmale und ihre
5. DIFFERENZIEREN UND INTEGRIEREN
 5. DIFFERENZIEREN UND INTEGRIEREN 1 Sei f eine auf R oder auf einer Teilmenge B R definierte Funktion: f : B R Die Funktion heißt differenzierbar in x 0 in B, falls sie in diesem Punkt x 0 lokal linear
5. DIFFERENZIEREN UND INTEGRIEREN 1 Sei f eine auf R oder auf einer Teilmenge B R definierte Funktion: f : B R Die Funktion heißt differenzierbar in x 0 in B, falls sie in diesem Punkt x 0 lokal linear
Naturwissenschaften Teil 1
 Naturwissenschaften Teil Auswertung von Messreihen Grafische Darstellung Die nachfolgende Tabelle enthält die Messwerte zur Aufnahme einer Abkühlungskurve für reines Zinn. Stelle die Messwerte in einem
Naturwissenschaften Teil Auswertung von Messreihen Grafische Darstellung Die nachfolgende Tabelle enthält die Messwerte zur Aufnahme einer Abkühlungskurve für reines Zinn. Stelle die Messwerte in einem
Die Magnitude. Markus Weidmann, Büro für Erdwissenschaftliche Öffentlichkeitsarbeit, Chur
 Die Magnitude Nicolas Deichmann, Donat Fäh, Domenico Giardini Schweizerischer Erdbebendienst, ETH-Zürich Markus Weidmann, Büro für Erdwissenschaftliche Öffentlichkeitsarbeit, Chur 1 Faktenblatt zum Thema
Die Magnitude Nicolas Deichmann, Donat Fäh, Domenico Giardini Schweizerischer Erdbebendienst, ETH-Zürich Markus Weidmann, Büro für Erdwissenschaftliche Öffentlichkeitsarbeit, Chur 1 Faktenblatt zum Thema
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Nachklausur zur Vorlesung. Statistik für Studierende der Biologie
 Institut für Mathematische Stochastik WS 1999/2000 Universität Karlsruhe 11. Mai 2000 Dr. Bernhard Klar Nachklausur zur Vorlesung Statistik für Studierende der Biologie Bearbeitungszeit: 90 Minuten Name:
Institut für Mathematische Stochastik WS 1999/2000 Universität Karlsruhe 11. Mai 2000 Dr. Bernhard Klar Nachklausur zur Vorlesung Statistik für Studierende der Biologie Bearbeitungszeit: 90 Minuten Name:
Chi-Quadrat-Verteilung
 Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Aufgabenpaket zum Crashkurs Mathematik
 Wilhelm-Hausenstein-Gymnasium Sprachliches und Naturwissenschaftlich-technologisches Gymnasium Elektrastraße 61 8195 München Telefon (089) 999690 Fa (089) 9996939 Aufgabenpaket zum Crashkurs Mathematik
Wilhelm-Hausenstein-Gymnasium Sprachliches und Naturwissenschaftlich-technologisches Gymnasium Elektrastraße 61 8195 München Telefon (089) 999690 Fa (089) 9996939 Aufgabenpaket zum Crashkurs Mathematik
Übungen Theoretische Physik I (Mechanik) Blatt 5 ( )
 TU München Prof. P. Vogl Beispiel 1: Übungen Theoretische Physik I (Mechanik) Blatt 5 (26.08.11) Nach Gompertz (1825) wird die Ausbreitung von Rostfraß auf einem Werkstück aus Stahl durch eine lineare
TU München Prof. P. Vogl Beispiel 1: Übungen Theoretische Physik I (Mechanik) Blatt 5 (26.08.11) Nach Gompertz (1825) wird die Ausbreitung von Rostfraß auf einem Werkstück aus Stahl durch eine lineare
Anhang 1: Einige mathematische Grundlagen
 Prof. Dr. H.-H. Kohler, WS 4/5 PC Anhang Anhang- Anhang : Einige mathematische Grundlagen. Funktion, Ableitung, Differential, Integral,. Näherung Wir schreiben eine Funktion f ( ) vereinfacht in der Form:
Prof. Dr. H.-H. Kohler, WS 4/5 PC Anhang Anhang- Anhang : Einige mathematische Grundlagen. Funktion, Ableitung, Differential, Integral,. Näherung Wir schreiben eine Funktion f ( ) vereinfacht in der Form:
Logarithmen und Exponentialgleichungen
 Logarithmen und Exponentialgleichungen W. Kippels 8. April 2011 Inhaltsverzeichnis 1 Definitionen 4 2 Gesetze 5 3 Logarithmen und Taschenrechner 5 4 Exponentialgleichungen 7 5 Übungsaufgaben zu Exponentialgleichungen
Logarithmen und Exponentialgleichungen W. Kippels 8. April 2011 Inhaltsverzeichnis 1 Definitionen 4 2 Gesetze 5 3 Logarithmen und Taschenrechner 5 4 Exponentialgleichungen 7 5 Übungsaufgaben zu Exponentialgleichungen
Das Rechnen mit Logarithmen
 Das Rechnen mit Logarithmen -E Mathematik, Vorkurs Spezielle Logarithmen Der natürliche Logarithmus ist von besonderer Bedeutung in den Anwendungen: Basiszahl ist die Eulersche Zahl e: log e x ln x gelesen:
Das Rechnen mit Logarithmen -E Mathematik, Vorkurs Spezielle Logarithmen Der natürliche Logarithmus ist von besonderer Bedeutung in den Anwendungen: Basiszahl ist die Eulersche Zahl e: log e x ln x gelesen:
Wirtschaftsmathematik: Mathematische Grundlagen
 Wirtschaftsmathematik: Mathematische Grundlagen 1. Zahlen 2. Potenzen und Wurzeln 3. Rechenregeln und Vereinfachungen 4. Ungleichungen 5. Intervalle 6. Beträge 7. Lösen von Gleichungen 8. Logarithmen 9.
Wirtschaftsmathematik: Mathematische Grundlagen 1. Zahlen 2. Potenzen und Wurzeln 3. Rechenregeln und Vereinfachungen 4. Ungleichungen 5. Intervalle 6. Beträge 7. Lösen von Gleichungen 8. Logarithmen 9.
Logarithmen. 1 Logarithmenbegriff
 Logarithmen 1 Logarithmenbegriff Beispiel Lösung Zeichnen Sie den Graphen der Funktion f: y = 2 x - 8 und bestimmen Sie die Nullstelle. Wertetabelle x - 2-1 0 1 2 3 4 y - 7,8-7,5-7 - 6-4 0 8 Bestimmung
Logarithmen 1 Logarithmenbegriff Beispiel Lösung Zeichnen Sie den Graphen der Funktion f: y = 2 x - 8 und bestimmen Sie die Nullstelle. Wertetabelle x - 2-1 0 1 2 3 4 y - 7,8-7,5-7 - 6-4 0 8 Bestimmung
Exponentialgleichungen und logarithmische Gleichungen
 mathe online Skripten http://www.mathe-online.at/skripten/ Exponentialgleichungen und logarithmische Gleichungen Franz Embacher Fakultät für Mathematik der Universität Wien E-mail: franz.embacher@univie.ac.at
mathe online Skripten http://www.mathe-online.at/skripten/ Exponentialgleichungen und logarithmische Gleichungen Franz Embacher Fakultät für Mathematik der Universität Wien E-mail: franz.embacher@univie.ac.at
Praktischer Test: TP2
 Praktischer Test: TP2 Praktischer Test: Die Sonne, eine einzigartige Energiequelle für das Sonnensystem Im Fall einer bemannten Mission zum Mars, scheint die Sonne die einzige unmittelbar verfügbare Energiequelle
Praktischer Test: TP2 Praktischer Test: Die Sonne, eine einzigartige Energiequelle für das Sonnensystem Im Fall einer bemannten Mission zum Mars, scheint die Sonne die einzige unmittelbar verfügbare Energiequelle
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Übung 7 1 Inhalt der heutigen Übung Statistik und Wahrscheinlichkeitsrechnung Vorrechnen der Hausübung D.9 Gemeinsames Lösen der Übungsaufgaben D.10: Poissonprozess
Statistik und Wahrscheinlichkeitsrechnung Übung 7 1 Inhalt der heutigen Übung Statistik und Wahrscheinlichkeitsrechnung Vorrechnen der Hausübung D.9 Gemeinsames Lösen der Übungsaufgaben D.10: Poissonprozess
Dieses Kapitel vermittelt:
 2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
Seismology - A statistical Vignette(Vorbereitungsmaterial) Benedikt Seifert 19. Januar 2012
 Seismology - A statistical Vignette(Vorbereitungsmaterial) Benedikt Seifert 19. Januar 2012 1 Inhaltsverzeichnis 1 Vorauseilende Gedanken 3 2 Kleine Einführung in die Seismologie 3 2.1 Grundbegriffe.................................
Seismology - A statistical Vignette(Vorbereitungsmaterial) Benedikt Seifert 19. Januar 2012 1 Inhaltsverzeichnis 1 Vorauseilende Gedanken 3 2 Kleine Einführung in die Seismologie 3 2.1 Grundbegriffe.................................
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = = 360 360 Das Bogenmaß eines Winkels ist
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = = 360 360 Das Bogenmaß eines Winkels ist
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = 2 = 360 360 Das Bogenmaß eines Winkels ist
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = 2 = 360 360 Das Bogenmaß eines Winkels ist
 Sinkt ein Körper in einer zähen Flüssigkeit mit einer konstanten, gleichförmigen Geschwindigkeit, so (A) wirkt auf den Körper keine Gewichtskraft (B) ist der auf den Körper wirkende Schweredruck gleich
Sinkt ein Körper in einer zähen Flüssigkeit mit einer konstanten, gleichförmigen Geschwindigkeit, so (A) wirkt auf den Körper keine Gewichtskraft (B) ist der auf den Körper wirkende Schweredruck gleich
Experimentelle Bestimmung der magnetischen Flussdichte
 Experimentelle Bestimmung der magnetischen Flussdichte Vorversuch: Um die magnetische Flussdichte zu bestimmen führen wir einen Vorversuch durch um die Kräftewirkung im magnetischen Feld zu testen. B F
Experimentelle Bestimmung der magnetischen Flussdichte Vorversuch: Um die magnetische Flussdichte zu bestimmen führen wir einen Vorversuch durch um die Kräftewirkung im magnetischen Feld zu testen. B F
Potenzen, Wurzeln & Logarithmen
 Potenzen, Wurzeln & Logarithmen 4. Kapitel aus meinem ALGEBRA - Lehrgang Sprachprofil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 22. November 2011 Überblick über die bisherigen
Potenzen, Wurzeln & Logarithmen 4. Kapitel aus meinem ALGEBRA - Lehrgang Sprachprofil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 22. November 2011 Überblick über die bisherigen
Jede physikalische Größe besteht aus Zahlenwert und Einheit!
 R. Brinkmann http://brinkmann-du.de Seite 1 26.11.201 Rechnen mit physikalischen Größen Jede physikalische Größe besteht aus Zahlenwert und Einheit! Basiseinheiten Größe ormelzeichen Grundeinheit Länge
R. Brinkmann http://brinkmann-du.de Seite 1 26.11.201 Rechnen mit physikalischen Größen Jede physikalische Größe besteht aus Zahlenwert und Einheit! Basiseinheiten Größe ormelzeichen Grundeinheit Länge
Merksatz Begriff der Funktion
 Der Begriff Funktion Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. Die Temperatur eines Gewässers wird in verschiedenen
Der Begriff Funktion Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. Die Temperatur eines Gewässers wird in verschiedenen
Schnellkurs und Übersicht zur Gröÿtfehlerabschätzung und Fehlerrechnung
 1 Schnellkurs und Übersicht zur Gröÿtfehlerabschätzung und Fehlerrechnung Zum Messergebnis gehören immer eine Fehlerangabe und nur signikante Stellen 1 Beim Messen arbeiten wir mit Näherungswerten! Selbst
1 Schnellkurs und Übersicht zur Gröÿtfehlerabschätzung und Fehlerrechnung Zum Messergebnis gehören immer eine Fehlerangabe und nur signikante Stellen 1 Beim Messen arbeiten wir mit Näherungswerten! Selbst
2. Freie gedämpfte Schwingungen
 2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
9 auf der Richterskala Erdbeben untersuchen II/A VORANSICHT
 1 von 24 9 auf der Richterskala Erdbeben untersuchen Jens Mittag, Oxbüll Ein Erdbeben der Stärke 9 auf der Richterskala ereignete sich 130 Kilometer östlich der japanischen Stadt Sendai. Einen Satz wie
1 von 24 9 auf der Richterskala Erdbeben untersuchen Jens Mittag, Oxbüll Ein Erdbeben der Stärke 9 auf der Richterskala ereignete sich 130 Kilometer östlich der japanischen Stadt Sendai. Einen Satz wie
Der Autor: Joachim Hönig Impressum
 Der Autor: Joachim Hönig - geboren 1972 - ist verheiratet und hat vier Söhne. Er arbeitet seit 17 Jahren an Förderschulen (zurzeit an der Almeschule in Büren). Neben seiner Arbeit als Lehrer ist er beim
Der Autor: Joachim Hönig - geboren 1972 - ist verheiratet und hat vier Söhne. Er arbeitet seit 17 Jahren an Förderschulen (zurzeit an der Almeschule in Büren). Neben seiner Arbeit als Lehrer ist er beim
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
