DIE NATÜRLICHEN ZAHLEN
|
|
|
- Henriette Morgenstern
- vor 7 Jahren
- Abrufe
Transkript
1 Natürliche Zahlen Herbert Paukert 1 DIE NATÜRLICHEN ZAHLEN Version 2.0 Herbert Paukert (1) Die natürlichen Zahlen [ 02 ] (2) Die Addition [ 06 ] (3) Die Geometrie der Zahlen [ 10 ] (4) Die Subtraktion [ 13 ] (5) Die Multiplikation [ 17 ] (6) Die Division [ 21 ] (7) Die Rechenregeln [ 26 ] Hinweis: Das vorliegende Skriptum besteht hauptsächlich aus Kopien aus dem interaktiven Lernprojekt paumath.exe, das von der Homepage des Autors heruntergeladen werden kann. Deswegen sind Texte und Grafiken teilweise nicht von höchster Qualität.
2 Natürliche Zahlen Herbert Paukert 2 (1) Die natürlichen Zahlen Die natürlichen Zahlen werden verwendet, um die Gegenstände (Elemente) einer Menge abzuzählen, d.h. die Anzahl der Elemente zu ermitteln. Betrachten wir beispielsweise eine Menge von Selbstlauten { a, e, i, o, u } oder eine Menge von Mitlauten { b, c, d }. Um eine Menge abzuzählen, können wir unsere Finger benutzen oder eine Strichliste anfertigen. Dabei schreiben wir für jedes gezählte Element einen Strich in die Liste. Für die Selbstlaute erhalten wir die Liste und wir nennen das Ergebnis die Zahl "Fünf (5)". Für die Mitlaute erhalten wir die Liste und wir nennen das Ergebnis die Zahl "Drei (3)". Diese Zähllisten werden fortlaufend mit Zahlennamen bezeichnet: Eins (1), Zwei (2), Drei (3), Vier (4), Fünf (5),... Sie geben die Anzahl der Elemente einer Menge an. Enthält eine Menge jedoch kein einziges Element (leere Menge), dann wird die Anzahl ihrer Elemente mit "Null (0)" bezeichnet. Um größere Mengen abzuzählen, brauchen wir ein Zahlensystem. Meistens wird das Zehnersystem verwendet, welches aus zehn Grundziffern besteht: 0 (Null) (Anzahl der Elemente der leeren Menge) 1 (Eins) (1 = "E", Einheit, Einerstelle) 2 (Zwei) 3 (Drei) 4 (Vier) 5 (Fünf) 6 (Sechs) 7 (Sieben) 8 (Acht) 9 (Neun) Die Zahl, welche einer bestimmten Zahl vorangeht, heißt ihr Vorgänger. Die Zahl, welche einer bestimmten Zahl nachfolgt, heißt ihr Nachfolger.
3 Natürliche Zahlen Herbert Paukert 3 Enthält eine Menge mehr als 9 Elemente, dann verwendet man für die Anzahl zwei Ziffernstellen: 10 (Zehn = "Z", Zehnerstelle) 11 (Zehn und Eins = Elf) 12 (Zehn und Zwei = Zwölf) 13 (Zehn und Drei = Dreizehn) 14 (Zehn und Vier = Vierzehn) 15 (Zehn und Fünf = Fünfzehn) 16 (Zehn und Sechs = Sechzehn) 17 (Zehn und Sieben = Siebzehn) 18 (Zehn und Acht = Achtzehn) 19 (Zehn und Neun = Neunzehn) Enthält eine Menge mehr als 19 Elemente, dann wird einfach weiter gezählt: 20 (Zwei Zehner = Zwanzig) 21 (Zwanzig und Eins = Einundzwanzig) 22 (Zwanzig und Zwei = Zweiundzwanzig) (Zwanzig und Neun = Neunundzwanzig) 30 (Drei Zehner = Dreißig) 31 (Dreißig und Eins = Einunddreißig) 32 (Dreißig und Zwei = Zweiunddreißig) (Dreißig und Neun = Neununddreißig) 40 (Vier Zehner = Vierzig) 41 (Vierzig und Eins = Einundvierzig) 42 (Vierzig und Zwei = Zweiundvierzig) (Vierzig und Neun = Neunundvierzig) (Neun Zehner = Neunzig) 91 (Neunzig und Eins = Einundneunzig) 92 (Neunzig und Zwei = Zweiundneunzig) (Neunzig und Neun = Neunundneunzig)
4 Natürliche Zahlen Herbert Paukert 4 Enthält eine Menge mehr als 99 Elemente, dann verwendet man für die Anzahl drei Ziffernstellen: 100 (Einhundert = "H", Hunderterstelle) 101 (Einhundert und Eins) (Einhundert und Neunundneunzig) 200 (Zweihundert) 201 (Zweihundert und Eins) (Zweihundert und Neunundneunzig) (Neunhundert) 901 (Neunhundert und Eins) (Neunhundert und Neunundneunzig) Enthält eine Menge mehr als 999 Elemente, dann verwendet man für die Anzahl vier oder noch mehr Ziffernstellen: 1000 (Tausend = "T", Tausenderstelle) (Zehntausend = "ZT")... Stellenwerte im Zehnersystem Das Zehnersystem besteht aus 10 Grundziffern { 0,1,2,3,4,5,6,7,8,9 }. Zahlen, welche größer als 9 sind, werden mit Hilfe von Stellenwerten dargestellt. 1, 2,.. 9, 10, 11,.. 99, 100, 101,.. 999, 1000, 1001,.. Einer (E): 1 = 1E Zehner (Z): 10 = 1Z = 10E Hunderter(H): 100 = 1H = 10Z = 100E Tausender (T): 1000 = 1T = 10H = 100Z = 1000E Beispiel: 4285 = 4T 2H 8Z 5E =
5 Natürliche Zahlen Herbert Paukert 5 Beispiel: 2537 = 2T 5H 3Z 7E = 2* * *10 + 7*1 Die Ziffer 7 hat in der Zahl 2537 den Stellenwert "Einer (E)". Die Ziffer 3 hat in der Zahl 2537 den Stellenwert "Zehner (Z)". Die Ziffer 5 hat in der Zahl 2537 den Stellenwert "Hunderter (H)". Die Ziffer 2 hat in der Zahl 2537 den Stellenwert "Tausender (T)". Merksatz: Zum Anschreiben einer natürlichen Zahl werden 10 Ziffern verwendet, welche nebeneinander an verschiedenen Stellen stehen. Der so genannte Stellenwert einer Ziffer erhöht sich schrittweise von rechts nach links um das Zehnfache. Beispiele für die Schreibweise im Zehnersystem: 37 = 3Z 7E, Drei Zehner (Z) und sieben Einer (E). 3Z = 3 * 10 = 30 7E = 7 * 1 = 7 3Z 7E = 3 * * 1 = = = 2H 8Z 5E, Zwei Hunderter (H), acht Zehner (Z), fünf Einer (E). 2H = 2 * 100 = 200 8Z = 8 * 10 = 80 5E = 5 * 1 = 5 2H 8Z 5E = 2 * * * 1 = = = 1Z 9E = 1*10 + 9*1 78 = 7Z 8E = 7*10 + 8*1 205 = 2H 0Z 5E = 2* *10 + 5*1 439 = 4H 3Z 9E = 4* *10 + 9* = 3T 0H 1Z 6E = 3* * *10 + 6* = 9T 9H 9Z 9E = 9* * *10 + 9*1
6 Natürliche Zahlen Herbert Paukert 6 (2) Die Addition von Zahlen Gegeben sind zwei Mengen. Eine neue Menge wird gebildet, welche alle Elemente der beiden Mengen enthält (Vereinigung). Zwei Mengen, die kein Element gemeinsam haben, heißen fremd. Beispielsweise sind die Mengen { a, e, i, o, u } und { b, c, d } fremd. Die erste Menge hat 5 Elemente. Die zweite Menge hat 3 Elemente. Legt man alle Elemente aus beiden Mengen zu einer neuen Menge zusammen, dann erhält man ihre Vereinigung { a, e, i, o, u, b, c, d }. Diese neue Menge hat genau 8 Elemente. Beispiele: 1. Menge: { a, e, i, o, u }, Anzahl = 5 2. Menge: { b, c, d }, Anzahl = 3 Vereinigung: { a, e, i, o, u, b, c, d }, Anzahl = 8 1. Menge: { A, O, U }, Anzahl = 3 2. Menge: { Ä, Ö, Ü }, Anzahl = 3 Vereinigung: { A, O, U, Ä, Ö, Ü }, Anzahl = 6 1. Menge: { +, -, *, / }, Anzahl = 4 2. Menge: { ß, µ,,, Ø, ƒ }, Anzahl = 6 Vereinigung: { +, -, *, /, ß, µ,,, Ø, ƒ }, Anzahl = 10 Merksatz: Wenn x und y die Elementanzahlen von zwei fremden Mengen sind, dann wird die Elementanzahl z ihrer Vereinigung als Summe x + y bezeichnet. Dazu sagt man "x plus y ist z". Auf diese Art und Weise kann man zu zwei Zahlen x und y eine neue Zahl z erzeugen. Diese Operation nennt man Addition. Das Ergebnis ist die Summe: x + y = z. Die zwei Zahlen x und y sind die Summanden. Beispielsweise ergibt "2 plus 3" die Zahl 5, d.h = 5.
7 Natürliche Zahlen Herbert Paukert 7 Additionen von kleinen Zahlen werden durch Strichlisten ermittelt: = 4, weil III und I genau IIII ergibt = 5, weil II und III genau IIIII ergibt = 12, weil IIIII und IIIIIII genau IIIIIIIIIIII ergibt. Hinweis: Addiert man zu einer Zahl (a) die Zahl Null (0), dann bleibt die Zahl unverändert: a + 0 = a. Schriftliche Addition Bei großen Zahlen muss schriftlich addiert werden. Dabei werden die Zahlen so untereinander geschrieben, dass die Ziffern mit dem gleichen Stellenwert immer genau untereinander stehen. Diese werden dann einzeln addiert. Dabei wird immer mit der Einer-Stelle (E) begonnen addiert man dann folgendermaßen: 2Z 5E + 1Z 7E Z 12E = 4Z 2E = 42 Das Beispiel zeigt, dass es bei der Addition der Einerziffern 5 und 7 zu einem so genannten Übertrag in die Zehnerstelle kommt: Man sagt: "5 plus 7 ist 12, daher 1 weiter". Der Übertrag wird dann zu der Summe der Zehnerziffern dazugezählt. Man sagt: "2 plus 1 ist 3, und 1 ist 4". Beispiele ohne Stellen-Übertrag: =? H Z E
8 Natürliche Zahlen Herbert Paukert =? H Z E Beispiele mit Stellen-Übertrag (Ü). Bei den Überträgen wandern immer Einheiten von einer Stelle zur benachbarten Stelle =? H Z E Ü Man sagt: "5 und 7 ist 12, 1 weiter. 3 und 2 ist 5 und 1 ist 6. 1 und 0 ist 1." =? H Z E Ü 1Ü Man sagt: "8 und 9 ist 17, 1 weiter. 6 und 5 ist 11 und 1 ist 12, 1 weiter." "3 und 1 ist 4 und 1 ist 5."
9 Natürliche Zahlen Herbert Paukert 9 Beim schriftlichen Addieren kann der Übertrag angeschrieben werden oder man addiert OHNE Anschreiben des Übertrags, was bei einiger Übung gelingen sollte Ü Ü Ü1Ü Ü1Ü Ü1Ü1Ü
10 Natürliche Zahlen Herbert Paukert 10 (3) Die Geometrie der Zahlen Der Zahlenstrahl Die natürlichen Zahlen { 0, 1, 2, 3, 4, 5, 6, 7,... } dienen in erster Linie zum Abzählen von Gegenständen oder Ereignissen. Die Menge der natürlichen Zahlen wird mit N bezeichnet. Sie beginnt mit der Zahl 0 (Null) und kann dann beliebig fortgesetzt werden, weil es zu jeder Zahl einen Nachfolger gibt. Ordnet man jeder natürlichen Zahl einen Punkt auf einer Geraden in der Zeichenebene zu, dann erhält man gleichweit entfernte Punkte auf einer halben Geraden, welche auch Zahlenstrahl genannt wird. a b Eine bestimmte Zahl a ist dann kleiner als eine zweite Zahl b, wenn sie auf dem Zahlenstrahl links von der zweiten Zahl liegt. Dadurch sind die Zahlen entsprechend ihrer Größe geordnet. Kleiner, Gleich, Größer Für zwei Zahlen a und b gibt es genau drei Möglichkeiten: (1) a ist kleiner als b. Man schreibt a < b. (2) a ist gleich b. Man schreibt a = b. (3) a ist größer als b. Man schreibt a > b. 0 < 1 < 2 < 3 < 4 < 5 < < < > > 299
11 Natürliche Zahlen Herbert Paukert 11 Die Zahlenpfeile Betrachten wir den Punkt "0" am linken Rand des Zahlenstrahls. Wir wollen ihn Ursprung "0" nennen. Wir zeichnen nun einen Pfeil von diesem Ursprung "0" zum Punkt "4". Dadurch erhalten wir die so genannte Pfeildarstellung der Zahl "4". Die Länge dieses Zahlenpfeiles beträgt genau 4 Einheiten. Der Zahlenpfeil "4": > Der Zahlenpfeil "7": > Der Pfeilanfang heißt immer "Fuß" des Pfeiles und die Pfeilspitze nennt man "Kopf" des Pfeiles. Der Zahlenpfeil "12": > Der Pfeilanfang heißt immer "Fuß" des Pfeiles und die Pfeilspitze nennt man "Kopf" des Pfeiles.
12 Natürliche Zahlen Herbert Paukert 12 Die Pfeiladdition Sowie man zwei Zahlen addieren kann, ist es auch möglich ihre Pfeile zu addieren. Wenn wir die Zahlenpfeile "4" und "3" addieren wollen, müssen wir den Fuß von "3" auf den Kopf von "4" stellen. Dadurch erhalten wir dann den Zahlenpfeil "7", der beim Ursprung "0" beginnt und beim Punkt "7" endet. Beispiel: = > > > Beispiel: = > > > Die Addition von Zahlenpfeilen erfolgt somit entsprechend der einfachen Pfeilregel: "Fuß des zweiten Pfeiles an den Kopf des ersten Pfeiles".
13 Natürliche Zahlen Herbert Paukert 13 Die Subtraktion Gegeben sind zwei Zahlen, beispielsweise 3 und 5. Welche Zahl muss man zu 3 addieren um 5 zu erhalten? Addition: 3 +? = 5 (Drei plus wieviel ist fünf?) Die gesuchte Zahl ist 2. Man nennt sie die Differenz von 5 und 3. Man schreibt 5-3 = 2. Man sagt "5 minus 3 ist 2". Diese Rechnung heißt Subtraktion. Die erste Zahl (5) heißt Minuend. Die zweite Zahl (3) heißt Subtrahend. Subtraktion: 5-3 = 2 Hinweis: Man kann keine größere Zahl von einer kleineren Zahl subtrahieren. So ist beispielsweise 3-5 nicht möglich, weil die Frage 5 +? = 3 nicht beantwortet werden kann. Schriftliche Subtraktion Bei größeren Zahlen muss schriftlich subtrahiert werden. Dazu schreiben wir die Zahlen so untereinander, dass Ziffern mit dem gleichen Stellenwert immer genau untereinander stehen. Diese werden dann einzeln subtrahiert. Dabei wird bei der Einer-Stelle begonnen. Beispiele ohne Stellen-Übertrag: =? Z E Man sagt: "2 und 7 ist 9. 1 und 3 ist 4."
14 Natürliche Zahlen Herbert Paukert =? Z E Man sagt: "4 und 3 ist 7. 2 und 5 ist 7." Bevor wir uns weiter mit der Subtraktion beschäftigen, wollen folgende Rechnungen betrachten: 6 2 = = = = = = 4 Diese Rechnungen zeigen uns, dass die Differenz von zwei Zahlen a b unverändert bleibt, wenn man beide Zahlen um denselben Wert c vermehrt. a b = (a + c) (b + c). Nun können wir auch Subtraktionen mit Stellen-Überträgen (Ü), ausführen, beispielsweise =? 7 6 7Z 6E 7Z 16E Z 9E - 3Z 9E ???? 4Z 7E 1Ü Weil an der Einer-Stelle die Subtraktion 6 9 nicht möglich ist, vermehren wir 76 und 29 um 10 (1Z). Das ergibt Z = 3Z 9E und Z = 8Z 6E = 7Z 16E. Dabei hat sich die Differenz nicht geändert. Jedoch kann die Subtraktion jetzt ausgeführt werden, weil = 7Z 16E 3Z 9E = 4Z 7E = 47. Man sagt: "9 und 7 ist 16, 1 weiter. 2 und 1 ist 3. 3 und 4 ist 7."
15 Natürliche Zahlen Herbert Paukert 15 Noch eine Subtraktion mit Übertrag (Ü): =? 8 3 8Z 3E 8Z 13E Z 4E - 6Z 4E ???? 2Z 9E 1Ü Kurze Schreibweise: Ü Man sagt: "4 und 9 ist 13, 1 weiter. 5 und 1 ist 6. 6 und 2 ist 8." Beim schriftlichen Subtrahieren kann der Übertrag angeschrieben werden, oder man subtrahiert OHNE Anschreiben des Übertrags Ü Man sagt: "7 und 8 ist 15, 1 weiter. 1 und 1 ist 2. 2 und 1 ist 3." Ü Man sagt: "5 und 7 ist 12, 1 weiter. 3 und 1 ist 4. 4 und 2 ist 6." Ü Man sagt: "6 und 3 ist 9, 0 weiter. 5 und 0 ist 5. 5 und 2 ist 7."
16 Natürliche Zahlen Herbert Paukert 16 Noch ein Beispiel mit Stellen-Übertrag (Ü): =? 1. Schritt 2. Schritt H 6Z 3E 5H 6Z 13E 5H 16Z 13E H 8Z 7E - 1H 9Z 7E - 2H 9Z 7E ???????? 6E 3H 7Z 6E 1Ü 1Ü 1Ü 1. Schritt: Weil an der Einer-Stelle die Subtraktion 3-7 nicht möglich ist, muss ein Übertrag der Einer-Stelle durchgeführt werden. Man sagt: "7 und 6 ist 13, 1 weiter. 8 und 1 ist 9." 2. Schritt: Weil an der Zehner-Stelle die Subtraktion 6-9 nicht möglich ist, muss ein Übertrag der Zehner-Stelle durchgeführt werden. Man sagt: "9 und 7 ist 16, 1 weiter. 1 und 1 ist 2. 2 und 3 ist 5." Beim schriftlichen Subtrahieren kann der Übertrag angeschrieben werden, oder man subtrahiert OHNE Anschreiben des Übertrags Ü 1Ü Man sagt: "7 und 6 ist 13, 1 weiter. 8 und 1 ist 9." "9 und 7 ist 16, 1 weiter. 1 und 1 ist 2. 2 und 3 ist 5."
17 Natürliche Zahlen Herbert Paukert 17 Die Multiplikation Betrachten wir nun eine Addition von lauter gleichen Zahlen, beispielsweise = 10. Statt kann man 5 * 2 ("5 Mal 2") schreiben und nennt das eine Multiplikation. Das Ergebnis 10 heißt das Produkt. Die Multiplikation ist nichts Anderes als die Addition von lauter gleichen Zahlen. Die Multiplikation mit Null ergibt immer Null. Als Multiplikationszeichen wird ein Kreuz x oder ein Stern * verwendet. Die beiden multiplizierten Zahlen heißen Faktoren. Multiplikation: 5 * 2 = 10 Beispiele: 0 * 2 = 0 1 * 2 = 2 2 * 2 = = 4 3 * 2 = = 6 4 * 2 = = 8 5 * 2 = = 10 0 * 3 = 0 1 * 3 = 3 2 * 3 = = 6 3 * 3 = = 9 4 * 3 = = 12 5 * 3 = = 15 0 * 4 = 0 1 * 4 = 4 2 * 4 = = 8 3 * 4 = = 12 4 * 4 = = 16 5 * 4 = = 20
18 Natürliche Zahlen Herbert Paukert 18 Die Multiplikation mit einer einstelligen Zahl 57 * 6 = = ( 5Z 7E) * 6 = ( 30Z 42E) = ( 34Z 2E) Übertrag von 40E = 4Z = ( 3H 4Z 2E) Übertrag von 30Z = 3H = * Ü 4Ü Man multipliziert dabei - mit der Einerstelle (E) beginnend - jede Ziffer von 57 mit der Zahl 6. Die Überträge addiert man dann schrittweise zur nächst höheren Stelle! 284 * 3 = = ( 2H 8Z 4E) * 3 = ( 6H 24Z 12E) = ( 6H 25Z 2E) Übertrag von 10E = 1Z = ( 8H 5Z 2E) Übertrag von 20Z = 2H = 852
19 Natürliche Zahlen Herbert Paukert * Ü 1Ü Man multipliziert dabei - mit der Einerstelle (E) beginnend - jede Ziffer von 284 mit der Zahl 3. Die Überträge addiert man dann schrittweise zur nächst höheren Stelle! Die Multiplikation mit einer zweistelligen Zahl 286 * 34 = Wir zerlegen 34 in (30 + 4) = (3Z 4E). Zuerst multiplizieren wir 286 mit 3Z, das ist 858Z = Dann multiplizieren wir 286 mit 4E, das ist 1144E = Zuletzt addieren wir beide Werte. (Unbedingt Überträge beachten.) 286 * (3Z 4E) = * (3Z 4E) Zehner-Zeile (Z) Einer-Zeile (E) = Ergebnis-Zeile = 9724
20 Natürliche Zahlen Herbert Paukert * 42 = Wir zerlegen 42 in (40 + 2) = (4Z 2E). Zuerst multiplizieren wir 1548 mit 4Z, das ist 6192Z = Dann multiplizieren wir 1548 mit 2E, das ist 3096E = Zuletzt addieren wir beide Werte. (Unbedingt Überträge beachten.) 1548 * (4Z 2E) = * (4Z 2E) Zehner-Zeile (Z) Einer-Zeile (E) = Ergebnis-Zeile = Beispiele von Multiplikationen: Mögliche Überträge werden nicht angeschrieben, sondern im Kopf richtig ausgerechnet! 2 3 * Zehnerzeile Einerzeile Ergebniszeile = Zehnerzeile + Einerzeile * Zehnerzeile Einerzeile Ergebniszeile = Zehnerzeile + Einerzeile
21 Natürliche Zahlen Herbert Paukert 21 Die Division Gegeben sind zwei Zahlen, beispielsweise 2 und 7. Wie oft ist die Zahl 2 in der Zahl 7 enthalten? Wir lösen das Problem, indem wir 2 von 7 so lange wie möglich subtrahieren: 7-2 = = = 1 Also ist 2 in 7 genau 3 Mal enthalten und es bleibt 1 als Rest. Man nennt die gesuchte Zahl 3 den Quotient von 7 und 2. Der Rest ist 1. Man sagt dazu "7 dividiert durch 2 ergibt 3 mit Rest 1". Diese Operation heißt Division. Als Divisionszeichen werden der Schrägstrich / oder der Doppelpunkt : verwendet. Die Zahl 7 heißt Dividend und die Zahl 2 heißt Divisor. Der Rest ist immer kleiner als der Divisor. Division 7 : 2 = 3, Rest 1 Gegeben sind zwei Zahlen, beispielsweise 3 und 14. Wie oft ist die Zahl 3 in der Zahl 14 enthalten? Wir lösen das Problem, indem wir 3 von 14 so lange wie möglich subtrahieren: 14-3 = = = = 2 Also ist 3 in 14 genau 4 Mal enthalten und es bleibt 2 als Rest. Division 14 : 3 = 4, Rest 2 Man kann die Division mit einer Multiplikation überprüfen: 14 = 4 * 3 + 2, d.h. Dividend = Quotient * Divisor + Rest.
22 Natürliche Zahlen Herbert Paukert 22 Ein Sonderfall liegt dann vor, wenn der Rest 0 ist, wie bei 6 : 2 = 3. Dann sagt man, dass der Divisor den Dividenden teilt. (2 ist ein Teiler von 6). Beispiele: 5 : 2 = 2 mit Rest 1 6 : 3 = 2 mit Rest 0 9 : 2 = 4 mit Rest 1 11 : 3 = 3 mit Rest 2 10 : 5 = 2 mit Rest 0 15 : 4 = 3 mit Rest 3 18 : 3 = 6 mit Rest 0 20 : 6 = 3 mit Rest 2 Will man größere Zahlen dividieren, dann wird folgende schriftliche Methode verwendet. Beispiel 325 : 7 =? 7 (1) Stellenwert-Zeile 325 : 7 = 4Z 6E = 46 (2) Divisions-Zeile -280 (3) 7 * 4Z = (4) = (5) 7 * 6E = Rest (6) = 3 In Zeile (1) wird ermittelt, in welcher Zifferngruppe von 325 die Zahl 7 das erste Mal enthalten ist. In 32 ist 7 dann 4 Mal enthalten. Der Divisor beginnt daher mit der Zehner-Stelle (Z). In Zeile 2 wird die Division angeschrieben. In Zeile (3) wird das Zwischenprodukt 7 * 4Z = 28Z = 280 gebildet und dann von 325 subtrahiert. Das ergibt den Zwischenrest 45 in Zeile (4). In Zeile (5) wird ermittelt, wie oft die Zahl 7 im Zwischenrest 45 enthalten ist. Das ist 6 Mal. Nun wird das Zwischenprodukt 7 * 6E = 42 gebildet und zuletzt von 45 subtrahiert. Das ergibt den letzten Rest 3 in Zeile (6).
23 Natürliche Zahlen Herbert Paukert 23 Beispiel 2675 : 42 =? 42 (1) Stellenwert-Zeile 2675 : 42 = 6Z 3E = 63 (2) Divisions-Zeile (3) 42 * 6Z = (4) = (5) 42 * 3E = Rest (6) = 29 In Zeile (1) wird ermittelt, in welcher Zifferngruppe von 2675 die Zahl 42 das erste Mal enthalten ist. In 267 ist 42 dann 6 Mal enthalten. Der Divisor beginnt daher mit der Zehner-Stelle (Z). In Zeile 2 wird die Division angeschrieben. In Zeile (3) wird das Zwischenprodukt 42 * 6Z = 252Z = 2520 gebildet und dann von 2675 subtrahiert. Das ergibt den Zwischenrest 155 in Zeile (4). In Zeile (5) wird ermittelt, wie oft die Zahl 42 im Zwischenrest 155 enthalten ist. ist. Das ist 3 Mal. Nun wird das Zwischenprodukt 42 * 3E = 126 gebildet und zuletzt von 155 subtrahiert. Das ergibt den letzten Rest 29 in Zeile (6). Beispiele von Divisionen: : 85 = 2H 7Z 3E = Rest Probe, = 273 *
24 Natürliche Zahlen Herbert Paukert : 317 = 5Z 2E = Rest Probe, = 52 * Sehr oft wird das hier beschriebene Divisions-Verfahren abgekürzt. Die Zwischenprodukte und die Subtraktionen werden dabei nicht angeschrieben, sondern im Kopf durchgeführt. Es werden nur die Zwischenreste angeschrieben. Abgekürztes Divisionsverfahren. Beispiel : 85 =? 85 (1) Stellenwertbestimmung : 85 = 273 (2) Divisions-Zeile 620 (3) Zwischenrest 257 (4) Zwischenrest 2 R (5) Letzter Rest Man sagt: 2 mal 5 ist 10 und 2 ist 12, 1 weiter. 2 mal 8 ist 16 und 1 ist 17, und 6 ist 23. Nächste Stelle 0 herab. 7 mal 5 ist 35 und 5 ist 40, 1 weiter. 7 mal 8 ist 56 und 4 ist 60, und 2 ist 62. Nächste Stelle 7 herab. 3 mal 5 ist 15 und 2 ist 17, 1 weiter. 3 mal 8 ist 24 und 1 ist 25, und 0 ist 25. Bleibt 2 Rest.
25 Natürliche Zahlen Herbert Paukert 25 Beispiele für das abgekürzte Divisionsverfahren: : 8 = R Probe, 173 = 21 * : 32 = R Probe, 401 = 12 * : 67 = R Probe, 6901 = 103 * : 72 = R Probe, 2935 = 40 * : 42 = R Probe, = 637 *
26 Natürliche Zahlen Herbert Paukert 26 (7) Die Rechenregeln Für das Rechnen mit natürlichen Zahlen werden folgende Regeln festgesetzt: [01] Grundsätzlich wird von links nach rechts gerechnet = = 6-4 = 2 [02] Punktrechnungen haben Vorrang vor Strichrechnungen 2 + 3*4 = = 14 [03] Rechnungen in Klammern werden zuerst durchgeführt (2 + 3) * 4 = 5 * 4 = 20 Für das Rechnen mit natürlichen Zahlen können weitere Gesetze direkt bewiesen werden. [04] Vertauschungsgesetz der Addition: a + b = b + a [05] Verbindungsgesetz der Addition: (a + b) + c = a + (b + c) [06] Vertauschungsgesetz der Multiplikation: a * b = b * a [07] Verbindungsgesetz der Multiplikation: (a * b) * c = a * (b * c) [08] Verteilungsgesetz: a * (b + c) = a * b + a * c Vertauschungsgesetz der Addition: a + b = b + a = II + III = IIIII = = III + II = IIIII = 5 Verbindungsgesetz der Addition: (a + b) + c = a + (b + c) (2 + 3) + 4 = = (3 + 4) = = 9 Vertauschungsgesetz der Multiplikation: a * b = b * a 3 * 2 = = 6 2 * 3 = = 6 Verbindungsgesetz der Multiplikation: (a * b) * c = a * (b * c) (2 * 3) * 4 = 6 * 4 = 24 2 * (3 * 4) = 2 * 12 = 24 Verteilungsgesetz: a * (b + c) = a * b + a * c 2 * (3 + 4) = 2 * 7 = 14 2 * * 4 = = 14
Herbert Paukert Schulmathematik in 8 Bänden Version 6.0, 2016 MATHE 1. Arithmetik - Unterstufe
 Herbert Paukert Schulmathematik in 8 Bänden Version 6.0, 2016 MATHE 1 Arithmetik - Unterstufe 2 Herbert Paukert: Schulmathematik, Band 1 Herbert Paukert: Schulmathematik, Band 1 3 MATHE, Band 1 Arithmetik
Herbert Paukert Schulmathematik in 8 Bänden Version 6.0, 2016 MATHE 1 Arithmetik - Unterstufe 2 Herbert Paukert: Schulmathematik, Band 1 Herbert Paukert: Schulmathematik, Band 1 3 MATHE, Band 1 Arithmetik
die ganze Zahl die rationale Zahl
 die ganze Zahl Beispiele für ganze Zahlen:..., 3, 2, 1, 0, 1, 2, 3,... Ganze Zahlen sind die natürlichen Zahlen und die negativen Zahlen (Minuszahlen). Z = {..., 3, 2, 1, 0, 1, 2, 3, } die rationale Zahl
die ganze Zahl Beispiele für ganze Zahlen:..., 3, 2, 1, 0, 1, 2, 3,... Ganze Zahlen sind die natürlichen Zahlen und die negativen Zahlen (Minuszahlen). Z = {..., 3, 2, 1, 0, 1, 2, 3, } die rationale Zahl
Begriffe, die auf eine Multiplikation oder Division hinweisen
 Fachbegriffe der Addition und Subtraktion Bei der Addition werden Zahlen zusammengezählt: 2 + 4 = 6 1. Summand 2. Summand Summe Bei der Subtraktion wird eine Zahl von einer anderen abgezogen. 7 2 = 5 Minuend
Fachbegriffe der Addition und Subtraktion Bei der Addition werden Zahlen zusammengezählt: 2 + 4 = 6 1. Summand 2. Summand Summe Bei der Subtraktion wird eine Zahl von einer anderen abgezogen. 7 2 = 5 Minuend
Terme, Gleichungen und Zahlenmengen
 Die natürlichen Zahlen Die natürlichen Zahlen werden mit dem Symbol N dargestellt. N = {1 ;2 ;3 ;4 ;5; 6;...} Zur einfachen Erfassung von Daten kann man eine Strichliste anfertigen. Beispiel: Größen der
Die natürlichen Zahlen Die natürlichen Zahlen werden mit dem Symbol N dargestellt. N = {1 ;2 ;3 ;4 ;5; 6;...} Zur einfachen Erfassung von Daten kann man eine Strichliste anfertigen. Beispiel: Größen der
1. Grundlagen der Arithmetik
 1. Grundlagen der Arithmetik Die vier Grundrechenarten THEORIE Addition (plus-rechnen, addieren, zusammenzählen): Summand + Summand = Summe Subtraktion (minus-rechnen, subtrahieren, wegzählen): Minuend
1. Grundlagen der Arithmetik Die vier Grundrechenarten THEORIE Addition (plus-rechnen, addieren, zusammenzählen): Summand + Summand = Summe Subtraktion (minus-rechnen, subtrahieren, wegzählen): Minuend
Darstellen, Ordnen und Vergleichen
 Darstellen, Ordnen und Vergleichen negative Zahlen positive Zahlen 1_ 6 < 3,5 3 < +2 +1 2 < +5 Um negative Zahlen darstellen zu können, wird der Zahlenstrahl zu einer Zahlengeraden erweitert. Wenn zwei
Darstellen, Ordnen und Vergleichen negative Zahlen positive Zahlen 1_ 6 < 3,5 3 < +2 +1 2 < +5 Um negative Zahlen darstellen zu können, wird der Zahlenstrahl zu einer Zahlengeraden erweitert. Wenn zwei
Regeln zur Bruchrechnung
 Regeln zur Bruchrechnung Brüche und Anteile Zur Beschreibung von Anteilen verwendet man Brüche (von gebrochen, z. B. eine Glasscheibe) wie 5 ; 5 oder 9. Die obere Zahl (über dem Bruchstrich) heißt Zähler,
Regeln zur Bruchrechnung Brüche und Anteile Zur Beschreibung von Anteilen verwendet man Brüche (von gebrochen, z. B. eine Glasscheibe) wie 5 ; 5 oder 9. Die obere Zahl (über dem Bruchstrich) heißt Zähler,
Bruchzahlen Herbert Paukert Die Grundlagen [ 02 ] 2. Kürzen und Erweitern [ 14 ] 3. Addieren und Subtrahieren [ 24 ]
![Bruchzahlen Herbert Paukert Die Grundlagen [ 02 ] 2. Kürzen und Erweitern [ 14 ] 3. Addieren und Subtrahieren [ 24 ] Bruchzahlen Herbert Paukert Die Grundlagen [ 02 ] 2. Kürzen und Erweitern [ 14 ] 3. Addieren und Subtrahieren [ 24 ]](/thumbs/49/25605643.jpg) Bruchzahlen Herbert Paukert 1 DIE BRUCHZAHLEN Version 2.0 Herbert Paukert 1. Die Grundlagen [ 02 ] 2. Kürzen und Erweitern [ 14 ] 3. Addieren und Subtrahieren [ 24 ] 4. Multiplizieren und Dividieren [
Bruchzahlen Herbert Paukert 1 DIE BRUCHZAHLEN Version 2.0 Herbert Paukert 1. Die Grundlagen [ 02 ] 2. Kürzen und Erweitern [ 14 ] 3. Addieren und Subtrahieren [ 24 ] 4. Multiplizieren und Dividieren [
Grundwissen JS 5 Algebra
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ math.-technolog. u. sprachl. Gymnasium Grundwissen JS 5 Algebra WILHELM-VON-HUMBOLDT-STRASSE 7 91257 PEGNITZ FERNRUF 09241/48333 FAX 09241/2564 Rechnen in N 29. Juli 2009
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ math.-technolog. u. sprachl. Gymnasium Grundwissen JS 5 Algebra WILHELM-VON-HUMBOLDT-STRASSE 7 91257 PEGNITZ FERNRUF 09241/48333 FAX 09241/2564 Rechnen in N 29. Juli 2009
Wie subtrahiert man ungleichnamige Brüche? Wie addiert man gemischte Zahlen? muss man Brüche auf den Hauptnenner bringen?
 A Was ist ein Hauptnenner? A Für welche Rechenarten muss man Brüche auf den Hauptnenner bringen? A9 Wie subtrahiert man ungleichnamige Brüche? A0 Wie addiert man gemischte Zahlen? A A A A Wie nennt man
A Was ist ein Hauptnenner? A Für welche Rechenarten muss man Brüche auf den Hauptnenner bringen? A9 Wie subtrahiert man ungleichnamige Brüche? A0 Wie addiert man gemischte Zahlen? A A A A Wie nennt man
Rechnen mit natürlichen Zahlen
 Addieren und Subtrahieren einer Zahl Fachausdrücke bei der Addition und Subtraktion: Addition (+) 52 + 27 = 79 1. Summand + 2. Summand = Summe Rechnen mit natürlichen Zahlen Subtraktion ( - ) Strichrechnungen
Addieren und Subtrahieren einer Zahl Fachausdrücke bei der Addition und Subtraktion: Addition (+) 52 + 27 = 79 1. Summand + 2. Summand = Summe Rechnen mit natürlichen Zahlen Subtraktion ( - ) Strichrechnungen
Rechengesetze und ihre Anwendungen. a + b = b + a. Assoziativgesetz ( Verbindungsgesetz ) a + ( b + c ) Distributivgesetz ( Verteilungsgesetz )
 Rechengesetze und ihre Anwendungen Es gibt 3 verschiedene Gesetze, die in der Mathematik angewandt werden. Es sind : Kommutativgesetz ( Vertauschungsgesetz ) a + b = b + a Assoziativgesetz ( Verbindungsgesetz
Rechengesetze und ihre Anwendungen Es gibt 3 verschiedene Gesetze, die in der Mathematik angewandt werden. Es sind : Kommutativgesetz ( Vertauschungsgesetz ) a + b = b + a Assoziativgesetz ( Verbindungsgesetz
Grundwissen 5. Klasse
 Grundwissen 5. Klasse 1/5 1. Zahlenmengen Grundwissen 5. Klasse Natürliche Zahlen ohne Null: N 1;2;3;4;5;... mit der Null: N 0 0;1;2;3;4;... Ganze Zahlen: Z... 3; 2; 1;0;1;2;3;.... 2. Die Rechenarten a)
Grundwissen 5. Klasse 1/5 1. Zahlenmengen Grundwissen 5. Klasse Natürliche Zahlen ohne Null: N 1;2;3;4;5;... mit der Null: N 0 0;1;2;3;4;... Ganze Zahlen: Z... 3; 2; 1;0;1;2;3;.... 2. Die Rechenarten a)
Grundrechnungsarten mit Dezimalzahlen
 Grundrechnungsarten mit Dezimalzahlen Vorrangregeln Die Rechnungsarten zweiter Stufe haben Vorrang vor den Rechnungsarten erster Stufe. Man sagt: "Punktrechnung geht vor Strichrechnung" Treten in einer
Grundrechnungsarten mit Dezimalzahlen Vorrangregeln Die Rechnungsarten zweiter Stufe haben Vorrang vor den Rechnungsarten erster Stufe. Man sagt: "Punktrechnung geht vor Strichrechnung" Treten in einer
1 Rechnen. Addition rationaler Zahlen gleicher Vorzeichen Summand + Summand = Summe
 Rationale Zahlen Die ganzen Zahlen zusammen mit allen positiven und negativen Bruchzahlen heißen rationale Zahlen. Die Menge der rationalen Zahlen wird mit Q bezeichnet. Je weiter links eine Zahl auf dem
Rationale Zahlen Die ganzen Zahlen zusammen mit allen positiven und negativen Bruchzahlen heißen rationale Zahlen. Die Menge der rationalen Zahlen wird mit Q bezeichnet. Je weiter links eine Zahl auf dem
Kopfrechenphase Wo ist das A? vorne, links, oben. (vorne, rechts) 2. Was wurde markiert? Fünf von sechs Teilen sind farbig. Also fünf Sechstel
 Kopfrechenphase 1 1. Wo ist das A? vorne, links, oben (vorne, rechts) 2. Was wurde markiert? Fünf von sechs Teilen sind farbig. Also fünf Sechstel 3. Fehler gesucht! a) 1kg sind 1000g b) 1m hat 1000mm
Kopfrechenphase 1 1. Wo ist das A? vorne, links, oben (vorne, rechts) 2. Was wurde markiert? Fünf von sechs Teilen sind farbig. Also fünf Sechstel 3. Fehler gesucht! a) 1kg sind 1000g b) 1m hat 1000mm
 II. Die Addition und Subtraktion natürlicher Zahlen ================================================================= 2.1 Die Addition +2 0 1 2 3 4 5 6 Zählen wir von 3 um 2 weiter, dann schreiben wir
II. Die Addition und Subtraktion natürlicher Zahlen ================================================================= 2.1 Die Addition +2 0 1 2 3 4 5 6 Zählen wir von 3 um 2 weiter, dann schreiben wir
Vorrangregeln der Grundrechnungsarten
 Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 8 1. Semester ARBEITSBLATT 8 RECHNEN MIT POTENZEN. 1) Potenzen mit negativer Basis
 ARBEITSBLATT 8 RECHNEN MIT POTENZEN ) Potenzen mit negativer Basis Zur Erinnerung: = = 6 Der Eponent gibt also an, wie oft die Basis mit sich selbst multipliziert werden muss. Die Basis muss natürlich
ARBEITSBLATT 8 RECHNEN MIT POTENZEN ) Potenzen mit negativer Basis Zur Erinnerung: = = 6 Der Eponent gibt also an, wie oft die Basis mit sich selbst multipliziert werden muss. Die Basis muss natürlich
Marcus lernt zählen und rechnen mit zig
 Marcus lernt zählen und rechnen mit zig Thomas Colignatus 1 / Übersetzt von Stefan Rollnik 2 und TC 28. August, und 5. & 8. September 2015, und 4. Oktober 2018 Nutzungsbedingungen sind in A child wants
Marcus lernt zählen und rechnen mit zig Thomas Colignatus 1 / Übersetzt von Stefan Rollnik 2 und TC 28. August, und 5. & 8. September 2015, und 4. Oktober 2018 Nutzungsbedingungen sind in A child wants
2 ZAHLEN UND VARIABLE
 Zahlen und Variable 2 ZAHLEN UND VARIABLE 2.1 Grundlagen der Mengenlehre Unter einer Menge versteht man die Zusammenfassung von unterscheidbaren Objekten zu einem Ganzen. Diese Objekte bezeichnet man als
Zahlen und Variable 2 ZAHLEN UND VARIABLE 2.1 Grundlagen der Mengenlehre Unter einer Menge versteht man die Zusammenfassung von unterscheidbaren Objekten zu einem Ganzen. Diese Objekte bezeichnet man als
Natürliche Zahlen und. Zahlenstrahl
 M 5.1 Natürliche Zahlen und Zahlenstrahl Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: 1; 2; 3; 4; Nimmt man auch die 0 hinzu, schreibt man: 0; 1; 2; 3; 4; Zahlenstrahl Je weiter rechts eine Zahl
M 5.1 Natürliche Zahlen und Zahlenstrahl Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: 1; 2; 3; 4; Nimmt man auch die 0 hinzu, schreibt man: 0; 1; 2; 3; 4; Zahlenstrahl Je weiter rechts eine Zahl
Rechnen und Sachaufgaben. Mathe. Rechnen und Sachaufgaben. in 15 Minuten. 5. Klasse
 Rechnen und Sachaufgaben 5. Klasse Mathe Rechnen und Sachaufgaben in 15 Minuten Klasse Mathe Duden in 15 Minuten Rechnen und Sachaufgaben 5. Klasse 2., aktualisierte Auflage Dudenverlag Mannheim Zürich
Rechnen und Sachaufgaben 5. Klasse Mathe Rechnen und Sachaufgaben in 15 Minuten Klasse Mathe Duden in 15 Minuten Rechnen und Sachaufgaben 5. Klasse 2., aktualisierte Auflage Dudenverlag Mannheim Zürich
fwg Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: Zahlenstrahl
 M 5.1 Die Zahlen Nimmt man auch die Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: hinzu, schreibt man: Zahlenstrahl 0 1 2 3 4 5 6 7 8 Je weiter rechts eine Zahl auf dem Zahlenstrahl liegt,
M 5.1 Die Zahlen Nimmt man auch die Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: hinzu, schreibt man: Zahlenstrahl 0 1 2 3 4 5 6 7 8 Je weiter rechts eine Zahl auf dem Zahlenstrahl liegt,
Fachrechnen für die Feuerwehr
 Die Roten Hefte e, Bd. 31 Fachrechnen für die Feuerwehr Bearbeitet von Kurt Klingsohr überarbeitet 2007. Taschenbuch. 145 S. Paperback ISBN 978 3 17 019903 3 Format (B x L): 10,5 x 14,8 cm Gewicht: 100
Die Roten Hefte e, Bd. 31 Fachrechnen für die Feuerwehr Bearbeitet von Kurt Klingsohr überarbeitet 2007. Taschenbuch. 145 S. Paperback ISBN 978 3 17 019903 3 Format (B x L): 10,5 x 14,8 cm Gewicht: 100
Voransicht. Grundrechen Führerschein: Aufwärmtraining
 Grundrechen Führerschein: Aufwärmtraining Mit dieser Seite kannst du dich auf den Grundrechen Führerschein vorbereiten. 1 Additionspuzzle. Zerschneide das Bild rechts, rechne die Aufgabe links in deinem
Grundrechen Führerschein: Aufwärmtraining Mit dieser Seite kannst du dich auf den Grundrechen Führerschein vorbereiten. 1 Additionspuzzle. Zerschneide das Bild rechts, rechne die Aufgabe links in deinem
Stoffverteilungsplan Mathematik Klasse 5
 Stoffverteilungsplan Mathematik Klasse 5 Lehrwerk: Mathematik heute; Schroedel Zeitraum Themen/Inhalte Begriffe/Bemerkungen Lehrbuch/KA Leitidee/Kompetenzen Weitere Hinweise 6 Wochen Natürliche Zahlen
Stoffverteilungsplan Mathematik Klasse 5 Lehrwerk: Mathematik heute; Schroedel Zeitraum Themen/Inhalte Begriffe/Bemerkungen Lehrbuch/KA Leitidee/Kompetenzen Weitere Hinweise 6 Wochen Natürliche Zahlen
Mathematik 1 -Arbeitsblatt 1-8: Rechnen mit Potenzen. 1F Wintersemester 2012/2013 Unterlagen: LehrerInnenteam GFB. Potenzen mit negativer Basis
 Schule Thema Personen Bundesgymnasium für Berufstätige Salzburg Mathematik -Arbeitsblatt -8: Rechnen mit Potenzen F Wintersemester 0/0 Unterlagen: LehrerInnenteam GFB ) Potenzen mit negativer Basis Zur
Schule Thema Personen Bundesgymnasium für Berufstätige Salzburg Mathematik -Arbeitsblatt -8: Rechnen mit Potenzen F Wintersemester 0/0 Unterlagen: LehrerInnenteam GFB ) Potenzen mit negativer Basis Zur
Natürliche Zahlen und. Zahlenstrahl
 M 5.1 Die Zahlen Nimmt man auch die Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: hinzu, schreibt man: Zahlenstrahl Je weiter rechts eine Zahl auf dem Zahlenstrahl liegt, desto größer
M 5.1 Die Zahlen Nimmt man auch die Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: hinzu, schreibt man: Zahlenstrahl Je weiter rechts eine Zahl auf dem Zahlenstrahl liegt, desto größer
Umgekehrter Dreisatz Der umgekehrte Dreisatz ist ein Rechenverfahren, das man bei umgekehrt proportionalen Zuordnungen anwenden kann.
 Dreisatz Der Dreisatz ist ein Rechenverfahren, das man bei proportionalen Zuordnungen anwenden kann. 3 Tafeln Schokolade wiegen 5 g. Wie viel Gramm wiegen 5 Tafeln? 1. Satz: 3 Tafeln wiegen 5 g.. Satz:
Dreisatz Der Dreisatz ist ein Rechenverfahren, das man bei proportionalen Zuordnungen anwenden kann. 3 Tafeln Schokolade wiegen 5 g. Wie viel Gramm wiegen 5 Tafeln? 1. Satz: 3 Tafeln wiegen 5 g.. Satz:
3 heißt 1. Faktor und 4 heißt 2. Faktor. 12 heißt Wert des Produkts. Beispiele : a) 4 5 = = 20. b) 3 12 = = 36
 VI. Die Multiplikation und Division natürlicher Zahlen ================================================================= 6.1 Die Multiplikation 3 4 Wir schreiben 4 + 4 + 4 = 3 4 und damit ist 3 4 = 12.
VI. Die Multiplikation und Division natürlicher Zahlen ================================================================= 6.1 Die Multiplikation 3 4 Wir schreiben 4 + 4 + 4 = 3 4 und damit ist 3 4 = 12.
0. Wiederholung 0.1 Rechnen in der Menge der positiven rationalen Zahlen lq + 0
 0. Wiederholung 0.1 Rechnen in der Menge der positiven rationalen Zahlen lq + 0 0.1.1 Formveränderungen von Brüchen Erweitern heißt Zähler und Nenner eines Bruches mit derselben Zahl multiplizieren. a
0. Wiederholung 0.1 Rechnen in der Menge der positiven rationalen Zahlen lq + 0 0.1.1 Formveränderungen von Brüchen Erweitern heißt Zähler und Nenner eines Bruches mit derselben Zahl multiplizieren. a
Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse Seite 1
 Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse Seite 1 1. Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 2. Zehnerschritte bis 1000: Von wo bis wo? 3. Zehnerschritte bis 1000: Wo ist
Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse Seite 1 1. Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 2. Zehnerschritte bis 1000: Von wo bis wo? 3. Zehnerschritte bis 1000: Wo ist
Inhalt. Natürliche Zahlen. Rechnen mit natürlichen Zahlen. Bruchteile und Bruchzahlen
 Inhalt A Natürliche Zahlen 1 Anzahlen 6 2 Große Zahlen 7 3 Besondere natürliche Zahlen 9 4 Potenzen 10 5 Teiler und Vielfache 11 6 Primzahlen 13 7 Runden 14 8 Die römische Zahlschreibweise 15 9 Natürliche
Inhalt A Natürliche Zahlen 1 Anzahlen 6 2 Große Zahlen 7 3 Besondere natürliche Zahlen 9 4 Potenzen 10 5 Teiler und Vielfache 11 6 Primzahlen 13 7 Runden 14 8 Die römische Zahlschreibweise 15 9 Natürliche
M 5.1. Natürliche Zahlen und Zahlenstrahl sfg
 M 5.1. Natürliche Zahlen und Zahlenstrahl sfg Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: N = {1; 2; 3; 4; } Nimmt man auch die 0 hinzu, schreibt man: N 0 = {0; 1; 2; 3; 4; } Zahlenstrahl 0 1 2
M 5.1. Natürliche Zahlen und Zahlenstrahl sfg Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: N = {1; 2; 3; 4; } Nimmt man auch die 0 hinzu, schreibt man: N 0 = {0; 1; 2; 3; 4; } Zahlenstrahl 0 1 2
sfg Natürliche Zahlen und Zahlenstrahl Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: N = {1; 2; 3; 4; }
 M 5.1 Natürliche Zahlen und Zahlenstrahl Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: N = {1; 2; 3; 4; } Nimmt man auch die 0 hinzu, schreibt man: N 0 = {0; 1; 2; 3; 4; } Zahlenstrahl 0 1 2 3 4
M 5.1 Natürliche Zahlen und Zahlenstrahl Die Zahlen 1, 2, 3, 4, nennt man natürliche Zahlen: N = {1; 2; 3; 4; } Nimmt man auch die 0 hinzu, schreibt man: N 0 = {0; 1; 2; 3; 4; } Zahlenstrahl 0 1 2 3 4
Aufgabe 8: Runden, schriftliches Rechnen
 Schüler/in Aufgabe 8: Runden, schriftliches Rechnen LERNZIELE: Zahlen runden und Resultate schätzen Die schriftlichen Verfahren kennen Achte darauf: 1. Du hältst dich beim Runden an die Rundungsregel (Aufgabe
Schüler/in Aufgabe 8: Runden, schriftliches Rechnen LERNZIELE: Zahlen runden und Resultate schätzen Die schriftlichen Verfahren kennen Achte darauf: 1. Du hältst dich beim Runden an die Rundungsregel (Aufgabe
Verstehst du die Sprache der Mathematik? Arbeitsblatt 1
 Verstehst du die Sprache der Mathematik? Arbeitsblatt 1 1. Erstelle für folgende Aufgabe einen Term: Die Rechnung ist nicht verlangt. Subtrahiere von der Summe der Zahlen 987 und 654 die Differenz der
Verstehst du die Sprache der Mathematik? Arbeitsblatt 1 1. Erstelle für folgende Aufgabe einen Term: Die Rechnung ist nicht verlangt. Subtrahiere von der Summe der Zahlen 987 und 654 die Differenz der
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 5 1. Semester ARBEITSBLATT 5 RECHNEN MIT BRÜCHEN. 1. Arten von Brüchen und Definition
 ARBEITSBLATT 5 RECHNEN MIT BRÜCHEN 1. Arten von Brüchen und Definition Beispiel: 3 5 Zähler Bruchstrich Nenner Definition: Jeder Bruch hat folgendes Aussehen: Zähler. Der Nenner gibt an, Nenner in wie
ARBEITSBLATT 5 RECHNEN MIT BRÜCHEN 1. Arten von Brüchen und Definition Beispiel: 3 5 Zähler Bruchstrich Nenner Definition: Jeder Bruch hat folgendes Aussehen: Zähler. Der Nenner gibt an, Nenner in wie
Grundwissen. 5. Jahrgangsstufe. Mathematik
 Grundwissen 5. Jahrgangsstufe Mathematik Grundwissen Mathematik 5. Jahrgangsstufe Seite 1 1 Natürliche Zahlen 1.1 Große Zahlen und Zehnerpotenzen eine Million = 1 000 000 = 10 6 eine Milliarde = 1 000
Grundwissen 5. Jahrgangsstufe Mathematik Grundwissen Mathematik 5. Jahrgangsstufe Seite 1 1 Natürliche Zahlen 1.1 Große Zahlen und Zehnerpotenzen eine Million = 1 000 000 = 10 6 eine Milliarde = 1 000
Merkstoff Mathematik: 5. Schulstufe, NMS Schörfling
 Merkstoff Mathematik: 5. Schulstufe Seite 2 Seite 3 Seite 4 Seite 5 Seite 6 Seite 7 Seite 8 Seite 9 Seite 0 Seite Seite 2 Seite 3 Seite 4 Zählen und Vergleichen von natürlichen Zahlen Darstellen von natürlichen
Merkstoff Mathematik: 5. Schulstufe Seite 2 Seite 3 Seite 4 Seite 5 Seite 6 Seite 7 Seite 8 Seite 9 Seite 0 Seite Seite 2 Seite 3 Seite 4 Zählen und Vergleichen von natürlichen Zahlen Darstellen von natürlichen
Mathematik 1 -Arbeitsblatt 1-4: Rechnen mit Brüchen. 1F Wintersemester 2012/2013 Unterlagen: LehrerInnenteam GFB RECHNEN MIT BRÜCHEN
 RECHNEN MIT BRÜCHEN. Arten von Brüchen und Definition Beispiel: 3 5 Zähler Bruchstrich Nenner Definition: Jeder Bruch hat folgendes Aussehen: Zähler Nenner. Der Nenner gibt an, in wie viele gleich große
RECHNEN MIT BRÜCHEN. Arten von Brüchen und Definition Beispiel: 3 5 Zähler Bruchstrich Nenner Definition: Jeder Bruch hat folgendes Aussehen: Zähler Nenner. Der Nenner gibt an, in wie viele gleich große
Bruchrechnen. 2.1 Teilbarkeit von Zahlen. Die Primfaktorzerlegung ist die Zerlegung einer natürlichen Zahl in ein Produkt von Primzahlen.
 ruchrechnen 2 2.1 Teilbarkeit von Zahlen Die Primfaktorzerlegung ist die Zerlegung einer natürlichen Zahl in ein Produkt von Primzahlen. Das kleinste gemeinsame Vielfache (kgv) mehrerer Zahlen ist die
ruchrechnen 2 2.1 Teilbarkeit von Zahlen Die Primfaktorzerlegung ist die Zerlegung einer natürlichen Zahl in ein Produkt von Primzahlen. Das kleinste gemeinsame Vielfache (kgv) mehrerer Zahlen ist die
Natürliche Zahlen und. Zahlenstrahl
 M 5.1 Natürliche Zahlen und Zahlenstrahl Die Zahlen fasst man zur Menge der natürlichen Zahlen zusammen: Nimmt man auch die hinzu, schreibt man: Die Zahl ist ein Element der Menge der natürlichen Zahlen
M 5.1 Natürliche Zahlen und Zahlenstrahl Die Zahlen fasst man zur Menge der natürlichen Zahlen zusammen: Nimmt man auch die hinzu, schreibt man: Die Zahl ist ein Element der Menge der natürlichen Zahlen
Addition und Subtraktion Addieren heißt zusammenzählen, plus rechnen oder die Summe bilden.
 1 Grundwissen Rechenarten Addition und Subtraktion Addieren heißt zusammenzählen, plus rechnen oder die Summe bilden. 418 + 2 987 = 3 405 + 2 987 418 Umkehraufgabe 3 405 Summe Ergebnis der Summe 2 987
1 Grundwissen Rechenarten Addition und Subtraktion Addieren heißt zusammenzählen, plus rechnen oder die Summe bilden. 418 + 2 987 = 3 405 + 2 987 418 Umkehraufgabe 3 405 Summe Ergebnis der Summe 2 987
1.Weiterentwicklung der Zahlvorstellung 1.1Die natürlichen Zahlen Mengenschreibweise: N = {1,2,3,...} N 0 = {0,1,2,3,...}
 1 Grundwissen Mathematik 5.Klasse Gymnasium SOB 1.Weiterentwicklung der Zahlvorstellung 1.1Die natürlichen Zahlen Mengenschreibweise: N = {1,2,3,...} N 0 = {0,1,2,3,...} Darstellung am Zahlenstrahl: Darstellung
1 Grundwissen Mathematik 5.Klasse Gymnasium SOB 1.Weiterentwicklung der Zahlvorstellung 1.1Die natürlichen Zahlen Mengenschreibweise: N = {1,2,3,...} N 0 = {0,1,2,3,...} Darstellung am Zahlenstrahl: Darstellung
b) Notieren Sie hier die Brüche aus der Tabelle, die sich noch kürzen lassen und kürzen Sie diese soweit als möglich: 1 2
 Addieren und Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen; Zähler subtrahieren. Füllen Sie die
Addieren und Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen; Zähler subtrahieren. Füllen Sie die
Zähler mal Zähler, Nenner mal Nenner
 Mathematik Klasse 6 Übersicht über die Bruchrechnung..20 1.) Pflichtbereich So viele Regeln zum Bruchrechnen, da kann man leicht schnell etwas durcheinander bringen! Das muss nicht sein: Verschaffe Dir
Mathematik Klasse 6 Übersicht über die Bruchrechnung..20 1.) Pflichtbereich So viele Regeln zum Bruchrechnen, da kann man leicht schnell etwas durcheinander bringen! Das muss nicht sein: Verschaffe Dir
1. Mathematik-Schularbeit, Name:. 1a) Gib den Vorgänger und Nachfolger folgender Zahl an!
 1. Mathematik-Schularbeit, Name:. am 13. 11. 2013 Klasse: 1. 1a) Gib den Vorgänger und Nachfolger folgender Zahl an! 4 532 2 399 1b) Stelle die folgende Zahlen am Zahlenstrahl dar. Setze ein Kreuz an die
1. Mathematik-Schularbeit, Name:. am 13. 11. 2013 Klasse: 1. 1a) Gib den Vorgänger und Nachfolger folgender Zahl an! 4 532 2 399 1b) Stelle die folgende Zahlen am Zahlenstrahl dar. Setze ein Kreuz an die
Beschreibung Prüfziffer Errechnung der Beitragskontonummer für BGKK
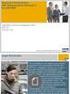 Beschreibung Prüfziffer Errechnung der Beitragskontonummer für BGKK Die Beitragskontonummer besteht aus einem 6-stelligen numerischen Begriff und einer Prüfziffer Die Prüfziffer wird auf folgende Art berechnet:
Beschreibung Prüfziffer Errechnung der Beitragskontonummer für BGKK Die Beitragskontonummer besteht aus einem 6-stelligen numerischen Begriff und einer Prüfziffer Die Prüfziffer wird auf folgende Art berechnet:
Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender?
 Arbeit mit der gelegten Zahl Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender? Wie heißen Nachbarzehntausender? Wie heißen die Nachbarzahlen?
Arbeit mit der gelegten Zahl Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender? Wie heißen Nachbarzehntausender? Wie heißen die Nachbarzahlen?
Marie Kilders. Grundwissen Klasse 5
 Grundwissen Klasse 5 1 Inhaltsverzeichnis 1. Natürliche und ganze Zahlen... 3 1.1 Dezimalsystem (Zehnersystem)... 4 1.2 Rechnen mit natürlichen Zahlen... 5 1.3 Diagramme... 8 1.4 Primfaktorzerlegung und
Grundwissen Klasse 5 1 Inhaltsverzeichnis 1. Natürliche und ganze Zahlen... 3 1.1 Dezimalsystem (Zehnersystem)... 4 1.2 Rechnen mit natürlichen Zahlen... 5 1.3 Diagramme... 8 1.4 Primfaktorzerlegung und
Lösungen zu den Tests 119 Stichwortverzeichnis 127. Lösungen zu den Übungen 78
 Inhalt 1 Anordnung der Zahlen am Zahlenstrahl 6 2 Große Zahlen 8 3 Runden 10 4 Stellenwertsysteme 12 5 Umrechnungen zwischen Zweier- und Zehnersystem 14 6 Addieren und Subtrahieren 16 7 Schriftliches Addieren
Inhalt 1 Anordnung der Zahlen am Zahlenstrahl 6 2 Große Zahlen 8 3 Runden 10 4 Stellenwertsysteme 12 5 Umrechnungen zwischen Zweier- und Zehnersystem 14 6 Addieren und Subtrahieren 16 7 Schriftliches Addieren
Inhaltsverzeichnis. Brüche Erweitern und Kürzen Bruchzahlen Rechnen mit Brüchen Dezimalzahlen Abbrechende und periodische Dezimalzahlen
 Inhaltsverzeichnis Große Zahlen und Stellentafel Vergleichen von Zahlen Runden von Zahlen Größen / Einheiten Die natürlichen Zahlen Addition Subtraktion Rechengesetze der Addition Multiplikation Division
Inhaltsverzeichnis Große Zahlen und Stellentafel Vergleichen von Zahlen Runden von Zahlen Größen / Einheiten Die natürlichen Zahlen Addition Subtraktion Rechengesetze der Addition Multiplikation Division
1. Füttere den Rechenwurm nacheinander mit den Zahlen 2, 4, 8, 3, 6, 5, 10, 7 und 9. : 6 : 4
 Terme und Gleichungen G NIVEAU 1. WIEDERHOLUNG DER GRUNDRECHENARTEN 1. Füttere den Rechenwurm nacheinander mit den Zahlen 2, 4, 8, 3, 6, 5, 10, 7 und 9. 8 : 4 3 : 6 : 5 3 10 : 6 7 = 2. Berechne im Heft
Terme und Gleichungen G NIVEAU 1. WIEDERHOLUNG DER GRUNDRECHENARTEN 1. Füttere den Rechenwurm nacheinander mit den Zahlen 2, 4, 8, 3, 6, 5, 10, 7 und 9. 8 : 4 3 : 6 : 5 3 10 : 6 7 = 2. Berechne im Heft
Zahlen und Operationen Grundaufgaben der Multiplikation und Division auf
 Zahlen und Operationen Grundaufgaben der Multiplikation und Division auf analoge Aufgaben im erweiterten Zahlenraum übertragen, Gesetzmäßigkeiten sowie Regeln erkennen und zur Lösung nutzen Inhaltsbezogene
Zahlen und Operationen Grundaufgaben der Multiplikation und Division auf analoge Aufgaben im erweiterten Zahlenraum übertragen, Gesetzmäßigkeiten sowie Regeln erkennen und zur Lösung nutzen Inhaltsbezogene
Natürliche Zahlen und. Zahlenstrahl
 M 5.1 Die Zahlen Nimmt man auch die Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: hinzu, schreibt man: Zahlenstrahl Je weiter rechts eine Zahl auf dem Zahlenstrahl liegt, desto größer
M 5.1 Die Zahlen Nimmt man auch die Natürliche Zahlen und Zahlenstrahl nennt man natürliche Zahlen: hinzu, schreibt man: Zahlenstrahl Je weiter rechts eine Zahl auf dem Zahlenstrahl liegt, desto größer
Negative Zahlen. Lösung: Ordne in einen Zahlenstrahl ein! 7;5; 3; 6. Das Dezimalsystem
 Negative Zahlen Negative Zahlen Ordne in einen Zahlenstrahl ein! 7;5; 3; 6 Das Dezimalsystem Zerlege in Stufen! Einer, Zehner, usw. a) 3.185.629 b) 24.045.376 c) 3.010.500.700 Das Dezimalsystem a) 3M 1HT
Negative Zahlen Negative Zahlen Ordne in einen Zahlenstrahl ein! 7;5; 3; 6 Das Dezimalsystem Zerlege in Stufen! Einer, Zehner, usw. a) 3.185.629 b) 24.045.376 c) 3.010.500.700 Das Dezimalsystem a) 3M 1HT
Vorrangregeln der Grundrechnungsarten
 Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Dezimalbrüche Dezimalzahlen für Gymnasiasten
 Dezimalbrüche Dezimalzahlen für Gymnasiasten Arbeitsblatt 1 1. Berechne: Runde das Ergebnis auf Zehntel. a) 4,22 + 8,751 = b) 924,68 (198,6 + 41,47) 8,82 = 2. Berechne: a) 10000 0,0025 = b) 45 0,2 = c)
Dezimalbrüche Dezimalzahlen für Gymnasiasten Arbeitsblatt 1 1. Berechne: Runde das Ergebnis auf Zehntel. a) 4,22 + 8,751 = b) 924,68 (198,6 + 41,47) 8,82 = 2. Berechne: a) 10000 0,0025 = b) 45 0,2 = c)
Lernzirkel Grundrechenarten und Terme Mathematik Nikolaus-von-Kues-Gymnasium Fachlehrer : W. Zimmer Blatt 1 /18. a + b = c
 Mathematik Nikolaus-von-Kues-Gymnasium Fachlehrer : W. Zimmer Blatt 1 /18 Station 1 Addition (lat. addere = dazutun) 1.1 Wie lauten die korrekten Bezeichnungen? a + b = c 1.2 Addiere schriftlich 3 5 6
Mathematik Nikolaus-von-Kues-Gymnasium Fachlehrer : W. Zimmer Blatt 1 /18 Station 1 Addition (lat. addere = dazutun) 1.1 Wie lauten die korrekten Bezeichnungen? a + b = c 1.2 Addiere schriftlich 3 5 6
GW Mathematik 5. Klasse
 Begriffe zur Gliederung von Termen Term Rechenart a heißt b heißt a + b (Summe) Addition 1. Summand 2. Summand a b (Differenz) Subtraktion Minuend Subtrahend a b ( Produkt) Multiplikation 1. Faktor 2.
Begriffe zur Gliederung von Termen Term Rechenart a heißt b heißt a + b (Summe) Addition 1. Summand 2. Summand a b (Differenz) Subtraktion Minuend Subtrahend a b ( Produkt) Multiplikation 1. Faktor 2.
1 Grundwissen 6 2 Dezimalbrüche (Dezimalzahlen) 9 3 Brüche 11 4 Rationale Zahlen 16 5 Potenzen und Wurzeln 20 6 Größen und Schätzen 24
 Inhalt A Grundrechenarten Grundwissen 6 Dezimalbrüche (Dezimalzahlen) 9 Brüche Rationale Zahlen 6 5 Potenzen und Wurzeln 0 6 Größen und Schätzen B Zuordnungen Proportionale Zuordnungen 8 Umgekehrt proportionale
Inhalt A Grundrechenarten Grundwissen 6 Dezimalbrüche (Dezimalzahlen) 9 Brüche Rationale Zahlen 6 5 Potenzen und Wurzeln 0 6 Größen und Schätzen B Zuordnungen Proportionale Zuordnungen 8 Umgekehrt proportionale
5. 7. Brüche und Dezimalzahlen. Mathematik. Das 3-fache Training für bessere Noten: Klasse. Klasse
 Das 3-fache Training für bessere Noten: WISSEN ÜBEN TESTEN Die wichtigsten Regeln zum Thema Brüche und Dezimalzahlen mit passenden Beispielen verständlich erklärt Zahlreiche Übungsaufgaben in drei Schwierigkeitsstufen
Das 3-fache Training für bessere Noten: WISSEN ÜBEN TESTEN Die wichtigsten Regeln zum Thema Brüche und Dezimalzahlen mit passenden Beispielen verständlich erklärt Zahlreiche Übungsaufgaben in drei Schwierigkeitsstufen
Addition und Subtraktion natürlicher Zahlen
 0 Minuten Addition und Subtraktion natürlicher Zahlen Kurztest : Addieren und Subtrahieren 1 Bei der linken Rechenmauer wird nach oben addiert, bei der rechten Rechenmauer nach oben subtrahiert. a) b)
0 Minuten Addition und Subtraktion natürlicher Zahlen Kurztest : Addieren und Subtrahieren 1 Bei der linken Rechenmauer wird nach oben addiert, bei der rechten Rechenmauer nach oben subtrahiert. a) b)
Bruchrechnen ohne Variablen Anwendungen 11
 Bruchrechnen ohne Variablen Anwendungen Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Bruchrechnen ohne Variablen Anwendungen Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Orientieren im Zahlenraum bis 1 Million
 Inhalt A Orientieren im Zahlenraum bis 1 Million 1 Stellentafel und Zahlenstrahl 6 2 Nachbarzahlen und Runden 8 3 Anordnen 10 B Addieren und Subtrahieren 1 Mündliches Addieren und Subtrahieren 12 2 Schriftliches
Inhalt A Orientieren im Zahlenraum bis 1 Million 1 Stellentafel und Zahlenstrahl 6 2 Nachbarzahlen und Runden 8 3 Anordnen 10 B Addieren und Subtrahieren 1 Mündliches Addieren und Subtrahieren 12 2 Schriftliches
Mathematik-Aufgabenpool > Grundrechnen mit Dezimalzahlen
 Michael Buhlmann Mathematik-Aufgabenpool > Grundrechnen mit Dezimalzahlen Einleitung: Dezimalzahlen (Dezimalbrüch sind (rational Zahlen von der Form Vorkommastellen-Komma- Nachkommastellen. Gerechnet wird
Michael Buhlmann Mathematik-Aufgabenpool > Grundrechnen mit Dezimalzahlen Einleitung: Dezimalzahlen (Dezimalbrüch sind (rational Zahlen von der Form Vorkommastellen-Komma- Nachkommastellen. Gerechnet wird
Bruchrechnen ohne Variablen Anwendungen 11 - Lösungen
 Bruchrechnen ohne Variablen Anwendungen - Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Bruchrechnen ohne Variablen Anwendungen - Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Lernzirkel Grundrechenarten und Terme Mathematik Cusanus-Gymnasium Wittlich Fachlehrer : W. Zimmer Blatt 1 /21
 Mathematik Cusanus-Gymnasium Wittlich Fachlehrer : W. Zimmer Blatt 1 /21 Station 1 Addition (lat. addere = dazutun) 1.1 Wie lauten die korrekten Bezeichnungen? a + b = c 1.2 Addiere schriftlich 3 5 6 8
Mathematik Cusanus-Gymnasium Wittlich Fachlehrer : W. Zimmer Blatt 1 /21 Station 1 Addition (lat. addere = dazutun) 1.1 Wie lauten die korrekten Bezeichnungen? a + b = c 1.2 Addiere schriftlich 3 5 6 8
= Rechne nach - das Ergebnis ist immer 1!
 Was ist ein Bruch? Bisher kennst du genau eine Art der Zahlen, die sogenannten "Natürlichen Zahlen". Unter den Natürlichen Zahlen versteht man die Zahlen 0, 1,,,... bis Unendlich. Mit diesen Zahlen lassen
Was ist ein Bruch? Bisher kennst du genau eine Art der Zahlen, die sogenannten "Natürlichen Zahlen". Unter den Natürlichen Zahlen versteht man die Zahlen 0, 1,,,... bis Unendlich. Mit diesen Zahlen lassen
M1 2a b Ko Potenzen Regeln/Gesetze 2.Teil bis Buch I S. 51 / II S. 43 / III S. 37
 M1 2a b Ko Potenzen Regeln/Gesetze 2.Teil bis Buch I S. 51 / II S. 43 / III S. 37 Dieses Blatt soll ohne TR-Einsatz gelöst werden. Da aber viele Schüler in den unteren Niveaus oft nicht einmal das Einmaleins
M1 2a b Ko Potenzen Regeln/Gesetze 2.Teil bis Buch I S. 51 / II S. 43 / III S. 37 Dieses Blatt soll ohne TR-Einsatz gelöst werden. Da aber viele Schüler in den unteren Niveaus oft nicht einmal das Einmaleins
Grundwissen Seite 1 von 11 Klasse5
 Grundwissen Seite 1 von 11 Klasse5 IN = {1; 2; 3; 4; 5; 6; } Menge der natürlichen Zahlen Beispiele: 5 ist eine natürliche Zahl kurz: 5 IN 5 ist ein Element von IN Natürliche Zahlen -2 ist keine natürliche
Grundwissen Seite 1 von 11 Klasse5 IN = {1; 2; 3; 4; 5; 6; } Menge der natürlichen Zahlen Beispiele: 5 ist eine natürliche Zahl kurz: 5 IN 5 ist ein Element von IN Natürliche Zahlen -2 ist keine natürliche
Grundwissenskatalog der 6. Jahrgangsstufe G8 - Mathematik Friedrich-Koenig-Gymnasium Würzburg
 Grundwissenskatalog der. Jahrgangsstufe G8 - Mathematik Friedrich-Koenig-Gymnasium Würzburg. Brüche und Dezimalzahlen Bruchteile Berechnung von Bruchteilen Bruchzahlen als Quotient Gemischte Zahlen Erweitern
Grundwissenskatalog der. Jahrgangsstufe G8 - Mathematik Friedrich-Koenig-Gymnasium Würzburg. Brüche und Dezimalzahlen Bruchteile Berechnung von Bruchteilen Bruchzahlen als Quotient Gemischte Zahlen Erweitern
ALGEBRA Lineare Gleichungen Teil 1. Klasse 8. Datei Nr Friedrich W. Buckel. Dezember 2005 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
 ALGEBRA Lineare Gleichungen Teil Klasse 8 Lineare Gleichungen mit einer Variablen Datei Nr. 40 Friedrich W. Buckel Dezember 005 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Inhalt DATEI 40 Grundlagen und ein
ALGEBRA Lineare Gleichungen Teil Klasse 8 Lineare Gleichungen mit einer Variablen Datei Nr. 40 Friedrich W. Buckel Dezember 005 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Inhalt DATEI 40 Grundlagen und ein
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lernzirkel Grundrechenarten - Übungen. Das komplette Material finden Sie hier:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernzirkel Grundrechenarten - Übungen Das komplette Material finden Sie hier: School-Scout.de Lernzirkel: inhaltlicher Aufbau Lernzirkel
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernzirkel Grundrechenarten - Übungen Das komplette Material finden Sie hier: School-Scout.de Lernzirkel: inhaltlicher Aufbau Lernzirkel
Schulinternes Fachcurriculum im Fach Mathematik Klasse 5
 Durch den Einsatz des gesamten Spektrums der neuen Aufgabenformate werden stets möglichst viele der geforderten Kompetenzbereiche K1 bis 1 der Rahmenbedingungen abgedeckt. Diesen sechs Kompetenzbereichen
Durch den Einsatz des gesamten Spektrums der neuen Aufgabenformate werden stets möglichst viele der geforderten Kompetenzbereiche K1 bis 1 der Rahmenbedingungen abgedeckt. Diesen sechs Kompetenzbereichen
Mathe Leuchtturm Übungsleuchtturm
 1 Mathe Leuchtturm-Übungen-3.&UE-Klasse-Nr.010-Tetgleichungen C by Joh Zerbs Mathe Leuchtturm Übungsleuchtturm 010 =Übungskapitel Ein Einstieg zum Kapitelblock Terme, Formeln und Gleichungen Erforderlicher
1 Mathe Leuchtturm-Übungen-3.&UE-Klasse-Nr.010-Tetgleichungen C by Joh Zerbs Mathe Leuchtturm Übungsleuchtturm 010 =Übungskapitel Ein Einstieg zum Kapitelblock Terme, Formeln und Gleichungen Erforderlicher
3.3 Lösungsstrategien für mündliches und halbschriftliches Rechnen Halbschriftliche Addition und Subtraktion
 3.3 Lösungsstrategien für mündliches und halbschriftliches Rechnen 3.3.1 Halbschriftliche Addition und Subtraktion 3.3.2 Halbschriftliche Multiplikation und Division Rahmenplan Rahmenplan Hessen S. 154:
3.3 Lösungsstrategien für mündliches und halbschriftliches Rechnen 3.3.1 Halbschriftliche Addition und Subtraktion 3.3.2 Halbschriftliche Multiplikation und Division Rahmenplan Rahmenplan Hessen S. 154:
Mathematik. Begriffe und Aufgaben
 Mathematik Begriffe und Zahlen Zahlen, Ziffern und Stellenwerte Definitionen Zahlen Zahlen, Ziffern und Stellenwerte Begriff Erklärung/Definition Beispiele Ziffern sind die Bausteine der Zahlenschreibweise
Mathematik Begriffe und Zahlen Zahlen, Ziffern und Stellenwerte Definitionen Zahlen Zahlen, Ziffern und Stellenwerte Begriff Erklärung/Definition Beispiele Ziffern sind die Bausteine der Zahlenschreibweise
Begriffe zur Gliederung von Termen, Potenzen 5
 Begriffe zur Gliederung von Termen, Potenzen 5 Begriffe zur Gliederung von Termen Term Rechenart Termbezeichnung a heißt b heißt a + b Addition Summe 1. Summand 2. Summand a b Subtraktion Differenz Minuend
Begriffe zur Gliederung von Termen, Potenzen 5 Begriffe zur Gliederung von Termen Term Rechenart Termbezeichnung a heißt b heißt a + b Addition Summe 1. Summand 2. Summand a b Subtraktion Differenz Minuend
7 Zehner-Packungen 70 Eier. 6 Zehner-Packungen 60 Eier. 5 Zehner-Packungen 50 Eier. 10 Einer = 1 Zehner. Name: Kreise immer 10 Würfel ein.
 Kreise immer 10 Würfel ein. Male sie mit der gleichen Farbe an. 10 Einer = 1 Zehner Wie viele Zehner-Packungen Eier liegen auf dem Tisch? Wie viele Eier sind das? 7 Zehner-Packungen Eier 5 Zehner-Packungen
Kreise immer 10 Würfel ein. Male sie mit der gleichen Farbe an. 10 Einer = 1 Zehner Wie viele Zehner-Packungen Eier liegen auf dem Tisch? Wie viele Eier sind das? 7 Zehner-Packungen Eier 5 Zehner-Packungen
A1 Aufbau des Zahlensystems
 ; Beherrschung der Grundrechenarten Grundbegriffe der Mengenlehre Von den Zeichen e, f, g, 2, %, k, #, s, r, können nicht alle sinnvoll zusammengefasst werden. Dagegen bilden e, f, g, k, s, r eine Menge
; Beherrschung der Grundrechenarten Grundbegriffe der Mengenlehre Von den Zeichen e, f, g, 2, %, k, #, s, r, können nicht alle sinnvoll zusammengefasst werden. Dagegen bilden e, f, g, k, s, r eine Menge
Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse
 Seite 1 Turmzimmer 1: Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 7. Hunderterschritte bis 10000: Wo ist die Zahl? 2. Zehnerschritte bis 1000: Von wo bis wo? 8. Hunderterschritte bis
Seite 1 Turmzimmer 1: Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 7. Hunderterschritte bis 10000: Wo ist die Zahl? 2. Zehnerschritte bis 1000: Von wo bis wo? 8. Hunderterschritte bis
Das kleine Lesebuch vom Rechnen für die Berufsvorbereitung
 Paul Koop: Das kleine Lesebuch vom Rechnen für die Berufsvorbereitung Seite Inhaltsverzeichnis: Das Dezimalsystem... Das Zählen... Das Zusammenzählen und Abziehen natürlicher Zahlen... Das Addieren natürlicher
Paul Koop: Das kleine Lesebuch vom Rechnen für die Berufsvorbereitung Seite Inhaltsverzeichnis: Das Dezimalsystem... Das Zählen... Das Zusammenzählen und Abziehen natürlicher Zahlen... Das Addieren natürlicher
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 1. Semester ARBEITSBLATT 6 VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q
 ARBEITSBLATT 6 VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q Dieser Punkt fällt in der Erklärung besonders leicht. Zusammengefasst kann man sagen, dass alles beim Alten bleibt. Es bleiben also sämtliche
ARBEITSBLATT 6 VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q Dieser Punkt fällt in der Erklärung besonders leicht. Zusammengefasst kann man sagen, dass alles beim Alten bleibt. Es bleiben also sämtliche
Deutsch. a hoch 3. a zum Quadrat. acht. achtzig. dividiert. drei. dreißig. dreizehn
 Deutsch Deutsch Plural a hoch 3 a zum Quadrat acht achtzig Addition, die Ar, das Basis, die Betrag von a, der Binom, das Bruch, der Bruchstrich, der Deckfläche, die Dekagramm, das Deltoid, das Dezimalbruch,
Deutsch Deutsch Plural a hoch 3 a zum Quadrat acht achtzig Addition, die Ar, das Basis, die Betrag von a, der Binom, das Bruch, der Bruchstrich, der Deckfläche, die Dekagramm, das Deltoid, das Dezimalbruch,
Mathematik-Dossier 2 Die Welt der natürlichen Zahlen Teil A (angepasst an das Lehrmittel Mathematik 1)
 Name: Mathematik-Dossier 2 Die Welt der natürlichen Zahlen Teil A (angepasst an das Lehrmittel Mathematik 1) Inhalt: Themenbereich 2a (Potenzen/Regeln und Gesetze) Die erste Stufe der Operationen: Addition
Name: Mathematik-Dossier 2 Die Welt der natürlichen Zahlen Teil A (angepasst an das Lehrmittel Mathematik 1) Inhalt: Themenbereich 2a (Potenzen/Regeln und Gesetze) Die erste Stufe der Operationen: Addition
Münchner Volkshochschule. Planung. Tag 02
 Planung Tag 02 Prof.Dr. Nils Mahnke Mathematischer Vorkurs Folie: 45 Mengenlehre VII Mengenoperationen: 1) Vereinigungsmenge: A B { x x A x B} 2) Schnittmenge: A 3) Differenzmenge: B { x x A x B} A \ B
Planung Tag 02 Prof.Dr. Nils Mahnke Mathematischer Vorkurs Folie: 45 Mengenlehre VII Mengenoperationen: 1) Vereinigungsmenge: A B { x x A x B} 2) Schnittmenge: A 3) Differenzmenge: B { x x A x B} A \ B
32 Die schriftliche Subtraktion
 Die schriftliche Subtraktion Lösungen von S. Einer 8 = Zehner 6 = Hunderter 4 = Tausender = Dem Herrn Scharfblick bleiben, für s Sparbuch. Wer rechnet, muss sich auch verständlich machen können: Der Fachausdruck
Die schriftliche Subtraktion Lösungen von S. Einer 8 = Zehner 6 = Hunderter 4 = Tausender = Dem Herrn Scharfblick bleiben, für s Sparbuch. Wer rechnet, muss sich auch verständlich machen können: Der Fachausdruck
2.Vorlesung Grundlagen der Informatik
 Christian Baun 2.Vorlesung Grundlagen der Informatik Hochschule Darmstadt WS1112 1/16 2.Vorlesung Grundlagen der Informatik Christian Baun Hochschule Darmstadt Fachbereich Informatik christian.baun@h-da.de
Christian Baun 2.Vorlesung Grundlagen der Informatik Hochschule Darmstadt WS1112 1/16 2.Vorlesung Grundlagen der Informatik Christian Baun Hochschule Darmstadt Fachbereich Informatik christian.baun@h-da.de
Umfang und Fläche von Rechtecken
 Umfang und Fläche von Rechtecken Herbert Paukert 1 Umfang und Fläche von Rechtecken Version 2.0 Herbert Paukert (1) Der Umfang von Rechtecken [02] Elemente der Geometrie [02] Fünf Übungsaufgaben [08] Das
Umfang und Fläche von Rechtecken Herbert Paukert 1 Umfang und Fläche von Rechtecken Version 2.0 Herbert Paukert (1) Der Umfang von Rechtecken [02] Elemente der Geometrie [02] Fünf Übungsaufgaben [08] Das
4.1 Teiler und Vielfache Primzahlen Primfaktorzerlegung Potenzen kgv und ggt Abschlusstest...
 Inhalt 1 Die natürlichen Zahlen 1.1 Der Zahlbegriff........................................... 6 1.2 Das Zehnersystem........................................ 7 1.3 Andere Stellenwertsysteme..................................
Inhalt 1 Die natürlichen Zahlen 1.1 Der Zahlbegriff........................................... 6 1.2 Das Zehnersystem........................................ 7 1.3 Andere Stellenwertsysteme..................................
1 Basiswissen aus der Sekundarstufe 1
 1 Basiswissen aus der Sekundarstufe 1 Check-in Methode M1 Finde den Fehler und erkläre, wie du vorgehst! Stelle das Beispiel richtig! 3 569,22 278,18 3 391,14 So rechne ich: Meine Erklärung: M2 So verschiebe
1 Basiswissen aus der Sekundarstufe 1 Check-in Methode M1 Finde den Fehler und erkläre, wie du vorgehst! Stelle das Beispiel richtig! 3 569,22 278,18 3 391,14 So rechne ich: Meine Erklärung: M2 So verschiebe
Rechnen mit natürlichen Zahlen 2
 . Rechnen mit natürlichen Zahlen L E R N - U N D A U F G A B E N P L A N Zum Gebrauch dieses Plans Hier wird kurz beschrieben, was im Unterricht gemacht wird und welche Aufgaben zu erledigen sind. Diese
. Rechnen mit natürlichen Zahlen L E R N - U N D A U F G A B E N P L A N Zum Gebrauch dieses Plans Hier wird kurz beschrieben, was im Unterricht gemacht wird und welche Aufgaben zu erledigen sind. Diese
Der Nenner eines Bruchs darf nie gleich 0 sein! Der Zähler eines Bruchs kann dagegen auch 0 sein. Dies besagt, dass kein Teil zu nehmen ist.
 Bruchteile Bruchteile von Ganzen lassen sich mit Hilfe von Brüchen angeben. Der Nenner gibt an, in wie viele gleiche Teile ein Ganzes zerlegt wird. Der Zähler gibt an, wie viele dieser gleichen Teile zu
Bruchteile Bruchteile von Ganzen lassen sich mit Hilfe von Brüchen angeben. Der Nenner gibt an, in wie viele gleiche Teile ein Ganzes zerlegt wird. Der Zähler gibt an, wie viele dieser gleichen Teile zu
Fragen und Aufgaben zum Grundwissen Mathematik
 Natürliche Zahlen Kapitel I ZÄHLEN UND ORDNEN GROßE ZAHLEN UND ZEHNERPOTENZEN Acht Schwimmer bestreiten einen Wettkampf. Miriam gewinnt die Bronzemedaille. Franz wird Vorletzter. Welche Platzierung haben
Natürliche Zahlen Kapitel I ZÄHLEN UND ORDNEN GROßE ZAHLEN UND ZEHNERPOTENZEN Acht Schwimmer bestreiten einen Wettkampf. Miriam gewinnt die Bronzemedaille. Franz wird Vorletzter. Welche Platzierung haben
5 25 Radizieren 25 5 und Logarithmieren log 25 2
 .1 Übersicht Operationen Addition und Subtraktion 7 Operationen. Stufe Multiplikation 3 1 und Division 1: 3 Operationen 3. Stufe Potenzieren, Radizieren und Logarithmieren log. Reihenfolge der Operationen
.1 Übersicht Operationen Addition und Subtraktion 7 Operationen. Stufe Multiplikation 3 1 und Division 1: 3 Operationen 3. Stufe Potenzieren, Radizieren und Logarithmieren log. Reihenfolge der Operationen
11 Szene. Schafe zählen oder wie Kasper beim Angeln einschlief. Kasper: Er sieht aus wie eine Mumie, eine pensionierte Mumie.
 Schafe zählen oder wie Kasper beim Angeln einschlief Glück haben 1 Heute Morgen haben wir Glück. Mein Nachbar steht nicht am Zaun. Vielleicht brummt ihm der Kopf, weil er sich mit der Angel das halbe Ohr
Schafe zählen oder wie Kasper beim Angeln einschlief Glück haben 1 Heute Morgen haben wir Glück. Mein Nachbar steht nicht am Zaun. Vielleicht brummt ihm der Kopf, weil er sich mit der Angel das halbe Ohr
