Kapitel 3. Kapitel 3 Graphentheorie
|
|
|
- Albert Linden
- vor 6 Jahren
- Abrufe
Transkript
1 Graphentheorie Inhalt Grundlagen Das Das Königsberger Brückenproblem Bäume Planare Graphen Färbungen Seite 2
2 3.1 Grundlagen Definition. Ein Ein Graph besteht aus aus Ecken und und Kanten; dabei verbindet jede jede Kante genau zwei zwei Ecken; je je zwei zwei Ecken können durch keine, eine eine oder oder mehr mehr als als eine eine Kante verbunden sein. sein. Beispiele: Seite 3 Anwendungen Städteverbindungen: Ecken = Städte, Kanten = Straßen. Typische (und (und schwere) Frage: Wie Wie kann kann man man eine eine Rundreise kürzester Länge finden? ( Travelling Salesman Problem ). Chemische Moleküle: Ecken = Atome, Kanten = Verbindungen. Wichtige Frage (die (die zur zur Entwicklung der der Graphentheorie entscheidend beigetragen hat): hat): Gegeben eine eine Summenformel (z.b. (z.b. C n H n 2n+1 OH), 2n+1 OH), wie wie viele viele verschiedene Strukturformeln gibt gibt es es dazu? Soziogramme: Ecken = Personen einer einer Gruppe, Kanten = Beziehungen zwischen den den Menschen (z.b. (z.b. bekannt sein sein mit ). mit ). Seite 4
3 Vollständige Graphen Definition. Ein Ein Graph heißt heißt vollständig, wenn jede jede Ecke Ecke mit mit jeder jeder anderen durch genau eine eine Kante verbunden ist. ist. Das Das heißt, bei bei einem vollständigen Graphen sind sind je je zwei zwei Ecken verbunden, aber aber nur nur durch eine eine Kante. Der Der vollständige Graph mit mit n Ecken wird wird mit mit K n bezeichnet. n Beispiele: K 1 K 1 2 K 2 3 K 3 4 K Seite 5 Zusammenhängende Graphen Definition. Ein Ein Graph heißt heißt zusammenhängend, wenn man man von von jeder jeder Ecke Ecke zu zu jeder jeder anderen über über eine eine Folge von von Kanten kommen kann. Das Das bedeutet: Ein Ein Graph ist ist zusammenhängend, wenn er er nicht nicht in in mehrere Teile Teile zerfällt. Beispiel: zusammenhängend unzusammenhängend Seite 6
4 Grad einer Ecke Definition. Der DerGrad einer einer Ecke Ecke ist ist die die Anzahl der der Kanten, die die von von dieser Ecke Ecke ausgehen. Beispiele: a) a) Der Der Grad Grad einer einer Ecke Ecke ist ist gleich 0, 0, falls falls von von ihr ihr keine Kante ausgeht. b) b) In In dem dem vollständigen Graphen K n hat n hat jede jede Ecke Ecke den den Grad Grad n 1, n 1, da da sie sie mit mit jeder jeder der der n 1 n 1 anderen durch genau eine eine Kante verbunden ist. ist. Im Im allgemeinen haben die die Ecken eines Graphen verschiedene Grade. Beispiel: Seite Das Königsberger Brückenproblem Dem Dem Mathematiker Leonhard Euler wurde folgendes Problem gestellt, das das ihn ihn zur zur Entwicklung der der ge- Graphentheorie geführt hat. hat. Durch Königsberg fließt fließt die die Pregel, die die sich sich teilt teilt und und zwei zwei Inseln umfließt. Diese sind sind untereinander und und mit mit den den Ufern wie wie abgebildet durch Brücken verbunden. Frage: Gibt Gibt es es einen Spaziergang, der der jede jede Brücke genau einmal überquert und und bei bei dem dem man man zum zum Ausgangspunkt zurückkehrt? Seite 8
5 Übersetzung der Karte in in einen Graphen Jedem Landteil wird wird eine eine Ecke Ecke zugeordnet: Jede Jede Brücke wird wird mit mit einer einer Kante identifiziert: Aus Aus der der Landkarte erhält man man so so den den folgenden Graphen: Seite 9 Übersetzung des Problems (I): Eulersche Kreise Definition. Sei Sei G ein ein Graph. Eine Eine Folge k 1, 1, k 2,..., 2,..., k s von s von Kanten von von G heißt heißt Kantenzug, falls falls es es Ecken e 0, 0, e 1, 1,..., e s gibt, s gibt, so so dass dass die die Kante k 1 die 1 die Ecken e 0 und 0 und e 1 verbindet, 1 die die Kante k 2 die 2 die Ecken e 1 1 und und e 2 verbindet, 2...,..., die die Kante k s die s die Ecken e s 1 und s 1 und e s verbindet. s e 1 e 0 k 1 k 2 k s e 2 e s-1 e s Ein Ein Kantenzug heißt ein ein eulerscher Kreis von von G, G, wenn jede jede Kante von von G genau einmal unter unter den den k 1, 1, k 2,..., 2,..., k s auftaucht s und und e s = s e 0 ist. 0 ist. Seite 10
6 Übersetzung des Problems (II): Eulersche Graphen Definition. Ein Ein eulerscher Graph ist ist ein ein Graph, der der einen eulerschen Kreis enthält. Mit Mit anderen Worten: Ein Ein Graph ist ist eulersch, wenn man man --seine Kanten in in einem Zug Zug zeichnen kann kann und und --am am Ende wieder am am Ausgangspunkt anlangt. Beispiel: K 5 ist 5 ist eulersch: Seite 11 Lösung des Königsberger Brückenproblems Der Der gesuchte Spaziergang, der der jede jede Brücke genau einmal überquert und und zum zum Startpunkt zurückkehrt, entspricht einem eulerschen Kreis. Die Die Frage lautet also: also: Ist Ist der der Graph des des Königsberger Brückenproblems eulersch? Satz Satz von von Euler (1736): Wenn ein ein Graph G eulersch ist, ist, dann dann hat hat jede jede Ecke Ecke von von G geraden Grad. Damit gelang Euler die dielösung des des Königsberger Brückenproblems: Der Der Graph des des Problems hat hat Ecken vom vom Grad Grad 3, 3, 3, 3, 3, 3, Also Also ist ist er er nicht nicht eulersch. Ein Ein solcher Spaziergang ist ist nicht nicht möglich! Seite 12
7 Beweis des Satzes von Euler Beweis. Wir Wir betrachten eine eine beliebige Ecke Ecke e von von G. G. Der Der eulersche Kreis Kreis durchquert die die Ecke Ecke e einige Male, sagen wir wir a mal. mal. Behauptung: Der Der Grad Grad der der Ecke Ecke e ist ist gleich 2a, 2a, also also eine eine gerade Zahl. Zahl. Denn: Bei Bei jedem Durchgang durch e verbraucht der der eulersche Kreis Kreis 2 Kanten; in in a Durchgängen werden also also 2a 2a Kanten erfasst. Da Da keine Kante zweimal benutzt wird, wird, ist ist der der Grad Grad von von e also also mindestens gleich 2a. 2a. Der Der Grad Grad kann kann aber aber auch auch nicht nicht größer sein, sein, da da jede jede Kante (also (also auch auch jede jede Kante, die die an an e angrenzt) in in dem dem eulerschen Kreis Kreis mindestens einmal vorkommt. Damit ist ist der der Grad Grad von von e wirklich gleich 2a, 2a, also also eine eine gerade Zahl. Zahl. Seite 13 Umkehrung des Satzes von Euler Es Es gilt gilt auch auch Umkehrung: Umkehrung des des Satzes von von Euler. Wenn in in einem zusammenhängenden Graphen G jede jede Ecke Ecke geraden Grad Grad hat, hat, dann dann ist ist G eulersch Folgerung: Jeder vollständige Graph K n mit n mit ungeradem n (also (also K 3, 3, K 5, 5, K 7, 7,..., K 2005, 2005,...) ist ist eulersch. Beweis. Jede Jede Ecke Ecke von von K n hat n hat den den Grad Grad n 1. n 1. Wenn n ungerade ist, ist, ist ist n 1 n 1 gerade. Seite 14
8 Offene eulersche Linien Definition. Eine Eine offene eulersche Linie ist ist ein ein Kantenzug, --der der jede jede Kante genau einmal durchquert, --und und die die Anfangsecke verschieden von von der der Endecke ist. ist. Also Also kann kann ein ein Graph genau dann dann in in einem Zug Zug gezeichnet werden, wenn er er einen eulerschen Kreis oder oder eine eine offene eulersche Linie Linie besitzt. Beispiel: Satz. Ein Ein zusammenhängender Graph besitzt genau dann dann eine eine offene eulersche Linie, wenn er er genau 2 Ecken ungeraden Grades besitzt. Wenn dies dies der der Fall Fall ist, ist, so so beginnt die die offene eulersche Linie Linie an an der der einen Ecke Ecke ungeraden Grades und und endet an an der der anderen. Seite 15 Beweis der Hinrichtung Beweis. Wir Wir müssen zwei zwei Richtungen zeigen Richtung: Wenn G eine eine offene eulersche Linie Linie hat, hat, dann dann gibt gibtes es genau 2 Ecken mit mit ungeradem Grad. Wir Wir betrachten eine eine offene eulersche Linie, die die von von a nach nach e führt. führt. Trick: Wir Wir denken uns uns eine eine zusätzliche Kante k* k* zwischen a und und e. e. Dann wird wird aus aus der der offenen eulerschen Linie Linie eine eine geschlossene. Nach Nach dem dem Satz Satz von von Euler hat hat dann dann also also jede jede Ecke Ecke geraden Grad. Nun Nun vergessen wir wir k* k* wieder. Jede Jede Ecke Ecke verschieden von von a und und e hat hat dann dann immer noch noch geraden Grad, während sich sich der der Grad Grad von von a und und e jeweils um um 1 erniedrigt hat, hat, also also jetzt jetzt ungerade ist. ist. Also Also sind sind a und und e die die einzigen Ecken mit mit ungeradem Grad. Seite 16
9 Beweis der Rückrichtung Richtung: Wenn G genau 2 Ecken mit mit ungeradem Grad Grad hat, hat, dann dann gibt gibt es es eine eine offene eulersche Linie. Sei Sei G ein ein zusammenhängender Graph, der der genau zwei zwei Ecken a und und e ungeraden Grades besitzt. Trick: Wir Wir denken uns uns eine eine zusätzliche Kante k* k* zwischen a und und e. e. Diese hat hat den den Effekt, dass dass jetzt jetzt jede jede Ecke Ecke geraden Grad Grad hat. hat. Nach der der Umkehrung des des Satzes von von Euler hat hat der der Graph mit mit der der Kante k* k* eine eine geschlossene eulersche Linie. Wenn wir wir k* k* wieder vergessen, wird wird aus aus der der geschlossenen eulerschen Linie Linie eine eine offene mit mit der der Anfangsecke a und und der der Endecke e. e. Also Also hat hat G eine eine offene eulersche Linie. Seite 17 Bsp.: Gibt es es offene Spaziergänge durch Königsberg? Der Der Graph des des Königsberger Brückenproblems hat hat vier vier Ecken ungeraden Grades. Also Also enthält er er auch auch keine offene Linie. Es Es gibt gibt also also keinen Spaziergang durch Königsberg, der der jede jede Brücke genau einmal überquert selbst wenn der der Startpunkt verschieden vom vom Endpunkt sein sein darf. darf. Seite 18
10 3.3 Bäume Definition. Ein Ein Baum ist ist ein ein Graph, der der zusammenhängend ist ist und und keinen Kreis enthält. Beispiel: Alle Alle Bäume mit mit höchstens fünf fünf Ecken sind: sind: Bemerkung: Wir Wir betrachten nur nur Bäume mit mit endlich vielen Ecken. Seite 19 Hilfssatz über Endecken Definition. Eine Eine Ecke Ecke eines Graphen vom vom Grad Grad 1 heißt eine eine Endecke Hilfssatz. Jeder Baum mit mit mindestens zwei zwei Ecken hat hat mindestens eine eine Endecke. Beweis. Wir Wir starten mit mit einer einer beliebigen Ecke Ecke e Wir Wir gehen von von e 0 0 aus aus über über eine eine Kante zu zu einer einer Ecke Ecke e Wenn e 1 eine 1 eine Endecke ist, ist, ist ist die die Behauptung richtig. Wenn nicht, gehen wir wir über über eine eine neue neue Kante von von e 1 aus 1 aus zu zu einer einer Ecke Ecke e Wenn e 2 eine 2 eine Endecke ist, ist, sind sind wir wir fertig. Sonst gehen wir wir über über eine eine neue neue Kante zu zu einer einer Ecke Ecke e Usw. Usw. Alle Alle diese Ecken sind sind verschieden (sonst gäbe gäbe es es einen Kreis). Da Da es es nur nur endlich viele viele Ecken gibt, gibt, muss die die Konstruktion einmal abbrechen. Die Die Ecke, an an der der es es nicht nicht weitergeht, ist ist eine eine Endecke. Seite 20
11 Satz über die Anzahl von Ecken und Kanten Satz: Für Für jeden Baum G mit mit n Ecken und und m Kanten gilt gilt n = m Beweis durch Induktion nach nach der der Anzahl n der der Ecken. Induktionsbasis: Im Im Fall Fall n = 1 besteht G nur nur aus aus einer einer Ecke Ecke und und keiner Kante; also also ist ist m = 0, 0, und und somit n = 1 und und m+1 m+1 = Induktionsschritt: Sei Sei n 1, 1, und und sei sei die die Behauptung richtig für für n. n. Sei Sei G ein ein Baum mit mit n+1 n+1 Ecken. Nach hat hat G eine eine Endecke e*. e*. Wir Wir entfernen e* e* und und die die an an e* e* angrenzende Kante k*, k*, und und erhalten einen Baum G* G* mit mit nur nur n Ecken. Nach Induktionsvoraussetzung hat hat G* G* also also genau n 1 n 1 Kanten. Da Da G genau eine eine Kante mehr mehr als als G* G* hat, hat, hat hat G genau n Kanten. Damit ist ist der der Induktionsschritt bewiesen, die die Aussage gilt gilt allgemein. Seite Planare Graphen Definition. Ein Ein Graph heißt heißt planar, falls falls er er ohne ohne Überschneidungen in in der der Ebene gezeichnet ist. ist. Beispiele: (a) (a) (b) (b) Projektionen konvexer Polyeder, z.b. z.b. eines Würfels: Projektion Seite 22
12 Plättbare Graphen Definition. Ein Ein Graph heißt heißtplättbar, wenn er er überschneidungsfrei in in die die Ebene gezeichnet werden kann. Beispiel: Der Der Graph ist ist plättbar, denn denn er er kann kann wie wie folgt folgt überschneidungsfrei gezeichnet werden: Definition. Ein Ein Graph heißt heißt einfach, wenn je je zwei zwei Ecken durch höchstens eine eine Kante verbunden sind. sind. Seite 23 Die Eulersche Polyederformel Jeder planare Graph zerlegt die die Ebene in in Gebiete. Wir Wir bezeichnen die die Anzahl der der Gebiete mit mit g. g. Es Es gibt gibt stets stets mindestens ein ein Gebiet, das das äußere Gebiet. D.h.: D.h.: g Beispiele: (a) (a) Der Der Graph hat hat g = (b) (b) Bäume haben g = Eulersche Polyederformel. Sei Sei G ein ein zusammenhängender planarer Graph mit mit n Ecken, m Kanten und und g Gebieten. Dann gilt: gilt: n m + g = Seite 24
13 Beweis der Eulerschen Polyederformel Beweis durch Induktion nach nach der der Anzahl g der der Gebiete. Induktionsbasis. Sei Sei g = Dann hat hat G keine Kreise, ist ist also also ein ein Baum. Nach ist ist n = m+1, m+1, also also n m + g = (m+1) m + 1 = Induktionsschritt: Sei Sei g 1, 1, und und sei sei die die Aussage richtig für für g. g. Sei Sei G ein ein Graph mit mit g+1 g+1 Gebieten. Da Da g+1 g+1 > 1 ist, ist, ist ist G kein kein Baum, enthält daher einen Kreis. Wir Wir entfernen eine eine Kante k* k* dieses Kreises. Da Da k* k* an an zwei zwei Gebiete von von G angrenzt, hat hat der der neue neue Graph G* G* nur nur noch noch g* g* = g Gebiete. Also Also können wir wir auf auf G* G* die die Induktionsvoraussetzung anwenden (G* (G* hat hat m 1 m 1 Kanten und und n Ecken). Das Das heißt: 2 = n (m 1) + g = n m + (g+1). Also Also gilt gilt die die Aussage für für g+1. g+1. Seite 25 Satz über planare Graphen Satz. Sei Sei G ein ein zusammenhängender einfacher planarer Graph mit mit n 3 Ecken und und m Kanten. Dann gilt: gilt: m 3n 3n Das Das heißt: Ein Ein planarer Graph hat hat nur nur wenige Kanten. M.a.W.: Graphen mit mit vielen Kanten können nicht nicht plättbar sein. sein. Beweis (durch trickreiche Abzählungen): Für Für ein ein Gebiet L (wie (wie Land ) bezeichnen wir wir mit mit m(l) m(l) die die Anzahl der der Kanten von von L. L. Da Da jedes Land Land mindestens drei drei Kanten hat, hat, gilt: gilt: m(l) 3g. L Gebiet Nun Nun zählen wir wir die die Paare (k, (k, L), L), wobei die die Kante k ein ein Teil Teil der der Grenze des des Gebiets L ist: ist: m(l) 2m. L Gebiet Zusammen folgt: folgt: 2m 2m 3g, 3g, d.h. d.h. g 2m/3. Einsetzen in in die die Eulersche Polyederformel: n m + 2m/3 2m/3 n m + g = 2, 2, also also m 3n 3n Seite 26
14 Folgerungen Folgerung: Der Der vollständige Graph K 5 ist 5 ist nicht nicht plättbar. Beweis. Wäre K 5 plättbar, 5 so so könnte nach nach obigem Satz Satz seine Anzahl 5 von von Kanten höchstens 3n 6 3n 6 = 9 sein. sein. K 5 hat 5 hat jedoch = Kanten Satz: Sei Sei G ein ein zusammenhängender einfacher planarer Graph. Dann gibt gibt es es mindestens eine eine Ecke, die die einen Grad Grad 5 hat. hat. Beweis. Die Die Behauptung ist ist klar klar für für n = 1 und und n = Sei Sei nun nun n 3: 3: Wenn jede jede Ecke Ecke mindestens den den Grad Grad 6 hätte, folgte aus aus dem dem vorigen Satz Satz 6 n Das Das ist ist ein ein Widerspruch. x Ecke Grad(x) = 2m 6n Seite 27 Anwendungsaufgabe Aufgabe: Drei Drei Häuser A, A, B, B, C sollen jeweils durch eine eine Leitung mit mit dem dem Gaswerk (G), (G), Elektrizitätswerk (E) (E) und und dem dem Wasserwerk (W) (W) verbunden werden. Kann man man dies dies so so machen, dass dass sich sich die die Leitungen nicht nicht überkreuzen? Graphentheoretische Formulierung: Ist Ist der der folgende Graph plättbar? Dieser Graph heißt vollständig bipartit und und wird wird mit mit K 3,3 bezeichnet. 3,3 Seite 28
15 Lösung der Aufgabe Es Es ist ist nicht nicht möglich! Beweis. Angenommen, wir wir könnten diesen Graphen als als planaren Graphen zeichnen. Dann hätte hätte dieser n = 6 Ecken, m = 9 Kanten, und und nach nach der der Eulerschen Polyederformel könnten wir wir die die Anzahl der der Länder ausrechnen: 2 = n m + g = g, g, also also g = Jedes Gebiet des des Graphen muss eine eine gerade Anzahl von von Ecken haben, denn denn Häuser und und Versorgungswerke wechseln sich sich ab. ab. Daher hat hat jedes Gebiet mindestens 4 Ecken und und also also auch auch mindestens 4 Kanten. Daher gilt m(l) 4g, gilt L Gebiet und und daher 2m 2m 4g. 4g. In In unserem Fall Fall bedeutet dies dies = 2m 2m 4g 4g = Dieser Widerspruch zeigt, dass dass K 3,3 nicht 3,3 nicht plättbar ist. ist. Seite Färbungen Ursprung: Mitte Mitte des des Jahrhunderts kam kam folgende Frage auf: auf: Wie Wie viele viele Farben braucht man man mindestens, um um eine eine beliebige Landkarte so so zu zu färben, dass dass je je zwei zwei benachbarte Länder verschiedene Farben haben? Vierfarbenvermutung: Vier Vier Farben genügen! dene Seite 30
16 Vierfarbenvermutung Beweisversuche 1852: Mathematikstudent F. F. Guthrie färbt färbt die die Karte von von England und und äußert zum zum ersten Mal Mal die die Vierfarbenvermutung. 1878: On On the the colouring of of maps von von A. A. Cayley. 1879: On On the the geographical problem of of the the four four colors von von A. A. B. B. Kempe: erster Beweis des des Vierfarbensatzes. 1890: P. P. J. J. Heawood entdeckt einen Fehler in in Kempes Beweis. Heawood kann kann den den Fünffarbensatz zeigen ( 5 ( 5 Farben reichen auf auf jeden Fall ). H. H. Heesch ( ): Entwickelt von von Kempes Methoden jahrzehntelang weiter und und kommt zu zu dem dem Schluss, dass dass das das Problem mit mit lang Hilfe Hilfe eines Rechners lösbar sein sein müsste. Seite 31 Der Beweis des Vierfarbensatzes mit dem Computer 1976: K. K. Apel Apelund W. W. Haken (University of of Illinois at at Urbana) bauen auf auf den den Arbeiten von von Heesch auf, auf, und und können das das Problem mit mit Hilfe Hilfe eines Computers lösen. Der Der Satz Satz ist ist endlich bewiesen! Der Der Beweis hat hat viel viel Aufsehen erregt: Zum Zum ersten Mal Mal beim beim Beweis eines Satzes wurde der der Computer essentiell eingesetzt. Auch Auch heute noch noch wünschen sich sich viele viele Mathematiker einen schönen, kurzen Beweis, den den man man z.b. z.b. in in einer einer Vorlesung darstellen könnte. Seite 32
17 Übersetzung der Landkarte in in einen Graphen Wir Wir zeichnen in in jedem Land Land einen Punkt (die (die Hauptstadt ) aus; aus; das das sind sind die die Ecken des des Graphen. Wir Wir verbinden zwei zwei Ecken durch eine eine Kante, wenn die die entsprechenden Länder ein ein Stück Grenze gemeinsam haben. Auf Auf diese Weise erhält man man einen planaren Graphen. Beispiel: Seite 33 Die chromatische Zahl χ(g) Definition. Eine Eine Färbung eines Graphen ist ist eine eine Zuordnung von von Farben zu zu den den Ecken, so so dass dass keine zwei zwei durch eine eine Kante verbundenen Ecken die die gleiche Farbe haben. Definition. Die Die chromatische Zahl Zahl χ(g) χ(g) eines Graphen G ist ist die die kleinste natürliche Zahl, Zahl, mit mit der der G gefärbt werden kann. (χ (χ ist ist der der griech. Buchstabe chi, chi, der der Anfangsbuchstabe des des Wortes chroma = Farbe.) Beispiele: (a) (a) Kreise gerader Länge haben χ = 2, 2, Kreise ungerader Länge χ = (b) (b) χ(k χ(k n ) n ) = n. n. Seite 34
18 Übersetzung des Färbungsproblems in in Graphentheorie Übersetzung des des Problems: Die Die Ecken des des Graphen sollen so so gefärbt werden, dass dass je je zwei zwei durch eine eine Kante verbundene Ecken verschiedene Farben haben. Wie Wie viele viele Farben benötigt eine eine solche Färbung? Die Die Vierfarbenvermutung lautet: Wenn G ein ein planarer Graph ist, ist, so so dene ist ist χ(g) χ(g) 4.. Folgendes Beispiel zeigt, dass dass nur nur 3 Farben nicht nicht genügen: Seite 35 Greedy Algorithmus Def. Def. Mit Mit (G) (G) ( delta ) bezeichnen wir wir den den maximalen Grad Grad von von G. G Satz: Für Für jeden Graphen G gilt gilt χ(g) χ(g) (G) (G) Beweis. Mit Mit folgendem Verfahren ( greedy Algorithmus ) kann kann man man jeden Graphen G mit mit höchstens (G)+1 Farben färben: Die Die Farben seien die die Zahlen 1, 1, 2, 2, 3, 3, Wir Wir nummerieren die die Ecken: e 1, 1, e 2, 2, e 3, 3,... Wir Wir färben e 1 mit 1 mit der der Farbe Wenn wir wir zu zu irgendeiner Ecke Ecke e i i kommen, färben wir wir sie sie mit mit der der kleinsten Farbe, die die nicht nicht verboten ist. ist. Wie Wie viele viele Farben sind sind für für e i verboten? i Schlimmstenfalls ist ist e i eine i eine Ecke Ecke mit mit maximalem Grad Grad = (G) (G) und und alle alle Nachbarecken von von e i i sind sind bereits verschieden gefärbt. In In diesem Fall Fall sind sind Farben verboten. Dann gibt gibt es es aber aber immer noch noch eine, eine, die die wir wir wählen können. Seite 36
19 Der Vierfarbensatz und der Fünffarbensatz Für Für planare Graphen gilt gilt etwas viel viel besseres: Vierfarbensatz (Apel und und Haken 1976). Jeder planare Graph kann kann mit mit 4 Farben gefärbt werden. D.h.: D.h.: Für Für jeden planaren Graphen G gilt: gilt: χ(g) χ(g) 4.. Das Das bedeutet: In In jeder jeder ebenen Landkarte können die die Länder so so mit mit 4 Farben gefärbt werden, dass dass je je zwei zwei benachbarte Länder verschieden gefärbt sind. sind Fünffarbensatz (Heawood, 1890). Jeder planare Graph kann kann mit mit 5 Farben gefärbt werden. Seite 37 Beweis des Fünffarbensatzes (I) (I) Beweis durch Induktion nach nach der der Eckenzahl n. n. Induktionsbasis. Für Für n 5 ist ist die die Aussage trivial: Jeder Graph mit mit höchstens 5 Ecken kann kann mit mit 5 Farben gefärbt werden. Induktionsschritt. Sei Sei n 5, n 5, und und sei sei die die Aussage richtig für für n Ecken. D.h.: D.h.: Jeder planare Graph mit mit n Ecken kann kann mit mit 5 Farben gefärbt werden. Sei Sei nun nun G ein ein planarer Graph mit mit n+1 n+1 Ecken. Wir Wir müssen zeigen, dass dass auch auch G mit mit 5 Farben gefärbt werden kann. Nach besitzt G eine eine Ecke Ecke e* e* vom vom Grad Grad Wir Wir entfernen e* e* und und alle alle an an e* e* anliegenden Kanten und und erhalten einen planaren Graphen G* G* mit mit nur nur n Ecken. Nach Induktionsvoraussetzung besitzt G* G* eine eine Färbung mit mit 5 Farben. Seite 38
20 Beweis des Fünffarbensatzes (II) (II) Ziel: Ziel: Mit Mit dieser Färbung (oder einer einer leichten Variation) erhalten wir wir eine eine Färbung von von G! G! Fall: Fall: Wenn die die ( ( 5) 5) zu zu e* e* benachbarten Ecken insgesamt mit mit höchstens 4 Farben gefärbt sind, sind, dann dann kann kann e* e* mit mit der der verbleibenden Farbe gefärbt werden Fall: Fall: e* e* hat hat 5 Nachbarecken e 1, 1, e 2, 2, e 3, 3, e 4, 4, e 5, 5, die die mit mit den den Farben 1, 1, 2, 2, 3, 3, 4, 4, 5 gefärbt sind. sind. Die Die Ecken e 1, 1,..., e 5 seien 5 gegen den den Uhrzeigersinn angeordnet. Wir Wir betrachten zunächst nur nur die die Menge aller aller Ecken der der Farben 1 oder oder 3, 3, die die von von e 1 aus 1 aus erreichbar sind. sind. Wir Wir unterscheiden zwei zwei (Unter-) Fälle. Seite 39 Beweis des Fünffarbensatzes (III) Guter Fall: Fall: Wenn man man von von e 1 ausgeht 1 und und nur nur Ecken der der Farben 1 oder oder 3 benützt, kommt man man nie nie zu zu e Dann kann kann man man die die Ecken der der Farben 1 oder oder 3, 3, die die man man von von e 1 aus 1 aus erreichen kann, umfärben (aus (aus 1 wird wird 3, 3, aus aus 3 wird wird 1). 1). Diese neue neue Färbung von von G* G* hat hat die die Eigenschaft, dass dass bei bei den den Ecken e 1, 1,..., e 5 nur 5 nur die die Farben 2, 2, 3, 3, 4, 4, 5 vorkommen. Also Also kann kann e* e* mit mit der der Farbe 1 gefärbt werden. Seite 40
21 Beweis des Fünffarbensatzes (IV) Schlechter Fall: Fall: Es Es gibt gibt einen Weg Weg von von e 1 nach 1 nach e 3, 3, der der nur nur Ecken der der Farben 1 und und 3 benutzt. Nun Nun betrachten wir wir die die Ecken e 2 und 2 und e Wegen der der Planarität von von G können diese Ecken nicht nicht durch einen Weg Weg verbunden sein, sein, der der nur nur Ecken der der Farben 2 und und 4 benutzt. Also Also kann kann man man alle alle Ecken der der Farben 2 oder oder 4, 4, die die von von e 2 aus 2 aus erreichbar sind, sind, umfärben (2 (2 wird wird 4, 4, 4 wird wird 2). 2). Damit erhält man man eine eine Färbung von von G*, G*, bei bei der der e 2 die 2 die Farbe 4 erhält. Nun Nun kann kann man man e* e* mit mit der der Farbe 2 färben. Damit ist ist der der Fünffarbensatz bewiesen! Seite 41
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie
 Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn
 Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn 1. Geschichte - Frage kommt Mitte des 19 Jahrhunderts auf Wie viele Farben benötigt man um eine Karte
Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn 1. Geschichte - Frage kommt Mitte des 19 Jahrhunderts auf Wie viele Farben benötigt man um eine Karte
Hausarbeit aus. Graphentheorie Formale Grundlagen Professor Franz Binder. zum Thema. Herbert Huber k Seite 1 von 21
 Hausarbeit aus 368.712 Formale Grundlagen Professor Franz Binder zum Thema Graphentheorie Herbert Huber k0455780 Seite 1 von 21 Inhaltsverzeichnis Graphen Grundlagen und Begriffsdefinitionen...3 Graphenstrukturen...6
Hausarbeit aus 368.712 Formale Grundlagen Professor Franz Binder zum Thema Graphentheorie Herbert Huber k0455780 Seite 1 von 21 Inhaltsverzeichnis Graphen Grundlagen und Begriffsdefinitionen...3 Graphenstrukturen...6
durch Einfügen von Knoten konstruiert werden kann.
 Satz von Kuratowski Definition Unterteilung eines Graphen Sei G = (V, E) und e = {u, v} E. 1 Das Einfügen eines neuen Knoten w in die Kante e führt zum Graphen G = (V {w}, E \ e {{u, w}, {w, v}}). 2 Der
Satz von Kuratowski Definition Unterteilung eines Graphen Sei G = (V, E) und e = {u, v} E. 1 Das Einfügen eines neuen Knoten w in die Kante e führt zum Graphen G = (V {w}, E \ e {{u, w}, {w, v}}). 2 Der
Der Vier-Farben-Satz
 , Samuel Hetterich, Felicia Raßmann Goethe-Universität Frankfurt, Institut für Mathematik 21.Juni 2013 Wieviele Farben braucht man zum Färben einer Landkarte? Spielregeln Länder mit einer gemeinsamen Grenze
, Samuel Hetterich, Felicia Raßmann Goethe-Universität Frankfurt, Institut für Mathematik 21.Juni 2013 Wieviele Farben braucht man zum Färben einer Landkarte? Spielregeln Länder mit einer gemeinsamen Grenze
Von den Kanten von Gewicht 4 wird nur noch eine ausgewählt, die zu dem letzten nicht ausgewählten Knoten führt: 1. Juni
 CHAPTER. GRAPHEN.. B Ä UME.. Bäume Ein schlichter Graph ohne Kreise heisst Wald, ist er noch zusätzlich zusammenhängend so wird er Baum genannt. Bevor wir Bäume genauer beschreiben ein kleines LEMMA...
CHAPTER. GRAPHEN.. B Ä UME.. Bäume Ein schlichter Graph ohne Kreise heisst Wald, ist er noch zusätzlich zusammenhängend so wird er Baum genannt. Bevor wir Bäume genauer beschreiben ein kleines LEMMA...
Kap. IV: Färbungen von Graphen
 Chr.Nelius: Graphentheorie (WS 2016/17) 46 Kap. IV: Färbungen von Graphen 12. Eckenfärbungen Bereits im 6 ten Paragraphen haben wir Eckenfärbungen benutzt, um bipartite Graphen charakterisieren zu können.
Chr.Nelius: Graphentheorie (WS 2016/17) 46 Kap. IV: Färbungen von Graphen 12. Eckenfärbungen Bereits im 6 ten Paragraphen haben wir Eckenfärbungen benutzt, um bipartite Graphen charakterisieren zu können.
4 Färbungen Begriffe Komplexität Greedy-Algorithmus Knotenreihenfolgen Das 4-Farben-Problem...
 Inhaltsverzeichnis 4 Färbungen 41 4.1 Begriffe....................... 41 4.2 Komplexität..................... 42 4.3 Greedy-Algorithmus................ 42 4.4 Knotenreihenfolgen................. 43 4.5
Inhaltsverzeichnis 4 Färbungen 41 4.1 Begriffe....................... 41 4.2 Komplexität..................... 42 4.3 Greedy-Algorithmus................ 42 4.4 Knotenreihenfolgen................. 43 4.5
Definition : Diechromatische Zahl eines Graphen G ist die kleinste Anzahl chromatische Zahl von Farben für eine zulässige Färbung.
 4 Definition : Eine zulässige Färbung ist eine Färbung der Knoten des ( un- zulässige Färbung gerichteten ) Graphen, so daß je zwei adjazente Knoten verschiedene Farben haben. Trivial ist, daß n verschiedene
4 Definition : Eine zulässige Färbung ist eine Färbung der Knoten des ( un- zulässige Färbung gerichteten ) Graphen, so daß je zwei adjazente Knoten verschiedene Farben haben. Trivial ist, daß n verschiedene
Achilles und die Schildkröte Sommersemester 2008
 Achilles und die Schildkröte Sommersemester 2008 Färbbarkeit planarer Graphen Alexander Damarowsky 20.05.2008 V6, 15.05.2008 Problemstellung /Ziel des Vortrags: Wie viele Farben werden benötigt, um jeden
Achilles und die Schildkröte Sommersemester 2008 Färbbarkeit planarer Graphen Alexander Damarowsky 20.05.2008 V6, 15.05.2008 Problemstellung /Ziel des Vortrags: Wie viele Farben werden benötigt, um jeden
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 6: Graphentheorie
 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Bemerkung: Der vollständige Graph K n hat n(n 1)
 Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Der Fünffarbensatz. Ausarbeitung des Seminarvortrags vom
 Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS Über klassische Probleme der Mathematik Leitung: Prof. Harald Upmeier, Benjamin Schwarz Referentin: Sabrina Klöpfel Wintersemester
Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS Über klassische Probleme der Mathematik Leitung: Prof. Harald Upmeier, Benjamin Schwarz Referentin: Sabrina Klöpfel Wintersemester
Fünf-Farben-Satz. Seminar aus reiner Mathematik, WS 13/14. Schweighofer Lukas, November Seite 1
 Der Fünf- Farben-Satz Seminar aus reiner Mathematik, WS 13/14 Schweighofer Lukas, November 2013 Seite 1 Inhaltsverzeichnis Vorwort...3 Graphentheoretische Grundlagen...4 Satz 2 (Eulerscher Polyedersatz)...7
Der Fünf- Farben-Satz Seminar aus reiner Mathematik, WS 13/14 Schweighofer Lukas, November 2013 Seite 1 Inhaltsverzeichnis Vorwort...3 Graphentheoretische Grundlagen...4 Satz 2 (Eulerscher Polyedersatz)...7
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Der Fünf-Farben-Satz. Lukas Schweighofer. Feb.2014
 Der Fünf-Farben-Satz Lukas Schweighofer Feb.2014 1 Contents 1 Vorwort 3 2 Graphentheoretische Grundlagen 4 3 Satz 2 (Eulerscher Polyedersatz) 8 4 Satz 3 9 5 Der Fnf-Farben-Satz 10 5.1 Beweis 1..............................
Der Fünf-Farben-Satz Lukas Schweighofer Feb.2014 1 Contents 1 Vorwort 3 2 Graphentheoretische Grundlagen 4 3 Satz 2 (Eulerscher Polyedersatz) 8 4 Satz 3 9 5 Der Fnf-Farben-Satz 10 5.1 Beweis 1..............................
16. Flächenfärbungen
 Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
1. Einleitung wichtige Begriffe
 1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
11: Die Euler sche Polyederformel für planare Graphen
 Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Hausaufgabe 2 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
5 Graphen und Polyeder
 5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Formale Grundlagen. bis , Lösungen. 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist.
 Formale Grundlagen 4. Übungsaufgaben bis 2011-06-03, Lösungen 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist. 2. Finden Sie einen Eulerschen Weg im Briefumschlag, d.h. in: { ((1,
Formale Grundlagen 4. Übungsaufgaben bis 2011-06-03, Lösungen 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist. 2. Finden Sie einen Eulerschen Weg im Briefumschlag, d.h. in: { ((1,
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter WS 2013/14 1 Eulersche Graphen Kantenzug Ein Kantenzug in einem Graphen (V, E) ist eine Folge (a 0, a 1,..., a n ) von Knoten
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter WS 2013/14 1 Eulersche Graphen Kantenzug Ein Kantenzug in einem Graphen (V, E) ist eine Folge (a 0, a 1,..., a n ) von Knoten
Knotenfärbung. Def.: Eine Knotenfärbung eines Graphen G=(V,E) mit k Farben ist eine Abbildung c:v {1,...,k}, so dass c(u) c(v) für alle {u,v} E.
 Knotenfärbung Def.: Eine Knotenfärbung eines Graphen G=(V,E) mit k Farben ist eine Abbildung c:v {1,...,k}, so dass c(u) c(v) für alle {u,v} E. Die chromatische Zahl χ(g) eines Graphen G ist die minimale
Knotenfärbung Def.: Eine Knotenfärbung eines Graphen G=(V,E) mit k Farben ist eine Abbildung c:v {1,...,k}, so dass c(u) c(v) für alle {u,v} E. Die chromatische Zahl χ(g) eines Graphen G ist die minimale
Westfählische Wilhelms-Universität. Eulersche Graphen. Autor: Jan-Hendrik Hoffeld
 Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Bernd Döring. Wege, Plätten, Färben. Vom Problem zur Theorie der Graphen
 Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen Bernd Döring, 2002-2005 Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg 28 26721 Emden - 2 - Inhaltsverzeichnis 0. Einleitung
Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen Bernd Döring, 2002-2005 Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg 28 26721 Emden - 2 - Inhaltsverzeichnis 0. Einleitung
Diskrete Mathematik. Hamiltonsche Graphen Teil I. Karina Arndt
 Diskrete Mathematik Hamiltonsche Graphen Teil I Karina Arndt 21.06.2006 Übersicht Einleitung Hamiltonsch und eulersch Hamiltonsche Kreise Hamiltonsche Graphen neu zeichnen Kreise und Wege Reguläre Graphen
Diskrete Mathematik Hamiltonsche Graphen Teil I Karina Arndt 21.06.2006 Übersicht Einleitung Hamiltonsch und eulersch Hamiltonsche Kreise Hamiltonsche Graphen neu zeichnen Kreise und Wege Reguläre Graphen
Ein Turnierplan mit fünf Runden
 Mathematik I für Informatiker Graphen p. 1 Ein Turnierplan mit fünf Runden c b a c b a c b a c b a c b a d e d e d e d e d e Mathematik I für Informatiker Graphen p. 2 Definition: Graph Ein (schlichter)
Mathematik I für Informatiker Graphen p. 1 Ein Turnierplan mit fünf Runden c b a c b a c b a c b a c b a d e d e d e d e d e Mathematik I für Informatiker Graphen p. 2 Definition: Graph Ein (schlichter)
2. Graphentheorie, Reinhard Diestel, Springer Verlag, 4. Auflage, 2012
 Das vorliegende Skript beschäftigt sich mit dem Thema Graphentheorie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Jahr 2013. Die vorliegende Version
Das vorliegende Skript beschäftigt sich mit dem Thema Graphentheorie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Jahr 2013. Die vorliegende Version
Vier-Farben-Vermutung (1)
 Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Graphen. Graphen und ihre Darstellungen
 Graphen Graphen und ihre Darstellungen Ein Graph beschreibt Beziehungen zwischen den Elementen einer Menge von Objekten. Die Objekte werden als Knoten des Graphen bezeichnet; besteht zwischen zwei Knoten
Graphen Graphen und ihre Darstellungen Ein Graph beschreibt Beziehungen zwischen den Elementen einer Menge von Objekten. Die Objekte werden als Knoten des Graphen bezeichnet; besteht zwischen zwei Knoten
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Daniel Platt Einführung in die Graphentheorie
 Einführung in die Für die Mathematische Schülergesellschaft Leonhard Euler Humboldt Universität zu Berlin, Institut für Mathematik Das vorliegende Skript beschäftigt sich mit dem Thema. Das Skript entsteht
Einführung in die Für die Mathematische Schülergesellschaft Leonhard Euler Humboldt Universität zu Berlin, Institut für Mathematik Das vorliegende Skript beschäftigt sich mit dem Thema. Das Skript entsteht
6. Planare Graphen und Färbungen
 6. Planare Graphen und Färbungen Lernziele: Den Begriff der Planarität verstehen und erläutern können, wichtige Eigenschaften von planaren Graphen kennen und praktisch einsetzen können, die Anzahl von
6. Planare Graphen und Färbungen Lernziele: Den Begriff der Planarität verstehen und erläutern können, wichtige Eigenschaften von planaren Graphen kennen und praktisch einsetzen können, die Anzahl von
Grundlagen der Graphentheorie. Thomas Kamps 6. Oktober 2008
 Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
4. Kreis- und Wegeprobleme
 4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung
4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung
Kapitel 1. Kapitel 1 Vollständige Induktion
 Vollständige Induktion Inhalt 1.1 1.1 Das Das Prinzip A(n) A(n) A(n+1) 1.2 1.2 Anwendungen 1 + 2 + 3 +...... + n =? 1.3 1.3 Landkarten schwarz-weiß 1.4 1.4 Fibonacci-Zahlen 1, 1, 1, 1, 2, 2, 3, 3, 5, 5,
Vollständige Induktion Inhalt 1.1 1.1 Das Das Prinzip A(n) A(n) A(n+1) 1.2 1.2 Anwendungen 1 + 2 + 3 +...... + n =? 1.3 1.3 Landkarten schwarz-weiß 1.4 1.4 Fibonacci-Zahlen 1, 1, 1, 1, 2, 2, 3, 3, 5, 5,
Lösungen zu Kapitel 5
 Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Der Eulersche Polyedersatz
 Der Eulersche Polyedersatz Def Die Anzahl der k Seiten eines konvexen Polytops P bezeichnen wir mit f k (P) oder kurz mit f k. Das n Tupel (f 0,f 1,...,f n 1 ) Z n heißt dann der f Vektor des (n dimensionalen)
Der Eulersche Polyedersatz Def Die Anzahl der k Seiten eines konvexen Polytops P bezeichnen wir mit f k (P) oder kurz mit f k. Das n Tupel (f 0,f 1,...,f n 1 ) Z n heißt dann der f Vektor des (n dimensionalen)
Elementargeometrie. Prof. Dr. Andreas Meister SS digital von: Frank Lieberknecht
 Prof. Dr. Andreas Meister SS 2004 digital von: Frank Lieberknecht Geplanter Vorlesungsverlauf...1 Graphentheorie...1 Beispiel 1.1: (Königsberger Brückenproblem)... 1 Beispiel 1.2: (GEW - Problem)... 2
Prof. Dr. Andreas Meister SS 2004 digital von: Frank Lieberknecht Geplanter Vorlesungsverlauf...1 Graphentheorie...1 Beispiel 1.1: (Königsberger Brückenproblem)... 1 Beispiel 1.2: (GEW - Problem)... 2
Vier-Farbenproblem. (c) Ein etwas schwereres Beispiel...
 Vier-Farbenproblem Kann man jede Landkarte mit vier Farben färben, sodass keine aneindander angrenzenden Länder die gleiche Farbe haben? Versuchen Sie die Karte Deutschlands oder eines der anderen Bilder
Vier-Farbenproblem Kann man jede Landkarte mit vier Farben färben, sodass keine aneindander angrenzenden Länder die gleiche Farbe haben? Versuchen Sie die Karte Deutschlands oder eines der anderen Bilder
Graphentheorie Graphentheorie. Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke
 Graphen Graphentheorie Graphentheorie Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke 2 Was ist ein Graph? Ein Graph ist in der Graphentheorie eine abstrakte Struktur,
Graphen Graphentheorie Graphentheorie Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke 2 Was ist ein Graph? Ein Graph ist in der Graphentheorie eine abstrakte Struktur,
Liegt eine Kante k auf einem Zyklus Z, so liegt k auf dem Rand genau zweier
 4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie.
4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie.
Anwendungen von Graphen
 Anwendungen von Graphen Strassen- und Verkehrsnetze Computernetzwerke elektrische Schaltpläne Entity-Relationship Diagramme Beweisbäume endliche Automaten Syntaxbäume für Programmiersprachen Entscheidungsbäume
Anwendungen von Graphen Strassen- und Verkehrsnetze Computernetzwerke elektrische Schaltpläne Entity-Relationship Diagramme Beweisbäume endliche Automaten Syntaxbäume für Programmiersprachen Entscheidungsbäume
Graphen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Ein Turnierplan mit fünf Runden c d b e a c d b e a c d b e a c d b b c a a d e e Das Diagramm beschreibt
Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Ein Turnierplan mit fünf Runden c d b e a c d b e a c d b e a c d b b c a a d e e Das Diagramm beschreibt
Gibt es in Königsberg einen Spaziergang, bei dem man jede der. Pregelbrücken. überquert?
 Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
Eulerweg, Eulerkreis. Das Königsberger Brückenproblem. Definition 3.1. Ein Weg, der jede Kante von G genau einmal
 3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
Diskrete Mathematik. Kryptographie und Graphentheorie
 Diskrete Matheatik Kryptographie und Graphentheorie Jochen Hores & Jonas Bühler 14.06.006 Jochen Hores, Jonas Bühler Kryptographie & Graphentherorie 1 Inhaltsverzeichnis Inhaltsverzeichnis 1. Kryptographie
Diskrete Matheatik Kryptographie und Graphentheorie Jochen Hores & Jonas Bühler 14.06.006 Jochen Hores, Jonas Bühler Kryptographie & Graphentherorie 1 Inhaltsverzeichnis Inhaltsverzeichnis 1. Kryptographie
Graphen und Algorithmen
 Graphen und Algorithmen Vorlesung #8: Färbungsprobleme Dr. Armin Fügenschuh Technische Universität Darmstadt WS 2007/2008 Übersicht Knotenfärbung (vs. Kanten- & Kartenfärbung) Satz von Brooks Algorithmen
Graphen und Algorithmen Vorlesung #8: Färbungsprobleme Dr. Armin Fügenschuh Technische Universität Darmstadt WS 2007/2008 Übersicht Knotenfärbung (vs. Kanten- & Kartenfärbung) Satz von Brooks Algorithmen
3 Die natürlichen Zahlen. Themen: Vollständige Induktion Varianten des Induktionsprinzips Induktion über den rekursiven Aufbau Die ganzen Zahlen
 3 Die natürlichen Zahlen Themen: Vollständige Induktion Varianten des Induktionsprinzips Induktion über den rekursiven Aufbau Die ganzen Zahlen Die natürlichen Zahlen Æ = {1, 2, 3,...}. sind die natürlichen
3 Die natürlichen Zahlen Themen: Vollständige Induktion Varianten des Induktionsprinzips Induktion über den rekursiven Aufbau Die ganzen Zahlen Die natürlichen Zahlen Æ = {1, 2, 3,...}. sind die natürlichen
Eulerscher Polyedersatz
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
3-Färbbarkeit. Korollar: Zu Entscheiden, ob ein Graph k-färbbar ist mit k 3, ist NP-vollständig.
 3-Färbbarkeit Wir wissen bereits, dass in polynomieller Zeit entschieden werden kann, ob ein Graph 2-färbbar ist. Satz: Zu Entscheiden, ob ein Graph 3-färbbar ist, ist NPvollständig. Beweis: Reduktion
3-Färbbarkeit Wir wissen bereits, dass in polynomieller Zeit entschieden werden kann, ob ein Graph 2-färbbar ist. Satz: Zu Entscheiden, ob ein Graph 3-färbbar ist, ist NPvollständig. Beweis: Reduktion
Graphentheorie. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
 Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Königsberger Brückenproblem
 Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS: Klassische Probleme der Mathematik Leitung: Prof. Dr. Harald Upmeier, Benjamin Schwarz Referentin: Lene Baur WS 2009/2010 Königsberger
Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS: Klassische Probleme der Mathematik Leitung: Prof. Dr. Harald Upmeier, Benjamin Schwarz Referentin: Lene Baur WS 2009/2010 Königsberger
Bäume und Wälder. Definition 1
 Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Listenfärbung von Graphen
 Listenfärbung von Graphen Martin Matković WS 2011/2012 Abstract Martin Matković 14. April 2012 In dieser Arbeit werden Definitionen und grundlegende Eigenschaften von Graphenfärbungen und speziell von
Listenfärbung von Graphen Martin Matković WS 2011/2012 Abstract Martin Matković 14. April 2012 In dieser Arbeit werden Definitionen und grundlegende Eigenschaften von Graphenfärbungen und speziell von
Mathematische Probleme, SS 2013 Montag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
$Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
Graphen. Leonhard Euler ( )
 Graphen Leonhard Euler (1707-1783) 2 Graph Ein Graph besteht aus Knoten (nodes, vertices) die durch Kanten (edges) miteinander verbunden sind. 3 Nachbarschaftsbeziehungen Zwei Knoten heissen adjazent (adjacent),
Graphen Leonhard Euler (1707-1783) 2 Graph Ein Graph besteht aus Knoten (nodes, vertices) die durch Kanten (edges) miteinander verbunden sind. 3 Nachbarschaftsbeziehungen Zwei Knoten heissen adjazent (adjacent),
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. wer das Problem löste 4
 Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen. Martin Oellrich. Warum eine Karte? 3. Warum stetige Grenzen?
 Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen Problemstellung Deutsche Bundesländer in vier Farben 4. April 06 Martin Oellrich Warum geht das immer? Gegeben: Karte eines Gebietes
Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen Problemstellung Deutsche Bundesländer in vier Farben 4. April 06 Martin Oellrich Warum geht das immer? Gegeben: Karte eines Gebietes
Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert?
 Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? Königsberger Brückenproblem Gibt es in Königsberg einen Spaziergang, bei dem man
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? Königsberger Brückenproblem Gibt es in Königsberg einen Spaziergang, bei dem man
Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume)
 WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Freie Bäume und Wälder
 (Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
(Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
2.4. Triangulierung von Polygonen
 Als drittes Problem haben wir in Kapitel 1 die Triangulierung von Polygonen identifiziert, die etwa bei der Überwachung eines Museums durch Kameras auftritt. F70 F71 Definition und Theorie: Definition
Als drittes Problem haben wir in Kapitel 1 die Triangulierung von Polygonen identifiziert, die etwa bei der Überwachung eines Museums durch Kameras auftritt. F70 F71 Definition und Theorie: Definition
OR für Wirtschaftsingenieure. Übungsserie 7: Färbungen von Graphen
 HTWD, Fakultät Informatik/Mathematik Prof. Dr. M. Voigt Operations Research allgemeine Optimierungsmethoden OR für Wirtschaftsingenieure Übungsserie : Färbungen von Graphen Aufgabe 1 : Wieviele Farben
HTWD, Fakultät Informatik/Mathematik Prof. Dr. M. Voigt Operations Research allgemeine Optimierungsmethoden OR für Wirtschaftsingenieure Übungsserie : Färbungen von Graphen Aufgabe 1 : Wieviele Farben
Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Esparza)
 WS 2013/14 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ws/ds/uebung/ 22. Januar 2014 ZÜ DS ZÜ XIII
WS 2013/14 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ws/ds/uebung/ 22. Januar 2014 ZÜ DS ZÜ XIII
Drei Vorlesungen über Bäume
 Bäume. Einleitung Drei Vorlesungen über Bäume Jens Vygen Nehmen wir einmal an, für einen neuen Zug wollen wir ein komplett neues Schienennetz bauen, das einige Städte miteinander verbindet. Oder ein neues
Bäume. Einleitung Drei Vorlesungen über Bäume Jens Vygen Nehmen wir einmal an, für einen neuen Zug wollen wir ein komplett neues Schienennetz bauen, das einige Städte miteinander verbindet. Oder ein neues
Drei Anwendungen der Eulerschen Polyederformel
 Drei Anwendungen der Eulerschen Polyederformel Seminar aus Reiner Mathematik Viktoria Weißensteiner 04. Dezember 2013 Inhaltsverzeichnis 1 Einleitung 2 2 Vorbereitende Theorie 3 2.1 ebene Graphen..........................
Drei Anwendungen der Eulerschen Polyederformel Seminar aus Reiner Mathematik Viktoria Weißensteiner 04. Dezember 2013 Inhaltsverzeichnis 1 Einleitung 2 2 Vorbereitende Theorie 3 2.1 ebene Graphen..........................
Minimal spannender Baum
 Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Elemente der Graphentheorie
 Universität Karlsruhe Elemente der Graphentheorie Schnupperkurs SS 2008 verfasst von Prof. Dr. Andreas Kirsch Institut für Algebra und Geometrie Universität Karlsruhe (TH) 1 Literaturliste über Graphentheorie
Universität Karlsruhe Elemente der Graphentheorie Schnupperkurs SS 2008 verfasst von Prof. Dr. Andreas Kirsch Institut für Algebra und Geometrie Universität Karlsruhe (TH) 1 Literaturliste über Graphentheorie
KARL-FRANZENS-UNIVERSITÄT GRAZ. Seminar aus Reiner Mathematik. Die Museumswächter. Krupic Mustafa Wintersemester 2013/14
 KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
2 Eulersche Polyederformel und reguläre Polyeder
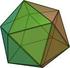 6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
 Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
WESTFÄLISCHE WILHELMS-UNIVERSITÄT MÜNSTER. Über 7 Brücken... wissen leben WWU Münster. Dietmar Lammers Hochschultag 201
 MÜNSTER Über 7 Brücken... Dietmar Lammers Hochschultag 201 MÜNSTER Über 7 Brücken... 2/29 > Dauerwerbeveranstaltung für ein Studium der Informatik- aber mit mathematischem Inhalt! Hier: Ein Auszug aus
MÜNSTER Über 7 Brücken... Dietmar Lammers Hochschultag 201 MÜNSTER Über 7 Brücken... 2/29 > Dauerwerbeveranstaltung für ein Studium der Informatik- aber mit mathematischem Inhalt! Hier: Ein Auszug aus
3 Klassifikation wichtiger Optimierungsprobleme
 3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
William Rowan Hamilton,
 3.2.2 Hamiltonkreise Definition 130. In einem Graph G = (V,E) nennt man einen Kreis, der alle Knoten aus V genau einmal durchläuft, einen Hamiltonkreis. Enthält ein Graph eine Hamiltonkreis, nennt man
3.2.2 Hamiltonkreise Definition 130. In einem Graph G = (V,E) nennt man einen Kreis, der alle Knoten aus V genau einmal durchläuft, einen Hamiltonkreis. Enthält ein Graph eine Hamiltonkreis, nennt man
6. Übung zur Linearen Optimierung SS08
 6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
1. Übung Graphentheorie WS2016/17
 1. Übung Graphentheorie WS2016/17 1. Schreiben Sie für jede Ecke der folgenden 7 Graphen den Grad auf! Welche der Graphen sind regulär? G 1 G 2 G 5 G 3 2. Bestimmen Sie alle paarweise nicht-isomorphen
1. Übung Graphentheorie WS2016/17 1. Schreiben Sie für jede Ecke der folgenden 7 Graphen den Grad auf! Welche der Graphen sind regulär? G 1 G 2 G 5 G 3 2. Bestimmen Sie alle paarweise nicht-isomorphen
3 Planare Graphen die Eulersche Polyederformel
 3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
Diskrete Mathematik 1
 Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May M. Ritzenhofen, M. Mansour Al Sawadi, A. Meurer Lösungsblatt zur Vorlesung Diskrete Mathematik 1 WS 2008/09 Blatt
Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May M. Ritzenhofen, M. Mansour Al Sawadi, A. Meurer Lösungsblatt zur Vorlesung Diskrete Mathematik 1 WS 2008/09 Blatt
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen)
 WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
9: Gewichtete Graphen
 Chr.Nelius: Graphentheorie (WS 06/7) 9 9: Gewichtete Graphen Beispiel: Eine Straßenkarte mit Entfernungsangaben zwischen den Orten ist ein Beispiel für einen gewichteten Graphen. (9.) DEF: Ein Graph G
Chr.Nelius: Graphentheorie (WS 06/7) 9 9: Gewichtete Graphen Beispiel: Eine Straßenkarte mit Entfernungsangaben zwischen den Orten ist ein Beispiel für einen gewichteten Graphen. (9.) DEF: Ein Graph G
Vorlesungen vom 5.Januar 2005
 Vorlesungen vom 5.Januar 2005 5 Planare Graphen 5.1 Beispiel: Gas, Wasser, Elektrik Drei eingeschworene Feinde, die im Wald leben, planen Trassen zu den Versorgungswerken für die drei Grundgüter Gas, Wasser
Vorlesungen vom 5.Januar 2005 5 Planare Graphen 5.1 Beispiel: Gas, Wasser, Elektrik Drei eingeschworene Feinde, die im Wald leben, planen Trassen zu den Versorgungswerken für die drei Grundgüter Gas, Wasser
Übungen zu Kombinatorik und Graphentheorie
 Übungen zu Kombinatorik und Graphentheorie Ilse Fischer, SS 07 (1) (a) In einer Schachtel sind 4 rote, 2 blaue, 5 gelbe und 3 grüne Stifte. Wenn man die Stifte mit geschlossenen Augen zieht, wieviele muss
Übungen zu Kombinatorik und Graphentheorie Ilse Fischer, SS 07 (1) (a) In einer Schachtel sind 4 rote, 2 blaue, 5 gelbe und 3 grüne Stifte. Wenn man die Stifte mit geschlossenen Augen zieht, wieviele muss
Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr)
 WS 2011/12 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/uebung/ 25. Januar 2012 ZÜ DS ZÜ XIII
WS 2011/12 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/uebung/ 25. Januar 2012 ZÜ DS ZÜ XIII
Diskrete Strukturen in der Informatik
 Diskrete Strukturen in der Informatik Markus Lohrey Universität Leipzig Wintersemester 2012/2013 Lohrey (Universität Leipzig) Diskrete Strukturen Wintersem. 2012/2013 1 / 287 Organisatorisches zur Vorlesung
Diskrete Strukturen in der Informatik Markus Lohrey Universität Leipzig Wintersemester 2012/2013 Lohrey (Universität Leipzig) Diskrete Strukturen Wintersem. 2012/2013 1 / 287 Organisatorisches zur Vorlesung
Das Vierfarbenproblem und verwandte Fragestellungen
 Eichstätter Kolloquium zur Februar 010 Didaktik der Mathematik Das Vierfarbenproblem und verwandte Fragestellungen Cornelia Minette Busch 1 Das Vierfarbenproblem Wenn Schüler eine politische Landkarte
Eichstätter Kolloquium zur Februar 010 Didaktik der Mathematik Das Vierfarbenproblem und verwandte Fragestellungen Cornelia Minette Busch 1 Das Vierfarbenproblem Wenn Schüler eine politische Landkarte
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul Einführung
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul Einführung
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel. Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien.
 Lösungen Übung 13 Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien. a) Strategie 1 (nächster Nachbar): Jedes Mal reist der Reisende vom Punkt, wo er gerade ist, zur nächstgelegenen Stadt,
Lösungen Übung 13 Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien. a) Strategie 1 (nächster Nachbar): Jedes Mal reist der Reisende vom Punkt, wo er gerade ist, zur nächstgelegenen Stadt,
Grundbegri e der Graphentheorie: Eckengrad, Wege und Kreise, Zusammenhang
 raphen- und Berechenbarkeitstheorie rundbegri e der raphentheorie: Eckengrad, Wege und Kreise, Zusammenhang 0.1 raphen Ein raph ist ein aar = (V, E) disjunkter Mengen mit E [V ]2, wobei [V ]2 die Menge
raphen- und Berechenbarkeitstheorie rundbegri e der raphentheorie: Eckengrad, Wege und Kreise, Zusammenhang 0.1 raphen Ein raph ist ein aar = (V, E) disjunkter Mengen mit E [V ]2, wobei [V ]2 die Menge
Nachbarschaft, Grad, regulär, Inzidenz
 Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter WS 2009/10 Isomorphie Zwei Graphen (V 1, E 1 ) und (V 2, E 2 ) heißen isomorph, wenn es eine bijektive, Kanten erhaltende und Kanten
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter WS 2009/10 Isomorphie Zwei Graphen (V 1, E 1 ) und (V 2, E 2 ) heißen isomorph, wenn es eine bijektive, Kanten erhaltende und Kanten
Eulerscher Polyedersatz
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Vervollständigung Lateinischer Quadrate
 Vervollständigung Lateinischer Quadrate Elisabeth Schmidhofer 01.12.2013 Inhaltsverzeichnis 1 Vorwort 3 2 Einleitung 4 2.1 Beispele.............................................. 4 3 Lateinische Quadrate
Vervollständigung Lateinischer Quadrate Elisabeth Schmidhofer 01.12.2013 Inhaltsverzeichnis 1 Vorwort 3 2 Einleitung 4 2.1 Beispele.............................................. 4 3 Lateinische Quadrate
Tutoraufgabe 1 (Suchen in Graphen):
 Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS14 F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe 1 (Suchen in Graphen): a) Geben Sie die Reihenfolge an, in der die Knoten besucht werden, wenn
Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS14 F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe 1 (Suchen in Graphen): a) Geben Sie die Reihenfolge an, in der die Knoten besucht werden, wenn
