Liegt eine Kante k auf einem Zyklus Z, so liegt k auf dem Rand genau zweier
|
|
|
- Clemens Peters
- vor 7 Jahren
- Abrufe
Transkript
1 4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie. Hier werden konkret Ecken als Punkte der Ebene angesehen und Kanten als Kurven in der Ebene, die diese Punkte verbinden und sich nicht überschneiden. Etwas genauer definieren wir: Definition 4.1 Ein planarer (oder ebener) Graph besteht aus einer Eckenmenge, einer Kantenmenge und einer Flächenmenge (alle endlich) in der Ebene, so dass sich die Kanten nicht überschneiden und folgendes gilt: Genau eine Fläche ist unbeschränkt. Der Rand jeder Fläche besteht aus endlich vielen Kanten. Liegt eine Kante k auf einem Zyklus Z, so liegt k auf dem Rand genau zweier Flächen. Liegt k auf keinem Zyklus, so liegt k auf dem Rand von genau einer Fläche. Im folgenden sei n die Anzahl der Ecken, m die Anzahl der Kanten, f die Anzahl der Flächen und q die Anzahl der Zusammenhangskomponenten. 4.1 Die Eulersche Polyederformel Der folgende Satz ist das Hauptthema dieses Abschnitts. Satz 4.2 (Eulersche Polyederformel) Sei G ein ebener Graph mit n Ecken, m Kanten, q Zusammenhangskomponenten und f Flächen. Dann gilt n+f m = 1+q. Beweis: Wir führen den Beweis durch vollständige Induktion nach m. m = 0: Dann ist q = n und f = 1 (weshalb?). Daher ist die Formel richtig für m = 0. Sei die Behauptung richtig für alle Graphen mit weniger als m Kanten, und sei G ein Graph mit m Kanten, m Fall:GbesitzteinenZyklusZ.Seik Z einekantedeszyklusunddefiniereg = G k, d.h. G entsteht aus G durch Streichen der Kante k. Dann ist zunächst m = m 1 und n = n. Da k Randkante von zwei verschiedenen Gebieten war, so ist f = f 1. Außerdem ist q = q, da die Endpunkte von k ja über den Kreis noch verbunden sind. Nach Induktionsvoraussetzung ist n +f m = 1+q, also n+(f 1) (m 1) = 1+q, also n+f m = 1+q. 2. Fall: G besitzt keinen Kreis. Dann besitzt keine Zusammenhangskomponente Kreise. Wegen m 1 existiert eine Zusammenhangskomponente mit mindestens einer Kante. In 21
2 dieser Komponente ist der Eckengrad jeder Ecke mindestens 1. Nach Satz?? existiert eine Ecke e in dieser Komponente mit d(e) = 1, denn der Fall d(e) = 0 scheidet aus. Sei k die (einzige) Kante, die an e hängt. Definiere G = G k. Dann ist zunächst n = n und m = m 1. Da e isolierte Ecke von G, aber nicht von G ist, so ist q = q + 1. Außerdem ist f = f. Die Induktionsvoraussetzung liefert n + f m = 1 + q, also n+f (m 1) = q +2, also n+f m = q +1. Bemerkung: Da n, m, q für jeden Graphen definiert sind, so liefert die Eulersche Polyederformel auch, dass die Anzahl der Flächen für jede Einbettung eines planaren Graphen gleich ist. Daher kann man von der Anzahl der Flächen eines planaren Graphen sprechen, und die Eulersche Polyederformel gilt für jeden planaren Graphen. Satz 4.3 Sei G ein planarer Graph ohne doppelte Kanten mit n Ecken und m Kanten. (a) Ist n 3, so ist m 3n 6. (b) Es gibt wenigstens eine Ecke e mit Grad d(e) 5. Beweis: (a) Wegen 3n 6 3 ist nur der Fall m 4 interessant (denn für m = 1, 2, 3 gilt die Ungleichung ja trivialerseise). Jede Fläche wird von mindestens 3 Kanten begrenzt (sonst gäbe es doppelte Kanten). Nach Definition gehört jede Kante zum Rand von höchstens 2 Flächen. Wenn man also jede Kante doppelt zeichnet, so kann man jedes Land mit verschiedenen Kanten begrenzen. Daher folgt 3f 2m. Die Polyederformel liefert n+f m = 1+q, also wegen q 1: also m 3n 6. m = n+f 1 q n+ 2 3 m 1 q n+ 2 3 m 2, (b) Wirkönnen n 3voraussetzen. Annahme, es sei d(e) 6für jedeecke e. DerSatz2.1 und Teil (a) würden dann 6n d(e) = 2m 6n 12 liefern, was nicht möglich ist. e Ecke Weiter unten werden wir zeigen, dass die Aussage (b) scharf ist, d.h. es gibt wirklich einen planaren Graphen ohne doppelte Kanten, in dem jede Ecke den Grad 5 hat. Beispiele 4.4 (a) K 5 ist nicht planar. Beweis: Andernfalls würde Teil (a) vom letzten Satz wegen n = 5 und m = 5 4 = 10 2 liefern: 10 = m 3n 6 = 9, ein Widerspruch. (b) K 3,3 ist nicht planar. Beweis: Annahme K 3,3 ist planar, also in die Ebene einbettbar. Jede Fläche wird dann von mindestens 4 Kanten berandet (sonst würden Kreise der Länge 3 existieren, was nicht möglich ist). Also können wir wie im Satz argumentieren und erhalten: 4f 2m, d.h. 2f m = 9, d.h. f 4. Auf der anderen Seite liefert die Polyederformel f = 2+m n = = 5, ein Widerspruch. 22
3 4.2 Die Platonischen Körper Ein Polytop ist eine beschränkte Menge, die sich als Durchschnitt endlich vieler Halbräume im Raum darstellen lässt. Unter einem platonischen Körper versteht man ein Polytop, dessen Seiten ebene kongruente regelmäßige Vielecke sind, z.b. Würfel (Quadrate), Tetraeder (gleichseitige Dreiecke), Dodekaeder (regelmäßige Fünfecke). Jedem platonischen Körper kann man in natürlicher Weise einen planaren Graphen zuordnen mit Ecken und Kanten. Man umschreibe nämlich dem Körper eine Kugel, nachdem man ihn so gedreht hat, dass der Strahl vom Mittelpunkt der Kugel durch den Nordpol der Kugel durch eine Seite stößt (und nicht durch eine Ecke oder Kante). Jetzt projiziere man Ecken und Kanten auf die Sphäre vom Mittelpunkt aus. Dies ergibt einen Graphen auf der Sphäre mit der Eigenschaft, dass der Nordpol innerhalb einer Fläche liegt. Letzt projiziere man vom Nordpol aus in die Äquatorebene. Dies liefert einen planaren Graph, die Fläche mit dem Nordpol wird die unbeschränkte äußere Fläche. Für den Würfel und den Dodekaeder sind z.b. isomorph zu Jetzt können wir zeigen: Satz 4.5 Es gibt genau 5 verschiedene platonische Körper, nämlich Tetraeder, Würfel, Oktaeder, Dodekaeder und Ikosaeder. Beweis:SeiwiederndieAnzahlderEcken, mdieanzahlderkantenundf dieanzahlder Seitenflächen. Wir betrachten als Seiten regelmäßige p-ecken, p 3. Beim platonischen Körper stoßen an jede Ecke gleich viele Kanten an, also d(e) = d für alle Ecken e. Damit reduziert sich die Formel von Satz 2.1 (nämlich e Ed(e) = 2m) auf dn = 2m. Da jede Fläche p Kanten hat, folgt pf = 2m, d.h. m = pf/2. In die erste Formel eingesetzt ergibt n = pf/d. Die Eulersche Polyederformel liefert pf d +f pf 2 = 2, d.h. 2pf +2df pdf = 4d, d.h. f = 4d 2p+2d pd. Wir gehen die Fälle für d durch: 23
4 d = 3: Dann f = 12 6 p. Da f N, so ist nur p = 3,4,5 f = 4,6,12 möglich. d = 4: Dann f = 16 = 8, also nur p = 3, f = 8 möglich. 8 2p 4 p d = 5: Dann f = 20, also nur p = 3, f = 20 möglich. 10 3p Für d 6 ist 2p+2d pd = 2p (p 2)d 2p 6(p 2) = 12 4p 0. Dies liefert kein positives f N. Damit haben wir alle Platonischen Körper gefunden: n m f d p Tetraeder Oktaeder Würfel Ikosaeder Dodekaeder Färbbarkeit ebener Graphen Ich halte mich in diesem Abschnitt an das interessante Buch von Aigner über Graphentheorie, der die Entwicklung dieses Gebietes aus dem 4-Farben Problem schildert. Beim 4-Farben Problem geht es bekanntlich darum, die Flächen eines ebenen Graphen mit insgesamt 4 Farben so zu färben, dass je zwei über Kanten berührende Flächen unterschiedliche Farben haben. Der erste, der behauptete, einen Beweis für das 4-Farben Problem gefunden zu haben, war ein gewisser A. Kempe 1 im Jahr Seine Lösung wurde mit Begeisterung aufgenommen, und er wurde sofort zum Fellow of the Royal Society gewählt. Erst 10 Jahre später zeigte Heawood einen Fehler auf. Trotzdem beinhaltet Kempe s Versuch gute Ideen, die z.b. beim Beweis des 5-Farben Satzes benutzt werden können. Definition 4.6 Ein ebener Graph mit den Flächen F = {F 1,...,F f } heißt q-färbbar, wenn es eine Abbildung ϕ : F {1,...,q} gibt mit ϕ(f) ϕ(f ) für alle Flächen F und F, die eine gemeinsame Randkante besitzen. Für Flächen sagen wir im folgende auch Länder. Ganz entscheidend ist der folgende Satz: Satz 4.7 Sei G ein ebener Graph mit Eckengrad d(e) 3 für alle Ecken e. Dann gibt es wenigstens eine Fläche mit höchstens 5 Randkanten. 1 Rechtanwalt und Mitglied der Londoner Mathematischen Gesellschaft. 24
5 Beweis: Sei f i, i = 1,2,..., die Anzahl der Flächen mit i Randkanten. Ist f die Gesamtzahl, so ist natürlich f = f i. Jede Kante von G begrenzt eine oder zwei Flächen. Ist m i die Zahl der Kanten, so folgt daraus if i 2m (abzählen!). Aus Satz 2.1 folgt wegen i d(e) 3 für alle Ecken: 3n d(e) = 2m. Multiplikation der Eulersche Polyederformel e mit 6 liefert 6(1+q) = 6n+6f 6m = (6n 4m }{{} ) + (6f 2m) 6f 2m 0 6f i if i = i 1(6 i)f i, also 0 < 6(1+q) i 1(6 i)f i. Wegen 6 i 0 für i 6 muss mindestens eines der f 1, f 2, f 3, f 4 oder f 5 positiv sein. Bemerkungen: (a) Die Voraussetzung d(e) 3 für alle e ist natürlich notwendig, denn sonst könnte man durch Unterteilung des Randes einer Fläche die Zahl der Randkanten beliebig erhöhen. (b) Die Aussage dieses Satzes entspricht genau der von Satz 4.3, dass jeder planare Graph ohne doppelte Kanten eine Ecke mit Grad 5 besitzt. Durch Dualisierung gehen beide Aussagen ineinander über. Der duale Graph G zu einem ebenen Graph G ist folgendermaßen erklärt: Die Ecken von G bestehen aus den Flächen von G, und zwei Ecken von G sind durch eine Kante verbunden, wenn die entsprechenden Flächen eine gemeinsame Randkante besitzen. Die Aussage des letzten Satzes ist scharf, denn das Dodekaeder hat 12 Flächen, bestehend nur aus Fünfecken. Auf Seite 23 ist seine Projektion in der Ebene gezeichnet. Durch Dualisierung gewinnen wir also auch ein Beispiel dafür, dass der Satz 4.3 scharf ist. Wir wollen jetzt Kempe s Beweisgang nachvollziehen. Er verläuft durch vollständige Induktion über f. Wir versuchen es zunächst mit 4 Farben. Die Fälle f 4 sind trivial, 4 Farben reichen für 4 Flächen natürlich aus. Wir setzen also jetzt voraus, jeder ebene Graph mit höchstens f 1 Flächen sei färbbar (mit 4 Farben), und es sei G ein ebener Graph mit f Flächen. Zunächst zeigen wir, dass wir ohne Beschränkung d(e) 3 für alle Ecken e voraussetzen können: Wir betrachten dafür zunächst G 0 = G {e : d(e) = 0}, d.h. wir entfernen von G alle isolierten Punkte. Haben wir G 0 gefärbt, so auch G. Jetzt betrachten wir nacheinander den Graphen G l+1 (l = 0,1,...), der aus G l entsteht, indem wir eine Ecke mit Grad 1 entfernen und die daran anstoßende Kante. Haben wir G l gefärbt, so auch G l+1, denn die an e l hängende Kante begrenzt ja nur eine Fläche. Der Iterationsprozess stoppt irgendwann mit einem Graphen G mit d(e) 2 für alle Ecken e. Eine Ecke e von G mit d(e) = 2 können wir 25
6 eliminieren, indem wir die beiden an e anstoßenden Kanten k 1 und k 2 verschmelzen falls die anderen Endpunkte von k 1 und k 2 verschieden sind. Sind diese Endpunkte gleich und nennen wir diesen ẽ, so sind e und ẽ durch eine Doppelkante verbunden und diese ragt bei e in eine Fläche F hinein. Haben wir den Rest gefärbt, so können wir das Innere dieser Schleife mit einer Farbe, der verschieden von der von F ist, färben. Man skizziere diese Fälle! Jetzt können wir Satz 4.7 anwenden. Daher gibt es eine Fläche F mit höchstens 5 Randkanten. Wir untersuchen jetzt die Fälle für 2, 3, 4 und 5 Randkanten getrennt. 1. Fall: F habe genau zwei Randkanten k 1 und k 2. Dann gibt es auch zwei Randecken e 1 und e 2. Wir bilden jetzt G k 1. Dieser neue Graph G hat f 1 Flächen und ist daher färbbar. Die Kante k 1 liegt in einer Fläche F mit Farbe 1. Die Kante k 2 stößt außer an F nur noch an eine weitere Fläche F an mit Farbe 2. Färbe jetzt F mit einer Farbe verschieden von 1 und 2. e 1 k 1 k 2 e 2 F e1 F e 2 k 2 Graph G Graph G 2. Fall: F habe genau drei Randkanten k 1, k 2, k 3 mit den angrenzenden Flächen A, B, C (siehe Bild). Wir benutzen jetzt eine auf Kempe zurückgehende Idee, die wir im folgenden Kontraktion nennen, und erzeugen einen Graphenmit f 1 Flächen auf folgende Weise: Zunächst fügen wir in F eine Ecke e ein und verbinden e mit den drei Ecken von F. Dann streichen wir die Randkanten zu A, B, C und schlagen damit F zu die Flächen A, B, C hinzu. Diese werden mit A, B, C bezeichnet. Der so konstruierte Graph G ist nach Induktionsvorauusetzung färbbar. Die drei ursprünglichen Randkanten von F liegen in den Ländern A, B, C, die mit drei verschiedenen Farben gefärbt sind. Gehen wir wieder zurück zu G, so ist also eine Farbe für F noch übrig. 26
7 A F B A B C C Graph G Graph G 3. Fall: F habe genau vier Randkanten mit angrenzenden Flächen A, B, C, D. Wieder kontrahieren wir und färben die Kontraktion G mit den Farben 1,2,3,4. Benötigen wir für die 4 Flächen nur drei Farben, so sind wir fertig, denn die 4. Farbe kann für F benutzt werden. Wir nehmen also an, alle 4 Farben 1,...,4 werden für die Färbung von A, B, C, D benötigt, und sie seien in dieser Reihenfolge gefärbt. Im Bild sind die Farben 1,2,3,4 durch rot, blau, grün, gelb repräsentiert. A F B 4 4 D 4 C Wir betrachten jetzt Ketten von aneinanderstoßenden Flächen. Es kann nicht sowohl eine 27
8 solche Kette von A nach C, die abwechselnd mit rot und grün gefärbt ist, geben als auch eine von B nach D, die abwechselnd mit blau und gelb gefärbt ist. Denn solche Ketten müssten sich schneiden, also eine gemeinsame Fläche haben, was natürlich nicht geht. Ohne Einschränkung nehmen wir an, es gebe keine blau-gelb-kette von B nach D. Betrachte jetzt die Menge F aller Flächen, die von B aus durch blau-gelb-ketten erreichbar sind. Im Plot sind sie gestrichelt gezeichnet. Die Flächen A, C und D gehören jedenfalls nicht dazu. In diesen Flächen von F vertauschen wir jetzt die Farben blau und gelb. Dann erhalten wir eine neue zulässige Färbung, denn: Jede Fläche F F ist blau oder gelb. Sei F eine Nachbarfläche. Ist sie rot oder blau gefärbt, so beeinflusst das Vertauschen von blau und gelb die Zulässigkeit nicht. Ist sie gelb (falls F blau) bzw. blau (falls F gelb), so ist auch F F und ihre Farbe wird ebenfalls vertauscht. Daher erhalten wir eine zulässige Färbung, bei der jetzt B die Farbe gelb erhält. Es bleibt also die Farbe blau übrig, mit der wir F färben können. Solche Ketten heißen Kempe-Ketten und wurden von ihm auch für den Fall benutzt, dass es Flächen mit 5 Randkanten gibt. Seine Argumenation enthielt aber einen Fehler (siehe unten). Allerdings können wir zeigen: Satz 4.8 (5 Farbensatz, Heawood 1890) Jeder ebene Graph kann mit 5 Farben gefärbt werden. Beweis: Wir führen den selben Induktionsschluss durch wie oben, nur für 5 statt für 4 Farben. Wir brauchen jetzt nur noch den 4 ten Fall betrachten, dass nämlich eine Fläche F mit 5 Randkanten und angrenzenden Flächen A, B, C, D, E existiert. Das Kontraktionsargument liefert die Färbbarkeit aller Flächen ohne F mit 5 Farben. Ohne Einschränkung können wir annehmen, dass die Nachbarflächen A, B, C, D, E mit den Farben rot, blau, grün, gelb und schwarz (in dieser Reihenfolge) belegt sind. Existiert nun keine rot-grün-kette von A nach C, so kann durch Vertauschung der Farben rot und grün eine Farbe eingespart werden. Falls es aber eine rot-grün-kette von A nach C gibt, so kann es sicher keine blau-gelb-kette von B nach D geben, und man kann hier eine Farbe einsparen, die für F verwendet werden kann. Damit ist der Satz bewiesen. Wir wollen zum Schluss dieses Kapitels noch auf Kempe s Argument für den 4 Farbensatz eingehen. Seien jetzt also wie beim Beweis des Satzes 4.8 die Fläche F von den Flächen A, B, C, D und E begrenzt und alle 4 verfügbaren Farben seien benötigt, um sie zu färben. Bei uns seien es rot, blau, grün und gelb(in dieser Reihenfolge). Durch Umfärbung können wir die folgende Situation erreichen: 28
9 E D A F 4 C B Falls keine rot-grün-kette von A nach C existiert, so können wir wie oben eine Farbe einsparen genau wie in dem Fall, dass keine rot-gelb-kette von A nach D existiert. Wir nehmen jetzt also an, dass sowohl eine rot-grün-kette von A nach C existiert als auch eine rot-gelb-kette von A nach D. Dann ist B von D getrennt und E von C. Dies bedeutet, dass die Klasse F B bl ge = {F : es gibt blau-gelb-kette von B nach F } nicht auch D oder E enthalten kann. Genauso enthält die Klasse F E bl gr = {F : es gibt blau-grün-kette von E nach F } weder B noch C. Vertausche also in F B bl ge die Farben blau und gelb und in F E bl gr die Farben blau und grün. Dann hat A die Farbe rot, B und D die Farbe gelb, C und E die Farbe grün. Es bleibt die Farbe blau für F übrig. Worin liegt der Fehler? (siehe Beispiel auf der nächsten Seite) 29
10 30
11: Die Euler sche Polyederformel für planare Graphen
 Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Achilles und die Schildkröte Sommersemester 2008
 Achilles und die Schildkröte Sommersemester 2008 Färbbarkeit planarer Graphen Alexander Damarowsky 20.05.2008 V6, 15.05.2008 Problemstellung /Ziel des Vortrags: Wie viele Farben werden benötigt, um jeden
Achilles und die Schildkröte Sommersemester 2008 Färbbarkeit planarer Graphen Alexander Damarowsky 20.05.2008 V6, 15.05.2008 Problemstellung /Ziel des Vortrags: Wie viele Farben werden benötigt, um jeden
Eulerscher Polyedersatz
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Planare Graphen und Färbungen. Kapitel 7. Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/ / 296
 Kapitel 7 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 256 / 296 Inhalt Inhalt 7 Färbungen Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 257 / 296 Jordankurve Zentrale Frage
Kapitel 7 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 256 / 296 Inhalt Inhalt 7 Färbungen Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 257 / 296 Jordankurve Zentrale Frage
Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn
 Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn 1. Geschichte - Frage kommt Mitte des 19 Jahrhunderts auf Wie viele Farben benötigt man um eine Karte
Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn 1. Geschichte - Frage kommt Mitte des 19 Jahrhunderts auf Wie viele Farben benötigt man um eine Karte
Mathematische Probleme, SS 2013 Montag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
$Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
Alexandra Kuhls Proseminar Das Buch der Beweise
 Der Fünf Farben Satz Alexandra Kuhls Proseminar Das Buch der Beweise 30.11.2017 Der Fünf Farben Satz Ist es möglich, die Gebiete einer ebenen Karte so Ist es möglich, die Gebiete einer ebenen Karte so
Der Fünf Farben Satz Alexandra Kuhls Proseminar Das Buch der Beweise 30.11.2017 Der Fünf Farben Satz Ist es möglich, die Gebiete einer ebenen Karte so Ist es möglich, die Gebiete einer ebenen Karte so
Fünf-Farben-Satz. Seminar aus reiner Mathematik, WS 13/14. Schweighofer Lukas, November Seite 1
 Der Fünf- Farben-Satz Seminar aus reiner Mathematik, WS 13/14 Schweighofer Lukas, November 2013 Seite 1 Inhaltsverzeichnis Vorwort...3 Graphentheoretische Grundlagen...4 Satz 2 (Eulerscher Polyedersatz)...7
Der Fünf- Farben-Satz Seminar aus reiner Mathematik, WS 13/14 Schweighofer Lukas, November 2013 Seite 1 Inhaltsverzeichnis Vorwort...3 Graphentheoretische Grundlagen...4 Satz 2 (Eulerscher Polyedersatz)...7
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Eulerscher Polyedersatz
 Eigenschaften als reguläre Parkettierungen der Sphäre Seien E die der Ecken, F die der Flächen und K die der Kanten eines konvexen Polyeders, dann gilt: K E = F 2 als reguläre Parkettierungen der Sphäre
Eigenschaften als reguläre Parkettierungen der Sphäre Seien E die der Ecken, F die der Flächen und K die der Kanten eines konvexen Polyeders, dann gilt: K E = F 2 als reguläre Parkettierungen der Sphäre
Polyeder, Konvexität, Platonische und archimedische Körper
 Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
Der Fünf-Farben-Satz. Lukas Schweighofer. Feb.2014
 Der Fünf-Farben-Satz Lukas Schweighofer Feb.2014 1 Contents 1 Vorwort 3 2 Graphentheoretische Grundlagen 4 3 Satz 2 (Eulerscher Polyedersatz) 8 4 Satz 3 9 5 Der Fnf-Farben-Satz 10 5.1 Beweis 1..............................
Der Fünf-Farben-Satz Lukas Schweighofer Feb.2014 1 Contents 1 Vorwort 3 2 Graphentheoretische Grundlagen 4 3 Satz 2 (Eulerscher Polyedersatz) 8 4 Satz 3 9 5 Der Fnf-Farben-Satz 10 5.1 Beweis 1..............................
Eulerscher Polyedersatz
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Eulerscher Polyedersatz Beweis durch planare Graphen und Anwendung auf platonische Körper Die oben abgebildete Briefmarke wurde
Kantengraphen und Planare Graphen. Seminararbeit
 Kantengraphen und Planare Graphen Seminararbeit in Mathematisches Seminar für LAK 621.378 SS 2018 vorgelegt von Anna Maria Gärtner bei: Baur, Karin, Univ.-Prof. Dr.phil. Graz, 2018 Inhaltsverzeichnis 1
Kantengraphen und Planare Graphen Seminararbeit in Mathematisches Seminar für LAK 621.378 SS 2018 vorgelegt von Anna Maria Gärtner bei: Baur, Karin, Univ.-Prof. Dr.phil. Graz, 2018 Inhaltsverzeichnis 1
6. Planare Graphen und Färbungen
 6. Planare Graphen und Färbungen Lernziele: Den Begriff der Planarität verstehen und erläutern können, wichtige Eigenschaften von planaren Graphen kennen und praktisch einsetzen können, die Anzahl von
6. Planare Graphen und Färbungen Lernziele: Den Begriff der Planarität verstehen und erläutern können, wichtige Eigenschaften von planaren Graphen kennen und praktisch einsetzen können, die Anzahl von
Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist:
 Svenja Hüning, Michael Kerber, Hannah Schreiber WS 2016/2017 Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist: Hinweise: Dieses Blatt präsentiert Beispiellösungen zu
Svenja Hüning, Michael Kerber, Hannah Schreiber WS 2016/2017 Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist: Hinweise: Dieses Blatt präsentiert Beispiellösungen zu
Univ.-Prof. Dr. Goulnara ARZHANTSEVA
 Diskrete Mathematik Univ.-Prof. Dr. Goulnara ARZHANTSEVA SS 2018 c Univ.-Prof. Dr. Goulnara Arzhantseva Kapitel 08: Menger, König und Hall / Planare Graphen 1 / 30 Der Satz von Menger: s t trennende Kantenmenge
Diskrete Mathematik Univ.-Prof. Dr. Goulnara ARZHANTSEVA SS 2018 c Univ.-Prof. Dr. Goulnara Arzhantseva Kapitel 08: Menger, König und Hall / Planare Graphen 1 / 30 Der Satz von Menger: s t trennende Kantenmenge
Polyeder und Platonische Körper
 Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
durch Einfügen von Knoten konstruiert werden kann.
 Satz von Kuratowski Definition Unterteilung eines Graphen Sei G = (V, E) und e = {u, v} E. 1 Das Einfügen eines neuen Knoten w in die Kante e führt zum Graphen G = (V {w}, E \ e {{u, w}, {w, v}}). 2 Der
Satz von Kuratowski Definition Unterteilung eines Graphen Sei G = (V, E) und e = {u, v} E. 1 Das Einfügen eines neuen Knoten w in die Kante e führt zum Graphen G = (V {w}, E \ e {{u, w}, {w, v}}). 2 Der
Definition : Diechromatische Zahl eines Graphen G ist die kleinste Anzahl chromatische Zahl von Farben für eine zulässige Färbung.
 4 Definition : Eine zulässige Färbung ist eine Färbung der Knoten des ( un- zulässige Färbung gerichteten ) Graphen, so daß je zwei adjazente Knoten verschiedene Farben haben. Trivial ist, daß n verschiedene
4 Definition : Eine zulässige Färbung ist eine Färbung der Knoten des ( un- zulässige Färbung gerichteten ) Graphen, so daß je zwei adjazente Knoten verschiedene Farben haben. Trivial ist, daß n verschiedene
Färbungen von Graphen: Die chromatische Zahl und der Satz von Brooks
 Färbungen on Graphen: Die chromatische Zahl und der Satz on Brooks Florian Seerin Heinrich-Heine-Uniersität Düsseldorf Mathe-Akademie 2018 Definition. Ein (endlicher) Graph besteht aus einer (endlichen)
Färbungen on Graphen: Die chromatische Zahl und der Satz on Brooks Florian Seerin Heinrich-Heine-Uniersität Düsseldorf Mathe-Akademie 2018 Definition. Ein (endlicher) Graph besteht aus einer (endlichen)
Aus dem binomischen Lehrsatz ergeben sich sofort interessante Beziehungen zwischen den Binomialkoeffizienten.
 11 Aussagen, Beweise, vollständige Induktion 13 Aus dem binomischen Lehrsatz ergeben sich sofort interessante Beziehungen zwischen den Binomialkoeffizienten 114 Folgerung n ( ) n = (1+1) n = 2 n und k
11 Aussagen, Beweise, vollständige Induktion 13 Aus dem binomischen Lehrsatz ergeben sich sofort interessante Beziehungen zwischen den Binomialkoeffizienten 114 Folgerung n ( ) n = (1+1) n = 2 n und k
1.1. Aussagen, Beweise, vollständige Induktion 15
 11 Aussagen, Beweise, vollständige Induktion 15 Man kann die Methode der vollständigen Induktion auch auf vielfältige Weise einsetzen, um geometrische Aussagen zu beweisen Hier ein prominentes Beispiel
11 Aussagen, Beweise, vollständige Induktion 15 Man kann die Methode der vollständigen Induktion auch auf vielfältige Weise einsetzen, um geometrische Aussagen zu beweisen Hier ein prominentes Beispiel
Drei Anwendungen der Eulerschen Polyederformel
 Drei Anwendungen der Eulerschen Polyederformel Seminar aus Reiner Mathematik Viktoria Weißensteiner 04. Dezember 2013 Inhaltsverzeichnis 1 Einleitung 2 2 Vorbereitende Theorie 3 2.1 ebene Graphen..........................
Drei Anwendungen der Eulerschen Polyederformel Seminar aus Reiner Mathematik Viktoria Weißensteiner 04. Dezember 2013 Inhaltsverzeichnis 1 Einleitung 2 2 Vorbereitende Theorie 3 2.1 ebene Graphen..........................
REGULÄRE UND SEMIREGULÄRE POLYTOPE
 REGULÄRE UND SEMIREGULÄRE POLYTOPE regulare und semireguläre polytope ANDREAS PAFFENHOLZ FU Berlin Germany Eulersche Polyederformel Theorem Für ein Polytop mit Ecken Eulersche Polyederformel Kanten und
REGULÄRE UND SEMIREGULÄRE POLYTOPE regulare und semireguläre polytope ANDREAS PAFFENHOLZ FU Berlin Germany Eulersche Polyederformel Theorem Für ein Polytop mit Ecken Eulersche Polyederformel Kanten und
Übungsaufgaben Graphentheorie, Wintersemester 2011/12
 Übungsaufgaben Graphentheorie, Wintersemester 2011/12 Frank Göring 25. Januar 2012 Zusammenfassung Übungsaufgaben zur Graphentheorievorlesung. 1 Bis 19.10.2011 1. Wir hatten einen Graphen G als zusammenhängend
Übungsaufgaben Graphentheorie, Wintersemester 2011/12 Frank Göring 25. Januar 2012 Zusammenfassung Übungsaufgaben zur Graphentheorievorlesung. 1 Bis 19.10.2011 1. Wir hatten einen Graphen G als zusammenhängend
KARL-FRANZENS-UNIVERSITÄT GRAZ. Seminar aus Reiner Mathematik. Die Museumswächter. Krupic Mustafa Wintersemester 2013/14
 KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
Ein Turnierplan mit fünf Runden
 Mathematik I für Informatiker Graphen p. 1 Ein Turnierplan mit fünf Runden c b a c b a c b a c b a c b a d e d e d e d e d e Mathematik I für Informatiker Graphen p. 2 Definition: Graph Ein (schlichter)
Mathematik I für Informatiker Graphen p. 1 Ein Turnierplan mit fünf Runden c b a c b a c b a c b a c b a d e d e d e d e d e Mathematik I für Informatiker Graphen p. 2 Definition: Graph Ein (schlichter)
Bastelbogen platonische Körper
 E s gibt in der Geometrie einige wenige Körper, die die größtmögliche Symmetrie besitzen. Sie wurden nach dem griechischen Philosophen Platon (428-348 v. Chr.) benannt und heißen deswegen platonische Körper.
E s gibt in der Geometrie einige wenige Körper, die die größtmögliche Symmetrie besitzen. Sie wurden nach dem griechischen Philosophen Platon (428-348 v. Chr.) benannt und heißen deswegen platonische Körper.
Freie Bäume und Wälder
 (Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
(Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
Naiver Algorithmus für Hamiltonkreis
 Naiver Algorithmus für Hamiltonkreis Algorithmus HAMILTON EINGABE: G = ([n], E) in Adjazenzmatrixdarstellung 1 Für alle Permutationen π : [n] [n]. 1 Falls (π(1), π(2),..., π(n)) ein Kreis in G ist, AUSGABE
Naiver Algorithmus für Hamiltonkreis Algorithmus HAMILTON EINGABE: G = ([n], E) in Adjazenzmatrixdarstellung 1 Für alle Permutationen π : [n] [n]. 1 Falls (π(1), π(2),..., π(n)) ein Kreis in G ist, AUSGABE
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/03 Institut für Informatik Aufgabenblatt 6 Prof. Dr. J. Csirik 18. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am
Technische Universität München WS 00/03 Institut für Informatik Aufgabenblatt 6 Prof. Dr. J. Csirik 18. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am
Der Eulersche Polyedersatz
 Der Eulersche Polyedersatz Def Die Anzahl der k Seiten eines konvexen Polytops P bezeichnen wir mit f k (P) oder kurz mit f k. Das n Tupel (f 0,f 1,...,f n 1 ) Z n heißt dann der f Vektor des (n dimensionalen)
Der Eulersche Polyedersatz Def Die Anzahl der k Seiten eines konvexen Polytops P bezeichnen wir mit f k (P) oder kurz mit f k. Das n Tupel (f 0,f 1,...,f n 1 ) Z n heißt dann der f Vektor des (n dimensionalen)
Von den Kanten von Gewicht 4 wird nur noch eine ausgewählt, die zu dem letzten nicht ausgewählten Knoten führt: 1. Juni
 CHAPTER. GRAPHEN.. B Ä UME.. Bäume Ein schlichter Graph ohne Kreise heisst Wald, ist er noch zusätzlich zusammenhängend so wird er Baum genannt. Bevor wir Bäume genauer beschreiben ein kleines LEMMA...
CHAPTER. GRAPHEN.. B Ä UME.. Bäume Ein schlichter Graph ohne Kreise heisst Wald, ist er noch zusätzlich zusammenhängend so wird er Baum genannt. Bevor wir Bäume genauer beschreiben ein kleines LEMMA...
Das Art Gallery Problem
 Dipl. Math. Timo de Wolff FB 12 Institut für Mathematik Mail: wolff(at)math.uni-frankfurt.de http://www.uni-frankfurt.de/fb/fb12/mathematik/dm/personen/dewolff/index.html Das Art Gallery Problem Mustervorlesung
Dipl. Math. Timo de Wolff FB 12 Institut für Mathematik Mail: wolff(at)math.uni-frankfurt.de http://www.uni-frankfurt.de/fb/fb12/mathematik/dm/personen/dewolff/index.html Das Art Gallery Problem Mustervorlesung
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Hausaufgabe 2 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
2 Eulersche Polyederformel und reguläre Polyeder
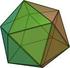 6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
Körper zum Selberbauen Polydron
 Körper zum Selberbauen Polydron Was versteht man unter Polydron? Polydron ist ein von Edward Harvey erfundenes intelligentes Spielzeug, mit dem man verschiedene geometrische Figuren bauen kann. Es ist
Körper zum Selberbauen Polydron Was versteht man unter Polydron? Polydron ist ein von Edward Harvey erfundenes intelligentes Spielzeug, mit dem man verschiedene geometrische Figuren bauen kann. Es ist
16. Platonische Körper kombinatorisch
 16. Platonische Körper kombinatorisch Ein Würfel zeigt uns, daß es Polyeder gibt, wo in jeder Ecke gleich viele Kanten zusammenlaufen, und jede Fläche von gleich vielen Kanten berandet wird. Das Tetraeder
16. Platonische Körper kombinatorisch Ein Würfel zeigt uns, daß es Polyeder gibt, wo in jeder Ecke gleich viele Kanten zusammenlaufen, und jede Fläche von gleich vielen Kanten berandet wird. Das Tetraeder
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Algorithmische Geometrie, SoSe 2005 Skriptmitschrift vom 29. April 2005
 Algorithmische Geometrie, SoSe 2005 Skriptmitschrift vom 29. April 2005 Antonia Wittmers Igor Savchenko Konvexe Hüllen Inkrementeller Algorithmus für die konvexe Hülle Dabei heißt inkrementeller Algorithmus,
Algorithmische Geometrie, SoSe 2005 Skriptmitschrift vom 29. April 2005 Antonia Wittmers Igor Savchenko Konvexe Hüllen Inkrementeller Algorithmus für die konvexe Hülle Dabei heißt inkrementeller Algorithmus,
WS 2015/16 Diskrete Strukturen Kapitel 4: Graphen (Planare Graphen, Färbung)
 WS 2015/16 Diskrete Strukturen Kapitel 4: Graphen (Planare Graphen, Färbung) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 4: Graphen (Planare Graphen, Färbung) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Kapitel 3. Kapitel 3 Graphentheorie
 Graphentheorie Inhalt 3.1 3.1 Grundlagen 3.2 3.2 Das Das Königsberger Brückenproblem 3.3 3.3 Bäume 3.4. 3.4. Planare Graphen 3.5 3.5 Färbungen Seite 2 3.1 Grundlagen Definition. Ein Ein Graph besteht aus
Graphentheorie Inhalt 3.1 3.1 Grundlagen 3.2 3.2 Das Das Königsberger Brückenproblem 3.3 3.3 Bäume 3.4. 3.4. Planare Graphen 3.5 3.5 Färbungen Seite 2 3.1 Grundlagen Definition. Ein Ein Graph besteht aus
Fußbälle, platonische und archimedische Körper
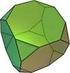 Fußbälle, platonische und archimedische Körper Prof. Dr. Wolfram Koepf http://www.mathematik.uni-kassel.de/~koepf Was ist ein Fußball? Sepp Herberger: Der Ball ist rund. Ist also ein Fußball eine Kugel?
Fußbälle, platonische und archimedische Körper Prof. Dr. Wolfram Koepf http://www.mathematik.uni-kassel.de/~koepf Was ist ein Fußball? Sepp Herberger: Der Ball ist rund. Ist also ein Fußball eine Kugel?
Grundlagen der Graphentheorie. Thomas Kamps 6. Oktober 2008
 Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
Bernd Döring. Wege, Plätten, Färben. Vom Problem zur Theorie der Graphen
 Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen Bernd Döring, 2002-2005 Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg 28 26721 Emden - 2 - Inhaltsverzeichnis 0. Einleitung
Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen Bernd Döring, 2002-2005 Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg 28 26721 Emden - 2 - Inhaltsverzeichnis 0. Einleitung
In diesem Kapitel bestimmen wir die multiplikative Struktur der Einheitengruppe (Z/Z) von Z/Z für eine beliebige positive Zahl Z >0.
 Kapitel 5: Die Einheitengruppe von Z/Z und Primitivwurzeln modulo In diesem Kapitel bestimmen wir die multiplikative Struktur der Einheitengruppe (Z/Z) von Z/Z für eine beliebige positive Zahl Z >0. 16
Kapitel 5: Die Einheitengruppe von Z/Z und Primitivwurzeln modulo In diesem Kapitel bestimmen wir die multiplikative Struktur der Einheitengruppe (Z/Z) von Z/Z für eine beliebige positive Zahl Z >0. 16
5 Graphen und Polyeder
 5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 6: Graphentheorie
 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie
 Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
5 Graphen. Repräsentationen endlicher Graphen. 5.1 Gerichtete Graphen. 5.2 Ungerichtete Graphen. Ordnung von Graphen
 Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
3 Planare Graphen die Eulersche Polyederformel
 3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
Kapitel 1. Grundlegendes
 Kapitel 1 Grundlegendes Abschnitt 1.4 Vollständige Induktion Charakterisierung der natürlichen Zahlen Die Menge N 0 = {0, 1, 2, 3,...} der natürlichen Zahlen läßt sich wie folgt charakterisieren: 1. 0
Kapitel 1 Grundlegendes Abschnitt 1.4 Vollständige Induktion Charakterisierung der natürlichen Zahlen Die Menge N 0 = {0, 1, 2, 3,...} der natürlichen Zahlen läßt sich wie folgt charakterisieren: 1. 0
Teilgebiete der Abbildungsgeometrie
 Teilgebiete der Abbildungsgeometrie In der Abbildungsgeometrie wird zur Klassifizierung von Eigenschaften des Raumes (bzw. der Ebene) und der in ihm enthaltenen Objekte (Geraden, Kreise, Polytope, usw.)
Teilgebiete der Abbildungsgeometrie In der Abbildungsgeometrie wird zur Klassifizierung von Eigenschaften des Raumes (bzw. der Ebene) und der in ihm enthaltenen Objekte (Geraden, Kreise, Polytope, usw.)
3.4 Kombinatorische Äquivalenz und Dualität von Polytopen
 222 Diskrete Geometrie (Version 3) 12. Januar 2012 c Rudolf Scharlau 3.4 Kombinatorische Äquivalenz und Dualität von Polytopen Dieser Abschnitt baut auf den beiden vorigen auf, indem er weiterhin den Seitenverband
222 Diskrete Geometrie (Version 3) 12. Januar 2012 c Rudolf Scharlau 3.4 Kombinatorische Äquivalenz und Dualität von Polytopen Dieser Abschnitt baut auf den beiden vorigen auf, indem er weiterhin den Seitenverband
Die Vermutungen von Hadwiger und
 Die Vermutungen von Hadwiger und Hajós David Müßig Seminar zur Graphentheorie, WS 09/10 Wir alle kennen die Gleichung χ(x) ω(x). Diese Gleichung ist nicht nur einläuchtend, sondern auch mehr oder weniger
Die Vermutungen von Hadwiger und Hajós David Müßig Seminar zur Graphentheorie, WS 09/10 Wir alle kennen die Gleichung χ(x) ω(x). Diese Gleichung ist nicht nur einläuchtend, sondern auch mehr oder weniger
Zur Zykelschreibweise von Permutationen
 Zur Zykelschreibweise von Permutationen Olivier Sète 16. Juni 2010 1 Grundlagen Definition 1.1. Eine Permutation von {1, 2,..., n} ist eine bijektive Abbildung σ : {1, 2,..., n} {1, 2,..., n}, i σ(i).
Zur Zykelschreibweise von Permutationen Olivier Sète 16. Juni 2010 1 Grundlagen Definition 1.1. Eine Permutation von {1, 2,..., n} ist eine bijektive Abbildung σ : {1, 2,..., n} {1, 2,..., n}, i σ(i).
Etwas Topologie. Thomas Jahn. LV Algebraische Topologie am 1. Dezember 2014
 Etwas Topologie Thomas Jahn LV Algebraische Topologie am 1. Dezember 214 1 Eulerscher Polyedersatz [2] Satz 1.1 (Eulerscher Polyedersatz). Sei G ein ebener Graph. (Multikanten und Schlingen sind erlaubt,
Etwas Topologie Thomas Jahn LV Algebraische Topologie am 1. Dezember 214 1 Eulerscher Polyedersatz [2] Satz 1.1 (Eulerscher Polyedersatz). Sei G ein ebener Graph. (Multikanten und Schlingen sind erlaubt,
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
17. Berliner Tag der Mathematik 2012 Wettbewerb Stufe III: Klassen 11 bis 12/13
 17. Berliner Tag der Mathematik 2012 Wettbewerb Stufe III: Klassen 11 bis 12/13 Aufgabe 1 Sei M eine Menge von in einem Dreieck verlaufenden Strecken, über die Folgendes vorausgesetzt wird: Die Kanten
17. Berliner Tag der Mathematik 2012 Wettbewerb Stufe III: Klassen 11 bis 12/13 Aufgabe 1 Sei M eine Menge von in einem Dreieck verlaufenden Strecken, über die Folgendes vorausgesetzt wird: Die Kanten
Diskrete Mathematik Graphentheorie (Übersicht)
 Diskrete Mathematik Graphentheorie (Übersicht) Dr. C. Löh 2. Februar 2010 0 Graphentheorie Grundlagen Definition (Graph, gerichteter Graph). Ein Graph ist ein Paar G = (V, E), wobei V eine Menge ist (die
Diskrete Mathematik Graphentheorie (Übersicht) Dr. C. Löh 2. Februar 2010 0 Graphentheorie Grundlagen Definition (Graph, gerichteter Graph). Ein Graph ist ein Paar G = (V, E), wobei V eine Menge ist (die
Diskrete Mathematik. Hamiltonsche Graphen Teil I. Karina Arndt
 Diskrete Mathematik Hamiltonsche Graphen Teil I Karina Arndt 21.06.2006 Übersicht Einleitung Hamiltonsch und eulersch Hamiltonsche Kreise Hamiltonsche Graphen neu zeichnen Kreise und Wege Reguläre Graphen
Diskrete Mathematik Hamiltonsche Graphen Teil I Karina Arndt 21.06.2006 Übersicht Einleitung Hamiltonsch und eulersch Hamiltonsche Kreise Hamiltonsche Graphen neu zeichnen Kreise und Wege Reguläre Graphen
8. Konvexe Polytope. Tobias Boelter. Mittwoch, 5. März TopMath Frühlingsschule
 1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
Graphen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Ein Turnierplan mit fünf Runden c d b e a c d b e a c d b e a c d b b c a a d e e Das Diagramm beschreibt
Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Ein Turnierplan mit fünf Runden c d b e a c d b e a c d b e a c d b b c a a d e e Das Diagramm beschreibt
Über ein Theorem von Hans Läuchli
 Über ein Theorem von Hans Läuchli Lorenz Halbeisen Abstract. Für natürliche Zahlen n sei P n die folgende Aussage: Ist G ein unendlicher Graph, all dessen endliche Teilgraphen n-färbbar sind, so ist auch
Über ein Theorem von Hans Läuchli Lorenz Halbeisen Abstract. Für natürliche Zahlen n sei P n die folgende Aussage: Ist G ein unendlicher Graph, all dessen endliche Teilgraphen n-färbbar sind, so ist auch
Abbildung 1: Reduktion: CLIQUE zu VERTEX-COVER. links: Clique V = {u, v, x, y}. rechts:der Graph Ḡ mit VC V \ V = {w, z}
 u v u v z w z w y x y x Abbildung 1: Reduktion: CLIQUE zu VERTEX-COVER. links: Clique V = {u, v, x, y}. rechts:der Graph Ḡ mit VC V \ V = {w, z} Definition 0.0.1 (Vertex Cover (VC)). Gegeben: Ein ungerichteter
u v u v z w z w y x y x Abbildung 1: Reduktion: CLIQUE zu VERTEX-COVER. links: Clique V = {u, v, x, y}. rechts:der Graph Ḡ mit VC V \ V = {w, z} Definition 0.0.1 (Vertex Cover (VC)). Gegeben: Ein ungerichteter
A Berlin, 10. April 2017
 A Berlin, 10. April 2017 Name:... Matr.-Nr.:... Wiederholung der schriftlichen Prüfung zur Vorlesung Diskrete Strukturen (Niedermeier/Molter/Froese, Wintersemester 2016/17) Einlesezeit: 15 Minuten Bearbeitungszeit:
A Berlin, 10. April 2017 Name:... Matr.-Nr.:... Wiederholung der schriftlichen Prüfung zur Vorlesung Diskrete Strukturen (Niedermeier/Molter/Froese, Wintersemester 2016/17) Einlesezeit: 15 Minuten Bearbeitungszeit:
8: Bipartite Graphen. s 1. bei dem es eine Kante zwischen s i und k gibt, wenn der Schüler s i die Note k für seine Arbeit bekommen hat.
 Chr.Nelius: Graphentheorie (WS 2018/19) 8 Bipartite Graphen 26 8: Bipartite Graphen In einer Schulklasse mit 24 Schülern s 1,s 2,s 3,...,s 24 wurde eine Mathe Arbeit geschrieben. Um das Ergebnis bildlich
Chr.Nelius: Graphentheorie (WS 2018/19) 8 Bipartite Graphen 26 8: Bipartite Graphen In einer Schulklasse mit 24 Schülern s 1,s 2,s 3,...,s 24 wurde eine Mathe Arbeit geschrieben. Um das Ergebnis bildlich
4 Färbungen Begriffe Komplexität Greedy-Algorithmus Knotenreihenfolgen Das 4-Farben-Problem...
 Inhaltsverzeichnis 4 Färbungen 41 4.1 Begriffe....................... 41 4.2 Komplexität..................... 42 4.3 Greedy-Algorithmus................ 42 4.4 Knotenreihenfolgen................. 43 4.5
Inhaltsverzeichnis 4 Färbungen 41 4.1 Begriffe....................... 41 4.2 Komplexität..................... 42 4.3 Greedy-Algorithmus................ 42 4.4 Knotenreihenfolgen................. 43 4.5
Einführung in die Diskrete Mathematik
 Einführung in die Diskrete Mathematik Sommersemester 2014 PD Dr. Nils Rosehr Inhaltsverzeichnis I Einleitung 5 II Kombinatorik 5 1 Grundlagen der Kombinatorik 6 1.1 Standardbezeichnungen......................
Einführung in die Diskrete Mathematik Sommersemester 2014 PD Dr. Nils Rosehr Inhaltsverzeichnis I Einleitung 5 II Kombinatorik 5 1 Grundlagen der Kombinatorik 6 1.1 Standardbezeichnungen......................
Diskrete Strukturen Kapitel 4: Graphentheorie (Euler-Hamilton)
 WS 2015/16 Diskrete Strukturen Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Planare Graphen. Ein Graph heißt planar, wenn er sich so in die Ebene einzeichnen lässt, dass sich die Kanten nicht schneiden.
 Planare Graphen Bei der Betrachtung des K 3,3 ergab sich die Frage, ob man diesen Graph so in die Ebene einzeichnen kann, dass sich die Kanten nicht schneiden. Das motiviert folgende Definition: Ein Graph
Planare Graphen Bei der Betrachtung des K 3,3 ergab sich die Frage, ob man diesen Graph so in die Ebene einzeichnen kann, dass sich die Kanten nicht schneiden. Das motiviert folgende Definition: Ein Graph
Vier-Farben-Vermutung (1)
 Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
16. Flächenfärbungen
 Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
Klausur. 18. Juli 2008, 10:15-12:15 Uhr. Name:... Matrikelnummer:... Anzahl beschriebener Blätter (ohne Aufgabenblatt):... D(p) : Y = p x X + p y
 GRUNDZÜGE DER ALGORITHMISCHEN GEOMETRIE Klausur 18. Juli 2008, 10:15-12:15 Uhr Name:................................... Matrikelnummer:................................... Anzahl beschriebener Blätter (ohne
GRUNDZÜGE DER ALGORITHMISCHEN GEOMETRIE Klausur 18. Juli 2008, 10:15-12:15 Uhr Name:................................... Matrikelnummer:................................... Anzahl beschriebener Blätter (ohne
Def. 1.1: Graph, Knoten, Kanten, adjazent. Notwendige Bedingungen für Isomorphie. Das 3-Brunnen Problem, der vollständige bipartite Graph K 3,3
 Stand: 27. Januar 2004 1. Kapitel: Was ist ein Graph? Beispiel: Mannschafts-Wettkämpfe Def. 1.1: Graph, Knoten, Kanten, adjazent Nullgraphen, vollständige Graphen K n, komplementäre Graphen Isomorphie
Stand: 27. Januar 2004 1. Kapitel: Was ist ein Graph? Beispiel: Mannschafts-Wettkämpfe Def. 1.1: Graph, Knoten, Kanten, adjazent Nullgraphen, vollständige Graphen K n, komplementäre Graphen Isomorphie
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
 Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Es sei P ein einfaches Polygon in der Ebene; P habe n Ecken. Hilfssatz: Zu jedem einfachen Polygon mit mehr als 3 Ecken existiert eine Diagonale.
 6. Polygontriangulierung: Wie bewacht man eine Kunstgalerie? 6.1. Grundlegendes zu Polygonen Es sei P ein einfaches Polygon in der Ebene; P habe n Ecken. Definition: Hilfssatz: Zu jedem einfachen Polygon
6. Polygontriangulierung: Wie bewacht man eine Kunstgalerie? 6.1. Grundlegendes zu Polygonen Es sei P ein einfaches Polygon in der Ebene; P habe n Ecken. Definition: Hilfssatz: Zu jedem einfachen Polygon
2.4A. Reguläre Polyeder (Platonische Körper)
 .A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
.A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Zweiter Zirkelbrief: Graphentheorie
 Matheschülerzirkel Universität Augsburg Schuljahr 2014/2015 Zweiter Zirkelbrief: Graphentheorie Inhaltsverzeichnis 1 Grundbegriffe 1 2 Eulerkreise 4 3 Hamiltonkreise 7 4 Planare Graphen 9 5 Färbbarkeit
Matheschülerzirkel Universität Augsburg Schuljahr 2014/2015 Zweiter Zirkelbrief: Graphentheorie Inhaltsverzeichnis 1 Grundbegriffe 1 2 Eulerkreise 4 3 Hamiltonkreise 7 4 Planare Graphen 9 5 Färbbarkeit
Vorlesungstermin 2: Graphentheorie II. Markus Püschel David Steurer. Algorithmen und Datenstrukturen, Herbstsemester 2018, ETH Zürich
 Vorlesungstermin 2: Graphentheorie II Markus Püschel David Steurer Algorithmen und Datenstrukturen, Herbstsemester 2018, ETH Zürich Wiederholung: Vollständige Induktion Ziel: zeige n N. A(n) für eine Aussage
Vorlesungstermin 2: Graphentheorie II Markus Püschel David Steurer Algorithmen und Datenstrukturen, Herbstsemester 2018, ETH Zürich Wiederholung: Vollständige Induktion Ziel: zeige n N. A(n) für eine Aussage
Chromatosaurier Lösungen
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Chromatosaurier Lösungen Aufgabe 1 (Tetrachromatosaurier (nur für die Klassen 7/8) [4 Punkte]). Bei Ausgrabungen wurde der folgende
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Chromatosaurier Lösungen Aufgabe 1 (Tetrachromatosaurier (nur für die Klassen 7/8) [4 Punkte]). Bei Ausgrabungen wurde der folgende
Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen. Martin Oellrich. Warum eine Karte? 3. Warum stetige Grenzen?
 Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen Problemstellung Deutsche Bundesländer in vier Farben 4. April 06 Martin Oellrich Warum geht das immer? Gegeben: Karte eines Gebietes
Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen Problemstellung Deutsche Bundesländer in vier Farben 4. April 06 Martin Oellrich Warum geht das immer? Gegeben: Karte eines Gebietes
Diskrete Mathematik 1
 Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May M. Ritzenhofen, M. Mansour Al Sawadi, A. Meurer Lösungsblatt zur Vorlesung Diskrete Mathematik 1 WS 2008/09 Blatt
Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May M. Ritzenhofen, M. Mansour Al Sawadi, A. Meurer Lösungsblatt zur Vorlesung Diskrete Mathematik 1 WS 2008/09 Blatt
GRUPPENTHEORIE AUFGABEN ZUR PRÜFUNGSVORBEREITUNG II
 Universität Bielefeld WS 2012/13 GRUPPENTHEORIE AUFGABEN ZUR PRÜFUNGSVORBEREITUNG II DR. PHILIPP LAMPE Rat sucht man deshalb, weil man die einzige Lösung kennt, aber nichts davon wissen will. Erica Jong
Universität Bielefeld WS 2012/13 GRUPPENTHEORIE AUFGABEN ZUR PRÜFUNGSVORBEREITUNG II DR. PHILIPP LAMPE Rat sucht man deshalb, weil man die einzige Lösung kennt, aber nichts davon wissen will. Erica Jong
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 8
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 8
Graphentheorie. Färbungen. Knoten- und Kantenfärbungen. Knoten- und Kantenfärbungen. Rainer Schrader. 28. Januar 2008
 Graphentheorie Rainer Schrader Färbungen Zentrum für Angewandte Informatik Köln 28. Januar 2008 1 / 57 2 / 57 wir wollen versuchen, die Knoten eines Graphen zu färben dabei dürfen keine zwei benachbarten
Graphentheorie Rainer Schrader Färbungen Zentrum für Angewandte Informatik Köln 28. Januar 2008 1 / 57 2 / 57 wir wollen versuchen, die Knoten eines Graphen zu färben dabei dürfen keine zwei benachbarten
Der Eulersche Polyedersatz in beliebiger Dimension
 Der Eulersche Polyedersatz in beliebiger Dimension Rolf Stefan Wilke 17. Juli 2007 Definition. Sei P R d ein Polytop der Dimension d. Es bezeichne f k (P ) die Anzahl der k-dimensionalen Seitenflächen.
Der Eulersche Polyedersatz in beliebiger Dimension Rolf Stefan Wilke 17. Juli 2007 Definition. Sei P R d ein Polytop der Dimension d. Es bezeichne f k (P ) die Anzahl der k-dimensionalen Seitenflächen.
3 Die natürlichen Zahlen. Themen: Vollständige Induktion Varianten des Induktionsprinzips Induktion über den rekursiven Aufbau Die ganzen Zahlen
 3 Die natürlichen Zahlen Themen: Vollständige Induktion Varianten des Induktionsprinzips Induktion über den rekursiven Aufbau Die ganzen Zahlen Die natürlichen Zahlen Æ = {1, 2, 3,...}. sind die natürlichen
3 Die natürlichen Zahlen Themen: Vollständige Induktion Varianten des Induktionsprinzips Induktion über den rekursiven Aufbau Die ganzen Zahlen Die natürlichen Zahlen Æ = {1, 2, 3,...}. sind die natürlichen
Triangulierungen von Punktmengen und Polyedern
 Triangulierungen von Punktmengen und Polyedern Vorlesung im Sommersemester 2000 Technische Universität Berlin Jörg Rambau 21.06.2000 Flipdefizit 10 In diesem Kapitel starten wir die Untersuchung von Triangulierungen,
Triangulierungen von Punktmengen und Polyedern Vorlesung im Sommersemester 2000 Technische Universität Berlin Jörg Rambau 21.06.2000 Flipdefizit 10 In diesem Kapitel starten wir die Untersuchung von Triangulierungen,
Beispiellösungen zu Blatt 55
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 55 Karsten hat zehn Zahnräder, je eines mit 7, 1,, 10, 179, 2, 299, 0,
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 55 Karsten hat zehn Zahnräder, je eines mit 7, 1,, 10, 179, 2, 299, 0,
Ilse Fischer. Fakultät für Mathematik, Universität Wien, Nordbergstraße 15, A-1090 Wien, Austria.
 GRAPHEN MÜSSEN NICHT IMMER FUNKTIONEN DARSTELLEN Ilse Fischer Fakultät für Mathematik, Universität Wien, Nordbergstraße 15, A-1090 Wien, Austria. E-mail: Ilse.Fischer@univie.ac.at Zusammenfassung. In der
GRAPHEN MÜSSEN NICHT IMMER FUNKTIONEN DARSTELLEN Ilse Fischer Fakultät für Mathematik, Universität Wien, Nordbergstraße 15, A-1090 Wien, Austria. E-mail: Ilse.Fischer@univie.ac.at Zusammenfassung. In der
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
: das Bild von ) unter der Funktion ist gegeben durch
 % 1.3 Funktionen Seien und Mengen nennt man Funktion oder Abbildung. Beachte: Zuordnung ist eindeutig. Bezeichnungen: : Definitionsbereich : Bildbereich (Zielmenge) von Der Graph einer Funktion: graph!
% 1.3 Funktionen Seien und Mengen nennt man Funktion oder Abbildung. Beachte: Zuordnung ist eindeutig. Bezeichnungen: : Definitionsbereich : Bildbereich (Zielmenge) von Der Graph einer Funktion: graph!
Algorithmische Geometrie: Delaunay Triangulierung (Teil 1)
 Algorithmische Geometrie: Delaunay Triangulierung (Teil 1) Nico Düvelmeyer WS 2009/2010, 26.1.2010 Überblick 1 Motivation Interpolation von Höhendaten 2 Triangulierungen von ebenen Punktmengen 3 Delaunay
Algorithmische Geometrie: Delaunay Triangulierung (Teil 1) Nico Düvelmeyer WS 2009/2010, 26.1.2010 Überblick 1 Motivation Interpolation von Höhendaten 2 Triangulierungen von ebenen Punktmengen 3 Delaunay
