Hauptseminar: Moderne Simulationsmethoden

Transkript

1 Hauptseminar: Moderne Simulationsmethoden Finite Elemente Methode von Galerkin Tanja Heich Fachbereich 08 Johannes Gutenberg-Universität Mainz 02. November 2017 Hauptseminar Moderne Simulationsmethoden 1

2 Inhaltsverzeichnis 1 2 Hauptseminar Moderne Simulationsmethoden 2

3 Inhaltsübersicht 1 2 Hauptseminar Moderne Simulationsmethoden 3

4 Idee Bisher Finite Elemente Methode für Zwei-Punkte-Randwertprobleme d dx ( p(x) du(x) dx ) + q(x)u(x) = f (x) für a < x < b mit homogenen Dirichlet-Randbedingungen u(a) = u(b) = 0. Jetzt analoge Theorie für zweidimensionale elliptische PDEs Hauptseminar Moderne Simulationsmethoden 4

5 Idee Sei D R 2 ein begrenztes Gebiet mit stückweise glattem Rand D. Gegeben seien geeignete Funktionen g : D R und a, f : D R mit a(x) > 0 für alle x D. Wir möchten ein u(x) finden, das die Gleichung (a(x) u(x)) = 2 j=1 x j ( a(x) u(x) x j ) = f (x) für x D mit Dirichlet-Randbedingungen u(x) = g(x) für x D erfüllt. Hauptseminar Moderne Simulationsmethoden 5

6 Regularität der Koeffizienten Annahme Der Streuungskoeffizient a(x) erfülle 0 < a min a(x) a max < für fast alle x D für reelle Konstanten a min und a max. Im Speziellen sei a L (D). Hauptseminar Moderne Simulationsmethoden 6

7 Variationsproblem Betrachten wir (a(x) u(x)) = f (x). Durch Multiplikation mit der Testfunktion φ Cc (D) und partieller Integration, erhalten wir a(x) u(x) φ(x)dx = f (x)φ(x)dx. D Jede Lösung u erfüllt das Variationsproblem a(u, φ) = l(φ) für alle φ C c (D), D wobei a(u, φ) := D l(φ) := f, φ L 2 (D). a(x) u(x) φ(x)dx, Hauptseminar Moderne Simulationsmethoden 7

8 Variationsproblem Betrachten wir (a(x) u(x)) = f (x). Durch Multiplikation mit der Testfunktion φ Cc (D) und partieller Integration, erhalten wir a(x) u(x) φ(x)dx = f (x)φ(x)dx. D Jede Lösung u erfüllt das Variationsproblem a(u, φ) = l(φ) für alle φ C c (D), D wobei a(u, φ) := D l(φ) := f, φ L 2 (D). a(x) u(x) φ(x)dx, Hauptseminar Moderne Simulationsmethoden 7

9 Lösungsraum und Spuroperator Betrachten wir die Dirichlet-Randbedingungen u(x) = g(x) für x D. Ist hier g 0, so können wir unsere Lösung u nicht in V = H 1 0 (D) suchen. Wir benötigen stattdessen W := H 1 g (D) := {w H 1 (D) : γw = g}. Definition Die Abbildung γ : H 1 (D) L 2 ( D) heißt Spuroperator und bildet Funktionen in D auf Funktionen in den Rand D ab. Hauptseminar Moderne Simulationsmethoden 8

10 Lösungsraum und Spuroperator Betrachten wir die Dirichlet-Randbedingungen u(x) = g(x) für x D. Ist hier g 0, so können wir unsere Lösung u nicht in V = H 1 0 (D) suchen. Wir benötigen stattdessen W := H 1 g (D) := {w H 1 (D) : γw = g}. Definition Die Abbildung γ : H 1 (D) L 2 ( D) heißt Spuroperator und bildet Funktionen in D auf Funktionen in den Rand D ab. Hauptseminar Moderne Simulationsmethoden 8

11 Hilbertraum Definition Für ein Gebiet D R d mit Rand D betrachten wir den Maßraum ( D, B( D), V ), wobei V (B) das Volumen der Borelmenge B B( D) ist. Dann ist L 2 ( D) ein Hilbertraum L 2 ( D, R) mit der Norm ( g L 2 ( D) := D g(x) 2 dv (x)) 1/2. Hauptseminar Moderne Simulationsmethoden 9

12 Spurorperator auf H 1 (D) Lemma Betrachte ein beschränktes Gebiet D R 2 mit genügend glattem Rand D. Dann existiert ein beschränkter linearer Operator γ : H 1 (D) L 2 ( D) so, dass γw = w D für alle w C 1 ( D). Hauptseminar Moderne Simulationsmethoden 10

13 Sobolevraum Definition Sei D R 2 ein beschränktes Gebiet. Der Sobolev-Raum H 1/2 ( D) ist definiert als H 1/2 ( D) := γ(h 1 (D)) = { } γw : w H 1 (D), wobei γ der Spuroperator auf H 1 (D) ist. H 1/2 ( D) ist ein Hilbertraum mit der Norm } g H 1/2 ( D) { w := inf H 1 (D) : γw = g und w H 1 (D). Hauptseminar Moderne Simulationsmethoden 11

14 Obere Schranke Nach dieser Definition gilt: Ist g H 1/2 ( D), so können wir eine H 1 (D)-Funktion finden, deren Spur g ist. Der Lösungsraum W = H 1 g (D) ist nicht leer. Lemma Es existiert ein K γ > 0 derart, dass wir für alle g H 1/2 ( D) ein u g H 1 (D) mit γu g = g und finden können. u g H 1 (D) K γ g H 1/2 ( D) Hauptseminar Moderne Simulationsmethoden 12

15 Obere Schranke Nach dieser Definition gilt: Ist g H 1/2 ( D), so können wir eine H 1 (D)-Funktion finden, deren Spur g ist. Der Lösungsraum W = H 1 g (D) ist nicht leer. Lemma Es existiert ein K γ > 0 derart, dass wir für alle g H 1/2 ( D) ein u g H 1 (D) mit γu g = g und finden können. u g H 1 (D) K γ g H 1/2 ( D) Hauptseminar Moderne Simulationsmethoden 12

16 Schwache Lösung Definition Eine schwache Lösung des Randwertproblems ist eine Funktion u W, die a(u, v) = l(v) für alle v V erfüllt, wobei a und l wie vorhin definiert sind als a(u, φ) := a(x) u(x) φ(x)dx, D l(φ) := f, φ L 2 (D). Hauptseminar Moderne Simulationsmethoden 13

17 Eindeutigkeit der Lösung u W = H 1 g(d) Theorem Sei die Regularität der Koeffizienten erfüllt, das heißt es gelte 0 < a min a(x) a max < für fast alle x D. Sei weiter f L 2 (D) und g H 1/2 ( D). Dann hat a(u, v) = l(v) für alle v V eine eindeutige Lösung u W = H 1 g (D). Hauptseminar Moderne Simulationsmethoden 14

18 Obere Schranke Theorem Sei u W mit a(u, v) = l(v) für alle v V. Gelten zudem die Bedingungen des vorigen Theorems, so gilt ( ) u H 1 (D) K f L 2 (D) + g H 1/2 ( D), { wobei K := max K p amin 1, K γ(1 + a max amin }. 1 ) Hauptseminar Moderne Simulationsmethoden 15

19 Inhaltsübersicht 1 2 Hauptseminar Moderne Simulationsmethoden 16

20 Idee Betrachte das ursprüngliche Randwertproblem mit Daten a und f : (a(x) u(x)) = f (x) für x D und Dirichlet-Randbedingungen u(x) = g(x) für x D. Das schwache Problem a(u, v) = l(v) für alle v V liefert uns den Startpunkt für die. Ist g 0, so sind der Lösungsraum und der Testraum verschieden. Wähle zwei endlichdimensionale Unterräume W h W = H 1 g (D) und V h V = H 1 0 (D). Hauptseminar Moderne Simulationsmethoden 17

21 Für die konstruieren wir die Unterräume so, dass v w V h für alle v, w W h. Definition Sei W h W und V h V. Angenommen v w V h sei für alle v, w W h erfüllt. Die für unser Randwertproblem ist dann die Funktion u h W h, die erfüllt. a(u h, v) = l(v) für alle v V h Hauptseminar Moderne Simulationsmethoden 18

22 Eindeutigkeit der Lösung u h W h Theorem Sei die Regularität der Koeffizienten erfüllt, das heißt es gelte 0 < a min a(x) a max < für fast alle x D. Sei weiter f L 2 (D) und g H 1/2 ( D). Dann hat eine eindeutige Lösung u h W h. a(u h, v) = l(v) für alle v V h Hauptseminar Moderne Simulationsmethoden 19

23 Bestapproximation Theorem Angenommen es sei V h V und W h W. Erfüllen zudem u W bzw. u h W h die Gleichungen a(u, v) = l(v) für alle v V bzw. a(u h, v) = l(v) für alle v V h. Ist v w V h für alle v, w W h erfüllt, so gilt u u h E = inf w W h u w E. Hauptseminar Moderne Simulationsmethoden 20

24 Quasi-Bestapproximation Theorem Sei die Regularität der Koeffizienten erfüllt, das heißt es gelte 0 < a min a(x) a max < für fast alle x D, und gelten weiter die Bedingungen von vorigem Theorem. Dann gilt u u h H 1 (D) amax a min u w H 1 (D) für alle w W h. Hauptseminar Moderne Simulationsmethoden 21

25 Beweis Beweisidee: Aus der Abschätzung amin w H 1 (D) w E a max w H 1 (D) und dem Ergebnis des vorigen Theorems u u h E = inf w W h u w E folgt leicht die zu zeigende Ungleichung u u h H 1 (D) amax a min u w H 1 (D). Hauptseminar Moderne Simulationsmethoden 22

26 Fehlerabschätzung bei approximierten Daten Wir erhalten folgende Fehlerabschätzung u ũ h H 1 (D) u ũ H 1 (D) + ũ ũ h H 1 (D). u ũ H 1 (D) ist der Fehler der schwachen Lösung bei Approximation der Daten ũ ũ h H 1 (D) ist der Fehler der bei Approximation der gestörten Lösung ũ W durch ũ h W h Alternativ: u ũ h H 1 (D) u u h H 1 (D) + u h ũ h H 1 (D) u h ũ h H 1 (D) ist der Fehler der bei Approximation von a(.,.) und l(.) Hauptseminar Moderne Simulationsmethoden 23

27 Fehlerabschätzung bei approximierten Daten Wir erhalten folgende Fehlerabschätzung u ũ h H 1 (D) u ũ H 1 (D) + ũ ũ h H 1 (D). u ũ H 1 (D) ist der Fehler der schwachen Lösung bei Approximation der Daten ũ ũ h H 1 (D) ist der Fehler der bei Approximation der gestörten Lösung ũ W durch ũ h W h Alternativ: u ũ h H 1 (D) u u h H 1 (D) + u h ũ h H 1 (D) u h ũ h H 1 (D) ist der Fehler der bei Approximation von a(.,.) und l(.) Hauptseminar Moderne Simulationsmethoden 23

28 Anpassung der Schranke Wir können unser letztes Theorem anpassen und erhalten ũ ũ h H 1 (D) ãmax ã min inf w W h ũ w H 1 (D). Nach der Wahl geeigneter Unterräume V h und W h können wir eine exakte Schranke finden. Hauptseminar Moderne Simulationsmethoden 24

29 Inhaltsübersicht 1 2 Hauptseminar Moderne Simulationsmethoden 25

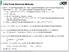
30 Trianguliertes Gitter auf D = (0, 1)x(0, 1) Abbildung: Beispiel mit n e = 32 Elementen, J = 9 innere Eckpunkte und J b = 16 Eckpunkte am Rand Hauptseminar Moderne Simulationsmethoden 26

31 Charakteristische Netzgröße Definition Betrachte eine Menge von n e nicht überlappenden Dreiecken T h := { 1,..., ne } derart, dass D = n e k=1 Verschiedene Dreiecke dürfen sich nur an einer Ecke treffen oder eine vollständige Kante teilen. Sei h k die Länge der längsten Kante von k und sei h := max k h k. Wir nennen T h ein zulässiges Gitter mit charakteristischer Gittergröße h. k. Hauptseminar Moderne Simulationsmethoden 27

32 Reguläres Gitter Definition Eine Folge von Gittern {T h } heißt regulär, wenn eine Konstante κ > 0 unabhängig von h derart existiert, dass ρ k h k κ für alle k T h, wobei ρ k der Radius des größten Innenkreises und h k die Größe von k sei. Abbildung: Trianguliertes Element k der Größe h k mit Innenkreis-Radius ρ k Hauptseminar Moderne Simulationsmethoden 28

33 Eine einfache Verfeinerungsstrategie Abbildung: Eine Folge von regulären Gittern Hauptseminar Moderne Simulationsmethoden 29

34 Inhaltsübersicht 1 2 Hauptseminar Moderne Simulationsmethoden 30

35 Gegeben sei ein endliches Gitter T h mit dreieckigen Elementen. Wir wählen V h H0 1 (D) als Menge von stetigen stückweise definierten Polynomen mit festem Totalgrad. Das heißt V h := {v C( D) mit v = 0 auf D und v k P r ( k ) für alle k T k }, wobei P r ( k ) Polynome in x = (x, y) mit Totalgrad r oder kleiner auf dem Dreieck k bezeichnet. Wir sind nicht verpflichtet, dass V h C( D), aber dies sichert uns, dass v D für alle v V h wohldefiniert ist. Hauptseminar Moderne Simulationsmethoden 31

36 Gegeben sei ein endliches Gitter T h mit dreieckigen Elementen. Wir wählen V h H0 1 (D) als Menge von stetigen stückweise definierten Polynomen mit festem Totalgrad. Das heißt V h := {v C( D) mit v = 0 auf D und v k P r ( k ) für alle k T k }, wobei P r ( k ) Polynome in x = (x, y) mit Totalgrad r oder kleiner auf dem Dreieck k bezeichnet. Wir sind nicht verpflichtet, dass V h C( D), aber dies sichert uns, dass v D für alle v V h wohldefiniert ist. Hauptseminar Moderne Simulationsmethoden 31

37 Knotenbasen Erneut benutzen wir Knotenbasen. Sei { } V h = span φ 1 (x),..., φ J (x), wobei φ j (x i ) = δ ij und {x 1,..., x J } eine Menge von Knoten ist, die an geeigenten Stellen in D positioniert sind um V h C( D) sicherzustellen. Der Polynomgrad r bestimmt die Funktion φ j genauso wie die Anzahl und Position der Knoten. Hauptseminar Moderne Simulationsmethoden 32

38 Beispiel: Stückweise lineare Elemente Beispiel Sei r = 1. Die globale Basisfunktion ist definiert als φ j k P 1 ( k ) und φ j (x i ) = δ ij, wobei x 1,..., x J die J inneren Eckpunkte des Gitters sind. Der Träger supp(φ j ) ist eine Stelle von Elementen, die sich an dem Eckpunkt x j treffen. Abbildung: Punkte der Dreiecke Hauptseminar Moderne Simulationsmethoden 33

39 Idee: Wahl der Knoten Betrachten wir zwei Elemente 1 und 2, die sich eine Kante ε teilen. Es gilt: φ j ist linear in beiden Argumenten und φ j 1 und φ j 2 stimmen an zwei Punkten auf ε (nämlich den Eckpunkten) überein. φ j (x) ist stetig entlang ε. Dies gilt für alle Kanten. v V h gehört zu C( D). Da aber keine Knoten auf dem Rand platziert sind, ist jedes v V h = span{φ 1,..., φ J } ebenfalls null auf D. Wahl der Knoten an den Eckpunkten Hauptseminar Moderne Simulationsmethoden 34

40 Wahl der Knoten Auf jedem Dreieck sind die Basisfunktionen zusammengesetzt aus den Monomen x a y b mit 0 a + b r. Beispiel Polynome von Grad r 2 sind Linearkombinationen von 1, x, y, x 2, xy und y 2. Für ein gegebenes r ist die Anzahl der Terme ( ) r + 2 (r + 2)(r + 1) n r := =. r 2 Hauptseminar Moderne Simulationsmethoden 35

41 Koeffizienten festlegen Für r = 1 ist n r = 3 und φ j (x, y) k = ax + by + c. Per Konstruktion kennen wir die Werte φ j (x j ) an drei Knoten x i in k (also den Eckpunkten). Festlegung der Koeffizienten a, b und c Im Allgemeinen benötigen wir n r Knoten in jedem Element. Gestaltung der Knoten so, dass r + 1 von diesen auf jeder Kante liegen. erhalten eine global stetige Approximation Hauptseminar Moderne Simulationsmethoden 36

42 Koeffizienten festlegen Für r = 1 ist n r = 3 und φ j (x, y) k = ax + by + c. Per Konstruktion kennen wir die Werte φ j (x j ) an drei Knoten x i in k (also den Eckpunkten). Festlegung der Koeffizienten a, b und c Im Allgemeinen benötigen wir n r Knoten in jedem Element. Gestaltung der Knoten so, dass r + 1 von diesen auf jeder Kante liegen. erhalten eine global stetige Approximation Abbildung: P 1, P 2 und P 3 Elemente mit 3, 6 und 10 Knoten Hauptseminar Moderne Simulationsmethoden 36

43 Koeffizienten festlegen Für r = 1 ist n r = 3 und φ j (x, y) k = ax + by + c. Per Konstruktion kennen wir die Werte φ j (x j ) an drei Knoten x i in k (also den Eckpunkten). Festlegung der Koeffizienten a, b und c Im Allgemeinen benötigen wir n r Knoten in jedem Element. Gestaltung der Knoten so, dass r + 1 von diesen auf jeder Kante liegen. erhalten eine global stetige Approximation Abbildung: P 1, P 2 und P 3 Elemente mit 3, 6 und 10 Knoten Hauptseminar Moderne Simulationsmethoden 36

44 Konstruktion von W h Hierzu: Einbeziehung der Randknoten x J+1,..., x J+Jb Im Fall der stückweise linearen Elemente sind das die Eckpunkte, die auf D liegen. (Nummerierung dieser erst nach Nummerierung der inneren Knoten) Genauer: durch Bereichern der Basis für V h mit den Polynomen φ j verbunden mit den J b Randknoten Hauptseminar Moderne Simulationsmethoden 37

45 Konstruktion von W h Hierzu: Einbeziehung der Randknoten x J+1,..., x J+Jb Im Fall der stückweise linearen Elemente sind das die Eckpunkte, die auf D liegen. (Nummerierung dieser erst nach Nummerierung der inneren Knoten) Genauer: durch Bereichern der Basis für V h mit den Polynomen φ j verbunden mit den J b Randknoten Im Speziellen hat jedes w W h die Form J J+J b w(x) = w i φ i (x) + w i φ i (x) =: w 0 (x) + w g (x). i=1 i=j+1 Hauptseminar Moderne Simulationsmethoden 37

46 Konstruktion von W h Hierzu: Einbeziehung der Randknoten x J+1,..., x J+Jb Im Fall der stückweise linearen Elemente sind das die Eckpunkte, die auf D liegen. (Nummerierung dieser erst nach Nummerierung der inneren Knoten) Genauer: durch Bereichern der Basis für V h mit den Polynomen φ j verbunden mit den J b Randknoten Im Speziellen hat jedes w W h die Form J J+J b w(x) = w i φ i (x) + w i φ i (x) =: w 0 (x) + w g (x). i=1 i=j+1 Hauptseminar Moderne Simulationsmethoden 37

47 Konstruktion von W h Im Speziellen hat jedes w W h die Form J J+J b w(x) = w i φ i (x) + w i φ i (x) =: w 0 (x) + w g (x). i=1 i=j+1 Nach Konstruktion ist w 0 V h auf dem Rand null und wir fixieren die Koeffizienten w B := [w J+1,..., w J+Jb ] T. Somit ist unsere Annahme v w V h für alle v, w W h erfüllt. Hauptseminar Moderne Simulationsmethoden 38

48 Konstruktion von W h Im Speziellen hat jedes w W h die Form J J+J b w(x) = w i φ i (x) + w i φ i (x) =: w 0 (x) + w g (x). i=1 i=j+1 Nach Konstruktion ist w 0 V h auf dem Rand null und wir fixieren die Koeffizienten w B := [w J+1,..., w J+Jb ] T. Somit ist unsere Annahme v w V h für alle v, w W h erfüllt. Hauptseminar Moderne Simulationsmethoden 38

49 Konstruktion von W h Im Speziellen hat jedes w W h die Form J J+J b w(x) = w i φ i (x) + w i φ i (x) =: w 0 (x) + w g (x). i=1 i=j+1 In vorigem Kapitel brauchten wir W h H 1 g (D). In der Praxis wird dies oft abgeschwächt. Mit der Konstruktion von w(x) haben wir w D = w g D = J+J b i=j+1 w i φ i D. Hauptseminar Moderne Simulationsmethoden 39

50 Konstruktion von W h Im Speziellen hat jedes w W h die Form J J+J b w(x) = w i φ i (x) + w i φ i (x) =: w 0 (x) + w g (x). i=1 i=j+1 In vorigem Kapitel brauchten wir W h H 1 g (D). In der Praxis wird dies oft abgeschwächt. Mit der Konstruktion von w(x) haben wir w D = w g D = J+J b i=j+1 w i φ i D. Hauptseminar Moderne Simulationsmethoden 39

51 Konstruktion von W h Mit der Konstruktion von w(x) haben wir w D = w g D = J+J b i=j+1 w i φ i D. Sofern g keine Linearkombination aus den gewählten Polynomen ist, wird die Randbedingung wird nur approximativ erfüllt und W h H 1 g (D). Hauptseminar Moderne Simulationsmethoden 40

52 Konstruktion von W h Mit der Konstruktion von w(x) haben wir w D = w g D = J+J b i=j+1 w i φ i D. Sofern g keine Linearkombination aus den gewählten Polynomen ist, wird die Randbedingung wird nur approximativ erfüllt und W h H 1 g (D). Möglichkeit: Annahme: w interpoliert g an den Randknoten und dazu fixieren wir w i := g(x i ) für i = J + 1,..., J + J b. Hauptseminar Moderne Simulationsmethoden 40

53 Konstruktion von W h Mit der Konstruktion von w(x) haben wir w D = w g D = J+J b i=j+1 w i φ i D. Sofern g keine Linearkombination aus den gewählten Polynomen ist, wird die Randbedingung wird nur approximativ erfüllt und W h H 1 g (D). Möglichkeit: Annahme: w interpoliert g an den Randknoten und dazu fixieren wir w i := g(x i ) für i = J + 1,..., J + J b. Hauptseminar Moderne Simulationsmethoden 40

54 Finite Elemente Approximation von Galerkin Die Finite Elemente Approximation von Galerkin kann nun geschrieben werden als J J+J b u h (x) = u i φ i (x) + w i φ i (x) = u 0 (x) + w g (x). i=1 i=j+1 Bringen wir dies nun in Form von a(u h, v) = l(v) für alle v V h und setzen v = φ j V h, so erhalten wir J J+J b u i a(φ i, φ j ) = l(φ j ) w i a(φ i, φ j ) für j = 1,..., J. i=1 i=j+1 Hauptseminar Moderne Simulationsmethoden 41

55 Finite Elemente Approximation von Galerkin Die Finite Elemente Approximation von Galerkin kann nun geschrieben werden als J J+J b u h (x) = u i φ i (x) + w i φ i (x) = u 0 (x) + w g (x). i=1 i=j+1 Bringen wir dies nun in Form von a(u h, v) = l(v) für alle v V h und setzen v = φ j V h, so erhalten wir J J+J b u i a(φ i, φ j ) = l(φ j ) w i a(φ i, φ j ) für j = 1,..., J. i=1 i=j+1 Hauptseminar Moderne Simulationsmethoden 41

56 Die Galerkin-Matrix Wir definieren die Galerkin-Matrix A R (J+J b)x(j+j b ) und den Vektor b R J+J b durch a ij := a(φ i, φ j ) = a(x) φ i (x) φ j (x)dx, i = 1,..., J + J b, D b i := l(φ i ) = f (x) φ i (x)dx, i = 1,..., J + J b. D Wird ein Reaktionsterm qu in unserem Randwertproblem addiert, so brauchen wir auch die Massematrix M, die als m ij := q(x) φ i (x) φ j (x)dx, i, j = 1,..., J + J b definiert ist. D Hauptseminar Moderne Simulationsmethoden 42

57 Die Galerkin-Matrix Wir definieren die Galerkin-Matrix A R (J+J b)x(j+j b ) und den Vektor b R J+J b durch a ij := a(φ i, φ j ) = a(x) φ i (x) φ j (x)dx, i = 1,..., J + J b, D b i := l(φ i ) = f (x) φ i (x)dx, i = 1,..., J + J b. D Wird ein Reaktionsterm qu in unserem Randwertproblem addiert, so brauchen wir auch die Massematrix M, die als m ij := q(x) φ i (x) φ j (x)dx, i, j = 1,..., J + J b definiert ist. D Hauptseminar Moderne Simulationsmethoden 42

58 Die Galerkin-Matrix Die Galerkin-Matrix A R (J+J b)x(j+j b ) ist durch a ij := a(φ i, φ j ) = a(x) φ i (x) φ j (x)dx, i = 1,..., J + J b definiert. Wir sehen: D a ij 0 ist nur dann, wenn sich die Träger supp(φ i ) und supp(φ j ) schneiden. Für r = 1 passiert dies nur, wenn x i und x j Eckpunkte des gleichen Dreiecks sind. A ist spärlich besetzt. Hauptseminar Moderne Simulationsmethoden 43

59 Die Galerkin-Matrix Die Galerkin-Matrix A R (J+J b)x(j+j b ) ist durch a ij := a(φ i, φ j ) = a(x) φ i (x) φ j (x)dx, i = 1,..., J + J b definiert. Wir sehen: D a ij 0 ist nur dann, wenn sich die Träger supp(φ i ) und supp(φ j ) schneiden. Für r = 1 passiert dies nur, wenn x i und x j Eckpunkte des gleichen Dreiecks sind. A ist spärlich besetzt. Hauptseminar Moderne Simulationsmethoden 43

60 Die Galerkin-Gleichung Unterteilen wir A und b in ( ) AII A A = IB, b = A BI A BB ( ) bi wobei A II R JxJ, A IB R JxJ b, b I R J und analog mit den anderen Blöcken. Die Galerkin Gleichung J J+J b u i a(φ i, φ j ) = l(φ j ) w i a(φ i, φ j ), j = 1,..., J i=1 i=j+1 kann dann als A II u I = b I A IB w B geschrieben werden, wobei w B die diskreten Randdaten sind, wie vorhin definiert. Hauptseminar Moderne Simulationsmethoden 44 b B,

61 Hauptseminar Moderne Simulationsmethoden Vielen Dank für Ihre Aufmerksamkeit! Hauptseminar Moderne Simulationsmethoden 45