Monte Carlo Finite Elemente Methode
|
|
|
- Nadja Goldschmidt
- vor 5 Jahren
- Abrufe
Transkript
1 Monte Carlo Finite Elemente Methode Lisa Eppler Johannes-Gutenberg Universität Mainz 18. Januar / 55
2 Inhalt Monte Carlo Finite Elemente Methode 1 Wiederholung 2 Monte Carlo 3 Beispiele 1-d 2-d 4 Fehleranalyse 2 / 55
3 Inhalt Monte Carlo Finite Elemente Methode 1 Wiederholung 2 Monte Carlo 3 Beispiele 1-d 2-d 4 Fehleranalyse 3 / 55
4 Wiederholung - stochastische Daten Elliptisches Randwertproblem mit stochastischen Daten: (a(x, ω) u(x, ω)) = f (x, ω) für x D u(x, ω) = g(x) für x D Variationsproblem mit stochastischen Daten: a(x, ω) u(x, ω) v(x) dx = f (x)v(x) dx D D v V := H 1 0 (D) 4 / 55
5 Wiederholung - stochastische Daten Elliptisches Randwertproblem mit stochastischen Daten: (a(x, ω) u(x, ω)) = f (x) für x D u(x, ω) = 0 für x D Variationsproblem mit stochastischen Daten: a(x, ω) u(x, ω) v(x) dx = f (x)v(x) dx D D v V := H 1 0 (D) 5 / 55
6 Wiederholung - stochastische Daten Elliptisches Randwertproblem mit stochastischen Daten: (a(x, ω) u(x, ω)) = f (x) für x D u(x, ω) = 0 für x D Variationsproblem mit stochastischen Daten: a(x, ω) u(x, ω) v(x) dx = f (x)v(x) dx D D v V := H 1 0 (D) 6 / 55
7 Wiederholung - stochastische Daten Annahme 9.5 Realisierungen a(, ω) des Diffusionskoeffizienten liegen in L (D) und erfüllen für fast alle ω Ω, wobei 0 < a min (ω) a(x, ω) a max (ω) < inf a min (ω) := ess inf x D a(x, ω), a max(ω) := ess sup a(x, ω) x D 7 / 55
8 Theorem 9.9 Falls Annahme 9.5 gilt, f L 2 (D) und g = 0, dann hat das Variationsproblem eine eindeutige Lösung u(, ω) V = H 1 0 (D). 8 / 55
9 Wiederholung - Galerkin FEM J V V h u h (x) = u i φ i (x), i=1 φ i Basisfunktionen von V h Löse LGS: Au = b mit a ij = b i = D D a(x) Φ i (x) Φ j (x)dx, f (x)φ i (x)dx, i, j = 1,..., J i = 1,..., J 9 / 55
10 Das Variationsproblem mit stochastischen Daten a(x, ω) u(x, ω) v(x) dx = D D f (x)v(x) dx v V := H0 1 (D) 10 / 55
11 Inhalt Monte Carlo Finite Elemente Methode 1 Wiederholung 2 Monte Carlo 3 Beispiele 1-d 2-d 4 Fehleranalyse 11 / 55
12 Monte Carlo Methode Idee: Wiederhole ein Experiment mit verschiedenen Eingabedaten und nehme den Durchschnitt der Ergebnisse als Lösung: X Q = X X Q Q 12 / 55
13 Monte Carlo Methode In unserem Fall: ã r := ã(, ω r ), für r = 1,..., Q i.i.d Löse die DGL für Q verschiedene ã r mit der Galerkin FEM. Erhalte ũ r h (x) := ũ h(x, ω r ), für r = 1,..., Q i.i.d 13 / 55
14 Monte Carlo Methode In unserem Fall: ã r := ã(, ω r ), für r = 1,..., Q i.i.d Löse die DGL für Q verschiedene ã r mit der Galerkin FEM. Erhalte ũ r h (x) := ũ h(x, ω r ), für r = 1,..., Q i.i.d 14 / 55
15 Monte Carlo Methode In unserem Fall: ã r := ã(, ω r ), für r = 1,..., Q i.i.d Löse die DGL für Q verschiedene ã r mit der Galerkin FEM. Erhalte ũ r h (x) := ũ h(x, ω r ), für r = 1,..., Q i.i.d 15 / 55
16 Monte Carlo Methode Berechne mit den erhaltenen ũ r h (x): und die Varianz: E[ũ(x)] µ Q,h (x) := 1 Q σ 2 Q,h (x) : = 1 Q 1 Q ũh r (x) r=w Q (ũh r (x) µ Q,h(x)) 2 r=1 = 1 ( Q ) (ũh r Q 1 (x)2 ) Qµ Q,h (x) 2 r=1 16 / 55
17 Monte Carlo Methode Berechne mit den erhaltenen ũ r h (x): und die Varianz: E[ũ(x)] µ Q,h (x) := 1 Q σ 2 Q,h (x) : = 1 Q 1 Q ũh r (x) r=w Q (ũh r (x) µ Q,h(x)) 2 r=1 = 1 ( Q ) (ũh r Q 1 (x)2 ) Qµ Q,h (x) 2 r=1 17 / 55
18 Inhalt Monte Carlo Finite Elemente Methode 1 Wiederholung 2 Monte Carlo 3 Beispiele 1-d 2-d 4 Fehleranalyse 18 / 55
19 Beispiel 1 d dx (a(x) d dx )u(x) = 1 für x (0, 1) R u(0) = 0, u(1) = 0 Approximiere a(x) mit a(x, ω) = µ + P k=1 σ k 2 π 2 cos(πkx)ξ k(ω), ξ k U( 1, 1) u.i.v 19 / 55
20 Beispiel 1 a(x, ω) = µ + P k=1 σ k 2 π 2 cos(πkx)ξ k(ω), ξ k U( 1, 1) u.i.v Gehe sicher, dass Annahme 9.5 erfüllt ist: 0 < a min (ω) a(x, ω) a max (ω) < inf 20 / 55
21 Beispiel 1 a(x, ω) = µ + P k=1 σ k 2 π 2 cos(πkx)ξ k(ω), ξ k U( 1, 1) u.i.v. Beziehungsweise, dass Annahme 9.3 erfüllt ist: Also: 0 < µ σ π 2 P 0 < a min a(x, ω) a max < k=1 Daraus ergibt sich die Bedingung: 1 k 2 a(x, ω) µ + σ π 2 σ < 6µ P k=1 1 k 2 < 21 / 55
22 Beispiel 1 a(x, ω) = µ + P k=1 σ k 2 π 2 cos(πkx)ξ k(ω), ξ k U( 1, 1) u.i.v. Beziehungsweise, dass Annahme 9.3 erfüllt ist: Also: 0 < µ σ π 2 P 0 < a min a(x, ω) a max < k=1 Daraus ergibt sich die Bedingung: 1 k 2 a(x, ω) µ + σ π 2 σ < 6µ P k=1 1 k 2 < 22 / 55
23 Beispiel 1 Algorithmus: [mean u, var u] = oned MC FEM(ne, sigma, mu, P, Q) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter h = 1/ne; x = [ h/2:h:1-h/2] ; Schritt 2 : for-schleife: j = 1,..., Q Zufalls-Vektor ξ ( 1, 1) P xi = -1+2.*rand(P,1); Berechne a(x, ω) (nochmal eine for-schleife) a = mu*ones(ne,1); a = a + sigma.*((i*pi).ˆ(-2)).*cos(pi*i.*x).*xi(i); Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u,a,b] = oned linear FEM(ne, a, zeros(ne,1), ones(ne,1),); Schritt 3: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 23 / 55
24 Beispiel 1 Algorithmus: [mean u, var u] = oned MC FEM(ne, sigma, mu, P, Q) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter h = 1/ne; x = [ h/2:h:1-h/2] ; Schritt 2 : for-schleife: j = 1,..., Q Zufalls-Vektor ξ ( 1, 1) P xi = -1+2.*rand(P,1); Berechne a(x, ω) (nochmal eine for-schleife) a = mu*ones(ne,1); a = a + sigma.*((i*pi).ˆ(-2)).*cos(pi*i.*x).*xi(i); Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u,a,b] = oned linear FEM(ne, a, zeros(ne,1), ones(ne,1),); Schritt 3: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 24 / 55
25 Beispiel 1 Algorithmus: [mean u, var u] = oned MC FEM(ne, sigma, mu, P, Q) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter h = 1/ne; x = [ h/2:h:1-h/2] ; Schritt 2 : for-schleife: j = 1,..., Q Zufalls-Vektor ξ ( 1, 1) P xi = -1+2.*rand(P,1); Berechne a(x, ω) (nochmal eine for-schleife) a = mu*ones(ne,1); a = a + sigma.*((i*pi).ˆ(-2)).*cos(pi*i.*x).*xi(i); Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u,a,b] = oned linear FEM(ne, a, zeros(ne,1), ones(ne,1),); Schritt 3: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 25 / 55
26 Beispiel 1 Algorithmus: [mean u, var u] = oned MC FEM(ne, sigma, mu, P, Q) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter h = 1/ne; x = [ h/2:h:1-h/2] ; Schritt 2 : for-schleife: j = 1,..., Q Zufalls-Vektor ξ ( 1, 1) P xi = -1+2.*rand(P,1); Berechne a(x, ω) (nochmal eine for-schleife) a = mu*ones(ne,1); a = a + sigma.*((i*pi).ˆ(-2)).*cos(pi*i.*x).*xi(i); Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u,a,b] = oned linear FEM(ne, a, zeros(ne,1), ones(ne,1),); Schritt 3: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 26 / 55
27 Beispiel 1 Algorithmus: [mean u, var u] = oned MC FEM(ne, sigma, mu, P, Q) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter h = 1/ne; x = [ h/2:h:1-h/2] ; Schritt 2 : for-schleife: j = 1,..., Q Zufalls-Vektor ξ ( 1, 1) P xi = -1+2.*rand(P,1); Berechne a(x, ω) (nochmal eine for-schleife) a = mu*ones(ne,1); a = a + sigma.*((i*pi).ˆ(-2)).*cos(pi*i.*x).*xi(i); Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u,a,b] = oned linear FEM(ne, a, zeros(ne,1), ones(ne,1),); Schritt 3: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 27 / 55
28 Inhalt Monte Carlo Finite Elemente Methode 1 Wiederholung 2 Monte Carlo 3 Beispiele 1-d 2-d 4 Fehleranalyse 28 / 55
29 Ausflug Stochastik Kovarianz Seien X, Y zwei relle Zufallsvariablen, dann ist Cov(X, Y ) := E [(X E(X ))(Y E(Y ))] die Kovarianz von X und Y. Cov(X, Y ) > 0 X wird größer, wenn Y größer wird Cov(X, Y ) < 0 X wird kleiner, wenn Y größer wird Cov(X, Y ) = 0 X und Y hängen nicht miteinander zusammen 29 / 55
30 Ausflug Stochastik Kovarianz Seien X, Y zwei relle Zufallsvariablen, dann ist Cov(X, Y ) := E [(X E(X ))(Y E(Y ))] die Kovarianz von X und Y. Cov(X, Y ) > 0 X wird größer, wenn Y größer wird Cov(X, Y ) < 0 X wird kleiner, wenn Y größer wird Cov(X, Y ) = 0 X und Y hängen nicht miteinander zusammen 30 / 55
31 Ausflug Stochastik Kovarianzmatrix Sei X = [X 1,..., X d ] T eine d-dimensionale Zufallsvariable. Die Matrix C = Cov(X) := E [(X ] E(X))(X E(X)) T heißt Kovarianzmatrix, wobei der Eintrag C ij = Cov(X i, X j ). 31 / 55
32 Ausflug Stochastik Gaußsches Zufallsfeld Ein Gaußsches Zufallsfeld {u(x) : x D} ist ein Zufallsfeld 2. Ordnung u = [u(x 1 ),..., u(x M )] T, das der multivariaten Gaußverteilung für jedes x 1,.., x M D folgt. u N(µ, C) mit µ i = µ(x i ) und C ij = Cov(x i, x j ) 32 / 55
33 Ausflug Stochastik Gaußsches Zufallsfeld - stationär und isotrop Ein Gaußsches Zufallsfeld ist stationär, falls µ unabhängig von x ist und isotrop, falls die Kovarianz invariant unter Rotation ist, also: C(x i, x j ) = c 0 (r), wobei r := x i x j 2 und c 0 : R + R die isotrope Kovarianz ist. 33 / 55
34 Beispiel 2 Sei D = (0, 1) (0, 1) und a(x) = e z(x), x D wobei z(x) ein stationäres Gaußsches Zufallsfeld ist mit µ = 0 und isotroper Kovarianz c 0 (r) = e r 2 /l / 55
35 Beispiel 2 Annahme 9.6 Sei D R 2 beschränkt und a(x) = e z(x), x D wobei z(x) ein Gaußsches Zufallsfeld ist, sodass für L, s > 0 gilt: E [ z(x) z(y) 2] L x y s 2 Theorem 9.9 Falls Annahme 9.6 gilt, so gilt auch Annahme / 55
36 Beispiel 2 Annahme 9.6 Sei D R 2 beschränkt und a(x) = e z(x), x D wobei z(x) ein Gaußsches Zufallsfeld ist, sodass für L, s > 0 gilt: E [ z(x) z(y) 2] L x y s 2 zeige: Dies gilt, falls z(x) ein Gaußsches Zufallsfeld ist mit µ = 0 und isotroper Kovarianz c 0 (r) = e r 2 /l 2 : 36 / 55
37 Beispiel 2 Sei D = (0, 1) (0, 1) und a(x) = e z(x), x D wobei z(x) ein Gaußsches Zufallsfeld ist mit µ = 0 und isotroper Kovarianz c 0 (r) = e r 2 /l 2. Approximiere a(x) auf dem gewählten Gitter T h durch ã(x, ω) k := a(ν k j, ω) j=1 k T wobei ν k j, j = 1, 2, 3 die Ecken des Dreiecks k sind. 37 / 55
38 Beispiel 2 Algorithmus: [mean u, var u] = twod MC FEM(ns,Q,ell,alpha) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter [xv, yv, elt2vert, nvtx, ne, h] = uniform mesh info(ns); Schritt 2: Erstelle ein (bzw. zwei) Gaußsche Zufallsfelder [z1, z2] = circ emb sample 2dB(C, n1, n2, m1, m2); Schritt 3: Berechne a(x) v1 = exp(z1); v2 = exp(z2); Schritt 4 : Berechne ã(x) a1 = (1/3).*(v1(elt2vert(:, 1)) + v1(elt2vert(:, 2)) + v1(elt2vert(:, 3))); a2 = (1/3).*(v2(elt2vert(:, 1)) + v2(elt2vert(:, 2)) + v2(elt2vert(:, 3))); 38 / 55
39 Beispiel 2 Algorithmus: [mean u, var u] = twod MC FEM(ns,Q,ell,alpha) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter [xv, yv, elt2vert, nvtx, ne, h] = uniform mesh info(ns); Schritt 2: Erstelle ein (bzw. zwei) Gaußsche Zufallsfelder [z1, z2] = circ emb sample 2dB(C, n1, n2, m1, m2); Schritt 3: Berechne a(x) v1 = exp(z1); v2 = exp(z2); Schritt 4 : Berechne ã(x) a1 = (1/3).*(v1(elt2vert(:, 1)) + v1(elt2vert(:, 2)) + v1(elt2vert(:, 3))); a2 = (1/3).*(v2(elt2vert(:, 1)) + v2(elt2vert(:, 2)) + v2(elt2vert(:, 3))); 39 / 55
40 Beispiel 2 Algorithmus: [mean u, var u] = twod MC FEM(ns,Q,ell,alpha) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter [xv, yv, elt2vert, nvtx, ne, h] = uniform mesh info(ns); Schritt 2: Erstelle ein (bzw. zwei) Gaußsche Zufallsfelder [z1, z2] = circ emb sample 2dB(C, n1, n2, m1, m2); Schritt 3: Berechne a(x) v1 = exp(z1); v2 = exp(z2); Schritt 4 : Berechne ã(x) a1 = (1/3).*(v1(elt2vert(:, 1)) + v1(elt2vert(:, 2)) + v1(elt2vert(:, 3))); a2 = (1/3).*(v2(elt2vert(:, 1)) + v2(elt2vert(:, 2)) + v2(elt2vert(:, 3))); 40 / 55
41 Beispiel 2 Algorithmus: [mean u, var u] = twod MC FEM(ns,Q,ell,alpha) Schritt 1: Diskretisiere den Raum mit einem uniformen Gitter [xv, yv, elt2vert, nvtx, ne, h] = uniform mesh info(ns); Schritt 2: Erstelle ein (bzw. zwei) Gaußsche Zufallsfelder [z1, z2] = circ emb sample 2dB(C, n1, n2, m1, m2); Schritt 3: Berechne a(x) v1 = exp(z1); v2 = exp(z2); Schritt 4 : Berechne ã(x) a1 = (1/3).*(v1(elt2vert(:, 1)) + v1(elt2vert(:, 2)) + v1(elt2vert(:, 3))); a2 = (1/3).*(v2(elt2vert(:, 1)) + v2(elt2vert(:, 2)) + v2(elt2vert(:, 3))); 41 / 55
42 Beispiel 2 [mean u, var u] = twod MC FEM(ns,Q,ell,alpha) Schritt 5: Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u1 int, A1, rhs1] = twod linear FEM(ns, xv, yv, elt2vert... nvtx, ne, h, a1, ones(ne,1)); [u2 int, A2, rhs1] = twod linear FEM(ns, xv, yv, elt2vert... nvtx, ne, h, a2, ones(ne,1)); Schritt 6: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 42 / 55
43 Beispiel 2 [mean u, var u] = twod MC FEM(ns,Q,ell,alpha) Schritt 5: Löse die DGL mit dem Galerkin-Verfahren aus Kapitel 2 mit linearen Basisfunktionen [u1 int, A1, rhs1] = twod linear FEM(ns, xv, yv, elt2vert... nvtx, ne, h, a1, ones(ne,1)); [u2 int, A2, rhs1] = twod linear FEM(ns, xv, yv, elt2vert... nvtx, ne, h, a2, ones(ne,1)); Schritt 6: Berechne µ Q,h (x) und die Varianz σ 2 Q,h (x) 43 / 55
44 Inhalt Monte Carlo Finite Elemente Methode 1 Wiederholung 2 Monte Carlo 3 Beispiele 1-d 2-d 4 Fehleranalyse 44 / 55
45 Fehlerabschätzung der Monte Carlo Methode E[u] µ Q,h H 1 0 (D) 45 / 55
46 Fehlerabschätzung der Monte Carlo Methode E[u] µ Q,h H 1 0 (D) E[u] E[ũ h] H 1 0 (D) + E[ũ h ] µ Q,h H1 0 }{{}}{{ (D) } =:E h,a =:E MC 46 / 55
47 Fehlerabschätzung der Monte Carlo Methode Jensen sche Ungleichung: Sei φ : R R eine konvexe Funktion und X eine reellwertige Zufallsvariable mit E[X ] <, dann gilt φ(e[x ]) E [φ(x )] L p (Ω, H0 1 (D)) Norm [ ] u L p (Ω,H0 1(D)) := E u p 1 p H0 1(D) 47 / 55
48 Fehlerabschätzung der Monte Carlo Methode Jensen sche Ungleichung: Sei φ : R R eine konvexe Funktion und X eine reellwertige Zufallsvariable mit E[X ] <, dann gilt φ(e[x ]) E [φ(x )] L p (Ω, H0 1 (D)) Norm [ ] u L p (Ω,H0 1(D)) := E u p 1 p H0 1(D) 48 / 55
49 Fehlerabschätzung der Monte Carlo Methode E[u] µ Q,h H 1 0 (D) E[u] E[ũ h] H 1 0 (D) + E[ũ h ] µ Q,h H 1 }{{} 0 (D) }{{} =:E h,a O(h) =:E MC 49 / 55
50 Fehlerabschätzung der Monte Carlo Methode Theorem 9.22 Es gelte die Annahme 9.6, f L 2 (D) und g = 0 und E MC := E[ũ h ] µ Q,h H 1 0 (D). Dann gilt: E[E 2 MC ] K Q für eine Konstante K > 0 unabhängig von h. 50 / 55
51 Fehlerabschätzung der Monte Carlo Methode Lemma 9.13 Es gelte die Annahme 9.6, f L 2 (D) und g = 0. Dann gilt: für alle p 1 und u h L p (Ω, H 1 0 (D)) u h L p (Ω,H 1 0 (D)) K p a 1 min L p (Ω) f L 2 (D) 51 / 55
52 Korollar Korollar 9.23 Es gelte die Annahme 9.6, f L 2 (D) und g = 0 und E MC := E[ũ h ] µ Q,h H 1 0 (D). Dann gilt für alle ε > 0: P(E MC Q 1 2 +ε ) LQ 2ε für ein L > 0, das unabhängig ist von h. 52 / 55
53 Aus der Stochastik Theorem 4.58(i) Falls für ein r, p > 0 und eine Konstante K gilt: E[ X n X p H0 1(D)]1/p K n r dann folgt für jedes ε > 0: P( X n X H 1 0 (D) n r+ε ) K p n pε 53 / 55
54 Fehlerabschätzung der Monte Carlo Methode E[u] µ Q,h H 1 0 (D) E[u] E[ũ h] H 1 0 (D) + E[ũ h ] µ Q,h H 1 }{{} 0 (D) }{{} =:E h,a O(h) =:E MC O(Q 1/2 ) 54 / 55
55 Ergebnis Aufwand Will man die Lösung mit der Monte Carlo Methode bis auf einen Fehler ε approximieren, so lässt sich mit den obigen Ergebnissen zeigen, dass der Aufwand bei O(ε 4 ) liegt. 55 / 55
Ausarbeitung Hauptseminar moderne Simulationsmethoden
 Ausarbeitung Hauptseminar moderne Simulationsmethoden Die Monte Carlo Finite Elemente Methode Lisa Eppler 18. Januar 2018 Der Vortrag, zu dem diese Ausarbeitung gehört, orientiert sich an den Seiten 380-386
Ausarbeitung Hauptseminar moderne Simulationsmethoden Die Monte Carlo Finite Elemente Methode Lisa Eppler 18. Januar 2018 Der Vortrag, zu dem diese Ausarbeitung gehört, orientiert sich an den Seiten 380-386
Hauptseminar: Moderne Simulationsmethoden
 Hauptseminar: Moderne Simulationsmethoden Finite Elemente Methode von Galerkin Tanja Heich Fachbereich 08 Johannes Gutenberg-Universität Mainz 02. November 2017 Hauptseminar Moderne Simulationsmethoden
Hauptseminar: Moderne Simulationsmethoden Finite Elemente Methode von Galerkin Tanja Heich Fachbereich 08 Johannes Gutenberg-Universität Mainz 02. November 2017 Hauptseminar Moderne Simulationsmethoden
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit
 3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
Vorlesung 8a. Kovarianz und Korrelation
 Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Unabhängige Zufallsvariablen
 Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Mathematische Ökonometrie
 Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Statistische Analyseverfahren Abschnitt 2: Zufallsvektoren und mehrdimensionale Verteilungen
 Statistische Analyseverfahren Abschnitt 2: Zufallsvektoren und mehrdimensionale Verteilungen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik Oktober 2018 Prof. Dr. Hans-Jörg
Statistische Analyseverfahren Abschnitt 2: Zufallsvektoren und mehrdimensionale Verteilungen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik Oktober 2018 Prof. Dr. Hans-Jörg
Varianz und Kovarianz
 KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
I Grundbegriffe 1 1 Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeiten und Unabhängigkeit Reellwertige Zufallsvariablen...
 Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Stochastische FEM mit elementaren Zufallselementen
 Stochastische FEM mit elementaren Zufallselementen Hans-Jörg Starkloff Westsächsische Hochschule Zwickau 13. Südostdeutsches Kolloquium zur Numerischen Mathematik 2007 Freiberg, 27. April 2007 Einführung
Stochastische FEM mit elementaren Zufallselementen Hans-Jörg Starkloff Westsächsische Hochschule Zwickau 13. Südostdeutsches Kolloquium zur Numerischen Mathematik 2007 Freiberg, 27. April 2007 Einführung
Kapitel 12 Erwartungswert und Varianz
 Kapitel 12 Erwartungswert und Varianz Vorlesung Wahrscheinlichkeitsrechnung I vom 4/10. Juni 2009 Lehrstuhl für Angewandte Mathematik 1 FAU 12.1 Der Erwartungswert Der Erwartungswert einer Zufallsvariablen
Kapitel 12 Erwartungswert und Varianz Vorlesung Wahrscheinlichkeitsrechnung I vom 4/10. Juni 2009 Lehrstuhl für Angewandte Mathematik 1 FAU 12.1 Der Erwartungswert Der Erwartungswert einer Zufallsvariablen
4. Verteilungen von Funktionen von Zufallsvariablen
 4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
Einführung und Grundlagen
 Kapitel 1 Einführung und Grundlagen Generelle Notation: Ω, A, P sei ein W-Raum im Hintergrund nie weiter spezifiziert Die betrachteten Zufallsvariablen seien auf Ω definiert, zb X : Ω, A M, A, wobei M,
Kapitel 1 Einführung und Grundlagen Generelle Notation: Ω, A, P sei ein W-Raum im Hintergrund nie weiter spezifiziert Die betrachteten Zufallsvariablen seien auf Ω definiert, zb X : Ω, A M, A, wobei M,
2.Tutorium Multivariate Verfahren
 2.Tutorium Multivariate Verfahren - Multivariate Verteilungen - Hannah Busen: 27.04.2015 und 04.05.2015 Nicole Schüller: 28.04.2015 und 05.05.2015 Institut für Statistik, LMU München 1 / 21 Gliederung
2.Tutorium Multivariate Verfahren - Multivariate Verteilungen - Hannah Busen: 27.04.2015 und 04.05.2015 Nicole Schüller: 28.04.2015 und 05.05.2015 Institut für Statistik, LMU München 1 / 21 Gliederung
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Vorlesung 12a. Zerlegung der Varianz
 Vorlesung 12a Zerlegung der Varianz 1 Im zufälligen Paar (X, Y ) 2 Im zufälligen Paar (X, Y ) sei Y reellwertig mit endlicher Varianz. Im zufälligen Paar (X, Y ) sei Y reellwertig mit endlicher Varianz.
Vorlesung 12a Zerlegung der Varianz 1 Im zufälligen Paar (X, Y ) 2 Im zufälligen Paar (X, Y ) sei Y reellwertig mit endlicher Varianz. Im zufälligen Paar (X, Y ) sei Y reellwertig mit endlicher Varianz.
Statistics, Data Analysis, and Simulation SS 2017
 Statistics, Data Analysis, and Simulation SS 2017 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 4. Mai 2017 Dr. Michael O. Distler
Statistics, Data Analysis, and Simulation SS 2017 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 4. Mai 2017 Dr. Michael O. Distler
2. Ein Zufallsvektor X IR d ist multivariat normal verteilt dann und nur dann wenn seine charakteristische Funktion folgendermaßen gegeben ist:
 Multivariate elliptische Verteilungen a) Die multivariate Normalverteilung Definition 2 Der Zufallsvektor (X 1, X 2,..., X d ) T hat eine multivariate Normalverteilung (oder eine multivariate Gauss sche
Multivariate elliptische Verteilungen a) Die multivariate Normalverteilung Definition 2 Der Zufallsvektor (X 1, X 2,..., X d ) T hat eine multivariate Normalverteilung (oder eine multivariate Gauss sche
Kapitel 8. Parameter multivariater Verteilungen. 8.1 Erwartungswerte
 Kapitel 8 Parameter multivariater Verteilungen 8.1 Erwartungswerte Wir können auch bei mehrdimensionalen Zufallsvariablen den Erwartungswert betrachten. Dieser ist nichts anderes als der vektor der Erwartungswerte
Kapitel 8 Parameter multivariater Verteilungen 8.1 Erwartungswerte Wir können auch bei mehrdimensionalen Zufallsvariablen den Erwartungswert betrachten. Dieser ist nichts anderes als der vektor der Erwartungswerte
Vorlesung 8b. Kovarianz, Korrelation und Regressionsgerade
 Vorlesung 8b Kovarianz, Korrelation und Regressionsgerade 1 1. Die Kovarianz und ihre Eigenschaften 2 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und
Vorlesung 8b Kovarianz, Korrelation und Regressionsgerade 1 1. Die Kovarianz und ihre Eigenschaften 2 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und
Reelle Zufallsvariablen
 Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
Johannes Veit. 8. Januar 2016
 Finite im Ein Blick über den Tellerrand... mit FreeFem++ 8. Januar 2016 im 1 2 im 3 4 Gliederung 5 im 1 2 im 3 4 Gliederung 5 dem Einheitsquadrat Laplace - Gleichung: im u(x) = 0 Man betrachte das Problem
Finite im Ein Blick über den Tellerrand... mit FreeFem++ 8. Januar 2016 im 1 2 im 3 4 Gliederung 5 im 1 2 im 3 4 Gliederung 5 dem Einheitsquadrat Laplace - Gleichung: im u(x) = 0 Man betrachte das Problem
Gaußsche Felder und Simulation
 3 2 data_2d_1.dat data_2d_2.dat data_2d_64.dat data_2d_128.dat 1-1 -2-3 1 2 3 4 5 6 7 Gaußsche Felder und Simulation Benedikt Jahn, Aaron Spettl 4. November 28 Institut für Stochastik, Seminar Zufällige
3 2 data_2d_1.dat data_2d_2.dat data_2d_64.dat data_2d_128.dat 1-1 -2-3 1 2 3 4 5 6 7 Gaußsche Felder und Simulation Benedikt Jahn, Aaron Spettl 4. November 28 Institut für Stochastik, Seminar Zufällige
Klausur,,Einführung in die W theorie
 Institut für angewandte Mathematik Wintersemester 017/18 Andreas Eberle, Maximilian Fels Klausur,,Einführung in die W theorie Bitte diese Felder in Druckschrift ausfüllen Name: Matrikelnr.: Vorname: Studiengang:
Institut für angewandte Mathematik Wintersemester 017/18 Andreas Eberle, Maximilian Fels Klausur,,Einführung in die W theorie Bitte diese Felder in Druckschrift ausfüllen Name: Matrikelnr.: Vorname: Studiengang:
Lineare Approximation
 Lineare Approximation Yasemin Hafizogullari 9. Januar 2009 Yasemin Hafizogullari () Lineare Approximation 9. Januar 2009 1 / 49 Übersicht 1 Erster Abschnitt: Lineare Approximation in beliebiger orthonormal
Lineare Approximation Yasemin Hafizogullari 9. Januar 2009 Yasemin Hafizogullari () Lineare Approximation 9. Januar 2009 1 / 49 Übersicht 1 Erster Abschnitt: Lineare Approximation in beliebiger orthonormal
Gauß-Prozess-Regression
 Bayessche Regression und Gaußprozesse Dr. rer. nat. Johannes Riesterer Motivation Kriging Der südafrikanische Bergbauingenieur Danie Krige versuchte 1951, eine optimale Interpolationsmethode für den Bergbau
Bayessche Regression und Gaußprozesse Dr. rer. nat. Johannes Riesterer Motivation Kriging Der südafrikanische Bergbauingenieur Danie Krige versuchte 1951, eine optimale Interpolationsmethode für den Bergbau
Übungen zu Partielle Differentialgleichungen, WS 2016
 Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Vorlesung Wahrscheinlichkeit und Statistik D-Math, ETH Überblick über den Stoff der einzelnen Stunden
 Vorlesung Wahrscheinlichkeit und Statistik D-Math, ETH Überblick über den Stoff der einzelnen Stunden Hansruedi Künsch Frühlingssemester 2013 Repetition vom 19. 2. Ein Wahrscheinlichkeitsraum besteht aus
Vorlesung Wahrscheinlichkeit und Statistik D-Math, ETH Überblick über den Stoff der einzelnen Stunden Hansruedi Künsch Frühlingssemester 2013 Repetition vom 19. 2. Ein Wahrscheinlichkeitsraum besteht aus
Vorlesung 9b. Kovarianz und Korrelation
 Vorlesung 9b Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X,Y]:= E [ (X EX)(Y EY) ] Insbesondere ist
Vorlesung 9b Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X,Y]:= E [ (X EX)(Y EY) ] Insbesondere ist
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 12. Übung SS 18: Woche vom
 Übungsaufgaben 12. Übung SS 18: Woche vom 2. 7. 6. 7. 2018 Stochastik VI: Zufallsvektoren; Funktionen von ZG Aufgaben: s. pdf auf der homepage von Dr. Vanselow http://www.math.tu-dresden.de/ vanselow/...
Übungsaufgaben 12. Übung SS 18: Woche vom 2. 7. 6. 7. 2018 Stochastik VI: Zufallsvektoren; Funktionen von ZG Aufgaben: s. pdf auf der homepage von Dr. Vanselow http://www.math.tu-dresden.de/ vanselow/...
1.3 Zufallsvariablen
 1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
Stochastik-Praktikum
 Stochastik-Praktikum Zufallszahlen und Monte Carlo Peter Frentrup Humboldt-Universität zu Berlin 17. Oktober 2017 (Humboldt-Universität zu Berlin) Zufallszahlen und Monte Carlo 17. Oktober 2017 1 / 23
Stochastik-Praktikum Zufallszahlen und Monte Carlo Peter Frentrup Humboldt-Universität zu Berlin 17. Oktober 2017 (Humboldt-Universität zu Berlin) Zufallszahlen und Monte Carlo 17. Oktober 2017 1 / 23
Finite Elemente Methode für elliptische Differentialgleichungen
 Finite Elemente Methode für elliptische Differentialgleichungen Michael Pokojovy 8. Oktober 2007 Das Ritzsche Verfahren Sei R n ein beschränktes offenes Gebiet mit abschnittsweise glattem Rand S. Betrachte
Finite Elemente Methode für elliptische Differentialgleichungen Michael Pokojovy 8. Oktober 2007 Das Ritzsche Verfahren Sei R n ein beschränktes offenes Gebiet mit abschnittsweise glattem Rand S. Betrachte
Multivariate Verteilungen
 Multivariate Verteilungen Zufallsvektoren und Modellierung der Abhängigkeiten Ziel: Modellierung der Veränderungen der Risikofaktoren X n = (X n,1, X n,2,..., X n,d ) Annahme: X n,i und X n,j sind abhängig
Multivariate Verteilungen Zufallsvektoren und Modellierung der Abhängigkeiten Ziel: Modellierung der Veränderungen der Risikofaktoren X n = (X n,1, X n,2,..., X n,d ) Annahme: X n,i und X n,j sind abhängig
Galerkin Finite-Elemente-Methode
 Leo-Paul Obame Ndong 9. November 2017 1 / 23 Inhaltsverzeichnis 2 / 23 1. Unterteilung von D = (a,b) in Teilintervalle oder Elemente 3 / 23 1. Unterteilung von D = (a,b) in Teilintervalle oder Elemente
Leo-Paul Obame Ndong 9. November 2017 1 / 23 Inhaltsverzeichnis 2 / 23 1. Unterteilung von D = (a,b) in Teilintervalle oder Elemente 3 / 23 1. Unterteilung von D = (a,b) in Teilintervalle oder Elemente
Spezifische innere Volumina
 Spezifische innere Volumina Stochastische Geometrie und ihre en - Zufallsfelder Regina Poltnigg und Henrik Haßfeld Universität Ulm 13. Januar 2009 1 Regina Poltnigg und Henrik Haßfeld 1 2 Berechnung von
Spezifische innere Volumina Stochastische Geometrie und ihre en - Zufallsfelder Regina Poltnigg und Henrik Haßfeld Universität Ulm 13. Januar 2009 1 Regina Poltnigg und Henrik Haßfeld 1 2 Berechnung von
Sind f X bzw. f Y die wie auf Folie 242 definierten Dichtefunktionen zur N(µ X, σx 2 )- bzw. N(µ Y, σy 2 )-Verteilung, so gilt (genau) im Fall ρ = 0
 Beispiel: Zweidimensionale Normalverteilung I Beispiel: Zweidimensionale Normalverteilung II Wichtige mehrdimensionale stetige Verteilung: mehrdimensionale multivariate Normalverteilung Spezifikation am
Beispiel: Zweidimensionale Normalverteilung I Beispiel: Zweidimensionale Normalverteilung II Wichtige mehrdimensionale stetige Verteilung: mehrdimensionale multivariate Normalverteilung Spezifikation am
Statistische Methoden
 Statistische Methoden Dr. C.J. Luchsinger 2 Beweis CLT Literatur Kapitel 2: Krengel: 12 2.1 Einführung Wir repetieren aus WTS, Kapitel 5: Fragestellung: Was geschieht mit dem Ausdruck n k=1 X k nµ, (2.1)
Statistische Methoden Dr. C.J. Luchsinger 2 Beweis CLT Literatur Kapitel 2: Krengel: 12 2.1 Einführung Wir repetieren aus WTS, Kapitel 5: Fragestellung: Was geschieht mit dem Ausdruck n k=1 X k nµ, (2.1)
Multivariate Verteilungen. Gerhard Tutz LMU München
 Multivariate Verteilungen Gerhard Tutz LMU München INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Multivariate Normalverteilung 3 Wishart Verteilung 7 3 Hotellings T Verteilung 11 4 Wilks Λ 14 INHALTSVERZEICHNIS
Multivariate Verteilungen Gerhard Tutz LMU München INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Multivariate Normalverteilung 3 Wishart Verteilung 7 3 Hotellings T Verteilung 11 4 Wilks Λ 14 INHALTSVERZEICHNIS
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Erwartungswert und Varianz von Zufallsvariablen
 Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Vorlesung 7a. Der Zentrale Grenzwertsatz
 Vorlesung 7a Der Zentrale Grenzwertsatz als Erlebnis und Das Schwache Gesetz der Großen Zahlen Wiederholung: Die Normalverteilung Dichtefunktion ϕ der Standardnormalverteilung ϕ(x) 0.0 0.1 0.2 0.3 0.4
Vorlesung 7a Der Zentrale Grenzwertsatz als Erlebnis und Das Schwache Gesetz der Großen Zahlen Wiederholung: Die Normalverteilung Dichtefunktion ϕ der Standardnormalverteilung ϕ(x) 0.0 0.1 0.2 0.3 0.4
Abhängigkeitsmaße Seien X 1 und X 2 zwei Zufallsvariablen. Es gibt einige skalare Maße für die Abhängigkeit zwischen X 1 und X 2.
 Abhängigkeitsmaße Seien X 1 und X 2 zwei Zufallsvariablen. Es gibt einige skalare Maße für die Abhängigkeit zwischen X 1 und X 2. Lineare Korrelation Annahme: var(x 1 ),var(x 2 ) (0, ). Der Koeffizient
Abhängigkeitsmaße Seien X 1 und X 2 zwei Zufallsvariablen. Es gibt einige skalare Maße für die Abhängigkeit zwischen X 1 und X 2. Lineare Korrelation Annahme: var(x 1 ),var(x 2 ) (0, ). Der Koeffizient
12 Ungleichungen. Wir beginnen mit einer einfachen Ungleichung über die Varianz. Satz 35 Es sei X eine zufällige Variable.
 12 Ungleichungen Wir beginnen mit einer einfachen Ungleichung über die Varianz. Satz 35 Es sei X eine zufällige Variable. Dann gilt: min c R E(X c)2 = Var X. Beweis: Für alle reellen Zahlen c R gilt: E(X
12 Ungleichungen Wir beginnen mit einer einfachen Ungleichung über die Varianz. Satz 35 Es sei X eine zufällige Variable. Dann gilt: min c R E(X c)2 = Var X. Beweis: Für alle reellen Zahlen c R gilt: E(X
Seminar Quantitatives Risikomanagement
 Seminar Quantitatives Risikomanagement Multivariate Modelle II Toni Bastgen Mathematisches Institut der Universität zu Köln Sommersemester 2008 Betreuung: Prof. Schmidli, J. Eisenberg Inhaltsverzeichnis
Seminar Quantitatives Risikomanagement Multivariate Modelle II Toni Bastgen Mathematisches Institut der Universität zu Köln Sommersemester 2008 Betreuung: Prof. Schmidli, J. Eisenberg Inhaltsverzeichnis
1 Erwartungswert und Kovarianzmatrix von Zufallsvektoren
 Erwartungswert und Kovarianzmatrix von Zufallsvektoren Erwartungswert und Kovarianzmatrix von Zufallsvektoren. Definition Ist X X,...,X p ein p-dimensionaler Zufallsvektor mit E X j < für alle j, so heißt
Erwartungswert und Kovarianzmatrix von Zufallsvektoren Erwartungswert und Kovarianzmatrix von Zufallsvektoren. Definition Ist X X,...,X p ein p-dimensionaler Zufallsvektor mit E X j < für alle j, so heißt
Beispiel 6 (Multivariate Normalverteilung)
 Beispiel 6 (Multivariate Normalverteilung) Sei X N(µ,Σ). Es existiert eine Matrix A IR d k, sodass X d = µ+az wobei Z N k (0,I) und AA T = Σ. Weiters gilt Z = RS wobei S ein gleichmäßig verteilter Zufallsvektor
Beispiel 6 (Multivariate Normalverteilung) Sei X N(µ,Σ). Es existiert eine Matrix A IR d k, sodass X d = µ+az wobei Z N k (0,I) und AA T = Σ. Weiters gilt Z = RS wobei S ein gleichmäßig verteilter Zufallsvektor
Maximumprinzip und Minimumprinzip
 Maximumprinzip und Minimumprinzip Daniela Rottenkolber LMU München Zillertal / 13.12.2012 16.12.2012 Daniela Rottenkolber Maximumprinzip und Minimumprinzip 1/14 Übersicht Motivation mit Beispielen Schwaches
Maximumprinzip und Minimumprinzip Daniela Rottenkolber LMU München Zillertal / 13.12.2012 16.12.2012 Daniela Rottenkolber Maximumprinzip und Minimumprinzip 1/14 Übersicht Motivation mit Beispielen Schwaches
1 Die direkte Methode der Variationsrechnung
 Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Modellierung elastischer Materialien Variationsformulierung Galerkin-Approximation FreeFem++ Ausblick: Lineare Thermoelastiz. Lineare Elastizität
 Lineare Elastizität Dominik Woznica Universität des Saarlandes 05.02.2016 Gliederung 1 Modellierung elastischer Materialien 2 Variationsformulierung 3 Galerkin-Approximation 4 FreeFem++ 5 Ausblick: Lineare
Lineare Elastizität Dominik Woznica Universität des Saarlandes 05.02.2016 Gliederung 1 Modellierung elastischer Materialien 2 Variationsformulierung 3 Galerkin-Approximation 4 FreeFem++ 5 Ausblick: Lineare
Erwartungswerte. Kapitel 5
 Kapitel 5 Erwartungswerte Wir haben bisher Erwartungswerte nur für diskrete und für absolut stetige Zufallsvariable definiert und berechnet. Ziel dieses Abschnitts ist die Erweiterung des Begriffs des
Kapitel 5 Erwartungswerte Wir haben bisher Erwartungswerte nur für diskrete und für absolut stetige Zufallsvariable definiert und berechnet. Ziel dieses Abschnitts ist die Erweiterung des Begriffs des
Gesetze der großen Zahlen
 Kapitel 0 Gesetze der großen Zahlen 0. Einführung Im ersten Kapitel wurde auf eine Erfahrungstatsache im Umgang mit zufälligen Erscheinungen aufmerksam gemacht, die man gewöhnlich als empirisches Gesetz
Kapitel 0 Gesetze der großen Zahlen 0. Einführung Im ersten Kapitel wurde auf eine Erfahrungstatsache im Umgang mit zufälligen Erscheinungen aufmerksam gemacht, die man gewöhnlich als empirisches Gesetz
Kapitel XII - Kennzahlen mehrdimensionaler Zufallsvariablen
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel XII - Kennzahlen mehrdimensionaler Zufallsvariablen Wahrscheinlichkeitstheorie Prof. Dr. W.-D. Heller Hartwig Senska
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel XII - Kennzahlen mehrdimensionaler Zufallsvariablen Wahrscheinlichkeitstheorie Prof. Dr. W.-D. Heller Hartwig Senska
13 Grenzwertsätze Das Gesetz der großen Zahlen
 13 Grenzwertsätze 13.1 Das Gesetz der großen Zahlen Der Erwartungswert einer zufälligen Variablen X ist in der Praxis meist nicht bekannt. Um ihn zu bestimmen, sammelt man Beobachtungen X 1,X 2,...,X n
13 Grenzwertsätze 13.1 Das Gesetz der großen Zahlen Der Erwartungswert einer zufälligen Variablen X ist in der Praxis meist nicht bekannt. Um ihn zu bestimmen, sammelt man Beobachtungen X 1,X 2,...,X n
Dynamische Systeme und Zeitreihenanalyse // Multivariate Normalverteilung und ML Schätzung 11 p.2/38
 Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
ALMA II - ÜBERBLICK STOCHASTIK. Jochen Garcke
 ALMA II - ÜBERBLICK STOCHASTIK Jochen Garcke GRUNDBEGRIFFE Wahrscheinlichkeitsraum (Ω, A, P) beschreibt Zufallssituation Realisierung, Stichprobe, Elementarereignis ω Ω Ergebnisraum zufälliges Ereignis
ALMA II - ÜBERBLICK STOCHASTIK Jochen Garcke GRUNDBEGRIFFE Wahrscheinlichkeitsraum (Ω, A, P) beschreibt Zufallssituation Realisierung, Stichprobe, Elementarereignis ω Ω Ergebnisraum zufälliges Ereignis
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Vorlesung 7b. Kovarianz und Korrelation
 Vorlesung 7b Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X,Y]:= E [ (X EX)(Y EY) ] Insbesondere ist
Vorlesung 7b Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X,Y]:= E [ (X EX)(Y EY) ] Insbesondere ist
x p 2 (x )dx, Hinweis: es ist nicht erforderlich, zu integrieren!
 Aufgabe T- Gegeben seien zwei normalverteilte Zufallsvariablen X N(µ, σ) 2 und X 2 N(µ 2, σ2) 2 mit pdf p (x) bzw. p 2 (x). Bestimmen Sie x (als Funktion der µ i, σ i, sodass x p (x )dx = + x p 2 (x )dx,
Aufgabe T- Gegeben seien zwei normalverteilte Zufallsvariablen X N(µ, σ) 2 und X 2 N(µ 2, σ2) 2 mit pdf p (x) bzw. p 2 (x). Bestimmen Sie x (als Funktion der µ i, σ i, sodass x p (x )dx = + x p 2 (x )dx,
Bootstrap-Methoden zur Ermittlung kritischer Werte für asymptotische FWER-Kontrolle
 Bootstrap-Methoden zur Ermittlung kritischer Werte für asymptotische FWER-Kontrolle [Dudoit, van der Laan, Pollard: Multiple Testing. Part I Single-Step Procedures for Control of General Type-I-Error Rates]
Bootstrap-Methoden zur Ermittlung kritischer Werte für asymptotische FWER-Kontrolle [Dudoit, van der Laan, Pollard: Multiple Testing. Part I Single-Step Procedures for Control of General Type-I-Error Rates]
Stochastik Wiederholung von Teil 1
 Stochastik Wiederholung von Teil 1 Andrej Depperschmidt Sommersemester 2016 Wahrscheinlichkeitsraum Definition Das Tripple (Ω, A, P) heißt Wahrscheinlichkeitsraum, falls gilt: (i) A ist eine σ-algebra,
Stochastik Wiederholung von Teil 1 Andrej Depperschmidt Sommersemester 2016 Wahrscheinlichkeitsraum Definition Das Tripple (Ω, A, P) heißt Wahrscheinlichkeitsraum, falls gilt: (i) A ist eine σ-algebra,
Kapitel 2.9 Der zentrale Grenzwertsatz. Stochastik SS
 Kapitel.9 Der zentrale Grenzwertsatz Stochastik SS 07 Vom SGGZ zum ZGWS Satz.4 (Schwaches Gesetz großer Zahlen) Sei (X i ) i eine Folge unabhängiger, identisch verteilter Zufallsvariablen mit E[X ]
Kapitel.9 Der zentrale Grenzwertsatz Stochastik SS 07 Vom SGGZ zum ZGWS Satz.4 (Schwaches Gesetz großer Zahlen) Sei (X i ) i eine Folge unabhängiger, identisch verteilter Zufallsvariablen mit E[X ]
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung
 2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
Partielle Differentialgleichungen
 Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
1 Multivariate Zufallsvariablen
 1 Multivariate Zufallsvariablen 1.1 Multivariate Verteilungen Definition 1.1. Zufallsvariable, Zufallsvektor (ZV) Sei Ω die Ergebnismenge eines Zufallsexperiments. Eine (univariate oder eindimensionale)
1 Multivariate Zufallsvariablen 1.1 Multivariate Verteilungen Definition 1.1. Zufallsvariable, Zufallsvektor (ZV) Sei Ω die Ergebnismenge eines Zufallsexperiments. Eine (univariate oder eindimensionale)
Stochastik Aufgaben zum Üben: Teil 2
 Prof. Dr. Z. Kabluchko Wintersemester 205/206 Hendrik Flasche Januar 206 Aufgabe Stochastik Aufgaben zum Üben: Teil 2 Es sei X eine Zufallsvariable mit Dichte f X (y) = cy 5 I y>. Bestimmen Sie c, P[2
Prof. Dr. Z. Kabluchko Wintersemester 205/206 Hendrik Flasche Januar 206 Aufgabe Stochastik Aufgaben zum Üben: Teil 2 Es sei X eine Zufallsvariable mit Dichte f X (y) = cy 5 I y>. Bestimmen Sie c, P[2
Statistik. Sommersemester Prof. Dr. Stefan Etschberger Hochschule Augsburg. für Betriebswirtschaft und internationales Management
 für Betriebswirtschaft und internationales Management Sommersemester 2015 Prof. Dr. Stefan Etschberger Hochschule Augsburg Normalverteilung Eine Zufallsvariable X mit einer Dichtefunktion und σ > 0 heißt
für Betriebswirtschaft und internationales Management Sommersemester 2015 Prof. Dr. Stefan Etschberger Hochschule Augsburg Normalverteilung Eine Zufallsvariable X mit einer Dichtefunktion und σ > 0 heißt
Übungsrunde 10, Gruppe 2 LVA , Übungsrunde 10, Gruppe 2, Markus Nemetz, TU Wien,
 Übungsrunde, Gruppe 2 LVA 7.369, Übungsrunde, Gruppe 2, 9..27 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 9..27 Anmerkung: Viele dieser Lösungsvorschläge stammen aus dem Informatik-Forum, Subforum
Übungsrunde, Gruppe 2 LVA 7.369, Übungsrunde, Gruppe 2, 9..27 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 9..27 Anmerkung: Viele dieser Lösungsvorschläge stammen aus dem Informatik-Forum, Subforum
Übungsrunde 11, Gruppe 2 LVA , Übungsrunde 10, Gruppe 2, Markus Nemetz, TU Wien,
 1 4.36 Übungsrunde 11, Gruppe 2 LVA 17.369, Übungsrunde 1, Gruppe 2, 16.1.27 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 16.1.27 1.1 Angabe Die logische Struktur eines Systems bestehend aus drei
1 4.36 Übungsrunde 11, Gruppe 2 LVA 17.369, Übungsrunde 1, Gruppe 2, 16.1.27 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 16.1.27 1.1 Angabe Die logische Struktur eines Systems bestehend aus drei
Konvergenz der diskreten Lösungen und Fehlerabschätzung
 Konvergenz der diskreten Lösungen und Fehlerabschätzung Michael de Mourgues LMU München Bruck am Ziller, 08.01.2015 Michael de Mourgues Konvergenz der diskreten Lösungen und Fehlerabschätzung 1/14 Das
Konvergenz der diskreten Lösungen und Fehlerabschätzung Michael de Mourgues LMU München Bruck am Ziller, 08.01.2015 Michael de Mourgues Konvergenz der diskreten Lösungen und Fehlerabschätzung 1/14 Das
Quantifizierung von Unsicherheiten Uncertainty Quantification
 Quantifizierung von Unsicherheiten Uncertainty Quantification Hermann G. Matthies Technische Universität Braunschweig wire@tu-bs.de http://www.wire.tu-bs.de Vorwort. Modelle der physikalischen Realität
Quantifizierung von Unsicherheiten Uncertainty Quantification Hermann G. Matthies Technische Universität Braunschweig wire@tu-bs.de http://www.wire.tu-bs.de Vorwort. Modelle der physikalischen Realität
Algorithmen für geographische Informationssysteme. 6. Vorlesung: 14. Mai 2014
 Algorithmen für geographische Informationssysteme 6. Vorlesung: 14. Mai 2014 Ausgleichung bei linearem funktionalen Modell Beispiel 2: Ausgleichung von Höhendifferenzen P 2 Δh 2,3 = 7.0 m P 3 Δh 1,2 =
Algorithmen für geographische Informationssysteme 6. Vorlesung: 14. Mai 2014 Ausgleichung bei linearem funktionalen Modell Beispiel 2: Ausgleichung von Höhendifferenzen P 2 Δh 2,3 = 7.0 m P 3 Δh 1,2 =
DWT 1.4 Rechnen mit kontinuierlichen Zufallsvariablen 234/467 Ernst W. Mayr
 1.4.2 Kontinuierliche Zufallsvariablen als Grenzwerte diskreter Zufallsvariablen Sei X eine kontinuierliche Zufallsvariable. Wir können aus X leicht eine diskrete Zufallsvariable konstruieren, indem wir
1.4.2 Kontinuierliche Zufallsvariablen als Grenzwerte diskreter Zufallsvariablen Sei X eine kontinuierliche Zufallsvariable. Wir können aus X leicht eine diskrete Zufallsvariable konstruieren, indem wir
Bezeichnungen und Hilfsmittel aus der Analysis
 Finite Elemente I 169 A Bezeichnungen und Hilfsmittel aus der Analysis A Bezeichnungen und Hilfsmittel aus der Analysis TU Bergakademie Freiberg, WS 2010/111 Finite Elemente I 170 A.1 Normierte Vektorräume
Finite Elemente I 169 A Bezeichnungen und Hilfsmittel aus der Analysis A Bezeichnungen und Hilfsmittel aus der Analysis TU Bergakademie Freiberg, WS 2010/111 Finite Elemente I 170 A.1 Normierte Vektorräume
3 Die Finite-Elemente-Methode
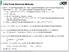 (3.1) Sei R 2 ein Polygongebiet, d.h. offen, zusammenhängend, und sei ein Polygonzug. Dann heißt T h = {K 1,...,K M } eine zulässige Triangulierung von, wenn a) K m = conv{z m,0,z m,1,z m,2 } Dreieck mit
(3.1) Sei R 2 ein Polygongebiet, d.h. offen, zusammenhängend, und sei ein Polygonzug. Dann heißt T h = {K 1,...,K M } eine zulässige Triangulierung von, wenn a) K m = conv{z m,0,z m,1,z m,2 } Dreieck mit
Riesz scher Darstellungssatz und Duale Räume
 Riesz scher Darstellungssatz und Duale Räume LV Numerik Partieller Differentialgleichungen Bärwolff SS 2010 14.06.2010 Julia Buwaya In der Vorlesung wurde der Riesz sche Dartsellungssatz als wichtiges
Riesz scher Darstellungssatz und Duale Räume LV Numerik Partieller Differentialgleichungen Bärwolff SS 2010 14.06.2010 Julia Buwaya In der Vorlesung wurde der Riesz sche Dartsellungssatz als wichtiges
2 Zufallsvariable und Verteilungsfunktionen
 8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
Erwartungswerte, Varianzen
 Kapitel 3 Erwartungswerte, Varianzen Wir wollen nun Zufallsvariablen eine Maßzahl zuordnen, die ihr typisches Verhalten in vager Weise angibt. Haben wir n Punkte x 1,...,x n R d, so ist der Schwerpunkt
Kapitel 3 Erwartungswerte, Varianzen Wir wollen nun Zufallsvariablen eine Maßzahl zuordnen, die ihr typisches Verhalten in vager Weise angibt. Haben wir n Punkte x 1,...,x n R d, so ist der Schwerpunkt
Stochastik-Praktikum
 Stochastik-Praktikum Markov Chain Monte Carlo Peter Frentrup Humboldt-Universität zu Berlin 16. Januar 2018 (Humboldt-Universität zu Berlin) Markov Chain Monte Carlo 16. Januar 2018 1 / 17 Übersicht 1
Stochastik-Praktikum Markov Chain Monte Carlo Peter Frentrup Humboldt-Universität zu Berlin 16. Januar 2018 (Humboldt-Universität zu Berlin) Markov Chain Monte Carlo 16. Januar 2018 1 / 17 Übersicht 1
4. Fortsetzung auf R N.
 4. Fortsetzung auf R N. Frage: Wann kann man Funktionen u W (Ω) zu ũ W (RN ) fortsetzen? Hier wird i.a. eine Fortsetzung durch 0 in R N \ Ω nicht zum Erfolg führen, da man die schwachen Ableitungen über
4. Fortsetzung auf R N. Frage: Wann kann man Funktionen u W (Ω) zu ũ W (RN ) fortsetzen? Hier wird i.a. eine Fortsetzung durch 0 in R N \ Ω nicht zum Erfolg führen, da man die schwachen Ableitungen über
Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator
 Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Methoden der Statistik Markov Chain Monte Carlo Methoden
 Methoden der Statistik Markov Chain Monte Carlo Methoden Humboldt-Universität zu Berlin 08.02.2013 Problemstellung Wie kann eine Zufallsstichprobe am Computer simuliert werden, deren Verteilung aus einem
Methoden der Statistik Markov Chain Monte Carlo Methoden Humboldt-Universität zu Berlin 08.02.2013 Problemstellung Wie kann eine Zufallsstichprobe am Computer simuliert werden, deren Verteilung aus einem
Stochastik Praktikum Markov Chain Monte Carlo Methoden
 Stochastik Praktikum Markov Chain Monte Carlo Methoden Humboldt-Universität zu Berlin 14.10.2010 Problemstellung Wie kann eine Zufallsstichprobe am Computer simuliert werden, deren Verteilung aus einem
Stochastik Praktikum Markov Chain Monte Carlo Methoden Humboldt-Universität zu Berlin 14.10.2010 Problemstellung Wie kann eine Zufallsstichprobe am Computer simuliert werden, deren Verteilung aus einem
Abhängigkeitsmaße Seien X 1 und X 2 zwei Zufallsvariablen. Es gibt einige skalare Maße für die Abhängigkeit zwischen X 1 und X 2.
 Abhängigkeitsmaße Seien X 1 und X 2 zwei Zufallsvariablen. Es gibt einige skalare Maße für die Abhängigkeit zwischen X 1 und X 2. Lineare Korrelation Annahme: var(x 1 ),var(x 2 ) (0, ). Der Koeffizient
Abhängigkeitsmaße Seien X 1 und X 2 zwei Zufallsvariablen. Es gibt einige skalare Maße für die Abhängigkeit zwischen X 1 und X 2. Lineare Korrelation Annahme: var(x 1 ),var(x 2 ) (0, ). Der Koeffizient
Existenz höherer Ableitungen
 Existenz höherer Ableitungen Bernhard Pfirsch LMU München Zillertal am 15.12.2012 Bernhard Pfirsch Existenz höherer Ableitungen 1/16 Definitionen: Sei der Operator L von der Form Lu = (A u), A : R n n,
Existenz höherer Ableitungen Bernhard Pfirsch LMU München Zillertal am 15.12.2012 Bernhard Pfirsch Existenz höherer Ableitungen 1/16 Definitionen: Sei der Operator L von der Form Lu = (A u), A : R n n,
Wahrscheinlichkeitsrechnung. Sommersemester Kurzskript
 Wahrscheinlichkeitsrechnung Sommersemester 2008 Kurzskript Version 1.0 S. Döhler 1. Juli 2008 In diesem Kurzskript sind Begriffe und Ergebnisse aus der Lehrveranstaltung zusammengestellt. Außerdem enthält
Wahrscheinlichkeitsrechnung Sommersemester 2008 Kurzskript Version 1.0 S. Döhler 1. Juli 2008 In diesem Kurzskript sind Begriffe und Ergebnisse aus der Lehrveranstaltung zusammengestellt. Außerdem enthält
Glättung durch iterative Verfahren
 Numerische Methoden in der Finanzmathematik II Sommersemester 211 Glättung durch iterative Verfahren Vorlesung Numerische Methoden in der Finanzmathematik II Sommersemester 211 Numerische Methoden in der
Numerische Methoden in der Finanzmathematik II Sommersemester 211 Glättung durch iterative Verfahren Vorlesung Numerische Methoden in der Finanzmathematik II Sommersemester 211 Numerische Methoden in der
Fakultät Verkehrswissenschaften Friedrich List Professur für Ökonometrie und Statistik, insb. im Verkehrswesen. Statistik II
 Statistik II 1. Ergänzungen zur Wahrscheinlichkeitstheorie Fakultät Verkehrswissenschaften Friedrich List Professur für Ökonometrie und Statistik, insb. im Verkehrswesen Statistik II 1. Ergänzungen zur
Statistik II 1. Ergänzungen zur Wahrscheinlichkeitstheorie Fakultät Verkehrswissenschaften Friedrich List Professur für Ökonometrie und Statistik, insb. im Verkehrswesen Statistik II 1. Ergänzungen zur
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik. PD Dr. U. Ludwig. Vorlesung 7 1 / 19
 Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
Zusammenfassung Stochastik I + II
 Zusammenfassung Stochastik I + II Stephan Kuschel Vorlesung von Dr. Nagel Stochastik I: WS 007/08 Stochastik II: SS 008 zuletzt aktualisiert: 7. Juli 009 Da diese Zusammenfassung den Menschen, die sie
Zusammenfassung Stochastik I + II Stephan Kuschel Vorlesung von Dr. Nagel Stochastik I: WS 007/08 Stochastik II: SS 008 zuletzt aktualisiert: 7. Juli 009 Da diese Zusammenfassung den Menschen, die sie
Strassen Type Theorems Proseminar Stochastik
 Strassen Type Theorems Proseminar Stochastik Cecelie Hector Universität Hamburg Fachbereich Mathematik SoSe 2004 Vortrag am 25.06.04 Definition (a). Ein topologischer Raum E heißt polnisch, wenn es eine
Strassen Type Theorems Proseminar Stochastik Cecelie Hector Universität Hamburg Fachbereich Mathematik SoSe 2004 Vortrag am 25.06.04 Definition (a). Ein topologischer Raum E heißt polnisch, wenn es eine
1.2 Summen von Zufallsvariablen aus einer Zufallsstichprobe
 1.2 Summen von Zufallsvariablen aus einer Zufallsstichprobe Nachdem eine Stichprobe X 1,..., X n gezogen wurde berechnen wir gewöhnlich irgendwelchen Wert damit. Sei dies T = T (X 1,..., X n, wobei T auch
1.2 Summen von Zufallsvariablen aus einer Zufallsstichprobe Nachdem eine Stichprobe X 1,..., X n gezogen wurde berechnen wir gewöhnlich irgendwelchen Wert damit. Sei dies T = T (X 1,..., X n, wobei T auch
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 8 Partielle
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 8 Partielle
1.5 Mehrdimensionale Verteilungen
 Poisson eine gute Näherung, da np = 0 und 500p = 5 00 = n. Wir erhalten somit als Näherung Exakte Rechnung ergibt P(2 X 0) = k=2 0 k=2 π (k) = 0,26424. 0 ( ) 00 P(2 X 0) = 0,0 k 0,99 00 k = 0,264238. k.4.2.4
Poisson eine gute Näherung, da np = 0 und 500p = 5 00 = n. Wir erhalten somit als Näherung Exakte Rechnung ergibt P(2 X 0) = k=2 0 k=2 π (k) = 0,26424. 0 ( ) 00 P(2 X 0) = 0,0 k 0,99 00 k = 0,264238. k.4.2.4
Klausur zur Vorlesung Stochastik II
 Institut für Stochastik WS 007/008 Universität Karlsruhe. 0. 008 r. B. Klar Klausur zur Vorlesung Stochastik II Muster-Lösung auer: 90 Minuten Name: Vorname: Matrikelnummer: iese Klausur hat bestanden,
Institut für Stochastik WS 007/008 Universität Karlsruhe. 0. 008 r. B. Klar Klausur zur Vorlesung Stochastik II Muster-Lösung auer: 90 Minuten Name: Vorname: Matrikelnummer: iese Klausur hat bestanden,
Prüfung. Wahrscheinlichkeit und Statistik. ETH Zürich HS 2015 Prof. Dr. P. Embrechts Januar Nachname. Vorname. Legi Nummer
 ETH Zürich HS 25 Prof. Dr. P. Embrechts Januar 26 Prüfung Wahrscheinlichkeit und Statistik BSc INFK Nachname Vorname Legi Nummer Das Folgende bitte nicht ausfüllen! Aufgabe Max. Punkte Summe Kontrolle
ETH Zürich HS 25 Prof. Dr. P. Embrechts Januar 26 Prüfung Wahrscheinlichkeit und Statistik BSc INFK Nachname Vorname Legi Nummer Das Folgende bitte nicht ausfüllen! Aufgabe Max. Punkte Summe Kontrolle
Gleichmäßige Berry-Esseen Schranken. Seminar zur Methode von Stein
 Gleichmäßige Berry-Esseen Schranken Seminar zur Methode von Stein Stefan Roth Institut für Stochastik 18. April, 2016 Universität Ulm Inhalt Wiederholung Gleichmäßige Berry-Essen Schranken Berry-Esseen
Gleichmäßige Berry-Esseen Schranken Seminar zur Methode von Stein Stefan Roth Institut für Stochastik 18. April, 2016 Universität Ulm Inhalt Wiederholung Gleichmäßige Berry-Essen Schranken Berry-Esseen
