Funktionale Zusammenhänge
|
|
|
- Klemens Busch
- vor 7 Jahren
- Abrufe
Transkript
1 Funktionale Zusammenhänge 5
2 Quadratische Funktionen und Gleichungen Will sehen, was ich weiß, vom Büblein auf dem Eis: Gefroren hat es heuer noch gar kein festes Eis. Das Büblein steht am Weiher und spricht ganz leis: Ich will es einmal wagen; das Eis, es muss doch tragen! Wer weiß? (Friedrich Güll, 8-879) Die Tragfähigkeit einer Eisfläche hängt von der Art des Eises und seiner Dicke d ab. Blaues Eis ist tragfähiger als weißes. Außerdem spielt die Größe der Fläche eine Rolle, auf welche die Last wirkt. Das höchstzulässige Gewicht G einer einzelnen Person, die das Eis gefahrlos betreten kann, lässt sich mit der folgenden Faustformel berechnen:. N G = 0 cm d Berechne zu folgenden Eisdicken d, das höchstzulässige Gewicht G d in cm G in N??????? Wie ändert sich die Tragfähigkeit des Eises, wenn sich die Eisdicke verdoppelt, verdreifacht? Zeichne den Graphen der Funktion d G für das Intervall 0 cm d 6 cm. Löse grafisch und rechnerisch: Daniel wiegt mit seiner Winterkleidung 60 kg. Wie dick muss das Eis mindestens sein, damit er es betreten darf? Wie viele Zentimeter sollte das Eis mindestens dick sein, wenn es ein Erwachsener bzw. eine Gruppe aus vier Erwachsenen betreten will? a) Wird die Tragfähigkeit des Eises größer oder kleiner, wenn sich die Last auf eine größere Fläche verteilt? b) Wie sollte sich eine Person verhalten, die eingebrochen ist und das rettende Ufer erreichen will? c) Wie sollten Retter vom Ufer aus vorgehen? (Interessante Informationen von der DRK-Wasserwacht dazu findest du im Internet.) 6
3 Quadratische Funktionen und Gleichungen. Reinquadratische Funktionen und Gleichungen Quadratische Funktionen Die Tragfähigkeit einer Eisfläche ist proportional zum Quadrat ihrer Dicke (Seite 6). Der Bremsweg eines Autos ist proportional zum Quadrat seiner Geschwindigkeit (Aufgabe ). Beide Abhängigkeiten lassen sich durch Funktionen der Form f(x) ax beschreiben. Den Anhalteweg eines Autos beschreibt eine Funktion der Form f(x) ax bx (Aufgabe e). Eine Funktion der Form f(x) ax bx c mita 0heißtquadratische Funktion. Ihren Graphen nennt man Parabel. ax heißt quadratisches Glied, bx lineares Glied und c konstantes Glied. Tritt das lineare Glied im Term einer quadratischen Funktion nicht auf (b 0), sprechen wir von einer reinquadratischen Funktion. DiereinquadratischeFunktionf(x) ax In unseren bisherigen Beispielen (Tragfähigkeit einer Eisfläche, Bremsweg eines Autos) hatten negative x-werte keine Bedeutung. Der Term ax ist aber für alle reellen Zahlen definiert: D. Beispiel f(x) x mit D Zum Zeichnen des Graphen legen wir eine Wertetabelle an: x,5,5 0,5 0 0,5,5,5,5,5 0,5 0,5 0 0,5 0,5,5,5 Weil das Quadrat x für beliebige reelle Zahlen x gleich dem Quadrat ( x) der Gegenzahl ist, ergeben x und x den gleichen - Wert. Die Parabel verläuft deshalb smmetrisch zur -Achse. Sie hat einen tiefsten Punkt, der im Nullpunkt des Koordinatensstems liegt. 5 0 x Der Wert des Parameters a wirkt sich auf den Verlauf der Parabel ax (Aufgabe ). aus 7
4 Funktionale Zusammenhänge = x x = x = x = x = x = x = 0,x Für a > 0 ist die Parabel nach oben geöffnet. Sie hat einen tiefsten Punkt. Für a < 0 ist die Parabel nach unten geöffnet. Sie hat einen höchsten Punkt. Der tiefste bzw. höchste Punkt heißt Scheitel der Parabel: S(0 0). Eine Parabel mit dem Parameter a oder a heißtnormalparabel. Durch den Parameter a wird die Parabel gestreckt: Für a > ist sie deshalb schlanker als die Normalparabel. Für a < ist die Parabel breiter als die Normalparabel. a heißt Streckfaktor. Der Scheitel der Parabel ax (a 0) liegt im Ursprung des Koordinatensstems.FürpositivenStreckfaktoraistdieParabelnachobengeöffnet,fürnegativen nach unten. Je größer a ist, desto schlanker ist die Parabel. DiereinquadratischeFunktionf(x) ax c Wir betrachten nun reinquadratische Funktionen mit konstantem Glied. Allgemein (Aufgabe ): = x Beispiel f(x) x mit D. Für alle reellen Zahlen x erhalten wir den Wert von x, indem wir zum Wert von x die Zahl addieren. Deshalb geht der Graph der Funktion f(x) x durch eine Verschiebung um zwei Einheiten nach oben aus dem Graphen der Funktion f(x) x hervor. Die Parabel mit der Gleichung x ist also smmetrisch zur -Achse und nach oben geöffnet. Ihr tiefster Punkt, ihr Scheitel, ist S(0 ). = x + 0 x Die Parabel mit der Gleichung ax c geht aus der Parabel ax durch eine Verschiebung um c in -Richtung hervor: Für c > 0 wird die Parabel nach oben und für c < 0 nach unten verschoben. Der Scheitel der Parabel ist S(0 c)
5 Quadratische Funktionen und Gleichungen Reinquadratische Gleichungen Bei der Berechnung einer Eisdicke (Seite 6) oder einer Geschwindigkeit aus der Länge einer Bremsspur (Aufgabe ) setzen wir einen reinquadratischen Term gleich einer Zahl. Wir erhalten eine reinquadratische Gleichung. Sie liefert für unsere beiden Beispiele jeweilis genau eine Lösung. Das ist aber bei quadratischen Gleichungen nicht immer der Fall. Beispiel x 0 mit D. Lösung: Grafisch. Lösung: Rechnerisch Wir zeichnen die Parabel mit der Gleichung x undsuchen alle x-werte, für die 0 ist. Es gibt zwei Lösungen: x und x x 0 Nach x auflösen x 8 x 6 Wurzel ziehen x oder x Die Gleichung hat zwei Lösungen, weil es zwei x-werte gibt, deren Quadrat gleich 6 ist. 0 x Die Anzahl der Lösungen reinquadratischer Gleichungen Das grafische Lösen reinquadratischer Gleichungen verschafft uns schnell einen Überblick über die Anzahl der Lösungen. Bringen wir die reinquadratische Gleichung auf die Form ax c 0, dann suchen wir die x-werte, bei denen die Parabel ax c die x-achse schneidet. Diese Stellen heißen bekanntlich Nullstellen der Funktion f(x) ax c (Aufgabe 0). Beispiel x 0 6 Grafisch 5 Rechnerisch Die Parabel mit der Gleichung x hat keine Nullstelle, dasienachoben geöffnet ist und den tiefsten Punkt S(0 ) hat. 0 x x 0 x L {} 9
6 Funktionale Zusammenhänge Beispiel x 0 Grafisch Der Scheitel der Parabel x liegt auf der x-achse: S(0 0). x 0istdie einzige Nullstelle. Sie ist die einzige Lösung x x Rechnerisch x 0 x 0 x 0 L {0} Beispiel x 0 6 Grafisch Die Parabel x ist nach oben geöffnet. Ihr Scheitel ist S(0 ). Also gibt es die zwei Nullstellen x und x. 5 Rechnerisch x 0 x x x oder x L { ; } 0 x Eine reinquadratische Gleichung hat keine, eine oder zwei Lösungen. Das Lösen durch Faktorisieren Wir können manche reinquadratische Gleichungen auch durch Faktorisieren lösen. Dabei verwenden wir die Plus-Minus-Formel und die Erkenntnis, dass ein Produkt nur dann null ist, wenn ein Faktor null ist: Beispiel x 0 Faktor ausklammern (x ) 0 Plus-Minus-Formel anwenden (x )(x ) 0 Klammern Null setzen x 0oderx 0 Lösungen angeben x oder x L { ; } 0
7 Quadratische Funktionen und Gleichungen Aufgaben :-) Fahrschulregeln Der Bremsweg eines Autos hängt von seiner Geschwindigkeit ab. Für trockene Straßen erhält man den Bremsweg in Metern, wenn man die vom Tacho angezeigte Zahl durch 0 dividiert und das Ergebnis quadriert. a) Bezeichne die vom Tacho angezeigte Zahl (die Geschwindigkeit in km/h) mit x. Gib den Bremsweg b(x) in Abhängigkeit von x an. b) Lege eine Wertetabelle an und berechne den Bremsweg b(x) für die Geschwindigkeiten von 0 km/h bis 00 km/h mit einer Schrittweite von 0 km/h. Wie lang ist der Bremsweg bei der doppelten, dreifachen Geschwindigkeit? c) Warum ist der Graph der Funktion x b(x) keine Gerade? Zeichne den Graphen. d) Vom Erkennen einer Gefahr bis zum Betätigen der Bremse verstreicht die Reaktionszeit. Der in der Reaktionszeit zurückgelegte Reaktionsweg in Metern ist gleich dem Dreifachen der vom Tacho angezeigten Zahl geteilt durch zehn. Gib den Reaktionsweg r(x) in Abhängigkeit von x an. Warum ist der Graph der Funktion x r(x) eine Gerade? Trage diese Gerade in das Diagramm von c) ein. e) Reaktionsweg und Bremsweg ergeben zusammen den Anhalteweg a(x). Gib a(x) in Abhängigkeit von x an. Ist der Graph der Funktion x a(x) eine Gerade? Trage den Graphen in das Diagramm ein. f) Nach einer Vollbremsung in einer geschlossenen Ortschaft hinterlässt Olivers Auto eine m lange Bremsspur. Ist Oliver zu schnell gefahren? :-) DieBedeutungdesParametersa Wir untersuchen die Bedeutung des Faktors a für den Verlauf der Parabel mit der Gleichung ax. a) Bestimme zu jeder Parabel den Wert von a mithilfe einer Wertetabelle. A B C 0 x 0 x 0 x D 0 x E 0 x
8 Funktionale Zusammenhänge b)übertragedietabelleindein Heft und gib an, ob die Parabeln nach oben oder nach unten geöffnet sind. Die Parabel mit a, die Mutter aller Parabeln, heißt Normalparabel. Gib an, ob die Parabeln schlanker oder breiter als die Normalparabel sind. ax Öffnung der Parabel Vergleich mit der Normalparabel a oben Normalparabel a>?? 0<a<?? <a<0?? a<?? :-) Funktionsplotter Mithilfe eines Funktionsplotters (oder mancher Geometrieprogramme) kann man sich den Graphen einer Funktion nach Eingabe ihrer Gleichung anzeigen lassen. Das ist besonders dann von Vorteil, wenn man die Abhängigkeit des Graphen von einem Parameter untersuchen möchte. a) Wir untersuchen die Abhängigkeit des Graphen der Funktion f(x) ax vom Parameter a. Wir definieren a zunächst durch einen Schieberegler. An ihm können wir durch Ziehen mit der Maus verschiedene a-werte einstellen, z. B. a.gebenwirnunindie Eingabezeile a*x^ ein, erhalten wir die abgebildete Parabel. Beobachte die Veränderungen der Parabel, wenn du den Parameter a im Zugmodus veränderst. Notiere deine Beobachtungen. Erhält man für jeden a- Wert eine Parabel? b) Untersuche jetzt analog die Graphen der Funktion f(x) x cinabhängigkeit vom Parameter c. Notiere deine Erkenntnisse. Parabeln zeichnen Berechne Wertetabellen folgender Funktionen für das Intervall [ ; ] mit der Schrittweite 0,5 und zeichne die vier Graphen in ein gemeinsames Koordinatensstem. Gib für alle Graphen die Lage des Scheitels an. a) f(x) x ; f(x) x ; f(x) x ; f(x) x b) f(x) 0,x ; f(x),5x ; f(x) 0,x ; f(x),5x c) f(x) x ; f(x) x ; f(x) x ; f(x) x d) f(x) x ; f(x) x ; f(x) x ; f(x) x 5 Who is who? Welcher Graph gehört zu welcher Gleichung? Begründe deine Entscheidung jeweils mit einem Satz. A) x B) x C) x D) x E) x F) x G) x H) x
9 Quadratische Funktionen und Gleichungen a) b) c) d) 0 x 0 x 0 x 0 x e) f) g) h) 0 x 0 x 0 x 0 x 5 6 Parabelgleichung gesucht Eine Parabel mit einer Gleichung der Form ax c verläuft durch die beiden angegebenen Punkte. Bestimme die Gleichung der Parabel. a) S(0,5); P(,5) b) S(0 ); P( ) c) S(0 ); P(,5) d) P( ); Q( 7) e) P( ); Q( ) f) P( 0); Q( 6) g) P( 0,5); Q( ) h) P( ); Q( 0) i) P( 0); Q( 0) 7 Reinquadratische Gleichungen a) x 9 b) x 9 c) x 5 d) x e) x f) x 0,9 g) x ( ) h) x ( 5) i) x k) x 5 l) 9x 0 m)50x 5 7 n) x 8 0 o) x 8 0 p) x q) x Kettenlinie Eine zwischen zwei Aufhängepunkten frei herabhängende Kette beschreibt eine Kurve, die man Kettenlinie nennt. Wir betrachten eine Kettenlinie zwischen den beiden Punkten A( 5 0) und B(5 0). Sie verläuft außerdem durch die Punkte mit den in der Tabelle angegebenen Koordinaten. a) Zeichne die Kettenlinie. x 0 b) Untersuche, ob die Kettenlinie eine Parabel ist: Stelle dazu die Gleichung der Parabel durch A, 0 0,5,,7 5, B und den Ursprung O auf. Berechne zu den x-werten der Tabelle die -Werte der Parabel. Zeichne die Parabel in das Koordinatensstem von a) ein.
10 Funktionale Zusammenhänge 9 DieBrückeüberdenSkjern Die Stahlseile von Hängebrücken, die durch die Fahrbahn belastet werden, verlaufen in der Form von Parabelbögen. Die rechts abgebildete Hängebrücke über den dänischen Fluss Skjern ist 60 m lang. Der Fußweg ist jeweils zwischen zwei parabelförmigen Stahlseilen aufgehängt. Alle,50 m sind die beiden Stahlseile durch einen vertikalen Stab miteinander verbunden. Wir führen ein Koordinatensstem ein: Der Ursprung O ist der Berührpunkt des unteren und des oberen Stahlseils (siehe rechts). Der -Wert des höchsten Punktes des oberen Stahlseils ist 7,0 Meter, der -Wert 0 des tiefsten Punktes des unteren Stahlseils 0,90 Meter. a) Stelle die Gleichungen der Parabeln auf, die den Verlauf des oberen und des untere Stahlseils beschreiben. b) Lege ein Koordinatensstem an (x-achse: cm 5 m, -Achse: cm m)und zeichnediebeidenstahlseileein. c) Berechne die Länge der vertikalen Stäbe für x 5m, 0m,..., 5m. d) Stelle eine Formel für die Länge der vertikalen Stäbe in Abhängigkeit von x auf. Überprüfe deine Formel mit einem in c) berechneten Wertepaar. e) An welchen Stellen der Brücke sind die vertikalen Stäbe ungefähr 50 cm bzw.,50 m lang? 7, 0,9 x :-) 0 Nullstellen a) Zeichne den Graphen der linearen Funktion f(x),5x,5. Welcher x-wert heißt Nullstelle einer Funktion? Bestimme die Nullstelle von f(x) grafisch und rechnerisch. b) Zeichne den Graphen der quadratischen Funktion f(x) x. Ermittle die Nullstellengrafischundrechnerisch. c) Wie viele Nullstellen kann eine lineare Funktion haben, wie viele eine quadratische? Skizziere zu jedem Fall ein Beispiel. Faktorisieren Löse die quadratische Gleichung durch Faktorisieren: a) x 75 0 b) x 0 c),5x 7,5 0 d) 7x 0 e) z f) 0,5z 8 0 g) u 0 h) u 8
11 Quadratische Funktionen und Gleichungen Gleichungen grafisch und rechnerisch Stelle die Gleichung der Parabel auf und berechne ihre Nullstellen. Welche Gleichungen werden durch den Schnitt der Parabel mit der eingezeichneten waagrechten Geraden grafisch gelöst? Stelle diese Gleichung auf und löse sie. Vergleiche deine Lösungen mit der Zeichnung. a) b) c) 0 x 0 x 0 x 5 Gleichung gesucht Stelle zu jeder Lösungsmenge mindestens drei reinquadratische Gleichungen auf. a) L { ; } b) L { 5; 5} c) L {0} d) L {} Manneken Pis Das Manneken Pis ist eines der Wahrzeichen der belgischen Hauptstadt Brüssel. Es wurde dort schon im 7. Jahrhundert aufgestellt. Rechts ist eine Kopie zu sehen. Die Längeneinheit des Koordinatensstems ist dm. a) Wie hoch ist das Manneken Pis? b) Der Wasserstrahl scheint parabelförmig zu verlaufen. Stelle die Gleichung einer zur -Achse smmetrischen Parabel auf, die durch die Punkte A und B verläuft. c) Überprüfe, ob der höchste Punkt des Wasserstrahls und zwei weitere, selbst gewählte Punkte auf der Parabel liegen. Was folgerst du daraus? d) Der Sockel, auf dem das Manneken steht, ist 0 cm hoch. Wie weit pisst das Manneken? 0 6 A 5 B 0 x 5
12 Funktionale Zusammenhänge Zum Intensivieren 5 Die Storebælt-Brücke Die Storebælt-Brücke ist die längste Hängebrücke Europas. Sie verbindet die beiden dänischen Inseln Fünen und Seeland. Ihre tragenden Stahlseile verlaufen in der Form von Parabelbögen. Zur mathematischen Beschreibung 0 führen wir ein Koordinatensstem ein: Die x-achse liegt genau auf der Wasseroberfläche mitten unter der Fahrbahn. Die -Achse verläuft genau in der Mitte zwischen den beiden Brückenpfeilern, die 6 m voneinander entfernt sind. Der Fuß der Pfeiler befindet sich 7 m unter dem Meeresspiegel. In diesem Koordinatensstem beschreibt die Gleichung,68 0 x 77 den Verlauf der tragenden Stahlseile zwischen den Brückenständern. a) Welche Werte darf x in dieser Gleichung annehmen? Welche Koordinaten haben die Fußpunkte der Brückenpfeiler? b) In welcher Höhe über dem Meeresspiegel verläuft die Fahrbahn ungefähr? c) Wie viele Meter ragen die Brückenpfeiler über das Wasser hinaus? Wie hoch sind sie insgesamt? x 6 Gleichungen rechnerisch und grafisch Löse zunächst die beiden Gleichungen rechnerisch. Zeichne anschließend die zugehörige Parabel. Überprüfe deine Rechenergebnisse anhand der Zeichnung. a) x 0 und x,5 b) x,5 0 und x,5 c) x 0und x 5 d) x 0 und x 6 7 Grundwissen: Lineare Funktionen a) Zeichne die Graphen der Funktionen f (x) x, f (x) x, f (x) x, f (x) xundf 5 (x) mithilfe des -Abschnitts und eines Steigungsdreiecks in ein gemeinsames Koordinatensstem ein. b) Welche besondere Lage haben die Graphen von f und f 5 im Koordinatensstem? Welche Lage haben die Graphen von f und f zueinander? c) Berechne die Nullstellen der fünf Funktionen und vergleiche deine Ergebnisse mit der Zeichnung. d) Berechne alle Schnittpunkte der Graphen und vergleiche deine Ergebnisse mit der Zeichnung. e) Liegt der Punkt P( 8) auf, oberhalb oder unterhalb des Graphen von f? f) Für welchen x-wert nimmt die Funktion f den Wert 0 an? 6
13 Quadratische Funktionen und Gleichungen. Quadratische Funktionen Die Funktion f(x) ax bx Der Anhalteweg eines Autos in Abhängigkeit von der Geschwindigkeit (Seite, Aufgabe e) und die Abhängigkeit der Anzahl der DNA-Brüche von der Strahlendosis (Aufgabe ) lassen sich durch quadratische Funktionen der Form f(x) ax bx beschreiben. Wir interessieren uns für diesen weiteren Sonderfall (c 0) quadratischer Funktionen. Als Definitionsmenge wählen wir die größtmögliche: D. Beispiel x x mit D Zum Zeichnen des Graphen legen wir eine Wertetabelle an: x x x,5 0 0,75 0,75 0,5 x 8 5,5,5 0 0,75 0,75 0 = x + x = x 6 5 Nullstellen 0 x S Der Scheitel S( ) der Parabel liegt nicht auf der -Achse. Die Parabel ist zur Geraden x smmetrisch. Das Diagramm legt die Vermutung nahe, dass sie aus der Parabel x durch eine Verschiebung um zwei Einheiten nach links hervorgeht (Aufgabe a). Wir ergänzen die Wertetabelle und tragen auch die Parabel x in das Koordinatensstem ein. Unsere Vermutung bestätigt sich. Da die Parabel x ihrerseits aus der Parabel x durch eine Verschiebung um nach unten hervorgeht, ist die Parabel x xzu Parabel x kongruent. Allgemein (Aufgabe b und c): Der Scheitel der Parabel mit der Gleichung ax bx liegt für b 0nichtauf der -Achse. Die Parabel ist zur Parabel ax kongruent. 7
14 Funktionale Zusammenhänge Die quadratische Gleichung ax bx 0 Die Nullstellen der Parabel x x lesen wir aus der Zeichnung ab: x 0und x. Wollen wir die Nullstellen berechnen, müssen wir die quadratische Gleichung x x 0 lösen. Weil wir die Variable x in dieser Gleichung nicht isolieren können, greifen wir auf die Methode des Faktorisierens zurück: x x 0 x( x ) 0 x 0 oder x 0 x 0 oder x Die Smmetrieachse einer Parabel verläuft immer durch ihren Scheitel. Die Nullstellen der Parabel liegen bezüglich dieser Achse smmetrisch zueinander. Folglich liegt die x-koordinate des Scheitels genau in der Mitte zwischen den Nullstellen, im obigen Beispiel also bei x S. Damit können wir auch die -Koordinate des Scheitels berechnen: S ( ). Kennen wir den Scheitel und den Streckfaktor a, dann können wir Parabeln vom Tp ax bx auch ohne Wertetabelle zeichnen. Beispiel x x Berechnung der Nullstellen: x x 0 x( x ) 0 x 0 oder x 0 x 0 oder x Der Scheitel S liegt somit bei x S x und S ( ) ( ). Der Streckfaktor der Parabel ist. WirkönnenPunktederParabelwie folgt finden: Gehen wir von S um nach rechts bzw. links, müssen wir um nach oben gehen. Gehen wir um nach rechts bzw. links, müssen wir um nachobengehenusw. = x + x Quadratische Gleichungen der Form ax bx 0 lösen wir, indem wir x ausklammern. x 0iststetseineLösung. Die zugehörige Parabel ax bx verläuft durch den Ursprung des Koordinatensstems. Die x-koordinate ihres Scheitels liegt in der Mitte zwischen den beiden Nullstellen. Die Funktion f(x) ax bx c Wir haben bisher die Sonderfälle b 0bzw.c 0 quadratischer Funktionen untersucht. Addieren wir das konstante Glied c zum Term der quadratischen Funktion f(x) ax bx, so bewirkt dieses eine Verschiebung der Parabel ax bx um c in 8
15 Quadratische Funktionen und Gleichungen -Richtung. Weil die Parabel ax bx stets durch den Ursprung verläuft, geht die Parabel ax bx c stets durch den Punkt (0 c). Der Parameter c ist folglich die -Koordinate des Schnittpunkts der Parabel mit der -Achse (Aufgabe 5). Beispiel x x ; Die Parabel x xwirdumzwei Einheiten nach unten verschoben: Sie schneidet die -Achse bei. Die Parameterwerte b und c wirken sich nur auf die Lage des Scheites aus. Allein der Streckfaktor bestimmt die Gestalt der Parabel. Alle Parabeln mit gleichem Streckfaktor a sind kongruent. = x + x x = x + x b) Aufgaben :-) Strahlenschäden Das Erbgut liegt in den menschlichen Zellen in Form der DNA vor. Durch Röntgenstrahlung kommt es zu Schäden an ihr, z. B. zu einem Bruch. In einem Labor wird in einer Gewebeprobe die mittlere Anzahl der Brüche pro DNA in Abhängigkeit von der verwendeten Strahlendosis x (in Joule pro kg) gemessen: x in J/kg 0, , 0, 0,8,8, 5,6 7, 8,9 0,8 a) Zeichne den Graphen der Funktion x mithilfe der Wertetabelle. b) Warum ist x keine lineare Funktion? Warum ist x keine reinquadratische Funktion? c) Setze an: ax bx c. Warum ist c 0? Bestimme a und b, indem du die Wertepaare (0,8) und (0,) einsetzt und das so entstehende Gleichungssstem löst. Zeige in Partnerarbeit, dass die Gleichung auch die anderen Wertepaare der Tabelle liefert. d) Strahlenbiologen sprechen von einer linear-quadratischen Abhängigkeit der DNA-Schäden von der Strahlendosis. Kannst du diese Bezeichnung erklären? :-) Funktionsplotter a) Lasse dir den Graphen der Funktion f(x) x x von einem Funktionsplotter oder einem dnamischen Geometrieprogramm anzeigen. Welche Smmetrie liegt vor? Welchen -Wert hat der Scheitel S? Aus welcher zur -Achse smmetrischen Parabel könnte der Graph durch Verschiebung hervorgegangen sein? Überprüfe deine Vermutung, indem du die Gleichung dieser Parabel in den Funktionsplotter eingibst. 9
16 Funktionale Zusammenhänge Definiere nun zwei Schieberegler a und b und stelle sie zunächst auf die Werte a 0,5 und b ein. Gib anschließend die Funktionsgleichung ax bx in die Eingabezeile ein. b) Verändere nun ausschließlich den Parameter b und beobachte, wie sich die Parabel verändert. Welche Eigenschaften der Parabel bleiben erhalten, welche nicht? c) Verändere nun ausschließlich den Parameter a und beobachte, wie sich die Parabel verändert. Welche Gemeinsamkeiten, welche Unterschiede kannst du jeweils erkennen? Quadratische Gleichungen ohne konstantes Glied Löse folgende quadratische Gleichungen rechnerisch. Was kannst du über die Lage des Scheitels der zugehörigen Parabel aussagen? Versuche, die Parabel ohne Wertetabelle zu zeichnen. a) x x 0 b) x 9x 0 c) x 5x 0 d) x 6x 0 e) x x f) 0,5 x x 0 g) x x 0 h) x x i) 8x 6x Auf dem Golfplatz Bernhard schlägt einen Golfball ab. Die Gleichung 5x 0x beschreibt dessen Flughöhe (in m) in Abhängigkeit von der Zeit x (in s). a) Zeichne den Graphen der Funktion mithilfe einer Wertetabelle. b) Berechne die Nullstellen der Funktion und überprüfe dein Ergebnis anhand der Zeichnung. Was besagen die Nullstellen über den Flug des geschlagenen Golfballs? c) Welche größte Höhe erreicht der Golfball? Zu welchem Zeitpunkt erreicht er sie? :-) 5 Untersuchung mithilfe eines Funktionsplotters Definiere in einem Funktionsplotter oder in einem dnamischen Geometrieprogramm drei Schieberegler a, b und c und stelle sie auf die Werte a, b und c ein. Gib anschließend die Funktionsgleichung ax bx c in die Eingabezeile ein. a) Verändere nun ausschließlich den Parameter c und beobachte genau, wie sich die Parabel verändert. Stelle dazu auch andere Werte für a und b ein und verändere wieder nur c im Zugmodus. Welche Gemeinsamkeiten, welche Unterschiede kannst du jeweils erkennen? Kannst du eine Aussage über die Bedeutung des Parameters c machen? b) Verändere abwechselnd die Parameter a, b und c. Welche Parameter haben Einfluss auf die Gestalt der Parabel? 50
17 Quadratische Funktionen und Gleichungen 6 Funktion gesucht Von einer Parabel mit einer Gleichung der Form x bx c sind zwei Nullstellen x und x bekannt. Bestimme die Koeffizienten b und c und den Scheitel der zugehörigen Parabel. a) x 0; x b) x ; x c) x, x d) x ; x e) x ; x f) x,x 7 Nullstellensuche Gegeben ist die Funktion mit der Gleichung x 7x. a) Berechne den Funktionswert an den Stellen x undx. b) Wie viele Nullstellen hat die Funktion? Begründe deine Antwort. c) Wo würdest du nach einer Nullstelle suchen? Zum Intensivieren 8 Wertetabellen a) Das folgende Bild zeigt die von einem Tabellenkalkulationsprogramm berechnete Wertetabelle einer quadratischen Funktion: Wie lautet die Gleichung der Funktion? Was kannst du über die Gestalt der zugehörigen Parabel aussagen? Wo schneidet sie die -Achse? Überprüfe deine Aussagen mithilfe der Wertetabelle und lies daraus auch die Koordinaten des Scheitels ab. Zeichne die Parabel. b) Was kannst du über die Graphen der folgenden Funktionen aussagen? A) f(x) x x 5 B) f(x) x x C) f(x) x x Welche x-koordinate könnte der Scheitel S jeweils haben? Berechne die zugehörige -Koordinate. Berechne anschließend nach obigem Vorbild für jede Funktion eine Wertetabelle mithilfe eines Tabellenkalkulationsprogramms. Zeichne den Graphen. Lies die Koordinaten des Scheitels und die Nullstellen so genau wie möglich ab. Vergleiche mit deiner Vermutung. 9 Gleichungen Löse folgende Gleichungen. Was ist das Besondere an den Aufgaben vom Tp A bzw. vom Tp B? Warum kannst du sie überhaupt lösen? A: a) x (x ) 5x 7(x ) b) x(x ) (x ) c) (x 5) ( x) d) (x ) (x ) 8 x( x) B: a) x 60x x x b) x (x ) x(x ) 9 c) (x ) ( x) x(x 5) d) (x 5) (x ) (x ) 5
18 Funktionale Zusammenhänge. Die Scheitelform der Funktionsgleichung Jede Parabel mit einer Gleichung der Form ax bx c istzurparabel ax kongruent. Für die Spezialfälle b 0oderc 0könnenwirdieLagedesScheitels und die Nullstellen bestimmen aber noch nicht für den allgemeinen Fall a 0, b 0undc 0. Wir gehen dieses Problem nun von der umgekehrten Richtung an: Wir betrachten Parabeln mit bekanntem Scheitel und überlegen uns die zugehörige Gleichung. Von Scheitel und Öffnungsfaktor zur Gleichung Wir verschieben Parabeln, deren Scheitel im Ursprung liegt, zunächst in x-richtung. Beispiel Die Normalparabel x wird um nach rechts verschoben. Wir zeichnen die Normalparabel und die verschobene Normalparabel mit einer Schablone. Bei der Suche und nach der Funktion f(x) der verschobenen Parabel hilft uns eine Wertetabelle: x 0 x f(x) Um den Funktionswert f(x) zu erhalten, müssen wir x vor dem Quadrieren um verringern. Also ist f(x) (x ). Der Graph der Funktion f(x) (x ) ist die nach oben geöffnete Normalparabel mit dem Scheitel S( 0). Multiplizieren wir den Funktionsterm mit der Minus-Formel aus, erhalten wir die normale Form der quadratischen Funktion: f(x) (x ) x x = x x 5 Die für die Funktion f(x) (x ) angestellten Überlegungen lassen sich auf jede Verschiebung in x-richtung übertragen (Aufgabe ). Ist die Parabel gegenüber der Normalparabel schlanker oder breiter (a ),müssenwirdenstreckfaktoraberücksichtigen (Aufgabe ). Beispielsweise ist (x ) die Gleichung der um nach rechts verschobenen Parabel x. Nun zum allgemeinen Fall: Wir verschieben eine Parabel, deren Scheitel im Ursprung liegt, in x- und in -Richtung.
19 Quadratische Funktionen und Gleichungen Beispiel Die Normalparabel x wird um nach rechts und um nach oben verschoben. Die Gleichung der um nach rechts verschobenen Parabel ist (x ). Um sie um nach oben zu schieben, addieren wir : (x ). Wird die Normalparabel zusätzlich mit dem Streckfaktor aufgebogen, lautet die Gleichung (x ). Durch Ausmultiplizieren und = x 6 5 = (x ) + = (x ) x Zusammenfassen können wir diese Form in die normale Form überführen: (x ) (x x ) x x x x In der ursprünglichen Form treten die Koordinaten des Scheitels auf. Man nennt sie deshalb Scheitelform. Für die normale Form sagen wir auch kurz Normalform. Unsere Überlegungen lassen sich verallgemeinern (Aufgabe 5): Die Scheitelform Die Gleichung einer Parabel mit dem Scheitel S(x S S ) und dem Streckfaktor a lautet a(x x S ) S. Liegt eine Parabelgleichung in Scheitelform vor, können wir sowohl den Scheitel als auch die Nullstellen der Parabel leicht bestimmen. Beispiel Von einer Parabel ist die Gleichung in der Scheitelform bekannt: (x ). Entweder entnehmen wir daraus sofort den Scheitel oder wir bedenken: Der kleinste Wert des quadratischen Anteils ist 0. Er wird für x angenommen. Wenn das Quadrat 0 ist, ergibt sich der -Wert. Also ist der Scheitel S( ). Der Streckfaktor ist a. Die Parabel ist folglich nach unten geöffnet und schlanker als die Normalparabel. Der Scheitel ist der höchste Punkt der Parabel. Er liegt über der x- Achse. Die Parabel hat somit zwei Nullstellen, die wir nun berechnen können: (x 0,5) 0 (x 0,5) : ( ) (x 0,5) Wurzelziehen x 0,5 oder x 0,5 x 0,5 oder x,5 S 0 x 5
20 Funktionale Zusammenhänge Quadratische Ergänzung Ist eine allgemeine quadratische Funktion in Normalform gegeben, müssen wir sie zur Bestimmung des Scheitels und der Nullstellen in die Scheitelform überführen. Dazu klammern wir zunächst den Faktor a aus. Dann ergänzen wir das quadratische und das lineare Glied so, dass sich der entstehende Term als Quadrat schreiben lässt. Beispiel x x,75 x x ( ) ( ),75 (x ) 9,75 (x,5) quadratische Ergänzung Es handelt sich um eine nach oben geöffnete Normalparabel mit dem Scheitel S(,5 ). Aus der Zeichnung entnehmen wir die beiden Nullstellen x 0,5 und S x,5. Für die rechnerische Nullstellenbestimmung müssen wir den Funktionsterm gleich 0 setzen: x x,75 0. Die Lösung dieser Gleichung durch Isolieren von x gelingt uns nicht unmittelbar. Hier hilft die Scheitelform: (x,5) 0 (x,5) x,5 oder x,5 x,5 oder x 0,5 = x x,75 Nullstellen 0 x Beispiel x x,5 [x x ] Streckfaktor ausklammern [x x ] quadratische Ergänzung [(x ) ] Ausmultiplizieren (x ) Scheitel S( ) Mithilfe des Scheitels und des Streckfaktors zeichnen wir die Parabel. Der Zeichnung entnehmen wir die beiden Nullstellen x und x. 5 Zur rechnerischen Nullstellenbestimmung verwenden wir wieder die Scheitelform: (x ) 0 (x ) (x ) Nullstellen x oder x 5 0 x x oder x S = x + x +,5 5
21 Quadratische Funktionen und Gleichungen Mit dem Verfahren der quadratischen Ergänzung sind wir in der Lage, beliebige quadratische Gleichungen zu lösen. Beispiel x 8x 0 : x x 5 quadratische Ergänzung x x 5 binomische Formel (x ) 9 Wurzel ziehen x oder x x oder x 5 Aufgaben :-) Schiebung Wie lautet die Gleichung der Normalparabel, die man durch Verschieben der Normalparabel x um a) nach rechts b) 5 nach rechts c) nach links d) nach oben e) nach unten f),5 nach links g) 0,5 nach rechts h) nach unten erhält? Wanted: Verschobene Normalparabel Zeichne die Normalparabeln mit den folgenden Gleichungen mithilfe einer Schablone. Forme den Term, falls nötig, zunächst in ein Quadrat um. a) (x ) b) (x,5) c) (x ) d) (x,5) e) x f) x g) x x h) x x i) x x,5 k) x,5 :-) Parabel gestaucht und verschoben a) Berechne für die Parabel x eine Wertetabelle von bismitderschrittweite und zeichne die Parabel. Zeichne die um nach rechts verschobene Parabel und gib zu ihr eine Wertetabelle an. b) Durch welche der folgenden Gleichungen wird die verschobene Parabel beschrieben? A) x B) x C) (x ) D) (x ) Überprüfe deine Vermutung mithilfe einer Wertetabelle oder mithilfe eines Funktionsplotters. c) Wie lautet die Gleichung der verschobenen Parabel, wenn man die ursprüngliche Parabel um 5 nach rechts bzw. nach links verschiebt? Wanted: Verschobene Parabeln Zeichne die Parabel mit der folgenden Gleichung. Klammere, falls nötig, zunächst den Streckfaktor aus und schreibe die Klammer als Quadrat. a) (x ) b) (x ) c) (x ) d) (x ) e) x x 8 f) x x g) x 6x,5 h) x x 9 i) x x 55
22 Funktionale Zusammenhänge :-) 5 VerschiebeninalleRichtungen a) Die Parabel mit der folgenden Gleichung soll jeweils um nach oben verschoben werden. Stelle die Gleichung der verschobenen Parabel auf. Überprüfe deine Gleichung mithilfe einer Wertetabelle oder mithilfe eines Funktionsplotters. A) x B) x x C) x x D) (x ) b) Die Parabel x wird um nach links und um nach oben verschobenen. Wie lautet die Gleichung der verschobenen Parabel? c) Die Parabel x wird um nach links und um nach oben verschobenen. Wie lautet die Gleichung der verschobenen Parabel? d) Die Parabel x wird um nach rechts und um nach oben verschobenen. Wie lautet die Gleichung der verschobenen Parabel? 6 Normalform gesucht a) Lies die Scheitelform jeweils aus demgraphenab.formesieindie Normalform um. b) Berechne die Nullstellen mithilfe der Scheitelform. Überprüfe deine Ergebnisse anhand der Zeichnung. c) b) 6 5 a) 7 Kongruente Parabeln I Gib die quadratische Funktion f(x) an, die einen zur Parabel x kongruenten Graphen mit dem Scheitel S besitzt. a) S( 0) b) S( ) c) S(,5,5) d) S(,5,5) 5 0 x d) 8 Kongruente Parabeln II Zeichne die Parabel x. Bestimme die Scheitel der folgenden Parabeln. Zeichne dieparabelnmithilfederparabel x. a) x b) x x 8 c) x x d) x x 5 e) x x 9 f) x x 9 Scheitelform durch quadratische Ergänzung Bringe die Funktionsgleichung in die Scheitelform. Zeichne die zugehörige Parabel. Ermittle die Nullstellen grafisch und rechnerisch. a) f(x) x x b) f(x) x x c) f(x) x x d) f(x) x x e) f(x) x x f) f(x) x 8x,5 g) f(x) x x h) f(x) x x i) f(x) x x k) f(x) x x l) f(x) x x m)f(x) x x 56
23 Quadratische Funktionen und Gleichungen 0 Quadratische Gleichungen Löse folgende quadratische Gleichungen: a) x x b) x 9x 78 c) x 6x 7 d) x x 88 0 e) x 6x 8 0 f) x x g) 5x 5 0x h) x 8x 8 i) x 0x Ausziehtisch Ein Tisch mit einer quadratischen Platte ist auf eine Länge von m ausziehbar. Wie groß ist die quadratische Platte, wenn die Tischfläche durch das Ausziehen um,6 m größer wird? (Zwei Lösungen!) Zum Intensivieren Ergänze zu einer binomischen Formel: a) x x... (...) b) x 8x... (...) c) x x... (...) d) x x... (...) e) x x... (...) f) 9x 5x... (...) Normalform gesucht Bestimme die Gleichung ax bx c der Parabel, die den Scheitel S besitzt und durchdenpunktpverläuft!(tipp:scheitelform!) a) S(0 0), P( 8) b) S(0 ), P( ) c) S(0 ), P( ) d) S( 0), P( 8) e) S( 0), P( ) f) S( ), P( 5) g) S( ), P( ) h) S( ), P( ) i) S( ), P( 0) Wanted: Gleichungen, Gleichungen, Gleichungen,... Im Folgenden sind Eigenschaften von Parabeln beschrieben. Gib dazu jeweils eine Gleichung oder falls möglich zwei Gleichungen verschiedener Parabeln an. Die Parabel ist a) eine nach unten geöffnete Normalparabel mit dem Scheitel S( ). b) eine Normalparabel mit dem Scheitel S( ). c) schlanker als die Normalparabel und hat den höchsten Punkt H(0 ). d) breiter als die Normalparabel und schneidet die -Achse im Punkt Q(0 ). e) kongruent zur Parabel x und verläuft durch den Punkt P( ). f) kongruent zur Parabel x x und schneidet die x-achse im Ursprung und im Punkt R( 0). g) kongruent zur Parabel x x 5 und smmetrisch zur Geraden x und verläuft ferner durch den Punkt P(8 ). 57
24 Funktionale Zusammenhänge 5 Alle Parabeln sind ähnlich! Die Parabel x isteineweiteparabel,dieparabel x isteineengeparabel. Carl Friedrich behauptet trotzdem, dass er jede Parabel mit der Schablone für die Normalparabel zeichnen kann. Er sucht zunächst den positiven x-wert, der gleich dem zugehörigen -Wert ist. a) Welcher x-wert ist das für x, welcher x? b) Dann wählt Carl Friedrich diesen Wert jeweils als Einheit auf der x- und der -Achse, legt die Schablone für die Normalparabel an und zeichnet: 8 = x = x = x 6,5 0,5 0 x 0 x 0,5 0 0,5 x Kontrolliere an mehreren Wertepaaren, dass Carl Friedrichs Behauptung richtig ist. c) Das gezeichnet Bild der Parabel x muss um den Faktor 0,5 verkleinert werden, damit man die gleichen Einheiten wie bei der Normalparabel erhält. Danach ist die Parabel enger als die Normalparabel. Wie muss entsprechend das Bild der Parabel x verändert werden? Wie verläuft sie danach im Vergleich zur Normalparabel? d) Warum folgt aus Carl Friedrichs Überlegung, dass die drei betrachteten Parabeln ähnlich sind? Dieses Ergebnis lässt sich auf alle Parabeln erweitern. 6 Wundersame Geldvermehrung Valentin behauptet sind genauso viel wie. Hier sein Beweis: ( 7 ) ( 7 ) 7 7 Wo steckt der Fehler? 7 Grundwissen: Potenzen mit negativen ganzzahligen Exponenten Forme in eine Summe um und gib das Ergebnis ohne negative Exponenten an. a) ( ) b) ( ) c) ( ) d) (a b ) e) (a b )(a b ) f) (a a ) g) (a a ) h) (x )(x ) i) (x a )(x ) k) x (x ) l) ( x ) m) ( x ) ( x ) 58
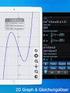
f : x y = mx + t Der Graph einer linearen Funktion ist eine Gerade, welche die y-achse im Punkt S schneidet. = m 2 x 2 m x 1
 III. Funktionen und Gleichungen ================================================================== 3.1. Lineare Funktionen Eine Funktion mit der Zuordnungvorschrift f : x y = mx + t und m, t R heißt lineare
III. Funktionen und Gleichungen ================================================================== 3.1. Lineare Funktionen Eine Funktion mit der Zuordnungvorschrift f : x y = mx + t und m, t R heißt lineare
Expertenpuzzle Quadratische Funktionen
 Phase 1 Aufgaben für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
Phase 1 Aufgaben für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
4.2. Quadratische Funktionen
 Definition: Normalform der Parabelgleichung.. Quadratische Funktionen Eine Funktion mit der Gleichung f() = a + b + c mit a R* und b,c R heißt quadratische Funktion oder ganzrationale Funktion. Grades
Definition: Normalform der Parabelgleichung.. Quadratische Funktionen Eine Funktion mit der Gleichung f() = a + b + c mit a R* und b,c R heißt quadratische Funktion oder ganzrationale Funktion. Grades
3 Lineare und quadratische Funktionen
 3 Lineare und quadratische Funktionen 31 Lineare Funktion Eine Funktion der Art f : mx + t, sind reelle Zahlen) x D heißt lineare Funktion (m und t Man kann die Funktionsgleichung auf zwei verschiedene
3 Lineare und quadratische Funktionen 31 Lineare Funktion Eine Funktion der Art f : mx + t, sind reelle Zahlen) x D heißt lineare Funktion (m und t Man kann die Funktionsgleichung auf zwei verschiedene
Graphen quadratischer Funktionen und deren Nullstellen
 Binomische Formeln Mithilfe der drei binomischen Formeln kann man Funktionen bzw. Gleichungen vereinfachen. 1. Binomische Formel ( Plusformel ) a 2 + 2 a b+ b 2 = (a+ b) 2 Herleitung: (a+ b) 2 = (a+ b)
Binomische Formeln Mithilfe der drei binomischen Formeln kann man Funktionen bzw. Gleichungen vereinfachen. 1. Binomische Formel ( Plusformel ) a 2 + 2 a b+ b 2 = (a+ b) 2 Herleitung: (a+ b) 2 = (a+ b)
Quadratische Funktionen Die Normalparabel
 Quadratische Funktionen Die Normalparabel Kreuze die Punkte an, die auf der Normalparabel liegen. A ( 9) B ( ) C ( 9) D ( ) E (9 ) F (0 0) Die Punkte A bis J sollen auf der Normalparabel liegen. Gib, falls
Quadratische Funktionen Die Normalparabel Kreuze die Punkte an, die auf der Normalparabel liegen. A ( 9) B ( ) C ( 9) D ( ) E (9 ) F (0 0) Die Punkte A bis J sollen auf der Normalparabel liegen. Gib, falls
Wertetabelle : x 0 0,5 1 2 3 4 0,5 1. y = f(x) = x 2 0 0,25 1 4 9 16 0,25 1. Graph der Funktion :
 Quadratische Funktionen ================================================================= 1. Die Normalparabel Die Funktion f : x y = x, D = R, heißt Quadratfunktion. Wertetabelle : x 0 0,5 1 3 4 0,5 1
Quadratische Funktionen ================================================================= 1. Die Normalparabel Die Funktion f : x y = x, D = R, heißt Quadratfunktion. Wertetabelle : x 0 0,5 1 3 4 0,5 1
Quadratische Funktionen
 Quadratische Funktionen 6. Die allgemeine quadratische Funktion Im Alltag sowie auch in den Naturwissenschaften treten vielfach Zusammenhänge auf, bei denen die Änderung einer Größe vom Quadrat der anderen
Quadratische Funktionen 6. Die allgemeine quadratische Funktion Im Alltag sowie auch in den Naturwissenschaften treten vielfach Zusammenhänge auf, bei denen die Änderung einer Größe vom Quadrat der anderen
Die gleiche Lösung erhält man durch Äquivalenzumformung:
 R. Brinkmann http://brinkmann-du.de Seite 3..0 Quadratische Gleichungen Reinquadratische Gleichung Lösen Sie die Gleichung x = 5 Durch probieren erhält man die Lösung: x = 5 oder x = 5 Denn x = 5 = 5 oder
R. Brinkmann http://brinkmann-du.de Seite 3..0 Quadratische Gleichungen Reinquadratische Gleichung Lösen Sie die Gleichung x = 5 Durch probieren erhält man die Lösung: x = 5 oder x = 5 Denn x = 5 = 5 oder
Repetitionsaufgaben: Quadratische Funktionen
 Kantonale Fachschaft Mathematik Repetitionsaufgaben: Quadratische Funktionen Zusammengestellt von Felix Huber, KSR Lernziele: - Sie wissen, dass der Graph einer quadratischen Funktion eine Parabel ist
Kantonale Fachschaft Mathematik Repetitionsaufgaben: Quadratische Funktionen Zusammengestellt von Felix Huber, KSR Lernziele: - Sie wissen, dass der Graph einer quadratischen Funktion eine Parabel ist
Expertenpuzzle Quadratische Funktionen
 Phase 1 Lösung für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
Phase 1 Lösung für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
A3.2 Quadratische Funktionen
 A. Quadratische Funktionen Die Quadratfunktion Definition: Eine reelle Funktion f: = a + b + c, D = R (a, b, c R a 0) heißt quadratische Funktion. Beispiele:. f: =. f: = 0,5 - + Die Quadratfunktion f:
A. Quadratische Funktionen Die Quadratfunktion Definition: Eine reelle Funktion f: = a + b + c, D = R (a, b, c R a 0) heißt quadratische Funktion. Beispiele:. f: =. f: = 0,5 - + Die Quadratfunktion f:
Übungsaufgaben zu quadratischen Gleichungen und Parabeln
 Übungsaufgaben zu quadratischen Gleichungen und Parabeln Binomische Formeln:. binomische Formel: ( a + b) = a + ab + b. binomische Formel:. binomische Formel: ( a b) = a ab + b ( a + b)(a b) = a b Lösungsformel
Übungsaufgaben zu quadratischen Gleichungen und Parabeln Binomische Formeln:. binomische Formel: ( a + b) = a + ab + b. binomische Formel:. binomische Formel: ( a b) = a ab + b ( a + b)(a b) = a b Lösungsformel
Quadratische Funktionen Arbeitsblatt 1
 Quadratische Funktionen Arbeitsblatt 1 Spezielle quadratische Funktion Die Funktionsgleichung einer speziellen quadratischen Funktion hat die Form y = 3 x 2. Der dazugehörige Graph heißt Parabel. Bei einer
Quadratische Funktionen Arbeitsblatt 1 Spezielle quadratische Funktion Die Funktionsgleichung einer speziellen quadratischen Funktion hat die Form y = 3 x 2. Der dazugehörige Graph heißt Parabel. Bei einer
+ 2. Bruchgleichungen
 Bruchgleichungen Gleichungen mit einer Lösungsvariablen im Nenner eines Bruchs heißen Bruchgleichungen. Definitionsmenge: Nenner 0 Lösungsweg: 1. Multiplikation mit dem Hauptnenner 2. Äquivalenzumformungen
Bruchgleichungen Gleichungen mit einer Lösungsvariablen im Nenner eines Bruchs heißen Bruchgleichungen. Definitionsmenge: Nenner 0 Lösungsweg: 1. Multiplikation mit dem Hauptnenner 2. Äquivalenzumformungen
Grundwissen Mathematik JS 11
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ math-naturw u neusprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 957 PEGNITZ FERNRUF 94/48 FAX 94/564 Grundwissen Mathematik JS Was versteht man allgemein unter einer
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ math-naturw u neusprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 957 PEGNITZ FERNRUF 94/48 FAX 94/564 Grundwissen Mathematik JS Was versteht man allgemein unter einer
4 Ganzrationale Funktionen
 FOS, Jahrgangsstufe (technisch) 4 Ganzrationale Funktionen 4 Polynomfunktionen Eine Funktion, die man auf die Form f : x a n x n + a n x n + + a 2 x 2 + a x + a 0 mit x R bringen kann, heißt ganzrationale
FOS, Jahrgangsstufe (technisch) 4 Ganzrationale Funktionen 4 Polynomfunktionen Eine Funktion, die man auf die Form f : x a n x n + a n x n + + a 2 x 2 + a x + a 0 mit x R bringen kann, heißt ganzrationale
f. y = 0,2x g. y = 1,5x + 5 h. y = 4 6x i. y = 4 + 5,5x j. y = 0,5x + 3,5
 11. Lineare Funktionen Übungsaufgaben: 11.1 Zeichne jeweils den Graphen der zugehörigen Geraden a. y = 0,5x 0,25 b. y = 0,1x + 2 c. y = 2x 2 d. 2x + 4y 5 = 0 e. y = x f. y = 0,2x g. y = 1,5x + 5 h. y =
11. Lineare Funktionen Übungsaufgaben: 11.1 Zeichne jeweils den Graphen der zugehörigen Geraden a. y = 0,5x 0,25 b. y = 0,1x + 2 c. y = 2x 2 d. 2x + 4y 5 = 0 e. y = x f. y = 0,2x g. y = 1,5x + 5 h. y =
Gleichsetzungsverfahren
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Parabeln - quadratische Funktionen
 Parabeln - quadratische Funktionen Roland Heynkes 9.11.005, Aachen Das Gleichsetzungsverfahren und die davon abgeleiteten Einsetzungs- und Additionsverfahren kennen wir als Methoden zur Lösung linearer
Parabeln - quadratische Funktionen Roland Heynkes 9.11.005, Aachen Das Gleichsetzungsverfahren und die davon abgeleiteten Einsetzungs- und Additionsverfahren kennen wir als Methoden zur Lösung linearer
Quadratische Funktionen Kompetenzorientiertes Üben
 Quadratische Funktionen Kompetenzorientiertes Üben Kompetenzen Quadratische Funktionen Die unten dargestellten Kompetenzen werden u. a. in einem Leistungsnachweis verlangt. Das Raster dient der Selbsteinschätzung.
Quadratische Funktionen Kompetenzorientiertes Üben Kompetenzen Quadratische Funktionen Die unten dargestellten Kompetenzen werden u. a. in einem Leistungsnachweis verlangt. Das Raster dient der Selbsteinschätzung.
x 0 0,5 1 2 3 4 0,5 1 2. Die Quadratfunktion ist für x 0 streng monoton fallend und für x 0 streng monoton steigend.
 Quadratische Funktionen ================================================================= 1. Die Normalparabel Die Funktion f : x y = x 2, D = R, heißt Quadratfunktion. Ihr Graph heißt Normalparabel. Wertetabelle
Quadratische Funktionen ================================================================= 1. Die Normalparabel Die Funktion f : x y = x 2, D = R, heißt Quadratfunktion. Ihr Graph heißt Normalparabel. Wertetabelle
Einfache quadratische Funktionen und Gleichungen. x y Wertetabelle. y-achse
 Einfache quadratische Funktionen und Gleichungen Eine quadratische Funktion hat allgemein die Funktion: y = ax 2 + bx + c Dabei gilt: a, b und c R und a 0 Der Graph, der hierbei entsteht ist eine Parabel.
Einfache quadratische Funktionen und Gleichungen Eine quadratische Funktion hat allgemein die Funktion: y = ax 2 + bx + c Dabei gilt: a, b und c R und a 0 Der Graph, der hierbei entsteht ist eine Parabel.
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Basistext Funktionen. Eine Funktion f ordnet jedem Element x aus einer Definitionsmenge D f genau ein Wert y zu.
 Basistext Funktionen Definition Eine Funktion f ordnet jedem Element x aus einer Definitionsmenge D f genau ein Wert y zu. Man schreibt: f: x -> y mit y = f(x) Die Wertemenge einer Funktion f besteht aus
Basistext Funktionen Definition Eine Funktion f ordnet jedem Element x aus einer Definitionsmenge D f genau ein Wert y zu. Man schreibt: f: x -> y mit y = f(x) Die Wertemenge einer Funktion f besteht aus
Ich kenne den Nullproduktsatz und kann ihn anwenden, um Gleichungen in faktorisierter Form (wie (2x+5) (7 5x)=0 ) zu lösen.
 Klasse 9c Mathematik Vorbereitung zur Klassenarbeit Nr. am 1..018 Themen: Quadratische Funktionen und Gleichungen Checkliste Was ich alles können soll Ich kenne die allgemeine Form f(x) = ax²+bx+c und
Klasse 9c Mathematik Vorbereitung zur Klassenarbeit Nr. am 1..018 Themen: Quadratische Funktionen und Gleichungen Checkliste Was ich alles können soll Ich kenne die allgemeine Form f(x) = ax²+bx+c und
1 Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an.
 Teste dich! - (/6) Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an. 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Gemeinsamkeiten: Beide
Teste dich! - (/6) Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an. 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Gemeinsamkeiten: Beide
y x oder y 3x. Nenne eine Gleichung einer Parabel, die den Scheitelpunkt im Ursprung hat und nach oben geöffnet ist.
 Parabeln Magische Wand Parabeln Magische Wand 10.1 10. 10.3 10.4 10.5 0.1 0. 0.3 0.4 0.5 30.1 30. 30.3 30.4 30.5 50.1 50. 50.3 50.4 50.5 70.1 70. 70.3 70.4 70.5 100.1 100. 100.3 100.4 100.5 10.1 10.1 10.1
Parabeln Magische Wand Parabeln Magische Wand 10.1 10. 10.3 10.4 10.5 0.1 0. 0.3 0.4 0.5 30.1 30. 30.3 30.4 30.5 50.1 50. 50.3 50.4 50.5 70.1 70. 70.3 70.4 70.5 100.1 100. 100.3 100.4 100.5 10.1 10.1 10.1
Die folgende Abbildung zeigt dir, wie man mit Hilfe des Brennstrahls und des Parallelstrahls das Bild bestimmen kann.
 Begleitmaterial zum Modul Bruchgleichungen Die folgende Abbildung zeigt dir, wie man mit Hilfe des Brennstrahls und des Parallelstrahls das Bild bestimmen kann.. Führe eine entsprechende Konstruktion selbst
Begleitmaterial zum Modul Bruchgleichungen Die folgende Abbildung zeigt dir, wie man mit Hilfe des Brennstrahls und des Parallelstrahls das Bild bestimmen kann.. Führe eine entsprechende Konstruktion selbst
Mathematik 9. Quadratische Funktionen
 Mathematik 9 Funktionen Eine Zuordnung f, die jedem x einer Menge D (Definitionsmenge) genau ein Element y = f(x) einer Menge Z (Zielmenge) zuordnet, heißt Funktion. Dabei heißt y = f(x) Funktionswert
Mathematik 9 Funktionen Eine Zuordnung f, die jedem x einer Menge D (Definitionsmenge) genau ein Element y = f(x) einer Menge Z (Zielmenge) zuordnet, heißt Funktion. Dabei heißt y = f(x) Funktionswert
Einführung der quadratischen Funktionen
 R. Brinkmann http://brinkmann-du.de Seite 08.0.008 Einführung der quadratischen Funktionen Jeder, der sich auf die Führerscheinprüfung vorbereitet sollte wissen, dass sich der Anhalteweg eines bremsenden
R. Brinkmann http://brinkmann-du.de Seite 08.0.008 Einführung der quadratischen Funktionen Jeder, der sich auf die Führerscheinprüfung vorbereitet sollte wissen, dass sich der Anhalteweg eines bremsenden
Thomas Wilkens Seite
 Thomas Wilkens Seite 08..007 Einführung der quadratischen Funktionen Sarah bereitet sich auf die Führerscheinprüfung vor. Sie hat gelernt, dass sich der Anhalteweg eines bremsenden Autos auf trockener
Thomas Wilkens Seite 08..007 Einführung der quadratischen Funktionen Sarah bereitet sich auf die Führerscheinprüfung vor. Sie hat gelernt, dass sich der Anhalteweg eines bremsenden Autos auf trockener
m und schneidet die y-achse im Punkt P(0/3).
 Aufgabe (Pflichtbereich 999) Eine Parabel hat die Gleichung y x 6x, 75. Bestimme rechnerisch die Koordinaten ihres Scheitelpunktes. Berechne die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
Aufgabe (Pflichtbereich 999) Eine Parabel hat die Gleichung y x 6x, 75. Bestimme rechnerisch die Koordinaten ihres Scheitelpunktes. Berechne die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
Quadratische Funktion
 Quadratische Funktion sind Funktionen die nur eine Variable enthalten, deren Exponent 2 ist und keine Variable die einen Exponenten enthält, der größer ist als 2. Zum Beispiel die quadratische Funktion
Quadratische Funktion sind Funktionen die nur eine Variable enthalten, deren Exponent 2 ist und keine Variable die einen Exponenten enthält, der größer ist als 2. Zum Beispiel die quadratische Funktion
und schneidet die -Achse im Punkt 0 3. Berechnen Sie die Koordinaten der Schnittpunkte von und. Lösung: 4 1;2 4
 7 Aufgaben im Dokument Aufgabe P5/2010 Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
7 Aufgaben im Dokument Aufgabe P5/2010 Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
Verschiedene Varianten von Aufgaben zu Parabeln
 Verschiedene Varianten von Aufgaben zu Parabeln 1) Gesucht werden die Nullstellen der Parabel mit der Gleichung: a) f(x) = 2x² 4x 16 b) f(x) = 5/3 (x 1) (x + 3) c) f(x) = - 1/2 (x + 4)² + 8 d) f(x) = 2x²
Verschiedene Varianten von Aufgaben zu Parabeln 1) Gesucht werden die Nullstellen der Parabel mit der Gleichung: a) f(x) = 2x² 4x 16 b) f(x) = 5/3 (x 1) (x + 3) c) f(x) = - 1/2 (x + 4)² + 8 d) f(x) = 2x²
1. Vereinfache wie im Beispiel: 3. Vereinfache wie im Beispiel: 4. Schreibe ohne Wurzel wie im Beispiel:
 1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
1. Selbsttest Heron-Verfahren Gleichungen
 1. Selbsttest 1.1. Heron-Verfahren Mit dem Heron-Verfahren soll ein Näherungswert für 15 gefunden werden. Führe die ersten drei Schritte des Heron- Verfahrens durch. Gib dann unter Verwendung der Werte
1. Selbsttest 1.1. Heron-Verfahren Mit dem Heron-Verfahren soll ein Näherungswert für 15 gefunden werden. Führe die ersten drei Schritte des Heron- Verfahrens durch. Gib dann unter Verwendung der Werte
7 Aufgaben im Dokument. Aufgabe P5/2010
 Aufgabe P5/2010 7 Aufgaben im Dokument Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
Aufgabe P5/2010 7 Aufgaben im Dokument Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
Quadratische Funktion
 Quadratische Funktion Wolfgang Kippels 6. Oktober 018 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3.1 Nullstellen................................... 3. Scheitelpunkt.................................
Quadratische Funktion Wolfgang Kippels 6. Oktober 018 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3.1 Nullstellen................................... 3. Scheitelpunkt.................................
Quadratische Funktion Aufgaben und Lösungen
 Quadratische Funktion Aufgaben und Lösungen http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Graph und Eigenschaften. y = a x + b x + c...............................................
Quadratische Funktion Aufgaben und Lösungen http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Graph und Eigenschaften. y = a x + b x + c...............................................
lineare Funktion: Graph: Gerade mit der Steigung a und dem y-achsenabschnitt b. quadratische Funktion: Graph: Parabel, sofern a 0
 1 7. Der Graph einer quadratischen Funktion lineare Funktion: Graph: Gerade mit der Steigung a und dem y-achsenabschnitt b. quadratische Funktion: Graph: Parabel, sofern a 0 Es wird im Folgenden untersucht,
1 7. Der Graph einer quadratischen Funktion lineare Funktion: Graph: Gerade mit der Steigung a und dem y-achsenabschnitt b. quadratische Funktion: Graph: Parabel, sofern a 0 Es wird im Folgenden untersucht,
Übungsaufgaben zur Linearen Funktion
 Übungsaufgaben zur Linearen Funktion Aufgabe 1 Bestimmen Sie den Schnittpunkt der beiden Geraden mit den Funktionsgleichungen f 1 (x) = 3x + 7 und f (x) = x 13! Aufgabe Bestimmen Sie den Schnittpunkt der
Übungsaufgaben zur Linearen Funktion Aufgabe 1 Bestimmen Sie den Schnittpunkt der beiden Geraden mit den Funktionsgleichungen f 1 (x) = 3x + 7 und f (x) = x 13! Aufgabe Bestimmen Sie den Schnittpunkt der
F u n k t i o n e n Quadratische Funktionen
 F u n k t i o n e n Quadratische Funktionen Eine Parabolantenne bündelt Radio- und Mikrowellen in einem Brennpunkt. Dort wird die Strahlung detektiert. Die Form einer Parabolantenne entsteht durch die
F u n k t i o n e n Quadratische Funktionen Eine Parabolantenne bündelt Radio- und Mikrowellen in einem Brennpunkt. Dort wird die Strahlung detektiert. Die Form einer Parabolantenne entsteht durch die
- G1 - Grundlagen der Mathematik - Bruchrechnen - MSS Böblingen. Einstiegsaufgaben: Merke: a) Addieren von Brüchen. b) Subtrahieren von Brüchen.
 MSS Böblingen - Bruchrechnen - - G - Einstiegsaufgaben: a a a) + = 6x 4x a + a b) = 6x x a a c) = 6x 4x a a d) : = 6x 4x e) 7 = Merke: a) Addieren von Brüchen b) Subtrahieren von Brüchen c) Multiplizieren
MSS Böblingen - Bruchrechnen - - G - Einstiegsaufgaben: a a a) + = 6x 4x a + a b) = 6x x a a c) = 6x 4x a a d) : = 6x 4x e) 7 = Merke: a) Addieren von Brüchen b) Subtrahieren von Brüchen c) Multiplizieren
Merksatz Begriff der Funktion
 Der Begriff Funktion Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. Die Temperatur eines Gewässers wird in verschiedenen
Der Begriff Funktion Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. Die Temperatur eines Gewässers wird in verschiedenen
Pflichtteil... 2. Wahlteil Analysis 1... 6. Wahlteil Analysis 2... 9. Wahlteil Analysis 3... 13. Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analsis 1... 6 Wahlteil Analsis... 9 Wahlteil Analsis 3... 13 Wahlteil Analtische Geometrie 1... 16 Wahlteil Analtische Geometrie... 3 Lösungen: 006 Pflichtteil Lösungen zur Prüfung
Pflichtteil... Wahlteil Analsis 1... 6 Wahlteil Analsis... 9 Wahlteil Analsis 3... 13 Wahlteil Analtische Geometrie 1... 16 Wahlteil Analtische Geometrie... 3 Lösungen: 006 Pflichtteil Lösungen zur Prüfung
Lösen einer Gleichung
 Zum Lösen von Gleichungen benötigen wir: mindestens einen Term eine Definition der in Frage kommenden Lösungen (Grundmenge) Die Grundmenge G enthält all jene Zahlen, die als Lösung für eine Gleichung in
Zum Lösen von Gleichungen benötigen wir: mindestens einen Term eine Definition der in Frage kommenden Lösungen (Grundmenge) Die Grundmenge G enthält all jene Zahlen, die als Lösung für eine Gleichung in
Relationen / Lineare Funktionen
 Relationen / Lineare Funktionen Relationen Werden Elemente aus einer Menge X durch eine Zuordnungsvorschrift anderen Elementen aus einer Menge Y zugeordnet, so wird durch diese Zuordnungsvorschrift eine
Relationen / Lineare Funktionen Relationen Werden Elemente aus einer Menge X durch eine Zuordnungsvorschrift anderen Elementen aus einer Menge Y zugeordnet, so wird durch diese Zuordnungsvorschrift eine
Grundwissen 8 - Lösungen
 Grundwissen 8 - Lösungen Bereich 1: Proportionalität 1) Die in den Tabellen dargestellten Größen sind in beiden Fällen proportional. Entscheide, welche Art von Proportionalität jeweils vorliegt und vervollständige
Grundwissen 8 - Lösungen Bereich 1: Proportionalität 1) Die in den Tabellen dargestellten Größen sind in beiden Fällen proportional. Entscheide, welche Art von Proportionalität jeweils vorliegt und vervollständige
1 Lineare Funktionen. 1 Antiproportionale Funktionen
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
9. Klasse TOP 10 Grundwissen 9 Lösen von Gleichungen 1
 Lösen von Gleichungen 1 Allgemein: Klammern auflösen, wenn sinnvoll (z. B. nicht sinnvoll, wenn im Nenner eines Bruchs bereits ein Produkt steht). Gleichartige Terme zusammenfassen (z. B. x bzw. x ausklammern).
Lösen von Gleichungen 1 Allgemein: Klammern auflösen, wenn sinnvoll (z. B. nicht sinnvoll, wenn im Nenner eines Bruchs bereits ein Produkt steht). Gleichartige Terme zusammenfassen (z. B. x bzw. x ausklammern).
PARABELN. 10. Klasse
 PARABELN 0. Klasse Jens Möller Owingen Tel. 0755-9 HUjmoellerowingen@aol.comU INHALTSVERZEICHNIS NORMALPARABEL PARABELN MIT FORMFAKTOR VERSCHIEBUNG IN Y-RICHTUNG VERSCHIEBUNG IN X-RICHTUNG 5 ALLGEMEINE
PARABELN 0. Klasse Jens Möller Owingen Tel. 0755-9 HUjmoellerowingen@aol.comU INHALTSVERZEICHNIS NORMALPARABEL PARABELN MIT FORMFAKTOR VERSCHIEBUNG IN Y-RICHTUNG VERSCHIEBUNG IN X-RICHTUNG 5 ALLGEMEINE
Wiederholung Quadratische Funktionen (Parabeln)
 SEITE 1 VON 7 Wiederholung Quadratische Funktionen (Parabeln) VON HEINZ BÖER 1. Regeln a) Funktionsvorschriften Normalform f(x) = a x² + b x + c Normalparabel: f(x) = x 2 Graf der Normalparabel Die einfachste
SEITE 1 VON 7 Wiederholung Quadratische Funktionen (Parabeln) VON HEINZ BÖER 1. Regeln a) Funktionsvorschriften Normalform f(x) = a x² + b x + c Normalparabel: f(x) = x 2 Graf der Normalparabel Die einfachste
Corinne Schenka Vorkurs Mathematik WiSe 2012/13. ausmultiplizieren. Anwenden von Potenzgesetzen, Wurzelgesetzen, Logarithmengesetzen
 3. Algebraische Grundlagen 3.1. Termumformungen Begriff Term: mathematischer Ausdruck, der aus Zahlen, Variablen, Rechenzeichen oder Klammern besteht Termumformungen dienen der Vereinfachung von komplexen
3. Algebraische Grundlagen 3.1. Termumformungen Begriff Term: mathematischer Ausdruck, der aus Zahlen, Variablen, Rechenzeichen oder Klammern besteht Termumformungen dienen der Vereinfachung von komplexen
Quadratische Funktionen (Parabeln)
 Quadratische Funktionen (Parabeln) Aufgabe: Gegeben ist die quadratische Funktion = () x. Berechne mit Hilfe einer Wertetabelle die Funktionswerte von bis + im Abstand 0,. Zeichne anschließend die Punkte
Quadratische Funktionen (Parabeln) Aufgabe: Gegeben ist die quadratische Funktion = () x. Berechne mit Hilfe einer Wertetabelle die Funktionswerte von bis + im Abstand 0,. Zeichne anschließend die Punkte
Über die Bedeutung der zwei Zahlen m und x 1 für das Aussehen des Graphen wird an anderer Stelle informiert.
 Lineare Funktionen - Term - Grundwissen Woran erkennt man, ob ein Funktionsterm zu einer Linearen Funktion gehört? oder Wie kann der Funktionsterm einer Linearen Funktion aussehen? Der Funktionsterm einer
Lineare Funktionen - Term - Grundwissen Woran erkennt man, ob ein Funktionsterm zu einer Linearen Funktion gehört? oder Wie kann der Funktionsterm einer Linearen Funktion aussehen? Der Funktionsterm einer
Inhalt. Vorwort 4. Quadratische Funktionen Einführung in das Thema 5-6. Ergänzung von Werten in Wertetabellen 9-10
 Inhalt Seite Vorwort 4 1 Quadratische Funktionen Einführung in das Thema 5-6 2 Die Funktionsgleichung = 2 7-8 Ergänzung von Werten in Wertetabellen 9-10 4 Erstellen von Wertetabellen und Zeichnen von Graphen
Inhalt Seite Vorwort 4 1 Quadratische Funktionen Einführung in das Thema 5-6 2 Die Funktionsgleichung = 2 7-8 Ergänzung von Werten in Wertetabellen 9-10 4 Erstellen von Wertetabellen und Zeichnen von Graphen
Nullstellen. Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt. Man schreibt
 Nullstellen Aufgabe 1 Gegeben ist die folgende quadratische Funktion: Bestimme die Nullstellen. f( x) x² 3 x² 3 : x² 16 16 x² 16 Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt.
Nullstellen Aufgabe 1 Gegeben ist die folgende quadratische Funktion: Bestimme die Nullstellen. f( x) x² 3 x² 3 : x² 16 16 x² 16 Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt.
Mathematik Quadratische Funktionen
 Mathematik Quadratische Funktionen und Quadratische Gleichungen ax + bx + c = 0 Stefan Gärtner 004 Gr Mathematik Quadratische Funktionen Seite Inhalt Inhaltsverzeichnis Seite Grundwissen 3 Definition Quadratische
Mathematik Quadratische Funktionen und Quadratische Gleichungen ax + bx + c = 0 Stefan Gärtner 004 Gr Mathematik Quadratische Funktionen Seite Inhalt Inhaltsverzeichnis Seite Grundwissen 3 Definition Quadratische
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
AUFGABENSAMMLUNG 9. KLASSE
 AUFGABENSAMMLUNG 9. KLASSE 1. Reelle Zahlen (1) Vereinfache soweit wie möglich. Alle Variablen sind aus R +. (a) 4a 4 a + ab a b (b) b : 7a (c) b + b + b ( 5 c 6 (d) c + ) () Schreibe ohne Wurzelzeichen
AUFGABENSAMMLUNG 9. KLASSE 1. Reelle Zahlen (1) Vereinfache soweit wie möglich. Alle Variablen sind aus R +. (a) 4a 4 a + ab a b (b) b : 7a (c) b + b + b ( 5 c 6 (d) c + ) () Schreibe ohne Wurzelzeichen
Quadratische Funktion - Übungen
 Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Bestimmung ganzrationaler Funktionen
 Bestimmung ganzrationaler Funktionen 30 0 0-50 -40-30 -0-0 0 0 30 40 50 x. Eine Brücke ist 30 m hoch und hat eine Spannweite von 00 m. Welche Parabel beschreibt die Krümmung des Stützbogens? Wir führen
Bestimmung ganzrationaler Funktionen 30 0 0-50 -40-30 -0-0 0 0 30 40 50 x. Eine Brücke ist 30 m hoch und hat eine Spannweite von 00 m. Welche Parabel beschreibt die Krümmung des Stützbogens? Wir führen
4.2. Aufgaben zu quadratischen Funktionen
 .. Aufgaben zu quadratischen Funktionen Aufgabe : Stauchung und Streckung der Normalparabel a) Zeichne die Schaubilder der folgenden Funktionen in das Koordinatensstem. b) Vervollständige die darunter
.. Aufgaben zu quadratischen Funktionen Aufgabe : Stauchung und Streckung der Normalparabel a) Zeichne die Schaubilder der folgenden Funktionen in das Koordinatensstem. b) Vervollständige die darunter
mathphys-online QUADRATISCHE FUNKTIONEN
 QUADRATICHE FUNKTIONEN Inhaltsverzeichnis Kapitel Inhalt eite Zuordnungsvorschriften, Funktionsgraph ymmetrie. ymmetrie zur. ymmetrie zu einer Parallelen zur Nullstellen Anzahl der Nullstellen 7 cheitel
QUADRATICHE FUNKTIONEN Inhaltsverzeichnis Kapitel Inhalt eite Zuordnungsvorschriften, Funktionsgraph ymmetrie. ymmetrie zur. ymmetrie zu einer Parallelen zur Nullstellen Anzahl der Nullstellen 7 cheitel
Bestimme dazu die Nullstellen, Scheitelpunkt und Schnittpunkt mit der y-achse und ergänze evtl. einige Punkte durch eine Wertetabelle.
 Klasse Art Schwierigkeit Mathematisches Schema Nr. 9 Üben xx Quadratische Funktion 1 Skizziere den Graphen der durch y = 0,5 x 2 + x - 4 gegebenen quadratischen Funktion. Bestimme dazu die Nullstellen,
Klasse Art Schwierigkeit Mathematisches Schema Nr. 9 Üben xx Quadratische Funktion 1 Skizziere den Graphen der durch y = 0,5 x 2 + x - 4 gegebenen quadratischen Funktion. Bestimme dazu die Nullstellen,
Einführungsphase Mathematik. Thema: Quadratische Funktionen. quadratische Gleichungen
 Thema: Quadratische Funktionen quadratische Gleichungen Normalform einer linearen Funktion Normalform einer quadratischen Funktion Handelt es sich um quadratische Funktionen??? Ja, denn a = 3, b = 0, c
Thema: Quadratische Funktionen quadratische Gleichungen Normalform einer linearen Funktion Normalform einer quadratischen Funktion Handelt es sich um quadratische Funktionen??? Ja, denn a = 3, b = 0, c
Papierfalten und Algebra
 Arbeitsblätter zum Thema Papierfalten und Algebra en Robert Geretschläger Graz, Österreich 009 Blatt 1 Lösen quadratischer Gleichungen mit Zirkel und Lineal AUFGABE 1 Zeige, dass die x-koordinaten der
Arbeitsblätter zum Thema Papierfalten und Algebra en Robert Geretschläger Graz, Österreich 009 Blatt 1 Lösen quadratischer Gleichungen mit Zirkel und Lineal AUFGABE 1 Zeige, dass die x-koordinaten der
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 50.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 50.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
d) Die Parabel verläuft symmetrisch zur Achse durch die Punkte ( 1 0,5) und (2 5,5).
 Dokument mit 26 Aufgaben Aufgabe A Der Wasserstrahl eines Springbrunnens hat eine Höhe von 6 und eine Weite von 6. Martin hat Lust unter dem Wasserstrahl durchzulaufen. a) Wähle ein geeigneters Koordinatensystem
Dokument mit 26 Aufgaben Aufgabe A Der Wasserstrahl eines Springbrunnens hat eine Höhe von 6 und eine Weite von 6. Martin hat Lust unter dem Wasserstrahl durchzulaufen. a) Wähle ein geeigneters Koordinatensystem
Realschulabschluss Funktionen (Pflichtteil) ab 2010 Lösung P5/2010 Lösungslogik Erstellung der Graphik. Die Parabel ist nach unten geöffnet, breiter u
 Lösung P5/2010 Erstellung der Graphik. Die Parabel ist nach unten geöffnet, breiter und in Richtung nicht verschoben, der Scheitel liegt somit bei 0 5. Aufstellung der Geradengleichung. Berechnung der
Lösung P5/2010 Erstellung der Graphik. Die Parabel ist nach unten geöffnet, breiter und in Richtung nicht verschoben, der Scheitel liegt somit bei 0 5. Aufstellung der Geradengleichung. Berechnung der
2.3 Quadratische Funktionen
 2.3 Quadratische Funktionen 2.3.1 Definition einer quadratischen Funktion Bisher hatten wir uns ganz auf lineare Funktionen beschränkt. Wir stellen sie im Koordinatensystem als Geraden dar.interessanter
2.3 Quadratische Funktionen 2.3.1 Definition einer quadratischen Funktion Bisher hatten wir uns ganz auf lineare Funktionen beschränkt. Wir stellen sie im Koordinatensystem als Geraden dar.interessanter
1 Analysis Kurvendiskussion
 1 Analysis Kurvendiskussion 1.1 Allgemeingültige Betrachtungen Die folgenden aufgezeigten Betrachtungen und Rechenschritte gelten für alle Arten von Funktionen. Funktion (z.b. Polynom n-ten Grades) Schreibweise
1 Analysis Kurvendiskussion 1.1 Allgemeingültige Betrachtungen Die folgenden aufgezeigten Betrachtungen und Rechenschritte gelten für alle Arten von Funktionen. Funktion (z.b. Polynom n-ten Grades) Schreibweise
MATHEMATIK GRUNDWISSEN 8. KLASSE LESSING-GYMNASIUM
 MATHEMATIK GRUNDWISSEN 8. KLASSE LESSING-GYMNASIUM NEU-ULM Lessing-Gmnasium Neu-Ulm Seite von I. Funktionen. Direkt proportionale Zuordnungen und sind direkt proportional, wenn, zum n-fachen Wert für der
MATHEMATIK GRUNDWISSEN 8. KLASSE LESSING-GYMNASIUM NEU-ULM Lessing-Gmnasium Neu-Ulm Seite von I. Funktionen. Direkt proportionale Zuordnungen und sind direkt proportional, wenn, zum n-fachen Wert für der
8. Klasse TOP 10 Grundwissen 8 Funktionen verstehen 1
 8. Klasse TOP 0 Grundwissen 8 Funktionen verstehen Wesentliches Kennzeichen einer Funktion ist: Zu jedem -Wert gehört genau ein -Wert. Meistens gibt es einen Funktionsterm (eine Formel), die angibt, wie
8. Klasse TOP 0 Grundwissen 8 Funktionen verstehen Wesentliches Kennzeichen einer Funktion ist: Zu jedem -Wert gehört genau ein -Wert. Meistens gibt es einen Funktionsterm (eine Formel), die angibt, wie
Formelsammlung Mathematik 9
 I Lineare Funktionen... 9.) Funktionen... 9.) Proportionale Funktionen... 9.) Lineare Funktionen... 9.4) Bestimmung von linearen Funktionen:... II) Systeme linearer Gleichungen... 9.5) Lineare Gleichungen
I Lineare Funktionen... 9.) Funktionen... 9.) Proportionale Funktionen... 9.) Lineare Funktionen... 9.4) Bestimmung von linearen Funktionen:... II) Systeme linearer Gleichungen... 9.5) Lineare Gleichungen
Die quadratische Funktion
 Die quadratische Funktion In einem Labor wird die Bewegung eines Versuchswagen aufgenommen. Es werden dabei die folgenden Messreihen aufgenommen: Messreihe 1 Messreihe 2 Messreihe 3 x in s 0,0 0,5 1,0
Die quadratische Funktion In einem Labor wird die Bewegung eines Versuchswagen aufgenommen. Es werden dabei die folgenden Messreihen aufgenommen: Messreihe 1 Messreihe 2 Messreihe 3 x in s 0,0 0,5 1,0
Grundwissen 9. Sabine Woellert
 Grundwissen 9 1. Quadratische Funktion... 2 1.1 Definition... 2 1.2 Eigenschaften der Normalparabel ( ):... 2 1.3 Veränderung der Normalparabel... 2 1.4 Normalform, Scheitelform... 4 1.5 Berechnung der
Grundwissen 9 1. Quadratische Funktion... 2 1.1 Definition... 2 1.2 Eigenschaften der Normalparabel ( ):... 2 1.3 Veränderung der Normalparabel... 2 1.4 Normalform, Scheitelform... 4 1.5 Berechnung der
Potenzen Potenzfunktionen und ihre Eigenschaften Abbilden von Funktionsgraphen
 Wie können Gleichungen der Form x n = a; a 0 n N gelöst werden? Wir benötigen die n-te Wurzel: n x = a Was ist, wenn n Q statt n N? (Q: rationale Zahlen; alle Brüche, auch negative N: natürliche Zahlen;
Wie können Gleichungen der Form x n = a; a 0 n N gelöst werden? Wir benötigen die n-te Wurzel: n x = a Was ist, wenn n Q statt n N? (Q: rationale Zahlen; alle Brüche, auch negative N: natürliche Zahlen;
Parabeln und quadratische. Gleichungen. 3.1 Die Gleichung y = ax 2
 Parabeln und quadratische Gleichungen In Klasse 7 hast du schon Geraden und Hperbeln als Funktionsgraphen kennen gelernt. Jetzt lernst du eine weitere Kurve kennen, und zwar die Parabel, zunächst aber
Parabeln und quadratische Gleichungen In Klasse 7 hast du schon Geraden und Hperbeln als Funktionsgraphen kennen gelernt. Jetzt lernst du eine weitere Kurve kennen, und zwar die Parabel, zunächst aber
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
1. Fall: 2. Fall: Lösungsblatt zu: Differentialquotient. Tipp: Nullstellen. Tipp: Es reicht, wenn einer der Faktoren Null wird.
 Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Vorbereitungsmappe. Grundlagen vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS
 Vorbereitungsmappe Grundlagen vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS Liebe Schülerinnen und Schüler, vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS stellt sich vor allem im Fach
Vorbereitungsmappe Grundlagen vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS Liebe Schülerinnen und Schüler, vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS stellt sich vor allem im Fach
Ganzrationale Funktionen
 Eine Dokumentation von Sandro Antoniol Klasse 3f Mai 2003 Inhaltsverzeichnis: 1. Einleitung...3 2. Grundlagen...4 2.1. Symmetrieeigenschaften von Kurven...4 2.1.1. gerade Exponenten...4 2.1.2. ungerade
Eine Dokumentation von Sandro Antoniol Klasse 3f Mai 2003 Inhaltsverzeichnis: 1. Einleitung...3 2. Grundlagen...4 2.1. Symmetrieeigenschaften von Kurven...4 2.1.1. gerade Exponenten...4 2.1.2. ungerade
Repetitionsaufgaben: quadratische Funktionen
 Kantonale Fachschaft Mathematik Repetitionsaufgaben: quadratische Funktionen Zusammengestellt von Bruno Wyrsch und Erich Huber, KS Seetal Inhaltsverzeichnis 1. Einführungsbeispiel.... Allgemeine Form der
Kantonale Fachschaft Mathematik Repetitionsaufgaben: quadratische Funktionen Zusammengestellt von Bruno Wyrsch und Erich Huber, KS Seetal Inhaltsverzeichnis 1. Einführungsbeispiel.... Allgemeine Form der
Demoseiten für
 Lineare Ungleichungen mit Variablen Anwendung (Vorübungen für das Thema Lineare Optimierung) Datei Nr. 90 bzw. 500 Stand 0. Dezember 009 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 90 / 500 Lineare Ungleichungen
Lineare Ungleichungen mit Variablen Anwendung (Vorübungen für das Thema Lineare Optimierung) Datei Nr. 90 bzw. 500 Stand 0. Dezember 009 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 90 / 500 Lineare Ungleichungen
Quadratische Funktionen und Gleichungen Mathematik Jahrgangsstufe 9 (G8) Bergstadt-Gymnasium Lüdenscheid. Friedrich Hattendorf
 Mathematik Jahrgangsstufe 9 (G8) Lüdenscheid Friedrich Hattendorf 4. September 2014 Vorbemerkung Die Datei entsteht noch; noch nicht alles ist optimal Hinweis zum Ausdruck: (Fast) Alles sollte noch gut
Mathematik Jahrgangsstufe 9 (G8) Lüdenscheid Friedrich Hattendorf 4. September 2014 Vorbemerkung Die Datei entsteht noch; noch nicht alles ist optimal Hinweis zum Ausdruck: (Fast) Alles sollte noch gut
Exemplar für Prüfer/innen
 Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2015 Mathematik Kompensationsprüfung Angabe für Prüfer/innen Hinweise zur Kompensationsprüfung
Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2015 Mathematik Kompensationsprüfung Angabe für Prüfer/innen Hinweise zur Kompensationsprüfung
Lineare Funktionen. Die lineare Funktion
 1 Die lineare Funktion Für alle m, t, aus der Zahlenmenge Q heißt die Funktion f: x m x + t lineare Funktion. Die Definitionsmenge ist Q (oder je nach Zusammenhang ein Teil davon). Der Graph der linearen
1 Die lineare Funktion Für alle m, t, aus der Zahlenmenge Q heißt die Funktion f: x m x + t lineare Funktion. Die Definitionsmenge ist Q (oder je nach Zusammenhang ein Teil davon). Der Graph der linearen
Funktionsgleichung in ABC-Form Funktionsgleichung in Scheitelform Funktionsgleichung in Nullstellenform. y 2 x 2x 3 2 ausklammern. Binom.
 Parabel zeichnen Parabel zeichnen Schritt für Schrittanleitungen unter www.fraengg.ch Klasse, GeoGebra) Funktionsgleichung in ABC-Form Funktionsgleichung in Scheitelform Funktionsgleichung in Nullstellenform
Parabel zeichnen Parabel zeichnen Schritt für Schrittanleitungen unter www.fraengg.ch Klasse, GeoGebra) Funktionsgleichung in ABC-Form Funktionsgleichung in Scheitelform Funktionsgleichung in Nullstellenform
Lineare Funktionen Arbeitsblatt 1
 Lineare Funktionen Arbeitsblatt 1 Eine Funktion mit der Gleichung y = m x + b heißt lineare Funktion. Ihr Graph ist eine Gerade mit der Steigung m. Die Gerade schneidet die y-achse im Punkt P(0 b). Man
Lineare Funktionen Arbeitsblatt 1 Eine Funktion mit der Gleichung y = m x + b heißt lineare Funktion. Ihr Graph ist eine Gerade mit der Steigung m. Die Gerade schneidet die y-achse im Punkt P(0 b). Man
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
Flächenberechnung mit Integralen
 Flächenberechnung mit Integralen W. Kippels 30. April 204 Inhaltsverzeichnis Übungsaufgaben 2. Aufgabe................................... 2.2 Aufgabe 2................................... 2.3 Aufgabe 3...................................
Flächenberechnung mit Integralen W. Kippels 30. April 204 Inhaltsverzeichnis Übungsaufgaben 2. Aufgabe................................... 2.2 Aufgabe 2................................... 2.3 Aufgabe 3...................................
Themenerläuterung. Die wichtigsten benötigten Formeln 1. Der Umgang mit der Mitternachtsformel
 Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Vorbereitung auf die erste Klassenarbeit
 01 QUADRATISCHE FUNKTIONEN Wiederholungen Alles um Quadratische Funktionen Vorbereitung auf die erste Klassenarbeit Aufgabe 1: Schuljahr 2017/18 Seite 1/12 Aufgabe 2: Schuljahr 2017/18 Seite 2/12 Aufgabe
01 QUADRATISCHE FUNKTIONEN Wiederholungen Alles um Quadratische Funktionen Vorbereitung auf die erste Klassenarbeit Aufgabe 1: Schuljahr 2017/18 Seite 1/12 Aufgabe 2: Schuljahr 2017/18 Seite 2/12 Aufgabe
Aufstellen von Funktionstermen
 Aufstellen von Funktionstermen Bisher haben wir uns mit der Untersuchung von Funktionstermen beschäftigt, um Eigenschaften des Graphen zu ermitteln. Nun wollen wir die Betrachtungsweise ändern. Wir gehen
Aufstellen von Funktionstermen Bisher haben wir uns mit der Untersuchung von Funktionstermen beschäftigt, um Eigenschaften des Graphen zu ermitteln. Nun wollen wir die Betrachtungsweise ändern. Wir gehen
