Lösungen, Aufgaben Kapitel 1. Semantik: Übungsaufgaben und Lösungen. Aufgaben Kapitel 1. Prof. Manfred Krifka, Sommersemester 2007
|
|
|
- Katja Sommer
- vor 7 Jahren
- Abrufe
Transkript
1 Prof. Manfred Krifka, Sommersemester 2007 Semantik: Übungsaufgaben und Lösungen Modul 4: Grammatik II: Der Satz Aufgaben Kapitel 1 1. Geben Sie drei Beispiele, in denen das, was ein Sprecher mit einem Ausdruck bezwecken will, und die wörtliche Bedeutung dieses Ausdrucks verschieden sind. Paraphrasieren Sie die die wörtliche Bedeutung, und erläutern Sie den intendierten Zweck. 2. Was haben Phonetik und Semantik als Bereiche der Sprachwissenschaft gemeinsam? 3. Warum scheint es attraktiv, den Begriff der Bedeutung auf den der beobachtbaren Handlung zu reduzieren? Warum muss diese Methode scheitern? 4. Wie werden Bedeutungen von Wörtern in einem Wörterbuch wiedergegeben? Begründen Sie, ob dies in (a) praktischer, (b) theoretischer Hinsicht eine befriedigende Methode ist, Bedeutungen zu erfassen. 5. Beschreiben Sie, weshalb nach Auffassung der Wahrheitsbedingungen-Semantik der Begriff der Wahrheit fundamental für den Begriff der Bedeutung ist. 6. Angenommen, wir haben eine gute Theorie der Bedeutung von Aussagesätzen wie Du isst einen Apfel. Wir können daraus eine Theorie von Entscheidungsfragen wie Isst du einen Apfel? entwickeln. Als Bedeutung einer solchen Frage könnten wir z.b. annehmen: Der Sprecher will wissen, ob der Aussagesatz Du isst einen Apfel wahr ist oder nicht. Wie kann man in ähnlicher Weise eine Theorie für Ergänzungsfragen und Befehle entwickeln? Diskutieren Sie das anhand der Beispiele (a) Was isst du? und (c) Iss einen Apfel! 7. Stellen Sie in dem folgenden Text Objektsprache, Metasprache und Bedeutungssprache nach den linguistischen Konventionen dar. Wenn jemand sagt, ihm sei hundeelend zumute, dann meint er, es geht mir schlecht. Und der Ausdruck der Himmel hängt voller Geigen ist sprichwörtlich geworden für: Ich bin sehr, sehr glücklich. Lösungen, Aufgaben Kapitel 1 1. Beispiel: Wenn man auf die Frage: Gehst du noch mit in die Kneipe? antwortet: Ich muss noch die Semantik-Hausaufgabe machen, gibt es zu der offensichtlichen wörtlichen Bedeutung den intendierten Sinn: Ich kann nicht mit in die Kneipe gehen. 2. Sowohl Phonetik als auch Semantik beschäftigen sich mit den Schnittstellen der Sprache zu nicht-sprachlichen Systemen: Die Phonetik mit der Produktion und Perzeption von sprachlichen Zeichen, also deren Realisierung im Artikulationsapparat und deren Wahrnehmung im Perzeptionsapparat. Die Semantik mit der Interpretation von sprachlichen Zeichen im kognitiven System des Menschen. 3. Bedeutungen sind nicht direkt beobachtbar, wenn aber Bedeutungen in Beziehung zu beobachtbaren Handlungen stehen, können wir diese Handlungen als Surrogat für Bedeutungen verstehen. Die Methode scheitert, weil viele Sätze, z.b. Behauptungen, nicht notwendig mit irgendwelchen beobachtbaren Handlungen korreliert. 4. Bedeutungen von Lemmata in Wörterbüchern werden in der Regel sprachlich beschrieben (Ausnahmen sind z.b. Bildwörterbücher). Dies ist praktisch befriedigend, wenn man davon ausgehen kann, dass der Leser die Ausdrücke, die zur Beschreibung verwendet werden, versteht oder nachschlagen kann (und dabei nicht in einen Zirkel gerät). In theoretischer Hinsicht kann das nicht befriedigend sein, da die Erklärung der Bedeutung eines Wortes dann immer schon einen Begriff von Bedeutung voraussetzt. 5. In der Wahrheitsbedingungen-Semantik als Bedeutung eines Aussagesatzes seine Wahrheitsbedingungen genommen, gemäß der Einsicht, dass jemand, der die Bedeutung eines Satzes versteht, auch wissen muß, unter welchen Umständen der Satz wahr bzw. falsch ist. Wahrheitsbedingungen kann man genauer und einfacher angeben als Bedeutungen. 6. Die Ergänzungsfrage Was isst du? kann man so auf Wahrheitsbedingungen zurückführen: Sprecher will vom Adressaten a, diejenigen x zu nennen, für die der Aussagesatz x isst einen Apfel wahr ist, d.h. für die die Wahrheitsbedingungen in der wirklichen Welt erfüllt sind. Der Befehl Iss einen Apfel! wird so verstanden, dass der Adressat a aufgefordert wird, die Bedeutung des Aussagesatzes a isst einen Apfel wahr zu machen. 7. Wenn jemand sagt, ihm sei hundeelend zumute, dann meint er, es geht mir schlecht. Und der Ausdruck der Himmel hängt voller Geigen ist sprichwörtlich geworden für: Ich bin sehr, sehr glücklich. Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
2 Aufgaben Kapitel 2: Aspekte der Bedeutung 1. Zeigen Sie durch die Präsuppositionstests, dass der folgende Satz die Präsupposition besitzt, dass es für Lola schwierig war, das Geld zu bekommen: Lola hat es geschafft, das Geld zu bekommen. 2. Welche skalare Implikatur wird ausgelöst in dem Satz Die meisten Kinder haben Schokoladeneis gegessen? Zeigen Sie genau, wie diese Implikatur zustandekommt, indem Sie sie als Alternativen die Sätze Alle Kinder haben Schokoladeneis gegegessen und Einige Kinder haben Schokoladeneis gegessen. 3. Argumentieren Sie dafür, dass die Tempora Präteritum und Futur deiktische Bedeutungen haben. 4. Finden Sie drei Paare von Beispielen mit gleicher deskriptiver aber unterschiedlicher expressiver Bedeutung. Beschreiben Sie die Unterschiede der expressiven Bedeutung. 5. Weshalb stellen sogenannte Idiome wie die Radieschen von unten angucken für tot sein ein Problem für das Kompositonalitätsprinzip dar? Lösungen, Aufgaben Kapitel 2 1. Wir wählen als Test den dialogischen Verneinungstest: A: Lola hat es geschafft, das Geld zu bekommen. B: Nein, das stimmt nicht. Sprecher B verneint lediglich, dass Lola das Geld bekommen hat, und nicht, dass es für sie schwierig war, das Geld zu bekommen. Andere Tests geben das gleiche Resultat, z.b. der Fragetest und der Test mit vielleicht. Aus Hat Lola es geschafft, das Geld zu bekommen? folgt, dass es für Lola schwierig war, das Geld zu bekommen. Desgleichan aus Lola hat es vielleicht geschafft, das Geld zu bekommen. 2. Die Äußerung des Satzes (a) Die meisten Kinder haben Schokoladeneis bekommen hat die Implikatur Nicht alle Kinder haben Schokoladeneis bekommen. Der Sprecher hat (a) geäußert und nicht den informativeren Satz (b) Alle Kinder haben Schokoladeneis bekommen. Der Sprecher soll so informativ wie möglich sein; da er den informativeren Satz (b) nicht geäußert hat, fehlt für diesen Satz offensichtlich die genügende Evidenz, oder der Sprecher weiß sogar, dass er falsch ist. Der Adressat kann also erschließen, dass Satz (b) falsch ist. 3. Ein Präteritumsatz wie Es regnete sagt, dass es zu einem Zeitpunkt vor dem Sprech - zeitpunkt geregnet hat. Ein Futursatz wie Es wird regnen sagt, dass es zu einem Zeitpunkt nach dem Sprechzeitpunkt regnen wird. In beiden Fällen beziehen wir uns also auf den Sprechzeitpunkt, und damit sind Präteritum und Futur deiktische Ausdrücke. 4. Ein Beispiel: Mädchen und Göre; letzteres ist eine abfällige (pejorative) Bezeichnung. 5. Die Bedeutung eines Idioms kann man nicht aus der Bedeutung der Bestandteile des Idioms ableiten, sondern die Bedeutung des Idioms muss unabhängig, also wie die Bedeutung eines Wortes, gelernt werden. (Da es aber nur endlich viele Idiome gibt. stellt dies kein besonderes Problem für die Lernbarkeit einer natürlichen Sprache dar.) Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
3 Aufgaben Kapitel 3: Logik und Semantik. Aussagenlogik. 1. Ist in den folgenden Fällen (i) oder (ii) die Negation des Satzes? a. Hier regnet es immer. (i) Hier regnet es nie. (ii) Hier regnet es nicht immer. b. Jemand hat mir geholfen. (i) Jemand hat mir nicht geholfen. (ii) Niemand hat mir geholfen. c. Es ist noch hell. (i) Es ist noch nicht hell. (ii) Es ist nicht mehr hell. d. Viele haben geklatscht. (i) Viele haben nicht geklatscht. (ii) Nicht viele haben geklatscht. 2. Definieren Sie die Beziehungen Φ und Ψ sind äquivalent, Φ und Ψ sind konträr, und Φ und Ψ sind kontradiktorisch mithilfe der logischen Folgerung, 3. Geben Sie die logischen Verhältnisse zwischen den folgenden Sätzen an (Implikation, Äquivalenz, Kontrarietät, Kontradiktion, Kontingenz). a. Das Glas ist leer. b. Das Glas ist halb voll. c. Das Glas ist halb leer. d. Das Glas ist voll. e. Das Glas ist nicht leer. f. Das Glas ist nicht voll. 4. Welche der folgenden Zeichenketten sind wohlgeformte Formeln (Sätze) der Aussagenlogik? a. [p 1 p 2 ] d. [p 1 p 2 p 3 ] b. [p 1 p 2 p 3 ] e. [p 1 p 2 ] p 1 c. p 1 [p 2 p 3 ] f. [p 1 p 3 ] p 4 ] 5. Berechnen Sie den Wahrheitswert des folgenden Satzes, unter der Annahme der folgenden Wahrheitswerte für die Teilsätze: p 1 : 0, p 2 : 1, p 3 : 0, p 4 : 1 [ [[p 1 p 2 ] p 4 ] [p 1 p 3 ]] 6. Welche der folgenden aussagenlogischen Formeln sind Tautologien, Kontradiktionen oder kontingente Sätze? a. [[p 1 p 2 ] p 2 ] d. [[p 1 p 2 ] [p 2 p 1 ]] b. [[p 1 p 2 ] p 2 ] e. [ [p 1 p 2 ] p 2 ] c. [p 1 [p 1 p 2 ]] f. [[p 1 p 2 ] [p 2 p 1 ]] 7. Desambiguieren Sie die folgenden Sätze mithilfe der aussagenlogischen Notation (wobei p 1 : Es regnet, p 2 : Es blitzt., p 3 : Es donnert ). a. Es regnet und es blitzt oder es donnert. b. Es regnet und blitzt nicht. Lösungen, Aufgaben Kapitel 3 1. a. Hier regnet es nicht immer. b. Niemand hat mir geholfen. b. Es ist nicht mehr hell. c. Nicht viele haben geklatscht. 2. a. Φ und Ψ sind äquivalent (Φ Ψ) gdw. Φ Ψ und Ψ Φ b. Φ und Ψ sind konträr gdw. Φ Ψ und Ψ Φ c. Φ und Ψ sind kontradiktorisch gdw. Φ Ψ, d.h. wenn Φ Ψ und Ψ Φ 3. Das Glas ist leer konträr zu Das Glas ist voll / halb voll / halb leer. kontradiktorisch zu Das Glas ist nicht leer. impliziert Das Glas ist nicht voll. Das Glas ist halb voll. äquivalent zu Das Glas ist halb leer. impliziert Das Glas ist nicht leer / nicht voll. kontradiktorisch zu Das Glas ist leer / voll. Das Glas ist halb leer. äquivalent zu Das Glas ist halb voll. impliziert Das Glas ist nicht leer / nicht voll. kontradiktorisch zu Das Glas ist leer / voll.. Das Glas ist voll. konträr zu Das Glas ist leer / halb voll / halb leer. kontradiktorisch zu Das Glas ist nicht voll. impliziert Das Glas ist nicht leer. Das Glas ist nicht leer. kontradiktorisch zu Das Glas ist leer. kontingent mit Das Glas ist voll / halb voll / halb leer. Das Glas ist nicht voll. kontradiktorisch zu Das Glas ist voll. kontingent mit Das Glas ist leer / halb leer / halb voll. 4. Wohlgeformt ist nur (a), bei den anderen fehlen Klammern. 5. [ [[p 1 p 2 ] p 4 ] [p 1 p 3 ]] a: Kontradiktion d: Kontingent b: Kontingent e: Tautologie c: Kontradiktion f: Kontingent 7. a. (i) [p 1 [p 2 p 3 ]] b. (i) [p 1 p 2 ] (ii) [[p 1 p 2 ] p 3 ] (ii) [p 1 p 2 ] Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
4 Aufgaben Kapitel 4: Beziehungen zwischen Wortbedeutungen 1. Finden Sie drei weitere Beispiele von Synonympaaren und diskutieren Sie mögliche Bedeutungs- und Verwendungsunterschiede. 2. Ist das folgende Gegenbeispiel gegen die Definition der Synonymität im Skript stichhaltig? Wenn nein, warum nicht? Das Wort Briefmarke hat 10 Buchstaben <=/=> Das Wort Postwertzeichen hat 10 Buchstaben. 3. Finden Sie drei Beispiele für Determinativkomposita mit unterschiedlichem semantischen Verhältnis zwischen Modifikatoren und Kopf, und beschreiben Sie dieses Verhältnis. 4. Zeigen Sie, ob die mit Punkten markierte Kontexte in den folgenden Beispielen auwärtsoder abwärtsimplizierend sind. Überprüfen Sie danach die Hypothese, dass negative Polaritätselemente nur in abwärtsimplizierenden Kontexten vorkommen. a. Es ist zweifelhaft, ob b. Es ist sicher, dass c. Kein Student c. Kein Student, der, hat seine Doktorarbeit abgeschlossen. 5. a. Identifizieren Sie den unmarkierten Ausdruck in den folgenden Antonympaaren. i. viel / wenig ii. breit / schmal iii. leicht / schwer iv. kurz / lang b. Beschreiben Sie die semantische Eigenschaft, die den unmarkierten Ausdruck gegenüber dem markierten kennzeichnet, und erklären Sie, warum es bei dem Paar hoch / tief keinen unmarkierten Ausdruck gibt. 6. Die Skalen von antonymen Adjektiven können sich danach unterscheiden, ob sie offen oder geschlossen sind. Beispielsweise kann man dafür argumentieren, dass die Skala billig / teuer so beschaffen ist, dass sie sie auf der billig -Seite geschlossen, auf der teuer -Seite offen ist. Es gibt einen Minimalwert beim Preis (nämlich, dass etwas gar nichts kostet, also umsonst ist), aber keinen Maximalwert. Die Intensifikatoren einer Sprache können sich auf diese Skaleneigenschaften beziehen: Im Deutschen wird sehr eher für offene Skalenenden verwendet, ganz hingegen für geschlossene. Aufgabe: Untersuchen Sie mit Google die Vorkommenshäufigkeit von ganz billig, sehr billig, ganz teuer, sehr teuer (Sie müssen die Zeichenketten mit Anführungszeichen schreiben, z.b. sehr billig ). Deuten Sie Ihren Befund. 7. Geben Sie eine Taxonomie für Kochgeschirr an. 8. Geben Sie eine Mereologie für Fahrrad an. Lösungen zu Aufgaben Kapitel 4 1. ( ) 2. Das Beispiel ist nicht stichhaltig, weil in dem Kontext, in dem die synynymen Ausdrücke vorkommen, nicht die Bedeutung der Ausdrücke zählt, sondern die Form. In dem Textkontext kommt insbesondere sowohl Metasprache als auch Objektsprache vor; dies muss vermieden werden. 3. Regenschirm: Ein Schirm gegen Regen. Holzpantoffeln: Pantoffeln aus Holz (Material) Abschlussprüfung: Eine Prüfung zum Abschluss eines Lehrgangs. 4. Tests mit dem Hyponym-Hyperonym-Paar Porsche Sportwagen Es ist zweifelhaft, ob Hans einen Sportwagen besitzt Es ist zweifelhaft, ob Hans einen Porsche besitzt, d.h. abwärtsimplizierend; daher: o.k.: Es ist zweifelhaft, ob er jemals in China war. Es ist sicher, dass Hans einen Porsche besitzt Es ist sicher, dass Hans einen Sportwagen besitzt., d.h. aufwärtsimplizierend; daher: *Es ist sicher, ob Hans jemals in China war. Kein Student hat einen Sportwagen Kein Student hat einen Porsche, d.h. abwärtsimplizierend; daher o.k.: Kein Student war jemals in China. Kein Student, der einen Sportwagen besitzt, hat seine Doktorarbeit abgeschlossen. Kein Student, der einen Porsche besitzt, hat seine Doktorarbeit abgeschlossen., d.h. abwärtsimplizierend. daher o.k: Kein Student, der jemals in China war, hat seine D.arbeit abgeschlossen. 5. a. Unmarkierte Ausdrücke: viel, breit, schwer, lang; z.b. Wie lang ist dieses Brett neutral; Wie kurz ist dieses Brett Das Brett ist kurz. b. Die Skalen der Beispiele haben jeweils einen Nullpunkt, z.b. ist der Nullpunkt bei lang/kurz die Null-Länge. Das Adjektiv, das den Bereich zum Nullpunkt hin abdeckt, ist das markierte Adjektiv. Bei hoch / tief gibt es keinen absoluten Nullpunkt, daher auch keinen markierten Ausdruck. 6. ganz billig: 131,000m sehr billig: 130,000, ganz teuer:1,720, sehr teuer: 438,000 Erklärung: ganz impliziert Erreichen eines Endpunkt, dieser besteht bei billig, aber kaum bei teuer. 7. Kochgeschirr Kochtopf Pfanne Römertopf Kokotte Fischpfanne Crêpepfanne 8. Fahrrad Rahmen Räder Lenker Gestell Sattel? Speichen Nabe Griffe Lenkstange Reifen Felge Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
5 Aufgaben zu Kapitel 5: Mengen, Relationen, Funktionen, semantische Beziehungen 1. Wir haben gesehen, dass die Hyponymie mithilfe des Begriffs der Teilmenge modelliert werden kann. Zeigen Sie, wie sie mit mengentheoretischen Begriffen die Beziehung von konträren Begriffen (Beispiel: reich und arm) und von komplementären Begriffen (Beispiel: reich und nicht reich) modellieren können. Gehen Sie dabei von der Grundmenge der Menge der Menschen aus. 2. Es sei A = {1, 2, 3, 4}, B = {4, 5, 6, 7}, U (Universum) = {x 0 x 10} Was ist A B, A B, A \ B, A, A (B )? 3. Definieren Sie, mithilfe der Operationen und. Das heißt, geben Sie eine Gleichung A B =..., wobei... das -Zeichen nicht enthält. 4. Die mengentheoretischen Regeln für und scheinen den Regeln der Addition + und Multiplikation ähnlich zu sein. Beispielsweise ist + kommutativ, da wir a+b = b+a haben. Vergleichen Sie die mengentheoretischen Gesetze (Kommutativität, Assoziativität, Distributivität, Idempotenz) mit den arithmetischen und stellen Sie Ähnlichkeiten und Unterschiede fest. 5. Welche der folgenden Paarmengen ist eine Funktion mit Argumentbereich {1,2,3,4}? i. { 1, a, 2, b, 3, c, 4, d } ii. { 1, a, 2, b, 3, c, 3, d, 4,d } iii. { 1, a, 2, b, 3, c, 4, c } iv. { 1, a, 2, b, 3, c } 6. Reduzieren Sie die folgenden Lambda-Ausdrücke so weit wie möglich: a) λx[2x + 3](7) b) λx[λy[2x + y](3)](4) (auch als λxλy[2x + y](3)(4) darstellbar) c) λf[f(7) + 4](λx[2x + 3]) d) λfλy[f(7) + y](4)(λx[2x + 3]) e) λf[f(7) + f(6)](λx[2x + 3]) f) λf[f(f(7))(λx[2x + 3]) 7. Definieren Sie die folgenden Begriffe mithilfe der angegebenen Begriffe, nach dem angegebenen Muster: [[Onkel]] definiert durch [[Elternteil]] und [[Bruder]]: λxλy[es gibt ein z mit [[Elternteil]](x)(z) und [[Bruder]](y)(z)], (d.h. y ist Onkel von x gdw. es ein z gibt sodass z Elternteil von x und y Bruder von z ist). a) [[Nichte]], durch [[Geschwister]], [[Tochter]] b) [[Kusine]], durch [[Elternteil]], [[Geschwister]], [[Tochter]] b) [[Enkelin]], durch [[Elternteil]] und [[weiblich]]. c) [[Schwiegermutter]], durch [[Ehegatte]] und [[Mutter]]. 8. Geben Sie die charakteristischen Funktion χ, χ {a, c}, χ {c, d}, and χ {a, b, c, d} an, d.h. die charakteristischen Funktionen der Mengen Ø, {a, c}, {c, d} and {a, b, c, d}, mit der Menge {a, b, c, d} als Universum. Lösungen zu Aufgaben Kapitel 5 1. Wenn zwei Begriffe A, B konträr sind, dann gilt: A B =, aber A B Zwei Begriffe A, B sind komplementär, wenn gilt: A = B 2. A B = {4} A B = {1, 2, 3, 4, 5, 6, 7}4} A \ B = {1, 2, 3} A = {0, 5, 6, 7, 8, 9, 10} A B = {0, 1, 2, 3, 4, 8, 9, 10} 3. A B = (A B ) (vgl. Regel von de Morgan) 4. Kommutativtiät: A B = B A, A B = B A a+b = b+a, a b = b a Assoziativität: A (B C) = (A B) C, A (B C) = (A B) C a+(b+c)= (a+b)+c, a (b c) = (a b) c Distributivität: A (B C) = (A B) (A C) A (B C) = (A B) (B C) a (b+c) = (a b) + (a c) a+(b c) (a+b) (a+c) (im allgemeinen) Idempotenz: A A = A A A = A a+a a (wenn a 0) a a a (wenn a 1) 5. i. { 1, a, 2, b, 3, c, 4, d } Funktion (eineindeutig) ii. { 1, a, 2, b, 3, c, 3, d, 4,d } keine Funktion, da 3, c und 3, d iii. { 1, a, 2, b, 3, c, 4, c } Funktion iv. { 1, a, 2, b, 3, c } keine Funktion mit Argumentbereich {1,2,3,4} b. Welche der obengenannten Mengen ist eine eineindeutige Funktion? 6. a. [ ] = 17 b. [λy[2 4 + y](3)] = [ ] = 11 c. [λx[2x + 3](7) + 4] = [[ ] + 4] = 21 d. λy[λx[2x + 3](7) + y](4) = λy[[ ] + y](4) = [[ ] + 4] = 21 e. [λx[2x + 3](7) + λx[2x + 3](6)] = [[ ] + [ ]] = 31 f. [λx[2x + 3](λx[2x + 3](7))] = [λx[2x + 3]( )] = λx[2x + 3](17) = [ ] = Definieren Sie die folgenden Begriffe mithilfe der angegebenen Begriffe, nach dem angegebenen Muster: [[Onkel]] definiert durch [[Elternteil]] und [[Bruder]]: λxλy[es gibt ein z mit [[Elternteil]](x)(z) und [[Bruder]](y)(z)], (d.h. y ist Onkel von x gdw. es ein z gibt sodass z Elternteil von x und y Bruder von z ist). a) [[Nichte]] = λxλy[es gibt ein z mit [[Geschwister]](z)(x) und [[Tochter]](z)(y)] b) [[Kusine]] = λxλy[es gibt ein z und es gibt ein z mit [[Elternteil]](x)(z) und [[Geschwister]](z)(z ) und [[Tochter]](z )(y)] c) Enkelin = λxλy[es gibt ein z mit Elternteil (z)(x) Elternteil (y)(z) weiblich (x)] c) [[Schwiegermutter]] = λxλy[es gibt ein z mit [[Ehegatte]](x)(z) und [[Mutter]](z)(y)] 8. χ = { a, 0, b, 0, c, 0, d, 0 } χ {a, c} = { a, 1, b, 0, c, 1, d, 0 } χ {c, d} = { a, 0, b, 0, c, 1, d, 1 } χ {a, b, c, d} = { a, 1, b, 1, c, 1, d, 1 } Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
6 Aufgaben zu Kapitel 6, Prädikation, Modifikation, Referenz 1. Im Seminar wurde gezeigt, wie intransitive und transitive Prädikationen kompositional interpretiert werden können. Zeigen Sie, wie die folgende ditransitive Prädikation unter der angegebenen Struktur kompositional interpretiert werden kann: (dass) [Manne [Lola [das Geld [schenkt]]] Dazu müssen Sie insbesondere eine Bedeutung für schenkt und eine Interpretationsregel für syntaktische Strukturen mit ditransitiven Verben angeben. 2. Im Seminar haben wir den Satz Lola rennt in Berlin abgeleitet. Betrachten Sie den folgenden Satz,: (dass) [Lola [Manne [auf der Straße [sieht]]] Dieser Satz hat eine Lesart, nach der sich Manne auf der Straße befindet und Lola ihn sieht. Geben Sie eine Bedeutung für auf der Straße an, welche mit dem transitiven Verb sieht kombiniert werden kann und dieses so modifiziert, dass angegeben wird, dass sich das Objekt auf der Straße befindet. Leiten Sie dann die Bedeutung des Satzes Schritt für Schritt ab. 3. Gibt es Verben ohne Argumente? 4. Argumentieren Sie, ob es sich bei den unterstrichenen Konstituenten um Komplemente (Argumentausdrücke) oder Adjunkte handelt. a. Hans steckte das Papier in den Ofen. b. Vincent schaute in die Sonne. c. Das Kind kleckerte auf den Teppich. d. Das Kind bekleckerte den Teppich. e. Fritz musiziert im Schloss. f. Fritz wohnt im Schloss. 5. Leiten Sie die Bedeutung der IP der Mann die Frau kennt ab. Lösungen zu Aufgaben Kapitel 6 1. Wir können das Verb schenken als dreistellige Relation repräsentieren: schenken s = λzλyλx[x schenkt y z in s] (wobei y der Rezipient und z die Gabe ist). Als syntaktische Struktur für ditransitive Verben kann man die folgende annehmen: [ VP [ NP (der) Lola] [ V [ NP das Geld] [ V0 schenkt]]] Wir können die Bedeutung des Satzes dann wie folgt kompositional ableiten: [ IP Manne [ VP Lola [ V das Geld [ V0 schenkt]]] s = schenkt s ( das Geld s )( Lola s )( Manne s ) = λzλyλx[x schenkt y z in s]( das Geld s 2. Bedeutung von auf der Straße als Modifikator eines zweistelligen Verbs: auf der Straße s = λrλyλx[[y ist auf der Straße in s] R(y)(x)] Bedeutung des Beispielsatzes: [ IP Lola [ VP Manne [ V0 [ PP auf der Straße] [ V0 sieht]]]] s = auf der Straße s ( sieht s )( Manne s )( Lola s ) = λrλyλx[[y ist auf der Straße in s] R(y)(x)] (λyλx[x sieht y in s])(manne)(lola) = λyλx[[y ist auf der Straße in s] [x sieht y in s]](manne)(lola) = [[Manne ist auf der Straße in s] [Lola sieht Manne in s]] 3. Sog. Witterungsverben wie regnen, blitzen, weihnachten sind nullstellig. Zwar müssen sie im Deutschen aus formalen Gründen mit einem Subjekt es realisiert werden (vgl. Es regnet, oder weil es regnet), dieses es bindet aber keine Argumentstelle dieser Prädikate. 4. a. in den Ofen ist nicht weglassbar, also Argument. b. in die Sonne ist weglassbar, daher eher Adjunkt. Allerdings muss die Richtung oder das Ziel des Schauens bereits in der Verbbedeutung angegeben sein, was für einen Argumentstatus spricht. Also: Fakultatives Argument. c. auf den Teppich ist weglassbar, also Adjunkt oder fakultatives Argument (s.o.) d. den Teppich ist nicht weglassbar, also Argument. e. im Schloss ist weglassbar, also Adjunkt. f. im Schloss ist nicht weglassbar, also Argument. g. den Schlager ist zwar weglassbar, muss aber bereits in der Verbbedeutung angegeben sein. Also fakultatives Argument. h. den ganzen Tag ist weglassbar und muss nicht in der Verbbedeutung angegeben sein, also Adjunkt. 5. [ IP [ NP der Mann] [ VP [ NP die Frau] [ V kennt]]] s = [ VP kennt [ NP die Frau]] s ( der Mann s ) = kennt s ( [ NP die Frau] s )( der Mann s ) = λyλx[x kennt y in s](ι{x x ist eine Frau in s})(ι{x x ist ein Mann in s}) = λx[x kennt ι{x x ist eine Frau in s} in s]( ι{x x ist ein Mann in s}) (definiert in Situationen s, in denen es genau einen Mann und genau eine Frau gibt) = [ι{x x ist ein Mann in s} kennt ι{x x ist eine Frau in s} in s} (statt ι{x x ist eine Frau in s} auch ι λx[x ist eine Frau in s] Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
7 Aufgaben zu Kapitel 7, Quantifikation Lösungen der Aufgaben zu Kapitel 7 1. Geben Sie die Bedeutung des Determinators zwischen fünf und sieben an. 2. Leiten Sie Schritt für Schritt die Bedeutung des Satzes ab: Zwischen fünf und sieben Äpfel sind verfault. 3. Geben Sie die Bedeutung des Determinators weniger als ein Viertel (der) an. 4. Leiten Sie Schritt für Schritt die Bedeutung des Satzes ab: Weniger als ein Viertel (der) Äpfel sind verfault. 5. Die übliche Art, die Wahrheit eines Satzes wie Jeder Rabe ist schwarz zu überprüfen, ist, sich die Raben anzusehen und zu prüfen, ob sie schwarz sind. Ein Philosoph hat jedoch eine andere Vorgehensweise vorgeschlagen: Wir können auch nachprüfen, ob jedes nicht-schwarze Ding ein Nicht-Rabe ist. a. Zeigen Sie (z.b. mithilfe eines Venn-Diagramms) dass die beiden Vorgehensweisen äquivalent sind. b. Begründen Sie, weshalb die zweite Vorgehensweise ungewöhnlich ist. (Stichwort: Konservativität von Determinatoren). 6. Leiten Sie die Bedeutung der folgenden IP ab: [ IP [ NP Manne] [ VP [ NP keine Abkürzungen] [ V kennt]]] 7. Leiten Sie die Bedeutung der folgenden IP ab: [ IP [ NP kein Mensch] [ VP [ NP die meisten Abkürzungen] [ V kennt]]] 8. Leiten Sie die Bedeutung der folgenden IP ab: [ IP [ NP die meisten Abkürzungen] 1 [ IP [ NP kein Mensch] [ VP t 1 [ V kennt]]] 9. Drücken Sie die Bedeutung der folgenden Sätze mithilfe der Prädikatenlogik aus: a. dass keine Frau jeden Mann liebt b. dass keine Frau zwei Männer liebt c. dass eine Frau einen Mann liebt, der sie liebt d. dass jede Frau jeden Mann liebt, der sie liebt. e. dass eine Frau weniger als drei Männer liebt f. dass keine Frau keinen Mann liebt 10. Drücken Sie die Bedeutung der folgenden Sätze in der Prädikatenlogik aus: a. dass eine Frau einen Mann kennt, der jede Frau liebt b. dass jede Frau einen Mann kennt, der keine Frau liebt c. dass jede Frau einen Mann kennt, der eine Frau kennt, die ihn liebt d. dass jede Frau denselben Mann liebt e. dass jede Frau einen anderen Mann liebt f. dass keine Zahl größer ist als alle anderen Zahlen (drücken Sie dabei x ist größer als y aus als: x > y) g. dass zwischen zwei verschiedenen Zahlen immer eine von beiden verschiedene Zahl liegt (für x liegt zwischen y und z : y < x x < z) 1. zwischen fünf und sieben s = λp λp[5 #(P P) 7] 2. [ S [ NP [ DET zwischen fünf und sieben] [ N Äpfel]] [ VP sind verfault]] s = zwischen fünf und sieben s ( Äpfel s )( sind verfault s ) = λp λp[5 #(P P ) 7](λx[x ist ein Apfel in s])(λx[x ist verfault in s]) = λp[5 #( λx[x ist ein Apfel in s] P) 7]() = 5 #( λx[x ist ein Apfel in s] λx[x ist verfault in s]) 7 3. weniger als ein Viertel der s = λp λp[#(p P) / #(P ) < ¼] 4. [ S [ NP [ DET weniger als ein Viertel der] [ N Äpfel]] [ VP sind verfault]]] s = weniger als ein Viertel der s ( Äpfel s )( sind verfault s ) = λp λp[#(p P) / #(P ) < ¼](λx[x ist ein Apfel in s])(λx[x ist verfault in s]) = λp[#(λx[x ist ein Apfel in s] P) / #( λx[x ist ein Apfel in s]) < ¼](λx[x ist verf. in s]) = #(λx[x ist ein Apfel in s] λx[x ist verfault in s]) / #( λx[x ist ein Apfel in s]) < ¼ 5. a. Die beiden Vorgehensweisen sind äquivalent: R S R S S R b. Die übliche Art der Überprüfung des Satzes Jeder Rabe ist schwarz macht sich die Konservativität des Determinators jeder zunutze, indem man sich auf die Raben konzentrieren kann und nachsehen kann, ob jedes Element in dieser Menge die durch die VP ausgedrückte Eigenschaft, schwarz zu sein, erfüllt. Die alternative Weise der Überprüfung dieses Satzes erfordert hingegen eine Überprüfung der Menge von Elementen, die keine Raben sind, man muss also gerade außerhalb der Menge suchen, die durch das Nomen angegeben wird. Man macht sich dabei die Eigenschaft der Konservativität nicht zunutze. 6. [ IP [ NP Manne] [ VP [ NP keine Abkürzungen] [ V kennt]]] s = λx[ keine Abkürzung s (λy[ kennt s (y)(x)])]( Manne s ) = λx[λp[λy[y ist eine Abkürzung in s] P = ](λy[x kennt y in s])](manne) = λx[λy[y ist eine Abkürzung in s] λy[x kennt y in s]= ](Manne) = [λy[y ist eine Abkürzung in s] λy[manne kennt y in s]= ] 7. [ IP [ NP kein Mensch] [ VP [ NP die meisten Abkürzungen] [ V kennt]]] s = kein Mensch s (λx[ die meisten Abkürzung s (λy[ kennt s (y)(x)])]) = kein Mensch s (λx[λp[#( Abk. s P)/# Abk. s > ½](λy[x kennt y in s])]) = kein Mensch s (λx[ #( Abk. s λy[x kennt y in s])/# Abk. s > ½]) = λp[ Mensch s P = ]( λx[ #( Abk. s λy[x kennt y in s])/# Abk. s > ½]) = Mensch s λx[ #( Abk. s λy[x kennt y in s])/# Abk. s > ½] = Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
8 8. [ IP [ NP die meisten Abkürzungen] 1 [ IP [ NP kein Mensch] [ VP t 1 [ V0 kennt]]]] s = die meisten Abkürzungen s (λx 1 ( kein Mensch s ( kennt s (x 1 ))) = λp[#( Abk. s P)/# Abk. s > ½](λx 1 [λp[ Mensch s P = ](λx[x kennt x 1 in s])]) = λp[#( Abk. s P)/# Abk. s > ½](λx 1 [ Mensch s λx[x kennt x 1 in s] = ]) = #( Abk. s λx 1 [ Mensch s λx[x kennt x 1 in s] = ]) / # Abk. s > ½ 9. a. x[frau(x) y[mann(y) liebt(x, y)]] b. x[frau(x) y z[mann(y) Mann(z) y=z liebt(x,y) liebt(x,z)]] c. x[frau(x) y[mann(y) liebt(x,y) lieby(y,x) d. x[frau(x) y[[mann(y) liebt(y,x)] liebt(x,y)]] e. x[frau(x) y z w[mann(y) Mann(z) Mann(w) liebt(x,y) liebt(x,z) liebt(x,w)]] f. x[frau(x) y[mann(y) liebt(x,y)]] 10. a. x y[frau(x) Mann(y) z[frau(z) liebt(y,z)] kennt(x,y)] b. x[frau(x) y[mann(y) z[frau(z) liebt(y,z)] kennt(x,y)] c. x[frau(x) y[mann(y) kennt(x,y) z[frau(z) kennt(y,z) liebt(z,y)]] d. y[mann(y) x[frau(x) liebt(x,y)]] e. x[frau(x) y[mann(y) liebt(x,y)]], genauer: x[frau(x) y[mann(y) liebt(x,y) z w[[frau(z) x=z Mann(w) liebt(z,w)] w=y]]] f. x[zahl(x) y[[zahl(y) x=y] x > y]] g. x y[[zahl(x) Zahl(y) x < y] z[zahl(z) x < z z < y]] Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
9 Aufgaben zu Kapitel 8, Summenindividuen 1. Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: (dass) Lola Manne sieht und rennt 2. Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: (dass) Lola und Manne einander hassen 3. Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: (dass) [ IP [ NP Lola und Manne] [ VP je [ VP [ NP einen Kuchen] essen]]] 4. Neben seiner reziproken Bedeutung hat sich vor allem auch die Bedeutung eines Reflexivpronomens, wie in Lola kämmt sich. a. Geben Sie die Bedeutung der VP kämmt sich an, also kämmt sich s, und zwar in Form eines Lambda-Ausdrucks auf der Basis der Bedeutung des transitiven Verbs kämmt, also kämmt s. b. Geben Sie eine Bedeutung für sich an, die folgender Regel genügt: [ VP [ NP sich] [ V kämmt]] s = sich s ( kämmt s ) c. Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: [ IP [ NP jede Frau] [ VP [ NP sich] [ V kämmt]]] 5. Geben Sie eine Bedeutung für das Puralmorphem er in Kinder an und leiten Sie die Bedeutung von Kind-er kompositional her. 1. [ IP Lola [ VP [ VP Manne [ V0 sieht]] und [ VP [ V0 rennt]]]] s = [ VP Manne [ V0 sieht]] und [ VP [ V0 rennt]]] s ( Lola s ) = λx[ [ VP Manne [ V0 sieht]] s (x) rennt s (x)](lola) = [ [ VP Manne [ V0 sieht]] s (Lola) rennt s (Lola)] = [λyλx[x sieht y in s](manne)(lola) λx[x rennt in s](lola)] = [Lola sieht Manne in s] [Lola rennt in s] 2. [ IP [ NP Lola und Manne] [ VP [ V0 einander [ V0 hassen]]]] s = [ VP [ V0 einander [ V0 hassen]]] s ( [ NP Lola und Manne] s ) = einander s ( hassen s )(Lola Manne) = λrλx y z[y x z x y z R(y)(z)](λyλx[x hasst y in s])(lola Manne) = λx y z[y x z x y z λyλx[x hasst y in s](y)(z)](lola Manne) = λx y z[y x z x y z [z hasst y in u]](lola Manne) = y z[y Lola Manne z Lola Manne y z [z hasst y in u]] 3. [ IP [ NP Lola und Manne] [ VP je [ VP [ NP einen Kuchen] [ V0 essen]]]] s = [ VP je [ VP [ NP einen Kuchen] [ V0 essen]]] s ( [ NP Lola und Manne] s ) = je s ( [ VP [ NP einen Kuchen] [ V0 essen]] s )(Lola Manne) = λpλx y[y a x P(y)](λx [ Kuchen s λy [x isst y in s] ])(Lola Manne) = λx y[y a x λx [ Kuchen s λy [x isst y in s] ](y)]](lola Manne) = y[y a Lola Manne [ Kuchen s λy [y isst y in s] ] 4. a. sich kämmt s = λx[ kämmt s (x)(x)], = λx[x kämmt x in s] b. sich s = λrλx[r(x)(x)] c. [ IP [ NP jede Frau] [ VP [ NP sich] [ V kämmt]]] s = jede Frau s ( sich s ( kämmt s )) = λp[ Frau s P](λRλx[R(x)(x)](λyλx [x kämmt y in s])) = λp[ Frau s P](λx[x kämmt x in s]) = Frau s λx[x kämmt x in s] 5. a. -er s = λpλx y[y a x P(x)] b. Kind-er s = -er s ( Kind s ) = λpλx y[y a x P(x)]( Kind s ) = λx y[y a x Kind s (x)] Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
10 Aufgaben zu Kapitel 9, Tempus 1. Charakterisieren Sie eine Zeitstruktur, die dicht ist, mithilfe einer prädikatenlogischen Formel. Eine Zeitstruktur ist dicht, wenn jeweils zwischen zwei Zeiten eine weitere, davon verschiedene Zeit liegt. 2. Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: [ IP [ NP Lola] [ I [ VP [ NP Manne] [ V0 heiraten]] [ I0 wird]] 3. Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: [ IP [ NP Lola] [ I [ VP [ AdvP morgen] [ VP [ V0 rennen]]] [ I0 wird]] 4. Betrachten Sie die folgende IP, die dem Satz Jedes Kind wird erwachsen sein zugrundeliegt: [ IP [ NP jedes Kind] [ I [ VP [ AP erwachsen] [ V0 sein]] [ I0 wird]]] Wir nehmen an, dass die beiden Prädikate Kind und erwachsen sich gegenseitig ausschließen. Trotzdem drückt der Satz Jedes Kind wird erwachsen sein keinen Widerspruch aus. Liefert unsere Interpretation die richtige Lesart für diesen Satz? Muss etwas verändert werden? 5. Leiten Sie die beiden Lesarten der folgenden IP ab: [ IP [ NP Lola] [ I [ VP [ AdvP um 10 Uhr] [ VP [ NP das Problem] [ V0 gelöst]] [ I0 hatte]]] 6. Im Englischen gibt es ein relatives Futur: a. Lola was going to run. b. Lola will be going to run. Geben Sie die Bedeutung des Satzes At 11:30 a.m. Lola was going to run an. 7. Geben Sie eine Bedeutung für den Partizip Präsens-Operator an, also den Operator, der einen Verbstamm wie renn- nimmt und daraus ein Partizip Präsens wie gerannt macht. Zeigen Sie, wie dieser Operator aus der Bedeutung des Verbstammes renn-, also renn- s,t, = λx[x rennt in s], die Bedeutung von gerannt, also gerannt s,t = λx[s < t x rennt in s], erzeugen kann. Lösungen zu Aufgaben zu Kapitel 9, Tempus 1. s s [s < s s [s < s < s ]] 2. [ IP [ NP Lola] [ I [ VP [ NP Manne] [ V0 heiraten]] [ I0 wird]] s,t = wird s,t ( heiraten s,t ( Manne s,t ))( Lola s,t ) = λpλx[t < s P(x)](λyλx[x heiratet y in s](manne))(lola) = λpλx[t < s P(x)](λx[x heiratet Manne in s])(lola) = λx[t < s [x heiratet Manne in s]](lola) = [t < s [Lola heiratet Manne in s]] 3. [ IP [ NP Lola] [ I [ VP [ AdvP morgen] [ VP [ V0 rennen]]] [ I0 wird]] s,t = wird s,t ( morgen s,t (( heiraten s,t ( Manne s,t )))( Lola s,t ) = λpλx[t < s P(x)](λPλx[s NACHTAG(t) P(x)] (λyλx[x heiratet y in s](manne)))(lola) = λpλx[t < s P(x)](λPλx[s NACHTAG(t) P(x)](λx[x heiratet Manne in s]))(lola) = λpλx[t < s P(x)](λx[s NACHTAG(t) [x heiratet Manne in s]])(lola) = λx[t < s s NACHTAG(t) [x heiratet Manne in s]](lola) = [t < s s NACHTAG(t) [Lola heiratet Manne in s]] 4. [ IP [ NP jedes Kind] [ I [ VP [ AP erwachsen] [ V0 sein]] [ I0 wird]]] s,t = jedes Kind s,t ( [ I [ VP [ AP erwachsen] [ V0 sein]] [ I0 wird]]] s,t ) = λp[λx[x ist ein Kind in s] P](λx[t < s x ist in s erwachsen]) = [λx[x ist ein Kind in s] λx[t < s x ist in s erwachsen]] Es wird von den Kindern in s gesagt, dass sie in s erwachsen sind, wobei s in der Zukunft liegt. Der Satz sagt also: Es gibt eine Situation s in der Zukunft, in der alle Kinder erwachsen sind. Dies ist die kontradiktorische Lesart. Wir wollen offensichtlich über die Kinder zur Sprechzeit t sprechen. Die Subjekts-NP braucht also ihren eigenen Tempusoperator. Eine Möglichkeit: jedes Kind s,t = λp[λx s [s =t x ist ein Kind in s ]] 5. Erste Lesart: [ IP [ NP Lola] [ I [ VP [ AdvP um 10 Uhr] [ VP [ NP das Problem] [ V0 gelöst I ]] [ I0 hatte]]] s,t = hatte s,t ( um 10 Uhr s,t ( gelöst I s,t ( das Problem s,t )))( Lola s,t ) = λpλx[s < t P(x)](λPλx[10 Uhr(s) P(x)](λyλx[s < t x löst y in s] (das Problem)))(Lola) = λpλx[s < t P(x)](λPλx[10 Uhr(s) P(x)] (λx[s < t x löst das Problem in s]))(lola) = λpλx[s < t P(x)](λx[10 Uhr(s) [s < t x löst das Problem in s]])(lola) = λx[s < t [10 Uhr(s) [s < t x löst das Problem in s]]](lola) = [s < t [10 Uhr(s) [s < t Lola löst das Problem in s]]] Zweite Lesart: [ IP [ NP Lola] [ I [ VP [ AdvP um 10 Uhr] [ VP [ NP das Problem] [ V0 gelöst II ]] [ I0 hatte]]] s,t = hatte s,t ( um 10 Uhr s,t ( gelöst II s,t ( das Problem s,t )))( Lola s,t ) = λpλx[s < t P(x)](λPλx[10 Uhr(s) P(x)](λyλx s [s < s x löst y in s ] (das Problem)))(Lola) = λpλx[s < t P(x)](λPλx[10 Uhr(s) P(x)] (λx s [s < s x löst das Problem in s ]))(Lola) = λpλx[s < t P(x)](λx[10 Uhr(s) s [s < s x löst das Problem in s ]])(Lola) = λx[s < t [10 Uhr(s) s [s < s x löst das Problem in s ]]](Lola) = [s < t [10 Uhr(s) s [s < s Lola löst das Problem in s ]]] 6. At 11:30 a.m. Lola was going to run. s,t = [s < t 11:30am(s) s [s < s Lola rennt in s ]] 7. ge- -t s,t = λpλx[s < t P(x)] ge- -t s,t ( renn- s,t ) = λpλx[s < t P(x)](λx[x rennt in s]) = λx[s < t x rennt in s] Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
11 Aufgaben zu Kapitel 10, Modalität 1. Geben Sie die Modalitätsart der folgenden Sätze an (epistemisch, deontisch, physisch, buletisch) und geben Sie an, ob es sich um starke oder schwache Modalität handelt. a. Peter darf heute ein Eis essen. b. Edith ist möglicherweise in Paris. c. Karl ist imstande, die Mondscheinsonate mit verbundenen Augen zu spielen. d. Das Kind muss die Masern haben. e. Egon würde gern einmal nach China fahren. f. Franz soll heute die Fenster streichen. 2. Die Sätze (a, b) sind übersetzungsäquivalent. Erklären Sie, welchen relativen Skopus der Modaloperator und die Negation in (a) und (b) jeweils zueinander haben, sodass die Übersetzungäquivalenz entsteht. Erklären Sie ferner die Skopusverhältnisse von Negation und Modaloperator in (c) und den Unterschied zwischen (a) und (b). a. John must not leave. b. John darf nicht gehen. c. John muss nicht gehen. 3. Betrachten Sie die folgenden Beispiele von Sätzen mit epistemischer Modalität. Diskutieren Sie, ob unsere Einteilung in starke vs. schwache Modalität genügt. Falls nicht, können Sie sich Methoden vorstellen, unseren Modalitätsbegriff entsprechend zu erweitern? a. Das Kind hat sicher die Masern. b. Das Kind hat wahrscheinlich die Masern. c. Das Kind hat möglicherweise die Masern. d. Das Kind könnte eventuell die Masern haben. 4. Leiten Sie die Bedeutung des folgenden Satzes Schritt für Schritt ab. Wählen Sie hierfür die buletische Zugänglichkeitsrelation Z B. (weil) Lola rennen wollte. Lösungen zu Aufgaben von Kapitel a. deontische Modalität, schwach b. epistemische Modalität, schwach c. physische Modalität (schwach) d. epistemische Modalität, stark e. bulethische Modalität, stark f. deontische Modalität, stark 2. Die Proposition, die John geht ausdrückt, wird durch John geht dargestellt. a. John must not leave. John geht b. John darf nicht gehen. John geht In (a) hat der Modaloperator Skopus über die Negation, in (b) hat die Negation Skopus über den Modaloperator Die beiden Sätze haben die gleiche Bedeutung, wegen der logischen Äquivalenz Φ Φ c. John muss nicht gehen. John geht In (c) hat die Negation Skopus über den Modaloperator anders als in (a), daher die unterschiedliche Bedeutung. Zusatzinformation (nicht Teil der Lösung): Die unterschiedliche Interpretation von (a) und (c) wird durch die unterschiedliche Syntax von Deutsch und Englisch verursacht. Wir können annehmen, dass im Deutschen in der für Skopusverhältnisse relevanten Nebensatzstellung die Negation das Modalverb in seinem Skopus hat: a. [ IP John [ I must [ VP not [ VP leave]]]] b. [ IP John [ I [ VP nicht [ VP gehen muss-] [ I0 PRÄS]]] (Nebensatzstellung) [ CP John [ C muss [ IP t 1 [ VP nicht [ VP gehen t 2 ] [ I0 t 2 ]]]] (Hauptsatzstellung) 3. Die einfache Einteilung in starke und schwache Modalität genügt nicht. Die Beispiele (a) bis (d) drücken vier verschiedene Arten von epistemischer Sicherheit aus, die durch zwei Operatoren allein nicht erfasst werden können. Bisher haben wir die Notwendigkeit als Allquantor über zugängliche mögliche Welten aufgefasst, und die Möglichkeit als Existenzquantor: i. Φ t = s Z(s) Φ s ii. Φ t = s Z(s) Φ s Mit (i) könnte man Beispiel (a) darstellen, mit (ii) Beispiel (d). Für (b) und (c) könnte man Quantoren über mögliche Situationen wie die meisten oder einige einführen, z.b. für (b): iii. WAHRSCHEINLICH Φ s = MEIST(Z(s), λs [ Φ s ]), wobei MEIST(A, B) gdw. #(A B) > #(A B), d.h. A B hat mehr Elemente als A B. 4. [ IP [ NP Lola] [ I [ VP rennen woll-] [ I0 -te]]] s,t = -te s,t ( woll- s,t (λs[ rennen s,t ]))( Lola s,t ) = λpλx[s < t P(x)](λRλx s [s Z B (x,s) R(s )(x)](λsλx[x rennt in s]))(lola) = λpλx[s < t P(x)](λx s [s Z B (x,s) x rennt in s ])(Lola) = λx[s < t s [s Z B (x,s) x rennt in s ]](Lola) = [s < t s [s Z B (Lola,s) Lola rennt in s ]] In der bulethischen Zugänglichkeitsrelation Z B ist wird hier auch der Träger des Wunschens (das Subjekt, Lola) festgehalten. Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
12 Klausur Juli 2006 zur Übung 1. Wahrheitsbedingungen und Kontextabhängigkeit (5 Punkte) a. Erläutern Sie anhand des Beispiels Die Ampel steht auf rot, wie die Bedeutung eines Satzes mithilfe des Begriffs der Wahrheit erklärt werden kann. (2 Punkte) b. Zeigen Sie anhand eines Beispiels einen Aspekt von Bedeutung auf, der nicht unmittelbar durch Wahrheitsbedingungen erfassbar ist. (1 Punkt) c. Inwieweit ist die Bedeutung des folgenden Satzes von Merkmalen des Äußerungskontexts abhängig? Ich hab dich gestern in der Kneipe um die Ecke gesehen. (2 Punkte) 2. Präsuppositionen und Implikaturen (5 Punkte) a. Identifizieren Sie die Präsuppositionen des folgenden Satzes: Von den drei Meerschweinchen von Peter ist eines in seinem Gartenteich ertrunken. (2 Punkte) 4. Wortbedeutungen (5 Punkte) a. Welche Bedeutungsbeziehungen besteht zwischen Klinke und Tür? b. Erläutern Sie den Begriff der Polysemie an einem Beispiel. c. In welcher Bedeutungsbeziehung stehen weit und eng? d. Erläutern Sie an einem Beispiel den Unterschied zwischen Vagheit und Ambiguität. (2 Punkte) 5. Aufbau komplexer Bedeutungen mit quantifizierter NP (5 Punkte) Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: [[ [ IP [ NP [ Det jeder] [ N Mann]] [ VP [ NP Lola] [ V0 kennt]]] ]] s Zur Erinnerung: [[jeder ]] s = λp λp [P P] 6. Tempus (5 Punkte) Leiten Sie die Bedeutung der folgenden IP Schritt für Schritt ab: [[ [ IP [ NP Lola] [ I [ Adv morgen] [ I [ VP rennen]] [ I0 wird]]] ]] s,t Zur Erinnerung: [[morgen ]] s,t = λpλx[s NACHTAG(t) P(x)] b. Welche Implikatur wird durch den folgenden Satz ausgelöst? Peter hat ein Meerschweinchen oder einen Wellensittich (2 Punkte) c. Erläutern Sie den Begriff der Aufhebung einer Implikatur an einem Beispiel. 3. Logik, Mengenlehre, Funktionen (5 Punkte) a. Zeigen Sie durch eine Untersuchung aller möglichen Wahrheitswerte, dass es sich bei der folgenden aussagenlogischen Formel um eine Tautologie handelt.: p 1 [p 1 p 2 ] b. Illustrieren Sie an einem Beispiel, wie man mithilfe mengentheoretischer Begriffe die Hyponymiebeziehung zwischen zwei Ausdrücken erfassen kann. (2 Punkte) c. Drücken Sie mithilfe der Prädikatenlogik die Bedeutung des folgenden Satzes aus: Jedes Mädchen tanzte mit einem Jungen, der ihr eine Blume gab. d. Geben Sie die folgende Beschreibung einer Funktion mit einem Lambda-Ausdruck an: Die Funktion, die eine Zahl x nimmt und auf eine Funktion abbildet, die eine Zahl y nimmt und auf die Summe von x und y abbildet. Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
13 Beispiel-Lösungen zur Klausur Hinweis: Antworten möglichst knapp halten; bei Material, das nicht zur Frage gehört, kann es Punktabzug geben! 1. Wahrheitsbedingungen und Kontextabhängigkeit a. Ein Sprecher, der die Bedeutung des Satzes Die Ampel steht auf rot kennt, muss dazu fähig sein, anzugeben, in welchen Situationen der Satz wahr ist. Er muss also z.b. auf ein Bild, in dem (genau) eine Ampel zu sehen ist, die auf rot steht, zustimmen, und auf ein Bild, in dem (genau) eine Ampel zu sehen ist, die auf grün und nicht auf rot steht, ablehnend reagieren. Allgemein: Die Bedeutung eines Satzes zu kennen schließt ein, die Wahrheitsbedingungen dieses Satzes zu kennen. (Dies heißt allerdings nicht, dazu in der Lage zu sein, auch zu überprüfen, ob der Satz in einer Situation wahr ist man kann z.b. nicht vollständiges Wissen über die Situation haben). b. Ein Beispiel sind Konnotationen, wie z.b. in Glücklicherweise stand die Ampel auf rot. Hier drückt glücklicherweise aus, dass der Sprecher es für einen glücklichen Umstand hält, dass der Restsatz wahr ist. (Weitere Beispiele: Präsuppositionen, Implikaturen). c. Es gibt in dem Beispiel eine Reihe von Ausdrücken, für deren spezifische Bedeutung man den Kontext kennen muss: ich bezieht sich auf den Sprecher, dich auf den Adressaten, gestern auf den Vortag, um die Ecke auf den Ort und das Tempus auf die Zeit vor der Äußerung. 2. Präsuppositionen und Implikaturen a. Präsuppositionen: (i) Peter hat drei Meerschweinchen, (ii) Peter hat einen Gartenteich. [Es ist hingegen keine Präsupposition (sondern eine Implikatur), dass nur eines und nicht alle seiner Meerschweinchen in seinem Gartenteich ertrunken sind.] b. Es wird die Implikatur ausgelöst, dass Peter nicht ein Meerschweinchen und einen Wellensittich hat. [Sonst hätte der Sprecher den informativeren Satz geäußert, dass Peter ein Meerschweinchen und einen Wellensittich hat.] c. Peter hat drei Meerschweinchen, vielleicht sogar vier. Der Zusatz vielleicht sogar vier hebt die Implikatur des ersten Satzes, dass Peter nicht mehr als drei Meerschweinchen hat, auf. 3. Logik, Mengenlehre, Funktionen a. p 1 p 2 p 1 p 1 p 2 p 1 [p 1 p 2 ] ein Objekt zutrifft, dann trifft auch β auf dieses Objekt zu, aber nicht umgekehrt. Wenn man die Bedeutung von α, β durch Mengen modelliert, gilt: α ist ein Hyponym zu β gdw. α β. c. x[mädchen(x) y[junge(y) z[blume(z) GAB(y,x,z)] TANZTE-MIT(x,y)] d. λx[λy[x+y]] 4. Wortbedeutungen a. Klinke ist ein Mereonym zu Tür. b. Ein Beispiel: Buch ist polysem; es kann z.b. ein konkretes Exemplar bedeuten (mein zerfleddertes Exemplar von Kafkas Prozess), und den Text selbst (Kafkas Prozess, wie er in vielen Buchexemplaren, Textdateien, Übersetzungen usw. existiert). Daneben gibt es weitere Bedeutungen, z.b. als Buch als Teil eines größeren Textes. c. Bei weit und eng handelt es sich um Antonyme, die einen großen bzw. einen kleinen Zwischenraum bezeichnen. [Dabei steht weit auch in einer Antonymbeziehung zu nah]. d. Ein Ausdruck heißt ambig, wenn er zwei klar geschiedene Bedeutungen besitzt; Beispiel: scharf (mit den Bedeutung spitzkantig, gut schneidend vs. durchdrigender, hitzerregender Geschmack ). Er trifft auf ein Objekt in einer Lesart zu oder nicht. Ein Ausdruck heißt vage, wenn er zu einem gewissen Grad auf ein Objekt zutrifft, Beispiel: scharf (in der ersten Lesart): Ein Messer kann zu einem gewissen Grade scharf sein; in unterschiedlichen Kontexten kann ein Messer scharf genannt werden oder auch nicht. 5. [ IP [ NP [ Det jeder] [ N Mann]] [ VP [ NP Lola] [ V0 kennt]]] s = jeder s ( Mann s )( kennt s ( Lola s )) = λp λp[p P](λx[x ist ein Mann in s])(λyλx[x kennt y in s])(lola)) = λp[λx[x ist ein Mann in s] P](λx[x kennt Lola in s]) = λx[x ist ein Mann in s] λx[x kennt Lola in s] 6. [ IP [ NP Lola] [ I [ Adv morgen] [ I [ VP rennen]] [ I0 wird]]] s,t = wird s,t ( morgen s,t ( rennen s,t ))( Lola s,t ) = λpλx[t < s P(x)](λPλx[s NACHTAG(t) P(x)](λx[x rennt in s])))(lola) = λpλx[t < s P(x)](λx[s NACHTAG(t) λx[x rennt in s](x)])(lola) = λpλx[t < s P(x)](λx[s NACHTAG(t) x rennt in s])(lola) = λx[t < s λx[s NACHTAG(t) x rennt in s](x)](lola) = λx[t < s [s NACHTAG(t) x rennt in s]](lola) = [t < s s NACHTAG(t) Lola rennt in s] b. Wenn ein Ausdruck α ein Hyponym eines Ausdrucks β ist, dann gilt: Wenn α auf Manfred Krifka, Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin,
(10) x 1[FRAU(x 1) RENNT(x 1)] Keine Frau rennt.
![(10) x 1[FRAU(x 1) RENNT(x 1)] Keine Frau rennt. (10) x 1[FRAU(x 1) RENNT(x 1)] Keine Frau rennt.](/thumbs/50/26484398.jpg) Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin, GK Semantik SS 2009, F.Sode Basierend auf Seminarunterlagen von Prof. Manfred Krifka Quantoren in der Prädikatenlogik (auch
Institut für deutsche Sprache und Linguistik, Humboldt-Universität zu Berlin, GK Semantik SS 2009, F.Sode Basierend auf Seminarunterlagen von Prof. Manfred Krifka Quantoren in der Prädikatenlogik (auch
Grundkurs Semantik. Sitzung 6: Prädikation, Modifikation, Referenz. Andrew Murphy
 Grundkurs Semantik Sitzung 6: Prädikation, Modifikation, Referenz Andrew Murphy andrew.murphy@uni-leizpig.de Grundkurs Semantik HU Berlin, Sommersemester 2015 http://www.uni-leipzig.de/ murphy/semantik15
Grundkurs Semantik Sitzung 6: Prädikation, Modifikation, Referenz Andrew Murphy andrew.murphy@uni-leizpig.de Grundkurs Semantik HU Berlin, Sommersemester 2015 http://www.uni-leipzig.de/ murphy/semantik15
Funktionen und sprachliche Bedeutungen
 Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Quantoren (6) (1) a. jede Frau b. eine Frau c. keine Fraue d. drei Frauen e. die meisten Frauen f. viele Frauen
 Quantoren (6) (1) a. jede Frau b. eine Frau c. keine Fraue d. drei Frauen e. die meisten Frauen f. viele Frauen Solche Ausdrücke werden im allgemeinen Quantoren oder quantifizierende Nominalphrasen genannt,
Quantoren (6) (1) a. jede Frau b. eine Frau c. keine Fraue d. drei Frauen e. die meisten Frauen f. viele Frauen Solche Ausdrücke werden im allgemeinen Quantoren oder quantifizierende Nominalphrasen genannt,
Einführung in die Semantik, 10. Sitzung Generalisierte Quanto
 Einführung in die Semantik, 10. Sitzung Generalisierte Quantoren, NPIs und Negation Göttingen 3. Januar 2007 Generalisierte Quantoren Prädikatenlogik Typentheorie Bedeutung von GQs Monotonizität GQs und
Einführung in die Semantik, 10. Sitzung Generalisierte Quantoren, NPIs und Negation Göttingen 3. Januar 2007 Generalisierte Quantoren Prädikatenlogik Typentheorie Bedeutung von GQs Monotonizität GQs und
Mengen, Prädikate, Relationen und Funktionen
 Wiederholung letzte Sitzung Mengen, Prädikate, Relationen und Funktionen Was sind Prädikate? Was sind Mengen? Wie kann man die Elemente einer Menge darstellen? Welche Beziehung zwischen Mengen haben wir
Wiederholung letzte Sitzung Mengen, Prädikate, Relationen und Funktionen Was sind Prädikate? Was sind Mengen? Wie kann man die Elemente einer Menge darstellen? Welche Beziehung zwischen Mengen haben wir
Grundlagen der Logik
 Grundlagen der Logik Denken Menschen logisch? Selektionsaufgabe nach Watson (1966): Gegeben sind vier Karten von denen jede auf der einen Seite mit einem Buchstaben, auf der anderen Seite mit einer Zahl
Grundlagen der Logik Denken Menschen logisch? Selektionsaufgabe nach Watson (1966): Gegeben sind vier Karten von denen jede auf der einen Seite mit einem Buchstaben, auf der anderen Seite mit einer Zahl
Linguistische Grundlagen 6. Semantik
 Linguistische Grundlagen 6. Semantik Gereon Müller Institut für Linguistik Universität Leipzig www.uni-leipzig.de/ muellerg Gereon Müller (Institut für Linguistik) 04-006-1001: Linguistische Grundlagen
Linguistische Grundlagen 6. Semantik Gereon Müller Institut für Linguistik Universität Leipzig www.uni-leipzig.de/ muellerg Gereon Müller (Institut für Linguistik) 04-006-1001: Linguistische Grundlagen
Mathematische und logische Grundlagen der Linguistik. Kapitel 3: Grundbegriffe der Aussagenlogik
 Mathematische und logische Grundlagen der Linguistik Kapitel 3: Grundbegriffe der Aussagenlogik Grundbegriffe der Aussagenlogik 1 Die Aussagenlogik ist ein Zweig der formalen Logik, der die Beziehungen
Mathematische und logische Grundlagen der Linguistik Kapitel 3: Grundbegriffe der Aussagenlogik Grundbegriffe der Aussagenlogik 1 Die Aussagenlogik ist ein Zweig der formalen Logik, der die Beziehungen
Mathematische und logische Grundlagen der Linguistik. Mathematische und logische Grundlagen der Linguistik. Karl Heinz Wagner. Hier Titel eingeben 1
 Grundbegriffe der Aussagenlogik 1 Mathematische und logische Grundlagen der Linguistik Kapitel 3: Grundbegriffe der Aussagenlogik Die Aussagenlogik ist ein Zweig der formalen Logik, der die Beziehungen
Grundbegriffe der Aussagenlogik 1 Mathematische und logische Grundlagen der Linguistik Kapitel 3: Grundbegriffe der Aussagenlogik Die Aussagenlogik ist ein Zweig der formalen Logik, der die Beziehungen
Satzsemantik. Semantik und Pragmatik. Satzsemantik. Satzsemantik
 Satzsemantik 8. Mai 2007 Gerhard Jäger Erklärungsanspruch der Satzsemantik Wahrheitsbedingungen von Aussagensätzen Bedeutungsbeziehungen zwischen (Aussage-)Sätzen Kompositionale Berechnung von Satzbedeutungen
Satzsemantik 8. Mai 2007 Gerhard Jäger Erklärungsanspruch der Satzsemantik Wahrheitsbedingungen von Aussagensätzen Bedeutungsbeziehungen zwischen (Aussage-)Sätzen Kompositionale Berechnung von Satzbedeutungen
Ein und derselbe Satz kann in Bezug auf unterschiedliche Situationen s 1. und s 2 unterschiedliche Wahrheitswerte haben.
 2 Aussagenlogik () 2.3 Semantik von [ Gamut 4-58, Partee 7-4 ] Ein und derselbe Satz kann in Bezug auf unterschiedliche Situationen s und s 2 unterschiedliche Wahrheitswerte haben. Beispiel: Es regnet.
2 Aussagenlogik () 2.3 Semantik von [ Gamut 4-58, Partee 7-4 ] Ein und derselbe Satz kann in Bezug auf unterschiedliche Situationen s und s 2 unterschiedliche Wahrheitswerte haben. Beispiel: Es regnet.
Semantik und Pragmatik
 1/17 Semantik und Pragmatik 15. Mai 2006 Gerhard Jäger Satzsemantik 2/17 Erklärungsanspruch der Satzsemantik Wahrheitsbedingungen von Aussagensätzen Bedeutungsbeziehungen zwischen (Aussage-)Sätzen Kompositionale
1/17 Semantik und Pragmatik 15. Mai 2006 Gerhard Jäger Satzsemantik 2/17 Erklärungsanspruch der Satzsemantik Wahrheitsbedingungen von Aussagensätzen Bedeutungsbeziehungen zwischen (Aussage-)Sätzen Kompositionale
7 Bedeutung und Logik
 7 Bedeutung und Logik 7.1 Logische Eigenschaften von Sätzen 7.2 Logische Beziehungen zwischen Sätzen 7.3 Logische Beziehungen und Bedeutungsbeziehungen 7.4 Formale Semantik Johannes Dölling: Semantik und
7 Bedeutung und Logik 7.1 Logische Eigenschaften von Sätzen 7.2 Logische Beziehungen zwischen Sätzen 7.3 Logische Beziehungen und Bedeutungsbeziehungen 7.4 Formale Semantik Johannes Dölling: Semantik und
Semantik und Pragmatik
 Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 3, 29. April 2005 Gerhard Jäger Semantik und Pragmatik p.1/26 Übersetzung Deutsch Aussagenlogik Motivation für Übersetzung: Deutsch als Objektsprache:
Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 3, 29. April 2005 Gerhard Jäger Semantik und Pragmatik p.1/26 Übersetzung Deutsch Aussagenlogik Motivation für Übersetzung: Deutsch als Objektsprache:
Einführung in die Semantik, 5. Sitzung Aussagenlogik
 Einführung in die, 5. Sitzung Aussagenlogik Göttingen 9. November 2006 Aussagenlogik Warum die formalen Sprachen der Logik? formale Sprachen haben wie jede Sprache ein Vokabular, eine und eine. Die Relation
Einführung in die, 5. Sitzung Aussagenlogik Göttingen 9. November 2006 Aussagenlogik Warum die formalen Sprachen der Logik? formale Sprachen haben wie jede Sprache ein Vokabular, eine und eine. Die Relation
Diskrete Strukturen. Sebastian Thomas RWTH Aachen https://www2.math.rwth-aachen.de/ds17/ Mathematische Logik
 Diskrete Strukturen Sebastian Thomas RWTH Aachen https://www2.math.rwth-aachen.de/ds17/ Mathematische Logik Aussagen Begriff Aussage: Ausdruck, welcher entweder wahr oder falsch ist e Die RWTH Aachen hat
Diskrete Strukturen Sebastian Thomas RWTH Aachen https://www2.math.rwth-aachen.de/ds17/ Mathematische Logik Aussagen Begriff Aussage: Ausdruck, welcher entweder wahr oder falsch ist e Die RWTH Aachen hat
Typengetriebene Interpretation. Arnim von Stechow Einführung in die Semantik
 Typengetriebene Interpretation Arnim von Stechow Einführung in die Semantik arnim.stechow@uni-tuebingen.de Programm Logische Typen Typengesteuerte Interpretation λ-schreibweise Prädikatsmodifikation (PM)
Typengetriebene Interpretation Arnim von Stechow Einführung in die Semantik arnim.stechow@uni-tuebingen.de Programm Logische Typen Typengesteuerte Interpretation λ-schreibweise Prädikatsmodifikation (PM)
Semantik einiger Konjunktionen. Arnim von Stechow Einführung in die Semantik
 Semantik einiger Konjunktionen Arnim von Stechow Einführung in die Semantik Programm Syntax und Semantik einiger AL-Junktoren Epistemisches müssen und können Strukturellen Mehrdeutigkeiten Extensionale
Semantik einiger Konjunktionen Arnim von Stechow Einführung in die Semantik Programm Syntax und Semantik einiger AL-Junktoren Epistemisches müssen und können Strukturellen Mehrdeutigkeiten Extensionale
Aussagenlogik. Übersicht: 1 Teil 1: Syntax und Semantik. 2 Teil 2: Modellierung und Beweise. Aussagenlogik H. Kleine Büning 1/25
 Aussagenlogik Übersicht: 1 Teil 1: Syntax und Semantik 2 Teil 2: Modellierung und Beweise Aussagenlogik H. Kleine Büning 1/25 Einführendes Beispiel Falls Lisa Peter trifft, dann trifft Lisa auch Gregor.
Aussagenlogik Übersicht: 1 Teil 1: Syntax und Semantik 2 Teil 2: Modellierung und Beweise Aussagenlogik H. Kleine Büning 1/25 Einführendes Beispiel Falls Lisa Peter trifft, dann trifft Lisa auch Gregor.
Formale Methoden 2. Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016
 Formale Methoden 2 Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016 Teil 2: Logik 1 Prädikatenlogik (Einleitung) 2 Aussagenlogik Motivation Grundlagen Eigenschaften Eigenschaften Normalformen
Formale Methoden 2 Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016 Teil 2: Logik 1 Prädikatenlogik (Einleitung) 2 Aussagenlogik Motivation Grundlagen Eigenschaften Eigenschaften Normalformen
Nur Aussagesätze, d.h. Deklarativ-, nicht aber Frage- oder Aufforderungs-sätze bringen das Zutreffen einer Aussage (oder Proposition) zum Ausdruck.
 2 Aussagenlogik (AL) 2. Wahrheitsfunktionale Konnektoren Nur Aussagesätze, d.h. Deklarativ-, nicht aber Frage- oder Aufforderungs-sätze bringen das Zutreffen einer Aussage (oder Proposition) zum Ausdruck.
2 Aussagenlogik (AL) 2. Wahrheitsfunktionale Konnektoren Nur Aussagesätze, d.h. Deklarativ-, nicht aber Frage- oder Aufforderungs-sätze bringen das Zutreffen einer Aussage (oder Proposition) zum Ausdruck.
ÜBUNG ZUM GRUNDKURS LOGIK WS 2015/16 GÜNTHER EDER
 ÜBUNG ZUM GRUNDKURS LOGIK WS 2015/16 GÜNTHER EDER WIEDERHOLUNG: SPRACHE DER PL Die Sprache der PL enthält (1) Einfache Individuenterme: Individuenkonstanten (a, b, c, ) und Individuenvariablen (x, y, z,
ÜBUNG ZUM GRUNDKURS LOGIK WS 2015/16 GÜNTHER EDER WIEDERHOLUNG: SPRACHE DER PL Die Sprache der PL enthält (1) Einfache Individuenterme: Individuenkonstanten (a, b, c, ) und Individuenvariablen (x, y, z,
Aussagen (und damit indirekt auch Aussagesätze) können wahr oder falsch sein. Wahr und falsch sind Wahrheitswerte von Aussagen.
 2 Aussagenlogik (AL) 2 Aussagenlogik (AL) 2. Wahrheitsfunktionale Konnektoren [ Gamut 28-35, Partee -6 ] Nur Aussagesätze, d.h. Deklarativ-, nicht aber Frage- oder Aufforderungssätze bringen das Zutreffen
2 Aussagenlogik (AL) 2 Aussagenlogik (AL) 2. Wahrheitsfunktionale Konnektoren [ Gamut 28-35, Partee -6 ] Nur Aussagesätze, d.h. Deklarativ-, nicht aber Frage- oder Aufforderungssätze bringen das Zutreffen
Formale Methoden II. Gerhard Jäger. SS 2008 Universität Bielefeld. Teil 1, 16. April Formale Methoden II p.1/30
 Formale Methoden II SS 2008 Universität Bielefeld Teil 1, 16. April 2008 Gerhard Jäger Formale Methoden II p.1/30 Sätze und Aussagen (1) Schon wieder Verona Feldbusch! (2) Hat die Vorlesung schon angefangen?
Formale Methoden II SS 2008 Universität Bielefeld Teil 1, 16. April 2008 Gerhard Jäger Formale Methoden II p.1/30 Sätze und Aussagen (1) Schon wieder Verona Feldbusch! (2) Hat die Vorlesung schon angefangen?
Lösungen 1 zum Mathematik-Brückenkurs für alle, die sich für Mathematik interessieren
 Lösungen 1 zum Mathematik-Brückenkurs für alle, die sich für Mathematik interessieren µfsr, TU Dresden Version vom 11. Oktober 2016, Fehler, Ideen, Anmerkungen und Verbesserungsvorschläge bitte an benedikt.bartsch@myfsr.de
Lösungen 1 zum Mathematik-Brückenkurs für alle, die sich für Mathematik interessieren µfsr, TU Dresden Version vom 11. Oktober 2016, Fehler, Ideen, Anmerkungen und Verbesserungsvorschläge bitte an benedikt.bartsch@myfsr.de
7 Bedeutung und Logik
 7.1 Logische Eigenschaften von Sätzen 7.2 Logische Beziehungen zwischen Sätzen 7.3 Logische Beziehungen und Bedeutungsbeziehungen 7.4 Formale Semantik 7.1 Logische Eigenschaften von Sätzen Ein Satz φ ist
7.1 Logische Eigenschaften von Sätzen 7.2 Logische Beziehungen zwischen Sätzen 7.3 Logische Beziehungen und Bedeutungsbeziehungen 7.4 Formale Semantik 7.1 Logische Eigenschaften von Sätzen Ein Satz φ ist
Logik I. Symbole, Terme, Formeln
 Logik I Symbole, Terme, Formeln Wie jede geschriebene Sprache basiert die Prädikatenlogik erster Stufe auf einem Alphabet, welches aus den folgenden Symbolen besteht: (a) Variabeln wie zum Beispiel v 0,v
Logik I Symbole, Terme, Formeln Wie jede geschriebene Sprache basiert die Prädikatenlogik erster Stufe auf einem Alphabet, welches aus den folgenden Symbolen besteht: (a) Variabeln wie zum Beispiel v 0,v
2.2.4 Logische Äquivalenz
 2.2.4 Logische Äquivalenz (I) Penélope raucht nicht und sie trinkt nicht. (II) Es ist nicht der Fall, dass Penélope raucht oder trinkt. Offenbar behaupten beide Aussagen denselben Sachverhalt, sie unterscheiden
2.2.4 Logische Äquivalenz (I) Penélope raucht nicht und sie trinkt nicht. (II) Es ist nicht der Fall, dass Penélope raucht oder trinkt. Offenbar behaupten beide Aussagen denselben Sachverhalt, sie unterscheiden
Syntax. 1 Jedes A AS AL ist eine (atomare) Formel. 2 Ist F eine Formel, so ist auch F eine Formel. 3 Sind F und G Formeln, so sind auch
 Formale der Informatik 1 Kapitel 15 Folgerbarkeit, Äquivalenzen und Normalformen Frank Heitmann heitmann@informatik.uni-hamburg.de 8. Juni 2015 Syntax Definition (Syntax der Aussagenlogik) Mit AS AL sei
Formale der Informatik 1 Kapitel 15 Folgerbarkeit, Äquivalenzen und Normalformen Frank Heitmann heitmann@informatik.uni-hamburg.de 8. Juni 2015 Syntax Definition (Syntax der Aussagenlogik) Mit AS AL sei
1 Aussagenlogik. 1.1 Aussagen. 15 ist eine Primzahl. 3 < 8 x < 15 (hängt von x ab, keine Aussage) Aussage = Behauptung Beispiele: Es regnet.
 Grundlagen der Mathematik für Informatiker 1 1 Aussagenlogik 1.1 Aussagen Aussage = Behauptung Beispiele: Es regnet. Die Straße ist naß. 15 ist eine Primzahl. 3 < 8 x < 15 (hängt von x ab, keine Aussage)
Grundlagen der Mathematik für Informatiker 1 1 Aussagenlogik 1.1 Aussagen Aussage = Behauptung Beispiele: Es regnet. Die Straße ist naß. 15 ist eine Primzahl. 3 < 8 x < 15 (hängt von x ab, keine Aussage)
Jeder Aussage p kann ein Wahrheitswert W(p) {0, 1} zugeordnet werden. Beispiele: W(Es regnet.) =? (je nach Lage der Dinge) W(Die Straße ist naß.) =?
 Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 2 1 Aussagenlogik 1.1 Aussagen Aussage = Behauptung Beispiele: Es regnet. Die Straße ist naß. 15 ist eine Primzahl.
Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 2 1 Aussagenlogik 1.1 Aussagen Aussage = Behauptung Beispiele: Es regnet. Die Straße ist naß. 15 ist eine Primzahl.
Aussagenlogik: Lexikon, Syntax und Semantik
 Einführung in die Logik - 2 Aussagenlogik: Lexikon, Syntax und Semantik Wiederholung: Was ist Logik? Logik : Die Lehre» vom formal korrekten Schließen» von den Wahrheitsbedingungen von Sätzen Unter welchen
Einführung in die Logik - 2 Aussagenlogik: Lexikon, Syntax und Semantik Wiederholung: Was ist Logik? Logik : Die Lehre» vom formal korrekten Schließen» von den Wahrheitsbedingungen von Sätzen Unter welchen
Mathematische Grundlagen der Computerlinguistik
 Mengen und Mengenoperationen (Teil I) Centrum für Informations- und Sprachverarbeitung (CIS) 2. Juni 2014 Table of Contents Mengen und ihre Darstellung Darstellung endlicher Mengen Darstellung unendlicher
Mengen und Mengenoperationen (Teil I) Centrum für Informations- und Sprachverarbeitung (CIS) 2. Juni 2014 Table of Contents Mengen und ihre Darstellung Darstellung endlicher Mengen Darstellung unendlicher
Was ist Logik? Was ist Logik? Aussagenlogik. Wahrheitstabellen. Geschichte der Logik eng verknüpft mit Philosophie
 Was ist Logik? Geschichte der Logik eng verknüpft mit Philosophie Begriff Logik wird im Alltag vielseitig verwendet Logik untersucht, wie man aus Aussagen andere Aussagen ableiten kann Beschränkung auf
Was ist Logik? Geschichte der Logik eng verknüpft mit Philosophie Begriff Logik wird im Alltag vielseitig verwendet Logik untersucht, wie man aus Aussagen andere Aussagen ableiten kann Beschränkung auf
Theorie der Informatik. Theorie der Informatik. 2.1 Äquivalenzen. 2.2 Vereinfachte Schreibweise. 2.3 Normalformen. 2.
 Theorie der Informatik 24. Februar 2014 2. Aussagenlogik II Theorie der Informatik 2. Aussagenlogik II 2.1 Äquivalenzen Malte Helmert Gabriele Röger 2.2 Vereinfachte Schreibweise Universität Basel 24.
Theorie der Informatik 24. Februar 2014 2. Aussagenlogik II Theorie der Informatik 2. Aussagenlogik II 2.1 Äquivalenzen Malte Helmert Gabriele Röger 2.2 Vereinfachte Schreibweise Universität Basel 24.
1 Aussagenlogik. 1.1 Aussagen. 15 ist eine Primzahl. 3 < 8 x < 15 (hängt von x ab, keine Aussage) Aussage = Behauptung Beispiele: Es regnet.
 Grundlagen der Mathematik für Informatiker 1 1 Aussagenlogik 1.1 Aussagen Aussage = Behauptung Beispiele: Es regnet. Die Straße ist naß. 15 ist eine Primzahl. 3 < 8 x < 15 (hängt von x ab, keine Aussage)
Grundlagen der Mathematik für Informatiker 1 1 Aussagenlogik 1.1 Aussagen Aussage = Behauptung Beispiele: Es regnet. Die Straße ist naß. 15 ist eine Primzahl. 3 < 8 x < 15 (hängt von x ab, keine Aussage)
Tilman Bauer. 4. September 2007
 Universität Münster 4. September 2007 und Sätze nlogik von Organisatorisches Meine Koordinaten: Sprechstunden: Di 13:30-14:30 Do 9:00-10:00 tbauer@uni-muenster.de Zimmer 504, Einsteinstr. 62 (Hochhaus)
Universität Münster 4. September 2007 und Sätze nlogik von Organisatorisches Meine Koordinaten: Sprechstunden: Di 13:30-14:30 Do 9:00-10:00 tbauer@uni-muenster.de Zimmer 504, Einsteinstr. 62 (Hochhaus)
Einführung in die Semantik, 8. Sitzung Typentheorie, F deutsch
 Einführung in die Semantik, 8. Sitzung, F deutsch Göttingen 1. Dezember 2006 Einführung in die Semantik, 8. Sitzung, F deutsch Semantik von F deutsch Satzoperatoren Negation Konjunktion und Disjunktion
Einführung in die Semantik, 8. Sitzung, F deutsch Göttingen 1. Dezember 2006 Einführung in die Semantik, 8. Sitzung, F deutsch Semantik von F deutsch Satzoperatoren Negation Konjunktion und Disjunktion
Lineare Algebra I. Anhang. A Relationen. Heinz H. GONSKA, Maria D. RUSU, Michael WOZNICZKA. Wintersemester 2009/10
 Fakultät für Mathematik Fachgebiet Mathematische Informatik Anhang Lineare Algebra I Heinz H. GONSKA, Maria D. RUSU, Michael WOZNICZKA Wintersemester 2009/10 A Relationen Definition A.1. Seien X, Y beliebige
Fakultät für Mathematik Fachgebiet Mathematische Informatik Anhang Lineare Algebra I Heinz H. GONSKA, Maria D. RUSU, Michael WOZNICZKA Wintersemester 2009/10 A Relationen Definition A.1. Seien X, Y beliebige
2 Theorie der semantischen Typen
 2 Theorie der semantischen Typen 2 Theorie der semantischen Typen [ Dowty 83-97, Gamut 75-9, Partee 338-34] 2. Typen Eine mögliche Erweiterung von PL ist die Prädikatenlogik der 2. Stufe (PL2). In PL2
2 Theorie der semantischen Typen 2 Theorie der semantischen Typen [ Dowty 83-97, Gamut 75-9, Partee 338-34] 2. Typen Eine mögliche Erweiterung von PL ist die Prädikatenlogik der 2. Stufe (PL2). In PL2
Semantik und Pragmatik
 Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 4, 6. Mai 2005 Gerhard Jäger Semantik und Pragmatik p.1/35 Prädikatenlogik: atomare Formeln Syntax JO, BERTIE, ETHEL, THE-CAKE... sind Individuenkonstanten
Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 4, 6. Mai 2005 Gerhard Jäger Semantik und Pragmatik p.1/35 Prädikatenlogik: atomare Formeln Syntax JO, BERTIE, ETHEL, THE-CAKE... sind Individuenkonstanten
Logic in a Nutshell. Christian Liguda
 Logic in a Nutshell Christian Liguda Quelle: Kastens, Uwe und Büning, Hans K., Modellierung: Grundlagen und formale Methoden, 2009, Carl Hanser Verlag Übersicht Logik - Allgemein Aussagenlogik Modellierung
Logic in a Nutshell Christian Liguda Quelle: Kastens, Uwe und Büning, Hans K., Modellierung: Grundlagen und formale Methoden, 2009, Carl Hanser Verlag Übersicht Logik - Allgemein Aussagenlogik Modellierung
Grundlagen der Theoretischen Informatik
 FH Wedel Prof. Dr. Sebastian Iwanowski GTI22 Folie 1 Grundlagen der Theoretischen Informatik Sebastian Iwanowski FH Wedel Kap. 2: Logik, Teil 2.2: Prädikatenlogik FH Wedel Prof. Dr. Sebastian Iwanowski
FH Wedel Prof. Dr. Sebastian Iwanowski GTI22 Folie 1 Grundlagen der Theoretischen Informatik Sebastian Iwanowski FH Wedel Kap. 2: Logik, Teil 2.2: Prädikatenlogik FH Wedel Prof. Dr. Sebastian Iwanowski
Grundkurs Semantik. Sitzung 3: Mengenlehre. Andrew Murphy
 Grundkurs Semantik Sitzung 3: Mengenlehre Andrew Murphy andrew.murphy@uni-leizpig.de Grundkurs Semantik HU Berlin, Sommersemester 2015 http://www.uni-leipzig.de/ murphy/semantik15 15. Mai 2015 Basiert
Grundkurs Semantik Sitzung 3: Mengenlehre Andrew Murphy andrew.murphy@uni-leizpig.de Grundkurs Semantik HU Berlin, Sommersemester 2015 http://www.uni-leipzig.de/ murphy/semantik15 15. Mai 2015 Basiert
THEORETISCHE INFORMATIK UND LOGIK
 Rückblick: Logelei Wir kehren zurück auf das Inselreich mit Menschen von Typ W (Wahrheitssager) und Typ L (Lügner). THEORETISCHE INFORMATIK UND LOGIK 14. Vorlesung: Modelltheorie und logisches Schließen
Rückblick: Logelei Wir kehren zurück auf das Inselreich mit Menschen von Typ W (Wahrheitssager) und Typ L (Lügner). THEORETISCHE INFORMATIK UND LOGIK 14. Vorlesung: Modelltheorie und logisches Schließen
Die neue Prädikatenlogik P2
 Joachim Stiller Die neue Prädikatenlogik P2 Versuch einer Begründung Alle Rechte vorbehalten Die neue Prädikatenlogik P2 In diesem Aufsatz möchte ich einmal versuchen, meine neue Prädikatenlogik P2 zu
Joachim Stiller Die neue Prädikatenlogik P2 Versuch einer Begründung Alle Rechte vorbehalten Die neue Prädikatenlogik P2 In diesem Aufsatz möchte ich einmal versuchen, meine neue Prädikatenlogik P2 zu
Natürliche Sprachen sind durch Ambiguitäten und Vagheiten beim Ausdruck von Denkinhalten charakterisiert.
 1 Einführung 1.1 Logik und Linguistik Natürliche Sprachen sind durch Ambiguitäten und Vagheiten beim Ausdruck von Denkinhalten charakterisiert. In der mathematischen, formalen Logik werden formale Sprachen,
1 Einführung 1.1 Logik und Linguistik Natürliche Sprachen sind durch Ambiguitäten und Vagheiten beim Ausdruck von Denkinhalten charakterisiert. In der mathematischen, formalen Logik werden formale Sprachen,
LÖSUNGEN ZU AUFGABE (41)
 DGB 40 Universität Athen, WiSe 2012-13 Winfried Lechner Handout #3 LÖSUNGEN ZU AUFGABE (41) 1. WIEDERHOLUNG: PARAPHRASEN, SITUATIONEN UND AMBIGUITÄT Ein Satz Σ ist ambig, wenn Σ mehr als eine Bedeutung
DGB 40 Universität Athen, WiSe 2012-13 Winfried Lechner Handout #3 LÖSUNGEN ZU AUFGABE (41) 1. WIEDERHOLUNG: PARAPHRASEN, SITUATIONEN UND AMBIGUITÄT Ein Satz Σ ist ambig, wenn Σ mehr als eine Bedeutung
Grundbegriffe für dreiwertige Logik
 Grundbegriffe für dreiwertige Logik Hans Kleine Büning Universität Paderborn 1.11.2011 1 Syntax und Semantik Die klassische Aussagenlogik mit den Wahrheitswerten falsch und wahr bezeichnen wir im weiteren
Grundbegriffe für dreiwertige Logik Hans Kleine Büning Universität Paderborn 1.11.2011 1 Syntax und Semantik Die klassische Aussagenlogik mit den Wahrheitswerten falsch und wahr bezeichnen wir im weiteren
1 K-Rahmen und K-Modelle
 Seminar: Einführung in die Modallogik (WS 15/16) Lehrender: Daniel Milne-Plückebaum, M.A. E-Mail: dmilne@uni-bielefeld.de Handout: K-Rahmen, K-Modelle & K-Wahrheitsbedingungen Im Folgenden werden wir uns
Seminar: Einführung in die Modallogik (WS 15/16) Lehrender: Daniel Milne-Plückebaum, M.A. E-Mail: dmilne@uni-bielefeld.de Handout: K-Rahmen, K-Modelle & K-Wahrheitsbedingungen Im Folgenden werden wir uns
Alphabet der Prädikatenlogik
 Relationen und Alphabet der Das Alphabet der besteht aus Individuenvariablen Dafür verwenden wir kleine Buchstaben vom Ende des deutschen Alphabets, auch indiziert, z. B. x, y, z, x 1, y 2,.... Individuenkonstanten
Relationen und Alphabet der Das Alphabet der besteht aus Individuenvariablen Dafür verwenden wir kleine Buchstaben vom Ende des deutschen Alphabets, auch indiziert, z. B. x, y, z, x 1, y 2,.... Individuenkonstanten
Semantik und Pragmatik
 Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 6, 20. Mai 2005 Gerhard Jäger Semantik und Pragmatik p.1/16 Typentheorie: Motivation Viele syntaktische Konstruktionen der natürlichen Sprachen
Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 6, 20. Mai 2005 Gerhard Jäger Semantik und Pragmatik p.1/16 Typentheorie: Motivation Viele syntaktische Konstruktionen der natürlichen Sprachen
THEORETISCHE INFORMATIK UND LOGIK
 THEORETISCHE INFORMATIK UND LOGIK 14. Vorlesung: Modelltheorie und logisches Schließen Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 31. Mai 2017 Rückblick: Logelei Wir kehren zurück auf
THEORETISCHE INFORMATIK UND LOGIK 14. Vorlesung: Modelltheorie und logisches Schließen Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 31. Mai 2017 Rückblick: Logelei Wir kehren zurück auf
Kapitel 1.0. Aussagenlogik: Einführung. Mathematische Logik (WS 2011/12) Kapitel 1.0: Aussagenlogik: Einführung 1/ 1
 Kapitel 1.0 Aussagenlogik: Einführung Mathematische Logik (WS 2011/12) Kapitel 1.0: Aussagenlogik: Einführung 1/ 1 Ziele der Aussagenlogik In der Aussagenlogik analysiert man die Wahrheitswerte zusammengesetzter
Kapitel 1.0 Aussagenlogik: Einführung Mathematische Logik (WS 2011/12) Kapitel 1.0: Aussagenlogik: Einführung 1/ 1 Ziele der Aussagenlogik In der Aussagenlogik analysiert man die Wahrheitswerte zusammengesetzter
Logik für Informatiker
 Vorlesung Logik für Informatiker 4. Aussagenlogik Syntax und Semantik der Aussagenlogik Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Syntax der Aussagenlogik:
Vorlesung Logik für Informatiker 4. Aussagenlogik Syntax und Semantik der Aussagenlogik Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Syntax der Aussagenlogik:
Logische Äquivalenz. Definition Beispiel 2.23
 Logische Äquivalenz Definition 2.22 Zwei aussagenlogische Formeln α, β A heißen logisch äquivalent, falls für jede Belegung I von α und β gilt: Schreibweise: α β. Beispiel 2.23 Aus Folgerung 2.6 ergibt
Logische Äquivalenz Definition 2.22 Zwei aussagenlogische Formeln α, β A heißen logisch äquivalent, falls für jede Belegung I von α und β gilt: Schreibweise: α β. Beispiel 2.23 Aus Folgerung 2.6 ergibt
Vorbereitungskurs Mathematik zum Sommersemester 2015 Aussagen, Logik und Beweistechniken
 Vorbereitungskurs Mathematik zum Sommersemester 2015 Aussagen, Logik und Beweistechniken Susanna Pohl Vorkurs Mathematik TU Dortmund 09.03.2015 Aussagen, Logik und Beweistechniken Aussagen und Logik Motivation
Vorbereitungskurs Mathematik zum Sommersemester 2015 Aussagen, Logik und Beweistechniken Susanna Pohl Vorkurs Mathematik TU Dortmund 09.03.2015 Aussagen, Logik und Beweistechniken Aussagen und Logik Motivation
4.1 Motivation. Theorie der Informatik. Theorie der Informatik. 4.1 Motivation. 4.2 Syntax der Prädikatenlogik. 4.3 Semantik der Prädikatenlogik
 Theorie der Informatik 3. März 2014 4. Prädikatenlogik I Theorie der Informatik 4. Prädikatenlogik I 4.1 Motivation Malte Helmert Gabriele Röger 4.2 Syntax der Prädikatenlogik Universität Basel 3. März
Theorie der Informatik 3. März 2014 4. Prädikatenlogik I Theorie der Informatik 4. Prädikatenlogik I 4.1 Motivation Malte Helmert Gabriele Röger 4.2 Syntax der Prädikatenlogik Universität Basel 3. März
Semantik und Pragmatik
 Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 9, 17. Juni 2005 Gerhard Jäger Semantik und Pragmatik p.1/31 Adverbien bisher kein wirklicher Fortschritt durch Übergang zu Typentheorie den selben
Semantik und Pragmatik SS 2005 Universität Bielefeld Teil 9, 17. Juni 2005 Gerhard Jäger Semantik und Pragmatik p.1/31 Adverbien bisher kein wirklicher Fortschritt durch Übergang zu Typentheorie den selben
Identität. Dr. Uwe Scheffler. Januar [Technische Universität Dresden]
![Identität. Dr. Uwe Scheffler. Januar [Technische Universität Dresden] Identität. Dr. Uwe Scheffler. Januar [Technische Universität Dresden]](/thumbs/95/125495871.jpg) Identität Dr. Uwe Scheffler [Technische Universität Dresden] Januar 2012 Freges Problem 1. Der Morgenstern ist der Morgenstern. 2. Der Morgenstern ist der Abendstern. 1. ist tautologisch. 2. ist nur in
Identität Dr. Uwe Scheffler [Technische Universität Dresden] Januar 2012 Freges Problem 1. Der Morgenstern ist der Morgenstern. 2. Der Morgenstern ist der Abendstern. 1. ist tautologisch. 2. ist nur in
Formale Logik. PD Dr. Markus Junker Abteilung für Mathematische Logik Universität Freiburg. Wintersemester 16/17 Sitzung vom 14.
 Formale Logik PD Dr. Markus Junker Abteilung für Mathematische Logik Universität Freiburg Wintersemester 16/17 Sitzung vom 14. Dezember 2016 Die formale Sprache der Prädikatenlogik: Zeichen Benutzt werden
Formale Logik PD Dr. Markus Junker Abteilung für Mathematische Logik Universität Freiburg Wintersemester 16/17 Sitzung vom 14. Dezember 2016 Die formale Sprache der Prädikatenlogik: Zeichen Benutzt werden
3.4 Direkte vs. indirekte Interpretation
 3 Theorie der λ -Repräsentation 3.4 Direkte vs. indirekte Interpretation In unserer semantischen Analyse natürlichsprachlicher Ausdrücke haben wir bisher die Methode der indirekten Interpretation zugrunde
3 Theorie der λ -Repräsentation 3.4 Direkte vs. indirekte Interpretation In unserer semantischen Analyse natürlichsprachlicher Ausdrücke haben wir bisher die Methode der indirekten Interpretation zugrunde
Sonst steht uns kein weiteres Symbol für die Bildung von AL-Formeln zur Verfügung.
 Seminar: Einführung in die Modallogik (WS 16/17) Lehrender: Daniel Milne-Plückebaum, M.A. E-Mail: dmilne@uni-bielefeld.de Handout: Syntax und Semantik der Aussagenlogik Die Syntax der Aussagenlogik Um
Seminar: Einführung in die Modallogik (WS 16/17) Lehrender: Daniel Milne-Plückebaum, M.A. E-Mail: dmilne@uni-bielefeld.de Handout: Syntax und Semantik der Aussagenlogik Die Syntax der Aussagenlogik Um
Formale Semantik. Anke Assmann Heim & Kratzer 1998, Kap. 2. Universität Leipzig, Institut für Linguistik
 1 / 52 Formale Semantik Heim & Kratzer 1998, Kap. 2 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.04.2013 2 / 52 Inhalt 1 Ein sanfter Einstieg 2 Ermittlung von
1 / 52 Formale Semantik Heim & Kratzer 1998, Kap. 2 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.04.2013 2 / 52 Inhalt 1 Ein sanfter Einstieg 2 Ermittlung von
TU7 Aussagenlogik II und Prädikatenlogik
 TU7 Aussagenlogik II und Prädikatenlogik Daniela Andrade daniela.andrade@tum.de 5.12.2016 1 / 32 Kleine Anmerkung Meine Folien basieren auf den DS Trainer von Carlos Camino, den ihr auf www.carlos-camino.de/ds
TU7 Aussagenlogik II und Prädikatenlogik Daniela Andrade daniela.andrade@tum.de 5.12.2016 1 / 32 Kleine Anmerkung Meine Folien basieren auf den DS Trainer von Carlos Camino, den ihr auf www.carlos-camino.de/ds
Einführung in die Logik
 Einführung in die Logik Klaus Madlener und Roland Meyer 24. April 2013 Inhaltsverzeichnis 1 Aussagenlogik 1 1.1 Syntax................................. 1 1.2 Semantik............................... 3 1.3
Einführung in die Logik Klaus Madlener und Roland Meyer 24. April 2013 Inhaltsverzeichnis 1 Aussagenlogik 1 1.1 Syntax................................. 1 1.2 Semantik............................... 3 1.3
Semantik. Sebastian Löbner. Eine Einführung. Walter de Gruyter Berlin New York 2003
 Sebastian Löbner 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Semantik Eine Einführung wde G Walter de Gruyter
Sebastian Löbner 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Semantik Eine Einführung wde G Walter de Gruyter
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 1 Logik,, Doris Bohnet Universität Hamburg - Department Mathematik Mo 6.10.2008 Zeitplan Tagesablauf: 9:15-11:45 Vorlesung Audimax I 13:00-14:30 Übung Übungsräume
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 1 Logik,, Doris Bohnet Universität Hamburg - Department Mathematik Mo 6.10.2008 Zeitplan Tagesablauf: 9:15-11:45 Vorlesung Audimax I 13:00-14:30 Übung Übungsräume
5. SITZUNG: AUSSAGENLOGIK
 5. SITZUNG: AUSSAGENLOGIK 1. Die Bedeutung komplexer Aussagen Die Bedeutung von atomaren Sätzen ist ein Wahrheitswert, welcher durch Überprüfung der Wahrheitsbedingungen relativ zu einer Situation ermittelt
5. SITZUNG: AUSSAGENLOGIK 1. Die Bedeutung komplexer Aussagen Die Bedeutung von atomaren Sätzen ist ein Wahrheitswert, welcher durch Überprüfung der Wahrheitsbedingungen relativ zu einer Situation ermittelt
Semantik. Anke Himmelreich Formale Semantik. Universität Leipzig, Institut für Linguistik 1 / 47
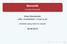 1 / 47 Semantik Formale Semantik Anke Himmelreich anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.06.2016 2 / 47 Inhaltsverzeichnis 1 Vorbemerkungen 2 Wahrheitskonditionale
1 / 47 Semantik Formale Semantik Anke Himmelreich anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.06.2016 2 / 47 Inhaltsverzeichnis 1 Vorbemerkungen 2 Wahrheitskonditionale
Klausur zur Vorlesung Mathematische Logik
 Universität Heidelberg 25. Januar 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Mathematische Logik LÖSUNGEN Aufgabe 1 (Aussagenlogik - 8 Punkte)
Universität Heidelberg 25. Januar 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Mathematische Logik LÖSUNGEN Aufgabe 1 (Aussagenlogik - 8 Punkte)
Grundbegriffe aus Logik und Mengenlehre
 Prof. Dr. B. Niethammer Dr. C. Seis, R. Schubert Institut fr Angewandte Mathematik Universitt Bonn Grundbegriffe aus Logik und Mengenlehre Wir wollen im Folgenden eine kurze Einführung in die Grundbegriffe
Prof. Dr. B. Niethammer Dr. C. Seis, R. Schubert Institut fr Angewandte Mathematik Universitt Bonn Grundbegriffe aus Logik und Mengenlehre Wir wollen im Folgenden eine kurze Einführung in die Grundbegriffe
Universität Heidelberg 12. April 2018 Institut für Informatik Klaus Ambos-Spies Nadine Losert. 2. Klausur zur Vorlesung Mathematische Logik
 Universität Heidelberg 12. April 2018 Institut für Informatik Klaus Ambos-Spies Nadine Losert 2. Klausur zur Vorlesung Mathematische Logik Es können maximal 48 Punkte erworben werden. Die Klausur ist bestanden,
Universität Heidelberg 12. April 2018 Institut für Informatik Klaus Ambos-Spies Nadine Losert 2. Klausur zur Vorlesung Mathematische Logik Es können maximal 48 Punkte erworben werden. Die Klausur ist bestanden,
Grundlagen der Programmierung
 GdP4 Slide 1 Grundlagen der Programmierung Vorlesung 4 vom 04.11.2004 Sebastian Iwanowski FH Wedel Grundlagen der Programmierung 1. Einführung Grundlegende Eigenschaften von Algorithmen und Programmen
GdP4 Slide 1 Grundlagen der Programmierung Vorlesung 4 vom 04.11.2004 Sebastian Iwanowski FH Wedel Grundlagen der Programmierung 1. Einführung Grundlegende Eigenschaften von Algorithmen und Programmen
4.3 NPn als Objekte oder als Prädikative
 4.3 NPn als Objekte oder als Prädikative 4.3.1 Quantifizierende NPn in Objektposition Steht eine quantifizierende NP nicht in Subjekt-, sondern in Objektposition, ist unter den bisher angenommenen Voraussetzungen
4.3 NPn als Objekte oder als Prädikative 4.3.1 Quantifizierende NPn in Objektposition Steht eine quantifizierende NP nicht in Subjekt-, sondern in Objektposition, ist unter den bisher angenommenen Voraussetzungen
Logik für Informatiker
 Vorlesung Logik für Informatiker 9. Prädikatenlogik Syntax und Semantik der Prädikatenlogik Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Syntax der
Vorlesung Logik für Informatiker 9. Prädikatenlogik Syntax und Semantik der Prädikatenlogik Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Syntax der
Vorsemesterkurs Informatik
 Vorsemesterkurs Informatik Ronja Düffel WS2018/19 01. Oktober 2018 Theoretische Informatik Wieso, weshalb, warum??!? 1 Modellieren und Formalisieren von Problemen und Lösungen 2 Verifikation (Beweis der
Vorsemesterkurs Informatik Ronja Düffel WS2018/19 01. Oktober 2018 Theoretische Informatik Wieso, weshalb, warum??!? 1 Modellieren und Formalisieren von Problemen und Lösungen 2 Verifikation (Beweis der
Mathematik-Vorkurs für Informatiker Aussagenlogik 1
 Christian Eisentraut & Julia Krämer www.vorkurs-mathematik-informatik.de Mathematik-Vorkurs für Informatiker Aussagenlogik 1 Aufgabe 1. (Wiederholung wichtiger Begriffe) Notieren Sie die Definitionen der
Christian Eisentraut & Julia Krämer www.vorkurs-mathematik-informatik.de Mathematik-Vorkurs für Informatiker Aussagenlogik 1 Aufgabe 1. (Wiederholung wichtiger Begriffe) Notieren Sie die Definitionen der
2. Theorie der Generalisierten Quantoren
 2. Theorie der Generalisierten Quantoren 2.1 Einleitung und Überblick Wie in Abschnitt 1.1 erläutert, kann man einen Quantor wie jed- als Relation zwischen zwei Mengen darstellen, bzw. eine quantifizierte
2. Theorie der Generalisierten Quantoren 2.1 Einleitung und Überblick Wie in Abschnitt 1.1 erläutert, kann man einen Quantor wie jed- als Relation zwischen zwei Mengen darstellen, bzw. eine quantifizierte
Syntax der Prädikatenlogik: Komplexe Formeln
 Syntax der Prädikatenlogik: Komplexe Formeln Σ = P, F eine prädikatenlogische Signatur Var eine Menge von Variablen Definition: Menge For Σ der Formeln über Σ Logik für Informatiker, SS 06 p.10 Syntax
Syntax der Prädikatenlogik: Komplexe Formeln Σ = P, F eine prädikatenlogische Signatur Var eine Menge von Variablen Definition: Menge For Σ der Formeln über Σ Logik für Informatiker, SS 06 p.10 Syntax
Mathem.Grundlagen der Computerlinguistik I, WS 2004/05, H. Leiß 1
 Mathem.Grundlagen der Computerlinguistik I, WS 2004/05, H. Leiß 1 1 Vorbemerkungen Mathematische Begriffe und Argumentationsweisen sind in vielen Fällen nötig, wo man über abstrakte Objekte sprechen und
Mathem.Grundlagen der Computerlinguistik I, WS 2004/05, H. Leiß 1 1 Vorbemerkungen Mathematische Begriffe und Argumentationsweisen sind in vielen Fällen nötig, wo man über abstrakte Objekte sprechen und
Einführung in die Semantik, 9. Sitzung Prädikate, definite NPs
 Einführung in die Semantik, 9. Sitzung Prädikate, definite NPs, Modifikatoren Göttingen 12. Dezember 2006 Prädikate Adjektive Präpositionalphrasen Attributive Adjektive Attributive Präpositionalphrasen
Einführung in die Semantik, 9. Sitzung Prädikate, definite NPs, Modifikatoren Göttingen 12. Dezember 2006 Prädikate Adjektive Präpositionalphrasen Attributive Adjektive Attributive Präpositionalphrasen
Logik für Informatiker
 Logik für Informatiker 2. Aussagenlogik Teil 4 7.05.2012 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Syntax der Aussagenlogik: Definition der Menge
Logik für Informatiker 2. Aussagenlogik Teil 4 7.05.2012 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Syntax der Aussagenlogik: Definition der Menge
Logik. Gabriele Kern-Isberner LS 1 Information Engineering. TU Dortmund Wintersemester 2014/15 WS 2014/15
 Logik Gabriele Kern-Isberner LS 1 Information Engineering TU Dortmund Wintersemester 2014/15 WS 2014/15 G. Kern-Isberner (TU Dortmund) Logik WS 2014/15 1 / 125 Übersicht Modallogik 5. Grundlagen 6. Erfüllbarkeit
Logik Gabriele Kern-Isberner LS 1 Information Engineering TU Dortmund Wintersemester 2014/15 WS 2014/15 G. Kern-Isberner (TU Dortmund) Logik WS 2014/15 1 / 125 Übersicht Modallogik 5. Grundlagen 6. Erfüllbarkeit
Übersichtsblatt Hertrampf/Bahrdt. 1 Mathematische Aussagen. Theoretische Informatik I WS2018/19
 Theoretische Informatik I WS2018/19 Übersichtsblatt Hertrampf/Bahrdt Institut für Formale Methoden der Informatik Theoretische Informatik Universität Stuttgart 1 Mathematische Aussagen Um mathematische
Theoretische Informatik I WS2018/19 Übersichtsblatt Hertrampf/Bahrdt Institut für Formale Methoden der Informatik Theoretische Informatik Universität Stuttgart 1 Mathematische Aussagen Um mathematische
Die Prädikatenlogik erster Stufe: Syntax und Semantik
 Die Prädikatenlogik erster Stufe: Syntax und Semantik 1 Mathematische Strukturen und deren Typen Definition 1.1 Eine Struktur A ist ein 4-Tupel A = (A; (R A i i I); (f A j j J); (c A k k K)) wobei I, J,
Die Prädikatenlogik erster Stufe: Syntax und Semantik 1 Mathematische Strukturen und deren Typen Definition 1.1 Eine Struktur A ist ein 4-Tupel A = (A; (R A i i I); (f A j j J); (c A k k K)) wobei I, J,
Logik für Informatiker
 Logik für Informatiker 2. Aussagenlogik Teil 2 28.04.2015 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Organisatorisches Termine Donnerstags: 30.04.2015 nicht
Logik für Informatiker 2. Aussagenlogik Teil 2 28.04.2015 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Organisatorisches Termine Donnerstags: 30.04.2015 nicht
Die Logik der Sprache PL
 II Die Logik der Sprache PL 16 Der Aufbau der Sprache PL Ein Beispiel Problem (1) Alle Menschen sind sterblich. Sokrates ist ein Mensch. Also: Sokrates ist sterblich. Intuitiv ist dieses Argument gültig.
II Die Logik der Sprache PL 16 Der Aufbau der Sprache PL Ein Beispiel Problem (1) Alle Menschen sind sterblich. Sokrates ist ein Mensch. Also: Sokrates ist sterblich. Intuitiv ist dieses Argument gültig.
Musterlösung Übungsblatt 1 ( )
 Seminar: Formale Semantik Modul 04-006-1006: Grammatiktheorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 1 (16.04.2013) Abgabe bis 26.04.2013 Institut für Linguistik Universität Leipzig 1 Funktionen
Seminar: Formale Semantik Modul 04-006-1006: Grammatiktheorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 1 (16.04.2013) Abgabe bis 26.04.2013 Institut für Linguistik Universität Leipzig 1 Funktionen
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 7 Sprachen erster Sufe Die in der letzten Vorlesung erwähnten Konstruktionsmöglichkeiten für Aussagen sind im Wesentlichen
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 7 Sprachen erster Sufe Die in der letzten Vorlesung erwähnten Konstruktionsmöglichkeiten für Aussagen sind im Wesentlichen
Musterlösung Übungsblatt 6 ( )
 Seminar: Formale Semantik Modul 04-006-1006: Grammatikorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 6 (05.06.2013) Abgabe bis 14.06.2013 Institut für Linguistik Universität Leipzig Hinweis:
Seminar: Formale Semantik Modul 04-006-1006: Grammatikorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 6 (05.06.2013) Abgabe bis 14.06.2013 Institut für Linguistik Universität Leipzig Hinweis:
Zweite und dritte Sitzung
 Zweite und dritte Sitzung Mengenlehre und Prinzipien logischer Analyse Menge Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohlunterschiedenen Objekten unserer Anschauung und unseres Denkens
Zweite und dritte Sitzung Mengenlehre und Prinzipien logischer Analyse Menge Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohlunterschiedenen Objekten unserer Anschauung und unseres Denkens
Geschichte der Logik ist eng verknüpft mit (Sprach-) Philosophie. Logik untersucht, wie aus wahren Aussagen andere wahre Aussagen folgen
 Was ist Logik? Geschichte der Logik ist eng verknüpft mit (Sprach-) Philosophie Logik untersucht, wie aus wahren Aussagen andere wahre Aussagen folgen Beschränkung auf "Aussage A folgt nach einer gegebenen
Was ist Logik? Geschichte der Logik ist eng verknüpft mit (Sprach-) Philosophie Logik untersucht, wie aus wahren Aussagen andere wahre Aussagen folgen Beschränkung auf "Aussage A folgt nach einer gegebenen
1 Einführung Aussagenlogik
 1 Einführung Aussagenlogik Denition 1. Eine Aussage ist ein Aussagesatz, der entweder wahr oder falsch ist. Welche der folgenden Sätze ist eine Aussage? 3+4=7 2*3=9 Angela Merkel ist Kanzlerin Stillgestanden!
1 Einführung Aussagenlogik Denition 1. Eine Aussage ist ein Aussagesatz, der entweder wahr oder falsch ist. Welche der folgenden Sätze ist eine Aussage? 3+4=7 2*3=9 Angela Merkel ist Kanzlerin Stillgestanden!
5.2 Logische Gültigkeit, Folgerung, Äquivalenz
 5.2 Logische Gültigkeit, Folgerung, Äquivalenz Durch Einsetzung von PL1-Formeln für die Metavariablen in AL-Gesetzen erhält man PL1-Instanzen von AL-Gesetzen. Beispiele: φ φ AL PL1-Instanzen: Pa () Pa
5.2 Logische Gültigkeit, Folgerung, Äquivalenz Durch Einsetzung von PL1-Formeln für die Metavariablen in AL-Gesetzen erhält man PL1-Instanzen von AL-Gesetzen. Beispiele: φ φ AL PL1-Instanzen: Pa () Pa
Wahrheitswertesemantik Einführung Aussagenlogik
 Wahrheitsbedingungen Wahrheitswertesemantik Einführung Aussagenlogik Sie haben sich in der ersten Sitzung mit verschiedenen Aspekten von Bedeutung auseinandergesetzt. Ein Aspekt, der dabei eine Rolle spielte,
Wahrheitsbedingungen Wahrheitswertesemantik Einführung Aussagenlogik Sie haben sich in der ersten Sitzung mit verschiedenen Aspekten von Bedeutung auseinandergesetzt. Ein Aspekt, der dabei eine Rolle spielte,
Kapitel 1. Aussagenlogik
 Kapitel 1 Aussagenlogik Einführung Mathematische Logik (WS 2012/13) Kapitel 1: Aussagenlogik 1/17 Übersicht Teil I: Syntax und Semantik der Aussagenlogik (1.0) Junktoren und Wahrheitsfunktionen (1.1) Syntax
Kapitel 1 Aussagenlogik Einführung Mathematische Logik (WS 2012/13) Kapitel 1: Aussagenlogik 1/17 Übersicht Teil I: Syntax und Semantik der Aussagenlogik (1.0) Junktoren und Wahrheitsfunktionen (1.1) Syntax
2.2.2 Semantik von TL. Menge der Domänen. Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs.
 2.2.2 Semantik von TL Menge der Domänen Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs. Diese Menge wird Domäne des betreffenden Typs genannt. Johannes Dölling: Formale
2.2.2 Semantik von TL Menge der Domänen Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs. Diese Menge wird Domäne des betreffenden Typs genannt. Johannes Dölling: Formale
1.1 Motivation. Theorie der Informatik. Theorie der Informatik. 1.1 Motivation. 1.2 Syntax. 1.3 Semantik. 1.4 Formeleigenschaften. 1.
 Theorie der Informatik 19. Februar 2014 1. Aussagenlogik I Theorie der Informatik 1. Aussagenlogik I Malte Helmert Gabriele Röger Universität Basel 19. Februar 2014 1.1 Motivation 1.2 Syntax 1.3 Semantik
Theorie der Informatik 19. Februar 2014 1. Aussagenlogik I Theorie der Informatik 1. Aussagenlogik I Malte Helmert Gabriele Röger Universität Basel 19. Februar 2014 1.1 Motivation 1.2 Syntax 1.3 Semantik
