Kalorimetrische Messungen
|
|
|
- Alwin Seidel
- vor 9 Jahren
- Abrufe
Transkript
1 Kalorimetrische Messungen 1 Kalorimetrische Messungen Durch Verfolgen des Temperaturverlaufs in einem Kalorimeter sollen die spezifische Wärmekapazität von Kupfer, die Schmelzwärme von Eis sowie die Lösungswärmen zweier Salze bestimmt werden. Aus dem Vergleich der Lösungswärmen wasserfreier und kristallwasserhaltiger Spezies kann die Hydratationswärme bestimmt werden. Stichworte Energie, Enthalpie, 1. Hauptsatz der Thermodynamik, Wärmekapazität, Temperatur, Temperaturmessung, Volumenarbeit, Wärme, Schmelzwärme, Hydratationswärme, Lösungswärme Experimentelle Bestimmung von Wärmemengen Kalorimetrische Messungen dienen zur Bestimmung von Wärmemengen, die von Substanzen unter konstanten äußeren Bedingungen aufgenommen werden, wenn diese entweder ihre Temperatur ändern (spezifische Wärme) oder sich selbst ändern (Wärmetönungen). Außerdem können in der Kalorimetrie Energien nicht thermischer Art (z.b. Strahlungsenergien) indirekt gemessen werden, wenn man den Grad der Umwandlung solcher Energieformen in Wärme kennt. Die empfohlene Einheit der Wärmemenge Q ist das Joule ( J ): 1 J = 1 VAs = 1/4,184 cal (1) Die alte Wärmeeinheit Kalorie (cal) ist durch (1) neu definiert. Bei allen kalorimetrischen Messungen ist der Wärmeaustausch des Kalorimeters mit seiner Umgebung zu kontrollieren. Bei den isothermen und adiabatischen Kalorimetern wird der Wärmeverlust experimentell weitgehend ausgeschaltet. Bei den isoperibolen Erwärmungskalorimetern in temperaturkonstanter Umgebung (Temperatur T 0 ) muss der Wärmeverlust rechnerisch oder graphisch ermittelt werden. Ein solches Kalorimeter wird im Praktikumsversuch verwendet. Es besteht aus einem Dewargefäß mit Deckel, Magnetrührer und einem elektrischen Heizelement. Die Temperatur wird mit einem Thermometer gemessen. Als Wärmeempfänger im Erwärmungskalorimeter kann ein Flüssigkeitsbad oder ein Metallblock dienen. Im hier verwendeten Versuchsaufbau wird dazu destilliertes Wasser eingesetzt. Bei einer Temperaturerhöhung ΔT des Wärmeempfängers beträgt die zugeführte Wärmemenge (Wärmetönung) Q, wenn C die Wärmekapazität des gesamten Kalorimeters ist: Q = C ΔT (2)
2 Kalorimetrische Messungen 2 Bestimmungen der Wärmekapazität C Die Wärmekapazität C eines Kalorimeters ist nach Gl. (2) diejenige Wärmemenge, die ein Kalorimeter bei einer Temperaturänderung von 1 K (bei Atmosphärendruck) aufnimmt bzw. abgibt. C ist für eine bestimmte Temperatur eine Apparatekonstante. Es gilt: C = k i= 1 m i c i (3) wenn das Kalorimeter aus k Teilen mit den Massen m i und den spezifischen Wärmen c i besteht (z.b. eigentlicher Wärmeempfänger, Thermometer, Rührer usw.). Nach Gl. (3) lässt sich C berechnen, wenn alle m i und c i bekannt sind. Einfacher und meist genauer ist jedoch eine experimentelle Bestimmung von C nach Gl. (2), indem man dem Kalorimeter eine genau bekannte Wärmemenge Q zuführt und die Temperaturänderung ΔT misst. Die genaueste Methode beruht auf der Wärmezuführung mit einem elektrischen Heizelement. Die elektrische Energie E, die vollständig in Wärme umgewandelt wird, ist für Gleichstrom durch E = U e.i.t gegeben, wenn I die Stromstärke, U die Spannung an den Enden des Heizelements und t die Zeitdauer der Energiezuführung sind. Misst man U e, I und t in den Einheiten V, A und s, so erhält man C aus Gl. (2) unmittelbar in der Einheit J/K: C = U e.i.t/δt (4) Bestimmungen der Temperaturänderung ΔT aus einer Gangbeobachtung Eine Gangbeobachtung besteht aus der Aufnahme einer Temperatur-Zeit-Kurve. Man unterscheidet bei kalorimetrischen Messungen drei Stadien (Abbildung 1): die Vorperiode, die Hauptperiode und die Nachperiode. Die Vorperiode beginnt, sobald sich die Temperatur im Kalorimeter durch Rühren ausgeglichen hat und sich nur noch linear mit der Zeit ändert. Die Hauptperiode beginnt, sobald die Wärmeentwicklung, die gemessen werden soll, in Gang gesetzt wird. Die Hauptperiode ist vorüber und die Nachperiode beginnt, wenn nach Beendigung der Wärmeentwicklung die Temperatur sich ausgeglichen hat und sich wieder nur noch linear mit der Zeit ändert. Im Idealfall (augenblicklicher Wärmeaustausch in einem trägheitslosen Kalorimeter bei trägheitsloser Temperaturmessung) wäre die Hauptperiode unendlich kurz. Der Temperatursprung an dieser Stelle wäre mit ΔT identisch und damit nach Gl. (2) der gesuchten Wärme-
3 Kalorimetrische Messungen 3 menge Q direkt proportional. Dieser Idealfall lässt sich jedoch streng nicht verwirklichen, da i.a. ein Wärmeaustausch mit der Umgebung (konstante Temperatur T 0 ) stattfindet. Die zeitliche Änderung der Temperatur im Kalorimeter erhält man in erster Näherung aus dem Newtonschen Abkühlungsgesetz dt/dt = K (T 0 T(t)) (5) T(t) ist die Temperatur der Kalorimeters zum Zeitpunkt t. Die Abkühlungskonstante K (Dimension t 1 ) ist nahezu nur solange konstant, wie T 0 -T < 6 K ist. Vorperiode Hauptperiode Nachperiode Temperatur T ΔT x Zeit t Abbildung 1: Flächenausgleichsverfahren zur genauen Bestimmung der Temperaturdifferenz ΔT In der Praxis benutzt man zur Bestimmung von ΔT häufig das Verfahren des Flächenausgleichs (s. Abb. 1). Man extrapoliert die Vorperiode vorwärts und die Nachperiode rückwärts, bis die beiden "Dreiecksflächen" beiderseits der Hauptperiode in Abbildung 1 gleich groß sind. Die Flächengleichheit kann man durch numerische oder graphische Integration sowie durch Auszählen von Quadraten auf Millimeterpapier feststellen. Der Temperatursprung an der markierten Stelle ist die gesuchte Temperaturdifferenz ΔT
4 Kalorimetrische Messungen 4 Sind außer der Wärmeleitung noch andere Vorgänge für den beobachteten Temperaturgang verantwortlich, so müssen sie auf der rechten Seite von Gl. (5) entsprechend berücksichtigt werden. Hierzu gehört z.b. auch die Rührwärme, die etwa mit der dritten Potenz der Rührgeschwindigkeit zunimmt. Wenn diese jedoch in allen Versuchen zeitlich konstant ist, so wird ihr Einfluss im Flächenausgleichsverfahren ausreichend berücksichtigt. Ebenso heben sich andere unkontrollierbare Effekte heraus, wenn man alle Versuche unter denselben Bedingungen durchführt, bei denen man die Wärmekapazität C des Kalorimeters bestimmt. Temperaturmessung in der Kalorimetrie Die Aufgabe besteht darin, eine Temperaturdifferenz ΔT möglichst genau zu messen. Außerdem muss i.a. eine absolute Bezugstemperatur bekannt sein, auf die man die kalorimetrisch gemessene Wärmemenge beziehen kann (z.b. T 0 ). Hier wird ein Pt100-Widerstandsthermometer verwendet, dessen temperaturabhängiger Widerstand gemessen wird. Dies geschieht mittels eines Messverstärkers, der eine Spannung U erzeugt, die dem Widerstand proportional ist und die über ein Digitalmultimeter von einem Computer registriert wird. Registrierten Spannungsdifferenzen ΔU entsprechen daher Temperaturdifferenzen ΔT. Für eine Absolutbestimmung der Temperaturen ist die Ermittlung einer Reihe von Temperatur-Spannungs- Wertepaaren (T,U) erforderlich, aus denen mittels linearer Regression eine Kalibriergerade T(U) = T 0 + ku erhalten wird, die eine eindeutige Zuordnung der gemessenen Spannungen zu den jeweiligen Temperaturwerten erlaubt. k ist ein experimentell zu bestimmender Kalibrierfaktor. Der erste Hauptsatz "In einem abgeschlossenen System ist du = 0 (Energieerhaltungssatz)." Die theoretische Grundlage für kalorimetrische Messungen ist der erste Hauptsatz der Thermodynamik (Energieerhaltungssatz), den man in differentieller Schreibweise so formulieren kann: du = δq + δw (6) In einem nicht abgeschlossenen System (wie z.b. einem Kalorimeter) führen das verrichten mechanischer Arbeit oder ein Wärmerein- oder austrag zu einer Änderung der inneren Energie und damit der im Kalorimeter gemessenen Temperatur. In Gl. (6) sind δq und δw keine vollständigen Differentiale (Q und W sind keine Zustandsfunktionen!). δw kann sich allgemein aus folgenden Anteilen zusammensetzen: mechanische, elektrische, magnetische, Schwerefeld- und Oberflächenarbeit. Im Folgenden wird nur eine (mechanische) Kompressionsarbeit δw = -pdv betrachtet. Dabei sind p der Druck des Systems (im mechanischen Gleichgewicht gleich dem Außendruck p ext ) und dv die Volumenänderung des Systems.
5 Kalorimetrische Messungen 5 Der Ausdruck (6) ist eine exakte Energiebilanz (Gleichheitszeichen) für beliebige Zustandsänderungen. Nach Gl. (6) erhält man du (nicht U selbst), wenn man den Zustand des Systems ändert, die dabei vom System auf genommene Wärme δq misst und die am System geleistete Arbeit δw hinzuzählt. Leistet das System Arbeit an seiner Umgebung (z.b. ein Motor), so gilt Gl. (6) unverändert mit δw < 0. Führt man einem materiellen System eine unendlich kleine Wärmemenge δq zu und erhöht sich dabei seine Temperatur um dt (latente Wärmeanteile seien ausgeschlossen), so heißt C = δq/dt die Wärmekapazität des Systems (s. Gl. 2). Ihre Einheit ist J/K. Zustandsänderungen bei konstantem Volumen (isochore Zustandsänderungen) In diesem Fall wird δw = -pdv = 0, und aus Gl. (6) erhält man du = δq V (7) Die Wärmekapazität bei konstantem Volumen C V erhält man aus der differentiellen Formulierung von Gl (2) zu C V = δq V /dt = du/dt (8) Entsprechend gilt für die spezifische Wärmekapazität c V und die molare Wärmekapazität C MV : c V = C V /m C MV = C V /n (9a) (9b) mit der Masse m bzw. der Stoffmenge n. Zustandsänderungen bei konstantem Druck (isobare Zustandsänderung) Für Zustandsänderungen bei konstantem Druck gilt nach dem ersten Hauptsatz der Thermodynamik δq p = du - δw = du + pdv (10) Man definiert zweckmäßig eine neue Funktion H(p,T), die Enthalpie:
6 Kalorimetrische Messungen 6 H = U + pv (11a) bzw. dh = du + pdv + Vdp (11b) was sich im hier betrachteten Fall (konstanter Druck: dp = 0) zu dh = du + pdv = δq p (12) reduziert. Analog zu Gl. (8) und (9) folgt aus Gl. (12) dann: C p = δq p /dt = dh/dt c p = C p /m C Mp = C p /n (13a) (13b) (13c) Gl. (9) und Gl. (13) sind Messvorschriften für C MV bzw. C Mp, wenn man die infinitesimalen Größen δq und dt durch (nicht allzu große) messbare Differenzen Q und ΔT ersetzt (s. Gl. 2). Ist ΔT = T 2 T 1 groß (T 1 = Temperatur des Ausgangszustands, T 2 = Temperatur des Endzustands), ist C M die mittlere Mol-/Atomwärme (bzw. spezifische Wärme) zwischen den Temperaturen T 1 und T 2. Spezifische Wärme von Gasen Die Molwärmen idealer Gase lassen sich mit Hilfe der kinetischen Gastheorie aus dem Molekülbau abschätzen. Nach dem Gleichverteilungssatz der Energie entfällt auf jeden Freiheitsgrad der Translation (f trans ) und Rotation (f rot ) die Energie ½kT und auf jeden Schwingungsfreiheitsgrad (f vib ) die Energie kt (wegen Addition von kinetischer und potentieller Energie der Vibration). Daraus folgt C Mv = ½R(f trans +f rot +2f vib ). R = N A k = Jmol -1 K -1 ist die allgemeine Gaskonstante, k die Boltzmann-Konstante und N A die Avogadrozahl. Einatomige Gase verfügen nur über drei Translationsfreiheitsgrade. Daraus folgt C Mv = (3/2)R 12,5 Jmol -1 K -1. Zweiatomige und lineare Gase weisen drei Translations-, zwei Rotations- und einen Schwingungsfreiheitsgrad auf, so dass C Mv = 7/2 R 29,1 Jmol -1 K -1. Drei- und mehratomige gewinkelte Moleküle haben drei Translations-, drei Rotations- und drei Schwingungsfreiheitsgrade, so dass C Mv = 6R 50 Jmol -1 K -1. Allerdings sind dies Grenzwerte für hohe Temperaturen. Rotations- und Vibrationsenergien sind gequantelt und leisten damit erst einen Beitrag zu C Mv, wenn die mittlere thermische Energie kt die Größenordnung der Energiequantisierung erreicht. Rotationsquanten sind energieärmer als Vibrationsquanten. Daher sind die meisten zwei- und dreiatomige Gase bei Zimmertemperatur nur rotations- und nicht schwingungsangeregt, so dass C Mv bei (5/2)R bzw. (6/2)R = 3R liegt und mit steigender Tem-
7 Kalorimetrische Messungen 7 peratur stetig wächst. Die Molwärmen realer Gase liegen im allgemeinen nur wenig über den für ideale Gase vorausgesagten Werten. Flüssigkeiten haben höhere Molwärmen als Gase und Feststoffe. Spezifische Wärme fester Körper - Dulong Petitsche Regel Die Atomwärme C MV hat für die meisten festen Elemente bei gewöhnlicher Temperatur (Zimmertemperatur) mit einigen Ausnahmen (z.b. B, C, Si) den allgemeinen Wert C MV = 3 R 25 J mol -1 K -1 (14) Auch diese Regel kann man mit dem Gleichverteilungssatz der Energie erklären, nach dem jedem Freiheitsgrad eines Atoms (Moleküls) im Mittel der gleiche Energiebetrag ½kT zukommt (k = Boltzmann-Konstante). Betrachtet man Atome im Kristallgitter als lineare harmonische Oszillatoren und rechnet jeweils 3 Freiheitsgrade (3 Raumrichtungen) für die potentielle und die kinetische Energie, so erhält man für ein Mol Substanz genau den durch Gl. (14) gegebenen Betrag für die Atom-/Molwärme C MV. Bei tieferen Temperaturen wird C MV kleiner und geht am absoluten Nullpunkt mit T 3 (Peter Debye) gegen Null (Nernst). Zwischen 0 K und 50 K gilt das Debyesche T 3 Gesetz: C MV = at 3 (a ist eine Stoffkonstante). Bei höheren Temperaturen nimmt C MV über den Wert von Gl. (14) zu, da die Schwingungen anharmonisch werden. Messungen von C Mp bzw. c p nach der Mischungsmethode Das Kalorimeter im Praktikum ist ein offenes Gefäß. Demzufolge misst man durch die Wärmetönungen ΔQ p Enthalpieänderungen ΔH nach Gl. (13). Man mischt dazu den zu untersuchenden Körper mit einer Flüssigkeit von bekannter spezifischer Wärme. Sind T 1 die Anfangstemperatur des Körpers (im Versuch die Siedetemperatur T S des Wassers) und T 2 die (gemeinsame) Endtemperatur nach dem Wärmeaustausch, so ist nach Gl. (13): c p = Q p /(mδt) mit ΔT = T 2 T 1 (15) Dabei ist Q p die ausgetauschte Wärmemenge (s. unten).
8 Kalorimetrische Messungen 8 Schmelzwärme Die spezifische Schmelzwärme λ S eines Körpers ist z.b. diejenige (latente) Wärme, die nötig ist, um seine Masseneinheit isotherm (bei der Schmelztemperatur T S ) vom festen in den flüssigen Zustand zu überführen. Analog sind Verdampfungs- und Sublimationswärmen definiert. Man kann λ S nach der Mischungsmethode messen. Liegt die anfängliche Kalorimetertemperatur T 1 oberhalb der Schmelztemperatur T S, so kühlt man den Körper etwas unter seinen Schmelzpunkt T S auf die Temperatur T 0 ab. Dann lässt man ihn in ein Flüssigkeitskalorimeter fallen, in dem er nach dem Schmelzen die Kalorimeter-Endtemperatur T 2 annimmt (T 0 < T S < T 2 < T 1 ). Man erhält nach dem ersten Hauptsatz folgende Energiebilanz: CΔT = m (λ S + c fl (T 2 -T S ) + c f (T S T 0 )) (16) C ist die Wärmekapazität und ΔT = T 2 T 1 die Temperaturänderung im Kalorimeter. Aus Gl. (16) kann man λ S und daraus die Schmelzentropie ΔS S = λ S /T S berechnen, wenn die mittleren spezifischen Wärmen c fl und c f im flüssigen bzw. festen Zustand in dem betreffenden Temperaturbereich bekannt sind. In der Praxis versucht man, die Temperaturdifferenz (T S T 0 ) in Gl. (16) so klein zu halten, dass der letzte Term in Gl. (16) gegen λ S vernachlässigt werden kann. Für den Praktikumsversuch mit Eis gilt z.b. in guter Näherung, dass T 0 = T S ist, wenn sich das Eis in einem offenen Dewargefäß 1 einige Zeit in flüssigem Wasser befand. Analog zu Gl. (16) kann man umgekehrt die Erstarrungswärme bestimmen. Im Prinzip können auch die bei Strukturänderungen fester Stoffe auftretenden Umwandlungswärmen so bestimmt werden. Diese Wärmen sind jedoch im Allgemeinen wesentlich kleiner und die Umwandlung kann sich über einen größeren Temperaturbereich erstrecken. Lösungs-, Verdünnungs- und Mischungswärmen Es seinen n 1 Mole einer festen Substanz in n 2 Molen eines Lösungsmittels gelöst. Wird das Stoffmengenverhältnis n 1 /n 2 dieser Lösung um einen unendlich kleinen Betrag dn 1 (Auflösung) oder dn 2 (Verdünnung) geändert, so erhält man eine Wärmetönung δq 1 bzw. δq 2. Man nennt und analog δq 1 /dn 1 die differentielle Lösungswärme δq 2 /dn 2 die differentielle Verdünnungswärme 1 Benannt nach dem schottischen Physikochemiker James Dewar, (sprich: dju:ar)
9 Kalorimetrische Messungen 9 der Lösung bei der Konzentration c. Da selbst bei endlichen Konzentrationsänderungen um Δn << n diese Wärmetönungen sehr gering sind, sind zu ihrer Messung sehr empfindliche Kalorimeter nötig. Einfacher lässt sich im allgemeinen die integrale Lösungswärme Q/n 1 bestimmen. Q ist die (meist negative) Wärmemenge, die bei der Auflösung von n 1 Molen fester Substanz in n 2 Molen Lösungsmittel insgesamt auftritt. Die integrale Mischungswärme ist definiert durch Q/(n 1 +n 2 ). n 1 und n 2 sind die Molzahlen der beiden Komponenten in der Mischung. Hydratationswärme eines Salzes Unter der molaren Hydratationswärme eines Salzes versteht man diejenige Wärmemenge, die man zur Bildung eines Mols festen Kristallhydrats aus dem festen wasserfreien Salz und der entsprechenden Menge Wasser benötigt. Wie diese Zustandsänderung bewirkt wird, ist nach dem ersten Hauptsatz oder auch nach dem Heßschen Satz von der Konstanz der Wärmesummen bei verschiedenen Wegen einer Reaktion belanglos. Die Hydratationswärme lässt sich aus den molaren integralen Lösungswärmen des wasserfreien und des hydratisierten Salzes bestimmen. Dies soll am Beispiel von Kupfersulfat erklärt werden. Zunächst wird 1 Mol festes Kupfersulfat gelöst. Es gilt CuSO 4 (fest) + n H 2 O CuSO 4 (gelöst) ΔH (17) Der Index soll andeuten, dass Wasser im Überschuss vorhanden ist (Molzahl n >> 1). Ebenfalls 1 Mol gelöstes Kupfersulfat erhält man durch Auflösen des festen Kristallhydrats, das aber zunächst gebildet werden muss: CuSO 4 (fest) + 5 H 2 O CuSO 4 5H 2 O(fest) ΔH hyd (18a) CuSO 4 5H 2 O(fest)+ (n-5) H 2 O CuSO 4 (gelöst) ΔH' (18b) Setzt man (18a) in (18b) ein und vergleicht mit (17), so erhält man die gesuchte Beziehung für die Hydratationswärme ΔH hyd = ΔH ΔH' (19) Alle Lösungsenthalpien in (17) bis (19) sind auf 1 Mol bezogen. Hat man Substanz der Masse m eingewogen, so erhält man also die molaren integralen Lösungsenthalpien (Lösungswärme) aus der Beziehung
10 Kalorimetrische Messungen 10 ΔH = Q M/m (20) Q ist die nach Gl. (2) gemessene Wärmetönung und M die Molmasse der Substanz. Wenn ein Salz gelöst wird, wird in einigen Fällen Energie frei (exothermer Vorgang) und in anderen Fällen wird Energie aufgenommen (endothermer Vorgang). Der Lösungsvorgang eines Salzes in einem Lösemittel wird dabei in zwei Schritte unterteilt. 1.Schritt: Das Salz liegt vor dem Lösen in kristalliner Form vor. Zwischen den unterschiedlich geladenen Ionen eines Salzkristalls herrschen starke Anziehungskräfte. Zur Aufspaltung des Kristallgitters müssen diese Kräfte überwunden werden. Die hierzu nötige Energie wird Gitterenergie genannt. Die Gitterenergie wird dem Lösemittel entzogen, wodurch sich die Lösung stark abkühlt. Da beim Aufspalten des Kristallgitters Energie benötigt wird, handelt es sich um einen endothermen Vorgang. 2.Schritt: Die abgespaltenen Ionen umgeben sich mit einer Hülle aus Lösemittelmolekülen (Solvathülle). Dieser exotherme Vorgang wird Solvatation genannt. Die hierbei an das Lösemittel abgegebene Energie heißt Solvatationsenergie. Handelt es sich bei dem Lösemittel um Wasser, spricht man von Hydratation bzw. Hydratationsenergie. Beide obengenannten Prozesse laufen parallel zueinander ab. Überwiegt die Gitterenergie, so ist der Gesamtvorgang des Lösens endotherm. Im umgekehrten Fall hat die Lösungsenthalpie ein negatives Vorzeichen (exotherm). Chemische Reaktionen laufen dann freiwillig ab, wenn die Änderung der Gibbschen Freien Enthalpie ΔG < 0 ist. Nach Definition ist ΔG = ΔH TΔS. Endotherme Lösungsprozesse (ΔH > 0) können somit dennoch als freiwillige Reaktionen ablaufen, wenn sich die Entropie im System stark vermehrt (ΔS >> 0). Ausführung und Auswertung der Messungen 1.) Kalibrierung des Widerstandsthermometers 2.) Bestimmung der Wärmekapazität des Kalorimeters 3.) Messung der spezifischen Wärme von Kupfer 4.) Bestimmung der Schmelzwärme von Eis 5.) Messung der Hydratationswärme von CuSO 4 6.) Messung der Hydratationswärme von NaAc Die Versuche erfolgen alle als Gangbeobachtung, die sich aus Vorperiode, Hauptperiode und Nachperiode zusammensetzt (siehe dazu den Abschnitt Bestimmung der Temperaturänderung aus einer Gangbeobachtung). Vor und Nachperiode sollen jeweils sechs Minuten dauern, die Hauptperiode dauert nur bei der Bestimmung der Wärmekapazität sechs Minuten.
11 Kalorimetrische Messungen 11 Versuchsablauf Zunächst werden zur Vorbereitung des Versuchsteils Nr. 4 einige Eiswürfel in ein separates Dewargefäß gebracht und dieses mit destilliertem Wasser aufgefüllt. 1.) Kalibrierung des Widerstandsthermometers Da für die Auswertung zum Teil absolute Temperaturen benötigt werden, ist eine Kalibrierung des Widerstandsthermometers erforderlich. Die Aufnahme der dazu erforderlichen Datenpunkte erfolgt während des Ablaufs der Versuchsteile 2-6. Ein geeichtes 2/10 C Thermometer ist am Kalorimeter fest montiert. Während der Messung der Versuche 2 6 notieren Sie für zehn verschiedene Temperaturen jeweils einen Spannungswert des Widerstandsthermometers und einen Wert des 2/10 C Thermometer. Es ist wichtig, vor jeder Temperaturablesung den Temperaturausgleich abzuwarten. 2.) Bestimmung der Wärmekapazität des Kalorimeters Das Dewar-Gefäß des Kalorimeters mit Rührkern wird ohne Wasser (gut trocken) mit 600 ml destilliertem Wasser von Umgebungstemperatur gefüllt. Anschließend wird es auf den Magnetrührer gestellt. Der am Stativ befestigte Teil des Deckels (Deckelteil I) mit dem Widerstandsthermometer wird vorsichtig abgesenkt, bis er auf dem Gefäß aufliegt. Danach wird das Kalorimeter mit dem zweiten Teil des Deckels (Deckelteil II) verschlossen und der Rührer eingeschaltet, der für alle Versuche mit der gleichen Geschwindigkeit laufen soll. Nachdem es im Kalorimeter zu einem Temperaturausgleich gekommen ist (erkennbar daran, dass sich die Temperatur noch linear mit der Zeit ändert), werden das Widerstandsthermometer und der Computer zur Aufnahme der Gangkurve vom Assistenten eingestellt. Notieren Sie die Temperaturanzeige am Widerstands- und am 2/10 C-Thermometer (für Aufgabe 1). Damit beginnt die Gangbeobachtung der Vorperiode. Zum Beginn der Hauptperiode schalten Sie mit dem Schalter ~ den Strom I ein und lesen Sie an den Messinstrumenten Strom I und Spannung U e ab. Kontrollieren Sie U e und I während der Hauptperiode häufiger, aber verändern Sie sie nicht! Wenn die Werte stark von 500 ma und 24 V abweichen, rufen Sie den Assistenten. Schalten Sie nach 6 Minuten den Strom ab und beobachten Sie die Nachperiode. Notieren Sie in der Nachperiode wieder die Anzeigen beider Thermometer. 3.) Messung der spezifischen Wärme von Kupfer Wiegen Sie den Kupferzylinder auf der Oberschalenwaage auf mindestens 0,1 g genau. Hängen Sie ihn anschließend an einem Faden in siedendes Wasser. Erhitzen Sie dazu Wasser in einem Becherglas mit dem Bunsenbrenner. Der Kupferzylinder muss dabei vollständig in das Wasser ein tauchen. Leeren Sie das Kalorimeter aus und befüllen es
12 Kalorimetrische Messungen 12 erneut mit 600 ml dest. Wasser und beginnen Sie mit der Messung der Vorperiode. Nachdem der Metallkörper im Becherglas die Siedetemperatur angenommen hat, heben Sie den Deckelteil II mit dem Haken ab, hängen den Kupferblock ein (dabei verbleibt er im Wasserbad) und lassen ihn von dem Assistenten in das Kalorimeter überführen. Setzen Sie die Gangbeobachtung wie gewöhnlich fort. Notieren Sie die Temperaturanzeigen beider Thermometer zu Beginn der Vorperiode und am Ende der Nachperiode. Nach der Messung heben Sie den Deckelteil II ab und haken den Kupferzylinder aus. 4.) Bestimmung der Schmelzwärme von Eis Befüllen Sie das Kalorimeter neu mit 600 ml Wasser. Wiegen Sie das Dewar-Gefäß mit Rührkern auf der Oberschalenwaage (im Wägeraum). Anschließend beobachten Sie wie gewohnt die Vorperiode und lassen zum Beginn der Hauptperiode möglichst "trockenes" Eis (anhaftendes Wasser verfälscht das Ergebnis) in das Kalorimeter fallen. Das Eis hierfür, etwa die Menge eines normalen Eiswürfels, entnehmen Sie die dem dafür zu Versuchsbeginn vorbereiteten Dewar-Gefäß. Beobachten Sie wie in den Versuchen vorher den Temperaturverlauf. Vergessen Sie nicht, sich die Anzeigen beider Thermometer bei Einstellung eines linearen Temperaturverlaufs (Vorperiode und Nachperiode) zu notieren. Bestimmen Sie durch Rückwiegen das Gewicht des eingesetzten Eiswürfels. 5.) Messung der Hydrationswärme von CuSO 4 Wiegen Sie ca. 7g CuSO 4 und 7g CuSO 4 5H 2 O in dafür bereitgestellte, beschriftete Kunststoffbecher im Wägeraum ein. Die Salze entnehmen Sie dem Chemikalienschrank. Stellen Sie dann das Dewar-Gefäß mit 600ml neuem, destilliertem. Wasser auf den Rührer, verschließen Sie es mit den beiden Deckelteilen und schalten Sie den Rührer ein. Warten Sie den Temperaturausgleich ab und beginnen dann mit der Messung der Vorperiode. Notieren Sie die Thermometeranzeigen. Öffnen Sie zum Beginn der Hauptperiode kurz den Deckelteil II und geben Sie das CuSO 4 in das Kalorimeter. Setzen Sie die Gangbeobachtung wie gewohnt fort. Wiederholen Sie den Versuch mit 7 g CuSO4 5H 2 O und 600ml neuem dest. Wasser. Kupfersulfat darf keinesfalls in den Ausguss gelangen. Es ist für Wasserorganismen sehr giftig und kann in Gewässern längerfristig schädliche Wirkungen haben (R50/53). Sammeln Sie die CuSO 4 Lösungen in einem Kanister zur Entsorgung. 6.) Messung der Hydratationswärme von NaAc. Wiederholen sie analog den vorherigen Versuch mit je ca. 10g Natriumacetat (NaAc) und NaAc 3H 2 O. Entsorgen Sie die Natriumacetat-Lösungen im Ausguss.
13 Kalorimetrische Messungen 13 Auswertung 1.) Tragen Sie die Spannungswerte des Widerstandsthermometers gegen die Temperaturen des geeichten 2/10 C Thermometers auf und stellen Sie mittels linearer Regression eine Geradengleichung auf, mit der Sie aus den Messwerten des Widerstandsthermometers absolute Temperaturen berechnen können. Setzen Sie die absoluten Temperaturen in die Gl. (15) und (16) ein. Die Temperaturdifferenzen ΔT können relativ angegeben werden. 2.) Berechnen Sie die Wärmekapazität des Kalorimeters aus der zugeführten elektrischen Energie. Bestimmen Sie ΔT graphisch aus der Gangkurve. 3.) Bestimmen Sie ΔT aus den Gangkurven. Berechnen Sie die spezifische Wärme c p der Metallprobe nach Gl. (15). Prüfen Sie die Gültigkeit der Dulong-Petit-Regel (Gl. 14). 4.) Bestimmen Sie analog zu 3.) die Schmelzwärme λ S von Eis aus Gl. (16) und berechnen Sie die Schmelzentropie ΔS S. 5.) Bestimmen Sie analog zu 3.) die integralen Lösungswärmen des nicht hydratisierten sowie des hydratisierten Kupfersulfats nach Gl. (19) und berechnen Sie die Hydratationswärme nach Gl. (18). Literaturwerte für diesen Versuchsteil finden Sie entweder in der Landolt-Börnstein- Buchreihe, Group IV Physical Chemistry, Volume 2: Heats of Mixing and Solution, Springer-Verlag, 1976, oder in der dort angeführten Originalarbeit von J.W.Larson, P. Cerutti, H.K. Garber und L.G. Helper, Journal of Physical Chemistry, 72, 2902 (1968). Beide Quellen sind aus dem Adressbereich der TU on-line zugänglich. 6.) Berechnen Sie analog zu 5.) die integralen Lösungswärmen des nicht hydratisierten sowie des hydratisierten Natriumacetats nach Gl (19) und berechnen Sie die Hydratationswärme nach Gl. (18). Literaturwerte für diesen Versuchsteil finden Sie in Kapitel VII bzw. in Tabelle XXI in "Thermal Properties of Aqueous Uni-Unilvalent Electrolytes", National Standard Reference Data Series (NSRDS) 2, Vivian Barfield Parker (1965). Das Dokument ist auf der Website des National Institute of Standards and Technology (NIST), des Äquivalents zur Physikalisch-Technischen Bundesanstalt (PTB), frei zugänglich. Diskutieren Sie alle Ergebnisse und vergleichen Sie sie mit den Literaturwerten (genaue Angabe der Literaturquelle). Berücksichtigen Sie in der Fehlerbetrachtung mögliche Quellen für Messungenauigkeiten (wie verlässlich ist die Thermometerkalibrierung?) und berechnen Sie die Fehler der ermittelten Größen nach dem Gaußschen Fehlerfortpflanzungsgesetz.
Kalorimetrische Messungen
 Kalorimetrische Messungen 1 Kalorimetrische Messungen Durch Verfolgen des Temperaturverlaufs in einem Kalorimeter werden die spezifische Wärmekapazität von Kupfer, die Schmelzwärme von Eis sowie die Lösungswärmen
Kalorimetrische Messungen 1 Kalorimetrische Messungen Durch Verfolgen des Temperaturverlaufs in einem Kalorimeter werden die spezifische Wärmekapazität von Kupfer, die Schmelzwärme von Eis sowie die Lösungswärmen
Protokoll zum Versuch 3.1
 Grundpraktikum Physikalische Chemie Studiengang: Chemie-Ingenieurwesen Technische Universität München SS 2003 Protokoll zum Versuch 3.1 Kalorimetrie Gruppe 3 Kim Langbein Oliver Gobin 11 April 2003 Inhaltsverzeichnis
Grundpraktikum Physikalische Chemie Studiengang: Chemie-Ingenieurwesen Technische Universität München SS 2003 Protokoll zum Versuch 3.1 Kalorimetrie Gruppe 3 Kim Langbein Oliver Gobin 11 April 2003 Inhaltsverzeichnis
Versuch Nr.53. Messung kalorischer Größen (Spezifische Wärmen)
 Versuch Nr.53 Messung kalorischer Größen (Spezifische Wärmen) Stichworte: Wärme, innere Energie und Enthalpie als Zustandsfunktion, Wärmekapazität, spezifische Wärme, Molwärme, Regel von Dulong-Petit,
Versuch Nr.53 Messung kalorischer Größen (Spezifische Wärmen) Stichworte: Wärme, innere Energie und Enthalpie als Zustandsfunktion, Wärmekapazität, spezifische Wärme, Molwärme, Regel von Dulong-Petit,
Kalorimetrische Messungen. Die Bestimmung von Enthalpieänderungen in Lösungen Praktikum physikalische Chemie für Pharmaziestudenten
 Kalorimetrische Messungen. Die Bestimmung von Enthalpieänderungen in Lösungen Praktikum physikalische Chemie für Pharmaziestudenten zusammengestellt von Soma Vesztergom 1.) Kurzbeschreibung Mit Hilfe eines
Kalorimetrische Messungen. Die Bestimmung von Enthalpieänderungen in Lösungen Praktikum physikalische Chemie für Pharmaziestudenten zusammengestellt von Soma Vesztergom 1.) Kurzbeschreibung Mit Hilfe eines
T5 - Hydratations- und Neutralisationsenthalpie
 T5 - Hydratations- und Neutralisationsenthalpie Aufgaben: 1. Messung der molaren integralen Lösungsenthalpie von Natriumhydrogenphosphat Na 2 HPO 4, Natriumhydrogenphosphat-dihydrat Na 2 HPO 4 2H 2 O,
T5 - Hydratations- und Neutralisationsenthalpie Aufgaben: 1. Messung der molaren integralen Lösungsenthalpie von Natriumhydrogenphosphat Na 2 HPO 4, Natriumhydrogenphosphat-dihydrat Na 2 HPO 4 2H 2 O,
TD 3: Neutralisationswärme
 TD 3: Neutralisationswärme Theoretische Einleitung Chemische Umsetzungen sind stets von einer Energieänderung begleitet, wobei der umgesetzte Energiebetrag entweder vom System aufgenommen (endotherme Reaktion)
TD 3: Neutralisationswärme Theoretische Einleitung Chemische Umsetzungen sind stets von einer Energieänderung begleitet, wobei der umgesetzte Energiebetrag entweder vom System aufgenommen (endotherme Reaktion)
Versuchsanleitungen zum Praktikum Physikalische Chemie für Anfänger 1
 Versuchsanleitungen zum Praktikum Physikalische Chemie für Anfänger 1 A 6 Kalorimetrie Aufgabe: Mittels eines Flüssigkeitskalorimeters ist a) die Neutralisationsenthalpie von säure b) die ösungsenthalpie
Versuchsanleitungen zum Praktikum Physikalische Chemie für Anfänger 1 A 6 Kalorimetrie Aufgabe: Mittels eines Flüssigkeitskalorimeters ist a) die Neutralisationsenthalpie von säure b) die ösungsenthalpie
PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test
 PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Lösungswärme wird dieses Vorgespräch durch einen Multiple Choice
PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Lösungswärme wird dieses Vorgespräch durch einen Multiple Choice
Bestimmung der spezifischen Wärmekapazität fester Körper
 - B02.1 - Versuch B2: Bestimmung der spezifischen Wärmekapazität fester Körper 1. Literatur: Demtröder, Experimentalphysik, Bd. I Bergmann-Schaefer, Lehrbuch der Physik, Bd.I Walcher, Praktikum der Physik
- B02.1 - Versuch B2: Bestimmung der spezifischen Wärmekapazität fester Körper 1. Literatur: Demtröder, Experimentalphysik, Bd. I Bergmann-Schaefer, Lehrbuch der Physik, Bd.I Walcher, Praktikum der Physik
Spezifische Wärme fester Körper
 1 Spezifische ärme fester Körper Die spezifische, sowie die molare ärme von Kupfer und Aluminium sollen bestimmt werden. Anhand der molaren ärme von Kupfer bei der Temperatur von flüssigem Stickstoff soll
1 Spezifische ärme fester Körper Die spezifische, sowie die molare ärme von Kupfer und Aluminium sollen bestimmt werden. Anhand der molaren ärme von Kupfer bei der Temperatur von flüssigem Stickstoff soll
PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test
 PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Neutralisationswärme wird dieses Vorgespräch durch einen
PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Neutralisationswärme wird dieses Vorgespräch durch einen
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 Vladimir Dyakonov #7 am 18.01.006 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 Vladimir Dyakonov #7 am 18.01.006 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Lösungswärme von Salzen
 Lösungswärme von Salzen In diesem Versuch wird die Lösungswärme von zwei Salzen, Calciumchlorid und Calciumchlorid-Hexahydrat ermittelt. Dabei wird die Temperaturänderung beim Lösen des Salzes kalorimetrisch
Lösungswärme von Salzen In diesem Versuch wird die Lösungswärme von zwei Salzen, Calciumchlorid und Calciumchlorid-Hexahydrat ermittelt. Dabei wird die Temperaturänderung beim Lösen des Salzes kalorimetrisch
ADIABATISCHE KALORIMETRIE
 VERSUCH 6 ADIABATISCHE KALORIMETRIE Thema Kalorimetrische Bestimmung von Lösungs- und Neutralisationswärmen Grundlagen Literatur 1. Hauptsatz der Thermodynamik adiabatische Kalorimetrie Lösungs-, Neutralisations-,
VERSUCH 6 ADIABATISCHE KALORIMETRIE Thema Kalorimetrische Bestimmung von Lösungs- und Neutralisationswärmen Grundlagen Literatur 1. Hauptsatz der Thermodynamik adiabatische Kalorimetrie Lösungs-, Neutralisations-,
1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen
 IV. Wärmelehre 1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen Historisch: Wärme als Stoff, der übertragen und in beliebiger Menge erzeugt werden kann. Übertragung: Wärmezufuhr Joulesche
IV. Wärmelehre 1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen Historisch: Wärme als Stoff, der übertragen und in beliebiger Menge erzeugt werden kann. Übertragung: Wärmezufuhr Joulesche
Physik für Mediziner im 1. Fachsemester
 Physik für Mediziner im 1. Fachsemester #10 30/10/2008 Vladimir Dyakonov [email protected] Thermisches Gleichgewicht Soll die Temperatur geändert werden, so muss dem System Wärme (kinetische
Physik für Mediziner im 1. Fachsemester #10 30/10/2008 Vladimir Dyakonov [email protected] Thermisches Gleichgewicht Soll die Temperatur geändert werden, so muss dem System Wärme (kinetische
Der Zustand eines Systems ist durch Zustandsgrößen charakterisiert.
 Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Verbrennungsenergie und Bildungsenthalpie
 Praktikum Physikalische Chemie I 1. Januar 2016 Verbrennungsenergie und Bildungsenthalpie Guido Petri Anastasiya Knoch PC111/112, Gruppe 11 Aufgabenstellung Die Bildungsenthalpie von Salicylsäure wurde
Praktikum Physikalische Chemie I 1. Januar 2016 Verbrennungsenergie und Bildungsenthalpie Guido Petri Anastasiya Knoch PC111/112, Gruppe 11 Aufgabenstellung Die Bildungsenthalpie von Salicylsäure wurde
3 Der 1. Hauptsatz der Thermodynamik
 3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
Mathematisch-Naturwissenschaftliche Grundlegung WS 2014/15 Chemie I Dr. Helge Klemmer
 Mathematisch-Naturwissenschaftliche Grundlegung WS 2014/15 Chemie I 12.12.2014 Gase Flüssigkeiten Feststoffe Wiederholung Teil 2 (05.12.2014) Ideales Gasgesetz: pv Reale Gase: Zwischenmolekularen Wechselwirkungen
Mathematisch-Naturwissenschaftliche Grundlegung WS 2014/15 Chemie I 12.12.2014 Gase Flüssigkeiten Feststoffe Wiederholung Teil 2 (05.12.2014) Ideales Gasgesetz: pv Reale Gase: Zwischenmolekularen Wechselwirkungen
Die innere Energie and die Entropie
 Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Wärmemenge, spezifische Wärmekapazität, molare Wärmekapazität, Kalorimetrie, Dulong-Petitsches Gesetz.
 W1 Spezifische Wärmekapazität von festen Stoffen Stoffgebiet: Wärmemenge, spezifische Wärmekapazität, molare Wärmekapazität, Kalorimetrie, Dulong-Petitsches Gesetz. Versuchsziel: Bestimmung der spezifischen
W1 Spezifische Wärmekapazität von festen Stoffen Stoffgebiet: Wärmemenge, spezifische Wärmekapazität, molare Wärmekapazität, Kalorimetrie, Dulong-Petitsches Gesetz. Versuchsziel: Bestimmung der spezifischen
Festkörper - System steht unter Atmosphärendruck gemessenen Wärmen erhalten Index p : - isoliert
 Kalorimetrie Mit Hilfe der Kalorimetrie können die spezifischen Wärmekapazitäten für Festkörper, Flüssigkeiten und Gase bestimmt werden. Kalorische Grundgleichung: ΔQ = c m ΔT Festkörper - System steht
Kalorimetrie Mit Hilfe der Kalorimetrie können die spezifischen Wärmekapazitäten für Festkörper, Flüssigkeiten und Gase bestimmt werden. Kalorische Grundgleichung: ΔQ = c m ΔT Festkörper - System steht
2 Wärmelehre. Reibungswärme Reaktionswärme Stromwärme
 2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
Versuch: Spezifische Wärmekapazität fester Körper
 ersuch T1 SPEZIFISHE WÄRMEKAPAZITÄT FESTER KÖRPER Seite 1 von 5 ersuch: Spezifische Wärmekapazität fester Körper Anleitung für folgende Studiengänge: Physik, L3 Physik, Biophysik, Meteorologie, hemie,
ersuch T1 SPEZIFISHE WÄRMEKAPAZITÄT FESTER KÖRPER Seite 1 von 5 ersuch: Spezifische Wärmekapazität fester Körper Anleitung für folgende Studiengänge: Physik, L3 Physik, Biophysik, Meteorologie, hemie,
1. Klausur ist am 5.12.! (für Vets sowie Bonuspunkte für Zahni-Praktikum) Jetzt lernen!
 1. Klausur ist am 5.12.! (für Vets sowie Bonuspunkte für Zahni-Praktikum) Jetzt lernen! http://www.physik.uni-giessen.de/dueren/ User: duerenvorlesung Password: ****** Druck und Volumen Gesetz von Boyle-Mariotte:
1. Klausur ist am 5.12.! (für Vets sowie Bonuspunkte für Zahni-Praktikum) Jetzt lernen! http://www.physik.uni-giessen.de/dueren/ User: duerenvorlesung Password: ****** Druck und Volumen Gesetz von Boyle-Mariotte:
11.2 Die absolute Temperatur und die Kelvin-Skala
 11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
T3 - Wärmekapazität. Nutzen Sie die Fachliteratur, um die nachfolgenden Fragen und Aufgaben zu beantworten:
 T3 - Wärmekapazität Ziel des Versuches In diesem Versuch sollen Sie sich mit den Konzepten der Wärmekapazität und der Kalorimetrie vertraut machen. Hierzu bestimmen Sie die Wärmekapazität des zur Verfügung
T3 - Wärmekapazität Ziel des Versuches In diesem Versuch sollen Sie sich mit den Konzepten der Wärmekapazität und der Kalorimetrie vertraut machen. Hierzu bestimmen Sie die Wärmekapazität des zur Verfügung
Versuch 2. Physik für (Zahn-)Mediziner. c Claus Pegel 13. November 2007
 Versuch 2 Physik für (Zahn-)Mediziner c Claus Pegel 13. November 2007 1 Wärmemenge 1 Wärme oder Wärmemenge ist eine makroskopische Größe zur Beschreibung der ungeordneten Bewegung von Molekülen ( Schwingungen,
Versuch 2 Physik für (Zahn-)Mediziner c Claus Pegel 13. November 2007 1 Wärmemenge 1 Wärme oder Wärmemenge ist eine makroskopische Größe zur Beschreibung der ungeordneten Bewegung von Molekülen ( Schwingungen,
TEMPERATUR UND WÄRMEKAPAZITÄT... 2 KALORIMETRIE I... 3 KALORIMETRIE II... 5 PHASENUMWANDLUNGEN... 6
 E-Mail: Homepage: [email protected] schroeder-doms.de München den 11. Mai 2009 W1 Kalorimetrie (Skript zur Vorbereitung) TEMPERATUR UND WÄRMEKAPAZITÄT... 2 Wärme und Temperatur, Kelvin-Skala:... 2
E-Mail: Homepage: [email protected] schroeder-doms.de München den 11. Mai 2009 W1 Kalorimetrie (Skript zur Vorbereitung) TEMPERATUR UND WÄRMEKAPAZITÄT... 2 Wärme und Temperatur, Kelvin-Skala:... 2
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti.
 (c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti [email protected] Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
(c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti [email protected] Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
(VIII) Wärmlehre. Wärmelehre Karim Kouz WS 2014/ Semester Biophysik
 Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Lösungsenthalpie / Lösungswärme unterschiedlicher Zinksulfat-Hydrate
 Lösungsenthalpie / Lösungswärme unterschiedlicher Zinksulfat-Hydrate Zeitbedarf für die Versuchsdurchführung: ca. 10 Min. Geräte: Magnetrührer mit Magnetrührstäbchen Thermometer (min. 0,5 C Genauigkeit)
Lösungsenthalpie / Lösungswärme unterschiedlicher Zinksulfat-Hydrate Zeitbedarf für die Versuchsdurchführung: ca. 10 Min. Geräte: Magnetrührer mit Magnetrührstäbchen Thermometer (min. 0,5 C Genauigkeit)
3. Berechnung der molaren Verbrennungsenthalpie. 4. Berechnung der Standardreaktionsenthalpie für die Hydrierung von Phthalsäureanhydrid
 Verbrennungswärme Aufgaben: 1. Ermittlung der Wärmekapazität des Kalorimeters durch Verbrennen einer Eichsubstanz. 2. Bestimmung der spezifischen Verbrennungswärmen von Phthalsäureanhydrid und Tetrahydrophthalsäureanhydrid.
Verbrennungswärme Aufgaben: 1. Ermittlung der Wärmekapazität des Kalorimeters durch Verbrennen einer Eichsubstanz. 2. Bestimmung der spezifischen Verbrennungswärmen von Phthalsäureanhydrid und Tetrahydrophthalsäureanhydrid.
Hochschule Düsseldorf University of Applied Sciences. 26. April 2017 HSD. Energiespeicher Wärme
 Energiespeicher 02 - Wärme Wiederholung Energiearten Primärenergie Physikalische Energie Kernenergie Chemische Energie Potentielle Energie Kinetische Energie Innere Energie Quelle: Innere Energie Innere
Energiespeicher 02 - Wärme Wiederholung Energiearten Primärenergie Physikalische Energie Kernenergie Chemische Energie Potentielle Energie Kinetische Energie Innere Energie Quelle: Innere Energie Innere
2 Grundbegriffe der Thermodynamik
 2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
1. Wärmelehre 1.1. Temperatur Wiederholung
 1. Wärmelehre 1.1. Temperatur Wiederholung a) Zur Messung der Temperatur verwendet man physikalische Effekte, die von der Temperatur abhängen. Beispiele: Volumen einer Flüssigkeit (Hg-Thermometer), aber
1. Wärmelehre 1.1. Temperatur Wiederholung a) Zur Messung der Temperatur verwendet man physikalische Effekte, die von der Temperatur abhängen. Beispiele: Volumen einer Flüssigkeit (Hg-Thermometer), aber
Elektromotorische Kraft und thermodynamische Zustandsfunktionen
 Praktikum Physikalische Chemie I 11. November 2015 Elektromotorische Kraft und thermodynamische Zustandsfunktionen Guido Petri Anastasiya Knoch PC111/112, Gruppe 11 Aufgabenstellung Die Reaktion des Daniell-Elements
Praktikum Physikalische Chemie I 11. November 2015 Elektromotorische Kraft und thermodynamische Zustandsfunktionen Guido Petri Anastasiya Knoch PC111/112, Gruppe 11 Aufgabenstellung Die Reaktion des Daniell-Elements
1. Wärmelehre 1.1. Temperatur. Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités)
 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
Versuchsprotokoll: Neutralisationsenthalpie
 Versuchsprotokoll: Neutralisationsenthalpie Patrik Wolfram TId: 0 Alina Heidbüchel TId: 19 Gruppe 10 01.06.13 1 Inhaltsverzeichnis 1. Einleitung...3. Theorie...3 3. Durchführung...6 4.Auswertung...7 4.1
Versuchsprotokoll: Neutralisationsenthalpie Patrik Wolfram TId: 0 Alina Heidbüchel TId: 19 Gruppe 10 01.06.13 1 Inhaltsverzeichnis 1. Einleitung...3. Theorie...3 3. Durchführung...6 4.Auswertung...7 4.1
Vorlesung Physik für Pharmazeuten PPh Wärmelehre
 Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Thermodynamik der Atmosphäre II
 Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre II Der erste Hauptsatz der Thermodynamik Die Gesamtenergie in einem geschlossenen System bleibt erhalten. geschlossen steht hier für thermisch
Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre II Der erste Hauptsatz der Thermodynamik Die Gesamtenergie in einem geschlossenen System bleibt erhalten. geschlossen steht hier für thermisch
Physik Erster Hauptsatz (mechanisches und elektrisches Wärmeäquivalent)
 Physik Erster Hauptsatz (mechanisches und elektrisches Wärmeäquivalent) 1. Ziel des Versuches Umwandlung von mechanischer Reibungsarbeit in Wärme, Umwandlung von elektrischer Arbeit bzw. Energie in Wärme,
Physik Erster Hauptsatz (mechanisches und elektrisches Wärmeäquivalent) 1. Ziel des Versuches Umwandlung von mechanischer Reibungsarbeit in Wärme, Umwandlung von elektrischer Arbeit bzw. Energie in Wärme,
Temperatur. Temperaturmessung. Grundgleichung der Kalorik. 2 ² 3 2 T - absolute Temperatur / ºC T / K
 Temperatur Temperatur ist ein Maß für die mittlere kinetische Energie der Teilchen 2 ² 3 2 T - absolute Temperatur [ T ] = 1 K = 1 Kelvin k- Boltzmann-Konst. k = 1,38 10-23 J/K Kelvin- und Celsiusskala
Temperatur Temperatur ist ein Maß für die mittlere kinetische Energie der Teilchen 2 ² 3 2 T - absolute Temperatur [ T ] = 1 K = 1 Kelvin k- Boltzmann-Konst. k = 1,38 10-23 J/K Kelvin- und Celsiusskala
4 Thermodynamik mikroskopisch: kinetische Gastheorie makroskopisch: System:
 Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Hochschule Düsseldorf University of Applied Sciences. 20. April 2016 HSD. Energiespeicher Wärme
 Energiespeicher 02 - Wärme Wiederholung Energiearten Primärenergie Physikalische Energie Kernenergie Chemische Energie Potentielle Energie Kinetische Energie Innere Energie Quelle: Innere Energie Innere
Energiespeicher 02 - Wärme Wiederholung Energiearten Primärenergie Physikalische Energie Kernenergie Chemische Energie Potentielle Energie Kinetische Energie Innere Energie Quelle: Innere Energie Innere
Allgemeines Gasgesetz. PV = K o T
 Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Praktikum Physik. Protokoll zum Versuch 5: Spezifische Wärme. Durchgeführt am Gruppe X
 Praktikum Physik Protokoll zum Versuch 5: Spezifische Wärme Durchgeführt am 10.11.2011 Gruppe X Name 1 und Name 2 ([email protected]) ([email protected]) Betreuer: Wir bestätigen hiermit, dass wir das
Praktikum Physik Protokoll zum Versuch 5: Spezifische Wärme Durchgeführt am 10.11.2011 Gruppe X Name 1 und Name 2 ([email protected]) ([email protected]) Betreuer: Wir bestätigen hiermit, dass wir das
Physikalische Chemie Praktikum. Thermodynamik: Verbrennungsenthalpie einer organischen Substanz
 Hochschule Emden/Leer Physikalische Chemie Praktikum Vers. Nr. 18 Nov. 2016 Thermodynamik: Verbrennungsenthalpie einer organischen Substanz Allgemeine Grundlagen 1. Hauptsatz der Thermodynamik, Enthalpie,
Hochschule Emden/Leer Physikalische Chemie Praktikum Vers. Nr. 18 Nov. 2016 Thermodynamik: Verbrennungsenthalpie einer organischen Substanz Allgemeine Grundlagen 1. Hauptsatz der Thermodynamik, Enthalpie,
PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe. W 3 - Kalorimetrie
 10.08.2008 PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe Versuch: W 3 - Kalorimetrie 1. Grundlagen Definition und Einheit von Wärme und Temperatur; Wärmekapazität (spezifische und molare); Regel von Dulong
10.08.2008 PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe Versuch: W 3 - Kalorimetrie 1. Grundlagen Definition und Einheit von Wärme und Temperatur; Wärmekapazität (spezifische und molare); Regel von Dulong
Physikdepartment. Ferienkurs zur Experimentalphysik 4. Daniel Jost 10/09/15
 Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Thermo Dynamik. Mechanische Bewegung (= Arbeit) Wärme (aus Reaktion) maximale Umsetzung
 Thermo Dynamik Wärme (aus Reaktion) Mechanische Bewegung (= Arbeit) maximale Umsetzung Aussagen der Thermodynamik: Quantifizieren von: Enthalpie-Änderungen Entropie-Änderungen Arbeit, maximale (Gibbs Energie)
Thermo Dynamik Wärme (aus Reaktion) Mechanische Bewegung (= Arbeit) maximale Umsetzung Aussagen der Thermodynamik: Quantifizieren von: Enthalpie-Änderungen Entropie-Änderungen Arbeit, maximale (Gibbs Energie)
8.4.5 Wasser sieden bei Zimmertemperatur ******
 8.4.5 ****** 1 Motivation Durch Verminderung des Luftdrucks siedet Wasser bei Zimmertemperatur. 2 Experiment Abbildung 1: Ein druckfester Glaskolben ist zur Hälfte mit Wasser gefüllt, so dass die Flüsigkeit
8.4.5 ****** 1 Motivation Durch Verminderung des Luftdrucks siedet Wasser bei Zimmertemperatur. 2 Experiment Abbildung 1: Ein druckfester Glaskolben ist zur Hälfte mit Wasser gefüllt, so dass die Flüsigkeit
Versuch W1: Kalorimetrie
 Versuch W1: Kalorimetrie Aufgaben: 1. Bestimmen Sie die Wärmekapazität zweier Kalorimeter (Kalorimeterkonstanten). 2. Bestimmen Sie die spezifische Wärmekapazität von 2 verschiedenen festen Stoffen. 3.
Versuch W1: Kalorimetrie Aufgaben: 1. Bestimmen Sie die Wärmekapazität zweier Kalorimeter (Kalorimeterkonstanten). 2. Bestimmen Sie die spezifische Wärmekapazität von 2 verschiedenen festen Stoffen. 3.
Reaktionsenthalpie der Hydratbildung von Salzen
 Übungen in physikalischer Chemie für B.Sc.-Studierende Versuch Nr.: S12 Version 2015 Kurzbezeichnung: Hydratation Reaktionsenthalpie der Hydratbildung von Salzen Aufgabenstellung Molare Lösungsenthalpien
Übungen in physikalischer Chemie für B.Sc.-Studierende Versuch Nr.: S12 Version 2015 Kurzbezeichnung: Hydratation Reaktionsenthalpie der Hydratbildung von Salzen Aufgabenstellung Molare Lösungsenthalpien
Kalorimetrische Untersuchung verschiedener Enthalpieformen anhand von Oxalsäure, atronlauge, Essigsäure, Kaliumchlorid und Wasser
 Kalorimetrische Untersuchung verschiedener Enthalpieformen anhand von Oxalsäure, atronlauge, Essigsäure, Kaliumchlorid und Wasser Lisa Kamber, D-CHAB, 1. Semester [email protected] Jorge Ferreiro,
Kalorimetrische Untersuchung verschiedener Enthalpieformen anhand von Oxalsäure, atronlauge, Essigsäure, Kaliumchlorid und Wasser Lisa Kamber, D-CHAB, 1. Semester [email protected] Jorge Ferreiro,
Physikalische Chemie Praktikum. Mischphasenthermodynamik: Gefrierpunktserniedrigung Molmassenbestimmung
 Hochschule Emden / Leer Physikalische Chemie Praktikum Mischphasenthermodynamik: Gefrierpunktserniedrigung Molmassenbestimmung Vers.Nr. 17 Sept. 2015 Allgemeine Grundlagen a) Reine Stoffe Bei reinen Stoffen
Hochschule Emden / Leer Physikalische Chemie Praktikum Mischphasenthermodynamik: Gefrierpunktserniedrigung Molmassenbestimmung Vers.Nr. 17 Sept. 2015 Allgemeine Grundlagen a) Reine Stoffe Bei reinen Stoffen
Einführung in die Physikalische Chemie: Inhalt. Einführung in die Physikalische Chemie:
 Einführung in die Physikalische Chemie: Inhalt Einführung in die Physikalische Chemie: Inhalt Kapitel 9: Prinzipien der Thermodynamik Inhalt: 9.1 Einführung und Definitionen 9.2 Der 0. Hauptsatz und seine
Einführung in die Physikalische Chemie: Inhalt Einführung in die Physikalische Chemie: Inhalt Kapitel 9: Prinzipien der Thermodynamik Inhalt: 9.1 Einführung und Definitionen 9.2 Der 0. Hauptsatz und seine
Hydrodynamik: bewegte Flüssigkeiten
 Hydrodynamik: bewegte Flüssigkeiten Wir betrachten eine stationäre Strömung, d.h. die Geschwindigkeit der Strömung an einem gegebenen Punkt bleibt konstant im Laufe der Zeit. Außerdem betrachten wir zunächst
Hydrodynamik: bewegte Flüssigkeiten Wir betrachten eine stationäre Strömung, d.h. die Geschwindigkeit der Strömung an einem gegebenen Punkt bleibt konstant im Laufe der Zeit. Außerdem betrachten wir zunächst
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
1. Klausur ist am 5.12.! Jetzt lernen! Klausuranmeldung: Bitte heute in Listen eintragen!
 1. Klausur ist am 5.12.! Jetzt lernen! Klausuranmeldung: Bitte heute in Listen eintragen! Aggregatzustände Fest, flüssig, gasförmig Schmelz -wärme Kondensations -wärme Die Umwandlung von Aggregatzuständen
1. Klausur ist am 5.12.! Jetzt lernen! Klausuranmeldung: Bitte heute in Listen eintragen! Aggregatzustände Fest, flüssig, gasförmig Schmelz -wärme Kondensations -wärme Die Umwandlung von Aggregatzuständen
Gefrierpunktserniedrigung
 Knoch, Anastasiya Datum der Durchführung: Petri, Guido 05.01.2016 (Gruppe 11) Datum der Korrektur: 02.02.2016 Praktikum Physikalische Chemie I. Thermodynamik Gefrierpunktserniedrigung 1. Aufgabenstellung
Knoch, Anastasiya Datum der Durchführung: Petri, Guido 05.01.2016 (Gruppe 11) Datum der Korrektur: 02.02.2016 Praktikum Physikalische Chemie I. Thermodynamik Gefrierpunktserniedrigung 1. Aufgabenstellung
C Metallkristalle. Allgemeine Chemie 60. Fluorit CaF 2 KZ(Ca) = 8, KZ(F) = 4. Tabelle 7: weiter Strukturtypen. kubisch innenzentriert KZ = 8
 Allgemeine Chemie 60 Fluorit CaF 2 KZ(Ca) = 8, KZ(F) = 4 Tabelle 7: weiter Strukturtypen C Metallkristalle kubisch primitiv KZ = 6 kubisch innenzentriert KZ = 8 kubisch flächenzentriert, kubisch dichteste
Allgemeine Chemie 60 Fluorit CaF 2 KZ(Ca) = 8, KZ(F) = 4 Tabelle 7: weiter Strukturtypen C Metallkristalle kubisch primitiv KZ = 6 kubisch innenzentriert KZ = 8 kubisch flächenzentriert, kubisch dichteste
T1: Wärmekapazität eines Kalorimeters
 Grundpraktikum T1: Wärmekapazität eines Kalorimeters Autor: Partner: Versuchsdatum: Versuchsplatz: Abgabedatum: Inhaltsverzeichnis 1 Physikalische Grundlagen und Aufgabenstellung 2 2 Messwerte und Auswertung
Grundpraktikum T1: Wärmekapazität eines Kalorimeters Autor: Partner: Versuchsdatum: Versuchsplatz: Abgabedatum: Inhaltsverzeichnis 1 Physikalische Grundlagen und Aufgabenstellung 2 2 Messwerte und Auswertung
Übung 2. Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen
 Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen Wärmekapazitäten isochore/isobare Zustandsänderungen Standardbildungsenthalpien Heizwert/Brennwert adiabatische Flammentemperatur WS 2013/14
Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen Wärmekapazitäten isochore/isobare Zustandsänderungen Standardbildungsenthalpien Heizwert/Brennwert adiabatische Flammentemperatur WS 2013/14
1.1 V 1 Überprüfung des Satzes von Hess mit der Reaktion von Calcium und Salzsäure
 1.1 V 1 Überprüfung des Satzes von Hess mit der Reaktion von Calcium und Salzsäure In diesem Versuch soll der Satz von Hess (die umgesetzte Wärmemenge ist bei einer chemischen Reaktion unabhängig vom Weg)
1.1 V 1 Überprüfung des Satzes von Hess mit der Reaktion von Calcium und Salzsäure In diesem Versuch soll der Satz von Hess (die umgesetzte Wärmemenge ist bei einer chemischen Reaktion unabhängig vom Weg)
Mode der Bewegung, Freiheitsgrade
 Mode der Bewegung, Freiheitsgrade Bewegungsmoden (normal modes of motion) : Jede UNABHÄNGIGE Bewegungsmöglichkeit der Atome (unabhängig: im quantenmechanischen Sinne durch orthogonale Wellenfunktionen
Mode der Bewegung, Freiheitsgrade Bewegungsmoden (normal modes of motion) : Jede UNABHÄNGIGE Bewegungsmöglichkeit der Atome (unabhängig: im quantenmechanischen Sinne durch orthogonale Wellenfunktionen
Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt
 1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
Thermodynamik. Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur
 Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Grundlagen der Physik II
 Grundlagen der Physik II Othmar Marti 12. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 12. 07. 2007 Klausur Die Klausur
Grundlagen der Physik II Othmar Marti 12. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 12. 07. 2007 Klausur Die Klausur
Die Innere Energie U
 Die Innere Energie U U ist die Summe aller einem System innewohnenden Energien. Es ist unmöglich, diese zu berechnen. U kann nicht absolut angegeben werden! Differenzen in U ( U) können gemessen werden.
Die Innere Energie U U ist die Summe aller einem System innewohnenden Energien. Es ist unmöglich, diese zu berechnen. U kann nicht absolut angegeben werden! Differenzen in U ( U) können gemessen werden.
T6 - Temperaturabhängigkeit der molaren Wärmekapazität
 6 - emperaturabhängigkeit der molaren Wärmekapazität Aufgaben: 1. Messung der molaren Wärmekapazität von Aluminium bzw. Kupfer als Funktion der emperatur im Bereich von 196 C bis Zimmertemperatur. 2. Berechnung
6 - emperaturabhängigkeit der molaren Wärmekapazität Aufgaben: 1. Messung der molaren Wärmekapazität von Aluminium bzw. Kupfer als Funktion der emperatur im Bereich von 196 C bis Zimmertemperatur. 2. Berechnung
Thermodynamik. Thermodynamics. Markus Arndt. Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008
 Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Spezifische Wärmekapazität fester Körper
 Version: 14. Oktober 2005 Spezifische Wärmekapazität fester Körper Stichworte Wärmemenge, spezifische Wärme, Schmelzwärme, Wärmekapazität, Wasserwert, Siedepunkt, innere Energie, Energiesatz, Hauptsätze
Version: 14. Oktober 2005 Spezifische Wärmekapazität fester Körper Stichworte Wärmemenge, spezifische Wärme, Schmelzwärme, Wärmekapazität, Wasserwert, Siedepunkt, innere Energie, Energiesatz, Hauptsätze
Formel X Leistungskurs Physik 2001/2002
 Versuchsaufbau: Messkolben Schlauch PI Barometer TI 1 U-Rohr-Manometer Wasser 500 ml Luft Pyknometer 2 Bild 1: Versuchsaufbau Wasserbad mit Thermostat Gegeben: - Länge der Schläuche insgesamt: 61,5 cm
Versuchsaufbau: Messkolben Schlauch PI Barometer TI 1 U-Rohr-Manometer Wasser 500 ml Luft Pyknometer 2 Bild 1: Versuchsaufbau Wasserbad mit Thermostat Gegeben: - Länge der Schläuche insgesamt: 61,5 cm
Energie und Energieerhaltung. Mechanische Energieformen. Arbeit. Die goldene Regel der Mechanik. Leistung
 - Formelzeichen: E - Einheit: [ E ] = 1 J (Joule) = 1 Nm = 1 Energie und Energieerhaltung Die verschiedenen Energieformen (mechanische Energie, innere Energie, elektrische Energie und Lichtenergie) lassen
- Formelzeichen: E - Einheit: [ E ] = 1 J (Joule) = 1 Nm = 1 Energie und Energieerhaltung Die verschiedenen Energieformen (mechanische Energie, innere Energie, elektrische Energie und Lichtenergie) lassen
Hochschule Düsseldorf University of Applied Sciences. 13. April 2016 HSD. Energiespeicher. Thermodynamik
 13. April 2016 Energiespeicher Thermodynamik Prof. Dr. Alexander Braun // Energiespeicher // SS 2016 26. April 2017 Thermodynamik Grundbegriffe Prof. Dr. Alexander Braun // Energiespeicher // SS 2017 26.
13. April 2016 Energiespeicher Thermodynamik Prof. Dr. Alexander Braun // Energiespeicher // SS 2016 26. April 2017 Thermodynamik Grundbegriffe Prof. Dr. Alexander Braun // Energiespeicher // SS 2017 26.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
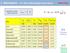 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
Physikalische Chemie 1
 Physikalische Chemie 1 Christian Lehmann 31. Januar 2004 Inhaltsverzeichnis 1 Einführung 2 1.1 Teilgebiete der Physikalischen Chemie............... 2 1.1.1 Thermodynamik (Wärmelehre)............... 2 1.1.2
Physikalische Chemie 1 Christian Lehmann 31. Januar 2004 Inhaltsverzeichnis 1 Einführung 2 1.1 Teilgebiete der Physikalischen Chemie............... 2 1.1.1 Thermodynamik (Wärmelehre)............... 2 1.1.2
O. Sternal, V. Hankele. 5. Thermodynamik
 5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
Phasenumwandlungsenthalpie
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 7 Phasenumwandlungsenthalpie Die Enthalpieänderung beim Übergang eines Systems in einen anderen Aggregatzustand kann unter der Voraussetzung,
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 7 Phasenumwandlungsenthalpie Die Enthalpieänderung beim Übergang eines Systems in einen anderen Aggregatzustand kann unter der Voraussetzung,
Physikalisches Praktikum Wirtschaftsingenieurwesen Physikalische Technik und Orthopädietechnik Prof. Dr. Chlebek, MSc. M. Gilbert
 Physikalisches Praktikum Wirtschaftsingenieurwesen Physikalische Technik und Orthopädietechnik Prof. Dr. Chlebek, MSc. M. Gilbert TH 01 Wärmekapazität und Wirkungsgrad (Pr_PhI_TH01_Wärmekapazität_6, 30.8.009)
Physikalisches Praktikum Wirtschaftsingenieurwesen Physikalische Technik und Orthopädietechnik Prof. Dr. Chlebek, MSc. M. Gilbert TH 01 Wärmekapazität und Wirkungsgrad (Pr_PhI_TH01_Wärmekapazität_6, 30.8.009)
Skript zur Vorlesung
 Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
E5: Faraday-Konstante
 E5: Faraday-Konstante Theoretische Grundlagen: Elektrischer Strom ist ein Fluss von elektrischer Ladung; in Metallen sind Elektronen die Ladungsträger, in Elektrolyten übernehmen Ionen diese Aufgabe. Befinden
E5: Faraday-Konstante Theoretische Grundlagen: Elektrischer Strom ist ein Fluss von elektrischer Ladung; in Metallen sind Elektronen die Ladungsträger, in Elektrolyten übernehmen Ionen diese Aufgabe. Befinden
Reaktion und Energie
 Reaktion und Energie Grundsätzliches Bei chemischen Reaktionen werden die Atome der Ausgangsstoffe neu angeordnet, d. h. Bindungen werden gespalten und neu geknüpft. Die Alltasgserfahrung legt nahe, dass
Reaktion und Energie Grundsätzliches Bei chemischen Reaktionen werden die Atome der Ausgangsstoffe neu angeordnet, d. h. Bindungen werden gespalten und neu geknüpft. Die Alltasgserfahrung legt nahe, dass
Physikalische Chemie in der Schule
 Universität Kassel, Grundpraktikum Physikalische Chemie Studiengang Lehramt Chemie Physikalische Chemie in der Schule I. Anfangsunterricht: Die Merkmale der chemischen Reaktion (Lit. Elemente chemie I
Universität Kassel, Grundpraktikum Physikalische Chemie Studiengang Lehramt Chemie Physikalische Chemie in der Schule I. Anfangsunterricht: Die Merkmale der chemischen Reaktion (Lit. Elemente chemie I
Zwei neue Basisgrössen in der Physik
 Nachtrag zur orlesung am vergangenen Montag Zwei neue Basisgrössen in der Physik 9. Wärmelehre, kinetische Gastheorie Temperatur T: Wärme ist verknüpft mit ungeordneter Bewegung der Atome oder Moleküle.
Nachtrag zur orlesung am vergangenen Montag Zwei neue Basisgrössen in der Physik 9. Wärmelehre, kinetische Gastheorie Temperatur T: Wärme ist verknüpft mit ungeordneter Bewegung der Atome oder Moleküle.
6.2 Zweiter HS der Thermodynamik
 Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
II. Der nullte Hauptsatz
 II. Der nullte Hauptsatz Hauptsätze... - sind thermodyn. Gesetzmäßigkeiten, die als Axiome (Erfahrungssätze) formuliert wurden - sind mathematisch nicht beweisbar, basieren auf Beobachtungen und Erfahrungen
II. Der nullte Hauptsatz Hauptsätze... - sind thermodyn. Gesetzmäßigkeiten, die als Axiome (Erfahrungssätze) formuliert wurden - sind mathematisch nicht beweisbar, basieren auf Beobachtungen und Erfahrungen
Reaktionsenthalpie der Hydratbildung von Salzen
 Übungen in physikalischer Chemie für B.Sc.-Studierende Versuch Nr.: S12 Version 2016 Kurzbezeichnung: Hydratbildung Reaktionsenthalpie der Hydratbildung von Salzen Aufgabenstellung Die molaren Lösungsenthalpien
Übungen in physikalischer Chemie für B.Sc.-Studierende Versuch Nr.: S12 Version 2016 Kurzbezeichnung: Hydratbildung Reaktionsenthalpie der Hydratbildung von Salzen Aufgabenstellung Die molaren Lösungsenthalpien
4.1.2 Quantitative Definition durch Wärmekapazitäten
 4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
Physikalische Chemie 0 Klausur, 22. Oktober 2011
 Physikalische Chemie 0 Klausur, 22. Oktober 2011 Bitte beantworten Sie die Fragen direkt auf dem Blatt. Auf jedem Blatt bitte Name, Matrikelnummer und Platznummer angeben. Zu jeder der 25 Fragen werden
Physikalische Chemie 0 Klausur, 22. Oktober 2011 Bitte beantworten Sie die Fragen direkt auf dem Blatt. Auf jedem Blatt bitte Name, Matrikelnummer und Platznummer angeben. Zu jeder der 25 Fragen werden
