MA 440 GEOMETRIE 2 HS 07
|
|
|
- David Beutel
- vor 6 Jahren
- Abrufe
Transkript
1 MA 440 GEOMETRIE 2 HS 07 Zielsetzung Die Stuierenen lernen, ass geometrische Ieen vielfach verwenet weren. Sie erweitern Ihr Wissen er Eukliischen Geometrie. Sie lernen, ass geometrisches Denken weitere Zweige er Mathematik eröffnet. Sie erwerben Fachwissen für en Geometrie-Unterricht er Sekunarstufe I Inhalt Golener Schnitt Kreiswinkelsätze Reguläre Polygone Symmetrien Eukliische un Nichteukliische Geometrie Graphen un Algorithmen Vorlesung mit Übungen Donnerstag, , UZI Hörsaal Y27 H 25 Jee 2. Woche finet von eine Übungsstune in Gruppen statt. Ganze Gruppe A Z im Raum??5 bei Christoph Schwarz, schwarz_ch@bluewin.ch Währen er Übungsstune können Sie Fragen zur laufenen Übungsserie stellen. Es gibt 6 Übungsserien, wobei Sie je etwa 20 Punkte erreichen können. Die gelösten Aufgaben geben Sie eine Woche später ab. Die korrigierten Aufgaben erhalten Sie in er nächsten Übungsstune zurück. Leistungsnachweis Der Leistungsnachweis, bzw. ie Testatbeingung ist erfüllt, wenn Sie minestens zwei Drittel aller möglichen Punkte, also 80 oer mehr Punkte, erreicht haben. Schriftliche Prüfung Sobal sie ie rei Mathematikmoule (Geometrie 2 un 3 un Zahlentheorie) besucht haben, weren alle rei Moule zusammen schriftlich geprüft. Die Prüfungsaufgaben sin im Stil er Übungsaufgaben. Die Prüfung finet meistens in er ersten Woche eines neuen Semesters statt. Bei ungenügener Leistung kann iese Prüfung einmal wieerholt weren. Das Prüfungsergebnis fliesst in ie Diplomnote ein. Denken Sie aran, ass Mathematik nur verstanen weren kann, wenn man selber Aufgaben zur präsentierten Theorie löst. Die Übungsserien bilen aher einen wichtigen Bestanteil jees Mathematikmouls. Johanna Schönenberger-Deuel Dr. sc. math Institut für Mathematik, Uni Zürich
2 2. Golener Schnitt Die Geometrie birgt zwei grosse Schätze: er eine ist er Satz von Pythagoras, er anere ist er Golene Schnitt. Den ersten können wir mit einem Scheffel Gol vergleichen, en zweiten ürfen wir ein kostbares Juwel nennen. Johannes Kepler, Der Golene Schnitt ist as wohl berühmteste Zahlenverhältnis. Das Pentagramm kommt nicht nur in er Geometrie vor, es ist ein wichtiges Zeichen in er Magie (Druenfuss: Schutzzeichen für Hexen un Druen). In er Antike ist as Pentagramm ein Symbol für unkle, unergrünliche Zusammenhänge. Es war as Erkennungszeichen es pythagoräischen Geheimbunes. Beim pythagoräischen Weltbil beruhen alle Harmonien auf ganzzahligen Verhältnissen.
3 3 Aufgabe: Untersuchen Sie as regelmässige Fünfeck. Zeichnen Sie ie Diagonalen. Welches ist as Verhältnis von Diagonale zu Seite?
4 4 Hippasos von Metapont hat aber schon um 450 v. Chr. enteckt, ass gerae im Pentagramm as Verhältnis von Diagonale zu Seite kein gemeinsames Mass enthält, as Verhältnis ist also irrational. Das haben Sie in er obigen Aufgabe herausgefunen.! = Seite Diagonale = s " = Diagonale Seite = s =! Die Verhältnisse σ un τ sin irrationale Zahlen. In er Geometrie kommen iese Verhältnisse auch in aneren Zusammenhängen vor. Definition: Der Punkt T teilt ie Strecke AB stetig oer im Golenen Schnitt, wenn gilt: Die ganze Strecke verhält sich zum längeren Abschnitt s, wie er längere Abschnitt s zum kürzeren - s. - s s A T B Der länger Abschnitt heisst Major, er kürzere Minor.
5 5 Ähnliche Dreiecke: ΔABD ~ ΔBTA! AD AB = AB BT! s = s " s! # = # "! # 2 " # " = 0! = s = 5 + =.68 2 " = s = 5 # =
6 6 Konstruktionen es Golenen Schnitts Die Strecke = 0 cm soll im Golenen Schnitt geteilt weren. Warum besitzen un s kein gemeinsames Mass m? Hätten un s ein gemeinsames Mass m, ann gäbe es natürliche Zahlen p un q, so ass = p. m un s = q. m. Dann wäre s = p q!!.
7 7 Beweisiee von Hippasos Hippasos von Metapont (ca. 450 v. Chr.) war ein griechischer Mathematiker aus em Kreis er Pythagoreer. Nach en Überlieferungen hat Hippasos zur glänzenen antiken Musiktheorie Wesentliches beigetragen. Er entwickelte Tonleitertheorien un Ähnliches. Auch wir heute angenommen, ass er es war, er ie berühmte Inkommensurabilität von Seite un Diagonale im Fünfeck (Pentagramm), em pythagoräischen Orenssymbol, fan. Versucht man nämlich urch Wechselwegnahme zwischen Seite un Diagonale eine kleinste gemeinsame Teilstrecke zu finen, so stößt man auf ein kleineres Pentagramm, in em ie Streckenverhältnisse wieer er Ausgangssituation gleich sin un so weiter. Es gibt ie Legene, ass ie Pythagoräer Hippasos im Meer ertränkt haben sollen, weil er iesen berühmten Beweis veröffentlicht hat. oer Fügt man Fünfecke so aneinaner, ass ie Seite s n es n-ten Fünfecks ie Diagonale n+ es (n+)-ten Fünfecks wir. Also gilt ann: n+ = s n! n s n = s n s n+ = n+ s n+ für jees n! " = n = n+ = s n s n+
8 Hätten n un s n ein gemeinsames Mass m, ann hätten es auch n+ un s n+. Nun weren aber ie Fünfecke mit wachsenem n immer kleiner, also kleiner als jees Mass m. Das ist nicht möglich, also gibt es kein gemeinsames Mass m. 8 Der Name Golener Schnitt ist im 9. Jahrhunert entstanen, wahrscheinlich aus sectio ivina (Kepler) un regula aurea (golene Regel). Der Golene Schnitt spielt in er Kunst eine grosse Rolle. Warum er Name stetige Teilung? - Trägt man bei einer stetig geteilten Strecke a en Minor (ie kleinere Strecke) auf em Major s (längere Strecke) ab, so wir iese wieer im Golenen Schnitt geteilt. (Beweis?)
9 9 Weitere Beziehungen von σ un τ! = =.68 " =! = 5 # 2 = 0.68 Da τ > 0 un τ 2 = + τ, erhalten wir für τ ie Wurzelfolge! = +! = + +! = + + +! = Für σ gilt = σ 2 + σ = σ(σ + ), also! = Kettenbruch! = +! = + +! = + +! un amit erhalten wir für σ en + +! = Näherungswerte für σ berechnen:! = =! 2 =! 3 = +! = 2 +! 2 = 2 3! 4 = 3 5,! 5 = 5 8,! 6 = 8 3,! 7 = 3 2,... σ 7 = ist ein guter Näherungswert für σ = Vergleichen Sie as Rechteck R mit en Seitenlängen 3 un 2 un as Golene Rechteck mit en Seitenlängen 3 un 3τ (= 2.034). Vergleichen Sie ie Zahlenfolge er Zähler sowie iejenige er Nenner. Kennen Sie ie Folge? Fibonacci-Folge.
10 0 Definition: Ein Rechteck mit Seitenverhältnis heisst Golenes Rechteck. Länge : Breite = : s =! = s Golene Dreiecke sin gleichschenklige Dreiecke mit Seitenverhältnis Schenkel : Basis = : s =! oer Schenkel : Basis = s : = " Somit gibt es spitzwinklige oer stumpfwinklige Golene Dreiecke. s s s Aufgabe: Zeichnen Sie im regulären Fünfeck ie beien Arten Golener Dreiecke ein.
11 Die Rechtecke R n mit en Seiten n un s n sin Golene Rechtecke. Die kürzere Seite es grösseren Rechtecks R n ist immer ie längere Seite es nachfolgenen kleineren Rechtecks R n-. Bemerkung: Mit Hilfe es Eukliischen Algorithmus zur Bestimmung es ggt zweier natürlicher Zahlen kann man schön zeigen, ass für Golene Rechtecke kein gemeinsames Mass er beien Seiten existiert. Eukliischen Algorithmus zur Bestimmung es ggt von a un b (a > b): ggt(a, b) = ggt(b, a - b) =... [enn aus ggt(a, b) = m, folgt a = pm un b = qm für p, q natürliche Zahlen, also a - b = m(p - q)] z.b. ggt(5, 9) = ggt(9, 6) = ggt(6, 3) = ggt(3, 3) = 3. Zeichnen Sie azu ein Rechteck mit Seitenlängen 5 un 9. Von iesem Rechteck nimmt man solange ein Quarat (Seitenlänge = kleinere Rechteckseite) weg, bis ein Quarat übrig bleibt. Mit iesem Quarat lässt sich as gegebene Rechteck auspflastern, seine Seite ist as grösste gemeinsame Mass er Rechteckseiten. Folgerung: Erscheint beim Verfahren es Eukliischen Algorithmus ein Rechteck, as zum gegebenen ähnlich ist, so kann nie ein Quarat übrig bleiben, es gibt also kein gemeinsames Mass er Rechteckseiten.
12 2 Die Vorerfront es Parthenon (Athen, 432 v. Chr.) passt fast exakt in ein Golenes Rechteck. Konstruktionen. Golenes Rechteck mit gegebener Breite b
13 3 2. Reguläres 5- Eck mit gegebener Seite s 3. Reguläres 5- Eck un 0-Eck mit gegebenem Umkreis r
2. Goldener Schnitt. Der Goldene Schnitt ist das wohl berühmteste Zahlenverhältnis.
 8 2. Golener Schnitt Die Geometrie birgt zwei grosse Schätze: er eine ist er Satz von Pythagoras, er anere ist er Golene Schnitt. Den ersten können wir mit einem Scheffel Gol vergleichen, en zweiten ürfen
8 2. Golener Schnitt Die Geometrie birgt zwei grosse Schätze: er eine ist er Satz von Pythagoras, er anere ist er Golene Schnitt. Den ersten können wir mit einem Scheffel Gol vergleichen, en zweiten ürfen
6 Lineare Kongruenzen
 6 Lineare Kongruenzen Sei m > 0 un a, b beliebig. Wir wollen ie Frage untersuchen, unter welchen Beingungen an a, b un m eine Zahl x 0 existiert, so aß ax 0 b mo m. Wenn ein solches x 0 existiert, sagen
6 Lineare Kongruenzen Sei m > 0 un a, b beliebig. Wir wollen ie Frage untersuchen, unter welchen Beingungen an a, b un m eine Zahl x 0 existiert, so aß ax 0 b mo m. Wenn ein solches x 0 existiert, sagen
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler Folie 1 /15 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 2. Die reellen Zahlen A. Filler Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2016
A. Filler Folie 1 /15 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 2. Die reellen Zahlen A. Filler Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2016
1 Goldener Schnitt. und a = m + M. 1, und wird im Allgemeinen mit τ (griechisch: tau) bezeichnet. Das Verhältnis M m hat den Wert 1+ 5
 1 Goldener Schnitt Definition und Satz 1.1 (Goldener Schnitt) Sei AB die Strecke zwischen den Punkten A und B. Ein Punkt S von AB teilt AB im Goldenen Schnitt, falls sich die größere Teilstrecke M (Major)
1 Goldener Schnitt Definition und Satz 1.1 (Goldener Schnitt) Sei AB die Strecke zwischen den Punkten A und B. Ein Punkt S von AB teilt AB im Goldenen Schnitt, falls sich die größere Teilstrecke M (Major)
B) Konstruktion des geometrischen Mittels und geometrisches Wurzelziehen :
 Seite I Einige interessante elementargeometrische Konstruktionen Ausgehend von einigen bekannten Sätzen aus der Elementargeometrie lassen sich einige hübsche Konstruktionen herleiten, die im folgenden
Seite I Einige interessante elementargeometrische Konstruktionen Ausgehend von einigen bekannten Sätzen aus der Elementargeometrie lassen sich einige hübsche Konstruktionen herleiten, die im folgenden
Der Satz des Pythagoras. Kein Darwinscher Zufall
 Der Satz des Pythagoras. Kein Darwinscher Zufall Detlef Dürr duerr@rz.mathematik.uni-muenchen.de 1. Mai 2012 1 Zahlen-Verhältnisse Die Grunderkenntnis der Gesetzmäßigkeit in der Natur ist Harmonie. Heute
Der Satz des Pythagoras. Kein Darwinscher Zufall Detlef Dürr duerr@rz.mathematik.uni-muenchen.de 1. Mai 2012 1 Zahlen-Verhältnisse Die Grunderkenntnis der Gesetzmäßigkeit in der Natur ist Harmonie. Heute
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 2. Übung/Lösung Mathematik für Studierende der Biologie
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anreas Herz, Dr. Stefan Häusler email: haeusler@biologie.uni-muenchen.e Department Biologie II Telefon: 089-80-74800 Großhaernerstr. Fa:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anreas Herz, Dr. Stefan Häusler email: haeusler@biologie.uni-muenchen.e Department Biologie II Telefon: 089-80-74800 Großhaernerstr. Fa:
1 Der Goldene Schnitt
 Goldener Schnitt 1 Der Goldene Schnitt 1 1.1 Das regelmäßige Zehneck 1 1. Ein anderer Name für den Goldenen Schnitt 4 1.3 Der Goldene Schnitt in Zahlen 6 1.4 Die Potenzen von und 8 1.5 Drei Beispiele 10
Goldener Schnitt 1 Der Goldene Schnitt 1 1.1 Das regelmäßige Zehneck 1 1. Ein anderer Name für den Goldenen Schnitt 4 1.3 Der Goldene Schnitt in Zahlen 6 1.4 Die Potenzen von und 8 1.5 Drei Beispiele 10
Aufgaben Geometrie Lager
 Schweizer Mathematik-Olympiade Aufgaben Geometrie Lager Aktualisiert: 26. Juni 2014 Starter 1. Zwei Städte A und B liegen auf verschiedenen Seiten eines Flusses. An welcher Stelle muss eine Brücke rechtwinklig
Schweizer Mathematik-Olympiade Aufgaben Geometrie Lager Aktualisiert: 26. Juni 2014 Starter 1. Zwei Städte A und B liegen auf verschiedenen Seiten eines Flusses. An welcher Stelle muss eine Brücke rechtwinklig
Arbeitsblatt 2 Übungen zu Mathematik I für das Lehramt an der Grund- und Mittelstufe sowie an Sonderschulen H. Strade, B. Werner WiSe 06/
 14. November 2006 Arbeitsblatt 2 Übungen zu Mathematik I für das Lehramt an der Grund- und Mittelstufe sowie an Sonderschulen H. Strade, B. Werner WiSe 06/07 31.10.06 Präsenzaufgaben: 1) Welche rationale
14. November 2006 Arbeitsblatt 2 Übungen zu Mathematik I für das Lehramt an der Grund- und Mittelstufe sowie an Sonderschulen H. Strade, B. Werner WiSe 06/07 31.10.06 Präsenzaufgaben: 1) Welche rationale
Geschichte Grundlagen Fibonacci-Zahlen Geometrischer Trugschluß Anwendung Fazit und Ausblick. Der Goldene Schnitt. Dario Jotanovic
 Der Goldene Schnitt Dario Jotanovic Mathematisches Proseminar Implementierung mathematischer Algorithmen Hochschule Darmstadt 19. Dezember 2013 Inhaltsangabe 1 Geschichte 2 Grundlagen Teilung im goldenen
Der Goldene Schnitt Dario Jotanovic Mathematisches Proseminar Implementierung mathematischer Algorithmen Hochschule Darmstadt 19. Dezember 2013 Inhaltsangabe 1 Geschichte 2 Grundlagen Teilung im goldenen
Vom goldenen Schnitt zum Alexanderplatz in Berlin
 Vom goldenen Schnitt zum Alexanderplatz in Berlin Mathematik von 1200 bis 2004 Stefan Kühling, Fachbereich Mathematik skuehling @ fsmath.mathematik.uni-dortmund.de Schnupper Uni 26. August 2004 1 1 Goldener
Vom goldenen Schnitt zum Alexanderplatz in Berlin Mathematik von 1200 bis 2004 Stefan Kühling, Fachbereich Mathematik skuehling @ fsmath.mathematik.uni-dortmund.de Schnupper Uni 26. August 2004 1 1 Goldener
Goldener Schnitt Was war das große Geheimnis der Pythagoräer?
 Das Pentagramm Der Drudenfuß Das Pentagramm war das Zeichen des Geheimbundes der Pythagoräer, und diese geheimnisvolle Figur gilt schon seit alters her als magisches Symbol. So fand es z.b. in früherer
Das Pentagramm Der Drudenfuß Das Pentagramm war das Zeichen des Geheimbundes der Pythagoräer, und diese geheimnisvolle Figur gilt schon seit alters her als magisches Symbol. So fand es z.b. in früherer
Binomische Formel mod p
 Binomische Formel mo p Lemma Binomische Formel mo p Seien a, b Z un p P. Dann gilt (a+b) p a p + b p mo p. Nach Binomischer Formel gilt (a+b) p = p p ) i=0( i a i b p i = a p + b p + p 1( p ) i=1 i a i
Binomische Formel mo p Lemma Binomische Formel mo p Seien a, b Z un p P. Dann gilt (a+b) p a p + b p mo p. Nach Binomischer Formel gilt (a+b) p = p p ) i=0( i a i b p i = a p + b p + p 1( p ) i=1 i a i
Zahlentheorie Aus der vorlesung von Lorenz Halbeisen Frühjahressemester 2014
 Zahlentheorie Aus der vorlesung von Lorenz Halbeisen Frühjahressemester 204 unai Csaba 3. Juni 204 ieses okument ist auf http://edunai.ch/?section=mitschriften&subsection=zahlentheorie verfügbar. ieses
Zahlentheorie Aus der vorlesung von Lorenz Halbeisen Frühjahressemester 204 unai Csaba 3. Juni 204 ieses okument ist auf http://edunai.ch/?section=mitschriften&subsection=zahlentheorie verfügbar. ieses
Dr. Neidhardt Thema: Parabeln. [ein Bindeglied zwischen Geometrie und Algebra ] Referent: Christian Schuster
![Dr. Neidhardt Thema: Parabeln. [ein Bindeglied zwischen Geometrie und Algebra ] Referent: Christian Schuster Dr. Neidhardt Thema: Parabeln. [ein Bindeglied zwischen Geometrie und Algebra ] Referent: Christian Schuster](/thumbs/55/35798812.jpg) Dr. Neihart 14.11.03 Thema: Parabeln [ein Bineglie zwischen Geometrie un Algebra ] Referent: Christian Schuster Glieerung: Anwenungsgebiete un Vorkommen von Parabel Erscheinungen in er Natur Parabeln:
Dr. Neihart 14.11.03 Thema: Parabeln [ein Bineglie zwischen Geometrie un Algebra ] Referent: Christian Schuster Glieerung: Anwenungsgebiete un Vorkommen von Parabel Erscheinungen in er Natur Parabeln:
3. Vorlesung. Die Existenz des Pentagons. (*)
 3. Vorlesung. ie Existenz des Pentagons. (*) In dieser Vorlesung werden wir sehen wie die Griechen bewiesen haben, dass es das Pentagon wirklich gibt. ieser eweis ist schon recht anspruchsvoll. So anspruchsvoll,
3. Vorlesung. ie Existenz des Pentagons. (*) In dieser Vorlesung werden wir sehen wie die Griechen bewiesen haben, dass es das Pentagon wirklich gibt. ieser eweis ist schon recht anspruchsvoll. So anspruchsvoll,
Geometrie Winkel und Vierecke PRÜFUNG 02. Ohne Formelsammlung! Name: Klasse: Datum: Punkte: Note: Klassenschnitt/ Maximalnote : Ausgabe: 2.
 GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
Kleiner Satz von Fermat
 Kleiner Satz von Fermat Satz Kleiner Satz von Fermat Sei p P. Dann gilt a p a mo p für alle a Z. Wir führen zunächst eine Inuktion für a 0 urch. IA a = 0: 0 p 0 mo p. IS a a+1: Nach vorigem Lemma gilt
Kleiner Satz von Fermat Satz Kleiner Satz von Fermat Sei p P. Dann gilt a p a mo p für alle a Z. Wir führen zunächst eine Inuktion für a 0 urch. IA a = 0: 0 p 0 mo p. IS a a+1: Nach vorigem Lemma gilt
PH Heidelberg, Fach Mathematik Modulprüfung 2, Einführung in die Geometrie, Wintersemester 09/10, Name Vorname Matrikelnummer
 Moulprüfung, Einführung in ie Geometrie, Wintersemester 09/0,.0.000 ufgae (Multiple hoice) a) Klaus, Gera, Max un Steffi führen inirekte eweise in er asoluten Geometrie. aei verwenen sie ie nachfolgenen
Moulprüfung, Einführung in ie Geometrie, Wintersemester 09/0,.0.000 ufgae (Multiple hoice) a) Klaus, Gera, Max un Steffi führen inirekte eweise in er asoluten Geometrie. aei verwenen sie ie nachfolgenen
Fächerverbindender Unterricht Renaissance
 Fächerverbindender Unterricht Renaissance Bereich Mathematik THEMA: Der Goldene Schnitt Zeit: Schüler bestimmen das Arbeitstempo selbst, müssen aber alle Aufgaben fertig stellen Bei 14 Tagen FvU haben
Fächerverbindender Unterricht Renaissance Bereich Mathematik THEMA: Der Goldene Schnitt Zeit: Schüler bestimmen das Arbeitstempo selbst, müssen aber alle Aufgaben fertig stellen Bei 14 Tagen FvU haben
1 Zahlentheorie. 1.1 Kongruenzen
 3 Zahlentheorie. Kongruenzen Der letzte Abschnitt zeigte, daß es sinnvoll ist, mit großen Zahlen möglichst einfach rechnen zu können. Oft kommt es nicht darauf, an eine Zahl im Detail zu kennen, sondern
3 Zahlentheorie. Kongruenzen Der letzte Abschnitt zeigte, daß es sinnvoll ist, mit großen Zahlen möglichst einfach rechnen zu können. Oft kommt es nicht darauf, an eine Zahl im Detail zu kennen, sondern
Montessori-Diplomkurs Inzlingen Geometrische Mappe Die metallenen Dreiecke
 Geometrische Mappe Die metallenen Dreiecke 1 Material 4 metallene Rahmen (14 cm X 14 cm) mit gleichseitigen Dreiecken (Seitenlänge 10 cm). Die Dreiecke sind wie folgt unterteilt Ganze Halbe Drittel Viertel
Geometrische Mappe Die metallenen Dreiecke 1 Material 4 metallene Rahmen (14 cm X 14 cm) mit gleichseitigen Dreiecken (Seitenlänge 10 cm). Die Dreiecke sind wie folgt unterteilt Ganze Halbe Drittel Viertel
Übungsaufgaben Repetitionen
 TG TECHNOLOGISCHE GRUNDLAGEN LÖSUNGSSATZ Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Übungsaufgaben Repetitionen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut
TG TECHNOLOGISCHE GRUNDLAGEN LÖSUNGSSATZ Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Übungsaufgaben Repetitionen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut
Von Sehnen und Sehnenlängen Konstruktion (mit Zirkel und Lineal) und Rechnung
 Die regelmäßige 5-Ecks - Konstruktion des Klaudios Ptolemaios (gelebt ca. 100 bis ca. 160 n. Chr. in Alexandria) 1 : Gegeben ein Kreis mit Durchmesser AB. D ist der Mittelpunkt der trecke MB. C ist Kreispunkt
Die regelmäßige 5-Ecks - Konstruktion des Klaudios Ptolemaios (gelebt ca. 100 bis ca. 160 n. Chr. in Alexandria) 1 : Gegeben ein Kreis mit Durchmesser AB. D ist der Mittelpunkt der trecke MB. C ist Kreispunkt
Determinanten. a e b f a c b d. b) x = , y = c) zu einem Spaltenvektor das Vielfache des anderen Spaltenvektors addiert wird,
 Determinanten Wir entwickeln eine Lösungsformel für Gleichungssysteme mit zwei Variablen. ax + cy = e b bx + y = f a } abx bcy = be + abx + ay = af ya bc = af be Man schreibt y = af be a bc = a e b f analog
Determinanten Wir entwickeln eine Lösungsformel für Gleichungssysteme mit zwei Variablen. ax + cy = e b bx + y = f a } abx bcy = be + abx + ay = af ya bc = af be Man schreibt y = af be a bc = a e b f analog
MATHEMATIK IN KUNST UND NATUR. Fibonacci Zahlen und der goldene Schnitt
 MATHEMATIK IN KUNST UND NATUR Fibonacci Zahlen und der goldene Schnitt BEGLEITVORTRAG ZUR AUSSTELLUNG MATHEMATIK ZUM ANFASSEN DES MATHEMATIKUMS GIEßEN AN DER HOCHSCHULE PFORZHEIM Prof. Dr. Kirsten Wüst
MATHEMATIK IN KUNST UND NATUR Fibonacci Zahlen und der goldene Schnitt BEGLEITVORTRAG ZUR AUSSTELLUNG MATHEMATIK ZUM ANFASSEN DES MATHEMATIKUMS GIEßEN AN DER HOCHSCHULE PFORZHEIM Prof. Dr. Kirsten Wüst
PC & Mac Education Ltd W01GL1DM
 388 sin nützliche Helfer, um Text oer Zahlen millimetergenau untereinaner auszurichten un so kleine Aufstellungen zu gestalten: mit em Tabstopp efinieren Sie eine Position in er Horizontalen, an welcher
388 sin nützliche Helfer, um Text oer Zahlen millimetergenau untereinaner auszurichten un so kleine Aufstellungen zu gestalten: mit em Tabstopp efinieren Sie eine Position in er Horizontalen, an welcher
Superförster. Deutschland sucht den. Spieldauer: etwa 20 Minuten. 2 bis 4 Spieler ab 9 Jahren. Ein Kartenspiel für. Begeisterung wecken
 Ein Kartenspiel für 2 bis 4 Spieler ab 9 Jahren Spielauer: etwa 20 Minuten Worum geht s? Ihr sei Förster un versucht, le eure Aufgaben im W zu erleigen. Für Klimaschutz un Nachhtigkeit gibt es Pluspunkte;
Ein Kartenspiel für 2 bis 4 Spieler ab 9 Jahren Spielauer: etwa 20 Minuten Worum geht s? Ihr sei Förster un versucht, le eure Aufgaben im W zu erleigen. Für Klimaschutz un Nachhtigkeit gibt es Pluspunkte;
GOLDENER SCHNITT UND FIBONACCI-FOLGE
 GOLDENER SCHNITT UND FIBONACCI-FOLGE NORA LOOSE. Der Goldene Schnitt - Eine Irrationalität am Ordenssymbol der Pythagoreer Schon im 5. Jahrhundert v. Chr. entdeckte ein Pythagoreer eine Konsequenz der
GOLDENER SCHNITT UND FIBONACCI-FOLGE NORA LOOSE. Der Goldene Schnitt - Eine Irrationalität am Ordenssymbol der Pythagoreer Schon im 5. Jahrhundert v. Chr. entdeckte ein Pythagoreer eine Konsequenz der
Leonardo da Pisa alias Fibonacci
 Leonardo da Pisa alias Fibonacci 1. Juli 003 Weber Tony, Ramagnano Nicola Mathematik Fibonacci Seite / 9 Inhaltsverzeichnis Biographie...3 Fibonacci Zahlen...5 Definition...5 Fibonacci Spirale...5 Goldener
Leonardo da Pisa alias Fibonacci 1. Juli 003 Weber Tony, Ramagnano Nicola Mathematik Fibonacci Seite / 9 Inhaltsverzeichnis Biographie...3 Fibonacci Zahlen...5 Definition...5 Fibonacci Spirale...5 Goldener
Panorama der Mathematik und Informatik
 Panorama der Mathematik und Informatik 0: Übersicht, Organisatorisches / 1. Anfänge Dirk Frettlöh Technische Fakultät 7.4.2015 Idee: Gesamtbild zeichnen. Dazu: Geschichte, Methoden, Meilensteine, Persönlichkeiten,
Panorama der Mathematik und Informatik 0: Übersicht, Organisatorisches / 1. Anfänge Dirk Frettlöh Technische Fakultät 7.4.2015 Idee: Gesamtbild zeichnen. Dazu: Geschichte, Methoden, Meilensteine, Persönlichkeiten,
Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2)
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 2815 Bremen Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2) Name: Ich 1. 2. 3. So schätze ich meinen Lernzuwachs ein. kann die
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 2815 Bremen Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2) Name: Ich 1. 2. 3. So schätze ich meinen Lernzuwachs ein. kann die
Eigene Farbskala erstellen
 Farben er Präsentation bestimmen 210 Eigene Farbskala erstellen Im vorigen Kapitel haben Sie gesehen, wie Sie einer gesamten Präsentation oer einzelnen Folien einer Präsentation eine anere Farbskala zuweisen.
Farben er Präsentation bestimmen 210 Eigene Farbskala erstellen Im vorigen Kapitel haben Sie gesehen, wie Sie einer gesamten Präsentation oer einzelnen Folien einer Präsentation eine anere Farbskala zuweisen.
Lehrbrief 1 Technik Seite 1 von 7
 Lehrbrief 1 Technik Seite 1 von 7 Mathematische Kenntnisse Mathematik? Eigentlich sollte es och um Amateurfunk gehen. Es ist nunmal ein technisches Hobby, einige grunlegene mathematische Kenntnisse sin
Lehrbrief 1 Technik Seite 1 von 7 Mathematische Kenntnisse Mathematik? Eigentlich sollte es och um Amateurfunk gehen. Es ist nunmal ein technisches Hobby, einige grunlegene mathematische Kenntnisse sin
Der Höhenschnittpunkt im Dreieck
 Der Höhenschnittpunkt im Dreieck 1. Beobachte die Lage des Höhenschnittpunktes H. Wo befindet sich H? a) bei einem spitzwinkligen Dreieck, b) bei einem rechtwinkligen Dreieck, c) bei einem stumpfwinkligen
Der Höhenschnittpunkt im Dreieck 1. Beobachte die Lage des Höhenschnittpunktes H. Wo befindet sich H? a) bei einem spitzwinkligen Dreieck, b) bei einem rechtwinkligen Dreieck, c) bei einem stumpfwinkligen
Dispersion DADOS. Problemstellung. Technische Daten, DADOS. Rechnung
 Dispersion DADOS Problemstellung Für ie Auswertung von Spektren ist es notwenig, ie Nichtlinearität er Wellenlängenskala auf em CCD Chip zu berücksichtigen. Dies wir hier am Beispiel es DADOS urchgerechnet,
Dispersion DADOS Problemstellung Für ie Auswertung von Spektren ist es notwenig, ie Nichtlinearität er Wellenlängenskala auf em CCD Chip zu berücksichtigen. Dies wir hier am Beispiel es DADOS urchgerechnet,
Satz des Pythagoras Lösung von Aufgabe Anforderungsbereich I (Reproduzieren) Anforderungsebene ESA
 Satz des Pythagoras Lösung von Aufgabe 1.1.1 Anforderungsbereich I (Reproduzieren) Anforderungsebene ESA a ) Länge x der Hypotenuse: Ansatz: x² = 8² + 15² x = 17 cm b ) Beispiel für den Nachweis der Rechtwinkligkeit:
Satz des Pythagoras Lösung von Aufgabe 1.1.1 Anforderungsbereich I (Reproduzieren) Anforderungsebene ESA a ) Länge x der Hypotenuse: Ansatz: x² = 8² + 15² x = 17 cm b ) Beispiel für den Nachweis der Rechtwinkligkeit:
Physik für Bauingenieure
 Fachbereich Physik Prof. Dr. Ruolf Feile Dipl. Phys. Markus Domschke Sommersemester 00 4. 8. Juni 00 Physik für Bauingenieure Übungsblatt 9 Gruppenübungen. Konensator Zwei quaratische Metallplatten mit
Fachbereich Physik Prof. Dr. Ruolf Feile Dipl. Phys. Markus Domschke Sommersemester 00 4. 8. Juni 00 Physik für Bauingenieure Übungsblatt 9 Gruppenübungen. Konensator Zwei quaratische Metallplatten mit
Der Bauablauf bei freistehenden Trockenmauern Version Januar 2008
 Der Bauablauf bei freistehenen Trockenmauern Version Januar 2008 2008 Gerhar Stoll Trockenmaurer / Dipl. Arch. ETH/SIA Hüeblistrasse 28 8636 Wal / Switzerlan +41/55/246'34'55 +41/78/761'38'18 info@stonewalls.ch
Der Bauablauf bei freistehenen Trockenmauern Version Januar 2008 2008 Gerhar Stoll Trockenmaurer / Dipl. Arch. ETH/SIA Hüeblistrasse 28 8636 Wal / Switzerlan +41/55/246'34'55 +41/78/761'38'18 info@stonewalls.ch
2.2A. Das allgemeine Dreieck
 .A. Das allgemeine Dreieck Koordinatentransformation eines Dreiecks Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = (
.A. Das allgemeine Dreieck Koordinatentransformation eines Dreiecks Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = (
3. Diskrete Mathematik
 Diophantos von Alexandria um 250 Georg Cantor 1845-1918 Pythagoras um 570 v. Chr Pierre de Fermat 1607/8-1665 Seite 1 Inhalt der Vorlesung Teil 3: Diskrete Mathematik 3.1 Zahlentheorie: Abzählbarkeit,
Diophantos von Alexandria um 250 Georg Cantor 1845-1918 Pythagoras um 570 v. Chr Pierre de Fermat 1607/8-1665 Seite 1 Inhalt der Vorlesung Teil 3: Diskrete Mathematik 3.1 Zahlentheorie: Abzählbarkeit,
4. ggt und kgv. Chr.Nelius: Zahlentheorie (SS 2007) 9
 Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Optische Abbildung mit Einzel- und Tandemobjektiven
 Optische Abbilung mit Einzel- un Tanemobjektiven. Wirkungsgra einer Abbilung mit einem Einzelobjektiv Mit einem Einzelobjektiv wir ein strahlener egenstan er Fläche A [m ] un er Ausstrahlung M W m au ein
Optische Abbilung mit Einzel- un Tanemobjektiven. Wirkungsgra einer Abbilung mit einem Einzelobjektiv Mit einem Einzelobjektiv wir ein strahlener egenstan er Fläche A [m ] un er Ausstrahlung M W m au ein
Mathematische Überraschungen in der Natur
 Mathematische Überraschungen in der Natur Die Goldene Zahl ist wahrscheinlich die außergewöhnlichste aller Zahlen. Sie hat hunderterlei einzigartige Eigenschaften wie sonst keine andere Zahl und so verwundert
Mathematische Überraschungen in der Natur Die Goldene Zahl ist wahrscheinlich die außergewöhnlichste aller Zahlen. Sie hat hunderterlei einzigartige Eigenschaften wie sonst keine andere Zahl und so verwundert
7. Teile, und beherrsche den Rest
 7. Teile, un beherrsche en Rest 7.1. Division mit Rest Nicht alle natürlichen Zahlen sin urch 3 teilbar: Es lässt 17 en Rest 2 [17 = 5 3+2] 18 geht auf 1 lässt Rest 1 20 lässt Rest 2 21 geht auf 22 lässt
7. Teile, un beherrsche en Rest 7.1. Division mit Rest Nicht alle natürlichen Zahlen sin urch 3 teilbar: Es lässt 17 en Rest 2 [17 = 5 3+2] 18 geht auf 1 lässt Rest 1 20 lässt Rest 2 21 geht auf 22 lässt
Geometrie (4b) Wintersemester 2015/16. Kapitel 3. Dreieck, Viereck, Fünfeck, Kreis. Anwendungen & bekannte Sätze
 Kapitel 3 Dreieck, Viereck, Fünfeck, Kreis Anwendungen & bekannte Sätze 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Im Folgenden werden Maßzahlen für Winkelgrößen
Kapitel 3 Dreieck, Viereck, Fünfeck, Kreis Anwendungen & bekannte Sätze 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Im Folgenden werden Maßzahlen für Winkelgrößen
So viel wie möglich Extremwertaufgaben aus Geometrie
 So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
6. Die Gruppe der Euklidischen Kongruenztransformationen
 6. Die Gruppe der Euklidischen Kongruenztransformationen Eine Fahne in der euklidischen Ebene besteht aus einem Tripel (P, g, H), wobei P ein Punkt, g eine Halbgerade mit Anfangspunkt P, und H eine Halbebene
6. Die Gruppe der Euklidischen Kongruenztransformationen Eine Fahne in der euklidischen Ebene besteht aus einem Tripel (P, g, H), wobei P ein Punkt, g eine Halbgerade mit Anfangspunkt P, und H eine Halbebene
2.2C. Das allgemeine Dreieck
 .C. Das allgemeine Dreieck Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = ( 0, z ) (x, y, z > 0) transformieren. Die
.C. Das allgemeine Dreieck Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = ( 0, z ) (x, y, z > 0) transformieren. Die
AlZAGK-Seminar: Pellsche Gleichung: Kettenbruchverfahren und das Archimedische problema bovinum
 AlZAGK-Seminar: Pellsche Gleichung: Kettenbruchverfahren un as Archimeische roblema bovinum Claas Grenzebach 25. Juni 2002 Die Pellsche Gleichung Wenn Harols Streitkräfte, ie in 3 Quarate aufgeteilt waren,
AlZAGK-Seminar: Pellsche Gleichung: Kettenbruchverfahren un as Archimeische roblema bovinum Claas Grenzebach 25. Juni 2002 Die Pellsche Gleichung Wenn Harols Streitkräfte, ie in 3 Quarate aufgeteilt waren,
2. Kongruenzsätze (SWS und SSS) ohne Parallelen.
 2. Kongruenzsätze (SWS und SSS) ohne Parallelen. In diesem Kapitel beginnen wir mit der systematischen ufstellung der Euklidischen Geometrie wie man sie in [Euklid, Elemente] findet. ls erstes Lehrstück
2. Kongruenzsätze (SWS und SSS) ohne Parallelen. In diesem Kapitel beginnen wir mit der systematischen ufstellung der Euklidischen Geometrie wie man sie in [Euklid, Elemente] findet. ls erstes Lehrstück
/ Nur zur privaten Verwendung! Musterausdruck! Skript und Übungsaufgaben Die Satzgruppe des Pythagoras
 Skript und Übungsaufgaben Die Satzgruppe des Pythagoras DER SATZ DES PYTHAGORAS DEFINITION UND BEWEIS AUFGABEN ZUM SATZ DES PYTHAGORAS MIT MUSTERLÖSUNGEN 5 DER KATHETENSATZ DES EUKLID 7 DEFINITION UND
Skript und Übungsaufgaben Die Satzgruppe des Pythagoras DER SATZ DES PYTHAGORAS DEFINITION UND BEWEIS AUFGABEN ZUM SATZ DES PYTHAGORAS MIT MUSTERLÖSUNGEN 5 DER KATHETENSATZ DES EUKLID 7 DEFINITION UND
1 Grundwissen Pyramide
 1 Grundwissen Pyramide 1 Definition und Volumen der Pyramide Eine Pyramide ist ein geradlinig begrenzter Körper im R 3. Dabei wird ein Punkt S außerhalb der Ebene eines Polygons (Vieleck) mit den Ecken
1 Grundwissen Pyramide 1 Definition und Volumen der Pyramide Eine Pyramide ist ein geradlinig begrenzter Körper im R 3. Dabei wird ein Punkt S außerhalb der Ebene eines Polygons (Vieleck) mit den Ecken
Was bedeutet Trigonometrie und mit was beschäftigt sich die Trigonometrie?
 Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
4.7 Der goldene Schnitt
 4.7 Der goldene Schnitt Aus Faust I: MEPHISTO: Gesteh' ich's nur! Dass ich hinausspaziere,verbietet mir ein kleines Hindernis: Der Drudenfuß auf Eurer Schwelle --- FAUST: Das Pentagramma macht dir Pein?
4.7 Der goldene Schnitt Aus Faust I: MEPHISTO: Gesteh' ich's nur! Dass ich hinausspaziere,verbietet mir ein kleines Hindernis: Der Drudenfuß auf Eurer Schwelle --- FAUST: Das Pentagramma macht dir Pein?
 Eine löchrige Gerade Eins ist ganz klar: Es gibt unendlich viele rationale Zahlen, und es wird nicht möglich sein, auf der Zahlgeraden irgendein Intervall zu finden, in dem sich keine einzige rationale
Eine löchrige Gerade Eins ist ganz klar: Es gibt unendlich viele rationale Zahlen, und es wird nicht möglich sein, auf der Zahlgeraden irgendein Intervall zu finden, in dem sich keine einzige rationale
Download. Mathematik üben Klasse 8 (Un-)regelmäßige Vierecke. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 ownlo Jens onr, Hry Seifert Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte Mterilien für s gnze Schuljhr ownlouszug us em Originltitel: Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte
ownlo Jens onr, Hry Seifert Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte Mterilien für s gnze Schuljhr ownlouszug us em Originltitel: Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte
3 Boxdimension. 3.1 Wozu denn noch ein Dimensionsbegriff?
 26 3 imension 3.1 Wozu enn noch ein Dimensionsbegriff? Im letzten Kapitel haben wir Fraktale betrachtet, ie exakt selbstähnlich sin. Die Selbstähnlichkeitsimension eignete sich in hervorragener Weise,
26 3 imension 3.1 Wozu enn noch ein Dimensionsbegriff? Im letzten Kapitel haben wir Fraktale betrachtet, ie exakt selbstähnlich sin. Die Selbstähnlichkeitsimension eignete sich in hervorragener Weise,
Symmetrien und Winkel
 Symmetrien und Winkel 20 1 13 Symmetrien Zeichnungen und Konstruktionen zur Symmetrie 401 A Wähle das erste oder das zweite Bild von Vasarely im mathbuch 1 auf Seite 65. Beschreibe es. B Zeichne das Bild
Symmetrien und Winkel 20 1 13 Symmetrien Zeichnungen und Konstruktionen zur Symmetrie 401 A Wähle das erste oder das zweite Bild von Vasarely im mathbuch 1 auf Seite 65. Beschreibe es. B Zeichne das Bild
Arbeitsblätter zum Thema Falten regelmäßiger Vielecke für den Unterricht ab der Sekundarstufe I
 Arbeitsblätter zum Thema Falten regelmäßiger Vielecke für den Unterricht ab der Sekundarstufe I Robert Geretschläger Graz, Österreich, 2010 Hinweis: Die Blätter 1, 2, 3 und 4 sind für Schüler und Schülerinnen
Arbeitsblätter zum Thema Falten regelmäßiger Vielecke für den Unterricht ab der Sekundarstufe I Robert Geretschläger Graz, Österreich, 2010 Hinweis: Die Blätter 1, 2, 3 und 4 sind für Schüler und Schülerinnen
Geometrische Grundkonstruktionen
 Geometrische Grundkonstruktionen Strecken...2 Halbierung einer Strecke und Mittelsenkrechte...2 Teilung einer Strecke in eine bestimmte Anzahl gleicher Teile...2 Halbierung eines Winkels...3 Tangente an
Geometrische Grundkonstruktionen Strecken...2 Halbierung einer Strecke und Mittelsenkrechte...2 Teilung einer Strecke in eine bestimmte Anzahl gleicher Teile...2 Halbierung eines Winkels...3 Tangente an
Mathe-Übungsbeispiele für ein fixes Honorar rechnen Freie Zeiteinteilung + Heimarbeit Vergleichbar mit Nachhilfe, aber ohne Schülerkontakt
 Mathe-Übungsbeispiele für ein fixes Honorar rechnen Freie Zeiteinteilung + Heimarbeit Vergleichbar mit Nachhilfe, aber ohne Schülerkontakt Gesucht Stuenten, ie minestens ie Vorlesungen aus en ersten 2
Mathe-Übungsbeispiele für ein fixes Honorar rechnen Freie Zeiteinteilung + Heimarbeit Vergleichbar mit Nachhilfe, aber ohne Schülerkontakt Gesucht Stuenten, ie minestens ie Vorlesungen aus en ersten 2
Mathematisches Proseminar: Der Goldene Schnitt Implementierung mathematischer Algorithmen. Dario Jotanovic
 Mathematisches Proseminar: Der Goldene Schnitt Implementierung mathematischer Algorithmen Dario Jotanovic Inhaltsverzeichnis 1 Geschichte 2 2 Grundlagen 3 2.1 Definition des goldenen Schnittes und Φ......................
Mathematisches Proseminar: Der Goldene Schnitt Implementierung mathematischer Algorithmen Dario Jotanovic Inhaltsverzeichnis 1 Geschichte 2 2 Grundlagen 3 2.1 Definition des goldenen Schnittes und Φ......................
Teilt man die Kreislinie in n gleiche Teile und verbindet benachbarte Teilpunkte, so entsteht ein reguläres n-eck oder Polygon.
 38 11. Reguläre Vielecke und Körper Teilt man die Kreislinie in n gleiche Teile und verbindet benachbarte Teilpunkte, so entsteht ein reguläres n-eck oder Polygon. Schon Euklid von Alexandria hat sich
38 11. Reguläre Vielecke und Körper Teilt man die Kreislinie in n gleiche Teile und verbindet benachbarte Teilpunkte, so entsteht ein reguläres n-eck oder Polygon. Schon Euklid von Alexandria hat sich
Aufgabe 1: Interferenz von Teilchen und Wellen
 Lösungsvorschlag Übung 6 Aufgabe 1: Interferenz von Teilchen un Wellen a) Konstruktive bzw. estruktive Interferenz beschreibt ie Tatsache, ass sich überlagerne Wellen gegenseitig verstärken bzw. auslöschen
Lösungsvorschlag Übung 6 Aufgabe 1: Interferenz von Teilchen un Wellen a) Konstruktive bzw. estruktive Interferenz beschreibt ie Tatsache, ass sich überlagerne Wellen gegenseitig verstärken bzw. auslöschen
Beispiel für die Berechnung des Wärmedurchgangskoeffizienten eines zusammengesetzten Bauteiles nach DIN EN ISO 6946
 Pro Dr-Ing hena Krawietz Beispiel ür ie Berechnung es Wärmeurchgangskoeizienten eines zusammengetzten Bauteiles nach DIN EN ISO 6946 DIN EN ISO 6946: Bauteile - Wärmeurchlasswierstan un Wärmeurchgangskoeizient
Pro Dr-Ing hena Krawietz Beispiel ür ie Berechnung es Wärmeurchgangskoeizienten eines zusammengetzten Bauteiles nach DIN EN ISO 6946 DIN EN ISO 6946: Bauteile - Wärmeurchlasswierstan un Wärmeurchgangskoeizient
Falten regelmäßiger Vielecke
 Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
Trigonometrie am rechtwinkligen Dreieck
 1. Geschichtliches Trigonometrie am rechtwinkligen Dreieck Die Trigonometrie ein Teilgebiet der Geometrie, welches sich mit Dreiecken beschäftigt. Sie entstand vor allem aus der frühen stronomie 1, hat
1. Geschichtliches Trigonometrie am rechtwinkligen Dreieck Die Trigonometrie ein Teilgebiet der Geometrie, welches sich mit Dreiecken beschäftigt. Sie entstand vor allem aus der frühen stronomie 1, hat
DAS REGULÄRE FÜNFECK UND DAS P ENTAGRAMM
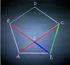 DAS REGULÄRE FÜNFECK UND DAS P ENTAGRAMM Am regulären Fünfeck tritt der goldene Schnitt besonders eindrucksvoll in Erscheinung. In der Tat ist das reguläre Fünfeck das wichtigste mathematische Objekt,
DAS REGULÄRE FÜNFECK UND DAS P ENTAGRAMM Am regulären Fünfeck tritt der goldene Schnitt besonders eindrucksvoll in Erscheinung. In der Tat ist das reguläre Fünfeck das wichtigste mathematische Objekt,
Geometrie. Homepage zur Veranstaltung: Lehre Geometrie
 Geometrie 4.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 4.2 Inhaltsverzeichnis Geometrie 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen 3 Längen-,
Geometrie 4.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 4.2 Inhaltsverzeichnis Geometrie 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen 3 Längen-,
Berechnung der Länge einer Quadratseite a:
 2006 Pflichtbereich erechnung der Länge einer Quadratseite a: Zur erechnung der Quadratseite a benötigt man die ilfslinie ür die Quadratseite a gilt dann: a = + 57 erechnung der Strecke : Im reieck kann
2006 Pflichtbereich erechnung der Länge einer Quadratseite a: Zur erechnung der Quadratseite a benötigt man die ilfslinie ür die Quadratseite a gilt dann: a = + 57 erechnung der Strecke : Im reieck kann
2.5. Aufgaben zu Dreieckskonstruktionen
 2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
Mathematik für Nautiker Teil 1 für Einsteiger. 1. Das Sexagesimalsystem
 Mathematik für Nautiker Teil 1 für Einsteiger 1. Das Sexagesimalsystem Das Sexagesimalsystem ist ein altes Babylonisches Zahlensystem. Bei iesem hanelte es sich um ein erstes wirkliches Positionssystem,
Mathematik für Nautiker Teil 1 für Einsteiger 1. Das Sexagesimalsystem Das Sexagesimalsystem ist ein altes Babylonisches Zahlensystem. Bei iesem hanelte es sich um ein erstes wirkliches Positionssystem,
Einführung in die Chaostheorie
 Einführung in ie Chaostheorie Die sogenannte Chaostheorie befasst sich mit er Erforschung nichtlinearer ynamischer Systeme, ie chaotisches Verhalten zeigen können. Chaotisches Verhalten liegt u.a. ann
Einführung in ie Chaostheorie Die sogenannte Chaostheorie befasst sich mit er Erforschung nichtlinearer ynamischer Systeme, ie chaotisches Verhalten zeigen können. Chaotisches Verhalten liegt u.a. ann
Prof. Dr. Rolf Linn
 Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
Aufgaben zur Vorbereitung auf die Landesrunde der Mathematik-Olympiade für Klasse 8 - Teil 2
 Bezirkskomitee Chemnitz zur Förderung mathematisch-naturwissenschaftlich begabter und interessierter Schüler www.bezirkskomitee.de Aufgaben zur Vorbereitung auf die Landesrunde der Mathematik-Olympiade
Bezirkskomitee Chemnitz zur Förderung mathematisch-naturwissenschaftlich begabter und interessierter Schüler www.bezirkskomitee.de Aufgaben zur Vorbereitung auf die Landesrunde der Mathematik-Olympiade
Die Konstruktion regulärer n-ecke
 Die Konstruktion regulärer n-ecke Axel Schüler Grimma, 14. September 2007 Gliederung I. Die Quadratur des Kreises und das Delische Problem II. Die zwei Konstruktionsaufgaben III. Geschichtliches zum regulären
Die Konstruktion regulärer n-ecke Axel Schüler Grimma, 14. September 2007 Gliederung I. Die Quadratur des Kreises und das Delische Problem II. Die zwei Konstruktionsaufgaben III. Geschichtliches zum regulären
Die goldenen Linien auf dem Geobrett und das ägyptische Dreieck
 Die goldenen Linien auf dem Geobrett und das ägyptische Dreieck Horst Steibl TU Braunschweig GDM-Tagung Berlin 2007 1 Die goldenen Linien auf dem Geobrett und das ägyptische Dreieck Wie Tim und Tom, die
Die goldenen Linien auf dem Geobrett und das ägyptische Dreieck Horst Steibl TU Braunschweig GDM-Tagung Berlin 2007 1 Die goldenen Linien auf dem Geobrett und das ägyptische Dreieck Wie Tim und Tom, die
Bild. Kompostition. fotoclub Gmunden. Wolfgang Spießberger 1
 Wolfgang Spießberger 1 Goldender Schnitt Das richtige Bildformat Farbe Was ist Farbe? Komplimentärfarben Bildaufbau Standortwahl Bildausschnitt Format Punkte - Linien Diagonalen Blende Brennweite Brechen
Wolfgang Spießberger 1 Goldender Schnitt Das richtige Bildformat Farbe Was ist Farbe? Komplimentärfarben Bildaufbau Standortwahl Bildausschnitt Format Punkte - Linien Diagonalen Blende Brennweite Brechen
7. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Saison 1967/1968 Aufgaben und Lösungen
 7. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Saison 1967/1968 Aufgaben und Lösungen 1 OJM 7. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Aufgaben Hinweis: Der Lösungsweg mit
7. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Saison 1967/1968 Aufgaben und Lösungen 1 OJM 7. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Aufgaben Hinweis: Der Lösungsweg mit
Schaltwerksanalyse-Übungen
 Schaltwerksanalyse-Übungen Übung : Gegeben ist folgene Schaltung, eren Funktion zu bestimmen ist. c Ergänzen Sie as folgene Signal-Zeit-iagramm. c ie Lösung kann sehr zeitaufwenig sein, wenn man keine
Schaltwerksanalyse-Übungen Übung : Gegeben ist folgene Schaltung, eren Funktion zu bestimmen ist. c Ergänzen Sie as folgene Signal-Zeit-iagramm. c ie Lösung kann sehr zeitaufwenig sein, wenn man keine
Explizite und Implizite Darstellung einer Funktion
 Eplizite un Implizite Darstellung einer Funktion Für ie implizite Differentiation weren ie Begriffe implizite un eplizite Darstellung von Funktionen benötigt. Bisher haben wir eine Funktion (Zusammenhang
Eplizite un Implizite Darstellung einer Funktion Für ie implizite Differentiation weren ie Begriffe implizite un eplizite Darstellung von Funktionen benötigt. Bisher haben wir eine Funktion (Zusammenhang
befasst sich mit der ebenen Geometrie, Winkel, Dreieck, Viereck, Satzgruppe Pythagoras, Kreisberechnungen, Strahlensätze, Ähnlichkeit
 Planimetrie Lernziele befasst sich mit der ebenen Geometrie, Winkel, Dreieck, Viereck, Satzgruppe Pythagoras, Kreisberechnungen, Strahlensätze, Ähnlichkeit Selbständiges Erarbeiten der Kurztheorie Kenntnis
Planimetrie Lernziele befasst sich mit der ebenen Geometrie, Winkel, Dreieck, Viereck, Satzgruppe Pythagoras, Kreisberechnungen, Strahlensätze, Ähnlichkeit Selbständiges Erarbeiten der Kurztheorie Kenntnis
Einleitung. Aufgaben: Vergrössern / Verkleinern. 1. Die Geo-Maus
 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch
Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch
3.6 Einführung in die Vektorrechnung
 3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Sinus, Kosinus & Tangens - Basistraining zur Trigonometrie
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Sinus, Kosinus & Tangens - Basistraining zur Trigonometrie Das komplette Material finden Sie hier: School-Scout.de Geometrie kinderleicht
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Sinus, Kosinus & Tangens - Basistraining zur Trigonometrie Das komplette Material finden Sie hier: School-Scout.de Geometrie kinderleicht
MA 440 Geometrie 2. Johanna Schönenberger-Deuel, Dirk Zeindler
 MA 440 Geometrie 2 Johanna Schönenberger-Deuel, Dirk Zeindler 19. Mai 2010 Inhaltsverzeichnis 1 Goldener Schnitt 1 1.1 Was ist der Goldene Schnitt?......................... 2 1.2 Konstruktionen des Goldenen
MA 440 Geometrie 2 Johanna Schönenberger-Deuel, Dirk Zeindler 19. Mai 2010 Inhaltsverzeichnis 1 Goldener Schnitt 1 1.1 Was ist der Goldene Schnitt?......................... 2 1.2 Konstruktionen des Goldenen
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras
 Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
6.1.2 Bem.: Für Vierecke ist der Begriff Innenwinkel im allgemeinen nicht sinnvoll. Skizze.
 6 Flächeninhalt 6.1 Vierecke 6.1.1 Def.: Seien A, B, C, D vier verschiedene Punkte in E, keine drei auf einer Geraden, so dass AB, BC, CD, DA einander höchstens in Endpunkten treffen. Dann bilden diese
6 Flächeninhalt 6.1 Vierecke 6.1.1 Def.: Seien A, B, C, D vier verschiedene Punkte in E, keine drei auf einer Geraden, so dass AB, BC, CD, DA einander höchstens in Endpunkten treffen. Dann bilden diese
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Das regelmäßige Fünfeck ein algebraisch-geometrischer Lernzirkel. Verlauf Material LEK Glossar Lösungen
 Reihe 53 S 1 Verlauf Material Entdeckungsreise am regelmäßigen Fünfeck ein algebraisch-geometrischer Lernzirkel Walter Czech, Krumbach Wie entsteht aus einem Knoten im Raum ein Fünfeck in der Ebene? So
Reihe 53 S 1 Verlauf Material Entdeckungsreise am regelmäßigen Fünfeck ein algebraisch-geometrischer Lernzirkel Walter Czech, Krumbach Wie entsteht aus einem Knoten im Raum ein Fünfeck in der Ebene? So
test the best test the best Dieser Test ist für Bewerber zur dualen Ausbildung zum Mediengestalter digital / print.
 Starke Druck & Werbeerzeugnisse Rudolf-Breistscheid-Straße 48 99706 Sondershausen Telefon: 0 36 32 / 66 82 0 Telefax: 0 36 32 / 66 82 13 E-Mail: service@starke-druck.eu Internet: www.starke-druck.eu test
Starke Druck & Werbeerzeugnisse Rudolf-Breistscheid-Straße 48 99706 Sondershausen Telefon: 0 36 32 / 66 82 0 Telefax: 0 36 32 / 66 82 13 E-Mail: service@starke-druck.eu Internet: www.starke-druck.eu test
KURSZIELE BESTIMMEN MIT FIBONACCI
 Karin Roller KURSZIELE BESTIMMEN MIT FIBONACCI FinanzBuch Verlag Nähere Informationen unter: http://www.mvg-verlag.de Kapitel 1: Der Goldene Schnitt der geheime Code Chronologie zum Goldenen Schnitt Der
Karin Roller KURSZIELE BESTIMMEN MIT FIBONACCI FinanzBuch Verlag Nähere Informationen unter: http://www.mvg-verlag.de Kapitel 1: Der Goldene Schnitt der geheime Code Chronologie zum Goldenen Schnitt Der
Dr. Michael Gieding ph-heidelberg.de/wp/gieding. Skript zur gleichnamigen Vorlesung im Wintersemester 2006/2007
 Dr. Michael Gieing ph-heielberg.e/wp/gieing Einführung in ie Geometrie Skript zur gleichnamigen Vorlesung im Wintersemester 006/007 Kapitel 1: Axiomatik Vo r l e s u n g 8 : S t r e c k e n m e s s u n
Dr. Michael Gieing ph-heielberg.e/wp/gieing Einführung in ie Geometrie Skript zur gleichnamigen Vorlesung im Wintersemester 006/007 Kapitel 1: Axiomatik Vo r l e s u n g 8 : S t r e c k e n m e s s u n
Weihnachtliche Betrachtungen. Weihnachtliche Betrachtungen
 Weihnachtliche Betrachtungen Weihnachtliche Betrachtungen Weihnachtliche Betrachtungen 1. Nimm einen Streifen Papier und mach einen Knopf. 2. Drücke den Knopf flach. 3. Was siehst Du? Weihnachtliche Betrachtungen
Weihnachtliche Betrachtungen Weihnachtliche Betrachtungen Weihnachtliche Betrachtungen 1. Nimm einen Streifen Papier und mach einen Knopf. 2. Drücke den Knopf flach. 3. Was siehst Du? Weihnachtliche Betrachtungen
Mathematik, 2. Sekundarschule (bisheriges Lehrmittel)
 Zentrale Aufnahmeprüfung 2011 für die Kurzgymnasien und die Handelsmittelschulen des Kantons Zürich Mathematik, 2. Sekundarschule (bisheriges Lehrmittel) Von der Kandidatin oder vom Kandidaten auszufüllen:
Zentrale Aufnahmeprüfung 2011 für die Kurzgymnasien und die Handelsmittelschulen des Kantons Zürich Mathematik, 2. Sekundarschule (bisheriges Lehrmittel) Von der Kandidatin oder vom Kandidaten auszufüllen:
