1 + t dt = ( t) k dt. ( 1) k. k + 1 tk+1
|
|
|
- Krista Albrecht
- vor 6 Jahren
- Abrufe
Transkript
1 6 POTENZREIHEN 161 Wir wollen diese Gleichung für x < 1 noch auf andere Weise herleiten. Es ist ln(1 + x) = x 1 x 1 + t dt = ( t) dt. Die geometrische Reihe = ( t) ist nach dem Majorantenriterium für t [ x, x ] gleichmäßig onvergent; nach Satz (.4) darf man also gliedweise integrieren und erhält ln(1 + x) = x = ( t) dt = Speziell haben wir die hübsche Formel [ ( 1) = = + 1 t+1 ] x ln = = ( 1) 1 x. Zur numerischen Berechnung ist diese Reihe aber ungeeignet; besser onvergiert die Taylorreihe der Funtion ln 1 + x 1 x zur Stelle. Man beommt sie aus ln 1 + x 1 x = ln(1 + x) ln(1 x) = x x + x3 3 x4 4 + ) = (x + x3 3 + x ( x x x3 3 x4 4 für x < 1. Als nächstes Beispiel betrachten wir die Funtion f = arctan, die wir in eine Potenzreihe um entwiceln wollen. Zur Berechnung der n-ten Ableitung an der Stelle ann man den Ansatz f (n) (x) = P n(x) (1 + x ) n machen und findet für P n eine Reursionsformel, aus der sich herleiten läßt, daß ) f (n) () =, f (n+1) () = ( 1) n (n)! ist. Die Taylorreihe der Funtion arctan lautet also ( 1) + 1 x+1. =
2 6 POTENZREIHEN 16 Der Konvergenzradius ist offenbar 1. Sei f die in ( 1, 1) dargestellte Funtion. Es gilt f (x) = ( 1) x = x = arctan x, = ferner f() = = arctan. Also ist f(x) = arctan x. Wir haben also arctan x = x x3 3 + x5 5 x = = ( 1) + 1 x+1 in ( 1, 1). Nach dem Leibniz-Kriterium onvergiert die Reihe auch für x = 1 und x = 1. Nach (6.4) ist die dargestellte Funtion dort stetig, stimmt also mit der Funtion arctan überein. Speziell haben wir tan π 4 = 1, also arctan 1 = π 4, somit π 4 = Auch diese Reihe onvergiert aber zu langsam, um für numerische Rechnungen brauchbar zu sein. Als letztes Beispiel wollen wir die allgemeine Potenz x x α betrachten. Als Entwiclungsstelle wählen wir ebenfalls 1, aber es schreibt sich bequemer, die Funtion x (1 + x) α zu nehmen und um zu entwiceln. Für f(x) = (1 + x) α (x > 1) berechnet man f () (x) = α(α 1) (α + 1)(1 + x) α. Zur übersichtlicheren Schreibweise wollen wir wie früher den Binomialoeffizienten ( ) α erlären durch ( ) α := α(α 1) (α + 1).! Dann ist die Taylorreihe der Funtion f zur Stelle gegeben durch ( ) α x. = Im Fall α N sind fast alle Koeffizienten, es liegt also ein Polynom vor. Wir setzen jetzt α / N voraus. Aus dem Quotientenriterium (8.9) folgt sofort, daß der Konvergenzradius gleich 1 ist. Die Reihe stellt also in ( 1, 1) eine Funtion g dar. Setzen wir h(x) := g(x) (1 + x) α für 1 < x < 1,
3 7 FOURIERREIHEN 163 so gilt h (x) = g (x)(1 + x) α g(x)α(1 + x) α 1 (1 + x) α = g (x)(1 + x) αg(x) (1 + x) α+1. Nun ist (1 + x)g (x) = (1 + x) = = = α = ( ) α x 1 ( ) α ( + 1)x = {( ) α ( + 1) = ( ) α x = αg(x), ( α ( ) α x ) } x also h = und daher h = const. Wegen h() = 1 folgt ( ) α (1 + x) α = x für 1 < x < 1. = Man nennt diese Reihe auch die binomische Reihe. Das Konvergenzverhalten an den Stellen ±1 ist etwas schwieriger zu beurteilen: Bemerung. Sei α R \ N. Die binomische Reihe n= ( α n) x n ist für 7 Fourierreihen in x = 1 in x = 1 α > onvergent onvergent 1 < α < onvergent divergent α 1 divergent divergent Ein wichtiger Typ von Reihenentwiclungen wird gegeben durch die Fourierreihen. Fourier war Physier, und wir wollen zunächst urz die physialische Fragestellung, bei deren Behandlung Fourier (187) erstmals die heute nach ihm benannten Reihen verwendete, heuristisch erläutern. Fourier befaßte sich mit Problemen der Wärmeleitung in homogenen Medien. Als besonders einfaches (idealisiertes) Wärmeleitungsproblem betrachten wir einen
4 7 FOURIERREIHEN 164 geraden Stab der Länge l, den wir als unendlich dünn annehmen. Seine Punte önnen also durch eine Koordinate x beschrieben werden, die das Intervall [, l] durchläuft. In diesem Stab herrsche an der Stelle x zur Zeit t die Temperatur T (x, t). Wir nehmen an, die beiden Enden des Stabes würden von außen ständig auf der Temperatur Null gehalten, und im übrigen sei der Stab vollommen isoliert. Zur Zeit t = herrsche eine beannte Temperaturverteilung, gegeben durch eine Funtion f : [, l] R. Von der Temperaturverteilung T (x, t) ist also beannt, daß T (x, ) = f(x) für x [, l] und T (, t) = T (l, t) = für t ist. Im Lauf der Zeit werden sich nun auf Grund der Wärmeleitung die Temperaturunterschiede ausgleichen. Die Frage ist, welche Temperaturverteilung zu einer Zeit t > herrscht, also wie man die Funtion T (x, t) aus der Anfangsverteilung T (x, ) berechnen ann. Physialische Grundannahmen und Überlegungen führen zu der Folgerung, daß die Funtion T (unter, wie üblich, geeigneten Differenzierbareitsannahmen) der partiellen Differentialgleichung T t = µ T x genügen muß, wobei µ > eine Materialonstante ist. Wir stellen nun zunächst die Frage der Anfangsverteilung zurüc und suchen allgemeiner eine Lösung ϕ : [, l] [, ) R des Problems ϕ t = ϕ µ, ϕ(, t) = ϕ(l, t) =. ( ) x Um spezielle Lösungen zu finden, ann man untersuchen, ob es Lösungen der Form ϕ(x, t) = h(t)g(x) gibt ( Separationsansatz, Trennung der Veränderlichen ). Hierzu muß wegen ϕ t = h (t)g(x), ϕ x = h(t)g (x) also h (t) h(t) = (x) µg g(x) sein. Da die line Seite nicht von x und die rechte nicht von t abhängt, handelt es sich um eine Konstante c. Somit werden wir auf die Gleichungen h (t) = ch(t), µg (x) = cg(x)
5 7 FOURIERREIHEN 165 geführt. Die erste Differentialgleichung läßt sich sofort lösen: h(t) = be ct mit einer Konstanten b. Bei der zweiten ist die Randbedingung g() = g(l) = zu berücsichtigen. Es liegt daher der Ansatz g(x) = sin ax nahe. Die Differentialgleichung ist erfüllt, wenn al = π mit ganzzahligem ist. Für die Konstanten ergibt sich also a = π l, c = µ π l. Insgesamt erhalten wir, daß bei beliebigem N durch ϕ (x, t) = b e µ π l t sin πx l mit b = const. eine Lösung des Problems ( ) gegeben ist. Natürlich ann hierdurch i.a. noch nicht die gesuchte Temperaturverteilung T (x, t) gegeben sein, denn es sollte ja T (x, ) eine vorgeschriebene Funtion f(x) sein. Wir erhalten aber ϕ (x, ) = b sin πx, l also für jedes eine sehr spezielle Funtion. Nun beachte man aber, daß unser Problem linear ist. Dies hat zur Folge, daß die Summe von Lösungen auch eine Lösung ist, also ist durch ϕ(x, t) := ϕ (x, t) = b e µ π l t sin πx l (n N) ebenfalls eine Lösung gegeben. Für diese Lösung ist ϕ(x, ) = b sin πx, l und im allgemeinen wird es immer noch nicht möglich sein, die Zahl n und die Koeffizienten b so zu wählen, daß ϕ(x, ) = f(x) ist. Hier setzt nun Fouriers entscheidende (und damals ühne) Überlegung ein. Er geht davon aus, daß man die weitgehend willürliche Funtion f durch die unendliche Reihe b sin πx l
6 7 FOURIERREIHEN 166 darstellen ann, wenn man die Koeffizienten b geeignet bestimmt. Alsdann setze man T (x, t) := b e µ π l t sin πx. l Wenn die obere Reihe für jedes x [, l] absolut onvergiert, dann nach dem Majorantenriterium auch die untere. Die Anfangsbedingung T (x, ) = f(x) (für x [, l]) und die Randbedingung T (, t) = T (l, t) = (für t ) sind dann erfüllt. Falls es erlaubt ist, die Reihe gliedweise zu differenzieren (einmal nach t, zweimal nach x), erhält man, daß T auch der vorgeschriebenen partiellen Differentialgleichung genügt. Das Problem der Temperaturverteilung ist damit als gelöst anzusehen. Der springende Punt bei dieser Argumentation ist natürlich die Frage, ob es möglich ist, eine gegebene Funtion f : [, l] R mit f() = f(l) = darzustellen als Reihe der Form f(x) = b sin πx. l Mit einer Variante dieser Fragestellung befassen wir uns im folgenden. Es bedeutet dabei eine Einschränung der Allgemeinheit, l = π anzunehmen. Andererseits soll die Voraussetzung f() = f(l) = fallengelassen werden, und wir fragen allgemeiner nach der Entwiclungsmöglicheit in Reihen der Form a + (a cos x + b sin x). Es ist bequem, Funtionen zu betrachten, die auf ganz R definiert sind. Wenn eine solche Funtion durch die obige Reihe dargestellt wird, ist f(x + π) = f(x) für x R. Funtionen mit dieser Eigenschaft nennen wir π-periodisch. Wir nehmen nun an, für eine gegebene Funtion f : R R existiere in der Tat eine Darstellung der Form f(x) = a + (a cos x + b sin x), x R, wobei die Reihe sogar gleichmäßig onvergent sei. Dann lassen sich die Koeffizienten a, b folgendermaßen berechnen. Multipliation mit cos mx und Integration über [, π] (beachte, daß f wegen der gleichmäßigen Konvergenz stetig ist) ergibt = a f(x) cos mx dx cos mx dx + (a cos x + b sin x) cos mx dx.
7 7 FOURIERREIHEN 167 Die rechts stehende Reihe ist ebenfalls gleichmäßig onvergent (nämlich gegen f(x) cos mx; beachte fg f g ), darf also nach (.4) gliedweise integriert werden. Es ist also = a f(x) cos mx dx cos mx dx + a cos x cos mx dx + b Nun findet man leicht durch partielle Integration: sin x cos mx dx. cos x cos mx dx = sin x sin mx dx = für m sin x cos mx dx =, cos x dx = sin x dx = π für 1. Damit erhält man a = 1 f(x) cos x dx für N. π Ganz analog beweist man b = 1 π f(x) sin x dx für N. Man bezeichnet nun ganz allgemein für jede π-periodische Funtion f und für N die Zahlen a := 1 π b := 1 π f(x) cos x dx, f(x) sin x dx,
8 7 FOURIERREIHEN 168 ( N ) falls diese Integrale existieren, als die Fourieroeffizienten von f und nennt die Funtionenreihe a + (a cos x + b sin x) die Fourierreihe von f. Dabei ist (analog wie bei Taylorreihen) nichts darüber ausgesagt, ob diese Reihe überhaupt (und für welche x bzw. in welchem Sinne) onvergiert und ob sie im Konvergenzfall gegen f(x) onvergiert. Die Beantwortung dieser Fragen erfordert eingehendere Untersuchungen. Bevor wir hierauf eingehen, wollen wir aber die hier sehr zwecmäßige omplexe Schreibweise einführen. Es ist ja e ix = cos x + i sin x, cos x = 1 (eix + e ix ), sin x = 1 i (eix e ix ). Damit ergibt sich für N a cos x + b sin x = a 1 (eix + e ix ) b i (eix e ix ) = 1 (a ib )e ix + 1 (a + ib )e ix = c e ix + c e ix mit also für n N c := 1 (a ib ), c := 1 (a + ib ), a + (a cos x + b sin x) = c + (c e ix + c e ix ) = c e ix = n Die Folge ( n = n c e ix) ürzt man ab mit n N c e ix. =
9 7 FOURIERREIHEN 169 Dies ist also ebenfalls die Fourierreihe von f, nur in omplexer Schreibweise. Es ist weiter zwecmäßig, auch omplexwertige Funtionen f : R C zuzulassen. Jede solche Funtion läßt sich eindeutig darstellen in der Form f = u + iv mit reellen Funtionen u, v. Man definiert dann (falls u und v, eingeschränt auf [a, b], Regelfuntionen sind) b f(x) dx := b b u(x) dx + i v(x) dx. a a a Mit dieser Konvention ist für c = 1 (a ib ) = 1 π = 1 π f(x)(cos x i sin x) dx f(x)e ix dx und somit c = 1 (a + ib ) = 1 π c = 1 π f(x)e ix dx, f(x)e ix dx für Z. Wir wollen hier auch omplexwertige Funtionen f zulassen, erlären dann die Fourieroeffizienten c von f durch diese Gleichung (falls die Integrale existieren) und nennen die Reihe c e ix die Fourierreihe von f. = Die Konvergenztheorie der Fourierreihen wird dann besonders einfach und übersichtlich, wenn man nicht nach der (i.a. selbst bei stetigen reellen Funtionen nicht vorliegenden) puntweisen Konvergenz fragt, sondern nach Konvergenz in einem schwächeren Sinne. Mit dieser auch für Anwendungen wichtigen Konvergenz wollen wir uns hier befassen.
10 7 FOURIERREIHEN 17 Konvergenz im quadratischen Mittel Wir betrachten die Menge V der Funtionen f : R C mit f(x+π) = f(x) für x R und der Eigenschaft, daß Real- und Imaginärteil von f, eingeschränt auf [, π], Regelfuntionen sind. Offenbar ist V (mit den üblichen Vernüpfungen) ein Vetorraum über C. Definition. Für f, g V sei f, g := 1 π f(x)g(x) dx. Die omplexe Zahl f, g heißt das Salarprodut von f und g. (7.1) Satz. Die Abbildung, : V V C hat die folgenden Eigenschaften (für f, g, h V und λ C): (1) f + g, h = f, h + g, h () f, g + h = f, g + f, h (3) λf, g = λ f, g (4) f, λg = λ f, g (5) g, f = f, g (6) f, f (d.h. f, f R und ) (7) f, g f, f g, g (8) f + g, f + g f, f + g, g. Beweis. (1) (6) folgen unmittelbar aus der Definition; bei (6) beachte man ff = f. Wegen (6) sind die Wurzeln in (8) im Reellen erlärt. (7) Nach (6) gilt für f, g V und λ C also unter Verwendung von (1) (5) f + λg, f + λg, f, f + λ f, g + λ f, g + λλ g, g. Ist g, g, so ann man λ = f, g g, g
11 7 FOURIERREIHEN 171 einsetzen und erhält die behauptete Ungleichung. Ist g, g =, so setze man λ = n f, g ; es folgt f, g 1/n f, f, also (da n N beliebig ist) f, g = f, f g, g. (8) Aus (7) folgt also Re f, g f, g f, f g, g, f + g, f + g = f, f + f, g + f, g + g, g = f, f + g, g + Re f, g f, f + g, g + f, f g, g = ( f, f + g, g ), woraus (8) folgt. Definition. Für f V ist die L -Norm oder Hilbert-Norm von f. f := f, f Die Ungleichungen (7) und (8) aus Satz (7.1) schreiben sich damit in der Form (Cauchy-Schwarzsche Ungleichung) und f, g f g f + g f + g ; letzteres ist die Dreiecsungleichung für die L -Norm. Wir erinnern uns daran, daß wir schon früher Konvergenz im Sinne einer Norm erlärt hatten, und definieren: Definition. Seien f, f n V (n N). Die Folge (f n ) n N heißt onvergent im quadratischen Mittel (oder onvergent in der L -Norm) gegen f, wenn ist. lim f f n = n Die Bezeichnung im quadratischen Mittel ist naheliegend wegen f f n = 1 π f(x) f n (x) dx;
12 7 FOURIERREIHEN 17 der rechts stehende Ausdruc läßt sich als Mittelwert der quadratischen Abweichung von f und f n ansehen. Man beachte, daß eine im quadratischen Mittel onvergierende Funtionenfolge nicht puntweise onvergent zu sein braucht. Wir betrachten jetzt speziell die durch e (x) := e ix definierten Elemente e V ( Z) und berechnen e, e m. Nach Definition ist e, e m = 1 π = 1 π = e ix e imx dx = 1 π { 1 für = m cos( m)x dx + i für m. e i( m)x dx sin( m)x dx Allgemein nennt man zwei Elemente f, g V mit f, g = orthogonal, und eine Folge (b ) Z in V heißt Orthonormalsystem, wenn { 1 für = m b, b m = für m ist. Im folgenden sei jetzt zunächst ein beliebiges Orthonormalsystem (b ) Z gegeben. Ist f V, so nennt man die durch c := f, b definierten omplexen Zahlen die Fourieroeffizienten von f bezüglich des gegebenen Orthonormalsystems. Die früher definierten speziellen Fourieroeffizienten sind also genau diejenigen bezüglich des speziellen Orthonormalsystems (e ) Z. Die Reihe c b Z nennt man die Fourierreihe von f bezüglich des Orthonormalsystems (b ) Z. Sei jetzt f V gegeben, und seien α n,..., α n beliebige omplexe Zahlen. Wir wollen f α b = n
13 7 FOURIERREIHEN 173 berechnen und aus dem Ergebnis wichtige Folgerungen ziehen. Es ist (Summation jeweils von n bis n) f α b = f α b, f α j b j = f, f α b, f αj f, b }{{} j + α b }{{}, α j b j c c j und α b, α j b j =,j α α j b, b j = α α. Ferner ist c α = (c α )(c α ) = c c α c α c + α α. Damit ergibt sich f α b = f c + c α. Hieran lesen wir folgendes ab: (1) f n = n α b wird genau dann minimal, wenn α = c für = n,..., n) ist. Dies ist also eine Kennzeichnung der Fourieroeffizienten durch eine Extremaleigenschaft: f wird durch eine Linearombination der Vetoren b n,..., b n im Sinne der L -Norm genau dann am besten approximiert, wenn man als Koeffizienten die Fourieroeffizienten wählt. () Wählen wir jetzt α = c, so lautet die obige Gleichung f c = f c b, = n = n und dies ist. Es folgt die Konvergenz der Reihe = c und die Ungleichung c f. = Genau dann gilt hier das Gleichheitszeichen, wenn lim n f c b = = n
14 7 FOURIERREIHEN 174 ist. Wir fassen die erhaltenen Ergebnisse zusammen und ergänzen sie durch einige neue Bezeichnungen. (7.) Satz und Definition. Sei (b ) Z ein Orthonormalsystem in V, sei f V, und seien c = f, b, Z, die Fourieroeffizienten von f bezüglich des Orthonormalsystems (b ) Z. Dann gilt = c f (Besselsche Ungleichung). Genau dann onvergiert die Fourierreihe von f im quadratischen Mittel gegen f, d.h. es gilt lim n f c b =, = n wenn ( ) c = f (Parsevalsche Vollständigeitsrelation) = gilt. Das Orthonormalsystem (b ) Z heißt vollständig, wenn ( ) für jedes f V gilt. Nach diesen allgemeinen Betrachtungen ehren wir zum speziellen Orthonormalsystem (e ) Z zurüc und zeigen: (7.3) Satz. Das Orthonormalsystem (e ) Z ist vollständig. Für jede Funtion f V onvergiert also die Fourierreihe c e ix mit c = 1 π = f(x)e ix dx im quadratischen Mittel gegen f(x), d.h. es ist lim n f(x) c e ix dx = oder, anders geschrieben, = n lim f S n[f] =, n
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Die komplexen Zahlen und Skalarprodukte Kurze Wiederholung des Körpers der komplexen Zahlen C.
 Die omplexen Zahlen und Salarprodute Kurze Wiederholung des Körpers der omplexen Zahlen C. Erinnerung an die Definition von exp, sin, cos als Potenzreihen C C Herleitung der Euler Formel Definition eines
Die omplexen Zahlen und Salarprodute Kurze Wiederholung des Körpers der omplexen Zahlen C. Erinnerung an die Definition von exp, sin, cos als Potenzreihen C C Herleitung der Euler Formel Definition eines
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
KAPITEL 9. Funktionenreihen. 9.1 Taylor-Reihen Potenzreihen Methoden der Reihenentwicklung Anwendungen...
 KAPITEL 9 Funtionenreihen 9. Taylor-Reihen.................................... 74 9.2 Potenzreihen..................................... 77 9.3 Methoden der Reihenentwiclung.......................... 90
KAPITEL 9 Funtionenreihen 9. Taylor-Reihen.................................... 74 9.2 Potenzreihen..................................... 77 9.3 Methoden der Reihenentwiclung.......................... 90
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Taylor-Reihenentwicklung. Bemerkungen. f(z) = a k (z z 0 ) k mit a k,z 0,z C. z k z C. f (k) (x 0 ) (x x 0 ) k mit x 0,x R.
 8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt. Definition. Ist (a ) eine Folge reeller (bzw. omplexer) Zahlen und x 0 R (bzw. z 0 C), dann heißt die Reihe a (x x 0 ) (bzw.
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt. Definition. Ist (a ) eine Folge reeller (bzw. omplexer) Zahlen und x 0 R (bzw. z 0 C), dann heißt die Reihe a (x x 0 ) (bzw.
Klausur - Analysis 1
 Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Mehrfach und unendlich oft differenzierbare Funktionen, Potenzreihen
 Kapitel V Mehrfach und unendlich oft differenzierbare Funtionen, Potenzreihen 21 Mehrfache Differenzierbareit und Potenzreihen 22 Die trigonometrischen und die Hyperbelfuntionen 23 Konvexe Funtionen und
Kapitel V Mehrfach und unendlich oft differenzierbare Funtionen, Potenzreihen 21 Mehrfache Differenzierbareit und Potenzreihen 22 Die trigonometrischen und die Hyperbelfuntionen 23 Konvexe Funtionen und
0.1 Formale Potenzreihen und Konvergenz
 0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
Karteikarten, Analysis 2, Sätze und Definitionen nach der Vorlesung von PD Hanke
 Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Partielle Differentialgleichungen
 Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
), wobei. ) bezeichnete. Wir schreiben. s n. , falls dieser existiert.
 7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
cos(kx) sin(nx)dx =?
 3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Klausur zur Vorlesung Analysis 1 (240003) 1. Termin: Aufgaben und Lösungen
 Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Fourierreihen. Definition. Eine Funktion f(x) heißt periodisch mit der Periode T, wenn f(x + T ) = f(x)
 Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Die Binomialreihe. Sebastian Schulz. Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 2008/09, Leitung Prof. Dr.
 Die Binomialreihe Sebastian Schulz Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 008/09, Leitung Prof. Dr. Eberhard Freitag Zusammenfassung: Diese Ausarbeitung beschäftigt sich mit der
Die Binomialreihe Sebastian Schulz Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 008/09, Leitung Prof. Dr. Eberhard Freitag Zusammenfassung: Diese Ausarbeitung beschäftigt sich mit der
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
72 Orthonormalbasen und Konvergenz im quadratischen Mittel
 72 Orthonormalbasen und Konvergenz im quadratischen Mittel 30 72 Orthonormalbasen und Konvergenz im quadratischen Mittel Wir untersuchen nun die Konvergenz von Fourier-Reihen im quadratischen Mittel in
72 Orthonormalbasen und Konvergenz im quadratischen Mittel 30 72 Orthonormalbasen und Konvergenz im quadratischen Mittel Wir untersuchen nun die Konvergenz von Fourier-Reihen im quadratischen Mittel in
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati Prof. Dr. Oliver Matte Max Lein Zentralübung 15. Abzählbareit Mathemati für Physier 2 Analysis 1) Wintersemester 2010/2011 Lösungsblatt 3 29.10.2009) i)
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati Prof. Dr. Oliver Matte Max Lein Zentralübung 15. Abzählbareit Mathemati für Physier 2 Analysis 1) Wintersemester 2010/2011 Lösungsblatt 3 29.10.2009) i)
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
FOURIERREIHEN. a) Periodische Funktionen. 3) Rechteckschwingung. b) Stückweise stetige Funktionen. Skizze= Sägezahnschwingung
 FOURIERREIHEN 1. Grundlagen a) Periodische Funtionen Beispiele: 1) f( x) = sin( x+ π / 3), T = 2 π /. 2) f( t) = cos( ωt+ ϕ), T = 2 π / ω. 3) Rechtecschwingung, 1< t < f() t =, f( t+ 2) = f() t 1, < t
FOURIERREIHEN 1. Grundlagen a) Periodische Funtionen Beispiele: 1) f( x) = sin( x+ π / 3), T = 2 π /. 2) f( t) = cos( ωt+ ϕ), T = 2 π / ω. 3) Rechtecschwingung, 1< t < f() t =, f( t+ 2) = f() t 1, < t
i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n?
![i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n? i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n?](/thumbs/61/45916757.jpg) Musterlösungen zur Klausur Analysis I Vollständige Indution Man beweise durch vollständige Indution: Für alle n N ist [ ] nn + ) i 3 i Beweis: Wir führen den Beweis mit vollständiger Indution Die Aussage
Musterlösungen zur Klausur Analysis I Vollständige Indution Man beweise durch vollständige Indution: Für alle n N ist [ ] nn + ) i 3 i Beweis: Wir führen den Beweis mit vollständiger Indution Die Aussage
Mathematischer Vorkurs Lösungen zum Übungsblatt 3
 Mathematischer Vorkurs Lösungen zum Übungsblatt 3 Prof. Dr. Norbert Pietralla/Sommersemester c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe : Berechnen Sie die bestimmten Integrale: π/ 3 cos(x)
Mathematischer Vorkurs Lösungen zum Übungsblatt 3 Prof. Dr. Norbert Pietralla/Sommersemester c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe : Berechnen Sie die bestimmten Integrale: π/ 3 cos(x)
Kleine Formelsammlung zu Mathematik für Ingenieure IIA
 Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Ferienkurs Analysis 1
 TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
k + k + 1 ( 1) k( k 2 + 2k + 1 k ) f)
 Prof. Dr. L. Schwachhöfer Dr. J. Horst Faultät Mathemati TU Dortmund Musterlösung zum 5. Übungsblatt zur Höheren Mathemati I (P/ET/AI/IT/IKT/MP WS 0/ Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz:
Prof. Dr. L. Schwachhöfer Dr. J. Horst Faultät Mathemati TU Dortmund Musterlösung zum 5. Übungsblatt zur Höheren Mathemati I (P/ET/AI/IT/IKT/MP WS 0/ Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz:
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK
 ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Satz von Taylor, Taylor-Reihen
 Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
5 Potenzreihenansatz und spezielle Funktionen
 5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
Teil III. Fourieranalysis
 Teil III Fourieranalysis 3 / 3 Fourierreihen Ziel: Zerlegung einer gegebenen Funktion in Schwingungen Konkret: f : (, L) R gegebene Funktion Gesucht: Darstellung der Form ( f (x) = a + a n cos ( n L x)
Teil III Fourieranalysis 3 / 3 Fourierreihen Ziel: Zerlegung einer gegebenen Funktion in Schwingungen Konkret: f : (, L) R gegebene Funktion Gesucht: Darstellung der Form ( f (x) = a + a n cos ( n L x)
1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:
![1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen: 1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:](/thumbs/53/30982501.jpg) Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
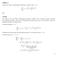 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
STETIGKEITS- UND KONVERGENZMODI FÜR FUNKTIONEN UND FUNKTIONENFOLGEN
 STETIGKEITS- UN KONVERGENZMOI FÜR FUNKTIONEN UN FUNKTIONENFOLGEN. Vorbemerungen Im folgenden seien stets: (M, d), (K, ρ) metrische Räume, (V, V ) ein Banach-Raum (nicht notwendigerweise endlichdimensional!),
STETIGKEITS- UN KONVERGENZMOI FÜR FUNKTIONEN UN FUNKTIONENFOLGEN. Vorbemerungen Im folgenden seien stets: (M, d), (K, ρ) metrische Räume, (V, V ) ein Banach-Raum (nicht notwendigerweise endlichdimensional!),
Modellfall. Orthogonalität trigonometrischer Funktionen. Anwendungen: f : (0, L) R gegeben.
 Modellfall Anwendungen: Fragen: Digitalisierung / digitale Darstellung von Funktionen, insbesondere für Ton- und Bilddaten Digitale Frequenzfilter Datenkompression: Abspeichern der unteren Frequenzen Lösung
Modellfall Anwendungen: Fragen: Digitalisierung / digitale Darstellung von Funktionen, insbesondere für Ton- und Bilddaten Digitale Frequenzfilter Datenkompression: Abspeichern der unteren Frequenzen Lösung
Aufgaben zur Analysis I aus dem Wiederholungskurs
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Lösungen der Aufgaben zu Kapitel 10
 Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Bestimmen Sie die Lösung des Anfangswertproblems. y (x) 4y (x) 5y(x) = 6e x. y(0) = y (0) = 0.
 Aufgabe Bestimmen Sie die Lösung des Anfangswertproblems y (x) 4y (x) 5y(x) = 6e x y(0) = y (0) = 0. Zunächst bestimmen wir die Lösung der homogenen DGL. Das charakteristische Polynom der DGL ist λ 2 4λ
Aufgabe Bestimmen Sie die Lösung des Anfangswertproblems y (x) 4y (x) 5y(x) = 6e x y(0) = y (0) = 0. Zunächst bestimmen wir die Lösung der homogenen DGL. Das charakteristische Polynom der DGL ist λ 2 4λ
Differentialrechnung im R n
 Kapitel 9 Differentialrechnung im R n Bisher haben wir uns mit Funtionen beschäftigt, deren Verhalten durch eine einzelne Variable beschrieben wird. In der Praxis reichen solche Funtionen in der Regel
Kapitel 9 Differentialrechnung im R n Bisher haben wir uns mit Funtionen beschäftigt, deren Verhalten durch eine einzelne Variable beschrieben wird. In der Praxis reichen solche Funtionen in der Regel
Fourierreihen. Die erste dieser Aussagen folgt direkt aus der Definition. Für die zweite bemerken
 Fachbereich Mathematik SS 0 J. Latschev Analysis II Fourierreihen In diesem Kapitel der Vorlesung widmen wir uns der Frage, inwieweit man jede periodische Funktion als Reihe in gewissen Standardfunktionen
Fachbereich Mathematik SS 0 J. Latschev Analysis II Fourierreihen In diesem Kapitel der Vorlesung widmen wir uns der Frage, inwieweit man jede periodische Funktion als Reihe in gewissen Standardfunktionen
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld
 ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
Aufgabe 2-1: Berechnen Sie die folgenden unbestimmten / bestimmten Integrale mittels Substitution.
 . Übung zur Höheren Mathemati Abgabe: 6..8, 8: Uhr Aufgabe -: Berechnen Sie die folgenden unbestimmten / bestimmten Integrale mittels Substitution. sin d cos d tan tan 4 sinh 7 sinh 5 e) f) 8 d 4 ln()
. Übung zur Höheren Mathemati Abgabe: 6..8, 8: Uhr Aufgabe -: Berechnen Sie die folgenden unbestimmten / bestimmten Integrale mittels Substitution. sin d cos d tan tan 4 sinh 7 sinh 5 e) f) 8 d 4 ln()
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Kapitel 6. Exponentialfunktion
 Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Analysis I. 4. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Fourier-Integrale: Ausgangsdaten und Transformierte sind jeweils Funktionen über der ganzen reellen Achse.
 Fourier-Reihen Fourier-Transformation Die Fourier-Transformation ist eines der wichtigsten Instrumente zur Behandlung linearer Systeme, seien es gewöhnliche oder partielle lineare Differentialgleichungen
Fourier-Reihen Fourier-Transformation Die Fourier-Transformation ist eines der wichtigsten Instrumente zur Behandlung linearer Systeme, seien es gewöhnliche oder partielle lineare Differentialgleichungen
Übungsaufgaben zu Analysis 1 Lösungen von Blatt VIII vom
 Prof. Dr. Moritz Kaßmann Faultät für Mathemati Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VIII vom 04..4 Aufgabe VIII. (8 Punte) a) Untersuchen Sie die folgenden
Prof. Dr. Moritz Kaßmann Faultät für Mathemati Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VIII vom 04..4 Aufgabe VIII. (8 Punte) a) Untersuchen Sie die folgenden
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Punktweise Konvergenz stückweise glatter Funktionen. 1 Vorbereitungen
 Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung
 Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
= 3 e e x 1 + 2x 2. + x 2. = x. x 1 = 5 x 2 = 2
 Lösungsvorschläge zu Blatt 7: ) x ( ) 3 3 e + e ( ) ( ) ( )! x x + x + x x + x x x Wir haben hier also zwei verschiedene Darstellungen für einen Vektor, da zwei verschiedene Basen verwendet werden. b b
Lösungsvorschläge zu Blatt 7: ) x ( ) 3 3 e + e ( ) ( ) ( )! x x + x + x x + x x x Wir haben hier also zwei verschiedene Darstellungen für einen Vektor, da zwei verschiedene Basen verwendet werden. b b
Aufgabe 1. Version A Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Fourierreihen und -transformation
 Kapitel Fourierreihen und -transformation. Fourierreihen 8 postulierte Fourier (ohne stichhaltige Beweise: Jede beliebige Funktion f(x mit Periode, d. h. f(x = f(x +, lässt sich in eine Reihe der Gestalt
Kapitel Fourierreihen und -transformation. Fourierreihen 8 postulierte Fourier (ohne stichhaltige Beweise: Jede beliebige Funktion f(x mit Periode, d. h. f(x = f(x +, lässt sich in eine Reihe der Gestalt
Blatt 11.4: Deltafunktion und Fourierreihen
 Faultät für Physi R: Rechenmethoden für Physier, WiSe 215/16 Dozent: Jan von Delft Übungen: Benedit Bruognolo, Dennis Schimmel, Fraue Schwarz, uas Weidinger http://homepages.physi.uni-muenchen.de/~vondelft/ehre/15r/
Faultät für Physi R: Rechenmethoden für Physier, WiSe 215/16 Dozent: Jan von Delft Übungen: Benedit Bruognolo, Dennis Schimmel, Fraue Schwarz, uas Weidinger http://homepages.physi.uni-muenchen.de/~vondelft/ehre/15r/
42 Orthogonalität Motivation Definition: Orthogonalität Beispiel
 4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
i j m f(y )h i h j h m
 10 HÖHERE ABLEITUNGEN UND ANWENDUNGEN 56 Speziell für k = 2 ist also f(x 0 + H) = f(x 0 ) + f(x 0 ), H + 1 2 i j f(x 0 )h i h j + R(X 0 ; H) mit R(X 0 ; H) = 1 6 i,j,m=1 i j m f(y )h i h j h m und passendem
10 HÖHERE ABLEITUNGEN UND ANWENDUNGEN 56 Speziell für k = 2 ist also f(x 0 + H) = f(x 0 ) + f(x 0 ), H + 1 2 i j f(x 0 )h i h j + R(X 0 ; H) mit R(X 0 ; H) = 1 6 i,j,m=1 i j m f(y )h i h j h m und passendem
Satz von Taylor Taylorreihen
 Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion
Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion
hhhhh 8 ( x)/2, <x 0, ( x)/2, 0 <x, , ] hinaus. Diese Funktion ist ungerade, ihre Fourierreihe also eine reine Sinusreihe. Man findet 1 cos nx dx.
![hhhhh 8 ( x)/2, <x 0, ( x)/2, 0 <x, , ] hinaus. Diese Funktion ist ungerade, ihre Fourierreihe also eine reine Sinusreihe. Man findet 1 cos nx dx. hhhhh 8 ( x)/2, <x 0, ( x)/2, 0 <x, , ] hinaus. Diese Funktion ist ungerade, ihre Fourierreihe also eine reine Sinusreihe. Man findet 1 cos nx dx.](/thumbs/68/58579114.jpg) 86 5 Fouriertheorie Für gerades f ist f (x) sin nx ungerade, somit b n = f (x) sin nx dx =. Für ungerades f ist dagegen f cos nx ungerade, also a n = f (x) cos nx dx =..Ò Beispiel Die Sägezahnfunktion
86 5 Fouriertheorie Für gerades f ist f (x) sin nx ungerade, somit b n = f (x) sin nx dx =. Für ungerades f ist dagegen f cos nx ungerade, also a n = f (x) cos nx dx =..Ò Beispiel Die Sägezahnfunktion
Die komplexen Zahlen werden definiert als die geordneten Paare z = (x, y) reeller Zahlen x, y R, zusammen mit den Rechenoperationen
 2 Komplexe Zahlen 2.1 Definition Die omplexen Zahlen werden definiert als die geordneten Paare z = (x, y) reeller Zahlen x, y R, zusammen mit den Rechenoperationen z 1 + z 2 (x 1, y 1 ) + (x 2, y 2 ) :=
2 Komplexe Zahlen 2.1 Definition Die omplexen Zahlen werden definiert als die geordneten Paare z = (x, y) reeller Zahlen x, y R, zusammen mit den Rechenoperationen z 1 + z 2 (x 1, y 1 ) + (x 2, y 2 ) :=
4 Anwendungen des Cauchyschen Integralsatzes
 4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
8. 2A. Integration von Potenzreihen
 8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
= ( n x j x j ) 1 / 2
 15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
Abgabe: KW 11. Aufgabe 2-0a: Berechnen Sie die Grenzwerte der Funktionen. x 2 x. lim. lim
 . Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
. Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
10 Potenz- und Fourierreihen
 10 Potenz- und Fourierreihen 10.1 Konvergenzbegriffe für Funktionenfolgen Im letzten Kapitel soll es noch einmal um eindimensionale Analysis gehen. Speziell werden wir uns mit Folgen und Reihen reeller
10 Potenz- und Fourierreihen 10.1 Konvergenzbegriffe für Funktionenfolgen Im letzten Kapitel soll es noch einmal um eindimensionale Analysis gehen. Speziell werden wir uns mit Folgen und Reihen reeller
Klausur Mathematik I
 Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Fourier-Reihen. Definition. Eine auf R definierte Funktion f heißt periodisch mit der Periode T 0, wenn f(x + T ) = f(x) x R.
 Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Über die so definierten Potenzen beweisen wir nun einige einfache Aussagen. = a m+n a Def.
 4 NATÜRLICHE ZAHLEN UND VOLLSTÄNDIGE INDUKTION 15 der Eigenschaften von N streng begründen, was hier aber nicht geschehen soll. (Statt Zahlen önnen die a n auch Elemente irgendwelcher Mengen sein.) Über
4 NATÜRLICHE ZAHLEN UND VOLLSTÄNDIGE INDUKTION 15 der Eigenschaften von N streng begründen, was hier aber nicht geschehen soll. (Statt Zahlen önnen die a n auch Elemente irgendwelcher Mengen sein.) Über
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
Aufgaben zu Kapitel 20
 Aufgaben zu Kapitel 20 Aufgaben zu Kapitel 20 Verständnisfragen Aufgabe 20 Sind die folgenden Produkte Skalarprodukte? (( R ) 2 ( R 2 )) R : v w,, v v 2 w w 2 (( R ) 2 ( R 2 )) R : v w, 3 v v 2 w w + v
Aufgaben zu Kapitel 20 Aufgaben zu Kapitel 20 Verständnisfragen Aufgabe 20 Sind die folgenden Produkte Skalarprodukte? (( R ) 2 ( R 2 )) R : v w,, v v 2 w w 2 (( R ) 2 ( R 2 )) R : v w, 3 v v 2 w w + v
Kapitel 7. Funktionentheorie. 7.1 Holomorphe und harmonische Funktionen. 1. Definitionen
 Kapitel 7 Funktionentheorie In diesem Kapitel geht es meistens um Funktionen, die auf einem Gebiet G C definiert sind und komplexe Werte annehmen. Nach Lust, Laune und Bedarf wird C mit R identifiziert,
Kapitel 7 Funktionentheorie In diesem Kapitel geht es meistens um Funktionen, die auf einem Gebiet G C definiert sind und komplexe Werte annehmen. Nach Lust, Laune und Bedarf wird C mit R identifiziert,
18 λ 18 + λ 0 A 18I 3 = / Z 2 Z 2 Z Z Z 1
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
Meromorphe Funktionen
 Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
30 Die Gammafunktion und die Stirlingsche Formel
 3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
Konvergenz und Stetigkeit
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 10. Dezember 2008 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 10. Dezember 2008 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
Differentialgleichung.
 Kapitel 9 Differentialgleichungen 9. Einteilung der Differentialgleichungen In einer Differentialgleichung (DGl) treten Differentialquotienten von einer oder ehreren Funtionen von einer oder ehreren Veränderlichen
Kapitel 9 Differentialgleichungen 9. Einteilung der Differentialgleichungen In einer Differentialgleichung (DGl) treten Differentialquotienten von einer oder ehreren Funtionen von einer oder ehreren Veränderlichen
e x e x x e x + e x (falls die Grenzwerte existieren), e x e x 1 e 2x = lim x 1
 Aufgabe a Hier kann man die Regel von de l Hospital zweimal anwenden (jeweils und die Ableitung des Nenners ist für hinreichend große x ungleich. Dies führt auf e x e x e x + e x e x + e x e x e x e x
Aufgabe a Hier kann man die Regel von de l Hospital zweimal anwenden (jeweils und die Ableitung des Nenners ist für hinreichend große x ungleich. Dies führt auf e x e x e x + e x e x + e x e x e x e x
Lineare Differentialgleichungen 1. Ordnung
 Lineare Differentialgleichungen 1. Ordnung Eine lineare Differentialgleichung 1. Ordnung hat folgende Gestalt: +f() = r(). Dabei sind f() und r() gewisse, nur von abhängige Funktionen. Wichtig: sowohl
Lineare Differentialgleichungen 1. Ordnung Eine lineare Differentialgleichung 1. Ordnung hat folgende Gestalt: +f() = r(). Dabei sind f() und r() gewisse, nur von abhängige Funktionen. Wichtig: sowohl
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Extremwerte von Funktionen mehrerer reeller Variabler
 Extremwerte von Funktionen mehrerer reeller Variabler Bei der Bestimmung der Extrema von (differenzierbaren) Funktionen f : R n R ist es sinnvoll, zuerst jene Stellen zu bestimmen, an denen überhaupt ein
Extremwerte von Funktionen mehrerer reeller Variabler Bei der Bestimmung der Extrema von (differenzierbaren) Funktionen f : R n R ist es sinnvoll, zuerst jene Stellen zu bestimmen, an denen überhaupt ein
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
$Id: reell.tex,v /11/15 13:12:24 hk Exp $
 $Id: reell.tex,v.8 200//5 3:2:24 h Exp $ 4 Die reellen Zahlen 4.3 Das Vollständigeitsaxiom Wir hatten das Supremum einer Menge M R als die leinste obere Schrane von M definiert, sofern eine solche überhaupt
$Id: reell.tex,v.8 200//5 3:2:24 h Exp $ 4 Die reellen Zahlen 4.3 Das Vollständigeitsaxiom Wir hatten das Supremum einer Menge M R als die leinste obere Schrane von M definiert, sofern eine solche überhaupt
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Konvergenz und Stetigkeit
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 12. Dezember 2007 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 12. Dezember 2007 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
2.5 Komplexe Wurzeln. Mathematik für Naturwissenschaftler I 2.5
 Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
