Einführung Die Power-Methode Lanczos Methode Anhang. Die Lanczos Methode. Wiebke Plenkers. 29. Mai 2008
|
|
|
- Mathias Meissner
- vor 5 Jahren
- Abrufe
Transkript
1 29. Mai 2008
2 Inhaltsverzeichnis Einführung 1 Einführung Motivation Exakte Diagonalisierung 2 Idee Mathematitische Vorgehensweise 3 4
3 Motivation Exakte Diagonalisierung Motivation Für die genaue Beschreibung von Vielteilchensystemen wird oft eine exakte Diagonalisierung des Hamiltonoperators gewünscht, z.b. bei der Beschreibung von Systemen Kondensierter Materie geringer Energie. Betrachte die Konfiguration von Teilchen auf N Gitterpunkten mit jeweils s Basiszuständen Ψ >= {α j } ψ(α 1, α 2,..., α N ) α 1, α 2,..., α N > Dimension der resultierenden Hamililton Matrix: N j=1 s j Problem der Hamiltonmatrix Die Dimension der Basis eines Vielteilchensystems wächst exponentiell mit N!
4 Motivation Exakte Diagonalisierung Kurze Erinnerung an den Hamiltonoperator H Ein Ansatz QM-Systeme zu lösen ist der, die Eigenwerte von H zu finden, also Lösen der Eigenwertgleichung H als Matrix : H ij =< v i H v j > H kann verschiedene Subsyteme miteinander verbinden H = l H1 l + l,m H2 l,m l,m,n,p H4 l,m,n,p +... Beispiele: simple tight-binding chain mit nearest-neighbour hopping H t,b = i,j t i,j(c + j+1 c j + c + j c j+1 ) mit Betrachtung des Spins : Hubbard model H = t j,m,σ (c+ j,σ c m,σ + c + m,σc j,σ ) + U j n j,, n j, des Weiteren gibt es z.b. Anderson Hamiltonien, Heisenberg Hamiltonien und mit Defekten z.b. das Kondo Model
5 Motivation Exakte Diagonalisierung Exakte Diagonalisierung Exakte Diagonalisierung = numerischer Ansatz zum Finden des exakten Ergebnisses für ein finites Gitter-System durch direkte Diagonalisierung von H 1) Einfachster Ansatz: Komplette Diagonalisierung, Problem: exponentieller Wachstum von H Lösen von det(h λe) = 0 2) Wenn nur niedrigen oder hohen Eigenzustände gesucht werden: Iterative Diagonalisierungs- Methoden Extreme Verkleinerung der Matrixdimension durch Projektion H wird duch die Benutzung von Symmetrien so weit wie möglich vereinfacht
6 Motivation Exakte Diagonalisierung Exakte Diagonalisierung Beispiel der Dimensionsreduktion von H, N=40,Heisenberg-H gesammter Hilbertraum: dim = 2 40 = Beschränkung auf S z=0 dim = Nutzung der Spininversion: dim = Nutzung von 40 Translationen: dim = 1, Nutzung aller 4 Rotationen: dim = Zur Berechnung auf Computern wird ein Zustand meist in einem Bit, bzw. einem Satz von Bits gespeichert Bisher können auf normalen Computern berechnet werden: Spin 1/2 - Modelle N=40 (lattice verschiedener Geometrien) Hubbard Modelle mit Halbfüllung N=20
7 Motivation Exakte Diagonalisierung Komplette Diagonalisierung Komplette Diagonalisierung wird z.b. in einem Schritt von DMRG gebraucht (Diagonaisierung der Dichtematrix) bekannte Programme für KD, wie z.b. LAPACK Solche Programme können zwar auch genutzt werden, um H zu diagonalisieren, aber sie sind weniger effizient als Interative Methoden Grenzen von kompletter Diagonalisierung: Die gesamte Matrix muss gespeichert und diagonalisiert werden ( exp.-wachstum!) Bsp. Hubbard-Kette: 10 (20) Plätze mit Supercomputer möglich (mit Symmetriebetrachtung) 1-D Systeme mit 1000 Plätzen mit DMRG auf normalem Computer
8 Motivation Exakte Diagonalisierung Iterative Diagonalisierung Idee Projektion der Matrix H auf einen Unterraum der Dimension M N!! (typisch auf M = 100) Der Unterraum muss dabei so gewählt sein, dass die extremen Eigenwerte innerhalb des Unterraums sehr schnell mit M zu den extremen Eigenwerten des Systems konvergieren Bedingung: Nur der Grundzustand und die niedrigen Anregungszustände werden gesucht Es gibt viele starke iterative Diagonalisierungs Prozeduren In der Physik sehr bekannt: die Lanczos-Methode So wie die meisten iterativen Diagonalisierungs-Methoden beruht auch die Lanczos-Methode auf der Power-Methode
9 Idee Mathematitische Vorgehensweise : Idee Sehr einfache Methode zum Finden des höchsten Eigenwerts mit entsprechendem Eigenvektor einer nxn-matrix Idee: Iterative Diagonalisierungs Methode Voraussetzung: A nxn hat n linear unabhängige Eigenvektoren A nxn hat einen dominanten Eigenwert Speicher-Vorteil: sehr effizient, da nur zwei Vektoren gespeichert werden müssen u i und u i 1
10 Idee Mathematitische Vorgehensweise Mathematitische Vorgehensweise 1 λ m 1 Sei X ein beliebiger Vektor : X 0 = c 1 V 1 + c 2 V c n V n mit {V 1, V 2,..., V n } sind linear unabhängigige Eigenvektoren Daraus folgt: AX 0 = c 1 λ 1 V 1 + c 2 λ 2 V c n λ n V n A 2 X 0 = c 1 λ 2 1 V 1 + c 2 λ 2 2 V c n λ 2 nv n... A m X 0 = c 1 λ m 1 V 1 + c 2 λ m 2 V c n λ m n V n dividiere durch λ m 1 A m X 0 = c 1 V 1 + c 2 ( λ 2 λ 1 ) m V c n ( λn λ 1 ) m V n wird nun m immer größer, so gehen die Brüche ( λ i λ 1 ) m gegen Null 1 λ m A m X 0 = c 1 V 1 1
11 Idee Mathematitische Vorgehensweise Mathematitische Vorgehensweise Ebenso verfärht man mit m+1 Bilde nun jeweils das Skalarprodukt mit einem beliebigen, nicht zu V 1 orthogonalen Vektor Y 1 A m X 0 Y = c 1 V 1 Y λ m 1 1 λ m+1 1 A m+1 X 0 Y = c 1 V 1 Y Gleichsetzen ergibt: A m+1 X 0 Y A m X 0 Y = λm+1 1 λ m 1 = λ 1 generiert den sogenannten Krylov-Unterraum : K n = span{u 0, Hu 0,..., H n 1 u 0 }
12 Einführung Gegeben sei eine Matrix H, zu der der minimale Eigenwert λ mit dem Eigenvektor x gesucht wird : Hx = λx Idee: benutze den n-ten Krylov-Raum (Dimension n) K n = span{u 0, Hu 0,..., H n 1 u 0 } mit einem beliebigen Startvektor u 0 konstruiere daraus eine orthogonale (nicht orthonormale Basis) von K n : {u 0, u 1,..., u n 1 } Nun werden die Zustände der mit folgender Rekursionsrelation gefunden: u i+1 = Hu i a i u i b 2 i u i 1 für i=0,...,n-1 mit a i = ut i Hu i u T i u i und b 2 i = ut i u i u T i 1 u i 1 für i=0,...,n-1 für i=1,...,n-1
13 Man wählt die Startwerte: u 1 = 0, b 0 = 0 Damit gilt u i K n für i=0,... n-1 Diese Rekursionsrelation wird nun wiederholt, bis die Vektoren zu einer beliebigen Genauigkeit konvergieren, dann n=m (maximale Dimension) u i+1 = Hu i ( ut i Hu i )u u T i u i b 2 i i u i 1 für i=0,...,n-1 Das Ergebnis ist eine Tridiagonale Matrix: T n = a 0 b 1 0 b 1 a 1 b 2 b 2 a 2 b n 1 0 b n 1 a n 1
14 Von dieser Tridimensionalen Matrix kann man nun numerisch leicht die Eigenwerte finden: det(h 1 ) det(h 0 ) = 1 a 0 b1 2 det(h 2 ) det(h 1 ) det(h i ) det(h i 1 ) = 1 a 0 b1 2 det(h i+1 ) det(h i ) det(h 0 ) = a 0 det(h 1 ) b 2 1det(H 2 ) Diese Iteration kann numerisch leicht gelöst werden
15 Induktionsvoraussetzung: {u 0, u 1,..., u n 1 } ist orthogonal damit ist u T i u i+1 = u T i (Hu i a i u i b 2 i u i 1) = a i u T i u i a i u T i u i 0 = 0 und für j=0,..., i-1 u T j u j+1 = u T j (Hu i a i u i b 2 i u i 1) = u T j Hu i b 2 i ut j u i 1 = u T i Hu j b 2 i ut j u i 1 = u T i (a j u j + u j+1 + b 2 i u i 1) b 2 i ut j u i 1 = u T i u j+1 b 2 i ut j u i 1 = 0 da bei j = i 1 die Definition von u i+1 greift und für j< i 1 Orthogonalität gilt paarweise Orthogonalität für alle i = 0,..., n 1
16 Normierung der Vektoren v i = u i u T i u i damit folgt für die Lanczos-Rekursionsbeziehung: a i = ut i Hu i = v T u T i u i i Hv i b i = v T i Hv i 1 v T i Hv j = 0 für i j und i j ± 1 T ij = v T i Hv j ist die schon genannte Tridimensionale Matrix
17 Einführung K n ist ein invarianter Unterraum: HK n K n in K n gilt: H = ij v it ij v T j und mit der Definition V = (v 0,..., v n 1 )(Mxn-Matrix, M: Dimension von H) ist H = VTV T wobei gilt: VTV T = 1 VV T, v i ist die i-te Spalte von V Nun definiert man die {q 0,..., q n 1 } durch T q i = λ i q i also ist T = i λ iq i q T i also: H = V ( i λ iq i q T ) i V T = i λ iv q i q T i V T also: H = i λ ix i x T i und Hx i = λ i x i mit x i = V q i
18 Vorteile der Lanczos-Methode: Die Näherung des extremen Eigenwerts ist meistens schon nach einer kleinen Iterationszahl sehr genau (typisch 100 Iterationen)!!! dim Lanczosmatrix << dim Hilbertraum Sehr speicher-effizient: Nur Speicherung von drei Vektoren notwendig: u i 1, u i, und u i+1 Mehrdimensionale Probleme können gelöst werden Aber es gibt auch große Nachteile: Konvergenz zu höheren Zuständen kann unregelmäßig sein ghost- Eigenwerte : Verlust an Orthogonalität der Lanczos-Vektoren aufgrund der finiten Rechnerpräzision
19 Lösung des Orthogonalitätsverlustes Reothogonalisierung der Lanzcos-Vektoren zueinander mit Hilfe des Gram-Schmidt-Verfahrens (allerdings müssen dann alle Vektoren gespeichert werden) teilweise Reothogonalisierung (Cullum und Willoughby) Modifizierte Lanzcos-Verfahren (z.b. Stopp nach Berechnung von zwei Vektoren, Diagonalisierung der 2x2-Matrix, resultierender Eigenwert=neuer Startpunkt für neue Iteration) andere Methoden wie z.b. implicitly restarted Lanczos method oder die Band- oder Block-
20 TFlops and 159-Billion-dimensional Exact-diagonalization for Trapped Fermion-Hubbard Model on the Earth Simulator - Susumu Yamada, Toshiyuki Imamura, Masahiko Machida - - Japan Atomic Energy Research Institute, The University of Electro-Communications - - Computer Society Goal: study a possibility of superfluidity in trapped atomic Fermi gases loaded on optical lattices, by implementation of an exact diagonalization code for the trapped Hubbard model on the Earth Simulator result: succes in solving a 159-billion-dimensional matrix by using the conventional Lanczos method. world-record!
21 Hubbard model with a trap potential: H = t j,m,σ (c+ j,σ c m,σ + c m,σc + j,σ ) + U j n j,, n j, + ( 2 ) 2 N V j,σ n ( ) j,σ i N 2 2 Berechnung des kleinsten Eigenwerts und des dazugehörigen Eigenvektors für Hv = λv mit der Lanczos- und der preconditioned conjugate gradient (PCG) Methode
22 Vergleich der beiden Methoden für ein System mit 12 Fermionen auf 20 Plätze (10 nodes of the Earth Simulator = 80 processor elements) Die PCG-Methode ist wesentlich besser außer für die Speichergröße Für die meisten Simulationen wird PCG benutzt und nur für sehr große Systeme Lanczos
23
24 - Ergebnisse Diagonalization of the Hubbard Hamiltonian H including the trapping potential and calculation of an binding energy, which is a probe for superfluidity, with varying the repulsive U(> 0) and V. Result: Find of a condition in which Cooper pair (superfluid) function develops based on the binding energy
25 - Ergebnisse The flat region is called Mott core below. Expectation:a superfluid phase emerges when the Mott core is formed as seen in the Figure. Cofirmation: scenario about the superfluidity by performing the exact diagonalization (Lanczos) on the repulsive Hubbard model with the trapping potential (fix the trapping strength, i.e., V/t = 29.7 and examine how the binding energy of two Fermions Eb [10] changes with varying U/t) A negative Eb is a probe for superfluidity Result: Eb goes to negative in a large U/t region and the amplitude of the negative Eb slightly increases with increasing NF up to NF = 10 ( negative Eb emerges only above a certain V)
26 Einführung * 2. Februar 1893 in Székesfehérvár, Österreich-Ungarn, 25. Juni 1974 in Budapest ungarischer Mathematiker und Physiker 1921 Ph.D. thesis über Relativitätstheorie Assistent von Albert Einstein Nach 1949 in Los Angeles im US National Bureau of Standards: Entwicklung einiger wichtigen Techniken für mathematische Rechnungen mit Hilfe von Computern 1950 und 1952 Veröffentlichung zweier Artikel über ein von ihm Verfahren der minimierten Iterierten genanntes Verfahren zur Lösung von Fredholmschen Integralgleichungen, linearen Gleichungssystemen und Eigenwertaufgaben heraus - Basis der Lanczos-Verfahren (ersten der heutzutage noch verwendeten Krylow-Unterraum-Verfahren) 1952 verlässt die USAWiebke an der Plenkers School Dieof Lanczos Theoretical Methode Physics at the
27 Einführung Vielen Dank! Fragen? Diskussion!
28 Lanczos Algorithmus Einführung Algorithmus für die Herstellung der Tridiagonalen Matrix Vorraussetzung: eine Funktion zur Berechnung des Skalarproduktes (x,y) und der Multiplikation A nxn v Wähle zu der zu diagonalisierenden Matrix A nxn einen beliebigen Vektor v der gleichen Dimension v v ; q(1 : n) = 0; β 0 = 0 v = for (i,1,m) w i = Av i β i v i 1 α i = (w i, v i ) w i = w i α i v i β i+1 = w i v i+1 = w i β i+1 return
Iterative Methoden zur Lösung von linearen Gleichungssystemen
 Iterative Methoden zur Lösung von linearen Gleichungssystemen (13.12.2011) Ziel Können wir wir die zeitabhängige Schrödinger-Gleichung lösen? φ(t) = e iht ψ(0) Typischerweise sind die Matrizen, die das
Iterative Methoden zur Lösung von linearen Gleichungssystemen (13.12.2011) Ziel Können wir wir die zeitabhängige Schrödinger-Gleichung lösen? φ(t) = e iht ψ(0) Typischerweise sind die Matrizen, die das
Der CG-Algorithmus (Zusammenfassung)
 Der CG-Algorithmus (Zusammenfassung) Michael Karow Juli 2008 1 Zweck, Herkunft, Terminologie des CG-Algorithmus Zweck: Numerische Berechnung der Lösung x des linearen Gleichungssystems Ax = b für eine
Der CG-Algorithmus (Zusammenfassung) Michael Karow Juli 2008 1 Zweck, Herkunft, Terminologie des CG-Algorithmus Zweck: Numerische Berechnung der Lösung x des linearen Gleichungssystems Ax = b für eine
51 Numerische Berechnung von Eigenwerten und Eigenvektoren
 5 Numerische Berechnung von Eigenwerten und Eigenvektoren 5. Motivation Die Berechnung der Eigenwerte einer Matrix A IR n n als Lösungen der charakteristischen Gleichung (vgl. Kapitel 45) ist für n 5 unpraktikabel,
5 Numerische Berechnung von Eigenwerten und Eigenvektoren 5. Motivation Die Berechnung der Eigenwerte einer Matrix A IR n n als Lösungen der charakteristischen Gleichung (vgl. Kapitel 45) ist für n 5 unpraktikabel,
Das Hubbard-Modell: Diagonalisierung mit Hilfe des Lanczos-Verfahrens Computational Physics-Praktikum WS 2007/08
 Das Hubbard-Modell: Diagonalisierung mit Hilfe des Lanczos-Verfahrens Computational Physics-Praktikum WS 2007/08 Johannes Märkle,Philipp Buchegger Betreuer Dr. Thomas Dahm Tübingen, den 25. Januar 2008
Das Hubbard-Modell: Diagonalisierung mit Hilfe des Lanczos-Verfahrens Computational Physics-Praktikum WS 2007/08 Johannes Märkle,Philipp Buchegger Betreuer Dr. Thomas Dahm Tübingen, den 25. Januar 2008
Inhalt. Mathematik für Chemiker II Lineare Algebra. Vorlesung im Sommersemester Kurt Frischmuth. Rostock, April Juli 2015
 Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Symmetrische Gleichungssysteme Das Verfahren konjugierter Gradienten
 Symmetrische Gleichungssysteme Das Verfahren konjugierter Gradienten 1 / 20 Lineares Gleichungssystem Ax = f, n A[i, j]x j = f i j=1 für i = 1,..., n Voraussetzungen Matrix A sei symmetrisch: A[i, j] =
Symmetrische Gleichungssysteme Das Verfahren konjugierter Gradienten 1 / 20 Lineares Gleichungssystem Ax = f, n A[i, j]x j = f i j=1 für i = 1,..., n Voraussetzungen Matrix A sei symmetrisch: A[i, j] =
Ausgewählte Lösungen zu den Übungsblättern 9-10
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
9 Eigenwerte und Eigenvektoren
 92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
9 Eigenwerte und Eigenvektoren
 92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
(also ) Oft wird Zusammenhang zwischen und mit einem Index angedeutet, z.b. wird der Eigenvektor v. durch gekennzeichnet.
 L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
Einführung in die Grundlagen der Numerik
 Einführung in die Grundlagen der Numerik Institut für Numerische Simulation Rheinische Friedrich-Wilhelms-Universität Bonn Wintersemester 2014/2015 Normierter Vektorraum Sei X ein R-Vektorraum. Dann heißt
Einführung in die Grundlagen der Numerik Institut für Numerische Simulation Rheinische Friedrich-Wilhelms-Universität Bonn Wintersemester 2014/2015 Normierter Vektorraum Sei X ein R-Vektorraum. Dann heißt
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
4 Lineare Abbildungen Basisdarstellungen
 4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
47 Singulärwertzerlegung
 47 Singulärwertzerlegung 47.1 Motivation Wir haben gesehen, dass symmetrische Matrizen vollständig mithilfe ihrer Eigenwerte und Eigenvektoren beschrieben werden können. Diese Darstellung kann unmittelbar
47 Singulärwertzerlegung 47.1 Motivation Wir haben gesehen, dass symmetrische Matrizen vollständig mithilfe ihrer Eigenwerte und Eigenvektoren beschrieben werden können. Diese Darstellung kann unmittelbar
42 Orthogonalität Motivation Definition: Orthogonalität Beispiel
 4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz. Serie 10
 D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz Serie 10 Abgabedatum: 23.5/24.5, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG G 46, luc.grosheintz@sam.math.ethz.ch Webpage:
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz Serie 10 Abgabedatum: 23.5/24.5, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG G 46, luc.grosheintz@sam.math.ethz.ch Webpage:
6 Hauptachsentransformation
 6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
Lanczos Methoden. Stefan Grell Im Rahmen eines Proseminar zur Numerischen Mathematik unter der Leitung von Prof. Wolf Hofmann. 15.
 Lanczos Methoden Stefan Grell Im Rahmen eines Proseminar zur Numerischen Mathematik unter der Leitung von Prof. Wolf Hofmann 15. Juni 2005 Lanczos-Methoden Lanczos-Methoden sind iterative Verfahren zur
Lanczos Methoden Stefan Grell Im Rahmen eines Proseminar zur Numerischen Mathematik unter der Leitung von Prof. Wolf Hofmann 15. Juni 2005 Lanczos-Methoden Lanczos-Methoden sind iterative Verfahren zur
Lineare Algebra und Numerische Mathematik für D-BAUG
 R Käppeli L Herrmann W Wu Herbstsemester Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 9 Aufgabe 9 Finden Sie eine Basis des Lösungsraums L R 5 des linearen
R Käppeli L Herrmann W Wu Herbstsemester Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 9 Aufgabe 9 Finden Sie eine Basis des Lösungsraums L R 5 des linearen
(also ) Oft wird Zusammenhang zwischen und mit einem Index angedeutet, z.b. wird der Eigenvektor v. durch gekennzeichnet.
 L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Anwendungen in der Physik: Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors - Normalmoden
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Anwendungen in der Physik: Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors - Normalmoden
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren. Gegeben. Gesucht: Diagonalform: Finde und! Definition: Eigenvektor, Eigenwert
 L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
Lineare Algebra II. Prof. Dr. M. Rost. Übungen Blatt 7 (SS 2011) Abgabetermin: Donnerstag, 2. Juni.
 Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 7 (SS 2011) Abgabetermin: Donnerstag, 2. Juni http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Eigenvektoren
Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 7 (SS 2011) Abgabetermin: Donnerstag, 2. Juni http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Eigenvektoren
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
Eigenwerte. Vorlesung Computergestützte Mathematik zur Linearen Algebra. Lehrstuhl für Angewandte Mathematik Sommersemester 2009
 Eigenwerte Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Sommersemester 2009 25. Juni + 2.+9. Juli 2009 Grundlagen Definition Ist für A C n,n, Ax = λx
Eigenwerte Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Sommersemester 2009 25. Juni + 2.+9. Juli 2009 Grundlagen Definition Ist für A C n,n, Ax = λx
Komplexe Lineare Algebra. Lösung allgemeiner Linearer Systeme (m n möglich) Die Lösbarkeit eines linearen Systems
 Determinante und Inverse Lösung allgemeiner Linearer Systeme (m n möglich) Die Lösbarkeit eines linearen Systems Ax = b R m, x R n, A R mn hängt sehr stark vom sogenannten Rang der m n Matrix A ab Diese
Determinante und Inverse Lösung allgemeiner Linearer Systeme (m n möglich) Die Lösbarkeit eines linearen Systems Ax = b R m, x R n, A R mn hängt sehr stark vom sogenannten Rang der m n Matrix A ab Diese
Lineare Algebra: Determinanten und Eigenwerte
 : und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
Ultrakalte Atome in optischen Gittern
 Ultrakalte Atome in optischen Gittern Seminarvortrag Matthias Küster Gliederung Motivation Beschreibung des Potentials optischer Gitter Tight-binding-Modell Bloch -Experiment Ausblick 2 Motivation Möglichkeit
Ultrakalte Atome in optischen Gittern Seminarvortrag Matthias Küster Gliederung Motivation Beschreibung des Potentials optischer Gitter Tight-binding-Modell Bloch -Experiment Ausblick 2 Motivation Möglichkeit
1.11 Eigenwertproblem Anwendungen von Eigenwerten und Eigenvektoren Lineare Rekursionen Lineare Differentialgleichungssysteme Bestimmung von
 1.11 Eigenwertproblem Anwendungen von Eigenwerten und Eigenvektoren Lineare Rekursionen Lineare Differentialgleichungssysteme Bestimmung von Wachstumsraten Bestimmung von Maximal- und Minimalwerten von
1.11 Eigenwertproblem Anwendungen von Eigenwerten und Eigenvektoren Lineare Rekursionen Lineare Differentialgleichungssysteme Bestimmung von Wachstumsraten Bestimmung von Maximal- und Minimalwerten von
Lineare Algebra und Numerische Mathematik für D-BAUG
 R Käppeli L Herrmann W Wu Herbstsemester Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe Beispiel einer Koordinatentransformation Gegeben seien zwei
R Käppeli L Herrmann W Wu Herbstsemester Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe Beispiel einer Koordinatentransformation Gegeben seien zwei
T2 Quantenmechanik Lösungen 7
 T2 Quantenmechanik Lösungen 7 LMU München, WS 7/8 7.. Lineare Algebra Prof. D. Lüst / Dr. A. Schmidt-May version: 28.. Gegeben sei ein komplexer Hilbert-Raum H der Dimension d. Sei { n } mit n,..., d eine
T2 Quantenmechanik Lösungen 7 LMU München, WS 7/8 7.. Lineare Algebra Prof. D. Lüst / Dr. A. Schmidt-May version: 28.. Gegeben sei ein komplexer Hilbert-Raum H der Dimension d. Sei { n } mit n,..., d eine
Numerische Lineare Algebra
 Numerische Lineare Algebra Oliver Ernst Professur Numerische Mathematik Wintersemester 2015/16 Inhalt I 1 Einleitung 1.1 Lineare Gleichungssysteme 1.2 Matrixfunktionen 1.3 Modellreduktion 1.4 Eigenwertaufgaben
Numerische Lineare Algebra Oliver Ernst Professur Numerische Mathematik Wintersemester 2015/16 Inhalt I 1 Einleitung 1.1 Lineare Gleichungssysteme 1.2 Matrixfunktionen 1.3 Modellreduktion 1.4 Eigenwertaufgaben
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski. Serie 9
 D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 9 Best Before: 24.5/25.5, in den Übungsgruppen (2 wochen) Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 9 Best Before: 24.5/25.5, in den Übungsgruppen (2 wochen) Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
Reduced-Rank Least Squares Modelle
 16.12.2008 Wiederholung Gegeben: Matrix A m n Paar Rechter Eigenvektor x, Eigenwert λ: A x = λ x mit x R n \ 0, λ N Paar Linker Eigenvektor y, Eigenwert λ: y T A = λ y T Singulärwertzerlegung (SVD): A
16.12.2008 Wiederholung Gegeben: Matrix A m n Paar Rechter Eigenvektor x, Eigenwert λ: A x = λ x mit x R n \ 0, λ N Paar Linker Eigenvektor y, Eigenwert λ: y T A = λ y T Singulärwertzerlegung (SVD): A
Parallelrechnern. 12. März Technische Universität Chemnitz. Der Jacobi-Davidson Algorithmus auf. Parallelrechnern. Patrick Kürschner.
 Technische Universität Chemnitz 12. März 2008 - sweise Gliederung - sweise - sweise Eigenwertprobleme Ziel: Lösung von Eigenwertproblemen Dabei: Ax = λx Matrix A C n n sehr groß, dünnbesetzt (sparse) Gesucht:
Technische Universität Chemnitz 12. März 2008 - sweise Gliederung - sweise - sweise Eigenwertprobleme Ziel: Lösung von Eigenwertproblemen Dabei: Ax = λx Matrix A C n n sehr groß, dünnbesetzt (sparse) Gesucht:
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 14. Übung: Woche vom (Lin.Alg.
 Übungsaufgaben 14. Übung: Woche vom 30. 1.-3. 2. 2017 (Lin.Alg. III): Heft Ü 3: 3.2.6.a,b,l,n; 3.2.12; 3.2.13; 5.4.1; 5.4.5.c; Hinweis 1: 3. Test (Integration, analyt. Geom.) ist seit 9.1. freigeschalten
Übungsaufgaben 14. Übung: Woche vom 30. 1.-3. 2. 2017 (Lin.Alg. III): Heft Ü 3: 3.2.6.a,b,l,n; 3.2.12; 3.2.13; 5.4.1; 5.4.5.c; Hinweis 1: 3. Test (Integration, analyt. Geom.) ist seit 9.1. freigeschalten
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10)
 Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme
 Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
46 Eigenwerte und Eigenvektoren symmetrischer Matrizen
 46 Eigenwerte und Eigenvektoren symmetrischer Matrizen 46.1 Motivation Symmetrische Matrizen (a ij = a ji für alle i, j) kommen in der Praxis besonders häufig vor. Gibt es für sie spezielle Aussagen über
46 Eigenwerte und Eigenvektoren symmetrischer Matrizen 46.1 Motivation Symmetrische Matrizen (a ij = a ji für alle i, j) kommen in der Praxis besonders häufig vor. Gibt es für sie spezielle Aussagen über
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 10. Aufgabe ETH Zürich D-MATH. Herbstsemester Dr. V. Gradinaru D.
 Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
6. Übungsblatt zur Mathematik II für Inf, WInf
 Fachbereich Mathematik Prof. Dr. Streicher Dr. Sergiy Nesenenko Pavol Safarik SS 5. 9. Mai 6. Übungsblatt zur Mathematik II für Inf, WInf Gruppenübung Aufgabe G (Standardskalarprodukt Sei v, e R und es
Fachbereich Mathematik Prof. Dr. Streicher Dr. Sergiy Nesenenko Pavol Safarik SS 5. 9. Mai 6. Übungsblatt zur Mathematik II für Inf, WInf Gruppenübung Aufgabe G (Standardskalarprodukt Sei v, e R und es
Fachhochschule Nordwestschweiz (FHNW) Hochschule Technik Lösungen Serie 10 (Lineare Abbildungen)
 Fachhochschule Nordwestschweiz (FHNW) Hochschule Technik Lösungen Serie (Lineare Abbildungen) Dozent/in: R. Burkhardt Büro:.6 Klasse: Semester: Datum: HS 8/9. Aufgabe Zeige, dass die folgenden Abbildungen
Fachhochschule Nordwestschweiz (FHNW) Hochschule Technik Lösungen Serie (Lineare Abbildungen) Dozent/in: R. Burkhardt Büro:.6 Klasse: Semester: Datum: HS 8/9. Aufgabe Zeige, dass die folgenden Abbildungen
Lernbuch Lineare Algebra und Analytische Geometrie, 2. Auflage 2012
 Lernbuch Lineare Algebra und Analytische Geometrie, 2 Auflage 22 Korrekturen 8 statt y M lies y N 2 statt m + n = m +(n )=m +(n ) lies m + n = m +(n ) 2 statt #P(M) lies #P (M) 4 7 statt Beispiel c) lies
Lernbuch Lineare Algebra und Analytische Geometrie, 2 Auflage 22 Korrekturen 8 statt y M lies y N 2 statt m + n = m +(n )=m +(n ) lies m + n = m +(n ) 2 statt #P(M) lies #P (M) 4 7 statt Beispiel c) lies
6 Symmetrische Matrizen und quadratische Formen
 Mathematik für Ingenieure II, SS 009 Dienstag 3.6 $Id: quadrat.tex,v.4 009/06/3 4:55:47 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6.3 Quadratische Funktionen und die Hauptachsentransformation
Mathematik für Ingenieure II, SS 009 Dienstag 3.6 $Id: quadrat.tex,v.4 009/06/3 4:55:47 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6.3 Quadratische Funktionen und die Hauptachsentransformation
Eigenwertprobleme. 25. Oktober Autoren: 1. Herrmann, Hannes ( ) 2. Kraus, Michael ( ) 3. Krückemeier, Paul ( )
 Eigenwertprobleme 5. Oktober Autoren:. Herrmann, Hannes (45969). Kraus, Michael (9). Krückemeier, Paul (899) 4. Niedzielski, Björn (7) Eigenwertprobleme tauchen in der mathematischen Physik an Stellen
Eigenwertprobleme 5. Oktober Autoren:. Herrmann, Hannes (45969). Kraus, Michael (9). Krückemeier, Paul (899) 4. Niedzielski, Björn (7) Eigenwertprobleme tauchen in der mathematischen Physik an Stellen
Klausur zu Grundlagen der Computermathematik
 Prof. Dr. Klaus Höllig. März 11 Klausur zu Grundlagen der Computermathematik en Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. a Die Folge A n x/ A n
Prof. Dr. Klaus Höllig. März 11 Klausur zu Grundlagen der Computermathematik en Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. a Die Folge A n x/ A n
Universität Tübingen Tübingen, den Mathematisches Institut D. Mansour, J. Seyrich
 Universität Tübingen Tübingen, den 03.07.2013 Mathematisches Institut D. Mansour, J. Seyrich Probeklausur zu Algorithmen der Numerischen Mathematik SS 2013 ID Nummer: 1 Name:.........................................
Universität Tübingen Tübingen, den 03.07.2013 Mathematisches Institut D. Mansour, J. Seyrich Probeklausur zu Algorithmen der Numerischen Mathematik SS 2013 ID Nummer: 1 Name:.........................................
38 Iterative Verfahren für lineare Gleichungssysteme
 38 Iterative Verfahren für lineare Gleichungssysteme 38.1 Motivation Viele praktische Probleme führen auf sehr große lineare Gleichungssysteme, bei denen die Systemmatrix dünn besetzt ist, d. h. nur wenige
38 Iterative Verfahren für lineare Gleichungssysteme 38.1 Motivation Viele praktische Probleme führen auf sehr große lineare Gleichungssysteme, bei denen die Systemmatrix dünn besetzt ist, d. h. nur wenige
Lineare Algebra I Lösungsvorschlag
 Aufgabe Lineare Algebra I Lösungsvorschlag Wir bezeichnen mit a, a 2, a 3 Q 4 die Spalten der Matrix A. Es ist 7 a + 2a 2 = 7 4 = 7a 3, und wir sehen im l A = a, a 2, a 3 = a, a 2. Da die Vektoren a und
Aufgabe Lineare Algebra I Lösungsvorschlag Wir bezeichnen mit a, a 2, a 3 Q 4 die Spalten der Matrix A. Es ist 7 a + 2a 2 = 7 4 = 7a 3, und wir sehen im l A = a, a 2, a 3 = a, a 2. Da die Vektoren a und
Übungsblatt
 Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
8. Vorlesung, 5. April Numerische Methoden I. Eigenwerte und Eigenvektoren
 8. Vorlesung, 5. April 2017 170 004 Numerische Methoden I Eigenwerte und Eigenvektoren 1 Eigenwerte und Eigenvektoren Gegeben ist eine n n-matrix A. Gesucht sind ein vom Nullvektor verschiedener Vektor
8. Vorlesung, 5. April 2017 170 004 Numerische Methoden I Eigenwerte und Eigenvektoren 1 Eigenwerte und Eigenvektoren Gegeben ist eine n n-matrix A. Gesucht sind ein vom Nullvektor verschiedener Vektor
Die Mathematik hinter Google
 Die Mathematik hinter Google Informationstag für Gymnasiastinnen und Gymnasiasten Universität Fribourg (Schweiz) georges.klein@unifr.ch Fribourg, 24. November 2010 georges.klein@unifr.ch Die Mathematik
Die Mathematik hinter Google Informationstag für Gymnasiastinnen und Gymnasiasten Universität Fribourg (Schweiz) georges.klein@unifr.ch Fribourg, 24. November 2010 georges.klein@unifr.ch Die Mathematik
= ( n x j x j ) 1 / 2
 15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme
 Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
Lösung 5: Gram-Schmidt Orthogonalisierung, adjungierte Abbildungen
 D-MATH Lineare Algebra II FS 7 Dr. Meike Akveld Lösung 5: Gram-Schmidt Orthogonalisierung, adjungierte Abbildungen. a) Wegen der Linearität im ersten Argument gilt sicherlich w S :, w =. Somit ist S und
D-MATH Lineare Algebra II FS 7 Dr. Meike Akveld Lösung 5: Gram-Schmidt Orthogonalisierung, adjungierte Abbildungen. a) Wegen der Linearität im ersten Argument gilt sicherlich w S :, w =. Somit ist S und
Eigenwerte/Eigenvektoren/Eigenräume/Diagonalisierung
 Zurück Stand 4.. 6 Eigenwerte/Eigenvektoren/Eigenräume/Diagonalisierung Im Allgemeinen werden Vektoren durch Multiplikation mit einer Matrix gestreckt und um einen bestimmten Winkel gedreht. Es gibt jedoch
Zurück Stand 4.. 6 Eigenwerte/Eigenvektoren/Eigenräume/Diagonalisierung Im Allgemeinen werden Vektoren durch Multiplikation mit einer Matrix gestreckt und um einen bestimmten Winkel gedreht. Es gibt jedoch
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Lineare Algebra und Numerische Mathematik für D-BAUG
 P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
Musterlösungen zur Linearen Algebra II Weihnachtszettel
 Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
3. Modalanalyse. Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen.
 3. Modalanalyse Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen. Bei der rechnerischen Modalanalyse muss ein Eigenwertproblem
3. Modalanalyse Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen. Bei der rechnerischen Modalanalyse muss ein Eigenwertproblem
Hauptachsentransformation: Eigenwerte und Eigenvektoren
 Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz SS 5 4.5.5 Höhere Mathematik II für die Fachrichtung Physik Lösungsvorschläge zum 4. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz SS 5 4.5.5 Höhere Mathematik II für die Fachrichtung Physik Lösungsvorschläge zum 4. Übungsblatt
Prüfung EM1 28. Jänner 2008 A :=
 1. Die Menge der Eigenwerte der Matrix ist Prüfung EM1 28. Jänner 2008 A := ( 0 1 ) 0 1 A. {1, 0} B. { 1} C. {0} D. {0, 1, 1} E. {0, 1} 2. Es seien V ein n-dimensionaler reeller Vektorraum, ein Skalarprodukt
1. Die Menge der Eigenwerte der Matrix ist Prüfung EM1 28. Jänner 2008 A := ( 0 1 ) 0 1 A. {1, 0} B. { 1} C. {0} D. {0, 1, 1} E. {0, 1} 2. Es seien V ein n-dimensionaler reeller Vektorraum, ein Skalarprodukt
Lineare Algebra und Numerische Mathematik für D-BAUG
 P. Grohs T. Welti F. Weber Herbstsemester 5 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe. Skalarprodukt und Orthogonalität.a) Bezüglich des euklidischen
P. Grohs T. Welti F. Weber Herbstsemester 5 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe. Skalarprodukt und Orthogonalität.a) Bezüglich des euklidischen
Störungstheorie. Kapitel Motivation. 8.2 Zeitunabhängige Störungstheorie (Rayleigh-Schrödinger) nicht-entartete Störungstheorie
 Kapitel 8 Störungstheorie 8.1 Motivation Die meisten quantenmechanischen Problemstellungen lassen sich (leider) nicht exakt lösen. So kommt zum Beispiel der harmonische Oszillator in der Natur in Reinform
Kapitel 8 Störungstheorie 8.1 Motivation Die meisten quantenmechanischen Problemstellungen lassen sich (leider) nicht exakt lösen. So kommt zum Beispiel der harmonische Oszillator in der Natur in Reinform
Modulteilprüfung Geometrie (BaM-GS), Probeklausur
 HRZ-Benutzername: Modulteilprüfung Geometrie (BaM-GS), Probeklausur Dr. Patrik Hubschmid // SoSe 2013, 4. Juli 2013 Kontrollieren Sie, ob Sie alle Blätter (8 einschlieÿlich zweier Deckblätter) erhalten
HRZ-Benutzername: Modulteilprüfung Geometrie (BaM-GS), Probeklausur Dr. Patrik Hubschmid // SoSe 2013, 4. Juli 2013 Kontrollieren Sie, ob Sie alle Blätter (8 einschlieÿlich zweier Deckblätter) erhalten
Lösung 23: Sylvesters Trägheitssatz & Singulärwertzerlegung
 D-MATH Lineare Algebra I/II HS 07/FS 08 Dr Meike Akveld Lösung 3: Sylvesters Trägheitssatz & Singulärwertzerlegung Wir wissen, dass eine Basis B von R n existiert, sodass p [β Q ] B I I q 0 n p q gilt
D-MATH Lineare Algebra I/II HS 07/FS 08 Dr Meike Akveld Lösung 3: Sylvesters Trägheitssatz & Singulärwertzerlegung Wir wissen, dass eine Basis B von R n existiert, sodass p [β Q ] B I I q 0 n p q gilt
2. Isotropie. Beweis: (i) (ii): β U ist nicht ausgeartet. U U = {0} (ii) (iii): β U ist nicht ausgeartet. Da β nicht ausgeartet ist, gilt U = U:
 2. Isotropie Im folgenden sei V ein K-Vektorraum der Dimension n. Es sei q eine quadratische Form darüber und β die zugehörige symmetrische Bilinearform. Zudem gelte in K: 1 + 1 0. Notation 2.0: Wir nennen
2. Isotropie Im folgenden sei V ein K-Vektorraum der Dimension n. Es sei q eine quadratische Form darüber und β die zugehörige symmetrische Bilinearform. Zudem gelte in K: 1 + 1 0. Notation 2.0: Wir nennen
Lösungshinweise zur Klausur. Mathematik für Informatiker III. (Dr. Frank Hoffmann) 18. Februar 2008
 Lösungshinweise zur Klausur Mathematik für Informatiker III (Dr. Frank Hoffmann) 8. Februar 8 Aufgabe Algebraisches I /6++ (a) Rechnen Sie zunächst nach, dass die Menge B = {,, von Vektoren eine Basis
Lösungshinweise zur Klausur Mathematik für Informatiker III (Dr. Frank Hoffmann) 8. Februar 8 Aufgabe Algebraisches I /6++ (a) Rechnen Sie zunächst nach, dass die Menge B = {,, von Vektoren eine Basis
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra und Numerische Mathematik für D-BAUG
 P Grohs T Welti F Weber Herbstsemester 25 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 8 Aufgabe 8 Basen für Bild und Kern Gegeben sind die beiden 2 Matrizen:
P Grohs T Welti F Weber Herbstsemester 25 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 8 Aufgabe 8 Basen für Bild und Kern Gegeben sind die beiden 2 Matrizen:
Singulärwert-Zerlegung
 Singulärwert-Zerlegung Zu jeder komplexen (reellen) m n-matrix A existieren unitäre (orthogonale) Matrizen U und V mit s 1 0 U AV = S = s 2.. 0.. Singulärwert-Zerlegung 1-1 Singulärwert-Zerlegung Zu jeder
Singulärwert-Zerlegung Zu jeder komplexen (reellen) m n-matrix A existieren unitäre (orthogonale) Matrizen U und V mit s 1 0 U AV = S = s 2.. 0.. Singulärwert-Zerlegung 1-1 Singulärwert-Zerlegung Zu jeder
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 6 Eigenwerte
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 6 Eigenwerte
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
So lösen Sie die Dichtematrix-Renormierungsgruppe
 Dichtematrixrenormierungsgruppe Andy Pster Vortrag im Rahmen der Vorlesung Numerische Methoden in der Festkörperphysik (N. Blümer) SS2008 13.07.2008 (O_ô) DMRG 13.07.2008 1 / 32 Gliederung 1 Die Theorie
Dichtematrixrenormierungsgruppe Andy Pster Vortrag im Rahmen der Vorlesung Numerische Methoden in der Festkörperphysik (N. Blümer) SS2008 13.07.2008 (O_ô) DMRG 13.07.2008 1 / 32 Gliederung 1 Die Theorie
Probeklausur Lineare Algebra 1 Achten Sie auf vollständige, saubere und schlüssige Argumentation! 100 Punkte sind 100%. Inhaltsverzeichnis
 Prof. Dr. Wolfgang Arendt Manuel Bernhard Wintersemester 5/6 Probeklausur Lineare Algebra Achten Sie auf vollständige, saubere und schlüssige Argumentation! Punkte sind %. Inhaltsverzeichnis Aufgabe Aufgabe
Prof. Dr. Wolfgang Arendt Manuel Bernhard Wintersemester 5/6 Probeklausur Lineare Algebra Achten Sie auf vollständige, saubere und schlüssige Argumentation! Punkte sind %. Inhaltsverzeichnis Aufgabe Aufgabe
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Unitäre und orthogonale Matrix
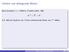 Unitäre und orthogonale Matrix Eine komplexe n n-matrix A heißt unitär, falls A 1 = A t = A, d.h. falls die Spalten von A eine orthonormale Basis von C n bilden. Unitäre und orthogonale Matrizen 1-1 Unitäre
Unitäre und orthogonale Matrix Eine komplexe n n-matrix A heißt unitär, falls A 1 = A t = A, d.h. falls die Spalten von A eine orthonormale Basis von C n bilden. Unitäre und orthogonale Matrizen 1-1 Unitäre
Lineare Algebra. 9. Übungsstunde. Steven Battilana. stevenb student.ethz.ch battilana.uk/teaching
 Lineare Algebra 9. Übungsstunde Steven Battilana stevenb student.ethz.ch battilana.uk/teaching November, 07 Erinnerung Ein Skalarprodukt ist eine Abbildung, : E n E n E, (v, w) v, w n k v kw k so dass:
Lineare Algebra 9. Übungsstunde Steven Battilana stevenb student.ethz.ch battilana.uk/teaching November, 07 Erinnerung Ein Skalarprodukt ist eine Abbildung, : E n E n E, (v, w) v, w n k v kw k so dass:
Quasi-exakt lösbare quantenmechanische Potentiale
 Quasi-exakt lösbare quantenmechanische Potentiale Ausarbeitung zum Seminar zur Theorie der Atome, Kerne und kondensierten Materie vom.10.014 Philipp Marauhn p_mara01@uni-muenster.de Inhaltsverzeichnis
Quasi-exakt lösbare quantenmechanische Potentiale Ausarbeitung zum Seminar zur Theorie der Atome, Kerne und kondensierten Materie vom.10.014 Philipp Marauhn p_mara01@uni-muenster.de Inhaltsverzeichnis
Alle Vektoren sind hier Spaltenvektoren. Eine Matrix besteht aus nebeneinandergeschrie-
 1 Vorbemerkungen Alle Vektoren sind hier Spaltenvektoren. Eine Matrix besteht aus nebeneinandergeschrie- benen Vektoren. Wird die Matrix A = ( a 1,..., a n ) mit dem Vektor c = c 1. c n multipliziert,
1 Vorbemerkungen Alle Vektoren sind hier Spaltenvektoren. Eine Matrix besteht aus nebeneinandergeschrie- benen Vektoren. Wird die Matrix A = ( a 1,..., a n ) mit dem Vektor c = c 1. c n multipliziert,
QR-Zerlegung Allgemeines. Householder-Spiegelung. Givens-Rotation. Gram-Schmidt-Orthogonalisierung. Fazit. QR-Zerlegung.
 20.0.2011 Inhaltsverzeichnis 1 2 3 4 1 2 3 4 der Matrix A R mxn, m n A = Q R Matrix Q: Q R nxn orthogonale Matrix (Spalten paarweise orthogonal) Q Q T = E Matrix R: R R mxn obere Dreiecksmatrix r 11 r
20.0.2011 Inhaltsverzeichnis 1 2 3 4 1 2 3 4 der Matrix A R mxn, m n A = Q R Matrix Q: Q R nxn orthogonale Matrix (Spalten paarweise orthogonal) Q Q T = E Matrix R: R R mxn obere Dreiecksmatrix r 11 r
Orthogonale Matrix. Definition 4.19
 Orthogonale Matrix Ausgleichsprobleme sind häufig schlecht konditioniert. Matrix des Normalengleichungssystems kann nahezu singulär sein. Spezielle Matrixzerlegung für höhere numerische Stabilität: QR-Zerlegung
Orthogonale Matrix Ausgleichsprobleme sind häufig schlecht konditioniert. Matrix des Normalengleichungssystems kann nahezu singulär sein. Spezielle Matrixzerlegung für höhere numerische Stabilität: QR-Zerlegung
Lineare Algebra und Numerische Mathematik D-BAUG Sommer 2014 Prof. R. Hiptmair. Name a a Note Vorname Studiengang Leginummer Datum
 Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Sommer 2014 Prof. R. Hiptmair Name a a Note Vorname Studiengang Leginummer Datum 13.08.2014 1 2 3 4 Total 12P 24P 26P 22P 84P Bitte füllen Sie zuerst
Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Sommer 2014 Prof. R. Hiptmair Name a a Note Vorname Studiengang Leginummer Datum 13.08.2014 1 2 3 4 Total 12P 24P 26P 22P 84P Bitte füllen Sie zuerst
4 Bilinearformen und Skalarprodukte
 4 Bilinearformen und Skalarprodukte 4 Grundlagen über Bilinearformen Definition 4 Sei V ein K-Vektorraum Eine Bilinearform b auf V ist eine Abbildung b : V V K mit folgenden Eigenschaften: (B) x, y, z
4 Bilinearformen und Skalarprodukte 4 Grundlagen über Bilinearformen Definition 4 Sei V ein K-Vektorraum Eine Bilinearform b auf V ist eine Abbildung b : V V K mit folgenden Eigenschaften: (B) x, y, z
Lösungshinweise zur Klausur
 Höhere Mathematik 1 und 4..14 Lösungshinweise zur Klausur für Studierende der Fachrichtungen el, kyb,mecha,phys Aufgabe 1 Entscheiden Sie, welche der folgenden Aussagen richtig und welche falsch sind.
Höhere Mathematik 1 und 4..14 Lösungshinweise zur Klausur für Studierende der Fachrichtungen el, kyb,mecha,phys Aufgabe 1 Entscheiden Sie, welche der folgenden Aussagen richtig und welche falsch sind.
2 Euklidische Vektorräume
 Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
1 Singulärwertzerlegung und Pseudoinverse
 Singulärwertzerlegung und Pseudoinverse Singulärwertzerlegung A sei eine Matrix mit n Spalten und m Zeilen. Zunächst sei n m. Bilde B = A A. Dies ist eine n n-matrix. Berechne die Eigenwerte von B. Diese
Singulärwertzerlegung und Pseudoinverse Singulärwertzerlegung A sei eine Matrix mit n Spalten und m Zeilen. Zunächst sei n m. Bilde B = A A. Dies ist eine n n-matrix. Berechne die Eigenwerte von B. Diese
Der LLL - Algorithmus. Seminar ganzzahlige Optimierung Wintersemester 2006/2007
 Der LLL - Algorithmus Seminar ganzzahlige Optimierung Wintersemester 2006/2007 Autor: Konrad Schade Betreuer: Prof. Dr. J. Rambau 1 Einführung 1.1 Motivation In dieser Arbeit soll die Verwendung des LLL-Algotithmuses
Der LLL - Algorithmus Seminar ganzzahlige Optimierung Wintersemester 2006/2007 Autor: Konrad Schade Betreuer: Prof. Dr. J. Rambau 1 Einführung 1.1 Motivation In dieser Arbeit soll die Verwendung des LLL-Algotithmuses
Lineare Algebra und Numerische Mathematik für D-BAUG
 R. Käppeli L. Herrmann W. Wu Herbstsemester 16 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Prüfung Name a a Note Vorname Leginummer Datum 18.8.17 1 3 4 Total 1P 1P 1P 1P 1P P
R. Käppeli L. Herrmann W. Wu Herbstsemester 16 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Prüfung Name a a Note Vorname Leginummer Datum 18.8.17 1 3 4 Total 1P 1P 1P 1P 1P P
3 Matrizenrechnung. 3. November
 3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
C orthogonal und haben die Länge 1). Dann ist die Länge von w = x u + y v gegeben durch w 2 Def. = w,w =
 1 v Die Länge Def. Sei (V,, ) ein Euklidscher Vektorraum. Für jeden Vektor v V heißt die Zahl v,v die Länge von v und wird v bezeichnet. Bemerkung. Die Länge des Vektors ist wohldefiniert, da nach Definition
1 v Die Länge Def. Sei (V,, ) ein Euklidscher Vektorraum. Für jeden Vektor v V heißt die Zahl v,v die Länge von v und wird v bezeichnet. Bemerkung. Die Länge des Vektors ist wohldefiniert, da nach Definition
D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys. Serie 13
 D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys Serie 13 1. Um einen Tisch sitzen 7 Zwerge. Vor jedem steht ein Becher mit Milch. Einer der Zwerge verteilt seine Milch gleichmässig auf alle
D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys Serie 13 1. Um einen Tisch sitzen 7 Zwerge. Vor jedem steht ein Becher mit Milch. Einer der Zwerge verteilt seine Milch gleichmässig auf alle
Eigenwerte und Diagonalisierung
 Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
