Grundbegriffe der Mathematischen Logik Hausaufgabenteil der Prüfung mit Lösungen
|
|
|
- Theodor Böhm
- vor 5 Jahren
- Abrufe
Transkript
1 Übungen zu Grundbegriffe der Mathematischen Logik Hausaufgabenteil der Prüfung mit Lösungen Teil I Rekursionstheorie Aufgabe 1. elche (totale) unktion f : N 2 N wird von dieser Registermaschine berechnet? Lösung: f(x, y) = max(x, y). 0: I R 2 = 0 THEN GOTO 1 ELSE GOTO 2 4: R 0 := R Aufgabe 2. Der Programmierer hat sich bei der Eingabe des obigen Programms in Zeile 0 vertippt. Das Resultat ist die folgende Registermaschine M: 0: I R 2 = 0 THEN GOTO 1 ELSE GOTO 4 4: R 0 := R wahr () oder falsch ()? M stoppt genau dann, wenn am Anfang R 2 = 0 ist. M berechnet die Identität id: N N, d.h. id(n) = n. M berechnet eine totale unktion von N 2 nach N. M berechnet eine partielle unktion g von N 3 nach N, so dass g(a, b, c) = max(a, b) wann immer g(a, b, c) definiert ist. Antwort Kommentar: enn am Anfang R 2 = 0 ist, dann bleibt das auch so, und die fehlerhafte Stelle wird nie erreicht. Andernfalls gerät das Programm in eine Schleife, in der R 2 nicht verändert wird. Das Programm ist offensichtlich für eine zweistellige unktion geschrieben, aber nach den formalen Definitionen kann man es auch als k-stellig auffassen für beliebiges k. ie immer wird dann am Anfang R i = 0 gesetzt für alle i > k. Es gilt max(n, 0) = n = id(n). Aufgabe 3. Hier sollten Sie insgesamt 12 Antworten geben. wahr (), falsch () oder sinnlos (S)? prim. rek. rek. rek. aufzb. Jedes Polynom p: N k N ist... S enn g : N 3 N primitiv rekursiv ist, f(x, 0) = 2x S und f(x, y + 1) = g(y, f(x, y), x), dann ist f... Die Ackermannfunktion A: N 2 N ist... S Die Menge {(x, y, z) N 3 y 2 x } ist... Sinnlos bedeutet, dass die Behauptung nicht einmal falsch ist. Beispiel: Jede reelle Zahl ist gleichschenklig. Kommentar: Eine Menge ist laut Definition in der Vorlesung primitiv rekursiv, wenn ihre charakteristische unktion es ist.
2 Teil II Prädikatenlogik Sei L = {R} die Sprache der Graphen, wobei R ein zweistelliges Relationssymbol ist. ir fassen (gerichtete) Graphen (allenfalls mit Schleifen, allenfalls unendlich) als L-Strukturen G = (G, R G ) auf. Hierbei ist G die Menge der Knoten und (a, b) R G gilt genau dann, wenn es eine Kante von a nach b gibt. Aufgabe 4. ir betrachten die folgenden vier Graphen: G 1 = (N, R G ) mit R G = {(a, b) N 2 b = a + 1}. G 4 (G 1 ist ein gerichteter Graph. Die gezeichneten Kanten in den Abbildungen sind ungerichtet, d.h. jede von ihnen steht für zwei entgegengesetzt gerichtete Kanten.) wahr () oder falsch ()? i = 1 i = 2 i = 3 i = 4 G i = xyz(r(x, y) R(y, z) R(x, z)) gilt für... G i = wxyz(r(w, x) R(x, y) R(y, z) R(z, w)) gilt für... G i = wxyz(w x w y w z x y x z y z) gilt für... Kommentar: Jeder der Graphen hat eine Kante aber keine Schleifen. Daher ist die erste ormel (Transitivität) für keinen der Graphen erfüllt. ür die zweite ormel genügt schon die Existenz einer Kante, weil dann sogar wxyz(r(w, x) R(x, y) R(y, z) R(z, w) w = y x = z) erfüllt ist. Aufgabe 5. Zeichnen Sie zwei nicht isomorphe Graphen, die beide die folgende L-Aussage erfüllen: G i = x( R(x, x)) xy(r(x, y) R(y, x)) wxyz ( R(w, x) R(x, y) R(y, z) R(z, w) u(u = w u = x u = y u = z) ). Kommentar: Gerichtet, ohne Schleifen, mit einem eg der Länge 4, der auch Überschneidungen erlaubt, und keinen Knoten von außerhalb des egs. Die ersten drei Lösungen enthalten jeweils nur die Kanten des egs. Die Liste ist vollständig. Aufgabe 6. Geben Sie für jeden Graphen G i eine ormel ϕ i an, so dass G i = ϕ j i = j. G 0 G 1 ϕ 0 x yz(y z R(x, y) R(x, z)) ϕ 1 x y( R(x, y)) ϕ 2 x 1... x 6 (x 1 x 2 x 1 x 3... x 5 x 6 R(x 1, x 2 ) R(x 2, x 3 )... R(x 5, x 6 )) ϕ 3 uxyz(x y x z y z R(u, x) R(u, y) R(u, z)) Kommentar: Die ormeln sind natürlich nur (möglichst einfache) Beispiele. ϕ 0 : Jeder Knoten hat mindestens Grad 2. ϕ 1 : Es gibt mindestens einen isolierten Knoten. ϕ 2 : Es gibt mindestens einen (überschneidungsfreien!) Pfad der Länge 5. ϕ 3 : Es gibt mindestens einen Knoten vom Grad 3. ormeln der Art ϕ 0 ϕ 1 ϕ 2 ϕ 3 sind eine Art Joker, den man für den schwersten all einsetzen kann.
3 Übungen zu Grundbegriffe der Mathematischen Logik Ungerade Seriennummern, mit Lösungen Teil I Rekursionstheorie Aufgabe 1. elche (totale) unktion f : N 2 N wird von dieser Registermaschine berechnet? 0: I R 1 = 0 THEN GOTO 6 4: R 0 := R : I R 2 = 0 THEN GOTO 6 5: GOTO 0 Lösung: f(x, y) = min(x, y). Aufgabe 2. Das obige Programm wurde aus einem alten Buch eingescannt. Dabei kam es zu einem ehler in Zeile 0. Das Resultat ist die folgende Registermaschine M: 0: I R 1 = 0 THEN GOTO 0 4: R 0 := R : I R 2 = 0 THEN GOTO 6 5: GOTO 0 wahr () oder falsch ()? M berechnet eine totale unktion von N 2 nach N. M stoppt genau dann, wenn am Anfang R 1 = 0 ist. M berechnet eine partielle unktion h von N 3 nach N, so dass h(a, b, c) genau dann definiert ist, wenn a > b. M berechnet eine partielle unktion g von N 2 nach N, so dass g(a, b) = min(a, b) wann immer g(a, b) definiert ist. Antwort Kommentar: Das Programm stoppt genau dann, wenn der ehler (sofortige Endlosschleife) nicht erreicht wird. Der ehler wird bspw. erreicht wenn am Anfang R 1 = 0 ist, aber auch, wenn R 1 mindestens so früh wie R 2 Null wird, d.h. falls am Anfang R 1 R 2 gilt. Sonst wie Hausaufgabe. Aufgabe 3. Hier sollten Sie insgesamt 12 Antworten geben. wahr (), falsch () oder sinnlos (S)? prim. rek. rek. rek. aufzb. Jede stetig differenzierbare unktion f : R k R ist... S S S enn f : N 3 N rekursiv ist, g(0, y) = f(y, 0, y) und S g(x + 1, y) = f(x, y, g(x, y)), dann ist g immer... Die totale unktion h: N 2 N, definiert durch h(0, y) = y! + y + 7, S h(x + 1, 0) = h(x, 1), h(x + 1, y + 1) = h(x, h(x + 1, y)) ist... Jede Menge der orm A \ B mit A primitiv rekursiv und B rekursiv aufzählbar ist... Kommentar: Zeile 1 ist etwas verunglückt, weil Jakob Kellner in der Vorlesung das Problem der Erweiterung der Definitionen auf reelle unktionen kurz angesprochen hatte; es gibt aber keine allgemein bekannten Standarddefinitionen. In Zeile 2 steht eine primitive Rekursion, wie in der Hausaufgabe. Die rekursiven unktionen sind unter primitiver Rekursion abgeschlossen, aber wenn man mit einer unktion anfängt, die selbst nicht einmal primitiv rekursiv ist, kann man natürlich im Allgemeinen keine primitive Rekursivität erwarten. Die unktion in Zeile 3 ist wie die Ackermannfunktion definiert, nur mit größeren Startwerten. Insbesonders ist das keine primitive Rekursion! Nach der Church-Turing-These muss die unktion natürlich rekursiv sein. Aber es gibt keinen Grund anzunehmen, dass sie primitiv rekursiv ist, und weil sie schneller wächst als die Ackermannfunktion ist sie das auch nicht. Zeile 4: enn B rekursiv aufzählbar aber nicht rekursiv ist, dann ist nicht einmal N \ B rekursiv aufzählbar. 1
4 Teil II Prädikatenlogik Sei L = {R} die Sprache der Graphen, wobei R ein zweistelliges Relationssymbol ist. ir fassen (gerichtete) Graphen (allenfalls mit Schleifen, allenfalls unendlich) als L-Strukturen G = (G, R G ) auf. Hierbei ist G die Menge der Knoten und (a, b) R G gilt genau dann, wenn es eine Kante von a nach b gibt. Aufgabe 4. ir betrachten die folgenden vier Graphen: G 1 = (N, R G ) mit R G = {(a, b) N 2 a ist Teiler von b}. G 4 (G 1 ist ein gerichteter Graph. Die gezeichneten Kanten in den Abbildungen sind ungerichtet, d.h. jede von ihnen steht für zwei entgegengesetzt gerichtete Kanten.) wahr () oder falsch ()? i = 1 i = 2 i = 3 i = 4 G i = xyz(r(x, y) R(y, z) R(x, z)) gilt für... G i = wxyz(r(w, x) R(x, y) R(y, z) R(z, w)) gilt für... G i = wxyz(w x w y w z x y x z y z) gilt für... Kommentar: R in G 1 ist eine partielle Ordnung, also transitiv. R in G 1 ist außerdem reflexiv, so dass dort auch die ormel in der zweiten Zeile gilt. Ansonsten alles genau wie in der Hausaufgabe. Aufgabe 5. Zeichnen Sie zwei nicht isomorphe Graphen, die beide die folgende L-Aussage erfüllen: G i = x( R(x, x)) xy(r(x, y) R(y, x)) x(x = x) ( w xyz x y x z y z R(w, x) R(w, y) R(w, z) ) u(r(w, u) u = x u = y u = z) Lösung: Hier gab es unendlich viele mögliche Lösungen. Die meisten Teilnehmer haben gemerkt, dass aus Aufgabe 4 eine Lösung ist. Die einfachste Variation bestand darin, den unzusammenhängenden Graphen zu nehmen, der aus zwei Kopien von besteht. Es gibt aber noch viele weitere Variationsmöglichkeiten wie beispielsweise ein 2n-Eck mit Diagonalen oder ein ürfel. Aufgabe 6. Geben Sie für jeden Graphen G i eine ormel ϕ i an, so dass G i = ϕ j i = j. G 0 G 1 ϕ 0 uxyz(x y x z y z R(u, x) R(u, y) R(u, z)) uxyz(u y x z R(u, x) R(x, y) R(y, z) R(z, u)) ϕ 1 x 1... x 6 (x 1 x 2 x 1 x 3... x 5 x 6 R(x 1, x 2 ) R(x 2, x 3 )... R(x 5, x 6 ) ϕ 2 xy(x y z R(x, z) z R(y, z)) ϕ 3 x y R(x, y) wxyz(w x w y w z x y x z y z R(w, x) R(x, y) R(y, z) R(z, w)) Kommentar: ϕ 0 : Es gibt einen Knoten vom Grad 3, aber keinen Zykel der Länge 4. (Letzteres abgekürzt. Die Abkürzung nutzt aus, dass alle vier Graphen keine Schleifen haben.) ϕ 1 : Es gibt einen (überschneidungsfreien!) eg der Länge 5. (ie ϕ 2 der Hausaufgabe.) ϕ 2 : Es gibt zwei (verschiedene!) isolierte Punkte. ϕ 3 : Es gibt einen isolierten Punkt und einen Zykel der Länge 4. 2
5 Übungen zu Grundbegriffe der Mathematischen Logik Prüfung am Mittwoch, Teil I Rekursionstheorie Aufgabe 1. elche (totale) unktion f : N 2 N wird von dieser Registermaschine berechnet? 0: I R 2 = 0 THEN GOTO 6 4: R 0 := R Lösung: f(x, y) = min(x, y). Aufgabe 2. Das obige Programm wurde aus einem alten Buch eingescannt. Dabei kam es zu einem ehler in Zeile 0. Das Resultat ist die folgende Registermaschine M: 0: I R 2 = 0 THEN GOTO 0 4: R 0 := R wahr () oder falsch ()? M berechnet eine totale unktion von N 2 nach N. M stoppt genau dann, wenn am Anfang R 2 = 0 ist. M berechnet eine partielle unktion h von N 2 nach N, so dass h(a, b) = min(a, b) wann immer h(a, b) definiert ist. M berechnet eine partielle unktion g von N 3 nach N, so dass g(a, b.c) genau dann definiert ist, wenn a < b. Antwort Kommentar: Das Programm stoppt genau dann, wenn der ehler (sofortige Endlosschleife) nicht erreicht wird. Der ehler wird bspw. erreicht wenn am Anfang R 2 = 0 ist, aber auch, wenn R 2 mindestens so früh wie R 1 Null wird, d.h. falls am Anfang R 1 R 2 gilt. Sonst wie Hausaufgabe. Aufgabe 3. Hier sollten Sie insgesamt 12 Antworten geben. wahr (), falsch () oder sinnlos (S)? prim. rek. rek. rek. aufzb. Jede stetig differenzierbare unktion f : R k R ist... S S S enn f : N 3 N rekursiv ist, g(0, y) = f(0, y, y) und S g(x + 1, y) = f(x, y, g(x, y)), dann ist g immer... Die totale unktion h: N 2 N, definiert durch h(0, y) = 3y + y + 2, S h(x + 1, 0) = h(x, 1), h(x + 1, y + 1) = h(x, h(x + 1, y)) ist... Jede Menge der orm A \ B mit A primitiv rekursiv und B rekursiv aufzählbar ist... Kommentar: Zeile 1 ist etwas verunglückt, weil Jakob Kellner in der Vorlesung das Problem der Erweiterung der Definitionen auf reelle unktionen kurz angesprochen hatte; es gibt aber keine allgemein bekannten Standarddefinitionen. In Zeile 2 steht eine primitive Rekursion, wie in der Hausaufgabe. Die rekursiven unktionen sind unter primitiver Rekursion abgeschlossen, aber wenn man mit einer unktion anfängt, die selbst nicht einmal primitiv rekursiv ist, kann man natürlich im Allgemeinen keine primitive Rekursivität erwarten. Die unktion in Zeile 3 ist wie die Ackermannfunktion definiert, nur mit größeren Startwerten. Insbesonders ist das keine primitive Rekursion! Nach der Church-Turing-These muss die unktion natürlich rekursiv sein. Aber es gibt keinen Grund anzunehmen, dass sie primitiv rekursiv ist, und weil sie schneller wächst als die Ackermannfunktion ist sie das auch nicht. Zeile 4: enn B rekursiv aufzählbar aber nicht rekursiv ist, dann ist nicht einmal N \ B rekursiv aufzählbar. 1
6 Teil II Prädikatenlogik Sei L = {R} die Sprache der Graphen, wobei R ein zweistelliges Relationssymbol ist. ir fassen (gerichtete) Graphen (allenfalls mit Schleifen, allenfalls unendlich) als L-Strukturen G = (G, R G ) auf. Hierbei ist G die Menge der Knoten und (a, b) R G gilt genau dann, wenn es eine Kante von a nach b gibt. Aufgabe 4. ir betrachten die folgenden vier Graphen: G 1 = (N, R G ) mit R G = {(a, b) N 2 a b}. G 4 (G 1 ist ein gerichteter Graph. Die gezeichneten Kanten in den Abbildungen sind ungerichtet, d.h. jede von ihnen steht für zwei entgegengesetzt gerichtete Kanten.) wahr () oder falsch ()? i = 1 i = 2 i = 3 i = 4 G i = xyz(r(x, y) R(y, z) R(x, z)) gilt für... G i = wxyz(r(w, x) R(x, y) R(y, z) R(z, w)) gilt für... G i = wxyz(w x w y w z x y x z y z) gilt für... Kommentar: R in G 1 ist eine partielle Ordnung, also transitiv. R in G 1 ist außerdem reflexiv, so dass dort auch die ormel in der zweiten Zeile gilt. Ansonsten alles genau wie in der Hausaufgabe. Aufgabe 5. Zeichnen Sie zwei nicht isomorphe Graphen, die beide die folgende L-Aussage erfüllen: G i = x(x = x) x( R(x, x)) xy(r(x, y) R(y, x)) ( w xyz R(w, x) R(w, y) R(w, z) x y x z y z ) u(r(w, u) u = x u = y u = z) Lösung: Hier gab es unendlich viele mögliche Lösungen. Die meisten Teilnehmer haben gemerkt, dass aus Aufgabe 4 eine Lösung ist. Die einfachste Variation bestand darin, den unzusammenhängenden Graphen zu nehmen, der aus zwei Kopien von besteht. Es gibt aber noch viele weitere Variationsmöglichkeiten wie beispielsweise ein 2n-Eck mit Diagonalen oder ein ürfel. Aufgabe 6. Geben Sie für jeden Graphen G i eine ormel ϕ i an, so dass G i = ϕ j i = j. G 0 G 1 ϕ 0 x y R(x, y) wxyz(w x w y w z x y x z y z R(w, x) R(x, y) R(y, z) R(z, w)) ϕ 1 uxyz(x y x z y z R(u, x) R(u, y) R(u, z)) uxyz(u y x z R(u, x) R(x, y) R(y, z) R(z, u)) ϕ 2 x 1... x 6 (x 1 x 2 x 1 x 3... x 5 x 6 R(x 1, x 2 ) R(x 2, x 3 )... R(x 5, x 6 ) ϕ 3 xy(x y z R(x, z) z R(y, z)) Kommentar: ϕ 0 : Es gibt einen isolierten Punkt und einen Zykel der Länge 4. ϕ 1 : Es gibt einen Knoten vom Grad 3, aber keinen Zykel der Länge 4. (Letzteres abgekürzt. Die Abkürzung nutzt aus, dass alle vier Graphen keine Schleifen haben.) ϕ 2 : Es gibt einen (überschneidungsfreien!) eg der Länge 5. (ie ϕ 2 der Hausaufgabe.) ϕ 3 : Es gibt zwei (verschiedene!) isolierte Punkte. 2
Nachklausur zur Vorlesung Einführung in die Theoretische Informatik
 Universität Heidelberg 11. Oktober 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Nachklausur zur Vorlesung Einführung in die Theoretische Informatik Musterlösungen
Universität Heidelberg 11. Oktober 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Nachklausur zur Vorlesung Einführung in die Theoretische Informatik Musterlösungen
Universität Heidelberg 23. Juli 2018 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl. Math. Martin Monath
 Universität Heidelberg 23. Juli 2018 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl. Math. Martin Monath Erste Klausur zur Vorlesung Einführung in die Theoretische Informatik Es können maximal
Universität Heidelberg 23. Juli 2018 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl. Math. Martin Monath Erste Klausur zur Vorlesung Einführung in die Theoretische Informatik Es können maximal
4. Funktionen und Relationen
 4. Funktionen und Relationen Nikolaus von Oresmes Richard Dedekind (1831-1916) René Descartes 1596-1650 Pierre de Fermat 1607/8-1665 Seite 1 Inhalt der Vorlesung Teil 4: Funktionen und Relationen 4.1 Funktionen:
4. Funktionen und Relationen Nikolaus von Oresmes Richard Dedekind (1831-1916) René Descartes 1596-1650 Pierre de Fermat 1607/8-1665 Seite 1 Inhalt der Vorlesung Teil 4: Funktionen und Relationen 4.1 Funktionen:
UE GRUNDBEGRIFFE DER MATHEMATISCHEN LOGIK SS 2016
 SS 206 VERA FISCHER Die Gesamtnote ergibt sich je zur Hälfte aus der Teilnote Kreuzerlliste und der Teilnote Zwischentest, gerundet auf freundlichen Weise. Für eine positive Benotung müssen beide Teilnoten
SS 206 VERA FISCHER Die Gesamtnote ergibt sich je zur Hälfte aus der Teilnote Kreuzerlliste und der Teilnote Zwischentest, gerundet auf freundlichen Weise. Für eine positive Benotung müssen beide Teilnoten
Injektiv, Surjektiv, Bijektiv
 Injektiv, Surjektiv, Bijektiv Aufgabe 1. Geben Sie einen ausführlichen Beweis für folgende Aussage: Wenn f A B surjektiv ist und R A A A eine reflexive Relation auf A ist, dann ist R B = {( f(x), f(y)
Injektiv, Surjektiv, Bijektiv Aufgabe 1. Geben Sie einen ausführlichen Beweis für folgende Aussage: Wenn f A B surjektiv ist und R A A A eine reflexive Relation auf A ist, dann ist R B = {( f(x), f(y)
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier
 Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/17 Rekursions- und Lerntheorie
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/17 Rekursions- und Lerntheorie
10. UNENTSCHEIDBARE PROBLEME:
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 10. UNENTSCHEIDBARE PROBLEME: DIAGONALISIERUNG UND REDUKTION Theoretische Informatik (SoSe 2011) 10. Unentscheidbare
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 10. UNENTSCHEIDBARE PROBLEME: DIAGONALISIERUNG UND REDUKTION Theoretische Informatik (SoSe 2011) 10. Unentscheidbare
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufgabe 45. Polynome sind stets stetig. Höhere Mathematik für Informatiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufgabe 45. Polynome sind stets stetig. Höhere Mathematik für Informatiker II (Sommersemester
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
Mächtigkeit von WHILE-Programmen
 Mächtigkeit von WHILE-Programmen und rekursive Funktionen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 16. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Mächtigkeit von WHILE-Programmen und rekursive Funktionen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 16. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Typen von Programmiersprachen
 Typen von Programmiersprachen Berechenbarkeitstheorie: Formalisierung des intuitiven Berechenbarkeitsbegriffs man kann vier Typen von Programmiersprachen zum Berechnen von Zahlenfunktionen unterscheiden:
Typen von Programmiersprachen Berechenbarkeitstheorie: Formalisierung des intuitiven Berechenbarkeitsbegriffs man kann vier Typen von Programmiersprachen zum Berechnen von Zahlenfunktionen unterscheiden:
Diskrete Strukturen Kapitel 2: Grundlagen (Relationen)
 WS 2016/17 Diskrete Strukturen Kapitel 2: Grundlagen (Relationen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 2: Grundlagen (Relationen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
1.3 Primitiv rekursive und µ-rekursive Funktionen
 Definition 1.11 Die Klasse der primitiv rekursiven Funktionen (a) Basisfunktionen: (1.) die konstanten Funktionen c (c N) (2.) die Projektionen Π m i (x 1,...,x m ) = x i (1 i m) (3.) die Nachfolgerfunktion
Definition 1.11 Die Klasse der primitiv rekursiven Funktionen (a) Basisfunktionen: (1.) die konstanten Funktionen c (c N) (2.) die Projektionen Π m i (x 1,...,x m ) = x i (1 i m) (3.) die Nachfolgerfunktion
2 Lösungen zu Kapitel 2
 2 Lösungen zu Kapitel 2 2. Lösung. Die Funktion f ist nicht injektiv. So gibt es (unendlich) viele Paare (x, y) mit f(x, y) = 0, etwa (0, 0) und (/2, ). Die Funktion f ist surjektiv. Zum Beispiel gilt
2 Lösungen zu Kapitel 2 2. Lösung. Die Funktion f ist nicht injektiv. So gibt es (unendlich) viele Paare (x, y) mit f(x, y) = 0, etwa (0, 0) und (/2, ). Die Funktion f ist surjektiv. Zum Beispiel gilt
Injektiv, Surjektiv, Bijektiv
 Injektiv, Surjektiv, Bijektiv Aufgabe 1. Geben Sie einen ausführlichen Beweis für folgende Aussage: Wenn f A B surjektiv ist und R A A A eine reflexive Relation auf A ist, dann ist R B = {( f(x), f(y)
Injektiv, Surjektiv, Bijektiv Aufgabe 1. Geben Sie einen ausführlichen Beweis für folgende Aussage: Wenn f A B surjektiv ist und R A A A eine reflexive Relation auf A ist, dann ist R B = {( f(x), f(y)
Klausur zur Vorlesung: Mathematische Logik SS 2011
 Klausur zur Vorlesung: Mathematische Logik SS 2011 Geben Sie am Ende Der Klausur Ihre Lösungen einschließlich dieses Deckblatts ab. Schreiben Sie auf jedes Blatt Ihren Namen und Ihre Matrikelnummer. Viel
Klausur zur Vorlesung: Mathematische Logik SS 2011 Geben Sie am Ende Der Klausur Ihre Lösungen einschließlich dieses Deckblatts ab. Schreiben Sie auf jedes Blatt Ihren Namen und Ihre Matrikelnummer. Viel
Theoretische Informatik SS 03 Übung 5
 Theoretische Informatik SS 03 Übung 5 Aufgabe 1 Im Buch von Schöning ist auf S. 106-108 beschrieben, wie eine Turing-Maschine durch ein GOTO-Programm simuliert werden kann. Zeigen Sie, wie dabei die Anweisungen
Theoretische Informatik SS 03 Übung 5 Aufgabe 1 Im Buch von Schöning ist auf S. 106-108 beschrieben, wie eine Turing-Maschine durch ein GOTO-Programm simuliert werden kann. Zeigen Sie, wie dabei die Anweisungen
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Diskrete Strukturen Endterm
 Technische Universität München I7 Winter 2013/14 Prof. J. Esparza / Dr. M. Luttenberger LÖSUNG Diskrete Strukturen Endterm Beachten Sie: Soweit nicht anders angegeben, ist stets eine Begründung bzw. der
Technische Universität München I7 Winter 2013/14 Prof. J. Esparza / Dr. M. Luttenberger LÖSUNG Diskrete Strukturen Endterm Beachten Sie: Soweit nicht anders angegeben, ist stets eine Begründung bzw. der
Aufgaben und Lösungen Ausarbeitung der Übungsstunde zur Vorlesung Analysis I
 Aufgaben und Lösungen Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 11 Einleitung Es wird eine 15-minütige Mikroklausur geschrieben. i) Sei D R oderd C. Wann heißt
Aufgaben und Lösungen Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 11 Einleitung Es wird eine 15-minütige Mikroklausur geschrieben. i) Sei D R oderd C. Wann heißt
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws13/14
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws13/14
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz Dr P C Kunstmann Dipl-Math M Uhl Sommersemester 009 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive Komplexe
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz Dr P C Kunstmann Dipl-Math M Uhl Sommersemester 009 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive Komplexe
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Existenz nicht rekursiv aufz. Sprachen
 S : Kardinalität einer Menge S (Anzahl ihrer Elemente) Wie vergleichen wir die Kardinalität unendlicher Mengen? A B : es gibt eine surjektive Abbildung von A nach B A = B : A B und B A Zwei Mengen A und
S : Kardinalität einer Menge S (Anzahl ihrer Elemente) Wie vergleichen wir die Kardinalität unendlicher Mengen? A B : es gibt eine surjektive Abbildung von A nach B A = B : A B und B A Zwei Mengen A und
Differenzierbarkeit im R n. Analysis III October 30, / 94
 Differenzierbarkeit im R n Analysis III October 30, 2018 36 / 94 Partielle Ableitungen Buch Kap. 5.5 Definition 5.23: (partielle Differenzierbarkeit) Sei die Funktion f : D R, D R n, wobei D eine offene
Differenzierbarkeit im R n Analysis III October 30, 2018 36 / 94 Partielle Ableitungen Buch Kap. 5.5 Definition 5.23: (partielle Differenzierbarkeit) Sei die Funktion f : D R, D R n, wobei D eine offene
Diskrete Strukturen. Vorlesung 7: Fixpunkte & Kardinalität. 27. November 2018
 Diskrete Strukturen Vorlesung 7: Fixpunkte & Kardinalität 27. November 2018 Nächste Termine Modul Diskrete Strukturen Hörsaalübung (Mo. 9:15) Vorlesung (Di. 17:15) 26.11. 27.11. Fixpunkte + Kardinalitäten
Diskrete Strukturen Vorlesung 7: Fixpunkte & Kardinalität 27. November 2018 Nächste Termine Modul Diskrete Strukturen Hörsaalübung (Mo. 9:15) Vorlesung (Di. 17:15) 26.11. 27.11. Fixpunkte + Kardinalitäten
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
1. Beschreiben Sie folgende Zahlenmengen durch Markierung auf der Zahlengeraden, der Zahlenebene bzw. durch Aufzählen der Elemente:
 Lösung 1. Übung Elemente der Algebra WS017/18 1. Beschreiben Sie folgende Zahlenmengen durch Markierung auf der Zahlengeraden, der Zahlenebene bzw. durch Aufzählen der Elemente: (e) {(x,y) IR 3x+4y 1}.
Lösung 1. Übung Elemente der Algebra WS017/18 1. Beschreiben Sie folgende Zahlenmengen durch Markierung auf der Zahlengeraden, der Zahlenebene bzw. durch Aufzählen der Elemente: (e) {(x,y) IR 3x+4y 1}.
Universelle Maschinen und universelle Funktionen
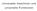 Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
Kapitel 5: Strukturen. 1.1 Zweistellige Relationen 1.2 Graphen 1.3 Algebren 1.4 Strukturen
 344 Kapitel 5: Strukturen 1.1 Zweistellige Relationen 1.2 Graphen 1.3 Algebren 1.4 Strukturen 5.1 Zweistellige Relationen 345 346 Erinnerung: Relationen Definition Seien k 1 und A eine Menge. 1. A k ist
344 Kapitel 5: Strukturen 1.1 Zweistellige Relationen 1.2 Graphen 1.3 Algebren 1.4 Strukturen 5.1 Zweistellige Relationen 345 346 Erinnerung: Relationen Definition Seien k 1 und A eine Menge. 1. A k ist
Theorie der Informatik Einleitung. Theorie der Informatik Basisfunktionen und Einsetzung Primitive Rekursion. 14.
 Theorie der Informatik 16. April 2014 14. primitive Rekursion und µ-rekursion Theorie der Informatik 14. primitive Rekursion und µ-rekursion 14.1 Einleitung 14.2 Basisfunktionen und Einsetzung Malte Helmert
Theorie der Informatik 16. April 2014 14. primitive Rekursion und µ-rekursion Theorie der Informatik 14. primitive Rekursion und µ-rekursion 14.1 Einleitung 14.2 Basisfunktionen und Einsetzung Malte Helmert
3. Relationen Erläuterungen und Schreibweisen
 3. Relationen Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob
3. Relationen Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob
Vorkurs Mathematik für Informatiker
 Vorkurs Mathematik für Informatiker 6. Ordnungsrelationen Thomas Huckle, Kilian Röhner Technische Universität München 9.10.2017 Graphen Graph besteht aus Knoten (Ecken) und Kanten (Verbindungen zwischen
Vorkurs Mathematik für Informatiker 6. Ordnungsrelationen Thomas Huckle, Kilian Röhner Technische Universität München 9.10.2017 Graphen Graph besteht aus Knoten (Ecken) und Kanten (Verbindungen zwischen
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Notation für Wörter w a is die Anzahl der Vorkommen von
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Notation für Wörter w a is die Anzahl der Vorkommen von
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Graphentheorie 1. Diskrete Strukturen. Sommersemester Uta Priss ZeLL, Ostfalia. Hausaufgaben Graph-Äquivalenz SetlX
 Graphentheorie 1 Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Graphentheorie 1 Slide 1/19 Agenda Hausaufgaben Graph-Äquivalenz SetlX Diskrete Strukturen Graphentheorie
Graphentheorie 1 Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Graphentheorie 1 Slide 1/19 Agenda Hausaufgaben Graph-Äquivalenz SetlX Diskrete Strukturen Graphentheorie
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Sicherheitsingenieure I A
 Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier
 Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/16 Rekursions- und Lerntheorie
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/16 Rekursions- und Lerntheorie
Übungen zu Analysis, SS 2015
 Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
Musterlösung 11.Übung Mathematische Logik
 Lehr- und Forschungsgebiet Mathematische Grundlagen der Informatik RWTH Aachen Prof. Dr. E. Grädel, F. Reinhardt SS 2015 Aufgabe 2 Musterlösung 11.Übung Mathematische Logik Geben Sie für die folgenden
Lehr- und Forschungsgebiet Mathematische Grundlagen der Informatik RWTH Aachen Prof. Dr. E. Grädel, F. Reinhardt SS 2015 Aufgabe 2 Musterlösung 11.Übung Mathematische Logik Geben Sie für die folgenden
Graphen. Im Rahmen dieser Vorlesung beschränken wir uns auf einfache ungerichtete Graphen, die wie folgt definiert werden können:
 Graphen Wir geben zunächst die allgemeinste Definition für den Begriff Graph an: Definition: Ein Graph ist ein 4-Tupel (V, E,, ), wobei V und E Mengen sind, und : E! V und : E! V totale Abbildungen. Im
Graphen Wir geben zunächst die allgemeinste Definition für den Begriff Graph an: Definition: Ein Graph ist ein 4-Tupel (V, E,, ), wobei V und E Mengen sind, und : E! V und : E! V totale Abbildungen. Im
Aufgabe Zusatz.1. Aufgabe Zusatz.2. Aufgabe Zusatz.3. Aufgabe Zusatz.4. HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz
 HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz sibylle.schwarz@htwk-leipzig.de Zusatz. Übung zur Vorlesung Modellierung Wintersemester 2018/19 Lösungen bis 13. Januar 2019 einzusenden im Opal-Kurs
HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz sibylle.schwarz@htwk-leipzig.de Zusatz. Übung zur Vorlesung Modellierung Wintersemester 2018/19 Lösungen bis 13. Januar 2019 einzusenden im Opal-Kurs
1.4 Gruppen, Ringe, Körper
 14 Gruppen, Ringe, Körper Definition 141 Eine Verknüpfung auf einer Menge M ist eine Abbildung : M M M : (a,b) a b Die Verknüpfung heißt assoziativ falls a,b,c M gilt: a (b c) = (a b) c; kommutativ falls
14 Gruppen, Ringe, Körper Definition 141 Eine Verknüpfung auf einer Menge M ist eine Abbildung : M M M : (a,b) a b Die Verknüpfung heißt assoziativ falls a,b,c M gilt: a (b c) = (a b) c; kommutativ falls
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Unentscheidbarkeitssätze der Logik
 Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Wichtige Klassen reeller Funktionen
 0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
Klausur zur Vorlesung Mathematische Logik
 Universität Heidelberg 13. Februar 2014 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Mathematische Logik Musterlösung Aufgabe 1 (Aussagenlogik
Universität Heidelberg 13. Februar 2014 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Mathematische Logik Musterlösung Aufgabe 1 (Aussagenlogik
Rekursive und primitiv rekursive Funktionen. Ein maschinenunabhängiges formales Berechnungsmodell auf den natürlichen Zahlen
 Rekursive und primitiv rekursive Funktionen Ein maschinenunabhängiges formales Berechnungsmodell auf den natürlichen Zahlen IDEE: Definiere eine Klasse von (partiell) berechenbaren Funktionen über N induktiv
Rekursive und primitiv rekursive Funktionen Ein maschinenunabhängiges formales Berechnungsmodell auf den natürlichen Zahlen IDEE: Definiere eine Klasse von (partiell) berechenbaren Funktionen über N induktiv
Theoretische Informatik SS 03 Übung 3
 Theoretische Informatik SS 03 Übung 3 Aufgabe 1 a) Sind die folgenden Funktionen f : partiell oder total: f(x, y) = x + y f(x, y) = x y f(x, y) = x y f(x, y) = x DIV y? Hierbei ist x DIV y = x y der ganzzahlige
Theoretische Informatik SS 03 Übung 3 Aufgabe 1 a) Sind die folgenden Funktionen f : partiell oder total: f(x, y) = x + y f(x, y) = x y f(x, y) = x y f(x, y) = x DIV y? Hierbei ist x DIV y = x y der ganzzahlige
Anwendungen der Logik, SS 2008, Martin Goldstern
 Anwendungen der Logik, SS 2008, Martin Goldstern Total geordnete Körper Ein total geordneter Körper ist ein Körper (K, +,, 0, 1, ) mit einer totalen (=linearen) Ordnung, die mit den Operationen verträglich
Anwendungen der Logik, SS 2008, Martin Goldstern Total geordnete Körper Ein total geordneter Körper ist ein Körper (K, +,, 0, 1, ) mit einer totalen (=linearen) Ordnung, die mit den Operationen verträglich
Aufgabe 3. Sei A eine Menge von Zahlen und neg das Tripel. neg = (A, A, R) A = N A = Z A = R A = R \ {0} mod : N 0 N N 0
 Funktionen Aufgabe 1. Finden Sie 3 Beispiele von Funktionen und 3 Beispiele von partiellen Funktionen, die nicht total sind. Es sollten auch mehrstellige Funktionen darunter sein. Aufgabe 2. Zeigen Sie,
Funktionen Aufgabe 1. Finden Sie 3 Beispiele von Funktionen und 3 Beispiele von partiellen Funktionen, die nicht total sind. Es sollten auch mehrstellige Funktionen darunter sein. Aufgabe 2. Zeigen Sie,
Notengebung. Teilnote Kreuzerlliste: 60% 69% 4; 70% 79% 3; 80% 89% 2; 90% 100% 1. Falls Sie weitere Fragen haben, bitte melden Sie sich bei mir.
 Notengebung Die Gesamtnote für die Übung ergibt sich je zur Hälfte aus der Teilnote Kreuzerlliste und der Teilnote Zwischentest, gerundet auf freundliche Weise; für eine positive Benotung müssen beide
Notengebung Die Gesamtnote für die Übung ergibt sich je zur Hälfte aus der Teilnote Kreuzerlliste und der Teilnote Zwischentest, gerundet auf freundliche Weise; für eine positive Benotung müssen beide
2 Mengen, Abbildungen und Relationen
 Vorlesung WS 08 09 Analysis 1 Dr. Siegfried Echterhoff 2 Mengen, Abbildungen und Relationen Definition 2.1 (Mengen von Cantor, 1845 1918) Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohl
Vorlesung WS 08 09 Analysis 1 Dr. Siegfried Echterhoff 2 Mengen, Abbildungen und Relationen Definition 2.1 (Mengen von Cantor, 1845 1918) Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohl
14. Rekursiv aufzählbare Mengen
 14. Rekursiv aufzählbare Mengen In diesem Abschnitt fassen wir einige Eigenschaften der rekursiv aufzählbaren d.h. der nach Churchscher These (effektiv) aufzählbaren Mengen zusammen. In Korollar 11.8 haben
14. Rekursiv aufzählbare Mengen In diesem Abschnitt fassen wir einige Eigenschaften der rekursiv aufzählbaren d.h. der nach Churchscher These (effektiv) aufzählbaren Mengen zusammen. In Korollar 11.8 haben
1 Mathematische Grundbegriffe
 1 1 Mathematische Grundbegriffe 1.1 Relationen und Funktionen Seien A 1,..., A n Mengen. Ein n-tupel über A 1,..., A n ist eine Folge (a 1,..., a n ) von Objekten a i A i, für i = 1,..., n. Zwei n-tupel
1 1 Mathematische Grundbegriffe 1.1 Relationen und Funktionen Seien A 1,..., A n Mengen. Ein n-tupel über A 1,..., A n ist eine Folge (a 1,..., a n ) von Objekten a i A i, für i = 1,..., n. Zwei n-tupel
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
GOTO simuliert Turingmaschinen
 GOTO simuliert Turingmaschinen Wir wissen bisher: LOOP ( GOTO = WHILE TM Jetzt zeigen wir, dass auch WHILE = TM gilt: Die Turingmaschine M =(Z,,,,z 1,, E) berechne f. Wir simulieren M mit einem GOTO-Programm
GOTO simuliert Turingmaschinen Wir wissen bisher: LOOP ( GOTO = WHILE TM Jetzt zeigen wir, dass auch WHILE = TM gilt: Die Turingmaschine M =(Z,,,,z 1,, E) berechne f. Wir simulieren M mit einem GOTO-Programm
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 7 Sprachen erster Sufe Die in der letzten Vorlesung erwähnten Konstruktionsmöglichkeiten für Aussagen sind im Wesentlichen
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 7 Sprachen erster Sufe Die in der letzten Vorlesung erwähnten Konstruktionsmöglichkeiten für Aussagen sind im Wesentlichen
Vorname Name Matrikelnummer 1. a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte)
 1 Aufgabe 1 (19 Punkte) a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte) Q, die endliche Zustandsmenge b) Was besagt die Church-Turing-These? (1 Punkt)
1 Aufgabe 1 (19 Punkte) a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte) Q, die endliche Zustandsmenge b) Was besagt die Church-Turing-These? (1 Punkt)
Mathematik II für Inf und WInf
 Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Grundlagen der Programmierung
 Grundlagen der Programmierung SS 05 Prof. Dr. K. Madlener Lösungshinweise zu Übungsblatt 6 Aufgabe 6.1. Sei f(x, b) = µy b.(y y x (y + 1) (y + 1) > x) f.a. x, b N. Sei weiter f(x) = f(x, x) f.a. x N. Aufgabe
Grundlagen der Programmierung SS 05 Prof. Dr. K. Madlener Lösungshinweise zu Übungsblatt 6 Aufgabe 6.1. Sei f(x, b) = µy b.(y y x (y + 1) (y + 1) > x) f.a. x, b N. Sei weiter f(x) = f(x, x) f.a. x N. Aufgabe
Klausur zur Vorlesung Einführung in die Theoretische Informatik
 Universität Heidelberg 19. Juli 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Einführung in die Theoretische Informatik LÖSUNGEN Es können
Universität Heidelberg 19. Juli 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Einführung in die Theoretische Informatik LÖSUNGEN Es können
Aufgabe 24 Die Wahrheitswerte von A A B und B sind immer gleich:
 Lösungen zu den Aufgaben von Anfang August Aufgabe 24 Die Wahrheitswerte von A A B und B sind immer gleich: Der Wahrheitswert von A A ist immer wahr, da immer entweder A oder A den Wahrheitswert wahr hat.
Lösungen zu den Aufgaben von Anfang August Aufgabe 24 Die Wahrheitswerte von A A B und B sind immer gleich: Der Wahrheitswert von A A ist immer wahr, da immer entweder A oder A den Wahrheitswert wahr hat.
Programmieren für Fortgeschrittene
 Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme Wintersemester 2011/12 Programmieren für Fortgeschrittene Rekursive Spezifikationen Die folgende
Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme Wintersemester 2011/12 Programmieren für Fortgeschrittene Rekursive Spezifikationen Die folgende
1.4 Gruppen, Ringe, Körper
 14 Gruppen, Ringe, Körper Definition 141 Eine Verknüpfung auf einer Menge M ist eine Abbildung : M M M : (a, b a b Die Verknüpfung heißt assoziativ falls gilt: a (b c = (a b c a, b, c M; kommutativ falls
14 Gruppen, Ringe, Körper Definition 141 Eine Verknüpfung auf einer Menge M ist eine Abbildung : M M M : (a, b a b Die Verknüpfung heißt assoziativ falls gilt: a (b c = (a b c a, b, c M; kommutativ falls
Klausur zur Vorlesung Grundbegriffe der Informatik 2. März 2016
 Klausurnummer Klausur zur Vorlesung Grundbegriffe der Informatik 2. März 2016 Nachname: Vorname: Matr.-Nr.: Diese Klausur ist mein 1. Versuch 2. Versuch in GBI Email-Adr.: nur falls 2. Versuch Aufgabe
Klausurnummer Klausur zur Vorlesung Grundbegriffe der Informatik 2. März 2016 Nachname: Vorname: Matr.-Nr.: Diese Klausur ist mein 1. Versuch 2. Versuch in GBI Email-Adr.: nur falls 2. Versuch Aufgabe
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Logik für Informatiker
 Vorlesung Logik für Informatiker 2. Induktion Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Induktion Zentrale Rolle Wesentliches Beweisprinzip in Mathematik
Vorlesung Logik für Informatiker 2. Induktion Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Induktion Zentrale Rolle Wesentliches Beweisprinzip in Mathematik
Vorlesung Diskrete Strukturen Relationen
 Vorlesung Diskrete Strukturen Relationen Bernhard Ganter WS 2009/10 Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B. Ein wichtiger Spezialfall ist
Vorlesung Diskrete Strukturen Relationen Bernhard Ganter WS 2009/10 Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B. Ein wichtiger Spezialfall ist
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 24-6. Sitzung Marcus Georgi tutorium@marcusgeorgi.de 04.12.2009 1 Repräsentation von Graphen im Rechner Adjazenzlisten Adjazenzmatrizen Wegematrizen 2 Erreichbarkeitsrelationen
Grundbegriffe der Informatik Tutorium 24-6. Sitzung Marcus Georgi tutorium@marcusgeorgi.de 04.12.2009 1 Repräsentation von Graphen im Rechner Adjazenzlisten Adjazenzmatrizen Wegematrizen 2 Erreichbarkeitsrelationen
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 18: Logik Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/35 Überblick Formeln in Prädikatenlogik erster Stufe Theorien und
Grundbegriffe der Informatik Einheit 18: Logik Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/35 Überblick Formeln in Prädikatenlogik erster Stufe Theorien und
Einführung in die Berechenbarkeitstheorie
 Einführung in die Berechenbarkeitstheorie Timo Kötzing 4. November 2013 1 Einleitung Dieses Dokument bietet eine kurze Einführung in die Grundlagen der Berechenbarkeitstheorie (für eine Ausführliche Behandlung
Einführung in die Berechenbarkeitstheorie Timo Kötzing 4. November 2013 1 Einleitung Dieses Dokument bietet eine kurze Einführung in die Grundlagen der Berechenbarkeitstheorie (für eine Ausführliche Behandlung
Theorie der Informatik
 Theorie der Informatik 15. Ackermannfunktion Malte Helmert Gabriele Röger Universität Basel 28. April 2014 Überblick: Vorlesung Vorlesungsteile I. Logik II. Automatentheorie und formale Sprachen III. Berechenbarkeitstheorie
Theorie der Informatik 15. Ackermannfunktion Malte Helmert Gabriele Röger Universität Basel 28. April 2014 Überblick: Vorlesung Vorlesungsteile I. Logik II. Automatentheorie und formale Sprachen III. Berechenbarkeitstheorie
e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme sin(x+y) = cos(x) sin(y)+sin(x) cos(y). und f. Für eine reelle Zahl x R gilt e ix = 1.
 8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
Technische Universität München. Ferienkurs Lineare Algebra 1. Mengenlehre, Aussagen, Relationen und Funktionen. Aufgaben mit Musterlösung
 Technische Universität München Ferienkurs Lineare Algebra 1 Mengenlehre, Aussagen, Relationen und Funktionen Aufgaben mit Musterlösung 21. März 2011 Tanja Geib 1 Aufgabe 1 Geben Sie zu B = {0, 2, 4} und
Technische Universität München Ferienkurs Lineare Algebra 1 Mengenlehre, Aussagen, Relationen und Funktionen Aufgaben mit Musterlösung 21. März 2011 Tanja Geib 1 Aufgabe 1 Geben Sie zu B = {0, 2, 4} und
Syntax von LOOP-Programmen
 LOOP-Berechenbarkeit Syntax von LOOP-Programmen Definition LOOP-Programme bestehen aus: Variablen: x 0, x 1, x 2, x 3,... Konstanten: 0, 1, 2, 3,... Trennsymbolen:; und := Operationen: + und Befehlen:
LOOP-Berechenbarkeit Syntax von LOOP-Programmen Definition LOOP-Programme bestehen aus: Variablen: x 0, x 1, x 2, x 3,... Konstanten: 0, 1, 2, 3,... Trennsymbolen:; und := Operationen: + und Befehlen:
Komplexitätstheorie WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018 23. November 2017 1/40 Satz 4.27 (Multinomialsatz) Seien r, n N 0. Dann gilt für
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018 23. November 2017 1/40 Satz 4.27 (Multinomialsatz) Seien r, n N 0. Dann gilt für
Funktionale Programmierung Teil 2 Methodik: Spezifikation, Implementierung, Verifikation
 Grundlagen der Programm- und Systementwicklung Funktionale Programmierung Teil 2 Methodik: Spezifikation, Implementierung, Verifikation Technische Universität München Institut für Informatik Software &
Grundlagen der Programm- und Systementwicklung Funktionale Programmierung Teil 2 Methodik: Spezifikation, Implementierung, Verifikation Technische Universität München Institut für Informatik Software &
2 Funktionen in mehreren Variablen: Differentiation
 Satz 2. (Richtungsableitung) Für jede auf der offenen Menge D R n total differenzierbaren Funktion f (insbesondere für f C 1 (D, R) und für jeden Vektor v R n, v 0, gilt: n v f(x) = f(x) v = f xi (x)v
Satz 2. (Richtungsableitung) Für jede auf der offenen Menge D R n total differenzierbaren Funktion f (insbesondere für f C 1 (D, R) und für jeden Vektor v R n, v 0, gilt: n v f(x) = f(x) v = f xi (x)v
min(a, b) H(a, b) G(a, b) A(a, b) Q(a, b) max(a, b), (1)
 FU Berlin: WiSe 13-14 (Analysis 1 - Lehr.) Übungsaufgaben Zettel 4 Aufgabe 15 Für zwei beliebige reelle Zahlen a > 0, b > 0 bezeichne A(a, b) := a+b, das arithmetische, G(a, b) := ab das geometrische,
FU Berlin: WiSe 13-14 (Analysis 1 - Lehr.) Übungsaufgaben Zettel 4 Aufgabe 15 Für zwei beliebige reelle Zahlen a > 0, b > 0 bezeichne A(a, b) := a+b, das arithmetische, G(a, b) := ab das geometrische,
Signatur einer prädikatenlogische Sprache
 Signatur einer prädikatenlogische Sprache Das Alphabet einer prädikatenlogische Sprache (erster Stufe) besteht aus den logischen Funktoren,,,,, and den Klammersymbolen ( und ) und dem Komma, einer (abzählbar
Signatur einer prädikatenlogische Sprache Das Alphabet einer prädikatenlogische Sprache (erster Stufe) besteht aus den logischen Funktoren,,,,, and den Klammersymbolen ( und ) und dem Komma, einer (abzählbar
Lösungen zur Vorlesung Berechenbarkeit und Komplexität
 Lehrstuhl für Informatik 1 WS 009/10 Prof. Dr. Berthold Vöcking 0.0.010 Alexander Skopalik Thomas Kesselheim Lösungen zur Vorlesung Berechenbarkeit und Komplexität. Zulassungsklausur Aufgabe 1: (a) Worin
Lehrstuhl für Informatik 1 WS 009/10 Prof. Dr. Berthold Vöcking 0.0.010 Alexander Skopalik Thomas Kesselheim Lösungen zur Vorlesung Berechenbarkeit und Komplexität. Zulassungsklausur Aufgabe 1: (a) Worin
Grundbegriffe der Mathematik - Blatt 1, bis zum
 Grundbegriffe der Mathematik - Blatt 1 bis zum 9.3.01 1. I.) Formalisieren Sie die folgenden Aussagen a) bis c) wie im folgenden Beispiel: Sei K ein Teilmenge der reellen Zahlen. Aussage: K ist genau dann
Grundbegriffe der Mathematik - Blatt 1 bis zum 9.3.01 1. I.) Formalisieren Sie die folgenden Aussagen a) bis c) wie im folgenden Beispiel: Sei K ein Teilmenge der reellen Zahlen. Aussage: K ist genau dann
1 Umkehrfunktionen und implizite Funktionen
 Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
1 Angeordnete Körper. 1.1 Anordnungen und Positivbereiche
 1 1 Angeordnete Körper 1.1 Anordnungen und Positivbereiche Definition 1.1. Eine zweistellige Relation auf einer Menge heißt partielle Ordnung, falls für alle Elemente a, b, c der Menge gilt: (i) a a (ii)
1 1 Angeordnete Körper 1.1 Anordnungen und Positivbereiche Definition 1.1. Eine zweistellige Relation auf einer Menge heißt partielle Ordnung, falls für alle Elemente a, b, c der Menge gilt: (i) a a (ii)
Probeklausur Mathematische Logik
 Lehr- und Forschungsgebiet Mathematische Grundlagen der Informatik RWTH Aachen Prof. Dr. E. Grädel SS 2015 Probeklausur Mathematische Logik Aufgabe 1 (a) (i) Seien R, zweistellige Relationssymbole. Ist
Lehr- und Forschungsgebiet Mathematische Grundlagen der Informatik RWTH Aachen Prof. Dr. E. Grädel SS 2015 Probeklausur Mathematische Logik Aufgabe 1 (a) (i) Seien R, zweistellige Relationssymbole. Ist
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Vektorräume und Lineare Abbildungen
 Vektorräume und Lineare Abbildungen Die angesprochene Thematik macht den Kern dieser Veranstaltung aus. Lineare Techniken sind zentral für weite Bereiche mathematischen Argumentierens. Durch in der Analysis
Vektorräume und Lineare Abbildungen Die angesprochene Thematik macht den Kern dieser Veranstaltung aus. Lineare Techniken sind zentral für weite Bereiche mathematischen Argumentierens. Durch in der Analysis
Rechenoperationen mit Folgen. Rekursion und Iteration.
 Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Aufgabe Bonus.1. Aufgabe Bonus.2. Aufgabe Bonus.3. Aufgabe Bonus.4. HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz
 HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz sibylle.schwarz@htwk-leipzig.de Bonus. Übung zur Vorlesung Modellierung Wintersemester 2017/18 Lösungen bis 3. Januar 2018 einzusenden im Opal-Kurs
HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz sibylle.schwarz@htwk-leipzig.de Bonus. Übung zur Vorlesung Modellierung Wintersemester 2017/18 Lösungen bis 3. Januar 2018 einzusenden im Opal-Kurs
Mathematik für Sicherheitsingenieure I A
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Prädikatenlogiken. Mathematische Logik. Vorlesung 7. Alexander Bors. 6. & 27. April A. Bors Logik
 Prädikatenlogiken Mathematische Logik Vorlesung 7 Alexander Bors 6. & 27. April 2017 1 Prädikatenlogiken Überblick 1 Formale Prädikatenlogiken erster Stufe (Quelle: Ziegler, pp. 3 24) (Abgeleitete) Axiome
Prädikatenlogiken Mathematische Logik Vorlesung 7 Alexander Bors 6. & 27. April 2017 1 Prädikatenlogiken Überblick 1 Formale Prädikatenlogiken erster Stufe (Quelle: Ziegler, pp. 3 24) (Abgeleitete) Axiome
