NP-vollst. u. NP-äquiv. Probleme
|
|
|
- Renate Albert
- vor 5 Jahren
- Abrufe
Transkript
1 NP-vollst. u. NP-äquiv. Probleme Literatur: Kapitel K6. Ziel: Weitere Probleme kennen lernen (und damit weitere Basisprobleme für eigene Reduktionen) Weitere Beispiele für NP-Vollständigkeitsbeweise kennen lernen. 235
2 Bisher bewiesen (vgl. Folie 189) Partition p BP SAT = p 3-SAT p p IS = p Clique = p VC DHC = p HC = p TSP 2,,sym NP-vollständig 2-SAT P (Übungen) 236
3 Folgerung Die Optimierungsvarianten von IS, Clique, VC und TSP sind NP-äquivalent. 237
4 Rucksackprobleme [K6.3] Subset Sum Problem (SSS) Eingabe: Zahlen a 1,...,a n, G. Frage: Gibt es eine Menge I {1,...,n}, so dass i I a i = G? Satz K6.3.1: SSS ist NP-vollständig. Beweis: 1. SSS NP. 2. Reduktion von 3-SAT. Reduktion mit verbundenen Komponenten 238
5 3. Angabe der Funktion f. Eingabe für 3-SAT: Variablen x 1,...,x n, Klauseln C 1,...,C m. Zahlen der SSS-Eingabe: - n+m Ziffern in Dezimaldarstellung. - Für jede Variable x i zwei Zahlen a i und b i : C 1 C 2... C j... C m... x i... a i b i x 1 x 2 falls C j x i enthält falls C j x i enthält x n 239
6 Für jede Variable x i : C 1 C 2... C j... C m... x i... a i b i Für jede Klausel C j : d j C 1 C 2... C j... C m e j Summe G: G C 1 3 x 1 x 1 x 1 x 2 x 2 x 2... x i... x n x n C 2... C j... C m... x i x n 240
7 C 1 x 4 b a a a d 1 e 1 1 e 2 d C 2 3 C 3 3 C 4 3 x 1 1 x 2 1 x C 1 = x 1 x 2 x 3, C 2 = x 1 x 2 x 4, C 3 = x 1 x 3 x 4, C 4 = x 2 x 3 x
8 Korrektheit : Sei z=(z 1,...,z n ) erfüllende Belegung. Wähle die Zahl a i, falls z i =1, b i, falls z i =0. Summe für Variablenstellen stimmt. Da z erfüllend, sind in jedem C j 1, 2 oder 3 Literale erfüllt. 1 erfülltes Literal: Wähle d j und e j. 2 erfüllte Literale: Wähle d j. Summe für die Klauselstellen stimmt. 242
9 Korrektheit : Sei Auswahl der Zahlen mit Summe G gegeben. Falls a i gewählt: z i =1. Falls b i gewählt: z i =0. Behauptung: Dies ist erfüllende Belegung. a i und b i können nicht beide gewählt sein. Für jede Klausel C j muss mindestens eine 1 von einem a i oder b i kommen Zugehöriges Literal erfüllt. 243
10 Spezialfälle/Restriktionen Allgemein gilt: Sei A NP, sei B NP-vollständig und ein Spezialfall von A. Dann ist auch A NPvollständig. Beweis: Es ist B p A: Spezialfall bedeutet: Eine Eingabe für A entsteht aus einer Eingabe für B durch Konstantsetzen einiger Teile. Diese Abbildung ist als Funktion f der Reduktion geeignet. 244
11 Rucksackproblem Knapsack (KP) Eingabe: n Objekte mit Nutzenwerten a 1,...,a n und Gewichten g 1,...,g n, Gesamtgewicht G, Nutzenschranke B. Frage: Gibt es eine Auswahl der Objekte mit Nutzen mindestens B und Gesamtgewicht höchstens G? KP*: Spezialfall mit G=B und a i =g i. 245
12 Folgerung K6.3.2: KP und KP* sind NP-vollständig. Beweis: KP* und SSS sind äquivalent. KP ist Verallgemeinerung von KP*. Restriktion 246
13 Partition Zur Erinnerung: Eingabe: Natürliche Zahlen a 1,...,a n. Frage: Gibt es I {1,...,n} mit Folgerung K6.3.2: Partition ist NP-vollständig. Problem: Partition ist ein Spezialfall von SSS. Verkehrte Richtung für Restriktion. 247
14 Beweis Reduktion SSS p Partition: Sei X=(a 1,...,a n,g) Eingabe für SSS. Sei S*=a a n. Konstruiere Partition-Eingabe: Y=(a 1,..., a n, a n+1 =2S* G, a n+2 =S*+G) erzwingende Komponenten Beob: a a n + a n+1 + a n+2 = 4S*. 248
15 X=(a 1,...,a n,g) Korrektheit: Y=(a 1,..., a n, a n+1 =2S* G, a n+2 =S*+G) : Sei I Lösung von X, also i I a i =G: Dann ist I {n+1} Lösung von Y. : Sei J Lösung für Y. Falls n+1 J, vertausche J und J={1,...,n+2} J. Dann ist J {n+1} eine Lösung für X. 249
16 Aufteilung u. Lastverteilung [K6.4] Wir haben bereits gezeigt: Partition p BP. Folgerung K6.4.1: BP ist NP-vollständig. BP Eingabe: n Objekte mit Größen a 1,...,a n, Kistengröße b, Zahl k. Aufgabe: Genügen k Kisten der Größe b, um alle Objekte zu verpacken? 250
17 Sequencing with Intervals (SWI) Eingabe: A={a 1,...,a n } Menge v. Aufgaben mit l(a): Bearbeitungsdauer von Aufgabe a, length r(a): frühester Bearbeitungszeitpunkt von a, d(a): Deadline für a release time Frage: Können die Aufgaben von einem Prozessor so bearbeitet werden, dass keine Aufgabe unterbrochen wird und alle Bedingungen eingehalten werden? 251
18 Satz K6.4.2: SWI ist NP-vollständig. Beweis: 1. SWI NP klar. 2. Reduktion Partition p SWI 3. Eingabe f. Partition: X=(s 1,...,s n ). Sei S = s s n, ist o.b.d.a. gerade Zahl. Erzeuge n+1 Aufgaben a 1,...,a n+1. Für 1 i n: l(a i )=s i, r(a i )=0, d(a i )=S+1, l(a n+1 )=1, r(a n+1 )=S/2, d(a n+1 )=S/2+1. a n+1 0 S/2 S/2+1 S+1 252
19 Cliquenprobleme [K6.5] Graphisomorphie (GI) Eingabe: Graphen G 1 =(V 1,E 1 ), G 2 =(V 2,E 2 ). Frage: Sind G 1 und G 2 isomorph, d.h., gibt es eine Funktion f : V 1 V 2 mit {v 1,v 2 } E 1 {f(v 1 ),f(v 2 )} E 2? GI NP klar. Für GI kennt man weder einen polyn. Algo., noch einen NP-Vollst.beweis. 253
20 Teilgraphisomorphie Subgraph Isomorphism (SI) Eingabe: Graphen G 1 =(V 1,E 1 ), G 2 =(V 2,E 2 ). Frage: Gibt es einen Teilgraphen von G 1, der zu G 2 isomorph ist? Teilgraph von G 1 : Knotenmenge V V 1. Kantenmenge: Alle Kanten aus E 1, die zwischen Knoten aus V verlaufen. 254
21 Satz K6.5.1: SI ist NP-vollständig. Beweis: 1. SI NP klar. 2. Reduktion Clique p SI. 3. Eingabe für Cliquenproblem: (G,k). Sei G 1 =G, G 2 =vollständiger Graph auf k Knoten. 4. G enthält k-clique Restriktion G 1 enthält zu G 2 isomorphen Subgraphen. 255
22 Graphfärbbarkeit Graph Colorability (GC) Eingabe: Unger. Graph G=(V,E), Zahl k. Frage: Können die Knoten von G mit k Farben gefärbt werden, so dass benachbarte Knoten verschieden gefärbt werden? 256
23 Bsp: Färben von Landkarten 257
24 Satz K6.5.2: GC ist NP-vollständig. Beweis: 1. GC NP klar. 2. Reduktion von 3-SAT. 3. Sei 3-SAT-Eingabe mit Variablen x 1,...,x n und Klauseln C 1,...,C m gegeben. Wähle k=3 (3 Farben) 258
25 Komponenten für Klauseln: v 1 v 2 w v 3 Beob. (für legale 3-Färbungen): 1.Wenn v 1, v 2 und v 3 dieselbe Farbe haben, dann hat auch w diese Farbe. 2.Wenn einer der v-knoten die Farbe 1 hat, kann auch w die Farbe 1 bekommen. 259
26 x 1 C 1 =x 1 x 2 x n 3 u x 2 x 1 x 2 C 2 w 1 x n x n 2 260
27 Korrektheit Sei erfüllende Belegung gegeben. x i =0: x i -Knoten bekommt Farbe 2, x i -Knoten bekommt Farbe 1. x i =1: x i -Knoten bekommt Farbe 1, x i -Knoten bekommt Farbe 2. Da die Belegung erfüllend ist, kann jede Klauselkomponente so gefärbt werden, dass w die Farbe 1 bekommt. 261
28 Korrektheit Sei legale Färbung gegeben. O.B.d.A.: w hat Farbe 1, u hat Farbe 3. Variablenknoten haben Farben 1 und 2. x i -Knoten hat Farbe 1: Belegung x i =1, x i -Knoten hat Farbe 2: Belegung x i =0. Annahme: C j dadurch nicht erfüllt. Alle v-knoten von C j haben Farbe 2 w hat Farbe 2. Widerspruch. 262
29 Spezialfall: festes k k-gc Eingabe: Graph G Frage: Ist G mit k Farben färbbar? Folgerung K6.5.3: 3-GC ist NP-vollständig. Übungsaufgaben: Zeige, dass 2-GC P. Zeige, dass k-gc für alle k 3 NP-vollständig ist. 263
30 Zusammenfassung Kompl.theorie Betrachtete Rechnermodelle: Turingmaschinen, Registermaschinen Varianten: deterministisch, randomisiert, nichtdeterministisch Komplexitätstheorie für randomisierte Algorithmen Komplexitätsklassen ZPP, RP, BPP, PP Probability Amplification Nichtdeterminismus als Spezialfall von Randomisierung 264
31 Zusammenfassung Kompl.theorie Zentrale Begriffe der NP- Vollständigkeitstheorie Turing-Reduktionen und polynomielle Reduktionen NP-vollständige und NP-schwere Probleme Satz von Cook, Vereinfachung von Beweisen der NP-Vollständigkeit Zahlreiche Reduktionen zwischen verschiedenen Problemen 265
32 Fazit NP-Vollständigkeit Ein Beweis der NP-Vollständigkeit liefert eine starken Hinweis darauf, dass ein Problem keinen polyn. Algo hat. Nutzen Keine Zeit dafür ver(sch)wenden, einen Algo zu suchen, den es wohl nicht gibt. Beweis liefert Hinweise darauf, was an dem Problem schwer ist Überlegen, ob wir das richtige Problem lösen. Fehlgeschlagene Versuche liefern Hinweise auf polynomielle Algos. 266
33 Fazit NP-Vollständigkeit (Forts.) Reduktionen mit verbundenen Komponenten erlauben es, Beziehungen zwischen nicht verwandten Problemen herzustellen. 3-SAT ist häufig ein Ausgangsproblem für Reduktionen. 267
Erfüllbarkeitsprobleme. Begriffe. Varianten von SAT
 Erfüllbarkeitsprobleme SAT (satisfiability problem) Eingabe: Formel F in konjunktiver Form. Frage: Gibt es eine Belegung x der Variablen in F mit F(x)=1? Beispiel: Begriffe erfüllbar satisfiable: Eigenschaft
Erfüllbarkeitsprobleme SAT (satisfiability problem) Eingabe: Formel F in konjunktiver Form. Frage: Gibt es eine Belegung x der Variablen in F mit F(x)=1? Beispiel: Begriffe erfüllbar satisfiable: Eigenschaft
Rechenzeit für A. Sei t B die Rechenzeit eines Algo für B. Seien p,q,r monotone Polynome ( +).
 Rechenzeit für A Sei t B die Rechenzeit eines Algo für B. Seien p,q,r monotone Polynome ( +). Rechenzeit des resultierenden Algo für A: t A (n) p(n) + q(n) t B (r(n)). Ist polynomiell, falls t B Polynom.
Rechenzeit für A Sei t B die Rechenzeit eines Algo für B. Seien p,q,r monotone Polynome ( +). Rechenzeit des resultierenden Algo für A: t A (n) p(n) + q(n) t B (r(n)). Ist polynomiell, falls t B Polynom.
Dank. Theoretische Informatik II. Teil VI. Vorlesung
 Dank Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Diese Vorlesungsmaterialien basieren zum Teil auf den Folien zu den Vorlesungen von Katrin Erk (gehalten an der Universität
Dank Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Diese Vorlesungsmaterialien basieren zum Teil auf den Folien zu den Vorlesungen von Katrin Erk (gehalten an der Universität
Zusammenfassung. Warum polynomielle Reduktionen? Definition NP-vollständig [K5.1.1] NP-Vollständigkeitstheorie [K5]
![Zusammenfassung. Warum polynomielle Reduktionen? Definition NP-vollständig [K5.1.1] NP-Vollständigkeitstheorie [K5] Zusammenfassung. Warum polynomielle Reduktionen? Definition NP-vollständig [K5.1.1] NP-Vollständigkeitstheorie [K5]](/thumbs/96/130567055.jpg) Warum polynomielle Reduktionen? erlauben feinere Unterteilungen von Komplexitätsklassen als Turing- Reduktionen, genügen für die betrachteten Probleme, für alle von uns betrachteten Komplexitätsklassen
Warum polynomielle Reduktionen? erlauben feinere Unterteilungen von Komplexitätsklassen als Turing- Reduktionen, genügen für die betrachteten Probleme, für alle von uns betrachteten Komplexitätsklassen
NP-vollständige Probleme. Michael Budahn - Theoretische Informatik 1
 NP-vollständige Probleme Michael Budahn - Theoretische Informatik 1 Motivation Michael Budahn - Theoretische Informatik 2 Motivation viele praxisrelevante Probleme sind NPvollständig und eine Lösung würde
NP-vollständige Probleme Michael Budahn - Theoretische Informatik 1 Motivation Michael Budahn - Theoretische Informatik 2 Motivation viele praxisrelevante Probleme sind NPvollständig und eine Lösung würde
Abbildung 1: Reduktion: CLIQUE zu VERTEX-COVER. links: Clique V = {u, v, x, y}. rechts:der Graph Ḡ mit VC V \ V = {w, z}
 u v u v z w z w y x y x Abbildung 1: Reduktion: CLIQUE zu VERTEX-COVER. links: Clique V = {u, v, x, y}. rechts:der Graph Ḡ mit VC V \ V = {w, z} Definition 0.0.1 (Vertex Cover (VC)). Gegeben: Ein ungerichteter
u v u v z w z w y x y x Abbildung 1: Reduktion: CLIQUE zu VERTEX-COVER. links: Clique V = {u, v, x, y}. rechts:der Graph Ḡ mit VC V \ V = {w, z} Definition 0.0.1 (Vertex Cover (VC)). Gegeben: Ein ungerichteter
NP-Vollständigkeit einiger Zahlprobleme
 NP-Vollständigkeit einiger Zahlprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 22. Januar 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
NP-Vollständigkeit einiger Zahlprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 22. Januar 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Kochrezept für NP-Vollständigkeitsbeweise
 Kochrezept für NP-Vollständigkeitsbeweise Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 11. Januar 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Kochrezept für NP-Vollständigkeitsbeweise Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 11. Januar 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V7, 5.12.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V7, 5.12.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Probleme aus NP und die polynomielle Reduktion
 Probleme aus NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 15. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Probleme aus NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 15. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Satz 227 3SAT ist N P-vollständig. Info IV 2 N P-Vollständigkeit 375/388 c Ernst W. Mayr
 Definition 6 3SAT ist die Menge der booleschen Formeln in konjunktiver Normalform, die in jeder Klausel höchstens drei Literale enthalten und die erfüllbar sind. Satz 7 3SAT ist N P-vollständig. Info IV
Definition 6 3SAT ist die Menge der booleschen Formeln in konjunktiver Normalform, die in jeder Klausel höchstens drei Literale enthalten und die erfüllbar sind. Satz 7 3SAT ist N P-vollständig. Info IV
Berechenbarkeit und Komplexität: Polynomielle Reduktion / NP-Vollständigkeit / Satz von Cook und Levin
 Berechenbarkeit und Komplexität: Polynomielle Reduktion / NP-Vollständigkeit / Satz von Cook und Levin Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 11. Januar 2008 Wiederholung
Berechenbarkeit und Komplexität: Polynomielle Reduktion / NP-Vollständigkeit / Satz von Cook und Levin Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 11. Januar 2008 Wiederholung
Die Klasse NP und die polynomielle Reduktion
 Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Dezember 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Dezember 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Die Klasse NP und die polynomielle Reduktion. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
 Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 26 Optimierungsprobleme und ihre Entscheidungsvariante Beim Rucksackproblem
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 26 Optimierungsprobleme und ihre Entscheidungsvariante Beim Rucksackproblem
Theoretische Grundlagen der Informatik. Vorlesung am 27. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 27.11.2018 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Letzte Vorlesung Die
Theoretische Grundlagen der Informatik 0 27.11.2018 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Letzte Vorlesung Die
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Reduktion. Komplexitätsklassen.
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 01. Dezember 2011 INSTITUT FÜR THEORETISCHE 0 KIT 01.12.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 01. Dezember 2011 INSTITUT FÜR THEORETISCHE 0 KIT 01.12.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 20. Vorlesung 12.01.2007 1 Komplexitätstheorie - Zeitklassen Die Komplexitätsklassen TIME DTIME, NTIME P NP Das Cook-Levin-Theorem Polynomial-Zeit-Reduktion
Informatik III Christian Schindelhauer Wintersemester 2006/07 20. Vorlesung 12.01.2007 1 Komplexitätstheorie - Zeitklassen Die Komplexitätsklassen TIME DTIME, NTIME P NP Das Cook-Levin-Theorem Polynomial-Zeit-Reduktion
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 5. Dezember 2017 INSTITUT FÜR THEORETISCHE 0 05.12.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 5. Dezember 2017 INSTITUT FÜR THEORETISCHE 0 05.12.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 06. Dezember 2011 INSTITUT FÜR THEORETISCHE 0 KIT 06.12.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 06. Dezember 2011 INSTITUT FÜR THEORETISCHE 0 KIT 06.12.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 22.12.2011 INSTITUT FÜR THEORETISCHE 0 KIT 09.01.2012 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Übung am 22.12.2011 INSTITUT FÜR THEORETISCHE 0 KIT 09.01.2012 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik
VL-13: Polynomielle Reduktionen. (Berechenbarkeit und Komplexität, WS 2018) Gerhard Woeginger
 VL-13: Polynomielle Reduktionen (Berechenbarkeit und Komplexität, WS 2018) Gerhard Woeginger WS 2018, RWTH BuK/WS 2018 VL-13: Polynomielle Reduktionen 1/46 Organisatorisches Nächste Vorlesungen: Donnerstag,
VL-13: Polynomielle Reduktionen (Berechenbarkeit und Komplexität, WS 2018) Gerhard Woeginger WS 2018, RWTH BuK/WS 2018 VL-13: Polynomielle Reduktionen 1/46 Organisatorisches Nächste Vorlesungen: Donnerstag,
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 16.12.2010 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Übung am 16.12.2010 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
NP-Vollständigkeit des Erfüllbarkeitsproblems
 NP-Vollständigkeit des Erfüllbarkeitsproblems Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 25 Def: NP-Härte Definition (NP-Härte) Ein Problem L heißt NP-hart,
NP-Vollständigkeit des Erfüllbarkeitsproblems Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 25 Def: NP-Härte Definition (NP-Härte) Ein Problem L heißt NP-hart,
Härte von Hamilton-Kreis und TSP Überblick über die Komplexitätslandschaft
 Härte von Hamilton-Kreis und TSP Überblick über die Komplexitätslandschaft Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 5. Februar 2010 Berthold Vöcking, Informatik
Härte von Hamilton-Kreis und TSP Überblick über die Komplexitätslandschaft Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 5. Februar 2010 Berthold Vöcking, Informatik
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 4 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 4 : Komplexitätsklassen Informatik III - WS07/08 Kapitel 4 2 Sprachen, Probleme, Zeitkomplexität
Informatik III - WS07/08 Kapitel 4 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 4 : Komplexitätsklassen Informatik III - WS07/08 Kapitel 4 2 Sprachen, Probleme, Zeitkomplexität
NP Vollständigkeit. Patryk Mazur
 NP Vollständigkeit Patryk Mazur 04.05.2010 0.Gliderung 1. Einführung 1. Definitionen P, NP, conp, EXP, NEXP 2. Bekannte Zusammenhänge zwischen dem Klassen 3. Hypothesen zu deren zusammenhängen und deren
NP Vollständigkeit Patryk Mazur 04.05.2010 0.Gliderung 1. Einführung 1. Definitionen P, NP, conp, EXP, NEXP 2. Bekannte Zusammenhänge zwischen dem Klassen 3. Hypothesen zu deren zusammenhängen und deren
Algorithmen und Komplexität
 Algorithmen und Komplexität Thema: NP-vollständige Probleme Erbschaftsproblem (Partition) von Jörg Winkler 17. Juli 2003 Inhaltsverzeichnis 1 GRUNDLEGENDES ZUM ERBSCHAFTSPROBLEM...3 1.1 PROBLEMVORSTELLUNG...
Algorithmen und Komplexität Thema: NP-vollständige Probleme Erbschaftsproblem (Partition) von Jörg Winkler 17. Juli 2003 Inhaltsverzeichnis 1 GRUNDLEGENDES ZUM ERBSCHAFTSPROBLEM...3 1.1 PROBLEMVORSTELLUNG...
Weitere NP-vollständige Probleme
 Weitere NP-vollständige Probleme Wir betrachten nun folgende Reduktionskette und weisen dadurch nach, daß alle diese Probleme NP-hart sind (sie sind auch in NP und damit NP-vollständig). SAT p 3-SAT p
Weitere NP-vollständige Probleme Wir betrachten nun folgende Reduktionskette und weisen dadurch nach, daß alle diese Probleme NP-hart sind (sie sind auch in NP und damit NP-vollständig). SAT p 3-SAT p
Das Rucksackproblem. Definition Sprache Rucksack. Satz
 Das Rucksackproblem Definition Sprache Rucksack Gegeben sind n Gegenstände mit Gewichten W = {w 1,...,w n } N und Profiten P = {p 1,...,p n } N. Seien ferner b, k N. RUCKSACK:= {(W, P, b, k) I [n] : i
Das Rucksackproblem Definition Sprache Rucksack Gegeben sind n Gegenstände mit Gewichten W = {w 1,...,w n } N und Profiten P = {p 1,...,p n } N. Seien ferner b, k N. RUCKSACK:= {(W, P, b, k) I [n] : i
Theorie der Informatik Übersicht. Theorie der Informatik SAT Graphenprobleme Routing-Probleme. 21.
 Theorie der Informatik 19. Mai 2014 21. einige NP-vollständige Probleme Theorie der Informatik 21. einige NP-vollständige Probleme 21.1 Übersicht 21.2 Malte Helmert Gabriele Röger 21.3 Graphenprobleme
Theorie der Informatik 19. Mai 2014 21. einige NP-vollständige Probleme Theorie der Informatik 21. einige NP-vollständige Probleme 21.1 Übersicht 21.2 Malte Helmert Gabriele Röger 21.3 Graphenprobleme
Statt Turingmaschinen anzugeben, genügt die Angabe eines C++ Programms oder die Angabe eines Pseudocodes.
 Turingmaschinen Wir haben Turingmaschinen eingeführt. Bis auf einen polynomiellen Anstieg der Rechenzeit haben Turingmaschinen die Rechenkraft von parallelen Supercomputern! Statt Turingmaschinen anzugeben,
Turingmaschinen Wir haben Turingmaschinen eingeführt. Bis auf einen polynomiellen Anstieg der Rechenzeit haben Turingmaschinen die Rechenkraft von parallelen Supercomputern! Statt Turingmaschinen anzugeben,
Grundlagen der Informatik Kapitel 20. Harald Krottmaier Sven Havemann
 Grundlagen der Informatik Kapitel 20 Harald Krottmaier Sven Havemann Agenda Klassen von Problemen Einige Probleme... Approximationsalgorithmen WS2007 2 Klassen P NP NP-vollständig WS2007 3 Klasse P praktisch
Grundlagen der Informatik Kapitel 20 Harald Krottmaier Sven Havemann Agenda Klassen von Problemen Einige Probleme... Approximationsalgorithmen WS2007 2 Klassen P NP NP-vollständig WS2007 3 Klasse P praktisch
Arbeitsheft zur NP-Vollständigkeit
 Arbeitsheft zur NP-Vollständigkeit (BuK / WS 2017 / RWTH Aachen) Gerhard J. Woeginger Dieses Arbeitsheft enthält einige Übungsaufgaben zur NP-Vollständigkeit. Jede Aufgabe besteht im Wesentlichen aus einem
Arbeitsheft zur NP-Vollständigkeit (BuK / WS 2017 / RWTH Aachen) Gerhard J. Woeginger Dieses Arbeitsheft enthält einige Übungsaufgaben zur NP-Vollständigkeit. Jede Aufgabe besteht im Wesentlichen aus einem
Berechenbarkeitstheorie 24. Vorlesung
 1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creatie Commons Attribution-NonCommercial 3.0 Unported Lizenz. DHC Eingabe:
1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creatie Commons Attribution-NonCommercial 3.0 Unported Lizenz. DHC Eingabe:
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Komplexitätstheorie Nico Döttling 8. Januar 2010 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in
Übung Theoretische Grundlagen Komplexitätstheorie Nico Döttling 8. Januar 2010 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in
Kurt Mehlhorn und Adrian Neumann Max Planck Institute for Informatics and Saarland University 1. Dezember 2013
 P versus NP Kurt Mehlhorn und Adrian Neumann Max Planck Institute for Informatics and Saarland University 1. Dezember 2013 Gliederung Informelle Formulierung des P = NP Problems Das Erfüllbarkeitsproblem
P versus NP Kurt Mehlhorn und Adrian Neumann Max Planck Institute for Informatics and Saarland University 1. Dezember 2013 Gliederung Informelle Formulierung des P = NP Problems Das Erfüllbarkeitsproblem
Das P=NP-Problem. Besitzen (Entscheidungs-)Probleme mit einer Nichtdeterministischen. deterministische Polynomielle Lösung?
 Das P=NP-Problem Besitzen (Entscheidungs-)Probleme mit einer Nichtdeterministischen Polynimiellen Lösung immer auch eine deterministische Polynomielle Lösung? Eines der bekanntesten offenen Probleme der
Das P=NP-Problem Besitzen (Entscheidungs-)Probleme mit einer Nichtdeterministischen Polynimiellen Lösung immer auch eine deterministische Polynomielle Lösung? Eines der bekanntesten offenen Probleme der
Das Rucksackproblem: schwache NP-Härte und Approximation
 Das Rucksackproblem: schwache NP-Härte und Approximation Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1. Februar 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Das Rucksackproblem: schwache NP-Härte und Approximation Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1. Februar 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Einführung (1/3) Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (1) Vorlesungen zur Komplexitätstheorie.
 Einführung (1/3) 3 Wir verfolgen nun das Ziel, Komplexitätsklassen mit Hilfe von charakteristischen Problemen zu beschreiben und zu strukturieren Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit
Einführung (1/3) 3 Wir verfolgen nun das Ziel, Komplexitätsklassen mit Hilfe von charakteristischen Problemen zu beschreiben und zu strukturieren Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Komplexitätstheorie (VI) 20.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 DTIME und NTIME / DSPACE und NSPACE DTIME(T(n)) ist die Klasse
Grundlagen der Theoretischen Informatik Komplexitätstheorie (VI) 20.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 DTIME und NTIME / DSPACE und NSPACE DTIME(T(n)) ist die Klasse
Theoretische Informatik. Exkurs: Komplexität von Optimierungsproblemen. Optimierungsprobleme. Optimierungsprobleme. Exkurs Optimierungsprobleme
 Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Einführung in Algorithmen und Komplexität
 Einführung in Algorithmen und Komplexität SS2004 w u v High Performance = Innovative Computer Systems + Efficient Algorithms Friedhelm Meyer auf der Heide 1 Was haben wir bisher gemacht? - Rechenmodell:
Einführung in Algorithmen und Komplexität SS2004 w u v High Performance = Innovative Computer Systems + Efficient Algorithms Friedhelm Meyer auf der Heide 1 Was haben wir bisher gemacht? - Rechenmodell:
Vorname Name Matrikelnummer 1. a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte)
 1 Aufgabe 1 (19 Punkte) a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte) Q, die endliche Zustandsmenge b) Was besagt die Church-Turing-These? (1 Punkt)
1 Aufgabe 1 (19 Punkte) a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte) Q, die endliche Zustandsmenge b) Was besagt die Church-Turing-These? (1 Punkt)
Lösungen zur 1. Klausur. Einführung in Berechenbarkeit, formale Sprachen und Komplexitätstheorie
 Hochschuldozent Dr. Christian Schindelhauer Paderborn, den 21. 2. 2006 Lösungen zur 1. Klausur in Einführung in Berechenbarkeit, formale Sprachen und Komplexitätstheorie Name :................................
Hochschuldozent Dr. Christian Schindelhauer Paderborn, den 21. 2. 2006 Lösungen zur 1. Klausur in Einführung in Berechenbarkeit, formale Sprachen und Komplexitätstheorie Name :................................
Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage. Ideen der Informatik Kurt Mehlhorn
 Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage Ideen der Informatik Kurt Mehlhorn Gliederung Ziele von Theorie Gibt es Probleme, die man prinzipiell nicht mit einem Rechner lösen kann?
Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage Ideen der Informatik Kurt Mehlhorn Gliederung Ziele von Theorie Gibt es Probleme, die man prinzipiell nicht mit einem Rechner lösen kann?
Komplexitätstheorie NP-Vollständigkeit: Reduktionen (2) Der Satz von Cook/Levin
 Komplexitätstheorie NP-Vollständigkeit: Reduktionen (2) Der Satz von Cook/Levin Helmut Veith Technische Universität München Organisatorisches Anmeldung zur Lehrveranstaltung: complexity@tiki.informatik.tu-muenchen.de
Komplexitätstheorie NP-Vollständigkeit: Reduktionen (2) Der Satz von Cook/Levin Helmut Veith Technische Universität München Organisatorisches Anmeldung zur Lehrveranstaltung: complexity@tiki.informatik.tu-muenchen.de
Approximationsalgorithmen für NP-harte Optimierungsprobleme
 Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 18 Was tun mit NP-harten Problemen? Viele praxisrelevante
Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 18 Was tun mit NP-harten Problemen? Viele praxisrelevante
Lösungen zur Vorlesung Berechenbarkeit und Komplexität
 Lehrstuhl für Informatik 1 WS 009/10 Prof. Dr. Berthold Vöcking 0.0.010 Alexander Skopalik Thomas Kesselheim Lösungen zur Vorlesung Berechenbarkeit und Komplexität. Zulassungsklausur Aufgabe 1: (a) Worin
Lehrstuhl für Informatik 1 WS 009/10 Prof. Dr. Berthold Vöcking 0.0.010 Alexander Skopalik Thomas Kesselheim Lösungen zur Vorlesung Berechenbarkeit und Komplexität. Zulassungsklausur Aufgabe 1: (a) Worin
14. Die polynomiell beschränkten Komplexitätsklassen. Die Grenzen der tatsächlichen Berechenbarkeit
 14. Die polynomiell beschränkten Komplexitätsklassen Die Grenzen der tatsächlichen Berechenbarkeit PRINZIPIELLE VS. TATSÄCHLICHE BERECHENBARKEIT Prinzipielle (theoretische) Berechenbarkeit: Eine Funktion
14. Die polynomiell beschränkten Komplexitätsklassen Die Grenzen der tatsächlichen Berechenbarkeit PRINZIPIELLE VS. TATSÄCHLICHE BERECHENBARKEIT Prinzipielle (theoretische) Berechenbarkeit: Eine Funktion
Wie komme ich von hier zum Hauptbahnhof?
 NP-Vollständigkeit Wie komme ich von hier zum Hauptbahnhof? P Wie komme ich von hier zum Hauptbahnhof? kann ich verwende für reduzieren auf Finde jemand, der den Weg kennt! Alternativ: Finde eine Stadtkarte!
NP-Vollständigkeit Wie komme ich von hier zum Hauptbahnhof? P Wie komme ich von hier zum Hauptbahnhof? kann ich verwende für reduzieren auf Finde jemand, der den Weg kennt! Alternativ: Finde eine Stadtkarte!
Approximationsalgorithmen für NP-harte Optimierungsprobleme
 Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 4. Januar 2011 Berthold Vöcking, Informatik 1 () Vorlesung
Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 4. Januar 2011 Berthold Vöcking, Informatik 1 () Vorlesung
Wie man das Poissonsche Problem löst
 Komplexitätstheorie 27.10.2004 Theorem 6 : Falls P = NP ist, dann ist auch E = NE. Padding : Technik zum übertragen von Kollapsresultaten nach oben Sei # є Σ ein neues Symbol. Für w є Σ* ist pad (w) :
Komplexitätstheorie 27.10.2004 Theorem 6 : Falls P = NP ist, dann ist auch E = NE. Padding : Technik zum übertragen von Kollapsresultaten nach oben Sei # є Σ ein neues Symbol. Für w є Σ* ist pad (w) :
Formale Grundlagen der Informatik 1 Kapitel 23 NP-Vollständigkeit (Teil 2)
 Formale Grundlagen der Informatik 1 Kapitel 23 (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Juli 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/37 Die Klassen P und NP P := {L
Formale Grundlagen der Informatik 1 Kapitel 23 (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Juli 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/37 Die Klassen P und NP P := {L
NP-Vollständigkeit und der Satz von Cook und Levin
 NP-Vollständigkeit und der Satz von Cook und Levin Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 17. Dezember 2010 Berthold Vöcking, Informatik 1 () Vorlesung
NP-Vollständigkeit und der Satz von Cook und Levin Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 17. Dezember 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Übungsblatt 4. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 4 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 6. Dezember 2017 Abgabe 19. Dezember 2017, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 4 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 6. Dezember 2017 Abgabe 19. Dezember 2017, 11:00 Uhr
Komplexitätstheorie P versus NP
 Komplexitätstheorie P versus NP Kurt Mehlhorn und Adrian Neumann Max Planck Institute for Informatics and Saarland University 6. Januar 2014 Gliederung Komplexitätstheorie und die Komplexitätslandschaft
Komplexitätstheorie P versus NP Kurt Mehlhorn und Adrian Neumann Max Planck Institute for Informatics and Saarland University 6. Januar 2014 Gliederung Komplexitätstheorie und die Komplexitätslandschaft
Formale Grundlagen der Informatik 1 Kapitel 21 P und NP
 Formale Grundlagen der Informatik 1 Kapitel 21 Frank Heitmann heitmann@informatik.uni-hamburg.de 28. Juni Frank Heitmann heitmann@informatik.uni-hamburg.de 1/41 Die Klassen Probleme in P := {L es gibt
Formale Grundlagen der Informatik 1 Kapitel 21 Frank Heitmann heitmann@informatik.uni-hamburg.de 28. Juni Frank Heitmann heitmann@informatik.uni-hamburg.de 1/41 Die Klassen Probleme in P := {L es gibt
Einführung Erfüllbarkeitsproblem NP-Vollständigkeit Definition von NP Was wäre, wenn Was tun? Ideen und Konzepte der Informatik.
 Ideen und Konzepte der Informatik P versus NP Die Grenzen der (effizienter) Berechnung? Antonios Antoniadis Basiert auf Folien von Kurt Mehlhorn 8. Jan. 2018 8. Jan. 2018 1/24 Gliederung Ziele von Theorie/Grundlagenforschung
Ideen und Konzepte der Informatik P versus NP Die Grenzen der (effizienter) Berechnung? Antonios Antoniadis Basiert auf Folien von Kurt Mehlhorn 8. Jan. 2018 8. Jan. 2018 1/24 Gliederung Ziele von Theorie/Grundlagenforschung
Komplexitätstheorie WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Knoten-Partitionierung in feste Eigenschaften ist NP-schwer
 Knoten-Partitionierung in feste Eigenschaften ist NP-schwer Seminar: Ausgewählte Kapitel der Informatik bei Prof. Dr. R. Schrader Seminarvortrag von Nils Rosjat Wintersemester 09 / 10 1 Einleitung Dieser
Knoten-Partitionierung in feste Eigenschaften ist NP-schwer Seminar: Ausgewählte Kapitel der Informatik bei Prof. Dr. R. Schrader Seminarvortrag von Nils Rosjat Wintersemester 09 / 10 1 Einleitung Dieser
Übungsblatt 4. Vorlesung Theoretische Grundlagen der Informatik im WS 18/19
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 4 Vorlesung Theoretische Grundlagen der Informatik im WS 18/19 Ausgabe 4. Dezember 2018 Abgabe 18. Dezember 2018, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 4 Vorlesung Theoretische Grundlagen der Informatik im WS 18/19 Ausgabe 4. Dezember 2018 Abgabe 18. Dezember 2018, 11:00 Uhr
durch Einfügen von Knoten konstruiert werden kann.
 Satz von Kuratowski Definition Unterteilung eines Graphen Sei G = (V, E) und e = {u, v} E. 1 Das Einfügen eines neuen Knoten w in die Kante e führt zum Graphen G = (V {w}, E \ e {{u, w}, {w, v}}). 2 Der
Satz von Kuratowski Definition Unterteilung eines Graphen Sei G = (V, E) und e = {u, v} E. 1 Das Einfügen eines neuen Knoten w in die Kante e führt zum Graphen G = (V {w}, E \ e {{u, w}, {w, v}}). 2 Der
Konjunktive Normalform
 Konjunktive Normalform Eine Formel α in konjunktiver Normalform hat die Form α k 1 k 2... k r. Die Klauseln k 1,..., k r sind Disjunktionen von Literalen, also Disjunktionen von Variablen oder negierten
Konjunktive Normalform Eine Formel α in konjunktiver Normalform hat die Form α k 1 k 2... k r. Die Klauseln k 1,..., k r sind Disjunktionen von Literalen, also Disjunktionen von Variablen oder negierten
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 4 Komplexitätstheorie Zeitkomplexität 3 Definition: Sei
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 4 Komplexitätstheorie Zeitkomplexität 3 Definition: Sei
Einführung in die Informatik 2
 Einführung in die Informatik 2 NP-Vollständigkeit Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz http://www.inf.uni-konstanz.de/algo/lehre/ss08/info2 Sommersemester 2008 Sven
Einführung in die Informatik 2 NP-Vollständigkeit Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz http://www.inf.uni-konstanz.de/algo/lehre/ss08/info2 Sommersemester 2008 Sven
Theoretische Informatik II
 Theoretische Informatik II Einheit 5.2 Das P N P Problem 1. Nichtdeterministische Lösbarkeit 2. Sind N P-Probleme handhabbar? 3. N P-Vollständigkeit Bei vielen schweren Problemen ist Erfolg leicht zu testen
Theoretische Informatik II Einheit 5.2 Das P N P Problem 1. Nichtdeterministische Lösbarkeit 2. Sind N P-Probleme handhabbar? 3. N P-Vollständigkeit Bei vielen schweren Problemen ist Erfolg leicht zu testen
3-Färbbarkeit. Korollar: Zu Entscheiden, ob ein Graph k-färbbar ist mit k 3, ist NP-vollständig.
 3-Färbbarkeit Wir wissen bereits, dass in polynomieller Zeit entschieden werden kann, ob ein Graph 2-färbbar ist. Satz: Zu Entscheiden, ob ein Graph 3-färbbar ist, ist NPvollständig. Beweis: Reduktion
3-Färbbarkeit Wir wissen bereits, dass in polynomieller Zeit entschieden werden kann, ob ein Graph 2-färbbar ist. Satz: Zu Entscheiden, ob ein Graph 3-färbbar ist, ist NPvollständig. Beweis: Reduktion
Einführung in die Informatik 2
 Einführung in die Informatik 2 NP-Vollständigkeit Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr, o.n.v.
Einführung in die Informatik 2 NP-Vollständigkeit Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr, o.n.v.
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V17, 10.12.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick:
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V17, 10.12.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick:
Wissenschaftliche Arbeitstechniken und Präsentation. NP-Vollständigkeit
 Wissenschaftliche Arbeitstechniken und Präsentation Dominik Fakner, Richard Hentschel, Hamid Tabibian, den 20.01.2012 Inhalt Definitionen Definition Nachweis Beispiel Reduktion Komplexitätsklasse Befasst
Wissenschaftliche Arbeitstechniken und Präsentation Dominik Fakner, Richard Hentschel, Hamid Tabibian, den 20.01.2012 Inhalt Definitionen Definition Nachweis Beispiel Reduktion Komplexitätsklasse Befasst
THEORETISCHE INFORMATIK UND LOGIK
 THEORETISCHE INFORMATIK UND LOGIK 9. Vorlesung: NP und NP-Vollständigkeit Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 10. Mai 2017 Rückblick PTime und LogSpace als mathematische Modelle
THEORETISCHE INFORMATIK UND LOGIK 9. Vorlesung: NP und NP-Vollständigkeit Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 10. Mai 2017 Rückblick PTime und LogSpace als mathematische Modelle
Vorlesung Theoretische Informatik (Info III)
 1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 6. Dezember 2007 Einleitung Motivation 2 Thema heute N P-Vollständigkeit weitere Reduktionen Einleitung
1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 6. Dezember 2007 Einleitung Motivation 2 Thema heute N P-Vollständigkeit weitere Reduktionen Einleitung
Rucksackproblem und Verifizierbarkeit
 Rucksackproblem und Verifizierbarkeit Gegeben: n Gegenstände mit Gewichten G={g 1,g 2,,g n } und Werten W={w 1,w 2,,w n } sowie zulässiges Gesamtgewicht g. Gesucht: Teilmenge S {1,,n} mit i i S unter der
Rucksackproblem und Verifizierbarkeit Gegeben: n Gegenstände mit Gewichten G={g 1,g 2,,g n } und Werten W={w 1,w 2,,w n } sowie zulässiges Gesamtgewicht g. Gesucht: Teilmenge S {1,,n} mit i i S unter der
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V5, 21.11.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V5, 21.11.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am..03 Randomisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Algorithmen II Vorlesung am..03 Randomisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Komplexitätstheorie WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Gliederung. 1. Einführung. 2. Polynominal Reduktion und NP-Vollständigkeit. 3. Geschichte. 4. Reale Probleme und Lösungsansetze 5.
 Gliederung 1. Einführung 1. Definitionen P, NP, conp, EXP, NEXP 2. Bekannte Zusammenhänge zwischen dem Klassen 3. Hypothesen zu deren zusammenhängen und deren Konsequenzen 2. Polynominal Reduktion und
Gliederung 1. Einführung 1. Definitionen P, NP, conp, EXP, NEXP 2. Bekannte Zusammenhänge zwischen dem Klassen 3. Hypothesen zu deren zusammenhängen und deren Konsequenzen 2. Polynominal Reduktion und
Einige Grundlagen der Komplexitätstheorie
 Deterministische Polynomialzeit Einige Grundlagen der Komplexitätstheorie Ziel: NP-Vollständigkeit als ressourcenbeschränktes Analagon zur RE-Vollständigkeit. Komplexitätstheorie untersucht den Ressourcenbedarf
Deterministische Polynomialzeit Einige Grundlagen der Komplexitätstheorie Ziel: NP-Vollständigkeit als ressourcenbeschränktes Analagon zur RE-Vollständigkeit. Komplexitätstheorie untersucht den Ressourcenbedarf
Theoretische Informatik SS 03 Übung 11
 Theoretische Informatik SS 03 Übung 11 Aufgabe 1 Zeigen Sie, dass es eine einfachere Reduktion (als die in der Vorlesung durchgeführte) von SAT auf 3KNF-SAT gibt, wenn man annimmt, dass die Formel des
Theoretische Informatik SS 03 Übung 11 Aufgabe 1 Zeigen Sie, dass es eine einfachere Reduktion (als die in der Vorlesung durchgeführte) von SAT auf 3KNF-SAT gibt, wenn man annimmt, dass die Formel des
Lösungen zur Ergänzung 12
 Theoretische Informati II SS 018 Carlos Camino Lösungen zur Ergänzung 1 Hinweise: In der Literatur sind zwei verschiedene Definitionen der natürlichen Zahlen gängig: N = {0, 1,,...} und N = {1,, 3,...}.
Theoretische Informati II SS 018 Carlos Camino Lösungen zur Ergänzung 1 Hinweise: In der Literatur sind zwei verschiedene Definitionen der natürlichen Zahlen gängig: N = {0, 1,,...} und N = {1,, 3,...}.
Kapitel L:II. II. Aussagenlogik
 Kapitel L:II II. Aussagenlogik Syntax der Aussagenlogik Semantik der Aussagenlogik Eigenschaften des Folgerungsbegriffs Äquivalenz Formeltransformation Normalformen Bedeutung der Folgerung Erfüllbarkeitsalgorithmen
Kapitel L:II II. Aussagenlogik Syntax der Aussagenlogik Semantik der Aussagenlogik Eigenschaften des Folgerungsbegriffs Äquivalenz Formeltransformation Normalformen Bedeutung der Folgerung Erfüllbarkeitsalgorithmen
Randomisierte Algorithmen Algorithmen, die Zufallsbits benutzen können. Fehlerfreie Algorithmen (Las-Vegas-Alg)
 Wiederholung Randomisierte Algorithmen Algorithmen, die Zufallsbits benutzen können. Fehlerfreie Algorithmen (Las-Vegas-Alg) Komplexitätsklassen: EP=ZPP Algorithmen mit Fehlern (Monte-Carlo-Alg) Zweiseitiger
Wiederholung Randomisierte Algorithmen Algorithmen, die Zufallsbits benutzen können. Fehlerfreie Algorithmen (Las-Vegas-Alg) Komplexitätsklassen: EP=ZPP Algorithmen mit Fehlern (Monte-Carlo-Alg) Zweiseitiger
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V11, 16.1.2012 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V11, 16.1.2012 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Komplexitätsklasse P. Manchmal wird mit P auch nur die Menge der Entscheidungsprobleme mit Polynomialzeitalgorithmen bezeichnet.
 Komplexitätsklasse P Definition K3.1.1: Ein Problem L gehört zur Komplexitätsklasse P, wenn es einen deterministischen Algorithmus mit polynomieller Rechenzeit für L gibt. Manchmal wird mit P auch nur
Komplexitätsklasse P Definition K3.1.1: Ein Problem L gehört zur Komplexitätsklasse P, wenn es einen deterministischen Algorithmus mit polynomieller Rechenzeit für L gibt. Manchmal wird mit P auch nur
Zeitkomplexität (1) Proseminar Theoretische Informatik. Proseminar Theoretische Informatik: Lisa Dohrmann 1
 Zeitkomplexität (1) Proseminar Theoretische Informatik Proseminar Theoretische Informatik: Lisa Dohrmann 1 Warum Komplexitätsbetrachtung? Ein im Prinzip entscheidbares und berechenbares Problem kann in
Zeitkomplexität (1) Proseminar Theoretische Informatik Proseminar Theoretische Informatik: Lisa Dohrmann 1 Warum Komplexitätsbetrachtung? Ein im Prinzip entscheidbares und berechenbares Problem kann in
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 15. DIE POLYNOMIELL BESCHRÄNKTEN KOMPLEXITÄTSKLASSEN Theoretische Informatik (SoSe 2011) 15. Polynomiell beschränkte
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 15. DIE POLYNOMIELL BESCHRÄNKTEN KOMPLEXITÄTSKLASSEN Theoretische Informatik (SoSe 2011) 15. Polynomiell beschränkte
Algorithmische Spieltheorie
 Algorithmische Spieltheorie Grundlagen der Komplexitätstheorie Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00
Algorithmische Spieltheorie Grundlagen der Komplexitätstheorie Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00
VL-18: Jenseits von P und NP. (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger
 VL-18: Jenseits von P und NP (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-18: Jenseits von P und NP 1/43 Organisatorisches Nächste (letzte) Vorlesung: Mittwoch,
VL-18: Jenseits von P und NP (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-18: Jenseits von P und NP 1/43 Organisatorisches Nächste (letzte) Vorlesung: Mittwoch,
Die Klassen P und NP. Formale Grundlagen der Informatik 1 Kapitel 11. Die Klassen P und NP. Die Klasse P
 Die Klassen Formale Grundlagen der Informatik 1 Kapitel 11 Frank Heitmann heitmann@informatik.uni-hamburg.de P := {L es gibt ein Polynom p und eine p(n)-zeitbeschränkte DTM A mit L(A) = L} = i 1 DTIME(n
Die Klassen Formale Grundlagen der Informatik 1 Kapitel 11 Frank Heitmann heitmann@informatik.uni-hamburg.de P := {L es gibt ein Polynom p und eine p(n)-zeitbeschränkte DTM A mit L(A) = L} = i 1 DTIME(n
Sudoku ist NP-vollständig
 Sudoku ist NP-vollständig Seminar über Algorithmen und Komplexität Freie Universität Berlin Institut für Informatik SS 007 Sarah Will 8.07.007 Einführung Sudoku ist ein japanisches Logikrätsel und hat
Sudoku ist NP-vollständig Seminar über Algorithmen und Komplexität Freie Universität Berlin Institut für Informatik SS 007 Sarah Will 8.07.007 Einführung Sudoku ist ein japanisches Logikrätsel und hat
Registermaschine. c(1) c(2) c(3) c(4) Speicher. Programm
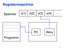 Registermaschine Speicher c(1) c(2) c(3) c(4) PC Akku Programm 1 Befehle einer Registermaschine LOAD i STORE i CLOAD i ILOAD i ISTORE i ADD i SUB i, MUL i, DIV i GOTO i IF (Akku? L) GOTO j END Lade c(i)
Registermaschine Speicher c(1) c(2) c(3) c(4) PC Akku Programm 1 Befehle einer Registermaschine LOAD i STORE i CLOAD i ILOAD i ISTORE i ADD i SUB i, MUL i, DIV i GOTO i IF (Akku? L) GOTO j END Lade c(i)
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V8, 12.12.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V8, 12.12.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Übungsblatt 5. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 5 Vorlesung Theoretische Grundlagen der Informatik im WS 16/17 Ausgabe 9. Dezember 2016 Abgabe 20. Dezember 2016, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 5 Vorlesung Theoretische Grundlagen der Informatik im WS 16/17 Ausgabe 9. Dezember 2016 Abgabe 20. Dezember 2016, 11:00 Uhr
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/03 Institut für Informatik Aufgabenblatt 6 Prof. Dr. J. Csirik 18. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am
Technische Universität München WS 00/03 Institut für Informatik Aufgabenblatt 6 Prof. Dr. J. Csirik 18. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am
Das große O. Aufwandsklasse O(g) für g : N R + enthält alle Funktionen f : N R + mit. f(n) c g(n) für alle n n 0
 1 Das große O Aufwandsklasse O(g) für g : N R + enthält alle Funktionen f : N R + mit f(n) c g(n) für alle n n 0 c, n 0 : konstant und größer als 0 O(g) beschreibt alle Probleme, die eine algorithmische
1 Das große O Aufwandsklasse O(g) für g : N R + enthält alle Funktionen f : N R + mit f(n) c g(n) für alle n n 0 c, n 0 : konstant und größer als 0 O(g) beschreibt alle Probleme, die eine algorithmische
Komplexität von Algorithmen Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekte mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekte mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Komplexitätstheorie. Kapitel 3: P vs NP
 Komplexitätstheorie Kapitel 3: P vs NP Einleitung Wir definieren die wichtigen Komplexitätsklassen P und NP und studieren deren Zusammenhang: Definitionen der Klassen Zusammenhang zwischen NP und Nichtdeterminismus
Komplexitätstheorie Kapitel 3: P vs NP Einleitung Wir definieren die wichtigen Komplexitätsklassen P und NP und studieren deren Zusammenhang: Definitionen der Klassen Zusammenhang zwischen NP und Nichtdeterminismus
