Numerische Integration
|
|
|
- Linda Heintze
- vor 7 Jahren
- Abrufe
Transkript
1 Numerische Integration Nikola Isenhardt Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 00/09, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: Mein Referat beschäftigt sich mit dem Thema der numerischen Integration. Wie der Name schon andeutet, ist dies ein Teilgebiet der numerischen Mathematik und bedeutet wörtlich übersetzt: Zahlenmäÿige Wiederherstellung eines Ganzen. Die Aufgabe der numerischen Integration ist es unter anderem, Integrale zu berechnen, welche mit den traditionellen Verfahren nicht berechnet werden können. Wir werden die vier grundlegenden Methoden kennenlernen, auf denen später komplexere Verfahren der numerischen Integration aufbauen: Die Rechteckmethode, die Trapezregel, die Tangentenregel und die Simpson-Regel. Nach Anwendung in einem Beispiel werden wir die Fehler unserer Berechnungsformen auch mathematisch abschätzen und durch die Vorstellung von ein paar ergänzenden Formeln zur Newton-Cotes-Formel gelangen, die die Struktur der Regeln aufgreift und in einer allgemeinen Form darstellt. Ein kleinerer Ausblick soll anschlieÿend die Gröÿe des Gebiets zeigen, welches mein Vortrag behandelt. Im Zeitalter der Computer und des Internets bekommen die hier vorgestellten Verfahren natürlich eine ganz andere Bedeutung. Wenn also vielleicht nach dem Lesen dieses Aufsatzes der Eindruck entsteht, dass die numerischen Methoden zur Berechnung eines Integrals sehr arbeitsaufwändig sind, ist es wichtig, sich vor Augen zu halten, dass es heutzutage durch Computer sehr viel einfacher ist, auf die Art und Weise, die hier beschrieben wird, Berechnungen durchzuführen. Gerade deshalb ist dieses Thema sehr aktuell. Abbildung 0.: Integral
2 Inhaltsverzeichnis Einleitung Quadraturformeln. Rechteckregel Trapezregel Tangentenregel Simpson-Regel Beispiel Fehlerabschätzung. Rechtecksregel Trapezregel Simpson-Regel Weitere Quadraturformeln 0 4. Newtonsche -tel-regel Milne-Regel Weddle-Regel Newton-Cotes-Formel 0 6 Ausblick 6. Gauÿformeln Rombergintegration Resümee Anhang Abbildungsverzeichnis 0. Integral Rechteckverfahren Trapezverfahren Simpson-Regel Tabellenverzeichnis Stützwerte und -punkte der Kurve f(x) = im Intervall [, ] x Zwischenwerte und -punkte des Intervalls [, ] der Kurve f(x) =.. 7 x Auistung der Newton-Cotes-Formeln für n=0,...,
3 Einleitung Oftmals stehen wir vor dem Problem, dass wir ein bestimmtes Integral b f(x)dx nicht a mit dem Hauptsatz der Dierential- und Integralrechnung auswerten können, da uns die Stammfunktion fehlt oder die betrachtete Kurve aus Messungen entstanden ist und wir somit keine explizite Funktion f(x) gegeben haben. Wir suchen also Verfahren zur Annäherung des Integrals, welche uns einen möglichst kleinen Fehler liefern. Quadraturformeln Diese Berechnungsformeln nennt man Quadraturformeln und werden im Folgenden vorgestellt. Hierbei geht man so vor: Zunächst teilen wir unseren Flächeninhalt in n Streifen der Länge h = b a. Die jeweiligen Werte dazu auf der x-achse nennen n wir Stützstellen x 0 = a, x = a + h,..., x n = b, die dazugehörigen Punkte auf der Funktion Stützpunkte f 0, f,..., f n. Es bleibt nun also, die Flächeninhalte der Streifen J ν = +h f(x)dx zu berechnen und diese aufzusummieren. So gelangen wir an unseren angenäherten Integralwert J.. Rechteckregel Die naheliegendste Methode, einen solchen Streifen anzunähern, ist das Rechteck mit Flächeninhalt hf ν zu betrachten. Diese Methode stammt unmittelbar von der Integraldenition (Obersumme und Untersumme). Es ist klar, dass bei einer steigenden Funktion der angenäherte Flächeninhalt kleiner als das Integral und bei einer fallenden Funktion gröÿer als das Integral ist. Abbildung.: Rechteckverfahren Der Flächeninhalt eines Rechtecks ist oensichtlich: J ν f ν h Und alle n Rechtecke aufsummiert ergeben: J h(f 0 + f f n )
4 . Trapezregel Eine etwas genauere Methode, den Streifenächeninhalt anzunähern, ist die Trapezregel. Man verbindet hierbei den ersten mit dem zweiten Stützpunkt unseres Streifen- Intervalls. Auch hier ist zu beachten, dass bei einer konvexen Kurve der berechnete Wert über dem Integralwert und bei einer konkaven Kurve unter dem Integralwert liegen wird. Abbildung.: Trapezverfahren Der Flächeninhalt eines Trapezes ist ebenfalls leicht zu berechnen. (Formel zur Berechnung des Flächeninhalts eines Trapezes: h(a + b), wobei a und b die Seitenlängen der parallelen Seiten sind): J ν h(f ν + f ν+ ) Wir summieren nun erneut alle n angenäherten Streifen auf und erhalten: J h(f + f f n ) + h (f 0 + f n ) (da bis auf f 0 und f n alle Werte zweimal vorkommen). Tangentenregel Noch exakter wird unsere Annäherung, wenn wir das Trapez nicht mit einer Geraden zwischen unseren Stützpunkten bilden, sondern die Tangente, die den Punkt durchläuft, der zum Stützwert + h gehört, als vierte Seite nehmen. Hier ist der Flächeninhalt bei konvexer Kurve zu klein und bei konkaver Kurve zu groÿ. Die Berechnung der Teilintegrale ist wieder sehr einfach: Und Aufsummieren liefert: J ν hf ν+ J h(f + f f n )
5 .4 Simpson-Regel Die nächste Idee, um den Fehler unserer Berechnung noch mehr zu verringern, ist mit einer Parabel, also einer Funktion zweiten Grades, unsere Funktion und danach durch Integration auch unseren Flächeninhalt anzunähern. Wie wir im Vortrag über Interpolation erfahren haben, hat Newton eine Formel zur Approximation einer Funktion mit drei Stützstellen, die sogenannte Interpolationsformel, erfunden. Der Astronom Johannes Kepler hat diese Formel nun verwendet, um ein Verfahren zur Berechnung eines Doppelstreifens herauszunden, die wiederrum Simpson dann zu einer Regel umfunktionierte, um einen beliebigen Flächeninhalt, solange er in eine gerade Anzahl von Streifen unterteilt war, zu berechnen. Hierbei ist nun n = m. Abbildung.: Simpson-Regel Die Newtonsche Interpolationsformel N(x) = y 0 + n k= k y 0 k!h k (x x 0)(x x )... (x x n ) mit den Stützstellen, + = + h und + = + h eingesetzt, ergibt: y = f ν }{{} T eil + (x ) f ν+ f ν h } {{ } T eil Und sieht integriert folgendermaÿen aus: +h ydx = hf }{{} ν + h(f ν+ f ν ) }{{} T eil + (x )(x h) f ν+ f ν+ + f ν } {{ h } T eil + T eil h h (f ν+ f ν+ + f ν ) } {{} T eil 5
6 = h(f ν + f ν+ f ν + 6 f ν+ f ν+ + 6 f ν) = h( 6 f ν + f ν+ + 6 f ν+) = 6 h(f ν + 4f ν+ + f ν+ ) = h (f ν + 4f ν+ + f ν+ ) = h (f ν + 4f ν+ + f ν+ ) (Die Integration der drei obigen Terme bendet sich als Nebenrechnung im Anhang.) Der berechnete Flächeninhalt ist also: J ν h (f ν + 4f ν+ + f ν+ ) Da wir nun wieder n = m dieser Intervallächeninhalte aufsummieren, müssen wir beachten, dass jeweils wieder der erste und letzte Stützpunkt nur einmal benötigt wird, die jeweils ungeraden Werte viermal und die restlichen zweimal. Die Simpson-Formel lautet folglich: J 4 h(f + f f m ) + h(f + f f m ) + h(f 0 + f m ) Nun wollen wir anhand eines Beispiels prüfen, welche Regel den kleinsten Fehler erzeugt:.5 Beispiel Wir wollen mit einem numerische Verfahren das Integral dx berechnen. Dafür teilen x wir das Integral in zehn gleichgroÿe Streifen der Länge h = und berechnen unseren Flächeninhalt mit der Trapez- und Tangentenformel, sowie anschlieÿend mit der 0 Simpson-Formel. Hierbei sind die Stützwerte und Stützpunkte gegeben durch: 6
7 x 0 =, 0 f 0 = x =, f = 0, x =, f = 0, x =, f = 0, 769 x 4 =, 4 f 4 = 0, 749 x 5 =, 5 f 5 = 0, x 6 =, 6 f 6 = 0, 65 x 7 =, 7 f 7 = 0, 54 x =, f = 0, x 9 =, 9 f 9 = 0, 56 x 0 =, 0 f 0 = 0, 5 Tabelle : Stützwerte und -punkte der Kurve f(x) = x im Intervall [, ] Die Trapezformel ergibt: dx 0, x Für die Tangentenregel benötigen auÿerdem wir die Stützwerte: x 0 + h =, 05 f = 0, 95 x + h =, 5 f = 0, 6957 x + h =, 5 f 5 = 0, x + h =, 5 f 7 = 0, x 4 + h =, 45 f 9 = 0, 6966 x 5 + h =, 55 f = 0, 6456 x 6 + h =, 65 f = 0, x 7 + h =, 75 f 5 = 0, 574 x + h =, 5 f 7 = 0, x 9 + h =, 95 f 9 = 0, 5 Tabelle : Zwischenwerte und -punkte des Intervalls [, ] der Kurve f(x) = x Eingesetzt in die Formel ergeben sie dies: dx 0, 694. x Die Simpson-Regel erzielt bei Verwendung der gleichen Anzahl von Stützstellen das genaueste Resultat mit: Tatsächlich ist dx 0, 695. x dx = log 0, 6947, der Fehler der Simpson-Regel ist also schon x bei Verwendung von 0 Stützwerten mit 0, deutlich geringer als die Fehler von Trapez- und Tangentenverfahren: 0, 0006 und 0,
8 Fehlerabschätzung Nun wollen wir den Fehler mathematisch bestimmen.. Rechtecksregel Der Fehler oder Rest eines Integralstreifens ist oensichtlich: R(h) = h 0 f(x)dx hf(0) Wenn man nun die Funktionen in ihrem Verlauf kennt, ist es recht einfach, den Fehler abzuschätzen. Sei also nun unsere Funktion f stetig dierenzierbar: R (h) = f(h) f(0) R (h) = f (h) Nun können wir eine obere Schranke M nden, die immer gröÿer als unser f (h) ist. Zum Beispiel M = sup f (t) mit t [0, h]. R (h) M R (h) M h R(h) M h Folglich ist eine Fehlerabschätzung bei der Rechteckregel: R(h) M h Der Fehler ist demnach noch ziemlich groÿ, da h eine zwei im Exponenten hat und somit nur verhältnismäÿig langsam kleiner werden kann.. Trapezregel Auch bei der Fehlerabschätzung der Trapezregel gehen wir ähnlich vor. Die Formel lautet: h 0 f(x)dx (f(0) + f(h))h Wir gehen diesmal davon aus, dass f zweimal stetig dierenzierbar ist, das heiÿt der Fehler ist: R(h) = h 0 f(x)dx (f(0) + f(h))h R (h) = f(h) f(0) ( (f (h)h + f(h)) = f(h) (f(0) + f(h)) h f (h) = f(h) f(0) h f (h) R (h) = f (h) (f (h) + hf (h)) = f (h) f (h) h f (h)) = h f (h)
9 Auch hier nden wir eine obere Schranke M, sodass diese immer gröÿer als unser f (h) ist. Sei also zum Beispiel M = sup f (t) mit t [0, h]. f (h) M R (h) = h f (h) hm R (h) 4 h M R(h) h M Die Fehlerabschätzung bei der Trapezregel lautet folglich: R(h) h M.. Simpson-Regel Als letztes betrachten wir den Fehler, der bei Anwendung der Simpson-Regel entsteht. Hier soll unsere Funktion f dreimal stetig dierenzierbar sein. Es gilt: R(h) = n n f(x)dx h (f( h) + 4f(0) + f(h)) R (h) = f(h) + f( h) (f( h) + h( f ( h)) 4f(0) (f(h) + hf (h)) = f(h) + f( h) f( h) + hf ( h) 4f(0) f(h) hf (h) = f(h) + f( h) h ( f ( h) + f (h)) 4 f(0) R (h) = f (h) f ( h) ( f ( h) + hf ( h)) (f (h) + hf (h)) = f (h) f ( h) h (f ( h) + f (h)) R (h) = f ( h) + f (h) (f ( h) hf ( h)) (f (h) + hf (h)) = f ( h) f ( h) h ( f ( h) + f (h)) = h ( f ( h) + f (h)) Sei hier nun analog M = sup f (t) mit t [ h, h] unsere obere Schranke. R (h) hm R (h) h M R (h) 9 h M R(h) 6 h4 M Die Abschätzung unseres Fehlers bei der Simpson-Regel ist demnach: R(h) 6 h4 M. Wenn man nun diese für ein Teilintervall abgeschätzten Fehler aufsummiert, gelangen wir an den gesuchten Fehler für unser Integral. Auÿerdem schreiben wir nun wieder für h = (b a) : n Fehler Rechteckregel : M h n = b am n Fehler Trapezregel : M h n = (b a) n M Fehler Tangentenregel : 4 M h n = (b a) 4n M Fehler Simpson-Regel : 6 M h 4 n = (b a)4 6n M Diese Übersicht der Fehlerabschätzungen zeigt uns, dass alle Fehler, sobald n 9
10 geht, im Unendlichen verschwinden. Jedoch wird auch klar, dass der Fehler der Simpson- Regel viel schneller klein wird, als beispielsweise der Fehler der Rechteckregel. Bei der Rechteckregel muss man, um den Fehler um eine Dezimalstelle zu verringern, n verzehnfachen. Bei der Simpson-Regel hingegen nimmt der Fehler proportional zu n ab, was zeigt, dass diese deutlich exakter ist. 4 Weitere Quadraturformeln Es gibt natürlich auÿer diesen vier vorgestellten Verfahren weitere Formeln, mit denen man den Flächeninhalt unseres Integrals annähern kann. 4. Newtonsche -tel-regel Newton zum Beispiel beschrieb eine Methode zur Berechnung von drei Integralstreifen. Da die Simpson-Regel ja nur im Fall n = m verwendet werden kann, ist diese sehr nützlich. 4. Milne-Regel 0 hf(x)dx h (f(0) + f(h) + f(h) + f(h)) Zur Berechnung von vier solcher Streifen hat Milne diese Formel aufgestellt: h 0 f(x)dx h Weddle-Regel ( 7f(0) + f ( ) h + f 4 ( ) h + f ( ) ) h + f(h) 4 Und im Fall n = 6, also sechs unserer Teilintervalle, gibt es folgende Formel: h f(x)dx h (f(0) + 6f ( ) ( h f h ) +7f ( ) ( h + 7f h ) ( + 6f 5h ) 6 + 4f(h)) 0 Wenn man die Formeln nebeneinander betrachtet, lässt sich eine gewisse Regelmäÿigkeit feststellen. Geht man nun davon aus, dass die Berechnung des Integrals unter der Verwendung von mehr Stützstellen die Verbesserung unseres Fehlers bringt, (wie bei der Simpson-Regel herausgefunden), so gelangt man zu der Newton-Cotes-Formel: 5 Newton-Cotes-Formel b a f(x)dx n j=0 g (n) j f(a + jh) Wir sehen, dass für n = 0,..., 6 diese Formel unter Verwendung bestimmter Koezienten gerade unsere Verfahren darstellt. 0
11 n Name Koezienten g j Fehlerabschätzung 0 Rechteckregel M h Trapezregel Simpson-Regel Newtonsche -tel-regel 4 Milne-Regel Weddle-Regel 4 40 M h 4 9 M 4 90 h M 4 0 h M h M h M h9 Tabelle : Auistung der Newton-Cotes-Formeln für n=0,...,6 Nun könnte man vermuten, dass der Fehler für immer gröÿer werdende n letztendlich verschwindet, jedoch treten dann negative Gewichte auf, und unsere Approximation mit der Newton-Cotes-Formel wird numerisch unbrauchbar, da durch die negativen Gewichte die Gefahr der Auslöschung von Gleitkommastellen besteht und die Verfahren damit instabil werden. 6 Ausblick Jetzt soll ein kleiner Ausblick auf weitere numerische Berechnungsverfahren gegeben werden, durch zwei hier kurz vorgestellte Methoden: 6. Gauÿformeln Bisher haben wir stets mit n Teilintegralen Polynome integriert, deren Grad höchstens n war. Mit den Gauÿformeln ist es möglich unter Verwendung von n + Stüztstellen Polynome bis zum Grad n + zu integrieren. b a f(x)w(x)dx n w j f(x j ) j=0 Hierbei ist w(x) die sogenannte Gewichtsfunktion, die im Intervall von a bis b stets positiv ist. Diese Formeln sind eine weitere Verbesserung bezogen auf den Wunsch, das optimale Verhältnis zwischen Aufwand und Fehler bei der numerischen Berechnung eines Integrals zu bekommen.
12 6. Rombergintegration Ein noch genaueres Verfahren, das ich auühren möchte, ist die Rombergintegration. Dabei macht man Folgendes: Man geht von der Trapezregel aus und berechnet das Trapez mit zwei Stützpunkten. Dann halbiert man h und hat zwei Trapeze, die man berechnet. Natürlich ist der Wert nun schon genauer. Anschlieÿend halbiert man h erneut. Durch Iteration dieses Verfahrens gelangt man an eine Folge von Werten, die graphisch gesehen eine Kurve darstellen. Man kann diese Werte nicht bis zuletzt ausrechnen, da irgendwann h zu klein wird. Wir können jedoch die Kurve weiter verfolgen und ohne explizite Berechnung der vorigen Werte an den gesuchten Wert gelangen. Dies nennt man Extrapolation. Eine genauere Darstellung des Rombergverfahrens und der Extrapolation würde den Rahmen dieses Aufsatzes jedoch sprengen. 7 Resümee Die Problematik, in welcher Form man an die numerische Berechnung von Integralen herangeht, beschäftigt Mathematiker immer wieder. Ob man in die Qualität oder die Quantität der Verfahren investieren soll, ist umstritten und es werden stets Ansätze für beide Schwerpunkte gesucht. Fest steht jedoch, die in diesem Aufsatz vorgestellten Methoden sind die Grundlegenden. Und wir kommen, genau wie wir nicht auf die numerische Integration verzichten können, nicht um die Verwendung dieser Verfahren herum, da es jede Menge von Funktionen gibt, deren Stammfunktion uns schlichtweg unbekannt sind. Abschlieÿend möchte ich noch anmerken, dass es für mich persönlich sehr aufschlussreich war, zu sehen, dass, so komplex auch die Arbeitsweise unserer Computer sein mag, doch hinter all dem vielen und schnellen Rechnen ein solides und verständliches Vorgehen steckt, welches man ohne Probleme (wie wir an unserem Beispiel gesehen haben) bis zu einem gewissen Punkt auch von Hand ausführen könnte. Literatur Courant, R.: Vorlesungen über Dierential- und Integralrechnung. Springer Verlag. (S.0-0) Kaballo, W.: Einführung in die Analysis, Bd.. Spektrum Akademischer Verlag. (S.45-5) (Stand: 05..0) (Stand: 05..0) Duden, Die deutsche Rechtschreibung. Bibliographisches Institut F. A. Brockhaus AG
13 Abbildungen: Abbildung 0.: Abbildung.: Abbildung.: Abbildung.: Tabellen: Anhang Tabelle : Courant, R.: Vorlesungen über Dierential- und Integralrechnung. Springer Verlag. (S. 05) Tabelle : Courant, R.: Vorlesungen über Dierential- und Integralrechnung. Springer Verlag. (S. 06) Tabelle : (S. 0) Integration des Terms y = f ν }{{} T eil + (x ) f ν+ f ν h } {{ } T eil + (x )(x h) f ν+ f ν+ + f ν } {{ h } T eil Teil : Teil : xν+ xν+ f ν dx = [f ν x] xν+h = f ν + f ν h f ν = f ν h (x ) f ν+ f ν dx = f ν+ f xν+ ν (x ) h h Betrachte nur den hinteren Teil: = xν+ (x ) [ ( ] xν+h x x) = (( ( + h) ( + h))) ( x ν) = ( + h + h x ν h ) ( ) = ( + h + ) = h
14 Teil : f ν+ f xν+ ν (x ) = h(f ν+ f ν ) h xν+h (x )(x h) = f ν+ f ν+ + f ν h Betrachte erneut nur den hinteren Teil: xν+h xν+h f ν+ f ν+ + f ν dx h (x )(x h)dx (x )(x h)dx = = xν+h (x x + x ν hx + h)dx [ x x + x νx x h + hx ] xν+h = ( + h) ( + h) + x ν( + h) ( + h) h + h( + h) x ν x ν + x ν h + x νh = ( + h)(x ν + 4 h + 4h ) (x ν + 4h + 4h ) + x ν + hx ν h( + 4 h + 4h ) +x νh + h ( x ν + h) = (x ν + hx ν + 4x νh + h + 4 h + h ) (x ν + 4hx ν + 4h ) + x ν + hx ν h h h + x νh + h x ν h = (x ν + 6hx ν + h + h ) hx ν 4h h x ν = h h f ν+ f ν+ + f ν h xν+h (x )(x h)dx = f ν+ f ν+ + f ν ( h h h ) = h (f ν+ f ν+ + f ν ) 4
15 Integriert sieht er also folgendermaÿen aus: +h + T eil ydx = hf }{{} ν + h(f ν+ f ν ) }{{} T eil h h (f ν+ f ν+ + f ν ) } {{} T eil 5
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KLAUSUR. Mathematik IV Wolfram Koepf. Name: Vorname: Matr. Nr.:
 KLAUSUR Mathematik IV 5. 3. 2007 Wolfram Koepf Name: Vorname: Matr. Nr.: Bitte lassen Sie genügend Platz zwischen den Aufgaben und beschreiben Sie nur die Vorderseite der Blätter! Zum Bestehen der Klausur
KLAUSUR Mathematik IV 5. 3. 2007 Wolfram Koepf Name: Vorname: Matr. Nr.: Bitte lassen Sie genügend Platz zwischen den Aufgaben und beschreiben Sie nur die Vorderseite der Blätter! Zum Bestehen der Klausur
Die Euler-Mascheroni-Konstante
 Die Euler-Mascheroni-Konstante Niloufar Rahi Ausarbeitung zum Vortrag in Überraschungen und Gegenbeispiele in der Analysis (Sommersemester 009, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: Wenn von der
Die Euler-Mascheroni-Konstante Niloufar Rahi Ausarbeitung zum Vortrag in Überraschungen und Gegenbeispiele in der Analysis (Sommersemester 009, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: Wenn von der
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
(x a) 3 + f (a) 4! x 4 4! Wir werden im Folgenden vor allem Maclaurin-Reihen betrachten, dies alles funktioniert aber auch. f (x) = sin x f (0) = 0
 Taylor-Reihen Einführung Mathematik GLF / 6 Christian Neukirchen Oft können wir bestimmte mathematische Funktionen nicht genau ausrechnen, besonders die trigonometrischen Funktionen wie, cos x, oder die
Taylor-Reihen Einführung Mathematik GLF / 6 Christian Neukirchen Oft können wir bestimmte mathematische Funktionen nicht genau ausrechnen, besonders die trigonometrischen Funktionen wie, cos x, oder die
Von mathematischer Modellierung und Computeralgebra - Die Lösung eines handfesten mathematischen Problems
 Von mathematischer Modellierung und Computeralgebra - Die Lösung eines handfesten mathematischen Problems Universität Paderborn Fakultät für Elektrotechnik, Informatik und Mathematik Institut für Mathematik
Von mathematischer Modellierung und Computeralgebra - Die Lösung eines handfesten mathematischen Problems Universität Paderborn Fakultät für Elektrotechnik, Informatik und Mathematik Institut für Mathematik
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Einführung in die Integralrechnung. Mag. Mone Denninger 13. November 2005
 Einführung in die Integralrechnung Mag. Mone Denninger. November 5 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis Einleitung Berechnung einfacher Stammfunktionen. Integrationsregeln.........................
Einführung in die Integralrechnung Mag. Mone Denninger. November 5 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis Einleitung Berechnung einfacher Stammfunktionen. Integrationsregeln.........................
Interpolation und Integration mit Polynomen
 Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
1/26. Integration. Numerische Mathematik 1 WS 2011/12
 1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
Kapitel 18 Numerisches Differenzieren und Integrieren
 Kapitel 8 Numerisches Differenzieren und Integrieren 8 8 8 Numerisches Differenzieren und Integrieren.......... 43 8. Numerische Differenziation... 43 8.. Differenzenformeln für die erste Ableitung...
Kapitel 8 Numerisches Differenzieren und Integrieren 8 8 8 Numerisches Differenzieren und Integrieren.......... 43 8. Numerische Differenziation... 43 8.. Differenzenformeln für die erste Ableitung...
Interpolation. Nadine Losert. Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 2008/09, Leitung PD Dr.
 Interpolation Nadine Losert Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 2008/09, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: Nachdem wir in den vorherigen Vorträgen verschiedene
Interpolation Nadine Losert Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 2008/09, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: Nachdem wir in den vorherigen Vorträgen verschiedene
Numerische Integration
 Numerische Integration Fakultät Grundlagen Januar 0 Fakultät Grundlagen Numerische Integration Übersicht Grundsätzliches Grundsätzliches Trapezregel Simpsonformel 3 Fakultät Grundlagen Numerische Integration
Numerische Integration Fakultät Grundlagen Januar 0 Fakultät Grundlagen Numerische Integration Übersicht Grundsätzliches Grundsätzliches Trapezregel Simpsonformel 3 Fakultät Grundlagen Numerische Integration
Numerische Integration
 Numerische Integration home/lehre/vl-mhs-1/folien/uebung/num_integration/cover_sheet_5a.tex Seite 1 von 12. p.1/12 Inhaltsverzeichnis 1. Einführung 2. Newton-Cotes Formeln Rechteckformel Trapezformel Simpsonsche
Numerische Integration home/lehre/vl-mhs-1/folien/uebung/num_integration/cover_sheet_5a.tex Seite 1 von 12. p.1/12 Inhaltsverzeichnis 1. Einführung 2. Newton-Cotes Formeln Rechteckformel Trapezformel Simpsonsche
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 21 Quadraturverfahren R. Steuding
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 21 Quadraturverfahren R. Steuding
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Übungen zu Splines Lösungen zu Übung 20
 Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 014 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 014 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Der Begriff des bestimmten Integrals
 Der Begriff des bestimmten Integrals Das ursprüngliche Problem, das zum Begriff des bestimmten Integrals führte, war ein geometrisches, die Bestimmung von Flächeninhalten. 1-E Archimedes von Syrakus Infinite
Der Begriff des bestimmten Integrals Das ursprüngliche Problem, das zum Begriff des bestimmten Integrals führte, war ein geometrisches, die Bestimmung von Flächeninhalten. 1-E Archimedes von Syrakus Infinite
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
2. Gauß-Integration. Prof. Dr. Wandinger 4. Scheibenelemente FEM 4.2-1
 Die analytische Integration der Steifigkeitsmatrix für das Rechteckelement ist recht mühsam. Für Polynome gibt es eine einfachere Methode zur Berechnung von Integralen, ohne dass die Stammfunktion benötigt
Die analytische Integration der Steifigkeitsmatrix für das Rechteckelement ist recht mühsam. Für Polynome gibt es eine einfachere Methode zur Berechnung von Integralen, ohne dass die Stammfunktion benötigt
Übungsblatt 4 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Einführung in die Integralrechnung
 Inhaltsverzeichnis 1. Das Problem der Flächenberechnung... 2 1.1 Problemstellung... 2 1.2 Abschätzung einer Fläche mit Vielecken... 3 1.3 Abschätzung einer Fläche mit einfachen Flächen... 4 1.4 Fläche
Inhaltsverzeichnis 1. Das Problem der Flächenberechnung... 2 1.1 Problemstellung... 2 1.2 Abschätzung einer Fläche mit Vielecken... 3 1.3 Abschätzung einer Fläche mit einfachen Flächen... 4 1.4 Fläche
Probe-Klausur 1 Mathematik f. Bau-Ing + Chem. Modul1
 Probe-Klausur 1 Mathematik f. Bau-Ing + Chem. Modul1 1. (a) Lösen Sie das lineare Gleichungssystem für die Werte a = 1, b = 2. x + 3y + 2z = 0 2x + ay + 3z = 1 3x + 4y + z = b (b) Für welche Werte von
Probe-Klausur 1 Mathematik f. Bau-Ing + Chem. Modul1 1. (a) Lösen Sie das lineare Gleichungssystem für die Werte a = 1, b = 2. x + 3y + 2z = 0 2x + ay + 3z = 1 3x + 4y + z = b (b) Für welche Werte von
$Id: integral.tex,v /05/12 16:36:04 hk Exp $ arctan x + + 4n n 2 2x + a. x 2 + ax + b Φ n 1. A n 1, Φ n (x) = xn 1 2n
 $Id: integral.te,v 1.9 9/5/1 16:36:4 hk Ep $ Integralrechnung.4 Integration rationaler Funktionen Am Ende der letzten Vorlesung hatten wir die Formel + a + b = 4n A n 1 n n arctan + + 4n 1 n 1 a + a +
$Id: integral.te,v 1.9 9/5/1 16:36:4 hk Ep $ Integralrechnung.4 Integration rationaler Funktionen Am Ende der letzten Vorlesung hatten wir die Formel + a + b = 4n A n 1 n n arctan + + 4n 1 n 1 a + a +
GMA. Grundlagen Mathematik und Analysis. Nullstellen und Fixpunkte Reelle Funktionen 3. Christian Cenker Gabriele Uchida
 GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
Analysis II. Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg
 Analysis II Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 2. Juni 2008 Beachtenswertes Die Veranstaltung ist eng angelehnt
Analysis II Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 2. Juni 2008 Beachtenswertes Die Veranstaltung ist eng angelehnt
Wendepunkte. Jutta Schlumberger
 Wendepunkte Jutta Schlumberger Ausarbeitung zum Vortrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemester 2009, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: In dieser Ausarbeitung
Wendepunkte Jutta Schlumberger Ausarbeitung zum Vortrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemester 2009, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: In dieser Ausarbeitung
[A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration
![[A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration [A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration](/thumbs/66/55829074.jpg) 1 Ableitung des Massenwirkungsgesetzes Mit dem Umfüllexperiment haben wir herausgefunden, dass die Stoffmengen oder die Stoffmengenkonzentrationen im Gleichgewicht auf einen Grenzwert zulaufen. Außerdem
1 Ableitung des Massenwirkungsgesetzes Mit dem Umfüllexperiment haben wir herausgefunden, dass die Stoffmengen oder die Stoffmengenkonzentrationen im Gleichgewicht auf einen Grenzwert zulaufen. Außerdem
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
19. Januar Universität Erlangen-Nürnberg Department Mathematik PD Dr. Markus Bause. . Danach liefert die Gauss-Elinination. .
 Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Polynominterpolation
 Polynominterpolation In der numerischen Mathematik versteht man unter Polynominterpolation die Suche nach einem Polynom, welches exakt durch vorgegebene Punkte (z. B. aus einer Messreihe) verläuft. Dieses
Polynominterpolation In der numerischen Mathematik versteht man unter Polynominterpolation die Suche nach einem Polynom, welches exakt durch vorgegebene Punkte (z. B. aus einer Messreihe) verläuft. Dieses
Polynome und ihre Nullstellen
 Polynome und ihre Nullstellen 29. Juli 2017 Inhaltsverzeichnis 1 Einleitung 2 2 Explizite Berechnung der Nullstellen 2.1 Polynome vom Grad 0............................. 2.2 Polynome vom Grad 1.............................
Polynome und ihre Nullstellen 29. Juli 2017 Inhaltsverzeichnis 1 Einleitung 2 2 Explizite Berechnung der Nullstellen 2.1 Polynome vom Grad 0............................. 2.2 Polynome vom Grad 1.............................
Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung. Lösungen zur Probeklausur 2.
 Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Heron-Verfahren. Inhaltsverzeichnis. Beispiel. aus Wikipedia, der freien Enzyklopädie
 1 of 7 28.05.2010 20:16 Heron-Verfahren aus Wikipedia, der freien Enzyklopädie Das Heron-Verfahren oder babylonische Wurzelziehen ist ein Rechenverfahren zur Berechnung einer Näherung der Quadratwurzel
1 of 7 28.05.2010 20:16 Heron-Verfahren aus Wikipedia, der freien Enzyklopädie Das Heron-Verfahren oder babylonische Wurzelziehen ist ein Rechenverfahren zur Berechnung einer Näherung der Quadratwurzel
Interpolation, numerische Integration
 Interpolation, numerische Integration 8. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 8. Mai 2014 Gliederung 1 Interpolation polynomial Spline 2 Numerische
Interpolation, numerische Integration 8. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 8. Mai 2014 Gliederung 1 Interpolation polynomial Spline 2 Numerische
Mehrdimensionale Integralrechnung 1
 Mehrdimensionale Integralrechnung Im - dimensionalen Fall wurde die Integralrechnung eingeführt, um Flächen unter Kurven zu berechnen. Eine ähnliche Fragestellung führt uns auf die mehrdimensionale Integralrechnung.
Mehrdimensionale Integralrechnung Im - dimensionalen Fall wurde die Integralrechnung eingeführt, um Flächen unter Kurven zu berechnen. Eine ähnliche Fragestellung führt uns auf die mehrdimensionale Integralrechnung.
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
(Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
Numerische Verfahren
 Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
ANALYSIS 2 VERSION 26. Juni 2018
 ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Oft können wir bestimmte mathematische Funktionen nicht genau
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Oft können wir bestimmte mathematische Funktionen nicht genau
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 20 Wiederholung: Fehlerbetrachtung.
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 20 Wiederholung: Fehlerbetrachtung.
Übungsblatt 1 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Klausur Numerische Methoden II Universität Siegen, Fachbereich Maschinenbau,
 Universität Siegen, Fachbereich Maschinenbau, 31.7.9 Name: Matrikelnummer: Aufgabe 1 (8 Punkte) Für die Abschätzung der Lebensdauer eines Wälzlagers wird die Bestimmungsgröße K gemäß der obenstehenden
Universität Siegen, Fachbereich Maschinenbau, 31.7.9 Name: Matrikelnummer: Aufgabe 1 (8 Punkte) Für die Abschätzung der Lebensdauer eines Wälzlagers wird die Bestimmungsgröße K gemäß der obenstehenden
Integral. Jörn Loviscach. Versionsstand: 5. Januar 2010, 16:36
 Integral Jörn Loviscach Versionsstand: 5. Januar 2010, 16:36 1 Idee des Integrals Gegeben eine Funktion f, die auf dem Intervall [a, b] definiert ist, soll das bestimmte Integral [definite integral] b
Integral Jörn Loviscach Versionsstand: 5. Januar 2010, 16:36 1 Idee des Integrals Gegeben eine Funktion f, die auf dem Intervall [a, b] definiert ist, soll das bestimmte Integral [definite integral] b
Die Bernoulli-Polynome
 Die Bernoulli-Polynome Lena Gerig Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 28/9, Leitung PD Dr. Gudrun Thäter) Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.
Die Bernoulli-Polynome Lena Gerig Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 28/9, Leitung PD Dr. Gudrun Thäter) Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.
Integrale. Mathematik Klasse 12. Fläche 1. Fläche 4. Fläche 2. Fläche 5 Fläche 3. Fläche 6. Ditmar Bachmann / Eurokolleg.
 Fläche 1 Fläche 4 Fläche 2 Fläche 5 Fläche 3 Fläche 6 aus Google maps Begriff des Integrals Die Wurzeln zur Integralrechnung reichen bis ins Altertum zurück. Damals ist man auf das Problem gestoßen, Flächen
Fläche 1 Fläche 4 Fläche 2 Fläche 5 Fläche 3 Fläche 6 aus Google maps Begriff des Integrals Die Wurzeln zur Integralrechnung reichen bis ins Altertum zurück. Damals ist man auf das Problem gestoßen, Flächen
Mehrfachintegrale 1-E1. Ma 2 Lubov Vassilevskaya
 Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Nachklausur zur Analysis 1, WiSe 2016/17
 BERGISCHE UNIVERSITÄT WUPPERTAL 04.04.7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis, WiSe 06/7 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 04.04.7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis, WiSe 06/7 Aufgabe
Analysis I Lösung von Serie 9
 FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Mathematik für Bauingenieure
 Mathematik für Bauingenieure von Kerstin Rjasanowa 1. Auflage Mathematik für Bauingenieure Rjasanowa schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 2006 Verlag C.H.
Mathematik für Bauingenieure von Kerstin Rjasanowa 1. Auflage Mathematik für Bauingenieure Rjasanowa schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 2006 Verlag C.H.
Didaktik der Mathematik der Sekundarstufe II
 Didaktik der Mathematik der Sekundarstufe II Teil 10: Integralrechnung Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur Vorlesung: http://www.mathematik.hu-berlin.de/
Didaktik der Mathematik der Sekundarstufe II Teil 10: Integralrechnung Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur Vorlesung: http://www.mathematik.hu-berlin.de/
Mathematik I Herbstsemester 2018 Kapitel 5: Integralrechnung
 Mathematik I Herbstsemester 208 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 70 5. Integralrechnung Grundbegriffe Das bestimmte Integral als Flächeninhalt Der Fundamentalsatz Partielle
Mathematik I Herbstsemester 208 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 70 5. Integralrechnung Grundbegriffe Das bestimmte Integral als Flächeninhalt Der Fundamentalsatz Partielle
Kapitel 8 Einführung der Integralrechnung über Flächenmaße
 8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
Didaktik der Mathematik der Sekundarstufe II
 Didaktik der Mathematik der Sekundarstufe II Teil 10: Integralrechnung Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur Vorlesung: http://www.mathematik.hu-berlin.de/
Didaktik der Mathematik der Sekundarstufe II Teil 10: Integralrechnung Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur Vorlesung: http://www.mathematik.hu-berlin.de/
Orthogonalpolynome Einführung, Eigenschaften und Anwendungen
 Anna Weller Orthogonalpolynome Einführung, Eigenschaften und Anwendungen 1 Orthogonalpolynome Einführung, Eigenschaften und Anwendungen Anna Weller Seminar zur Numerik im SS 2018, Universität zu Köln 10.
Anna Weller Orthogonalpolynome Einführung, Eigenschaften und Anwendungen 1 Orthogonalpolynome Einführung, Eigenschaften und Anwendungen Anna Weller Seminar zur Numerik im SS 2018, Universität zu Köln 10.
Übungsblatt 3 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA4 - SS6 Übungsblatt Musterlösung Sei M,N N und f C M+N+ (B) eine komplexe Funktion, B eine kompakte Menge. Die Padé Approximation PN M (f)(x) ist die rationale
Numerik gewöhnlicher Differentialgleichungen MA4 - SS6 Übungsblatt Musterlösung Sei M,N N und f C M+N+ (B) eine komplexe Funktion, B eine kompakte Menge. Die Padé Approximation PN M (f)(x) ist die rationale
Polynominterpolation. Allgemeines Problem: Beispiel 1 (Teil 1):
 . Großübung Polynominterpolation Allgemeines Problem: Aufgrund gegebener Messwerte (Paare aus Werten i und Funktionswerten f( i )) soll ein Funktionsverlauf rekonstruiert bzw. zumeist angenähert werden.
. Großübung Polynominterpolation Allgemeines Problem: Aufgrund gegebener Messwerte (Paare aus Werten i und Funktionswerten f( i )) soll ein Funktionsverlauf rekonstruiert bzw. zumeist angenähert werden.
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Flächenberechnung mittels Untersummen und Obersummen
 Flächenberechnung mittels Untersummen und Obersummen Ac Einstieg: Fläche unter einer Normalparabel mit f(x) = x 2 Wir approximieren durch Rechtecksflächen, wobei zunächst senkrecht zur x-achse 10 Streifen
Flächenberechnung mittels Untersummen und Obersummen Ac Einstieg: Fläche unter einer Normalparabel mit f(x) = x 2 Wir approximieren durch Rechtecksflächen, wobei zunächst senkrecht zur x-achse 10 Streifen
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Interpolation, numerische Integration, Eigenwerte
 Neunte Vorlesung, 29. Mai 2008, Inhalt Interpolation, numerische Integration, Eigenwerte Polynomiale Interpolation (Lagrange, Newton, Neville) Splines und weitere Interpolationsverfahren numerische Integration
Neunte Vorlesung, 29. Mai 2008, Inhalt Interpolation, numerische Integration, Eigenwerte Polynomiale Interpolation (Lagrange, Newton, Neville) Splines und weitere Interpolationsverfahren numerische Integration
Gemischte Aufgaben zur Differentialund Integralrechnung
 Gemischte Aufgaben zur Differentialund Integralrechnung W. Kippels 0. Mai 04 Inhaltsverzeichnis Aufgaben. Aufgabe.................................... Aufgabe.................................... Aufgabe...................................
Gemischte Aufgaben zur Differentialund Integralrechnung W. Kippels 0. Mai 04 Inhaltsverzeichnis Aufgaben. Aufgabe.................................... Aufgabe.................................... Aufgabe...................................
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Erste Schularbeit Mathematik Klasse 8D WIKU am
 Erste Schularbeit Mathematik Klasse 8D WIKU am 3.1.215 KORREKTUR UND KOMMENTAR Aufgabe 1. (2P) Parameter einer linearen Funktion bestimmen. Gegeben ist die Funktion f(x) = ax 4, wobei a R +. Bestimmen
Erste Schularbeit Mathematik Klasse 8D WIKU am 3.1.215 KORREKTUR UND KOMMENTAR Aufgabe 1. (2P) Parameter einer linearen Funktion bestimmen. Gegeben ist die Funktion f(x) = ax 4, wobei a R +. Bestimmen
Einführung des Integrals Stammfunktionen Hauptsatz Flächen Mittelwerte Rotationsvolumen
 14 Integralrechnung Einführung des Integrals Stammfunktionen Hauptsatz Flächen Mittelwerte Rotationsvolumen E-Mail: klaus_messner@web.de, Internet: www.elearning-freiburg.de Einführung des Integrals 15
14 Integralrechnung Einführung des Integrals Stammfunktionen Hauptsatz Flächen Mittelwerte Rotationsvolumen E-Mail: klaus_messner@web.de, Internet: www.elearning-freiburg.de Einführung des Integrals 15
$Id: integral.tex,v /05/05 13:36:42 hk Exp $
 $Id: integral.tex,v.5 07/05/05 3:36:4 hk Exp $ Integralrechnung.4 Integration rationaler Funktionen In diesem Abschnitt wollen wir die Integration rationaler Funktionen diskutieren. Es wird sich herausstellen
$Id: integral.tex,v.5 07/05/05 3:36:4 hk Exp $ Integralrechnung.4 Integration rationaler Funktionen In diesem Abschnitt wollen wir die Integration rationaler Funktionen diskutieren. Es wird sich herausstellen
Mathematik 1 für Bauingenieure
 Mathematik 1 für Bauingenieure Name (bitte ausfüllen): Prüfung am 3.3.2017 Reinhard Winkler Matrikelnummer (bitte ausfüllen): Wichtige Hinweise bevor Sie beginnen: Die Prüfung besteht aus vier Aufgaben
Mathematik 1 für Bauingenieure Name (bitte ausfüllen): Prüfung am 3.3.2017 Reinhard Winkler Matrikelnummer (bitte ausfüllen): Wichtige Hinweise bevor Sie beginnen: Die Prüfung besteht aus vier Aufgaben
$Id: integral.tex,v /05/05 14:57:29 hk Exp hk $ ln(1 + t) 2 = ln 2 ln 3 + ln 2 = ln
 $Id: integral.tex,v.5 2009/05/05 4:57:29 hk Exp hk $ 2 Integralrechnung 2.3 Die Integrationsregeln Wir wollen noch eine letzte kleine Anmerkung zur Substitutionsregel machen. Der letzte Schritt bei der
$Id: integral.tex,v.5 2009/05/05 4:57:29 hk Exp hk $ 2 Integralrechnung 2.3 Die Integrationsregeln Wir wollen noch eine letzte kleine Anmerkung zur Substitutionsregel machen. Der letzte Schritt bei der
Übungen zur Ingenieur-Mathematik II SS 2017 Blatt Aufgabe 13: Betrachten Sie die Funktion. f(x) =
 Übungen zur Ingenieur-Mathematik II SS 2017 Blatt 6 2.5.2017 Aufgabe 1: Betrachten Sie die Funktion Lösung: f(x) = 1, x [, 1]. 1 + 25x2 a) Bestimmen Sie die Interpolationspolynome vom Grad m p m (x) =
Übungen zur Ingenieur-Mathematik II SS 2017 Blatt 6 2.5.2017 Aufgabe 1: Betrachten Sie die Funktion Lösung: f(x) = 1, x [, 1]. 1 + 25x2 a) Bestimmen Sie die Interpolationspolynome vom Grad m p m (x) =
A Differenzialrechnung
 A Differenzialrechnung Seite 1 Stetigkeit und Differenzierbarkeit... 2 Nullstellensatz und Intervallhalbierung... Newton - Verfahren... 8 Funktionsverkettung... 1 5 Kettenregel... 11 Produktregel... 1
A Differenzialrechnung Seite 1 Stetigkeit und Differenzierbarkeit... 2 Nullstellensatz und Intervallhalbierung... Newton - Verfahren... 8 Funktionsverkettung... 1 5 Kettenregel... 11 Produktregel... 1
23 Integral. 1 Idee des Integrals
 23 Integral Jörn Loviscach Versionsstand: 21. September 2013, 15:56 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen beim Ansehen der Videos: http://www.j3l7h.de/videos.html This work is licensed
23 Integral Jörn Loviscach Versionsstand: 21. September 2013, 15:56 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen beim Ansehen der Videos: http://www.j3l7h.de/videos.html This work is licensed
Mathematik III für Physiker. Vorlesung
 Mathematik III für Physiker Wintersemester /3 Vorlesung..3 Satz 6 (iduensatz) Sei f holomorph in G := C \ {z,..., z N } und G ein geschlossener, stückweise stetig dierenzierbarer Weg. Dann gilt f(ξ)dξ
Mathematik III für Physiker Wintersemester /3 Vorlesung..3 Satz 6 (iduensatz) Sei f holomorph in G := C \ {z,..., z N } und G ein geschlossener, stückweise stetig dierenzierbarer Weg. Dann gilt f(ξ)dξ
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV Aufgabe N1 (LR-Zerlegung mit Pivotisierung) Gegeben seien R 3.
 Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.
Bernstein-Polynome. Autor: Johannes Erath. Schriftliche Ausarbeitung zum Vortrag vom
 Bernstein-Polynome Autor: Johannes Erath Schriftliche Ausarbeitung zum Vortrag vom 07.04.2009 1 Inhaltsverzeichnis 1 Einleitung 3 2 Einführung 3 2.1 Etwas Geschichte........................... 3 2.2 Denition
Bernstein-Polynome Autor: Johannes Erath Schriftliche Ausarbeitung zum Vortrag vom 07.04.2009 1 Inhaltsverzeichnis 1 Einleitung 3 2 Einführung 3 2.1 Etwas Geschichte........................... 3 2.2 Denition
Die Binomialreihe. Sebastian Schulz. Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 2008/09, Leitung Prof. Dr.
 Die Binomialreihe Sebastian Schulz Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 008/09, Leitung Prof. Dr. Eberhard Freitag Zusammenfassung: Diese Ausarbeitung beschäftigt sich mit der
Die Binomialreihe Sebastian Schulz Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 008/09, Leitung Prof. Dr. Eberhard Freitag Zusammenfassung: Diese Ausarbeitung beschäftigt sich mit der
Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[
![Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[ Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[](/thumbs/76/73058958.jpg) Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Seminar Stochastische Unternehmensmodelle Varianzreduzierende Techniken
 Seminar Stochastische Unternehmensmodelle Varianzreduzierende Techniken 25. Juni 2015 1 / 37 Übersicht 1. Ziel des Vortrags 2. Einleitung 3. Varianzreduzierende Techniken Bedingtes Monte Carlo Importance
Seminar Stochastische Unternehmensmodelle Varianzreduzierende Techniken 25. Juni 2015 1 / 37 Übersicht 1. Ziel des Vortrags 2. Einleitung 3. Varianzreduzierende Techniken Bedingtes Monte Carlo Importance
Musterlösungen zur Leistungsnachweisklausur vom Studiengang Informatik, Ingenieurinformatik, Lehramt
 TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
Tangente als Näherung
 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 1 Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion p 1 (x) eine Näherung für f(x): f(x) p 1 (x)
Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 1 Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion p 1 (x) eine Näherung für f(x): f(x) p 1 (x)
Bewegungen. Freier Fall eines Massenpunktes. Daniel Wunderlich. Wintersemester 2008/2009,
 Bewegungen Freier Fall eines Massenpunktes Daniel Wunderlich Universität Heidelberg Proseminar Analysis Leitung: PD Dr. Grudrun Thäter Wintersemester 2008/2009, 25.11.2008 Daniel Wunderlich (Uni Heidelberg)
Bewegungen Freier Fall eines Massenpunktes Daniel Wunderlich Universität Heidelberg Proseminar Analysis Leitung: PD Dr. Grudrun Thäter Wintersemester 2008/2009, 25.11.2008 Daniel Wunderlich (Uni Heidelberg)
Integralrechnung und das Riemannintegral
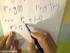 Integralrechnung und das Riemannintegral Vorlesung zur Didaktik der Analysis Oliver Passon Oliver Passon Integralrechnung 1 Inhalt Historisches Archimedes (Parabel) Hippokrates ( Möndchen ) Cavalerie Aktuell
Integralrechnung und das Riemannintegral Vorlesung zur Didaktik der Analysis Oliver Passon Oliver Passon Integralrechnung 1 Inhalt Historisches Archimedes (Parabel) Hippokrates ( Möndchen ) Cavalerie Aktuell
1.4 Schaubild von Schaubild von Schaubild von 1., /
 Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
ur Ingenieure (Maschinenbau und Sicherheitstechnik) 2. Semester Apl. Prof. Dr. G. Herbort Dr. T. Pawlaschyk
 Mathematik f ur Ingenieure (Maschinenbau und Sicherheitstechnik) 2. Semester Apl. Prof. Dr. G. Herbort Dr. T. Pawlaschyk www.math.uni-wuppertal.de/ herbort SoSe16 Arbeitsheft Blatt 1 Tutorium Hinweis:
Mathematik f ur Ingenieure (Maschinenbau und Sicherheitstechnik) 2. Semester Apl. Prof. Dr. G. Herbort Dr. T. Pawlaschyk www.math.uni-wuppertal.de/ herbort SoSe16 Arbeitsheft Blatt 1 Tutorium Hinweis:
Arbeitsblatt 1. Ergebnisse: a) Schätzen:... b) Abzählen:... c) Berechnen: (unter Angabe der geometrischen Figuren)
 Arbeitsblatt 1 Für das nächste Frequency-Festival pachtet der Veranstalter zusätzliche Fläche für die Besucherzelte beim benachbarten Landwirt. Zur Ermittlung des Pachtpreises muss die Fläche ausgemessen
Arbeitsblatt 1 Für das nächste Frequency-Festival pachtet der Veranstalter zusätzliche Fläche für die Besucherzelte beim benachbarten Landwirt. Zur Ermittlung des Pachtpreises muss die Fläche ausgemessen
Musterlösung. Modulprüfung MA2302. Numerik. 8. Oktober Prüfer: Prof. Dr. Bernd Simeon. Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral
 Modulprüfung MA2302 Numerik 8. Oktober 2009 Musterlösung Prüfer: Prof. Dr. Bernd Simeon Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral soll durch die Quadraturformel approximiert werden. I n
Modulprüfung MA2302 Numerik 8. Oktober 2009 Musterlösung Prüfer: Prof. Dr. Bernd Simeon Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral soll durch die Quadraturformel approximiert werden. I n
5. DIFFERENZIEREN UND INTEGRIEREN
 5. DIFFERENZIEREN UND INTEGRIEREN 1 Sei f eine auf R oder auf einer Teilmenge B R definierte Funktion: f : B R Die Funktion heißt differenzierbar in x 0 in B, falls sie in diesem Punkt x 0 lokal linear
5. DIFFERENZIEREN UND INTEGRIEREN 1 Sei f eine auf R oder auf einer Teilmenge B R definierte Funktion: f : B R Die Funktion heißt differenzierbar in x 0 in B, falls sie in diesem Punkt x 0 lokal linear
Lösungen zur Klausur zur Analysis 1, WiSe 2016/17
 BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
Integralrechnung. integral12.pdf, Seite 1
 Integralrechnung Beispiel Zusammenhang WegGeschwindigkeit: Ist F (t) der zur Zeit t zurückgelegte Weg und v(t) die Geschwindigkeit, so ist v(t) = F (t) Geometrisch: Steigung der Tangente an der Kurve y
Integralrechnung Beispiel Zusammenhang WegGeschwindigkeit: Ist F (t) der zur Zeit t zurückgelegte Weg und v(t) die Geschwindigkeit, so ist v(t) = F (t) Geometrisch: Steigung der Tangente an der Kurve y
Lösungsblatt Aufgabe 1.32
 Aufgabenstellung: Die Geschwindigkeit eines Körpers ist für t 1 durch v t = 10 10 gegeben. t 1. Schätze die Länge des im Zeitintervall [1 4] zurückgelegten Weges durch Ober- und Untersumme ab, wobei das
Aufgabenstellung: Die Geschwindigkeit eines Körpers ist für t 1 durch v t = 10 10 gegeben. t 1. Schätze die Länge des im Zeitintervall [1 4] zurückgelegten Weges durch Ober- und Untersumme ab, wobei das
1 Polynome III: Analysis
 1 Polynome III: Analysis Definition: Eine Eigenschaft A(x) gilt nahe bei a R, falls es ein δ > 0 gibt mit A(x) gilt für alle x (a δ, a + δ)\{a} =: U δ (a) Beispiele: x 2 5 nahe bei 0 (richtig). Allgemeiner:
1 Polynome III: Analysis Definition: Eine Eigenschaft A(x) gilt nahe bei a R, falls es ein δ > 0 gibt mit A(x) gilt für alle x (a δ, a + δ)\{a} =: U δ (a) Beispiele: x 2 5 nahe bei 0 (richtig). Allgemeiner:
Skript Analysis. sehr einfach. Erstellt: Von:
 Skript Analysis sehr einfach Erstellt: 2017 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Funktionen... 3 2. Geraden... 6 3. Parabeln... 9 4. Quadratische Gleichungen... 11 5. Ableitungen...
Skript Analysis sehr einfach Erstellt: 2017 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Funktionen... 3 2. Geraden... 6 3. Parabeln... 9 4. Quadratische Gleichungen... 11 5. Ableitungen...
Satz von Taylor Taylorreihen
 Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion
Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion
Prof. Dr. Rolf Linn
 Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
