Tangente als Näherung
|
|
|
- Arthur Waltz
- vor 5 Jahren
- Abrufe
Transkript
1 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 1 Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion p 1 (x) eine Näherung für f(x): f(x) p 1 (x) für x a.
2 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 2 sin x x für kleine x Beispielsweise ist für f(x) := sin x die Tangente an der Stelle a := 0 die Winkelhalbierende und man hat folglich p 1 (x) = x sin x x für kleine x. Besonders raffiniert sind diese Näherungsformeln nicht. Für die Cosinusfunktion erhält man beispielsweise mit der selben Argumentation cosx 1 für kleine x.
3 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 3 Fehlerbetrachtung Eine Näherungsformel ist auch wenig wert, wenn man nichts über den Fehler weiß. Wir leiten deshalb eine Abschätzung her. Dazu betrachten wir eine Stelle b, wobei wir a < b voraussetzen. Die Argumentation für a > b verläuft völlig analog. Wenn a b gilt, ist f(b) p 1 (b). Bezeichnen wir den Fehler ( Rest ), der dabei gemacht wird mit R 1 (b), dann haben wir ausführlicher also f(b) = p 1 (b) + R 1 (b), f(b) = f(a) + f (a)(b a) + R 1 (b).
4 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 4 Restgliedabschätzung Um etwas über R 1 (b) herauszubekommen, erweist sich folgender Ansatz als erfolgreich: wir führen eine neue Zahl k ein, die durch R 1 (b) = k (b a) 2 bestimmt ist und definieren dann eine neue Funktion g(x) durch g(x) := f(x) + f (x)(b x) + k(b x) 2. Es ist nicht schwierig, diese Funktion abzuleiten, man muss allerdings voraussetzen, dass die zweite Ableitung von f(x) existiert.
5 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 5 g (x) g (x) = f (x) f (x) + f (x)(b x) 2k(b x) = [ f (x) 2k ] (b x). Durch Einsetzen findet man, dass g(a) = g(b) (= f(b)) gilt. Nach dem Mittelwertsatz der Differenzialrechnung existiert deshalb eine Zahl c mit a < c < b und g (c) = g(b) g(a) b a = 0.
6 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 6 Ergebnis der Abschätzung Das Ergebnis ist also folgendes: Es gibt eine Zahl c zwischen a und b, für die gilt. R 1 (b) = 1 2 f (c)(b a) 2 Nun wissen wir etwas über R 1 (b), aber es erscheint schwierig, diese Information auszunutzen, denn man hat ja keine Information über die genaue Lage der Stelle c.
7 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 7 Oft genügt es jedoch, einfach den schlechtesten aller in Frage kommenden Werte zu nehmen: Kennt man eine Schranke M, so dass f (x) M für alle x zwischen a und b gilt, dann ist sicher R 1 (b) 1 2 M(b a)2. Dies kann man in einen Lehrsatz gießen.
8 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 8 Satz über die Approximation Satz: Wenn f (x) in einer Umgebung U von a existiert, dann gilt für jedes x U f(x) = f(a) + f (a)(x a) + R 1 (x), wobei R 1 (x) = 1 2 f (c)(x a) 2 für eine Zahl c zwischen a und x ist.
9 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 8 Satz über die Approximation Satz: Wenn f (x) in einer Umgebung U von a existiert, dann gilt für jedes x U f(x) = f(a) + f (a)(x a) + R 1 (x), wobei R 1 (x) = 1 2 f (c)(x a) 2 für eine Zahl c zwischen a und x ist. Ist außerdem f (x) M für alle x U, dann gilt auch für alle x U. R 1 (x) 1 M(x a)2 2
10 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 9 Anwendungsbeispiel (1) Damit können wir nun im Einzelfall eine Abschätzung angeben, was wir am Beispiel der Näherung sin demonstrieren: In diesem Fall ist f(x) = sin x, a = 0, p 1 (x) = x. Wegen f (x) = sin x ist M := 1 eine Schranke, die die Bedingungen des Satzes erfüllt.
11 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 10 Anwendungsbeispiel (2) Man hat also R 1 (x) 1 2 x2, was für x := 0.2 den Wert R 1 (0.2) 0.02 ergibt. Wir erhalten also sin 0.2 = 0.2 ± 0.02, d.h. sin 0.2 [0.18, 0.22]. Der wirkliche Wert ist
12 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 11 Anwendungsbeispiel (3) Man kann sich über dieses Beispiel ärgern, denn offenbar gibt es noch Verbesserungsbedarf. Einerseits ist die Näherung sin viel besser als uns die Abschätzung verspricht. Der wirkliche Fehler ist ja mehr als zehnmal kleiner als abgeschätzt. Man wünscht sich also eine wirkungsvollere Fehlerabschätzung. Andererseits zeigt das Beispiel der Cosinusfunktion dafür Grenzen auf. Mit der gleichen Methode erhalten wir die Abschätzung cos 0.2 = 1 ± 0.02, was der Wahrheit ziemlich nahe kommt: der wahre Wert ist cos 0.2 =
13 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 12 Von der linearen Approximation... Bei der linearen Approximation wird eine Funktion f(x) an einer Stelle a durch eine lineare Funktion p 1 (x) := a 0 + a 1 x angenähert. Das führt auf f(x) f(a) + f (a)(x a) für x a. Dies ergibt sich aus den Bedingungen f(a) = p 1 (a),f (a) = p 1(a).
14 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 13 über die quadratische Approximation... Versucht man allgemeiner, f(x) an der Stelle a durch ein quadratisches Polynom p 2 (x) := a 0 + a 1 x + a 2 x 2 anzunähern, dann fordert man naheliegenderweise f(a) = p 2 (a),f (a) = p 2(a),f (a) = p 2(a), was natürlich nur sinnvoll ist, wenn f (x) existiert. Daraus erhält man p 2 (x) = f(a) + f (a)(x a) + f (a)(x a) 2.
15 Mathematik I für Informatiker Satz von Taylor Taylorreihen p zum Taylorschen Satz Gegeben sei eine Funktion f(x), die in einer Umgebung der Stelle a n + 1-mal differenzierbar ist. Wir suchen ein Polynom p n (x) vom Grade n mit f(a) = p n (a),f (a) = p n(a),f (a) = p n(a),...,f (n) (a) = p (n) n (a). In Analogie zum Satz über die lineare Approximation erhält man folgendes wichtige Ergebnis:
16 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 15 Satz von Taylor Satz: Wenn f (n+1) (x) in einer Umgebung U von a existiert, dann gilt für jedes x U f(x) = f(a) + f (a)(x a) f (a)(x a) ! f (a)(x a) 3 wobei n! f(n) (a)(x a) n + R n (x), R n (x) = für ein c zwischen a und x gilt. 1 (n + 1)! f(n+1) (c)(x a) n+1
17 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 16 Zusatz Ist außerdem f (n+1) (x) M n+1 für alle x U, dann gilt auch 1 R n (x) (n + 1)! M n+1 x a n+1 für alle x U.
18 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 17 Der Satz bedeutet... Als Näherung für die Funktion f(x) an der Stelle a erhält man für vorgegebenen Grad n das Polynom p n (x) = f(a)+f (a)(x a)+ 1 2 f (a)(x a) ! f (a)(x a) n! f(n) (a)(x Der Näherungsfehler wird durch die Funktion R n (x) angegeben; diese kann man mit Hilfe der (n + 1)-ten Ableitung von f(x) abschätzen.
19 für alle x U. Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 18 Satz von Taylor für a := 0 Wenn f (n+1) (x) in einer Umgebung U von 0 existiert, dann gilt für jedes x U dass f(x) = f(0)+f (0)x+ 1 2 f (0)x ! f (0)x n! f(n) (0)x n +R n (x), wobei R n (x) = für ein c zwischen 0 und x gilt. 1 (n + 1)! f(n+1) (c)x n+1 Ist außerdem f (n+1) (x) M n+1 für alle x U, dann gilt auch 1 R n (x) (n + 1)! M n+1 x n+1
20 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 19 Anwendungsbeispiel Als erstes Anwendungsbeispiel untersuchen wir den Fall f(x) := cosx, a := 0, n := 2. Als Näherung erhält man cos x x2 für x 0, im Falle x := 0.2 also cos
21 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 20 Fehleabschätzung für das Beispiel Den Fehler schätzen wir mit Hilfe von M 3 := 1 ab zu (gerundet) R 2 (0.2) 1 3! = Diese Näherung ist viel besser als die im vorigen Abschnitt gewonnene (zur Erinnerung: der wirkliche Wert ist cos 0.2 = ).
22 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 21 Noch besser (1) Weil die dritte Ableitung der Cosinusfunktion (also sin x) an der Stelle a := 0 verschwindet, erhalten wir für n := 3 das gleiche Näherungspolynom wie oben, nämlich p 3 (x) = x2 und damit cos x = x2 + R 3 (x),
23 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 22 (2) wobei (mit M 4 := 1) R 3 (x) 1 4! 1 x4, was für x := 0.2 R 3 (x) 1 4! (0.2)4 = ergibt, eine wirklich gute Abschätzung. Nochmal das Ergebnis cos 0.2 = 0.98 ± und zum Vergleich den wirklichen Wert cos 0.2 =
24 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 23 Potenzreihen Potenzreihen (in x) sind Reihen der Form a 0 + a 1 x + a 2 x a n x n +..., wobei x,a 0,a 1,... Zahlen sind. Eine solche Reihe kann konvergent oder divergent sein, je nach Wahl der a i und von x. Schon die Bezeichnungsweise legt nahe, dass wir eine Potenzreihe nicht nur für ein festes x betrachten, sondern verschiedene Werte von x einsetzen wollen, während die a i festgehalten werden.
25 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 24 Polynome unendlichen Grades Man schreibt eine Potenzreihe deshalb als eine Art unendliches Polynom, wie in folgendem Beispiel: x + x2 2 + x3 3 + x4 4 +.
26 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 25 Konvergenz Man kann dann fragen, für welche x die Reihe konvergiert, und findet folgendes Ergebnis: Satz Eine Potenzreihe konvergiert entweder a 0 + a 1 x + a 2 x a n x n nur für x = 0 und divergiert für alle anderen Werte von x oder 2. für x < r und divergiert für alle x > r, für eine reelle Zahl r, oder 3. konvergiert für alle x.
27 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 26 Konvergenzradius Die Menge der x, für die die Reihe konvergiert, ist also in jedem Fall ein Intervall, das Konvergenzintervall der Reihe. Die halbe Länge dieses Intervalls nennt man den Konvergenzradius der Reihe. Eine Potenzreihe hat also den Konvergenzradius Null, den Konvergenzradius r R, oder unendlichen Konvergenzradius ( Konvergenzradius r = ).
28 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 27 Beispiel Die geometrische Reihe 1 + x + x 2 + x konvergiert für x < 1 und divergiert für x 1. Ihr Konvergenzradius ist also gleich 1, ihr Konvergenzintervall ist ( 1, +1).
29 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 28 Potenzreihen als Funktionen Es liegt nahe, Potenzreihen als Beschreibungen von Funktionen aufzufassen. f(x) := a 0 + a 1 x + a 2 x a n x n +... Der Definitionsbereich einer solchen Funktion ist das Konvergenzintervall, der Funktionswert an der Stelle x ist der jeweilige Grenzwert der Reihe.
30 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 29 Ableiten wie Polynome Satz Hat die Potenzreihe f(x) := a 0 + a 1 x + a 2 x a n x n +... den Konvergenzradius r > 0, dann gilt: 1. Die Funktion f(x) ist stetig auf dem Intervall ( r,r). 2. f(x) ist auf dem Intervall ( r,r) differenzierbar, und die Ableitung ist f (x) = a 1 + 2a 2 x + 3a 3 x na n x n 1 +. Der Konvergenzradius dieser Reihe ist ebenfalls r.
31 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 30 Eindeutigkeit der Reihe Eine unmittelbare Folgerung aus diesem Satz ist, dass eine Funktion f(x) wenn überhaupt, dann nur durch eine Potenzreihe beschrieben werden kann, denn man hat für f(x) := a 0 + a 1 x + a 2 x a n x n +... ja nach dem Satz, dass a n = 1 n! f(n) (0). Diese Darstellung der Koeffizienten erinnert uns sofort an den Satz von Taylor (für a := 0)!
32 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 31 Taylor-Reihen Es wird nun deutlich, was beim diesem Satz geschieht: das Näherungspolynom p n (x) ist jeweils ein Anfangsstück der Potenzreihe! Die Potenzreihe für eine Funktion f(x) nennt man deshalb auch die Taylor-Reihe für f(x) (am Entwicklungspunkt a := 0).
33 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 32 Andere Entwicklungspunkte Man kann den Begriff der Potenzreihe verallgemeinern auf Reihen der Form f(x) := a 0 + a 1 (x a) + a 2 (x a) a n (x a) n +... Dann ist die Beziehung zum Taylorschen Satz besonders deutlich. Wir konzentrieren uns hier auf den Fall a := 0.
34 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 33 Beispiel Für f(x) := sin x haben wir f(0) = 0, f (0) = 1, f (0) = 0, f (0) = 1 und f (4) (x) = f(x). Die Folge (f (i) (0) i N 0 ) ist also eine endlose Wiederholung von 0, 1, 0, 1. Die Taylor-Reihe für sin x ist 0 + x + 0 x3 3! x5 5! + 0 x7 7! +.
35 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 34 Konvergenz der Sinusreihe Was ist der Konvergenzradius dieser Reihe? Die Sinusfunktion ist für alle x R definiert, aber unser Zugang zur Taylorreihe war der, die Funktion in der Nähe von a := 0 zu approximieren. Wir können also eigentlich nicht erwarten, dass die Taylorreihe weit entfernt von a noch konvergiert.
36 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 35 Restglied Konvergenz haben wir offenbar genau dort, wo der Fehler gegen Null geht, also an den Stellen x, an denen lim R n(x) = 0 n gilt. Alle Ableitungen f (n) (x) der Sinusfunktion sind beschränkt und erfüllen f (n) (x) 1 für alle x R. Deshalb können wir im Satz von Taylor alle M n gleich 1 setzen und erhalten R n (x) x n+1 (n + 1)!.
37 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 36 Überall konvergent! Folglich gilt für jedes x R lim R n(x) = lim n n x n+1 (n + 1)! = 0. Die Taylor-Reihe für sin x konvergiert also für alle x R, der Konvergenzradius ist unendlich.
38 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 37 Taylorreihe für cos x Für alle x gilt also sin x = x x3 3! + x5 5! x7 7! +. Mit Hilfe des Satzes über die Ableitung erhalten wir daraus sogleich eine ebenfalls überall konvergente Potenzreihe für den Cosinus: cosx = 1 x2 2! + x4 4! x6 6! +.
39 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 38 Exponentialfunktion Wir haben für f(x) := e x : f(x) := e x f(0) = 1 f (x) := e x f (0) = 1 f (x) := e x f (0) = 1 f (x) := e x f (0) = 1.. f (n) (x) := e x f (n) (0) = 1..
40 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 39 Koeffizienten Wegen a n = 1 n! f(n) (0) erhalten wir a n = 1 n!. Wenn es also eine Taylorreihe für die Exponentialfunktion gibt, dann lautet sie 1 + x + x2 2! + x3 3! + x4 4! +...
41 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 40 Quotientenkritrium anwenden! r bezeichne den Konvergenzradius der Potenzreihe n=0 a n(x a) n. Dann gilt: Falls lim n a n+1 a n = 0, dann ist r =. Mit a n = xn n! und a n+1 = xn+1 (n+1)! lim n a n+1 a n = lim n ergibt sich x n+1 (n + 1)! n! x n = lim n x n + 1 = 0. Die Potenzreihe der Exponentialfunktion konvergiert überall!
42 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 41 Vergleich der Reihen Wir haben gefunden: sin x = x x3 3! + x5 5! x7 7! + cosx = 1 x2 2! + x4 4! x6 6! + e x = 1 + x + x2 2! + x3 3! + x4 4! +...
43 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 42 Kombinationen von sin und cos (1) sin x = x x3 3! + x5 5! x7 7! + cosx = 1 x2 2! + x4 4! x6 6! + cosx + sin x = 1 + x x2 2! x3 3! + x4 4! + x5 5!...
44 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 43 Kombinationen von sin und cos (2) sin x = x x3 3! + x5 5! x7 7! + cosx = 1 x2 2! + x4 4! x6 6! + cosx sin x = 1 x x2 2! + x3 3! + x4 4! x5 5!...
45 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 44 Komplexe Argumente Man kann in eine Potenzreihe auch komplexe Zahlen als Argumente einsetzen. Die Konvergenzüberlegungen verallgemeinern sich. Wir gehen darauf hier nicht weiter ein.
46 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 45 Komplexe Exponentialfunktion e ix = 1 + ix + (ix)2 2! + (ix)3 3! + (ix)4 4! + (ix)5 5! +... = 1 + ix + i2 x 2 2! + i3 x 3 3! + i4 x 4 4! + i5 x 5 5! +... = 1 + ix + x2 2! + ix3 3! = 1 x2 2! + x4 4!... + i + x4 4! + ix5 5! +... ) (x x3 3! + x5 5! +...
47 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 46 Erneuter Vergleich der Reihen sin x = x x3 3! + x5 5! x7 7! + cos x = 1 x2 2! + x4 4! x6 6! + e ix = 1 x2 2! + x4 4!... + i ) (x x3 3! + x5 5! +...
48 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 46 Erneuter Vergleich der Reihen sin x = x x3 3! + x5 5! x7 7! + cos x = 1 x2 2! + x4 4! x6 6! + e ix Daraus folgt: = 1 x2 2! + x4 4!... + i ) (x x3 3! + x5 5! +... e ix = cosx + i sin x
49 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 47 Eulersche Formel Die schönste Formel der Welt:
50 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 47 Eulersche Formel Die schönste Formel der Welt: e iπ = 1.
Satz von Taylor Taylorreihen
 Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion
Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Michael Karow Thema: Satz von Taylor Die Taylor-Entwicklung I Satz von Taylor. Sei f : R D R an der Stelle x n-mal differenzierbar. Dann gilt für x D, n f (k) (x )
Vorlesung: Analysis I für Ingenieure Michael Karow Thema: Satz von Taylor Die Taylor-Entwicklung I Satz von Taylor. Sei f : R D R an der Stelle x n-mal differenzierbar. Dann gilt für x D, n f (k) (x )
Mathematik für Bauingenieure
 Mathematik für Bauingenieure von Kerstin Rjasanowa 1. Auflage Mathematik für Bauingenieure Rjasanowa schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 2006 Verlag C.H.
Mathematik für Bauingenieure von Kerstin Rjasanowa 1. Auflage Mathematik für Bauingenieure Rjasanowa schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 2006 Verlag C.H.
Die Taylorreihe einer Funktion
 Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
(b) Bestimmen Sie mit Hilfe des Newton-Verfahrens eine Nullstelle von f auf 6 Nachkommastellen
 Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Karteikarten, Analysis 2, Sätze und Definitionen nach der Vorlesung von PD Hanke
 Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
a 0 +a 1 x+a 2 x n=0 a n x n := lim
 1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Folgen. Eine (unendliche) (Zahlen)folge ist eine Abbildung. dann als. notiert, und das wird abgekürzt mit. nennt man die Folgenglieder.
 Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
konvergent falls Sei eine allgemeine ("gutmütige") Funktion. Frage: kann man sie in der Nähe des Punktes darstellen mittels einer Potenzreihe in
 C5 Funktionen: Reihenentwicklungen C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich
C5 Funktionen: Reihenentwicklungen C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich
konvergent falls eine allgemeine ("gutmütige") Funktion. Frage: kann man sie in der darstellen mittels einer Potenzreihe in
 C5 Funktionen: Taylorreihen & Fourieranalysis C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen
C5 Funktionen: Taylorreihen & Fourieranalysis C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen
11. Anwendungen der Differentialrechnung
 124 Andreas Gathmann 11. Anwendungen der Differentialrechnung Im letzten Kapitel haben wir gesehen, wie wir von nahezu allen Funktionen ihre Ableitung berechnen können und welche elementaren Eigenschaften
124 Andreas Gathmann 11. Anwendungen der Differentialrechnung Im letzten Kapitel haben wir gesehen, wie wir von nahezu allen Funktionen ihre Ableitung berechnen können und welche elementaren Eigenschaften
Mathematik für Anwender. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 4. Januar 0 Prof. Dr. H. Brenner Mathematik für Anwender Testklausur mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden
Fachbereich Mathematik/Informatik 4. Januar 0 Prof. Dr. H. Brenner Mathematik für Anwender Testklausur mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden
11. Anwendungen der Differentialrechnung
 122 Andreas Gathmann 11. Anwendungen der Differentialrechnung Im letzten Kapitel haben wir gesehen, wie wir von nahezu allen Funktionen ihre Ableitung berechnen können und welche elementaren Eigenschaften
122 Andreas Gathmann 11. Anwendungen der Differentialrechnung Im letzten Kapitel haben wir gesehen, wie wir von nahezu allen Funktionen ihre Ableitung berechnen können und welche elementaren Eigenschaften
Fehlerabschätzung für Taylorpolynome der e-funktion
 Fehlerabschätzung für Talorpolnome der e-funktion f() = e R () = e g() = ++ - -. Wir approimieren die Funktion f() = e durch g() = +! +! und schätzen den Fehler R() auf dem Intervall [,] ab. Sei also e
Fehlerabschätzung für Talorpolnome der e-funktion f() = e R () = e g() = ++ - -. Wir approimieren die Funktion f() = e durch g() = +! +! und schätzen den Fehler R() auf dem Intervall [,] ab. Sei also e
Freie Universität Berlin Wintersemester 11/12 Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke
 Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen zu Aufgabenblatt 10P
 Analysis Prof. Dr. Peter Becker Fachbereich Informatik Sommersemester 05 9. Juni 05 Lösungen zu Aufgabenblatt 0P Aufgabe (Funktionsgrenzwerte) Berechnen Sie die folgenden Grenzwerte: cos(x) x cos( x )
Analysis Prof. Dr. Peter Becker Fachbereich Informatik Sommersemester 05 9. Juni 05 Lösungen zu Aufgabenblatt 0P Aufgabe (Funktionsgrenzwerte) Berechnen Sie die folgenden Grenzwerte: cos(x) x cos( x )
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Taylorentwicklung von Funktionen einer Veränderlichen
 Taylorentwicklung von Funktionen einer Veränderlichen 17. Januar 2013 KAPITEL 1. MATHEMATISCHE GRUNDLAGEN 1 Kapitel 1 Mathematische Grundlagen 1.1 Stetigkeit, Differenzierbarkeit und C n -Funktionen Der
Taylorentwicklung von Funktionen einer Veränderlichen 17. Januar 2013 KAPITEL 1. MATHEMATISCHE GRUNDLAGEN 1 Kapitel 1 Mathematische Grundlagen 1.1 Stetigkeit, Differenzierbarkeit und C n -Funktionen Der
P n (1) P j (1) + ε 2, j=0. P(1) P j (1) + ε 2 < ε. log(1+x) =
 Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
MIA Analysis einer reellen Veränderlichen WS 06/07. Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen
 Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Mathematik I. k=0 c k(x a) k bilden die Teilpolynome n k=0 c k(x a) k polynomiale Approximationen für die Funktion f
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 30 Zu einer konvergenten Potenzreihe f(x) = c k(x a) k bilden die Teilpolynome n c k(x a) k polynomiale Approximationen für die Funktion
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 30 Zu einer konvergenten Potenzreihe f(x) = c k(x a) k bilden die Teilpolynome n c k(x a) k polynomiale Approximationen für die Funktion
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
Stetigkeit von Funktionen
 Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
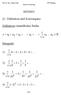 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Kapitel 16 : Differentialrechnung
 Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Mathematik zum Mitnehmen
 Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Mathematik I - Woche 10
 Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Animation: Approximation von sin(x) durch Polynome 1-25.Grades
 of 1 19/03/14 09:00 Taylorpolynome zurück Approximation durch Polynome höheren Grades Erklärung Bis jetzt haben wir Funktionen nur durch Polynome 1. und 2.Grades approximiert, nämlich durch die Tangentengerade
of 1 19/03/14 09:00 Taylorpolynome zurück Approximation durch Polynome höheren Grades Erklärung Bis jetzt haben wir Funktionen nur durch Polynome 1. und 2.Grades approximiert, nämlich durch die Tangentengerade
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Differentiation und Taylorentwicklung. Thomas Fehm
 Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Analysis I. Vorlesung 20. Konvexe Funktionen
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 20 Konvexe Funktionen Eine konvexe Teilmenge. Eine nichtkonvexe Teilmenge. Definition 20.1. Eine Teilmenge T R n heißt konvex, wenn mit
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 20 Konvexe Funktionen Eine konvexe Teilmenge. Eine nichtkonvexe Teilmenge. Definition 20.1. Eine Teilmenge T R n heißt konvex, wenn mit
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Oft können wir bestimmte mathematische Funktionen nicht genau
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Oft können wir bestimmte mathematische Funktionen nicht genau
4.7 Der Taylorsche Satz
 288 4 Differenziation 4.7 Der Taylorsche Satz Die Differenzierbarkeit, also die Existenz der ersten Ableitung einer Funktion, erlaubt bekanntlich, diese Funktion lokal durch eine affine Funktion näherungsweise
288 4 Differenziation 4.7 Der Taylorsche Satz Die Differenzierbarkeit, also die Existenz der ersten Ableitung einer Funktion, erlaubt bekanntlich, diese Funktion lokal durch eine affine Funktion näherungsweise
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Mathematik IT 3 (Analysis) Probeklausur
 Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen
 Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
HM I Tutorium 6. Lucas Kunz. 28. November 2018
 HM I Tutorium 6 Lucas Kunz 28. November 208 Inhaltsverzeichnis Theorie 2. Exponentialfunktion.............................. 2.2 Trigonometrische Funktionen......................... 2.3 Potenzreihen...................................
HM I Tutorium 6 Lucas Kunz 28. November 208 Inhaltsverzeichnis Theorie 2. Exponentialfunktion.............................. 2.2 Trigonometrische Funktionen......................... 2.3 Potenzreihen...................................
Vorlesung Mathematik für Ingenieure 1 (Wintersemester 2008/09)
 Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Kapitel 6 Folgen und Stetigkeit
 Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
ANALYSIS 2 VERSION 26. Juni 2018
 ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
5 Differenzialrechnung für Funktionen einer Variablen
 5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
2 Stetigkeit und Differenzierbarkeit
 2.1) Sei D R. a) x 0 R heißt Häufungspunkt von D, wenn eine Folge x n ) n N existiert mit x n D,x n x 0 und lim n x n = x 0. D sei die Menge der Häufungspunkte von D. b) x 0 D heißt innerer Punkt von D,
2.1) Sei D R. a) x 0 R heißt Häufungspunkt von D, wenn eine Folge x n ) n N existiert mit x n D,x n x 0 und lim n x n = x 0. D sei die Menge der Häufungspunkte von D. b) x 0 D heißt innerer Punkt von D,
AM3: Differenzial- und Integralrechnung im R n. 1 Begriffe. 2 Norm, Konvergenz und Stetigkeit. x 1. x 2. f : x n. aus Platzgründen schreibt man:
 AM3: Differenzial- und Integralrechnung im R n 1 Begriffe f : x 1 f 1 x 1, x 2,..., x n ) x 2... f 2 x 1, x 2,..., x n )... x n f m x 1, x 2,..., x n ) }{{}}{{} R n R m aus Platzgründen schreibt man: f
AM3: Differenzial- und Integralrechnung im R n 1 Begriffe f : x 1 f 1 x 1, x 2,..., x n ) x 2... f 2 x 1, x 2,..., x n )... x n f m x 1, x 2,..., x n ) }{{}}{{} R n R m aus Platzgründen schreibt man: f
Thema 5 Differentiation
 Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Mathematik I Herbstsemester 2018 Kapitel 6: Potenzreihen
 Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Beispielaufgaben rund um Taylor
 Beispielaufgaben rund um Taylor Mirko Getzin Universität Bielefeld Fakultät für Mathematik 19. Februar 014 Keine Gewähr auf vollständige Richtigkeit und perfekter Präzision aller (mathematischen) Aussagen.
Beispielaufgaben rund um Taylor Mirko Getzin Universität Bielefeld Fakultät für Mathematik 19. Februar 014 Keine Gewähr auf vollständige Richtigkeit und perfekter Präzision aller (mathematischen) Aussagen.
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 22 3. Funktionen. Grenzwerte.
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 22 3. Funktionen. Grenzwerte.
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu. MC-Fragen Serie 1. Einsendeschluss: Freitag, der :00 Uhr
 D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt.
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt.
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
c < 1, (1) c k x k0 c k = x k0
 4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
Kapitel 3. Reihen und ihre Konvergenz
 Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
15 Restabschätzung nach Taylor. Potenzreihen
 15 Restabschätzung nach Taylor. Potenzreihen Jörn Loviscach Versionsstand: 21. März 2014, 21:09 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen beim Ansehen der Videos: http://www.j3l7h.de/videos.html
15 Restabschätzung nach Taylor. Potenzreihen Jörn Loviscach Versionsstand: 21. März 2014, 21:09 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen beim Ansehen der Videos: http://www.j3l7h.de/videos.html
9. Übungsblatt zur Vorlesung Mathematik I für Informatik
 Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Anleitung zu Blatt 2, Analysis II
 Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu. MC-Fragen Serie 1. Einsendeschluss: Freitag, der :00 Uhr
 D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
Kapitel 5 Trigonometrie
 Mathematischer Vorkurs TU Dortmund Seite / 7 Schenkel Winkelbereich Scheitel S α Winkel werden in Grad oder im Bogenmaß (auch Rad) angegeben: 360 =. y cot α r = sin α α cos α tan α x Durch diese Betrachtungen
Mathematischer Vorkurs TU Dortmund Seite / 7 Schenkel Winkelbereich Scheitel S α Winkel werden in Grad oder im Bogenmaß (auch Rad) angegeben: 360 =. y cot α r = sin α α cos α tan α x Durch diese Betrachtungen
Analysis I. 7. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Abbildung 11.1: Approximation einer Tangente
 Analysis, Woche Differentialrechnung I A. Ableitung einer Funktion Sei f : R R eine Funktion. Die Gerade durch die Punkte (a, f (a)) und (b, f (b)) findet man als Graph der Funktion l : R R mit l (x) =
Analysis, Woche Differentialrechnung I A. Ableitung einer Funktion Sei f : R R eine Funktion. Die Gerade durch die Punkte (a, f (a)) und (b, f (b)) findet man als Graph der Funktion l : R R mit l (x) =
Polynome, Stetigkeit, Dierenzierbarkeit
 Polynome, Stetigkeit, Dierenzierbarkeit Inhaltsverzeichnis 1 Polynome 1 1.1 Denitionen...................................................... 1 1.2 Nullstellen.......................................................
Polynome, Stetigkeit, Dierenzierbarkeit Inhaltsverzeichnis 1 Polynome 1 1.1 Denitionen...................................................... 1 1.2 Nullstellen.......................................................
Ferienkurs der TU München- - Analysis 2 Fourierreihen und Taylorreihen. Marcus Jung, Jonas J. Funke
 Ferienkurs der U München- - Analysis Fourierreihen und aylorreihen Lösung Marcus Jung, Jonas J. Funke 3.8. FOURIERREIHEN Fourierreihen Aufgabe. Sei f : R R stetig und periodisch mit Fourierkoeffizienten
Ferienkurs der U München- - Analysis Fourierreihen und aylorreihen Lösung Marcus Jung, Jonas J. Funke 3.8. FOURIERREIHEN Fourierreihen Aufgabe. Sei f : R R stetig und periodisch mit Fourierkoeffizienten
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Lösen von Differentialgleichungen durch Reihenentwicklung
 Lösen von Differentialgleichungen durch Reihenentwicklung Thomas Wassong FB17 Mathematik Universität Kassel 30. April 2008 Einführung Reihen in der Mathematik Reihen zum Lösen von Differentialgleichungen
Lösen von Differentialgleichungen durch Reihenentwicklung Thomas Wassong FB17 Mathematik Universität Kassel 30. April 2008 Einführung Reihen in der Mathematik Reihen zum Lösen von Differentialgleichungen
