Sensitivitätsanalyse in der Linearen Optimierung

Transkript

1 Sensitivitätsanalyse in der Linearen Optimierung Bei der Sensitivitätsanalyse werden i. allg. Größen des Ausgangsproblems variiert, und es wird untersucht, welche Wirkung eine derartige Modifikation auf die Lösung eines Problems besitzt. Man kann diese Frage auch etwas anders stellen: In welchem Maße kann man eine Größe ändern, ohne daß sich die Änderung auf die wesentlichen Eigenschaften der Lösung auswirkt? Da man in einem Problem i.d.r. nicht alle Daten gleichzeitig modifizieren kann, wird nur eine Größe unter Konstanthaltung aller anderen ( ceteris paribus ) geändert und die Frage gestellt: In welchem Bereich kann die betreffende Größe variiert werden, ohne daß damit die Lösung ihre Gültigkeit verliert? Unter gültig werden hier die qualitativen Merkmale einer Lösung verstanden und nicht die quantitativen. Das heißt, eine Lösung unterscheidet sich qualitativ (strukturell) erst dann von einer anderen, wenn mindestens eine Pivotoperation nötig ist, um Zulässigkeit und/oder Optimalität wieder herzustellen, wenn sie durch die Änderung verloren ging. Diese in LP-Software-Systemen i.allg. als RANGE bezeichnete Prozedur wird stets unter Konstanthaltung aller übrigen Daten bezüglich eines Koeffizienten durchgeführt. Besondere Bedeutung kommt hierbei den sog. Randkoeffizienten eines LP-Modells zu, d.h. den Koeffizienten der Rechten Seite und der Zielfunktion. Da in der rein algorithmischen Behandlung jedoch alle Zeilen und Spalten gleich behandelbar sind, läßt sich die Analyse im Prinzip auf jeden anderen Koeffizienten ausweiten. Allerdings unterscheiden sich die Ränder von den übrigen Zeilen und Spalten dadurch, daß sie nie Pivotzeile bzw. Pivotspalte werden, so daß sie nicht bewegt werden. Die Sensitivitätsanalyse ist dann für die Zeilen und Spalten komplizierter, die während des Lösungsprozesses von der Basis in die Nichtbasis wechseln. Wir diskutieren in der Hauptsache die Sensitivitätsanalyse der Rechten Seite (RS) (Abschnitt 1) und der Zielfunktion (ZF) (Abschnitt 2). Beides wird i.d.r. auch zusammen mit LP-Software angeboten. Um den Schwankungsbereich eines Koeffizienten bestimmen zu können, werden stets sowohl der Ausgangszustand als auch die Optimallösung des betreffenden Problems benötigt. Wir gehen im folgenden von den in Tab. 1a und b dargestellten Bezeichnungen aus. Max x j x s RS Max x j x r RS z d j d s z 0 z d j d r z 0 x r a rj a rs b r x s a sj a sr b s x i a ij a is b i x i a ij a ir b i Tab. 1a: Ausgangszustand Tab. 1b: Optimalzustand Die vier in den Tableaus benutzten Variablen x i, x r, x j und x s stehen stellvertretend für ganze Mengen von Variablen mit folgenden Eigenschaften: x i ist eine logische Basisvariable, d.h. eine ursprüngliche Schlupfvariable, die auch in der Optimallösung noch Basisvariable (BV) ist.

2 2 Sensitivitätsanalyse in LP x r ist eine logische Basisvariable, d.h. entweder eine Schlupfvariable oder eine künstliche Variable, die im Optimalzustand Nichtbasisvariable (NBV) ist. x j ist eine Entscheidungsvariable, d.h. eine ursprüngliche Strukturvariable, Aktivitätenvariable etc., die im Optimalzustand noch NBV ist. x s ist eine Entscheidungsvariable, die im Optimalzustand als BV erscheint. Für die Randkoeffizienten (b i, b r, d j, d s ) werden die Schwankungsbereiche dadurch bestimmt, daß man zu der betreffenden Größe einen zunächst variablen Wert δ addiert (bzw. subtrahiert) und die Änderung auf die Optimallösung berechnet. Sodann wird gefragt, wie groß die Wirkung maximal sein darf, ohne daß sie eine Iteration notwendig macht. Auf diese Weise wird für jede der betrachteten vier Größen ein Intervall berechnet, dessen Grenzen diejenigen Werte darstellen, deren Unter- bzw. Überschreitung einen Basiswechsel erfordern. Wir werden diese Grenzwerte als Iterationsgrenzen bezeichnen. Zusammen mit diesen Werten wird i.allg. festgelegt, welche Aktivität bzw. welche Variable von der nächsten notwendigen Iteration betroffen ist, d.h. welche Variable ggfs. die Basis verläßt oder in sie aufgenommen wird. Die untere bzw. obere Iterationsgrenze wird nachfolgend durch die Hochindizes ( u ) bzw. ( o ) gekennzeichnet, während die variierte Größe unterstrichen ist. 1 Sensitivitätsanalyse der Rechten Seite Im Hinblick auf die Koeffizienten der Rechten Seite wird gefragt, in welchen Bereichen b i bzw. b r schwanken können, bevor eine Iteration ausgelöst wird. Dabei ist zu unterscheiden, ob die ursprüngliche Basisvariable in der Optimallösung noch immer Basisvariable (x i ) ist oder nicht (x r ). Fall 1.1: Sensitivitätsanalyse der Koeffizienten b i Eine ursprüngliche Basisvariable x i ist noch in der Basis und hat den Wert x i = b i. Die Variable x i kann als Schlupfvariable angesehen werden und der Wert b i als Restkapazität. Der Faktor i ist also nicht knapp, sondern kann im Gegenteil um b i konsequenzlos im Angebot verringert werden: δ u = b i Verringert man b i noch mehr, wird x i die Basis verlassen. Bei einer Vergrößerung von b i wird die Restkapazität b i entsprechend größer. Das heißt, die Obergrenze ist unendlich. Der gesamte Schwankungsbereich beträgt also: δ u = b i : x i verläßt die Basis b i δ u b i < (keine Änderung)

3 3 Sensitivitätsanalyse in LP Fall 1.2: Sensitivitätsanalyse der Koeffizienten b r Als NBV ist x r gleich null, d.h. der entsprechende Faktor r ist knapp. Würde man x r = δ erzwingen, so würde sich dies laut Tab. 1b auf die Rechte Seite wie folgt auswirken: x r = δ d a a r sr ir RS(δ) z0 δ dr bs δ asr b i δ air Mit δ > 0 würde Restkapazität geschaffen, d.h. das ursprüngliche Angebot verringert ( Untergrenze u ). Für δ < 0 würde (fiktive) Restkapazität beseitigt, d.h. das Angebot im Ausgangszustand vergrößert ( Obergrenze o ). Somit stellt sich die Frage, wann in beiden Fällen der erste Koeffizient der Rechten Seite gleich null wird: b i bp min air > 0 = > 0 (u) δ > 0: δ u i air apr,falls air 0 i Es wird angenommen, daß sich das Minimum in der Spalte mit x p als BV ergäbe. b i bq max air < 0 = < 0 (o) δ < 0: δ o i air aqr,falls air 0 i Es wird angenommen, daß sich das Maximum in der Spalte mit x q als BV ergäbe. Zusammengefaßt ergibt sich das Intervall: x p verläßt die Basis b r δ u b r b r δo x q verläßt die Basis Die Rechenregeln sind nachstehend algorithmisch zusammengefaßt:

4 4 Sensitivitätsanalyse in LP Sensitivitätsanalyse der Rechten Seite b Input: Output: Simplex-Tableau eines Maximierungsproblems der optimalen Lösung zur Basis B Schwankungsbereiche für alle Koeffizienten des Vektors b Markierung: Größen des Optimaltableaus sind mit Stern (), die variierten Größen durch Unterstrich gekennzeichnet. Methode: Schritt 1: Die Sensitivitätsanalyse untersucht Wertänderungen der logischen Variablen, d.h. der ursprünglichen Basisvariablen (Schlupfvariablen und künstliche Variablen). Logische Variablen in der Basis: x i mit i B x i b i - δ u b i < Schritt 2: Logische Variablen als NBV: x r mit r N 2.1 Berechne δ u b b i p min air > 0 = i air a pr, falls air 0 i Der minimale (positive) Quotient ergebe sich in der Zeile p. δ o b b i q max air < 0 = i air aqr, falls air 0 i Der maximale (negative) Quotient ergebe sich in der Zeile q. 2.2 Als Schwankungsbereich ergibt sich: x p b r δ u b r b r δo x q Algorithmus 1: Sensitivitätsanalyse der Rechten Seite

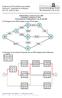
5 5 Sensitivitätsanalyse in LP Beispiel: Im folgenden sind für ein Problem das Ausgangs- und das Optimaltableau gegeben: Max x 1 x 2 x 3 RS z x R x T x M Tab. 2: Ausgangstableau Max x M x 2 x T RS Var r x M x T z x R (o) x bi (u) a x (u) 500 (o) Tab. 3a: Optimaltableau Tab. 3b: Quotiententableau Das Ergebnis der Sensitivitätsanalyse ist für alle Koeffizienten der RS in der nachstehenden Tab. 4 zusammengefaßt: x p b i δ u Var. i RS b i b i δ o x q Fall x R x R (1,1) x x T x 1 (1,2) x x M x R (1,2) ir Tab. 4: Zusammenfassung der Ergebnisse der Sensitivitätsanalyse der Rechten Seite Die Sensitivitätsanalyse der Koeffizienten b i läßt sich geometrisch eindrucksvoll erklären. Variiert man den absoluten Wert (= Rechte Seite b i ) einer Nebenbedingung, so verschiebt man diese parallel. Qualitativ ändert sich nichts an der Lösung, so lange von der Verschiebung kein Eckpunkt betroffen ist, der nicht auf der Nebenbedingung liegt. Das bedeutet z.b. in Abb. 1, daß die Nebenbedingung (i) in dem Korridor zwischen der Lage (u unterer Iterationswert) und (o oberer Iterationswert) bewegt werden kann, ohne die Eckpunkte 1 und 2 zu tangieren. Da die Eckpunkte 3, 4 und 5 auf der Nebenbedingung (i) liegen, verschieben sich diese mit.

6 6 Sensitivitätsanalyse in LP x P 4 (o) x1 (u) (i) Abb. 1: Sensitivitätsanalyse von Rechter Seite b i {or1ab401.pre} An der unteren Iterationsgrenze wird der Eckpunkt 2 erreicht. Unterschreitet man ihn, so muß die zur Ordinate gehörende Schlupfvariable aus der Basis eliminiert werden. An der oberen Iterationsgrenze wird der Eckpunkt 1 erreicht. Bei einer darüber hinausgehenden Vergrößerung von b i stellt die Nebenbedingung (i) keine Beschränkung mehr dar. Ihre Schlupfvariable x i wird daher größer null werden und damit Basisvariable.

7 7 Sensitivitätsanalyse in LP 2 Sensitivitätsanalyse der Zielfunktion Wie zuvor sollen nun die Bewertungsgrößen der Zielfunktion bezüglich ihrer Wirkung auf die Optimallösung analysiert werden. Dabei kommt es - wie im übrigen fast immer, wenn mit der Zielfunktion argumentiert wird - zu einem Sprachproblem, das mit dem (umgekehrten) Vorzeichen der Zielfunktionskoeffizienten im Tableau zusammenhängt. Dadurch wird ein positiver Bewertungskoeffizient im Tableau negativ und eine obere Schranke desselben ergäbe sich im Tableau als untere Schranke. In diesem Sinne ist genau die Sensitivitätsanalyse betroffen, bei der ja derartige Schranken gesucht sind. Wir unterscheiden daher im weiteren zwischen dem Zielzeilenkoeffizient (ZZK) d j, der im Tableau erscheint, und dem Zielfunktionskoeffizient (ZFK) c j, der im Sinne des Zielkriteriums interpretiert wird. Bei der Sensitivitätsanalyse der Zielzeilenkoeffizienten fragen wir: In welchem Bereich darf δ in dem Ausdruck d j = d j + δ schwanken, ohne die Lösung strukturell zu beeinflussen? Gesucht sind also die oberen und unteren Schranken für den Änderungsbetrag δ, bei deren Über- bzw. Unterschreitung eine Iteration ausgelöst wird. Auch in diesem Abschnitt muß man zwei Fälle unterscheiden, je nachdem, ob die betreffende Strukturvariable x j im Optimalzustand Nichtbasisvariable (NBV und damit x j = 0) ist oder Basisvariable (BV und damit i.allg. x j > 0) ist. Zusätzlich kann man die Sensitivitätsanalyse auf ursprüngliche Schlupfvariablen ausdehnen, die im Optimalzustand größer null sind. Dies läßt eine interessante Interpretation zu. Fall 2.1: Sensitivitätsanalyse der Zielfunktionskoeffizienten d j Die Aktivität j wird im Optimalzustand nicht genutzt, weil der ZZK d j um den Betrag d j > 0, d.h. den reduzierten Kosten, zu groß ist. Verringert man den ZZK um d j, d.h. auf d j d j, so wird im Optimalzustand in der Spalte j der ZZK gleich null werden, d.h. eine mehrdeutige Lösung anzeigen. Eine Änderung darüber hinaus ergibt einen negativen Zielzeilenkoeffizient, der eine Iteration auslöst. Bei jeder Vergrößerung von d j würde der Zielzeilenkoeffizient d j nur umso größer werden, so daß hieraus kein Einfluß auf die Lösungsstruktur resultiert. Zusammengefasst: δ u = d j : x j geht in die Basis d j δ u = d j d j d j < (keine Änderung!) Fall 2.2: Sensitivitätsanalyse der Zielfunktionskoeffizienten d s Das Auftreten der Strukturvariablen x s in der Basis bedeutet, daß die Aktivität s auf entsprechendem Niveau x s = b s > 0 genutzt wird. Eine Änderung des Zielzeilenkoeffizienten d s um δ auf d s = d s + δ bedeutet für δ > 0 eine Vergrößerung des ZZK (= eine Verkleinerung des ZFK!) und für δ < 0 eine Verkleinerung des ZZK (= eine Vergrößerung des ZFK!).

8 8 Sensitivitätsanalyse in LP Max x j x r RS z d j + δ a sj d r + δ a sr z 0 + δ b r x s a sj a sr b r Tab. 5: Änderung der Zielfunktion Welchen Wert kann δ annehmen, bis der erste modifizierte ZZK in Tab. 5 gleich Null sein wird? Für δ < 0 wird der ZZK kleiner, d.h. man berechnet die Untergrenze δ u der Änderung; dann kann nur für positive Koeffizienten a sj > 0 einer der ZZK gleich Null werden: d j dj + δ asj = 0 δ= >0 für asj > 0 a sj Der kleinste derartige Quotient zeigt an, um welchen Betrag der zugehörige ZZK maximal verkleinert werden kann, bevor eine Iteration notwendig wird. (u) δ > 0: d u d j cv min asj > 0 = > 0 j asj asv, falls a 0 j Es wird angenommen, daß sich das Minimum in der Spalte mit x v als NBV ergibt. sj Für δ > 0 wird der ZZK größer, d.h. man berechnet die Obergrenze δ o der Änderung; dann kann nur für negative Koeffizienten a sj < 0 einer der ZZK gleich Null werden: (o) δ < 0: d o d j dw max asj < 0 = < 0 j asj asw, falls a 0 j Es wird angenommen, daß sich das Maximum in der Spalte mit x w als NBV ergibt. Für die Zielzeilenkoeffizienten d s ergibt sich damit folgender Schwankungsbereich: sj x v geht in die Basis d s + δ u d s d s + δ o x w geht in die Basis Im Fall 2.2 kann man noch eine sehr informative Sonderbetrachtung anschließen. Eine logische Basisvariable ist entweder eine künstliche Variable oder eine Schlupfvariable. Als künstliche Variable darf sie im Optimalzustand nicht BV sein. Eine Schlupfvariable kann jedoch sowohl NBV (eines knappen Faktors Fall 1.2) als auch BV sein. Letzteres bedeutet, daß von dem betreffenden Faktor ein Restschlupf existiert.

9 9 Sensitivitätsanalyse in LP Eine Schlupfvariable x i unterscheidet sich von einer Strukturvariable hauptsächlich dadurch, daß der Zielfunktionskoeffizient anfangs gleich Null ist. In den folgenden beiden Fällen könnte man sich vorstellen, daß der Schlupf in einem Maximierungsproblem anders als mit null bewertet ist: Einen positiven ZFK (c i > 0) könnte man als Erlös interpretieren mit der Idee, den Rest in jedem Fall zu dem Preis c i > 0 absetzen zu können. Einen negativen ZFK (c i < 0) könnte man als Kosten ansehen, die proportional zur Restmenge entstehen, wie z.b. Lagerkosten. Für eine Schlupfvariable in der optimalen Basis kann man nun durch die Sensitivitätsanalyse ermitteln, in welchem Bereich (zwischen minimalen Kosten und maximalem Erlös) die Bewertung des Restfaktors schwanken kann, ohne die Lösungsstruktur zu ändern. Dazu wendet man auf Zeilen i mit x i > 0 die Abweichungsanalyse wie für Strukturvariablen in der Basis an. Die untere (δ u ) bzw. obere Iterationsgrenze ( δ o ) bestimmen dann den Schwankungsbereich: x v geht in die Basis δ u d i δ o x w geht in die Basis Die Rechenregeln sind nachstehend algorithmisch zusammengefaßt:

10 10 Sensitivitätsanalyse in LP Sensitivitätsanalyse der Zielfunktion d T Input: Output: Simplex-Tableau eines Maximierungsproblems der optimalen Lösung zur Basis B Schwankungsbereiche für alle Koeffizienten des Vektors d T Markierung: Größen des Optimaltableaus sind mit Stern (), die variierten Größen durch Unterstrich gekennzeichnet. Methode: Schritt 1: Die Sensitivitätsanalyse untersucht Wertänderungen der Strukturvariablen, d.h. der ursprünglichen Nichtbasisvariablen (Entscheidungsvariablen) und der Schlupfvariablen, die in der Basis bleiben. Strukturvariable als NBV: x j mit j N δ u = d j : x j geht in die Basis d j δ u = d j d j d j < Schritt 2: Strukturvariable in der Basis: x s mit s B 2.1 Berechne d u d j cv min asj > 0 = > 0 j asj asv, falls a 0 j sj Der minimale positive Quotient ergebe sich in der Spalte v. d o d j dw max asj < 0 = < 0 j asj asw, falls a 0 j sj Der minimale negative Quotient ergebe sich in der Spalte w. 2.2 Als Schwankungsbereich ergibt sich: x v Schritt 3: Logische Variable in der Basis: x i mit i B 3.1 Berechne nach den Regeln 2.1 δ u und δ o für Zeile i: 3.2 Als Schwankungsbereich für die Bewertung des Schlupfs ergibt sich: x v Algorithmus 2: Sensitivitätsanalyse der Zielfunktion

11 11 Sensitivitätsanalyse in LP Beispiel: Das Beispiel des vorausgegangenen Abschnitts soll auch hier zur Illustration dienen. Max x M x 2 x T RS z x R x x Tab. 6: Optimaltableau Var j x R 2,5 (o) 2 (u) x (u) x (u) (o) c a j ij Tab. 7: Quotiententableau Die Sensitivitätsanalyse der Zielfunktionskoeffizienten (ZFK) ergibt also: x v d j + δ u Var j d j d j + δ o x w x x x T x x 2 x x x 2 2 x R 0 2,5 x M Tab. 8: Zusammenfassung der Ergebnisse der Sensitivitätsanalyse der Zielfunktion Auch zur Zielfunktionsanalyse gibt es eine sehr anschauliche geometrische Deutung. Modifikation eines Zielfunktionskoeffizienten c j heißt in jedem Fall, die Neigung der Zielhyperebene in entsprechender Koordinatenrichtung zu ändern; man also dreht die Zielebene um den optimalen Punkt. An der zweidimensionalen Abb. 2 kann man die Wirkung einer Drehung besonders deutlich erkennen. Die Zielfunktion kann um den optimalen Punkt 4 gedreht werden, bis sie parallel zu einer den Optimalpunkt bestimmenden Nebenbedingungen verläuft. Dann hat man den Fall mehrdeutiger Lösungen erreicht. Kippt man die Zielfunktion weiter, d.h. über die Punkte 2 bzw. 3 hinaus, so ändert sich der Optimalpunkt in einen dieser Eckpunkte, was eine Iteration auslösen würde.

12 12 Sensitivitätsanalyse in LP x P x1 Abb. 2: Sensitivitätsanalyse der Zielfunktion {or1ab402.pre}