Transportoptimierung

Transkript

1 Transportoptimierung Mathematisches Modell Konstruktionsverfahren für einen zulässigen Transportplan Duale Aufgabe des TOP Verbesserungsverfahren: MODI-Verfahren 1

2 Transport ein zentrales Element jedes logistischen Systems Transport ist durch die folgenden Elemente charakterisiert: Aufkommensorte A i mit Aufkommensmengen a i [t], i=1,2,,m Bedarfsorte B j mit Bedarfsmengen b j [t], j = 1,2,,n Transportverbindungen zwischen A i und B j (Länge in km) Transportleistung [t km] 2

3 Klassisches Transportproblem Welche Aufkommensorte A i müssen welchen Bedarfsorten B j welche Mengen x ij eines einheitlichen Transportgutes liefern, damit die Gesamttransportleistung [tkm] minimal wird, die Aufkommensorte A i ihre Aufkommensmenge a i absetzen können, die Bedarfsorte B j ihre Bedarfsmenge b j decken können. 3

4 Annahmen des klassischen TOP Jeder Bedarfsort B j kann von jedem Aufkommensort A i beliefert werden. Die Transportkosten c ij von den Orten A i zu den Orten B j sind proportional zur Entfernung von A i nach B j. Die Summe der Aufkommensmengen a i (i=1,2,..., m) muss gleich der Summe der Bedarfsmengen b j (j=1,2,..., n) sein (geschlossenes Transportproblem): a i = b j 4

5 Beispiel 4 Baustellen (B-Orte) beziehen Zement aus 3 Zementwerken (A-Orte). Die Bedarfe der Baustellen betragen dabei im betrachteten Zeitraum b 1 =10 t, b 2 =12 t, b 3 =8 t und b 4 =20 t Zement. Die Aufkommen der Produktionsstätten sind a 1 =11 t, a 2 =15 t und a 3 =24 t Zement. Die Entfernungen zwischen den A-Orten und den B-Orten betragen (in km): c ij [km] B1 B2 B3 B4 A A A Wie viele Tonnen an (gleichwertigem) Zement müssen die B-Orte jeweils aus welchem A-Orte beziehen, damit der Gesamttransportaufwand (gemessen in tkm) minimal wird? 5

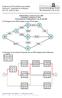
6 Transportnetz A 1 11 t B 1 10 t B 2 12 t 70 Entfernung c ij von A i nach B j in km cij B1 B2 B3 B4 A A A B 4 20 t A 2 15 t A 3 24 t B 3 8 t Ort ai/bj A1 11 A2 15 A B1 10 B2 12 B3 8 B Wichtig a i = b j 6

7 Mathematisches Modell des Transportproblems für m=3 A-Orte und n=4 B-Orte 52 B4 20 t A1 11 t 70 B1 10 t A2 B2 15 t 12 t 70 Entfernung cij von Ai nach Bj in km cij B1 B2 B3 B4 A A A Ges.: m n = 3 4=12 Entscheidungsvariable x ij x ij Liefermenge [t] von A i nach B j i = 1(1)3, j = 1(1)4 A3 24 t B3 8 t Ort ai/bj A1 11 A2 15 A B1 10 B2 12 B3 8 B x 11, x 12, x 13, x 14, x 21, x 22, x 23, x 24, x 31, x 32, x 33, x 34 Lineare Zielfunktion: min z = 70 x x x 34 Nebenbedingungen: m+n =7 lineare Gleichungen mit n m =12 Unbekannten A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 B1: x 11 + x 21 + x 31 = 10 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 Nichtnegativitätsbedingungen: alle x ij 0 7

8 Bemerkung zu den Nebenbedingungsgleichungen Von den m + n Gleichungen ist eine Gleichung stets überflüssig, da sie von den restlichen Gleichungen linear abhängig ist. Warum? m = 3 n = 4 B1: x 11 + x 21 + x 31 = 10 A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 = 10 m i 1 beim klass. TOP wird gefordert: a i m i 1 n a i b j 1 j n j 1 b j es sind m+n-1 Gleichungen linear unabhängig m+n-1 Basisvariable 8

9 allg. mathematisches Modell des klassischen TOP Zielfunktion: m n i 1 j 1 c ij x ij min m+n Nebenbedingungen: n j 1 xij ai, i 1,2,..., m m i 1 xij bj, j 1,2,... n Nichtnegativitätsbedingungen: x ij 0, i 1,2,..., m, j 1,2,..., n. 9

10 Überführung in die Standardaufgabe max und Form Zielfunktion: m n i 1 j 1 c ij x ij min max m n i 1 j 1 c x ij ij max Nebenbedingungen: n j 1 xij ai, i 1,2,..., m n j 1 n j 1 xij ai, i 1,2,..., m xij ai, i 1,2,..., m m i 1 xij bj, j 1,2,... n m i 1 m i 1 xij bj, j 1,2,... n xij bj, j 1,2,... n Nichtnegativitätsbedingungen: x ij 0, i 1,2,..., m, j 1,2,..., n. 10

11 Lösung der Aufgabe mittels primalem Simplexalgorithmus Ges.: 12 Entscheidungsvariable x ij x ij Liefermenge [t] von A i nach B j i = 1(1)3, j = 1(1)4 A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 B1: x 11 + x 21 + x 31 = 10 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 Starttabelle des primalen LOP min z= 70 x x x Entscheidungsvariable 14 Schlupfvariable, weil 14 NB. BV x11 x12 x13 x14 x21 x22 x23 x24 x31 x32 x33 x34 y 1 y 1 y 2 y 2 y 3 y 3 y 4 y 4 y 5 y 5 y 6 y 6 y 7 y 7 b y y y y y y y y y y y y y y z PS PZ 11

12 nach 8.Iteration BV x11 x12 x13 x14 x21 x22 x23 x24 x31 x32 x33 x34 y 1 y 1 y 2 y 2 y 3 y 3 y 4 y 4 y 5 y 5 y 6 y 6 y 7 y 7 b y x y y y x y x y x x y y x z Geben Sie den optimalen Transportplan an. x 22 = 12 t, x 33 =8 t, x 21 =3 t, x 31 =7 t, x 34 = 9 t, x 14 = 11 t Z= 4220 tkm 12

13 Optimaler Transportplan A 1 11t B 1 10 t B 2 12 t 70 m+n-1 = 6 Straßen werden befahren B 4 20 t A 2 15 t Liefermengen von A i -B j x 14 = 11 t x 21 = 3 t, x 22 = 12 t, x 31 = 7 t x 33 = 8 t, x 34 = 9 t, 8 68 B 3 8 t Z =GTL=4220tkm A 3 24 t 13

14 Merke (1) Jede zulässige Basislösung des allgemeinen Transportproblems mit m A-Orten und n B-Orten besitzt genau m + n 1 Basisvariable. 14

15 Empfehlung Löse das klassische Transportproblem über die Transport-Simplexmethode Vorteil: viel schneller als die Standard-Simplexmethode Vergleich: Standard-Simplexmethode: 2(m + n) + 1 Zeilen m n +2(m+n) + 1 Spalten Transport-Simplexmethode: m + 2 Zeilen n + 2 Spalten 15

16 Die Transport-Simplexmethode läuft in zwei Schritten ab: Schritt 1: Bestimmung einer zulässigen Basislösung mit Hilfe eines Konstruktions-(Eröffnungs-) Verfahrens. Schritt 2: Optimierung der zulässigen Basislösung mit Hilfe eines Verbesserungsverfahrens. 16

17 Ges.: m n = 3 4=12 Entscheidungsvariable x ij x ij Liefermenge [t] von A i nach B j i = 1(1)3, j = 1(1)4 x 11, x 12, x 13, x 14, x 21, x 22, x 23, x 24, x 31, x 32, x 33, x 34 Lineare Zielfunktion: min z = 70 x x x 34 Nebenbedingungen: m+n =7 lineare Gleichungen mit n m =12 Unbekannten A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 Nichtnegativitätsbedingungen: alle x ij 0 B1: x 11 + x 21 + x 31 = 10 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 Zusammenfassung aller Bedingungen in einer Tabelle B1 B2 B3 B4 a i A x 11 x 12 x 13 x 14 =Summe 11 A x 21 x 22 x 23 x 24 =Summe 15 A x 31 x 32 x 33 x 34 =Summe 24 =Summe =Summe =Summe =Summe b j z SS cij xij setze m+n-1 von den m * n Variablen so, dass sie mit den m+n Zeilen- und Spaltensummen übereinstimmen. So erhalten wir einen zulässigen Transportplan. 17

18 52 B4 20 t A1 11 t 70 B1 10 t A2 B2 15 t 12 t 70 Entfernung cij von Ai nach Bj in km cij B1 B2 B3 B4 A A A Schritt 1 Konstruktion eines zulässigen Transportplanes A3 24 t B3 8 t Ort ai/bj A1 11 A2 15 A B1 10 B2 12 B3 8 B Trage die a i, b j und c ij -Werte in die entsprechenden Felder ein B1 B1 B2 B2 B3 a B3 B4 B4 i A1 A A2 A A3 A b j zum Bsp. Die Bj-Orte bestellen nacheinander bei ihren nächsten Ai-Orten. B1 beginnt. Belege m+n-1 Felder mit positiven Liefermengen x ij so, dass die Summe der Zeile i dem a i -Wert und die Summe der Spalte j dem b j -Wert entspricht (i=1,2,3, j= 1,2,3,4) (gilt für den nichtdegenerierten Fall) B1 A1 70 x 11 =10 A2 74 x 21 =0 A3 131 x 31 =0 bj 10 B2 135 x 12 =0 70 x 22 = x 32 =0 12 B3 150 x 13 =0 64 x 23 =3 68 x 33 =5 8 B4 52 x 14 =1 147 x 24 =0 125 x 34 =19 20 a i Gesamttransportleistung =70*10+52*1+70*12+64*3+68*5+125*19=4499 tkm 18

19 Übliche Konstruktionsverfahren für zulässige Transportpläne Nordwesteckenregel Zeilen-Spalten Sukzession Spaltenfolge-Verfahren Spaltenminimumverfahren (=Modifiziertes Spaltenfolge-Verfahren) Matrixminimum-Methode Vogel sche Approximationsmethode (besonders geeignet) 19

20 Konstruktionsverfahren 1 für einen zulässigen Transportplan Nordwesteckenregel: Stelle die Aufkommensort-Bedarfsort-Tabelle auf. Belege m+n-1 Felder der A-B Tabelle stufenförmig von links oben (Nord-West) nach rechts unten (Süd-Ost) mit der jeweiligen maximal möglichen Transportmenge x ij.(auch x ij = 0 möglich). Die c ij -Werte bleiben unberücksichtigt (Nachteil dieser Regel). 20

21 zulässiger Transportplan mittels Nordwesteckenregel Belege m+n-1 Felder der A-B Tabelle stufenförmig von links oben (Nord-West) nach rechts unten (Süd-Ost) mit der jeweiligen maximal möglichen Transportmenge x ij. (auch x ij = 0 möglich) Die c ij -Werte bleiben unberücksichtigt (Nachteil dieser Regel). B1 B2 B3 B4 ai A A A bj /50 Rest 11 4 Rest Transportmengen: (=zulässige Basislösung) x 11 =10t, x 12 =1t, x 22 =11t, x 23 =4t, x 33 =4t, x 34 =20t Gesamttransportleistung = 70*10+135*1+70*11+64*4+68*4+125*20=4633 tkm 21

22 Konstruktionsverfahren 2 für einen zulässigen Transportplan Zeilen-Spalten Sukzession Ordne dem günstigsten Feld der A-B Tabelle die maximal mögliche Menge zu. Ordne dem zweit günstigsten Feld in der Zeile oder Spalte die Restmenge zu. Solange zuordnen bis Bedarf für alle Spalten gedeckt ist. (auch x ij = 0 möglich). Markiere Spalte und Zeile, wenn in ihr Rest Null ist. 22

23 zulässiger Transportplan mittels Zeilen- Spalten Sukzession Ordne dem günstigsten Feld der A-B Tabelle die maximal mögliche Menge zu. Ordne dem zweit günstigsten Feld in der Zeile oder Spalte die Restmenge zu. Solange zuordnen bis Bedarf für alle Spalten gedeckt ist. (auch x ij = 0 möglich). Markiere Spalte und Zeile, wenn Rest Null. B1 B2 B3 B4 A Rest A x 21 = 3 5 x 22 = 12 6 A x 31 = 7 4 x 33 = 8 3 x 14 = 11 1 x 34 = Rest / 7 6 Transportmengen: x 14 =11t, x 21 =3t, x 22 =12t, x 31 =7t, x 33 =8t, x 34 =9t Gesamttransportleistung = 52*11+74*3+70*12+131*7+68*8+125*9=4220 tkm 23

24 Konstruktionsverfahren 3 für einen zulässigen Transportplan Spaltenfolge-Verfahren: Ordne dem günstigsten Feld der 1. Spalte der A-B Tabelle die maximal mögliche Menge zu. Verteile die Restmengen auf die jeweils nächst günstigen Felder der 1. Spalte. Wiederhole diese Prozedur für jede nachfolgende Spalte. (auch x ij = 0 möglich). Markiere Spalte und Zeile, wenn Rest Null. 24

25 zulässiger Transportplan mittels Spalten-Folge Verfahren Ordne in der B1 Spalte dem günstigsten Feld die maximal mögliche Menge zu. Verteile die Restmengen auf die jeweils nächst günstigen Felder der 1. Spalte. Wiederhole diese Prozedur für jede der nachfolgenden Bj Spalte. (auch x ij = 0 möglich). Markiere Spalte und Zeile, wenn Rest Null. B1 B2 B3 B4 A Rest x 11 = 10 1 A x 22 = 12 2 x 23 = 3 3 A x 14 = 1 5 x 33 = 5 4 x 34 = Rest Transportmengen: x 11 =10t, x 14 =1t, x 22 =12t, x 23 =3t, x 33 =5t, x 34 =19t Gesamttransportleistung = 70*10+52*1+70*12+64*3+68*5+125*19=4499 tkm 25

26 Konstruktionsverfahren 4 für einen zulässigen Transportplan Spaltenminimum-Verfahren (= Modifiziertes Spaltenfolge-Verfahren) Beginnend mit der 1. Spalte werden allen Spalten die maximal mögliche Menge ihrem günstigsten Feld zugeordnet (auch x ij = 0 möglich). ( Falls die Spaltensumme gleich der Bedarfsmenge markiere diese Spalte. Bei nicht markierten Spalten beginne wieder von vorne und setze einen weiteren Wert beim nächst günstigsten Feld. Wiederhole diese Prozedur für jede nachfolgende Spalte Bj solange bis alle Spalten markiert sind. 26

27 zulässiger Transportplan mittels Spaltenminimum- Verfahren Beginnend mit der 1. Spalte werden allen Spalten die maximal mögliche Menge ihrem günstigsten Feld zugeordnet (auch x ij = 0 möglich). ( Falls die Spaltensumme gleich der Bedarfsmenge markiere diese Spalte. Bei nicht markierten Spalten beginne wieder von vorne und setze einen weiteren Wert beim nächst günstigsten Feld. Wiederhole diese Prozedur für jede nachfolgende Spalte Bj solange bis alle Spalten markiert sind. B1 B2 B3 B4 A x 11 =10 1 A x 22 = 12 2 x 23 = 3 3 A x 14 = 1 4 x 33 = 5 5 x 34 = Rest Rest Transportmengen: x 11 =10t, x 14 =1t, x 22 =12t, x 23 =3t, x 33 =5t, x 34 =19t Gesamttransportleistung = 70*10+52*1+70*12+64*3+68*5+125*19=4499 tkm 27

28 Konstruktionsverfahren 5 für einen zulässigen Transportplan Matrixminimum-Verfahren: Das Matrixminimumverfahren folgt dem Prinzip des besten Nachfolgers. In der A-B Tabelle wird das günstigste Feld gesucht und mit der maximal zulässigen Liefermenge belegt. Danach sucht man das zweit günstigste Feld der Rest A-B Tabelle und ordnet diesem Feld die maximal zulässige Menge zu usw. Bei den einzelnen Schritten sind die Beträge der Nachfragemengen bzw. der Angebotsmengen an die bereits vergebenen Mengen anzupassen. 28

29 zulässiger Transportplan mittels Matrixminimum -Verfahren In der A-B Tabelle wird das günstigste Feld gesucht und mit der maximal zulässigen Liefermenge belegt. Danach sucht man das zweit günstigste Feld der Rest A-B Tabelle und ordnet diesem Feld die maximal zulässige Menge zu usw. Bei den einzelnen Schritten sind die Beträge der Nachfragemengen bzw. der Angebotsmengen an die bereits vergebenen Mengen anzupassen. B1 B2 B3 B4 A A A Transportmengen: x 14 =11t, x 22 =7t, x 23 =8t, x 31 =10t, x 32 =5t, x 34 =9t Gesamttransportleistung= 52*11+70*7+64*8+131*10+187*5+125*9=4.944 tkm 29

30 zulässiger Transportplan mittels Spaltenminimum-Verfahren bei Entartung B1 B2 B3 B4 A A A Rest x 11 =10 1 x 22 = 12 2 x 23 = 4 3 x 33 = 4 5 x 14 = 0 4 x 34 = Rest Transportmengen: x 11 =10, x 14 =0, x 22 =12, x 23 =4, x 33 =4, x 34 =20 Gesamttransportleistung= 70*10+52*0+70*12+64*4+68*4+125*20=4568 tkm Allg.: Falls weniger als (m+n-1) positive x ij, so belege Felder mit Nullen so, dass gewährleistet wird, dass kein Element als einziges in einer Zeile und Spalte steht. 30

31 zulässiger Transportplan mittels Spaltenminimum-Verfahren bei Entartung B1 B2 B3 B4 A A A Rest x 11 =20 1 x 22 = 20 2 x 23 = 0 3 x 33 = 10 5 x 14 = 0 4 x 34 = Rest Transportmengen: x 11 =20, x 14 =0, x 22 =20, x 23 =0, x 33 =10, x 34 =10 Gesamttransportleistung= 70*20+52*0+70*20+64*0+68*10+125*10=4730tkm Allg.: Falls weniger als (m+n-1) positive xij, so belege Felder mit Nullen so, dass gewährleistet wird, dass kein Element als einziges in einer Zeile und Spalte steht. 31

32 zulässiger Transportplan mittels Nordwesteckenregel bei Entartung B1 B2 B3 B4 A A A3 4 a i b j /50 Rest Rest 0 Transportmengen: (=zulässige Basislösung) x 11 =10t, x 12 =0, x 22 =11t, x 23 =5t, x 33 =4t, x 34 =20t oder x 11 =10t, x 21 =0, x 22 =11t, x 23 =5t, x 33 =4t, x 34 =20t Wenn a i = b j so fährt man bei A i+1 und B j+1 fort, nimmt aber x i+1,j oder x i,j+1 als Basisvariable mit Wert 0 in die Basis auf. Die Basislösung ist dann entartet. Gesamttransportleistung = 70*10+70*11+64*5+68*4+125*20=4562 tkm 32

33 Merke (2) Unter den m + n -1 Basisvariablen x ij können auch Variable mit dem Wert Null sei. (sog. degeneriertes Problem). Degeneration tritt auf, wenn eine Mengenzuweisung gleich zwei Gleichungen erfüllt, nämlich Zeilen- und Spaltengleichung. allg.: Zur Belegung mit Nullen sind solche freien Felder auszuwählen, die gewährleisten, dass kein x ij >0 als einzige Variable in einer Zeile und Spalte steht. 33

34 Überprüfung auf Optimalität des Transportplanes durch Berechnung der Opportunitätskosten Zulässiger TP nach Spaltenminimum-Verfahren B1 B2 B3 B4 A A D A bj ai Hinweis: Zur Erhaltung der Zeilen- und Spaltensumme muss jeweils eine 1 bei den entsprechenden besetzten Feldern addiert oder subtrahiert werden. (=nach jedem Schritt rechtwinklig die Richtung wechseln Entstehung eines Zyklus) Lösungsidee: Stepping-Stone (=Distributionsmethode) Da die kurze Strecke von A2 nach B1 mit c 21 =74 km nicht vorgeschlagen wurde, stellt sich die Frage Was wäre, wenn dort eine Tonne transportiert wird, also x 21 = 1 ist?. Wir bestimmen die Opportunitätskosten oc 21. Ist oc 21 <0, so kann der Transportplan noch verbessert werden. Berechne die Opportunitätskosten: ioc 21 = = -65 Die Gesamttransportleistung könnte um 65 tkm reduziert werden. 34

35 Die Transport-Simplexmethode läuft in zwei Schritten ab: Schritt 1: Bestimmung einer zulässigen Basislösung mit Hilfe eines Konstruktions-(Eröffnungs-) verfahrens. nun zum Schritt 2: Optimierung der zulässigen Basislösung mit Hilfe eines Verbesserungsverfahrens. 35

36 Modifizierte Distributionsmethode (MODI-Methode) ist ein iteratives exaktes Verbesserungsverfahren, das in Analogie zum Simplex-Algorithmus in jeder Iteration eine Basisvariable (BV) gegen eine Nichtbasisvariable (NBV) austauscht. Dies geschieht so lange, wie dadurch eine Verminderung der Gesamttransportleistung [tkm] erzielt werden kann. Um die von einem Tausch betroffene BV zu identifizieren, nutzt die Methode Erkenntnisse der Dualitätstheorie. 36

37 Prinzip der MODI-Methode 1. Zu einer zulässigen Basislösung x wird ein duale Lösung (u,v) konstruiert. 2. Danach werden für alle Nichtbasisvariablen mit Hilfe der dualen Lösung die Opportunitätskosten bestimmt. Sind alle Opportunitätskosten größer oder gleich Null, so ist die aktuelle Basislösung optimal. 3. Ist die aktuelle Basislösung nicht optimal, wird durch eine Umverteilung der Transportmengen die Nichtbasisvariable mit den kleinsten negativen Opportunitätskosten in die Basis aufgenommen und eine Basisvariable herausgenommen. Die Methode beginnt von vorne. denke an z-zeile in Simplex-Tabelle 37

38 Ökonomische Formulierung der dualen Aufgabe Versorgung durch Transaktionen (Beschaffung/Verkauf) Der Transport wurde bisher durch eine Spedition realisiert. Anstelle des Transports ist folgendes denkbar: die Produktmengen a i der A i -Orte werden jeweils am A i -Ort an ein anderes Unternehmen verkauft: Preis pro ME: - u i, i=1,2,3 und die Bedarfsmengen b j der B j -Orte werden jeweils am B j -Ort von diesem Unternehmen gekauft: Preis pro ME: + v j, j=1,2,3,4 Die Preisdifferenz v j (- u i ) =(u i + v j ) pro ME sollte für die Spedition nicht größer als die Transportkosten c ij pro ME sein. Das Unternehmen will sein Ergebnis maximieren. 38

39 Primale - Duale Aufgabe des TOP Primale Aufgabe Ges.: 12 Entscheidungsvariable x ij x ij Liefermenge [t] von A i nach B j i = 1(1)3, j = 1(1)4 Duale Aufgabe Ges.: 7 Entscheidungsvariable Kaufpreis u i, und Verkaufspreis v j pro ME u i v j i = 1(1)3, j = 1(1)4 unter Beachtung von 7 Nb.: A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 B1: x 11 + x 21 + x 31 = 10 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 min z= 70 x x x 34 x11 x12 x13 x14x21x22x23 x24 x31 x32 x33 x34 b A A A B B B B z F unter Beachtung von 12 Nb.: u 1 + v 1 + oc 11 = 70 u 1 + v 2 + oc 12 = 135 u 1 + v 3 + oc 13 = 150 u 1 + v 4 + oc 14 = 52 u 2 + v 1 + oc 21 = 74 u 2 + v 2 + oc 22 = 70 u 2 + v 3 + oc 23 = 64 u 2 + v 4 + oc 24 = 147 u 3 + v 1 + oc 31 = 131 u 3 + v 2 + oc 32 = 187 u 3 + v 3 + oc 33 = 68 u 3 + v 4 + oc 34 = 125 Preisdifferenz nicht größer als Transportkosten pro ME max F= 11u 1 +15u 2 +24u 3 +10v 1 +12v 2 +8v 3 +20v 4 Tabelle zunächst vertikal kippen und dann Rechtsdrehung um 90 x ij 0 u i, v j R 39

40 Duale Formulierung der Standard- Simplexmethode primales Problem: 7 lin. Nebenbedingungen A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 B1: x 11 + x 21 + x 31 = 10 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 min. lin. Zielfunktion mit 12 Variablen min z =70x x x 34 duales Problem: 7 Entscheidungsvariable u 1 u 2 u 3 v 1 v 2 v 3 v 4 max. lin. Zielfunktion mit 7 Variablen max F =11u u u v v v v 4 12 Variable x 11,x 12,,x 33,x 34 u 1 + v 1 70 mit c ij [km] B1 B2 B3 B4 x ij 0 A A A i = 1(1)3, j = 1(1)4 12 Nebenbedingungen u 1 + v u 1 + v u 1 + v 4 52 u i, v j R u 2 + v 1 74 u 2 + v 2 70 u 2 + v 3 64 u 2 + v u 3 + v u 3 + v u 3 + v 3 68 u 3 + v

41 Duale Formulierung der Standard- Simplexmethode primales Problem: 7 lin. Nebenbedingungen A1: x 11 + x 12 + x 13 + x 14 = 11 A2: x 21 + x 22 + x 23 + x 24 = 15 A3: x 31 + x 32 + x 33 + x 34 = 24 B1: x 11 + x 21 + x 31 = 10 B2: x 12 + x 22 + x 32 = 12 B3: x 13 + x 23 + x 33 = 8 B4: x 14 + x 24 + x 34 = 20 min. lin. Zielfunktion mit 12 Variablen min z =70x x x 34 duales Problem: 7 Entscheidungsvariable u 1 u 2 u 3 v 1 v 2 v 3 v 4 max. lin. Zielfunktion mit 7 Variablen max F =11u u u v v v v 4 12 Variable x 11,x 12,,x 33,x 34 u 1 + v 1 70 mit c ij [km] B1 B2 B3 B4 x ij 0 A A A i = 1(1)3, j = 1(1)4 12 Nebenbedingungen u 1 + v u 1 + v u 1 + v 4 52 u i, v j R u 2 + v 1 74 u 2 + v 2 70 u 2 + v 3 64 u 2 + v u 3 + v u 3 + v u 3 + v 3 68 u 3 + v

42 42 Merke Es gilt für die 12 Nebenbedingungen: u 1 + v 1 + oc 11 = c 11 x11 u 2 + v 1 + oc 21 = c 21 x21 u 3 + v 1 + oc 31 = c 31 x31 u 1 + v 2 + oc 12 = c 12 x12 u 2 + v 2 + oc 22 = c 22 x22 u 3 + v 2 + oc 32 = c 32 u 1 + v 3 + oc 13 = c 13 u 2 + v 3 + oc 23 = c 23 u 3 + v 3 + oc 33 = c 33 x13 x23 x32 x33 u 1 + v 4 + oc 14 = c 14 x14 u 2 + v 4 + oc 24 = c 24 x24 u 3 + v 4 + oc 34 = c 34 x34 Kennen wir eine zulässige primale Basislösung (= zulässiger Transportplan m + n -1 positive x ij Werte), so sind in den entsprechenden m + n 1 Ungleichungen des Ungleichungssystems die oc ij gleich null. Es werden also m+n-1 Ungleichungen zu m+n-1 Gleichungen mit m+n Variablen. Setzten wir eine der Variablen gleich null, im allg. u 1 = 0, so erhalten wir eine zugehörige duale Lösung zur zulässigen primalen Lösung.

43 Tabelle des Modi-Verfahrens B 1 B 2... B n ai Dual variable A 1 c 11 c 12 c 1n u 1 x 11 x x 1n a 1 A 2 c 21 c 22 c 2n u 2... a A m c m1 c m2 c mn u m x m1 x m2... x mn a m bj b 1 b 2... b n Z Dual variable v 1 v 2... v n 43

44 Schritt 2.1 Berechnung der Dualvariablen u i und v j in der Transport-Simplextabelle Basisvariablen x ij aus dem Spalten-Minimum-Verfahren B1 B2 B3 B4 A A A vj ui Falls x ij > 0, so ist u i +v j = c ij gesetzt: u 1 = 0 x 11 = 10 v 1 = 70 0 = 70 x 14 = 1 v 4 = 52 0 = 52 x 34 = 19 u 3 = = 73 x 33 = 5 v 3 = = -5 x 23 = 3 u 2 = 64 (-5) = 69 x 22 = 12 v 2 = = 1 44

45 Schritt 2.2 Berechnung der Opportunitätskosten oc ij in der Transport-Simplextabelle Für x ij = 0 (Nichtbasisvariablen) Opportunitätskosten oc ij ermitteln: oc ij = c ij (u i + v j ) B1 B2 B3 B4 ui A A A vj oc 12 = 135-(0+1) =

46 Schritt 2.3 Optimalitätstest mittels Opportunitätskosten oc ij in der Transport-Simplextabelle B1 B2 B3 B4 ui A A A vj Negative Opportunitätskosten geben an, um wie viel sich die Transportkosten vermindern, wenn das zugehörige Mengenelement x ij (Nichtbasisvariable) mit einer Einheit belegt wird. Wenn alle oc ij > 0 eindeutige optimale Lösung, oc ij 0 mehrere optimale Lösungen. wenn oc ij < 0 so Optimallösung noch nicht erreicht 46

47 Schritt 2.4 Basistausch Ein freies Feld mit den negativsten Opportunitätskosten wird mit einer Transportmenge D belegt Aufnahme einer Nichtbasisvariable in die Basislösung. Durch die Besetzung eines Feldes muss ein bisher besetztes Feld wieder frei werden. eine Basisvariable wird zur Nichtbasisvariablen. Durch den Austausch der Variablen dürfen die Nebenbedingungen für Aufkommens- und Bedarfsorte nicht verletzt werden. 47

48 Basistausch B1 B2 B3 B4 A D D 3 11 A D -65 +D D A D D 4 24 bj ai Im Feld mit dem negativsten Opportunitätskostenwert wird x ij keine der zu verändernden Variablen negativ wird x ij =+D Wähle D = min{10,19,3} = 3 Veränderung = oc 21 *3 = -65*3 = -195 so gewählt, dass Die Zahl D kreist nun rum, es ist darauf zu achten, dass durch diese Zahl die aiund bj-werte nicht verändert werden. neue Gesamttransportleistung = = 4304 tkm 48

49 Verbesserter TP B1 B2 B3 B4 ai A A A bj Ist dieser TP optimal? 49

50 Opportunitätskostenberechnung, Optimalitätstest und Basistausch B1 B2 B3 B4 ui A D D 0 A A D D 73 vj nicht optimal, da noch negativer Opportunitätskostenwert => weitere Verbesserung nötig. Wir belegen das leere Feld A3-B1 mit D = min{7,16} = 7 und vollziehen einen Ringtausch. 50

51 Verbesserter TP und Optimalitätstest B1 B2 B3 B4 A A x21 = 3 x22 =12 A vj x14 =11 X31 = 7 x33 = 8 x34 = 9 ui Beachte, hier wurde u 3 = 0 gesetzt, weil sofort v 4, v 3 und v 1 bestimmt werden können. Da alle Opportunitätskostenwerte positiv sind, liegt nun ein optimaler Transportplan vor. 51

52 Vergleich optimale Tabelle nach MODI-Methode und Simplex- Methode B1 B2 B3 B4 ui A x14 =11-73 A x21 = 3 x22 = A X31 = 7 60 x33 = 8 x34 = 9 vj x 14 = 11 tx 21 =3 t, x 22 = 12 t, x 31 =7 t, x 33 =8 t,, x 34 = 9 t, Z= 4220 tkm BV x11 x12 x13 x14 x21 x22 x23 x24 x31 x32 x33 x34 y 1 y 1 y 2 y 2 y 3 y 3 y 4 y 4 y 5 y 5 y 6 y 6 y 7 y 7 b y x y y y x y x y x x y y x z

53 Zusammenfassung 1. Zu jeder Zeile i und zu jeder Spalte j der A i B j Tabelle ist eine Dualvariable u i bzw. v j zu berechnen und zwar derart, dass für alle besetzten Felder (Variablen der Basislösung) gilt: c ij = u i + v j. 2. Für alle unbenutzten Felder (Nicht-Basisvariablen) ist aus den Dualvariablen ein Opportunitätswert oc ij = c ij (u i + v j ) zu berechnen. Dieser Wert gibt an, um wie viel sich die Gesamttransportleistung ändert, wenn man einen gegenwärtig unbenutzten Transportweg mit einer Transporteinheit durch Änderung des Transportplanes in Anspruch nähme. 3. Eine Lösung ist optimal, in der keine negativen oc ij vorkommen. Kommen negative oc ij vor, so ist eine neue Basislösung zu bilden und mit Vorschrift 1 erneut zu beginnen. 53

54 Beachte: Sind die Aufkommensmengen a i und die Bedarfsmengen b j ganze Zahlen, dann ist jede Basislösung und insbesondere der optimale Transportplan ganzzahlig. Satz 2.13: Jede Basislösung eines linearen Programms ist genau dann ganzahlig, wenn bei ganzzahligen rechten Seiten b i die Koeffizientenmatrix A total unimodular * ist. * Eine Matrix A heißt total unimodular wenn die Determinanten aller quadratischen Teilmatrizen von A nur die Werte 0, 1 oder -1 annehmen. 54

55 Übung Die drei Aufkommensorte A1, A2 und A3 mit den Aufkommensmengen a1 = 60, a2 = 80, a3 = 100 haben die vier Bedarfsorte B1, B2, B3 und B4 mit den Bedarfsmengen b1 = 40, b2 = 100, b3 = 30 und b4 = 70 mit einem einheitlichen Gut zu beliefern. Die Entfernungen der A-Orte zu den B-Orten sind der Entfernungstabelle zu entnehmen. B1 B2 B3 B4 A A A Stellen Sie eine zulässigen Transportplan nach der NW-Eckenregel oder nach dem Spaltenminimum-Verfahren auf und bestimmen Sie dann die optimale Lösung mittels Modi-Verfahren. 55

56 zulässiger Transportplan mittels Spaltenminimum-Verfahren B1 B2 B3 B4 A A A bj aj Transportmengen: x 14 =60, x 21 =40,x 23 =30, x 24 = 10, x 32 =100, x 33 =0, Gesamttransportleistung = 10*60+70*40+80*30+80*10+60*100+70*0= GE 56

57 Anwendung des Verbesserungsverfahrens MODI B1 B2 B3 B4 ui A A A vj Z =