Räumliche Indexstrukturen
|
|
|
- Roland Fried
- vor 7 Jahren
- Abrufe
Transkript
1 Referat Räumliche Indexstrukturen Alexander Bau 2. Juli 2008
2 Inhaltsverzeichnis 1 Einführung 3 2 Grundlagen Anforderungen Minimal umspannende Rechtecke Clipping Nachteile Punkttransformationen Nachteile Z-Ordnung FASS-Kurven Z-Werte Nachteile Quadtrees PR-Quadtree Einbettung einer Z-Ordnung Überlappende Blockregionen R-Baum R-Baum-Varianten R -Baum R + -Baum Quellen 16 2
3 1 Einführung Die Speicherung, Verwaltung und Abfrage von räumlichen Strukturen stellt eine besondere Herausforderung an ein Datenbankmanagementsystem (DBMS). So müssen viele Operatoren und Strukturen, die beim Umgang mit flachen Daten eingesetzt werden, erweitert oder sogar ersetzt werden, um diesen neuen Herausforderungen gerecht zu werden. Dieses Dokument stellt eine Auswahl von gebräuchlichen Indexstrukturen vor, die in heutigen DBMS zum Einsatz kommen. Anwendung finden die vorgestellten Verfahrung bspw. in Geodatenbanksystemen, CAD-Anwendungen (Computer Aided Design), aber auch in hochdimensionalen Problemen der Mathematik und Bioinformatik. 2 Grundlagen Indexstrukturen haben innerhalb eines Datenbankmanagementsystems zwei wichtige Aufgaben. Zum einen sollen sie eine effiziente Speicherplatzausnutzung der zugrunde liegenden Datenträger gewährleisten, andererseits sollen die Zugriffszeiten auf die gespeicherten Daten minimiert werden. Die Güte der Lösung dieser beiden Aufgaben stellt ein wichtiges Qualitätsmerkmal eines DBMS dar. Daher wurden Standardlösungen entwickelt, welche auch in vielen anderen Bereichen der Informatik Anwendung finden. Dazu gehören B-Bäume und Hashtabellen. Beide Ansätze werden in heutigen DBMS erfolgreich umgesetzt, stellen aber eine essentielle Anforderung an die zu speichernden Daten: Es muss eine Ordnungsrelation R (Lineare Ordnung bzw. Totalordnung) zwischen den Elementen der zu speichernden Datenmenge M definiert sein. x y {x M, y M, x y (x, y) R (y, x) R} Diese Bedingung ist für einfache Datenypen erfüllt. Bspw. können Strings durch eine lexikographische Ordnung und Zahlen anhand ihrer natürlichen Reihenfolge sortiert werden. Bei mehrdimensionalen Daten ist eine solche Ordnung aber nicht mehr gegeben. So kann z.b. nicht entschieden werden, welcher von zwei Punkten einer Ebene kleiner ist. Daher wäre es nicht möglich, diese Punkte in einem B-Baum zu speichern. Die im folgenden vorgestellten Indexstrukturen lassen sich anhand unterschiedlicher Kriterien klassifizieren. So spielt die Art der zu speichernden Daten eine wichtige Rolle. Dabei sind die Rechteckstrukturen von besonderer Bedeutung. Sie werden in Anwendungsfällen genutzt, bei denen es um die Speicherung von ausgedehnten Geometrien, wie z.b. Polygone und Linienzüge, geht. Durch die räumliche Ausdehnung dieser Objekte entstehen weitere Probleme, die von den einzelnen Strukturen jeweils anders behandelt werden. Falls jedoch ausschließlich Punktwolken zu speichern sind, können spezielle, meist weniger komplexe, Indexstrukturen genutzt werden. 3
4 2.1 Anforderungen Unabhängig von der Klassifizierung stellen die oben aufgeführten Anwendungsgebiete weitere Anforderungen an die jeweils gewählte räumliche Indexstruktur. So spielt die Suche bezüglich geometrischer Attribute eine wichtige Rolle. In der Praxis kommen hauptsächlich zwei Abfrageformen zum Einsatz: die Punktabfrage und die Rechteckanfrage. Bei der Punktabfrage sind alle Objekte von Interesse, die einen Abfragepunkt P schneiden. In den meisten Strukturen ist diese Abfrageform wesentlich einfacher zu verarbeiten als die Rechteckabfrage, bei der alle Objekte gesucht sind, die ein gegebenes Abfragerechteck R schneiden. Wie beide Abfragen in den einzelnen Verfahren umgesetzt wurden, wird an späterer Stelle beleuchtet. Der effiziente Umgang mit dynamischen Datenmanipulationen stellt eine weitere Herausforderung an die gewählte Indexstruktur dar. So muss die Struktur auf Einfüge-, Änderungs- und Löschoperationen entsprechend reagieren können. Viele Datenstrukturen sind von der Abarbeitungsreihenfolge solcher Operationen abhängig, so dass es im Worst-Case zu einer degenerierten Struktur kommen kann, die negative Laufzeiten zur Folge hat. Eine weitere Ursache für solche Abnormalitäten ist eine extreme Ungleichverteilung der Daten im Datenraum. 2.2 Minimal umspannende Rechtecke Die oben angesprochenen Rechteckstrukturen arbeiten meist nicht auf den rohen Anwendungsdaten, sondern nutzen eine angemessene Approximation. Dies hat mehrere Gründe: So gestaltet sich bspw. der Überlappungstest zwischen einem Anfragerechteck und einem komplexen Polygon als äußert schwierig. Da in vielen Datenbanken die Anfrage die am häufigsten genutzte Operation ist, würde ein solcher Test sich negativ auf die Laufzeit auswirken. Ein weiterer Grund stellt die Abstraktion von konkreten Daten dar. Da in Rechteckstrukturen unterschiedlich geartete Geometriedaten gespeichert werden können, ist es hilfreich, von der konkreten Form der Daten zu abstrahieren, um das System generisch zu halten und für eventuelle Weiterentwicklungen zu öffnen. Eine solche Abstraktion stellt der Ansatz der Konservativen Approximation dar. Bei dieser Form der Approximation wird eine umfassende Fläche F (bzw. Körper im R 3 ) um das zu speichernde Objekt O gelegt, welche gerade so groß ist, dass alle Punkte von O innerhalb von F liegen. Im R 2 wird häufig ein achsenausgerichtetes Rechteck genutzt, welches minimal umspannendes Rechteck (MUR) genannt wird. Als achsenausgerichtet bezeichnet man ein MUR, falls alle Kanten des MUR parallel zu den Koordinatenachsen sind. Im R 3 ist häufig auch von Axis Aligned Bounding Boxes die Rede. Diese und weitere Formen der konservativen Approximation sind in Bild 1 illustriert. Eine davon sind die gedrehten minimal umspannenden Rechtecke. Durch ihre stärkere Ausrichtung an der von ihnen umgebenen Geometrie werden sie häufig auch Object Oriented Bounding Boxes genannt. Eine weitere Form sind die konvexen Hüllen, die das von ihnen umgebene Objekt durch ein konvexes Polygon annähern. Beide Ausprägungen versuchen den offensichtlichen Nachteil der MUR zu minimieren, dass sie Punkte einschließen, die nicht zum approximierten Objekt gehören. Dadurch würde auch die 4
5 Abbildung 1: Verschiedene konservative Approximationen Wahrscheinlichkeit von Fehltreffern bei Abfragen verkleinert werden. Dieser Erfolg wird jedoch durch eine schwierigere Berechenbarkeit und eine aufwendige Verwaltung der Approximationen erkauft. Daher spielen bei den weiteren Verfahren nur die normalen MUR eine Rolle. 3 Clipping Eines der einfachsten Verfahren stellt das Clipping dar. Hierbei wird zunächst der Datenraum in gleichgroße, disjunkte Blöcke aufgeteilt. Die zentrale Idee beim Clipping ist, dass ein Objekt allen Blöcken des Datenraumes zugeordnet wird, die die MUR des betreffenden Objektes schneiden. Falls ein Objekt (bzw. dessen MUR) jedoch mehrere Blöcke überlappt, so wird das entsprechende Objekt an den Blockgrenzen zerschnitten und die einzelnen Teile werden den jeweiligen Blöcken zugeordnet. In Bild 2 ist ein einfacher Anwendungsfall illustriert. Im Beispiel wurde eine Auflösung von 3 * 3 Blöcken gewählt, um den kompletten Datenraum zu unterteilen. Man erkennt, dass bspw. das Rechteck R 2 von vier Blockregionen geschnitten wird. Demzufolge wird R 2 in R 2.1, R 2.2, R 2.3 und R 2.4 aufgeteilt und die einzelnen Teile werden nun den jeweils überlappenden Blöcken zugeordnet. Dadurch ergibt sich eine einfache 1:n-Beziehung zwischen den einzelnen Blockregionen und den Objektteilen (ein Objektteil ist genau einer Blockregion zugeordnet und eine Blockregionen speichert n Objektteile). Für eine Punktanfrage mit dem Punkt P muss geklärt werden, in welcher Blockregion P liegt. Alle Objekte, die in diesem Block gespeichert sind, müssen auf Überschneidung mit P getestet und ggf. der Ergebnismenge hinzugefügt werden. Bei einer Rechteckanfrage betrifft dies jedoch mehrere Blöcke. Daher muss hier über alle Blöcke iteriert werden, die sich mit dem Anfragerechteck R überschneiden. 5
6 Abbildung 2: Beispielanwendung des Clipping-Verfahrens 3.1 Nachteile Dem Vorteil der relativ einfachen Arbeitsweise dieses Verfahrens stehen eine Reihe Nachteile gegenüber. Der Offensichtlichste betrifft die getrennte Speicherung von Objekten. Das hat zur Folge das bei Rechteckanfragen das selbe Objekt mehrfach in der Ergebnismenge auftauchen kann, weil mehrere Teile des Objektes in unterschiedlichen Blockregionen das Anfragerechteck geschnitten haben. Daher müssen Duplikate in einem weiteren Arbeitsschritt erkannt und ggf. entfernt werden. Zwei wesentliche Faktoren beeinflussen die Effizienz dieses Verfahrens. Zum einen ist das die Auflösung der Datenraumaufteilung und zum anderen die durchschnittliche Größe der zu speichernden Objekte. Falls einer der beiden Faktoren ungünstig gewählt wurde, kann es entweder passieren, dass große Objekte sehr oft aufgeteilt werden müssen, was eine schlechte Speicherplatzausnutzung bedeutet, oder, dass viele Objekte in zu großen Blockregion gespeichert werden, was bei Rechteckanfragen Überlappungstest für viele Objekte nach sich zieht. Das würde eine sehr schlechte Antwortzeit für solche Anfrageformen bedeuten. 4 Punkttransformationen Um die Nachteile des Clippings bei Objekten mit geometrischer Ausdehnung zu vermeiden, bedient man sich der Punkttransformation in einen höherdimensionalen Raum. Bei dieser Operation werden achsenparallele Rechtecke im R 2 zu vierdimensionalen Punkten und achsenparallele Quader im R 3 zu sechsdimensionalen Punkten transformiert. Der Grund für diesen Aufwand ist die Idee, dass sich höherdimensionale Punkte einfacher verwalten lassen, als niederdimensionale Körper bzw. Flächen. Daher werden zur Spei- 6
7 cherung der transformierten Objekte mehrdimensionale Punktstrukturen genutzt, wie bspw. der k-d-baum zur Speicherung von Punkten im R k. Bild 3 zeigt am Beispiel der Mittentransformation, wie sich ein Rechteck in einen höherdimensionalen Punkt transformieren lässt. Abbildung 3: Parameter, die ein Rechteck eindeutig beschreiben (Mittentransformation) Bei der Mittentransformation wird ein Rechteck durch seinen Mittelpunkt M und seine Ausdehnung D in beide Dimensionen beschrieben. Da M und D zwei Koordinatenpaare bilden, lassen sich diese vier Zahlen als Punkt im R 4 auffassen und in einer entsprechenden Struktur speichern. Äquivalent arbeitet die Eckentransformation, die ein Rechteck durch zwei gegenüberliegende Eckpunkte beschreibt. 4.1 Nachteile Die Punkttransformation besitzt zwei erhebliche Nachteile. Zum einen geht die räumliche Beziehung zwischen Objekten im ursprünglichen Datenraum verloren. Diese Tatsache soll in Bild 4 verdeutlicht werden. Abbildung 4: Verlust räumlicher Beziehungen bei der Transformation von eindimensionalen Intervallen In diesem Beispiel wurden zur besseren Übersicht eindimensionale Intervalle (statt zwei- 7
8 dimensionaler Rechtecke) transformiert. I 2 und I 3 liegen dabei auf I 1, d.h. die räumliche Beziehung zwischen I 1 und I 2 und zwischen I 1 und I 3 ist höher als zwischen I 2 und I 3. Jedes Intervall wird durch die Abszisse der Intervallmitte und die Ausdehnung repräsentiert. Z. Bsp. hat I 1 eine Ausdehnung von 0.4 und die Mitte befindet sich bei x = 0.5. Diese beiden Parameter werden nun als Punkt im R 2 aufgefasst. Das rechte Bild zeigt die transformierten Intervalle (I x P x ), wobei alle Punkte P x unterhalb des eingezeichneten Dreiecks liegen. Nun ist erkennbar, dass bspw. die räumliche Beziehung zwischen I 1 und I 2 verloren gegeangen ist, da der Abstand zwischen P 1 und P 2 größer ist als der Abstand zwischen P 2 und P 3. Das hat zur Folge, dass Anfrageintervalle im transformierten Raum größer sein müssen, als Anfrageintervalle im Ursprungsraum, was wiederum eine schlechtere Laufzeit zur Folge hat. Ein weiterer bedeutender Nachteil ist die extreme Ungleichverteilung der Daten im transformierten Raum. Unter realen Bedingungen würden sich die meisten der transformierten Punkte P x knapp überhalb der Abszissenachse befinden. 5 Z-Ordnung Die Z-Ordnungen gehen einen anderen Weg als die bisher vorgestellten Verfahren. Bei dieser Indexstruktur wird eine lineare Ordnung, basierend auf einer FASS-Kurve, eingeführt. 5.1 FASS-Kurven Eine FASS-Kurve (space-f illing, self-avoiding, simple, self-similar - raumfüllend, selbstausweichend, einfach, selbstähnlich) ist eine eindimensionale Linie, die eine Gitterstruktur im R 2 oder R 3 komplett durchläuft. Sie besitzt eine Berechnungsvorschrift, die beliebig oft, rekursiv angewendet werden kann. Daher nähert sich eine FASS-Kurve jedem Punkt in der gewählten Dimension beliebig genau an. Zwei wichtige Kriterien, nach denen die Menge aller FASS-Kurve klassifiziert werden kann, sind die Güte der Nachbarschaftserhaltung (s.u.) und die Komplexität der Berechnungsvorschrift. Obwohl die Hilbert-Kurve eine bessere Nachbarschafterhaltung aufweist als die Z-Kurve, ist sie schwerer zu berechnen. Somit stellt die Z-Kurve einen guten Kompromiss zwischen beiden Anforderungen dar und gibt dem Verfahren daher seinen Namen. 5.2 Z-Werte Ähnlich wie beim Clipping wird bei diesem Verfahren der Datenraum zunächst durch eine Gitterstruktur aufgeteilt. Bei den Z-Ordnungen wird diese Gitterstruktur durch reguläre Binärregionen beschrieben. Reguläre Binärregionen der Auflösung n teilen den Datenraum in 2 n Blöcke. Im Bild 5 sind einige Beispiele für unterschiedliche Auflösungen angegeben. 8
9 Abbildung 5: Die Z-Ordnung bei verschiedenen Auflösungen Eine Binärregion x im Gitter wird durch ein Wertepaar (index x, auflösung x ), dem sog. Z-Wert, dargestellt, wobei index x durch die Durchlaufreihenfolge der Z-Kurve gegeben ist, d.h. die erste durchlaufende Binärregion bekommt den Index 0 zugewisen, die Nächste den Index 1 und die letzte Binärregion den Index 2 n 1. Für jede Binärregion wird ebenfalls die Auflösung des Gitters gespeichert. Der Grund für dieses Verhalten wird im Abschnitt Quadtrees erklärt. Das mittlere Beispiel in Bild 5 zeigt die Z-Werte für eine Gitteraufteilung der Auflösung 4. Hier ist die nachbarschaftserhaltende Eigenschaft der Z-Kurve gut erkennbar, da bspw. in unmittelbarer Umgebung von (1, 4) ebenfalls die Z-Werte (0, 4) und (2, 4) zu finden sind. Natürlich gilt dies nicht für alle Blöcke, da z.bsp. die Werte (3, 4) und (9, 4) ebenfalls nebeneinander liegen. Durch die Enumeration der einzelnen Binärregionen kann eine Ordnungsrelation basierend auf der Durchlaufreihenfolge der Z-Kurve definiert werden. X < Y index x < index y Durch diese Ordnungsrelation ist es nun möglich die einzelnen Binärregionen in einer herkömmlichen Indexstruktur, wie z.b. dem B + -Baum zu speichern. Bild 6 zeigt eine beispielhafte Situation bei der Nutzung der Z-Ordnung. Im Beispiel soll das Polygon P 1 und die Linie L 1 gespeichert werden, aber beide Objekte schneiden mehrere Binärregionen. In einem solchen Fall wird ähnlich verfahren wie beim Clipping. Es werden alle betroffenen Binärregionen mit einem Verweis auf das jeweilige Objekt im B + -Baum gespeichert. Da bspw. P 1 vier Binärregionen schneidet, existieren vier Verweise im Baum auf P 1. Um eine Punktanfrage zu bearbeiten, wird der entsprechende Z-Wert des Anfragepunktes 9
10 Abbildung 6: Beispielhafter Anwendungsfall berechnet und alle Objekte die im Baum durch die entsprechende Binärregion referenziert werden, müssen in weiteren Arbeitsschritten bedacht werden (Überschneidungstests etc.). Bei Rechteckanfragen muss die Menge M aller Binärregionen berechnet werden, die das Anfragerechteck approximieren. Aus M lassen sich dann mehrere (mindestens eine) Bereichsanfragen an den B + -Baum ableiten, die zur Ermittlung aller gewünschten Objekte führt. Dabei kann es jedoch vorkommen, dass es durch die mehrfache Speicherung gleicher Objekte zu Duplikaten innerhalb der Ergebnismenge kommt. Diese müssen in einem weiteren Arbeitsschritt erkannt und entfernt werden. 5.3 Nachteile Durch die ähnliche Verfahrensweise wie beim Clipping werden auch dessen Nachteile übernommen. D. h. dass bei einer zu hohen Auflösung der Binärregionen oder bei zu großen Objekten sehr viele Verweise auf das jeweilige Objekt im Baum existieren. Das hat negative Auswirkungen auf die Laufzeit und die Speicherausnutzung (siehe Clipping). 6 Quadtrees Quadtrees verfolgen einen anderen Ansatz als die bisher vorgestellten Verfahren um deren Nachteile zu umgehen. Die angesprochenen Laufzeit- und Speicherausnutzungsdefizite dieser Indexstrukturen begründen sich hauptsächlich auf der Tatsache, dass der Datenraum anhand eines statischen Faktors (z. Bsp. die Auflösung der Binärregionen bei der Z-Ordnung) aufgeteilt wurde. Dieser Faktor musste vor der eigentlichen Arbeit mit dieser Struktur passend zur erwarteten, durchschnittlichen Objektgröße gewählt werden. Bei den Quadtrees verzichtet man daher auf einen solchen konstanten Faktor und teilt den Datenraum anhand der bereits gespeicherten Objekte auf. Dabei legt man eine einfache Berechnungsvorschrift zugrunde: Jede Ebene im Quadtree wird in vier Teile geteilt (daher auch der Name Quadtree). Im Beispiel in Bild 7 wurden diese vier Teile mit NW (Nordwest), NO (Nordost), SO (Südost) und SW (Südwest) gekennzeichnet. Jedes dieser 10
11 vier Teile kann nun rekusiv weiter aufgeteilt werden bis eine bestimmte Tiefe erreicht oder eine Abbruchbedingung erfüllt ist. Ein Beispiel für eine solche Abbruchbedingung soll im nächsten Abschnitt vorgestellt werden. 6.1 PR-Quadtree Ein PR-Quadtree (Point-Region-Quadtree) ist ein Quadtree zur Speicherung von Punktwolken. Wie der Name bereits andeutet, wird dabei jeder Blockregion im Baum maximal ein Punkt zugeordnet. D. h. jede Blockregion wird so oft geteilt, bis alle in ihr enthaltenen Punkte sich allein in einer Blockregion befinden. In Bild 7 ist ein PR-Baum illustriert. Abbildung 7: Beispielhafter PR-Quadtree Es ist erkennbar, dass bspw. die größere Blockregion unten links nicht weiter aufgeteilt werden muss, da bereits nur ein Punkt in ihr gespeichert ist, wo hingegen ein Block am rechten Rand besonders weit aufgeteilt werden musste, da sich hier zwei Punkte in unmittelbarer Nähe befinden. Da die Speicherung von Punkten weniger interessant ist, wird im Folgenden auf eine Quadtree-Variante eingegangen, die auch zur Speicherung ausgedehnter Geometrien geeignet ist. 6.2 Einbettung einer Z-Ordnung Um nun auch Polygone oder Linienzüge im Quadtree zu speichern, wird versucht, diese Objekte durch rekursive Aufteilung einzelner Blockregionen so gut wie möglich zu approximieren. Dabei wird meist eine maximale Rekursionstiefe vorgegeben. In Bild 8 wird dies am Beispiel des Polygons P 1 und der Linie L 1 gezeigt. 11
12 Abbildung 8: Quadtree mit eingebetteter Z-Ordnung Um diese Objekte in einer herkömmlichen Indexstruktur speichern zu können, wird in den Quadtree eine Z-Ordnung eingebettet. Dabei werden den einzelnen Blockregionen des Baumes nun Z-Werte unterschiedlicher Auflösung zugewiesen. Dies funktioniert, da jede Blockregion als reguläre Binärregion innerhalb einer Z-Ordnung aufgefasst werden kann. Bspw. wird das Polygon P 1 in Bild 8 durch vier Blöcke der Auflösung 6 und einen Block der Auflösung 4 bestmöglich repräsentiert. Um nun einen B + -Baum nutzen zu können muss eine Ordnungsrelation zwischen Z-Werten unterschiedlicher Auflösung definiert werden: X < Y index x 2 auflösungx a < index y 2 auflösungy a Dabei steht für die ganzzahlige Division und a = min(auflösung x, auflösung y ). Durch diese Relation wird der höheraufgelöste Z-Wert auf die Ebene des Anderen umgerechnet, da der Vergleich von Z-Werten gleicher Aufflösung wohldefiniert ist (s.o.). Nun ist es möglich, alle Blöcke, die ein gegebenes Objekt O überlappen, mit einem Verweis auf O in einem B + -Baum zu speichern. Dabei kann es wie beim Clipping zur mehrfachen Speicherung gleicher Objekte kommen, aber durch die unterschiedlich aufgelösten Regionen im Quadtree tritt diese Situation weniger häufig auf als bei anderen Verfahren. 7 Überlappende Blockregionen Alle bisher vorgestellten Verfahren haben den Datenraum in disjunkte Teile aufgeteilt. Dieser Umstand führt jedoch dazu, dass es oft nötig ist, Objekte, die die Grenzen dieser disjunkten Blöcke überlappen, mehrfach gespeichert werden müssen. Das zieht, wie bereits beschrieben, einige Probleme nach sich. Daher existieren einige Indexstrukturen, welche einen anderen Ansatz wählen: Sie unterteilen den Datenraum ebenfalls in Blöcke, 12
13 aber diese dürfen sich überschneiden. Ein beliebter Vertreter dieser Art von Indexstrukturen soll im folgenden Abschnitt vorgestellt werden. 7.1 R-Baum Der R-Baum weist viele Parallelen zum B + -Baum auf. Er unterscheidet ebenso zwischen Verzeichniss- und Datenknoten. Letztere liegen alle auf einer Ebene. Die Verzeichnissknoten beinhalten neben den Verweisen auf ihre unmittelbaren Kinder auch ein minimal umspannendes Rechteck, welches den gesamten Teilbaum unter ihnen umspannt. Bild 9 zeigt ein Beispiel, dass diese Idee skizziert. Beispielsweise umspannt das MUR des Verzeichnissknotens a die Knoten c und d und die Datenknoten 1-5. Abbildung 9: Ein einfacher R-Baum (Verzeichnissknoten sind mit Kleinbuchstaben, Datenknoten mit Zahlen markiert) Ein Unterschied ergibt sich aus den überlappenden Blockregionen der R-Bäume gegenüber den Quadtrees. Während bei den Quadtrees die Reihenfolge der Einfügeoperationen keine Rolle für die resultierende Datenstruktur spielt, ist diese Reihenfolge bei den R- Bäumen relavant. Einen viel höheren Einfluss auf die Laufzeit der Indexstruktur hat jedoch weniger die Reihenfolge der Einfügeoperationen, als die Wahl des Datenknotens bzw. des Teilbaums in den ein neues Objekt gespeichert werden soll. Es lassen sich innerhalb dieser Operation drei Fälle unterscheiden: Das zu speichernde Objekt bzw. sein MUR liegt komplett innerhalb eines MUR eines Verzeichnissknotens. In diesem Fall wird dieser Knoten gewählt und es wird rekusiv weiterverfahren. Das zu speichernde Objekt bzw. sein MUR überlappen mehrere Verzeichnissknoten- MUR. Dann können zur Entscheidung verschiedene Heuristiken angewandt wer- 13
14 den, bspw. kann derjenige Knoten ausgewählt werden, dessen MUR den kleinsten Flächeninhalt hat. Das zu speichernde Objekt bzw. sein MUR überlappt kein Verzeichnissknoten- MUR. In diesem Fall können erneut verschiedene Heuristiken angewandt werden. So kann zum Beispiel derjenige Knoten gewählt werden, dessen MUR sich beim Hinzufügen des zu speichernden Objektes am wenigsten vergrößert. Eine weitere Operation ist für die Effizienz des R-Baumes von Bedeutung: Falls durch häufiges Hinzufügen von neuen Objekten ein Verzeichnissknoten seine maximale Kapazität (abhängig von der Ordnung des Baumes) erreicht, so muss dieser aufgeteilt werden. Es existieren verschieden Ansätze, wie räumlich am günstigsten aufgeteilt werden kann. Ein Vorteil von R-Bäumen sind die relativ einfach zu implementierenden Anfrageformen. So muss lediglich durch ein Überlappungstest zwischen der Anfragegeometrie und den MUR entschieden werden, welche Teilbäume rekursiv weiter untersucht werden müssen. Falls man auf ein Blattknoten stößt, ergibt sich die Ergebnismenge aus den erfolgreichen Überlappungstests zwischen der Anfragegeometrie und den gespeicherten Objekten. Da jedes Objekt nur einmal im gesamten Baum gespeichert wird, entfällt ein zweiter Arbeitsschritt zum Erkennen und Entfernen eventueller Duplikate. 7.2 R-Baum-Varianten R -Baum Der R -Baum versucht einige kritische Punkte des gewöhnlichen R-Baumes zu vermeiden. So kann es passieren, dass zu große Überlappungen dazu führen, dass bei Anfragen mehrere Teilbäume untersucht werden müssen. Daher ist eine Minimierung der Überlappungen erwünscht. Weiterhin soll die Fläche und die Anzahl der Blöcke minimiert werden, da kleinere Blöcke auch weniger oft gefunden werden. Es besteht ebenfalls in der Form der einzelnen Blockregionen Optimierungspotential. So soll versucht werden, eine möglichst quadratische Form der Blöcke zu erreichen. Diese Forderung wird mit der meist (fast) quadratischen Form der Anfragerechtecke begründet. Diese Annahme resultiert bspw. aus der annähernd quadratischen Form heutiger Bildschirmfenster oder Kartenblätter. So kann gezeigt werden, dass quadratische Blockregionen im Mittel weniger häufig gefunden werden, falls das Anfragerechteck ebenfalls annähernd quadratisch ist. Bei diesen konträren Forderungen muss ein passender Konsens zwischen allen Optimierungswünschen gefunden werden. Der R -Baum erreicht dies unter Ausnutzung bestimmer Heuristiken während der Einfüge und Splitoperationen. Diese erfolgreiche Umsetzung aller gewünschten Anforderungen mach diese Variante des R-Baumes zu einer sehr verbreiteten Indexstruktur in heutigen Datenbanksystemen. 14
15 7.2.2 R + -Baum Der R + -Baum vermeidet Überlappungen vollständig, in dem ein Verfahren, ähnlich dem Clipping, genutzt wird. Seine Struktur ist zwar äquivalent zum R-Baum, aber die MUR der Verzeichnissknoten dürfen sich nicht überlappen. Das hat Auswirkungen auf die Überlaufbehandlung von Knoten. So wird mittels Partitionierungslinien entlang jeder Dimension und einer zughörigen Kostenfunktion entschieden, wie ein Knoten aufgeteilt wird. Die Kostenfunktion gewichtet meist die Anzahl der Objekte, die durch die aktuelle Partitionierungslinie geschnitten werden. Diese Kosten sollen minimiert werden, d. h. es sollen so wenige Objekte wie möglich geschnitten werden. Häufig ist es jedoch nicht möglich eine günstige Partitionierungslinie zu finden. In einem solchen Fall muss unterschieden werden, ob der übergelaufene Knoten ein Daten- oder Verzeichnissknoten war. Ist ein Datenknoten übergelaufen, werden alle Objekte, die die Partitionierungslinie schneiden in beiden resultierenden Datenknoten gespeichert. Ist ein Verzeichnissknoten V übergelaufen, wird die Partitionierung rekursiv für alle Kindknoten von V fortgesetzt, unabhängig davon, ob diese ebenfalls voll sind oder nicht. Das kann dazu führen, dass entlang solcher Partitionierungslinien viele, nur sehr gering gefüllte Knoten gibt, was sich wiederum negativ auf das Laufzeitverhalten auswirken kann. 15
16 8 Quellen Thomas Brinkhoff: Geodatenbanksysteme in Theorie und Praxis. Herbert Wichmann Verlag, Heidelberg 2005 Geo-Anfrageverabeitung. marburg.de/teaching/vl/sonst/ 05WS_geodb/Folien/spatialIndexingAll.pdf (Zugriff: 3. Juni 2008) 16
{0,1} rekursive Aufteilung des Datenraums in die Quadranten NW, NE, SW und SE feste Auflösung des Datenraums in 2 p 2 p Gitterzellen
 4.4 MX-Quadtrees (I) MatriX Quadtree Verwaltung 2-dimensionaler Punkte Punkte als 1-Elemente in einer quadratischen Matrix mit Wertebereich {0,1} rekursive Aufteilung des Datenraums in die Quadranten NW,
4.4 MX-Quadtrees (I) MatriX Quadtree Verwaltung 2-dimensionaler Punkte Punkte als 1-Elemente in einer quadratischen Matrix mit Wertebereich {0,1} rekursive Aufteilung des Datenraums in die Quadranten NW,
Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE)
 4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
4.4 Quadtrees. Literatur
 4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
Kollisionserkennung
 1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
Indizierung von Geodaten - Raumbezogene Indexstrukturen. Seminar mobile Geoinformationssystem Vortrag von Markus Steger
 Indizierung von Geodaten - Raumbezogene Indexstrukturen Seminar mobile Geoinformationssystem Vortrag von Markus Steger Index wozu ist er gut? Index allgemein Effizienter Zugriff auf Daten, i.d.r. mit B-Baum
Indizierung von Geodaten - Raumbezogene Indexstrukturen Seminar mobile Geoinformationssystem Vortrag von Markus Steger Index wozu ist er gut? Index allgemein Effizienter Zugriff auf Daten, i.d.r. mit B-Baum
4.3 Splitstrategien für R-Bäume (I)
 4.3 Splitstrategien für R-Bäume (I) Der Knoten K läuft mit K = M+1 über: Aufteilung auf zwei Knoten K 1 und K 2, sodaß K 1 m und K 2 m Erschöpfender Algorithmus Suche unter den O(2 M ) Möglichkeiten die
4.3 Splitstrategien für R-Bäume (I) Der Knoten K läuft mit K = M+1 über: Aufteilung auf zwei Knoten K 1 und K 2, sodaß K 1 m und K 2 m Erschöpfender Algorithmus Suche unter den O(2 M ) Möglichkeiten die
4.3 R-Bäume (I) Idee. basiert auf der Technik überlappender Seitenregionen verallgemeinert die Idee des B + -Baums auf den 2-dimensionalen Raum
 4.3 R-Bäume (I) Idee basiert auf der Technik überlappender Seitenregionen verallgemeinert die Idee des B + -Baums auf den 2-dimensionalen Raum Geo-Informationssysteme 98 4.3 R-Bäume (I) Definition Ein
4.3 R-Bäume (I) Idee basiert auf der Technik überlappender Seitenregionen verallgemeinert die Idee des B + -Baums auf den 2-dimensionalen Raum Geo-Informationssysteme 98 4.3 R-Bäume (I) Definition Ein
B+-Baum mit Z-Ordnung. B+-Baum mit Z-Ordnung. Anforderungen. 7.3 Räumliche Zugriffsstrukturen
 B+-Baum mit Z-Ordnung Window Query: 1. Ansatz Benutze den gewöhnlichen Algorithmus für Bereichsanfragen im B + -Baum: Suche mit dem kleinsten Z-Wert des Suchrechtecks (entspricht dem linken unteren Eckpunkt)
B+-Baum mit Z-Ordnung Window Query: 1. Ansatz Benutze den gewöhnlichen Algorithmus für Bereichsanfragen im B + -Baum: Suche mit dem kleinsten Z-Wert des Suchrechtecks (entspricht dem linken unteren Eckpunkt)
Datenbanken II Ausarbeitung: Räumliche Indexstrukturen
 Datenbanken II Ausarbeitung: Räumliche Indexstrukturen Rico Tilgner Matrikelnummer: 39212 10.06.2008 Inhaltsverzeichnis 1 Einleitung 3 1.1 Geoinformationssysteme............................ 3 2 Indexstrukturen
Datenbanken II Ausarbeitung: Räumliche Indexstrukturen Rico Tilgner Matrikelnummer: 39212 10.06.2008 Inhaltsverzeichnis 1 Einleitung 3 1.1 Geoinformationssysteme............................ 3 2 Indexstrukturen
Algorithmen und Datenstrukturen Bereichsbäume
 Algorithmen und Datenstrukturen Bereichsbäume Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Überblick Einführung k-d Baum BSP Baum R Baum Motivation
Algorithmen und Datenstrukturen Bereichsbäume Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Überblick Einführung k-d Baum BSP Baum R Baum Motivation
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am 03.12.2013 Algorithmische Geometrie: Schnitte von Strecken Sweep-Line INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Algorithmen II Vorlesung am 03.12.2013 Algorithmische Geometrie: Schnitte von Strecken Sweep-Line INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Indexe in Dateien. Thomas Behr. 19.November c 2015 FernUniversität in Hagen
 Indexe in Dateien Fakultät für Mathematik und Informatik Datenbanksysteme für neue Anwendungen FernUniversität in Hagen 19.November 2015 c 2015 FernUniversität in Hagen Indexe ermöglichen schnellen Zugriff
Indexe in Dateien Fakultät für Mathematik und Informatik Datenbanksysteme für neue Anwendungen FernUniversität in Hagen 19.November 2015 c 2015 FernUniversität in Hagen Indexe ermöglichen schnellen Zugriff
4. Räumliche Indexstrukturen
 4. Räumliche Indexstrukturen 4.1 Einführung 4.2 Z-Ordnung 4.3 R-Bäume 4.4 Quadtrees Geo-Informationssysteme 66 4.1 Einführung (I) Grundlegende Ideen konventionelle Zugriffsstrukturen sind für die Verwaltung
4. Räumliche Indexstrukturen 4.1 Einführung 4.2 Z-Ordnung 4.3 R-Bäume 4.4 Quadtrees Geo-Informationssysteme 66 4.1 Einführung (I) Grundlegende Ideen konventionelle Zugriffsstrukturen sind für die Verwaltung
WINTERSEMESTER 2006/2007. Mehrdimensionale Bäume
 ALGORITHMISCHE ANWENDUNGEN WINTERSEMESTER 2006/2007 Team: B_blau_Ala0607 Wilhelm Faber 11032935 Ioannis Chouklis 11042438 1 Inhaltsverzeichnis Inhaltsverzeichnis...2 1. Der k-d Baum...3 1.1. Inhomogene
ALGORITHMISCHE ANWENDUNGEN WINTERSEMESTER 2006/2007 Team: B_blau_Ala0607 Wilhelm Faber 11032935 Ioannis Chouklis 11042438 1 Inhaltsverzeichnis Inhaltsverzeichnis...2 1. Der k-d Baum...3 1.1. Inhomogene
Indexstrukturen in Datenbanken
 für Zeichendaten und Texte sowie mehrdimensionale Dateiorganisation und Zugriffspfade 3. Juli 2014 Inhaltsverzeichnis 1 Einleitung 2 Präfix B+-Baum 3 Tries 4 k-dimensionale Bäume 5 Grid-File 6 mehrdimensionales
für Zeichendaten und Texte sowie mehrdimensionale Dateiorganisation und Zugriffspfade 3. Juli 2014 Inhaltsverzeichnis 1 Einleitung 2 Präfix B+-Baum 3 Tries 4 k-dimensionale Bäume 5 Grid-File 6 mehrdimensionales
Geodatenbanksysteme in Theorie und Praxis
 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Thomas Brinkhoff Geodatenbanksysteme in Theorie und Praxis Einführung
2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Thomas Brinkhoff Geodatenbanksysteme in Theorie und Praxis Einführung
Geodatenbanksysteme in Theorie und Praxis
 Themas Brinkheff Geodatenbanksysteme in Theorie und Praxis Einführung in objektrelationale Geodatenbanken unter besonderer Berücksichtigung von Grade Spatial 2., überarbeitete und erweiterte Auflage @
Themas Brinkheff Geodatenbanksysteme in Theorie und Praxis Einführung in objektrelationale Geodatenbanken unter besonderer Berücksichtigung von Grade Spatial 2., überarbeitete und erweiterte Auflage @
B / B* - Bäume. Guido Hildebrandt Seminar Datenbanksysteme
 B / B* - Bäume Guido Hildebrandt Seminar Datenbanksysteme 25.11.2010 Gliederung Einleitung Binärbaum B - Baum B* - Baum Varianten Zusammenfassung Quellen Gliederung Einleitung Binärbaum B - Baum B* - Baum
B / B* - Bäume Guido Hildebrandt Seminar Datenbanksysteme 25.11.2010 Gliederung Einleitung Binärbaum B - Baum B* - Baum Varianten Zusammenfassung Quellen Gliederung Einleitung Binärbaum B - Baum B* - Baum
Mehrdimensionale Zugriffspfade und Dateiorganisation
 Mehrdimensionale Zugriffspfade und Dateiorganisation Gliederung Begriffe, Anforderungen und Probleme, Anwendungsgebiete Konkrete Techniken Bäume Grid-File Mehrdimensionales Hashing Begriffe Eindimensionale
Mehrdimensionale Zugriffspfade und Dateiorganisation Gliederung Begriffe, Anforderungen und Probleme, Anwendungsgebiete Konkrete Techniken Bäume Grid-File Mehrdimensionales Hashing Begriffe Eindimensionale
Geodatenbanksysteme in Theorie und Praxis
 Thomas Brinkhoff Geodatenbanksysteme in Theorie und Praxis Einführung in objektrelationale Geodatenbanken unter besonderer Berücksichtigung von Orade Spatial 3., überarbeitete und erweiterte Auflage @
Thomas Brinkhoff Geodatenbanksysteme in Theorie und Praxis Einführung in objektrelationale Geodatenbanken unter besonderer Berücksichtigung von Orade Spatial 3., überarbeitete und erweiterte Auflage @
Suchbäume. Suchbäume. Einfügen in Binären Suchbäumen. Suchen in Binären Suchbäumen. Prinzip Suchbaum. Algorithmen und Datenstrukturen
 Suchbäume Suchbäume Prinzip Suchbaum Der Wert eines Knotens wird als Schlüssel verstanden Knoten kann auch weitere Daten enthalten, die aber hier nicht weiter betrachtet werden Werte der Schlüssel müssen
Suchbäume Suchbäume Prinzip Suchbaum Der Wert eines Knotens wird als Schlüssel verstanden Knoten kann auch weitere Daten enthalten, die aber hier nicht weiter betrachtet werden Werte der Schlüssel müssen
Was bisher geschah. 1. Zerlegung in monotone Polygone 2. Triangulierung der monotonen Teilpolygone
 Was bisher geschah Motivation, Beispiele geometrische Objekte im R 2 : Punkt, Gerade, Halbebene, Strecke, Polygon, ebene Zerlegung in Regionen (planare Graphen) maschinelle Repräsentation geometrischer
Was bisher geschah Motivation, Beispiele geometrische Objekte im R 2 : Punkt, Gerade, Halbebene, Strecke, Polygon, ebene Zerlegung in Regionen (planare Graphen) maschinelle Repräsentation geometrischer
Datenbanken: Indexe. Motivation und Konzepte
 Datenbanken: Indexe Motivation und Konzepte Motivation Warum sind Indexstrukturen überhaupt wünschenswert? Bei Anfrageverarbeitung werden Tupel aller beteiligter Relationen nacheinander in den Hauptspeicher
Datenbanken: Indexe Motivation und Konzepte Motivation Warum sind Indexstrukturen überhaupt wünschenswert? Bei Anfrageverarbeitung werden Tupel aller beteiligter Relationen nacheinander in den Hauptspeicher
12. Hashing. Hashing einfache Methode um Wörtebücher zu implementieren, d.h. Hashing unterstützt die Operationen Search, Insert, Delete.
 Hashing einfache Methode um Wörtebücher zu implementieren, d.h. Hashing unterstützt die Operationen Search, Insert, Delete. Worst-case Zeit für Search: Θ(n). In der Praxis jedoch sehr gut. Unter gewissen
Hashing einfache Methode um Wörtebücher zu implementieren, d.h. Hashing unterstützt die Operationen Search, Insert, Delete. Worst-case Zeit für Search: Θ(n). In der Praxis jedoch sehr gut. Unter gewissen
Ein Secondo-basierter Routenplaner mit Berücksichtigung von Steigungen
 Ein Secondo-basierter Routenplaner mit Berücksichtigung von Steigungen Holger Hennings, Fabio Valdés Fachpraktikum Erweiterbare Datenbanksysteme (WS 2017/18) Lehrgebiet Datenbanksysteme für neue Anwendungen
Ein Secondo-basierter Routenplaner mit Berücksichtigung von Steigungen Holger Hennings, Fabio Valdés Fachpraktikum Erweiterbare Datenbanksysteme (WS 2017/18) Lehrgebiet Datenbanksysteme für neue Anwendungen
Quadtrees. Christian Höner zu Siederdissen
 Quadtrees Christian Höner zu Siederdissen Quadtrees Zum Verständnis benötigt... Was sind Quadtrees Datenstruktur Wofür Quadtrees Operationen auf dem Baum Vor- und Nachteile (spezialisierte Formen) Zum
Quadtrees Christian Höner zu Siederdissen Quadtrees Zum Verständnis benötigt... Was sind Quadtrees Datenstruktur Wofür Quadtrees Operationen auf dem Baum Vor- und Nachteile (spezialisierte Formen) Zum
Geometrie 2. Julian Fischer Julian Fischer Geometrie / 30
 Geometrie 2 Julian Fischer 6.7.2009 Julian Fischer Geometrie 2 6.7.2009 1 / 30 Themen 1 Bereichssuche und kd-bäume 1 Bereichssuche 2 kd-bäume 2 Divide and Conquer 1 Closest pair 2 Beispiel: Points (IOI
Geometrie 2 Julian Fischer 6.7.2009 Julian Fischer Geometrie 2 6.7.2009 1 / 30 Themen 1 Bereichssuche und kd-bäume 1 Bereichssuche 2 kd-bäume 2 Divide and Conquer 1 Closest pair 2 Beispiel: Points (IOI
5 BINÄRE ENTSCHEIDUNGS- DIAGRAMME (BDDS)
 5 BINÄRE ENTSCHEIDUNGS- DIAGRAMME (BDDS) Sommersemester 2009 Dr. Carsten Sinz, Universität Karlsruhe Datenstruktur BDD 2 1986 von R. Bryant vorgeschlagen zur Darstellung von aussagenlogischen Formeln (genauer:
5 BINÄRE ENTSCHEIDUNGS- DIAGRAMME (BDDS) Sommersemester 2009 Dr. Carsten Sinz, Universität Karlsruhe Datenstruktur BDD 2 1986 von R. Bryant vorgeschlagen zur Darstellung von aussagenlogischen Formeln (genauer:
Inhaltsverzeichnis. Vorwort...
 Vorwort... V 1 Einleitung... 1 1.1 Geoinformationssysteme und -dienste... 1 1.1.1 Geoinformationssysteme... 1 1.1.2 Offene Geoinformationssysteme... 4 1.1.3 Geodienste... 5 1.2 Datenbanksysteme... 7 1.2.1
Vorwort... V 1 Einleitung... 1 1.1 Geoinformationssysteme und -dienste... 1 1.1.1 Geoinformationssysteme... 1 1.1.2 Offene Geoinformationssysteme... 4 1.1.3 Geodienste... 5 1.2 Datenbanksysteme... 7 1.2.1
Übungsblatt 7 - Voronoi Diagramme
 Karlsruher Institut für Technologie Algorithmische Geometrie Fakultät für Informatik Sommersemester 2012 ITI Wagner Martin Nöllenburg/Andreas Gemsa Übungsblatt 7 - Voronoi Diagramme 1 Voronoi-Zellen Sei
Karlsruher Institut für Technologie Algorithmische Geometrie Fakultät für Informatik Sommersemester 2012 ITI Wagner Martin Nöllenburg/Andreas Gemsa Übungsblatt 7 - Voronoi Diagramme 1 Voronoi-Zellen Sei
Kollisionserkennung - Broad Phase
 Kollisionserkennung - road Phase Alexander van Renen Fakultät für Informatik Technische Universität München oltzmannstr. 3 85748 Garching, Deutschland renen@in.tum.de 21. Juli 2012 Zusammenfassung Kollisionserkennung
Kollisionserkennung - road Phase Alexander van Renen Fakultät für Informatik Technische Universität München oltzmannstr. 3 85748 Garching, Deutschland renen@in.tum.de 21. Juli 2012 Zusammenfassung Kollisionserkennung
Geometrische Algorithmen Segmentschnitt. Lernmodul 7: Geo-Algorithmen und -Datenstrukturen - Segmentschnitt
 Folie 1 von 37 Geometrische Algorithmen Segmentschnitt Folie 2 von 37 Segmentschnitt Übersicht Zwei Segmente Lage zweier Segmente Prüfung auf Schnittfreiheit Formeln zum Geradenschnitt Feststellen des
Folie 1 von 37 Geometrische Algorithmen Segmentschnitt Folie 2 von 37 Segmentschnitt Übersicht Zwei Segmente Lage zweier Segmente Prüfung auf Schnittfreiheit Formeln zum Geradenschnitt Feststellen des
Geradenarrangements und Dualität von Punkten und Geraden
 Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Parallele Algorithmen in der Bildverarbeitung
 Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Dualität + Quad-trees
 Übung Algorithmische Geometrie Dualität + Quad-trees LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Andreas Gemsa 30.06.2011 Übersicht Übungsblatt 10 - Dualität
Übung Algorithmische Geometrie Dualität + Quad-trees LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Andreas Gemsa 30.06.2011 Übersicht Übungsblatt 10 - Dualität
Geradenarrangements und Dualität von Punkten und Geraden
 Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Mobile Objekte Indexstrukturen
 Verteilung und Integration von Informationen im Verkehrsbereich Mobile Objekte Indexstrukturen Ingo Beutler 07.06.2004 Anfragen: z.b. Welche Transporter befinden sich in der Nähe des HSaF? Wie können räumliche
Verteilung und Integration von Informationen im Verkehrsbereich Mobile Objekte Indexstrukturen Ingo Beutler 07.06.2004 Anfragen: z.b. Welche Transporter befinden sich in der Nähe des HSaF? Wie können räumliche
Geradenarrangements und Dualität von Punkten und Geraden
 Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 17.06.2014 1 Dualitätsabbildung Bisher haben wir Dualität für planare
Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 17.06.2014 1 Dualitätsabbildung Bisher haben wir Dualität für planare
Geometrische Algorithmen Segmentschnitt
 Folie 1 von 36 Geometrische Algorithmen Segmentschnitt Folie 2 von 36 Segmentschnitt Übersicht Zwei Segmente Lage zweier Segmente Prüfung auf Schnittfreiheit Formeln zum Geradenschnitt Feststellen des
Folie 1 von 36 Geometrische Algorithmen Segmentschnitt Folie 2 von 36 Segmentschnitt Übersicht Zwei Segmente Lage zweier Segmente Prüfung auf Schnittfreiheit Formeln zum Geradenschnitt Feststellen des
Geometrische Algorithmen Segmentschnitt
 Folie 1 von 36 Geometrische Algorithmen Segmentschnitt Folie 2 von 36 Segmentschnitt Übersicht Zwei Segmente! Lage zweier Segmente! Prüfung auf Schnittfreiheit! Formeln zum Geradenschnitt! Feststellen
Folie 1 von 36 Geometrische Algorithmen Segmentschnitt Folie 2 von 36 Segmentschnitt Übersicht Zwei Segmente! Lage zweier Segmente! Prüfung auf Schnittfreiheit! Formeln zum Geradenschnitt! Feststellen
Inhalt. 1. Einführung in die Informatik. 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele.
 1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
13. Hashing. AVL-Bäume: Frage: Suche, Minimum, Maximum, Nachfolger in O(log n) Einfügen, Löschen in O(log n)
 AVL-Bäume: Ausgabe aller Elemente in O(n) Suche, Minimum, Maximum, Nachfolger in O(log n) Einfügen, Löschen in O(log n) Frage: Kann man Einfügen, Löschen und Suchen in O(1) Zeit? 1 Hashing einfache Methode
AVL-Bäume: Ausgabe aller Elemente in O(n) Suche, Minimum, Maximum, Nachfolger in O(log n) Einfügen, Löschen in O(log n) Frage: Kann man Einfügen, Löschen und Suchen in O(1) Zeit? 1 Hashing einfache Methode
Bereichsabfragen. Dr. Martin Nöllenburg Vorlesung Algorithmische Geometrie
 Vorlesung Algorithmische Geometrie LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 17.05.2011 Geometrie in Datenbanken In einer Personaldatenbank
Vorlesung Algorithmische Geometrie LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 17.05.2011 Geometrie in Datenbanken In einer Personaldatenbank
4.1 Einführung. 4.2 Z-Ordnung. 4.3 R-Bäume. 4.4 Quadtrees. Kapitel 3: Räumliche Indexstrukturen. 4. Räumliche Indexstrukturen
 LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS Kapitel 3: Räumliche Indexstrukturen Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2011/12 Ludwig-Maximilians-Universität
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS Kapitel 3: Räumliche Indexstrukturen Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2011/12 Ludwig-Maximilians-Universität
Informatik II Bäume zum effizienten Information Retrieval
 lausthal Informatik II Bäume zum effizienten Information Retrieval. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Binäre Suchbäume (binary search tree, BST) Speichere wieder Daten als "Schlüssel
lausthal Informatik II Bäume zum effizienten Information Retrieval. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Binäre Suchbäume (binary search tree, BST) Speichere wieder Daten als "Schlüssel
Voronoi-Diagramme. Dr. Martin Nöllenburg Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK
 Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 29.05.2011 Das Postamt-Problem b(p, q) = {x R 2 : xp = xq } p q h(p, q) h(q, p) = {x :
Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 29.05.2011 Das Postamt-Problem b(p, q) = {x R 2 : xp = xq } p q h(p, q) h(q, p) = {x :
Seminar. Algorithmische Geometrie
 Seminar Algorithmische Geometrie WS 2000/2001 Thema: Konvexe Hülle Mirko Dennler 21439 Inhaltsverzeichnis Konvexe Hülle 1. Problemstellung 3 2. GRAHAMS SCAN 4-5 3. JARVIS' MARCH 5-6 4. QUICK HULL 6-7 5.
Seminar Algorithmische Geometrie WS 2000/2001 Thema: Konvexe Hülle Mirko Dennler 21439 Inhaltsverzeichnis Konvexe Hülle 1. Problemstellung 3 2. GRAHAMS SCAN 4-5 3. JARVIS' MARCH 5-6 4. QUICK HULL 6-7 5.
Beschleunigungsverfahren für Raytracing Grids Hierarchische Grids Bewertung Fazit
 Überblick Einführung Beschleunigungsverfahren für Raytracing Grids Hierarchische Grids Fazit Einführung Gewöhnliche Beschleunigungsverfahren & Raumunterteilung entworfen und optimiert für effizientes Traversieren
Überblick Einführung Beschleunigungsverfahren für Raytracing Grids Hierarchische Grids Fazit Einführung Gewöhnliche Beschleunigungsverfahren & Raumunterteilung entworfen und optimiert für effizientes Traversieren
Punkt-in-Polygon-Suche Übersicht
 Folie 1 von 19 Punkt-in-Polygon-Suche Übersicht Praxisbeispiel/Problemstellung Zählen von Schnittpunkten Schnitt einer Halbgerade mit der Masche Aufwandsbetrachtung Streifenkarte Vorgehen und Eigenschaften
Folie 1 von 19 Punkt-in-Polygon-Suche Übersicht Praxisbeispiel/Problemstellung Zählen von Schnittpunkten Schnitt einer Halbgerade mit der Masche Aufwandsbetrachtung Streifenkarte Vorgehen und Eigenschaften
Algorithmische Geometrie: Delaunay Triangulierung (Teil 2)
 Algorithmische Geometrie: Delaunay Triangulierung (Teil 2) Nico Düvelmeyer WS 2009/2010, 2.2.2010 Überblick 1 Delaunay Triangulierungen 2 Berechnung der Delaunay Triangulierung Randomisiert inkrementeller
Algorithmische Geometrie: Delaunay Triangulierung (Teil 2) Nico Düvelmeyer WS 2009/2010, 2.2.2010 Überblick 1 Delaunay Triangulierungen 2 Berechnung der Delaunay Triangulierung Randomisiert inkrementeller
Ein Secondo-basierter Routenplaner mit Berücksichtigung von Steigungen
 Ein Secondo-basierter Routenplaner mit Berücksichtigung von Steigungen Holger Hennings, Fabio Valdés Fachpraktikum Erweiterbare Datenbanksysteme (WS 2015/16) Lehrgebiet Datenbanksysteme für neue Anwendungen
Ein Secondo-basierter Routenplaner mit Berücksichtigung von Steigungen Holger Hennings, Fabio Valdés Fachpraktikum Erweiterbare Datenbanksysteme (WS 2015/16) Lehrgebiet Datenbanksysteme für neue Anwendungen
2.1. Konvexe Hülle in 2D
 Wir wollen die konvexe Hülle einer Menge von Punkten P = {p 1,..., p n } in der Ebene R 2 bestimmen. y y x x Def. 21: Eine Teilmenge S der Ebene ist konvex gdw für jedes Paar das Liniensegment pq in S
Wir wollen die konvexe Hülle einer Menge von Punkten P = {p 1,..., p n } in der Ebene R 2 bestimmen. y y x x Def. 21: Eine Teilmenge S der Ebene ist konvex gdw für jedes Paar das Liniensegment pq in S
Wiederholung. Objekte) Hauptkosten beim Pathtracing Ziel: Beschleunigung durch Reduktion der Schnittpunktstestzahl. Ansätze
 Wiederholung Pathtracing = Schnittpunktstests mit Geometrie: primäre Augstrahlen, Schattenstrahlen, sekundäre Strahlen Problem: Komplexität! (mindestens linear mit der Anzahl der Objekte) Hauptkosten beim
Wiederholung Pathtracing = Schnittpunktstests mit Geometrie: primäre Augstrahlen, Schattenstrahlen, sekundäre Strahlen Problem: Komplexität! (mindestens linear mit der Anzahl der Objekte) Hauptkosten beim
Stud.-Nummer: Datenstrukturen & Algorithmen Seite 1
 Stud.-Nummer: Datenstrukturen & Algorithmen Seite 1 Aufgabe 1. / 16 P Instruktionen: 1) In dieser Aufgabe sollen Sie nur die Ergebnisse angeben. Diese können Sie direkt bei den Aufgaben notieren. 2) Sofern
Stud.-Nummer: Datenstrukturen & Algorithmen Seite 1 Aufgabe 1. / 16 P Instruktionen: 1) In dieser Aufgabe sollen Sie nur die Ergebnisse angeben. Diese können Sie direkt bei den Aufgaben notieren. 2) Sofern
Algorithmen und Datenstrukturen 1
 Algorithmen und Datenstrukturen 1 7. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@informatik.uni-leipzig.de aufbauend auf den Kursen der letzten Jahre von E. Rahm, G. Heyer,
Algorithmen und Datenstrukturen 1 7. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@informatik.uni-leipzig.de aufbauend auf den Kursen der letzten Jahre von E. Rahm, G. Heyer,
Dynamischer Speicher
 In diesem Abschnitt werden (1) Felder fester Länge und Dynamischer Speicher (2) Felder mit variabler Länge, die sich erst zu Laufzeit des Programms ergibt gegenübergestellt Für (2) benötigt man Funktionen
In diesem Abschnitt werden (1) Felder fester Länge und Dynamischer Speicher (2) Felder mit variabler Länge, die sich erst zu Laufzeit des Programms ergibt gegenübergestellt Für (2) benötigt man Funktionen
Vorlesung Geometrische Algorithmen Generierung von Nicht-uniformen Netzen Sven Schuierer
 Vorlesung Geometrische Algorithmen Generierung von Nicht-uniformen Netzen Sven Schuierer Uberblick 1. Anwendung 2. Anforderungen an Netze 3. Quadrantenbaume Quadrantenbaume fur Punktemengen Bestimmung
Vorlesung Geometrische Algorithmen Generierung von Nicht-uniformen Netzen Sven Schuierer Uberblick 1. Anwendung 2. Anforderungen an Netze 3. Quadrantenbaume Quadrantenbaume fur Punktemengen Bestimmung
Im weiteren wird insbesondere auf die Verwaltung und Speicherung von einfachen Polygonen mit Löchern eingegangen.
 Skript Index- und Speicherungsstrukturen Seite 99 7 Raumzugriffsstrukturen Ausgedehnte Objekte In Nichtstandard-Datenbankssytemen, wie z.b. in Geographischen Datenbanksystemen, werden nicht nur Punktobjekte,
Skript Index- und Speicherungsstrukturen Seite 99 7 Raumzugriffsstrukturen Ausgedehnte Objekte In Nichtstandard-Datenbankssytemen, wie z.b. in Geographischen Datenbanksystemen, werden nicht nur Punktobjekte,
Übung zur Vorlesung Algorithmische Geometrie
 Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Einführung in die linearen Funktionen. Autor: Benedikt Menne
 Einführung in die linearen Funktionen Autor: Benedikt Menne Inhaltsverzeichnis Vorwort... 3 Allgemeine Definition... 3 3 Bestimmung der Steigung einer linearen Funktion... 4 3. Bestimmung der Steigung
Einführung in die linearen Funktionen Autor: Benedikt Menne Inhaltsverzeichnis Vorwort... 3 Allgemeine Definition... 3 3 Bestimmung der Steigung einer linearen Funktion... 4 3. Bestimmung der Steigung
Darstellungsarten für 3D-Körper. Boundary Representation (BRep):
 Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Theoretische Informatik 1 WS 2007/2008. Prof. Dr. Rainer Lütticke
 Theoretische Informatik 1 WS 2007/2008 Prof. Dr. Rainer Lütticke Inhalt der Vorlesung Grundlagen - Mengen, Relationen, Abbildungen/Funktionen - Datenstrukturen - Aussagenlogik Automatentheorie Formale
Theoretische Informatik 1 WS 2007/2008 Prof. Dr. Rainer Lütticke Inhalt der Vorlesung Grundlagen - Mengen, Relationen, Abbildungen/Funktionen - Datenstrukturen - Aussagenlogik Automatentheorie Formale
R-Baum eine dynamische Index-Strukur für räumliche Suche
 Gabriele Wilke-Müller Klufternerstraße 73 88048 Friedrichshafen wilke-mueller@t-online.de Matrikel-Nr. 01/482681 Support for Non-Standard Data Types in DBMSs WS 2003/2004 bei Prof. Dr. Marc H. Scholl Thema:
Gabriele Wilke-Müller Klufternerstraße 73 88048 Friedrichshafen wilke-mueller@t-online.de Matrikel-Nr. 01/482681 Support for Non-Standard Data Types in DBMSs WS 2003/2004 bei Prof. Dr. Marc H. Scholl Thema:
Relationen und Graphentheorie
 Seite Graphentheorie- Relationen und Graphentheorie Grundbegriffe. Relationen- und Graphentheorie gehören zu den wichtigsten Hilfsmitteln der Informatik, die aus der diskretenmathematik stammen. Ein Graph
Seite Graphentheorie- Relationen und Graphentheorie Grundbegriffe. Relationen- und Graphentheorie gehören zu den wichtigsten Hilfsmitteln der Informatik, die aus der diskretenmathematik stammen. Ein Graph
Amortisierte Analysen
 Amortisierte Analysen 26. Mai 2016 1 Einleitung Es gibt viele Datenstrukturen, bei deren Komplexitätsanalyse das Problem auftaucht, dass die Ausführung mancher Operationen Einfluss auf die Komplexität
Amortisierte Analysen 26. Mai 2016 1 Einleitung Es gibt viele Datenstrukturen, bei deren Komplexitätsanalyse das Problem auftaucht, dass die Ausführung mancher Operationen Einfluss auf die Komplexität
Felder fester Länge (1)
 Felder fester Länge (1) Felder: Aneinanderreihung von mehreren Variablen gleichen Typs Ursprünglich als 1-dimensionale Organisationsform gedacht, aber auch zwei- und höherdimensional (Matrizen u.ä.) Benutzung
Felder fester Länge (1) Felder: Aneinanderreihung von mehreren Variablen gleichen Typs Ursprünglich als 1-dimensionale Organisationsform gedacht, aber auch zwei- und höherdimensional (Matrizen u.ä.) Benutzung
t-äre Bäume können - wie Binärbäume - degenerieren, d.h. durch ungünstige Einfügereihenfolge kann ein unausgewogener Baum mit großer Höhe entstehen.
 .3 B-Bäume t-äre Bäume können - wie Binärbäume - degenerieren, d.h. durch ungünstige Einfügereihenfolge kann ein unausgewogener Baum mit großer Höhe entstehen. Wird der t-äre Baum zur Verwaltung von Daten
.3 B-Bäume t-äre Bäume können - wie Binärbäume - degenerieren, d.h. durch ungünstige Einfügereihenfolge kann ein unausgewogener Baum mit großer Höhe entstehen. Wird der t-äre Baum zur Verwaltung von Daten
TU München, Fakultät für Informatik Lehrstuhl III: Datenbanksysteme Prof. Alfons Kemper, Ph.D.
 TU München, Fakultät für Informatik Lehrstuhl III: Datenbanksysteme Prof. Alfons Kemper, Ph.D. Blatt Nr. 10 Übung zur Vorlesung Grundlagen: Datenbanken im WS15/16 Harald Lang, Linnea Passing (gdb@in.tum.de)
TU München, Fakultät für Informatik Lehrstuhl III: Datenbanksysteme Prof. Alfons Kemper, Ph.D. Blatt Nr. 10 Übung zur Vorlesung Grundlagen: Datenbanken im WS15/16 Harald Lang, Linnea Passing (gdb@in.tum.de)
Packalgorithmen für quaderförmige Objekte. Ilia Belozerov
 Packalgorithmen für quaderförmige Objekte Ilia Belozerov 1. Motivation 2. Definitionen und Sätze 3. Exakte Lösungsverfahren 4. Heuristische Methoden 5. Vergleich der Heuristiken Übersicht Bedeutung von
Packalgorithmen für quaderförmige Objekte Ilia Belozerov 1. Motivation 2. Definitionen und Sätze 3. Exakte Lösungsverfahren 4. Heuristische Methoden 5. Vergleich der Heuristiken Übersicht Bedeutung von
Algorithmische Geometrie: Arrangements und
 Algorithmische Geometrie: Arrangements und Dualität Nico Düvelmeyer WS 2009/2010, 19.1.2010 Überblick 1 Strahlenverfolgung und Diskrepanz 2 Dualität Dualitäts-Abbildung Transformation des Problems zur
Algorithmische Geometrie: Arrangements und Dualität Nico Düvelmeyer WS 2009/2010, 19.1.2010 Überblick 1 Strahlenverfolgung und Diskrepanz 2 Dualität Dualitäts-Abbildung Transformation des Problems zur
Organisationsformen der Speicherstrukturen
 Organisationsformen der Speicherstrukturen Bäume und Hashing 1 Motivation Ablage von Daten soll einfachen, schnellen und inhaltsbezogenen Zugriff ermöglichen (z.b. Zeige alle Schüler des Lehrers X am heutigen
Organisationsformen der Speicherstrukturen Bäume und Hashing 1 Motivation Ablage von Daten soll einfachen, schnellen und inhaltsbezogenen Zugriff ermöglichen (z.b. Zeige alle Schüler des Lehrers X am heutigen
Lernmodul 7 Algorithmus von Dijkstra
 Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Hallo Welt für Fortgeschrittene
 Hallo Welt für Fortgeschrittene Geometrie II Benjamin Zenke Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Inhalt Closest Pair Divide & Conquer Bereichssuche Gitterverfahren k-d-tree Sweep-Line-Algorithmen
Hallo Welt für Fortgeschrittene Geometrie II Benjamin Zenke Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Inhalt Closest Pair Divide & Conquer Bereichssuche Gitterverfahren k-d-tree Sweep-Line-Algorithmen
1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie
 Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/3, Folie 1 2010 Prof. Steffen Lange - HDa/FbI
Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/3, Folie 1 2010 Prof. Steffen Lange - HDa/FbI
Voronoi-Diagramme INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK. Dr. Martin Nöllenburg Vorlesung Algorithmische Geometrie
 Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 03.06.2014 1 Das Postamt-Problem b(p, q) = {x 2 R 2 : xp = xq } p q h(p, q) h(q, p) = {x
Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 03.06.2014 1 Das Postamt-Problem b(p, q) = {x 2 R 2 : xp = xq } p q h(p, q) h(q, p) = {x
Quad-trees. Benjamin Niedermann Übung Algorithmische Geometrie
 Übung Algorithmische Geometrie Quad-trees LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Benjamin Niedermann 02.07.2014 Übersicht Übungsblatt 11 - Quadtrees Motivation:
Übung Algorithmische Geometrie Quad-trees LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Benjamin Niedermann 02.07.2014 Übersicht Übungsblatt 11 - Quadtrees Motivation:
Mehrwegbäume Motivation
 Mehrwegbäume Motivation Wir haben gute Strukturen (AVL-Bäume) kennen gelernt, die die Anzahl der Operationen begrenzen Was ist, wenn der Baum zu groß für den Hauptspeicher ist? Externe Datenspeicherung
Mehrwegbäume Motivation Wir haben gute Strukturen (AVL-Bäume) kennen gelernt, die die Anzahl der Operationen begrenzen Was ist, wenn der Baum zu groß für den Hauptspeicher ist? Externe Datenspeicherung
Welche Objekte treffen in der nächsten Stunde aufeinander?
 324Anfragen 3.2.4 an die nahe Zukunft Beispiel: Wer befindet sich in der nächsten Stunde in Region A? Welche Objekte treffen in der nächsten Stunde aufeinander? Eigenschaften: Zukünftige Bewegung von Objekten
324Anfragen 3.2.4 an die nahe Zukunft Beispiel: Wer befindet sich in der nächsten Stunde in Region A? Welche Objekte treffen in der nächsten Stunde aufeinander? Eigenschaften: Zukünftige Bewegung von Objekten
Kapitel 6: Algorithmen der Computer-Geometrie
 LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS Kapitel 6: Algorithmen der Computer-Geometrie Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2015/16 Ludwig-Maximilians-Universität
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS Kapitel 6: Algorithmen der Computer-Geometrie Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2015/16 Ludwig-Maximilians-Universität
1. Sichtbarkeitsproblem beim Rendern einer dreidimensionalen Szene auf einer zweidimensionalen
 3D-Rendering Ulf Döring, Markus Färber 07.03.2011 1. Sichtbarkeitsproblem beim Rendern einer dreidimensionalen Szene auf einer zweidimensionalen Anzeigefläche (a) Worin besteht das Sichtbarkeitsproblem?
3D-Rendering Ulf Döring, Markus Färber 07.03.2011 1. Sichtbarkeitsproblem beim Rendern einer dreidimensionalen Szene auf einer zweidimensionalen Anzeigefläche (a) Worin besteht das Sichtbarkeitsproblem?
Entscheidungsverfahren für die Software-Verifikation. 4 - BDDs
 Entscheidungsverfahren für die Software-Verifikation 4 - BDDs Datenstruktur BDD 1986 von R. Bryant vorgeschlagen zur Darstellung von aussagenlogischen Formeln (genauer: Booleschen Funktionen) Boolesche
Entscheidungsverfahren für die Software-Verifikation 4 - BDDs Datenstruktur BDD 1986 von R. Bryant vorgeschlagen zur Darstellung von aussagenlogischen Formeln (genauer: Booleschen Funktionen) Boolesche
9 Minimum Spanning Trees
 Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Graphen (1) Darstellung Traversierung Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 441 Generalisierung von Bäumen Verallgemeinerung (von Listen zu Graphen)
Vorlesung Datenstrukturen Graphen (1) Darstellung Traversierung Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 441 Generalisierung von Bäumen Verallgemeinerung (von Listen zu Graphen)
Boolesche Operationen und lokale Manipulationen
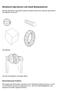 1 Boolesche Operationen und lokale Manipulationen Mit Hilfe Boolescher Operatoren werden komplexe Körper aus Instanzen generischer Grundkörper konstruiert.. Grundkörper Aus den Grundkörpern erzeugter Körper
1 Boolesche Operationen und lokale Manipulationen Mit Hilfe Boolescher Operatoren werden komplexe Körper aus Instanzen generischer Grundkörper konstruiert.. Grundkörper Aus den Grundkörpern erzeugter Körper
Datenbanksysteme II Multidimensionale Indizes (Kapitel 14) Felix Naumann
 Datenbanksysteme II Multidimensionale Indizes (Kapitel 14) 14.5.2007 Felix Naumann Motivation 2 Annahme bisher: Eine Dimension Ein einziger Suchschlüssel Suchschlüssel kann auch Kombination von Attributen
Datenbanksysteme II Multidimensionale Indizes (Kapitel 14) 14.5.2007 Felix Naumann Motivation 2 Annahme bisher: Eine Dimension Ein einziger Suchschlüssel Suchschlüssel kann auch Kombination von Attributen
Universität Trier. Fachbereich IV. Wintersemester 2004/2005. Wavelets made easy. Kapitel 2 Mehrdimensionale Wavelets und Anwendungen
 Universität Trier Fachbereich IV Wintersemester 2004/2005 Wavelets made easy Kapitel 2 Mehrdimensionale Wavelets und Anwendungen Thomas Queckbörner 16.11.2004 Übersicht des Kapitels: 1. Einführung 2. Zweidimensionale
Universität Trier Fachbereich IV Wintersemester 2004/2005 Wavelets made easy Kapitel 2 Mehrdimensionale Wavelets und Anwendungen Thomas Queckbörner 16.11.2004 Übersicht des Kapitels: 1. Einführung 2. Zweidimensionale
Effizienter Planaritätstest Vorlesung am
 Effizienter Planaritätstest Vorlesung am 23.04.2014 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER Satz Gegebenen einen Graphen G = (V, E) mit n Kanten und m Knoten, kann in O(n + m) Zeit
Effizienter Planaritätstest Vorlesung am 23.04.2014 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER Satz Gegebenen einen Graphen G = (V, E) mit n Kanten und m Knoten, kann in O(n + m) Zeit
WS 2014/15 FINITE-ELEMENT-METHODE JUN.-PROF. D. JUHRE
 Eigenschaften Der wesentliche Nachteil neunknotiger biquadratischer Lagrange Elemente ist die gegenüber dem bilinearen Element erhöhte Anzahl von Elementfreiheitsgraden. Insbesondere die beiden Freiheitsgrade
Eigenschaften Der wesentliche Nachteil neunknotiger biquadratischer Lagrange Elemente ist die gegenüber dem bilinearen Element erhöhte Anzahl von Elementfreiheitsgraden. Insbesondere die beiden Freiheitsgrade
Algorithmen und Komplexität
 Algorithmen und Komplexität Dynamische Programmierung Markus Ullrich Norbert Baum Fachbereich Informatik - IIb07 Hochschule Zittau/Görlitz 28. Mai 2009 1 / 29 Wie sieht es mit langen Ketten aus? A 1 A
Algorithmen und Komplexität Dynamische Programmierung Markus Ullrich Norbert Baum Fachbereich Informatik - IIb07 Hochschule Zittau/Görlitz 28. Mai 2009 1 / 29 Wie sieht es mit langen Ketten aus? A 1 A
Berechnung approximierter Voronoi-Zellen auf geometrischen Datenströmen
 Definition Berechnung approximierter Voronoi-Zellen auf geometrischen Datenströmen Seminar über Algorithmen WS 2005/2006 Vorgetragen von Oliver Rieger und Patrick-Thomas Chmielewski basierend auf der Arbeit
Definition Berechnung approximierter Voronoi-Zellen auf geometrischen Datenströmen Seminar über Algorithmen WS 2005/2006 Vorgetragen von Oliver Rieger und Patrick-Thomas Chmielewski basierend auf der Arbeit
Kapitel 3 Anfragen auf räumlichen Objekten
 Kapitel 3 Anfragen auf räumlichen Objekten Skript zur Vorlesung: Spatial, Temporal, and Multimedia Databases Sommersemester 2011, LMU München 2007 Prof. Dr. Hans-Peter Kriegel, Dr. Peer Kröger, Dr. Peter
Kapitel 3 Anfragen auf räumlichen Objekten Skript zur Vorlesung: Spatial, Temporal, and Multimedia Databases Sommersemester 2011, LMU München 2007 Prof. Dr. Hans-Peter Kriegel, Dr. Peer Kröger, Dr. Peter
Bäume, Suchbäume und Hash-Tabellen
 Im folgenden Fokus auf Datenstrukturen, welche den assoziativen Zugriff (über einen bestimmten Wert als Suchkriterium) optimieren Bäume: Abbildung bzw. Vorberechnung von Entscheidungen während der Suche
Im folgenden Fokus auf Datenstrukturen, welche den assoziativen Zugriff (über einen bestimmten Wert als Suchkriterium) optimieren Bäume: Abbildung bzw. Vorberechnung von Entscheidungen während der Suche
Bäume. 2006 Jiri Spale, Algorithmen und Datenstrukturen - Bäume 1
 Bäume 2006 Jiri Spale, Algorithmen und Datenstrukturen - Bäume 1 Inhalt Grundbegriffe: Baum, Binärbaum Binäre Suchbäume (Definition) Typische Aufgaben Suchaufwand Löschen allgemein, Methode Schlüsseltransfer
Bäume 2006 Jiri Spale, Algorithmen und Datenstrukturen - Bäume 1 Inhalt Grundbegriffe: Baum, Binärbaum Binäre Suchbäume (Definition) Typische Aufgaben Suchaufwand Löschen allgemein, Methode Schlüsseltransfer
4. Segmentierung von Objekten Video - Inhaltsanalyse
 4. Segmentierung von Objekten Video - Inhaltsanalyse Stephan Kopf Inhalt Vorgehensweise Berechnung der Kamerabewegungen zwischen beliebigen Bildern Transformation eines Bildes Hintergrundbilder / Panoramabilder
4. Segmentierung von Objekten Video - Inhaltsanalyse Stephan Kopf Inhalt Vorgehensweise Berechnung der Kamerabewegungen zwischen beliebigen Bildern Transformation eines Bildes Hintergrundbilder / Panoramabilder
Geometrie II. Deniz Neufeld Deniz Neufeld Geometrie II / 39
 Geometrie II Deniz Neufeld 20.06.2016 Deniz Neufeld Geometrie II 20.06.2016 1 / 39 Ziel Umgehen mit großen, mehrdimensionalen Datenmengen Bereichssuche Nearest-Neighbour-Search Mehrdimensionale Datenverarbeitung
Geometrie II Deniz Neufeld 20.06.2016 Deniz Neufeld Geometrie II 20.06.2016 1 / 39 Ziel Umgehen mit großen, mehrdimensionalen Datenmengen Bereichssuche Nearest-Neighbour-Search Mehrdimensionale Datenverarbeitung
Dynamische Geometrie
 Dynamische Geometrie 1) Die Mittelsenkrechten, die Seitenhalbierenden, die Höhen und die Winkelhalbierenden eines beliebigen Dreiecks schneiden sich jeweils in einem Punkt. a) Untersuchen Sie die Lage
Dynamische Geometrie 1) Die Mittelsenkrechten, die Seitenhalbierenden, die Höhen und die Winkelhalbierenden eines beliebigen Dreiecks schneiden sich jeweils in einem Punkt. a) Untersuchen Sie die Lage
Conservative Volumetric Visibility with Occluder Fusion
 Conservative Volumetric Visibility with Occluder Fusion Worum geht es? Ausgangspunkt komplexe Szene, wie Städte, Straßenzüge, etc. Ziel effiziente Berechnung von nicht sichtbaren Regionen Begriffe / Definitionen
Conservative Volumetric Visibility with Occluder Fusion Worum geht es? Ausgangspunkt komplexe Szene, wie Städte, Straßenzüge, etc. Ziel effiziente Berechnung von nicht sichtbaren Regionen Begriffe / Definitionen
Geometrische Algorithmen Einige einfache Definitionen: Ist ein Punkt in einem Polygon? Punkt-in-Polygon-Problem. Das Punkt-in-Polygon-Problem
 Geometrische Algorithmen Einige einfache Definitionen: Punkt: im n-dimensionalen Raum ist ein n-tupel (n Koordinaten) Gerade: definiert durch zwei beliebige Punkte auf ihr Strecke: definiert durch ihre
Geometrische Algorithmen Einige einfache Definitionen: Punkt: im n-dimensionalen Raum ist ein n-tupel (n Koordinaten) Gerade: definiert durch zwei beliebige Punkte auf ihr Strecke: definiert durch ihre
