Austauschprozesse Kapitalfluss
|
|
|
- Christoph Scholz
- vor 7 Jahren
- Abrufe
Transkript
1 Austauschprozesse Kapitalfluss Zwischen den Filialen F und F 2 einer Bank findet pro Monat ein Kapitalfluss statt. Die Übergangsmatrix lautet: 4 A = Der Startvektor sei z.b. x 0 = 4 F F 2 4 (in Millionene. Wie sieht die weitere Entwicklung aus? Variiere die Anfangsverteilung. Mit x n+ = A x n und gegebenem x 0 entsteht durch Iteration eine Punktfolge. 4 y (, 4 ( 2 2 ( ( (0 x a Warum liegen die Punktfolgen jeweils auf einer Geraden? Wie lautet der Richtungsvektor dieser Geraden? b Was bedeuten in diesem Kontext negative Zahlen? c Die Grenzvektoren scheinen auch auf einer Geraden zu liegen. Untersuche dies. Beachte, dass für die Grenzvektoren x gilt: x = A x. d In dem Gleichungssystem in c ist eine Gleichung überflüssig. Warum? Durch welche wird sie zweckmäßigerwiese ersetzt? 2 e Ermittle λ, so dass für x 0 = gilt: A x 2 0 = λ x 0. Gilt diese Beziehung auch für Vektoren, die zu x 0 kollinear sind? f Stelle x 0 = als Linearkombination von Vektoren aus c und e dar und untersuche hiermit die weitere Entwicklung.
2 Austauschprozesse, Methodisches Mit x 0 als Anfangszustand (Anfangsverteilung erhalten wir nach einer Zeiteinheit x = A x 0, nach 2 Zeiteinheiten: x 2 = A x = A (A x 0, usw. GTR: [A] [B] [B], ENTER-Taste (wiederholt, der Startvektor ist eine 2-Matrix. Die Grenzverteilung ist hiermit erkennbar. F F 2,000,000,0 2,40, 2,4 2,09,9 2,0,90 2,6,9 2,,2 2,4,796 2,22,7 2,27,7 2,29,7 2,22,779 2,22,779 F F 2,000,000 0,00 2,00 0,47,2 0,760,240 0,9,02,00 0,99,0 0,947,079 0,92,09 0,907,0 0,99,06 0,94,0 0,92,09 0,9 F F 2 2,000 2,000,00,00 0,60 0,60 0, 0, 0, 0, 0,0 0,0 0,0 0,0 0,00 0,00 0,07 0,07 0,009 0,009 0,00 0,00 0,00 0,00 0,002 0,002 λ = 0, = 4 Wie muss die Multiplikation A A = A 2 von Matrizen beschaffen sein, damit gilt: A (A x 0 = A 2 x 0? Die Frage beantwortet das Blatt Matrizenmultiplikation (Vektorrechnung Markow. Für die grafische Darstellung der Punktfolgen eignen sich Excel, Derive, GeoGebra oder ein GTR: (siehe GTR Folgen nmin = 0 u(n = 4 u(n + 4 v(n u(nmin = v(n = u(n + 4 v(n v(nmin = 2nd FORMAT uv Die zweite Möglichkeit, die Konvergenz zu untersuchen, besteht im Potenzieren der Matrix A. Die Spalten von A sind gleich. Sie stimmen mit dem stationären Vektor Durch Multiplikation mit S erhalten wir jede Grenzverteilung zu gegebener Spaltensumme. 4 + ( 4 (Spaltensumme überein. 2
3 Eigenvektoren Zwischen den Filialen F und F 2 einer Bank findet pro Monat ein Kapitalfluss statt. Die Übergangsmatrix lautet: 4 A = Der Startvektor sei x 0 = 4 F F (in Millionene. 6 Der Austauschprozess soll mit einer weiterführenden Methode untersucht werden, die in unübersichtlichen Situationen nutzbringend angewandt werden kann. Hierzu ermitteln wir (z. B. aus der Gleichgewichtsbedingung A x = x einen Fixvektor und einen Richtungsvektor (x+y = const für den Prozess. Der Startvektor kann als Linearkombination dieser Vektoren dargestellt werden. y x 0 x 0 = = +4 = + Ermittle λ: A = λ Was folgt für: x = A [ + ], x 2, x,...? 6
4 Eigenvektoren Ergebnisse A = 0 x 0 = 6 = + 6 x = A [ + ] = A +A 6 6 = + 6 ( x 2 = ( 2... ( x n = ( n Die Vektoren und 6 heißen Eigenvektoren. Ihre zugehörigen Eigenwerte sind und. Wird ein Startvektor als Linearkombination von Eigenvektoren dargestellt, dann ist die weitere Entwicklung offensichtlich. Das gilt natürlich nicht nur für 22-Matrizen. Die Kenntnis der Eigenwerte einer Übergangsmatrix erlaubt Aussagen über die langfristige Entwicklung, z.b. wenn alle Eigenwerte kleiner sind oder ein Eigenwert größer ist. Wie verhält es sich vermutlich bei Matrizen der Austauschprozesse (Spaltensumme? 4
5 Eigenvektoren Fortsetzung Ein Vektor mit der Eigenschaft A x = λ x heißt Eigenvektor zum Eigenwert λ. Für die Matrix A = ( a b c d ax + by = λx cx + dy = λy bedeutet das: bzw. (a λx + by = 0 cx + (d λy = 0 d.h. (a λx = by cx = (d λy Durch eine Division beider Seiten fallen x und y heraus: d.h. (a λ(d λ bc = 0 oder in anderer Schreibweise: det(a λe = 0 a λ c = b d λ Es müssen also zuerst mit dieser Gleichung die Eigenwerte ermittelt werden und dann mit ihnen mit dem Gleichungssystem A x = λ x die zugehörigen Eigenvektoren. Zu einem Eigenvektor ist auch ein Vielfaches Eigenvektor zum selben Eigenwert. Sei x 0 = e + e 2, Eigenwert von e sei λ, Eigenwert von e 2 sei λ 2. Ermittle x, x 2, x,... Mit dem GTR werden Eigenwerte als Nullstellen ermittelt: Y-Editor: Y=det([A]-identity(2X. Ermittle für die Matrix A = ( 2 2 Eigenwerte und Eigenvektoren. 2. Die Eigenwerte der Matrix B = 2 0 lauten:, 2 und 4. Bestimme die Eigenvektoren Eine Bevölkerungsentwicklung werde durch eine Matrix A beschrieben. a Die Grenzmatrix A enthalte eine Nullspalte. Was bedeutet das? b Es soll eine jährliche, konstante Einwanderung c berücksichtigt werden. Die Anfangsverteilung sei v 0. Wie sieht die weitere Entwicklung aus?
6 Aufgaben 4. Die Matrix beschreibt die Entwicklung einer Population. C = a Überpüfe, ob e =, e 2 =, e = 2 Eigenvektoren sind b Stelle den Startvektor v 0 = 6 als Linearkombination von e, e 2 und e dar. Wie lautet v n? Gibt es eine Grenzverteilung? Wenn ja, wie wäre sie?. Zwei Anbieter A, B eines Produktes teilen sich den Markt. Innerhalb eines Monats wechselt ein Anteil p der Kunden von A zu B, während p+0,2 der Kunden von B aufgrund geringerer Markentreue zu A wechseln. Die übrigen Kunden verbleiben bei dem jeweiligen Anbieter. Die Gesamtzahl der Kunden bleibt gleich. Langfristig kann sich jeder der Anbieter nur dann am Markt halten, wenn er mindestens 0% Marktanteil aufweist. Für welche Werte p wird B vom Markt verschwinden? 6. Für einen Startvektor v gelte: A v = q v. Was kann über v in Abhängigkeit von q ausgesagt werden? 7. Wie kann ein vermuteter Grenzvektor eines Austauschprozesses auf einfache Weise (ohne GTR nachgewiesen werden?. Sei M = p p p p 2 p 2 p 2 p p p, Startvektor a = a a 2 a, Spaltensumme a +a 2 +a = S Die Grenzverteilung ist unabhängig von der Anfangsverteilung. Erläutere dies. M a = p a +p a 2 +p a p 2 a +p 2 a 2 +p 2 a = p a +p a 2 +p a p (a +a 2 +a p 2 (a +a 2 +a = S p (a +a 2 +a p p 2 p 6
7 Aufgaben Ergebnisse. A = ( 2 2 Eigenwert, Eigenvektor 2 ew =, e = ew 2 = 4, e 2 = 2. B = Eigenwert, Eigenvektor ew = 4, e =, ew 2 =, e 2 =, 2 ew = 2, e = 0 4. C = a Eigenwert, Eigenvektor ew = 2, e =, ew 2 = 2 6 4, e 2 =, ew =, e = b v 0 = 6 = e +6 e 2 + e, v = q < = v ist der Nullvektor, das System zerfällt q > = v existiert nicht, das System expandiert q = = v = v q = = periodische Entwicklung mit ± v 7. A v = v 7
8 Konvergenzverhalten stochastischer Matrizen Die Veranschaulichung des Grenzprozesses für eine -Matrix gelingt im R. Die Punktfolge liegt auf der Ebene x+y +z = S, wobei S die Spaltensumme des Startvektors ist. Die Grenzverteilung ergibt sich als Schnitt der Ebene mit einer Ursprungsgeraden, deren Richtungs- vektor der Eigenvektor zum Eigenwert ist. Auf dieser Geraden liegen die stationären Verteilungen. Um den Konvergenzprozess näher zu untersuchen, wird der Startvektor als Linearkombination der Eigenvektoren dargestellt. z S S y x S Bei stochastischen Matrizen bleibt die Spaltensumme durch den Übergang von x nach A x erhalten. Für einen Eigenvektor u bedeutet dies, dass seine Spaltensumme mit der von λ u übereinstimmt. Das ist nur möglich, wenn λ = oder die Spaltensumme Null ist, d.h. u +u 2 +u = 0, der Eigenvektor also parallel zur Ebene x +x 2 +x = S verläuft (beachte den Normalenvektor. Da der Prozess konvergiert, müssen die Eigenwerte dieser Eigenvektoren kleiner Null sein. Nun ist auch ersichtlich, dass die Grenzverteilung von der Anfangsverteilung (bei gleicher Spaltensumme unabhängig ist. Zeige: S 0 0 Aus A 0 = A S = A 0 folgt, dass die Spalten von A gleich sind und 0 0 S mit der stationären Verteilung übereinstimmen.
9 Grenzmatrix Betrachte die. Zeilen (2. Zeilen der Matrizen. Welche Vermutung liegt nahe? Beweis? A = 0,2 0,7 0, 0, A 2 = 0,6 0, 0,4 0,6 A = 0,4 0,2 0,6 0,47 A 4 = 0, 0,4 0, 0,6 0,4 0,4 A = 0, 0,9 0,467 0,466 A 0 = 0, 0,4 0,467 0,467 A = 0, 0, 9
10 Grenzmatrix Die kleinere Zahl der jeweils. Zeile (2. Zeile wird mit höheren Potenzen immer größer, die größere Zahl wird immer kleiner. Die Differenzen streben vermutlich gegen Null (d n 0, d <, siehe 4., Aufg., Seite. ( p. p. = A ( a b (. A n =.... = A n+ Sei a < b = a p+b ( p > a (Gleichheit für a = b Für N N-Matrizen wächst die kleinste Zahl je Zeile monoton, die Größte fällt monoton. ( Sei also A p p = p 2 p 2 Für einen Startvektor a =. ( a a 2 mit der Spaltensumme a +a 2 = S ist dann die Grenzverteilung unabhängig von der Anfangsverteilung. Erläutere dies. lim x (An a = A a = ( p p p 2 p 2 a p a = +p a 2 = a 2 p 2 a +p 2 a 2 p (a +a 2 p 2 (a +a 2 p = S p 2 0
11 . Die Bevölkerung eines Landes mit 0 Millionen Einwohnern sei gleichmäßig in Männer, Frauen und Kinder aufgeteilt. lm beobachteten Zeitraum von einem Jahr erreichen jeweils % der männlichen und weiblichen Kinder das Erwachsenenalter. lm Durchschnitt bekommen 2% der Frauen in diesem Jahr ein Kind. Die Sterblichkeit betrage bei den Männern % und bei den Frauen 0%. Wie wird sich die Bevölkerung weiter entwickeln? Die im Text gegebenen lnformationen lassen sich in einem Übergangsgraphen veranschaulichen. 94% K % % 2% M F % 90% und in einer Übergangsmatrix übersichtlich anordnen: A = 0, 0 0,0 0 0,9 0,0 0 0,2 0,94 y M n+ = 0,M n F n+ = K n+ = + 0,0K n 0,9F n + 0,0K n 0,2F n + 0,94K n v0 = 0, 0,, v0 = 0, 0,226, 0,62 v = 0 0,2 0,22 0,79 x Kinder Frauen Männer Für den Zustandsvektor zur anfänglichen Gleichverteilung können absolute oder relative Werte verwendet werden. Die durch die Grafik nahegelegte Vermutung hinsichtlich der weiteren Entwicklung ist falsch.
12 Die Einwohnerzahl wächst schließlich immer weiter an, desgleichen die Zahl der Männer und Frauen. y 0, 0, Kinder Frauen Männer x v0 =, v = 0,2 0,22, 0,79 v 0 = 0,9 0,29,,047 v 00 = 0,0 0,449,629 Eine Grenzmatrix existiert nicht. Die Bevölkerungsentwicklung ist natürlich von der Anfangsverteilung abhängig. Die Matrix A 0 = 0 0,4 0,0 0 0,60 0,26 0 2, 0,9 belegt, dass die Bevölkerungszahl nach 0 Jahren weitgehend unabhängig von der anfänglichen Anzahl der Männer ist. Im vorliegenden Beispiel ist die Zeilensumme in der dritten Zeile der Übergangsmatrix A größer als, die hohe Geburtenrate sichert das Wachstum der Bevölkerung. Die Einträge in der Ubergangsmatrix A sind nicht kleiner als Null. Allgemein gilt dann, dass das durch die Matrix beschriebene System (bei positiven Startkomponenten ( konvergiert, wenn alle Zeilensummen gleich sind, (2 expandiert, wenn alle Zeilensummen größer als sind, ( zerfällt, wenn alle Zeilensummen der Matrix kleiner als sind. 2
13 Eine Betrachtung der Eigenwerte und -vektoren der Matrix A ist aufschlussreich.,9 0,9 ew = 0,, e = 0, ew 2 = 0,, e 2 = 0,46, ew =,009, e = 0,276 0 Begründe: Die Verteilung der Einwohner auf die betrachteten Bevölkerungsgruppen bleibt schließlich stabil. Der Anteil der Männer an der Gesamtbevölkerung konvergiert gegen 2,9%, der Anteil der Frauen gegen,% und der der Kinder gegen 6,%.
14 2. Für eine Haftpflichtversicherung gibt es die Tarifklassen A, B und C. C ist die Ungünstigste. Bleibt man während eines Kalenderjahres schadensfrei, steigt man im folgenden Jahr in die nächstgünstigere Klasse auf oder verbleibt in A. Im Schadensfall ist es umgekehrt. Der Übergangsgraph enthält die Umstufungsanteile. Die Gesamtzahl der Versicherten sei als konstant anzunehmen. 0, 0,4 0, A B C 0,4 0,6 0,6 a Die Gesamtzahl der Versicherten betrage 400. Im Jahr 09 sind dabei 00 Versicherte in die Tarifklasse A, 00 in B und der Rest in C eingestuft. Berechnen Sie die Verteilungen der Jahre 0, 0 und. b Welche Verteilung stellt sich auf lange Sicht ein? c Die langfristig sich einstellende Anzahl der Versicherten in der Tarifklasse A ist dem Unternehmen zu hoch. Es erwägt, bei größeren Schadensfällen eine direkte Rückstufung von A nach C einzuführen. Wie groß müsste dieser Anteil sein (mit dem die Schadensgrenze ermittelt werden könnte, damit sich langfristig nur noch 600 Versicherte in Klasse A befänden? Wie viele Versicherte wären dann in den übrigen Klassen?. Zwei Firmen stellen die miteinander konkurrierenden Kaffeemischungen K und K 2 her. Marktuntersuchungen haben ergeben, dass 0% der Kunden der Kaffeesorte K je Übergangsperiode treu bleiben, während0% von K 2 nach K wechseln. Die Firma, diek 2 produziert, plantdie Einführung einer neuen Kaffeemischung K, um ihren Marktanteil zu erhöhen. Hierbei ergab eine vorbereitende Marktanalyse, dass bei einer Einführung von K 0% bei K bleiben und 0% von K zu K wechseln. Die Kunden von K 2 bleiben zu 60% ihrer Marke treu, sie lehnen K ab. Die neue Marke K behält zu 0% ihre neuen Kunden, 40% wechseln zu K 2. Zur Zeit (vor Einführung der neuen Sorte liegt der Marktanteil bei 6% für K und % für K 2. a Welche Marktstrategie sollte der Produzent von K 2 verfolgen, wenn er einen größeren Marktanteil erzielen will? b Bewerte das zugrundeliegende mathematische Modell für die Einführung einer neuen Kaffeesorte. 4
15 2. Für eine Haftpflichtversicherung gibt es die Tarifklassen A, B und C. C ist die Ungünstigste. Bleibt man während eines Kalenderjahres schadensfrei, steigt man im folgenden Jahr in die nächstgünstigere Klasse auf oder verbleibt in A. Im Schadensfall ist es umgekehrt. Der Übergangsgraph enthält die Umstufungsanteile. Die Gesamtzahl der Versicherten sei als konstant anzunehmen. 0, 0,4 0, A B C 0,4 0,6 0,6 a Die Gesamtzahl der Versicherten betrage 400. Im Jahr 09 sind dabei 00 Versicherte in die Tarifklasse A, 00 in B und der Rest in C eingestuft. Berechnen Sie die Verteilungen der Jahre 0, 0 und v 0 = 62, v 0 = 0, v = b Welche Verteilung stellt sich auf lange Sicht ein? 00 v = c Die langfristig sich einstellende Anzahl der Versicherten in der Tarifklasse A ist dem Unternehmen zu hoch. Es erwägt, bei größeren Schadensfällen eine direkte Rückstufung von A nach C einzuführen. Wie groß müsste dieser Anteil sein (mit dem die Schadensgrenze ermittelt werden könnte, damit sich langfristig nur noch 600 Versicherte in Klasse A befänden? Wie viele Versicherte wären dann in den übrigen Klassen? M = 0, 0,6 0 a 0 0,6 0, a 0,4 0,4 v = 600 b 2700 b M v = v = b =,, a = 0,2 v = 600, 67,67
16 . Zwei Firmen stellen die miteinander konkurrierenden Kaffeemischungen K und K 2 her. Marktuntersuchungen haben ergeben, dass 0% der Kunden der Kaffeesorte K je Übergangsperiode treu bleiben, während 0% von K 2 nach K wechseln. Die Firma, die K 2 produziert, plant die Einführung einer neuen Kaffeemischung K, um ihren Marktanteil zu erhöhen. Hierbei ergab eine vorbereitende Marktanalyse, dass bei einer Einführung von K 0% bei K bleiben und 0% von K zu K wechseln. Die Kunden von K 2 bleiben zu 60% ihrer Marke treu, sie lehnen K ab. Die neue Marke K behält zu 0% ihre neuen Kunden, 40% wechseln zu K 2. Zur Zeit (vor Einführung der neuen Sorte liegt der Marktanteil bei 6% für K und % für K 2. a Welche Marktstrategie sollte der Produzent von K 2 verfolgen, wenn er einen größeren Marktanteil erzielen will? 0, 0, A = 0,2 0,7 langfristige Marktanteile vor Einführung der neuen Sorte: K = 60%, K 2 = 40% B = 0, 0,4 0, 0, 0,6 0,4 0, 0 0, langfristige Anteile mit Einführung von K : K = 60,%, K 2 = 27,%, K = 2,% Gesamtanteil von K 2 und K : 9,4% Durch die Einführung der neuen Sorte verkleinert sich der Marktanteil etwas. b Bewerte das zugrundeliegende mathematische Modell für die Einführung einer neuen Kaffeesorte. 6
17 4. Für einen Austauschprozess sei A = 0,7 0,4 0, 0,6. Der Startvektor, sei x 0 = 0. 0 a Bestimmen Sie x, x, x, x 2, A und damit x (Was muss zu x 2 angemerkt werden?. b Weisen Sie nach, dass a = können? 0 ein Fixvektor ist. Wie hätte man ihn ohne GTR errechnen 0 c Ermitteln Sie k, so dass für b = gilt: A b = k b. Gilt diese Beziehung auch für Vektoren, die zu b kollinear sind? 600 d Stellen Sie y 0 = als Linearkombination der Vektoren a und 00 b (aus b und c dar und beschreiben Sie hiermit die weitere Entwicklung. 7
18 4. Für einen Austauschprozess sei A = 0,7 0,4 0, 0,6. Der Startvektor, sei x 0 = 0. 0 a Bestimmen Sie x, x, x, x 2, A und damit x (Was muss zu x 2 angemerkt werden?. b Weisen Sie nach, dass a = können? 99,,,6 x =, x 6 =, x 0,2 =, x 6,66 2 = 70, 6 0,7 0,7 A = 0,7 0 99,, x = = 0,4 0,4 0,4 0 0, 0 ein Fixvektor ist. Wie hätte man ihn ohne GTR errechnen 0 A a = a A x = x, zweite Zeile durch x+y = 0 ersetzen ansonsten gilt für stochastische Matrizen: A x 0 = a Als Startvektor kann jeder Vektor mit derselben Spaltensumme genommen werden. c Ermitteln Sie k, so dass für b = gilt: A b = k b. Gilt diese Beziehung auch für Vektoren, die zu b kollinear sind? k = 0, ja 600 d Stellen Sie y 0 = als Linearkombination der Vektoren a und 00 b (aus b und c dar und beschreiben Sie hiermit die weitere Entwicklung. y 0 = 2 a 0 b 400 y n = +0, 00 n y x 0 0
19 . In einem abgeschlossenen Wildreservat - unterteilt in die Bereiche A, B und C - untersuchen Biologen die monatliche Wanderungsbewegung der Bären. Die Ergebnisse sind in dem Diagramm festgehalten. % C 0% 0% A B 60% 60% 40% a Ergänzen Sie das Diagramm und stellen Sie das Wechselverhalten in einer Übergangsmatrix Q dar. b Bestimmen Sie alle Fixvektoren zur Matrix Q. c ln einem bestimmten Monat halten sich in A 400, in B und C jeweils 0 Bären auf. Berechnen Sie für die nächsten drei Monate die Verteilung (gerundet der Bären auf die drei Gebiete. Welche Verteilung stellt sich langfristig ein? d ln einem bestimmten Monat halten sich 00 Bären in A, B und C im Verhältnis 4 : : 2 auf. Wie viele Bären sind das in den einzelnen Bereichen? e Einige Biologen streben folgende Grenzverteilung an: in A 00, in B 20 und in C 240 Bären. Hierzu sollen die markierten Übergänge ( verändert werden (in A könnten z.b. die Lebensbedingungen erschwert werden. Untersuchen Sie, ob dies möglich ist. f Einige Biologen vermuten, dass sich die ursprüngliche Übergangsmatrix verändert hat zu: Q = a b Erörtern Sie (ohne Rechnung die möglichen Konsequenzen (Fallunterscheidung a, b größer null Prozent, a, b nahezu null. Nennen Sie auch mögliche Ursachen. Gehen Sie jeweils auf die Existenz einer Grenzverteilung ein. 9
20 . In einem abgeschlossenen Wildreservat - unterteilt in die Bereiche A, B und C - untersuchen Biologen die monatliche Wanderungsbewegung der Bären. Die Ergebnisse sind in dem Diagramm festgehalten. % C 0% 0% 0% 0% 0% A B 60% 60% 40% a Ergänzen Sie das Diagramm und stellen Sie das Wechselverhalten in einer Übergangsmatrix Q dar. Q = 0,6 0,6 0, 0, 0,4 0, 0, 0 0,2 4 b Bestimmen Sie alle Fixvektoren zur Matrix Q. x = λ2 c ln einem bestimmten Monat halten sich in A 400, in B und C jeweils 0 Bären auf. Berechnen Sie für die nächsten drei Monate die Verteilung (gerundet der Bären auf die drei Gebiete. Welche Verteilung stellt sich langfristig ein? p0 = 400 0, 0 p = 4 2, 60 p2 = 42, p = 4 6, 6 4 p = 7 62 d ln einem bestimmten Monat halten sich 00 Bären in A, B und C im Verhältnis 4 : : 2 auf. Wie viele Bären sind das in den einzelnen Bereichen? A 00, B 600, C 400 e Einige Biologen streben folgende Grenzverteilung an: in A 00, in B 20 und in C 240 Bären. Hierzu sollen die markierten Übergänge ( verändert werden (in A könnten z.b. die Lebensbedingungen erschwert werden. Untersuchen Sie, ob dies möglich ist. a 0,6 0, 0, 0,4 0, b 0 0, = a = 0,26, b = 0,64
21 f Einige Biologen vermuten, dass sich die ursprüngliche Übergangsmatrix verändert hat zu: Q = a b Erörtern Sie (ohne Rechnung die möglichen Konsequenzen (Fallunterscheidung a, b größer null Prozent, a, b nahezu null. Nennen Sie auch mögliche Ursachen. Gehen Sie jeweils auf die Existenz einer Grenzverteilung ein. Es wandern keine Bären mehr aus C ab. Falls a und b ungleich Null sind, ist C absorbierend, Ursachen... Es existiert eine Grenzverteilung. Falls a und b nahezu Null sind, findet keine Wanderbewegung zwischen C und den anderen Gebieten statt. Eine Grenzverteilung muss nicht existieren; die Tiere können zwischen den Bereichen A und B periodisch wechseln. alternativ f Einige Biologen vermuten, dass sich die ursprüngliche Übergangsmatrix in der. Zeile und in der. Spalte verändert hat:.. 0 Q =.. 0 0,04 0,04 Beschreiben Sie (ohne Rechnung die langfristigen Auswirkungen. Die Gesamtanzahl der Bären in den Gebieten A und B sei anfänglich 600. Welche Funktion B(t erfasst die Gesamtanzahl der Bären in diesen Gebieten? C ist absorbierend. B(t = 600 0,96 t 2
22 ohne GTR 0,4 0,6 A B In einem System verteilt sich ein Gesamtbestand auf die Zustände A und B. Pro Zeiteinheit finden zwischen den Zuständen die in der Abbildung dargestellten Übergänge statt. a Geben Sie die Übergangsmatrix M an. Bestimmen Sie die Matrix N, die die Übergänge in zwei aufeinanderfolgenden Zeiteinheiten zusammenfassend beschreibt. b Weisen Sie nach, dass die Grenzmatrix ist. G = 22
23 ohne GTR 0,4 0,6 A B In einem System verteilt sich ein Gesamtbestand auf die Zustände A und B. Pro Zeiteinheit finden zwischen den Zuständen die in der Abbildung dargestellten Übergänge statt. a Geben Sie die Übergangsmatrix M an. Bestimmen Sie die Matrix N, die die Übergänge in zwei aufeinanderfolgenden Zeiteinheiten zusammenfassend beschreibt. M = 0,4 0,76 0,4, N = M 2 = 0,6 0 0,24 0,6 b Weisen Sie nach, dass die Grenzmatrix ist. G = 0,4 0,6 0 ( = ( (Grenzverteilung 2
24 ohne GTR Gegeben ist die Matrix M = Ermitteln Sie die fehlenden Einträge in der zugehörigen inversen Matrix: M =
25 ohne GTR Gegeben ist die Matrix M = Ermitteln Sie die fehlenden Einträge in der zugehörigen inversen Matrix: M = M = Es fällt auf, dass die Spaltensumme wieder ist. Ist das Zufall? 2
Matrizenrechnung Umfüllprozesse
 Matrizenrechnung Umfüllprozesse In Messzylindern A und B befinden sich anfänglich die Flüssigkeitsmengen m und m. Aus A wird der Anteil a entnommen, aus B der Anteil b weitere Gefäße sind daher erforderlich.
Matrizenrechnung Umfüllprozesse In Messzylindern A und B befinden sich anfänglich die Flüssigkeitsmengen m und m. Aus A wird der Anteil a entnommen, aus B der Anteil b weitere Gefäße sind daher erforderlich.
Stochastische Prozesse Einführung
 Stochastische Prozesse Einführung Der Kurs wird in 2 Gruppen aufgeteilt siehe Excel-Blatt, z.b. A = 2 und B = 20, und es werden die Wechsel-Anteile festgelegt: Pro Takt wechseln z.b. 4 von A nach B und
Stochastische Prozesse Einführung Der Kurs wird in 2 Gruppen aufgeteilt siehe Excel-Blatt, z.b. A = 2 und B = 20, und es werden die Wechsel-Anteile festgelegt: Pro Takt wechseln z.b. 4 von A nach B und
Populationsentwicklung
 Populationsentwicklung Lewis (942) und Leslie (945) entwickelten ein Modell, mit dem die Entwicklung einer Population unter Einbeziehung der Altersstruktur untersucht werden kann. Die Population wird z.b.
Populationsentwicklung Lewis (942) und Leslie (945) entwickelten ein Modell, mit dem die Entwicklung einer Population unter Einbeziehung der Altersstruktur untersucht werden kann. Die Population wird z.b.
1. a) Ergänzen Sie das Diagramm eines Austauschprozesses und ermitteln Sie die Übergangsmatrix.
 Matrizenrechnung Aufgaben 15% C 50% 40% 60% A B 20% 30% 1. a) Ergänzen Sie das Diagramm eines Austauschprozesses und ermitteln Sie die Übergangsmatrix. b) Bestimmen Sie die Grenzverteilung. 200 c) Der
Matrizenrechnung Aufgaben 15% C 50% 40% 60% A B 20% 30% 1. a) Ergänzen Sie das Diagramm eines Austauschprozesses und ermitteln Sie die Übergangsmatrix. b) Bestimmen Sie die Grenzverteilung. 200 c) Der
In Anwendungen müssen oft hohe Potenzen einer quadratischen Matrix berechnet werden = = 83 79
 Matrixpotenzen n Anwendungen müssen oft hohe Potenzen einer quadratischen Matrix berechnet werden. a) terative Berechnung = 2 = 2 2 2 5 = 7 = 2 2 2 2 = 5 4 4 5 = 5 4 4 5 5 = 29 25 = 5 4 4 5 2 3 = 4 2 3
Matrixpotenzen n Anwendungen müssen oft hohe Potenzen einer quadratischen Matrix berechnet werden. a) terative Berechnung = 2 = 2 2 2 5 = 7 = 2 2 2 2 = 5 4 4 5 = 5 4 4 5 5 = 29 25 = 5 4 4 5 2 3 = 4 2 3
Ba-Wü: BG Neuer Lehrplan Mathematik Modul-5: Prozesse Teil 3a: stochastische Übergangsprozesse. Februar und März
 Ba-Wü: BG Neuer Lehrplan Mathematik Modul-5: Prozesse Teil 3a: stochastische Übergangsprozesse Februar und März 216 1 Stoffverteilungsplan 1 Woche Inhalte 1 + 2 Einstufige Prozesse Darstellung mit Tabellen,
Ba-Wü: BG Neuer Lehrplan Mathematik Modul-5: Prozesse Teil 3a: stochastische Übergangsprozesse Februar und März 216 1 Stoffverteilungsplan 1 Woche Inhalte 1 + 2 Einstufige Prozesse Darstellung mit Tabellen,
B =(b1,1. + b 1,2. + b 1,3 1,3. + b 2,4 + b 3,1. + b 2,2. + b 2,3. + b 3,2. + b 3,3
 Matrizen Matrizen sind zunächst einmal einfach eine rechteckige Anordnung von Zahlen, Elementen oder mathematischen Operationen, die lineare Zusammenhänge zwischen verschiedenen Größen übersichtlich darstellen.
Matrizen Matrizen sind zunächst einmal einfach eine rechteckige Anordnung von Zahlen, Elementen oder mathematischen Operationen, die lineare Zusammenhänge zwischen verschiedenen Größen übersichtlich darstellen.
Klausur DI/LA F 2006 LA : 1
 Klausur DI/LA F 26 LA : Aufgabe (4+2=6 Punkte): Gegeben seien die Matrix A und der Vektor b mit λ A = λ und b = λ a) Bestimmen Sie die Werte λ R, für welche das Gleichungssystem Ax = b genau eine, keine
Klausur DI/LA F 26 LA : Aufgabe (4+2=6 Punkte): Gegeben seien die Matrix A und der Vektor b mit λ A = λ und b = λ a) Bestimmen Sie die Werte λ R, für welche das Gleichungssystem Ax = b genau eine, keine
Mathematik Matrizenrechnung
 Mathematik Matrizenrechnung Einstufige Prozesse Rechenregeln für Matrizen Mehrstufige Prozesse Inverse Matrix Stochastische Prozesse 6 Zyklisches Verhalten Einstufige Prozesse Einstufige Prozesse Zur Beschreibung
Mathematik Matrizenrechnung Einstufige Prozesse Rechenregeln für Matrizen Mehrstufige Prozesse Inverse Matrix Stochastische Prozesse 6 Zyklisches Verhalten Einstufige Prozesse Einstufige Prozesse Zur Beschreibung
Lineare Algebra (Zentralabitur 2009: Abibienen) (knappe Lösung)
 Lineare lgebra (Zentralabitur 2009: bibienen) (knappe Lösung) bibienen Ein aus den fleißigen Bienen mutierter Insektenstamm, die nachtaktiven bibienen", wurde im Jahr 2009 auf der Insel Bremensia" über
Lineare lgebra (Zentralabitur 2009: bibienen) (knappe Lösung) bibienen Ein aus den fleißigen Bienen mutierter Insektenstamm, die nachtaktiven bibienen", wurde im Jahr 2009 auf der Insel Bremensia" über
Ergänzende Aufgaben zur Planarbeit Stochastische Matrizen I 1 I 3 0,8 0,2 0,2 0,1 0,7 0,2 0,1 0,1 0,6. und I
 Ergänzende Aufgaben zur Planarbeit Stochastische Matrizen Ergänzende Aufgaben zur Planarbeit Stochastische Matrizen Aufgabe Das Kaufverhalten bei den Lesern der drei marktbeherrschenden Illustrierten sei
Ergänzende Aufgaben zur Planarbeit Stochastische Matrizen Ergänzende Aufgaben zur Planarbeit Stochastische Matrizen Aufgabe Das Kaufverhalten bei den Lesern der drei marktbeherrschenden Illustrierten sei
Matrix-Potenzen und größter Eigenwert
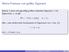 Matrix-Potenzen und größter Eigenwert Besitzt A einen betragsmäßig größten einfachen Eigenwert λ mit Eigenvektor v, so gilt A n x = λ n (cv + o(1)), n, falls x eine nichttriviale Komponente im Eigenraum
Matrix-Potenzen und größter Eigenwert Besitzt A einen betragsmäßig größten einfachen Eigenwert λ mit Eigenvektor v, so gilt A n x = λ n (cv + o(1)), n, falls x eine nichttriviale Komponente im Eigenraum
Prozesse dieser Art sind in der Informatik z.b. bei der Untersuchung der Auslastung von Servern wichtig (Warteschlangenmodelle).
 77 Markowketten 77 Motivation Der Zustand eines Systems zur Zeit n N werde durch eine Zufallsvariable X n beschrieben und soll nur von X n abhängen (nicht jedoch von früheren Zuständen X n, X n 3, ) Wir
77 Markowketten 77 Motivation Der Zustand eines Systems zur Zeit n N werde durch eine Zufallsvariable X n beschrieben und soll nur von X n abhängen (nicht jedoch von früheren Zuständen X n, X n 3, ) Wir
2 Aufgaben. 2.1 Analysis. BE Aufgaben zum Aufgabenpool 1. 1 Die Abbildung zeigt den Graphen G f einer in
 Übungsklausur 013/014 im Fach Mathematik Länderübergreifender gemeinsamer Aufgabenpool Aufgaben.1 Analysis 1 Die Abbildung zeigt den Graphen G f einer in 1;3 definierten Funktion f, die die Nullstellen
Übungsklausur 013/014 im Fach Mathematik Länderübergreifender gemeinsamer Aufgabenpool Aufgaben.1 Analysis 1 Die Abbildung zeigt den Graphen G f einer in 1;3 definierten Funktion f, die die Nullstellen
Determinanten. a e b f a c b d. b) x = , y = c) zu einem Spaltenvektor das Vielfache des anderen Spaltenvektors addiert wird,
 Determinanten Wir entwickeln eine Lösungsformel für Gleichungssysteme mit zwei Variablen. ax + cy = e b bx + y = f a } abx bcy = be + abx + ay = af ya bc = af be Man schreibt y = af be a bc = a e b f analog
Determinanten Wir entwickeln eine Lösungsformel für Gleichungssysteme mit zwei Variablen. ax + cy = e b bx + y = f a } abx bcy = be + abx + ay = af ya bc = af be Man schreibt y = af be a bc = a e b f analog
Eigenwerte und Eigenvektoren von Matrizen
 Eigenwerte und Eigenvektoren von Matrizen Betrachtet wird eine (n,n)-matrix A. Eine Zahl λ heißt Eigenwert von A, wenn ein Vektor v existiert, der nicht der Nullvektor ist und für den gilt: A v = λ v.
Eigenwerte und Eigenvektoren von Matrizen Betrachtet wird eine (n,n)-matrix A. Eine Zahl λ heißt Eigenwert von A, wenn ein Vektor v existiert, der nicht der Nullvektor ist und für den gilt: A v = λ v.
Grundlagen der Mathematik II (LVA U)
 Dr. Marcel Dettling 3.4. Dr. Daniel Haase FS daniel.haase@math.ethz.ch Grundlagen der Mathematik II (LVA 4-6- U) 8 Zur Übungsstunde vom 3.4. Aufgabe (Ausgleichsrechnung) Gegeben sei das lineare Gleichungssystem
Dr. Marcel Dettling 3.4. Dr. Daniel Haase FS daniel.haase@math.ethz.ch Grundlagen der Mathematik II (LVA 4-6- U) 8 Zur Übungsstunde vom 3.4. Aufgabe (Ausgleichsrechnung) Gegeben sei das lineare Gleichungssystem
Behörde für Bildung und Sport Abitur 2008 Lehrermaterialien zum Leistungskurs Mathematik
 II2 Einkommensgruppen LA/AG 2 Die Familien eines fiktiven Landes werden einer der drei angegebenen Einkommensgruppen zugeordnet In statistischen Erhebungen hat man festgestellt, dass Kinder der Eltern
II2 Einkommensgruppen LA/AG 2 Die Familien eines fiktiven Landes werden einer der drei angegebenen Einkommensgruppen zugeordnet In statistischen Erhebungen hat man festgestellt, dass Kinder der Eltern
Musterlösungen Blatt Mathematischer Vorkurs. Sommersemester Dr. O. Zobay. Matrizen
 Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
9 Eigenwerte und Eigenvektoren
 92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
9 Eigenwerte und Eigenvektoren
 92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
92 9 Eigenwerte und Eigenvektoren Wir haben im vorhergehenden Kapitel gesehen, dass eine lineare Abbildung von R n nach R n durch verschiedene Darstellungsmatrizen beschrieben werden kann (je nach Wahl
Satz. Wie wirkt sich ein Basiswechsel auf die Darstellungsmatrix einer linearen Abbildung F : V n V n aus?
 Wie wirkt sich ein Basiswechsel auf die Darstellungsmatrix einer linearen Abbildung F : V n V n aus? Seien [F] B und [F] B die Darstellungsmatrizen von F bezüglich zweier Basen B und B. Weiter sei T die
Wie wirkt sich ein Basiswechsel auf die Darstellungsmatrix einer linearen Abbildung F : V n V n aus? Seien [F] B und [F] B die Darstellungsmatrizen von F bezüglich zweier Basen B und B. Weiter sei T die
Ausführliche Lösungen
 Bohner Ott Deusch Mathematik für berufliche Gymnasien Lineare Algebra Mathematische Beschreibung von Prozessen durch Matrizen Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab. Auflage 6 ISBN
Bohner Ott Deusch Mathematik für berufliche Gymnasien Lineare Algebra Mathematische Beschreibung von Prozessen durch Matrizen Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab. Auflage 6 ISBN
Lösung 1. 65% A 20% 5% 15% 5% 25% 90%B C 70% 5% 2. A= 28,25% B=35,5% C=21,25%
 Felix Hasenau, Q2, 2015/16 X Übergangsmatrizen Einen Monat vor den undestagswahlen liegt die Partei in Umfragen bei 40%, die Partei bei 25 % und die Partei bei 20%. Die restlichen 15% verteilen sich auf
Felix Hasenau, Q2, 2015/16 X Übergangsmatrizen Einen Monat vor den undestagswahlen liegt die Partei in Umfragen bei 40%, die Partei bei 25 % und die Partei bei 20%. Die restlichen 15% verteilen sich auf
Endliche Markov-Ketten - eine Übersicht
 Endliche Markov-Ketten - eine Übersicht Diese Übersicht über endliche Markov-Ketten basiert auf dem Buch Monte Carlo- Algorithmen von Müller-Gronbach et. al. und dient als Sammlung von Definitionen und
Endliche Markov-Ketten - eine Übersicht Diese Übersicht über endliche Markov-Ketten basiert auf dem Buch Monte Carlo- Algorithmen von Müller-Gronbach et. al. und dient als Sammlung von Definitionen und
Klausur 2 Kurs 13Ma1e Mathematik
 29--24 Klausur 2 Kurs Mae Mathematik Lösung Version 29-2-5 Gegeben sind zwei Ebenen E und E 2 : E : 2 x x 2 x =6 E 2 : x = a) Berechnen Sie die Gleichung der Schnittgerade der beiden Ebenen. Plan: E 2
29--24 Klausur 2 Kurs Mae Mathematik Lösung Version 29-2-5 Gegeben sind zwei Ebenen E und E 2 : E : 2 x x 2 x =6 E 2 : x = a) Berechnen Sie die Gleichung der Schnittgerade der beiden Ebenen. Plan: E 2
4x 1 + 2x 2 + 3x 3 = 1, x 2 + ax 3 = 1, ax 2 + x 3 = a 1. 0 a 1 1 Wir führen nun den Gauÿalgorithmus durch:
 Aufgabe 8 Punkte Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R des folgenden linearen Gleichungssystems: 4x + x + 3x 3 =, x + ax 3 =, ax + x 3 =. Lösung. Wir schreiben das lineare Gleichungssystem
Aufgabe 8 Punkte Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R des folgenden linearen Gleichungssystems: 4x + x + 3x 3 =, x + ax 3 =, ax + x 3 =. Lösung. Wir schreiben das lineare Gleichungssystem
f(x)dx F(b) F(3) F(b).
 Aufgaben aus dem Aufgabenpool. Analysis A_ Die Abbildung zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für 5 f(x)dx. ( ) Die Funktion F
Aufgaben aus dem Aufgabenpool. Analysis A_ Die Abbildung zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für 5 f(x)dx. ( ) Die Funktion F
n x n y n Tab.1: Zwei Beispiele
 Hans Walser, [0404] Konvergente Fibonacci-Folgen Worum geht es? Die klassische Fibonacci-Folge,,,, 5, 8,,,... ist divergent. Wir untersuchen Beispiele von konvergenten Folgen mit der Rekursion: a n = pa
Hans Walser, [0404] Konvergente Fibonacci-Folgen Worum geht es? Die klassische Fibonacci-Folge,,,, 5, 8,,,... ist divergent. Wir untersuchen Beispiele von konvergenten Folgen mit der Rekursion: a n = pa
DynaTraffic Lösungen Einstiegsaufgaben
 DynaTraffic Lösungen Einstiegsaufgaben 1. Interpretation von Verkehrssituation und Übergangsgraph a) Die Übergangswahrscheinlichkeit P(A,B)=0.1 bedeutet für ein Auto, das sich auf Spur A befindet, dass
DynaTraffic Lösungen Einstiegsaufgaben 1. Interpretation von Verkehrssituation und Übergangsgraph a) Die Übergangswahrscheinlichkeit P(A,B)=0.1 bedeutet für ein Auto, das sich auf Spur A befindet, dass
Lineare Algebra und Numerische Mathematik D-BAUG Winter 2013 Prof. H.-R. Künsch. Regeln Multiple Choice:
 b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Winter 03 Prof. H.-R. Künsch c Alle Aufgaben haben das gleiche Gewicht. Die Lösungswege müssen, abgesehen von Aufgabe, nachvollziehbar dargestellt
b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Winter 03 Prof. H.-R. Künsch c Alle Aufgaben haben das gleiche Gewicht. Die Lösungswege müssen, abgesehen von Aufgabe, nachvollziehbar dargestellt
) (1 BE) 1 2 ln 2. und somit
 1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 54 Stochastische Matrizen Definition 54.. Eine reelle quadratische Matrix M a ij i,j n heißt spaltenstochastisch,
Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 54 Stochastische Matrizen Definition 54.. Eine reelle quadratische Matrix M a ij i,j n heißt spaltenstochastisch,
Randomisierte Algorithmen
 Randomisierte Algorithmen Randomisierte Algorithmen Thomas Worsch Fakultät für Informatik Karlsruher Institut für Technologie Wintersemester 2018/2019 1 / 40 Überblick Überblick Grundlegendes zu Markov-Ketten
Randomisierte Algorithmen Randomisierte Algorithmen Thomas Worsch Fakultät für Informatik Karlsruher Institut für Technologie Wintersemester 2018/2019 1 / 40 Überblick Überblick Grundlegendes zu Markov-Ketten
Übungsklausur 2013/2014 im Fach Mathematik Länderübergreifender gemeinsamer Aufgabenpool
 STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN Abteilung Gymnasium Referat Mathematik Länderübergreifende gemeinsame Aufgaben in den Abiturprüfungen der Länder Bayern, Hamburg, Mecklenburg-Vorpommern,
STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN Abteilung Gymnasium Referat Mathematik Länderübergreifende gemeinsame Aufgaben in den Abiturprüfungen der Länder Bayern, Hamburg, Mecklenburg-Vorpommern,
Grenzmatrix und Fixvektor Modellierung eines Umschüttvorgangs
 S 1 Grenzmatrix und Fixvektor interessante Entdeckungen bei der Modellierung eines Umschüttvorgangs Dr. Peter Scholl, Siegburg M 1 Leckerer Milchkaffee einen Umschüttvorgang modellieren In einem Krug sind
S 1 Grenzmatrix und Fixvektor interessante Entdeckungen bei der Modellierung eines Umschüttvorgangs Dr. Peter Scholl, Siegburg M 1 Leckerer Milchkaffee einen Umschüttvorgang modellieren In einem Krug sind
Abitur Matrizen und Prozesse (Teil 4 mit Hilfsmittel) Musteraufgaben Lösung A1 1.1 Übergangsmatrix Die Übergangsmatrix lautet (vgl.
 Lösung A1 1.1 Übergangsmatrix Die Übergangsmatrix lautet (vgl. Diagramm): 0,4 0,2 0,1 0,5 0,7 0,5 0,4 0,1 0,1 0,4 0,2 0,1 0,5 0,1 0,7 0,4 Verteilung der Haushalte im Jahr 2015 Stand 2014: 1000 Haushalte
Lösung A1 1.1 Übergangsmatrix Die Übergangsmatrix lautet (vgl. Diagramm): 0,4 0,2 0,1 0,5 0,7 0,5 0,4 0,1 0,1 0,4 0,2 0,1 0,5 0,1 0,7 0,4 Verteilung der Haushalte im Jahr 2015 Stand 2014: 1000 Haushalte
Vermischte Aufgaben zu Mathematische Grundlagen der Ökonomie
 Aufgabe : Vermischte Aufgaben zu Mathematische Grundlagen der Ökonomie Bilden die Lösungsmengen der folgenden linearen Gleichungssysteme jeweils einen Unterraum des IR 3? Begründen Sie. (i) (ii) + 3 =
Aufgabe : Vermischte Aufgaben zu Mathematische Grundlagen der Ökonomie Bilden die Lösungsmengen der folgenden linearen Gleichungssysteme jeweils einen Unterraum des IR 3? Begründen Sie. (i) (ii) + 3 =
2 a 6. a 4 a Wir führen nun den Gauÿalgorithmus durch: 2 a a 2 4a 2 4a a a 2 2a 0 2 a
 Aufgabe 8 Punkte). Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R) des folgenden linearen Gleichungssystem: x + ax + 6x = 4, ax + 4x + ax =, x + 4x =. Lösung. Wir schreiben das lineare Gleichungssystem
Aufgabe 8 Punkte). Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R) des folgenden linearen Gleichungssystem: x + ax + 6x = 4, ax + 4x + ax =, x + 4x =. Lösung. Wir schreiben das lineare Gleichungssystem
1 Einstimmung 2. 2 Allgemeine Eigenwertprobleme Berechnung von Eigenwerten und Eigenvektoren Wichtige Eigenschaften...
 Wirtschaftswissenschaftliches Zentrum 4 Universität Basel Mathematik 2 Dr Thomas Zehrt Eigenwerte und Eigenvektoren Inhaltsverzeichnis Einstimmung 2 2 Allgemeine Eigenwertprobleme 5 2 Berechnung von Eigenwerten
Wirtschaftswissenschaftliches Zentrum 4 Universität Basel Mathematik 2 Dr Thomas Zehrt Eigenwerte und Eigenvektoren Inhaltsverzeichnis Einstimmung 2 2 Allgemeine Eigenwertprobleme 5 2 Berechnung von Eigenwerten
10 Kapitel I: Anschauliche Vektorrechnung
 10 Kapitel I: Anschauliche Vektorrechnung haben. In Mengenschreibweise ist G = {x x = a + tb für ein t R}. Wir werden für diese einführenden Betrachtungen im Interesse einer knappen Redeweise jedoch häufig
10 Kapitel I: Anschauliche Vektorrechnung haben. In Mengenschreibweise ist G = {x x = a + tb für ein t R}. Wir werden für diese einführenden Betrachtungen im Interesse einer knappen Redeweise jedoch häufig
Zulassungsprüfung in Mathematik
 der Deutschen Aktuarvereinigung e V Hinweise: Als Hilfsmittel sind ein Taschenrechner, eine mathematische Formelsammlung sowie entsprechende Literatur zugelassen Die Gesamtpunktzahl beträgt 9 Punkte Die
der Deutschen Aktuarvereinigung e V Hinweise: Als Hilfsmittel sind ein Taschenrechner, eine mathematische Formelsammlung sowie entsprechende Literatur zugelassen Die Gesamtpunktzahl beträgt 9 Punkte Die
Rekursive Folgen. Ermittle jeweils drei weitere Elemente. Gegen welchen Wert könnte die Folge streben? c Roolfs 3 2, 7 5, 17 12,...
 Rekursive Folgen Ermittle jeweils drei weitere Elemente. Gegen welchen Wert könnte die Folge streben? a) b) c) d) e), 7 5, 7,... 4, 9 5, 9 4,..., 5, 4 8,..., 5, 7,..., 7, 0,... Rekursive Folgen Ermittle
Rekursive Folgen Ermittle jeweils drei weitere Elemente. Gegen welchen Wert könnte die Folge streben? a) b) c) d) e), 7 5, 7,... 4, 9 5, 9 4,..., 5, 4 8,..., 5, 7,..., 7, 0,... Rekursive Folgen Ermittle
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 12. Aufgabe Herbstsemester Dr. V. Gradinaru D. Devaud.
 Dr. V. Gradinaru D. Devaud Herbstsemester 15 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie 1 Aufgabe 1.1 1.1a) Sei A eine n n-matrix. Das Gleichungssystem Ax = b sei
Dr. V. Gradinaru D. Devaud Herbstsemester 15 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie 1 Aufgabe 1.1 1.1a) Sei A eine n n-matrix. Das Gleichungssystem Ax = b sei
Lösungen zu Mathematik I/II
 Prof. Dr. E. W. Farkas ETH Zürich, Februar 11 D BIOL, D CHAB Lösungen zu Mathematik I/II Aufgaben 1. 1 Punkte a Wir berechnen lim x x + x + 1 x + x 3 + x = 1. b Wir benutzen L Hôpital e x e x lim x sinx
Prof. Dr. E. W. Farkas ETH Zürich, Februar 11 D BIOL, D CHAB Lösungen zu Mathematik I/II Aufgaben 1. 1 Punkte a Wir berechnen lim x x + x + 1 x + x 3 + x = 1. b Wir benutzen L Hôpital e x e x lim x sinx
8. Vorlesung, 5. April Numerische Methoden I. Eigenwerte und Eigenvektoren
 8. Vorlesung, 5. April 2017 170 004 Numerische Methoden I Eigenwerte und Eigenvektoren 1 Eigenwerte und Eigenvektoren Gegeben ist eine n n-matrix A. Gesucht sind ein vom Nullvektor verschiedener Vektor
8. Vorlesung, 5. April 2017 170 004 Numerische Methoden I Eigenwerte und Eigenvektoren 1 Eigenwerte und Eigenvektoren Gegeben ist eine n n-matrix A. Gesucht sind ein vom Nullvektor verschiedener Vektor
DynaTraffic Modelle und mathematische Prognosen. Simulation der Verteilung des Verkehrs mit Hilfe von Markov-Ketten
 DynaTraffic Modelle und mathematische Prognosen Simulation der Verteilung des Verkehrs mit Hilfe von Markov-Ketten Worum geht es? Modelle von Verkehrssituationen Graphen: Kanten, Knoten Matrixdarstellung
DynaTraffic Modelle und mathematische Prognosen Simulation der Verteilung des Verkehrs mit Hilfe von Markov-Ketten Worum geht es? Modelle von Verkehrssituationen Graphen: Kanten, Knoten Matrixdarstellung
Eigenwerte. Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1)
 Eigenwerte 1 Eigenwerte und Eigenvektoren Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1) für einen Vektor x 0. Vektor x heißt ein
Eigenwerte 1 Eigenwerte und Eigenvektoren Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1) für einen Vektor x 0. Vektor x heißt ein
Matrizen. Stefan Keppeler. 28. November Mathematik I für Biologen, Geowissenschaftler und Geoökologen
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen Matrizen 28. November 2007 Summe & Produkt Beispiel: Einwohnerzahlen Beispiel Addition Multiplikation Inverse Addition & Multiplikation Anwendung
Mathematik I für Biologen, Geowissenschaftler und Geoökologen Matrizen 28. November 2007 Summe & Produkt Beispiel: Einwohnerzahlen Beispiel Addition Multiplikation Inverse Addition & Multiplikation Anwendung
Analytische Geometrie
 Der fx-991 DE X im Mathematik- Unterricht Analytische Geometrie Station 1 Schnittgerade zweier Ebenen Da der Taschenrechner nur eindeutige Lösungen eines Gleichungssystems liefert, kann er nur Schnittpunkte
Der fx-991 DE X im Mathematik- Unterricht Analytische Geometrie Station 1 Schnittgerade zweier Ebenen Da der Taschenrechner nur eindeutige Lösungen eines Gleichungssystems liefert, kann er nur Schnittpunkte
Vorkurs Mathematik. Vektoren, lineare Gleichungssysteme und Matrizen
 Dorfmeister, Boiger, Langwallner, Pfister, Schmid, Wurtz Vorkurs Mathematik TU München WS / Blatt Vektoren, lineare Gleichungssysteme und Matrizen. In einem kartesischen Koordinatensystem des R sei eine
Dorfmeister, Boiger, Langwallner, Pfister, Schmid, Wurtz Vorkurs Mathematik TU München WS / Blatt Vektoren, lineare Gleichungssysteme und Matrizen. In einem kartesischen Koordinatensystem des R sei eine
Bereich Schwierigkeit Thema Matrizen XXX Übergangsprozesse. Rinderzucht II (aus Abi 2010) Mögliche Lösung
 Matrizen XXX Übergangsprozesse Rinderzucht II (aus Abi 21) Bei der Aufzucht von Rindern unterscheidet man zwischen Neugeborenen (N), ein- jährigen Kälbern (K) und geschlechtsreifen erwachsenen Tieren (E).
Matrizen XXX Übergangsprozesse Rinderzucht II (aus Abi 21) Bei der Aufzucht von Rindern unterscheidet man zwischen Neugeborenen (N), ein- jährigen Kälbern (K) und geschlechtsreifen erwachsenen Tieren (E).
1/2 2 v 1/5 0 0 E H I E H I
 Lineare Algebra 1. Chemische Reaktionen Bei einer hypothetischen Reaktion zwischen Molekülen A und Molekülen B geht pro Zeiteinheit der Bruchteil p = 0.3 der Moleküle A in Moleküle B und der Bruchteil
Lineare Algebra 1. Chemische Reaktionen Bei einer hypothetischen Reaktion zwischen Molekülen A und Molekülen B geht pro Zeiteinheit der Bruchteil p = 0.3 der Moleküle A in Moleküle B und der Bruchteil
3.6 Eigenwerte und Eigenvektoren
 3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Aufgaben für das Fach Mathematik
 Niedersächsisches Kultusministerium Referat / Logistikstelle für zentrale Arbeiten November 06 Aufgaben für das Fach Mathematik Eingesetzte Abituraufgaben aus dem länderübergreifenden Abituraufgabenpool
Niedersächsisches Kultusministerium Referat / Logistikstelle für zentrale Arbeiten November 06 Aufgaben für das Fach Mathematik Eingesetzte Abituraufgaben aus dem länderübergreifenden Abituraufgabenpool
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Aufgabe Summe Note Punkte
 Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Klausur Ingenieurmathematik am. September 5 (mit Lösungen) Name Matr.-Nr. Vorname Unterschrift Aufgabe 3 5 7 Summe Note Punkte Die Klausur
Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Klausur Ingenieurmathematik am. September 5 (mit Lösungen) Name Matr.-Nr. Vorname Unterschrift Aufgabe 3 5 7 Summe Note Punkte Die Klausur
37 Gauß-Algorithmus und lineare Gleichungssysteme
 37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P.
![Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P. Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P.](/thumbs/64/51976840.jpg) 2.2 Berechnung von Übergangswahrscheinlichkeiten Wir beschreiben die Situation zum Zeitpunkt t durch einen Zustandsvektor q t (den wir als Zeilenvektor schreiben). Die i-te Komponente (q t ) i bezeichnet
2.2 Berechnung von Übergangswahrscheinlichkeiten Wir beschreiben die Situation zum Zeitpunkt t durch einen Zustandsvektor q t (den wir als Zeilenvektor schreiben). Die i-te Komponente (q t ) i bezeichnet
LANGZEITVERHALTEN VON MARKOW-KETTEN
 LANGZEITVERHALTEN VON MARKOW-KETTEN NORA LOOSE. Buchstabensalat und Definition Andrei Andreewitsch Markow berechnete Anfang des 20. Jahrhunderts die Buchstabensequenzen in russischer Literatur. 93 untersuchte
LANGZEITVERHALTEN VON MARKOW-KETTEN NORA LOOSE. Buchstabensalat und Definition Andrei Andreewitsch Markow berechnete Anfang des 20. Jahrhunderts die Buchstabensequenzen in russischer Literatur. 93 untersuchte
1.2 Ein Institut prüft jährlich die Wasserqualität von Stränden in einer 6P Urlaubsregion und vergibt hierfür ein bis drei Sterne.
 Aufgabe A1/2017 1.1 Ein Unternehmen stellt aus den beiden Rohstoffen und die drei Zwischenprodukte, und her. Aus den drei Zwischenprodukten entstehen die beiden Endprodukte und. Die benötigten Rohstoffe
Aufgabe A1/2017 1.1 Ein Unternehmen stellt aus den beiden Rohstoffen und die drei Zwischenprodukte, und her. Aus den drei Zwischenprodukten entstehen die beiden Endprodukte und. Die benötigten Rohstoffe
Eigenwerte und Eigenvektoren
 Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20: Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte
Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20: Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 2
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 25): Lineare Algebra und analytische Geometrie 2 2. (Frühjahr 29, Thema 3, Aufgabe 3) Gegeben sei die reelle 3 3 Matrix 4 2 A = 2 7 2 R 3 3. 2 2 a)
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 25): Lineare Algebra und analytische Geometrie 2 2. (Frühjahr 29, Thema 3, Aufgabe 3) Gegeben sei die reelle 3 3 Matrix 4 2 A = 2 7 2 R 3 3. 2 2 a)
TECHNISCHE UNIVERSITÄT MÜNCHEN. Einführung in die Matrizenrechnung
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra WS 006/07 en Blatt 3.0.006 Einführung in die Matrizenrechnung Zentralübungsaufgaben
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra WS 006/07 en Blatt 3.0.006 Einführung in die Matrizenrechnung Zentralübungsaufgaben
Klausur zum Grundkurs Höhere Mathematik I
 Name, Vorname: Studiengang: Matrikelnummer: 2 4 5 6 Z Punkte Note Klausur zum Grundkurs Höhere Mathematik I für BNC, GtB, MB, EC, TeM, VT, KGB, WWT, ESM, FWK, BGi, WiW 22. Februar 2007, 8.00 -.00 Uhr Zugelassene
Name, Vorname: Studiengang: Matrikelnummer: 2 4 5 6 Z Punkte Note Klausur zum Grundkurs Höhere Mathematik I für BNC, GtB, MB, EC, TeM, VT, KGB, WWT, ESM, FWK, BGi, WiW 22. Februar 2007, 8.00 -.00 Uhr Zugelassene
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Serie 1 Musterlösung
 Serie 1 Musterlösung Lineare Algebra www.adams-science.org Klasse: 1Ea, 1Eb, 1Sb Datum: HS 17 1. Kollinear RIMDII Bestimme ob die Vektoren kollinear sind, indem du die erste Komponente eliminierst. u =
Serie 1 Musterlösung Lineare Algebra www.adams-science.org Klasse: 1Ea, 1Eb, 1Sb Datum: HS 17 1. Kollinear RIMDII Bestimme ob die Vektoren kollinear sind, indem du die erste Komponente eliminierst. u =
Übergangsmatrizen. October 27, 2014
 Übergangsmatrizen October 27, 214 Der Begriff Übergangsmatrix wird (unter anderem) für die Matrizen, die das Wechselverhalten von z.b. Käufern oder Wählern darstellen. Bei Wikipedia wird eine Übergangsmatrix
Übergangsmatrizen October 27, 214 Der Begriff Übergangsmatrix wird (unter anderem) für die Matrizen, die das Wechselverhalten von z.b. Käufern oder Wählern darstellen. Bei Wikipedia wird eine Übergangsmatrix
Lösungen zu Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Sommer 4 Lösungen zu Prüfung Lineare Algebra I/II für D-MAVT. [ Punkte] Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in
Prof. N. Hungerbühler ETH Zürich, Sommer 4 Lösungen zu Prüfung Lineare Algebra I/II für D-MAVT. [ Punkte] Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Diplomvorprüfung LA H 06 VD : 1
 Diplomvorprüfung LA H 6 VD : Aufgabe : (3 + + = 6 Punkte) Gegeben sei die Matrix A = a) Bestimmen Sie die Eigenwerte von A b) Bestimmen Sie alle Eigenvektoren der Matrix A c) Ist die Matrix A invertierbar?
Diplomvorprüfung LA H 6 VD : Aufgabe : (3 + + = 6 Punkte) Gegeben sei die Matrix A = a) Bestimmen Sie die Eigenwerte von A b) Bestimmen Sie alle Eigenvektoren der Matrix A c) Ist die Matrix A invertierbar?
1 Lineare Gleichungssysteme und Matrizen
 1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
Orientierung der Vektoren b 1,..., b n. Volumen des von den Vektoren aufgespannten Parallelotops
 15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Mathematik I. Vorlesung 16. Eigentheorie
 Prof Dr H Brenner Osnabrück WS 009/00 Mathematik I Vorlesung 6 Eigentheorie Unter einer Achsenspiegelung in der Ebene verhalten sich gewisse Vektoren besonders einfach Die Vektoren auf der Spiegelungsachse
Prof Dr H Brenner Osnabrück WS 009/00 Mathematik I Vorlesung 6 Eigentheorie Unter einer Achsenspiegelung in der Ebene verhalten sich gewisse Vektoren besonders einfach Die Vektoren auf der Spiegelungsachse
DisMod-Repetitorium Tag 3
 DisMod-Repetitorium Tag 3 Markov-Ketten 21. März 2018 1 Markov-Ketten Was ist eine Markov-Kette? Was gehört alles dazu? Darstellung als Graph und als Matrix Stationäre Verteilung und Grenzverteilung Ergodizität
DisMod-Repetitorium Tag 3 Markov-Ketten 21. März 2018 1 Markov-Ketten Was ist eine Markov-Kette? Was gehört alles dazu? Darstellung als Graph und als Matrix Stationäre Verteilung und Grenzverteilung Ergodizität
Iterative Verfahren, Splittingmethoden
 Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem
Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem
1.1 Veranschaulichen Sie diese Informationen in einem Übergangsgraphen 4P und ergänzen Sie die fehlenden Angaben.
 Aufgabe A1 (nicht für TG) 1.1 Drei Energieversorger, und konkurieren in einer 4P Gemeinde um 2800 Haushalte. Werbeaktionen veranlassen am Jahresende viele Verbraucher, den Energieversorger zu wechseln.
Aufgabe A1 (nicht für TG) 1.1 Drei Energieversorger, und konkurieren in einer 4P Gemeinde um 2800 Haushalte. Werbeaktionen veranlassen am Jahresende viele Verbraucher, den Energieversorger zu wechseln.
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2012/2013
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Inhalt. Mathematik für Chemiker II Lineare Algebra. Vorlesung im Sommersemester Kurt Frischmuth. Rostock, April Juli 2015
 Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Probeklausur zu Mathematik 2 für Informatik
 Gunter Ochs Wintersemester 4/5 Probeklausur zu Mathematik für Informatik Lösungshinweise wie immer ohne Garantie auf Fehlefreiheit. Gegeben sei das Dreieck im R mit den Eckpunkten A a Berechnen Sie die
Gunter Ochs Wintersemester 4/5 Probeklausur zu Mathematik für Informatik Lösungshinweise wie immer ohne Garantie auf Fehlefreiheit. Gegeben sei das Dreieck im R mit den Eckpunkten A a Berechnen Sie die
4 Lineare Algebra (Teil 2): Quadratische Matrizen
 4 Lineare Algebra (Teil : Quadratische Matrizen Def.: Eine (n n-matrix, die also ebensoviele Zeilen wie Spalten hat, heißt quadratisch. Hat sie außerdem den Rang n, sind also ihre n Spalten linear unabhängig,
4 Lineare Algebra (Teil : Quadratische Matrizen Def.: Eine (n n-matrix, die also ebensoviele Zeilen wie Spalten hat, heißt quadratisch. Hat sie außerdem den Rang n, sind also ihre n Spalten linear unabhängig,
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
10.2 Linearkombinationen
 147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
Lösungshinweise zur Klausur. Mathematik für Informatiker III. (Dr. Frank Hoffmann) 18. Februar 2008
 Lösungshinweise zur Klausur Mathematik für Informatiker III (Dr. Frank Hoffmann) 8. Februar 8 Aufgabe Algebraisches I /6++ (a) Rechnen Sie zunächst nach, dass die Menge B = {,, von Vektoren eine Basis
Lösungshinweise zur Klausur Mathematik für Informatiker III (Dr. Frank Hoffmann) 8. Februar 8 Aufgabe Algebraisches I /6++ (a) Rechnen Sie zunächst nach, dass die Menge B = {,, von Vektoren eine Basis
Aussagenlogik. 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl. C: 2 ist eine Primzahl D: 7 7. F: 3 ist Teiler von 9
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Lineare Algebra 1. . a n1 a n2 a n3 a nm
 Lineare Algebra 1 Lineare Algebra Hilfreiche Konzepte zur Vereinfachung der Darstellung und Berechnung stellt die lineare Algebra bereit. Auch wenn sie nur an wenigen Stellen des Buches verwendet wurden,
Lineare Algebra 1 Lineare Algebra Hilfreiche Konzepte zur Vereinfachung der Darstellung und Berechnung stellt die lineare Algebra bereit. Auch wenn sie nur an wenigen Stellen des Buches verwendet wurden,
D-INFK Lineare Algebra HS 2017 Özlem Imamoglu Olga Sorkine-Hornung. Musterlösung 13. (A ± I)x = 0 Ax ± x = 0 Ax = ±x Ax = λx
 D-INFK Lineare Algebra HS 2017 Özlem Imamoglu Olga Sorkine-Hornung Musterlösung 13 1. Die Matrix A±I ist singulär falls es einen Vektor x 0 gibt der die Gleichung (A±I)x = 0 erfüllt, d.h. wenn A ± I als
D-INFK Lineare Algebra HS 2017 Özlem Imamoglu Olga Sorkine-Hornung Musterlösung 13 1. Die Matrix A±I ist singulär falls es einen Vektor x 0 gibt der die Gleichung (A±I)x = 0 erfüllt, d.h. wenn A ± I als
Eigenwerte (Teschl/Teschl 14.2)
 Eigenwerte Teschl/Teschl 4. Ein Eigenvektor einer quadratischen n nmatrix A ist ein Vektor x R n mit x 0, für den Ax ein skalares Vielfaches von x ist, es also einen Skalar λ gibt mit Ax = λ x Ax λ x =
Eigenwerte Teschl/Teschl 4. Ein Eigenvektor einer quadratischen n nmatrix A ist ein Vektor x R n mit x 0, für den Ax ein skalares Vielfaches von x ist, es also einen Skalar λ gibt mit Ax = λ x Ax λ x =
Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich:
![Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich:](/thumbs/67/57409595.jpg) Lineare Algebra D-MATH, HS 04 Prof. Richard Pink Lösung zu Serie. [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: a) F (X) := X 5 X in R[X] und C[X]. b) F (X) := X 4 +X 3 +X in
Lineare Algebra D-MATH, HS 04 Prof. Richard Pink Lösung zu Serie. [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: a) F (X) := X 5 X in R[X] und C[X]. b) F (X) := X 4 +X 3 +X in
Skript Lineare Algebra
 Skript Lineare Algebra sehr einfach Erstellt: 2018/19 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Vektoren... 3 2. Geraden... 6 3. Ebenen... 8 4. Lagebeziehungen... 10 a) Punkt - Gerade...
Skript Lineare Algebra sehr einfach Erstellt: 2018/19 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Vektoren... 3 2. Geraden... 6 3. Ebenen... 8 4. Lagebeziehungen... 10 a) Punkt - Gerade...
, v 3 = und v 4 =, v 2 = V 1 = { c v 1 c R }.
 154 e Gegeben sind die Vektoren v 1 = ( 10 1, v = ( 10 1. Sei V 1 = v 1 der von v 1 aufgespannte Vektorraum in R 3. 1 Dann besteht V 1 aus allen Vielfachen von v 1, V 1 = { c v 1 c R }. ( 0 ( 01, v 3 =
154 e Gegeben sind die Vektoren v 1 = ( 10 1, v = ( 10 1. Sei V 1 = v 1 der von v 1 aufgespannte Vektorraum in R 3. 1 Dann besteht V 1 aus allen Vielfachen von v 1, V 1 = { c v 1 c R }. ( 0 ( 01, v 3 =
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Serie a) Welche der folgenden Vektoren sind Eigenvektoren der Matrix 1 0 1? 0 1 1
 Prof. Norbert Hungerbühler Serie Lineare Algebra II ETH Zürich - D-MAVT. a Welche der folgenden Vektoren sind Eigenvektoren der Matrix? i (,,. ii (,,. iii (,,. iv (, 3,. v (,,. Ein Vektor v ist Eigenvektor
Prof. Norbert Hungerbühler Serie Lineare Algebra II ETH Zürich - D-MAVT. a Welche der folgenden Vektoren sind Eigenvektoren der Matrix? i (,,. ii (,,. iii (,,. iv (, 3,. v (,,. Ein Vektor v ist Eigenvektor
