Extrapolation von Beanspruchungskollektiven
|
|
|
- Rosa Becker
- vor 7 Jahren
- Abrufe
Transkript
1 Extrapolation von Beanspruchungskollektiven Karsten Hinkelmann, Christian Müller, Rainer Masendorf, Alfons Esderts Technical Report Series Fac3--02
2 Impressum Publisher: Fakultät für Mathematik/Informatik und Maschinenbau, Technische Universität Clausthal Am Regenbogen 5, Clausthal-Zellerfeld, Germany Editor-in-chief: Alfons Esderts Technical editor: Martina Wächter Contact: URL: ISSN: The Faculty of Mathematics/Computer Science and Mechanical Engineering Review Board Prof. Dr. Frank Endres Prof. Dr. Alfons Esderts Prof. Dr. Stefan Hartmann apl. Prof. Dr. Günter Kemnitz Prof. Dr. Armin Lohrengel Prof. Dr. Norbert Müller Prof. Dr. Volker Wesling Prof. Dr. Oliver Zirn
3 Extrapolation von Beanspruchungskollektiven Dipl.-Math. Karsten Hinkelmann Dipl.-Ing. Christian Müller Dr.-Ing. Rainer Masendorf Prof. Dr.-Ing. Alfons Esderts TU Clausthal Institut für Maschinelle Anlagentechnik und Betriebsfestigkeit Leibnizstraße 32 D Clausthal-Zellerfeld / Abstract The extrapolation of load collectives is an important tool in the design process of cyclically loaded parts. It is used to create design collectives. The article at hand will take an in-depth look at the extreme value extrapolation based on Gumbel. Numerical simulations are used to analyse the influence of the number of load segments in a load-time history. For collectives that can be mathematically described, the optimum number of segments can be determined independently of the actual collective. This method of extrapolation is valid only if the collective at hand can be mathematically described. In this case the extrapolation can also be described as an analytical progression of the mathematical collective. This case is discussed in the last chapter.
4 Einleitung Für sicherheitsrelevante Bauteile müssen Festigkeitsnachweise erbracht werden, um einen ausfallsicheren Betrieb über ihre Nutzungsdauer zu gewährleisten. Ein Festigkeitsnachweis stellt immer einen Vergleich zwischen Beanspruchung und Festigkeit dar. Werden Bauteile schwingend beansprucht, ist neben dem statischen Nachweis auch ein Ermüdungsfestigkeitsnachweis gegen zyklische Beanspruchung zu erbringen. Beim Ermüdungsfestigkeitsnachweis wird zwischen dauerfester und betriebsfester Bemessung unterschieden, Abbildung. Dauerfeste Auslegung bedeutet, dass alle Beanspruchungsamplituden einen Mindestsicherheitsabstand zur Dauerfestigkeit einhalten. Bauteile werden meist dann dauerfest ausgelegt, wenn sie während ihrer Nutzungsdauer hohe Schwingspielzahlen erreichen. Demgegenüber steht der Betriebsfestigkeitsnachweis. Hierbei werden bewusst Beanspruchungsamplituden oberhalb der Dauerfestigkeit zugelassen, mit dem Ziel weiteres Leichtbaupotential zu nutzen. Abbildung : Festigkeitsnachweise gegen statische und zyklische Beanspruchung Die statische und dauerfeste Bemessung beruht auf dem Vergleich von Kennwerten. Bei einer betriebsfesten Auslegung müssen Kennfunktionen für Beanspruchung und Festigkeit betrachtet werden. Festigkeitsseitig sind Wöhlerlinien oft die Grundlage eines Betriebsfestigkeitsnachweises. Für die Beanspruchung wird i. A. ein Kollektiv verwendet. Mit den Amplituden und ihrer Häufigkeit enthält das Beanspruchungskollektiv wesentliche Größen einer Beanspruchungszeitfunktion in reduzierter Form. Zur Abschätzung von Beanspruchungen stehen mehrere Methoden zur Verfügung, Abbildung 2. Abbildung 2: Möglichkeiten einer Lastannahme Hierbei können die aufgeführten Methoden auch kombiniert eingesetzt werden. Im Entwicklungsprozess eines Bauteils oder eines Systems wird häufig auf hybride Verfahren zurückgegriffen. Alte Betriebsmessungen von existierenden Vorgängerbauteilen dienen beispielsweise als Eingangsdaten einer rechnergestützten Simulation für einen Prototypen. FACULTY 3 2
5 Im Folgenden wird die Vorgehensweise zur Ermittlung eines Bemessungskollektivs am Beispiel eines PKW näher erläutert, Abbildung 3. Im Idealfall enthält das Bemessungskollektiv alle während der Nutzungsdauer auftretenden Beanspruchungen in ihrer Höhe und Häufigkeit. Zu Beginn müssen relevante Betriebszustände definiert werden. Für das Beispiel eines Kraftfahrzeugs ergeben sich beispielsweise fünf relevante Betriebszustände: Autobahn, gute Landstraße, Stadtverkehr, schlechte Landstraße und Schlechtweg. Im nächsten Schritt sind Teilkollektive zu erstellen, Abbildung 3. Für die festgelegten Betriebszustände müssen Teilkollektive ermittelt werden, Abbildung 3. Dies kann messtechnisch, über Simulationen oder Regelwerke geschehen. Um eine repräsentative Messung zu erhalten, ist es erforderlich jeden Betriebszustand ausreichend lang messtechnisch zu erfassen. Eine nichtrepräsentative Messung kann nicht zuverlässig extrapoliert werden. Die Überführung der gemessenen Beanspruchungszeitfunktionen in Kollektive erfolgt mithilfe von Zählverfahren. Ein umfangreicher Überblick zu Zählverfahren ist in [Köhl ] gegeben. Anschließend erfolgt die Festlegung der Bauteilnutzungsdauer und die Gewichtung der Teilkollektive, Abbildung 3. Repräsentative Gesamtnutzungsdauern können sich aus Kundenansprüchen oder auch Gewährleistungsvorgaben ergeben und müssen vor der Superposition (Überlagerung) und der Gewichtung der Teilkollektive festgelegt werden. Die Gewichtung gibt an, welchen Anteil ein Teilkollektiv am Bemessungskollektiv hat. Für Schienenfahrzeuge oder Kräne existieren beispielsweise Standardeinsatzspiegel. Die Gesamtnutzungsdauer für den PKW ist im CARLOS (CARLOadStandard) auf km festgelegt [Schü 90]. Dabei besitzen die fünf Betriebszustände die folgenden Anteile: Autobahn 30 % (2 000 km) Gute Landstraße 29 % ( 600 km) Stadtverkehr 23 % (9 200 km) Schlechte Landstraße 4 % (5 600 km) Schlechtweg 4 % ( 600 km) Mit der Gesamtnutzungsdauer und der Gewichtung ist bekannt, für welche Streckenlänge die Teilkollektive gelten müssen (Teilfolgenumfänge). Die messtechnisch ermittelten Teilkollektive gelten aber nur für den Zeitraum der Messung, sodass eine Extrapolation erforderlich wird, Abbildung 3. Dazu stehen verschiedene Methoden zur Verfügung, Kapitel 3. Liegen alle extrapolierten Teilkollektive vor, müssen sie durch Superposition zu einem Bemessungskollektiv überlagert werden, indem alle Stufen der Teilkollektive in ein gemeinsames Bemessungskollektiv zusammengefasst werden. 3 Technical Report
6 Abbildung 3: Herleitung von Bemessungskollektiven FACULTY 3 4
7 2 Mathematisch beschreibbare Lastkollektive Ein Lastkollektiv enthält mit seinen Amplituden und Häufigkeiten die Größen, welche als wesentlich für die Werkstoffschädigung erachtet werden. Man kann es aus Messungen oder Simulationen ableiten, indem Zählverfahren eingesetzt werden, Abbildung 4. Abbildung 4: Von der Messung zum Lastkollektiv Ein Kollektiv beschreibt den Zusammenhang zwischen der Beanspruchungsamplitude S a und der zugehörigen Summenhäufigkeit H oder Stufenhäufigkeit h (Häufigkeit mit der die Spannungsamplitude S a auftritt), [Gude 99]. Oft können gemessene oder simulierte Lastkollektive durch sogenannte Einheitskollektive angenähert werden, die mathematisch beschrieben werden können, Gleichung ( ), [Hank 70], [Hück 88]. Dabei beschreiben Ŝ a den Kollektivhöchstwert und H 0 den Kollektivumfang. Der Formparameter υ beschreibt den Verlauf des Kollektivs zwischen dem Kollektivhöchstwert Ŝ a und dem Kollektivumfang H 0, Abbildung 5. H = υ S a Sa H 0 ( ),0 0,8 0,6 0,4 ν = 0,7 ν = ν = 3 ν = 2 ν = 4 ν = 0,2 0, Summenhäufigkeit H (log) Abbildung 5: Mathematisch beschreibbare Kollektive für verschiedene Formparameter υ Das härteste Lastkollektiv ist ein Einstufenkollektiv (υ = ), Abbildung 5. Kollektive mit einem Formparameter von υ = 2 werden auch als Normkollektive bezeichnet. Sie treten nach [Buxb 92] typischerweise bei stationären Prozessen auf. Kollektive mit 5 Technical Report
8 Formparameter υ = werden als Geradlinienkollektive bezeichnet, da sie in der üblichen halblogarithmischen Darstellung als Gerade erscheinen. Weitere Möglichkeiten Lastkollektive mathematisch zu beschreiben sind in [FKM 03] und [Haib 06] gegeben. 3 Verfahren zur Extrapolation von Lastzeitreihen In der Literatur sind Vorschläge zur Extrapolation gegeben: Grafische Extrapolation eines Lastkollektivs [Gude 99], Extremwertextrapolation in Anlehnung an Gumbel [Buxb 92], Rainflowmatrixextrapolation nach Krüger [Krüg 85], Rainflowmatrixextrapolation nach Dreßler [Dreß 96]. Alle genannten Methoden enthalten Parameter, die vom Anwender frei wählbar sind und das Endergebnis stark beeinflussen können. Grafische Extrapolation: Wahl des Höchstwerts des extrapolierten Kollektivs Extremwertextrapolation in Anlehnung an Gumbel: Wahl der Lastabschnittanzahl Rainflowmatrixextrapolation nach Krüger: Wahl des exponentiellen Verteilungsgesetzes Rainflowmatrixextrapolation nach Dreßler: Wahl der Gewichtungsfunktion Im Weiteren soll nur die Extremwertextrapolation in Anlehnung an Gumbel betrachtet werden. In [Buxb 92] und [Gude 99] wird das Verfahren zur Extremwertextrapolation beschrieben, welches auf der Extremwertstatistik nach Gumbel [Gumb 58] basiert. In der Betriebsfestigkeit wird das Verfahren in abgewandelter Form eingesetzt. Streng genommen, erfüllt die nachfolgende Vorgehensweise die von Gumbel gestellten Voraussetzungen nicht vollständig. Weiterhin wird das von Gumbel vorgegebenen Verteilungsgesetz der Extremwerte (Gumbelverteilung) durch eine logarithmische Normalverteilung angenähert. Für die Belange der Betriebsfestigkeit ist nach Buxbaum die oben beschriebene Vorgehensweise dennoch hinreichend zuverlässig, [Buxb 92]. Ziel der Extremwertextrapolation ist es, den Kollektivhöchstwert Ŝ an des Nutzungsdauerkollektivs möglichst gut abzuschätzen, indem das aufgenommene Messsignal verwendet wird. Das Extrapolationsverfahren ist nach [Buxb 92] nur für mathematische Kollektive und deren Linearkombinationen anwendbar, wobei nach folgenden Schritten vorzugehen ist, Abbildung 6. FACULTY 3 6
9 Abbildung 6: Extremwertextrapolation in Anlehnung an Gumbel Eine vorliegende Beanspruchungszeitfunktion mit der Messlänge H M wird in m Lastabschnitte gleicher Länge eingeteilt. In jedem Abschnitt wird die größte auftretende Spannungsamplitude Ŝ ae ermittelt. Die Extremwerte Ŝ ae werden in der Regel in ein logarithmisch-normalverteilt geteiltes Wahrscheinlichkeitspapier eingetragen, Abbildung 6. Dabei kann ihre Überschreitenswahrscheinlichkeit P Ü beispielsweise mithilfe der Formel nach Rossow abgeschätzt werden, die nur von der Ordnungszahl i und der Anzahl der Abschnitte m abhängt, Gleichung ( 2 ). 3 i P Ü = ( 2 ) 3 m+ Der Kollektivhöchstwert des Nutzungsdauerkollektivs kann nach der Berechnung seiner Überschreitenswahrscheinlichkeit P Ü im Wahrscheinlichkeitsdiagramm abgeschätzt werden. Sind während der Nutzungsdauer n Lastabschnitte zu erwarten, so berechnet sich die Überschreitenswahrscheinlichkeit des Nutzdauerkollektivhöchstwerts gemäß Gleichung ( 3 ). 7 Technical Report
10 2 P S Ü an = ( 3 ) 3 n+ Im Wahrscheinlichkeitspapier kann mit diesem Ergebnis der Nutzdauerkollektivhöchstwert Ŝ an abgelesen werden, Abbildung 6. Das extrapolierte Kollektiv setzt sich zusammen aus dem Nutzdauerkollektivhöchstwert Ŝ an und dem mit dem Extrapolationsfaktor e multiplizierten Lastkollektiv aus der Messung. Der Extrapolationsfaktor e stellt hierbei das Verhältnis aus Nutzungs- und Messdauer dar, Gleichung ( 4 ). H N e = ( 4 ) H M Abbildung 7: Nicht definierter Bereich zwischen rechtsverschobenem Messkollektiv und Nutzungsdauerkollektivhöchstwert Die zu Beginn gewählte Abschnittanzahl m hat einen entscheidenden Einfluss auf die Vorhersagegüte des durch Extrapolation abgeschätzten Nutzdauerkollektivhöchstwert Ŝ an, [Buxb 92]. In der Literatur sind keine Vorschriften angegeben, wie die Abschnittanzahl m anzunehmen ist, damit gute Schätzungen erzielt werden können. Weiterhin fehlen Hinweise darauf, wie der nicht definierte Bereich, Abbildung 7, zwischen rechtsverschobenem Messkollektiv und dem Nutzdauerkollektivhöchstwert zu schließen ist. Diese Fragestellungen werden in den folgenden Kapiteln diskutiert. FACULTY 3 8
11 4 Simulation von Lastzeitreihen und Extrapolation der generierten Kollektive Im folgenden Abschnitt wird untersucht, welchen Einfluss die verwendete Abschnittanzahl auf die Güte der Kollektivhöchstwertschätzung hat. Einerseits stellt sich die Frage wie sensitiv die Höchstwertschätzung auf die Wahl der Abschnittanzahl reagiert, anderseits soll die optimale Abschnittanzahl gefunden werden, mit der die Schätzung am besten gelingt. Dabei werden die Messdauer H M, die Kollektivform ν und der Extrapolationsfaktor e (Verhältnis aus Nutzungs- und Messdauer) variiert. Um den Einfluss der Abschnittanzahl auf die Güte der Kollektivhöchstwertschätzung untersuchen zu können, werden Simulationen durchgeführt, Abbildung 8. In die Simulation gehen die Messdauer H M, die Nutzungsdauer H N und die Kollektivform ν ein. Weiterhin werden Grenzen festgesetzt in denen die Abschnittanzahl m in m delta Schritten variiert wird. Mit den Eingaben zum Kollektiv ist das mathematische Kollektiv der Nutzungsdauer vollständig beschrieben, sofern der Kollektivhöchstwert Ŝ an zu eins festgesetzt wird. Hieraus lässt sich wiederum die Lastfolge für die Nutzungsdauer mithilfe von Zufallszahlen rekonstruieren, indem H N Amplituden aus dem Nutzungsdauerkollektiv gezogen werden, Abbildung 8. Aus dieser Nutzungsdauerlastfolge der Länge H N wird eine kürzere Lastfolge der Länge H M entnommen, welche das gemessene Signal repräsentiert. Das entnommene Messsignal kann in Abschnitte unterteilt und nach der Vorschrift aus Kapitel 3 extrapoliert werden. Die Extrapolation erfolgt mit unterschiedlichen Abschnittanzahlen innerhalb vorgegebener Grenzen, Abbildung 8. Da der Rekonstruktion der Lastfolge ein Zufallsprozess zugrunde liegt, muss das Generieren der Lastfolgen, das Entnehmen des Messsignals und dessen Extrapolation mit unterschiedlichen Abschnittanzahlen mehrfach (Anzahl der Wiederholungen = wdh, Abbildung 8) durchgeführt werden. Somit liegt an Ende der Simulation für jede Abschnittanzahl eine Verteilung der geschätzten Höchstwerte vor. Die optimale Abschnittanzahl, mit der der Kollektivhöchstwert im Mittel getroffen wird, ist somit bekannt, Abbildung 8. 9 Technical Report
12 Abbildung 8: Simulation zur Untersuchung des Einflusses der Abschnittanzahl auf die Höchstwertschätzung FACULTY 3 0
13 geschätzter Höchstwert / Vorgabe e = 0 ν = % Quantil % Quantil 90% Quantil Abschnittanzahl geschätzter Höchstwert / Vorgabe e = 0 ν = 0.8 0% Quantil % Quantil 90% Quantil Abschnittanzahl geschätzter Höchstwert / Vorgabe e = 500 ν = % Quantil % Quantil 90% Quantil Abschnittanzahl geschätzter Höchstwert / Vorgabe e = 500 ν = 0.8 0% Quantil % Quantil 90% Quantil Abschnittanzahl Abbildung 9: Einfluss der Abschnittanzahl auf die Kollektivhöchstwertschätzung (Messumfang H M =konst.=0 3, wdh=0.000) Welchen Einfluss die Abschnittanzahl auf die Kollektivhöchstwertschätzung hat, kann Abbildung 9 entnommen werden. Die mittlere Kollektivhöchstwertschätzung ist mit dem 50%-Quantil (durchgezogene Linie) gegeben. Innerhalb der gestrichelten Linien liegen 80% aller Schätzungen. Grundsätzlich lässt sich feststellen, dass mit zunehmender Abschnittanzahl der Höchstwert größer geschätzt wird. Für die hier untersuchten mathematischen Kollektive existiert ein Optimum, welches unabhängig vom Extrapolationsfaktor e und von der Kollektivform ν ist. Im gezeigten Beispiel sind ca. 50 Abschnitte optimal. Bei der vorgegebenen Messlänge von H M =0 3 ergibt sich die Häufigkeit der Amplituden in einem Abschnitt zu 20. Die Schätzung wird umso sicherer, je völliger das Kollektiv und je kleiner der Extrapolationsfaktor ist. Weiterhin reagieren weniger völlige Kollektive und große Extrapolationsfaktoren viel empfindlicher auf die falsche Wahl der Abschnittanzahl (steilerer Verlauf der Linien). Der Einfluss des Messumfangs H M wurde bisher noch nicht betrachtet, da er konstant gehalten wurde. Abbildung 0 zeigt zwei Simulationen mit unterschiedlichen Messumfängen. Die bisherige Simulation mit einem Messumfang von H M =0 3 Lastwechseln wird einer weiteren Simulation mit H M =3x0 3 Zyklen gegenübergestellt. Erwartungsgemäß ist die Schätzung auf Grundlage der längeren Messung zuverlässiger. Die optimale Abschnittanzahl unterscheidet sich allerdings erheblich. Die Wahl der Abschnittanzahl, sollte also nicht unabhängig vom Messumfang erfolgen. Technical Report
14 geschätzter Höchstwert / Vorgabe H M = 000 e = 0 ν = 0.8 0% Quantil % Quantil 90% Quantil Abschnittanzahl geschätzter Höchstwert / Vorgabe H M = 3000 e = 0 ν = 0.8 0% Quantil % Quantil 90% Quantil Abschnittanzahl Abbildung 0: Einfluss des Messumfangs H M auf die optimale Abschnittanzahl (wdh=0.000) optimale Abschnittanzahl (log) ν = e = 0 ν = 2 e = 0 ν = e = 500 ν = 2 e = 500 Näherung ANZ opt = 0 (log(h M ) -.3) H M = 000, siehe Abbildung 0 links H M = 3000, siehe Abbildung 0 rechts Messlänge (log) Abbildung : Optimale Abschnittanzahl in Abhängigkeit der Messlänge Für mathematisch beschreibbare Kollektive wurde gezeigt, dass die optimale Abschnittanzahl unabhängig von der Kollektivform ν und dem Extrapolationsfaktor e ist, jedoch stark von der Messlänge H M beeinflusst wird. Daher wird im Folgenden die Messlänge H M zwischen 0 2,5 H M 0 4,5 variiert und die jeweils zugehörige optimale Abschnittanzahl ermittelt. In Abbildung ist die optimale Abschnittanzahl über der Messlänge H M für verschiedene Kollektivformen ν und Extrapolationsfaktoren e aufgetragen. Im doppeltlogarithmischen Papier ergibt sich zwischen optimaler Abschnittanzahl ANZ opt und Messlänge H M ein linearer Zusammenhang, der in guter Näherung mit Gleichung ( 5 ) beschrieben werden kann. ( log( H M ),3) ANZ = 0 ( 5 ) opt FACULTY 3 2
15 Aus Gleichung ( 5 ) geht hervor, dass die Abschnittanzahl bei der Extrapolation mathematischer Kollektive,3 Dekaden kleiner gewählt werden sollte als die Häufigkeit der Messlänge H M. Dies ist gleichbedeutend mit einer Amplitudenhäufigkeit von 20 je Abschnitt, unabhängig von der Messlänge H M. Liegt ein Messkollektiv vor, welches nicht näherungsweise mit Gleichung ( ) beschrieben werden kann, ist die Anwendung von Gleichung ( 5 ) unzulässig. Das folgende hypothetische Beispiel zeigt die Auswirkungen, falls die beschriebene Vorgehensweise dennoch angewendet wird. In Abbildung 2 links ist ein Nutzungsdauerkollektiv gegeben, welches aus der Überlagerung zweier mathematischer Kollektive konstruiert wurde. Entnimmt man dem Nutzungsdauerkollektiv (Kollektiv mit durchgezogener Linie in Abbildung 2 links) eine Messung und versucht daraus den Nutzungsdauerhöchstwert zu schätzen, vgl. auch Abbildung 8, so werden sich die Abschnitthöchstwerte der Messung nicht mehr entlang einer Geraden im lognormalverteilten Wahrscheinlichkeitspapier anordnen, Abbildung 2 rechts. Dies liegt in den unterschiedlichen Teilgrundgesamtheiten des Nutzungsdauerkollektivs begründet. Die Stichprobe (Messung) enthält nur noch sehr wenige Abschnitthöchstwerte, welche dem Teilkollektiv der Überlast entstammen. Das Abschätzen des Kollektivhöchstwertes entlang der Regressionsgeraden ist somit fehlerhaft. 0.8 Überlagertes Nutzungsdauerkollektiv Teilkollektiv Überlast, ν = 3 Teilkollektiv Normallast, ν = 5 Amplitude Summenhäufigkeit H (log) Abbildung 2: Optimale Abschnittanzahl in Abhängigkeit der Messlänge In solchen Fällen sollte versucht werden, das gemessene Kollektiv in mathematisch beschreibbare Teilkollektive zu zerlegen (inverse Superposition), um diese anschließend einzeln zu extrapolieren. Die extrapolierten Teilkollektive können anschließend wieder zu dem gesamten extrapolierten Kollektiv überlagert werden. Eine weitere Möglichkeit besteht darin, die Verteilungsfunktion, Abbildung 2 rechts mit Hilfe von Kerndichteschätzern (Überlagerung mehrerer Wahrscheinlichkeitsdichtefunktionen) zu beschreiben, [Silv 84]. 3 Technical Report
16 5 Verlauf des Amplitudenkollektivs zwischen extrapolierten und gemessenem Höchstwert Bisher wurde gezeigt, wie der Kollektivhöchstwert des Nutzungsdauerkollektivs geschätzt werden sollte. Über den verbleibenden Bereich zwischen dem gemessenen Höchstwert und dem Nutzungsdauerhöchstwert wurden noch keine Aussagen getroffen. Um diesen nicht definierten Abschnitt zu belegen, wird der Extrapolationsfaktor aufsteigend bis zum Endwert variiert, um Stützstellen zu berechnen (hier von e=0 0. bis e=0 2 ). Die Berechnung erfolgt hierbei immer mit der optimalen Abschnittanzahl nach Kapitel 4. Das jeweilige Zwischenergebnis (Höchstwert für einen eingefügten Extrapolationsfaktor) wird nach rechts verschoben und agiert somit als Stützstelle zwischen gemessenem und extrapoliertem Höchstwert. Abbildung 3 zeigt, dass mit dieser Vorgehensweise das rechtsverschobene Messkollektiv erwartungsgemäß seiner mathematischen Beschreibung folgt. Das heißt, der Formparameter ν bleibt bei der Extrapolation mathematischer Kollektive erhalten. Da die vorgestellte Extrapolationsmethode nur für die nach Gleichung ( ) beschriebenen Kollektive in Kombination mit der Näherungslösung zuverlässig ist, können die mathematischen Messkollektive auch analytisch bis zur Nutzungsdauer beschrieben werden. Somit entfällt die Einteilung in Abschnitte, das Sortieren der Höchstwerte und das anschließende Abschätzen des Nutzungskollektivhöchstwertes. Amplitude Rechtsverschobenes Messkollektiv Schließen des nicht definierten Bereichs durch sukzessive Extrapolation mit Näherungsformel H M = 000 ν = 2 e = Summenhäufigkeit (log) Amplitude Rechtsverschobenes Messkollektiv Schließen des nicht definierten Bereichs durch sukzessive Extrapolation mit Näherungsformel H M = 000 ν = e = Summenhäufigkeit (log) Abbildung 3: Nicht definierter Bereich zwischen Messkollektiv und Nutzungsdauerkollektivhöchstwert durch sukzessive Extrapolation belegen, links: Normkollektiv ν=2, rechts: Geradlinienkollektiv ν= FACULTY 3 4
17 6 Mathematische Kollektive analytisch extrapolieren Ziel soll es sein den Nutzungsdauerkollektivhöchstwert Ŝ an aus den bekannten Größen: Messdauerkollektivhöchstwert Ŝ am, Messumfang H M, Kollektivform ν und Nutzungsumfang H N analytisch zu bestimmen. Für die folgenden Betrachtungen wird die Ordinate auf den Kollektivhöchstwert des zu bestimmenden Nutzungskollektivs Ŝ an bezogen, Abbildung 4. Das Nutzungsdauerkollektiv besitzt demnach immer den Höchstwert eins und kann gemäß Gleichung ( 6 ) beschrieben werden. H = υ S a SaN H N Wie auch in den vorangegangen Kapiteln wird das Messkollektiv um den Extrapolationsfaktor e nach rechts verschoben, Abbildung 4. In Gleichung ( 6 ) kann somit der Punkt (e, Ŝ am / Ŝ an ) eingesetzt werden. ( 6 ) Abbildung 4: Analytische Extrapolation e = H N υ SaM S an Der Extrapolationsfaktor beschreibt das Verhältnis aus Nutzungsdauer H N und Messdauer H M, Gleichung ( 8 ). H ( 7 ) N e = ( 8 ) H M Durch Einsetzen von Gleichung ( 7 ) in Gleichung ( 8 ) ergibt sich: e = H υ SaM S an N H H N M = H υ SaM S an N H M = H υ SaM S an N Das Logarithmieren und weitere Umformen von Gleichung ( 9 ) führt zum gesuchten Zusammenhang. Der Überhöhungsfaktor der Kollektivhöchstwerte Ŝ an / Ŝ am steigt mit dem Verhältnis der logarithmierten Kollektivumfänge an. Erwartungsgemäß fällt die Überhöhung bei härteren Kollektiven geringer aus. log am ( H ) = log( H ) M S S an υ N SaN am S log = log ( H N ) ( H ) M υ S an = S am log log ( H N ) ( H ) M υ ( 9 ) ( 0 ) 5 Technical Report
18 Wird beispielsweise bei einer Messung ein Geradlinienkollektiv mit einem Messumfang von H M =0 4 ermittelt und ein Nutzungsdauerkollektiv mit dem Umfang H N =0 6 benötigt, so wird der Kollektivhöchstwert des Nutzungsdauerkollektivs um den Faktor,5 größer sein, als der des Messkollektivs, Abbildung 5. Abbildung 5: Analytische Kollektivhöchstwertschätzung FACULTY 3 6
19 7 Zusammenfassung Im vorliegenden Beitrag wird die Extremwertextrapolation untersucht, wie sie in der Betriebsfestigkeit angewendet wird. Anhand einer Simulation mit mathematisch beschreibbaren Kollektiven wird gezeigt, welchen Einfluss die Wahl der Abschnittanzahl auf das Extrapolationsergebnis hat. Die Abschnittslänge sollte so gewählt werden, dass in jedem Abschnitt 20 Amplituden enthalten sind. Die optimale Abschnittanzahl lässt sich demnach mit Gleichung ( ) berechnen. ( log( H M ),3) ANZopt = 0 ( ) Die beschriebene Vorgehensweise und die Gleichung zur Bestimmung der optimalen Abschnittanzahl sind nur für mathematisch beschreibbare Kollektive nach Gleichung ( ) zulässig. Der Bereich zwischen dem extrapolierten und gemessenen Höchstwert kann durch sukzessive Rechtsverschiebung und mehrfaches Extrapolieren geschlossen werden, indem Stützstellen berechnet werden. In diesem Bereich folgt das extrapolierte Kollektiv der vorgegebenen Kollektivform. D. h., das extrapolierte Kollektiv kann auch direkt mit der Vorschrift des rechtsverschobenen Messkollektivs analytisch beschrieben werden, Abbildung 6. Abbildung 6: Extrapoliertes Kollektiv mathematisch beschreiben 7 Technical Report
20 Literaturverzeichnis [Buxb 92] [Dreß 96] [FKM 03] [Gude 99] [Gumb 58] [Haib 06] [Hank 70] [Hück 88] [Köhl ] [Krüg 85] [Schü 90] [Silv 84] O. Buxbaum: Betriebsfestigkeit: Sichere und wirtschaftliche Bemessung schwingbruchgefährdeter Bauteile 2. Auflage, Verlag Stahleisen, Düsseldorf, 992 K. Dreßler; B. Gründer; M. Hack, V. B. Köttgen: Extrapolation of Rainflow Matrices SAE, Detroit, 996 B. Hänel, E. Haibach, T. Seeger, G. Wirthgen und H. Zenner: Rechnerischer Festigkeitsnachweis für Maschinenbauteile 5. Auflage, VDMA-Verlag, Frankfurt, 2003 H. Gudehus, H. Zenner: Leitfaden für die Betriebsfestigkeitsrechnung 4. Auflage, Verlag Stahleisen, Düsseldorf, 999 E. J. Gumbel: Statistics of Extremes Columbia University Press, New York, 958 E. Haibach: Betriebsfestigkeit: Verfahren und Daten zur Bauteilberechnung 2. Auflage, Berlin, Springer Verlag, 2002 M. Hanke: Eine Methode zur Beschreibung der Betriebslastkollektive als Grundlage für Betriebsfestigkeitsversuche ATZ 72, Heft 3, 970 M. Hück, J. Bergmann, W. Schütz Relative Miner-Regel Gemeinschaftsarbeit PKW-Industrie / IABG, IABG-Bericht TF 2022, Teil I, 988 M. Köhler, S. Jenne, K. Pötter, H. Zenner Zählverfahren und Lastannahme in der Betriebsfestigkeit Springer-Verlag, Berlin, 20 W. Krüger; J. Petersen: Simulation und Extrapolation von Rainflow-Matrizen Kaiserslautern : Universität Kaiserslautern, 985 D. Schütz, H. Klätschke, H. Steinhilber, P. Heuler, W. Schütz: Standardisierte Lastabläufe für Bauteile von PKW Radaufhängungen LBF-Bericht Nr. FB-9, 990 B. W. Silverman Density Estimation for Statistics and Data Analysis Crc Pr Inc; 2. Auflage, 986 FACULTY 3 8
Kapitel 5_1 Mehrstufenbeanspruchung (Lastkollektiv) 5.1- Mehrstufen - Schwingbeanspruchung
 5.1- Mehrstufen - Schwingbeanspruchung 1 Kapitel 5 Kapitel 5_1 Mehrstufenbeanspruchung (Lastkollektiv) Vom Beanspruchungs-Zeit Verlauf zum Beanspruchungskollektiv 2 statistische Grundbegriffe - Klassenhäufigkeitsverteilung
5.1- Mehrstufen - Schwingbeanspruchung 1 Kapitel 5 Kapitel 5_1 Mehrstufenbeanspruchung (Lastkollektiv) Vom Beanspruchungs-Zeit Verlauf zum Beanspruchungskollektiv 2 statistische Grundbegriffe - Klassenhäufigkeitsverteilung
Robustheit der Freigabeprüfung mit wenigen Proben
 Robustheit der Freigabeprüfung mit wenigen Proben C. Müller, R. Masendorf, A. Esderts Technical Report Series Fac3-14-03 Impressum Publisher: Fakultät für Mathematik/Informatik und Maschinenbau, Technische
Robustheit der Freigabeprüfung mit wenigen Proben C. Müller, R. Masendorf, A. Esderts Technical Report Series Fac3-14-03 Impressum Publisher: Fakultät für Mathematik/Informatik und Maschinenbau, Technische
Zählverfahren und Lastannahme in der Betriebsfestigkeit
 Zählverfahren und Lastannahme in der Betriebsfestigkeit Michael Köhler Sven Jenne Kurt Pötter Harald Zenner Zählverfahren und Lastannahme in der Betriebsfestigkeit 1 3 Dipl.-Ing. Michael Köhler Haldenweg
Zählverfahren und Lastannahme in der Betriebsfestigkeit Michael Köhler Sven Jenne Kurt Pötter Harald Zenner Zählverfahren und Lastannahme in der Betriebsfestigkeit 1 3 Dipl.-Ing. Michael Köhler Haldenweg
Zur Treffsicherheit der experimentellen Dauerfestigkeitsschätzung
 Zur Treffsicherheit der experimentellen Dauerfestigkeitsschätzung C. Müller, K. Hinkelmann, R. Masendorf, A. Esderts Technical Report Series Fac3-14-02 Impressum Publisher: Fakultät für Mathematik/Informatik
Zur Treffsicherheit der experimentellen Dauerfestigkeitsschätzung C. Müller, K. Hinkelmann, R. Masendorf, A. Esderts Technical Report Series Fac3-14-02 Impressum Publisher: Fakultät für Mathematik/Informatik
Monte-Carlo Tests. Diplomarbeit. Wiebke Werft. Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf
 Monte-Carlo Tests Diplomarbeit Wiebke Werft Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Düsseldorf im Dezember 2003 Betreuung: Prof. Dr. Arnold Janssen Inhaltsverzeichnis Einleitung
Monte-Carlo Tests Diplomarbeit Wiebke Werft Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Düsseldorf im Dezember 2003 Betreuung: Prof. Dr. Arnold Janssen Inhaltsverzeichnis Einleitung
1 Grundprinzipien statistischer Schlußweisen
 Grundprinzipien statistischer Schlußweisen - - Grundprinzipien statistischer Schlußweisen Für die Analyse zufallsbehafteter Eingabegrößen und Leistungsparameter in diskreten Systemen durch Computersimulation
Grundprinzipien statistischer Schlußweisen - - Grundprinzipien statistischer Schlußweisen Für die Analyse zufallsbehafteter Eingabegrößen und Leistungsparameter in diskreten Systemen durch Computersimulation
Übungen mit dem Applet Wahrscheinlichkeitsnetz
 Wahrscheinlichkeitsnetz 1 Übungen mit dem Applet Wahrscheinlichkeitsnetz 1 Statistischer Hintergrund... 1.1 Verteilungen... 1. Darstellung von Daten im Wahrscheinlichkeitsnetz...4 1.3 Kurzbeschreibung
Wahrscheinlichkeitsnetz 1 Übungen mit dem Applet Wahrscheinlichkeitsnetz 1 Statistischer Hintergrund... 1.1 Verteilungen... 1. Darstellung von Daten im Wahrscheinlichkeitsnetz...4 1.3 Kurzbeschreibung
Logarithmische Skalen
 Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert
 Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Statistics, Data Analysis, and Simulation SS 2017
 Mainz, 8. Juni 2017 Statistics, Data Analysis, and Simulation SS 2017 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Dr. Michael O. Distler
Mainz, 8. Juni 2017 Statistics, Data Analysis, and Simulation SS 2017 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Dr. Michael O. Distler
Hydrologie und Flussgebietsmanagement
 Hydrologie und Flussgebietsmanagement o.univ.prof. DI Dr. H.P. Nachtnebel Institut für Wasserwirtschaft, Hydrologie und konstruktiver Wasserbau Wiederholung Statistische Grundlagen Definitionen der statistischen
Hydrologie und Flussgebietsmanagement o.univ.prof. DI Dr. H.P. Nachtnebel Institut für Wasserwirtschaft, Hydrologie und konstruktiver Wasserbau Wiederholung Statistische Grundlagen Definitionen der statistischen
Lehrveranstaltung Betriebsfestigkeit und Bruchmechanik
 Fakultät Maschinenbau Professur Festkörpermechanik Lehrveranstaltung Betriebsfestigkeit und Bruchmechanik Vorlesung 8 26.05.2016 Ergänzende Folien zur Lehrveranstaltung Dr.-Ing. Thomas Lehmann Betriebsfestigkeit
Fakultät Maschinenbau Professur Festkörpermechanik Lehrveranstaltung Betriebsfestigkeit und Bruchmechanik Vorlesung 8 26.05.2016 Ergänzende Folien zur Lehrveranstaltung Dr.-Ing. Thomas Lehmann Betriebsfestigkeit
Analyse eines zweistufigen, regionalen Clusteralgorithmus am Beispiel der Verbundenen Wohngebäudeversicherung
 Analyse eines zweistufigen, regionalen Clusteralgorithmus am Beispiel der Verbundenen Wohngebäudeversicherung Zusammenfassung der Diplomarbeit an der Hochschule Zittau/Görlitz Maria Kiseleva Motivation
Analyse eines zweistufigen, regionalen Clusteralgorithmus am Beispiel der Verbundenen Wohngebäudeversicherung Zusammenfassung der Diplomarbeit an der Hochschule Zittau/Görlitz Maria Kiseleva Motivation
Zur Auswertung von Schwingfestigkeitsversuchen
 BETRIEBSFESTIGKEIT 513 Zur Auswertung von Schwingfestigkeitsversuchen im Zeitfestigkeitsbereich Teil : Wie zuverlässig kann die Standardabweichung aus experimentellen Daten geschätzt werden? Andreas Martin
BETRIEBSFESTIGKEIT 513 Zur Auswertung von Schwingfestigkeitsversuchen im Zeitfestigkeitsbereich Teil : Wie zuverlässig kann die Standardabweichung aus experimentellen Daten geschätzt werden? Andreas Martin
Statistische Tests (Signifikanztests)
 Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Fallzahlplanung bei unabhängigen Stichproben
 Fallzahlplanung bei unabhängigen Stichproben Seminar Aktuelle biometrische Probleme Benjamin Hofner benjamin.hofner@stat.uni-muenchen.de 12. Januar 2005 Übersicht 1. Einführung und Grundlagen der Fallzahlplanung
Fallzahlplanung bei unabhängigen Stichproben Seminar Aktuelle biometrische Probleme Benjamin Hofner benjamin.hofner@stat.uni-muenchen.de 12. Januar 2005 Übersicht 1. Einführung und Grundlagen der Fallzahlplanung
Grundlegende Eigenschaften von Punktschätzern
 Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Wahrscheinlichkeitsverteilungen
 Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Statistische Auswertung in der Betriebsprüfung
 Dr. Harald Krehl Der Einsatz verteilungsbezogener Verfahren Der Einsatz verteilungsbezogener Verfahren etwa des Benford- Newcomb Verfahrens oder der Normalverteilung bzw. der LogNormalverteilung in der
Dr. Harald Krehl Der Einsatz verteilungsbezogener Verfahren Der Einsatz verteilungsbezogener Verfahren etwa des Benford- Newcomb Verfahrens oder der Normalverteilung bzw. der LogNormalverteilung in der
Stochastische Approximation des Value at Risk
 Stochastische Approximation des Value at Risk Annemarie Bitter Motivation Eines der wichtigsten Projekte der Versicherungswirtschaft ist derzeit die sogenannte Solvency-II-Richtlinie der Versicherungsaufsicht.
Stochastische Approximation des Value at Risk Annemarie Bitter Motivation Eines der wichtigsten Projekte der Versicherungswirtschaft ist derzeit die sogenannte Solvency-II-Richtlinie der Versicherungsaufsicht.
Belastungsmessungen am 3-Ring-System eines Sprungfallschirms
 Belastungsmessungen am 3-Ring-System eines Sprungfallschirms Prof. Dr.-Ing. Egon Füglein Dipl.-Ing. Christian Scheller Einführung Dynamisch beanspruchte Bauteile können durch Ermüdung (fatigue) versagen.
Belastungsmessungen am 3-Ring-System eines Sprungfallschirms Prof. Dr.-Ing. Egon Füglein Dipl.-Ing. Christian Scheller Einführung Dynamisch beanspruchte Bauteile können durch Ermüdung (fatigue) versagen.
Vorlesung Stetige Verteilungen / Mathematische Behandlung
 B E A C D Z Faultät Verehrswissenschaften Friedrich List Professur für Verehrsströmungslehre Verehrssystemtheorie I+II (V.-Wirtschaft) Vorlesung..0 Stetige Verteilungen / Mathematische Behandlung Neufert,
B E A C D Z Faultät Verehrswissenschaften Friedrich List Professur für Verehrsströmungslehre Verehrssystemtheorie I+II (V.-Wirtschaft) Vorlesung..0 Stetige Verteilungen / Mathematische Behandlung Neufert,
Mathematischer Vorkurs Lösungen zum Übungsblatt 5
 Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Deutscher Ausschuß für Stahlbau
 Deutscher DAS Deutscher Probabilistische Erfassung der Schadensakkumulation für Schweißverbindungen unter Mehrstufenbeanspruchung und besonderer Berücksichtigung der Dauerfestigkeit ZUSAMMENFASSUNG Die
Deutscher DAS Deutscher Probabilistische Erfassung der Schadensakkumulation für Schweißverbindungen unter Mehrstufenbeanspruchung und besonderer Berücksichtigung der Dauerfestigkeit ZUSAMMENFASSUNG Die
Verarbeitung von Messdaten
 HTL Steyr Verarbeitung von Messdaten Seite von 8 Bernhard Nietrost, HTL Steyr Verarbeitung von Messdaten Mathematische / Fachliche Inhalte in Stichworten: Regression, Polynominterpolation, Extremwertberechnung,
HTL Steyr Verarbeitung von Messdaten Seite von 8 Bernhard Nietrost, HTL Steyr Verarbeitung von Messdaten Mathematische / Fachliche Inhalte in Stichworten: Regression, Polynominterpolation, Extremwertberechnung,
Zur Wiederverwendung von Durchläufern im Treppenstufenversuch
 786 BETRIEBSFESTIGKEIT Zur Wiederverwendung von Durchläufern im Treppenstufenversuch Christian Müller, Karsten Hinkelmann, Michael Wächter, Rainer Masendorf und Alfons Esderts, Clausthal-Zellerfeld Zyklisch
786 BETRIEBSFESTIGKEIT Zur Wiederverwendung von Durchläufern im Treppenstufenversuch Christian Müller, Karsten Hinkelmann, Michael Wächter, Rainer Masendorf und Alfons Esderts, Clausthal-Zellerfeld Zyklisch
Übungsscheinklausur,
 Mathematik IV für Maschinenbau und Informatik (Stochastik) Universität Rostock, Institut für Mathematik Sommersemester 27 Prof. Dr. F. Liese Übungsscheinklausur, 3.7.27 Dipl.-Math. M. Helwich Name:...
Mathematik IV für Maschinenbau und Informatik (Stochastik) Universität Rostock, Institut für Mathematik Sommersemester 27 Prof. Dr. F. Liese Übungsscheinklausur, 3.7.27 Dipl.-Math. M. Helwich Name:...
unabhängigen Variablen Eine Funktion dient der Beschreibung von Zusammenhängen zwischen mehreren verschiedenen Faktoren.
 Funktionsbegriff 2.1 2 Funktionen mit einer unabhängigen Variablen 2.1 Funktionsbegriff Eine Funktion dient der Beschreibung von Zusammenhängen zwischen mehreren verschiedenen Faktoren. In den Wirtschaftswissenschaften
Funktionsbegriff 2.1 2 Funktionen mit einer unabhängigen Variablen 2.1 Funktionsbegriff Eine Funktion dient der Beschreibung von Zusammenhängen zwischen mehreren verschiedenen Faktoren. In den Wirtschaftswissenschaften
Schließende Statistik
 Schließende Statistik [statistical inference] Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
Schließende Statistik [statistical inference] Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
Interpolation und Integration mit Polynomen
 Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Gerätetechnisches Praktikum: Leichtbau
 Gerätetechnisches Praktikum: Leichtbau LEICHTBAUPROFILE Universität der Bundeswehr München Fakultät für Luft- und Raumfahrttechnik Institut für Leichtbau Prof.Dr.-Ing. H. Rapp Stand: 14. Januar 2011 Gerätetechnisches
Gerätetechnisches Praktikum: Leichtbau LEICHTBAUPROFILE Universität der Bundeswehr München Fakultät für Luft- und Raumfahrttechnik Institut für Leichtbau Prof.Dr.-Ing. H. Rapp Stand: 14. Januar 2011 Gerätetechnisches
2.3 Intervallschätzung
 2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
1 Fähigkeitskennwerte und deren Bedeutung
 1 Fähigkeitskennwerte und deren Bedeutung (in Anlehnung an Textband DIHT Naturwissenschaftliche Grundlagen) 1.1 Fähigkeitsuntersuchungen Die Qualitätsforderungen in der Serien- und Massenfertigung können
1 Fähigkeitskennwerte und deren Bedeutung (in Anlehnung an Textband DIHT Naturwissenschaftliche Grundlagen) 1.1 Fähigkeitsuntersuchungen Die Qualitätsforderungen in der Serien- und Massenfertigung können
U-Wert Bestimmung für eine unbekannte Gebäudehülle mit dem gskin U-Value KIT der
 U-Wert Bestimmung für eine unbekannte Gebäudehülle mit dem gskin U-Value KIT der greenteg AG Dr. Zoltán Nagy, Architektur und Gebäudesysteme, ETH Zürich http://systems.arch.ethz.ch nagy@arch.ethz.ch +41
U-Wert Bestimmung für eine unbekannte Gebäudehülle mit dem gskin U-Value KIT der greenteg AG Dr. Zoltán Nagy, Architektur und Gebäudesysteme, ETH Zürich http://systems.arch.ethz.ch nagy@arch.ethz.ch +41
9. Logarithmische Normalverteilung
 Seite 1 9. Logarithmische Normalverteilung 9 Logarithmische Normalverteilung 9.1 Transformationen 9. Logarithmische Transformation linksgipfelig verteilter Daten 9..1 Die logarithmische Skala 9.. Konstruktion
Seite 1 9. Logarithmische Normalverteilung 9 Logarithmische Normalverteilung 9.1 Transformationen 9. Logarithmische Transformation linksgipfelig verteilter Daten 9..1 Die logarithmische Skala 9.. Konstruktion
Kapitel 8 Einführung der Integralrechnung über Flächenmaße
 8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
k np g(n, p) = Pr p [T K] = Pr p [T k] Φ. np(1 p) DWT 4.1 Einführung 359/467 Ernst W. Mayr
![k np g(n, p) = Pr p [T K] = Pr p [T k] Φ. np(1 p) DWT 4.1 Einführung 359/467 Ernst W. Mayr k np g(n, p) = Pr p [T K] = Pr p [T k] Φ. np(1 p) DWT 4.1 Einführung 359/467 Ernst W. Mayr](/thumbs/52/28946049.jpg) Die so genannte Gütefunktion g gibt allgemein die Wahrscheinlichkeit an, mit der ein Test die Nullhypothese verwirft. Für unser hier entworfenes Testverfahren gilt ( ) k np g(n, p) = Pr p [T K] = Pr p
Die so genannte Gütefunktion g gibt allgemein die Wahrscheinlichkeit an, mit der ein Test die Nullhypothese verwirft. Für unser hier entworfenes Testverfahren gilt ( ) k np g(n, p) = Pr p [T K] = Pr p
Seminar im Wintersemester 2010/2011: Quantitative und implementierte Methoden der Marktrisikobewertung
 M.Sc. Brice Hakwa hakwa@uni-wuppertal.de Seminar im Wintersemester 2010/2011: Quantitative und implementierte Methoden der Marktrisikobewertung - Zusammenfassung zum Thema: Berechnung von Value-at-Risk
M.Sc. Brice Hakwa hakwa@uni-wuppertal.de Seminar im Wintersemester 2010/2011: Quantitative und implementierte Methoden der Marktrisikobewertung - Zusammenfassung zum Thema: Berechnung von Value-at-Risk
Numerische Bestimmung des Zahnkopffaktors für kreisförmige Fußausrundung an Zahnstangen
 IMW - Institutsmitteilung Nr. 36 (2011) 21 Numerische Bestimmung des Zahnkopffaktors für kreisförmige Fußausrundung an Zahnstangen Arslan, G.; DIN 3990 erlaubt u.a. die Berechnung der Zahnfußbiegespannung
IMW - Institutsmitteilung Nr. 36 (2011) 21 Numerische Bestimmung des Zahnkopffaktors für kreisförmige Fußausrundung an Zahnstangen Arslan, G.; DIN 3990 erlaubt u.a. die Berechnung der Zahnfußbiegespannung
Binomialverteilung Vertrauensbereich für den Anteil
 Übungen mit dem Applet Binomialverteilung Vertrauensbereich für den Anteil Binomialverteilung Vertrauensbereich für den Anteil 1. Statistischer Hintergrund und Darstellung.... Wie entsteht der Vertrauensbereich?...
Übungen mit dem Applet Binomialverteilung Vertrauensbereich für den Anteil Binomialverteilung Vertrauensbereich für den Anteil 1. Statistischer Hintergrund und Darstellung.... Wie entsteht der Vertrauensbereich?...
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
FEM-Modellbildung und -Berechnung von Kehlnähten
 FEM-Modellbildung und -Berechnung von Kehlnähten 1. Problemstellung und Lösungskonzept Die wesentliche Schwierigkeit bei der Berechnung einer Kehlnaht ist die Diskrepanz zwischen der tatsächlichen Geometrie
FEM-Modellbildung und -Berechnung von Kehlnähten 1. Problemstellung und Lösungskonzept Die wesentliche Schwierigkeit bei der Berechnung einer Kehlnaht ist die Diskrepanz zwischen der tatsächlichen Geometrie
Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n (2k 1) = n 2.
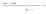 Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k=1 (2k 1) = n 2. Aufgabe 2. (7 Punkte) Gegeben sei das lineare Gleichungssystem x + 2z = 0 ay
Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k=1 (2k 1) = n 2. Aufgabe 2. (7 Punkte) Gegeben sei das lineare Gleichungssystem x + 2z = 0 ay
WWT Frank Sandig Agricolastr. 16, 2310A Freiberg. 1. Belegaufgabe.
 Frank Sandig Agricolastr. 16, 310A 09599 Freiberg 4817 4.WWT sandigf@mailserver.tu-freiberg.de Maschinen- und Apparateelemente 1. Belegaufgabe Aufgabenstellung: Abgabezeitraum: 6.11. - 30.11.007 Übungsleiter:
Frank Sandig Agricolastr. 16, 310A 09599 Freiberg 4817 4.WWT sandigf@mailserver.tu-freiberg.de Maschinen- und Apparateelemente 1. Belegaufgabe Aufgabenstellung: Abgabezeitraum: 6.11. - 30.11.007 Übungsleiter:
Drehzahl- und Drehrichtungserfassung Richtungserkennung mit Hall-Schalter
 Drehzahl- und Drehrichtungserfassung Richtungserkennung mit Hall-Schalter In vielen Anwendungsfällen müssen die Drehzahl und die Drehrichtung eines Motors bekannt sein. Diese Parameter können komfortabel
Drehzahl- und Drehrichtungserfassung Richtungserkennung mit Hall-Schalter In vielen Anwendungsfällen müssen die Drehzahl und die Drehrichtung eines Motors bekannt sein. Diese Parameter können komfortabel
Kapitel 2. Mittelwerte
 Kapitel 2. Mittelwerte Im Zusammenhang mit dem Begriff der Verteilung, der im ersten Kapitel eingeführt wurde, taucht häufig die Frage auf, wie man die vorliegenden Daten durch eine geeignete Größe repräsentieren
Kapitel 2. Mittelwerte Im Zusammenhang mit dem Begriff der Verteilung, der im ersten Kapitel eingeführt wurde, taucht häufig die Frage auf, wie man die vorliegenden Daten durch eine geeignete Größe repräsentieren
Duplizieren von Report-Vorlagen für die Erstellung umfangreicher Reports (ab ArtemiS SUITE 7.2)
 02/16 für die Erstellung umfangreicher Reports (ab ArtemiS SUITE 7.2) In der ArtemiS SUITE steht eine sehr flexible Report-Funktion zur Verfügung, die Ihnen die übersichtliche Darstellung Ihrer Analyse-Ergebnisse
02/16 für die Erstellung umfangreicher Reports (ab ArtemiS SUITE 7.2) In der ArtemiS SUITE steht eine sehr flexible Report-Funktion zur Verfügung, die Ihnen die übersichtliche Darstellung Ihrer Analyse-Ergebnisse
Wegen fehlender Extremstellen von und positiver Steigung im Intervall ( &0; 11' ist eine größere Produktionsmenge stets mit höheren Gesamtkosten
 Aufgabe 1 Die Gesamtkosten eines Unternehmens bei der Herstellung eines Produktes werden durch die Funktion mit = 10 + 40 +100; [0;11] beschrieben. Dabei bezeichnen die Produktionsmenge in Mengeneinheiten
Aufgabe 1 Die Gesamtkosten eines Unternehmens bei der Herstellung eines Produktes werden durch die Funktion mit = 10 + 40 +100; [0;11] beschrieben. Dabei bezeichnen die Produktionsmenge in Mengeneinheiten
Statistics, Data Analysis, and Simulation SS 2015
 Mainz, June 11, 2015 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Dr. Michael O. Distler
Mainz, June 11, 2015 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Dr. Michael O. Distler
Funktionen in der Mathematik
 R. Brinkmann http://brinkmann-du.de Seite 05.0.008 Funktionen in der Mathematik Bei der mathematischen Betrachtung natürlicher, technischer oder auch alltäglicher Vorgänge hängt der Wert einer Größe oft
R. Brinkmann http://brinkmann-du.de Seite 05.0.008 Funktionen in der Mathematik Bei der mathematischen Betrachtung natürlicher, technischer oder auch alltäglicher Vorgänge hängt der Wert einer Größe oft
- Normalverteilung (Gaußverteilung) kann auf sehr viele Zufallsprozesse angewendet werden.
 Normalverteilung und Standardnormalverteilung als Beispiel einer theoretischen Verteilung - Normalverteilung (Gaußverteilung) kann auf sehr viele Zufallsprozesse angewendet werden. - Stetige (kontinuierliche),
Normalverteilung und Standardnormalverteilung als Beispiel einer theoretischen Verteilung - Normalverteilung (Gaußverteilung) kann auf sehr viele Zufallsprozesse angewendet werden. - Stetige (kontinuierliche),
Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 2011 Mathematik
 ZK M A1 (mit CAS) Seite 1 von 5 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung siehe Prüfungsaufgabe. Materialgrundlage
ZK M A1 (mit CAS) Seite 1 von 5 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung siehe Prüfungsaufgabe. Materialgrundlage
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Übung 3 1 Inhalt der heutigen Übung Vorrechnen der Hausübung B.7 Beschreibende Statistik Gemeinsames Lösen der Übungsaufgaben C.1: Häufigkeitsverteilung C.2: Tukey
Statistik und Wahrscheinlichkeitsrechnung Übung 3 1 Inhalt der heutigen Übung Vorrechnen der Hausübung B.7 Beschreibende Statistik Gemeinsames Lösen der Übungsaufgaben C.1: Häufigkeitsverteilung C.2: Tukey
1 Wahrscheinlichkeitsrechnung. 2 Zufallsvariablen und ihre Verteilung. 3 Statistische Inferenz. 4 Intervallschätzung
 0 Einführung 1 Wahrscheinlichkeitsrechnung Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung Motivation und Hinführung Der wahre Anteil der rot-grün Wähler 009 war genau
0 Einführung 1 Wahrscheinlichkeitsrechnung Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung Motivation und Hinführung Der wahre Anteil der rot-grün Wähler 009 war genau
vertikale effektive Spannung log σ' z [kpa] M E ' 1
![vertikale effektive Spannung log σ' z [kpa] M E ' 1 vertikale effektive Spannung log σ' z [kpa] M E ' 1](/thumbs/73/69529928.jpg) Aufgabe 1: Ödometerversuch Im Labor wurde an einem Seebodenlehm ein Ödometerversuch durchgeführt. Im Folgenden ist eine kure Übersicht der Messresultate usammengestellt, mit denen im Weiteren dieses Musterbeispieles
Aufgabe 1: Ödometerversuch Im Labor wurde an einem Seebodenlehm ein Ödometerversuch durchgeführt. Im Folgenden ist eine kure Übersicht der Messresultate usammengestellt, mit denen im Weiteren dieses Musterbeispieles
SPSS-Beispiel zum Kapitel 4: Deskriptivstatistische Evaluation von Items (Itemanalyse) und Testwertverteilungen
 SPSS-Beispiel zum Kapitel 4: Deskriptivstatistische Evaluation von Items (Itemanalyse) und Testwertverteilungen Augustin Kelava 22. Februar 2010 Inhaltsverzeichnis 1 Einleitung zum inhaltlichen Beispiel:
SPSS-Beispiel zum Kapitel 4: Deskriptivstatistische Evaluation von Items (Itemanalyse) und Testwertverteilungen Augustin Kelava 22. Februar 2010 Inhaltsverzeichnis 1 Einleitung zum inhaltlichen Beispiel:
Einführung: Extremwertstatistik in der Hydrologie
 1 Einführung: Extremwertstatistik in der Hydrologie Aufgaben der Extremwertstatistik in der Hydrologie Grundbegriffe Ermittlung der Verteilungsfunktion für hydrologische Extremwerte Anwendung der bekannten
1 Einführung: Extremwertstatistik in der Hydrologie Aufgaben der Extremwertstatistik in der Hydrologie Grundbegriffe Ermittlung der Verteilungsfunktion für hydrologische Extremwerte Anwendung der bekannten
8. Konfidenzintervalle und Hypothesentests
 8. Konfidenzintervalle und Hypothesentests Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Beispiel. Sie wollen den durchschnittlichen Fruchtsaftgehalt eines bestimmten Orangennektars
8. Konfidenzintervalle und Hypothesentests Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Beispiel. Sie wollen den durchschnittlichen Fruchtsaftgehalt eines bestimmten Orangennektars
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
2. Mathematik-Schularbeit für die 6. Klasse Autor: Gottfried Gurtner
 2. Mathematik-Schularbeit für die 6. Klasse Autor: Gottfried Gurtner Arbeitszeit: 100 Minuten Lernstoff: Mathematische Grundkompetenzen: AG2.1, AG2.2, AG2.3 FA1.1, FA1.5, FA1.6, FA1.7, FA1.9 FA2.1, FA2.2,
2. Mathematik-Schularbeit für die 6. Klasse Autor: Gottfried Gurtner Arbeitszeit: 100 Minuten Lernstoff: Mathematische Grundkompetenzen: AG2.1, AG2.2, AG2.3 FA1.1, FA1.5, FA1.6, FA1.7, FA1.9 FA2.1, FA2.2,
DWT 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen 330/467 Ernst W. Mayr
 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
1 Zielfunktionen und Restriktionen. Beispiel 1 Beispiel 2 Anna Berta Cäsar Dirk Zielfunktion U A Y A U B =X B Y B X B
 Seite 1 Ausführliche formal-analytische Herleitungen anhand von zwei Beispielen zum Kapitel 3.2 zum Kurs 42110 Preisbildung auf unvollkommenen Märkten und allgemeines Gleichgewicht Inhaltsverzeichnis 1
Seite 1 Ausführliche formal-analytische Herleitungen anhand von zwei Beispielen zum Kapitel 3.2 zum Kurs 42110 Preisbildung auf unvollkommenen Märkten und allgemeines Gleichgewicht Inhaltsverzeichnis 1
Dioden Gleichrichtung und Stabilisierung
 Fachbereich Elektrotechnik und Informatik Praktikum für Messtechnik u. Elektronik Semester: Prof. Dr.-Ing. Heckmann Name: Gruppe: Fach: BME, MME Matr. Nr.: Datum: Versuch 2 Testat: Dioden Gleichrichtung
Fachbereich Elektrotechnik und Informatik Praktikum für Messtechnik u. Elektronik Semester: Prof. Dr.-Ing. Heckmann Name: Gruppe: Fach: BME, MME Matr. Nr.: Datum: Versuch 2 Testat: Dioden Gleichrichtung
Statistik. Ronald Balestra CH St. Peter
 Statistik Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch 17. Januar 2010 Inhaltsverzeichnis 1 Statistik 1 1.1 Beschreibende Statistik....................... 1 1.2 Charakterisierung von Häufigkeitsverteilungen...........
Statistik Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch 17. Januar 2010 Inhaltsverzeichnis 1 Statistik 1 1.1 Beschreibende Statistik....................... 1 1.2 Charakterisierung von Häufigkeitsverteilungen...........
Hauptklausur zur Stochastik für Lehramt
 Universität Duisburg-Essen Essen, den 20.02.203 Fakultät für Mathematik Dr. Daniel Herden Dipl.-Inf. Christian Thiel Matthias aus der Wiesche Hauptklausur zur Stochastik für Lehramt Bearbeitungszeit: mind.
Universität Duisburg-Essen Essen, den 20.02.203 Fakultät für Mathematik Dr. Daniel Herden Dipl.-Inf. Christian Thiel Matthias aus der Wiesche Hauptklausur zur Stochastik für Lehramt Bearbeitungszeit: mind.
MATHEMATIK 3 STUNDEN
 EUROPÄISCHES ABITUR 2013 MATHEMATIK 3 STUNDEN DATUM : 10. Juni 2013, Vormittag DAUER DER PRÜFUNG: 2 Stunden (120 Minuten) ERLAUBTES HILFSMITTEL Prüfung mit technologischem Hilfsmittel 1/6 DE AUFGABE B1
EUROPÄISCHES ABITUR 2013 MATHEMATIK 3 STUNDEN DATUM : 10. Juni 2013, Vormittag DAUER DER PRÜFUNG: 2 Stunden (120 Minuten) ERLAUBTES HILFSMITTEL Prüfung mit technologischem Hilfsmittel 1/6 DE AUFGABE B1
Aussagen hierzu sind mit einer unvermeidbaren Unsicherheit behaftet, die statistisch über eine Irrtumswahrscheinlichkeit bewertet wird.
 Stichprobenumfang Für die Fragestellung auf Gleichheit von ein oder zwei Stichproben wird auf Basis von Hypothesentests der notwendige Stichprobenumfang bestimmt. Deshalb werden zunächst die Grundlagen
Stichprobenumfang Für die Fragestellung auf Gleichheit von ein oder zwei Stichproben wird auf Basis von Hypothesentests der notwendige Stichprobenumfang bestimmt. Deshalb werden zunächst die Grundlagen
Kapitel XIV - Anpassungstests
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel XIV - Anpassungstests Induktive Statistik Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh 2. Grundannahme:
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel XIV - Anpassungstests Induktive Statistik Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh 2. Grundannahme:
NIEDERSCHLAG. Hausübung 1
 Hausübung 1 NIEDERSCHLAG Abgabe: 25.10.2017 Niederschlag wird nahezu weltweit mit einem Netz von Messstationen erfasst. Dabei handelt es sich um punktuelle Messungen. Für grundlegende Fragen der Ingenieurhydrologie
Hausübung 1 NIEDERSCHLAG Abgabe: 25.10.2017 Niederschlag wird nahezu weltweit mit einem Netz von Messstationen erfasst. Dabei handelt es sich um punktuelle Messungen. Für grundlegende Fragen der Ingenieurhydrologie
unendlich-dimensionalen lästigen Parameter auffassen.
 Näherungen mit Bootstrap Werner Stahel, Seminar für Statistik, ETH Zürich, 8. 4. 2009 Dieser Text kann dazu dienen, die Ideen des Bootstrap zusammenzufassen. Es fehlen hier Beispiele. 1 Fragestellung a
Näherungen mit Bootstrap Werner Stahel, Seminar für Statistik, ETH Zürich, 8. 4. 2009 Dieser Text kann dazu dienen, die Ideen des Bootstrap zusammenzufassen. Es fehlen hier Beispiele. 1 Fragestellung a
Einsatz von Varianzreduktionstechniken II
 Einsatz von Varianzreduktionstechniken II Stratified Sampling und Common Random Numbers Bastian Bluhm Betreuer: Christiane Barz Ausgewählte technische, rechtliche und ökonomische Aspekte des Entwurfs von
Einsatz von Varianzreduktionstechniken II Stratified Sampling und Common Random Numbers Bastian Bluhm Betreuer: Christiane Barz Ausgewählte technische, rechtliche und ökonomische Aspekte des Entwurfs von
Satz über implizite Funktionen und seine Anwendungen
 Satz über implizite Funktionen und seine Anwendungen Gegeben sei eine stetig differenzierbare Funktion f : R 2 R, die von zwei Variablen und abhängt. Wir betrachten im Folgenden die Gleichung f(,) = 0.
Satz über implizite Funktionen und seine Anwendungen Gegeben sei eine stetig differenzierbare Funktion f : R 2 R, die von zwei Variablen und abhängt. Wir betrachten im Folgenden die Gleichung f(,) = 0.
Klaus Palme Tel. +49 (0) Fax Nr. +49 (0)
 Datum 06.12.2011 Bericht Auftraggeber 2011/016-B-5 / Kurzbericht Palme Solar GmbH Klaus Palme Tel. +49 (0) 73 24-98 96-433 Fax Nr. +49 (0) 73 24-98 96-435 info@palme-solar.de Bestellungsnummer 7 Auftragnehmer
Datum 06.12.2011 Bericht Auftraggeber 2011/016-B-5 / Kurzbericht Palme Solar GmbH Klaus Palme Tel. +49 (0) 73 24-98 96-433 Fax Nr. +49 (0) 73 24-98 96-435 info@palme-solar.de Bestellungsnummer 7 Auftragnehmer
Lösungen zum Arbeitsblatt: y = mx + b Alles klar???
 I. Zeichnen von Funktionen a) Wertetabelle x -4-3 - -1 0 1 3 4 y =,5x -10-7,5-5 -,5 0,5 5 7,5 10 y = - x,7 1,3 0,7 0-0,7-1,3 - -,7 3 y = x 1,5-9,5-7,5-5,5-3,5-1,5 0,5,5 4,5 6,5 y = - 1 x + 4 3,5 3,5 1,5
I. Zeichnen von Funktionen a) Wertetabelle x -4-3 - -1 0 1 3 4 y =,5x -10-7,5-5 -,5 0,5 5 7,5 10 y = - x,7 1,3 0,7 0-0,7-1,3 - -,7 3 y = x 1,5-9,5-7,5-5,5-3,5-1,5 0,5,5 4,5 6,5 y = - 1 x + 4 3,5 3,5 1,5
Untersuchung der Auswahl der Hauptfreiheitsgrade zum Import eines Modells von ANSYS nach SIMPACK
 IMW - Institutsmitteilung Nr. 35 (2010) 103 Untersuchung der Auswahl der Hauptfreiheitsgrade zum Import eines Modells von ANSYS nach SIMPACK M. Leng; Z. Liang Die Auswahl der Hauptfreiheitsgrade spielt
IMW - Institutsmitteilung Nr. 35 (2010) 103 Untersuchung der Auswahl der Hauptfreiheitsgrade zum Import eines Modells von ANSYS nach SIMPACK M. Leng; Z. Liang Die Auswahl der Hauptfreiheitsgrade spielt
Stochastik für die Naturwissenschaften
 Stochastik für die Naturwissenschaften Dr. C.J. Luchsinger 7. n (Konvergenz, LLN, CLT) Literatur Kapitel 7 n heisst für uns n gross * Statistik in Cartoons: Kapitel 5, Seite 114 in Kapitel 6 * Stahel:
Stochastik für die Naturwissenschaften Dr. C.J. Luchsinger 7. n (Konvergenz, LLN, CLT) Literatur Kapitel 7 n heisst für uns n gross * Statistik in Cartoons: Kapitel 5, Seite 114 in Kapitel 6 * Stahel:
Inhaltsverzeichnis. Inhaltsverzeichnis. 3
 Inhaltsverzeichnis Inhaltsverzeichnis Vorwort 4 1 Der Taschenrechner 5 1.1 Erste Rechnungen.................................. 5 1.2 Bearbeiten und Löschen der Eingaben....................... 7 1.3 Mehrere
Inhaltsverzeichnis Inhaltsverzeichnis Vorwort 4 1 Der Taschenrechner 5 1.1 Erste Rechnungen.................................. 5 1.2 Bearbeiten und Löschen der Eingaben....................... 7 1.3 Mehrere
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Anleitung zum Applet
 Anleitung zum Applet Wahrscheinlichkeitsnetz bearbeitet von: WS 2006/2007 E/TI-7, betreut von: Prof. Dr. Wilhelm Kleppmann Inhaltsverzeichnis Anleitung zum Applet... 1 1 Vorwort... 3 2 Grafische Benutzeroberfläche
Anleitung zum Applet Wahrscheinlichkeitsnetz bearbeitet von: WS 2006/2007 E/TI-7, betreut von: Prof. Dr. Wilhelm Kleppmann Inhaltsverzeichnis Anleitung zum Applet... 1 1 Vorwort... 3 2 Grafische Benutzeroberfläche
Die erhobenen Daten werden zunächst in einer Urliste angeschrieben. Daraus ermittelt man:
 Die erhobenen Daten werden zunächst in einer Urliste angeschrieben. Daraus ermittelt man: a) Die absoluten Häufigkeit: Sie gibt an, wie oft ein Variablenwert vorkommt b) Die relative Häufigkeit: Sie erhält
Die erhobenen Daten werden zunächst in einer Urliste angeschrieben. Daraus ermittelt man: a) Die absoluten Häufigkeit: Sie gibt an, wie oft ein Variablenwert vorkommt b) Die relative Häufigkeit: Sie erhält
Biomechanik im Sporttheorieunterricht
 Betrifft 22 DR. MARTIN HILLEBRECHT Biomechanik im Sporttheorieunterricht - Grafische Schwerpunktbestimmung - 1. EINLEITUNG Im ersten Teil diese Artikels (vgl. Betrifft Sport 4/ 98) wurden zwei Verfahren
Betrifft 22 DR. MARTIN HILLEBRECHT Biomechanik im Sporttheorieunterricht - Grafische Schwerpunktbestimmung - 1. EINLEITUNG Im ersten Teil diese Artikels (vgl. Betrifft Sport 4/ 98) wurden zwei Verfahren
3.3 Absenkungsverlauf
 3.3 Absenkungsverlauf 3.3.1 Aufgabe 3.3.1.1 Verzögerungsfunktion Der Absenkungsverlauf des Grundwassers auf Grund einer Entnahme aus einem Brunnen (z.b. durch einen so genannten Pumpversuch) kann in erster
3.3 Absenkungsverlauf 3.3.1 Aufgabe 3.3.1.1 Verzögerungsfunktion Der Absenkungsverlauf des Grundwassers auf Grund einer Entnahme aus einem Brunnen (z.b. durch einen so genannten Pumpversuch) kann in erster
1 Fraktale Eigenschaften der Koch-Kurve
 Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
4 Statistik der Extremwertverteilungen
 In diesem Kapitel beschäftigen wir uns mit statistischen Anwendungen der Extremwerttheorie. Wir werden zwei verschiedene Zugänge zur Modellierung von Extremwerten betrachten. Der erste Zugang basiert auf
In diesem Kapitel beschäftigen wir uns mit statistischen Anwendungen der Extremwerttheorie. Wir werden zwei verschiedene Zugänge zur Modellierung von Extremwerten betrachten. Der erste Zugang basiert auf
Mathematik für Biologen und Chemiker Prof. Scheltho - Übungen Mathe 2
 Mathematik für Biologen und Chemiker Prof. Scheltho - Übungen Mathe 2 Fortsetzung der komlexen Zahlen : 9. Radizieren und Potenzen a) Berechnen Sie (1+i) 20 und geben Sie das Resultat als Polarkoordinaten
Mathematik für Biologen und Chemiker Prof. Scheltho - Übungen Mathe 2 Fortsetzung der komlexen Zahlen : 9. Radizieren und Potenzen a) Berechnen Sie (1+i) 20 und geben Sie das Resultat als Polarkoordinaten
Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung
 R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
Exemplar für Prüfer/innen
 Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2015 Mathematik Kompensationsprüfung Angabe für Prüfer/innen Hinweise zur Kompensationsprüfung
Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2015 Mathematik Kompensationsprüfung Angabe für Prüfer/innen Hinweise zur Kompensationsprüfung
Mathematische und statistische Methoden II
 Statistik & Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte
Statistik & Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte
57. Mathematik-Olympiade 1. Runde (Schulrunde) Lösungen
 nolympiadeklasse 11 1 57. Mathematik-Olympiade 1. Runde (Schulrunde) Lösungen c 017 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 57111 Lösung
nolympiadeklasse 11 1 57. Mathematik-Olympiade 1. Runde (Schulrunde) Lösungen c 017 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 57111 Lösung
Musterlösung: Partikelbewegung im Fluid
 Musterlösung: Partikelbewegung im Fluid 0. Januar 016 Wiederholung Ein Ausschnitt notwendiger Grundlagen für die Berechnung stationärer Sinkgeschwindigkeiten von Partikeln im Fluid. Annahmen: Partikel
Musterlösung: Partikelbewegung im Fluid 0. Januar 016 Wiederholung Ein Ausschnitt notwendiger Grundlagen für die Berechnung stationärer Sinkgeschwindigkeiten von Partikeln im Fluid. Annahmen: Partikel
0.1 Versuch 4C: Bestimmung der Gravitationskonstante mit dem physikalischen Pendel
 0.1 Versuch 4C: Bestimmung der Gravitationskonstante mit dem physikalischen Pendel 0.1.1 Aufgabenstellung Man bestimme die Fallbeschleunigung mittels eines physikalischen Pendels und berechne hieraus die
0.1 Versuch 4C: Bestimmung der Gravitationskonstante mit dem physikalischen Pendel 0.1.1 Aufgabenstellung Man bestimme die Fallbeschleunigung mittels eines physikalischen Pendels und berechne hieraus die
Schnittpunkt zweier Einzelfunktionen einer zerlegten speziellen bilogarithmischen Funktion
 chnittpunkt zweier Einzelfunktionen einer zerlegten speziellen bilogarithmischen Funktion Dipl.- Ing. Björnstjerne Zindler, M.c. Erstellt: 28. Januar 205 Letzte Revision: 5. Februar 205 Inhaltsverzeichnis
chnittpunkt zweier Einzelfunktionen einer zerlegten speziellen bilogarithmischen Funktion Dipl.- Ing. Björnstjerne Zindler, M.c. Erstellt: 28. Januar 205 Letzte Revision: 5. Februar 205 Inhaltsverzeichnis
3. Kraftgrößenverfahren
 .Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
.Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
7.7 Spezielle diskrete Wahrscheinlichkeitsverteilungen
 7.7 Spezielle diskrete Wahrscheinlichkeitsverteilungen 7.7.1 Die Laplace-Verteilung Sei X eine gleich verteilte Zufallsvariable mit den Werten in der Menge Ω X = {x i R : i = 1,...,n}, d.h. f (x i = 1
7.7 Spezielle diskrete Wahrscheinlichkeitsverteilungen 7.7.1 Die Laplace-Verteilung Sei X eine gleich verteilte Zufallsvariable mit den Werten in der Menge Ω X = {x i R : i = 1,...,n}, d.h. f (x i = 1
