Kurzbeschreibung. Eingaben zur Berechnung. Das Optionspreismodell. Mit dem Eurex-OptionMaster können Sie
|
|
|
- Victor Brahms
- vor 8 Jahren
- Abrufe
Transkript
1 Kurzbeschreibung Mit dem Eurex-OptionMaster können Sie - theoretische Optionspreise - Optionskennzahlen ( Griechen ) und - implizite Volatilitäten von Optionen berechnen und die errechneten Preise bei verschiedenen Kurs- und Volatilitäts- Szenarien simulieren. Die Ergebnisse werden anschaulich in der so genannten Kurs/Vola-Matrix dargestellt. Sie erhalten dadurch eine Vielzahl möglicher Preisentwicklungen auf einen Blick, die erhöhte Transparenz verbessert Ihr Gespür für die Preissensitivität von Optionen. Das Optionspreismodell Der Eurex-OptionMaster berechnet die Optionspreise anhand des Black/Scholes- Optionspreismodells. Mit diesem Modell können theoretische Preise von europäischen Aktien- oder Aktienindexoptionen, beispielsweise der Option auf den DAX, den Benchmark-Index der Deutsche Börse AG, berechnet werden, bei denen während der Laufzeit keine Dividendenzahlungen anfallen. Der Eurex-OptionMaster kann jedoch auch Dividenden zumindest näherungsweise bei der Berechnung berücksichtigen. Der Wert von tief im Geld liegenden europäischen Verkaufsoptionen (Put-Optionen) liegt bei der Nutzung des Black/Scholes-Optionspreismodells unter dem inneren Wert der Optionen. Für amerikanische Optionen (beispielsweise Eurex-Aktienoptionen) ist die Wertuntergrenze, sofern keine Dividende gezahlt wird, jedoch durch den inneren Wert der Option Basispreis minus Aktienpreis definiert. Das Black/Scholes-Optionspreismodell wird in der Praxis häufig verwandt; andere Modelle berücksichtigen weitere Faktoren bei der Preisbestimmung. Keines der Modelle kann Ihnen jedoch ein genaues Ergebnis garantieren. Bedenken Sie daher, dass der Eurex-OptionMaster unter anderem auch aus diesem Grunde nicht zu Handelszwecken oder zur Unterstützung bei Handelsentscheidungen heran gezogen werden sollte. Eingaben zur Berechnung Tragen Sie in die Eingabefelder im oberen Drittel des Eurex-OptionMaster die von Ihnen gewünschten Werte ein und klicken auf den Button Berechnung starten. Die Ergebnisse (Optionspreis und implizite Volatilität) und die Optionskennzahlen (Griechen Delta, Gamma, Rho, Theta und Vega) für Kaufoptionen (Calls) und Verkaufsoptionen (Puts) werden im mittleren Bereich angezeigt; im unteren Drittel veranschaulicht die Kurs/Vola-Matrix die vom Eurex-OptionMaster berechneten Preise, wiederum getrennt nach Calls und Puts.
2 Kaufdatum Hier geben Sie das Kaufdatum der Option ein. Voreingestellt ist stets das aktuelle Datum, das Sie jederzeit ändern können, indem Sie entweder in die Datumszeile selbst klicken und das Datum eingeben, oder aber auf das Kalendersymbol klicken und im sich öffnenden Kalender das gewünschte Datum festlegen. Letzter Handelstag / Restlaufzeit Hier können Sie entweder den letzten Handelstag der Option über einen Kalender auswählen oder aber die Restlaufzeit der Option in Tagen inklusive des Kaufdatums eingeben. Der OptionMaster zeigt Ihnen in beiden Fällen den letzten Handelstag als Datum an. Beispiel: Sie geben am 16. April 30 Tage Restlaufzeit für die Option an. Der OptionMaster ermittelt den 15. Mai als letzten Handelstag. Der 16. April ist der erste Tag der Restlaufzeit, der 15. Mai der letzte Tag. Bei der Eingabe von einem Tag Restlaufzeit sind Kaufdatum und letzter Handelstag identisch. Kurs Basiswert Hier geben Sie den aktuellen Kurs des Basiswertes (Aktie, Futures et cetera) ein. Beispiel: Eingabe des Aktienkurses EUR 100,50. Ausübungspreis Hier geben Sie den Ausübungspreis der Option ein. Beispiel: Ausübungspreis einer Aktienoption: EUR 100 (die Eingabe der Nachkommastellen ist nicht erforderlich, wenn es sich um volle Beträge handelt). Zins Als Zins geben Sie den kurzfristigen für die Optionslaufzeit relevanten inländischen Refinanzierungssatz ein. In der Praxis wird hier häufig mit der so genannten Repo-Rate gerechnet. Beispiele: Für eine Option mit einem Monat Restlaufzeit ist ein kurzfristiger Zinssatz für einen Monat einzugeben, beispielsweise eine 2 für 2 Prozent. Für eine Option mit Restlaufzeit von einem Jahr ist analog der Zinssatz für ein Jahr einzugeben, hier beispielweise eine 2,5 für 2,5 Prozent. Volatilität Einer der wichtigsten Faktoren zur Berechnung des Optionspreises ist die Volatilität. Unterschieden wird zwischen der historischen Volatilität und der für die Zukunft angenommenen Volatilität (implizite Volatilität): Die historische Volatilität misst die Schwankungsintensität (Standardabweichung) eines Basiswertes über einen bestimmten Zeitraum in der Vergangenheit, zum Beispiel 250 Tage. Die Angabe erfolgt in Prozent per annum.
3 Die historischevolatilität ist zur Berechnung von Optionspreisen jedoch nur bedingt geeignet, denn entscheidend hierfür ist die zukünftige Volatilität des Basiswerts. Sie kann von den Marktteilnehmern nur geschätzt werden, wobei als Grundlage der Schätzung die historische Volatilität genutzt wird. Je höher die Volatilität geschätzt wird, desto höher ist auch der Optionspreis. Aus jedem angebotenen Optionspreis Bid oder Ask sowie aus jedem Handelspreis kann zurückgerechnet werden, mit welcher Volatilität dieser Optionspreis berechnet wurde. Diese im Optionspreis enthaltene Volatilität wird als implizite Volatilität bezeichnet. Die implizite Volatilität lässt sich mit dem Eurex-OptionMaster bei Eingabe des aktuellen Optionspreises Call (für implizite Vola) und Put (für implizite Vola) berechnen. Hinweis: Hier geben Sie Ihre angenommene Volatilität (implizite Volatilität) per annum ein. Die Angabe erfolgt in Prozent. Beispiel: Für 25 Prozent geben Sie die Zahl 25 ein. Berechnung starten Mit den bisher eingegebenen Daten können Sie bereits die Ergebnisse und Optionskennzahlen für Calls und Puts berechnen lassen; die Werte der Kurs/Vola- Matrix können jedoch erst ermittelt werden, wenn Sie auch in den Feldern Volatilitätsintervall und Kursintervall Eintragungen vorgenommen haben. Diese Eingabefelder inklusive der Berücksichtigung einer Dividendenzahlung werden im Folgenden beschrieben: Dividende Zur Berechnung von Aktienoptionen, bei denen während der Optionslaufzeit eine Dividende gezahlt wird, können Sie eine erwartete Dividende (Bardividende) eingeben. Erwarten Sie beispielsweise, dass eine Dividende von EUR 2 ausgeschüttet wird, geben Sie in das Feld Dividende eine 2 ein. Weitere Informationen hierzu finden Sie unter Optionspreismodell. Dividendendatum Wie bei der Eingabe des Kaufdatums und des letzten Handelstages können Sie an dieser Stelle das Datum einer möglichen Dividendenzahlung über einen Kalender auswählen, oder Sie klicken wiederum in die Datumszeile selbst und geben das Datum der Dividendenzahlung manuell ein. Alternativ können Sie auch die Tage bis zur Dividendenzahlung eingeben. Call (für implizite Vola) Wenn Sie nicht nur den theoretischen Preis eines Call berechnen möchten, sondern zusätzlich die implizite Volatilität des gehandelten Call (bei identischen Daten), dann geben Sie unter Call (für implizite Vola) den aktuellen Preis des Call ein.
4 Beispiel: Kaufdatum Letzter Handelstag Kurs Basiswert EUR 100,50 Ausübungspreis EUR 100 Zins 3% Volatilität 25% Call-Optionspreis EUR 5,6805 Bei Eingabe eines Optionspreises von EUR 7 unter Call (für implizite Vola) berechnet der OptionMaster automatisch die in diesem Preis enthaltene Volatilität und zeigt diese unter Implizite Volatilität bei den Ergebnissen für Calls an: 31,60%. Put (für implizite Vola) Wenn Sie nicht nur den theoretischen Preis eines Put berechnen möchten, sondern zusätzlich die implizite Volatilität des gehandelten Put (bei identischen Daten), dann geben Sie unter Put (für implizite Vola) den aktuellen Preis des Put ein. Volatilitätsintervall In dem Feld Volatilitätsintervall definieren Sie, wie der Eurex-OptionMaster die Kurs/Vola-Matrix für Calls und Puts aufbauen soll. Wenn Sie zur Berechnung des theoretischen Optionspreises unter Volatilität zum Beispiel 30 Prozent eingegeben haben und jetzt unter Volatilitätsintervall eine 2 für 2 Prozent eintragen, dann erzeugt der Eurex-OptionMaster die Kurs/Vola-Matrix in der Form, dass die Optionspreise jeweils für Volatilitäten in einem Abstand von 2 Prozent angegeben werden, beginnend bei 22 Prozent bis hin zu einem Optionspreis für eine Volatilität von 38 Prozent. Kursintervall In dem Feld Kursintervall legen Sie den Abstand der Kurse des Basiswertes fest, mit denen der Eurex-OptionMaster in der Kurs/Vola-Matrix Optionspreise berechnen soll. Wenn Sie zur Berechnung des theoretischen Optionspreises unter Kurs Basiswert zum Beispiel EUR 100 als Aktienkurs eingegeben haben und unter Kursintervall eine 5 für 5 Euro eintragen, dann erzeugt der Eurex-OptionMaster die Kurs/Vola-Matrix in der Form, dass die Optionspreise jeweils für Kurse des Basiswertes in einem Abstand von 5 Euro angegeben werden, in diesem Falle beginnend bei 80 Euro bis hin zu einem Kurs von 120 Euro.
5 Ergebnisse für Calls/Ergebnisse für Puts Nach Anklicken des Buttons Berechnung starten erscheinen in den Feldern Call- Optionspreis beziehungsweise Put-Optionspreis die Ergebnisse für Call und Put. Falls Sie zusätzlich in der rechten Spalte im Markt gehandelte Preise für Call und Put eingegeben haben, wird außerdem die implizite Volatilität dieser Optionen angezeigt. Call-Optionspreis Gemeint ist der theoretische Call-Optionspreis, wie er sich anhand des Black/Scholes-Optionspreismodells für die von Ihnen eingegebenen Basisdaten ergibt. Put-Optionspreis Gemeint ist der theoretische Put-Optionspreis, wie er sich anhand des Black/Scholes-Optionspreismodells für die von Ihnen eingegebenen Basisdaten ergibt. Implizite Volatilität Zeigt die implizite Volatilität einer Option an, wenn unter Call (für implizite Vola) oder unter Put (für implizite Vola) ein Optionspreis eingegeben wurde, für den die implizite Volatilität berechnen werden sollte. Optionskennzahlen für Calls und Puts Delta Das Delta bezeichnet die voraussichtliche absolute Veränderung des theoretischen Optionspreises bei einer Veränderung des Basiswertes um eine Einheit. Mathematisch betrachtet, ist das die erste Ableitung der Optionspreisformel nach dem Kurs des Basiswertes. Ein angezeigtes Delta von 0,53 bei einem Call bedeutet, dass der Call um 0,53 Einheiten im Preis steigen wird, wenn der Kurs des Basiswertes um eine Einheit steigt. Der Preis eines Put hingegen sinkt für den Fall, dass der Kurs des Basiswertes um eine Einheit steigen sollte (negatives Delta von zum Beispiel 0,45). Das Delta ist nicht konstant und nimmt bei einem Call Werte zwischen 0 und 1, bei einem Put Werte zwischen 1 und 0 ein. Die Veränderung des Delta wird durch das ebenfalls berechnete Gamma gemessen. Gamma Das Gamma bezeichnet die erwartete Veränderungsrate des Delta bei einer Veränderung des Kurses des Basiswertes um eine Einheit.
6 Beispiel: Der Kurs einer Aktie steigt von EUR 100 auf EUR 101. Anfänglich hat ein Call ein Delta von 0,50. Durch den Anstieg der Aktie auf EUR 101 verändert sich das Delta auf 0,55. Das Gamma beträgt 0,05. Mit anderen Worten: Die Option wird zukünftige Veränderungen des Basiswertes in dieselbe Richtung absolut in stärkerem Maße nachvollziehen. Das Gamma ist sowohl für Calls als auch für Puts positiv, da sich das Delta des Call von 0 in Richtung +1 und das Delta des Put von 1 Richtung 0 verändert (und damit in beiden Fällen größer wird). Unterstellt wird in jedem Fall eine stetig steigende Preisbewegung. Rho Das Rho misst die erwartete Veränderung des Optionspreises bei einer angenommenen Zinsveränderung von einem Prozentpunkt. Der Einfluss ist bei Optionen mit kurzer Restlaufzeit generell geringer als bei Optionen mit einer längeren Restlaufzeit. Grundsätzlich gilt: Je länger die Restlaufzeit ist, desto stärker ist der Einfluss einer Zinsveränderung. Theta Das Theta misst die erwartete absolute Veränderung des Optionspreises, wenn die Restlaufzeit der Option um einen Tag abnimmt. Da mit abnehmender Restlaufzeit Optionen in der Regel niedrigere Preise aufweisen, weist das Theta (im Gegensatz zum Delta oder Vega, die positive Werte annehmen) normalerweise einen negativen Wert auf. Vega Das Vega (häufig auch als Kappa bezeichnet) gibt die erwartete absolute Veränderung des Optionspreises bei einer Veränderung der Volatilität um einen Prozentpunkt an. Calls und Puts werden bei einer Erhöhung der Volatilität gleichermaßen teurer. Das Vega ist daher positiv und stellt neben dem Delta und Gamma die wichtigste Optionskennzahl dar. Kurs/Vola-Matrix für Call- und Put-Preise Mit der Kurs/Vola-Matrix können Sie eine Vielzahl von Optionspreisen gleichzeitig in einem Arbeitsschritt berechnen. Das bedeutet, dass Sie verschiedene Szenarien mit veränderten Preisen und unterschiedlichen Volatilitäten in einer einzigen Übersicht vergleichen können. Sie können dem OptionMaster die Intervalle vorgeben, für die einzelne Optionspreise berechnet werden sollen. Die Berechnung der zwei Matrizen erfolgt automatisch, wenn Sie oben unter Volatilitätsintervall und Kursintervall Werte eingetragen und auch die übrigen zur Berechnung von Optionspreisen notwendigen Daten eingegeben haben. Wenn Sie einen der Preise in der Matrix anklicken, wird er automatisch in die Mitte der Matrix gesetzt. Dadurch werden neue Preise sichtbar und weitere Vergleiche möglich.
Aufgaben Brealey/Myers [2003], Kapitel 21
![Aufgaben Brealey/Myers [2003], Kapitel 21 Aufgaben Brealey/Myers [2003], Kapitel 21](/thumbs/25/5752225.jpg) Quiz: 1, 2, 4, 6, 7, 10 Practice Questions: 1, 3, 5, 6, 7, 10, 12, 13 Folie 0 Lösung Quiz 7: a. Das Optionsdelta ergibt sich wie folgt: Spanne der möglichen Optionspreise Spanne der möglichen Aktienkurs
Quiz: 1, 2, 4, 6, 7, 10 Practice Questions: 1, 3, 5, 6, 7, 10, 12, 13 Folie 0 Lösung Quiz 7: a. Das Optionsdelta ergibt sich wie folgt: Spanne der möglichen Optionspreise Spanne der möglichen Aktienkurs
Sensitivitätsfaktoren
 Sensitivitätsfaktoren Überblick Sensitivitätsfaktoren zeigen die Änderungen des Optionspreises, wenn sich eine Einflussgröße ändert Sensitivitätsfaktoren werden mit einem Optionspreismodell errechnet Einflussgrößen:
Sensitivitätsfaktoren Überblick Sensitivitätsfaktoren zeigen die Änderungen des Optionspreises, wenn sich eine Einflussgröße ändert Sensitivitätsfaktoren werden mit einem Optionspreismodell errechnet Einflussgrößen:
Dynamik von Optionen
 Dynamik von Optionen Plan Der Optionspreis und seine Einflussfaktoren Wert des Calls / Puts bei unterschiedlichen Marktbedingungen Änderung des Optionspreises bei Änderung eines oder mehrerer Einflussfaktoren
Dynamik von Optionen Plan Der Optionspreis und seine Einflussfaktoren Wert des Calls / Puts bei unterschiedlichen Marktbedingungen Änderung des Optionspreises bei Änderung eines oder mehrerer Einflussfaktoren
Volatilitätsstrategie mit Optionen
 MT AG MANAGING TECHNOLOGY IMPROVING BUSINESS PERFORMANCE Volatilitätsstrategie mit Optionen Referent: Guido Neander, Senior-Berater, MT AG, Ratingen Agenda Begriffsdefinitionen Optionen Volatilität Preisbestimmungsfaktoren
MT AG MANAGING TECHNOLOGY IMPROVING BUSINESS PERFORMANCE Volatilitätsstrategie mit Optionen Referent: Guido Neander, Senior-Berater, MT AG, Ratingen Agenda Begriffsdefinitionen Optionen Volatilität Preisbestimmungsfaktoren
Internationale Finanzierung 7. Optionen
 Übersicht Kapitel 7: 7.1. Einführung 7.2. Der Wert einer Option 7.3. Regeln für Optionspreise auf einem arbitragefreien Markt 7.3.1. Regeln für Calls 7.3.2. Regeln für Puts 7.3.3. Die Put Call Parität
Übersicht Kapitel 7: 7.1. Einführung 7.2. Der Wert einer Option 7.3. Regeln für Optionspreise auf einem arbitragefreien Markt 7.3.1. Regeln für Calls 7.3.2. Regeln für Puts 7.3.3. Die Put Call Parität
Finanzmanagement 5. Optionen
 Übersicht Kapitel 5: 5.1. Einführung 5.2. Der Wert einer Option 5.3. Regeln für Optionspreise auf einem arbitragefreien Markt 5.3.1. Regeln für Calls 5.3.2. Regeln für Puts 5.3.3. Die Put Call Parität
Übersicht Kapitel 5: 5.1. Einführung 5.2. Der Wert einer Option 5.3. Regeln für Optionspreise auf einem arbitragefreien Markt 5.3.1. Regeln für Calls 5.3.2. Regeln für Puts 5.3.3. Die Put Call Parität
Vertical-Spreads Iron Condor Erfolgsaussichten
 www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
Aufgaben Brealey/Myers [2003], Kapitel 20
![Aufgaben Brealey/Myers [2003], Kapitel 20 Aufgaben Brealey/Myers [2003], Kapitel 20](/thumbs/33/16561217.jpg) Folie 0 Quiz: 1, 2, 3, 4, 5, 8, 9, 11, 12, 13, 14 Practice Questions: 2, 3, 4, 5, 6, 8, 9, 11, 13, 14, 15, 17, 18, 21 Challenge Questions: 2 Folie 1 Lösungshinweis zu Quiz 4: Put-Call Parität: Fälligkeit
Folie 0 Quiz: 1, 2, 3, 4, 5, 8, 9, 11, 12, 13, 14 Practice Questions: 2, 3, 4, 5, 6, 8, 9, 11, 13, 14, 15, 17, 18, 21 Challenge Questions: 2 Folie 1 Lösungshinweis zu Quiz 4: Put-Call Parität: Fälligkeit
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können.
 Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Lehrer: Einschreibemethoden
 Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Bedienungsanleitung Rückabwicklungsrechner
 1 Eingaben Zelle C2 Auszahlungsbetrag Hier muss der erste Auszahlungsbetrag eingegeben werden. Weitere Auszahlungen siehe Weiter unten. Zelle C3 Zeitpunkt der Auszahlung Datum der ersten Auszahlung Zelle
1 Eingaben Zelle C2 Auszahlungsbetrag Hier muss der erste Auszahlungsbetrag eingegeben werden. Weitere Auszahlungen siehe Weiter unten. Zelle C3 Zeitpunkt der Auszahlung Datum der ersten Auszahlung Zelle
Orderarten im Wertpapierhandel
 Orderarten im Wertpapierhandel Varianten bei einer Wertpapierkauforder 1. Billigst Sie möchten Ihre Order so schnell wie möglich durchführen. Damit kaufen Sie das Wertpapier zum nächstmöglichen Kurs. Kurs
Orderarten im Wertpapierhandel Varianten bei einer Wertpapierkauforder 1. Billigst Sie möchten Ihre Order so schnell wie möglich durchführen. Damit kaufen Sie das Wertpapier zum nächstmöglichen Kurs. Kurs
Private Banking. Region Ost. Risikomanagement und Ertragsverbesserung durch Termingeschäfte
 Private Banking Region Ost Risikomanagement und Ertragsverbesserung durch Termingeschäfte Ihre Ansprechpartner Deutsche Bank AG Betreuungscenter Derivate Region Ost Vermögensverwaltung Unter den Linden
Private Banking Region Ost Risikomanagement und Ertragsverbesserung durch Termingeschäfte Ihre Ansprechpartner Deutsche Bank AG Betreuungscenter Derivate Region Ost Vermögensverwaltung Unter den Linden
EMIS - Langzeitmessung
 EMIS - Langzeitmessung Every Meter Is Smart (Jeder Zähler ist intelligent) Inhaltsverzeichnis Allgemeines 2 Bedienung 3 Anfangstand eingeben 4 Endstand eingeben 6 Berechnungen 7 Einstellungen 9 Tarife
EMIS - Langzeitmessung Every Meter Is Smart (Jeder Zähler ist intelligent) Inhaltsverzeichnis Allgemeines 2 Bedienung 3 Anfangstand eingeben 4 Endstand eingeben 6 Berechnungen 7 Einstellungen 9 Tarife
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Programmteil Zeiterfassung für Projekt und Mitarbeiter
 Programmteil Zeiterfassung für Projekt und Mitarbeiter Version: 2.01 Datum: 24.02.2004 Modul: Projektverwaltung, Zeiterfassung Programmaufruf: Stammdaten Grunddaten Lohnarten Stammdaten Mitarbeiter Belege
Programmteil Zeiterfassung für Projekt und Mitarbeiter Version: 2.01 Datum: 24.02.2004 Modul: Projektverwaltung, Zeiterfassung Programmaufruf: Stammdaten Grunddaten Lohnarten Stammdaten Mitarbeiter Belege
AZK 1- Freistil. Der Dialog "Arbeitszeitkonten" Grundsätzliches zum Dialog "Arbeitszeitkonten"
 AZK 1- Freistil Nur bei Bedarf werden dafür gekennzeichnete Lohnbestandteile (Stundenzahl und Stundensatz) zwischen dem aktuellen Bruttolohnjournal und dem AZK ausgetauscht. Das Ansparen und das Auszahlen
AZK 1- Freistil Nur bei Bedarf werden dafür gekennzeichnete Lohnbestandteile (Stundenzahl und Stundensatz) zwischen dem aktuellen Bruttolohnjournal und dem AZK ausgetauscht. Das Ansparen und das Auszahlen
DAB Margin Trader. die neue Handelsplattform der DAB bank AG. Margin Trading. DAB Margin Trader 1. die neue Handelsplattform der DAB bank
 DAB Margin Trader AG Margin Trading DAB Margin Trader 1 Inhaltsverzeichnis Inhaltsverzeichnis... 2 1 Einloggen... 3 2 Anforderung mobiletan... 3 3 Einsehen von Details der Devisenpaare... 4 4 Ordereingabe
DAB Margin Trader AG Margin Trading DAB Margin Trader 1 Inhaltsverzeichnis Inhaltsverzeichnis... 2 1 Einloggen... 3 2 Anforderung mobiletan... 3 3 Einsehen von Details der Devisenpaare... 4 4 Ordereingabe
Vertrieb durch: h+f Informatik und Elektrotechnik Washingtonstrasse 32 CH-9400 Rorschach Tel: +41 (0)71 845 45 40 Mobile: +41 (0)79 600 80 57
 ELEKTRONISCHES RESERVIERUNGSSYSTEM Reservierung Version 9.0 Vertrieb durch: h+f Informatik und Elektrotechnik Washingtonstrasse 32 CH-9400 Rorschach Tel: +41 (0)71 845 45 40 Mobile: +41 (0)79 600 80 57
ELEKTRONISCHES RESERVIERUNGSSYSTEM Reservierung Version 9.0 Vertrieb durch: h+f Informatik und Elektrotechnik Washingtonstrasse 32 CH-9400 Rorschach Tel: +41 (0)71 845 45 40 Mobile: +41 (0)79 600 80 57
Tilgungsplan im NTCS Controlling
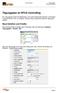 im Der bietet die Möglichkeit, neue oder bestehende Darlehen und Kredite in übersichtlicher Form zu erfassen. Ebenso können gewährte Darlehen dargestellt werden. Neue Darlehen und Kredite Der Einstieg
im Der bietet die Möglichkeit, neue oder bestehende Darlehen und Kredite in übersichtlicher Form zu erfassen. Ebenso können gewährte Darlehen dargestellt werden. Neue Darlehen und Kredite Der Einstieg
Diese Ansicht erhalten Sie nach der erfolgreichen Anmeldung bei Wordpress.
 Anmeldung http://www.ihredomain.de/wp-admin Dashboard Diese Ansicht erhalten Sie nach der erfolgreichen Anmeldung bei Wordpress. Das Dashboard gibt Ihnen eine kurze Übersicht, z.b. Anzahl der Beiträge,
Anmeldung http://www.ihredomain.de/wp-admin Dashboard Diese Ansicht erhalten Sie nach der erfolgreichen Anmeldung bei Wordpress. Das Dashboard gibt Ihnen eine kurze Übersicht, z.b. Anzahl der Beiträge,
Um sich zu registrieren, öffnen Sie die Internetseite www.doodle.de und wählen Sie dort rechts oben
 Doodle Anleitung Konto erstellen Die Registrierung eines Benutzerkontos ist für Umfragen nicht erforderlich. Sollten Sie jedoch öfters Umfragen erstellen, ist dies aus Gründen der Übersicht und Einfachheit
Doodle Anleitung Konto erstellen Die Registrierung eines Benutzerkontos ist für Umfragen nicht erforderlich. Sollten Sie jedoch öfters Umfragen erstellen, ist dies aus Gründen der Übersicht und Einfachheit
2. Im Admin Bereich drücken Sie bitte auf den roten Button Webseite bearbeiten, sodass Sie in den Bearbeitungsbereich Ihrer Homepage gelangen.
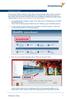 Bildergalerie einfügen Wenn Sie eine Vielzahl an Bildern zu einem Thema auf Ihre Homepage stellen möchten, steht Ihnen bei Schmetterling Quadra das Modul Bildergalerie zur Verfügung. Ihre Kunden können
Bildergalerie einfügen Wenn Sie eine Vielzahl an Bildern zu einem Thema auf Ihre Homepage stellen möchten, steht Ihnen bei Schmetterling Quadra das Modul Bildergalerie zur Verfügung. Ihre Kunden können
Excel Pivot-Tabellen 2010 effektiv
 7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 1)
 1 Lösungshinweise zur Einsendearbeit 1: SS 2012 Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 1) Fristentransformation 50 Punkte Die Bank B gibt im Zeitpunkt t = 0 einen Kredit mit einer Laufzeit
1 Lösungshinweise zur Einsendearbeit 1: SS 2012 Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 1) Fristentransformation 50 Punkte Die Bank B gibt im Zeitpunkt t = 0 einen Kredit mit einer Laufzeit
teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep
 teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Anwendungshinweise zur Anwendung der Soziometrie
 Anwendungshinweise zur Anwendung der Soziometrie Einführung Die Soziometrie ist ein Verfahren, welches sich besonders gut dafür eignet, Beziehungen zwischen Mitgliedern einer Gruppe darzustellen. Das Verfahren
Anwendungshinweise zur Anwendung der Soziometrie Einführung Die Soziometrie ist ein Verfahren, welches sich besonders gut dafür eignet, Beziehungen zwischen Mitgliedern einer Gruppe darzustellen. Das Verfahren
Handbuch. NAFI Online-Spezial. Kunden- / Datenverwaltung. 1. Auflage. (Stand: 24.09.2014)
 Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Bedienungsanleitung für den Online-Shop
 Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Hilfe zur Urlaubsplanung und Zeiterfassung
 Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Stammdatenanlage über den Einrichtungsassistenten
 Stammdatenanlage über den Einrichtungsassistenten Schritt für Schritt zur fertig eingerichteten Hotelverwaltung mit dem Einrichtungsassistenten Bitte bereiten Sie sich, bevor Sie starten, mit der Checkliste
Stammdatenanlage über den Einrichtungsassistenten Schritt für Schritt zur fertig eingerichteten Hotelverwaltung mit dem Einrichtungsassistenten Bitte bereiten Sie sich, bevor Sie starten, mit der Checkliste
Fallbeispiel: Eintragen einer Behandlung
 Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor
 Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
ClubWebMan Veranstaltungskalender
 ClubWebMan Veranstaltungskalender Terminverwaltung geeignet für TYPO3 Version 4. bis 4.7 Die Arbeitsschritte A. Kategorien anlegen B. Veranstaltungsort und Veranstalter anlegen B. Veranstaltungsort anlegen
ClubWebMan Veranstaltungskalender Terminverwaltung geeignet für TYPO3 Version 4. bis 4.7 Die Arbeitsschritte A. Kategorien anlegen B. Veranstaltungsort und Veranstalter anlegen B. Veranstaltungsort anlegen
Geben Sie in dem offenen Suchfeld den Namen Ihrer Einrichtung ein und klicken Sie auf Suchen.
 Erläuterungen zur Online-Pflege im Weiterbildungsportal Die Online-Pflege erlaubt sowohl das Bearbeiten bereits vorhandener Kurse als auch das Anlegen neuer Kurse. Wichtig ist, dass ein Kurs, der an mehreren
Erläuterungen zur Online-Pflege im Weiterbildungsportal Die Online-Pflege erlaubt sowohl das Bearbeiten bereits vorhandener Kurse als auch das Anlegen neuer Kurse. Wichtig ist, dass ein Kurs, der an mehreren
Kurzbeschreibung CIC-Kalkulator
 C.I.C. Software GmbH Kurzbeschreibung CIC-Kalkulator C.I.C. Software GmbH Bajuwarenring 12 82041 Oberhaching Fon +49 89 63839 100 Fax +49 89 63839 101 Mail info@cic-software.de www.cic-software.de Inhaltsübersicht
C.I.C. Software GmbH Kurzbeschreibung CIC-Kalkulator C.I.C. Software GmbH Bajuwarenring 12 82041 Oberhaching Fon +49 89 63839 100 Fax +49 89 63839 101 Mail info@cic-software.de www.cic-software.de Inhaltsübersicht
Kapitel I: Registrierung im Portal
 Kapitel I: Registrierung im Portal Um zu unserem Portal zu gelangen, rufen Sie bitte die folgende Internetseite auf: www.arag-forderungsmanagement.de Bei Ihrem ersten Besuch des ARAG Portals ist es notwendig,
Kapitel I: Registrierung im Portal Um zu unserem Portal zu gelangen, rufen Sie bitte die folgende Internetseite auf: www.arag-forderungsmanagement.de Bei Ihrem ersten Besuch des ARAG Portals ist es notwendig,
Anwendungsbeispiele Buchhaltung
 Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Dokumentation Typo3. tt - news - Nachrichtenmodul
 Dokumentation Typo3 tt - news - Nachrichtenmodul 2 Inhaltsverzeichnis 1.1 Erstellen neuer News Beiträge... 3 1.2 Bearbeiten des Textes... 4 1.3 Einstellen Datum, Archivdatum, Sprache... 5 1.4 Einfügen
Dokumentation Typo3 tt - news - Nachrichtenmodul 2 Inhaltsverzeichnis 1.1 Erstellen neuer News Beiträge... 3 1.2 Bearbeiten des Textes... 4 1.3 Einstellen Datum, Archivdatum, Sprache... 5 1.4 Einfügen
Der Kalender im ipad
 Der Kalender im ipad Wir haben im ipad, dem ipod Touch und dem iphone, sowie auf dem PC in der Cloud einen Kalender. Die App ist voreingestellt, man braucht sie nicht laden. So macht es das ipad leicht,
Der Kalender im ipad Wir haben im ipad, dem ipod Touch und dem iphone, sowie auf dem PC in der Cloud einen Kalender. Die App ist voreingestellt, man braucht sie nicht laden. So macht es das ipad leicht,
Vertreterabrechnung DdD Cowis backoffice
 Vertreterabrechnung DdD Cowis backoffice Seite 1 von 5 Inhaltsverzeichnis Bereich Adressen... 3 Übergeordnete Vertreter... 3 Provisionen... 4 Bereich Aufträge... 4 Seite 2 von 5 Bereich Adressen In der
Vertreterabrechnung DdD Cowis backoffice Seite 1 von 5 Inhaltsverzeichnis Bereich Adressen... 3 Übergeordnete Vertreter... 3 Provisionen... 4 Bereich Aufträge... 4 Seite 2 von 5 Bereich Adressen In der
Arbeitsschritte EAÜ Leistungserbringer Einnahmen erfassen
 Arbeitsschritte EAÜ Leistungserbringer Einnahmen erfassen 1. Das Projekt auswählen Nach dem Anmelden in der Datenbank im Menü [Vorhaben] den Untermenüpunkt [Vorhabenübersicht] wählen. Dort bitte das entsprechende
Arbeitsschritte EAÜ Leistungserbringer Einnahmen erfassen 1. Das Projekt auswählen Nach dem Anmelden in der Datenbank im Menü [Vorhaben] den Untermenüpunkt [Vorhabenübersicht] wählen. Dort bitte das entsprechende
LSF-Anleitung für Studierende
 LSF-Anleitung für Studierende 1. Veranstaltungen Beim Anklicken der Option Veranstaltung finden Sie unter der Navigationsleiste: Vorlesungsverzeichnis Suche nach Veranstaltungen Stundenpläne Stundenpläne
LSF-Anleitung für Studierende 1. Veranstaltungen Beim Anklicken der Option Veranstaltung finden Sie unter der Navigationsleiste: Vorlesungsverzeichnis Suche nach Veranstaltungen Stundenpläne Stundenpläne
So wähle ich die EINE richtige Option aus
 So wähle ich die EINE richtige Option aus Rainer Heißmann, Dresden, 16.01.2016 Experten. Sicherheit. Kompetenz. So wähle ich die EINE richtige Option aus Seite 2 von 18 Geld machen Voltaire (französischer
So wähle ich die EINE richtige Option aus Rainer Heißmann, Dresden, 16.01.2016 Experten. Sicherheit. Kompetenz. So wähle ich die EINE richtige Option aus Seite 2 von 18 Geld machen Voltaire (französischer
E-MAIL VERWALTUNG. Postfächer, Autoresponder, Weiterleitungen, Aliases. http://www.athost.at. Bachstraße 47, 3580 Mödring office@athost.
 E-MAIL VERWALTUNG Postfächer, Autoresponder, Weiterleitungen, Aliases http://www.athost.at Bachstraße 47, 3580 Mödring office@athost.at Loggen Sie sich zunächst unter http://www.athost.at/kundencenter
E-MAIL VERWALTUNG Postfächer, Autoresponder, Weiterleitungen, Aliases http://www.athost.at Bachstraße 47, 3580 Mödring office@athost.at Loggen Sie sich zunächst unter http://www.athost.at/kundencenter
Dow Jones am 13.06.08 im 1-min Chat
 Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Zinsrechner. Bedienungsanleitung
 Zinsrechner Bedienungsanleitung Medcontroller Dragonerstraße 35 30163 Hannover Telefon: 0511 397 0990 kundenservice@medcontroller.de www.medcontroller.de Inhaltsverzeichnis Hintergrund... 2 Nutzungsbedingungen
Zinsrechner Bedienungsanleitung Medcontroller Dragonerstraße 35 30163 Hannover Telefon: 0511 397 0990 kundenservice@medcontroller.de www.medcontroller.de Inhaltsverzeichnis Hintergrund... 2 Nutzungsbedingungen
104 WebUntis -Dokumentation
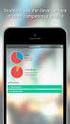 104 WebUntis -Dokumentation 4.1.9.2 Das elektronische Klassenbuch im Betrieb Lehrer Aufruf Melden Sie sich mit Ihrem Benutzernamen und Ihrem Passwort am System an. Unter den aktuellen Tagesmeldungen erscheint
104 WebUntis -Dokumentation 4.1.9.2 Das elektronische Klassenbuch im Betrieb Lehrer Aufruf Melden Sie sich mit Ihrem Benutzernamen und Ihrem Passwort am System an. Unter den aktuellen Tagesmeldungen erscheint
Musterlösung Übung 3
 Musterlösung Übung 3 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Musterlösung Übung 3 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Aufgaben zur Vorlesung Finanzmanagement
 Aufgaben zur Vorlesung Finanzmanagement B. rke FH Gelsenkirchen, Abteilung Bocholt February 4, 006 Aufgabenblatt: "Bewertung von Optionen" 1 Lösungshinweise 1 uropean Put Option Zeichnen Sie den einer
Aufgaben zur Vorlesung Finanzmanagement B. rke FH Gelsenkirchen, Abteilung Bocholt February 4, 006 Aufgabenblatt: "Bewertung von Optionen" 1 Lösungshinweise 1 uropean Put Option Zeichnen Sie den einer
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Outlook 2000 Thema - Archivierung
 interne Schulungsunterlagen Outlook 2000 Thema - Inhaltsverzeichnis 1. Allgemein... 3 2. Grundeinstellungen für die Auto in Outlook... 3 3. Auto für die Postfach-Ordner einstellen... 4 4. Manuelles Archivieren
interne Schulungsunterlagen Outlook 2000 Thema - Inhaltsverzeichnis 1. Allgemein... 3 2. Grundeinstellungen für die Auto in Outlook... 3 3. Auto für die Postfach-Ordner einstellen... 4 4. Manuelles Archivieren
Stundenerfassung Version 1.8
 Stundenerfassung Version 1.8 Anleitung Überstunden Ein Modul der Plusversion 2008 netcadservice GmbH netcadservice GmbH Augustinerstraße 3 D-83395 Freilassing Dieses Programm ist urheberrechtlich geschützt.
Stundenerfassung Version 1.8 Anleitung Überstunden Ein Modul der Plusversion 2008 netcadservice GmbH netcadservice GmbH Augustinerstraße 3 D-83395 Freilassing Dieses Programm ist urheberrechtlich geschützt.
Aufruf der Buchungssystems über die Homepage des TC-Bamberg
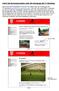 Aufruf der Buchungssystems über die Homepage des TC-Bamberg Das Online-Buchungssystem erreichen Sie einfach über die Homepage des TC-Bamberg (www.tennis-club-bamberg.de).über den Link (siehe Bild 1) gelangen
Aufruf der Buchungssystems über die Homepage des TC-Bamberg Das Online-Buchungssystem erreichen Sie einfach über die Homepage des TC-Bamberg (www.tennis-club-bamberg.de).über den Link (siehe Bild 1) gelangen
QR-FUNKTION. Informationen über zu erledigende Aufgaben an das Reinigungspersonal senden.
 QR-FUNKTION Informationen über zu erledigende Aufgaben an das Reinigungspersonal senden. Informationen über erledigte Aufgaben vom Reinigungspersonal erhalten. Verwaltung regelmäßiger Aufgaben Der Hauptzweck
QR-FUNKTION Informationen über zu erledigende Aufgaben an das Reinigungspersonal senden. Informationen über erledigte Aufgaben vom Reinigungspersonal erhalten. Verwaltung regelmäßiger Aufgaben Der Hauptzweck
Kurze Anleitung zum Guthaben-Aufladen bei. www.blau.de
 Kurze Anleitung zum Guthaben-Aufladen bei www.blau.de Seite 1 von 8 Inhaltsverzeichnis 1 blau.de aufrufen... 3 2 Ihr Konto bei blau.de... 4 2.1 Aufladen über das Internet... 5 2.2 Aufladen direkt am Mobiltelefon
Kurze Anleitung zum Guthaben-Aufladen bei www.blau.de Seite 1 von 8 Inhaltsverzeichnis 1 blau.de aufrufen... 3 2 Ihr Konto bei blau.de... 4 2.1 Aufladen über das Internet... 5 2.2 Aufladen direkt am Mobiltelefon
1 Einleitung. Lernziele. automatische Antworten bei Abwesenheit senden. Einstellungen für automatische Antworten Lerndauer. 4 Minuten.
 1 Einleitung Lernziele automatische Antworten bei Abwesenheit senden Einstellungen für automatische Antworten Lerndauer 4 Minuten Seite 1 von 18 2 Antworten bei Abwesenheit senden» Outlook kann während
1 Einleitung Lernziele automatische Antworten bei Abwesenheit senden Einstellungen für automatische Antworten Lerndauer 4 Minuten Seite 1 von 18 2 Antworten bei Abwesenheit senden» Outlook kann während
e LEARNING Kurz-Anleitung zum Erstellen eines Wikis 1. Wiki erstellen
 Kurz-Anleitung zum Erstellen eines Wikis Die Aktivität Wiki verschafft Ihnen die Möglichkeit, Wissen zu sammeln und zu strukturieren. Dabei können Sie die Teilnehmer Ihres Kurses an der Erstellung des
Kurz-Anleitung zum Erstellen eines Wikis Die Aktivität Wiki verschafft Ihnen die Möglichkeit, Wissen zu sammeln und zu strukturieren. Dabei können Sie die Teilnehmer Ihres Kurses an der Erstellung des
Musterlösung Übung 2
 Musterlösung Übung 2 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Musterlösung Übung 2 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
GE Capital Equipment Financing. GE Capital Leasing-Tool Schulungsunterlagen
 GE Capital Equipment Financing GE Capital Leasing-Tool Schulungsunterlagen Sie befinden sich im ALSO Online-Shop (2 Objekte liegen in Ihrem Merkzettel) Wechsel vom ALSO Online-Shop zum GE Capital Leasingantrag:
GE Capital Equipment Financing GE Capital Leasing-Tool Schulungsunterlagen Sie befinden sich im ALSO Online-Shop (2 Objekte liegen in Ihrem Merkzettel) Wechsel vom ALSO Online-Shop zum GE Capital Leasingantrag:
Hilfedatei der Oden$-Börse Stand Juni 2014
 Hilfedatei der Oden$-Börse Stand Juni 2014 Inhalt 1. Einleitung... 2 2. Die Anmeldung... 2 2.1 Die Erstregistrierung... 3 2.2 Die Mitgliedsnummer anfordern... 4 3. Die Funktionen für Nutzer... 5 3.1 Arbeiten
Hilfedatei der Oden$-Börse Stand Juni 2014 Inhalt 1. Einleitung... 2 2. Die Anmeldung... 2 2.1 Die Erstregistrierung... 3 2.2 Die Mitgliedsnummer anfordern... 4 3. Die Funktionen für Nutzer... 5 3.1 Arbeiten
1.5 Umsatzsteuervoranmeldung
 1.5 Umsatzsteuervoranmeldung In diesem Abschnitt werden die Arbeitschritte zum Erstellen des MwSt Abrechnungsschemas erläutert. Es wird gezeigt, wie die Werte für die monatliche Umsatzsteuervoranmeldung
1.5 Umsatzsteuervoranmeldung In diesem Abschnitt werden die Arbeitschritte zum Erstellen des MwSt Abrechnungsschemas erläutert. Es wird gezeigt, wie die Werte für die monatliche Umsatzsteuervoranmeldung
Optionen am Beispiel erklärt
 Optionen am Beispiel erklärt Long Call Short Call Long Put Short Put von Jens Kürschner Grundlagen 2 Definition einer Option Eine Option bezeichnet in der Wirtschaft ein Recht, eine bestimmte Sache zu
Optionen am Beispiel erklärt Long Call Short Call Long Put Short Put von Jens Kürschner Grundlagen 2 Definition einer Option Eine Option bezeichnet in der Wirtschaft ein Recht, eine bestimmte Sache zu
Ablauf Bestellungen im Radiokiosk von Radio Central und Radio Eviva
 Ablauf Bestellungen im Radiokiosk von Radio Central und Radio Eviva 1 2 1. Mit einem Klick auf den Einkaufs-Button (Einkaufswagen) beim Produkt wird diese Auswahl 2. in den Warenkorb (rechte Seite) eingefügt.
Ablauf Bestellungen im Radiokiosk von Radio Central und Radio Eviva 1 2 1. Mit einem Klick auf den Einkaufs-Button (Einkaufswagen) beim Produkt wird diese Auswahl 2. in den Warenkorb (rechte Seite) eingefügt.
Ihr Ideen- & Projektmanagement-Tool
 Planungsbox 2.9 Ihr Ideen- & Projektmanagement-Tool Planungsbox verknüpft Notizen, Termine, Dateien, email- & Internetadressen, ToDo-Listen und Auswertungen Planungsbox verwaltet ToDo-Listen, Termine und
Planungsbox 2.9 Ihr Ideen- & Projektmanagement-Tool Planungsbox verknüpft Notizen, Termine, Dateien, email- & Internetadressen, ToDo-Listen und Auswertungen Planungsbox verwaltet ToDo-Listen, Termine und
Datenerfassung (mehrere Merkmale) 1/5
 Datenerfassung (mehrere Merkmale) 1/5 Ziel: Ziel dieser Aufgabe ist es, die Möglichkeiten der linearen Transformation, der Merkmalsverknüpfung und des Erstellens zusätzlicher Merkmale kennen zu lernen.
Datenerfassung (mehrere Merkmale) 1/5 Ziel: Ziel dieser Aufgabe ist es, die Möglichkeiten der linearen Transformation, der Merkmalsverknüpfung und des Erstellens zusätzlicher Merkmale kennen zu lernen.
Erfolgreich handeln mit Optionen
 Erfolgreich handeln mit Optionen INHALT 01 GRUNDLAGEN VON 05 OPTIONEN 02 GRIECHEN 13 Delta 14 Gamma 18 Vega 21 Theta 24 03 VOLATILITÄT 27 Historische Volatilität 29 Implizite Volatilität 31 Volatility
Erfolgreich handeln mit Optionen INHALT 01 GRUNDLAGEN VON 05 OPTIONEN 02 GRIECHEN 13 Delta 14 Gamma 18 Vega 21 Theta 24 03 VOLATILITÄT 27 Historische Volatilität 29 Implizite Volatilität 31 Volatility
Manager. von Peter Pfeifer, Waltraud Pfeifer, Burkhard Münchhagen. Spielanleitung
 Manager von Peter Pfeifer, Waltraud Pfeifer, Burkhard Münchhagen Spielanleitung Manager Ein rasantes Wirtschaftsspiel für 3 bis 6 Spieler. Das Glück Ihrer Firma liegt in Ihren Händen! Bestehen Sie gegen
Manager von Peter Pfeifer, Waltraud Pfeifer, Burkhard Münchhagen Spielanleitung Manager Ein rasantes Wirtschaftsspiel für 3 bis 6 Spieler. Das Glück Ihrer Firma liegt in Ihren Händen! Bestehen Sie gegen
Beispiel Shop-Eintrag Ladenlokal & Online-Shop im Verzeichnis www.wir-lieben-shops.de 1
 Beispiel Shop-Eintrag Ladenlokal & Online-Shop. Als Händler haben Sie beim Shop-Verzeichnis wir-lieben-shops.de die Möglichkeit einen oder mehrere Shop- Einträge zu erstellen. Es gibt 3 verschiedene Typen
Beispiel Shop-Eintrag Ladenlokal & Online-Shop. Als Händler haben Sie beim Shop-Verzeichnis wir-lieben-shops.de die Möglichkeit einen oder mehrere Shop- Einträge zu erstellen. Es gibt 3 verschiedene Typen
Anleitung zur Daten zur Datensicherung und Datenrücksicherung. Datensicherung
 Anleitung zur Daten zur Datensicherung und Datenrücksicherung Datensicherung Es gibt drei Möglichkeiten der Datensicherung. Zwei davon sind in Ges eingebaut, die dritte ist eine manuelle Möglichkeit. In
Anleitung zur Daten zur Datensicherung und Datenrücksicherung Datensicherung Es gibt drei Möglichkeiten der Datensicherung. Zwei davon sind in Ges eingebaut, die dritte ist eine manuelle Möglichkeit. In
Folgeanleitung für Fachlehrer
 1. Das richtige Halbjahr einstellen Folgeanleitung für Fachlehrer Stellen sie bitte zunächst das richtige Schul- und Halbjahr ein. Ist das korrekte Schul- und Halbjahr eingestellt, leuchtet die Fläche
1. Das richtige Halbjahr einstellen Folgeanleitung für Fachlehrer Stellen sie bitte zunächst das richtige Schul- und Halbjahr ein. Ist das korrekte Schul- und Halbjahr eingestellt, leuchtet die Fläche
Zimmertypen. Zimmertypen anlegen
 Zimmertypen anlegen Hier legen Sie Ihre Zimmer an, damit sie auf der Homepage dargestellt werden und online buchbar gemacht werden können. Wobei wir ausdrücklich darauf hinweisen möchten, dass es ganz
Zimmertypen anlegen Hier legen Sie Ihre Zimmer an, damit sie auf der Homepage dargestellt werden und online buchbar gemacht werden können. Wobei wir ausdrücklich darauf hinweisen möchten, dass es ganz
Funktionsbeschreibung. Lieferantenbewertung. von IT Consulting Kauka GmbH
 Funktionsbeschreibung Lieferantenbewertung von IT Consulting Kauka GmbH Stand 16.02.2010 odul LBW Das Modul LBW... 3 1. Konfiguration... 4 1.1 ppm... 4 1.2 Zertifikate... 5 1.3 Reklamationsverhalten...
Funktionsbeschreibung Lieferantenbewertung von IT Consulting Kauka GmbH Stand 16.02.2010 odul LBW Das Modul LBW... 3 1. Konfiguration... 4 1.1 ppm... 4 1.2 Zertifikate... 5 1.3 Reklamationsverhalten...
Investition und Finanzierung
 Tutorium Investition und Finanzierung Sommersemester 2014 Investition und Finanzierung Tutorium Folie 1 Inhaltliche Gliederung des 3. Tutorium Investition und Finanzierung Tutorium Folie 2 Aufgabe 1: Zwischenform
Tutorium Investition und Finanzierung Sommersemester 2014 Investition und Finanzierung Tutorium Folie 1 Inhaltliche Gliederung des 3. Tutorium Investition und Finanzierung Tutorium Folie 2 Aufgabe 1: Zwischenform
Der naldo-offline-handyfahrplan
 Der naldo-offline-handyfahrplan Erste Schritte mit dem neuen naldo-offline-handyfahrplan Bedienungsanleitung Inhaltsverzeichnis: 1. Erster Programmstart 2. Die Programmbedienung 3. Favoriten 4. Meine Fahrten
Der naldo-offline-handyfahrplan Erste Schritte mit dem neuen naldo-offline-handyfahrplan Bedienungsanleitung Inhaltsverzeichnis: 1. Erster Programmstart 2. Die Programmbedienung 3. Favoriten 4. Meine Fahrten
Kostenstellen verwalten. Tipps & Tricks
 Tipps & Tricks INHALT SEITE 1.1 Kostenstellen erstellen 3 13 1.3 Zugriffsberechtigungen überprüfen 30 2 1.1 Kostenstellen erstellen Mein Profil 3 1.1 Kostenstellen erstellen Kostenstelle(n) verwalten 4
Tipps & Tricks INHALT SEITE 1.1 Kostenstellen erstellen 3 13 1.3 Zugriffsberechtigungen überprüfen 30 2 1.1 Kostenstellen erstellen Mein Profil 3 1.1 Kostenstellen erstellen Kostenstelle(n) verwalten 4
Hin zum perfekten Preis
 Hin zum perfekten Preis Ein Blick auf den Preis entscheidet oft darüber, ob ein Besucher Ihres Inserats sich weiterhin für Ihr Angebot interessiert oder nicht. Entscheidend ist nicht nur die Höhe der angegebenen
Hin zum perfekten Preis Ein Blick auf den Preis entscheidet oft darüber, ob ein Besucher Ihres Inserats sich weiterhin für Ihr Angebot interessiert oder nicht. Entscheidend ist nicht nur die Höhe der angegebenen
XONTRO Newsletter. Kreditinstitute. Nr. 18
 XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
20 Modul Lager und Inventur
 20 Modul Lager und Inventur Alle Lagerbewegungen (Verkauf, Einkauf, Umbuchungen, Inventur) werden aufgezeichnet um die Lagerstände von Artikeln nachvollziehbar zu machen. Das Modul ist ab Version Standard
20 Modul Lager und Inventur Alle Lagerbewegungen (Verkauf, Einkauf, Umbuchungen, Inventur) werden aufgezeichnet um die Lagerstände von Artikeln nachvollziehbar zu machen. Das Modul ist ab Version Standard
Support-Ticket-System. - Anleitung zur Benutzung -
 Support-Ticket-System - Anleitung zur Benutzung - Anschrift Netzwerkservice Schmidt Münsterstr. 170 44534 Lünen-Wethmar Telefon (02306) 308380-99 Telefax (02306) 308380-44 Mobil (0178) 71 88 344 ICQ 173452919
Support-Ticket-System - Anleitung zur Benutzung - Anschrift Netzwerkservice Schmidt Münsterstr. 170 44534 Lünen-Wethmar Telefon (02306) 308380-99 Telefax (02306) 308380-44 Mobil (0178) 71 88 344 ICQ 173452919
Dokumentation Bonuspunkteverwaltung. Verfasser(in) / Autor: Check it Consulting
 Dokumentation Bonuspunkteverwaltung Verfasser(in) / Autor: Check it Consulting Stand 05/2006 1 In Jack können die erreichten Bonuspunkte je nach Vorgabe und Bedarf des Büros automatisch berechnet werden.
Dokumentation Bonuspunkteverwaltung Verfasser(in) / Autor: Check it Consulting Stand 05/2006 1 In Jack können die erreichten Bonuspunkte je nach Vorgabe und Bedarf des Büros automatisch berechnet werden.
Fotostammtisch-Schaumburg
 Der Anfang zur Benutzung der Web Seite! Alles ums Anmelden und Registrieren 1. Startseite 2. Registrieren 2.1 Registrieren als Mitglied unser Stammtischseite Wie im Bild markiert jetzt auf das Rote Register
Der Anfang zur Benutzung der Web Seite! Alles ums Anmelden und Registrieren 1. Startseite 2. Registrieren 2.1 Registrieren als Mitglied unser Stammtischseite Wie im Bild markiert jetzt auf das Rote Register
Senkung des technischen Zinssatzes und des Umwandlungssatzes
 Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Teaser-Bilder erstellen mit GIMP. Bildbearbeitung mit GIMP 1
 Teaser-Bilder erstellen mit GIMP 08.08.2014 Bildbearbeitung mit GIMP 1 Auf den folgenden Seiten werden die wichtigsten Funktionen von GIMP gezeigt, welche zur Erstellung von Bildern für die Verwendung
Teaser-Bilder erstellen mit GIMP 08.08.2014 Bildbearbeitung mit GIMP 1 Auf den folgenden Seiten werden die wichtigsten Funktionen von GIMP gezeigt, welche zur Erstellung von Bildern für die Verwendung
Benutzerhandbuch. Leitfaden zur Benutzung der Anwendung für sicheren Dateitransfer.
 Benutzerhandbuch Leitfaden zur Benutzung der Anwendung für sicheren Dateitransfer. 1 Startseite Wenn Sie die Anwendung starten, können Sie zwischen zwei Möglichkeiten wählen 1) Sie können eine Datei für
Benutzerhandbuch Leitfaden zur Benutzung der Anwendung für sicheren Dateitransfer. 1 Startseite Wenn Sie die Anwendung starten, können Sie zwischen zwei Möglichkeiten wählen 1) Sie können eine Datei für
Anleitung zum LPI ATP Portal www.lpi-training.eu
 Anleitung zum LPI ATP Portal www.lpi-training.eu Version 1.0 vom 01.09.2013 Beschreibung des Anmeldevorgangs und Erklärung der einzelnen Menüpunkte. Anmeldevorgang: 1. Gehen Sie auf die Seite http://www.lpi-training.eu/.
Anleitung zum LPI ATP Portal www.lpi-training.eu Version 1.0 vom 01.09.2013 Beschreibung des Anmeldevorgangs und Erklärung der einzelnen Menüpunkte. Anmeldevorgang: 1. Gehen Sie auf die Seite http://www.lpi-training.eu/.
XONTRO Newsletter. Makler. Nr. 16
 XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
Ihre Interessentendatensätze bei inobroker. 1. Interessentendatensätze
 Ihre Interessentendatensätze bei inobroker Wenn Sie oder Ihre Kunden die Prozesse von inobroker nutzen, werden Interessentendatensätze erzeugt. Diese können Sie direkt über inobroker bearbeiten oder mit
Ihre Interessentendatensätze bei inobroker Wenn Sie oder Ihre Kunden die Prozesse von inobroker nutzen, werden Interessentendatensätze erzeugt. Diese können Sie direkt über inobroker bearbeiten oder mit
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Handbuch. Anlegen von Vermittlern, Gruppen und Anwendern. 1. Auflage. (Stand: 24.09.2014)
 Handbuch NAFI Online-Spezial Anlegen von Vermittlern, Gruppen und Anwendern 1. Auflage (Stand: 24.09.2014) Copyright 2015 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung...
Handbuch NAFI Online-Spezial Anlegen von Vermittlern, Gruppen und Anwendern 1. Auflage (Stand: 24.09.2014) Copyright 2015 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung...
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
2.1 Erstellung einer Gutschrift über den vollen Rechnungsbetrag
 1. Einführung Manchmal ist es notwendig, dem Kunden eine Gutschrift zu einer bestimmten Rechnung, über einzelne Positionen oder auch völlig frei von einer Basis-Rechnung zu erstellen. Die verschiedenen
1. Einführung Manchmal ist es notwendig, dem Kunden eine Gutschrift zu einer bestimmten Rechnung, über einzelne Positionen oder auch völlig frei von einer Basis-Rechnung zu erstellen. Die verschiedenen
FORUM HANDREICHUNG (STAND: AUGUST 2013)
 FORUM HANDREICHUNG (STAND: AUGUST 2013) Seite 2, Forum Inhalt Ein Forum anlegen... 3 Forumstypen... 4 Beiträge im Forum schreiben... 5 Beiträge im Forum beantworten... 6 Besondere Rechte der Leitung...
FORUM HANDREICHUNG (STAND: AUGUST 2013) Seite 2, Forum Inhalt Ein Forum anlegen... 3 Forumstypen... 4 Beiträge im Forum schreiben... 5 Beiträge im Forum beantworten... 6 Besondere Rechte der Leitung...
Monitoring-Service Anleitung
 Anleitung 1. Monitoring in CrefoDirect Wie kann Monitoring über CrefoDirect bestellt werden? Bestellung von Monitoring beim Auskunftsabruf Beim Auskunftsabruf kann das Monitoring direkt mitbestellt werden.
Anleitung 1. Monitoring in CrefoDirect Wie kann Monitoring über CrefoDirect bestellt werden? Bestellung von Monitoring beim Auskunftsabruf Beim Auskunftsabruf kann das Monitoring direkt mitbestellt werden.
Kurzanleitung MAN E-Learning (WBT)
 Kurzanleitung MAN E-Learning (WBT) Um Ihr gebuchtes E-Learning zu bearbeiten, starten Sie bitte das MAN Online- Buchungssystem (ICPM / Seminaris) unter dem Link www.man-academy.eu Klicken Sie dann auf
Kurzanleitung MAN E-Learning (WBT) Um Ihr gebuchtes E-Learning zu bearbeiten, starten Sie bitte das MAN Online- Buchungssystem (ICPM / Seminaris) unter dem Link www.man-academy.eu Klicken Sie dann auf
Kleines Handbuch zur Fotogalerie der Pixel AG
 1 1. Anmelden an der Galerie Um mit der Galerie arbeiten zu können muss man sich zuerst anmelden. Aufrufen der Galerie entweder über die Homepage (www.pixel-ag-bottwartal.de) oder über den direkten Link
1 1. Anmelden an der Galerie Um mit der Galerie arbeiten zu können muss man sich zuerst anmelden. Aufrufen der Galerie entweder über die Homepage (www.pixel-ag-bottwartal.de) oder über den direkten Link
Anleitung für den Zugriff auf Mitgliederdateien der AG-KiM
 Anleitung für den Zugriff auf Mitgliederdateien der AG-KiM Hinweise: - Dies ist eine schrittweise Anleitung um auf den Server der Ag-Kim zuzugreifen. Hierbei können Dateien ähnlich wie bei Dropbox hoch-
Anleitung für den Zugriff auf Mitgliederdateien der AG-KiM Hinweise: - Dies ist eine schrittweise Anleitung um auf den Server der Ag-Kim zuzugreifen. Hierbei können Dateien ähnlich wie bei Dropbox hoch-
