s p f Σ p f S p f, also auch für jede Folge (p n ) n N0 von Partitionen, für die die Feinheit gegen 0 geht.
|
|
|
- Regina Schubert
- vor 5 Jahren
- Abrufe
Transkript
1 Satz: Äquivalenz von Riemann- und Darboux-Integral f : [a, b] R. Dann sind äquivalent: (a) f Riemann-integrierbar. (b) f beschränkt und Darbouxintegrierbar. Gilt (a) oder (b), so ist I(f) = Sf = sf. Beweis: einfacher ist (b) (a) : Für alle Partitionen p von [a, b] gilt: s p f Σ p f S p f, also auch für jede Folge (p n ) n N0 von Partitionen, für die die Feinheit gegen 0 geht. Damit gilt: lim n s p n f = lim Σ n pn f = lim S n pn f. Folglich ist f Riemann-integrierbar und I(f) = Sf = sf. (a) (b) : Vorab: f Riemannintegrierbar f beschränkt.
2 Es reicht, zu zeigen: S p f und s p f sind durch Riemann-Summen Σ p f beliebig genau approximierbar. Da f Riemannintegrierbar ist, ist dann Sf = sf. Wir zeigen: S p f ist durch Riemann- Summen Σ p f beliebig genau approximierbar. Sei ε > 0 vorgegeben. Zu zeigen ist: Zu der Partition p gibt es eine Riemann-Summe Σ p f mit S p f Σ p f < ε. Einfach wäre es, wenn für k n sup f(x) = x [x k,x k+1 ] Tafelskizze max f(x) x [x k,x k+1 ] Für jede Partition p von [a, b] gilt: Für jedes ϕ > 0 gibt es in [t k, t k+1 ] eine Stützstelle x k mit sup f(x) f(x k ) < ϕ. x [x k,x k+1 ] (Def. des Supremums)
3 Wähle ϕ so, dass ϕ (b a) < ε. Dann ist S p f Σ p f = = k n(t k+1 t k ) ( sup f(x) f(x k )) < x [x k,x k+1 ] < k n(t k+1 t k ) ϕ = (b a) ϕ < ε Bei Partitionen werden die Stützpunkte oft nicht gebraucht. Daher: Def.: Ist a = t 0 t 1... t n+1 = b, so heißt p := (t k ) k n eine (stützpunktfreie) Partition von [a, b]. Jordan-Inhalt ebener Flächenstücke: Für jedes δ > 0 kann man R 2 pflastern mit δ-quadraten, mit Mengen Q der Gestalt: Q = [mδ, (m + 1)δ] [nδ, (n + 1)δ] mit ganzen Zahlen m und n.
4 Ad-hoc-Sprechweise: Für jedes beschränkte P R 2 sei N(P ) die Anzahl aller δ-quadrate Q mit Q P und n(p ) die Anzahl aller δ-quadrate Q mit Q P. Dann ist n(p ) N(P ) N. Def.: Sei P R 2 beschränkt. J(P ) := inf δ>0 (δ2 N(P )) j(p ) := sup(δ 2 n(p )) δ>0 J(P )... äußerer Jordan-Inhalt von P j(p )... innerer Jordan-Inhalt von P Ist J(P ) = j(p ), so heißt P Jordanmessbar und J(P ) = j(p ) der Jordan- Inhalt von P. Ohne Beweis: Die Definition ist unabhängig vom kartesischen Koordinatensystem in der Ebene.
5 Satz: Sei f : [a, b] R beschränkt mit f(x) 0 für alle x [a, b]. Sei P := {(x, y) R 2 : a x b, 0 y f(x)}. Dann sind äquivalent: (a) f ist Riemann-integrierbar. (b) P ist Jordan-messbar. Gilt (a) oder (b), so ist I(f) = J(P ). Bew.: aus Zeitgründen ohne
6 2 Untersuchung des Integrals Integrierbare Funktionen Zu Treppenfunktionen: Aus Analysis 1 kennen wir Treppenfunktionen. Aus dem Satz über die Äquivalenz von Riemann- und Darboux-Integrierbarkeit entnehmen wir: Satz: Treppenfunktionen und Riemann-Integral Sei f : [a, b] R. Dann sind äquivalent: (a) f ist Riemann-integrierbar. (b) Für alle ε > 0 gibt es Treppenfunktionen g und h auf [a, b] mit g f h und I(h g) < ε. In Analysis 1 wurde das Integral für Regelfunktionen eingeführt. Regelfunktionen sind solche Funktionen, die durch Treppenfunktionen gleichmäßig approximiert werden können.
7 (Das ist eine Formulierung ohne Verwendung von Banachräumen.) Das führt auf die Fragen: (1) Ist jede Regelfunktion Riemannintegrierbar? (2) Ist jede Riemann-integrierbare Funktion eine Regelfunktion? Der letzte Satz beantwortet diese Fragen nicht. Er besagt: Jede Riemannintegrierbare Funktion f lässt sich durch Treppenfunktionen so annähern, dass das Integral über der Treppenfunktion das Integral über f beliebig genau annähert. Satz: Jede Regelfunktion ist Riemannintegrierbar. Bew.: Das ist Aufgabe H06 von Blatt 02.
8 Stetige Funktionen: Satz: (Integrierbarkeit stetiger Funktionen) Vor.: f : [a, b] R stetig. Beh.: f ist gleichmäßig durch Treppenfunktionen approximierbar, also Riemannintegrierbar. Bew.:... Def.: (stückweise stetig) f : [a, b] R heißt stückweise stetig, falls gilt: Es gibt eine Partition p von [a, b], so dass für k n gilt: (a) f ]t k, t k+1 [ ist stetig. (b) lim f(x) und x t k,x>t k existieren. lim f(x) x t k+1,x<t k+1 Korollar: (Integrierbarkeit stückweise stetiger Funktionen) Vor.: f : [a, b] R stückweise stetig. Beh.: f ist gleichmäßig durch Treppenfunktionen approximierbar, also Riemannintegrierbar.
Analysis II (FS 2015): MEHRFACHE INTEGRALE
 Analysis II (FS 2015): MEHRFACHE INTEGRALE Dietmar A. Salamon ETH-Zürich 27. April 2015 Zusammenfassung Das Ziel dieses Manuskriptes ist es, das Riemannsche Integral einer Funktion von mehreren Variablen
Analysis II (FS 2015): MEHRFACHE INTEGRALE Dietmar A. Salamon ETH-Zürich 27. April 2015 Zusammenfassung Das Ziel dieses Manuskriptes ist es, das Riemannsche Integral einer Funktion von mehreren Variablen
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Stetige Funktionen. Definition. Seien (X, d) und (Y, D) metrische Räume und f : X Y eine Abbildung. i) f heißt stetig in x 0 (x 0 D(f)), wenn
 Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
3. Übungsblatt - Lösungsskizzen. so, dass f tatsächlich eine Wahrscheinlichkeitsdichte
 Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
1.3 Zufallsvariablen
 1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
Serie 5 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
2 Allgemeine Integrationstheorie
 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
Definition 3.1. Sei A X. Unter einer offenen Überdeckung von A versteht man eine Familie (U i ) i I offener Mengen U i X mit U i
 3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Unterricht 13: Wiederholung.
 , 1 I Unterricht 13: Wiederholung. Erinnerungen: Die kleinen Übungen nden diese Woche statt. Zur Prüfung müssen Sie Lichtbildausweis (Personalausweis oder Reisepass) Studierendenausweis mitbringen. I.1
, 1 I Unterricht 13: Wiederholung. Erinnerungen: Die kleinen Übungen nden diese Woche statt. Zur Prüfung müssen Sie Lichtbildausweis (Personalausweis oder Reisepass) Studierendenausweis mitbringen. I.1
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung
 Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
6 Räume integrierbarer Funktionen
 $Id: L.tex,v 1.5 2012/01/19 15:07:43 hk Ex $ $Id: green.tex,v 1.3 2012/01/19 15:18:26 hk Ex hk $ 6 Räume integrierbarer Funktionen In der letzten Sitzung hatten wir die sogenannte L -Norm ( 1/ f := f(x)
$Id: L.tex,v 1.5 2012/01/19 15:07:43 hk Ex $ $Id: green.tex,v 1.3 2012/01/19 15:18:26 hk Ex hk $ 6 Räume integrierbarer Funktionen In der letzten Sitzung hatten wir die sogenannte L -Norm ( 1/ f := f(x)
Lösung zum Tutorium für Topologie und Differentialrechnung mehrerer Variablen SS y. Mit A ist der Flächeninhalt des von
 Blatt Nr. Markus Nöth Lösung zum Tutorium für Topologie und Differentialrechnung mehrerer Variablen SS 1 Aufgabe 1 1 8 6 X w - 6 8 Abbildung 1: Cauchy-Schwarz-Ungl. A In der nebenstehenden Graphik sind
Blatt Nr. Markus Nöth Lösung zum Tutorium für Topologie und Differentialrechnung mehrerer Variablen SS 1 Aufgabe 1 1 8 6 X w - 6 8 Abbildung 1: Cauchy-Schwarz-Ungl. A In der nebenstehenden Graphik sind
Wiederholungsklausur zur Analysis I
 Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
53 Die Parsevalsche Gleichung
 53 Die Parsevalsche Gleichung 53 Die Parsevalsche Gleichung 5 53. Skalarprodukte auf Räumen quadratintegrierbarer Funktionen. a) Die Orthogonalitätsrelationen (5.5) legen die Interpretation des Ausdrucks
53 Die Parsevalsche Gleichung 53 Die Parsevalsche Gleichung 5 53. Skalarprodukte auf Räumen quadratintegrierbarer Funktionen. a) Die Orthogonalitätsrelationen (5.5) legen die Interpretation des Ausdrucks
Kapitel A. Konstruktion und Eigenschaften von Integralen
 Kapitel A Konstruktion und Eigenschaften von Integralen Inhalt dieses Kapitels A000 Wie misst man Flächen- und Rauminhalt? Absolut integrierbare Funktionen Integration: Theorie und Anwendung A001 Bildquelle:
Kapitel A Konstruktion und Eigenschaften von Integralen Inhalt dieses Kapitels A000 Wie misst man Flächen- und Rauminhalt? Absolut integrierbare Funktionen Integration: Theorie und Anwendung A001 Bildquelle:
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
4 Differenzierbarkeit einer konjugierten Funktion
 4 Differenzierbarkeit einer konjugierten Funktion (Eingereicht von Corinna Vits) 4.1 Differenzierbarkeit 1.Ordnung Theorem 4.1.1: Sei f ConvR n strikt konvex. Dann ist int dom und f ist stetig differenzierbar
4 Differenzierbarkeit einer konjugierten Funktion (Eingereicht von Corinna Vits) 4.1 Differenzierbarkeit 1.Ordnung Theorem 4.1.1: Sei f ConvR n strikt konvex. Dann ist int dom und f ist stetig differenzierbar
Das Lebesgue-Integral
 Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Topologische Grundbegriffe II. Inhaltsverzeichnis
 Vortrag zum Seminar zur Analysis, 03.05.2010 Dennis Joswig, Florian Goy Aufbauend auf den Resultaten des Vortrages Topologische Grundbegriffe I untersuchen wir weitere topologische Eigenschaften von metrischen
Vortrag zum Seminar zur Analysis, 03.05.2010 Dennis Joswig, Florian Goy Aufbauend auf den Resultaten des Vortrages Topologische Grundbegriffe I untersuchen wir weitere topologische Eigenschaften von metrischen
Wiederholungsklausur zur Analysis I
 Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Zusammenfassung Analysis 2
 Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
10 Der Satz von Radon-Nikodym
 uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
Schwache Konvergenz von Wahrscheinlichkeitsmaßen
 Schwache Konvergenz von Wahrscheinlichkeitsmaßen 6. Juli 2010 Inhaltsverzeichnis 1 Definition 2 3 Lindeberg-Bedingung Interpretation Definition Motivation (Konvergenz von Wahrscheinlichkeitsmaßen) Sind
Schwache Konvergenz von Wahrscheinlichkeitsmaßen 6. Juli 2010 Inhaltsverzeichnis 1 Definition 2 3 Lindeberg-Bedingung Interpretation Definition Motivation (Konvergenz von Wahrscheinlichkeitsmaßen) Sind
Analysis 2. Vorlesungsausarbeitung zum SS von Prof. Dr. Klaus Fritzsche. Inhaltsverzeichnis
 Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Lösungen zur Klausur zur Analysis 1, WiSe 2016/17
 BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
( ) ( ) < b k, 1 k n} (2) < x k
 Technische Universität Dortmund Fakultät für Mathematik Proseminar Analysis Prof. Dr. Röger Benjamin Czyszczon Satz von Heine Borel Gliederung 1. Zellen und offene Überdeckungen 2. Satz von Heine Borel
Technische Universität Dortmund Fakultät für Mathematik Proseminar Analysis Prof. Dr. Röger Benjamin Czyszczon Satz von Heine Borel Gliederung 1. Zellen und offene Überdeckungen 2. Satz von Heine Borel
KAPITEL 18 UND 19 H. KOCH. Kapitel 18. x>a. x<y
 KAPITEL 18 UND 19 H. KOCH 1. VORLESUNG VOM 08.01.2018 Kpitel 18 Definition 1 (Zerlegungen, Treppenfunktionen, Regelfunktionen) Sei < b. 1. Eine Zerlegung τ von [, b] besteht us einer Zhl N N und (N + 1)
KAPITEL 18 UND 19 H. KOCH 1. VORLESUNG VOM 08.01.2018 Kpitel 18 Definition 1 (Zerlegungen, Treppenfunktionen, Regelfunktionen) Sei < b. 1. Eine Zerlegung τ von [, b] besteht us einer Zhl N N und (N + 1)
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
4 Das Riemann-Integral im R n
 $Id: nintegral.tex,v 1.7 2012/11/20 16:08:44 hk Exp hk $ 4 Das Riemann-Integral im R n 4.1 Das n-dimensionale Riemann-Integral In der letzten Sitzung hatten wir die Definition des n-dimensionalen Riemann-Integrals
$Id: nintegral.tex,v 1.7 2012/11/20 16:08:44 hk Exp hk $ 4 Das Riemann-Integral im R n 4.1 Das n-dimensionale Riemann-Integral In der letzten Sitzung hatten wir die Definition des n-dimensionalen Riemann-Integrals
Wichtige Klassen reeller Funktionen
 0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
Analysis I. 7. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 207 Erinnerung Satz. (Zwischenwertsatz) Sei f : [a, b] R stetig mit f(a) f(b). Dann gibt es zu jedem
Analysis I 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 207 Erinnerung Satz. (Zwischenwertsatz) Sei f : [a, b] R stetig mit f(a) f(b). Dann gibt es zu jedem
9 Metrische und normierte Räume
 9 Metrische und normierte Räume Idee: Wir wollen Abstände zwischen Punkten messen. Der Abstand soll eine reelle Zahl 0 sein (ohne Dimensionsangabe wie Meter...). 9.1 Definition Sei X eine Menge. Eine Metrik
9 Metrische und normierte Räume Idee: Wir wollen Abstände zwischen Punkten messen. Der Abstand soll eine reelle Zahl 0 sein (ohne Dimensionsangabe wie Meter...). 9.1 Definition Sei X eine Menge. Eine Metrik
Darstellungssatz von Riesz in vollständig regulären Räumen. Carina Pöll Wintersemester 2012
 Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Stetigkeit von Funktionen
 9 Stetigkeit von Funktionen Definition 9.1 : Sei D R oder C und f : D R, C. f stetig in a D : ε > 0 δ > 0 mit f(z) f(a) < ε für alle z D, z a < δ. f stetig auf D : f stetig in jedem Punkt a D. f(a) ε a
9 Stetigkeit von Funktionen Definition 9.1 : Sei D R oder C und f : D R, C. f stetig in a D : ε > 0 δ > 0 mit f(z) f(a) < ε für alle z D, z a < δ. f stetig auf D : f stetig in jedem Punkt a D. f(a) ε a
D-MATH, D-PHYS, D-CHAB Analysis I HS 2017 Prof. Manfred Einsiedler. Lösung 4
 D-MATH, D-PHYS, D-CHAB Analysis I HS 017 Prof. Manfred Einsiedler Lösung 4 Hinweise 1. Zeigen Sie, dass inf X die kleinste obere Schranke von X ist.. Dass z 1, z Lösungen sind, kann man durch Einsetzen
D-MATH, D-PHYS, D-CHAB Analysis I HS 017 Prof. Manfred Einsiedler Lösung 4 Hinweise 1. Zeigen Sie, dass inf X die kleinste obere Schranke von X ist.. Dass z 1, z Lösungen sind, kann man durch Einsetzen
Reelle Zufallsvariablen
 Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
1. Übungsblatt zur Analysis 3
 Hannover, den 2. Oktober 23 Aufgabe. Übungsblatt zur Analysis 3 Abgabe am 27./28. Oktober 23 vor den Stundenübungen (je 5 Punkte) Man zeige: a) Die Funktion f : N N N, f(m, n) := 2 (m + n)(m + n + ) +
Hannover, den 2. Oktober 23 Aufgabe. Übungsblatt zur Analysis 3 Abgabe am 27./28. Oktober 23 vor den Stundenübungen (je 5 Punkte) Man zeige: a) Die Funktion f : N N N, f(m, n) := 2 (m + n)(m + n + ) +
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
1 Konvergenz im p ten Mittel
 Konvergenz im p ten Mittel 1 1 Konvergenz im p ten Mittel In diesem Paragraphen werden zunächst in Abschnitt 1.1 die L p Räume eingeführt. Diese erweisen sich als vollständige, lineare Räume über R. In
Konvergenz im p ten Mittel 1 1 Konvergenz im p ten Mittel In diesem Paragraphen werden zunächst in Abschnitt 1.1 die L p Räume eingeführt. Diese erweisen sich als vollständige, lineare Räume über R. In
Analysis 2. Contents. Torsten Wedhorn. June 12, Notation. Es bezeichne K immer den Körper R der reellen Zahlen oder den Körper C der komplexen
 Analysis 2 Torsten Wedhorn June 12, 2012 Notation Es bezeichne K immer den Körper R der reellen Zahlen oder den Körper C der komplexen Zahlen. Contents 12 Metrische Räume 2 (A) Definition metrischer Räume........................
Analysis 2 Torsten Wedhorn June 12, 2012 Notation Es bezeichne K immer den Körper R der reellen Zahlen oder den Körper C der komplexen Zahlen. Contents 12 Metrische Räume 2 (A) Definition metrischer Räume........................
Schwartz-Raum (Teil 1)
 Schwartz-Raum (Teil 1) Federico Remonda, Robin Krom 10. Januar 2008 Zusammenfassung Der Schwartz-Raum ist ein Funktionenraum, der besondere Regularitätseigenschaften besitzt, die uns bei der Fouriertransformation
Schwartz-Raum (Teil 1) Federico Remonda, Robin Krom 10. Januar 2008 Zusammenfassung Der Schwartz-Raum ist ein Funktionenraum, der besondere Regularitätseigenschaften besitzt, die uns bei der Fouriertransformation
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Faltung und Approximation von Funktionen
 Faltung und Approximation von Funktionen Lisa Bauer und Anja Moldenhauer 9. Juni 2008 1 Die Faltung von Funktionen 1.1 Die Faltung Eine kleine Widerholung mit einem Zusatz: Vergleiche den Vortrag von Benjamin
Faltung und Approximation von Funktionen Lisa Bauer und Anja Moldenhauer 9. Juni 2008 1 Die Faltung von Funktionen 1.1 Die Faltung Eine kleine Widerholung mit einem Zusatz: Vergleiche den Vortrag von Benjamin
Schwache Konvergenz von W-Verteilungen auf der Zahlengeraden
 Kapitel 5 Schwache Konvergenz von W-Verteilungen auf er Zahlengeraen 5.1 Schwache Konvergenz bzw. Verteilungskonvergenz Bezeichne W(, B 1 ie Menge aller W-Verteilungen auf (, B 1. Definition 5.1 (Schwache
Kapitel 5 Schwache Konvergenz von W-Verteilungen auf er Zahlengeraen 5.1 Schwache Konvergenz bzw. Verteilungskonvergenz Bezeichne W(, B 1 ie Menge aller W-Verteilungen auf (, B 1. Definition 5.1 (Schwache
Erwartungswert als Integral
 Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Inverse Fourier Transformation
 ETH Zürich HS 27 Departement Mathematik Seminararbeit Inverse Fourier Transformation Patricia Hinder Sandra König Oktober 27 Prof. M. Struwe Im Vortrag der letzten Woche haben wir gesehen, dass die Faltung
ETH Zürich HS 27 Departement Mathematik Seminararbeit Inverse Fourier Transformation Patricia Hinder Sandra König Oktober 27 Prof. M. Struwe Im Vortrag der letzten Woche haben wir gesehen, dass die Faltung
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung. Lösungen zur Probeklausur 2.
 Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Analysis III. Vorlesungsskriptum WS 2006/07. Fakultät für Mathematik, Ruhr-Universität Bochum
 Analysis III Vorlesungsskriptum WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel IX. Integralrechnung mehrerer Veränderlicher 5 IX.1. Nullmengen 5 IX.2.
Analysis III Vorlesungsskriptum WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel IX. Integralrechnung mehrerer Veränderlicher 5 IX.1. Nullmengen 5 IX.2.
6.1 Zerlegungen Ober- und Unterintegrale Existenz des Integrals
 Kapitel 6 Das Riemann-Integral In diesem Abschnitt wollen wir einen Integralbegriff einführen. Dieser Integralbegriff geht auf Riemann 1 zurück und beruht auf einer naheliegenden Anschauung. Es wird sich
Kapitel 6 Das Riemann-Integral In diesem Abschnitt wollen wir einen Integralbegriff einführen. Dieser Integralbegriff geht auf Riemann 1 zurück und beruht auf einer naheliegenden Anschauung. Es wird sich
30 Die Gammafunktion und die Stirlingsche Formel
 3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
Der Satz von FEJÉR und die CESÀRO- Summation
 Schriftliche Ausarbeitung im Rahmen des Seminars zur Fourieranalysis Der Satz von FEJÉR und die CESÀRO- Summation vorgelegt von SEBASIAN MESS dem Lehrstuhl A für Mathematik der RWH AACHEN Betreuer: PROF.
Schriftliche Ausarbeitung im Rahmen des Seminars zur Fourieranalysis Der Satz von FEJÉR und die CESÀRO- Summation vorgelegt von SEBASIAN MESS dem Lehrstuhl A für Mathematik der RWH AACHEN Betreuer: PROF.
Kapitel I. Maßtheorie
 Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
(Lebesgue - ) Integration
 25 (Lebesgue - ) Integration ist ein allgemeines Konzept zur Definition von fdλ, wenn λ ein Maß auf X ist und f eine λ-messbare Funktion X R. Als,,Spezialfälle bekommen wir b a f(t) dt für Regelfunktionen
25 (Lebesgue - ) Integration ist ein allgemeines Konzept zur Definition von fdλ, wenn λ ein Maß auf X ist und f eine λ-messbare Funktion X R. Als,,Spezialfälle bekommen wir b a f(t) dt für Regelfunktionen
34 Äquivalenz von Normen; Stetigkeit und Kompaktheit in endlich-dimensionalen
 34 Äquivalenz von Normen; Stetigkeit und Kompaktheit in endlich-dimensionalen R-Vektorräumen 34.1 Äquivalenz von Normen 34.3 Stetigkeit und Normen linearer Abbildungen 34.4 Äquivalente Normen sind gegeneinander
34 Äquivalenz von Normen; Stetigkeit und Kompaktheit in endlich-dimensionalen R-Vektorräumen 34.1 Äquivalenz von Normen 34.3 Stetigkeit und Normen linearer Abbildungen 34.4 Äquivalente Normen sind gegeneinander
Maß- und Integrationstheorie
 Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn
Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn
Lebesgue-Integral und L p -Räume
 Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
8.1. DER RAUM R N ALS BANACHRAUM 17
 8.1. DER RAUM R N ALS BANACHRAUM 17 Beweis. Natürlich ist d 0 und d(x, y) = 0 genau dann, wenn x = y. Wegen (N2) ist x = x und damit d(x, y) = d(y, x). Die letzte Eigenschaft einer Metrik schließt man
8.1. DER RAUM R N ALS BANACHRAUM 17 Beweis. Natürlich ist d 0 und d(x, y) = 0 genau dann, wenn x = y. Wegen (N2) ist x = x und damit d(x, y) = d(y, x). Die letzte Eigenschaft einer Metrik schließt man
D-ITET Analysis II FS 13 Prof. Horst Knörrer. Musterlösung 1. 3xy 2 = 2 x 2. y y. 3 y y. 3 x v x + v = 2 3 v v.
 D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
Faltung und Gute Kerne. 1 Faltung
 Vortrag zum Proseminar zur Analysis, 9.07.200 Lars Grötschel, Elisa Friebel Im ersten Abschnitt Faltung definieren und beschäftigen wir uns mit der Faltung, die die grundliegende Operation des zweiten
Vortrag zum Proseminar zur Analysis, 9.07.200 Lars Grötschel, Elisa Friebel Im ersten Abschnitt Faltung definieren und beschäftigen wir uns mit der Faltung, die die grundliegende Operation des zweiten
ANALYSIS 3. Carsten Schütt WS 2008/9
 1. Es sei f : R 3 R 3 durch f 1 (r, φ 1,φ 2 ) = r cos φ 1 f 2 (r, φ 1,φ 2 ) = r sin φ 1 cos φ 2 f 3 (r, φ 1,φ 2 ) = r sin φ 1 sin φ 2 gegeben. Für welche (r, φ 1,φ 2 ) ist f lokal invertierbar? Ist f global
1. Es sei f : R 3 R 3 durch f 1 (r, φ 1,φ 2 ) = r cos φ 1 f 2 (r, φ 1,φ 2 ) = r sin φ 1 cos φ 2 f 3 (r, φ 1,φ 2 ) = r sin φ 1 sin φ 2 gegeben. Für welche (r, φ 1,φ 2 ) ist f lokal invertierbar? Ist f global
Stochastische Prozesse
 Albert-Ludwigs-Universität Freiburg Vorlesungsskript Stochastische Prozesse apl. Prof. Dr. Stefan Tappe Wintersemester 2017/18 Abteilung für Mathematische Stochastik Inhaltsverzeichnis 1 Grundlegende
Albert-Ludwigs-Universität Freiburg Vorlesungsskript Stochastische Prozesse apl. Prof. Dr. Stefan Tappe Wintersemester 2017/18 Abteilung für Mathematische Stochastik Inhaltsverzeichnis 1 Grundlegende
Lösungen zur Übungsserie 9
 Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag,? November Lösungen zur Übungsserie 9 Aufgaben 1,2,3,5,6,8,9,11 Aufgabe 1. Sei a R. Berechnen Sie die folgenden Grenzwerte, falls sie existieren.
Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag,? November Lösungen zur Übungsserie 9 Aufgaben 1,2,3,5,6,8,9,11 Aufgabe 1. Sei a R. Berechnen Sie die folgenden Grenzwerte, falls sie existieren.
Integralrechnung und das Riemannintegral
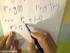 Integralrechnung und das Riemannintegral Vorlesung zur Didaktik der Analysis Oliver Passon Oliver Passon Integralrechnung 1 Inhalt Historisches Archimedes (Parabel) Hippokrates ( Möndchen ) Cavalerie Aktuell
Integralrechnung und das Riemannintegral Vorlesung zur Didaktik der Analysis Oliver Passon Oliver Passon Integralrechnung 1 Inhalt Historisches Archimedes (Parabel) Hippokrates ( Möndchen ) Cavalerie Aktuell
Kapitel III. Stetige Funktionen. 14 Stetigkeit und Rechenregeln für stetige Funktionen. 15 Hauptsätze über stetige Funktionen
 Kapitel III Stetige Funktionen 14 Stetigkeit und Rechenregeln für stetige Funktionen 15 Hauptsätze über stetige Funktionen 16 Konvergenz von Funktionen 17 Logarithmus und allgemeine Potenz C 1 14 Stetigkeit
Kapitel III Stetige Funktionen 14 Stetigkeit und Rechenregeln für stetige Funktionen 15 Hauptsätze über stetige Funktionen 16 Konvergenz von Funktionen 17 Logarithmus und allgemeine Potenz C 1 14 Stetigkeit
Wir wünschen viel Erfolg!
 Dr. Felix Schwenninger WS 2018/2019 Bergische Universität Wuppertal Probeklausur Analysis II Name: Vorname: Matrikelnummer: Studiengang: Wichtige Hinweise: Sofern nicht anders angegeben, müssen alle Rechnungen,
Dr. Felix Schwenninger WS 2018/2019 Bergische Universität Wuppertal Probeklausur Analysis II Name: Vorname: Matrikelnummer: Studiengang: Wichtige Hinweise: Sofern nicht anders angegeben, müssen alle Rechnungen,
12 Aufgaben zu linearen Funktionalen
 266 12. Aufgaben zu linearen Funktionalen A B C 12 Aufgaben zu linearen Funktionalen 12.1 Stetige Funktionale (siehe auch 11.6.E, 12.2, 13.4.A) Sei E ein topologischer Vektorraum und ϕ: E K (ϕ ) linear.
266 12. Aufgaben zu linearen Funktionalen A B C 12 Aufgaben zu linearen Funktionalen 12.1 Stetige Funktionale (siehe auch 11.6.E, 12.2, 13.4.A) Sei E ein topologischer Vektorraum und ϕ: E K (ϕ ) linear.
Analysis III. Vorlesung 69. Integrierbare Funktionen
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
5 Die Transformationsformel
 $Id: transform.tex,v 1.6 1/1/11 15:47:59 hk Exp hk $ 5 Die Transformationsformel In der letzten Sitzung haben wir die Transformationsformel als n-dimensionale Erweiterung der bekannten Substitutionsregel
$Id: transform.tex,v 1.6 1/1/11 15:47:59 hk Exp hk $ 5 Die Transformationsformel In der letzten Sitzung haben wir die Transformationsformel als n-dimensionale Erweiterung der bekannten Substitutionsregel
nennt man eine Zerlegung (Partition, Unterteilung) des Intervalls [a, b]. Die Feinheit der Zerlegung ist dabei
![nennt man eine Zerlegung (Partition, Unterteilung) des Intervalls [a, b]. Die Feinheit der Zerlegung ist dabei nennt man eine Zerlegung (Partition, Unterteilung) des Intervalls [a, b]. Die Feinheit der Zerlegung ist dabei](/thumbs/64/52033315.jpg) Kpitel 8: Integrtion Erläuterung uf Folie 8.1 Ds bestimmte Integrl Sei f : [, b] R eine beschränkte Funktion uf einem (zunächst) kompkten Intervll [, b]. Definition: 1) Eine Menge der Form Z = { = x 0
Kpitel 8: Integrtion Erläuterung uf Folie 8.1 Ds bestimmte Integrl Sei f : [, b] R eine beschränkte Funktion uf einem (zunächst) kompkten Intervll [, b]. Definition: 1) Eine Menge der Form Z = { = x 0
Topologische Grundbegriffe II. 1 Begriffe auf Mengen
 Vortrag zum Seminar zur Analysis, 03.05.2010 Dennis Joswig, Florian Goy Aufbauend auf den Resultaten der Vorlesung Topologische Grundbegriffe I untersuchen wir weitere topologische Eigenschaften von metrischen
Vortrag zum Seminar zur Analysis, 03.05.2010 Dennis Joswig, Florian Goy Aufbauend auf den Resultaten der Vorlesung Topologische Grundbegriffe I untersuchen wir weitere topologische Eigenschaften von metrischen
Serie 1 Lösungsvorschläge
 D-Math Mass und Integral FS 2014 Prof. Dr. D. A. Salamon Serie 1 Lösungsvorschläge 1. a) Seien A, B X zwei Mengen, so dass keine der Mengen A \ B, B \ A, A B und X \ (A B) leer ist. Bestimmen Sie die Kardinalität
D-Math Mass und Integral FS 2014 Prof. Dr. D. A. Salamon Serie 1 Lösungsvorschläge 1. a) Seien A, B X zwei Mengen, so dass keine der Mengen A \ B, B \ A, A B und X \ (A B) leer ist. Bestimmen Sie die Kardinalität
Eigenschaften stetiger Funktionen Buch Kap. 2.5
 Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
Nachklausur Analysis I
 SS 008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Nachklausur Analysis I 07.0.008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
SS 008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Nachklausur Analysis I 07.0.008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Beispiele zur Konvergenzuntersuchung bei Reihen.
 Beispiele zur Konvergenzuntersuchung bei Reihen Beispiel: Wir untersuchen die Konvergenz der Exponentialreihe z k k! für z C Anwendung des Quotientenkriteriums ergibt z k+1 (k + 1! z k = z k+1 k! z k (k
Beispiele zur Konvergenzuntersuchung bei Reihen Beispiel: Wir untersuchen die Konvergenz der Exponentialreihe z k k! für z C Anwendung des Quotientenkriteriums ergibt z k+1 (k + 1! z k = z k+1 k! z k (k
f(x nk ) = lim y nk ) = lim Bemerkung 2.14 Der Satz stimmt nicht mehr, wenn D nicht abgeschlossen oder nicht beschränkt ist, wie man z.b.
 Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
Der Primzahlsatz, Teil 2
 Vortrag zum Seminar zur Funktionentheorie, 4.5.22 Maike Gerhard Ziel dieses Vortrags ist es den Primzahlsatz zu beweisen. Dieser besagt π() π(), d.h. lim ln /ln =, wobei π() die Anzahl der Primzahlen kleiner
Vortrag zum Seminar zur Funktionentheorie, 4.5.22 Maike Gerhard Ziel dieses Vortrags ist es den Primzahlsatz zu beweisen. Dieser besagt π() π(), d.h. lim ln /ln =, wobei π() die Anzahl der Primzahlen kleiner
Kapitel 19. Das Lebesgue Maß σ Algebren und Maße
 Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Klausur - Analysis 1
 Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
4 Absolutstetige Verteilungen und Zufallsvariablen 215/1
 4 Absolutstetige Verteilungen und Zufallsvariablen 215/1 23. Bemerkung Integralbegriffe für Funktionen f : R d R (i) Lebesgue-Integral (Vorlesung Analysis IV). Spezialfall: (ii) Uneigentliches Riemann-Integral
4 Absolutstetige Verteilungen und Zufallsvariablen 215/1 23. Bemerkung Integralbegriffe für Funktionen f : R d R (i) Lebesgue-Integral (Vorlesung Analysis IV). Spezialfall: (ii) Uneigentliches Riemann-Integral
Stetigkeit, Konvergenz, Topologie
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Stetigkeit, Konvergenz, Topologie 21.03.2012 Inhaltsverzeichnis 1 Stetigkeit und Konvergenz
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Stetigkeit, Konvergenz, Topologie 21.03.2012 Inhaltsverzeichnis 1 Stetigkeit und Konvergenz
Proseminar: Normierte Vektorräume und Banachräume Vortrag: L und Maß-Räume
 Proseminar: Normierte Vektorräume und Banachräume Vortrag: L und Maß-Räume Dozent: Prof.Dr.Hans Crauel Student: Yassin El Karrouchi Goethe-Universität-Frankfurt am Main nhaltsverzeichnis 1 Einleitung 1.1
Proseminar: Normierte Vektorräume und Banachräume Vortrag: L und Maß-Räume Dozent: Prof.Dr.Hans Crauel Student: Yassin El Karrouchi Goethe-Universität-Frankfurt am Main nhaltsverzeichnis 1 Einleitung 1.1
sign: R R, sign(x) := 0 falls x = 0 1 falls x < 0 Diese ist im Punkt x 0 = 0 nicht stetig, denn etwa zu ε = 1 finden wir kein δ > 0
 ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 81 3. Stetigkeit 3.1. Stetigkeit. Im Folgenden sei D R eine beliebige nichtleere Teilmenge. Typischerweise wird D ein allgemeines Intervall sein, siehe Abschnitt
ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 81 3. Stetigkeit 3.1. Stetigkeit. Im Folgenden sei D R eine beliebige nichtleere Teilmenge. Typischerweise wird D ein allgemeines Intervall sein, siehe Abschnitt
Mathematik III. Vorlesung 74. Folgerungen aus dem Satz von Fubini. (( 1 3 x3 1 2 x2 y +2y 3 x) 1 2)dy. ( y +2y y +4y3 )dy
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Übungsblatt 2 - Analysis 2, Prof. G. Hemion
 Tutor: Martin Friesen, martin.friesen@gmx.de Übungsblatt 2 - Analysis 2, Prof. G. Hemion Um die hier gestellten Aufgaben zu lösen brauchen wir ein wenig Kentnisse über das Infimum bzw. Supremum einer Menge.
Tutor: Martin Friesen, martin.friesen@gmx.de Übungsblatt 2 - Analysis 2, Prof. G. Hemion Um die hier gestellten Aufgaben zu lösen brauchen wir ein wenig Kentnisse über das Infimum bzw. Supremum einer Menge.
Gleichmäßige Konvergenz und Funktionenräume
 Gleichmäßige Konvergenz und Funktionenräume Isabella Lukasewitz und Andreas Brack 07.06.2010 Vortrag zum Proseminar zur Analysis Konvergenz und Funktionenräume INHALTSVERZEICHNIS Bereits in den Vorlesungen
Gleichmäßige Konvergenz und Funktionenräume Isabella Lukasewitz und Andreas Brack 07.06.2010 Vortrag zum Proseminar zur Analysis Konvergenz und Funktionenräume INHALTSVERZEICHNIS Bereits in den Vorlesungen
Universität Ulm Abgabe: Mittwoch,
 Universität Ulm Abgabe: Mittwoch, 8.5.23 Prof. Dr. W. Arendt Jochen Glück Sommersemester 23 Punktzahl: 36+4* Lösungen Halbgruppen und Evolutionsgleichungen: Blatt 2. Sei X ein Banachraum und (T (t)) t
Universität Ulm Abgabe: Mittwoch, 8.5.23 Prof. Dr. W. Arendt Jochen Glück Sommersemester 23 Punktzahl: 36+4* Lösungen Halbgruppen und Evolutionsgleichungen: Blatt 2. Sei X ein Banachraum und (T (t)) t
