Zusammenfassung: Kapitel 5, Zusammenhangsmaße
|
|
|
- Bertold Schmitt
- vor 5 Jahren
- Abrufe
Transkript
1 Zusammenfassung: Kapitel 5, Zusammenhangsmaße Kovarianz s xy = 1 n n (x i x)(y i ȳ) i=1 Korrelationskoeffizient nach Bravais-Pearson r xy = s xy s x s y = n (x i x)(y i ȳ) i=1 n (x i x) 2 i=1 n (y i ȳ) 2 i=1 Dr. Matthias Arnold 294
2 Zusammenfassung: Kapitel 5, Zusammenhangsmaße Kovarianz und Korrelation Maßzahlen für den linearen Zusammenhang Korrelation: standardisiert Korrelation Kausalität Rangkorrelationskoeffizient nach Spearman n ( R(xi ) R )( x R(yi ) R ) y r R xy = i=1 n ( R(xi ) R ) 2 x n ( R(yi ) R ) 2 y i=1 i=1 Maß für monotonen Zusammenhang Dr. Matthias Arnold 295
3 Zusammenfassung: Kapitel 6, Preisindizes Preisindex nach Laspeyres P L 0t = n p t (i) q 0 (i) i=1 n p 0 (i) q 0 (i) i=1 Preisindex nach Paasche P P 0t = n p t (i) q t (i) i=1 n p 0 (i) q t (i) i=1 Dr. Matthias Arnold 296
4 Zusammenfassung: Kapitel 6, Preisindizes Preisindizes Darstellung als gewichtetes arithmetisches Mittel Inflationsrate Warenkorb und Verbraucherpreisindex praktische Umsetzung Dr. Matthias Arnold 297
5 Zusammenfassung: Kapitel 7, Zufällige Ereignisse und ihre Wahrscheinlichkeiten Grundlegende Begriffe Zufallsexperiment Elementarereignisse ω i Ergebnismenge Ω Ereignisse Ereignisse A und B Schnittmenge A B Vereinigungsmenge A B Differenzmenge A \ B Komplementärmenge Ā disjunkte Mengen Dr. Matthias Arnold 298
6 Zusammenfassung: Kapitel 7, Zufällige Ereignisse und ihre Wahrscheinlichkeiten Wahrscheinlichkeiten Laplace Axiome von Kolmogoroff Rechenregeln bedingte Wahrscheinlichkeiten stochastische Unabhängigkeit Interpretation bedingter Wahrscheinlichkeiten Dr. Matthias Arnold 299
7 Zusammenfassung: Kapitel 8, Zufallsvariablen Zufallsvariable X Abbildung: Ω R diskrete und stetige Zufallsvariablen diskrete Zufallsvariable: Wahrscheinlichkeitsfunktion f(x i )=P (X = x i ), i =1,...,k, diskrete Zufallsvariable: Verteilungsfunktion F (x) =P (X x) = x i x f(x i ), x R Dr. Matthias Arnold 300
8 Zusammenfassung: Kapitel 8, Zufallsvariablen stetige Zufallsvariable: Dichtefunktion f(x) =F (x), x R, stetige Zufallsvariable: Verteilungsfunktion F (x) =P (X x) = x f(t) dt, x R Dr. Matthias Arnold 301
9 Zusammenfassung: Kapitel 8, Zufallsvariablen Wahrscheinlichkeitsfunktion, Dichtefunktion, Verteilungsfunktion Eigenschaften Rechenregeln stochastische Unabhängigkeit Dr. Matthias Arnold 302
10 Zusammenfassung: Kapitel 9, Erwartungswert, Varianz und Kovarianz von Zufallsvariablen Erwartungswert, diskrete Zufallsvariable E (X) = i I x i f(x i ) Erwartungswert, stetige Zufallsvariable E (X) = x f(x) dx Eigenschaften des Erwartungswertes Gesetz der großen Zahl p-quantile Dr. Matthias Arnold 303
11 Zusammenfassung: Kapitel 9, Erwartungswert, Varianz und Kovarianz von Zufallsvariablen Varianz einer Zufallsvariablen σ 2 X = Var (X) =E [ (X E (X)) 2] Standardabweichung σ X = σ 2 X Eigenschaften Dr. Matthias Arnold 304
12 Zusammenfassung: Kapitel 9, Erwartungswert, Varianz und Kovarianz von Zufallsvariablen Kovarianz zweier Zufallsvariablen σ XY = Cov (X, Y )=E [(X E (X))(Y E (Y ))] Korrelation zweier Zufallsvariablen ρ XY = σ XY σ X σ Y Kovarianz und Korrelation Maße für den linearen Zusammenhang Rechenregeln, Eigenschaften Unkorreliertheit und Unabhängigkeit Dr. Matthias Arnold 305
13 Zusammenfassung: Kapitel 10, Ausgewählte Verteilungen Binomialverteilung Bernoulli-Experiment, n-mal wiederholt Stetige Gleichverteilung Normalverteilung Standardnormalverteilung Zentraler Grenzwertsatz Approximationen Dr. Matthias Arnold 306
14 Teil C: Induktive Statistik Dr. Matthias Arnold 307
15 Motivation Teil B: Verteilung F einer Zufallsvariablen X ist bekannt sämtliche Parameter von F (Erwartungswert, Varianz, Quantile,... ) lassen sich direkt angeben Teil C: Verteilung F einer Zufallsvariablen X ist unbekannt Stichprobe X 1,..., X n uiv F Realisationen x 1,..., x n sollen Rückschlüsse auf unbekannte Parameter von F liefern Dr. Matthias Arnold 308
16 Motivation (Fortsetzung) Dr. Matthias Arnold 309
17 Kapitel 11: Punktschätzung Beispiel 11.1 (S1-Verspätung, vgl. u.a. Beispiel 9.5 b)) X = S1-Verspätung (in min) Haltestelle Dortmund Universität Kapitel 8&9: X R[0, 20] Jetzt: X F, wobei F unbekannt Messe nun stichprobenartig folgende Verspätungen (in Min.): 2, 14, 10, 0, 9, 20, 8, 2, 3, 2 gesucht: Durchschnittliche Verspätung, also E (X)??? Dr. Matthias Arnold 310
18 Definition 11.1 X 1,..., X n Stichprobenvariablen aus Grundgesamtheit mit unbekannter Verteilung F = F θ. Dann heißt eine Funktion ˆθ = g (X 1,..., X n ) Schätzfunktion (kurz Schätzer) für den unbekannten Parameter θ. Der sich aus den Realisationen x 1,..., x n ergebende Wert g (x 1,..., x n ) heißt Schätzwert für θ. Dr. Matthias Arnold 311
19 Beispiel 11.2 (S1-Verspätung, Situation wie in Beispiel 11.1) X i = S1-Verspätung (in min) bei i ter Messung uiv X 1,..., X 10 X F (F unbekannt) Von Interesse: μ = E (X i ) einige mögliche Kandidaten: ˆμ 1 = X = 7 ˆμ 2 = X 1 = 2 ˆμ 3 = 3 X 8 = 6 ˆμ 4 = i=1 X i = 7, 56 Welcher Schätzer ist am besten? Dr. Matthias Arnold 312
20 Definition 11.2 Ein Schätzer ˆθ, für den E (ˆθ) =θ gilt, heißt erwartungstreu (oder unverzerrt) für θ. Für einen Schätzer ˆθ heißt Bias (ˆθ) =E (ˆθ) θ Verzerrung (oder Bias) vonˆθ. Dr. Matthias Arnold 313
21 Bemerkung a) Grafische Darstellung erwartungstreue Schätzung f(θ^) Dr. Matthias Arnold 314 θ
22 Bemerkung (Fortsetzung) b) Grafische Darstellung verzerrte Schätzung f(θ^) θ Dr. Matthias Arnold 315
23 Beispiel 11.3 (S1-Verspätung, Situation wie in Beispiel 11.2) Für die vier vorgeschlagenen Schätzer gilt: ( ) E (ˆμ 1 ) = E X i 1 10 i=1 = 1 10 i=1 E (X i )= μ = μ E (ˆμ 2 ) = E (X 1 ) = μ E (ˆμ 3 ) = E (3 X 8 )=3 E (X 8 )=3 μ μ E (ˆμ 4 ) = E ( 1 9 ) 9 X i i=1 = 1 9 i=1 9 E (X i )= μ = μ ˆμ 1, ˆμ 2 und ˆμ 4 erwartungstreu welchen Schätzer bevorzugen? Dr. Matthias Arnold 316
24 Definition 11.3 Seien ˆθ 1 und ˆθ 2 erwartungstreue Schätzer für θ. Wenn Var (ˆθ 1 ) < Var (ˆθ 2 ), so heißt ˆθ 1 effizienter zur Schätzung von θ als ˆθ 2. Bemerkung Grafische Darstellung Effizienz (hier ˆθ 1 effizienter als ˆθ 2 ) f(θ^1) f(θ^2) Dr. Matthias Arnold 317 θ
25 Beispiel 11.4 (S1-Verspätung, Situation wie in Beispiel 11.3) Für die erwartungstreuen Schätzer ˆμ 1, ˆμ 2 und ˆμ 4 gilt: ( ) Var (ˆμ 1 ) = Var X i Var (X i ) 1 10 i=1 = = σ2 = 1 10 σ2 Var (ˆμ 2 ) = Var (X 1 )=σ 2 Var (ˆμ 4 ) = Var ( 1 9 ) 9 X i i=1 = σ2 = 1 9 σ2 = 1 81 i=1 9 Var (X i ) Güte der Schätzer (gemäß Effizienzkrit.): 1) ˆμ 1, 2) ˆμ 4, 3) ˆμ 2 i=1 Dr. Matthias Arnold 318
26 Bemerkung a) Betrachte Zufallsvariablen X 1,..., X n (uiv) mit E (X i )=μ. Gemäß Beispiel 11.4 ist ˆμ 1 = X effizienter als zwei andere erwartungstreue Schätzer für μ. Allgemein ist X der effizienteste Schätzer unter allen erwartungstreuen Schätzern für μ, d.h.esgilt: Var ( X) Var ( μ) für alle μ mit E ( μ) =μ. b) Spezialfall von a) bei Bernoulliverteilung: uiv X 1,..., X n Bin(1,p) E (X i )=p X erwartungstreuer (und außerdem effizientester) Schätzer für p Dr. Matthias Arnold 319
27 Bemerkung (Fortsetzung) c) Betrachte Zufallsvariablen X 1,..., X n (uiv) mit E (X i )=μ bekannt und σ 2 = Var (X i ) unbekannt. Dannist ˆσ 2 = S 2 X = 1 n n (X i μ) 2 i=1 ein erwartungstreuer Schätzer für σ 2. d) Betrachte Zufallsvariablen X 1,..., X n (uiv) mit E (X i )=μ unbekannt und σ 2 = Var (X i ) unbekannt. Dannist ˆσ 2 = S 2 X = 1 n 1 n (X i X) 2 i=1 ein erwartungstreuer Schätzer für σ 2. Dr. Matthias Arnold 320
28 Beispiel 11.5 (S1-Verspätung, Situation wie in 11.1) a) X i = S1-Verspätung bei i ter Messung (i =1,..., 10), X i F (unbekannt) Schätze Varianz σ 2 (gem. Bem. d) nach Bsp. 11.1) erwartungstreu mit S 2 X S 2 X = 1 9 ( (2 7) 2 +(14 7) 2 +(10 7) 2 +(0 7) 2 +(9 7) 2 +(20 7) 2 +(8 7) 2 +(2 7) 2 +(3 7) 2 +(2 7) 2 ) = 1 ( ) 9 = = 41, 34 Dr. Matthias Arnold 321
29 Beispiel 11.5 (Fortsetzung) b) Situation wie in a), unterstelle jedoch, dass der aus den zehn Messungen resultierende Mittelwert ( x =7)dem wahren Erwartungswert entspricht verwende diese Zusatzinfo und schätze die Varianz σ 2 (gem. Bem. c) nach Bsp. 11.1) erwartungstreu mit S 2 X S 2 X = 1 n n (X i μ) 2 = 1 10 i=1 372 = 37, 2 Dr. Matthias Arnold 322
30 Beispiel 11.5 (Fortsetzung) c) Mit welcher Wahrscheinlichkeit verspätet sich S1 um höchstens 5 Minuten? { 1, Verspätung 5 min Definiere Y i = 0, sonst Also Y 1,..., Y 10 uiv Bin(1,p); Von Interesse: p (Wahrscheinlichkeit, dass S1 max. 5 min. zu spät) Gemäß Bem. b) nach Bsp ist X effizientester Schätzer für p ˆp = 1 10 ( )= 1 2 (Zur Erinnerung: P(Versp. max. 5 min) =0, 25 bei Unterstellung einer Gleichverteilung) Dr. Matthias Arnold 323
31 Bemerkung Fazit/Zusammenfassung Kapitel 11 Schätzer = Funktion der Stichprobenvariablen, selbst ebenfalls Zufallsvariable Erwartungstreue als Konzept zum Vergleich von Schätzern Effizienz als Konzept zum Vergleich von erwartungstreuen Schätzern Dr. Matthias Arnold 324
32 Kapitel 12: Intervallschätzung Motivation Bisher: Schätzung des unbekannten Parameters θ durch ˆθ auf einen Punkt P(ˆθ = θ) =0(falls ˆθ stetig verteilt), darüber hinaus keine Informationen, wie wahrscheinlich sich ˆθ zumindest in der Nähe von θ realisiert Jetzt: Konstruiere (basierend auf Punktschätzer) Intervall, das unbekannten Parameter mit hoher Wahrscheinlichkeit überdeckt liefert Information über Präzision des Schätzers Dr. Matthias Arnold 325
33 Definition 12.1 X 1,..., X n Stichpr. aus Grundges. mit X i F θ (unbekannt). V u = g(x 1,X 2,...,X n ) und V o = h(x 1,X 2,...,X n ) Stichprobenfunktionen mit V u <V o. Dann heißt das Intervall [V u,v o ] Konfidenzintervall für den unbekannten Parameter θ. Weiter heißt Irrtumswahrscheinlichkeit und α = P (θ / [V u,v o ]) 1 α = P (θ [V u,v o ]) Vertrauenswahrscheinlichkeit oder Konfidenzniveau. Dr. Matthias Arnold 326
34 Beispiel 12.1 Das Zentrum für Studienangelegenheiten an der TU Dortmund behauptet, dass die mittlere Wartezeit von Besuchern nicht mehr als zehn Minuten beträgt. Eine Befragung von 16 zufällig ausgewählten Besuchern ergab folgende Wartezeiten (in Minuten): 12, 20, 5, 15, 8, 1, 30, 25, 10, 4, 17, 11, 20, 10, 6, 2. Gesucht: 95%-Konfidenzintervall für die mittlere Wartezeit Annahme: Wartezeiten Stichprobenrealisationen einer normalverteilten Grundgesamtheit mit Standardabweichung σ =5 bekannt. Dr. Matthias Arnold 327
35 Bemerkung Herleitung eines Konfidenzintervalls für μ bei bekannter Varianz (normalverteilte Grundgesamtheit) uiv Ausgangssituation: X 1,..., X n N ( μ, σ 2) n i=1 X i N ( n μ, n σi 2 ) (vgl. Bem. d) nach Def. 10.4) X ( ) N μ, σ2 n (vgl. Bem. d) nach Bsp. 9.1 und Bem. a), Punkt ii), nach Beispiel 9.5) n X μ σ N(0, 1) (vgl. Bem. c) nach Def. 10.4) ( P u α n X ) μ u 2 σ 1 α =1 α 2 mit u γ = γ-quantil der N (0, 1)-Verteilung Dr. Matthias Arnold 328
36 Bemerkung (Fortsetzung) uiv Herleitung Konfidenzintervall für μ bei X i N ( μ, σ 2), σ 2 bekannt (Fortsetzung) 1 α = ( P u 1 α n ( X ) μ) u 2 1 α 2 = ( ) σ P u 1 α X σ μ u 2 1 α n 2 n = P = P ( u 1 α 2 X σ u 1 α 2 n }{{} = V u σ n X μ u 1 α 2 μ X + u 1 α 2 ) σ X n σ n } {{ } = V o Dr. Matthias Arnold 329
37 Bemerkung (Fortsetzung) uiv Somit gilt: Wenn X 1,..., X n N(μ, σ 2 ), Varianz σ 2 bekannt, dann ist ein Konfidenzintervall für den unbekannten Erwartungswert μ zum Konfidenzniveau 1 α gegeben durch [ ] σ KI 1 α (μ) = X u 1 α, X σ + u 2 1 α n 2 n Interpretation μ ist ein fester Wert (obwohl unbekannt), zufällig sind die Intervallgrenzen deshalb: Das Intervall [V u,v o ] überdeckt den unbekannten Parameter μ mit vorgegebener Wahrscheinlichkeit 1 α Dr. Matthias Arnold 330
38 Beispiel 12.2 (Wartezeiten ZfS, vgl. Bsp. 12.1) X i = Wartezeit i-ter Besucher (in Minuten), dann gilt nach Annahme: uiv X 1,X 2,...,X 16 N(μ, 25) Konfidenzintervall Varianz σ 2 bekannt, also: [ KI 1 α (μ) = X u 1 α 2 Berechnung für diese Daten: σ n, X + u 1 α 2 ] σ n Dr. Matthias Arnold 331
39 Beispiel 12.2 (Fortsetzung) Hier ist X = 1 ( )=12, und für α =0, 05 gilt nach Tabelle KI 0,95 (μ) = 1 α =0, 95 u 1 α = u 0,975 =1, 96 2 [ 12, 25 1, ;12, , 96 = [12, 25 2, 45; 12, , 45] ] 5 16 = [9, 8; 14, 7]=[9 Min.&48 Sek.; 14 Min.&42 Sek.] Intervall derart konstruiert, dass es unter den getroffenen Annahmen die (unbekannte, aber feste) mittlere Wartezeit beim ZfS mit 95 % Wahrscheinlichkeit überdeckt Dr. Matthias Arnold 332
40 Bemerkung Frage: Wie lässt sich analoges Konfidenzintervall für mittlere Wartezeit finden, wenn Varianz σ 2 unbekannt? Idee: Ersetze in Bemerkung nach Beispiel 12.1 die unbekannte Varianz σ 2 durch erwartungstreuen Schätzer, z.b. S 2 X (siehe Bem. d) nach Bsp. 11.4) Problem: n X μ S X N (0, 1) Aber: n X μ S X besitzt andere, leicht handhabbare Verteilung Dr. Matthias Arnold 333
41 Definition 12.2 X 1,..., X n uiv N(0, 1), dann heißt die Zufallsvariable Y = n i=1 X 2 i χ 2 -verteilt mit n Freiheitsgraden, kurz: Y χ 2 n. Weiter sei W ebenfalls N (0, 1) verteilt und Y wie oben definiert (also Y χ 2 n). Sind W und Y stochastisch unabhängig, so heißt die Zufallsvariable Z = W 1 n Y t-verteilt mit n Freiheitsgraden, kurz: Z t n. Dr. Matthias Arnold 334
42 Bemerkung 1 a) Dichten ausgesuchter χ 2 n Verteilungen f(x) n=1 n=2 n=3 n=4 n=6 n= Dr. Matthias Arnold 335 x
43 Bemerkung 1 (Fortsetzung) b) Dichten ausgesuchter t n Verteilungen f(x) n = 2 f(x) n = x x f(x) n = 10 f(x) n = x Dr. Matthias Arnold 336 x
44 Bemerkung 2 a) Konfidenzintervall für μ bei Normalverteilung, σ 2 unbekannt uiv Betrachte Problem aus Bem. nach Bsp. 12.2: X i N(μ, σ 2 ) mit μ und σ 2 unbekannt; Gesucht: Konfidenzintervall für μ Bekannt: n X μ σ N(0, 1); außerdem leicht zu zeigen: (n 1) S 2 X σ 2 χ 2 n 1 Weiter sind X und S 2 X stochastisch unabhängig n X μ σ n 1 n 1 und somit P S X 2 σ 2 = n X μ σ S Xσ ( t n 1, α 2 n X μ S X = n X μ S X t n 1 (vgl. Def. 12.2) t n 1,1 α 2 ) =1 α Dr. Matthias Arnold 337
45 Bemerkung 2 (Fortsetzung) a) Konfidenzintervall bei N (μ, σ 2 ), σ 2 unbekannt (Fortsetzung) uiv Somit gilt: Wenn X 1,..., X n N(μ, σ 2 ), Varianz σ 2 unbekannt, dann ist ein Konfidenzintervall für den unbekannten Erwartungswert μ zum Konfidenzniveau 1 α gegeben durch [ ] S X KI 1 α (μ) = X t n 1,1 α, X S + t 2 n 1,1 α X n 2 n b) Für n konvergiert t n Verteilung gegen N (0, 1) Verteilung; Faustregel: Approximation bei n 30 akzeptabel wenn n 30, so kann im Konfidenzintervall aus Teil a) anstelle des (1 α/2) Quantils der t n Verteilung das entsprechende N (0, 1) Quantil verwendet werden Dr. Matthias Arnold 338
46 Beispiel 12.3 (Wartezeiten ZfS, vgl. Bsp und 12.2) X i = Wartezeit i-ter Besucher (in Minuten) ; unterstelle weiterhin Normalverteilung, nehme nun jedoch an, dass σ 2 unbekannt X 1,..., X 16 uiv N(μ, σ 2 ) Gesucht: Konfidenzintervall für μ wende Bem. 2 a) nach Def an X =12, 25 und n =16(vgl. Bsp. 12.2), weiterhin gilt t 15,0.975 =2, 131; berechne nun außerdem S X 2 S 2 X = 1 15 = 69, 933 ( (12 12, 25) 2 +(20 12, 25) (2 12, 25) 2) Dr. Matthias Arnold 339
47 Beispiel 12.3 (Fortsetzung) Somit gilt 69, 933 KI 0,95 (μ) = 12, 25 ± t 15, [ ] 69, , 933 = 12, 25 2, 131 ;12, , = [12, 25 4, 455; 12, , 455] = [7, 795; 16, 705] = [7 Min.&48 Sek.; 16 Min.&42 Sek.] Beachte: Bei bekannter Varianz umschloss das Konfidenzintervall den Bereich [9 Min.&48 Sek.; 14 Min.&42 Sek.], vgl. Bsp dieses Intervall liegt komplett in dem Konfidenzintervall, welches bei unbekannter Varianz berechnet wurde (klar: weniger Informationen größere Unsicherheit) Dr. Matthias Arnold 340
48 Beispiel 12.4 Bei einer Umfrage unter 65 mittelständischen Unternehmen geben 26 Betriebe an, zusätzliche Mitarbeiter einstellen zu wollen, falls der Kündigungsschutz gelockert wird. Gesucht: 90%-Konfidenzintervall für den unbekannten Anteil der Betriebe, die nach einer Gesetzesänderung zusätzliche Arbeitsplätze schaffen wollen { 1 i-ter Betrieb möchte zusätzl. Mitarb. einstellen Definiere X i = 0 sonst X 1,..., X 65 uiv Bin (1,p) 65 i=1 X i Bin (65,p) Gemäß Fragestellung also benötigt: Konfidenzintervall für p Dr. Matthias Arnold 341
49 Bemerkung uiv Seien X 1,..., X n Bin (1,p), dann ist ein (approximatives) Konfidenzintervall für den unbekannten Anteil p zum Konfidenzniveau 1 α gegeben durch: KI 1 α (p) = [ ˆp u 1 α 2 ˆσ n, ˆp + u 1 α 2 ] ˆσ n Dabei ist ˆp = X, ˆσ = ˆp (1 ˆp) und u γ das γ-quantil der Standardnormalverteilung. Weiterhin gilt die Approximation als akzeptabel, wenn (1) n 30, (2) nˆp 10, (3) n (1 ˆp) 10 Dr. Matthias Arnold 342
50 Beispiel 12.5 (Umfrage in mittelständischen Unternehmen, vgl. Bsp. 12.4) X i wie in Bsp X 1,..., X 65 uiv Bin (1,p) Gesucht: Konfidenzintervall für p Nutze Bem. nach Bsp. 12.4: 65 i=1 Überprüfung der Voraussetzungen: X i =26 ˆp = X = =0, 4 (1) n = (2) n ˆp = (3) n (1 ˆp) = Dr. Matthias Arnold 343
51 Beispiel 12.5 (Fortsetzung) Weiter gilt und somit ˆσ = 0, 4(1 0, 4) = 0, 24 = 0, 49 1 α =0, 9 u 1 α 2 = u 0,95 =1, 645 KI 0,9 (p) = [ ] 0, 49 0, 49 0, 4 1, 645 ;0, 4+1, = [0, 4 0, 1; 0, 4+0, 1] = [0, 3; 0, 5] Das 90 % Konfidenzintervall für den Anteil an Betrieben, die nach einer Gesetzesänderung zusätzliches Personal einstellen würden, geht von 30 % bis 50 %. Dr. Matthias Arnold 344
52 Wahlumfragen Politbarometer (Forschungsgruppe Wahlen) Angabe: Bei Befragten beträgt die Fehlertoleranz für Parteien mit 40% Stimmenanteil +/ 3% für Parteien mit 10% Stimmenanteil +/ 2% Berechnung n = 1250 α =0, 05 (Konvention) u 1 α 2 = u = ˆσ u 1 α 2 n 2 p (1 p) bzw. 2 = 2 n p (1 p) n =2 0, , 028 Dr. Matthias Arnold 345
53 Wahlumfragen Infratest Dimap (ARD-DeutschlandTREND) Angabe: Bei Befragten beträgt die Fehlertoleranz für Parteien mit 5% Stimmenanteil +/ 1, 4% für Parteien mit 50% Stimmenanteil +/ 3, 1% Berechnung n = 1000 α =0, 05 (Konvention) u 1 α 2 = u = ˆσ u 1 α 2 n 2 p (1 p) bzw. 2 = 2 n p (1 p) n =2 0, , 0138 Dr. Matthias Arnold 346
54 Das Konfidenzintervall [ KI 1 α (μ) = X u 1 α 2 σ n, X + u 1 α 2 ] σ n hat die Breite ( V o V u = X + u 1 α 2 ) ( σ X u 1 α n 2 σ n ) =2 u 1 α 2 σ n und ist deshalb umso schmaler, je größer α ist (größere Irrtumswahrscheinlichkeit bedeutet kleineres Intervall) kleiner σ 2 ist (präzisere Schätzung gibt mehr Sicherheit) größer n ist (mehr Stichprobe bedeutet mehr Information) Dr. Matthias Arnold 347
55 erforderlicher Stichprobenumfang In der Praxis häufig: gewünschte Breite des Konfidenzintervalles vorgegeben: V o V u = c mit einer Konstante c daraus: erforderlichen Stichprobenumfang berechnen c = V o V u = 2 u 1 α 2 n = ( 2 u 1 α 2 σ n σ ) 2 c bei unbekanntem σ: durch Schätzwert ersetzen Zusammenhang ist quadratisch: Intervallbreite halbieren erfordert vierfachen Stichprobenumfang Dr. Matthias Arnold 348
Kapitel 3 Schließende Statistik
 Motivation Grundgesamtheit mit unbekannter Verteilung F Stichprobe X 1,...,X n mit Verteilung F Realisation x 1,...,x n der Stichprobe Rückschluss auf F Dr. Karsten Webel 160 Motivation (Fortsetzung) Kapitel
Motivation Grundgesamtheit mit unbekannter Verteilung F Stichprobe X 1,...,X n mit Verteilung F Realisation x 1,...,x n der Stichprobe Rückschluss auf F Dr. Karsten Webel 160 Motivation (Fortsetzung) Kapitel
Kapitel 3 Schließende Statistik
 Beispiel 3.4: (Fortsetzung Bsp. 3.) bekannt: 65 i=1 X i = 6, also ˆp = X = 6 65 = 0, 4 Überprüfen der Voraussetzungen: (1) n = 65 30 () n ˆp = 6 10 (3) n (1 ˆp) = 39 10 Dr. Karsten Webel 194 Beispiel 3.4:
Beispiel 3.4: (Fortsetzung Bsp. 3.) bekannt: 65 i=1 X i = 6, also ˆp = X = 6 65 = 0, 4 Überprüfen der Voraussetzungen: (1) n = 65 30 () n ˆp = 6 10 (3) n (1 ˆp) = 39 10 Dr. Karsten Webel 194 Beispiel 3.4:
6. Schätzverfahren für Parameter
 6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
2.3 Intervallschätzung
 2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
Kapitel 3 Schließende Statistik
 Bemerkung 3.34: Die hier betrachteten Konfidenzintervalle für unbekannte Erwartungswerte sind umso schmaler, je größer der Stichprobenumfang n ist, je kleiner die (geschätzte) Standardabweichung σ (bzw.
Bemerkung 3.34: Die hier betrachteten Konfidenzintervalle für unbekannte Erwartungswerte sind umso schmaler, je größer der Stichprobenumfang n ist, je kleiner die (geschätzte) Standardabweichung σ (bzw.
2.3 Intervallschätzung
 2.3.1 Motivation und Hinführung Bsp. 2.15. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler unter allen Wählern war 2009 auf eine Nachkommastelle gerundet genau 33.7%. Wie groß ist die Wahrscheinlichkeit,
2.3.1 Motivation und Hinführung Bsp. 2.15. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler unter allen Wählern war 2009 auf eine Nachkommastelle gerundet genau 33.7%. Wie groß ist die Wahrscheinlichkeit,
Statistik. Sommersemester Prof. Dr. Stefan Etschberger HSA. für Betriebswirtschaft und International Management
 Statistik für Betriebswirtschaft und International Management Sommersemester 2014 Prof. Dr. Stefan Etschberger HSA Streuungsparameter Varianz Var(X) bzw. σ 2 : [x i E(X)] 2 f(x i ), wenn X diskret Var(X)
Statistik für Betriebswirtschaft und International Management Sommersemester 2014 Prof. Dr. Stefan Etschberger HSA Streuungsparameter Varianz Var(X) bzw. σ 2 : [x i E(X)] 2 f(x i ), wenn X diskret Var(X)
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Statistik I für Betriebswirte Vorlesung 14
 Statistik I für Betriebswirte Vorlesung 14 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 13. Juli 017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 14 Version: 8. Juli
Statistik I für Betriebswirte Vorlesung 14 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 13. Juli 017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 14 Version: 8. Juli
Philipp Sibbertsen Hartmut Lehne. Statistik. Einführung für Wirtschafts- und. Sozialwissenschaftler. 2., überarbeitete Auflage. 4^ Springer Gabler
 Philipp Sibbertsen Hartmut Lehne Statistik Einführung für Wirtschafts- und Sozialwissenschaftler 2., überarbeitete Auflage 4^ Springer Gabler Inhaltsverzeichnis Teil I Deskriptive Statistik 1 Einführung
Philipp Sibbertsen Hartmut Lehne Statistik Einführung für Wirtschafts- und Sozialwissenschaftler 2., überarbeitete Auflage 4^ Springer Gabler Inhaltsverzeichnis Teil I Deskriptive Statistik 1 Einführung
Statistik I für Betriebswirte Vorlesung 13
 Statistik I für Betriebswirte Vorlesung 13 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 4. Juli 2016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
Statistik I für Betriebswirte Vorlesung 13 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 4. Juli 2016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
1 Wahrscheinlichkeitsrechnung. 2 Zufallsvariablen und ihre Verteilung. 3 Statistische Inferenz. 4 Intervallschätzung
 0 Einführung 1 Wahrscheinlichkeitsrechnung Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung Motivation und Hinführung Der wahre Anteil der rot-grün Wähler 009 war genau
0 Einführung 1 Wahrscheinlichkeitsrechnung Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung Motivation und Hinführung Der wahre Anteil der rot-grün Wähler 009 war genau
Kapitel 2 Wahrscheinlichkeitsrechnung
 Definition 2.77: Normalverteilung & Standardnormalverteilung Es sei µ R und 0 < σ 2 R. Besitzt eine stetige Zufallsvariable X die Dichte f(x) = 1 2 πσ 2 e 1 2 ( x µ σ ) 2, x R, so heißt X normalverteilt
Definition 2.77: Normalverteilung & Standardnormalverteilung Es sei µ R und 0 < σ 2 R. Besitzt eine stetige Zufallsvariable X die Dichte f(x) = 1 2 πσ 2 e 1 2 ( x µ σ ) 2, x R, so heißt X normalverteilt
Inhaltsverzeichnis. Robert Galata, Sandro Scheid. Deskriptive und Induktive Statistik für Studierende der BWL. Methoden - Beispiele - Anwendungen
 Inhaltsverzeichnis Robert Galata, Sandro Scheid Deskriptive und Induktive Statistik für Studierende der BWL Methoden - Beispiele - Anwendungen Herausgegeben von Robert Galata, Markus Wessler ISBN (Buch):
Inhaltsverzeichnis Robert Galata, Sandro Scheid Deskriptive und Induktive Statistik für Studierende der BWL Methoden - Beispiele - Anwendungen Herausgegeben von Robert Galata, Markus Wessler ISBN (Buch):
Man kann also nicht erwarten, dass man immer den richtigen Wert trifft.
 2.2.2 Gütekriterien Beurteile die Schätzfunktionen, also das Verfahren an sich, nicht den einzelnen Schätzwert. Besonders bei komplexeren Schätzproblemen sind klar festgelegte Güteeigenschaften wichtig.
2.2.2 Gütekriterien Beurteile die Schätzfunktionen, also das Verfahren an sich, nicht den einzelnen Schätzwert. Besonders bei komplexeren Schätzproblemen sind klar festgelegte Güteeigenschaften wichtig.
Zufallsvariablen. Diskret. Stetig. Verteilung der Stichprobenkennzahlen. Binomial Hypergeometrisch Poisson. Normal Lognormal Exponential
 Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Stetige Zufallsvariable Verteilungsfunktion: Dichtefunktion: Integralrechnung:
Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Stetige Zufallsvariable Verteilungsfunktion: Dichtefunktion: Integralrechnung:
Mehrdimensionale Zufallsvariablen
 Mehrdimensionale Zufallsvariablen Im Folgenden Beschränkung auf den diskreten Fall und zweidimensionale Zufallsvariablen. Vorstellung: Auswerten eines mehrdimensionalen Merkmals ( ) X Ỹ also z.b. ω Ω,
Mehrdimensionale Zufallsvariablen Im Folgenden Beschränkung auf den diskreten Fall und zweidimensionale Zufallsvariablen. Vorstellung: Auswerten eines mehrdimensionalen Merkmals ( ) X Ỹ also z.b. ω Ω,
So berechnen Sie einen Schätzer für einen Punkt
 htw saar 1 EINFÜHRUNG IN DIE STATISTIK: SCHÄTZEN UND TESTEN htw saar 2 Schätzen: Einführung Ziel der Statistik ist es, aus den Beobachtungen eines Merkmales in einer Stichprobe Rückschlüsse über die Verteilung
htw saar 1 EINFÜHRUNG IN DIE STATISTIK: SCHÄTZEN UND TESTEN htw saar 2 Schätzen: Einführung Ziel der Statistik ist es, aus den Beobachtungen eines Merkmales in einer Stichprobe Rückschlüsse über die Verteilung
Vorlesung: Statistik II für Wirtschaftswissenschaft
 Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 017 4 Spezielle Zufallsgrößen Einführung 1 Wahrscheinlichkeit: Definition
Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 017 4 Spezielle Zufallsgrößen Einführung 1 Wahrscheinlichkeit: Definition
Fit for Abi & Study Stochastik
 Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
Stochastik Praktikum Parametrische Schätztheorie
 Stochastik Praktikum Parametrische Schätztheorie Thorsten Dickhaus Humboldt-Universität zu Berlin 05.10.2010 Prolog Momentenmethode X : Ω 1 Ω Zufallsgröße, die Experiment beschreibt. Ein statistisches
Stochastik Praktikum Parametrische Schätztheorie Thorsten Dickhaus Humboldt-Universität zu Berlin 05.10.2010 Prolog Momentenmethode X : Ω 1 Ω Zufallsgröße, die Experiment beschreibt. Ein statistisches
Statistik. Sommersemester Stefan Etschberger. für Betriebswirtschaft, Internationales Management, Wirtschaftsinformatik und Informatik
 Stefan Etschberger für Betriebswirtschaft, Internationales Management, Wirtschaftsinformatik und Informatik Sommersemester 2017 Rechenregeln für den Erwartungswert Ist f symmetrisch bzgl. a, so gilt E(X)
Stefan Etschberger für Betriebswirtschaft, Internationales Management, Wirtschaftsinformatik und Informatik Sommersemester 2017 Rechenregeln für den Erwartungswert Ist f symmetrisch bzgl. a, so gilt E(X)
Lösung Semesterendprüfung
 MAE4 Mathematik: Analysis für Ingenieure 4 Frühlingssemester 26 Dr. Christoph Kirsch ZHAW Winterthur Aufgabe : Lösung Semesterendprüfung Wir betrachten die Ergebnismenge Ω : {, 2,, 4, 5, 6} 2 6 2 6 Elemente,
MAE4 Mathematik: Analysis für Ingenieure 4 Frühlingssemester 26 Dr. Christoph Kirsch ZHAW Winterthur Aufgabe : Lösung Semesterendprüfung Wir betrachten die Ergebnismenge Ω : {, 2,, 4, 5, 6} 2 6 2 6 Elemente,
FORMELSAMMLUNG STATISTIK B
 Somersemester 2012 FORMELSAMMLUNG STATISTIK B Prof. Kneip / Dr. Scheer / Dr. Arns Version vom April 2012 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 2 2 Diskrete Zufallsvariablen 5 3 Stetige Zufallsvariablen
Somersemester 2012 FORMELSAMMLUNG STATISTIK B Prof. Kneip / Dr. Scheer / Dr. Arns Version vom April 2012 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 2 2 Diskrete Zufallsvariablen 5 3 Stetige Zufallsvariablen
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Wahrscheinlichkeit und Statistik: Zusammenfassung
 HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
Fakultät Verkehrswissenschaften Friedrich List Professur für Ökonometrie und Statistik, insb. im Verkehrswesen. Statistik II. Prof. Dr.
 Statistik II Fakultät Verkehrswissenschaften Friedrich List Professur für Ökonometrie und Statistik, insb. im Verkehrswesen Statistik II 2. Parameterschätzung: 2.1 Grundbegriffe; 2.2 Maximum-Likelihood-Methode;
Statistik II Fakultät Verkehrswissenschaften Friedrich List Professur für Ökonometrie und Statistik, insb. im Verkehrswesen Statistik II 2. Parameterschätzung: 2.1 Grundbegriffe; 2.2 Maximum-Likelihood-Methode;
FORMELSAMMLUNG STATISTIK B
 Somersemester 2010 FORMELSAMMLUNG STATISTIK B Dr. Scheer / J. Arns Version vom April 2010 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 2 2 Zufallsvariablen 5 3 Diskrete Verteilungsmodelle 7 4 Parameterschätzung
Somersemester 2010 FORMELSAMMLUNG STATISTIK B Dr. Scheer / J. Arns Version vom April 2010 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 2 2 Zufallsvariablen 5 3 Diskrete Verteilungsmodelle 7 4 Parameterschätzung
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Wintersemester 206 Prof. Dr. Stefan Etschberger HSA Unabhängigkeit von Ereignissen A, B unabhängig: Eintreten von A liefert keine Information über P(B). Formal: P(A
Einführung in einige Teilbereiche der Wintersemester 206 Prof. Dr. Stefan Etschberger HSA Unabhängigkeit von Ereignissen A, B unabhängig: Eintreten von A liefert keine Information über P(B). Formal: P(A
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert
 Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Goethe-Universität Frankfurt
 Goethe-Universität Frankfurt Fachbereich Wirtschaftswissenschaft PD Dr. Martin Biewen Dr. Ralf Wilke Sommersemester 2006 Klausur Statistik II 1. Alle Aufgaben sind zu beantworten. 2. Bitte runden Sie Ihre
Goethe-Universität Frankfurt Fachbereich Wirtschaftswissenschaft PD Dr. Martin Biewen Dr. Ralf Wilke Sommersemester 2006 Klausur Statistik II 1. Alle Aufgaben sind zu beantworten. 2. Bitte runden Sie Ihre
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 9. Dezember 2010 1 Konfidenzintervalle Idee Schätzung eines Konfidenzintervalls mit der 3-sigma-Regel Grundlagen
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 9. Dezember 2010 1 Konfidenzintervalle Idee Schätzung eines Konfidenzintervalls mit der 3-sigma-Regel Grundlagen
Vorwort zur 3. Auflage 15. Vorwort zur 2. Auflage 15. Vorwort 16 Kapitel 0 Einführung 19. Teil I Beschreibende Statistik 29
 Inhaltsübersicht Vorwort zur 3. Auflage 15 Vorwort zur 2. Auflage 15 Vorwort 16 Kapitel 0 Einführung 19 Teil I Beschreibende Statistik 29 Kapitel 1 Eindimensionale Häufigkeitsverteilungen 31 Kapitel 2
Inhaltsübersicht Vorwort zur 3. Auflage 15 Vorwort zur 2. Auflage 15 Vorwort 16 Kapitel 0 Einführung 19 Teil I Beschreibende Statistik 29 Kapitel 1 Eindimensionale Häufigkeitsverteilungen 31 Kapitel 2
Parameterschätzung. Kapitel 14. Modell Es sei {P θ θ Θ}, Θ R m eine Familie von Verteilungen auf χ (sog. Stichprobenraum),
 Kapitel 14 Parameterschätzung Modell Es sei {P θ θ Θ}, Θ R m eine Familie von Verteilungen auf χ (sog. Stichprobenraum), = ( 1,..., n ) sei eine Realisierung der Zufallsstichprobe X = (X 1,..., X n ) zu
Kapitel 14 Parameterschätzung Modell Es sei {P θ θ Θ}, Θ R m eine Familie von Verteilungen auf χ (sog. Stichprobenraum), = ( 1,..., n ) sei eine Realisierung der Zufallsstichprobe X = (X 1,..., X n ) zu
Wahrscheinlichkeitstheorie und Statistik
 Wahrscheinlichkeitstheorie und Statistik Definitionen und Sätze Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2018 2.5.2018 Diskrete Wahrscheinlichkeitsräume Diskreter
Wahrscheinlichkeitstheorie und Statistik Definitionen und Sätze Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2018 2.5.2018 Diskrete Wahrscheinlichkeitsräume Diskreter
Statistik I für Betriebswirte Vorlesung 4
 Statistik I für Betriebswirte Vorlesung 4 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 25. April 2016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
Statistik I für Betriebswirte Vorlesung 4 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 25. April 2016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
0 sonst. a) Wie lautet die Randwahrscheinlichkeitsfunktion von Y? 0.5 y = 1
 Aufgabe 1 (2 + 2 + 2 + 1 Punkte) Gegeben sei folgende gemeinsame Wahrscheinlichkeitsfunktion f(x, y) = P (X = x, Y = y) der Zufallsvariablen X und Y : 0.2 x = 1, y = 1 0.3 x = 2, y = 1 f(x, y) = 0.45 x
Aufgabe 1 (2 + 2 + 2 + 1 Punkte) Gegeben sei folgende gemeinsame Wahrscheinlichkeitsfunktion f(x, y) = P (X = x, Y = y) der Zufallsvariablen X und Y : 0.2 x = 1, y = 1 0.3 x = 2, y = 1 f(x, y) = 0.45 x
1.8 Mehrdimensionale Zufallsvariablen
 1.8 Mehrdimensionale Zufallsvariablen 1.8 Mehrdimensionale Zufallsvariablen Im Folgenden Beschränkung auf den diskreten Fall und zweidimensionale Zufallsvariablen. Schnelldurchgang unter Bezug auf das
1.8 Mehrdimensionale Zufallsvariablen 1.8 Mehrdimensionale Zufallsvariablen Im Folgenden Beschränkung auf den diskreten Fall und zweidimensionale Zufallsvariablen. Schnelldurchgang unter Bezug auf das
Kapitel 9:Erwartungswert, Varianz und Kovarianz von Zufallsvariablen
 Kapitel 9:Erwartungswert, Varianz und Kovarianz von Zufallsvariablen Motivation Erwartungswert: Welchen Wert nimmt Zufallsvariable durchschnittlich an? Populärstes Lagemaß aus Teil A: Arithmetisches Mittel
Kapitel 9:Erwartungswert, Varianz und Kovarianz von Zufallsvariablen Motivation Erwartungswert: Welchen Wert nimmt Zufallsvariable durchschnittlich an? Populärstes Lagemaß aus Teil A: Arithmetisches Mittel
7. Übung: Aufgabe 1. b), c), e) Aufgabe 2. a), c), e) Aufgabe 3. c), e) Aufgabe 4. Aufgabe 5. Aufgabe 6. Aufgabe 7. Aufgabe 8. Aufgabe 9.
 7. Übung: Aufgabe 1 b), c), e) Aufgabe a), c), e) Aufgabe 3 c), e) Aufgabe 4 b) Aufgabe 5 a) Aufgabe 6 b) Aufgabe 7 e) Aufgabe 8 c) Aufgabe 9 a), c), e) Aufgabe 10 b), d) Aufgabe 11 a) Aufgabe 1 b) Aufgabe
7. Übung: Aufgabe 1 b), c), e) Aufgabe a), c), e) Aufgabe 3 c), e) Aufgabe 4 b) Aufgabe 5 a) Aufgabe 6 b) Aufgabe 7 e) Aufgabe 8 c) Aufgabe 9 a), c), e) Aufgabe 10 b), d) Aufgabe 11 a) Aufgabe 1 b) Aufgabe
1 Grundlagen der Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsräume. Ein erster mathematischer Blick auf Zufallsexperimente...
 Inhaltsverzeichnis 1 Grundlagen der Wahrscheinlichkeitsrechnung 1 1.1 Wahrscheinlichkeitsräume Ein erster mathematischer Blick auf Zufallsexperimente.......... 1 1.1.1 Wahrscheinlichkeit, Ergebnisraum,
Inhaltsverzeichnis 1 Grundlagen der Wahrscheinlichkeitsrechnung 1 1.1 Wahrscheinlichkeitsräume Ein erster mathematischer Blick auf Zufallsexperimente.......... 1 1.1.1 Wahrscheinlichkeit, Ergebnisraum,
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Statistik II für Studierende der Soziologie
 Name: Matrikelnummer: Formelsammlung zur Vorlesung Statistik II für Studierende der Soziologie Dr. Carolin Strobl SoSe 2009 1 Wahrscheinlichkeitsrechnung 1.1 Mengen und elementare Mengenoperationen Definition:
Name: Matrikelnummer: Formelsammlung zur Vorlesung Statistik II für Studierende der Soziologie Dr. Carolin Strobl SoSe 2009 1 Wahrscheinlichkeitsrechnung 1.1 Mengen und elementare Mengenoperationen Definition:
JosefPuhani. Kleine Formelsammlung zur Statistik. 10. Auflage. averiag i
 JosefPuhani Kleine Formelsammlung zur Statistik 10. Auflage averiag i Inhalt- Vorwort 7 Beschreibende Statistik 1. Grundlagen 9 2. Mittelwerte 10 Arithmetisches Mittel 10 Zentral wert (Mediän) 10 Häufigster
JosefPuhani Kleine Formelsammlung zur Statistik 10. Auflage averiag i Inhalt- Vorwort 7 Beschreibende Statistik 1. Grundlagen 9 2. Mittelwerte 10 Arithmetisches Mittel 10 Zentral wert (Mediän) 10 Häufigster
1.5.4 Quantile und Modi. Bem [Quantil, Modus]
![1.5.4 Quantile und Modi. Bem [Quantil, Modus] 1.5.4 Quantile und Modi. Bem [Quantil, Modus]](/thumbs/77/75975909.jpg) 1.5.4 Quantile und Modi 1.5 Erwartungswert und Varianz Bem. 1.73. [Quantil, Modus] und Vertei- Analog zu Statistik I kann man auch Quantile und Modi definieren. Gegeben sei eine Zufallsvariable X mit Wahrscheinlichkeitsverteilung
1.5.4 Quantile und Modi 1.5 Erwartungswert und Varianz Bem. 1.73. [Quantil, Modus] und Vertei- Analog zu Statistik I kann man auch Quantile und Modi definieren. Gegeben sei eine Zufallsvariable X mit Wahrscheinlichkeitsverteilung
Statistik I für Betriebswirte Vorlesung 14
 Statistik I für Betriebswirte Vorlesung 14 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 11. Juli 016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
Statistik I für Betriebswirte Vorlesung 14 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 11. Juli 016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
70 Wichtige kontinuierliche Verteilungen
 70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
Übungen zur Vorlesung Statistische Methoden Kapitel 1-2
 TECHNISCHE UNIVERSITÄT DORTMUND Sommersemester 2011 FAKULTÄT STATISTIK Dr. M. Arnold Dipl.-Stat. R. Walter Übungen zur Vorlesung Statistische Methoden Kapitel 1-2 Aufgabe 1: Gegeben ist eine diskrete Zufallsvariable
TECHNISCHE UNIVERSITÄT DORTMUND Sommersemester 2011 FAKULTÄT STATISTIK Dr. M. Arnold Dipl.-Stat. R. Walter Übungen zur Vorlesung Statistische Methoden Kapitel 1-2 Aufgabe 1: Gegeben ist eine diskrete Zufallsvariable
3 Statistische Schätzungen
 3 Statistische Schätzungen In der Wahrscheinlichkeitstheorie geht es darum, über Modelle Ereignisse zu bewerten bzw. Voraussagen über ihr Eintreten zu treffen. Sind nun umgekehrt Daten bekannt, und wollen
3 Statistische Schätzungen In der Wahrscheinlichkeitstheorie geht es darum, über Modelle Ereignisse zu bewerten bzw. Voraussagen über ihr Eintreten zu treffen. Sind nun umgekehrt Daten bekannt, und wollen
Teil VIII. Zentraler Grenzwertsatz und Vertrauensintervalle. Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle. Lernziele. Typische Situation
 Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Statistik. Sommersemester Prof. Dr. Stefan Etschberger Hochschule Augsburg. für Betriebswirtschaft und internationales Management
 für Betriebswirtschaft und internationales Management Sommersemester 2015 Prof. Dr. Stefan Etschberger Hochschule Augsburg Normalverteilung Eine Zufallsvariable X mit einer Dichtefunktion und σ > 0 heißt
für Betriebswirtschaft und internationales Management Sommersemester 2015 Prof. Dr. Stefan Etschberger Hochschule Augsburg Normalverteilung Eine Zufallsvariable X mit einer Dichtefunktion und σ > 0 heißt
Inhaltsverzeichnis. Inhalt Teil I: Beschreibende (Deskriptive) Statistik Seite. 1.0 Erste Begriffsbildungen Merkmale und Skalen 5
 Inhaltsverzeichnis Inhalt Teil I: Beschreibende (Deskriptive) Statistik Seite 1.0 Erste Begriffsbildungen 1 1.1 Merkmale und Skalen 5 1.2 Von der Urliste zu Häufigkeitsverteilungen 9 1.2.0 Erste Ordnung
Inhaltsverzeichnis Inhalt Teil I: Beschreibende (Deskriptive) Statistik Seite 1.0 Erste Begriffsbildungen 1 1.1 Merkmale und Skalen 5 1.2 Von der Urliste zu Häufigkeitsverteilungen 9 1.2.0 Erste Ordnung
3 Grundlagen statistischer Tests (Kap. 8 IS)
 3 Grundlagen statistischer Tests (Kap. 8 IS) 3.1 Beispiel zum Hypothesentest Beispiel: Betrachtet wird eine Abfüllanlage für Mineralwasser mit dem Sollgewicht µ 0 = 1000g und bekannter Standardabweichung
3 Grundlagen statistischer Tests (Kap. 8 IS) 3.1 Beispiel zum Hypothesentest Beispiel: Betrachtet wird eine Abfüllanlage für Mineralwasser mit dem Sollgewicht µ 0 = 1000g und bekannter Standardabweichung
Theorie Parameterschätzung Ausblick. Schätzung. Raimar Sandner. Studentenseminar "Statistische Methoden in der Physik"
 Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
5. Stichproben und Statistiken
 5. Stichproben und Statistiken Problem: Es sei X eine ZV, die einen interessierenden Zufallsvorgang repräsentiere Man möchte die tatsächliche Verteilung von X kennenlernen (z.b. mittels der VF F X (x)
5. Stichproben und Statistiken Problem: Es sei X eine ZV, die einen interessierenden Zufallsvorgang repräsentiere Man möchte die tatsächliche Verteilung von X kennenlernen (z.b. mittels der VF F X (x)
Stochastik für Mathematiker Teil 2: Wahrscheinlichkeitstheorie
 Stochastik für Mathematiker Teil 2: Wahrscheinlichkeitstheorie Sommersemester 2018 Kapitel 8: Elemente der mathematischen Statistik Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik
Stochastik für Mathematiker Teil 2: Wahrscheinlichkeitstheorie Sommersemester 2018 Kapitel 8: Elemente der mathematischen Statistik Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik
Vorlesung: Statistik II für Wirtschaftswissenschaft
 Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2
Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2
Aufgabe 1 (8= Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten:
 Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
Schließende Statistik
 Schließende Statistik [statistical inference] Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
Schließende Statistik [statistical inference] Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
Statistik im iadhetocr-studi der BWL und VWl
 Max C. Wewel Statistik im iadhetocr-studi der BWL und VWl Methoden, Anwendung, Interpretation 2., erweiterte Auflage Mit herausnehmbarer Formelsammlung ein Imprint von Pearson Education München Boston
Max C. Wewel Statistik im iadhetocr-studi der BWL und VWl Methoden, Anwendung, Interpretation 2., erweiterte Auflage Mit herausnehmbarer Formelsammlung ein Imprint von Pearson Education München Boston
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management
 Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg Lageparameter: Erwartungswert d) Erwartungswert
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg Lageparameter: Erwartungswert d) Erwartungswert
Dynamische Systeme und Zeitreihenanalyse // Multivariate Normalverteilung und ML Schätzung 11 p.2/38
 Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Einführung in die Statistik
 Einführung in die Statistik Analyse und Modellierung von Daten von Prof. Dr. Rainer Schlittgen Universität Hamburg 12., korrigierte Auflage Oldenbourg Verlag München Inhaltsverzeichnis 1 Statistische Daten
Einführung in die Statistik Analyse und Modellierung von Daten von Prof. Dr. Rainer Schlittgen Universität Hamburg 12., korrigierte Auflage Oldenbourg Verlag München Inhaltsverzeichnis 1 Statistische Daten
Statistik I für Betriebswirte Vorlesung 13
 Statistik I für Betriebswirte Vorlesung 13 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 6. Juli 2017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 13 Version: 7. Juli
Statistik I für Betriebswirte Vorlesung 13 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 6. Juli 2017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 13 Version: 7. Juli
Häufigkeiten. Verteilungen. Lageparameter Mittelwert. oder
 Formelsammlung Beschreibende Statistik Univariate Häufigkeitsverteilungen X ist ein diskretes Merkmal, mit k Ausprägungen TR: Mode 2 1 = AC absolute relative Häufigkeit Häufigkeiten Bivariate Häufigkeitsverteilungen
Formelsammlung Beschreibende Statistik Univariate Häufigkeitsverteilungen X ist ein diskretes Merkmal, mit k Ausprägungen TR: Mode 2 1 = AC absolute relative Häufigkeit Häufigkeiten Bivariate Häufigkeitsverteilungen
Zentraler Grenzwertsatz/Konfidenzintervalle
 / Statistik I Sommersemester 2009 Statistik I ZGWS/ (1/37) Kann Ahmadinejad die Wahl gewonnen haben? Im wesentlichen Dreiteilung der polit. Elite 2005: 17.3 Millionen Stimmen (Stichwahl), Wahlbeteiligung
/ Statistik I Sommersemester 2009 Statistik I ZGWS/ (1/37) Kann Ahmadinejad die Wahl gewonnen haben? Im wesentlichen Dreiteilung der polit. Elite 2005: 17.3 Millionen Stimmen (Stichwahl), Wahlbeteiligung
1.1.1 Ergebnismengen Wahrscheinlichkeiten Formale Definition der Wahrscheinlichkeit Laplace-Experimente...
 Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Hans-Friedrich Eckey / Reinhold Kosfeld / Christian Dreger. Statistik. Grundlagen - Methoden - Beispiele GABLER
 Hans-Friedrich Eckey / Reinhold Kosfeld / Christian Dreger Statistik Grundlagen - Methoden - Beispiele GABLER INHALTSVERZEICHNIS TEIL I: DESKRIPTIVE STATISTIK 1. GEGENSTAND UND GRUNDBEGRIFFE DER STATISTIK
Hans-Friedrich Eckey / Reinhold Kosfeld / Christian Dreger Statistik Grundlagen - Methoden - Beispiele GABLER INHALTSVERZEICHNIS TEIL I: DESKRIPTIVE STATISTIK 1. GEGENSTAND UND GRUNDBEGRIFFE DER STATISTIK
I. Deskriptive Statistik 1
 I. Deskriptive Statistik 1 1. Einführung 3 1.1. Grundgesamtheit und Stichprobe.................. 5 1.2. Merkmale und Verteilungen..................... 6 1.3. Tabellen und Grafiken........................
I. Deskriptive Statistik 1 1. Einführung 3 1.1. Grundgesamtheit und Stichprobe.................. 5 1.2. Merkmale und Verteilungen..................... 6 1.3. Tabellen und Grafiken........................
Chi-Quadrat-Verteilung
 Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Modellanpassung und Parameterschätzung. A: Übungsaufgaben
 7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
Binomialverteilung. Häufigkeit, mit der Ereignis A bei n unabhängigen Versuchen eintritt. Träger von X : X = {0, 1, 2,..., n}.
 Binomialverteilung Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder nicht. X = Häufigkeit, mit
Binomialverteilung Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder nicht. X = Häufigkeit, mit
Einführung in die computergestützte Datenanalyse
 Karlheinz Zwerenz Statistik Einführung in die computergestützte Datenanalyse 6., überarbeitete Auflage DE GRUYTER OLDENBOURG Vorwort Hinweise zu EXCEL und SPSS Hinweise zum Master-Projekt XI XII XII TEIL
Karlheinz Zwerenz Statistik Einführung in die computergestützte Datenanalyse 6., überarbeitete Auflage DE GRUYTER OLDENBOURG Vorwort Hinweise zu EXCEL und SPSS Hinweise zum Master-Projekt XI XII XII TEIL
WS 2014/15. (d) Bestimmen Sie die Wahrscheinlichkeitsfunktion von X. (e) Bestimmen Sie nun den Erwartungswert und die Varianz von X.
 Fragenkatalog zur Übung Methoden der empirischen Sozialforschung WS 2014/15 Hier finden Sie die denkbaren Fragen zum ersten Teil der Übung. Das bedeutet, dass Sie zu diesem Teil keine anderen Fragen im
Fragenkatalog zur Übung Methoden der empirischen Sozialforschung WS 2014/15 Hier finden Sie die denkbaren Fragen zum ersten Teil der Übung. Das bedeutet, dass Sie zu diesem Teil keine anderen Fragen im
Wahrscheinlichkeitsräume und Zufallsvariablen
 Kapitel Wahrscheinlichkeitsräume und Zufallsvariablen. W-Raum Unter einem Zufallsexperiment verstehen wir einen vom Zufall beeinflussten Vorgang, der ein entsprechend zufälliges Ergebnis hervorbringt.
Kapitel Wahrscheinlichkeitsräume und Zufallsvariablen. W-Raum Unter einem Zufallsexperiment verstehen wir einen vom Zufall beeinflussten Vorgang, der ein entsprechend zufälliges Ergebnis hervorbringt.
7.2 Theoretische Kennwerte
 7.2 Theoretische Kennwerte Theoretische Varianz und Standardabweichung Definition und Notation Verschiebungsformel für die theoretische Varianz 391 7.2 Theoretische Kennwerte Interpretation der theoretischen
7.2 Theoretische Kennwerte Theoretische Varianz und Standardabweichung Definition und Notation Verschiebungsformel für die theoretische Varianz 391 7.2 Theoretische Kennwerte Interpretation der theoretischen
2.2 Punktschätzung. Gegeben sei die in Kapitel 2.1 beschriebene Situation, also eine i.i.d. Stichprobe X 1,...,X n eines Merkmales X.
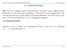 Ziel: Finde ein möglichst gutes Schätzverfahren und damit einen möglichst guten Schätzwert für eine bestimmte Kenngröße ϑ (Parameter) der Grundgesamtheit, z.b. den wahren Anteil der rot/grün-wähler, den
Ziel: Finde ein möglichst gutes Schätzverfahren und damit einen möglichst guten Schätzwert für eine bestimmte Kenngröße ϑ (Parameter) der Grundgesamtheit, z.b. den wahren Anteil der rot/grün-wähler, den
Statistik I für Betriebswirte Vorlesung 3
 Statistik I für Betriebswirte Vorlesung 3 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 15. April 2019 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 3 Version: 1. April
Statistik I für Betriebswirte Vorlesung 3 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 15. April 2019 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 3 Version: 1. April
Grundlagen der Statistik
 www.nwb.de NWB Studium Betriebswirtschaft Grundlagen der Statistik Band 2: Wahrscheinlichkeitsrechnung und induktive Statistik Von Professor Dr. Jochen Schwarze 9., vollständig überarbeitete Auflage STUDIUM
www.nwb.de NWB Studium Betriebswirtschaft Grundlagen der Statistik Band 2: Wahrscheinlichkeitsrechnung und induktive Statistik Von Professor Dr. Jochen Schwarze 9., vollständig überarbeitete Auflage STUDIUM
Einführung in die Statistik
 Einführung in die Statistik Analyse und Modellierung von Daten Von Prof. Dr. Rainer Schlittgen 4., überarbeitete und erweiterte Auflage Fachbereich Materialwissenschaft! der Techn. Hochschule Darmstadt
Einführung in die Statistik Analyse und Modellierung von Daten Von Prof. Dr. Rainer Schlittgen 4., überarbeitete und erweiterte Auflage Fachbereich Materialwissenschaft! der Techn. Hochschule Darmstadt
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Wahrscheinlichkeitsrechnung und schließende Statistik
 Springer-Lehrbuch Wahrscheinlichkeitsrechnung und schließende Statistik Bearbeitet von Karl Mosler, Friedrich Schmid 4., verb. Aufl. 2010. Taschenbuch. XII, 347 S. Paperback ISBN 978 3 642 15009 8 Format
Springer-Lehrbuch Wahrscheinlichkeitsrechnung und schließende Statistik Bearbeitet von Karl Mosler, Friedrich Schmid 4., verb. Aufl. 2010. Taschenbuch. XII, 347 S. Paperback ISBN 978 3 642 15009 8 Format
1 Einleitung und Grundlagen 1
 Inhaltsverzeichnis Vorwort vii 1 Einleitung und Grundlagen 1 1.1 Einführende Beispiele 1 1.2 Statistischer Prozess 2 1.3 Grundlagen 2 1.4 Unterscheidung von Merkmalen 3 1.4.1 Skalenniveaus 3 1.4.2 Stetige
Inhaltsverzeichnis Vorwort vii 1 Einleitung und Grundlagen 1 1.1 Einführende Beispiele 1 1.2 Statistischer Prozess 2 1.3 Grundlagen 2 1.4 Unterscheidung von Merkmalen 3 1.4.1 Skalenniveaus 3 1.4.2 Stetige
Inhaltsverzeichnis Inhaltsverzeichnis VII Erst mal locker bleiben: Es f angt ganz einfach an! Keine Taten ohne Daten!
 Inhaltsverzeichnis Inhaltsverzeichnis VII 1 Erst mal locker bleiben: Es fängt ganz einfach an! 1 1.1 Subjektive Wahrscheinlichkeit - oder warum...?..... 4 1.2 Was Ethik mit Statistik zu tun hat - Pinocchio
Inhaltsverzeichnis Inhaltsverzeichnis VII 1 Erst mal locker bleiben: Es fängt ganz einfach an! 1 1.1 Subjektive Wahrscheinlichkeit - oder warum...?..... 4 1.2 Was Ethik mit Statistik zu tun hat - Pinocchio
Über dieses Buch Die Anfänge Wichtige Begriffe... 21
 Inhalt Über dieses Buch... 12 TEIL I Deskriptive Statistik 1.1 Die Anfänge... 17 1.2 Wichtige Begriffe... 21 1.2.1 Das Linda-Problem... 22 1.2.2 Merkmale und Merkmalsausprägungen... 23 1.2.3 Klassifikation
Inhalt Über dieses Buch... 12 TEIL I Deskriptive Statistik 1.1 Die Anfänge... 17 1.2 Wichtige Begriffe... 21 1.2.1 Das Linda-Problem... 22 1.2.2 Merkmale und Merkmalsausprägungen... 23 1.2.3 Klassifikation
Trim Size: 176mm x 240mm Lipow ftoc.tex V1 - March 9, :34 P.M. Page 11. Über die Übersetzerin 9. Einleitung 19
 Trim Size: 176mm x 240mm Lipow ftoc.tex V1 - March 9, 2016 6:34 P.M. Page 11 Inhaltsverzeichnis Über die Übersetzerin 9 Einleitung 19 Was Sie hier finden werden 19 Wie dieses Arbeitsbuch aufgebaut ist
Trim Size: 176mm x 240mm Lipow ftoc.tex V1 - March 9, 2016 6:34 P.M. Page 11 Inhaltsverzeichnis Über die Übersetzerin 9 Einleitung 19 Was Sie hier finden werden 19 Wie dieses Arbeitsbuch aufgebaut ist
Klausur zu Statistik II
 GOETHE-UNIVERSITÄT FRANKFURT FB Wirtschaftswissenschaften Statistik und Methoden der Ökonometrie Prof. Dr. Uwe Hassler Wintersemester 03/04 Klausur zu Statistik II Matrikelnummer: Hinweise Hilfsmittel
GOETHE-UNIVERSITÄT FRANKFURT FB Wirtschaftswissenschaften Statistik und Methoden der Ökonometrie Prof. Dr. Uwe Hassler Wintersemester 03/04 Klausur zu Statistik II Matrikelnummer: Hinweise Hilfsmittel
Statistik Workshop. 12. und 14. Januar Prof. Dr. Stefan Etschberger HSA
 Workshop Mini-Einführung und Auffrischung zu einigen Teilen der angewandten 12. und 14. Prof. Dr. Stefan Etschberger HSA Outline 1 : Einführung Fehler durch Gute und schlechte Grafiken Begriff Grundbegriffe
Workshop Mini-Einführung und Auffrischung zu einigen Teilen der angewandten 12. und 14. Prof. Dr. Stefan Etschberger HSA Outline 1 : Einführung Fehler durch Gute und schlechte Grafiken Begriff Grundbegriffe
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.)
 Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Statistik Klausur Sommersemester 2013 Hamburg, BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN!
 Statistik 2 1. Klausur Sommersemester 2013 Hamburg, 26.07.2013 A BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................ Vorname:.............................................................................
Statistik 2 1. Klausur Sommersemester 2013 Hamburg, 26.07.2013 A BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................ Vorname:.............................................................................
Uwe Hassler. Statistik im. Bachelor-Studium. Eine Einführung. für Wirtschaftswissenschaftler. ^ Springer Gabler
 Uwe Hassler Statistik im Bachelor-Studium Eine Einführung für Wirtschaftswissenschaftler ^ Springer Gabler 1 Einführung 1 2 Beschreibende Methoden univariater Datenanalyse 5 2.1 Grundbegriffe 5 2.2 Häufigkeitsverteilungen
Uwe Hassler Statistik im Bachelor-Studium Eine Einführung für Wirtschaftswissenschaftler ^ Springer Gabler 1 Einführung 1 2 Beschreibende Methoden univariater Datenanalyse 5 2.1 Grundbegriffe 5 2.2 Häufigkeitsverteilungen
