Elektrotechnik I Formelsammlung
|
|
|
- Jörn Bösch
- vor 9 Jahren
- Abrufe
Transkript
1 Elektrotechnik I Formelsammlung Andreas itter und Marco Weber. Dezember 009 Inhaltsverzeichnis Physikalische Gesetze Physikalische Konstanten Physikalische Zusammenhänge Mathematische Formeln Doppelbrüche Komplexe echnung Netzwerk-Analysis 3 Serieschaltung Spannungsteilerregel Parallelschaltung Stromteilerregel Kirchhoff sche egeln Superpositions-Theoreme Verfahren zur Analyse Gleichstrom DC 6 Leistung Kondensatoren Spulen Wechselstrom AC 8 Zeigerdarstellung Polarform Impedanz / Admittanz Widerstand Kondensator / Kapazität Spule / Induktivität Serienschwingkreis Parallelschwingkreis Netzwerk-Analysis mit Wechselgrössen Leistung
2 Seite. Dezember 009 Physikalische Gesetze Physikalische Konstanten Einheitsladung: e = C [C] = [As] Influenzkonstante: ε 0 = C Nm Phsyikalische Zusammenhänge Ohmsches Gesetz: U = I U =[V ]= [ ] [ ] C F = Nm m [ ] Nm As [ ] kg m, = [Ω] = A s 3 Kraft zwischen zwei Ladungen: Kraft in einem elektrischen Feld: Strom: Widerstand eines Leiters: F = q q 4πε 0 r F = q E =[N] =[N] ( ) Q I = lim = dq t t dt =[A] = ρ L A = [Ω] Sheet esistance: s = ρ d = [Ω] = L s b = [Ω] mit Breite b Mathematische Formeln Doppelbrüche x + = x x x x + x x + x + = x 3 x x x 3 x x + x x 3 + x 3 x Komplexe echnung Betrag: Argument: Eulersche Umwandlung: Z = a + jb c + jd Z = a + b c + d Z = a + jb ( ) bc ad c + jd (Z) = arctan ac bd Falls gilt: sign(bc ad) = sign(ac bd) = müssen 80 zur Phase addiert werden. cis ϕ = cos ϕ + j sin ϕ = e jϕ
3 Seite 3. Dezember Netzwerk-Analysis Serieschaltung Schaltbild: Widerstände: tot = i = Strom: I = I = I 3 = Spannung: V = V i = V + V + V 3 + ichtung beachten! Spannungsteilerregel V i = V i tot Parallelschaltung bei zwei Widerständen: V V = Schaltbild: Widerstände: tot = wenn alle gleich: tot = i Anz. für zwei Widerstände: tot = + Strom: I = I i = I + I + I 3 + Spannung: V = V = V 3 = Leitfähigkeit: G = =[S] Siemens Stromteilerregel I i = I tot i mit zwei Widerständen: I = + I bzw. I = + I
4 Seite 4. Dezember 009 Kirchhoff sche egeln KCL-Knotenregel: Die Summe aller zufliessenden Ströme in einem Knoten ist Null. Dabei Nützlich: Über einen Widerstand gilt: I = V V V I V KVL-Maschenregel: Die Summe der Potentiale, die über einen geschlossenen Kreislauf an- und abfallen ist Null. 0 V =0 Superpositions-Theoreme Verschiedene Strom- und Spannungsquellen können einzeln betrachtet werden (Achtung AC bei unterschiedlichen Frequenzen!) Die nicht zu berechnenden Strom und Spannungsquellen werden folgendermassen gehandhabt. E I Thévenin-Theorem: Jedes linear elektrische Netzwerk kann bezüglich zweier Klemmen zu einer Ersatzspannungsquelle, dem Thévenin- Äquivalent, bestehend aus einer Spannungsquelle und einem Widerstand in Serie, umgeformt werden. Ersatzwiderstand Th : Alle Strom- und Spannungsquellen gemäss Superposition behandeln. Widerstand an offenen Klemmen berechnen. Entspricht No. Ersatzspannung E Th : Gemäss Superpositionsprinzip offene Stromkreisspannungen an offenen Klemmen berechnen und Summe bilden. E Th Th Norton-Theorem: Ähnlich dem Thévenin-Theorem mit dem Unterschied, dass Ersatzstromquelle und Ersatzwiderstand parallel sind. Ersatzwiderstand No : Entspricht Th des Thévenin- Theorems. Ersatzstromquelle I No : Gemäss Superpositionsprinzip Kurzschlussströme berechnen an geschlossenen Klemmen und Summe bilden. I No No
5 Seite 5. Dezember 009 Umwandlung zwischen Thévenin und Norton: I N = E Th Th E Th = I N Th No = Th Maximale Leistungsübertragung: L = Th E Th Th L E L = E Th L = No I No No L I L = I No Verfahren zur Analyse Ast-Strom-Analyse:. Nummeriere in jedem Ast einen Strom. Wende in jeder Masche das KVL an 3. Wende das KCL an (an einem Minimum der Knoten (alle Äste)) 4. Löse die Gleichungen Maschen-Analyse:. Nummeriere jede unabhängige geschlossene Masche. Wende KVL in jeder Masche an Knoten-Analyse:. Nummeriere die Knoten. Wähle einen eferenzknoten und setze Potential Null 3. KCL an restlichen Knoten V,V,V 3, Löse das Gleichungssystem Brückenschaltungen: Falls das Verhältnis : 3 = : 4 gilt, fliesst kein Strom durch 5 und der Widerstand kann aus dem Schaltbild entfernt werden.
6 Seite 6. Dezember Gleichstrom DC Strom und Spannung mit konstanter ichtung und Betrag Leistung P = u t = I V P = I P = V [ W = J ] s Kondensatoren Symbol: Kapazität: Differentialgleichungen: Lade- und Entladevorgang: C i = Q i V i =[F ] Faraday (gilt in jedem Kondensator i) i C (t) = dq C dt = C dv C dt v C (t) = C i C (t) dt Zum Zeitpunkt t = t 0 wird der Schalter umgeschaltet, sodass sich der bis dahin vollständig aufgeladene Kondensator wieder vollständig entlädt. + - E t < t 0 t! t 0 C i C (t) v C (t) Ladephase: Entladephase: E i C (t) v C (t) =0 i C (t) + v C (t) = 0 C d (v dt C(t)) + v C (t) =E C d (v dt C(t)) = v C (t) v C (t) =E ( ) e t / C v C (t) =E ( ) e t / C ( ) i C (t) = E / C i e t C (t) = E e t / C t =0: v C (t) = 0 t = t 0 : v C (t) =E t : v C (t) =0 i C (t) = E i C (t) = 0 i C (t) = E v (t) =E v (t) =0 v (t) =E Graphische Darstellung:
7 Seite 7. Dezember 009 Serieschaltung: + - E + 3 Parallelschaltung: - E 3 Spulen Gespeicherte Energie: Q T = Q = Q = Q 3 Q T = Q + Q + Q 3 E = Q + Q + Q 3 CV = C V + C V + C 3 V C C C 3 E = V + V + V 3 E = V = V = V 3 = C tot = C i C tot C i U = QV = CV = Q C Plattenkondensator: V = E d E = V d = F Q gespeichert im elektrischen Feld C = Q V = ε 0 ε r A d Symbol: Induktivität: L = dφ [ di = H = Vs ] A Henry (Φ magnetischer Fluss) Spulengüte: Q L = w L L (gilt in jeder Spule) Differentialgleichungen: i L (t) = L v L (t) dt v L (t) =L di L dt Lade- und Entladevorgang: Zum Zeitpunkt t = t 0 wird der Schalter umgeschaltet, sodass sich die bis dahin vollständig aufgeladene Spule wieder vollständig entlädt. + - E t < t 0 t! t 0 L i L (t) v L (t) Ladephase: Entladephase: E i L (t) v L (t) = 0 i L (t) + v L (t) = 0 i L (t) + L d (i L d dt L(t)) = E dt L(t)) = i L (t) i L (t) = E ( e t L ) i L (t) = E e t L v L (t) =Ee t L v L (t) =E( e t L ) t =0: v L (t) =E t = t 0 : v L (t) = 0 t : v L (t) =E i L (t) =0 i L (t) = E i L (t) =0 v (t) = 0 v (t) =E v (t) =0
8 Seite 8. Dezember 009 Graphische Darstellung: Serieschaltung: + - E + 3 Parallelschaltung: - E 3 L tot = L i L tot = L i Gespeicherte Energie: U = L I gespeichert im Magnetfeld Solenoid: B = µ 0 I n Toroid: B = µ 0 I n πr n Anzahl Windungen h Dicke des ings a Aussenradius i Innenradius r mittlerer adius A Querschnittsfläche n L = µ 0 l A L = µ 0 n h π ln a i 7 Vs µ 0 =4π 0 Am 5 Wechselstrom AC Zeigerdarstellung Polarform Frequenz: Kreisfrequenz: f = T = [Hz] ω = π =πf = [ ] T s Phasenverschiebung: Der Phasenverschiebungswinkel θ ist die Spannung gegenüber dem Strom! θ = (V ) (I)
9 Seite 9. Dezember 009 Zeitsignal: a(t) =A m cos (ωt + θ) Phasor: A = A m (cos θ + j sin θ) =A m e jθ Amplitude: A m = e(a) + Im(A) Phase: θ = (A) = arctan ( ) Im(A) e(a) Impedanz / Admittanz Im xl Z induktiv Komplexer Widerstand: Z = V I = [Ω] e xc kapazitiv Admittanz: Y = Z =[S] Siemens Z Serieschaltung: Z = i Z i Parallelschaltung: Z = i Z i Y = i Y i = i Z i Widerstand x =0 Phasenverschiebung: θ =0 Impedanz: Z = Kondensator / Kapazität x C = ωc Phasenverschiebung: θ = 90 Impedanz: Z C = jωc Ein Kondensator ist ein Kurzschluss für hohe Frequenzen und ein Leerlauf für tiefe Frequenzen (= Gleichstrom).
10 Seite 0. Dezember 009 Spule / Induktivität x L = ωl Phasenverschiebung: Impedanz: θ = +90 Z L = jωl Eine Spule ist ein Leerlauf für hohe Frequenzen und ein Kurzschluss für tiefe Frequenzen (= Gleichstrom). Serienschwingkreis S C L Z = S + jωl + jωc = S + j ( ωl ) ωc esonanzfrequenz: f S = ω S π ω S = LC Güte Q = S ω S C = L S C = ω SL S Bandbreite: BW 3dB = S L = ω S Q ω, = ω S + (Q) ± S L mit: 3dB = Frequenzgänge:
11 Seite. Dezember 009 Parallelschwingkreis P C L Z = P + jωl + jωc = jωl P P ( ω LC)+jωL esonanzfrequenz: f P = ω P π ω P = LC Güte Bandbreite: Q = P ω P C = P C L = P ω P L BW 3dB = ω P Q ω, = ω P mit: 3dB = + (Q) ± ω P Q Frequenzgänge: Netzwerk-Analysis mit Wechselgrössen Unterschiedliche Frequenzen: Befinden sich in einem Netzwerk Elemente mit unterschiedlichen Frequenzen, so müssen sie in zwei unabhängigen echenschritten behandelt werden und könnenerst am Schluss kombiniert werden. Hierzu wird das Superpositionsprinzip verwendet. Die Lösungen der Aufgabe mit den unterschiedlichen Frequenzen ergeben addiert die Lösung.
12 Seite. Dezember 009 Allgemeines Vorgehen: eaktive Elemente mit Impedanzen ersetzen Falls Phasenverschiebungen vorhanden sind müssen diese nur für die Berechnung der Phase beachtet werden und werden ganz zum Schluss addiert oder subtrahiert. Netzwerk mit normaler Netzwerkanalysis lösen! Frequenzen in algebrahische Lösung einsetzen. Komplexe Lösung in eal- und Imaginärteil, Polarform oder am gebräuchlichsten in Betrag und Phase darstellen Mit der letzteren Form kann dann die gesuchte Grösse wieder als Zeitsignal dargestellt werden. Leistung Effektivwerte: Erzeugt ein Wechselstrom in einem Widerstand im Mittel die gleiche Leistung, wie ein Gleichstrom, so ist der Effektivwert des Stromes gleich dem Wert des Gleichstromes. T p(t) =ī(t) = P = I T 0 i(t) dt = I π i(t) dt = I π 0 π I m π = I I eff = Im V eff = Vm Scheinleistung: Die Scheinleistung ist die vektorielle Summe aus Wirkleistung und Blindleistung. P S = S = I eff V eff = I m V m = V m Z = I m Z Wirkleistung: Die Wirkleistung ist die Leistung, die über den Widerstand genutzt werden kann. Sie ist in Phase mit dem Strom. P W = P = P S cos θ = e(p S ) Blindleistung: Die Blindleistung bleibt im System und kann nicht genutzt werden. P B = Q = P S sin θ = Im(P S ) Leistungsfaktor: F = cos θ = P W P S
Kapitel 6: Grundlagen der Wechselstromtechnik
 Inhalt Kapitel 6: Grundlagen der technik Sinusförmige Signale Zeigerdarstellung Darstellung mit komplexen Zahlen komplexe Widerstände Grundschaltungen Leistung im kreis Ortskurven Übertragungsfunktion
Inhalt Kapitel 6: Grundlagen der technik Sinusförmige Signale Zeigerdarstellung Darstellung mit komplexen Zahlen komplexe Widerstände Grundschaltungen Leistung im kreis Ortskurven Übertragungsfunktion
Kleine Formelsammlung für IuK
 Kleine Formelsammlung für IuK Florian Franzmann 17. März 4 Inhaltsverzeichnis 1 Dezimale Vielfache und Teile von Einheiten Konstanten 3 Shannon 3.1 Informationsgehalt...................................
Kleine Formelsammlung für IuK Florian Franzmann 17. März 4 Inhaltsverzeichnis 1 Dezimale Vielfache und Teile von Einheiten Konstanten 3 Shannon 3.1 Informationsgehalt...................................
GRUNDLAGEN DER WECHSELSTROMTECHNIK
 ELEKTROTECHNIK M GLEICHSTROM. ELEKTRISCHE GRÖßEN UND GRUNDGESETZE. ELEKTRISCHE LADUNG UND STROM.3 ELEKTRISCHES FELD UND STROM.4 ELEKTRISCHES SPANNUNG UND POTENTIAL.5 ELEKTRISCHES LEISTUNG UND WIRKUNGSGRAD.6
ELEKTROTECHNIK M GLEICHSTROM. ELEKTRISCHE GRÖßEN UND GRUNDGESETZE. ELEKTRISCHE LADUNG UND STROM.3 ELEKTRISCHES FELD UND STROM.4 ELEKTRISCHES SPANNUNG UND POTENTIAL.5 ELEKTRISCHES LEISTUNG UND WIRKUNGSGRAD.6
/U Wie groß ist den beiden unter 6. genannten Fällen der von der Spannungsquelle U 1 gelieferte Strom? als Formel. 1 + jωc = R 2.
 Aufgabe Ü6 Gegeben ist die angegebene Schaltung:. Berechnen Sie allgemein (als Formel) /. 2. Wie groß ist der Betrag von /? R 3. Um welchen Winkel ist gegenüber phasenverschoben? 4. Skizzieren Sie die
Aufgabe Ü6 Gegeben ist die angegebene Schaltung:. Berechnen Sie allgemein (als Formel) /. 2. Wie groß ist der Betrag von /? R 3. Um welchen Winkel ist gegenüber phasenverschoben? 4. Skizzieren Sie die
Lösungen zu Kapitel 2
 Elektrotechnik für Studium und Praxis: Lösungen Lösungen zu Kapitel Aufgabe.1 Aus der Maschengleichung ergibt sich: I 4 = U q1 + U q R 1 I 1 R I R I R 4 I 4 = 4 V + 1 V Ω 5 A Ω, A 5 Ω 4 A Ω I 4 = (4 +
Elektrotechnik für Studium und Praxis: Lösungen Lösungen zu Kapitel Aufgabe.1 Aus der Maschengleichung ergibt sich: I 4 = U q1 + U q R 1 I 1 R I R I R 4 I 4 = 4 V + 1 V Ω 5 A Ω, A 5 Ω 4 A Ω I 4 = (4 +
Grundlagen der Elektrotechnik 2 Seminaraufgaben
 ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2005.10 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2005.10 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
Grundlagen der Elektrotechnik für Maschinenbauer
 Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 12 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 3. Februar 2005 Klausurdauer : 2 Stunden Hilfsmittel : 5 Blätter Formelsammlung
Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 12 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 3. Februar 2005 Klausurdauer : 2 Stunden Hilfsmittel : 5 Blätter Formelsammlung
FH Giessen-Friedberg StudiumPlus Dipl.-Ing. (FH) M. Beuler Grundlagen der Elektrotechnik Wechselstromtechnik
 4 4. Wechselgrößen Nimmt eine Wechselgröße in bestimmten aufeinander folgenden Zeitabständen wieder denselben Augenblickswert an, nennt man sie periodische Wechselgröße. Allgemeine Darstellung periodischer
4 4. Wechselgrößen Nimmt eine Wechselgröße in bestimmten aufeinander folgenden Zeitabständen wieder denselben Augenblickswert an, nennt man sie periodische Wechselgröße. Allgemeine Darstellung periodischer
Elektrotechnik II Formelsammlung
 Elektrotechnik II Formelsammlung Achim Enthaler 20.03.2007 Gleichungen Allgemeine Gleichungen aus Elektrotechnik I siehe Formelsammlung Elektrotechnik I, SS2006 Maxwell Gleichungen in Integralform Durchutungsgesetz
Elektrotechnik II Formelsammlung Achim Enthaler 20.03.2007 Gleichungen Allgemeine Gleichungen aus Elektrotechnik I siehe Formelsammlung Elektrotechnik I, SS2006 Maxwell Gleichungen in Integralform Durchutungsgesetz
Aufgabe Summe Note Mögliche Punkte Erreichte Punkte
 Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 12 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 30. 3. 2006 Klausurdauer : 2 Stunden Hilfsmittel : 5 Blätter Formelsammlung
Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 12 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 30. 3. 2006 Klausurdauer : 2 Stunden Hilfsmittel : 5 Blätter Formelsammlung
Technische Universität München Lehrstuhl für Technische Elektrophysik. Tutorübungen zu Elektromagnetische Feldtheorie. (Prof.
 Technische Universität München Lehrstuhl für Technische Elektrophysik Tutorübungen zu Elektromagnetische Feldtheorie Prof. Wachutka Wintersemester 08/09 Lösung Blatt 0 Allgemeines zum Thema komplexe Wechselstromrechnung
Technische Universität München Lehrstuhl für Technische Elektrophysik Tutorübungen zu Elektromagnetische Feldtheorie Prof. Wachutka Wintersemester 08/09 Lösung Blatt 0 Allgemeines zum Thema komplexe Wechselstromrechnung
1.2) Bestimmen Sie die Leistung, welche in Abhängigkeit der Frequenz ω am Widerstand abfällt und stellen Sie diesen Zusammenhang graphisch dar.
 Übung /Grundgebiete der Elektrotechnik 3 (WS7/8 Frequenzabhängiges Übertragungsverhalten Dr. Alexander Schaum, Lehrstuhl für vernetzte elektronische Systeme Christian-Albrechts-Universität zu Kiel Aufgabe
Übung /Grundgebiete der Elektrotechnik 3 (WS7/8 Frequenzabhängiges Übertragungsverhalten Dr. Alexander Schaum, Lehrstuhl für vernetzte elektronische Systeme Christian-Albrechts-Universität zu Kiel Aufgabe
Praktikum II RE: Elektrische Resonanz
 Praktikum II E: Elektrische esonanz Betreuer: Dr. Torsten Hehl Hanno ein [email protected] Florian Jessen [email protected] 29. März 2004 Made with L A TEX and Gnuplot Praktikum
Praktikum II E: Elektrische esonanz Betreuer: Dr. Torsten Hehl Hanno ein [email protected] Florian Jessen [email protected] 29. März 2004 Made with L A TEX and Gnuplot Praktikum
2 Komplexe Rechnung in der Elektrotechnik
 Komplexe echnung in der Elektrotechnik. Einleitung Wechselstromnetwerke sind Netwerke, in denen sinusförmige Spannungen oder ströme gleicher Frequen auf ohmsche, induktive und kapaitive Widerstände wirken.
Komplexe echnung in der Elektrotechnik. Einleitung Wechselstromnetwerke sind Netwerke, in denen sinusförmige Spannungen oder ströme gleicher Frequen auf ohmsche, induktive und kapaitive Widerstände wirken.
Experimentalphysik II Zeitlich veränderliche Felder und Wechselstrom
 Experimentalphysik II Zeitlich veränderliche Felder und Wechselstrom Ferienkurs Sommersemester 009 Martina Stadlmeier 09.09.009 Inhaltsverzeichnis 1 Zeitlich veränderliche Felder 1.1 Faradaysches Induktionsgesetz.....................
Experimentalphysik II Zeitlich veränderliche Felder und Wechselstrom Ferienkurs Sommersemester 009 Martina Stadlmeier 09.09.009 Inhaltsverzeichnis 1 Zeitlich veränderliche Felder 1.1 Faradaysches Induktionsgesetz.....................
Anwendungen zu komplexen Zahlen
 HM an der HWS. Hj 08/9 Dr. Timo Essig, Dr. Marinela Wong [email protected], [email protected] Aufgabenblatt 7 Anwendungen zu komplexen Zahlen Achtung: Auf diesem Blatt schreiben wir die komplexe Einheit
HM an der HWS. Hj 08/9 Dr. Timo Essig, Dr. Marinela Wong [email protected], [email protected] Aufgabenblatt 7 Anwendungen zu komplexen Zahlen Achtung: Auf diesem Blatt schreiben wir die komplexe Einheit
Physik-Department. Ferienkurs zur Experimentalphysik 2 - Musterlösung
 Physik-Department Ferienkurs zur Experimentalphysik 2 - Musterlösung Daniel Jost 27/08/13 Technische Universität München Aufgaben zur Magnetostatik Aufgabe 1 Bestimmen Sie das Magnetfeld eines unendlichen
Physik-Department Ferienkurs zur Experimentalphysik 2 - Musterlösung Daniel Jost 27/08/13 Technische Universität München Aufgaben zur Magnetostatik Aufgabe 1 Bestimmen Sie das Magnetfeld eines unendlichen
ET II Übung 1 Überlagerung von Quellen
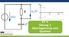 ET II Übung 1 Überlagerung von Quellen Allgemeines zum Kurs Übungen sind freiwillig Einreichung der Übungen ist freiwillig Alle Dokumente sind auf MOODLE hochgestellt!!! Kontakt: Silvan Plüss e-mail: [email protected]
ET II Übung 1 Überlagerung von Quellen Allgemeines zum Kurs Übungen sind freiwillig Einreichung der Übungen ist freiwillig Alle Dokumente sind auf MOODLE hochgestellt!!! Kontakt: Silvan Plüss e-mail: [email protected]
Musterlösung Grundlagen der Elektrotechnik B
 Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 06.0.206 06.0.206 Musterlösung Grundlagen der Elektrotechnik B Seite von 3 Aufgabe : Gleichstrommaschine (20 Punkte) In dieser
Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 06.0.206 06.0.206 Musterlösung Grundlagen der Elektrotechnik B Seite von 3 Aufgabe : Gleichstrommaschine (20 Punkte) In dieser
Aufgabe Summe Note Mögliche Punkte Erreichte Punkte
 Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 1 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 7. April 005 Klausurdauer : Stunden Hilfsmittel : 5 Blätter Formelsammlung DIN
Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 1 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 7. April 005 Klausurdauer : Stunden Hilfsmittel : 5 Blätter Formelsammlung DIN
RE - Elektrische Resonanz Praktikum Wintersemester 2005/06
 RE - Elektrische Resonanz Praktikum Wintersemester 5/6 Philipp Buchegger, Johannes Märkle Assistent Dr. Torsten Hehl Tübingen, den 8. November 5 Einführung Ziel dieses Versuches ist es, elektrische Resonanz
RE - Elektrische Resonanz Praktikum Wintersemester 5/6 Philipp Buchegger, Johannes Märkle Assistent Dr. Torsten Hehl Tübingen, den 8. November 5 Einführung Ziel dieses Versuches ist es, elektrische Resonanz
1 Elektrostatik TUM EM-Tutorübung SS 10. Formelsammlung EM SS Fabian Steiner, Paskal Kiefer
 TUM EM-Tutorübung SS 1 1.5.21 Formelsammlung EM SS 21 Diese Formelsammlung dient nur zur Orientierung und stellt keinen nspruch auf ollständigkeit. Zudem darf sie während der Prüfung nicht benutzt werden,
TUM EM-Tutorübung SS 1 1.5.21 Formelsammlung EM SS 21 Diese Formelsammlung dient nur zur Orientierung und stellt keinen nspruch auf ollständigkeit. Zudem darf sie während der Prüfung nicht benutzt werden,
Technische Universität Clausthal
 Technische Universität Clausthal Klausur im Wintersemester 2012/2013 Grundlagen der Elektrotechnik I Datum: 18. März 2013 Prüfer: Prof. Dr.-Ing. Beck Institut für Elektrische Energietechnik Univ.-Prof.
Technische Universität Clausthal Klausur im Wintersemester 2012/2013 Grundlagen der Elektrotechnik I Datum: 18. März 2013 Prüfer: Prof. Dr.-Ing. Beck Institut für Elektrische Energietechnik Univ.-Prof.
Übungen zur Klassischen Physik II (Elektrodynamik) SS 2016
 Institut für Experimentelle Kernphysik, KIT Übungen zur Klassischen Physik II Elektrodynamik) SS 206 Prof. Dr. T. Müller Dr. F. Hartmann 2tes und letztes Übungsblatt - Spulen, Wechselstrom mit komplexen
Institut für Experimentelle Kernphysik, KIT Übungen zur Klassischen Physik II Elektrodynamik) SS 206 Prof. Dr. T. Müller Dr. F. Hartmann 2tes und letztes Übungsblatt - Spulen, Wechselstrom mit komplexen
NTB Druckdatum: ELA II. Zeitlicher Verlauf Wechselgrösse: Augenblickswert ändert sich periodisch und der zeitliche Mittelwert ist Null.
 WECHSELSTROMLEHRE Wechselgrössen Zeitlicher Verlauf Wechselgrösse: Augenblickswert ändert sich periodisch und der zeitliche Mittelwert ist Null. Zeigerdarstellung Mittelwerte (Gleichwert, Gleichrichtwert
WECHSELSTROMLEHRE Wechselgrössen Zeitlicher Verlauf Wechselgrösse: Augenblickswert ändert sich periodisch und der zeitliche Mittelwert ist Null. Zeigerdarstellung Mittelwerte (Gleichwert, Gleichrichtwert
Diplomvorprüfung WS 2009/10 Grundlagen der Elektrotechnik Dauer: 90 Minuten
 Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 8 Hochschule München Fakultät 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung WS 2009/10
Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 8 Hochschule München Fakultät 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung WS 2009/10
2. Parallel- und Reihenschaltung. Resonanz
 Themen: Parallel- und Reihenschaltungen RLC Darstellung auf komplexen Ebene Resonanzerscheinungen // Schwingkreise Leistung bei Resonanz Blindleistungskompensation 1 Reihenschaltung R, L, C R L C U L U
Themen: Parallel- und Reihenschaltungen RLC Darstellung auf komplexen Ebene Resonanzerscheinungen // Schwingkreise Leistung bei Resonanz Blindleistungskompensation 1 Reihenschaltung R, L, C R L C U L U
Formelsammlung. Experimentalphysik II. Zur Vorlesung bei Prof. Dr. M. Wuttig, Sommersemester Pascal Del Haye 27.
 Formelsammlung Experimentalphysik II Zur Vorlesung bei Prof. Dr. M. Wuttig, Sommersemester 2003 Pascal Del Haye www.delhaye.de 27. Juli 2003 Inhaltsverzeichnis Thermodynamik 3. Ideale Gasgleichung........................
Formelsammlung Experimentalphysik II Zur Vorlesung bei Prof. Dr. M. Wuttig, Sommersemester 2003 Pascal Del Haye www.delhaye.de 27. Juli 2003 Inhaltsverzeichnis Thermodynamik 3. Ideale Gasgleichung........................
3.5. Prüfungsaufgaben zur Wechselstromtechnik
 3.5. Prüfungsaufgaben zur Wechselstromtechnik Aufgabe : Impedanz (4) Erkläre die Formel C i C und leite sie aus der Formel C Q für die Kapazität eines Kondensators her. ösung: (4) Betrachtet man die Wechselspannung
3.5. Prüfungsaufgaben zur Wechselstromtechnik Aufgabe : Impedanz (4) Erkläre die Formel C i C und leite sie aus der Formel C Q für die Kapazität eines Kondensators her. ösung: (4) Betrachtet man die Wechselspannung
Technische Universität Kaiserslautern Lehrstuhl Entwurf Mikroelektronischer Systeme Prof. Dr.-Ing. N. Wehn. Probeklausur
 Technische Universität Kaiserslautern Lehrstuhl Entwurf Mikroelektronischer Systeme Prof. Dr.-Ing. N. Wehn 22.02.200 Probeklausur Elektrotechnik I für Maschinenbauer Name: Vorname: Matr.-Nr.: Fachrichtung:
Technische Universität Kaiserslautern Lehrstuhl Entwurf Mikroelektronischer Systeme Prof. Dr.-Ing. N. Wehn 22.02.200 Probeklausur Elektrotechnik I für Maschinenbauer Name: Vorname: Matr.-Nr.: Fachrichtung:
Grundlagen der Elektrotechnik 2 Übungsaufgaben
 ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2006.07 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2006.07 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
Serie 12 Musterlösung
 Serie 2 Musterlösung ineare Algebra www.adams-science.org Klasse: Ea, Eb, Sb Datum: HS 7 In dieser Serie werden alle echnungen in der Basis und in SI-Einheiten durchgeführt. e ˆ cos(ω t) und e 2 ˆ sin(ω
Serie 2 Musterlösung ineare Algebra www.adams-science.org Klasse: Ea, Eb, Sb Datum: HS 7 In dieser Serie werden alle echnungen in der Basis und in SI-Einheiten durchgeführt. e ˆ cos(ω t) und e 2 ˆ sin(ω
Elektrotechnik I MAVT
 Prof. Dr. Q. Huang Elektrotechnik MAVT Prüfung H07 BSc 23.08.2007 1. [30P] DC-Aufgaben (a) [9P] Betrachten Sie die Schaltung in Abbildung 1 und lösen Sie die nachfolgenden Aufgaben. Vereinfachen Sie die
Prof. Dr. Q. Huang Elektrotechnik MAVT Prüfung H07 BSc 23.08.2007 1. [30P] DC-Aufgaben (a) [9P] Betrachten Sie die Schaltung in Abbildung 1 und lösen Sie die nachfolgenden Aufgaben. Vereinfachen Sie die
Grundlagen der Elektrotechnik B
 Prof. Dr. Ing. Joachim Böcker Grundlagen der Elektrotechnik B 13.03.013 Name: Matrikelnummer: Vorname: Studiengang: Fachprüfung Leistungsnachweis Aufgabe: (Punkte 1 (11 (17 3 (14 4 (1 5 (13 Punkte Klausur
Prof. Dr. Ing. Joachim Böcker Grundlagen der Elektrotechnik B 13.03.013 Name: Matrikelnummer: Vorname: Studiengang: Fachprüfung Leistungsnachweis Aufgabe: (Punkte 1 (11 (17 3 (14 4 (1 5 (13 Punkte Klausur
Formelsammlung Elektrotechnik von Sascha Spors V1.3 /
 Formelsammlung Elektrotechnik von Sascha Spors V.3 /..96 Mathematische Formeln : arctan( b a Z a + jb Y arg(z ; arctan( b a arctan( b < a für a >, b +π für a π für a
Formelsammlung Elektrotechnik von Sascha Spors V.3 /..96 Mathematische Formeln : arctan( b a Z a + jb Y arg(z ; arctan( b a arctan( b < a für a >, b +π für a π für a
Gegeben ist die dargestellte Schaltung mit nebenstehenden Werten. Daten: U AB. der Induktivität L! und I 2. , wenn Z L. = j40 Ω ist? an!
 Grundlagen der Elektrotechnik I Aufgabe K4 Gegeben ist die dargestellte Schaltung mit nebenstehenden Werten. R 1 A R 2 Daten R 1 30 Ω R 3 L R 2 20 Ω B R 3 30 Ω L 40 mh 1500 V f 159,15 Hz 1. Berechnen Sie
Grundlagen der Elektrotechnik I Aufgabe K4 Gegeben ist die dargestellte Schaltung mit nebenstehenden Werten. R 1 A R 2 Daten R 1 30 Ω R 3 L R 2 20 Ω B R 3 30 Ω L 40 mh 1500 V f 159,15 Hz 1. Berechnen Sie
17. Wechselströme. me, 18.Elektromagnetische Wellen. Wechselstromtransformation. = = (gilt bei Ohm schen Lasten
 Wechselstromtransformation Idee: Anwendung der Induktion und der Feldführung in einem Eisenkern zur verlustarmen Transformation der Amplitude von Wechselspannungen Anwendung (n >>n 1 ): Hochspannungserzeugung
Wechselstromtransformation Idee: Anwendung der Induktion und der Feldführung in einem Eisenkern zur verlustarmen Transformation der Amplitude von Wechselspannungen Anwendung (n >>n 1 ): Hochspannungserzeugung
Uebungsserie 1.3 RLC-Netzwerke und komplexe Leistung
 15. September 2017 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.3 RLC-Netzwerke und komplexe Leistung Aufgabe 1. Komplexe Impedanz von Zweipolen Bestimmen Sie für die nachfolgenden Schaltungen
15. September 2017 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.3 RLC-Netzwerke und komplexe Leistung Aufgabe 1. Komplexe Impedanz von Zweipolen Bestimmen Sie für die nachfolgenden Schaltungen
Diplomvorprüfung SS 2010 Fach: Grundlagen der Elektrotechnik Dauer: 90 Minuten
 Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 8 Hochschule München FK 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung SS 2010 Fach: Grundlagen
Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 8 Hochschule München FK 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung SS 2010 Fach: Grundlagen
Klausur Grundlagen der Elektrotechnik I (MB, SB, VT, EUT, BVT, LUM) Seite 1 von 5 R 3 U 3. Antwort hier eintragen R 3
 Klausur 06.09.2010 Grundlagen der Elektrotechnik I (MB, SB, VT, EUT, BVT, LUM) Seite 1 von 5 Aufgabe 1 (4 Punkte) Folgendes Netzwerk ist gegeben: U 2 Name: Matr.-Nr.: 1 I 4 2 1 = 10 Ω 2 = 10 Ω 3 = 10 Ω
Klausur 06.09.2010 Grundlagen der Elektrotechnik I (MB, SB, VT, EUT, BVT, LUM) Seite 1 von 5 Aufgabe 1 (4 Punkte) Folgendes Netzwerk ist gegeben: U 2 Name: Matr.-Nr.: 1 I 4 2 1 = 10 Ω 2 = 10 Ω 3 = 10 Ω
Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt
 DHBW Karlsruhe Grundlagen der Elektrotechnik II Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt 5 Hoch und Tiefpässe 5. L--Hoch und Tiefpass Abbildung
DHBW Karlsruhe Grundlagen der Elektrotechnik II Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt 5 Hoch und Tiefpässe 5. L--Hoch und Tiefpass Abbildung
Übungen zur Physik II PHY 121, FS 2017
 Übungen zur Physik II PHY, FS 07 Serie Abgabe: Dienstag, 3. Mai 00 Impedanz = impedance Phasenlage = phasing Wirkleistung = active power Blindleistung = reactive power Scheinleistung = apparent power Schaltung
Übungen zur Physik II PHY, FS 07 Serie Abgabe: Dienstag, 3. Mai 00 Impedanz = impedance Phasenlage = phasing Wirkleistung = active power Blindleistung = reactive power Scheinleistung = apparent power Schaltung
Uebungsserie 1.4 Ersatzzweipole, Resonanz und Blindleistungskompensation
 1. Oktober 2015 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.4 Ersatzzweipole, Resonanz und Blindleistungskompensation Aufgabe 1. Ersatzzweipole a) Berechnen Sie die Bauteilwerte für R r und L
1. Oktober 2015 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.4 Ersatzzweipole, Resonanz und Blindleistungskompensation Aufgabe 1. Ersatzzweipole a) Berechnen Sie die Bauteilwerte für R r und L
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 23. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 23. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 23. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 23. 06.
Uebungsserie 1.4 Ersatzzweipole, Resonanz und Blindleistungskompensation
 15. September 2017 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.4 Ersatzzweipole, Resonanz und Blindleistungskompensation Aufgabe 1. Ersatzzweipole a) Berechnen Sie die Bauteilwerte für R r und
15. September 2017 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.4 Ersatzzweipole, Resonanz und Blindleistungskompensation Aufgabe 1. Ersatzzweipole a) Berechnen Sie die Bauteilwerte für R r und
Musterlösung Grundlagen der Elektrotechnik B
 Fachgebiet Leistungselektronik und Elektrische Antriebstechnik Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 7.08.200 7.08.200 Musterlösung Grundlagen der Elektrotechnik B
Fachgebiet Leistungselektronik und Elektrische Antriebstechnik Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 7.08.200 7.08.200 Musterlösung Grundlagen der Elektrotechnik B
1 Elektrostatik Elektrische Feldstärke E Potential, potentielle Energie Kondensator... 4
 Inhaltsverzeichnis 1 Elektrostatik 3 1.1 Elektrische Feldstärke E............................... 3 1.2 Potential, potentielle Energie............................ 4 1.3 Kondensator.....................................
Inhaltsverzeichnis 1 Elektrostatik 3 1.1 Elektrische Feldstärke E............................... 3 1.2 Potential, potentielle Energie............................ 4 1.3 Kondensator.....................................
Induktion. Bewegte Leiter
 Induktion Bewegte Leiter durch die Kraft werden Ladungsträger bewegt auf bewegte Ladungsträger wirkt im Magnetfeld eine Kraft = Lorentzkraft Verschiebung der Ladungsträger ruft elektrisches Feld hervor
Induktion Bewegte Leiter durch die Kraft werden Ladungsträger bewegt auf bewegte Ladungsträger wirkt im Magnetfeld eine Kraft = Lorentzkraft Verschiebung der Ladungsträger ruft elektrisches Feld hervor
Grundlagen der Elektrotechnik. Übungsaufgaben
 Grundlagen der Elektrotechnik Sönke Carstens-Behrens Wintersemester 2009/2010 RheinAhrCampus 1 Grundlagen der Elektrotechnik, WiSe 2009/2010 Aufgabe 1: Beantworten Sie folgende Fragen: a) Wie viele Elektronen
Grundlagen der Elektrotechnik Sönke Carstens-Behrens Wintersemester 2009/2010 RheinAhrCampus 1 Grundlagen der Elektrotechnik, WiSe 2009/2010 Aufgabe 1: Beantworten Sie folgende Fragen: a) Wie viele Elektronen
Musterlösung Grundlagen der Elektrotechnik B
 Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 01.04.2015 01.04.2015 Musterlösung Grundlagen der Elektrotechnik B Seite 1 von 14 Aufgabe 1: Gleichstrommaschine (20 Punkte) LÖSUNG
Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 01.04.2015 01.04.2015 Musterlösung Grundlagen der Elektrotechnik B Seite 1 von 14 Aufgabe 1: Gleichstrommaschine (20 Punkte) LÖSUNG
Elektrotechnik: Übungsblatt 3 - Gleichstromschaltungen
 Elektrotechnik: Übungsblatt 3 - Gleichstromschaltungen 1. Aufgabe: Nennen sie die Kirchhoffschen Gesetzte und erläutern sie ihre physikalischen Prinzipien mit eigenen Worten. Lösung: Knotenregel: Die vorzeichenrichtige
Elektrotechnik: Übungsblatt 3 - Gleichstromschaltungen 1. Aufgabe: Nennen sie die Kirchhoffschen Gesetzte und erläutern sie ihre physikalischen Prinzipien mit eigenen Worten. Lösung: Knotenregel: Die vorzeichenrichtige
Grundlagen der Elektrotechnik
 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Ingo Wolff Grundlagen der Elektrotechnik Einführung in die elektrischen
2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Ingo Wolff Grundlagen der Elektrotechnik Einführung in die elektrischen
Aufgaben zur Experimentalphysik II: Elektromagnetische Schwingungen und Wellen
 Aufgaben zur Experimentalphysik II: Elektromagnetische Schwingungen und Wellen Musterlösung William Hefter - 10/09/009 1. Elektromagnetische Schwingungen 1. Die dafür benötigte Zeit ist t = T 4, wobei
Aufgaben zur Experimentalphysik II: Elektromagnetische Schwingungen und Wellen Musterlösung William Hefter - 10/09/009 1. Elektromagnetische Schwingungen 1. Die dafür benötigte Zeit ist t = T 4, wobei
Seite 1 von 8 FK 03. W. Rehm. Name, Vorname: Taschenrechner, Unterschrift I 1 U 1. U d U 3 I 3 R 4. die Ströme. I 1 und I
 Diplomvorprüfung GET Seite 1 von 8 Hochschule München FK 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung SS 2011 Fach: Grundlagen der Elektrotechnik,
Diplomvorprüfung GET Seite 1 von 8 Hochschule München FK 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung SS 2011 Fach: Grundlagen der Elektrotechnik,
Grundlagen der Elektrotechnik I
 Prof. Dr.-Ing. B. Schmülling Musterlösung zur Klausur Grundlagen der Elektrotechnik I im Wintersemester 27 / 28 Aufgabe : Die Lösungen zu Aufgabe folgen am Ende. Aufgabe 2:. U q = 3 V 2. R i = Ω 3. P =
Prof. Dr.-Ing. B. Schmülling Musterlösung zur Klausur Grundlagen der Elektrotechnik I im Wintersemester 27 / 28 Aufgabe : Die Lösungen zu Aufgabe folgen am Ende. Aufgabe 2:. U q = 3 V 2. R i = Ω 3. P =
Praktikum EE2 Grundlagen der Elektrotechnik. Name: Testat : Einführung
 Fachbereich Elektrotechnik Ortskurven Seite 1 Name: Testat : Einführung 1. Definitionen und Begriffe 1.1 Ortskurven für den Strom I und für den Scheinleistung S Aus den Ortskurven für die Impedanz Z(f)
Fachbereich Elektrotechnik Ortskurven Seite 1 Name: Testat : Einführung 1. Definitionen und Begriffe 1.1 Ortskurven für den Strom I und für den Scheinleistung S Aus den Ortskurven für die Impedanz Z(f)
Musterlösung Grundlagen der Elektrotechnik B
 Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 7.4.2 7.4.2 Musterlösung Grundlagen der Elektrotechnik B Seite von 4 Version vom 6. Mai 2 Aufgabe : Ausgleichsvorgang 2 Punkte).
Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 7.4.2 7.4.2 Musterlösung Grundlagen der Elektrotechnik B Seite von 4 Version vom 6. Mai 2 Aufgabe : Ausgleichsvorgang 2 Punkte).
1 Allgemeine Grundlagen
 Allgemeine Grundlagen. Gleichstromkreis.. Stromdichte Die Stromdichte in einem stromdurchflossenen Leiter mit der Querschnittsfläche A ist definiert als: j d d :Stromelement :Flächenelement.. Die Grundelemente
Allgemeine Grundlagen. Gleichstromkreis.. Stromdichte Die Stromdichte in einem stromdurchflossenen Leiter mit der Querschnittsfläche A ist definiert als: j d d :Stromelement :Flächenelement.. Die Grundelemente
Ferienkurs Experimentalphysik II Elektrodynamik
 Ferienkurs Experimentalphysik II Elektrodynamik Lennart Schmidt 07.09.2011 Inhaltsverzeichnis 1 Zeitlich veränderliche Felder 3 1.1 Induktion.................................... 3 1.2 Die Maxwell-Gleichungen...........................
Ferienkurs Experimentalphysik II Elektrodynamik Lennart Schmidt 07.09.2011 Inhaltsverzeichnis 1 Zeitlich veränderliche Felder 3 1.1 Induktion.................................... 3 1.2 Die Maxwell-Gleichungen...........................
Name:...Vorname:... Seite 1 von 8. Hochschule München, FK 03 Grundlagen der Elektrotechnik WS 2008/2009
 Name:...Vorname:... Seite 1 von 8 Hochschule München, FK 03 Grundlagen der Elektrotechnik WS 2008/2009 Matrikelnr.:... Hörsaal:...Platz:... Stud. Gruppe:... Zugelassene Hilfsmittel: beliebige eigene A
Name:...Vorname:... Seite 1 von 8 Hochschule München, FK 03 Grundlagen der Elektrotechnik WS 2008/2009 Matrikelnr.:... Hörsaal:...Platz:... Stud. Gruppe:... Zugelassene Hilfsmittel: beliebige eigene A
Zusammenfassung EPII. Elektromagnetismus
 Zusammenfassung EPII Elektromagnetismus Elektrodynamik: Überblick Dynamik (Newton): Elektromagnetische Kräfte zw. Ladungen: Definition EFeld: Kraft auf ruhende Testladung Q: BFeld: Kraft auf bewegte Testladung:
Zusammenfassung EPII Elektromagnetismus Elektrodynamik: Überblick Dynamik (Newton): Elektromagnetische Kräfte zw. Ladungen: Definition EFeld: Kraft auf ruhende Testladung Q: BFeld: Kraft auf bewegte Testladung:
rtllh Grundlagen der Elektrotechnik Gert Hagmann AULA-Verlag
 Gert Hagmann Grundlagen der Elektrotechnik Das bewährte Lehrbuch für Studierende der Elektrotechnik und anderer technischer Studiengänge ab 1. Semester Mit 225 Abbildungen, 4 Tabellen, Aufgaben und Lösungen
Gert Hagmann Grundlagen der Elektrotechnik Das bewährte Lehrbuch für Studierende der Elektrotechnik und anderer technischer Studiengänge ab 1. Semester Mit 225 Abbildungen, 4 Tabellen, Aufgaben und Lösungen
IV. Elektrizität und Magnetismus
 IV. Elektrizität und Magnetismus IV.4 Wechselstromkreise Physik für Mediziner Ohmscher Widerstand bei Wechselstrom Der Ohmsche Widerstand verhält sich bei Wechselstrom genauso wie bei Gleichstrom zu jedem
IV. Elektrizität und Magnetismus IV.4 Wechselstromkreise Physik für Mediziner Ohmscher Widerstand bei Wechselstrom Der Ohmsche Widerstand verhält sich bei Wechselstrom genauso wie bei Gleichstrom zu jedem
Versuchsvorbereitung: P1-83,84: Ferromagnetische Hysteresis
 Praktikum Klassische Physik I Versuchsvorbereitung: P1-83,84: Ferromagnetische Hysteresis Jingfan Ye Gruppe Mo-11 Karlsruhe, 23. November 2009 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer
Praktikum Klassische Physik I Versuchsvorbereitung: P1-83,84: Ferromagnetische Hysteresis Jingfan Ye Gruppe Mo-11 Karlsruhe, 23. November 2009 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer
Name:...Vorname:... Seite 1 von 8. FH München, FB 03 Grundlagen der Elektrotechnik SS 2003
 Name:...Vorname:... Seite 1 von 8 FH München, FB 03 Grundlagen der Elektrotechnik SS 2003 Matrikelnr.:... Hörsaal:... Platz:... Zugelassene Hilfsmittel: beliebige eigene A 1 2 3 4 Σ N Aufgabensteller:
Name:...Vorname:... Seite 1 von 8 FH München, FB 03 Grundlagen der Elektrotechnik SS 2003 Matrikelnr.:... Hörsaal:... Platz:... Zugelassene Hilfsmittel: beliebige eigene A 1 2 3 4 Σ N Aufgabensteller:
ETiT Praktikum. Durchsprache der elektrotechnischen Grundlagen
 ETiT Praktikum Durchsprache der elektrotechnischen Grundlagen Prof. Dr.-Ing. habil. Dr. h.c. Andreas Binder Tel. : 65 / 6-267 [email protected] V2/ ETiT Praktikum Versuch 2 Kapazitäten und Induktivitäten
ETiT Praktikum Durchsprache der elektrotechnischen Grundlagen Prof. Dr.-Ing. habil. Dr. h.c. Andreas Binder Tel. : 65 / 6-267 [email protected] V2/ ETiT Praktikum Versuch 2 Kapazitäten und Induktivitäten
Grundlagenwissen Elektrotechnik
 Marlene Marinescu I Jürgen Winter Grundlagenwissen Elektrotechnik Gleich-, Wechsel- und Drehstrom 3., bearbeitete und erweiterte Auflage Mit 281 Abbildungen und ausführlichen Beispielen STUDIUM 11 VIEWEG+
Marlene Marinescu I Jürgen Winter Grundlagenwissen Elektrotechnik Gleich-, Wechsel- und Drehstrom 3., bearbeitete und erweiterte Auflage Mit 281 Abbildungen und ausführlichen Beispielen STUDIUM 11 VIEWEG+
Klausur Grundlagen der Elektrotechnik I (MB, SB, VT, EUT, BVT, LUM) Seite 1 von 5 R 3 U 3. Antwort hier eintragen R 3
 Klausur 06.09.2010 Grundlagen der Elektrotechnik I (MB, SB, VT, ET, BVT, LM) Seite 1 von 5 Aufgabe 1 (4 Punkte) Folgendes Netzwerk ist gegeben: 2 Name: Matr.-Nr.: Mit Lösung 1 I 4 2 1 = 10 Ω 2 = 10 Ω 3
Klausur 06.09.2010 Grundlagen der Elektrotechnik I (MB, SB, VT, ET, BVT, LM) Seite 1 von 5 Aufgabe 1 (4 Punkte) Folgendes Netzwerk ist gegeben: 2 Name: Matr.-Nr.: Mit Lösung 1 I 4 2 1 = 10 Ω 2 = 10 Ω 3
Übungen zu Experimentalphysik 2
 Physik Department, Technische Universität München, PD Dr. W. Schindler Übungen zu Experimentalphysik 2 SS 13 - Lösungen zu Übungsblatt 4 1 Schiefe Ebene im Magnetfeld In einem vertikalen, homogenen Magnetfeld
Physik Department, Technische Universität München, PD Dr. W. Schindler Übungen zu Experimentalphysik 2 SS 13 - Lösungen zu Übungsblatt 4 1 Schiefe Ebene im Magnetfeld In einem vertikalen, homogenen Magnetfeld
Grundlagen der Elektrotechnik I im Wintersemester 2017 / 2018
 +//6+ Prof. Dr.-Ing. B. Schmülling Klausur Grundlagen der Elektrotechnik I im Wintersemester 7 / 8 Bitte kreuzen Sie hier Ihre Matrikelnummer an (von links nach rechts). Vor- und Nachname: 3 4 3 4 3 4
+//6+ Prof. Dr.-Ing. B. Schmülling Klausur Grundlagen der Elektrotechnik I im Wintersemester 7 / 8 Bitte kreuzen Sie hier Ihre Matrikelnummer an (von links nach rechts). Vor- und Nachname: 3 4 3 4 3 4
Lehr- und Übungsbuch Elektrotechnik
 Lehr- und Übungsbuch Elektrotechnik Prof. Dr.-Ing. habil. Siegfried Altmann Prof. Dr.-Ing. Detlef Schlayer 2., bearbeitete Auflage mit 689 Bildern, 7 Tabellen, 186 Beispielen und Lösungen Fachbuchverlag
Lehr- und Übungsbuch Elektrotechnik Prof. Dr.-Ing. habil. Siegfried Altmann Prof. Dr.-Ing. Detlef Schlayer 2., bearbeitete Auflage mit 689 Bildern, 7 Tabellen, 186 Beispielen und Lösungen Fachbuchverlag
Reihenschwingkreis. In diesem Versuch soll das Verhalten von ohmschen, kapazitiven und induktiven Widerständen im Wechselstromkreis untersucht werden.
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum E 13 Reihenschwingkreis In diesem Versuch soll das Verhalten von ohmschen, kapazitiven und induktiven Widerständen im Wechselstromkreis
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum E 13 Reihenschwingkreis In diesem Versuch soll das Verhalten von ohmschen, kapazitiven und induktiven Widerständen im Wechselstromkreis
Wechselstromwiderstände
 Wechselstromwiderstände Wirkwiderstand, ideale Spule und idealer Kondensator im Wechselstromkreis Wirkwiderstand R In einem Wirkwiderstand R wird elektrische Energie in Wärmeenergie umgesetzt. Er verursacht
Wechselstromwiderstände Wirkwiderstand, ideale Spule und idealer Kondensator im Wechselstromkreis Wirkwiderstand R In einem Wirkwiderstand R wird elektrische Energie in Wärmeenergie umgesetzt. Er verursacht
Aufgabe 1 Transiente Vorgänge
 Aufgabe 1 Transiente Vorgänge S 2 i 1 i S 1 i 2 U 0 u C C L U 0 = 2 kv C = 500 pf Zum Zeitpunkt t 0 = 0 s wird der Schalter S 1 geschlossen, S 2 bleibt weiterhin in der eingezeichneten Position (Aufgabe
Aufgabe 1 Transiente Vorgänge S 2 i 1 i S 1 i 2 U 0 u C C L U 0 = 2 kv C = 500 pf Zum Zeitpunkt t 0 = 0 s wird der Schalter S 1 geschlossen, S 2 bleibt weiterhin in der eingezeichneten Position (Aufgabe
Übung Grundlagen der Elektrotechnik B
 Übung Grundlagen der Elektrotechnik B Themengebiet E: Komplexe Zahlen Aufgabe 1: echnen mit komplexen Zahlen Stellen Sie die folgenden komplexen Zahlen in der arithmetischen Form (z = x + jy und der exponentiellen
Übung Grundlagen der Elektrotechnik B Themengebiet E: Komplexe Zahlen Aufgabe 1: echnen mit komplexen Zahlen Stellen Sie die folgenden komplexen Zahlen in der arithmetischen Form (z = x + jy und der exponentiellen
E2: Wärmelehre und Elektromagnetismus 20. Vorlesung
 E2: Wärmelehre und Elektromagnetismus 20. Vorlesung 28.06.2018 Barlow-Rad Heute: Telefon nach Bell - Wechselstrom - Transformatoren - Leistungsverluste - R, L, C im Wechselstromkreis 28.06.2018 https://xkcd.com/2006/
E2: Wärmelehre und Elektromagnetismus 20. Vorlesung 28.06.2018 Barlow-Rad Heute: Telefon nach Bell - Wechselstrom - Transformatoren - Leistungsverluste - R, L, C im Wechselstromkreis 28.06.2018 https://xkcd.com/2006/
Wechselstromwiderstände (Impedanzen) Parallel- und Reihenschaltungen. RGes = R1 + R2 LGes = L1 + L2
 Wechselstromwiderstände (Impedanzen) Ohm'scher Widerstand R: Kondensator mit Kapazität C: Spule mit Induktivität L: RwR = R RwC = 1/(ωC) RwL = ωl Parallel- und Reihenschaltungen bei der Reihenschaltung
Wechselstromwiderstände (Impedanzen) Ohm'scher Widerstand R: Kondensator mit Kapazität C: Spule mit Induktivität L: RwR = R RwC = 1/(ωC) RwL = ωl Parallel- und Reihenschaltungen bei der Reihenschaltung
Elektrotechnik für Studierende Inhalt. Vorwort...11
 5 Inhalt Vorwort...11 1 Signale...13 1.1 Definitionen zu Signalen...13 1.2 Klassifizierung von Signalen...15 1.2.1 Klassifizierung nach dem Signalverlauf...15 1.2.1.1 Determinierte Signale...15 1.2.1.2
5 Inhalt Vorwort...11 1 Signale...13 1.1 Definitionen zu Signalen...13 1.2 Klassifizierung von Signalen...15 1.2.1 Klassifizierung nach dem Signalverlauf...15 1.2.1.1 Determinierte Signale...15 1.2.1.2
Wechselspannungen und -ströme
 Überblick Grundlagen: Spannung, Strom, Widerstand, IV-Kennlinien Elektronische Messgeräte im Elektronikpraktikum Passive Filter Signaltransport im Kabel Transistor Operationsverstärker Sensorik PID-egler
Überblick Grundlagen: Spannung, Strom, Widerstand, IV-Kennlinien Elektronische Messgeräte im Elektronikpraktikum Passive Filter Signaltransport im Kabel Transistor Operationsverstärker Sensorik PID-egler
Basiswissen Gleich- und Wechselstromtechnik
 Marlene Marinescu Jürgen Winter Basiswissen Gleich- und Wechselstromtechnik Mit ausführlichen Beispielen Mit 217 Abbildungen Studium Technik vieweg VII Inhaltsverzeichnis I. Grundlegende Begriffe 1 1.
Marlene Marinescu Jürgen Winter Basiswissen Gleich- und Wechselstromtechnik Mit ausführlichen Beispielen Mit 217 Abbildungen Studium Technik vieweg VII Inhaltsverzeichnis I. Grundlegende Begriffe 1 1.
Versuch E Bei einer unbelasteten Spannungsquelle liegt kein geschlossener Stromkreis vor. Außer dem Innenwiderstand
 1 Spannungsquelle Belastete und unbelastete Spannungsquelle: Unbelastete Spannungsquelle Bei einer unbelasteten Spannungsquelle liegt kein geschlossener Stromkreis vor. Außer dem Innenwiderstand R i der
1 Spannungsquelle Belastete und unbelastete Spannungsquelle: Unbelastete Spannungsquelle Bei einer unbelasteten Spannungsquelle liegt kein geschlossener Stromkreis vor. Außer dem Innenwiderstand R i der
Wellen und Elektrodynamik für Chemie- und Bioingenieure und Verfahrenstechniker WS 11/12 Übung 6
 Wellen und Elektrodynamik für Chemie- und Bioingenieure und Verfahrenstechniker WS 11/12 Übung 6 KIT University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz Association
Wellen und Elektrodynamik für Chemie- und Bioingenieure und Verfahrenstechniker WS 11/12 Übung 6 KIT University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz Association
Technische Universität Clausthal
 Technische Universität Clausthal Klausur im Wintersemester 2013/2014 Grundlagen der Elektrotechnik I Datum: 20. Februar 2014 Prüfer: Prof. Dr.-Ing. Beck Institut für Elektrische Energietechnik und Energiesysteme
Technische Universität Clausthal Klausur im Wintersemester 2013/2014 Grundlagen der Elektrotechnik I Datum: 20. Februar 2014 Prüfer: Prof. Dr.-Ing. Beck Institut für Elektrische Energietechnik und Energiesysteme
20. Vorlesung. III Elektrizität und Magnetismus. 21. Wechselstrom 22. Elektromagnetische Wellen IV. Optik 22. Elektromagnetische Wellen (Fortsetzung)
 20. Vorlesung III Elektrizität und Magnetismus 21. Wechselstrom 22. Elektromagnetische Wellen IV. Optik 22. Elektromagnetische Wellen (Fortsetzung) Versuche: Aluring (Nachtrag zur Lenzschen Regel, s.20)
20. Vorlesung III Elektrizität und Magnetismus 21. Wechselstrom 22. Elektromagnetische Wellen IV. Optik 22. Elektromagnetische Wellen (Fortsetzung) Versuche: Aluring (Nachtrag zur Lenzschen Regel, s.20)
Elektrische Messverfahren
 Vorbereitung Elektrische Messverfahren Carsten Röttele 20. Dezember 2011 Inhaltsverzeichnis 1 Messungen bei Gleichstrom 2 1.1 Innenwiderstand des µa-multizets...................... 2 1.2 Innenwiderstand
Vorbereitung Elektrische Messverfahren Carsten Röttele 20. Dezember 2011 Inhaltsverzeichnis 1 Messungen bei Gleichstrom 2 1.1 Innenwiderstand des µa-multizets...................... 2 1.2 Innenwiderstand
Bundestechnologiezentrum für Elektro- und Informationstechnik e.v.
 Lernprogramm Wechselstromtechnik Themenübersicht Wechselstromtechnik Einführung und Begriffe Wechselgrößen Merkmale Wechselgröße Vorteile der Wechselspannung Momentanwert-Scheitelwert-Periodendauer-Frequenz
Lernprogramm Wechselstromtechnik Themenübersicht Wechselstromtechnik Einführung und Begriffe Wechselgrößen Merkmale Wechselgröße Vorteile der Wechselspannung Momentanwert-Scheitelwert-Periodendauer-Frequenz
Übungsblatt 8. = d(i 0 I) Nach Integration beider Seiten und beachtung der Anfangswerte t = 0, I = 0 erhält man:
 Aufgabe 29 Ein Stromkreis bestehe aus einer Spannungsquelle mit Spannung U 0 in Reihe mit einer Induktivität(Spule) L = 0.8H und einem Widerstand R = 10Ω. Zu dem Zeitpunkt t = 0 werde die Spannungsquelle
Aufgabe 29 Ein Stromkreis bestehe aus einer Spannungsquelle mit Spannung U 0 in Reihe mit einer Induktivität(Spule) L = 0.8H und einem Widerstand R = 10Ω. Zu dem Zeitpunkt t = 0 werde die Spannungsquelle
Filter. Ortsverband Pulheim G40
 Filter Ortsverband Pulheim G40 Filter, Einführung 16.02.2018 Filter 2 Vierpol I e I a U e Vierpol U a Übertragungsverhalten bei I a = 0 ist A(jω) A jω = U a U e 16.02.2018 Filter 3 Streuparameter it wissen.de
Filter Ortsverband Pulheim G40 Filter, Einführung 16.02.2018 Filter 2 Vierpol I e I a U e Vierpol U a Übertragungsverhalten bei I a = 0 ist A(jω) A jω = U a U e 16.02.2018 Filter 3 Streuparameter it wissen.de
Experimentalphysik II Elektromagnetische Schwingungen und Wellen
 Experimentalphysik II Elektromagnetische Schwingungen und Wellen Ferienkurs Sommersemester 2009 Martina Stadlmeier 10.09.2009 Inhaltsverzeichnis 1 Elektromagnetische Schwingungen 2 1.1 Energieumwandlung
Experimentalphysik II Elektromagnetische Schwingungen und Wellen Ferienkurs Sommersemester 2009 Martina Stadlmeier 10.09.2009 Inhaltsverzeichnis 1 Elektromagnetische Schwingungen 2 1.1 Energieumwandlung
Wechselstrom und Zeigerdiagramme ohne Ballast. von. Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials
 Wechselstrom und Zeigerdiagramme ohne Ballast von Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses
Wechselstrom und Zeigerdiagramme ohne Ballast von Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses
Elektrotechnische Grundlagen, WS 00/01. Musterlösung Übungsblatt 1. Hieraus läßt sich der Strom I 0 berechnen:
 Elektrotechnische Grundlagen, WS 00/0 Prof. aitinger / Lammert esprechung: 06..000 ufgabe Widerstandsnetzwerk estimmen Sie die Werte der Spannungen,, 3 und 4 sowie der Ströme, I, I, I 3 und I 4 in der
Elektrotechnische Grundlagen, WS 00/0 Prof. aitinger / Lammert esprechung: 06..000 ufgabe Widerstandsnetzwerk estimmen Sie die Werte der Spannungen,, 3 und 4 sowie der Ströme, I, I, I 3 und I 4 in der
Repetitionen. Widerstand, Drosseln und Kondensatoren
 Kapitel 16.1 epetitionen Widerstand, Drosseln und Kondensatoren Verfasser: Hans-udolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausgabe: Oktober 2011 1 1.702 Serieschaltung
Kapitel 16.1 epetitionen Widerstand, Drosseln und Kondensatoren Verfasser: Hans-udolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausgabe: Oktober 2011 1 1.702 Serieschaltung
Maßeinheiten der Elektrizität und des Magnetismus
 Maßeinheiten der Elektrizität und des Magnetismus elektrische Stromstärke I Ampere A 1 A ist die Stärke des zeitlich unveränderlichen elektrischen Stromes durch zwei geradlinige, parallele, unendlich lange
Maßeinheiten der Elektrizität und des Magnetismus elektrische Stromstärke I Ampere A 1 A ist die Stärke des zeitlich unveränderlichen elektrischen Stromes durch zwei geradlinige, parallele, unendlich lange
(2 π f C ) I eff Z = 25 V
 Physik Induktion, Selbstinduktion, Wechselstrom, mechanische Schwingung ösungen 1. Eine Spule mit der Induktivität = 0,20 mh und ein Kondensator der Kapazität C = 30 µf werden in Reihe an eine Wechselspannung
Physik Induktion, Selbstinduktion, Wechselstrom, mechanische Schwingung ösungen 1. Eine Spule mit der Induktivität = 0,20 mh und ein Kondensator der Kapazität C = 30 µf werden in Reihe an eine Wechselspannung
Leistung bei Wechselströmen
 Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 27 VL #4 am 6.7.27 Vladimir Dyakonov Leistung bei Wechselströmen I(t) I(t) Wechselspannung U Gleichspannung
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 27 VL #4 am 6.7.27 Vladimir Dyakonov Leistung bei Wechselströmen I(t) I(t) Wechselspannung U Gleichspannung
