4.3 Affine Punkträume
|
|
|
- Frida Adler
- vor 9 Jahren
- Abrufe
Transkript
1 4.3. AFFINE PUNKTRÄUME Affine Punkträume Es wird jetzt der Übergang von der linearen Algebra zur analytischen Geometrie beschrieben Definition (affiner Punktraum) Sei V ein K-Vektorraum, A eine nicht leere Menge und : A A V, (P, Q) P Q eine Abbildung. Dann heißt (A, ) affiner Punktraum zu V, wenn gilt: 1. P A, v V 1 Q A : (Kurz: Q = P + v.) 2. P, Q, R A : P Q = v. P Q + QR = P R. Die Elemente von A heißen Punkte. Ist V n dimensional, so heißt auch A n dimensional: dim K (A) := dim K (V ). V wird zur Verdeutlichung auch mit V (A) bezeichnet Beispiel Zu V sei A := V und : A A = V V V, (v0, v 1 ) v 0 v 1 := v 1 v 0. Dieser affine Punktraum zu V wird mit D(V ) bezeichnet. Leicht nachzuprüfen ist Hilfssatz Ist (A, ) affiner Raum zu V und sind P, Q, R, S A, dann gilt: 1. P Q = 0V P = Q, 2. P Q = QP, 3. P Q = RS = P R = QS (Parallelogrammregel). Greifen wir uns einen Punkt 0 A als Ursprungspunkt heraus, so ist nach P A eindeutig durch den Vektor p := OP V bestimmt, seinen Ortsvektor. P kann dann mit p identifiziert werden, d.h. wir haben die Bijektion A V, P p := OP. Der Differenzvektor P Q von P und Q genügt dann der Gleichung P Q = q p.
2 186 O Q P Q P Wie man nun damit die lineare Algebra auf die Elementargeometrie anwenden kann zeigt folgendes Beispiel: Beispiel Wir wollen beweisen, daß die Diagonale und die Seitenhalbierende sich in nicht ausgearteten Parallelogrammen im Verhältnis 1:2 schneiden. Beweis: Wir betrachten das Parallelogramm, dessen Punkte wie skizziert bezeichnet seien: D C M P A B Gesucht sind λ, µ R mit P M = λ BM und AP = µ AC. Dazu betrachten wir das Dreieck AMP, für welches gilt: AM + MP + P A = 0, bzw. 1 AD λbm µac = 0. 2 Das ist nach ii) äquivalent zu 1 AD λ( BA + AM) µ( AB + BC) = 0. 2 Da es sich um ein Parallelogramm handelt, gilt BC = AD, so daß sich hieraus folgendes ergibt: ( 1 2 λ µ) AD + (λ µ) AB = 0. 2 Das Parallelogramm ist genau dann nicht ausgeartet, wenn ( AD, AB) linear unabhängig ist, so daß wir schließlich folgendes Gleichungssystem für die gesuchten Parameter bekommen: λ µ = 0
3 4.3. AFFINE PUNKTRÄUME λ 2 µ = 0. Die einzige Lösung ist λ = µ = 1 3, wie behauptet Definition (affine Koordinaten, Unterräume und Abbildungen) A sei ein affiner Punktraum zu V. i) Ein Ursprungspunkt O A ergibt zusammen mit irgendeiner Basisfolge B = (b 0,..., b n 1 ) von V = V (A) ein affines Koordinatensystem (O; B) = (O; b 0,..., b n 1 ). Die diesbezüglichen Komponenten p i des Ortsvektors p = OP von P A : OP = i p i b i heißen die affinen Koordinaten von P bezüglich (0; b 0,..., b n 1 ). ii) B A heißt affiner Unterraum von A, (kurz: B A), wenn gilt: P 0 B : { P 0 Q Q B} V (A). Dieser Vektorraum { P 0 Q Q B} ist offenbar unabhängig von der getroffenen Auswahl von P 0 B und kann deshalb mit V (B) bezeichnet werden, er heißt auch die Richtung von B. In Anlehnung an die Elementargeometrie heißen eindimensionale affine Unterräume Geraden, zweidimensionale heißen Ebenen. (n 1) dimensionale Unterräume n die Dimension von A heißen Hyperebenen. iii) Sind B 0,..., B m affine Unterräume von A, dann heißt der kleinste affine Unterraum, der i B i umfaßt, der Verbindungsraum der B i. Er wird mit B 0... B m bezeichnet. Beispielsweise sind Punkte P, Q A (nulldimensionale) affine Unterräume. Der Verbindungsraum P Q heißt deren Verbindungsgerade, usw. iv) Zwei Unterräume B 0, B 1 eines affinen Punktraumes A heißen parallel, kurz B 0 B 1, wenn die Richtung eines von ihnen in der Richtung des anderen enthalten ist: i: V (B i ) V (B j ), j i. (B 0 und B 1 sind dann offenbar disjunkt oder einer ist im anderen enthalten.) Disjunkte und nicht zueinander parallele Unterräume heißen windschief.
4 188 v) Eine Abbildung f: A A, P P heißt affine Abbildung, wenn und die von f induzierte Abbildung P 1 Q 1 = P 2 Q 2 = P 1Q 1 = P 2Q 2 ϕ: V V, P Q P Q linear ist, also die Abbildung ϕ, die folgendes Diagramm kommutativ ergänzt: A A V (f f) V ϕ Beispiele Für irgend zwei Punkte aus einem affinen Raum A zu einem Vektorraum V über GF (2) gilt: P Q = {P, Q}. Demnach enthält jede Teilmenge eines solchen affinen Unterraums mit zwei Punkten auch deren Verbindungsgerade. Es ist jedoch nicht jede Teilmenge eines affinen Raums zu GF (2) 2 ein affiner Unterraum. Das liegt an der Charakteristik von GF (2), denn bei char(k) 2 folgt aus der Tatsache, daß B A nicht leer ist und mit je zwei Punkten auch deren Verbindungsgerade enthält, daß B ein affiner Unterraum ist (vgl. Übungsblatt) Hilfssatz Zu jedem ϕ End K (V ) und jedem Punktepaar (O, O ) A 2 gibt es genau eine affine Abbildung f: A A, mit f(o) = O, die gemäß v) die lineare Abbildung ϕ induziert, nämlich f: P P, mit OP = OO + ϕ( OP ). Mit Hilfe von Ortsvektoren p = OP läßt sich diese Abbildung auch wie folgt schreiben: f: x x = ϕ(x) + t, mit t := OO. Affine Abbildungen f: x x = ϕ(x) + t mit ϕ = id V heißen Translationen. Offenbar ist die affine Abbildung f genau dann injektiv, surjektiv, bijektiv, wenn dies für die induzierte lineare Abbildung ϕ gilt. Die Inverse f 1 einer affinen
5 4.3. AFFINE PUNKTRÄUME 189 Abbildung f induziert die Inverse ϕ 1 der von f induzierten linearen Abbildung ϕ. Die bijektiven affinen Abbildungen ergeben, zusammen mit der Komposition als Verknüpfung, eine Gruppe, die affine Gruppe Aff(A) von A. Unter den Teilmengen affiner Räume sind solche der folgenden Form besonders wichtig: Definition (allgemeine Lage, Parallelepiped, Simplex) A sei ein affiner Raum, P 0,..., P m A. i) Die P ν heißen Punkte in allgemeiner Lage, wenn sie in keinem (m 1) dimensionalen Unterraum liegen, d.h. wenn die Folge ( P 0 P 1,..., P 0 P m ) linear unabhängig ist, bzw. wenn dim(p 0 P 1... P m ) = m. ii) Sind P 0,..., P m, Punkte in allgemeiner Lage und ist K = R, dann heißt {P 0 + m i=1 κ i P 0 P i 0 κ i 1} das von den P i aufgespannte Parallelepiped. Die Teilmenge {P 0 + m i=1 ρ i P 0 P i 0 κ i 1, i κ i = 1} heißt das von den P i aufgespannte Simplex. Affine Räume A mit euklidischen Vektorräumen V (A) nennt man euklidische Räume. Die hier definierte Metrik ergibt eine Distanzfunktion ρ(p, Q) := P Q, und auch die anderen für euklidische Vektorräume behandelten metrischen Konzepte erfahren eine geometrische Interpretation. Affine Abbildungen, die die Distanzen erhalten, heißen starre Bewegungen. Die zugehörigen linearen ϕ gehören zu der folgenden Klasse linearer Abbildungen: Definition (Isometrie) f Hom R (V, W ) heißt Isometrie, wenn f das innere Produkt invariant läßt: f(v 1 ) f(v 2 ) = v 1 v 2. Aus den vorangegangenen Überlegungen über lineare Abbildungen zwischen euklidischen Vektorräumen ergeben sich leicht die folgenden Eigenschaften von Isometrien:
6 Satz i) Genau die die Norm erhaltenden linearen Abbildungen sind Isometrien. ii) Isometrien sind injektiv. iii) Isometrien f zwischen euklidischen Vektorräumen derselben Dimension sind Isomorphismen, und für sie gilt f = f 1. iv) Gilt für f Hom R (V, W ) die Gleichung f = f 1, dann ist f Isometrie. v) Isometrien zwischen euklidischen Vektorräumen derselben Dimension bilden Orthonormalbasisfolgen auf Orthonormalbasisfolgen ab, und umgekehrt sind Isomorphismen mit dieser Eigenschaft Isometrien. vi) Ist f End R (V ) eine Isometrie, dann ist det(f) {1, 1} und Eigenwerte sind ggf. auch aus der Menge {1, 1} Definition (Rotation) f End R (V ) heißt Rotation, wenn f isometrisch ist. Die Rotationen f mit det(f) = 1 heißen dabei eigentliche, die anderen uneigentliche Rotationen. Es gibt natürlich auch Rotationen, die überhaupt keine Eigenwerte im vorgegebenen Grundkörper haben, z. B. die Abbildung f mit ( ) 0 1 M(E, f, E) :=. 1 0 Sie beschreibt eine eigentliche Rotation des euklidischen Vektorraums R 2 mit Standardskalarprodukt v w := v i w i und besitzt keinerlei Eigenwert in R. Aus den Ergebnissen über die Existenz von Eigenwerten im Reellen, die mittels Zwischenwertsatz erzielt worden waren, erhalten wir (weil das Quadrat eines Eigenwerts λ einer Isometrie gleich 1 ist): Folgerung Eigentliche (uneigentliche) Rotationen von Räumen ungerader Dimension besitzen einen Eigenwert 1( 1). Uneigentliche Rotationen auf Räumen gerader Dimension besitzen die beiden Eigenwerte ±1. Eine weitere leicht einzusehende Folgerung formuliert Hilfssatz Ist U V invariant unter der Rotation f, dann auch U. Sind f, g End R (V ) Rotationen, dann auch f 1 und g f 1. Die Rotationen bilden also eine Untergruppe O(V ) in der Gruppe GL(V ) der regulären linearen Automorphismen von V, sie heißt die (volle) orthogonale Gruppe von V, denn die Rotationen sind, wegen f = f 1 orthogonale Abbildungen: O(V ) GL(V ).
7 4.3. AFFINE PUNKTRÄUME 191 Den Kern der Abbildungen det : GL(V ) R bilden die eigentlichen Rotationen, er heißt die spezielle orthogonale Gruppe und wird mit SO(V ) bezeichnet: SO(V ) := Kern(det GL(V )) = {A GL(V ) det(a) = 1} Falls V {0 V } ist, gilt i) SO(V ) := {f O(V ) det(f) = 1} O(V ), ii) O(V )/SO(V ) = 2. Es soll nun gezeigt werden, daß eine Rotation f End R (V ) eine direkte Zerlegung von V ergibt in invariante und orthogonale Unterräume der Dimension 1 oder Satz Ist f Aut R (V ) eine Rotation, dann gibt es eine Orthonormalbasisfolge B von V mit M(B, f, B) =... ɛ 0 0 ɛm 1 cos(ω 1 ) sin(ω 1 ) sin(ω 1 ) cos(ω 1 )... cos(ωr) sin(ωr) 0 sin(ω r ) cos(ω r ), wobei ɛ ν {1, 1}, 0 ν m 1. Beweis: i) Wir bemerken zunächst, daß die Summe der Eigenräume E(1), E( 1) direkt ist: U := E(1) + E( 1) = E(1) E( 1). Nach dem letzten Hilfssatz ist die entsprechende Zerlegung V = U U = E(1) E( 1) (E(1) E( 1)) eine Zerlegung in invariante Unterräume. Die Wahl einer an U und an die Zerlegung von U in die Eigenräume angepaßten Basisfolge B ergibt den ersten
8 192 diagonalen Teil der Matrix von f mit den Einträgen ɛ i, wie behauptet: M(B, f, B) = ii) Da die Einschränkung f U = f (E(1) E( 1)) keinen Eigenwert besitzt, hat dieser Raum gerade Dimension. Wir zeigen, daß dieser Unterraum eine unter f invariante Ebene enthält: Die Einschränkung F von f + f = f +f 1 auf (E(1) E( 1)) ist selbstadjungiert, besitzt also einen Eigenvektor e, λ sei der zugehörige Eigenwert. Da f in (E(1) E( 1)) keinen Eigenvektor besitzt, sind e und f(e) linear unabhängig: Diese Ebene ist invariant unter f, denn W := e, f(e) = dim R (W ) = 2. F (e) = f(e) + f 1 (e) = λ e = f 2 (e) = λ f(e) e. Die Einschränkung von f auf W ist eine eigentliche Rotation, W also ebenfalls invariant unter f, so daß wir eine verfeinerte Zerlegung von V in invariante Unterräume erhalten: V = U W W. Wir haben also von U einen invarianten Unterraum der Dimension 2 abspalten können, so daß die Einschränkung von f auf diesen wegen der geraden Dimension eine eigentliche Rotation ist. Dies können wir iterieren und erhalten die Behauptung damit per Induktion und mit dem folgenden Hilfssatz Hilfssatz Ist W zweidimensional euklidisch, 0 die normierte Determinantenform, die eine Orientierung repräsentiert, sowie ϕ End R (W ) definiert durch ϕ(v) w = 0 (v, w), dann ist ϕ eigentliche Rotation mit ϕ 2 = id. Beweis: i) Wir beweisen als erste die Identität ϕ = ϕ : v ϕ(w) = ϕ(v) w = 0 (v, w) = 0 (w, v) = ϕ(w) v = v ϕ(w). ii) Es zeigt sich jetzt, daß ϕ eine Isometrie ist: v w 2 + ϕ(v) w 2 = v w (v, w) 2 = v 2 w 2.
9 4.3. AFFINE PUNKTRÄUME 193 Setzen wir jetzt w := ϕ(v), so ergibt sich (mit v ϕ(v) = 0, nach i)): ϕ(v) 4 = ϕ(v) ϕ(v) 2 = ϕ(v) 2 v 2. Das ergibt ϕ(v) = v, ϕ erhält also die Norm und ist demnach Isometrie. iii) Zum Nachweis von ϕ 2 = id: ϕ 2 = i) ϕ ϕ = ii) ϕ ϕ 1 = id. iv) Mit Hilfe von iii) erhalten wir schließlich det(ϕ) 0 (v, w) = 0 (ϕ(v), ϕ(w)) = ϕ 2 (v) ϕ(w) = v ϕ(w) = 0 (v, w), was det(ϕ) = 1 ergibt und den Beweis vervollständigt. Diese Abbildung ϕ heißt auch die kanonische Komplexstruktur der euklidischen Ebene W. Sei nun f eine eigentliche Drehung von W, v W \{0 V } und ω der orientierte Winkel zwischen v und f(v). Für ihn gilt cos(ω) = v f(v) v f(v), sin(ω) = 0(v, f(v)) ϕ(v) f(v) = v f(v) v f(v). Da, für jedes v W der Norm 1, (v, ϕ(v)) eine ON-Basisfolge ist, gilt also für jede eigentliche Rotation f und die kanonische Komplexstruktur ϕ zu der Orientierung, bei der diese ON-Basisfolge positiv orientiert ist (beachte v = f(v) = 1): v cos(ω) + ϕ(v) sin(ω) = v v f(v) + ϕ(v) ϕ(v) f(v) = f(v). Mit ϕ 2 = id V ergibt sich daraus f(ϕ(v)) = ϕ(v) cos(ω) v sin(ω). Das ergibt die behauptete Matrixform: ( ) cos(ω) sin(ω) M((v, ϕ(v)), f, (v, ϕ(v))) = sin(ω) cos(ω) Tatsächlich sind diese Matrixelemente unabhängig von der Wahl von v : cos(ω) = 1 2 Spur(ϕ), sin(ω) = 1 Spur(f ϕ). 2 Der Winkel ω kann deshalb als der Drehwinkel von f bezeichnet werden, kurz ω(f) := ω. Insbesondere haben wir ω(id) = 0, ω( id) = π, ω(ϕ) = π/2. Für die Beschreibung von Rotationen in dreidimensionalen euklidischen Räumen gehen wir vom allgemeinen Satz über die Form von Rotationen f aus: M(B, ϕ, B) = ± cos(ω) sin(ω) 0 sin(ω) cos(ω).
10 194 Links oben steht ±1, je nachdem ob f eine eigentliche oder eine uneigentliche Rotation beschreibt. Dabei ist B = (b 0, b 1, b 2 ) eine ON-Basisfolge, der Unterraum b 0 heißt Drehachse von f.
4.2 Die adjungierte Abbildung
 4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
3.5 Duale Vektorräume und Abbildungen
 3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 34 Die Diagonalisierbarkeit von Isometrien im Komplexen Satz 34.1. Es sei V ein endlichdimensionaler C-Vektorraum
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 34 Die Diagonalisierbarkeit von Isometrien im Komplexen Satz 34.1. Es sei V ein endlichdimensionaler C-Vektorraum
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Prüfung Lineare Algebra 2
 1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Jede symmetrische Bilinearform b definiert eine quadratische Form q durch. q(x) := b(x, x).
 1 Kapitel 1 Clifford-Algebren 1 Innere Produkte Sei k {R, C}, V stets ein endlich-dimensionaler k-vektorraum. Fehlende Beweise finden sich in der Literatur ([Art1], [Bou1], [Brie], [Cohn]). Definition.
1 Kapitel 1 Clifford-Algebren 1 Innere Produkte Sei k {R, C}, V stets ein endlich-dimensionaler k-vektorraum. Fehlende Beweise finden sich in der Literatur ([Art1], [Bou1], [Brie], [Cohn]). Definition.
Definition und gemeinsame Eigenschaften der Symplektischen und Orthogonalen Geometrie
 Universität Duisburg-Essen, Campus Essen, Fachbereich Mathematik, IEM AG Zahlentheorie Definition und gemeinsame Eigenschaften der Symplektischen und Orthogonalen Geometrie Proseminar Algebra WS 2008/2009,
Universität Duisburg-Essen, Campus Essen, Fachbereich Mathematik, IEM AG Zahlentheorie Definition und gemeinsame Eigenschaften der Symplektischen und Orthogonalen Geometrie Proseminar Algebra WS 2008/2009,
Kapitel V. Affine Geometrie
 Kapitel V Affine Geometrie 1 Affine Räume Betrachte ein lineares Gleichungssystem Γ : a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a m2 x 2 + + a mn x n = b
Kapitel V Affine Geometrie 1 Affine Räume Betrachte ein lineares Gleichungssystem Γ : a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a m2 x 2 + + a mn x n = b
Analytische Geometrie
 21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
Wir verallgemeinern jetzt den Begriff bilinear zu multilinear. Unser Ziel ist dabei insbesondere die Einführung der sogenannten Determinante.
 118 36 Determinanten Wir verallgemeinern jetzt den Begriff bilinear zu multilinear Unser Ziel ist dabei insbesondere die Einführung der sogenannten Determinante 361 Definition (alternierend, symmetrisch,
118 36 Determinanten Wir verallgemeinern jetzt den Begriff bilinear zu multilinear Unser Ziel ist dabei insbesondere die Einführung der sogenannten Determinante 361 Definition (alternierend, symmetrisch,
18 λ 18 + λ 0 A 18I 3 = / Z 2 Z 2 Z Z Z 1
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
Lineare Algebra II Lösungen zu ausgewählten Aufgaben
 Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
 Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Projektive Räume und Unterräume
 Projektive Räume und Unterräume Erik Slawski Proseminar Analytische Geometrie bei Prof. Dr. Werner Seiler und Marcus Hausdorf Wintersemester 2007/2008 Fachbereich 17 Mathematik Universität Kassel Inhaltsverzeichnis
Projektive Räume und Unterräume Erik Slawski Proseminar Analytische Geometrie bei Prof. Dr. Werner Seiler und Marcus Hausdorf Wintersemester 2007/2008 Fachbereich 17 Mathematik Universität Kassel Inhaltsverzeichnis
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 0/06 Lineare Algebra und analytische Geometrie I Vorlesung... und ein guter Lehrer kann auch einem schlechten Schüler was beibringen Beziehung zwischen Eigenräumen Wir
Prof. Dr. H. Brenner Osnabrück WS 0/06 Lineare Algebra und analytische Geometrie I Vorlesung... und ein guter Lehrer kann auch einem schlechten Schüler was beibringen Beziehung zwischen Eigenräumen Wir
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 03.12.2013 Alexander Lytchak 1 / 16 Wiederholung und Beispiele Der Spaltenrang einer Matrix ist gleich ihrem Zeilenrang.
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 03.12.2013 Alexander Lytchak 1 / 16 Wiederholung und Beispiele Der Spaltenrang einer Matrix ist gleich ihrem Zeilenrang.
a) Ein Gruppenhomomorphismus von G nach H ist eine Abbildung Φ : G H, sodass für alle g 1, g 2 G die Gleichung Φ(g 1 g 2 ) = Φ(g 1 ) Φ(g 2 )
 I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 2015
 sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
4 Orthogonale Endormorphismen
 4 Orthogonale Endormorphismen Frage: Bei welchen Abbildungen R R bzw. R 3 R 3 bleibt der Abstand zwischen zwei Punkten erhalten? Für α R setzen wir cosα sin α D(α) = und S(α) := sin α cosα ( cos α sin
4 Orthogonale Endormorphismen Frage: Bei welchen Abbildungen R R bzw. R 3 R 3 bleibt der Abstand zwischen zwei Punkten erhalten? Für α R setzen wir cosα sin α D(α) = und S(α) := sin α cosα ( cos α sin
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 10 Bewegungen Wir haben schon mehrfach die Würfelgruppe betrachtet, also die Gruppe der eigentlichen Symmetrien an einem Würfel.
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 10 Bewegungen Wir haben schon mehrfach die Würfelgruppe betrachtet, also die Gruppe der eigentlichen Symmetrien an einem Würfel.
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Eigenwerte und Diagonalisierung
 Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum
 Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Lineare Algebra und Analytische Geometrie I für die Fachrichtung Informatik
 Universität Karlsruhe (TH) Institut für Algebra und Geometrie Dr. Klaus Spitzmüller Dipl.-Inform. Wolfgang Globke Lineare Algebra und Analytische Geometrie I für die Fachrichtung Informatik Lösungen zum
Universität Karlsruhe (TH) Institut für Algebra und Geometrie Dr. Klaus Spitzmüller Dipl.-Inform. Wolfgang Globke Lineare Algebra und Analytische Geometrie I für die Fachrichtung Informatik Lösungen zum
Drehachse und Drehwinkel
 Drehachse und Drehwinkel Jede Drehung Q im R 3 besitzt eine Drehachse, d.h. lässt einen Einheitsvektor u invariant, und entspricht einer ebenen Drehung um einen Winkel ϕ in der zu u orthogonalen Ebene.
Drehachse und Drehwinkel Jede Drehung Q im R 3 besitzt eine Drehachse, d.h. lässt einen Einheitsvektor u invariant, und entspricht einer ebenen Drehung um einen Winkel ϕ in der zu u orthogonalen Ebene.
Lineare Algebra und analytische Geometrie
 Lineare Algebra und analytische Geometrie von Günther Eisenreich Mit 107 Abbildungen und 2 Tabellen 3., erweiterte und berichtigte Auflage Akademie Verlag Inhaltsverzeichnis A. Allgemeine Vorbemerkungen
Lineare Algebra und analytische Geometrie von Günther Eisenreich Mit 107 Abbildungen und 2 Tabellen 3., erweiterte und berichtigte Auflage Akademie Verlag Inhaltsverzeichnis A. Allgemeine Vorbemerkungen
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Invariantentheorie. Bewegungen
 Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invariantentheorie Vorlesung 21 In den folgenden Vorlesungen werden wir die endlichen Untergruppen G SL 2 (C) und ihre Invariantenringe klassifizieren. Dieses
Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invariantentheorie Vorlesung 21 In den folgenden Vorlesungen werden wir die endlichen Untergruppen G SL 2 (C) und ihre Invariantenringe klassifizieren. Dieses
4.4 Symmetrische Bilinearformen
 4.4. SYMMETRISCHE BILINEARFORMEN 195 4.4 Symmetrische Bilinearformen Alle betrachteten Vektorräume seien euklidisch. Wir betrachten Bilinearformen Φ: V V R, von denen wir nur voraussetzen, daß sie symmetrisch
4.4. SYMMETRISCHE BILINEARFORMEN 195 4.4 Symmetrische Bilinearformen Alle betrachteten Vektorräume seien euklidisch. Wir betrachten Bilinearformen Φ: V V R, von denen wir nur voraussetzen, daß sie symmetrisch
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall
 44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
Lineare Algebra II 11. Übungsblatt
 Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
4 Affine Koordinatensysteme
 4 Affine Koordinatensysteme Sei X φ ein affiner Raum und seien p,, p r X Definition: Nach ( c ist der Durchschnitt aller affinen Unterräume Z X, welche die Menge {p,,p r } umfassen, selbst ein affiner
4 Affine Koordinatensysteme Sei X φ ein affiner Raum und seien p,, p r X Definition: Nach ( c ist der Durchschnitt aller affinen Unterräume Z X, welche die Menge {p,,p r } umfassen, selbst ein affiner
Musterlösungen Klausur Geometrie
 Musterlösungen Klausur Geometrie Aufgabe 1 (Total: 8 Punkte). Seien A, B, C die Eckpunkte eines nichtentarteten Dreiecks in der euklidischen Ebene. Seien D, E, F derart gewählt, dass folgende Teilverhältnisse
Musterlösungen Klausur Geometrie Aufgabe 1 (Total: 8 Punkte). Seien A, B, C die Eckpunkte eines nichtentarteten Dreiecks in der euklidischen Ebene. Seien D, E, F derart gewählt, dass folgende Teilverhältnisse
EXKURS: MATRIZEN UND LINEARE GLEICHUNGSSYSTEME
 EXKURS: MATRIZEN UND LINEARE GLEICHUNGSSYSTEME In diesem Abschnitt wiederholen wir zunächst grundlegende Definitionen und Eigenschaften im Bereich der Matrizenrechnung, die wahrscheinlich bereits in Ansätzen
EXKURS: MATRIZEN UND LINEARE GLEICHUNGSSYSTEME In diesem Abschnitt wiederholen wir zunächst grundlegende Definitionen und Eigenschaften im Bereich der Matrizenrechnung, die wahrscheinlich bereits in Ansätzen
10. Affine und euklidische Geometrie.
 10. Affine und euklidische Geometrie. In der analytischen Geometrie beschreibt man nach Wahl eines Koordinatensystems Punkte durch n-tupel von Zahlen (n = 2 für die Ebene, n = 3 für den 3-dimensionalen
10. Affine und euklidische Geometrie. In der analytischen Geometrie beschreibt man nach Wahl eines Koordinatensystems Punkte durch n-tupel von Zahlen (n = 2 für die Ebene, n = 3 für den 3-dimensionalen
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Prüfung Lineare Algebra , B := ( ), C := 1 1 0
 1. Es seien 1 0 2 0 0 1 3 0 A :=, B := ( 1 2 3 4 ), C := 1 1 0 0 1 0. 0 0 0 1 0 0 1 0 0 0 0 Welche der folgenden Aussagen ist richtig? A. A und C haben Stufenform, B nicht. B. A und B haben Stufenform,
1. Es seien 1 0 2 0 0 1 3 0 A :=, B := ( 1 2 3 4 ), C := 1 1 0 0 1 0. 0 0 0 1 0 0 1 0 0 0 0 Welche der folgenden Aussagen ist richtig? A. A und C haben Stufenform, B nicht. B. A und B haben Stufenform,
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG [email protected] http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG [email protected] http://www2.mathematik.uni-wuerzburg.de
1. und 2. Fundamentalform
 1. und 2. Fundamentalform regulärer Flächen Proseminar Differentialgeometrie Von Daniel Schliebner Herausgabe: 05. Dezember 2007 Daniel Schliebner 1. und 2. Fundamentalform regulärer Flächen Seite 1 6.1
1. und 2. Fundamentalform regulärer Flächen Proseminar Differentialgeometrie Von Daniel Schliebner Herausgabe: 05. Dezember 2007 Daniel Schliebner 1. und 2. Fundamentalform regulärer Flächen Seite 1 6.1
Affine und projektive Räume
 Affine und projektive Räume W. Kühnel Literatur hierzu: G.Fischer, Analytische Geometrie, 7. Aufl., Vieweg 2001 Zur Motivation: Wenn man in einem Vektorraum die Elemente nicht als Vektoren, sondern als
Affine und projektive Räume W. Kühnel Literatur hierzu: G.Fischer, Analytische Geometrie, 7. Aufl., Vieweg 2001 Zur Motivation: Wenn man in einem Vektorraum die Elemente nicht als Vektoren, sondern als
Lineare Algebra und Numerische Mathematik für D-BAUG
 P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Modulteilprüfung Geometrie (BaM-GS, L3M-RF)
 Modulteilprüfung Geometrie (BaM-GS, L3M-RF) Prof. Dr. Martin Möller SoSe 2011 // 05. Juli 2011 Kontrollieren Sie, ob Sie alle Blätter (12 einschließlich zweier Deckblätter) erhalten haben, und geben Sie
Modulteilprüfung Geometrie (BaM-GS, L3M-RF) Prof. Dr. Martin Möller SoSe 2011 // 05. Juli 2011 Kontrollieren Sie, ob Sie alle Blätter (12 einschließlich zweier Deckblätter) erhalten haben, und geben Sie
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 33 Das Kreuzprodukt Eine Besonderheit im R 3 ist das sogenannte Kreuzprodukt, das zu zwei gegebenen Vektoren
Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 33 Das Kreuzprodukt Eine Besonderheit im R 3 ist das sogenannte Kreuzprodukt, das zu zwei gegebenen Vektoren
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
Zeigen Sie, dass der einzige Gruppenhomomorphismus von (G, ) nach (Z 5, +) die Abbildung Φ : G Z 5
 Aufgabe I (4 Punkte) Es sei G : {e, g, g, g } eine 4-elementige Gruppe mit neutralem Element e Die Verknüpfung auf G werde mit bezeichnet Außerdem seien in G folgende Gleichungen erfüllt: g g g und g g
Aufgabe I (4 Punkte) Es sei G : {e, g, g, g } eine 4-elementige Gruppe mit neutralem Element e Die Verknüpfung auf G werde mit bezeichnet Außerdem seien in G folgende Gleichungen erfüllt: g g g und g g
3 Definition: 1. Übungsblatt zur Vorlesung Lineare Algebra I. im WS 2003/2004 bei Prof. Dr. S. Goette
 1. Übungsblatt zur Vorlesung Abgabe Donnerstag, den 30.10.03 1 Finden 2 Sei Sie reelle Zahlen a, b, c, so dass a (2, 3, 1) + b (1, 2, 2) + c (2, 5, 3) = (3, 7, 5). (V,, ) ein euklidischer Vektorraum. Zeigen
1. Übungsblatt zur Vorlesung Abgabe Donnerstag, den 30.10.03 1 Finden 2 Sei Sie reelle Zahlen a, b, c, so dass a (2, 3, 1) + b (1, 2, 2) + c (2, 5, 3) = (3, 7, 5). (V,, ) ein euklidischer Vektorraum. Zeigen
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
43911: Lineare Algebra/Geometrie Prüfungstermin Herbst 2015 Lösungsvorschlag
 Dr. Erwin Schörner 49: Lineare Algebra/Geometrie Prüfungstermin Herbst 5 Lösungsvorschlag I.. a Die in Abhängigkeit vom Parameter t R für t t A t t t R und b R t + t t + t zu betrachtende Menge F t { x
Dr. Erwin Schörner 49: Lineare Algebra/Geometrie Prüfungstermin Herbst 5 Lösungsvorschlag I.. a Die in Abhängigkeit vom Parameter t R für t t A t t t R und b R t + t t + t zu betrachtende Menge F t { x
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4 Lineare Algebra/Analytische Geometrie II SoSe 2016
 Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4 Lineare Algebra/Analytische Geometrie II SoSe 2016 Bearbeiten Sie bitte zwei
Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4 Lineare Algebra/Analytische Geometrie II SoSe 2016 Bearbeiten Sie bitte zwei
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
AUFGABENSAMMLUNG ZU VEKTORRECHNUNG FÜR USW
 AUFGABENSAMMLUNG ZU VEKTORRECHNUNG FÜR USW Lineare Gleichungssysteme Lösen Sie folgende Gleichungssysteme über R: a) x + x + x = 6x + x + x = 4 x x x = x 7x x = 7 x x = b) x + x 4x + x 4 = 9 x + 9x x x
AUFGABENSAMMLUNG ZU VEKTORRECHNUNG FÜR USW Lineare Gleichungssysteme Lösen Sie folgende Gleichungssysteme über R: a) x + x + x = 6x + x + x = 4 x x x = x 7x x = 7 x x = b) x + x 4x + x 4 = 9 x + 9x x x
4.3 Bilinearformen. 312 LinAlg II Version Juni 2006 c Rudolf Scharlau
 312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
Aufgabe I.1 (4 Punkte) Gegeben seien die Matrix H := und die Menge L := {A R 4 4 A HA = H} Zeigen Sie:
 Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Proseminar Lineare Algebra II, SS 11. Blatt
 Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Klausurenkurs zum Staatsexamen (WS 2013/14): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Vorlesung 27. Der projektive Raum. Wir werden den projektiven Raum zunehmend mit mehr Strukturen versehen.
 Vorlesung 27 Der projektive Raum Definition 1. Sei K ein Körper. Der projektive n-dimensionale Raum P n K besteht aus allen Geraden des A n+1 K durch den Nullpunkt, wobei diese Geraden als Punkte aufgefasst
Vorlesung 27 Der projektive Raum Definition 1. Sei K ein Körper. Der projektive n-dimensionale Raum P n K besteht aus allen Geraden des A n+1 K durch den Nullpunkt, wobei diese Geraden als Punkte aufgefasst
Lineare Abbildungen und Darstellungsmatrizen
 KAPITEL 4 Lineare Abbildungen und Darstellungsmatrizen 1. Lineare Abbildungen Definition 4.1 (Lineare Abbildungen). Seien V und W zwei Vektorräume über den selben Körper K. Eine Abbildung f : V W heißt
KAPITEL 4 Lineare Abbildungen und Darstellungsmatrizen 1. Lineare Abbildungen Definition 4.1 (Lineare Abbildungen). Seien V und W zwei Vektorräume über den selben Körper K. Eine Abbildung f : V W heißt
4.2 Quotientenvektorräume
 306 LinAlg II Version 1 6. Juni 2006 c Rudolf Scharlau 4.2 Quotientenvektorräume Zum Verständnis der folgenden Konstruktion ist es hilfreich, sich noch einmal den Abschnitt 1.4 über Restklassen vom Beginn
306 LinAlg II Version 1 6. Juni 2006 c Rudolf Scharlau 4.2 Quotientenvektorräume Zum Verständnis der folgenden Konstruktion ist es hilfreich, sich noch einmal den Abschnitt 1.4 über Restklassen vom Beginn
Zusammenfassung: Geometrie.
 Zusammenfassung: Geometrie. Gabriele Nebe und Sebastian Thomas Lineare Algebra II, WS 2009/10 nach dem Skript von Prof. W. Plesken Affine Geometrie Definition. Ein affiner Raum ist eine Menge A, auf der
Zusammenfassung: Geometrie. Gabriele Nebe und Sebastian Thomas Lineare Algebra II, WS 2009/10 nach dem Skript von Prof. W. Plesken Affine Geometrie Definition. Ein affiner Raum ist eine Menge A, auf der
Aufgaben zur Vorlesung: Lineare Algebra und analytische Geometrie I
 Institut für Mathematik Blatt Prof. Dr. B. Martin, H. Süß Abgabe: 0.4. Aufgaben zur Vorlesung: Lineare Algebra und analytische Geometrie I Aufgabe : 2 Punkte Stellen Sie die Gleichung der Ebene auf, in
Institut für Mathematik Blatt Prof. Dr. B. Martin, H. Süß Abgabe: 0.4. Aufgaben zur Vorlesung: Lineare Algebra und analytische Geometrie I Aufgabe : 2 Punkte Stellen Sie die Gleichung der Ebene auf, in
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
1 Die Jordansche Normalform
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
r i w i (siehe (3.7)). r i v, w i = 0.
 Orthogonales Komplement und Orthogonalprojektion Wir betrachten weiterhin einen euklidischen Vektorraum V,,. (6.13) Def.: Ist M V, so heißt das orthogonale Komplement von M. (6.14) Fakt. (i) M ist Untervektorraum
Orthogonales Komplement und Orthogonalprojektion Wir betrachten weiterhin einen euklidischen Vektorraum V,,. (6.13) Def.: Ist M V, so heißt das orthogonale Komplement von M. (6.14) Fakt. (i) M ist Untervektorraum
VII.2. INNERE PRODUKTE 227
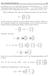 VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
Eigenwerttheorie. Martin Gubisch Lineare Algebra I WS 2007/2008
 Eigenwerttheorie Martin Gubisch Lineare Algebra I WS 27/28 Motivation Gegeben seien ein K-Vektorraum V der Dimension n < und eine K-lineare Abbildung f : V V Wir suchen eine Basis V = v 1,, v n von V,
Eigenwerttheorie Martin Gubisch Lineare Algebra I WS 27/28 Motivation Gegeben seien ein K-Vektorraum V der Dimension n < und eine K-lineare Abbildung f : V V Wir suchen eine Basis V = v 1,, v n von V,
Aufgaben zur linearen Algebra und analytischen Geometrie I
 Aufgaben zur linearen Algebra und analytischen Geometrie I Es werden folgende Themen behandelt:. Formale und logische Grundlagen 2. Algebraische Grundlagen 3. Vektorräume und LGS 4. Homomorphismen und
Aufgaben zur linearen Algebra und analytischen Geometrie I Es werden folgende Themen behandelt:. Formale und logische Grundlagen 2. Algebraische Grundlagen 3. Vektorräume und LGS 4. Homomorphismen und
Klausurvorbereitungsblatt Lineare Algebra
 Klausurvorbereitungsblatt Lineare Algebra Sommersemester 25 Aufgabe 2 2 Sei A 3 3 8 2 4 3 R4 5. 5 2 a) Bestimmen Sie die Lösungsmenge des linearen Gleichungssystems Ax b) Ist Ax b mit b lösbar? (Begründen
Klausurvorbereitungsblatt Lineare Algebra Sommersemester 25 Aufgabe 2 2 Sei A 3 3 8 2 4 3 R4 5. 5 2 a) Bestimmen Sie die Lösungsmenge des linearen Gleichungssystems Ax b) Ist Ax b mit b lösbar? (Begründen
Symmetrien. Transformationen. Affine und euklidische Räume
 Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
13. Lineare Algebra und Koordinatenwechsel.
 3. Lineare Algebra und Koordinatenwechsel. In dieser Vorlesung behandeln wir die Vorzüge von Koordinatenwechseln. Insbesondere werden wir über geeignete Koordinatenwechsle zu einer Klassifikation der lineare
3. Lineare Algebra und Koordinatenwechsel. In dieser Vorlesung behandeln wir die Vorzüge von Koordinatenwechseln. Insbesondere werden wir über geeignete Koordinatenwechsle zu einer Klassifikation der lineare
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 2016
 Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
Wiederholungsblatt Elementargeometrie LÖSUNGSSKIZZE
 Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
Kapitel 3 Lineare Algebra
 Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 29.11.2013 Alexander Lytchak 1 / 13 Wiederholung Der Rang einer linearen Abbildung ist gleich dem Spaltenrang der darstellenden
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 29.11.2013 Alexander Lytchak 1 / 13 Wiederholung Der Rang einer linearen Abbildung ist gleich dem Spaltenrang der darstellenden
Lineare Algebra II 6. Übungsblatt
 Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
Musterlösung der Klausur zur linearen Algebra II
 David Blottière SS 7 Patrick Schützdeller Universität Paderborn Julia Sauter Musterlösung der Klausur zur linearen Algebra II Aufgabe 1 Bestimmen Sie Jordan-Normalformen der folgenden Matrizen, und schreiben
David Blottière SS 7 Patrick Schützdeller Universität Paderborn Julia Sauter Musterlösung der Klausur zur linearen Algebra II Aufgabe 1 Bestimmen Sie Jordan-Normalformen der folgenden Matrizen, und schreiben
Ausgewählte Lösungen zu den Übungsblättern 4-5
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Ausgewählte en zu den Übungsblättern -5 Aufgabe, Lineare Unabhängigkeit
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Ausgewählte en zu den Übungsblättern -5 Aufgabe, Lineare Unabhängigkeit
7. Wie lautet die Inverse der Verkettung zweier linearer Abbildungen? 9. Wie kann die Matrixdarstellung einer linearen Abbildung aufgestellt werden?
 Kapitel Lineare Abbildungen Verständnisfragen Sachfragen Was ist eine lineare Abbildung? Erläutern Sie den Zusammenhang zwischen Unterräumen, linearer Unabhängigkeit und linearen Abbildungen! 3 Was ist
Kapitel Lineare Abbildungen Verständnisfragen Sachfragen Was ist eine lineare Abbildung? Erläutern Sie den Zusammenhang zwischen Unterräumen, linearer Unabhängigkeit und linearen Abbildungen! 3 Was ist
gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren
 Stefan K. 4.Übungsblatt Algebra I Aufgabe 1 gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler von G zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren Beweis: Seien
Stefan K. 4.Übungsblatt Algebra I Aufgabe 1 gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler von G zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren Beweis: Seien
3 Geometrische Klassifikation der Bewegungen im R 2 und R 3
 3 Geometrische Klassifikation der Bewegungen im R 2 und R 3 Sei f : R n R n eine Bewegung Sie kann beschrieben werden in der Form Dabei ist T (f)(x) = A x f(x) = Ax + b mit A O(n) und b R n Definition:
3 Geometrische Klassifikation der Bewegungen im R 2 und R 3 Sei f : R n R n eine Bewegung Sie kann beschrieben werden in der Form Dabei ist T (f)(x) = A x f(x) = Ax + b mit A O(n) und b R n Definition:
13. Vorlesung. Lineare Algebra und Koordinatenwechsel.
 3. Vorlesung. Lineare Algebra und Koordinatenwechsel. In dieser Vorlesung behandeln wir die Vorzüge von Koordinatenwechseln. Insbesondere werden wir über geeignete Koordinatenwechsle zu einer Klassifikation
3. Vorlesung. Lineare Algebra und Koordinatenwechsel. In dieser Vorlesung behandeln wir die Vorzüge von Koordinatenwechseln. Insbesondere werden wir über geeignete Koordinatenwechsle zu einer Klassifikation
Inhalt. Mathematik für Chemiker II Lineare Algebra. Vorlesung im Sommersemester Kurt Frischmuth. Rostock, April Juli 2015
 Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Bild, Faser, Kern. Stefan Ruzika. 23. Mai Mathematisches Institut Universität Koblenz-Landau Campus Koblenz
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 23. Mai 2016 Stefan Ruzika 7: Bild, Faser, Kern 23. Mai 2016 1 / 11 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume 4 Basis
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 23. Mai 2016 Stefan Ruzika 7: Bild, Faser, Kern 23. Mai 2016 1 / 11 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume 4 Basis
Projektive Abbildungen, Beziehung zwischen anen und projektiven Räumen, Projektive Unabhängigkeit.
 Projektive Abbildungen, Beziehung zwischen anen und projektiven Räumen, Projektive Unabhängigkeit. Agnieszka Wenska 2008-02-19 1 Wir wissen bereits: Was projektive Räume und Unterräume sind Wie man die
Projektive Abbildungen, Beziehung zwischen anen und projektiven Räumen, Projektive Unabhängigkeit. Agnieszka Wenska 2008-02-19 1 Wir wissen bereits: Was projektive Räume und Unterräume sind Wie man die
