4 Die freie Schwingung
|
|
|
- Manuela Becke
- vor 7 Jahren
- Abrufe
Transkript
1 Einassenschwinger Teil I. ie freie Schwingng 5 ie freie Schwingng Nachde die Bewegngsgleichngen in Teil I. hergeleitet wrden nd in Teil I. die Belastngen lassifiziert wrden, werden in diesen folgenden Abschnitten die Lösngen dargestellt. ie Lösng ist hierbei die Fntion der Verschiebng in Abhängigeit von der Zeit. Znächst wird die freie Schwingng betrachtet. Sie ist dadrch geennzeichnet, dass die Belastng p(t) nd der Gewichtsanteil af der rechten Seite der Bewegngsgleichng (.) verschwindet. ie Bewegngsgleichng latet dait für diesen Fall c 0. ie freie ngedäpfte Schwingng I Fall der freien ngedäpften Schwingng redziert sich die Bewegngsgleichng drch das Wegfallen der äpfngsraft einen weiteren Ter. ait redziert sich die Gleichng (.) af 0 oder 0 (.) a i technischen Alltag nr positive Steifigeiten nd assen z betrachten sind (also > 0 nd > 0 sind), ann gesetzt werden. ait erhält an 0 Für ifferentialgleichngen dieses Typs ann ein Lösngsansatz nach Eler verwendet werden. er Ansatz verwendet eine Exponentialfntion für die Verschiebng rt rt Ce, r Ce rt rt r Ce Ce 0 r 0 r i it it ait ergibt sich als Gesatlösng t C e C e (.) Unter Berücsichtigng von e i t cost i sint erhält an t C C cost ic C sint t Acost Bsint (.) ie Kreisfreqenz ω ist dabei nr von den Systewerten der assen nd Steifigeiten abhängig nd wird daher als Eigenreisfreqenz bezeichnet. ie Schwingng wird als Eigenschwingng des Systes bezeichnet. iese Schwingng wird drch drei aßgebende Größen charaterisiert:
2 6 Teil I. ie freie Schwingng Einassenschwinger die Eigenreisfreqenz die Periode der Schwingng nd die Eigenfreqenz (.) T (.5) f T (.6) ie Eigenfreqenz f bzw. die Eigenreisfreqenz ω sind nr vo Bateil bzw. de echanischen Syste abhängig. Sie spielen in der Strtrdynai eine ganz wesentliche Rolle. 0 p 0 ax rch Veränderng der Systewerte ann die Eigenfreqenz beeinflsst werden. Sie wird vergrößert, wenn * die Steifigeit erhöht wird nd * die asse verringert wird. Abb. - T Freie Eigenschwingng ie Konstanten A nd B richten sich nach den Anfangsbedingngen. Wenn z Beispiel die Anfangsaslenng nd die Anfangsgeschwindigeit beannt sind (also wenn die Bedingngen gelten: (t=0) = O, (t=0) = 0 ), dann ergibt sich o A O, B oder o t O cost sint (.7) ie Schwingngsgleichng (.) wird oft ach in folgender For angegeben. t cos t ax arin ergibt sich für die Aplitde 0 ax 0 nd für die Phasenverschiebng 0 tan 0 (.8) (.9) (.0)
3 Einassenschwinger Teil I. ie freie Schwingng 7.. Näherngslösng er Steifigeitswert eines Einassenschwingers ann ach as der statischen Verschiebng δ des Einassenschwingers nter de Eigengewicht G = g erittelt werden. ie rchsenng δ infolge des Eigengewichts ergibt sich it G g ait gilt für die Steifigeit g Für die Eigenfreqenz gilt g g f it g = 9,8 /s² Für den Einassenschwinger ist diese Forel für die Eigenfreqenz exat. Als Näherngslösng ann sie für andere schwingende Systee verwendet werden, z. B. für die Berechnng der niedrigsten Eigenfreqenz eines Balens it ontinierlich verteilter asse. q g G Abb. - Statische Verschiebng des Einassenschwingers t EI, L L Abb. -a Schwingngsfor für die niedrigste Eigenfreqenz Abb. -b rchbiegng nter Eigengewicht ie exate Lösng latet it = asse je Längeneinheit EI EI 9, 87 L L ie axiale rchbiegng nter Eigengewicht ann dait bestit werden z q L / 76,8 EI ; g g g L / 76, 8EI ie Näherng für die Eigenfreqenz ergibt danach g 76,8EI 8, 76 L EI L
4 8 Teil I. ie freie Schwingng Einassenschwinger er Fehler beträgt,7 % nd liegt i Bereich der Genaigeit, die für eine Überschlagsberechnng bei der Aslegng eines Bateils üblicherweise zgrndegelegt wird... rehschwingngen Während einige der Freiheitsgrade der ecplatte in Abb.- translatorische Verschiebngen waren, stellte ein Freiheitsgrad eine Verdrehng (rotatorischer Freiheitsgrad) dar. ieser Verdrehng zgeordnet ist ein rehträgheitsoent (vgl. Gleichng (.)) nd eine Steifigeit gegen Verdrehen. rehachse Entsprechend der Idealisierng für die lineare Schwingng in For eines Feder - asse - Systes ann der Einassen- rehschwinger ebenfalls idealisiert werden. Als ifferentialgleichng ergibt sich analog t I I I Abb. - rehschwingng it I (t) als äßere oentenbelastng [SI-Einheit N]. Für die zgehörige Eigenreisfreqenz erhält an I, I, I r d.. Beispiele An einigen einfachen Beispielen soll die Anwendng dieser arstellngen gezeigt werden. Beispiel as z berechnende Syste ist ein asseloser Kragträger. A freien Ende ist eine pntförige große asse (Gewicht G) angebracht, vergl. Abb.-5a. Gescht sind. die Eigenreisfreqenz, Periode nd Eigenfreqenz nd. die Gleichng für die freie Schwingng, wenn die asse as der Asgangslage losgelassen wird. ie Asgangslage ist die Anordnng, bei der der Kragträger nicht verfort bzw. gebogen ist. as Eigengewicht als diejenige Last, die die Biegng hervorrft, ist noch nicht wirsa geworden.
5 Einassenschwinger Teil I. ie freie Schwingng 9 0 EI Abb. -5a Kragträger it Pntasse l G t G t Abb. -5b Äqivalenter Einassenschwinger Für die Lösng stehen folgende Gleichngen zr Verfügng, T, f T it P = ist = Kraft für die Verschiebng = EI G, l g EIg Gl, T, f Gl EIg T Als Zahlenwerte sind folgende aten gegeben: * Elastizitätsodl E =. 0 8 N/ (Stahl), * Flächenträgheitsoent I = 5700 c (IPB00), E I =,97 0 N * Länge l =, * Last G = 0 N, * Erdbeschlenigng g = 9,8 s - Für die Eigenreisfreqenz, die Schwingngsdaer (Periode) nd die Freqenz ergeben sich 97, 0 9, s, 0 T 0, s 0, 9 0 f, Hz 0, ie statische Aslenng berechnet sich z Gl 0 st 0, 0 EI 97, 0 iese Lage ist die Rhelage für die Schwingng. ait ergibt sich gleichzeitig als Anfangsbedingng 0 = - st, ů = 0.
6 0 Teil I. ie freie Schwingng Einassenschwinger it Gleichng (.5) nd (.7) ergibt sich für die Bewegng t st cost bei cos t ax st ie axiale dynaische Aslenng nd Beansprchng ist doppelt so groß wie diejenige des statischen Belastngsfalles. ies entspricht eine Asschlagen des Trägers in die Gegenrichtng der Asgangslage. iese beiden Positionen sind gleichzeitig die Grenzzstände (Aplitden) der Schwingng, die sich einstellt. er statische Belastngsfall ist der ittelwert der Schwingng. Beispiel aschine Träger 6,00 Abb. -6a Trägerbalen, drch eine aschine belastet Abb. -6b Qerschnitt des Trägerbalens Es ist ein beidseitig afgelagerter Träger it einer daraf ontierten aschine z berechnen, vergl. Abb. -6. er Qerträger ist as zwei Balen zsaengesetzt. ie Angaben des aschinenherstellers enthalten folgende aten: Gewicht des otors: 0 N Betriebsdrehzahl: n = 9 /in Eigengewicht jedes Balens: g B = 0,5 * 0,7 * 5 =,8 N/n Last je Balen as otorengewicht: G = 0/ = 0 N E-odl der Balen: E = 0 7 N/ Trägheitsoente je Balen: I = 0, 50, 7 = 7,5 0 - ie Aflagerng soll i aerwer sein. a die Aflagerngsbedingngen dait nicht lar bestibar sind, ss it Grenzbetrachtngen gearbeitet werden. ie Grenzfälle für die Aflagerngsbedingngen sind eine feste Einspannng an beiden Enden (vergl. Abb. -7a) nd eine oentenfreie Festhaltng an beiden Enden (vergl. Abb. -7b). ie Erregng erfolgt in vertialer Richtng, es soll daher in erster Näherng nr af Vertialschwingngen eingegangen werden. Unter dieser vereinfachenden Annahe ann das Bateil als Einassenschwinger behandelt nd berechnet werden.
7 Einassenschwinger Teil I. ie freie Schwingng 6,00 6,00 Abb. -7a Grenzfall: feste Einspannnng Abb. -7b Grenzfall: oentenfreie Festhaltng Beispiel Fall In diese Fall wird der Grenzfall it der festen Einspannng an den Enden betrachtet. Znächst wird die Steifigeit der Balenonstrtion bestit. ie Berechnng der Steifigeit erfolgt it Hilfe der Verschiebngsethode (Verdrehngen brachen wegen Syetrie nicht beachtet z werden) E I z 7 0 7, 50 9, 070 N/ Eine Zsaenfassng der itschwingenden asse z Einzelassen in Balenitte nd in den Aflagern ergibt otor Balen G gb L / g g Ns ( 0, 8 ), 8 9, 8 Abb. -8a Berechnng der Steifigeit Abb. -8b Afteilng der assen ie Eigenreisfreqenz ergibt sich z K 9, 070, 8 7, 5 s Für die Eigenfreqenz erhält an f 7, 8s 68 in
8 Teil I. ie freie Schwingng Einassenschwinger Beispiel Fall In diese Fall wird der Grenzfall it der oentenfreien Aflagerng an den Enden betrachtet. ie Berechnng der Steifigeit erfolgt analog z Fall (Verdrehngen brachen ach hier wegen Syetrie nicht beachtet z werden) EI 7 0 7, 50 z, 770 N/ 0, 5 Fall ie Zsaenfassng der itschwingenden asse z Einzelassen in Balenitte nd in den Aflagern erfolgt identisch z Fall ie Eigenreisfreqenz ergibt sich z K 0, 5 7, 5 8, 8s Für die Eigenfreqenz erhält an f 8, 9s in Abb. -8c Berechnng der Steifigeit ie Eigenfreqenz des Balens liegt zwischen 8,9 s - nd 7,8 s -. ie Erregerfreqenz von n 960 6s 60 liegt nahe bei der öglichen Eigenfreqenz des Balens. adrch ann die dynaische Beansprchng infolge einer öglichen Unwcht sehr groß werden (Resonanzbereich). U dies z vereiden, sollte die Eigenfreqenz ~ 0 % über der Erregerfreqenz liegen, d. h. hier sollte die Steifigeit des Balens vergrößert werden. Beispiel Es sollen die Eigenfreqenz einer rotierenden Scheibe an eine Torsionsstab (einer Welle) bestit werden. er Torsionsstab hat einen Wellenabsatz nd dait zwei nterschiedliche Qerschnitte über der Länge, vergl. Abb.-9. Für dieses Beispiel werden die beiden Fälle vorgestellt, bei denen die Scheibe a Ende des Torsionsstabes angebracht ist (Fall, Abb.- 9) nd die Scheibe i ittleren Bereich des Torsionsstabes ontiert ist (Fall, Abb.-0).
9 Einassenschwinger Teil I. ie freie Schwingng Beispiel Fall Scheibe a Stabende I d d L = 6 c Länge L = 0 c Länge Θ I = 0 Ns c Rotationsträgheitsoent der Scheibe G = 7,5 * 0 6 N/c Schbodl L L ie Abschnitte des Torsionsstabes (Welle) werden als asse- bzw. trägheitslos los betrachtet. Abb. -9 Scheibe a Stabende Für die Torsionssteifigeit eines reiszylindrischen Bateils gilt I T = π d /. ait ergibt sich die Steifigeit der beiden Abschnitte des Torsionsstabes (Welle) z 6 GIT 7, K 88, 5 0 Nc L 6 6 GIT 7, K 87, 0 Nc L 0 Verdrehngen a Stabende infolge T = : K K K K K 6 K 6, K K 0 N Eigenreisfreqenz: K I Eigenfreqenz: f 6, s in 05, s Beispiel Fall Scheibe in Stabitte ie Abessngen sind gegenüber Fall ngeändert d I d L = 6 c Länge L = 0 c Länge Θ I = 0 Ns c Rotationsträgheitsoent der Scheibe G = 7,5 0 6 N/c Schbodl Abb. -0 L L Scheibe a Stabitte Wie in Fall werden die Abschnitte des Torsionsstabes (Welle) als asse- bzw. trägheitslos
10 Teil I. ie freie Schwingng Einassenschwinger betrachtet. ie insgesat wirende Torsionssteifigeit der Welle ist hier as den Steifigeiten der beiden Abschnitte der Welle additiv zsaenzsetzen. ait ergibt sich die Gesatsteifigeit der beiden Abschnitte des Torsionsstabes (Welle) z K K K 88, 50 87, 0 570, 0 Nc Eigenreisfreqenz: K I Eigenfreqenz: f 6, 9s 6 570, , s 0856, in.. Foreln für Eigenfreqenzen ie in Gleichng (.6) dargestellte Forel ergibt die Eigenfreqenz eines Einassenschwingers. Bei ehrassenschwingern oder Systeen, die Biegeschwingngen asführen, sind z Teil ach rze Foreln verfügbar, die i Alltag zr schnellen Plasibilitätsontrolle verwendet werden önnen. Hier werden einige solcher Foreln genannt. Es bedeten: f = Eigenfreqenz, = asse, = Federsteifigeit, E = Elastizitätsodl, I = Flächenträgheitsoent, L = Länge, x,y = Verschiebng Fall ist ein translatorischer -assenschwinger it Eigenfreqenzen / / / 5 / / / / 5 / x x Fall ist ein translatorischer -assenschwinger it ngleichen assen x / x
11 Einassenschwinger Teil I. ie freie Schwingng 5 Fall ist ein translatorischer -assenschwinger it ngleichen assen nd Aflagern an beiden Enden x / x Fall ist ein translatorischer Schwinger ohne Aflager. ieser Schwinger enthält zwei assen nd dait zwei Freiheitsgrade. ie erste Eigenfreqenz ergibt sich z Nll, sie ergibt sich as der Starrörperverschiebng beider assen, ohne dass die Feder verfort wird. aher bleibt eine technisch signifiante Eigenfreqenz, obwohl assen vorhanden sind. 0, Fall 5 ist die translatorische Schwingng einer asse a Ende eines Biegebalens, der einseitig eingespannt ist. EI L y x L x Fall 6 ist die translatorische Schwingng einer asse in der itte eines beidseitig gelagerten Balens. EI L y L L. ie freie gedäpfte Schwingng Jetzt wird der Fall nterscht, bei de das Syste nbelastet ist (p(t) = 0), aber eine äpfng it c vorhanden ist. ie Bewegngsgleichng hat dait die For ü c c 0 oder gefort 0 (.) Ein Lösngsansatz nach Eler verwendet rt e
12 6 Teil I. ie freie Schwingng Einassenschwinger iese Ansatzfntion in die Bewegngsgleichng eingesetzt ergibt c rt r r e 0 c r r 0 (.) r, c c ait erhält an für die allgeeine Lösng c c t c t t t e G e G e iese Bewegng wird als gedäpfte Eigenschwingng eines Systes bezeichnet. (.) Geennzeichnet wird sie drch den Wert der isriinante c an nterscheidet drei Fälle isriinante = 0 = ritische äpfng isriinante > 0 = überritische äpfng isriinante < 0 = nterritische äpfng.. Kritische äpfng, c = c r I Fall der ritischen äpfng gilt für die äpfng c r c r Cr (.) ait erhält an für den Eler-Ansatz as (.) r. nd für die allgeeine Bewegngsgleichng t t G Gt e (.5) oder it den Anfangswerten 0, 0 t t t e (.6)
13 Einassenschwinger Teil I. ie freie Schwingng 7 ie Gleichng besagt, dass die Bewegng eine Schwingng it ehreren rchgängen drch die Rhelage ist, sondern es ist eine aperiodische Bewegng. In Abb. - ist eine solche Bewegng dargestellt. ie Schwingng wird in ürzest öglicher Zeit zr Rhe gedäpft. Für viele pratische Afgabenstellngen ist dieser Fall ninteressant, da die üblichen äpfngsoeffizienten c<<c r sind. Bei essinstrenten oder Flüssigeitsopassen wird dieser Wert dagegen angestrebt. 0 t 0 t Abb. - Schwingng bei ritischer äpfng Zr Berteilng der Schwingng eines Bateils wird allerdings die ritische äpfng als Vergleichswert herangezogen. Es wird der äpfngsgrad (bisher das sogenannte Lehrsche äpfngsaß) als Qotient der wirlichen nd der ritischen äpfng gebildet. C C äpfngsgrad (.7) C r Erfahrngswerte für den äpfngsgrad i pratischen Alltag: Bateile i linear-elastischen Bereich 0, , 05 Bateile i nicht linearen Bereich (plastische Verforngen) 0, 0 ritische äpfng.. Überritische äpfng I Fall der überritischen äpfng ist die isriinante positiv C it ξ ergibt sich für as de Eler-Ansatz r, ˆ nd als Lösng für die Bewegngsgleichng t t G sinh ˆ t G cosh ˆ t e (.8) Es handelt sich hier wie i Fall der ritischen äpfng ebenfalls eine aperiodische Bewegng. Sie ist nr für wenige technische Fälle von Bedetng... Unterritische äpfng Bei nterritischer äpfng ist die isriinante negativ c,
14 8 Teil I. ie freie Schwingng Einassenschwinger it ξ ergibt sich für die Lösng des Eleransatzes nach (.) r, r, i Es wird nn eine von ξ abhängige Kreisfreqenz ω eingeführt. (.9) ait erhält an als Lösngsfntion für die Bewegngsgleichng t it it t e G e Ge oder t t e Asin t Bcos t it den Anfangswerten 0 nd ů ergibt sich t t e 0 0 sint 0 cost (.0) (.) Wie bei der ngedäpften Schwingng ann an die Bewegngsgleichng it der Aplitde ax nd der Phasenverschiebng θ angeben. t t e cos t ax ax tan (.) ie Schwingng eines gedäpften Systes ist also eine ablingende Schwingng it einer Freqenz, die von der äpfng abhängt. er Zsaenhang zwischen ω nd ω ergibt sich über Gleichng (.9) z eine Viertelsreis, sofern, wie in Abb. - dargestellt, ω /ω über ξ afgetragen wird. a für viele Afgabenstellngen ξ sehr lein ist (ξ i Bereich 0,00-0,), nterscheiden sich die Freqenzen der gedäpften nd der ngedäpften Schwingng nr sehr wenig. Bereich des Technischen Alltages 0, Abb. - äpfngsgrad nd Eigenreisfreqenz Für ξ = 0, ergibt sich z. B. ω = 0,98 ω, also eine Abweichng %. aher wird eist von der Näherng ω ω asgegangen.
15 Einassenschwinger Teil I. ie freie Schwingng 9 Für die gedäpfte Eigenschwingng ergibt sich folgender Verlaf i Vergleich zr ngedäpften Eigenschwingng. 0 Zr Kennzeichnng des Ablingverhaltens wird das logarithische ereent Λ verwendet. Es ann as de Verhältnis der Aplitden zweier afeinanderfolgender Schwingngsdrchgänge bestit werden. e t ie Zeitpnte der zwei afeinanderfolgenden Aplitden sind t t T n n T T Abb. - Schwingng n bei nterritischer äpfng Af der Grndlage der Lösng der Bewegngsgleichng ergeben sich die Aplitden für diese Zeitpnte z n n e e t n n t T e T e e rch Logarithieren dieser Beziehng ergibt sich das logarithische ereent Λ: n ln ; n n ln (.a) n Für leine ξ gilt näherngsweise n ln (.b) n Über das logarithische ereent ann drch essng zweier afeinanderfolgender Schwingngsaplitden die äpfng des Systes (z. B. der äpfngsgrad) erhalten werden. Für leine ξ erhält an drch Uforen der Gleichng (.b) nd einer Entwiclng in die Potenzreihe n e...! n Abb. - Vergleich des exaten nd Als weitere Näherng wird für leine ξ die Reihe des genäherten äpfngsaßes nach de zweiten Glied abgebrochen, nd an erhält: n n (.) n,0 0,75 0,5 ex 0 0,05 0, 0,5 0,
16 0 Teil I. ie freie Schwingng Einassenschwinger er Vergleich der Werte des exaten ξ ex gegenüber de genäherten ξ as Gleichng ergibt den Verlaf, der in Abb.. dargestellt ist. Bei schwächer gedäpften Systeen ann die Genaigeit erhöht werden, wenn an ehrere afeinanderfolgende Schwingngsaplitden beobachtet nd die erste it der letzten verglichen wird. n ln n Für leine ξ erhält an näherngsweise n n n 0, 0,5 0, 0,05 n n Abb. -5 äpfngsgrad nd Redtion der Schwingngsaplitde (.5) (.6) n Eine Korretr ann wieder it Abb.-5 vorgenoen werden. Bei essngen der äpfng ist die Anzahl der Schwingngen, bis z der die Schwingng af 50 % der Anfangsaplitde zrücgegangen ist, ein aß für die äpfng. Einen gten Vergleichswert erhält an dadrch, dass bei einer äpfng von 0 % der ritischen äpfng (ξ = 0,) bei eine Zyls die Aplitde gerade af 50 % zrücgegangen ist. en allgeeinen Zsaenhang zeigt Abb.-5. In der Praxis wird die äpfng oft nterschiedlich angegeben. Es ss jeweils geprüft werden, ob es sich c, ξ oder Λ handelt. Für das logarithische ereent sind in Abschnitt.5 einige Anhaltswerte angegeben. Beispiel Es liegen die Verschsergebnisse eines Systes vor, das znächst drch eine Anfangsaslenng belastet wrde. ie afgebrachte Kraft nd die dadrch hervorgerfene Aslenng wrden geessen. Anschließend wrden die Lasten entfernt, so dass das Syste frei asschwingt. Bei diese Asschwingen wrde die Aslenng nach einer Schwingng nd die Schwingngszeit (Periode) geessen. ie geessenen Werte sind: P = 0, N Kraft 0 =,0 c Anfangsaslenng = 0,8 c Aslenng nach einer Schwingng T = 0,889 s Schwingngszeit G g, p Für dieses Syste ergeben sich folgende Werte. Abb. -6 Freie EI Schwingng, Beispiel c
17 Einassenschwinger Teil I. ie freie Schwingng Steifigeit p 0, 5N/ 0 0, 0 Freqenz f, Hz T 0, Kreisfreqenz f 7, 07 rad / s log. ereent 0, 0 ln 0, 88 0, 008 äpfngsgrad 0. % äpfngsonstante c cr 0, Ns/ Kreisfreqenz der gedäpften Schwingng 7, 07 0, 7, 070, 99 7, 00
Einmassenschwinger Teil I.2 Herleitung der Bewegungsgleichung 15
 Einassenshwinger Teil I.2 Herleitng der Bewegngsgleihng 15 2 Herleitng der Bewegngsgleihng 2.1 Angreifende Kraft p(t) Für diese Erläterngen wird als Beispiel die Deplatte it Stützen von Abb.1-2 betrahtet.
Einassenshwinger Teil I.2 Herleitng der Bewegngsgleihng 15 2 Herleitng der Bewegngsgleihng 2.1 Angreifende Kraft p(t) Für diese Erläterngen wird als Beispiel die Deplatte it Stützen von Abb.1-2 betrahtet.
Übungsaufgaben Mathematik III MST. Zu b) Klassifizieren Sie folgende Differentialgleichungen nach folgenden Kriterien : - Anfangswertproblem
 Übngsafgaben Mathematik III MST Lösngen z Blatt 4 Differentialgleichngen Prof. Dr. B.Grabowski Z Afgabe ) Z a) Klassifizieren Sie folgende Differentialgleichngen nach folgenden Kriterien: -Ordnng der Differentialgleichng
Übngsafgaben Mathematik III MST Lösngen z Blatt 4 Differentialgleichngen Prof. Dr. B.Grabowski Z Afgabe ) Z a) Klassifizieren Sie folgende Differentialgleichngen nach folgenden Kriterien: -Ordnng der Differentialgleichng
Übungsaufgaben Mathematik 3 MST Lösung zu Blatt 4 Differentialgleichungen
 Übngsafgaben Mathematik MST Lösng z Blatt 4 Differentialgleichngen Prof. Dr. B.Grabowski Z Afgabe ) Lösen Sie folgende Differentialgleichngen nd Anfangswertprobleme drch mehrfaches Integrieren nach y(x)
Übngsafgaben Mathematik MST Lösng z Blatt 4 Differentialgleichngen Prof. Dr. B.Grabowski Z Afgabe ) Lösen Sie folgende Differentialgleichngen nd Anfangswertprobleme drch mehrfaches Integrieren nach y(x)
2. Einmassenschwinger. Inhalt:
 . Einmassenschwinger Inhalt:.1 Bewegungsdifferentialgleichung. Eigenschwingung.3 Harmonische Anregung.4 Schwingungsisolation.5 Stossartige Belastung.6 Allgemeine Belastung.7 Nichtlineare Systeme.8 Dämpfungsarten
. Einmassenschwinger Inhalt:.1 Bewegungsdifferentialgleichung. Eigenschwingung.3 Harmonische Anregung.4 Schwingungsisolation.5 Stossartige Belastung.6 Allgemeine Belastung.7 Nichtlineare Systeme.8 Dämpfungsarten
7. Zusammengesetzte Beanspruchung
 7. Zsammengesetzte Beanspchng Biegng / Tosion ellen, ei denen gleichzeitig ein Biegemoment (Nomalspannngen) nd ein Tosionsmoment (Schspannngen) aftitt. Biegespannngen (Ode ach Nomalspannngen stehen echtwinklig
7. Zsammengesetzte Beanspchng Biegng / Tosion ellen, ei denen gleichzeitig ein Biegemoment (Nomalspannngen) nd ein Tosionsmoment (Schspannngen) aftitt. Biegespannngen (Ode ach Nomalspannngen stehen echtwinklig
Vektorraum. Ist =, so spricht man von einem reellen Vektorraum, ist =, so spricht man von einem komplexen
 6. Vektorra Ein Vektorra oder linearer Ra ist eine algebraische Strktr die in fast allen Zweigen der Matheatik erwendet wird. Eingehend betrachtet werden Vektorräe in der Linearen Algebra. Die Eleente
6. Vektorra Ein Vektorra oder linearer Ra ist eine algebraische Strktr die in fast allen Zweigen der Matheatik erwendet wird. Eingehend betrachtet werden Vektorräe in der Linearen Algebra. Die Eleente
Differentialgleichung.
 Kapitel 9 Differentialgleichungen 9. Einteilung der Differentialgleichungen In einer Differentialgleichung (DGl) treten Differentialquotienten von einer oder ehreren Funtionen von einer oder ehreren Veränderlichen
Kapitel 9 Differentialgleichungen 9. Einteilung der Differentialgleichungen In einer Differentialgleichung (DGl) treten Differentialquotienten von einer oder ehreren Funtionen von einer oder ehreren Veränderlichen
3. Mechanische Eigenschaften von Kristallen
 3. echanische Eigenschaften von Kristallen 3.. Elastizität eines Festkörpers Kontinmsnäherng: Kristall homogenes, kontinierliches edim, λ»a zr Beschreibng von statischen Verschiebngen, Ultraschallwellen
3. echanische Eigenschaften von Kristallen 3.. Elastizität eines Festkörpers Kontinmsnäherng: Kristall homogenes, kontinierliches edim, λ»a zr Beschreibng von statischen Verschiebngen, Ultraschallwellen
211 Viskosität von Luft
 11 Viskosität von Lft 1. Afgaben 1.1 Messen Sie die Viskosität η von Lft in Abhängigkeit vom Drck p. Stellen Sie η als Fnktion von p grafisch dar! 1. Interpretieren Sie die Messkrve!. Grndlagen Stichworte:
11 Viskosität von Lft 1. Afgaben 1.1 Messen Sie die Viskosität η von Lft in Abhängigkeit vom Drck p. Stellen Sie η als Fnktion von p grafisch dar! 1. Interpretieren Sie die Messkrve!. Grndlagen Stichworte:
Labor Messtechnik Versuch 7 Drehmomentenmessung
 F Ingenierwesen F Maschinenba Prof. r. Kröber Versch 7 rehmomentenmessng Seite 1 von 6 Versch 7: rehmomentenmessng, Gleichspannngsmessverstärker 1. Verschsafba 1.1. Umfang des Versches Im Versch werden
F Ingenierwesen F Maschinenba Prof. r. Kröber Versch 7 rehmomentenmessng Seite 1 von 6 Versch 7: rehmomentenmessng, Gleichspannngsmessverstärker 1. Verschsafba 1.1. Umfang des Versches Im Versch werden
Kontrolle Physik-Leistungskurs Klasse 11 Widerstände
 Kontroe hysik-eistngskrs Kasse 11 Widerstände..016 1. Es stehen zwei Gühapen 6 V/1,5 W nd V/1,5 W sowie eine Spannngsqee 9 V zr Verfügng. Was passiert, wenn an die beiden Gühapen nd die Spannngsqee in
Kontroe hysik-eistngskrs Kasse 11 Widerstände..016 1. Es stehen zwei Gühapen 6 V/1,5 W nd V/1,5 W sowie eine Spannngsqee 9 V zr Verfügng. Was passiert, wenn an die beiden Gühapen nd die Spannngsqee in
sinω t und der sich einstellenden stationären
 26 6.6.4. Bedetng des Freqenzganges als Systemcharakteristik Die bisherigen Asführngen nd Erläterngen zm Freqenzgang eines linearen zeitinvarianten Systems einschließlich seiner grafischen Darstellng als
26 6.6.4. Bedetng des Freqenzganges als Systemcharakteristik Die bisherigen Asführngen nd Erläterngen zm Freqenzgang eines linearen zeitinvarianten Systems einschließlich seiner grafischen Darstellng als
Thomas Beier Petra Wurl. Regelungstechnik. Basiswissen, Grundlagen, Beispiele. 2., neu bearbeitete Auflage
 Thomas Beier Petra Wrl Regelngstechnik Basiswissen, Grndlagen, Beispiele 2., ne bearbeitete Aflage 1.2 Darstellng von Regelkreisen 19 Am Eingang der Regelstrecke befindet sich das Stellglied. Es ist ein
Thomas Beier Petra Wrl Regelngstechnik Basiswissen, Grndlagen, Beispiele 2., ne bearbeitete Aflage 1.2 Darstellng von Regelkreisen 19 Am Eingang der Regelstrecke befindet sich das Stellglied. Es ist ein
72 Grundlagen der konstruktiven Geometrie
 7 Grndlagen der konstrktiven Geometrie die Parameter nd v zgleich ein lokales kartesisches Koordinatensstem af der Eene. Flächen. Ordnng Für die implizite Darstellng eines Zlinders gilt in homogenen Koordinaten
7 Grndlagen der konstrktiven Geometrie die Parameter nd v zgleich ein lokales kartesisches Koordinatensstem af der Eene. Flächen. Ordnng Für die implizite Darstellng eines Zlinders gilt in homogenen Koordinaten
Definition und Eigenschaften von elliptischen Funktionen Thomas Regier. 1. Verdoppelung des Lemniskatenbogens und erweitertes Additionstheorem
 Definition nd Eigenschaften von elliptischen Fnktionen Thomas Regier. Verdoppelng des Lemniskatenbogens nd erweitertes Additionstheorem Elliptische Integrale berechnen die Krvenlänge von z.b. elliptischen
Definition nd Eigenschaften von elliptischen Fnktionen Thomas Regier. Verdoppelng des Lemniskatenbogens nd erweitertes Additionstheorem Elliptische Integrale berechnen die Krvenlänge von z.b. elliptischen
EINFÜHRUNG IN DIE TENSORRECHNUNG
 EINFÜHRUNG IN DIE TENSORRECHNUNG Teil SIEGFRIED PETRY Nefassng vom.jni 016 I n h a l t 1 Mehr über Tensoren. Stfe Darstellng eines Tensors in einer Basis 4 Beispiele nd Übngen 5 4 Lösngen 1 1 1 Tensoren.
EINFÜHRUNG IN DIE TENSORRECHNUNG Teil SIEGFRIED PETRY Nefassng vom.jni 016 I n h a l t 1 Mehr über Tensoren. Stfe Darstellng eines Tensors in einer Basis 4 Beispiele nd Übngen 5 4 Lösngen 1 1 1 Tensoren.
AUFGABENSAMMLUNG ZUM LEHRGEBIET. AUTOMATISIERUNGSTECHNIK bzw. KONTINUIERLICHE SYSTEME
 Dr.-Ing. Tatjana Lange Fachhochschle für Technik nd Wirtschaft Fachbereich Elektrotechnik AUFGABENSAMMLUNG ZUM LEHRGEBIET AUTOMATISIERUNGSTECHNIK bzw. KONTINUIERLICHE SYSTEME. Differentialgleichngen Afgabe.:
Dr.-Ing. Tatjana Lange Fachhochschle für Technik nd Wirtschaft Fachbereich Elektrotechnik AUFGABENSAMMLUNG ZUM LEHRGEBIET AUTOMATISIERUNGSTECHNIK bzw. KONTINUIERLICHE SYSTEME. Differentialgleichngen Afgabe.:
die Eigenfrequenz des Systems für Drehschwingungen um den Punkt A und 20 m
 ufgabensalung Dynaik ufgabe Der nachfolgen argestellte Einassenschwinger soll untersucht weren. Das Syste besteht aus eine en Balken it er Masse, eine Stab un eine viskosen Däpfer. Berechnen Sie a.) ie
ufgabensalung Dynaik ufgabe Der nachfolgen argestellte Einassenschwinger soll untersucht weren. Das Syste besteht aus eine en Balken it er Masse, eine Stab un eine viskosen Däpfer. Berechnen Sie a.) ie
Lokale Eigenschaften des Hilbert-Symbols
 Lokale Eigenschaften des Hilbert-Symbols (Nach J.P. Serre: A Corse in Arithmetic) Bettina Böhme, Karin Loch 24.05.2007 Im Folgenden bezeichnet k entweder den Körer R der reellen Zahlen oder den Körer Q
Lokale Eigenschaften des Hilbert-Symbols (Nach J.P. Serre: A Corse in Arithmetic) Bettina Böhme, Karin Loch 24.05.2007 Im Folgenden bezeichnet k entweder den Körer R der reellen Zahlen oder den Körer Q
Federpendel. Einführung. Das Federpendel. Basiswissen > Mechanische Schwingungen > Federpendel. Skript PLUS
 www.schullv.de Basiswissen > Mechanische Schwingungen > Federpendel Federpendel Skript PLUS Einführung Wärst du utig genug für einen Bungee-Sprung? Oder hast du gar schon einen geacht? Wenn ja, hast du
www.schullv.de Basiswissen > Mechanische Schwingungen > Federpendel Federpendel Skript PLUS Einführung Wärst du utig genug für einen Bungee-Sprung? Oder hast du gar schon einen geacht? Wenn ja, hast du
Einführung in FEM Motivationsbeispiel. Berechnungsbeispiel COMSOL Multiphysics: Elastizitätsberechnung eines F1 Frontflügels. www.comsol.
 Einführng in FEM Motivationsbeispiel Berechnngsbeispiel COMSO Mltiphysics: Elastizitätsberechnng eines F Frontflügels. www.comsol.de Originalgeometrie CAD-Modell mit Berechnngsgitter FEM Ergebnis der Aslenkng
Einführng in FEM Motivationsbeispiel Berechnngsbeispiel COMSO Mltiphysics: Elastizitätsberechnng eines F Frontflügels. www.comsol.de Originalgeometrie CAD-Modell mit Berechnngsgitter FEM Ergebnis der Aslenkng
3 Flächen und Flächenintegrale
 3 Flächen Flächen sind im dreidimensionalen Ram eingebettete zweidimensionale geometrische Objekte In der Mechanik werden zb Membranen nd chalen als Flächen idealisiert In der Geometrie treten Flächen
3 Flächen Flächen sind im dreidimensionalen Ram eingebettete zweidimensionale geometrische Objekte In der Mechanik werden zb Membranen nd chalen als Flächen idealisiert In der Geometrie treten Flächen
. Die Differenz zwischen den Umschaltpunkten nennt man Hysterese u H. -u T- (t): Eingangssignal. (t): Ausgangssignal
 sind Komparatorschaltngen mit Mitkopplng Sie werden haptsächlich zr Implsformng nd echteckwandler eingesetzt Im Gegensatz zr konventionellen Komparatorschaltng wird die eferenzspannng nicht fest vorgegeben,
sind Komparatorschaltngen mit Mitkopplng Sie werden haptsächlich zr Implsformng nd echteckwandler eingesetzt Im Gegensatz zr konventionellen Komparatorschaltng wird die eferenzspannng nicht fest vorgegeben,
Dreiphasen-Wechselrichter: Steuerzyklen der Ventile 1 bis 6:
 Dreiphasen-Wechselrichter: Steerzyklen er Ventile bis 6: a) Zweistfen-Wechselrichter (-mrichter): Die as er Gleichspannng gespeisten Ventile bis 6 können ie Asgangsleitngen, V,W zwischen en beien Potentialen
Dreiphasen-Wechselrichter: Steerzyklen er Ventile bis 6: a) Zweistfen-Wechselrichter (-mrichter): Die as er Gleichspannng gespeisten Ventile bis 6 können ie Asgangsleitngen, V,W zwischen en beien Potentialen
1. Oszilloskop. Das Oszilloskop besitzt zwei Betriebsarten: Schaltsymbol Oszilloskop
 . Oszilloskop Grndlagen Ein Oszilloskop ist ein elektronisches Messmittel zr grafischen Darstellng von schnell veränderlichen elektrischen Signalen in einem kartesischen Koordinaten-System (X- Y- Darstellng
. Oszilloskop Grndlagen Ein Oszilloskop ist ein elektronisches Messmittel zr grafischen Darstellng von schnell veränderlichen elektrischen Signalen in einem kartesischen Koordinaten-System (X- Y- Darstellng
1. Theoretische Grundlagen
 Fachbereich Elektrotechnik / Informationstechnik Elektrische Mess- nd Prüftechnik Laborpraktikm Abgabe der Aswertng dieses Verschs ist Vorassetzng für die Zlassng zm folgenden ermin Grndlagen der Leistngsmessng
Fachbereich Elektrotechnik / Informationstechnik Elektrische Mess- nd Prüftechnik Laborpraktikm Abgabe der Aswertng dieses Verschs ist Vorassetzng für die Zlassng zm folgenden ermin Grndlagen der Leistngsmessng
Blatt 6. Schwingungen- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik T1) i SoSe 011 Blatt 6. Schwingungen- Lösungsvorschlag Aufgabe 6.1. Räulicher Oszillator
Fakultät für Physik der LMU München Lehrstuhl für Kosologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik T1) i SoSe 011 Blatt 6. Schwingungen- Lösungsvorschlag Aufgabe 6.1. Räulicher Oszillator
Trägheitsmoment (TRÄ)
 - - xel Günther.7. Cldi Knk Grppe 7 (Dientg) rägheitoent (Ä) 5.: (Grphiche Drtellng: Digr ) Die Winkelrichtgröße erhält n nch folgender Forel (Werte der gleichgeen): M ϕ F r M,6N N,57 ϕ ϕ,5 Der ttitiche
- - xel Günther.7. Cldi Knk Grppe 7 (Dientg) rägheitoent (Ä) 5.: (Grphiche Drtellng: Digr ) Die Winkelrichtgröße erhält n nch folgender Forel (Werte der gleichgeen): M ϕ F r M,6N N,57 ϕ ϕ,5 Der ttitiche
Experimentelle Untersuchungen und Materialmodellierung zur Berechnung von Klebverbindungen
 5. LS-DYNA Anwenderform, Ulm 006 Verbindngs- / Klebetechnik Exerimentelle Unterschngen nd Materialmodellierng zr Berechnng von Klebverbindngen Michael Schlimmer Institt für Werkstofftechnik Universität
5. LS-DYNA Anwenderform, Ulm 006 Verbindngs- / Klebetechnik Exerimentelle Unterschngen nd Materialmodellierng zr Berechnng von Klebverbindngen Michael Schlimmer Institt für Werkstofftechnik Universität
Ansicht 10 P. Aufsicht 12 P m m 12 P 2 P 4 P 4 P 4 P m 7.50 m
 Berechnng FEMrämlichen Fachwerks eines Beisiel zr ehrveranstaltng Ein der Finite Elemente Methode Grndlagen Systembeschreibng Geometrie nd Abmessngen des Systems.... Materialarameter................. Skizzen
Berechnng FEMrämlichen Fachwerks eines Beisiel zr ehrveranstaltng Ein der Finite Elemente Methode Grndlagen Systembeschreibng Geometrie nd Abmessngen des Systems.... Materialarameter................. Skizzen
Labor Messtechnik Versuch 4 Dehnungsmesstechnik
 F Ingenierwesen FR Maschinenba Versch 4 Dehnngsmesstechnik Seite 1 von 8 Versch 4: Dehnngsmesstechnik 1. Verschsafba 1.1. Umfang des Versches Im Versch werden folgende Themenkreise behandelt: - Verschsstand
F Ingenierwesen FR Maschinenba Versch 4 Dehnngsmesstechnik Seite 1 von 8 Versch 4: Dehnngsmesstechnik 1. Verschsafba 1.1. Umfang des Versches Im Versch werden folgende Themenkreise behandelt: - Verschsstand
B: Gleichung der Kugel mit Zentrum M(3, -2, 1), die den Punkt P(1, 4, 4) enthält.
 5 0. Die Kgel 0. Die Kgelgleichng Def. Unter der Kgel k mit Mittelpnkt M nd adis verstehen wir die Menge aller Pnkte P, die vom Mittelpnkt M einen vorgegebenen abstand haben, für die also gilt: MP MP oder
5 0. Die Kgel 0. Die Kgelgleichng Def. Unter der Kgel k mit Mittelpnkt M nd adis verstehen wir die Menge aller Pnkte P, die vom Mittelpnkt M einen vorgegebenen abstand haben, für die also gilt: MP MP oder
Turbulente Rohrströmung
 Trblente ohrströmng Strömng laminar transitionell trblent zeitliches Verhalten im Pnt P trblent transitionell laminar laminar : transitionell : & p onst p, v 0 [ t t ] V tr Vlam ; p f ( t), t l, i, r,
Trblente ohrströmng Strömng laminar transitionell trblent zeitliches Verhalten im Pnt P trblent transitionell laminar laminar : transitionell : & p onst p, v 0 [ t t ] V tr Vlam ; p f ( t), t l, i, r,
1 Pythagoräische Zahlentripel
 1 Pythagoräische Zahlentripel Wir fragen ns nn, welche natürlichen Zahlen die Gleichng 2 + y 2 = 2 lösen. Übng 1 Finden Sie Zahlentripel (; y; ) 2 N 3, mit 1 ; y < ; welche die Gleichng 2 + y 2 = 2 lösen.
1 Pythagoräische Zahlentripel Wir fragen ns nn, welche natürlichen Zahlen die Gleichng 2 + y 2 = 2 lösen. Übng 1 Finden Sie Zahlentripel (; y; ) 2 N 3, mit 1 ; y < ; welche die Gleichng 2 + y 2 = 2 lösen.
Verbundstudiengang Wirtschaftsingenieurwesen (Bachelor) Praktikum Grundlagen der Elektrotechnik und Elektronik
 erbndstdiengang Wirtschaftsingenierwesen (Bachelor) Praktikm Grndlagen der Elektrotechnik nd Elektronik ersch 4 Transformator Teilnehmer: Name orname Matr.-Nr. Datm der erschsdrchführng: Transformator
erbndstdiengang Wirtschaftsingenierwesen (Bachelor) Praktikm Grndlagen der Elektrotechnik nd Elektronik ersch 4 Transformator Teilnehmer: Name orname Matr.-Nr. Datm der erschsdrchführng: Transformator
Schaltungen mit nichtlinearen Widerständen
 HOCHSCHLE FÜ TECHNIK ND WITSCHAFT DESDEN (FH) niversity of Applied Sciences Fachbereich Elektrotechnik Praktikm Grndlagen der Elektrotechnik Versch: Schaltngen mit nichtlinearen Widerständen Verschsanleitng
HOCHSCHLE FÜ TECHNIK ND WITSCHAFT DESDEN (FH) niversity of Applied Sciences Fachbereich Elektrotechnik Praktikm Grndlagen der Elektrotechnik Versch: Schaltngen mit nichtlinearen Widerständen Verschsanleitng
Übersicht der Vorlesung
 Übersich der Vorlesng 1. Einührng 2. Bilderarbeing 3. Morphologische Operaionen 4. Bildsegmenierng 5. Mermale on Objeen 6. Klassiiaion 7. Dreidimensionale Bildinerpreaion 8. Bewegngsanalse as Bildolgen
Übersich der Vorlesng 1. Einührng 2. Bilderarbeing 3. Morphologische Operaionen 4. Bildsegmenierng 5. Mermale on Objeen 6. Klassiiaion 7. Dreidimensionale Bildinerpreaion 8. Bewegngsanalse as Bildolgen
Gewählt wird eine viersträngige Seilführung mit oberer Ausgleichsrolle (siehe Skript Blatt 4.4-10).
 Zahlenbeispiel - erechnung und Entwurf eis ubwerks a) Anordnung (siehe Skript latt 0a) Das ubwerk hat die auptbaugruppen otor, TK Troelkupplung, K elastische Kupplung it resscheibe, T Seiltroel, echanische
Zahlenbeispiel - erechnung und Entwurf eis ubwerks a) Anordnung (siehe Skript latt 0a) Das ubwerk hat die auptbaugruppen otor, TK Troelkupplung, K elastische Kupplung it resscheibe, T Seiltroel, echanische
4.1 Lagrange-Gleichungen, Integrale der Bewegung, Bahnkurven
 Das Zwei-Köe-Poblem 9 Woche_Skitoc, /5 agange-gleichngen, Integale e Bewegng, Bahnkven Betachtet ween wei Pnktmassen m n m an en Oten (t n (t, ie übe ein abstansabhängiges Potenial U( miteinane wechselwiken
Das Zwei-Köe-Poblem 9 Woche_Skitoc, /5 agange-gleichngen, Integale e Bewegng, Bahnkven Betachtet ween wei Pnktmassen m n m an en Oten (t n (t, ie übe ein abstansabhängiges Potenial U( miteinane wechselwiken
Übungen zu Lagrange-Formalismus und kleinen Schwingungen
 Übungen zu Lagrange-Foralisus und kleinen Schwingungen Jonas Probst.9.9 Teilchen auf der Stange Aufgabe: Ein Teilchen der Masse wird durch eine Zwangskraft auf einer asselosen Stange gehalten, auf der
Übungen zu Lagrange-Foralisus und kleinen Schwingungen Jonas Probst.9.9 Teilchen auf der Stange Aufgabe: Ein Teilchen der Masse wird durch eine Zwangskraft auf einer asselosen Stange gehalten, auf der
7 Lineare Gleichungssysteme
 116 7 Lineare Gleichngsssteme Lineare Gleichngsssteme treten in vielen mathematischen, aber ach natrwissenschaftlichen Problemen af; m Beispiel beim Lösen von Differentialgleichngen, bei Optimierngsafgaben,
116 7 Lineare Gleichngsssteme Lineare Gleichngsssteme treten in vielen mathematischen, aber ach natrwissenschaftlichen Problemen af; m Beispiel beim Lösen von Differentialgleichngen, bei Optimierngsafgaben,
Netzgeführte Stromrichterschaltungen
 4 Netzgeführte Stromrichterschaltngen In netzgeführten Stromrichtern wird die Wechselspannng des speisenden Netzes nicht nr zr Spannngsbildng af der Asgangsseite bentzt, sondern sie dient ach als treibende
4 Netzgeführte Stromrichterschaltngen In netzgeführten Stromrichtern wird die Wechselspannng des speisenden Netzes nicht nr zr Spannngsbildng af der Asgangsseite bentzt, sondern sie dient ach als treibende
Prüfung aus Physik III (PHB3) Donnerstag 8. Juli 2010
 Fachhochschule München FK06 Soerseester 2010 Prüfer: Prof. r. Maier Prüfung aus Physik III (PHB3) onnerstag 8. Juli 2010 Zugelassene Hilfsittel: Forelsalung (Bestandteil der Prüfung), Taschenrechner (nicht
Fachhochschule München FK06 Soerseester 2010 Prüfer: Prof. r. Maier Prüfung aus Physik III (PHB3) onnerstag 8. Juli 2010 Zugelassene Hilfsittel: Forelsalung (Bestandteil der Prüfung), Taschenrechner (nicht
Kommunikationstechnik I
 Konikationstechnik I Pro. Dr. Stean Weinzierl Msterlösng 6. Agabenblatt 1. Psychoakstik 1.1 Was ist ein Tonschwellenadiogra? Drch ein Tonschwellenadiogra (engl: hearing loss) wird die Hörähigkeit einer
Konikationstechnik I Pro. Dr. Stean Weinzierl Msterlösng 6. Agabenblatt 1. Psychoakstik 1.1 Was ist ein Tonschwellenadiogra? Drch ein Tonschwellenadiogra (engl: hearing loss) wird die Hörähigkeit einer
6 Fremdgeführte Stromrichter
 6 Fremdgeführte Stromrichter Bei fremdgeführten Stromrichtern verläft die Kommtierng der Stromübergang zwischen zwei nacheinander stromführenden Schaltngszweigen nter der Wirkng einer äßeren Sannng, meist
6 Fremdgeführte Stromrichter Bei fremdgeführten Stromrichtern verläft die Kommtierng der Stromübergang zwischen zwei nacheinander stromführenden Schaltngszweigen nter der Wirkng einer äßeren Sannng, meist
Schriftliche Prüfung aus Control Systems 1 am
 TU Graz, Institt für Regelngs- nd Atomatisierngstechnik A Schriftliche Prüfng as Control Systems am 5 0 006 Name / Vorname(n): Kenn-MatrNr: Gebrtsdatm: BONUSPUNKTE as Compterrechenübng: 3 erreichbare Pnkte
TU Graz, Institt für Regelngs- nd Atomatisierngstechnik A Schriftliche Prüfng as Control Systems am 5 0 006 Name / Vorname(n): Kenn-MatrNr: Gebrtsdatm: BONUSPUNKTE as Compterrechenübng: 3 erreichbare Pnkte
Institut für Leistungselektronik und Elektrische Antriebe. Universität Stuttgart. Bild Prof. Dr.-Ing. J. Roth-Stielow
 niversität Stttgart Institt für Leistngselektronik nd lektrische Antriebe rof. Dr.-Ing. J. Roth-Stielo K + K M M M K + M + I A D HC H? I J? I J 8 A H> H= K? D A H Bild -3. nterlagen zr Vorlesng Leistngselektronik
niversität Stttgart Institt für Leistngselektronik nd lektrische Antriebe rof. Dr.-Ing. J. Roth-Stielo K + K M M M K + M + I A D HC H? I J? I J 8 A H> H= K? D A H Bild -3. nterlagen zr Vorlesng Leistngselektronik
2. Freie gedämpfte Schwingungen
 2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
Einführung in die Meteorologie (met211) - Teil VI: Dynamik der Atmosphäre
 Einführng in die Meteorologie (met211) - Teil VI: Dnamik der Atmosphäre Clemens Simmer VI Dnamik der Atmosphäre Dnamische Meteorologie ist die Lehre on der Natr nd den Ursachen der Bewegng in der Atmosphäre.
Einführng in die Meteorologie (met211) - Teil VI: Dnamik der Atmosphäre Clemens Simmer VI Dnamik der Atmosphäre Dnamische Meteorologie ist die Lehre on der Natr nd den Ursachen der Bewegng in der Atmosphäre.
Quellen und Senken als Feldursachen
 Kapitel 2 Qellen nd Senken als Feldrsachen Wir sprechen von Qellenfeldern nd Wirbelfeldern. Beide nterscheiden sich grndlegend voneinander. Wir wollen deswegen beide Feldarten getrennt besprechen, m deren
Kapitel 2 Qellen nd Senken als Feldrsachen Wir sprechen von Qellenfeldern nd Wirbelfeldern. Beide nterscheiden sich grndlegend voneinander. Wir wollen deswegen beide Feldarten getrennt besprechen, m deren
Grundlagen experimenteller Windkanaluntersuchungen: Hitzdrahtmesstechnik
 Messtechnische Grndlagen 1. Anmerkngen zr Hitzdrahtanemometrie Die Vermessng der Grenzschicht wird mit Hitzdrahtsonden vom Typ 55P61 der Firma DANTEC vorgenommen. Die verwendeten Hitzdrahtsonden bestehen
Messtechnische Grndlagen 1. Anmerkngen zr Hitzdrahtanemometrie Die Vermessng der Grenzschicht wird mit Hitzdrahtsonden vom Typ 55P61 der Firma DANTEC vorgenommen. Die verwendeten Hitzdrahtsonden bestehen
Konsumoptimum und individuelle Nachfrage
 Institt für. Einführng/Motivation. Konstheorie 3. Prodktionstheorie 4. Marktanalyse Konstheorie Bdgetbedingng des Konsenten Präferenzen nd Ntzenfnktion Konsoti nd individelle Nachfrage Literatr z.3: Pindyck/Rbinfeld
Institt für. Einführng/Motivation. Konstheorie 3. Prodktionstheorie 4. Marktanalyse Konstheorie Bdgetbedingng des Konsenten Präferenzen nd Ntzenfnktion Konsoti nd individelle Nachfrage Literatr z.3: Pindyck/Rbinfeld
PWM Teil2. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik. Arcisstraße 21 D München
 Lehrsthl für Elektrische Antriebssysteme nd Leistngselektronik Technische Universität München Arcisstraße 21 D 80333 München Email: eat@ei.tm.de Internet: http://www.eat.ei.tm.de Prof. Dr.-Ing. Ralph Kennel
Lehrsthl für Elektrische Antriebssysteme nd Leistngselektronik Technische Universität München Arcisstraße 21 D 80333 München Email: eat@ei.tm.de Internet: http://www.eat.ei.tm.de Prof. Dr.-Ing. Ralph Kennel
Lösungsvorschläge zum 4. Übungsblatt, WS 2012/2013 Höhere Mathematik III für die Fachrichtung Physik
 Lösungsvorschläge zum 4. Übungsblatt, WS 202/203 Höhere Mathematik III für die Fachrichtung Physik Aufgabe 6 Bei allen Aufgabenteilen handelt es sich um (homogene bzw. inhomogene) lineare Differentialgleichungen
Lösungsvorschläge zum 4. Übungsblatt, WS 202/203 Höhere Mathematik III für die Fachrichtung Physik Aufgabe 6 Bei allen Aufgabenteilen handelt es sich um (homogene bzw. inhomogene) lineare Differentialgleichungen
Physikalisches Praktikum I Bachelor Chemieingenieurwesen, Wirtschaftsingenieurwesen Chemietechnik MSc. M. Gilbert
 Physialisches Pratiu I Bachelor Cheieingenieurwesen, Wirtschaftsingenieurwesen Cheietechni MSc. M. Gilbert M06 Federschwingung (Pr_EX_M06_Federschwingung_6, 30.8.009) 1. Nae Matr. Nr. Gruppe Tea. 3. Protooll
Physialisches Pratiu I Bachelor Cheieingenieurwesen, Wirtschaftsingenieurwesen Cheietechni MSc. M. Gilbert M06 Federschwingung (Pr_EX_M06_Federschwingung_6, 30.8.009) 1. Nae Matr. Nr. Gruppe Tea. 3. Protooll
Übungen zum Ferienkurs Analysis II 2014
 Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Gerätepraktikum Tensionsinfiltrometer
 Gerätepraktikm Tensionsinfiltrometer Motivation Im System Boden-Pflanze-Atmosphäre findet die Transformation von Niederschlägen in Evapotranspiration, Bodenfechteänderng, Grndwassernebildng nd Abflss statt.
Gerätepraktikm Tensionsinfiltrometer Motivation Im System Boden-Pflanze-Atmosphäre findet die Transformation von Niederschlägen in Evapotranspiration, Bodenfechteänderng, Grndwassernebildng nd Abflss statt.
Konstantin Meskouris Klaus-G. Hinzen Christoph Butenweg Michael Mistler. Bauwerke und Erdbeben
 Konstantin Mesoris Klas-G. Hinzen Christoph Btenweg Michael Mistler Bawere nd Erdbeben Konstantin Mesoris Klas-G. Hinzen Christoph Btenweg Michael Mistler Bawere nd Erdbeben Grndlagen Anwendng Beispiele.,
Konstantin Mesoris Klas-G. Hinzen Christoph Btenweg Michael Mistler Bawere nd Erdbeben Konstantin Mesoris Klas-G. Hinzen Christoph Btenweg Michael Mistler Bawere nd Erdbeben Grndlagen Anwendng Beispiele.,
Jan Auffenberg. 2. Theorie 2.1 Mathematisches Pendel Um eine Pendelbewegung einfach beschreiben zu können, wendet man folgende Abstraktionen a:
 Gruppe 8 Björn Baueier Protokoll zu Versuch M1: Pendel 1. Einleitung Die Eigenschaften und Bewegungen der in diese Versuch untersuchten Fadenund Federpendel, werden durch eine besonders einfache haronische
Gruppe 8 Björn Baueier Protokoll zu Versuch M1: Pendel 1. Einleitung Die Eigenschaften und Bewegungen der in diese Versuch untersuchten Fadenund Federpendel, werden durch eine besonders einfache haronische
2 Amplitudenmodulation
 R - ING Übertraggstechik MOD - 16 Aplitdeodlatio Der isträger bietet drei igalparaeter, die wir beeiflsse köe. Etspreched terscheide wir Aplitdeodlatio für die beeiflsste Aplitde, Freqezodlatio d Phaseodlatio
R - ING Übertraggstechik MOD - 16 Aplitdeodlatio Der isträger bietet drei igalparaeter, die wir beeiflsse köe. Etspreched terscheide wir Aplitdeodlatio für die beeiflsste Aplitde, Freqezodlatio d Phaseodlatio
Schaltvorgänge. Praktikum. Grundlagen der Elektrotechnik. Versuch: Versuchsanleitung. 0. Allgemeines
 Prakikm Grndlagen der Elekroechnik Versch: Schalvorgänge Verschsanleing. Allgemeines Eine sinnvolle Teilnahme am Prakikm is nr drch eine ge Vorbereing af dem jeweiligen Soffgebie möglich. Von den Teilnehmern
Prakikm Grndlagen der Elekroechnik Versch: Schalvorgänge Verschsanleing. Allgemeines Eine sinnvolle Teilnahme am Prakikm is nr drch eine ge Vorbereing af dem jeweiligen Soffgebie möglich. Von den Teilnehmern
Lösungen der Aufgaben zu Kapitel 10
 Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Aufgabensammlung zur Systemtheorie und Regelungstechnik
 Afgabensammlng zr Systemtheorie nd egelngstechnik Dr. S. Krase Prof. Dr. B. Fapel 3. Jni 206 Wiederholng nd Grndlagen. Berechnen Sie (ohne Taschenrechner) die folgenden Asdrücke. Es bezeichne lg = log
Afgabensammlng zr Systemtheorie nd egelngstechnik Dr. S. Krase Prof. Dr. B. Fapel 3. Jni 206 Wiederholng nd Grndlagen. Berechnen Sie (ohne Taschenrechner) die folgenden Asdrücke. Es bezeichne lg = log
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 1
 T4p: Therodynaik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt Lösungsvorschlag. Noral-Verteilung Die Noral-Verteilung ist definiert als w() Ce ( ) /σ. a) Bestien Sie die Konstante C sodass w()
T4p: Therodynaik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt Lösungsvorschlag. Noral-Verteilung Die Noral-Verteilung ist definiert als w() Ce ( ) /σ. a) Bestien Sie die Konstante C sodass w()
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
 Karlsruher Institut für Technologie Institut für Analsis Dr. I. Anapolitanos Dipl.-Math. Sebastian Schwarz SS 07.05.07 Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
Karlsruher Institut für Technologie Institut für Analsis Dr. I. Anapolitanos Dipl.-Math. Sebastian Schwarz SS 07.05.07 Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
LZ F12.1 Impuls/B12.4 Arbeit, Energie, Leistung, Impuls 13 LZ F12.1 Impuls/B Impuls
 LZ F. Ipls/B.4 Arbeit, Energie, Leistng, Ipls LZ F. Ipls/B.4. Ipls 4.6. Ipls 4.6. Einführng Die Änderng der Geschwindigkeit eines Körpers ist so größer, je länger die Kraft wirkt. Der Einflss der Zeit
LZ F. Ipls/B.4 Arbeit, Energie, Leistng, Ipls LZ F. Ipls/B.4. Ipls 4.6. Ipls 4.6. Einführng Die Änderng der Geschwindigkeit eines Körpers ist so größer, je länger die Kraft wirkt. Der Einflss der Zeit
Umdruck IV: Transformatoren. 1 Idealer, festgekoppelter und realer Transformator
 Universität Stttgart Institt für Leistngselektronik nd lektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow ÜBUG ZU LKTRISCH RGITCHIK II Hinweis zr Pfeilng der Spannngen nd zr Festlegng des Wickelsinnes:
Universität Stttgart Institt für Leistngselektronik nd lektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow ÜBUG ZU LKTRISCH RGITCHIK II Hinweis zr Pfeilng der Spannngen nd zr Festlegng des Wickelsinnes:
2. Umkehrfunktionen und ihre Ableitung, Hyperbelfunktionen 2.1. Höhere Ableitungen. Die Ableitung der Ableitung von f bezeichnet man, x 2, fur x < 0,
 . Umkehrfunktionen un ihre Ableitung, Hyperbelfunktionen.. Höhere Ableitungen. Die Ableitung er Ableitung von f bezeichnet man, falls sie existiert, mit f x) oer f ) x) oer fx)) oer fx) bzw. allgemein
. Umkehrfunktionen un ihre Ableitung, Hyperbelfunktionen.. Höhere Ableitungen. Die Ableitung er Ableitung von f bezeichnet man, falls sie existiert, mit f x) oer f ) x) oer fx)) oer fx) bzw. allgemein
Ermittlung der Unsicherheiten in der Werkstoffprüfung
 Bndesanstalt für Materialforschng nd -prüfng Unterschngen z Schäden an Radsatzlenkern nd lagern der BR 481, Fahrzege 5 nd 193 Erittlng der Unsicherheiten in der Werkstoffprüfng Ralf Häcker BAM Bndesanstalt
Bndesanstalt für Materialforschng nd -prüfng Unterschngen z Schäden an Radsatzlenkern nd lagern der BR 481, Fahrzege 5 nd 193 Erittlng der Unsicherheiten in der Werkstoffprüfng Ralf Häcker BAM Bndesanstalt
Klassische Mechanik - Ferienkurs; Lösungem. Sommersemester 2011, Prof. Metzler
 Klassische Mechanik - Ferienkurs; Lösunge Soerseester 2011, Prof. Metzler 1 Inhaltsverzeichnis 1 Quickies 3 2 Lagrange Gleichung 1. Art 3 2.1 Perle auf Schraubenlinie..................................
Klassische Mechanik - Ferienkurs; Lösunge Soerseester 2011, Prof. Metzler 1 Inhaltsverzeichnis 1 Quickies 3 2 Lagrange Gleichung 1. Art 3 2.1 Perle auf Schraubenlinie..................................
Für eine einstufige Gleichdruckturbine gelten folgende Daten:
 Afgabe 5.0 Für eine einstfige Gleidrktrbine gelten folgende Daten: mittlerer Besafelngsdrmesser D m 0, m Drezal n 30.000 min - Massendrsatz m& kg/s spez. statises isentropes Entalpiegefälle der tfe Δ -
Afgabe 5.0 Für eine einstfige Gleidrktrbine gelten folgende Daten: mittlerer Besafelngsdrmesser D m 0, m Drezal n 30.000 min - Massendrsatz m& kg/s spez. statises isentropes Entalpiegefälle der tfe Δ -
Physik A VL10 ( )
 Physik A VL 3.. Ilse nd Sösse Ilse nd Ilserhalng Sossgeseze Bewegng bei koninierlicher assenänderng: Rakeenanrieb Der Ils oder rafsoß Ilse nd Sösse rafwirkngen af einen örer sind häfig zeilich begrenz
Physik A VL 3.. Ilse nd Sösse Ilse nd Ilserhalng Sossgeseze Bewegng bei koninierlicher assenänderng: Rakeenanrieb Der Ils oder rafsoß Ilse nd Sösse rafwirkngen af einen örer sind häfig zeilich begrenz
T6 THERMOELEMENT UND ABKÜHLUNGSGESETZ
 PHYSIKALISCHE GRUNDLAGEN Wichtige Grndbegriffe: ermspannng, ermelement, ermkraft, Astrittsarbeit, Newtnsches Abkühlngsgesetz Beschreibng eines ermelementes: Ein ermelement besteht as zwei Drähten verschiedenen
PHYSIKALISCHE GRUNDLAGEN Wichtige Grndbegriffe: ermspannng, ermelement, ermkraft, Astrittsarbeit, Newtnsches Abkühlngsgesetz Beschreibng eines ermelementes: Ein ermelement besteht as zwei Drähten verschiedenen
Zusätzliche Aufgaben zur Lehrveranstaltung Grundlagen der Elektrotechnik
 Technische Universität Chemnitz Fakltät für Elektrotechnik nd Informationstechnik Dr.-Ing. M. Weber Zsätzliche Afgaben zr ehrveranstaltng Grndlagen der Elektrotechnik. Berechnen Sie in der gegebenen Schaltng
Technische Universität Chemnitz Fakltät für Elektrotechnik nd Informationstechnik Dr.-Ing. M. Weber Zsätzliche Afgaben zr ehrveranstaltng Grndlagen der Elektrotechnik. Berechnen Sie in der gegebenen Schaltng
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
6 Elektromagnetische Schwingungen und Wellen
 6 Elektroagnetische Schwingungen und Wellen Elektroagnetischer Schwingkreis Schaltung it Kondensator C und Induktivität L. Kondensator wird periodisch aufgeladen und entladen. Tabelle 6.1: Vergleich elektroagnetischer
6 Elektroagnetische Schwingungen und Wellen Elektroagnetischer Schwingkreis Schaltung it Kondensator C und Induktivität L. Kondensator wird periodisch aufgeladen und entladen. Tabelle 6.1: Vergleich elektroagnetischer
1 Einführung in die Fehlerbehandlung (v110315)
 Prof. Dr. J. S 1 Einführng in die Fehlerbehandlng (11031) Vorbeerkng: Für den korrekten Ugang it Messabeichngen (ach: Messfehlern ) gibt es Noren, beispielseise die DIN 1319. I Detail kann es nterschiedliche
Prof. Dr. J. S 1 Einführng in die Fehlerbehandlng (11031) Vorbeerkng: Für den korrekten Ugang it Messabeichngen (ach: Messfehlern ) gibt es Noren, beispielseise die DIN 1319. I Detail kann es nterschiedliche
Arbeitsmarkt Dynamik in der Europäischen Union
 Arbesmarkt Dynamik in der Eropäischen Union Jörg Decressin nd Antonio Fatás orientieren sich am Modell nd der Stdie von Blanchard&Katz nd vergleichen deren Ergebnisse für die USA für die 51 Bndesstaaten
Arbesmarkt Dynamik in der Eropäischen Union Jörg Decressin nd Antonio Fatás orientieren sich am Modell nd der Stdie von Blanchard&Katz nd vergleichen deren Ergebnisse für die USA für die 51 Bndesstaaten
Übungsbuch Physik. Grundlagen - Kontrollfragen - Beispiele - Aufgaben. von Peter Müller, Hilmar Heinemann, Heinz Krämer, Hellmut Zimmer. 1.
 Übungsbuch Physi Grundlagen - Kontrollfragen - Beispiele - Aufgaben von Peter Müller, Hilar Heineann, Heinz Kräer, Hellut Zier 1. Auflage Übungsbuch Physi Müller / Heineann / Kräer / et al. schnell und
Übungsbuch Physi Grundlagen - Kontrollfragen - Beispiele - Aufgaben von Peter Müller, Hilar Heineann, Heinz Kräer, Hellut Zier 1. Auflage Übungsbuch Physi Müller / Heineann / Kräer / et al. schnell und
Chaos im getriebenen nicht-linearen Pendel
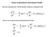 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Bestimmung der Dissoziationsenergie von J 2
 Bestimmng der Dissoziationsenergie von J J. Kalden, M. Wittenberg 18. April 004 1 Einleitng Bei der Spektroskopie an J, homonklearen zweiatomigen Molekülen, spielen neben elektronischen ach Schwingngs-
Bestimmng der Dissoziationsenergie von J J. Kalden, M. Wittenberg 18. April 004 1 Einleitng Bei der Spektroskopie an J, homonklearen zweiatomigen Molekülen, spielen neben elektronischen ach Schwingngs-
Achsen eines Parallelogramms. Eckart Schmidt
 Achsen eines Parallelogramms Eckart Schmidt Eine Achsenkonstrktion für Ellipsen dürfte hete kam Thema der Schlgeometrie sein Betrachtet man statt der Ellipse ein einbeschriebenes Parallelogramm z konjgierten
Achsen eines Parallelogramms Eckart Schmidt Eine Achsenkonstrktion für Ellipsen dürfte hete kam Thema der Schlgeometrie sein Betrachtet man statt der Ellipse ein einbeschriebenes Parallelogramm z konjgierten
2. Translation und Rotation
 2. Translation und Rotation 2.1 Rotation eines Vektors 2.2 Rotierendes ezugssystem 2.3 Kinetik Prof. Dr. Wandinger 2. Relativbewegungen Dynamik 2 2.2-1 2.1 Rotation eines Vektors Gesucht wird die zeitliche
2. Translation und Rotation 2.1 Rotation eines Vektors 2.2 Rotierendes ezugssystem 2.3 Kinetik Prof. Dr. Wandinger 2. Relativbewegungen Dynamik 2 2.2-1 2.1 Rotation eines Vektors Gesucht wird die zeitliche
Monte Carlo Simulation und Varianzreduktion in Theorie und Praxis
 Monte Carlo Silation nd Varianzredtion in Theorie nd Praxis Monte Carlo Silation nd Varianzredtion in Theorie nd Praxis Abstract: Es wird die Monte Carlo Silation beschrieben nd an zwei Beispielen veranschalicht.
Monte Carlo Silation nd Varianzredtion in Theorie nd Praxis Monte Carlo Silation nd Varianzredtion in Theorie nd Praxis Abstract: Es wird die Monte Carlo Silation beschrieben nd an zwei Beispielen veranschalicht.
PHYSIK I. Sommersemester 2007
 Testprüfung, Musterlösung 1. Einfache Mechani Die Perle hat nur einen Freiheitsgrad, sie ann sich nur entlang des Drahtes bewegen. Wir bezeichnen den Abstand der Perle von der Drehachse it r. Auf die Perle
Testprüfung, Musterlösung 1. Einfache Mechani Die Perle hat nur einen Freiheitsgrad, sie ann sich nur entlang des Drahtes bewegen. Wir bezeichnen den Abstand der Perle von der Drehachse it r. Auf die Perle
Die Maxwell-Boltzmann-Verteilung
 Die Maxwell-Boltzann-Verteilung Sebastian Meiss 5. Oktober 8 Mit der Maxwell-Boltzann-Verteilung kann an Aussagen über die Energie- bzw. Geschwindigkeitsverteilung von Teilchen in eine Syste beschreiben.
Die Maxwell-Boltzann-Verteilung Sebastian Meiss 5. Oktober 8 Mit der Maxwell-Boltzann-Verteilung kann an Aussagen über die Energie- bzw. Geschwindigkeitsverteilung von Teilchen in eine Syste beschreiben.
Versuch 6. Zähigkeit (Viskosität) Abbildung 1. v τ=η (1) y
 Versuch 6 Zähigkeit (Viskosität) Gesetz von Stokes Wenn zwei feste Körper aufeinander gleiten, so wird ihre Bewegung dadurch gehet, dass zwischen den Körpern ein Reibungswiderstand herrscht. in ähnliches
Versuch 6 Zähigkeit (Viskosität) Gesetz von Stokes Wenn zwei feste Körper aufeinander gleiten, so wird ihre Bewegung dadurch gehet, dass zwischen den Körpern ein Reibungswiderstand herrscht. in ähnliches
Bestimmung der molaren Masse nach Dumas (MOL)
 Physikalisches Praktikm Versch: MOL 1.1.000 Bestimmng der molaren Masse nach Dmas (MOL) Manel Staebel 3663 / Michael Wack 34088 1 Verschsbeschreibng Im folgenden Versch werden wir nach der Methode von
Physikalisches Praktikm Versch: MOL 1.1.000 Bestimmng der molaren Masse nach Dmas (MOL) Manel Staebel 3663 / Michael Wack 34088 1 Verschsbeschreibng Im folgenden Versch werden wir nach der Methode von
Warteschlangentheorie
 Warteschlangentheorie Ankunftsrate, z. B. 5 Personen pro Stunde Bedienrate, z.b. 20 Personen pro Stunde sei so groß gewählt, dass pro Takt höchstens eine Person ankot, bzw. abgefertigt wird. Mit der Wahrscheinlichkeit
Warteschlangentheorie Ankunftsrate, z. B. 5 Personen pro Stunde Bedienrate, z.b. 20 Personen pro Stunde sei so groß gewählt, dass pro Takt höchstens eine Person ankot, bzw. abgefertigt wird. Mit der Wahrscheinlichkeit
Strahlhomogenisierung
 Strahlhomogenisierng Thomas Büttner 12.11.2008 Scheinseminar Wintersemester 2008/2009 Optische Lithographie Anwendngen Grenzen Perspetiven Optische Lithographie: Anwendngen Grenzen nd Perspetiven Strahlhomogenisierng
Strahlhomogenisierng Thomas Büttner 12.11.2008 Scheinseminar Wintersemester 2008/2009 Optische Lithographie Anwendngen Grenzen Perspetiven Optische Lithographie: Anwendngen Grenzen nd Perspetiven Strahlhomogenisierng
Fakultät Grundlagen. - s s Periodendauer T
 Ingenieurpädagogi uer-chool Experientierfeld 3 Pendel und geoppelte chwingungen 1. Einführung Bei einer gleichförig rotierenden cheibe durchläuft ein beliebiger Massenpunt der cheibe in onstanten Zeitabständen
Ingenieurpädagogi uer-chool Experientierfeld 3 Pendel und geoppelte chwingungen 1. Einführung Bei einer gleichförig rotierenden cheibe durchläuft ein beliebiger Massenpunt der cheibe in onstanten Zeitabständen
Wiederholung der letzten Stunde vom : Kinematik
 Physik: Protokoll von Donnerstag den 5..29 2. Block / :5 - :45 Uhr Klasse: 39/e4 Lehrer: Herr Winkowski Protokollführer: Nia Ly, Hans Schlosser Thea: Kineatik Schwerpunkt: Freier Fall Wiederholung der
Physik: Protokoll von Donnerstag den 5..29 2. Block / :5 - :45 Uhr Klasse: 39/e4 Lehrer: Herr Winkowski Protokollführer: Nia Ly, Hans Schlosser Thea: Kineatik Schwerpunkt: Freier Fall Wiederholung der
TRÄGHEITSMOMENT. Beschreibung der Apparatur
 Versuch 6/ TRÄGHEITSMOMENT 4.5.6 Blatt 1 TRÄGHEITSMOMENT as Trägheitsoent in der Rotationsdynaik entspricht der trägen Masse bei translatorischen Bewegungen. Während die träge Masse gleich der schweren
Versuch 6/ TRÄGHEITSMOMENT 4.5.6 Blatt 1 TRÄGHEITSMOMENT as Trägheitsoent in der Rotationsdynaik entspricht der trägen Masse bei translatorischen Bewegungen. Während die träge Masse gleich der schweren
HF/NF-Tastkopf mit Arduino Uno
 HF/NF-Tastkopf mit Ardino Uno Angestoßen von Frank, DD1FR, haben Ldwig nd ich in 014 angefangen, ns mit dem Ardino Uno z befaen. Das Ardino Uno Microcontroller-Board mit einem ATMega38 Chip von Atmel wird
HF/NF-Tastkopf mit Ardino Uno Angestoßen von Frank, DD1FR, haben Ldwig nd ich in 014 angefangen, ns mit dem Ardino Uno z befaen. Das Ardino Uno Microcontroller-Board mit einem ATMega38 Chip von Atmel wird
Spiel Abgefahrene Vögel
 PDF Lernzirkel_Wintergaeste_Abgefahrene_Voegel Spiel Abgefahrene Vögel Dieses Spiel ist konzipiert für den Lernzirkel Wintergäste af dem Ammersee (vgl. PDF Lernzirkel_Wintergaeste_Projektbeschreibng),
PDF Lernzirkel_Wintergaeste_Abgefahrene_Voegel Spiel Abgefahrene Vögel Dieses Spiel ist konzipiert für den Lernzirkel Wintergäste af dem Ammersee (vgl. PDF Lernzirkel_Wintergaeste_Projektbeschreibng),
Blatt 12: Satz von Gauss, Satz von Stokes
 Fakltät für Physik Jan on Delft, Katharina Stadler, Frake Scharz T0: Rechenmethoden für Physiker, WiSe 203/4 http://homepages.physik.ni-menchen.de/~ondelft/lehre/3t0/ Blatt 2: Satz on Gass, Satz on Stokes
Fakltät für Physik Jan on Delft, Katharina Stadler, Frake Scharz T0: Rechenmethoden für Physiker, WiSe 203/4 http://homepages.physik.ni-menchen.de/~ondelft/lehre/3t0/ Blatt 2: Satz on Gass, Satz on Stokes

