Die Entdeckung des Chaos
|
|
|
- Nikolas Egger
- vor 6 Jahren
- Abrufe
Transkript
1 Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per kontakt verfügbare Programm Feigenbaum ermöglicht die Untersuchung solcher Systeme. Eingeschlossen ist darin auch die grafische Aufbereitung in Form von Liapunov-Diagrammen. Bis vor relativ kurzer Zeit erschien die Welt wohlgeordnet und in allen ihren Teilen berechenbar. In jeder Größenordnung ist das Universum angefüllt mit stabilen Strukturen. Auf der kleinsten bekannten Ebene binden sich die Elementarteilchen, die Quarks, zu Protonen und Neutronen, die die Kerne der Elemente bilden. Zusammen mit den Elektronen ergeben sich daraus die Atome als Voraussetzung für die Bildung komplexerer Strukturen aus Atomen und Molekülen. Gaswolken aus Atomen und Molekülen haben sich infolge der Schwerkraft zu kugelförmigen Objekten zusammengezogen und haben Sonnen, Planeten, Monde und Kometen geboren. Zumindest auf einem der Planeten haben sich aus den gleichen Grundbestandteilen komplizierte biologische Systeme etabliert, die so weit gekommen sind, dass sie über ihre eigene Existenz nachdenken können. Sie halten sich für die Krone der Schöpfung und glauben spätestens seit der Verbreitung der Newtonschen Gesetze an eine berechenbare, deterministische Welt, die prinzipiell wie ein Uhrwerk funktioniert. Newtons Weltbild wurde zwar durch Quantentheorie und Relativitätstheorie starken Veränderungen unterworfen, die man Revolutionen nannte, im Prinzip hat sich aber nichts an der Methode verändert, aus dem Verhalten der kleinsten Teilchen auf das Verhalten des gesamten Systems zu schließen. In den letzten zwanzig Jahren sind aber die Grenzen dieser Einstellung deutlich zutage getreten. Diese Grenzen zeigen sich in der Existenz und dem Verhalten von zahlreichen chaotischen Systemen, die gegenüber den geordneten Systemen in der Mehrheit sind. Beispiele sind das Wetter mit Stürmen, Turbulenzen und Wolkenbildung, die Entwicklung biologischer Arten, die Ausbreitung von Epidemien, Entstehung von Lawinen, eine unter Lebewesen ausbrechende Panik, die Entwicklung von Börsenkursen, Herzrhythmusstörungen wie auch der plötzliche Zerfall von Staaten und Weltreichen (Jugoslawien, UdSSR). Trotz ihrer Vielzahl wurden die chaotischen Systeme in den Wissenschaften einfach als Sonderfälle, als Störung des normalen Verhaltens ausgeklammert und unbehandelt zur Seite geschoben; notfalls mit einer linearen Näherung gerechnet. So werden auch in den klassischen Schulfächern bisher chaotische Systeme wenig beachtet. Im Nachhinein erscheint es angesichts der anderen Möglichkeiten geradezu als Wunder, dass es überhaupt relativ stabile Strukturen gibt. Nun, wenn es sie nicht gäbe, könnte man diese Überlegungen gar nicht anstellen. Bisher gibt es keine geschlossene Chaostheorie, aber in den letzten zwanzig Jahren wurden Ansätze entwickelt, deren Grundlagen bereits Ende des 19. Jahrhunderts von dem französischen Mathematiker Henri Poincaré erdacht wurden. Dabei ging es um die Beantwortung der
2 Frage, ob unser Planetensystem stabil sei. Für die Lösung des Vielkörperproblems hatte der schwedische König Oskar II einen lukrativen Preis ausgesetzt, den schließlich Poincaré erhielt, obwohl er nachweisen konnte, dass das entsprechende Gleichungssystem praktisch nicht lösbar ist. Das bedeutet, dass man bis heute nicht weiß, ob sich unser Planetensystem bis zum Ausbrennen der Sonne periodisch verhalten wird. Was ist nun Chaos und welche Systeme sind chaotisch? Zur Untersuchung dieser Frage stellen wir uns ein einfaches System als eine Blackbox vor, die einen Eingang und einen Ausgang besitzt. Der Ausgang wird mit dem Eingang verbunden, das nennt man eine Rückkopplung. Der am Ausgang gebildete Wert wird so dem System zugeführt und erneut vom System verarbeitet. Was daraus entstehen kann, zeigt sich an dem bekannten Beispiel mit Mikrofon, Verstärker und Lautsprecher. Verhulst-Gleichung als Rückkopplungs-System Untersuchungen haben ergeben, dass rückgekoppelte Systeme dann chaotisch reagieren können, wenn sie nichtlineare Komponenten besitzen. Als einfaches Beispiel soll das Verhalten das Systems durch die mathematische Gleichung repräsentiert werden. Sie ist Biologen als Verhulst-Gleichung bekannt und dient als Modell für die Entwicklung einer biologischen Population. Die Systemgröße x n bedeutet darin die Anzahl der Individuen der biologischen Art. B ist die Geburtenrate und damit eine Stellgröße oder ein Parameter des Systems. B = 2 bedeutet beispielsweise, dass sich die Rasse im betrachteten Zeitraum verdoppelt. x n+1 ist dann die neue Anzahl. Wäre die Gleichung einfach nur x n+1 = B x n, würde die Anzahl unbeschränkt wachsen. In der Natur trifft dies im allgemeinen aber nicht zu. Der Faktor (1 - x n ) begrenzt daher das Wachstum, denn Nahrung und Raum sind nicht unbegrenzt verfügbar. Die Gleichung ist normiert, d.h. dass der Höchstwert für x n die Zahl 1 ist, was 100% des Tragbaren für das System entspricht. Rechnen wir einmal ein Beispiel: Die Geburtenrate sei konstant B = 2 und der Startwert sei x = 0,8: Wenn man einmal bei dem Ergebnis 0,5 angelangt ist, ergeben weitere Rechnungen keine Veränderungen mehr; das System hat einen stabilen Zustand, genannt Attraktor, erreicht. Auch andere Startwerte kleiner als 1 und größer als 0 führen zum selben Ergebnis. Da das System nichtlinear ist, kann es aber auch chaotische Folgen erzeugen. Steigert man die Geburtenrate B beispielsweise auf den Wert 3.7, erhält man mit jedem beliebigen Startwert zwischen 0 und 1 eine chaotische Folge.
3 Chaotisch bedeutet, dass die Ergebnisse dann im Bereich von 0 bis 1 hin und her springen und keinen Attraktor finden. Obwohl die Zahlen theoretisch streng bestimmt sind, erhält jeder, der nachrechnet, unterschiedliche Werte, die vom verwendeten Rechner abhängen. Schon kleinste Abweichungen in den Zwischenwerten führen zu völlig unterschiedlichen Zahlenfolgen. Dieses Verhalten nennt man die Sensitivität oder Empfindlichkeit des Chaos. Das sogenannte Feigenbaum-Diagramm (benannt nach dem Mathematiker Mitchell Feigenbaum) zeigt das Verhalten der Verhulstgleichung bei Veränderung der Geburtenrate B. Feigenbaum-Diagramm: Der Punkt im Diagramm zeigt beispielsweise unsere vorhergehende Rechnung mit B = 2 und einem beliebigen Startwert x. Aufgetragen ist nur der Endwert (Attraktor) der Rückkopplung (Iteration). An der Grafik, in der nur die Endzustände der Rückkopplung aufgezeichnet sind, erkennt man, dass das System bis zur Geburtenrate B = 3 nach einigen Zyklen einen stabilen Wert erreicht, der sich bei festem B nicht verändert. Das heißt praktisch, dass die Population schließlich auf einem bestimmten Niveau stagniert. Steigt aber die Geburtenrate über 3, schwankt die Anzahl plötzlich von Generation zu Generation zwischen zwei Werten hin und her. Dieses Verhalten kann man durchaus noch als Stabilität deuten. Die Zahl B = 3,45 bedeutet die Überschreitung einer weiteren Grenze; jetzt schwankt die Population zwischen vier Werten. In immer kleineren Abständen folgen weitere Gabelungen und fortgesetzte Verdopplungen der Anzahl möglicher Systemzustände. Schließlich gibt es eine Grenzzahl, ab der das System in das Chaos eintritt. In der Grafik entspricht dies dem schwarzen Bereich. Hier kann praktisch nicht mehr vorhergesagt werden, welche Größe die Population in der nächsten Generation annehmen wird. Bei B = 4 wird sogar das ganze Intervall der Werte zwischen 0 und 1 ausgefüllt. Das Chaos scheint perfekt. Wenn man genau hinsieht, erkennt man im chaotischen Bereich helle Streifen. Sie werden Fenster der Ordnung genannt. Durch ein rotes Rechteck habe ich einen Ausschnitt markiert, den wir uns jetzt durch genauere Rechnung vergrößert ansehen wollen.
4 Dieser kleine Ausschnitt zwischen B = 3,35 und B = 3,78 umfasst einen Teil des Verzweigungsbaums und ein solches Fenster der Ordnung. Zoom: Oben sieht man den vergrößerten Ausschnitt, der im vorigen Bild rot markiert ist. Ein erneutes Zoomen (rotes Rechteck) ergibt das folgende Bild im Ordnungsfenster des Chaos: Hier zeigt sich mitten im Chaos wieder ein stabiles Systemverhalten, das sich allerdings erneut mit einem Feigenbaumszenario in die Fänge des Chaos begibt, wenn man die Größe B nur ein klein wenig erhöht. Der Übergang ist wieder geprägt vom Verdopplungsweg der zunehmenden möglichen Systemgrößen, genannt der Verdopplungsweg ins Chaos. Auffällig ist, dass der Feigenbaum im Kleinen wieder kleine Feigenbäume enthält, die prinzipiell
5 wie das Ganze aussehen. Man spricht von Selbstähnlichkeit oder von einem Fraktal, ein Begriff, zu dem ich gleich mehr sagen möchte. Man könnte den Zoomvorgang noch mehrere Male wiederholen und würde, bevor man die Rechenkünste des Computers überfordert, noch einige Feigenbäume in den Feigenbäumen entdecken. Wenn eine so einfache Gleichung Chaos produzieren kann, gilt das erst recht für kompliziertere Systeme mit vielen Freiheitsgraden. Kleinste Veränderungen an den Systemgrößen zeigen im Chaosbereich unvorhersagbare Folgen. So wurde die von Kritikern oft missverstandene Metapher vom Flügelschlag eines Schmetterlings in China, der einen Wirbelsturm in den USA auslösen kann, geboren. Die verallgemeinerte Untersuchung chaotischer Systeme hat zu völlig neuen überraschenden Ergebnissen geführt und einen Umdenkungsprozess in unserer Weltanschauung ausgelöst. Es zeigte sich, dass eine ganze Gruppe von Systemen dem Feigenbaumszenario folgt, dass ein Verdopplungsweg ins Chaos führen kann, wenn man einen Systemparameter verändert. Dabei bleibt dieses Verhalten nicht auf mathematische Gleichungen beschränkt, sondern findet seine Entsprechung in natürlichen Systemen. Das konnte in den 80 er Jahren insbesondere in Strömungsexperimenten nachgewiesen werden. Ein Beispiel dafür könnte auch die Veränderung unserer Atmosphäre durch Einbringen von Schadstoffen sein, woraufhin das Klima in chaotische Schwankungen geriete. Also liefert auch die Mathematik genug Gründe, mit unseren Lebensgrundlagen vorsichtiger umzugehen. U. Schwebinghaus Weitere Informationen zum Programm Feigenbaum in Ulli's Fractal Home
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Wie lang ist die Küste Großbritanniens?
 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Diskrete Populationsmodelle für Einzelspezies
 Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Stringtheorie: Auf der Suche nach der Weltformel
 Stringtheorie: Auf der Suche nach der Weltformel Jan Louis Universität Hamburg Sylt, Juli 2005 2 Physik des 20. Jahrhunderts Quantentheorie (QT) Planck, Bohr, Heisenberg,... Physik von kleinen Skalen (Mikrokosmos)
Stringtheorie: Auf der Suche nach der Weltformel Jan Louis Universität Hamburg Sylt, Juli 2005 2 Physik des 20. Jahrhunderts Quantentheorie (QT) Planck, Bohr, Heisenberg,... Physik von kleinen Skalen (Mikrokosmos)
Übungen zur Mathematik Blatt 1
 Blatt 1 Aufgabe 1: Bestimmen Sie die Fourier-Reihe der im Bild skizzierten periodischen Funktion, die im Periodenintervall [ π, π] durch die Gleichung f(x) = x beschrieben wird. Zeichnen Sie die ersten
Blatt 1 Aufgabe 1: Bestimmen Sie die Fourier-Reihe der im Bild skizzierten periodischen Funktion, die im Periodenintervall [ π, π] durch die Gleichung f(x) = x beschrieben wird. Zeichnen Sie die ersten
Gewöhnliche Differentialgleichungen: Einleitung
 Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Logistisches Wachstum
 Informationsblatt für die Lehrkraft Logistisches Wachstum Informationsblatt für die Lehrkraft Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Logistisches Wachstum und Chaos Mittelschule, technische
Informationsblatt für die Lehrkraft Logistisches Wachstum Informationsblatt für die Lehrkraft Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Logistisches Wachstum und Chaos Mittelschule, technische
+ + Personalmanagement Stuff-Turnover. Simulation im Excel. Organizational Headcount. Turnover. Recruitment
 Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Heron-Verfahren. Inhaltsverzeichnis. Beispiel. aus Wikipedia, der freien Enzyklopädie
 1 of 7 28.05.2010 20:16 Heron-Verfahren aus Wikipedia, der freien Enzyklopädie Das Heron-Verfahren oder babylonische Wurzelziehen ist ein Rechenverfahren zur Berechnung einer Näherung der Quadratwurzel
1 of 7 28.05.2010 20:16 Heron-Verfahren aus Wikipedia, der freien Enzyklopädie Das Heron-Verfahren oder babylonische Wurzelziehen ist ein Rechenverfahren zur Berechnung einer Näherung der Quadratwurzel
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Durch Simulation dynamische Systeme entdecken Labor 6
 Institut für Automatik D-ITET, 2. Sem. ETH Zürich Dr. F. J. Kraus 28. Mai 2004 Durch Simulation dynamische Systeme entdecken Labor 6 In diesem Labor wollen wir einen kleinen Einblick in die Chaostheorie
Institut für Automatik D-ITET, 2. Sem. ETH Zürich Dr. F. J. Kraus 28. Mai 2004 Durch Simulation dynamische Systeme entdecken Labor 6 In diesem Labor wollen wir einen kleinen Einblick in die Chaostheorie
0.1.1 Exzerpt von B. S. 414: Unendlich hoher Potenzialtopf
 1 15.11.006 0.1 119. Hausaufgabe 0.1.1 Exzerpt von B. S. 414: Unendlich hoher Potenzialtopf (Siehe 118. Hausaufgabe.) 0.1. Exzerpt von B. S. 414: Wellenlängen der Wellenfunktion im Fall stehender Wellen
1 15.11.006 0.1 119. Hausaufgabe 0.1.1 Exzerpt von B. S. 414: Unendlich hoher Potenzialtopf (Siehe 118. Hausaufgabe.) 0.1. Exzerpt von B. S. 414: Wellenlängen der Wellenfunktion im Fall stehender Wellen
Wie lange wird unsere Warmzeit, das Holozän, noch dauern?
 Wie lange wird unsere Warmzeit, das Holozän, noch dauern? Das Klima der vergangenen vielen Hunderttausend Jahre ist gekennzeichnet durch die Abwechslung von Warmzeiten und Eiszeiten, wie Bild 1 zeigt.
Wie lange wird unsere Warmzeit, das Holozän, noch dauern? Das Klima der vergangenen vielen Hunderttausend Jahre ist gekennzeichnet durch die Abwechslung von Warmzeiten und Eiszeiten, wie Bild 1 zeigt.
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
 Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie
 Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie Daniela Schimming, Jennifer Richter, Juliana Schmidt Gliederung 1. Grundlagen 2. Nachrichtenjournalismus und
Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie Daniela Schimming, Jennifer Richter, Juliana Schmidt Gliederung 1. Grundlagen 2. Nachrichtenjournalismus und
Relative Atommassen. Stefan Pudritzki Göttingen. 8. September 2007
 Relative Atommassen Stefan Pudritzki Göttingen 8. September 2007 Berechnung der relativen Atommassen Nach dem derzeitigen Kenntnisstand können die relativen Atommassen der chemischen Elemente mit einem
Relative Atommassen Stefan Pudritzki Göttingen 8. September 2007 Berechnung der relativen Atommassen Nach dem derzeitigen Kenntnisstand können die relativen Atommassen der chemischen Elemente mit einem
Zusätzliche Aufgabe 5:
 D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas Zusätzliche Aufgabe 5: Populationsmodelle Um die Entwicklung einer Population zu modellieren, gibt es diskrete Modelle, wobei die Zeit t bei diskreten
D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas Zusätzliche Aufgabe 5: Populationsmodelle Um die Entwicklung einer Population zu modellieren, gibt es diskrete Modelle, wobei die Zeit t bei diskreten
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
2. Quadratische Lagrangefunktionen und Fourierreihe.
 0. Einführung Wir haben gerade das klassische Wirkungsprinzip betrachtet, nachdem wir wissen, dass der dynamische Verlauf eines Teilchens in dem Diagramm die Kurve darstellen soll, die die minimale Wirkung
0. Einführung Wir haben gerade das klassische Wirkungsprinzip betrachtet, nachdem wir wissen, dass der dynamische Verlauf eines Teilchens in dem Diagramm die Kurve darstellen soll, die die minimale Wirkung
Gewöhnliche Differentialgleichungen. Teil II: Lineare DGLs mit konstanten Koeffizienten
 - 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
- 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
String Theorie - Die Suche nach der großen Vereinheitlichung
 String Theorie - Die Suche nach der großen Vereinheitlichung Ralph Blumenhagen Max-Planck-Institut für Physik String Theorie - Die Suche nach der großen Vereinheitlichung p.1 Das Ziel der Theoretischen
String Theorie - Die Suche nach der großen Vereinheitlichung Ralph Blumenhagen Max-Planck-Institut für Physik String Theorie - Die Suche nach der großen Vereinheitlichung p.1 Das Ziel der Theoretischen
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Serie 4 2 = 10. ) ist). Dann gilt für alle n n 0
 Serie 4. Aufgabe 336 Punkte) Gegeben seien zwei reelle Zahlenfolgen durch a n : 0 n, n N b n : n n, n N Bestimmen Sie die Grenzwerte a bzw. b der Folgen a n ) n N bzw. b n ) n N. Geben Sie jeweils zu gegebenem
Serie 4. Aufgabe 336 Punkte) Gegeben seien zwei reelle Zahlenfolgen durch a n : 0 n, n N b n : n n, n N Bestimmen Sie die Grenzwerte a bzw. b der Folgen a n ) n N bzw. b n ) n N. Geben Sie jeweils zu gegebenem
Wachstum mit oberer Schranke
 1 1.1 exponentielles Wir haben das eines Kontos mit festem Zinssatz untersucht. Der jährliche Zuwachs (hier die Zinsen) sind proportional zum Bestand (hier dem jeweiligen Kontostand). Die Annahme, daß
1 1.1 exponentielles Wir haben das eines Kontos mit festem Zinssatz untersucht. Der jährliche Zuwachs (hier die Zinsen) sind proportional zum Bestand (hier dem jeweiligen Kontostand). Die Annahme, daß
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Die Erde, ein lebendiger Planet األرض: الكوكب اليح
 Die Erde, ein lebendiger Planet األرض: الكوكب اليح [أملاين - German [Deutsch - A.O. ايه. أوه. Übersetzer: Eine Gruppe von Übersetzern ترمجة: جمموعة من املرتمجني 1432-2011 Beschreibung: Die Erde wurde speziell
Die Erde, ein lebendiger Planet األرض: الكوكب اليح [أملاين - German [Deutsch - A.O. ايه. أوه. Übersetzer: Eine Gruppe von Übersetzern ترمجة: جمموعة من املرتمجني 1432-2011 Beschreibung: Die Erde wurde speziell
Otto-von-Guericke-Universität Magdeburg. Fakultät für Informatik Institut für Simulation und Grafik. Seminararbeit. Der Weg ins Chaos und zurück
 Otto-von-Guericke-Universität Magdeburg Fakultät für Informatik Institut für Simulation und Grafik Seminararbeit Der Weg ins Chaos und zurück Verfasser: Fabian Schmidt 13. Dezember 2007 Betreuer: Dipl.-Ing.
Otto-von-Guericke-Universität Magdeburg Fakultät für Informatik Institut für Simulation und Grafik Seminararbeit Der Weg ins Chaos und zurück Verfasser: Fabian Schmidt 13. Dezember 2007 Betreuer: Dipl.-Ing.
Einführung in die Chaostheorie
 Einführung in ie Chaostheorie Die sogenannte Chaostheorie befasst sich mit er Erforschung nichtlinearer ynamischer Systeme, ie chaotisches Verhalten zeigen können. Chaotisches Verhalten liegt u.a. ann
Einführung in ie Chaostheorie Die sogenannte Chaostheorie befasst sich mit er Erforschung nichtlinearer ynamischer Systeme, ie chaotisches Verhalten zeigen können. Chaotisches Verhalten liegt u.a. ann
Ferienkurs Experimentalphysik 4
 Ferienkurs Experimentalphysik 4 Probeklausur Markus Perner, Markus Kotulla, Jonas Funke Aufgabe 1 (Allgemeine Fragen). : (a) Welche Relation muss ein Operator erfüllen damit die dazugehörige Observable
Ferienkurs Experimentalphysik 4 Probeklausur Markus Perner, Markus Kotulla, Jonas Funke Aufgabe 1 (Allgemeine Fragen). : (a) Welche Relation muss ein Operator erfüllen damit die dazugehörige Observable
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Die wahre Geschichte der Antimaterie
 Die wahre Geschichte der Antimaterie Philip Bechtle 8. Juli 2009 Öffentlicher Abendvortrag 08.07.2009 1 Die Handlung des Films Antimaterie wird vom Large Hadron Collider (LHC) am CERN gestohlen und im
Die wahre Geschichte der Antimaterie Philip Bechtle 8. Juli 2009 Öffentlicher Abendvortrag 08.07.2009 1 Die Handlung des Films Antimaterie wird vom Large Hadron Collider (LHC) am CERN gestohlen und im
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Die Welt der kleinsten Teilchen
 Die Welt der kleinsten Teilchen Woraus ist die Welt, woraus sind wir selbst gemacht? (Dank an Prof. Kolanoski und Prof. Kobel fuer die Ueberlassung einiger Folien) 1 Die Welt der kleinsten Teilchen Woraus
Die Welt der kleinsten Teilchen Woraus ist die Welt, woraus sind wir selbst gemacht? (Dank an Prof. Kolanoski und Prof. Kobel fuer die Ueberlassung einiger Folien) 1 Die Welt der kleinsten Teilchen Woraus
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
Konstante Zu- und Abflüsse (Veränderungen)
 Konstante Zu- und Abflüsse (Veränderungen) Unser erstes Modell: Ein (großer) Eimer wird unter einen Wasserhahn gestellt. Der Wasserhahn wird geöffnet und ein konstanter Wasserstrom von 2 Litern pro Minute
Konstante Zu- und Abflüsse (Veränderungen) Unser erstes Modell: Ein (großer) Eimer wird unter einen Wasserhahn gestellt. Der Wasserhahn wird geöffnet und ein konstanter Wasserstrom von 2 Litern pro Minute
Rekursive Folgen. Ermittle jeweils drei weitere Elemente. Gegen welchen Wert könnte die Folge streben? c Roolfs 3 2, 7 5, 17 12,...
 Rekursive Folgen Ermittle jeweils drei weitere Elemente. Gegen welchen Wert könnte die Folge streben? a) b) c) d) e), 7 5, 7,... 4, 9 5, 9 4,..., 5, 4 8,..., 5, 7,..., 7, 0,... Rekursive Folgen Ermittle
Rekursive Folgen Ermittle jeweils drei weitere Elemente. Gegen welchen Wert könnte die Folge streben? a) b) c) d) e), 7 5, 7,... 4, 9 5, 9 4,..., 5, 4 8,..., 5, 7,..., 7, 0,... Rekursive Folgen Ermittle
Lernziele zu Radioaktivität 1. Radioaktive Strahlung. Entdeckung der Radioaktivität. Entdeckung der Radioaktivität
 Radioaktive Strahlung Entstehung Nutzen Gefahren du weisst, Lernziele zu Radioaktivität 1 dass Elementarteilchen nur bedingt «elementar» sind. welche unterschiedlichen Arten von radioaktiven Strahlungen
Radioaktive Strahlung Entstehung Nutzen Gefahren du weisst, Lernziele zu Radioaktivität 1 dass Elementarteilchen nur bedingt «elementar» sind. welche unterschiedlichen Arten von radioaktiven Strahlungen
Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage. Ideen der Informatik Kurt Mehlhorn
 Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage Ideen der Informatik Kurt Mehlhorn Gliederung Ziele von Theorie Gibt es Probleme, die man prinzipiell nicht mit einem Rechner lösen kann?
Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage Ideen der Informatik Kurt Mehlhorn Gliederung Ziele von Theorie Gibt es Probleme, die man prinzipiell nicht mit einem Rechner lösen kann?
Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten
 http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
Nichtlineare Phänomene und Selbstorganisation
 Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Chaos Oder Mandelbrot und Peitsche
 Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Folgen und Reihen. Wirtschaftswissenschaftliches Zentrum Universität Basel. Mathematik für Ökonomen 1 Dr. Thomas Zehrt
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen Dr. Thomas Zehrt Folgen und Reihen Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band, 7. Auflage,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen Dr. Thomas Zehrt Folgen und Reihen Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band, 7. Auflage,
Wie arbeitet ein Teilchenphysiker? Das Standardmodell, Detektoren und Beschleuniger.
 Grafik 2 Vorstellung des Instituts für Kern- und Teilchenphysik Wie arbeitet ein Teilchenphysiker? Das Standardmodell, Detektoren und Beschleuniger. Dipl. Phys. Kathrin Leonhardt 1 Grafik 2 Auf den Spuren
Grafik 2 Vorstellung des Instituts für Kern- und Teilchenphysik Wie arbeitet ein Teilchenphysiker? Das Standardmodell, Detektoren und Beschleuniger. Dipl. Phys. Kathrin Leonhardt 1 Grafik 2 Auf den Spuren
Wettbewerbs- und Symbiose-Modelle Von Jakob Foss
 Wettbewerbs- und Symbiose-Modelle Von Jakob Foss Wettbewerbsmodell Das einfachste Wettbewerbsmodell für zwei Spezies lässt sich aus dem Lotka- Volterra Modell ableiten und sieht folgendermaßen aus: dn1
Wettbewerbs- und Symbiose-Modelle Von Jakob Foss Wettbewerbsmodell Das einfachste Wettbewerbsmodell für zwei Spezies lässt sich aus dem Lotka- Volterra Modell ableiten und sieht folgendermaßen aus: dn1
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Juliamengen und Mandelbrotmenge
 Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
numerische Berechnungen von Wurzeln
 numerische Berechnungen von Wurzeln. a) Berechne x = 7 mit dem Newtonverfahren und dem Startwert x = 4. Mache die Probe nach jedem Iterationsschritt. b) h sei eine kleine Zahl, d.h. h. Wir suchen einen
numerische Berechnungen von Wurzeln. a) Berechne x = 7 mit dem Newtonverfahren und dem Startwert x = 4. Mache die Probe nach jedem Iterationsschritt. b) h sei eine kleine Zahl, d.h. h. Wir suchen einen
5. Raum-Zeit-Symmetrien: Erhaltungssätze
 5. Raum-Zeit-Symmetrien: Erhaltungssätze Unter Symmetrie versteht man die Invarianz unter einer bestimmten Operation. Ein Objekt wird als symmetrisch bezeichnet, wenn es gegenüber Symmetrieoperationen
5. Raum-Zeit-Symmetrien: Erhaltungssätze Unter Symmetrie versteht man die Invarianz unter einer bestimmten Operation. Ein Objekt wird als symmetrisch bezeichnet, wenn es gegenüber Symmetrieoperationen
Die Darstellung nichtlinearer Bewegungsabläufe
 Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Abiturprüfung Physik, Leistungskurs. Aufgabe: Anregung von Vanadium und Silber durch Neutronen
 Seite 1 von 6 Abiturprüfung 2013 Physik, Leistungskurs Aufgabenstellung: Aufgabe: Anregung von Vanadium und Silber durch Neutronen Vanadium besteht in der Natur zu 99,75 % aus dem stabilen Isotop 51 23
Seite 1 von 6 Abiturprüfung 2013 Physik, Leistungskurs Aufgabenstellung: Aufgabe: Anregung von Vanadium und Silber durch Neutronen Vanadium besteht in der Natur zu 99,75 % aus dem stabilen Isotop 51 23
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION
 Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Inhaltsverzeichnis Vorwort Einleitung Kapitel 1: Sonnensystem Kapitel 2: Sterne, Galaxien und Strukturen aus Galaxien
 Inhaltsverzeichnis Vorwort Einleitung Kapitel 1: Sonnensystem Objekte des Sonnensystems Sonne Innere Gesteinsplaneten und deren Monde Asteroidengürtel Äußere Gas- und Eisplaneten und deren Monde Zentauren
Inhaltsverzeichnis Vorwort Einleitung Kapitel 1: Sonnensystem Objekte des Sonnensystems Sonne Innere Gesteinsplaneten und deren Monde Asteroidengürtel Äußere Gas- und Eisplaneten und deren Monde Zentauren
Relativitätstheorie und Kosmologie Teil 2 Unterricht
 Relativitätstheorie und Kosmologie Teil 2 Unterricht F. Herrmann und M. Pohlig S www.physikdidaktik.uni-karlsruhe.de 9 DER GEKRÜMMTE RAUM 10 KOSMOLOGIE 9 DER GEKRÜMMTE RAUM Raum und Zeit getrennt behandeln
Relativitätstheorie und Kosmologie Teil 2 Unterricht F. Herrmann und M. Pohlig S www.physikdidaktik.uni-karlsruhe.de 9 DER GEKRÜMMTE RAUM 10 KOSMOLOGIE 9 DER GEKRÜMMTE RAUM Raum und Zeit getrennt behandeln
Masse von Newton und Einstein zu Higgs und dunkler Materie
 von Newton und Einstein zu Higgs und dunkler Materie Institut f. Kern- und Teilchenphysik Dresden, 13.11.2008 Inhalt 1 Einleitung 2 Newton träge und schwere 3 Einstein bewegte und Ruhemasse 4 Higgs Ruhemasse
von Newton und Einstein zu Higgs und dunkler Materie Institut f. Kern- und Teilchenphysik Dresden, 13.11.2008 Inhalt 1 Einleitung 2 Newton träge und schwere 3 Einstein bewegte und Ruhemasse 4 Higgs Ruhemasse
Maße des Modellmondes Radius Modellmond Abstand Modellmond-Modellsonne
 Rechnungen zuofi-box Im Folgenden finden Sie die Herleitung und Berechnung zum Abschnitt Die SoFi-Box symbolisch aus dem Artikel Die SoFi-Box Ein Modellexperiment zum fächerverbindenden Unterricht von
Rechnungen zuofi-box Im Folgenden finden Sie die Herleitung und Berechnung zum Abschnitt Die SoFi-Box symbolisch aus dem Artikel Die SoFi-Box Ein Modellexperiment zum fächerverbindenden Unterricht von
Wozu brauchen wir theoretische Physik? Ziele der Physik
 Wozu brauchen wir theoretische Physik? Wolfgang Kinzel Lehrstuhl für theoretische Physik III Universität Würzburg Ziele der Physik Die Physik sucht nach allgemeinen Naturgesetzen. Sie möchte die Natur
Wozu brauchen wir theoretische Physik? Wolfgang Kinzel Lehrstuhl für theoretische Physik III Universität Würzburg Ziele der Physik Die Physik sucht nach allgemeinen Naturgesetzen. Sie möchte die Natur
Schulbücher, Themen- und Arbeitshefte für den Physikunterricht (Sekundarstufe II) (ohne Reihenfolge)
 Schulbücher, Themen- und Arbeitshefte für den Physikunterricht (Sekundarstufe II) (ohne Reihenfolge) Schulbuch Themen Klasse 11 Verlag: Klett 2002 3-12-772510-8 Kinematik Dynamik Elektrisches Feld modell
Schulbücher, Themen- und Arbeitshefte für den Physikunterricht (Sekundarstufe II) (ohne Reihenfolge) Schulbuch Themen Klasse 11 Verlag: Klett 2002 3-12-772510-8 Kinematik Dynamik Elektrisches Feld modell
Was ist Gravitation?
 Was ist Gravitation? Über die Einheit fundamentaler Wechselwirkungen zur Natur schwarzer Löcher Hans Peter Nilles Physikalisches Institut, Universität Bonn Was ist Gravitation, UniClub Bonn, März. 2011
Was ist Gravitation? Über die Einheit fundamentaler Wechselwirkungen zur Natur schwarzer Löcher Hans Peter Nilles Physikalisches Institut, Universität Bonn Was ist Gravitation, UniClub Bonn, März. 2011
(in)stabile Kerne & Radioaktivität
 Übersicht (in)stabile Kerne & Radioaktivität Zerfallsgesetz Natürliche und künstliche Radioaktivität Einteilung der natürlichen Radionuklide Zerfallsreihen Zerfallsarten Untersuchung der Strahlungsarten
Übersicht (in)stabile Kerne & Radioaktivität Zerfallsgesetz Natürliche und künstliche Radioaktivität Einteilung der natürlichen Radionuklide Zerfallsreihen Zerfallsarten Untersuchung der Strahlungsarten
Fixpunkt-Iterationen
 Fixpunkt-Iterationen 2. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 27. Februar 2014 Gliederung Wiederholung: Gleichungstypen, Lösungsverfahren Grundprinzip
Fixpunkt-Iterationen 2. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 27. Februar 2014 Gliederung Wiederholung: Gleichungstypen, Lösungsverfahren Grundprinzip
N.BORGHINI Version vom 20. November 2014, 21:56 Kernphysik
 II.4.4 b Kernspin und Parität angeregter Zustände Im Grundzustand besetzen die Nukleonen die niedrigsten Energieniveaus im Potentialtopf. Oberhalb liegen weitere Niveaus, auf welche die Nukleonen durch
II.4.4 b Kernspin und Parität angeregter Zustände Im Grundzustand besetzen die Nukleonen die niedrigsten Energieniveaus im Potentialtopf. Oberhalb liegen weitere Niveaus, auf welche die Nukleonen durch
1 Die Mandelbrotmenge
 1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
DIE THERMISCHE GESCHICHTE DES UNIVERSUMS & FREEZE-OUT. 14. Dezember Kim Susan Petersen. Proseminar Theoretische Physik & Astroteilchenphysik
 DIE THERMISCHE GESCHICHTE DES UNIVERSUMS & FREEZE-OUT 14. Dezember 2010 Kim Susan Petersen Proseminar Theoretische Physik & Astroteilchenphysik INHALT 1. Das Standardmodell 2. Die Form des Universums 3.
DIE THERMISCHE GESCHICHTE DES UNIVERSUMS & FREEZE-OUT 14. Dezember 2010 Kim Susan Petersen Proseminar Theoretische Physik & Astroteilchenphysik INHALT 1. Das Standardmodell 2. Die Form des Universums 3.
Markov-Prozesse. Markov-Prozesse. Franziskus Diwo. Literatur: Ronald A. Howard: Dynamic Programming and Markov Processes
 Markov-Prozesse Franziskus Diwo Literatur: Ronald A. Howard: Dynamic Programming and Markov Processes 8.0.20 Gliederung Was ist ein Markov-Prozess? 2 Zustandswahrscheinlichkeiten 3 Z-Transformation 4 Übergangs-,
Markov-Prozesse Franziskus Diwo Literatur: Ronald A. Howard: Dynamic Programming and Markov Processes 8.0.20 Gliederung Was ist ein Markov-Prozess? 2 Zustandswahrscheinlichkeiten 3 Z-Transformation 4 Übergangs-,
NIGEL CALDER. Einsteins Universum. Aus dem Englischen von Wolfram Knapp UMSCHAU VERLAG FRANKFURT AM MAIN
 NIGEL CALDER Einsteins Universum Aus dem Englischen von Wolfram Knapp ^ UMSCHAU VERLAG FRANKFURT AM MAIN INHALT i Kosmischer Wirbelsturm 11 Gravitation und höchste Geschwindigkeit verändern das Weltbild
NIGEL CALDER Einsteins Universum Aus dem Englischen von Wolfram Knapp ^ UMSCHAU VERLAG FRANKFURT AM MAIN INHALT i Kosmischer Wirbelsturm 11 Gravitation und höchste Geschwindigkeit verändern das Weltbild
Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1. 1 Grundlagen 2. 2 Der Graph einer Funktion 4. 3 Umkehrbarkeit 5
 Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1 Inhaltsverzeichnis 1 Grundlagen 2 2 Der Graph einer Funktion
Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1 Inhaltsverzeichnis 1 Grundlagen 2 2 Der Graph einer Funktion
2. Eigenschaften von Zahlenfolgen
 . Eigenschaften von Zahlenfolgen.. Monotone Folgen ) Definition Eine Folge heisst streng monoton wachsend, wenn für alle n gilt: an+ > an. (D.h. jedes Folgenglied ist grösser als sein Vorgänger. Man sagt
. Eigenschaften von Zahlenfolgen.. Monotone Folgen ) Definition Eine Folge heisst streng monoton wachsend, wenn für alle n gilt: an+ > an. (D.h. jedes Folgenglied ist grösser als sein Vorgänger. Man sagt
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
REFERAT FÜR INNOVATIVE ARCHIKETUREN
 REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
Anwendung der Infinitesimalrechnung in der Physik (besonders geeignet für Kernfach Physik Kurshalbjahr Mechanik Anforderung auf Leistungskursniveau)
 Anwendung der Infinitesimalrechnung in der Physik (besonders geeignet für Kernfach Physik Kurshalbjahr Mechanik Anforderung auf Leistungskursniveau) Vorbemerkung Die nachfolgenden Darstellungen dienen
Anwendung der Infinitesimalrechnung in der Physik (besonders geeignet für Kernfach Physik Kurshalbjahr Mechanik Anforderung auf Leistungskursniveau) Vorbemerkung Die nachfolgenden Darstellungen dienen
7. Das Bohrsche Modell des Wasserstoff-Atoms. 7.1 Stabile Elektronbahnen im Atom
 phys4.08 Page 1 7. Das Bohrsche Modell des Wasserstoff-Atoms 7.1 Stabile Elektronbahnen im Atom Atommodell: positiv geladene Protonen (p + ) und Neutronen (n) im Kern negative geladene Elektronen (e -
phys4.08 Page 1 7. Das Bohrsche Modell des Wasserstoff-Atoms 7.1 Stabile Elektronbahnen im Atom Atommodell: positiv geladene Protonen (p + ) und Neutronen (n) im Kern negative geladene Elektronen (e -
Würfelt Gott oder würfelt er nicht? p.1/35
 Würfelt Gott oder würfelt er nicht? Die Rolle des Zufalls im Weltbild der Physik Claus Grupen Universität Siegen Dortmund, den 21. Mai 2005 Würfelt Gott oder würfelt er nicht? p.1/35 Eine uralte Frage...
Würfelt Gott oder würfelt er nicht? Die Rolle des Zufalls im Weltbild der Physik Claus Grupen Universität Siegen Dortmund, den 21. Mai 2005 Würfelt Gott oder würfelt er nicht? p.1/35 Eine uralte Frage...
Die Chaostheorie und Fraktale in der Natur
 Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
2. Übung zur Vorlesung Steuer- und Regelungstechnik
 2. Übung zur Vorlesung Steuer- und Regelungstechnik Aufstellen von DGL s, lineare und nichtlineare Systeme Felix Goßmann M.Sc. Institut für Steuer- und Regelungstechnik Fakultät für Luft- und Raumfahrttechnik
2. Übung zur Vorlesung Steuer- und Regelungstechnik Aufstellen von DGL s, lineare und nichtlineare Systeme Felix Goßmann M.Sc. Institut für Steuer- und Regelungstechnik Fakultät für Luft- und Raumfahrttechnik
VL Klimasysteme 12 April Wettersysteme: ihre Bedeutung und Vorhersage. Stephan Pfahl. Gruppe Atmospheric Dynamics
 VL Klimasysteme 12 April 2017 Wettersysteme: ihre Bedeutung und Vorhersage Stephan Pfahl Gruppe Atmospheric Dynamics Was sind Wettersysteme? Zyklone = Tiefdruckgebiet Blocking = Hochdruckgebiet Front Föhn
VL Klimasysteme 12 April 2017 Wettersysteme: ihre Bedeutung und Vorhersage Stephan Pfahl Gruppe Atmospheric Dynamics Was sind Wettersysteme? Zyklone = Tiefdruckgebiet Blocking = Hochdruckgebiet Front Föhn
Allgemeine Relativitätstheorie und Quantenphysik
 Allgemeine Relativitätstheorie und Quantenphysik Franz Embacher Fakultät für Physik der Universität Wien Vortrag am Bundes-Oberstufenrealgymnasium Wien 3, 26. April 2016 Vortrag an der Österreichischen
Allgemeine Relativitätstheorie und Quantenphysik Franz Embacher Fakultät für Physik der Universität Wien Vortrag am Bundes-Oberstufenrealgymnasium Wien 3, 26. April 2016 Vortrag an der Österreichischen
Die Beschreibung von Signalen und Systemen kann in verschiedenen Bereichen erfolgen:
 1 Grundlegende Begriffe 1.1 Signale und Systeme ein Signal: ein System: ist ein Satz von Daten setzt Signale in Beziehung Darstellung: Die Beschreibung von Signalen und Systemen kann in verschiedenen Bereichen
1 Grundlegende Begriffe 1.1 Signale und Systeme ein Signal: ein System: ist ein Satz von Daten setzt Signale in Beziehung Darstellung: Die Beschreibung von Signalen und Systemen kann in verschiedenen Bereichen
Nichtlineare Prozesse in der Elektrochemie II
 Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Nichtlineare Gleichungen
 Nichtlineare Gleichungen Ein wichtiges Problem in der Praxis ist die Bestimmung einer Lösung ξ der Gleichung f(x) =, () d.h. das Aufsuchen einer Nullstelle ξ einer (nicht notwendig linearen) Funktion f.
Nichtlineare Gleichungen Ein wichtiges Problem in der Praxis ist die Bestimmung einer Lösung ξ der Gleichung f(x) =, () d.h. das Aufsuchen einer Nullstelle ξ einer (nicht notwendig linearen) Funktion f.
Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide
 Daniel Janocha Aus der Reihe: e-fellows.net stipendiaten-wissen e-fellows.net (Hrsg.) Band 1064 Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide Weak solution of the Stokes equations
Daniel Janocha Aus der Reihe: e-fellows.net stipendiaten-wissen e-fellows.net (Hrsg.) Band 1064 Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide Weak solution of the Stokes equations
1 Lineare Gleichungssysteme
 1 Lineare Gleichungssysteme Wenn man in der Schule an den Punkt der lineare Gleichungssysteme kommt, hat man normale Gleichungen und deren Umformungen schon behandelt. Und das nicht ohne Grund, denn die
1 Lineare Gleichungssysteme Wenn man in der Schule an den Punkt der lineare Gleichungssysteme kommt, hat man normale Gleichungen und deren Umformungen schon behandelt. Und das nicht ohne Grund, denn die
: Quantenmechanische Lösung H + 2. Molekülion und. Aufstellen der Schrödingergleichung für das H + 2
 H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
Radioaktiver Zerfall des Atomkernes: α-zerfall
 Radioaktiver Zerfall des Atomkernes: α-zerfall Schwere Atomkerne (hohes Z, hohes N) sind instabil gegen spontanen Zerfall. Die mögliche Emission einzelner Protonen oder einzelner Neutronen ist nicht häufig.
Radioaktiver Zerfall des Atomkernes: α-zerfall Schwere Atomkerne (hohes Z, hohes N) sind instabil gegen spontanen Zerfall. Die mögliche Emission einzelner Protonen oder einzelner Neutronen ist nicht häufig.
Versuch 3: Beugung am Spalt und Kreisblende
 Versuch 3: Beugung am Spalt und Kreisblende Dieser Versuch soll der Einführung der allgemeinen Beugungstheorie dienen. Beugungsphänomene werden in verschiedenen Erscheinungsformen zunächst nur beobachtet.
Versuch 3: Beugung am Spalt und Kreisblende Dieser Versuch soll der Einführung der allgemeinen Beugungstheorie dienen. Beugungsphänomene werden in verschiedenen Erscheinungsformen zunächst nur beobachtet.
Einführung in die Quantentheorie der Atome und Photonen
 Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
Bernstein. Elektronen sind die wohl bekanntesten Elementarteilchen.
 Bernstein Elektronen sind die wohl bekanntesten Elementarteilchen. Der Name kommt vom griechischen elektron und bedeutet Bernstein. Bernstein ist eine goldgelbe organische Substanz aus dem fossilen Harz
Bernstein Elektronen sind die wohl bekanntesten Elementarteilchen. Der Name kommt vom griechischen elektron und bedeutet Bernstein. Bernstein ist eine goldgelbe organische Substanz aus dem fossilen Harz
exponentielle Wachstumsphase Abbildung 1: Wachstumskurve einer Bakterienkultur
 Bakterienwachstum Mathematische Schwerpunkte: Teil 1: Folgen; vollständige Induktion; rekursiv definierte Folgen Teil 2: Exponentialfunktionen Teil 3: Extremwertbestimmung; Integration einer rationalen
Bakterienwachstum Mathematische Schwerpunkte: Teil 1: Folgen; vollständige Induktion; rekursiv definierte Folgen Teil 2: Exponentialfunktionen Teil 3: Extremwertbestimmung; Integration einer rationalen
Radioaktiver Zerfall
 11.3.2 Radioaktiver Zerfall Betrachtet man einen einzelnen instabilen Atomkern, so kann nicht vorhergesagt werden zu welchem Zeitpunkt der Atomkern zerfällt. So könnte der Atomkern im nächsten Moment,
11.3.2 Radioaktiver Zerfall Betrachtet man einen einzelnen instabilen Atomkern, so kann nicht vorhergesagt werden zu welchem Zeitpunkt der Atomkern zerfällt. So könnte der Atomkern im nächsten Moment,
I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N
 Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Chaos im getriebenen nicht-linearen Pendel
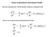 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
ÜBER EINE TECHNISCHE ANWENDUNG DER DISTRffiUTIONENTHEORIE
 ÜBER EINE TECHNISCHE ANWENDUNG DER DISTRffiUTIONENTHEORIE Von 1. FENYO Lehrstuhl für jlathelllatik, Technische Universität, Budapest (Eingegangen am 24. August, 1964.) 1. FODOR hat in einem Aufsatz [1]
ÜBER EINE TECHNISCHE ANWENDUNG DER DISTRffiUTIONENTHEORIE Von 1. FENYO Lehrstuhl für jlathelllatik, Technische Universität, Budapest (Eingegangen am 24. August, 1964.) 1. FODOR hat in einem Aufsatz [1]
Hybride Etafunktionen und Isotopie G. Schulz VII. Teil, Angewandte Zahlenlehre Universität des Saarlandes Fakultät 7 für Physik und Mechatronik 2015
 1 Hybride Etafunktionen und Isotopie G. Schulz VII. Teil, Angewandte Zahlenlehre Universität des Saarlandes Fakultät 7 für Physik und Mechatronik 215 Wenn zahlentheoretisch gesicherte Strukturen im Raum
1 Hybride Etafunktionen und Isotopie G. Schulz VII. Teil, Angewandte Zahlenlehre Universität des Saarlandes Fakultät 7 für Physik und Mechatronik 215 Wenn zahlentheoretisch gesicherte Strukturen im Raum
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
