FC3 - Duffing Oszillator
|
|
|
- Erica Waldfogel
- vor 7 Jahren
- Abrufe
Transkript
1 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik
2 leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007
3 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme Der Begriff Theorie komplexer Systeme bezeichnet eine umfassende Theorie, in der die Chaostheorie nur einen Teil darstellt. Ursprünglich ist der Begriff in der statistischen Mechanik verortet, wie es schon im vorigen Versuch zu erkennen war. Diese behandelt Systeme mit großer Anzahl von Teilchen, die nicht mehr trivial bzw. linear untereinander wechselwirken. Hierbei treten unterschiedliche und zum Teil chaotische Effekte auf. Schließlich kommt es zu Selbstorganisationsprozesse, wie im Falle eines Wassertropfens. Auch im Beispiel der Planetenbewegungen kommt es zu nicht linearen Wechselwirkungen. Betrachtet man zwei Planeten, ist die Lösung der Differentialgleichung noch trivial. Zieht man beispielsweise die Sonne mit in Betracht, lässt sich das System nur noch mit Hilfe von iterativen Gleichungen lösen. Da es in diesem Fall labile energetische Tiefpunkte gibt, kann es zum chaotischen Verhalten kommen. 2 Fraktale - Das Sierpinski Dreieck Der etymologische Ursprung des Wortes Fraktal liegt im lateinischen fractus, was soviel bedeutet wie gebrochen. Geprägt wurde der Begriff durch Benoît Mandelbrot und bezeichnet natürliche bzw. künstliche Gebilde, die einen hohen Grad von Selbstähnlichkeit aufweisen. Beispielsweise bildet ein Blumenkohl ein Fraktal, da seine Röschen in der Form dem des ganzen Kopfes ähneln. Diese wiederum lassen sich auch wieder in kleine Röschen zerlegen, die ihrem Ursprung ähneln. Das bedeutet, auch wenn man ein Fraktal sehr stark vergrößert, zeigt es gleiche Strukturen wie vor der Vergrößerung. Ein bekanntes klassisches Fraktal bildet das nachdem polnischen Mathematiker Waclaw Sierpinski benannte Sierpinski-Dreieck. Dieses wird wie folgt konstruiert: Man beginnt mit einem Dreieck in der Ebene. Nun werden die Mittelpunkte der drei Seiten miteinander verbunden, so dass vier kongruente Dreiecke entstehen. Nun wird das dasselbe Schema auf die drei erhaltenen äußeren Dreiecke angewandt. Man beginnt sich iterativ dem Sierpinski-Dreieck zu nähern. Neben dieser klassischen Methode zur Konstruktion, gibt es auch eine andere Möglichkeit für die Erstellung. Dazu definiert man drei Punkte p i im Raum (möglichst die Eckpunkte eines Dreiecks) und weist ihnen jeweils eine Zahl zu. Nun startet mit an einem beliebigen Punkt P und bestimmt zufällig einen der drei Punkte p i. Auf der Hälfte der Strecke von Punkt P zum speziellen Punkt p j wird ein schwarzer Punkt gezeichnet. Anschließend wird dieser Prozess iterativ fortgeführt, wobei jeweils der gezeichnete Punkt als neuer Startpunkt zu sehen ist. Da Fraktale unter anderem derart komplex sein können, dass die üblichen Messbegriffe ihren Sinn verlieren, gilt es nun eine neue Maßeinheit zu definieren. Hierbei gibt es die Möglichkeit, den Grad der Komplexität zu messen, unter Berücksichtigung der Längen-, Oberflächen- oder Volumenänderung bei immer kleineren Maßstäben. Hierfür gibt es mehrere Dimensionsbegriffe, wobei an dieser Stelle sich auf der der Selbstähnlichkeits- Dimension beschränkt wird. Dieser wird aus dem Verkleinerungsfaktor s und der Anzahl
4 4 FC3 - Duffing Oszillator der Teile a, in welche die Struktur zerlegt werden kann, bestimmt: Aufgaben zur Vorbereitung a = 1 s D = ln a. (1) D ln s 1 Machen Sie sich mit den Begrifflichkeiten aus dem Text vertraut. Schauen Sie sich in der Literatur die Koch sche Schneeflocke genauer an. Aufgaben Programmieren Sie eine Darstellung des Sierpinski Dreiecks in C und stellen Sie diese anschließend mit einem Grafikprogramm dar. Berechnen Sie die Selbstähnlichkeits-Dimension des Dreiecks. 3 Bifurkationen - Populationsdynamik Bifurkationen, bzw. Verzweigungen bezeichnen eine Zustandsänderung eines nichtlinearen Systems unter Einfluss eines definierten Parameters. Der Begriff wurde ursprünglich von Heneri Poincaré eingeführt. Ein klassischen Beispiel stellt hier die Populationsdynamik dar. Hier betrachtet man eine Fuchspopulation mit einer gewissen Geburtenrate b. Da diese Population natürlich durch die Nahrungsverfügbarkeit begrenzt wird, kommt es zur so genannten logistischen Abbildung: Ausgehend von einem exponentiellen Wachstum x n+1 = bx n (1 x n ). (2) dx dt = rx (3) wird hinführend zum logistischen Wachstum zusätzlich eine Kapazität k eingeführt: dx dt = rx(1 x ). (4) k Die Diskretisierung der Differentialgleichung 4 führt zu der zuvor erwähnten Gleichung 2. Variiert man nun die Geburtenrate, kommt es zu entsprechenden Gleichgewichten nach einer bestimmten Zeit. Diese lassen sich in einem Bifurkations-Diagramm darstellen, wobei hier die Abszisse die Geburtenrate b und die Ordinate den Gleichgewichtszustand darstellt. Dabei kommt es bei dynamischen Systemen meist zu einer Periodenverdopplung, sobald ein kritischer Punkt überschritten ist.
5 FC3 - Duffing Oszillator 5 Aufgaben zur Vorbereitung Machen Sie sich mit den Begrifflichkeiten aus dem Text vertraut. Schauen Sie sich in der Literatur den Begriff des Attraktors an. Aufgaben Programmieren Sie die Populationsdynamik und visualisieren Sie anschließend die erhaltenen Ergebnisse in einem Bifurkations-Diagramm (Startwert der Population p 0 = 0.5). 4 Physikalische Systeme - Der Duffing Oszillator Im Folgenden soll nun ein physikalisches nichtlineares System betrachtet werden. Es handelt sich um den Duffing-Oszillator (harmonischer Oszillator mit weicher Feder), der in der Realität über ein Fadenpendel und zwei Permanentmagneten realisiert werden kann. Die zugehörige Differentialgleichung lautet: d 2 x dt 2 + α 1x + α 2 x 3 = 0, (5) mit den Konstanten α 1 und α 2. Die treibende Kraft des Oszillators ist folglich mit dem zugehörigen Potential F (x) = α 1 x α 2 x 3, (6) V (x) = α 1 2 x2 + α 2 4 x4. (7) Für den Fall α 1 < 0 und α 2 > 0 erhält man drei Extrema (x = 0 und x = ± α 1 α 2 ) für das System. Wie in Abbildung 1 zu erkennen ist, existieren zwei Minima und ein labiler Punkt am Nullpunkt, es entsteht ein so genanntes Doppelmuldenpotential. Die Definition des allgeimeinen Duffing-Oszillators lautet nun wie folgt: mit den Konstanten: r Reibungsparameter ω 0 Eigenfrequenz β Stärke der Nichtlinearität f Stärke der von aussen treibenden Kraft Ω Frequenz der von aussen treibenden Kraft ẍ + rẋ + ω 2 0x + βx 3 = fcos(ωt), (8) Dynamische Systeme lassen sich an dieser Stelle mit dem so genannte Poincaré-Schnitt näher untersuchen. Hierbei wird durch eine stroboskopische Aufnahme des Phasenraums
6 6 FC3 - Duffing Oszillator 0,6 0,4 0,2-1,4-1,2-1 -0,8-0,6-0,4-0,2 0 0,2 0,4 0,6 0,8 1 1,2 1,4 Abbildung 1: Doppelmulden-Potential des reibungsfreien Duffing-Oszillators. eine diskrete Anzahl von Punkten erstellt. Der Poincaré-Schnitt hat den Vorteil, dass er aufgrund der kleineren Datenmenge einfacher zu untersuchen ist. Abhängig von der Wahl der Parameter kann es nun zu einem chaotischen Verhalten der Oszillators kommen. Wie bereits erwähnt, lassen sich diese Systeme mit der fraktalen Dimension beschreiben. Allerdings stellt sich hier die Anwendung der Selbstähnlichkeits- Dimension als nicht durchführbar heraus. Daher benutzt man die so genannte Korrelations- Dimension. Da der Attraktor durch die im Phasenraum dichtliegenden Punkte definiert ist, lässt sich ein Größe C(R) definieren als: C(R) = lim, j N Θ(R x i x j ). (9) N i Hierbei wird jeder Längeneinheit R die Zahl von Punktepaaren zugeordnet deren Abstand zueinander kleiner als R ist. Damit lässt sich die Dimension mit Hilfe des Potenz-Gesetzes aus 1 bestimmen: D = ln C(R) ln R. (10) Um nun die numerische Modellierung des Problems anzugehen, soll im Folgenden das
7 FC3 - Duffing Oszillator 7 Runge-Kutta Verfahren 4. Ordnung verwendet werden: k 1 = hf(t n, x n, v n ) l 1 = hg(t n, x n, v n ) mit ẋ = f(t, x, v) und v = g(t, x, v). Aufgaben k 2 = hf(t n + h 2, x n + k 1 2, v n + l 1 l 2 = hg(t n + h 2, x n + k 1 2, v n + l 1 k 3 = hf(t n + h 2, x n + k 2 2, v n + l 2 l 3 = hg(t n + h 2, x n + k 2 2, v n + l 2 k 4 = hf(t n + h 2, x n + k 3 2, v n + l 3 l 4 = hg(t n + h 2, x n + k 3 2, v n + l 3 x n+1 = x n (k 1 + 2k 2 + 2k 3 + k 4 ) + O(h 5 ) v n+1 = x n (l 1 + 2l 2 + 2l 3 + l 4 ) + O(h 5 ), (11) Programmieren Sie die Simulation des Duffing-Oszillators mit Hilfe des Runge-Kutta Verfahrens 4. Ordnung. Realisieren Sie den freien Duffing Oszillator (f = 0.0) ohne treibende Kraft von aussen mit folgenden Parametern: einfacher fokaler Grenzpunkt: ω 2 0 0, r > 0 (1) r=0.1, ω 2 0=β=Ω=0.0, f=0.0, x 0 =1.5, v 0 =0.0 zwei fokale Grenzpunkte (Doppelmulden-Potential): ω (2) r=0.0, ω 2 0= β=ω=1.0, f=0.0, x 0 = , v 0 =0.0 (3) r=0.1, ω 2 0= β=ω=1.0, f=0.0, x 0 = , v 0 =0.0 Realisieren Sie den Ueda Oszillator als spezielle Form des Duffing-Oszillators (Ω = 1.0, ω 2 0 = 0.0). Es wird sichtbar, dass für diese Form es zu stabile koexistierenden Grenzzyklen und seltsamen Attraktoren in Abhängigkeit von den Parametern kommt. Zeichnen Sie aus diesem Grund jeweils die Trajektorie und den zugehörigen Poincaré- Schnitt mit der Frequenz Ω nach entsprechender Einschwingzeit. stabile koexistierende Grenzzyklen mit verschiedenen Perioden (1) r=0.08, ω 2 0=0.0, β=ω=1.0, f=0.2, x 0 =1.0, v 0 =0.0: stabiler Einergrenzzyklus (2) r=0.08, ω 2 0=0.0, β=ω=1.0, f=0.2, x 0 =-0.7, v 0 =0.0: stabiler Zweiergrenzzyklus (3) r=0.08, ω 2 0=0.0, β=ω=1.0, f=0.2, x 0 =-1.0, v 0 =0.0: stabiler Dreiergrenzzyklus
8 8 FC3 - Duffing Oszillator seltsamer Attraktor (4) r=0.05, ω 2 0=0.0, β=ω=1.0, f=7.5, x 0 =1.5, v 0 =0.0: seltsamer Attraktor Realisieren Sie den getriebenen Duffing-Oszillator. Hierbei soll die Bifurkation bzw. Periodenverdopplung verdeutlicht werden (Variation des Paramters f). Zeichen Sie auch hier die Trajektorie und den Poincaré-Schnitt erst nach der Einschwingzeit. (1) r=0.25, ω 2 0=-1.0, β=1.0, f=0.35, Ω=1.4, x 0 =1.0, v 0 =0.0: Einerperiode (2) r=0.25, ω 2 0=-1.0, β=1.0, f=0.37, Ω=1.4, x 0 =1.0, v 0 =0.0: Zweierperiode (3) r=0.25, ω 2 0=-1.0, β=1.0, f=0.39, Ω=1.4, x 0 =1.0, v 0 =0.0: Dreierperiode (4) r=0.25, ω 2 0=-1.0, β=1.0, f=0.40, Ω=1.4, x 0 =1.0, v 0 =0.0: seltsamer Attraktor Berechnen Sie die Korrelationsdimension im Falle des seltsamen Attraktors am Beispiel des Ueda-Oszillators (r=0.05, ω 2 0=0.0, β=ω=1.0, f=7.5, x 0 =1.5, v 0 =0.0). Zu diesem Zweck bestimmen Sie die Steigung der von ln C(R) über ln R) aufgetragenen Graden.
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Ökologische Gleichungen für zwei Spezies
 Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Jan Henrik Sylvester. 10. Februar 2003
 Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Seminar Fraktale. Kapitel 13 Dynamical Systems. Von Dirk Simon
 Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Wie lang ist die Küste Großbritanniens?
 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Differenzialgleichungen
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
BERÜHMTE KURVEN Logarithmische Spirale. Die Logarithmische Spirale wird durch eine Gleichung in Polarkoordinaten angegeben: r(φ)=a*e k φ
 BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Chaos im getriebenen nicht-linearen Pendel
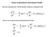 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Juliamengen und Mandelbrotmenge
 Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
2 Selbstähnlichkeit, Selbstähnlichkeitsdimension
 9 2 Selbstähnlichkeit, Selbstähnlichkeitsdimension und Fraktale 2.1 Selbstähnlichkeit Bei den Betrachtungen zur Dimension in Kapitel 1 haben wir ähnliche (im geometrischen Sinn) Figuren miteinander verglichen.
9 2 Selbstähnlichkeit, Selbstähnlichkeitsdimension und Fraktale 2.1 Selbstähnlichkeit Bei den Betrachtungen zur Dimension in Kapitel 1 haben wir ähnliche (im geometrischen Sinn) Figuren miteinander verglichen.
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
 Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Die Chaostheorie und Fraktale in der Natur
 Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
INSTITUT FÜR THEORETISCHE PHYSIK. Prof. Dr. U. Motschmann Dr. M. Feyerabend. Theoretische Mechanik SS 2017
 INSTITUT FÜR THEORETISCHE PHYSIK Prof. Dr. U. Motschmann Dr. M. Feyerabend Theoretische Mechanik SS 2017 Klausurvorbereitung Bearbeitungszeit: 180 Minuten 1. Wissensfragen (20 Punkte) Benennen Sie alle
INSTITUT FÜR THEORETISCHE PHYSIK Prof. Dr. U. Motschmann Dr. M. Feyerabend Theoretische Mechanik SS 2017 Klausurvorbereitung Bearbeitungszeit: 180 Minuten 1. Wissensfragen (20 Punkte) Benennen Sie alle
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
 Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
 3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Stabile periodische Bewegungen (Grenzzyklen)
 Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
Aufgaben zum Wochenende (1)
 Aufgaben zum Wochenende (1) 1. Schreiben Sie das Polynom (x 1) 5 geordnet nach Potenzen von x auf. (Binomialkoeffizienten!). Welche Bedingung müssen a, b, c erfüllen, damit die Lösungsmenge der Bestimmungsgleichung
Aufgaben zum Wochenende (1) 1. Schreiben Sie das Polynom (x 1) 5 geordnet nach Potenzen von x auf. (Binomialkoeffizienten!). Welche Bedingung müssen a, b, c erfüllen, damit die Lösungsmenge der Bestimmungsgleichung
Zusätzliche Aufgabe 5:
 D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas Zusätzliche Aufgabe 5: Populationsmodelle Um die Entwicklung einer Population zu modellieren, gibt es diskrete Modelle, wobei die Zeit t bei diskreten
D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas Zusätzliche Aufgabe 5: Populationsmodelle Um die Entwicklung einer Population zu modellieren, gibt es diskrete Modelle, wobei die Zeit t bei diskreten
Klausur zur T1 (Klassische Mechanik)
 Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
1 Die logistische Gleichung X t+1 = λx t (1 X t )
 1 Die logistische Gleichung X t+1 = X t (1 X t ) Bisher haben wir Rekursionen mit mehr oder weniger einfachem Verhalten betrachtet; wir konnten entweder eine explizite Lösungsformel aufstellen oder ohne
1 Die logistische Gleichung X t+1 = X t (1 X t ) Bisher haben wir Rekursionen mit mehr oder weniger einfachem Verhalten betrachtet; wir konnten entweder eine explizite Lösungsformel aufstellen oder ohne
SINIS Simulation nichtlinearer Systeme
 In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
Beispiele. Strecke A R 1 (genauso für R d ):
 Definition 6.1.1 (fraktale Dimension). Sei A R d beschränkt und für ε > 0 sei N A (ε) die minimale Anzahl der d-dimensionalen Kugeln vom Radius ε, mit denen A überdeckt werden kann. Die fraktale Dimension
Definition 6.1.1 (fraktale Dimension). Sei A R d beschränkt und für ε > 0 sei N A (ε) die minimale Anzahl der d-dimensionalen Kugeln vom Radius ε, mit denen A überdeckt werden kann. Die fraktale Dimension
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Lösung 05 Klassische Theoretische Physik I WS 15/16. y a 2 + r 2. A(r) =
 Karlsruher Institut für Technologie Institut für theoretische Festkörperphsik www.tfp.kit.edu Lösung Klassische Theoretische Phsik I WS / Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler Besprechung...
Karlsruher Institut für Technologie Institut für theoretische Festkörperphsik www.tfp.kit.edu Lösung Klassische Theoretische Phsik I WS / Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler Besprechung...
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I
 Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Versuchsprotokoll: Modellierung molekularer Schwingungen
 Versuchsprotokoll: Modellierung molekularer Schwingungen Teammitglieder: Nicole Schai und Cristina Mercandetti Datum: 11.12.12 Versuchsleiter: Claude Ederer 1. Einleitung Dieser Versuch befasste sich mit
Versuchsprotokoll: Modellierung molekularer Schwingungen Teammitglieder: Nicole Schai und Cristina Mercandetti Datum: 11.12.12 Versuchsleiter: Claude Ederer 1. Einleitung Dieser Versuch befasste sich mit
Gleichgewichte von Differentialgleichungen
 Gleichgewichte von Differentialgleichungen Gleichgewichte von Differentialgleichungen Teil 1 Zur Erinnerung: Zur Erinnerung: Wir hatten lineare Differentialgleichungen betrachtet: in R 1 : Zur Erinnerung:
Gleichgewichte von Differentialgleichungen Gleichgewichte von Differentialgleichungen Teil 1 Zur Erinnerung: Zur Erinnerung: Wir hatten lineare Differentialgleichungen betrachtet: in R 1 : Zur Erinnerung:
Der Duffing-Oszillator
 11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
(dφ) 2 + (dz) 2. φ 2 dφ mit z=z(φ).
 PD Dr. S. Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt 5 WS 8/9.. 8. Strecke auf Zylinder. Bestimmen Sie die kürzeste Verbindung zwischen zwei Punkten auf Pkt.) dem Zylinder.
PD Dr. S. Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt 5 WS 8/9.. 8. Strecke auf Zylinder. Bestimmen Sie die kürzeste Verbindung zwischen zwei Punkten auf Pkt.) dem Zylinder.
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
 Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Serie 13. Analysis D-BAUG Dr. Cornelia Busch FS 2016
 Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Martin-Anderson-Nexö-Gymnasium, Dresden
 Fraktale Wechselspiel zwischen Chaos und Ordnung Teilnehmer: David Burgschweiger Tim Gabriel Welf Garkisch Anne Kell Leonard König Erik Lorenz Sofie Martins Niklas Schelten Heinrich-Hertz-Oberschule, Berlin
Fraktale Wechselspiel zwischen Chaos und Ordnung Teilnehmer: David Burgschweiger Tim Gabriel Welf Garkisch Anne Kell Leonard König Erik Lorenz Sofie Martins Niklas Schelten Heinrich-Hertz-Oberschule, Berlin
Modellbildung und Simulation, Kap (S ) 10 Zwei-Spezies-Modelle
 Erratum zu Modellbildung und Simulation, Kap. 1.3 (S. 256 261) 1 Zwei-Spezies-Modelle Interessanter als einzelne Populationen sind Modelle mit mehreren Arten, die miteinander in Wechselwirkung stehen,
Erratum zu Modellbildung und Simulation, Kap. 1.3 (S. 256 261) 1 Zwei-Spezies-Modelle Interessanter als einzelne Populationen sind Modelle mit mehreren Arten, die miteinander in Wechselwirkung stehen,
Fraktale. Mathe Fans an die Uni. Sommersemester 2009
 Fraktale Mathe Fans an die Uni Ein Fraktal ist ein Muster, das einen hohen Grad Selbstähnlichkeit aufweist. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst
Fraktale Mathe Fans an die Uni Ein Fraktal ist ein Muster, das einen hohen Grad Selbstähnlichkeit aufweist. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst
Vorkurs Mathematik Übungsaufgaben. Dozent Dr. Arne Johannssen
 Vorkurs Mathematik Übungsaufgaben 2 Dozent Dr. Arne Johannssen Lehrstuhl für Betriebswirtschaftslehre, insbesondere Mathematik und Statistik in den Wirtschaftswissenschaften Neues Logo: ie gesamte Universität
Vorkurs Mathematik Übungsaufgaben 2 Dozent Dr. Arne Johannssen Lehrstuhl für Betriebswirtschaftslehre, insbesondere Mathematik und Statistik in den Wirtschaftswissenschaften Neues Logo: ie gesamte Universität
durch Ratengleichungen der Form t t = F 2 N 1 t, N 2 t d N 1 t
 5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
Lineare und nichtlineare Schwingungen und Wellen
 Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Fraktale und Julia-Mengen
 Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Parameterdef. an nichtl. Zweipolkennl.
 Parameterdef. an nichtl. Zweipolkennl. nichtlin. Zweipole Typen von Approximationsfunktionen KENNLINIENAPPROXIMATION Rektifikationsmethode y 5α 4α FUNKTION β < β > y = αx β β = 3α 2α α β < β =.5.5 2 2.5
Parameterdef. an nichtl. Zweipolkennl. nichtlin. Zweipole Typen von Approximationsfunktionen KENNLINIENAPPROXIMATION Rektifikationsmethode y 5α 4α FUNKTION β < β > y = αx β β = 3α 2α α β < β =.5.5 2 2.5
Klausur zu Theoretische Physik 2 Klassische Mechanik
 Klausur zu Theoretische Physik Klassische Mechanik 30. September 016 Prof. Marc Wagner Goethe-Universität Frankfurt am Main Institut für Theoretische Physik 5 Aufgaben mit insgesamt 5 Punkten. Die Klausur
Klausur zu Theoretische Physik Klassische Mechanik 30. September 016 Prof. Marc Wagner Goethe-Universität Frankfurt am Main Institut für Theoretische Physik 5 Aufgaben mit insgesamt 5 Punkten. Die Klausur
Versuch 6 - Nichtlineares Pendel
 UNIVERSITÄT REGENSBURG Naturwissenschaftliche Fakultät II - Physik Anleitung zum Anfängerpraktikum A1 Versuch 6 - Nichtlineares Pendel 23. überarbeitete Auflage 2009 Dr. Stephan Giglberger Prof. Dr. Christian
UNIVERSITÄT REGENSBURG Naturwissenschaftliche Fakultät II - Physik Anleitung zum Anfängerpraktikum A1 Versuch 6 - Nichtlineares Pendel 23. überarbeitete Auflage 2009 Dr. Stephan Giglberger Prof. Dr. Christian
7 Die Hamilton-Jacobi-Theorie
 7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
Klassische Theoretische Physik I WS 2013/ Nicht so schnell (10 Punkte) Ein kleiner
 Karlsruher Institut für Technologie www.tkm.kit.edu/lehre/ Klassische Theoretische Physik I WS 23/24 Prof. Dr. J. Schmalian Blatt, Punkte Dr. P. P. Orth Abgabe und Besprechung 24..24. Nicht so schnell
Karlsruher Institut für Technologie www.tkm.kit.edu/lehre/ Klassische Theoretische Physik I WS 23/24 Prof. Dr. J. Schmalian Blatt, Punkte Dr. P. P. Orth Abgabe und Besprechung 24..24. Nicht so schnell
Partialbruchzerlegung
 Partialbruchzerlegung Lucas Kunz 27. Januar 207 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Nullstellen höheren Grades........................... 2.3 Residuen-Formel................................
Partialbruchzerlegung Lucas Kunz 27. Januar 207 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Nullstellen höheren Grades........................... 2.3 Residuen-Formel................................
Bewegung auf Paraboloid 2
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 8 vom 17.06.13 Abgabe: 24.06. Aufgabe 34 4 Punkte Bewegung auf Paraboloid 2 Ein Teilchen der Masse m bewege sich reibungsfrei unter
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 8 vom 17.06.13 Abgabe: 24.06. Aufgabe 34 4 Punkte Bewegung auf Paraboloid 2 Ein Teilchen der Masse m bewege sich reibungsfrei unter
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Dieses Kapitel vermittelt:
 2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
Theoretische Physik I/II
 Theoretische Physik I/II Prof. Dr. M. Bleicher Institut für Theoretische Physik J. W. Goethe-Universität Frankfurt Aufgabenzettel XI 27. Juni 2011 http://th.physik.uni-frankfurt.de/ baeuchle/tut Lösungen
Theoretische Physik I/II Prof. Dr. M. Bleicher Institut für Theoretische Physik J. W. Goethe-Universität Frankfurt Aufgabenzettel XI 27. Juni 2011 http://th.physik.uni-frankfurt.de/ baeuchle/tut Lösungen
2. Fraktale Geometrie
 2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
2.3 Chaos und Lyapunov-Exponent. d dx f(x) λ = lim n n . (1) Programm. k=0. PROGRAM lyapunov ...
 2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
Fraktale und Chaos. Wir beschftigten uns mit Fraktalen, die aus dem Studium komplexer dynamischer
 Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Übungsklausur Analysis & Geometrie Bevölkerungsdichte & Pyramide Pflichtteil (ohne Hilfsmittel)
 Pflichtteil (ohne Hilfsmittel) ) Berechne die erste Ableitung. 3x a) f(x) e cos(x x) b) 3x f(x) e cos(x x) (5VP) ) Berechne und vereinfache. a) cos x dx b) 5 dx (4VP) x 3) Bestimme die Lösungsmenge der
Pflichtteil (ohne Hilfsmittel) ) Berechne die erste Ableitung. 3x a) f(x) e cos(x x) b) 3x f(x) e cos(x x) (5VP) ) Berechne und vereinfache. a) cos x dx b) 5 dx (4VP) x 3) Bestimme die Lösungsmenge der
Hamilton-Systeme. J. Struckmeier
 Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK. K. Taubert Universität Hamburg SS08
 Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
Kunst und Wissenschaft
 Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
PROBEPRÜFUNG MATHEMATIK I UND II
 PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
9 Fourier-Transformation
 9 Fourier-Transformation Zoltán Zomotor Versionsstand: 5. September 2015, 18:26 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
9 Fourier-Transformation Zoltán Zomotor Versionsstand: 5. September 2015, 18:26 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
exponentielle Wachstumsphase Abbildung 1: Wachstumskurve einer Bakterienkultur
 Bakterienwachstum Mathematische Schwerpunkte: Teil 1: Folgen; vollständige Induktion; rekursiv definierte Folgen Teil 2: Exponentialfunktionen Teil 3: Extremwertbestimmung; Integration einer rationalen
Bakterienwachstum Mathematische Schwerpunkte: Teil 1: Folgen; vollständige Induktion; rekursiv definierte Folgen Teil 2: Exponentialfunktionen Teil 3: Extremwertbestimmung; Integration einer rationalen
Vorwissen Lineare Modelle zweier Bevölkerungen
 Reiser Stephan 1 Ablauf Vorwissen Lineare Modelle zweier Bevölkerungen Das Konkurrenzmodell von Volterra Ein allgemeineres Konkurrenzmodell Periodische Bahnen für die allgemeine Volterra-Lotka- Gleichung
Reiser Stephan 1 Ablauf Vorwissen Lineare Modelle zweier Bevölkerungen Das Konkurrenzmodell von Volterra Ein allgemeineres Konkurrenzmodell Periodische Bahnen für die allgemeine Volterra-Lotka- Gleichung
Chaos am invertierten Pendel
 Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Gitterfeldtheoretische Behandlung des harmonischen Oszillators in der Pfadintegralformulierung in Euklidischer Raum-Zeit
 Gitterfeldtheoretische Behandlung des harmonischen Oszillators in der Pfadintegralformulierung in Euklidischer Raum-Zeit Präsentation zur Bachelorarbeit September 2014 Einleitung Modelle in der Physik
Gitterfeldtheoretische Behandlung des harmonischen Oszillators in der Pfadintegralformulierung in Euklidischer Raum-Zeit Präsentation zur Bachelorarbeit September 2014 Einleitung Modelle in der Physik
Lösung - Serie 2. D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Welche der folgenden Funktionen ( 1, 1) R sind strikt monoton wachsend?
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
Physik der sozio-ökonomischen Systeme mit dem Computer. 7. Vorlesung
 Physik der sozio-ökonomischen Systeme mit dem Computer PC-POOL RAUM 01.120 JOHANN WOLFGANG GOETHE UNIVERSITÄT 01.12.2017 7. Vorlesung MATTHIAS HANAUSKE FRANKFURT INSTITUTE FOR ADVANCED STUDIES JOHANN WOLFGANG
Physik der sozio-ökonomischen Systeme mit dem Computer PC-POOL RAUM 01.120 JOHANN WOLFGANG GOETHE UNIVERSITÄT 01.12.2017 7. Vorlesung MATTHIAS HANAUSKE FRANKFURT INSTITUTE FOR ADVANCED STUDIES JOHANN WOLFGANG
ETHZ, D-MATH. Numerische Methoden D-PHYS, WS 2015/16 Dr. V. Gradinaru
 ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
Funktion Abbildung genau ein und nur ein
 Definition des Begriffs Funktion In der Mathematik ist eine Funktion (lateinisch functio) oder Abbildung eine Beziehung (Relation) zwischen zwei Mengen, die jedem Element der Definitionsmenge (Funktionsargument,
Definition des Begriffs Funktion In der Mathematik ist eine Funktion (lateinisch functio) oder Abbildung eine Beziehung (Relation) zwischen zwei Mengen, die jedem Element der Definitionsmenge (Funktionsargument,
Moderne Theoretische Physik IIIa WS 18/19
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik IIIa WS 8/9 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 7 Dr. Stefan Rex Besprechung: 9..9.
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik IIIa WS 8/9 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 7 Dr. Stefan Rex Besprechung: 9..9.
Diskrete Populationsmodelle für Einzelspezies
 Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
ẋ = αx(t) + βx(t τ) (1.3) 1.1 DDE als diskrete Abbildung x(t + h) = x(t) + hẋ(t) (1.2)
 1 Lyapunovspektrum Wir wollen im folgenden Kapitel das Lyapunovspektrum am Beispiel der einfachsten retardierten Dierentialgleichung (Dierential Delay Equation) betrachten: ẋ(t) = αx(t) + βx(t τ) (11)
1 Lyapunovspektrum Wir wollen im folgenden Kapitel das Lyapunovspektrum am Beispiel der einfachsten retardierten Dierentialgleichung (Dierential Delay Equation) betrachten: ẋ(t) = αx(t) + βx(t τ) (11)
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
1 Fraktale Eigenschaften der Koch-Kurve
 Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Zusatzmaterial zu Kapitel 6
 ZU KAPITEL 62: METHODEN ZUR STABILITÄTSPRÜFUNG Zusatzmaterial zu Kapitel 6 Zu Kapitel 62: Methoden zur Stabilitätsprüfung Einleitung Bei der Feststellung der asymptotischen Stabilität (siehe Kapitel 63)
ZU KAPITEL 62: METHODEN ZUR STABILITÄTSPRÜFUNG Zusatzmaterial zu Kapitel 6 Zu Kapitel 62: Methoden zur Stabilitätsprüfung Einleitung Bei der Feststellung der asymptotischen Stabilität (siehe Kapitel 63)
1 Debye-Abschirmung. 1.1 Grundlagen. Φ = q r exp ( r/λ D), λ D =
 1 Debye-Abschirmung Bringt man eine zusätzliche estladung in ein Plasma ein, so wird deren elektrisches Feld durch die Ladungen des Plasmas mit entgegengesetztem Vorzeichen abgeschirmt. Die charakteristische
1 Debye-Abschirmung Bringt man eine zusätzliche estladung in ein Plasma ein, so wird deren elektrisches Feld durch die Ladungen des Plasmas mit entgegengesetztem Vorzeichen abgeschirmt. Die charakteristische
