Fraktale und Beispiele aus der Physik
|
|
|
- Gerhard Hartmann
- vor 7 Jahren
- Abrufe
Transkript
1 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien und das Pseudo-Fraktal Jetzt wird s komplex Fraktale in der komplexen Ebene: Mandelbrotmenge und Juliamengen Knut Müller 12/2004
2 Schon lange bekannt: Mathematische Beschreibung der Natur durch usw... ganzzahlige Dimensionen: Euklidische Geometrie VIEL ERFOLG:
3
4 Fraktale Geometrie Für die mathematische Naturbeschreibung scheint weniger die resultierende Form entscheidend zu sein als ein simples, oft iteriertes Aufbauprinzip
5 Fraktale Geometrie Für die mathematische Naturbeschreibung scheint weniger die resultierende Form entscheidend zu sein als ein simples, oft iteriertes Aufbauprinzip Fraktale... (1) haben nicht-ganzzahlige Dimension (a) Fraktale Dim. (b) Box - Dim. (c)..... (2) sind oft [statistisch] selbstähnlich (3) treten häufig in chaotischen Systemen auf (Nichtlinearität, Komplexität)
6 Das Magnetpendel Experimenteller Aufbau z L Annahmen: (1) L >> r(t), langes Pendel, d.h. m bewegt sich planar (z = 0). r(t) m z = 0 (2) Jeder Magnet erzeugt zum Abstand reziprokes Potential. y x O (x,y,-d) 3 3 z = -d (3) m ruht irgendwann aufgrund Stokes scher Reibung. (x 1,y 1,-d) (x 2,y 2,-d)
7 Das Magnetpendel Aufstellen der DGL
8 Einschub im Nachhinein: Die Trajektorien auf der übernächsten Folie wurden hiermit gemacht Numerische Lösung der Differentialgleichungen mit MAPLE 7 # # Trajektorien für das Magnetpendel mit 3 Magneten # Knut Müller 15/12/2004 # # Vorgeplenkel > restart: > with(plots): > with(plottools): > with(detools): # # Parameter # > l:=2: Abstand der Magneten voneinander > x1:=0: x1,x2,x3,y1,y2,y3: Positionen der Magneten > x2:=l/2: auf den Ecken eines gleichseitigen Dreiecks > x3:=-l/2: > y1:=l*sqrt(1/3): > y2:=-l*sqrt(1/12): > y3:=-l*sqrt(1/12): > reib:=0.01: Reibungskoeffizient > gravi:=0.8: Stärke der Rückstell-(Gravitations-)kraft > feld:=5: Magnet-/Coulombfeldstärke > dist:=0.25: vertikaler Abstand der Magneten von z = 0 > > startx:=0.2: startx,starty: Koordinaten, wo das Pendel startet > starty:=-1.1: > dauer:=100: solange lässt MAPLE es pendeln # # Differentialgleichungen # > xkomp:=diff(diff(x(t),t),t) + reib*diff(x(t),t) + gravi*x(t) + > feld*((x(t)-x1)^2+(y(t)-y1)^2+dist^2)^(-3/2)*(x(t)-x1) + > feld*((x(t)-x2)^2+(y(t)-y2)^2+dist^2)^(-3/2)*(x(t)-x2) + > feld*((x(t)-x3)^2+(y(t)-y3)^2+dist^2)^(-3/2)*(x(t)-x3)=0: > ykomp:=diff(diff(y(t),t),t) + reib*diff(y(t),t) + gravi*y(t) + > feld*((x(t)-x1)^2+(y(t)-y1)^2+dist^2)^(-3/2)*(y(t)-y1) + > feld*((x(t)-x2)^2+(y(t)-y2)^2+dist^2)^(-3/2)*(y(t)-y2) + > feld*((x(t)-x3)^2+(y(t)-y3)^2+dist^2)^(-3/2)*(y(t)-y3)=0: > > Digits:=8: mit sovielen Nachkommastellen rechnet MAPLE > > t:='t': > sys:=[xkomp,ykomp,x(0)=startx,y(0)=starty,d(x)(0)=0,d(y)(0)=0]: > > lsg:=dsolve(sys,{x(t),y(t)},numeric): > > Trajektorie:=odeplot(lsg,[x(t),y(t)],0..dauer,view=[-2..2,-2..2],axes= > boxed): > > magnet1:=circle([x1,y1],1.5/10,color=red,thickness=3): > magnet2:=circle([x2,y2],1.5/10,color=blue,thickness=3): > magnet3:=circle([x3,y3],1.5/10,color=yellow,thickness=3): > display({magnet1,magnet2,magnet3,trajektorie},numpoints=500,axes=boxed >,scaling=constrained);
9 Das Magnetpendel Trajektorien und Vorhersagbarkeit chaotischer Verlauf der Trajektorie des Pendels: Winzige Änderungen der Anfangsbedingungen zeigen große Abweichungen in der Bahnkurve. (hervorgerufen durch die Nichtlinearität ) [Illustration des chaotischen Verlaufs der Trajektorien mit einem Maple-Programm an dieser Stelle]
10 Das Magnetpendel Trajektorien und Vorhersagbarkeit
11 Das Magnetpendel Trajektorien und Vorhersagbarkeit chaotischer Verlauf der Trajektorie des Pendels: Winzige Änderungen der Anfangsbedingungen zeigen große Abweichungen in der Bahnkurve. (hervorgerufen durch Nichtlinearität) Zwei stabile Bereiche sind stets so getrennt, daß der des dritten Attraktors dazwischenliegt.
12 Das Magnetpendel Vorhersagbarkeit
13 Das Magnetpendel Vorhersagbarkeit chaotischer Verlauf der Trajektorie des Pendels: Winzige Änderungen der Anfangsbedingungen zeigen große Abweichungen in der Bahnkurve. (hervorgerufen durch Nichtlinearität r 3 ) Zwei stabile Bereiche sind stets so getrennt, daß der des dritten Attraktors dazwischenliegt. Die Größe des instabilen Bereichs A(s) hängt ab von (negativ) (positiv) Reibungskoeffizient /m Konstante der Rückstellkraft g/l
14 Das Magnetpendel Vorhersagbarkeit Reibungsabhängigkeit 0,2 0,3 Abhängigkeit von der Rückstellkraft 0,3 0,2 0,4 0,5 0,1 0,0
15 Das Magnetpendel Fraktale Grenzen chaotischer Verlauf der Trajektorie des Pendels: Winzige Änderungen der Anfangsbedingungen zeigen große Abweichungen in der Bahnkurve. (hervorgerufen durch Nichtlinearität) Zwei stabile Bereiche sind stets so getrennt, daß der des dritten Attraktors dazwischenliegt. Die Größe des instabilen Bereichs A(s) hängt ab von (negativ) Reibungskoeffizient /m (positiv) Konstante der Rückstellkraft g/l Die Grenzen spalten sich mit zunehmender Vergrößerung immer weiter auf. Allerdings ist irgendwann ein Ende erreicht, wie wir es von Fraktalen in der Natur kennen.
16 Das Magnetpendel Fraktale Grenzen (zur Konstruktion der Cantormenge)
17 Feigenbaumdiagramm Anschaulicher Spezialfall: Entwicklung von Populationen z Feigenbaum Diagramm z n+1 = z n ² + c Realteil Wachstumsparameter als Variable c
18 Fraktale in der komplexen Ebene Mandelbrotmenge Jetzt ein weiterer Spezialfall: Erweiterung auf komplexe Ebene Mandelbrot Menge Im z n+1 = z n ² + c z, c C 0 Re (Start: z 0 = 0 Þ z 1 = c)
19
20 Fraktale in der komplexen Ebene Juliamengen Ausgangspunkt erneut: Logistische Abbildung im Komplexen z n+1 = z n ² + c (z, c C) Aber: Setze nun c fest und erstelle eine Karte von z Startwerten, deren Folge beschränkt ist. Für jedes c erhält man nun eine eigene Menge, genannt Juliamenge J c entweder zusammenhängend oder total unzusammenhängend ( Punktwolken )
21 Fraktale in der komplexen Ebene Juliamengen M Juliamengen c = 0,4 + 0,3i M total unzusammenhängend c = 0, ,58679i M zusammenhängend
22 Fraktale in der komplexen Ebene Juliamengen «Mandelbrotmenge Noch einmal: Bei der Mandelbrotmenge startet man mit z 1 = c und erstellt eine Karte aller c, für die die Folge z n+1 = z n ² + c endlich bleibt. In jeder Juliamenge für sich ist c = const. und es wird eine Karte aller z 0 Startwerte erstellt, für die die Folge endlich bleibt. c variiert lediglich von Juliamenge zu Juliamenge. Þ Insbesondere gibt es zu jedem Punkt in der Mandelbrotmenge auch eine Juliamenge mit folgender Eigenschaft: Þ Nur die aus c M entstehenden Juliamengen sind zusammenhängend, alle anderen sind total unzusammenhängend. Also:
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Ökologische Gleichungen für zwei Spezies
 Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
Gleichgewichte von Differentialgleichungen
 Gleichgewichte von Differentialgleichungen Gleichgewichte von Differentialgleichungen Teil 1 Zur Erinnerung: Zur Erinnerung: Wir hatten lineare Differentialgleichungen betrachtet: in R 1 : Zur Erinnerung:
Gleichgewichte von Differentialgleichungen Gleichgewichte von Differentialgleichungen Teil 1 Zur Erinnerung: Zur Erinnerung: Wir hatten lineare Differentialgleichungen betrachtet: in R 1 : Zur Erinnerung:
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
 Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Differentialgleichungen I
 Differentialgleichungen I Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 5. Januar 2009 Beachtenswertes Die Veranstaltung
Differentialgleichungen I Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 5. Januar 2009 Beachtenswertes Die Veranstaltung
Bifurkationstheorie. 1. Verzweigungen stationärer Zustände
 Bifurkationstheorie 1. Verzweigungen stationärer Zustände Die Lage, Anzahl und Stabilität der stationären Zustände von nichtlinearen Systemen hängt in der Regel noch von bestimmten Systemparametern ab.
Bifurkationstheorie 1. Verzweigungen stationärer Zustände Die Lage, Anzahl und Stabilität der stationären Zustände von nichtlinearen Systemen hängt in der Regel noch von bestimmten Systemparametern ab.
Chaos - Nichtlineare Dynamik
 Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Juliamengen und Mandelbrotmenge
 Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Abbildung 1: Feigenbaum-Diagramm
 Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
Vortragsthemen. Reelle Dynamik
 Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
BERÜHMTE KURVEN Logarithmische Spirale. Die Logarithmische Spirale wird durch eine Gleichung in Polarkoordinaten angegeben: r(φ)=a*e k φ
 BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Big Data Science in und außerhalb der Physik
 Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Ausarbeitung zum Vortrag im Rahmen des Hauptseminars Big Data Science in und außerhalb der Physik an der Fakultät für Physik am Karlsruher Institut
Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Ausarbeitung zum Vortrag im Rahmen des Hauptseminars Big Data Science in und außerhalb der Physik an der Fakultät für Physik am Karlsruher Institut
Nichtlineare Dynamik in biologischen Systemen
 Universität Leipzig Fakultät für Physik und Geowissenschaften Bereich Didaktik der Physik 29. August 2006 11 Nichtlineare Dynamik in biologischen Systemen Erster Gutachter: Prof. Dr. Wolfgang Oehme, Universität
Universität Leipzig Fakultät für Physik und Geowissenschaften Bereich Didaktik der Physik 29. August 2006 11 Nichtlineare Dynamik in biologischen Systemen Erster Gutachter: Prof. Dr. Wolfgang Oehme, Universität
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
 Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Einführung in die Physik I. Schwingungen und Wellen 1
 Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Einführung in die objektorientierte Programmierung mit C++
 Prof. Dr. Thomas Klinker FB Elektrotechnik und Informatik 08. 03. 2007 Projekt im 4. Semester Elektrotechnik: Einführung in die objektorientierte Programmierung mit C++ Aufgabe 1: Schreiben Sie ein Programm,
Prof. Dr. Thomas Klinker FB Elektrotechnik und Informatik 08. 03. 2007 Projekt im 4. Semester Elektrotechnik: Einführung in die objektorientierte Programmierung mit C++ Aufgabe 1: Schreiben Sie ein Programm,
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: , Abgabe am )
 Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Vorlesung Theoretische Mechanik
 Julius-Maximilians-Universität Würzburg Vorlesung Theoretische Mechanik Wintersemester 17/18 Prof. Dr. Johanna Erdmenger Vorläufiges Skript 1 (Zweite Vorlesung, aufgeschrieben von Manuel Kunkel, 23. 10.
Julius-Maximilians-Universität Würzburg Vorlesung Theoretische Mechanik Wintersemester 17/18 Prof. Dr. Johanna Erdmenger Vorläufiges Skript 1 (Zweite Vorlesung, aufgeschrieben von Manuel Kunkel, 23. 10.
Spezielle Kinetik MC 1.3. Prof. Dr. B. Dietzek. Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie. Wintersemester 2016/2017
 Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
1. Funktionen und Stetigkeit
 1. Funktionen und Stetigkeit Um Funktionen mit mehreren Variablen auf ihr Grenzwertverhalten, wie Stetigkeit und Differenzierbarkeit, untersuchen zu können, ist es sinnvoll, sie auf kleinen Umgebungen,
1. Funktionen und Stetigkeit Um Funktionen mit mehreren Variablen auf ihr Grenzwertverhalten, wie Stetigkeit und Differenzierbarkeit, untersuchen zu können, ist es sinnvoll, sie auf kleinen Umgebungen,
3. Vorlesung Wintersemester
 3. Vorlesung Wintersemester 1 Parameterdarstellung von Kurven Wir haben gesehen, dass man die Bewegung von Punktteilchen durch einen zeitabhängigen Ortsvektor darstellen kann. Genauso kann man aber auch
3. Vorlesung Wintersemester 1 Parameterdarstellung von Kurven Wir haben gesehen, dass man die Bewegung von Punktteilchen durch einen zeitabhängigen Ortsvektor darstellen kann. Genauso kann man aber auch
FRAKTALE. Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier
 FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Wir erinnern zunächst an die verschiedenen Arten von Funktionen, die uns bisher begegnet sind: V : r 0 3 V ( r) 0 3
 3 1. Mathematische Grundlagen Zur Vorbereitung fassen wir in diesem ersten Kapitel die wichtigsten mathematischen Konzepte zusammen, mit denen wir in der Elektrodynamik immer wieder umgehen werden. 1.1.
3 1. Mathematische Grundlagen Zur Vorbereitung fassen wir in diesem ersten Kapitel die wichtigsten mathematischen Konzepte zusammen, mit denen wir in der Elektrodynamik immer wieder umgehen werden. 1.1.
Der Duffing-Oszillator
 11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
PW2 Grundlagen Vertiefung. Kinematik und Stoÿprozesse Version
 PW2 Grundlagen Vertiefung Kinematik und Stoÿprozesse Version 2007-09-03 Inhaltsverzeichnis 1 Vertiefende Grundlagen zu den Experimenten mit dem Luftkissentisch 1 1.1 Begrie.....................................
PW2 Grundlagen Vertiefung Kinematik und Stoÿprozesse Version 2007-09-03 Inhaltsverzeichnis 1 Vertiefende Grundlagen zu den Experimenten mit dem Luftkissentisch 1 1.1 Begrie.....................................
) auf dem Band auf Osiris zu, während Osiris sich auf dem Weg in die Unterwelt mit der Geschwindigkeit 0.35 Schoinen pro Stunde (v 2 = 1 m s
 1 Das Rätsel vom Käfer auf dem Gummiband Die alten Ägypter glaubten angeblich, Osiris habe am Tempel in Luor ein unsichtbares Gummiband der Länge L = 1m befestigt, auf dessen Anfang er einen Scarabaeus
1 Das Rätsel vom Käfer auf dem Gummiband Die alten Ägypter glaubten angeblich, Osiris habe am Tempel in Luor ein unsichtbares Gummiband der Länge L = 1m befestigt, auf dessen Anfang er einen Scarabaeus
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
 Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 7 vom Abgabe:
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
Die grasende Ziege am Seil
 ) H F * Die grasende Ziege am Seil von Ingmar Rubin 4. Oktober 003 Eine Ziege befindet sich auf einer eingezäunten Weideläche, die von einem Wassergraben durchzogen wird. In den Punkten A und B befindet
) H F * Die grasende Ziege am Seil von Ingmar Rubin 4. Oktober 003 Eine Ziege befindet sich auf einer eingezäunten Weideläche, die von einem Wassergraben durchzogen wird. In den Punkten A und B befindet
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Chaos im getriebenen nicht-linearen Pendel
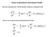 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Dass die Rotation eines konservativen Kraftfeldes null ist, folgt direkt aus der Identität C 1 C 2 C 2 C 1
 I.1 Grundbegriffe der newtonschen Mechanik 11 I.1.3 c Konservative Kräfte Definition: Ein zeitunabhängiges Kraftfeld F ( r) wird konservativ genannt, wenn es ein Skalarfeld (3) V ( r) gibt, das F ( r)
I.1 Grundbegriffe der newtonschen Mechanik 11 I.1.3 c Konservative Kräfte Definition: Ein zeitunabhängiges Kraftfeld F ( r) wird konservativ genannt, wenn es ein Skalarfeld (3) V ( r) gibt, das F ( r)
I.6.3 Kepler-Problem. V ( x ) = G Nm 1 m 2. (I.91a) mit dem Potential. . (I.91b)
 38 Newton sche Mechanik I.6.3 Kepler-Problem Die Newton sche Gravitationskraft zwischen zwei Massenpunkten mit Massen m 1, m 2 ist eine konservative Zentralkraft, gegeben durch mit dem Potential F ( x
38 Newton sche Mechanik I.6.3 Kepler-Problem Die Newton sche Gravitationskraft zwischen zwei Massenpunkten mit Massen m 1, m 2 ist eine konservative Zentralkraft, gegeben durch mit dem Potential F ( x
Herbert Zeitler Wolfgang Neidhardt. Fraktale und Chaos. Eine Einführung. Wissenschaftliche Buchgesellschaft Darmstadt
 Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
 3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
 Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Abbildung 14: Ein Vektorfeld im R 2
 Vektoranalysis 54 Vektoranalysis Wir wollen nun Vektorfelder betrachten. Es sei U R n. Ein Vektorfeld im R n ist eine Abbildung v : U R n, die jedem Punkt x ihres sbereichs U einen Vektor v(x) zuordnet.
Vektoranalysis 54 Vektoranalysis Wir wollen nun Vektorfelder betrachten. Es sei U R n. Ein Vektorfeld im R n ist eine Abbildung v : U R n, die jedem Punkt x ihres sbereichs U einen Vektor v(x) zuordnet.
Einführendes Beispiel zum lösen einer DGL n-ter Ordnung Dokumentation zum Dreikörperproblem (Sonne, Erde, Mond)
 Projektarbeit zur grafischen Beschreibung des Dreikörperproblems durch numerisches lösen der Bewegungsgleichungen Joachim N. WS 07/08 Einführendes Beispiel zum lösen einer DGL n-ter Ordnung Dokumentation
Projektarbeit zur grafischen Beschreibung des Dreikörperproblems durch numerisches lösen der Bewegungsgleichungen Joachim N. WS 07/08 Einführendes Beispiel zum lösen einer DGL n-ter Ordnung Dokumentation
Blatt 1. Kinematik- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
REFERAT FÜR INNOVATIVE ARCHIKETUREN
 REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Fraktale und Chaos. Wir beschftigten uns mit Fraktalen, die aus dem Studium komplexer dynamischer
 Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
1 Lagrange-Formalismus
 Lagrange-Formalismus SS 4 In der gestrigen Vorlesung haben wir die Beschreibung eines physikalischen Systems mit Hilfe der Newton schen Axiome kennen gelernt. Oft ist es aber nicht so einfach die Kraftbilanz
Lagrange-Formalismus SS 4 In der gestrigen Vorlesung haben wir die Beschreibung eines physikalischen Systems mit Hilfe der Newton schen Axiome kennen gelernt. Oft ist es aber nicht so einfach die Kraftbilanz
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Das mathematische Pendel
 1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
1 Die drei Bewegungsgleichungen
 1 Die drei Bewegungsgleichungen Unbeschleunigte Bewegung, a = 0: Hier gibt es nur eine Formel, nämlich die für den Weg, s. (i) s = s 0 + v t s ist der zurückgelegte Weg, s 0 der Ort, an dem sich der Körper
1 Die drei Bewegungsgleichungen Unbeschleunigte Bewegung, a = 0: Hier gibt es nur eine Formel, nämlich die für den Weg, s. (i) s = s 0 + v t s ist der zurückgelegte Weg, s 0 der Ort, an dem sich der Körper
Abbildung 5.1: stabile und instabile Ruhelagen
 Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
Oberstufe Mathematik - Fraktale Annika Maier, Anja Schmid; Abitur 2004. Fraktale
 Fraktale 1 Einleitung : Um solche grafischen Gebilde handelt es sich in unserem mathematischen Referat Wir werden in möglichst nicht-mathematischer Sprache, also für jedermann zugänglich, beschreiben,
Fraktale 1 Einleitung : Um solche grafischen Gebilde handelt es sich in unserem mathematischen Referat Wir werden in möglichst nicht-mathematischer Sprache, also für jedermann zugänglich, beschreiben,
Vorbereitung für Olympische Spiele auf dem Mars oder Mond
 Vorbereitung für Olympische Spiele auf dem Mars oder Mond Martin Sust Karl-Franzens Franzens-Universität Graz Interessierende Fragen für Sport auf der Erde: 1. Welche Abmessungen müssen Sportanlagen haben?
Vorbereitung für Olympische Spiele auf dem Mars oder Mond Martin Sust Karl-Franzens Franzens-Universität Graz Interessierende Fragen für Sport auf der Erde: 1. Welche Abmessungen müssen Sportanlagen haben?
6 Differentialgleichungen
 88 6 Differentialgleichungen Eine Differentialgleichung ist eine Gleichung, in der eine unbekannte Funktion y = y(x) und Ableitungen (die erste oder auch höhere) von y vorkommen. Lösungen einer Differentialgleichung
88 6 Differentialgleichungen Eine Differentialgleichung ist eine Gleichung, in der eine unbekannte Funktion y = y(x) und Ableitungen (die erste oder auch höhere) von y vorkommen. Lösungen einer Differentialgleichung
Harmonische Schwingungen
 Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
Thema: Visualisierung mit MAPLE
 Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Kapitel 2. Kinematik des Massenpunktes. 2.1 Einleitung. 2.2 Massenpunkt. 2.3 Ortsvektor
 Kapitel 2 Kinematik des Massenpunktes 2.1 Einleitung In diesem Kapitel behandeln wir die Bewegung von einem oder mehreren Körpern im Raum. Wir unterscheiden dabei zwischen Kinematik und Dynamik. Die Kinematik
Kapitel 2 Kinematik des Massenpunktes 2.1 Einleitung In diesem Kapitel behandeln wir die Bewegung von einem oder mehreren Körpern im Raum. Wir unterscheiden dabei zwischen Kinematik und Dynamik. Die Kinematik
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 25/6 Dörte Hansen Seminar 1 Dissipative Kräfte I Reibung Wenn wir in der theoretischen Mechanik die Bewegung eines Körpers beschreiben wollen,
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 25/6 Dörte Hansen Seminar 1 Dissipative Kräfte I Reibung Wenn wir in der theoretischen Mechanik die Bewegung eines Körpers beschreiben wollen,
1 Die Mandelbrotmenge
 1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
Übungen mit dem Applet Kurven in Parameterform
 Kurven in Parameterform 1 Übungen mit dem Applet Kurven in Parameterform 1 Ziele des Applets... Wie entsteht eine Kurve in Parameterform?... 3 Kurvenverlauf für ausgewählte x(t) und y(t)... 3 3.1 x(t)
Kurven in Parameterform 1 Übungen mit dem Applet Kurven in Parameterform 1 Ziele des Applets... Wie entsteht eine Kurve in Parameterform?... 3 Kurvenverlauf für ausgewählte x(t) und y(t)... 3 3.1 x(t)
Kausalität: Verhältnis von Ursache und Wirkung
 Kausalität: Verhältnis von Ursache und Wirkung Einleitung Wenn jemand einen Ball fallen lässt wisst ihr sicherlich jedesmal ungefähr, wohin der Ball fällt. Wisst ihr das auch, wenn ein Blatt Papier fallengelassen
Kausalität: Verhältnis von Ursache und Wirkung Einleitung Wenn jemand einen Ball fallen lässt wisst ihr sicherlich jedesmal ungefähr, wohin der Ball fällt. Wisst ihr das auch, wenn ein Blatt Papier fallengelassen
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
Rekurrente Neuronale Netze. Rudolf Kruse Neuronale Netze 227
 Rekurrente Neuronale Netze Rudolf Kruse Neuronale Netze 227 Rekurrente Netze: Abkühlungsgesetz Ein Körper der Temperaturϑ wird in eine Umgebung der Temperaturϑ A eingebracht. Die Abkühlung/Aufheizung des
Rekurrente Neuronale Netze Rudolf Kruse Neuronale Netze 227 Rekurrente Netze: Abkühlungsgesetz Ein Körper der Temperaturϑ wird in eine Umgebung der Temperaturϑ A eingebracht. Die Abkühlung/Aufheizung des
Übungen zu Lagrange-Formalismus und kleinen Schwingungen
 Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Anwendung: Gedämpfter, getriebener harmonischer Oszillator Unendlich viele Anwendungen in der Physik, auch außerhalb der Mechanik!
 Anwendung: Gedämpfter, getriebener harmonischer Oszillator Unendlich viele Anwendungen in der Physik, auch außerhalb der Mechanik! Bewegungsgleichung: Dämpfungsrate: Einheit: Kreisfrequenz des Oszillators:
Anwendung: Gedämpfter, getriebener harmonischer Oszillator Unendlich viele Anwendungen in der Physik, auch außerhalb der Mechanik! Bewegungsgleichung: Dämpfungsrate: Einheit: Kreisfrequenz des Oszillators:
BASISPRÜFUNG MATHEMATIK I UND II
 ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
Wie man dieses (Weg-)Integral berechnet, kann man sich mit der folgenden Merkregel im Kopf halten. Man schreibt d~r = d~r
 Vektoranalysis 3 Die Arbeit g Zum Einstieg eine kleine Veranschaulichung. Wir betrachten ein Flugzeug, das irgendeinen beliebigen Weg zurücklegt. Ausserdem seien gewisse Windverhältnisse gegeben, so dass
Vektoranalysis 3 Die Arbeit g Zum Einstieg eine kleine Veranschaulichung. Wir betrachten ein Flugzeug, das irgendeinen beliebigen Weg zurücklegt. Ausserdem seien gewisse Windverhältnisse gegeben, so dass
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle. zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"):
 Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
Mathematik Teil 2: Differentialgleichungen
 Mathematik Teil 2: Differentialgleichungen M. Gutting Fakultät IV, Department Mathematik 19. Juni 2017 Natürliches Wachstum/Zerfall Wachstum/Zerfall (Zinsen, Population / Radioaktiver Zerfall) verhält
Mathematik Teil 2: Differentialgleichungen M. Gutting Fakultät IV, Department Mathematik 19. Juni 2017 Natürliches Wachstum/Zerfall Wachstum/Zerfall (Zinsen, Population / Radioaktiver Zerfall) verhält
2. Kinematik. Inhalt. 2. Kinematik
 2. Kinematik Inhalt 2. Kinematik 2.1 Arten der Bewegung 2.2 Mittlere Geschwindigkeit (1-dimensional) 2.3 Momentane Geschwindigkeit (1-dimensional) 2.4 Beschleunigung (1-dimensional) 2.5 Bahnkurve 2.6 Bewegung
2. Kinematik Inhalt 2. Kinematik 2.1 Arten der Bewegung 2.2 Mittlere Geschwindigkeit (1-dimensional) 2.3 Momentane Geschwindigkeit (1-dimensional) 2.4 Beschleunigung (1-dimensional) 2.5 Bahnkurve 2.6 Bewegung
D-MATH, D-PHYS, D-CHAB Analysis II FS 2017 Prof. Manfred Einsiedler. Übungsblatt 5 A := u = Au, u(0) = 1. 1
 D-MATH, D-PHYS, D-CHAB Analysis II FS 2017 Prof. Manfred Einsiedler Übungsblatt 5 1. Gegeben sei die Matrix 1 1 0 A := 0 1 0 0 0 2 a) Bestimmen Sie ein Fundamentalsystem (das heisst eine Basis des Lösungsraums)
D-MATH, D-PHYS, D-CHAB Analysis II FS 2017 Prof. Manfred Einsiedler Übungsblatt 5 1. Gegeben sei die Matrix 1 1 0 A := 0 1 0 0 0 2 a) Bestimmen Sie ein Fundamentalsystem (das heisst eine Basis des Lösungsraums)
Ferienkurs Theoretische Mechanik Sommer 2010 Newton/Koordinaten/Dgl s
 Fakultät für Physik Friedrich Wulschner Technische Universität München Vorlesung Montag Ferienkurs Theoretische Mechanik Sommer 2010 Newton/Koordinaten/Dgl s Inhaltsverzeichnis 1 Newtons 3 Axiome 2 2 Lösungsverfahren
Fakultät für Physik Friedrich Wulschner Technische Universität München Vorlesung Montag Ferienkurs Theoretische Mechanik Sommer 2010 Newton/Koordinaten/Dgl s Inhaltsverzeichnis 1 Newtons 3 Axiome 2 2 Lösungsverfahren
11.3. Variablentrennung, Ähnlichkeit und Trajektorien
 3 Variablentrennung, Ähnlichkeit und Trajektorien Trennung der Veränderlichen (TdV) Es seien zwei stetige Funktionen a (der Variablen ) und b (der Variablen ) gegeben Die Dgl a( ) b( ) b( ) d d läßt sich
3 Variablentrennung, Ähnlichkeit und Trajektorien Trennung der Veränderlichen (TdV) Es seien zwei stetige Funktionen a (der Variablen ) und b (der Variablen ) gegeben Die Dgl a( ) b( ) b( ) d d läßt sich
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraft und Beschleunigung Masse: Seit 1889 ist die Einheit der Masse wie folgt festgelegt: Das Kilogramm ist die Einheit der Masse; es ist gleich der Masse des Internationalen Kilogrammprototyps.
Masse, Kraft und Beschleunigung Masse: Seit 1889 ist die Einheit der Masse wie folgt festgelegt: Das Kilogramm ist die Einheit der Masse; es ist gleich der Masse des Internationalen Kilogrammprototyps.
1 Debye-Abschirmung. 1.1 Grundlagen. Φ = q r exp ( r/λ D), λ D =
 1 Debye-Abschirmung Bringt man eine zusätzliche estladung in ein Plasma ein, so wird deren elektrisches Feld durch die Ladungen des Plasmas mit entgegengesetztem Vorzeichen abgeschirmt. Die charakteristische
1 Debye-Abschirmung Bringt man eine zusätzliche estladung in ein Plasma ein, so wird deren elektrisches Feld durch die Ladungen des Plasmas mit entgegengesetztem Vorzeichen abgeschirmt. Die charakteristische
Newton-Beschreibung: Bewegung eines Massenpunkts auf einer Oberfläche
 Newton-Beschreibung: Bewegung eines Massenpunkts auf einer Oberfläche R. Mahnke (Univ. Rostock), J. Kaupužs (Lettische Univ. Riga) 3. Mai 24 Zusammenfassung Ziel dieses Kommentars ist es, die Newtonschen
Newton-Beschreibung: Bewegung eines Massenpunkts auf einer Oberfläche R. Mahnke (Univ. Rostock), J. Kaupužs (Lettische Univ. Riga) 3. Mai 24 Zusammenfassung Ziel dieses Kommentars ist es, die Newtonschen
Chaos Seminar Wetter und Klima. Dominik Fröschl
 Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Selbstähnliche Strukturen in der Natur
 Selbstähnliche Strukturen in der Natur Selbstähnliche Objekte werden in der Mathematik durch fraktale Strukturen und einer sogenannten fraktalen Dimension (Hausdorff Dimension) beschrieben. Ziel dieser
Selbstähnliche Strukturen in der Natur Selbstähnliche Objekte werden in der Mathematik durch fraktale Strukturen und einer sogenannten fraktalen Dimension (Hausdorff Dimension) beschrieben. Ziel dieser
2. Potentialströmungen
 2. Potentialströmungen Bei der Umströmung schlanker Körper ist Reibung oft nur in einer dünnen Schicht um den Körper signifikant groß. Erinnerung: Strömung um ein zweidimensionales Tragflügelprofil: 1
2. Potentialströmungen Bei der Umströmung schlanker Körper ist Reibung oft nur in einer dünnen Schicht um den Körper signifikant groß. Erinnerung: Strömung um ein zweidimensionales Tragflügelprofil: 1
4.2 Der Harmonische Oszillator
 Dieter Suter - 208 - Physik B3, SS03 4.2 Der Harmonische Oszillator 4.2.1 Harmonische Schwingungen Die Zeitabhängigkeit einer allgemeinen Schwingung ist beliebig, abgesehen von der Periodizität. Die mathematische
Dieter Suter - 208 - Physik B3, SS03 4.2 Der Harmonische Oszillator 4.2.1 Harmonische Schwingungen Die Zeitabhängigkeit einer allgemeinen Schwingung ist beliebig, abgesehen von der Periodizität. Die mathematische
Experimentalphysik 1
 Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg (ronja.berg@tum.de) Katharina Scheidt (katharina.scheidt@tum.de) Aufgabe 1: Superposition
Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg (ronja.berg@tum.de) Katharina Scheidt (katharina.scheidt@tum.de) Aufgabe 1: Superposition
2. Übung zur Vorlesung Steuer- und Regelungstechnik
 2. Übung zur Vorlesung Steuer- und Regelungstechnik Aufstellen von DGL s, lineare und nichtlineare Systeme Felix Goßmann M.Sc. Institut für Steuer- und Regelungstechnik Fakultät für Luft- und Raumfahrttechnik
2. Übung zur Vorlesung Steuer- und Regelungstechnik Aufstellen von DGL s, lineare und nichtlineare Systeme Felix Goßmann M.Sc. Institut für Steuer- und Regelungstechnik Fakultät für Luft- und Raumfahrttechnik
Analysis und Lineare Algebra mit MuPAD
 Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Gewöhnliche Differentialgleichungen Aufgaben, Teil 1
 Gewöhnliche Differentialgleichungen Aufgaben, Teil 1 4-E1 4-E2 4-E3 Gewöhnliche Differentialgleichung: Aufgaben Bestimmen Sie allgemeine und spezielle Lösungen der folgenden Differentialgleichungen Aufgabe
Gewöhnliche Differentialgleichungen Aufgaben, Teil 1 4-E1 4-E2 4-E3 Gewöhnliche Differentialgleichung: Aufgaben Bestimmen Sie allgemeine und spezielle Lösungen der folgenden Differentialgleichungen Aufgabe
Experimente, Ideen und Entwicklung der Chaostheorie
 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Übungsblatt 02. Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik
 Übungsblatt 0 Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik 4.04.008 Aufgaben. Berechnen Sie, ausgehend vom Coulomb-Gesetz, das elektrische Feld um einen
Übungsblatt 0 Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik 4.04.008 Aufgaben. Berechnen Sie, ausgehend vom Coulomb-Gesetz, das elektrische Feld um einen
Dynamische Systeme eine Einführung
 Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Abbildung 11.1: Farnblatt
 Kapitel 11 Fraktale 11.1 Selbstähnlichkeit Viele in der Natur vorkommende Strukturen weisen eine starke Selbstähnlichkeit auf. Beispiele sind Gebirgsformationen, Meeresküsten oder Pflanzenblätter. Solche
Kapitel 11 Fraktale 11.1 Selbstähnlichkeit Viele in der Natur vorkommende Strukturen weisen eine starke Selbstähnlichkeit auf. Beispiele sind Gebirgsformationen, Meeresküsten oder Pflanzenblätter. Solche
3. Berechnen Sie auch die Beschleunigung a als Funktion der Zeit t. 4. Erstellen Sie ein SIMULINK Modell, das x(t) numerisch berechnet.
 unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
Beispiel: Evolution infizierter Individuen
 Differentialgleichungen sind sehr nützlich in der Modellierung biologischer Prozesse, denn: damit kann man auch sehr komplizierte Systeme beschreiben die Mathematik liefert mit der gut entwickelten Theorie
Differentialgleichungen sind sehr nützlich in der Modellierung biologischer Prozesse, denn: damit kann man auch sehr komplizierte Systeme beschreiben die Mathematik liefert mit der gut entwickelten Theorie
y (t) Wie berechnet sich die Ableitung von F aus den Ableitungen von x (t) und y (t)? Die Antwort gibt die erste Kettenregel
 103 Differenzialrechnung 553 1035 Kettenregeln Die Kettenregel bei Funktionen einer Variablen erlaubt die Berechnung der Ableitung von verketteten Funktionen Je nach Verkettung gibt es bei Funktionen von
103 Differenzialrechnung 553 1035 Kettenregeln Die Kettenregel bei Funktionen einer Variablen erlaubt die Berechnung der Ableitung von verketteten Funktionen Je nach Verkettung gibt es bei Funktionen von
Gymnasium Fränkische Schweiz Abiturjahrgang 2011 Ebermannstadt SEMINARARBEIT. im W-Seminar Mathematik: Komplexe Zahlen. Thema. Die Mandelbrotmenge
 Gymnasium Fränkische Schweiz Abiturjahrgang 2011 Ebermannstadt SEMINARARBEIT im W-Seminar Mathematik: Komplexe Zahlen Thema Die Mandelbrotmenge Verfasser/in: Seminarleiter/in: Michael Hübschmann Herr Hümmer
Gymnasium Fränkische Schweiz Abiturjahrgang 2011 Ebermannstadt SEMINARARBEIT im W-Seminar Mathematik: Komplexe Zahlen Thema Die Mandelbrotmenge Verfasser/in: Seminarleiter/in: Michael Hübschmann Herr Hümmer
6 Julia-Mengen. 114 Kapitel 2 Konforme Abbildungen
 114 Kapitel 2 Konforme Abbildungen 6 Julia-Mengen Sei G C ein Gebiet. Eine holomorphe Abbildung f : G G kann eine holomorphe oder eine meromorphe Funktion auf G sein. Definition. Zwei holomorphe Abbildungen
114 Kapitel 2 Konforme Abbildungen 6 Julia-Mengen Sei G C ein Gebiet. Eine holomorphe Abbildung f : G G kann eine holomorphe oder eine meromorphe Funktion auf G sein. Definition. Zwei holomorphe Abbildungen
