Chaos - Nichtlineare Dynamik
|
|
|
- Lennart Fried
- vor 7 Jahren
- Abrufe
Transkript
1 Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102
2 Inhaltsverzeichnis Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 2/102
3 Einführung Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 3/102
4 Einführung Äg Chaostheorie Chaostheorie beschäftigt sich mit Systemen, denen zwar deterministische Gesetzmäßigkeiten zugrunde liegen, deren Verhalten jedoch irregulär und langfristig nicht vorhersagbar ist. Chaos - Nichtlineare Dynamik 4/102
5 Einführung Äg Chaostheorie Chaostheorie beschäftigt sich mit Systemen, denen zwar deterministische Gesetzmäßigkeiten zugrunde liegen, deren Verhalten jedoch irregulär und langfristig nicht vorhersagbar ist. Die zugrunde liegende DGLs sind nicht nicht linear (= Nichtlineare Dynamik). Folge: kleine Variation in den Anfangsbedingungen verstärken sich exponentiell. Vorhersage über genauen Systemzustand nur begrenzt berechenbar bzw. unmöglich. Chaos - Nichtlineare Dynamik 4/102
6 Einführung Äg Chaostheorie Chaostheorie beschäftigt sich mit Systemen, denen zwar deterministische Gesetzmäßigkeiten zugrunde liegen, deren Verhalten jedoch irregulär und langfristig nicht vorhersagbar ist. Die zugrunde liegende DGLs sind nicht nicht linear (= Nichtlineare Dynamik). Folge: kleine Variation in den Anfangsbedingungen verstärken sich exponentiell. Vorhersage über genauen Systemzustand nur begrenzt berechenbar bzw. unmöglich. Chaostheorie untersucht dieses Verhalten mit dem Ziel, statistische Aussagen über das System zu treffen. Chaos - Nichtlineare Dynamik 4/102
7 Einführung Äg Chaos ursprünglich: altgriech., der ungeordnete Urstoff vor der Weltschöpfung heute: schwer vorhersehbarer Zustand Chaos - Nichtlineare Dynamik 5/102
8 Einführung Äg Chaos ursprünglich: altgriech., der ungeordnete Urstoff vor der Weltschöpfung heute: schwer vorhersehbarer Zustand Determinismus Ein Algorithmus heißt deterministisch, wenn es zu jeder (Programm-)Situation höchstens eine nachfolgende Situation geben kann, wenn also zu jedem Zeitpunkt der Folgeschritt eindeutig bestimmt ist. Chaos - Nichtlineare Dynamik 5/102
9 Einführung Äg Chaos ursprünglich: altgriech., der ungeordnete Urstoff vor der Weltschöpfung heute: schwer vorhersehbarer Zustand Determinismus Ein Algorithmus heißt deterministisch, wenn es zu jeder (Programm-)Situation höchstens eine nachfolgende Situation geben kann, wenn also zu jedem Zeitpunkt der Folgeschritt eindeutig bestimmt ist. Deterministisches Chaos Verhalten, bei dem einfache deterministische Gesetze zu irregulären Bewegungen führen, wird als Deterministisches Chaos bezeichnet. Chaos - Nichtlineare Dynamik 5/102
10 Einführung Äg Beispiele für Deterministisches Chaos Verkehrschaos viele Verkehrsteilnehmer mit ihren Bewegungsmöglichkeiten (Freiheitsgrade). periodisch getriebenes Pendel System mit wenigen Freiheitsgraden; Position auf längere Sicht unvorhersehbar. Chaos - Nichtlineare Dynamik 6/102
11 Einführung Äg Beispiele für Deterministisches Chaos Verkehrschaos viele Verkehrsteilnehmer mit ihren Bewegungsmöglichkeiten (Freiheitsgrade). periodisch getriebenes Pendel System mit wenigen Freiheitsgraden; Position auf längere Sicht unvorhersehbar. tropfendes Wasserhahn durch das Zittern des einzelnen Tropfens wird der nachfolgende beeinflußt. Schmetterlingseffekt Kann der Flügelschlag eines Schmetterlings in Brasilien einen Tornado in Texas hervorrufen? (Edward N. Lorenz) Chaos - Nichtlineare Dynamik 6/102
12 Einführung Äg Beispiele für Deterministisches Chaos Verkehrschaos viele Verkehrsteilnehmer mit ihren Bewegungsmöglichkeiten (Freiheitsgrade). periodisch getriebenes Pendel System mit wenigen Freiheitsgraden; Position auf längere Sicht unvorhersehbar. tropfendes Wasserhahn durch das Zittern des einzelnen Tropfens wird der nachfolgende beeinflußt. Schmetterlingseffekt Kann der Flügelschlag eines Schmetterlings in Brasilien einen Tornado in Texas hervorrufen? (Edward N. Lorenz) Kleine Ursache - große, meist unvorhersehbare Wirkung Chaos - Nichtlineare Dynamik 6/102
13 Einführung - Strukturelle Stabilität Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 7/102
14 Einführung - Strukturelle Stabilität Äg Stabilitäts-Dogma galt bis ca mathematische Modelle, die strukturelle Instabilität aufweisen haben nichts mit der Realität zu tun Verhaltensabhängigkeit von Modellparametern (bisher konstant) Chaos - Nichtlineare Dynamik 8/102
15 Einführung - Strukturelle Stabilität Äg 1. Beispiel: ẋ = f (x, λ) = x 3 + λx (1) = x(x 2 + λ) (2) Chaos - Nichtlineare Dynamik 9/102
16 Einführung - Strukturelle Stabilität Äg 1. Beispiel: ẋ = f (x, λ) = x 3 + λx (1) = x(x 2 + λ) (2) stationäre Zustände (Fixpunkte) für ẋ = 0 x 0 = x = = 0 (3) x + = x = + λ (4) x = x = λ (5) für λ = 0 fallen die Lösungen x + und x zusammen Chaos - Nichtlineare Dynamik 9/102
17 Einführung - Strukturelle Stabilität Äg (Gabel- bzw. Pitchfork-)Bifurkation x ist für λ < 0 global asymptotisch stabil für λ > 0 ist x 0 instabil und für λ > 0 sind x + und x asymptotisch lokal stabil (nicht global) Chaos - Nichtlineare Dynamik 10/102
18 Einführung - Strukturelle Stabilität Äg beim Übergang λ = 0 ändert sich das qualitative Verhalten des System-Modells Widerspruch zum Stabilitäts-Dogma solche Modelle waren bis 1950 nicht erlaubt, weil sie als unnatürlich galten Rene Thom: Katastrophentheorie Chaos - Nichtlineare Dynamik 11/102
19 Einführung - Strukturelle Stabilität Äg 2. Beispiel: ẋ = x 2 + µ (6) (7) Chaos - Nichtlineare Dynamik 12/102
20 Einführung - Strukturelle Stabilität Äg 2. Beispiel: ẋ = x 2 + µ (6) (7) stationäre Zustände (Fixpunkte) für ẋ = 0 x + = x = + λ (8) x = x = λ (9) Chaos - Nichtlineare Dynamik 12/102
21 Einführung - Strukturelle Stabilität Äg x + : stabiler Zweig x instabiler Zweig (Grenzpunkt-)Bifurkation Chaos - Nichtlineare Dynamik 13/102
22 Einführung - Strukturelle Stabilität Äg 3. Beispiel: ẋ = x 3 + λx + µ (10) stationäre Zustände für kubische Gleichung (kanonische Form): bis zu 3 reelle Lösungen Chaos - Nichtlineare Dynamik 14/102
23 Einführung - Strukturelle Stabilität Äg Ursprung 0 bildet Spitzensingularität für λ < 0: 1 Lösung für λ > 0: 3 Lösungen Chaos - Nichtlineare Dynamik 15/102
24 Einführung - Strukturelle Stabilität Äg λ > 0 (Hyterese) µ 0 Grenzkurve im (µ, λ)-paramterraum zwischen den beiden Lösungsbereichen: 4λ µ 2 = 0 (11) Chaos - Nichtlineare Dynamik 16/102
25 Einführung - Grenzzyklen Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 17/102
26 Einführung - Grenzzyklen Äg In dissipativen Systemmodellen mit Phasenraumdimension 2 gibt es außer Fokus und Knoten noch einen dritten Attraktortyp: Grenzzyklus Alle Bahnen münden in einen (stabilen) Grenzzyklus, der einen instabilen Fixpunkt P umgibt. (entdeckt von Poincaré) Chaos - Nichtlineare Dynamik 18/102
27 Einführung - Grenzzyklen Äg Beispiel: x 1 = ν cos(ϕ); x 2 = ν sin(ϕ) 1. ν = λν ν 3 ν > 0 2. ϕ = ω aus 2. folgt: ϕ(t) = ϕ 0 + ωt aus 1. lassen sich Fixpunkte ermitteln: ν = 0 und ν = λ Chaos - Nichtlineare Dynamik 19/102
28 Einführung - Grenzzyklen Äg Beispiel: x 1 = ν cos(ϕ); x 2 = ν sin(ϕ) für λ < 0 ist ν = 0, (d.h. ( x 1 x 2 ) = ( 0 0) ein stabiler Fixpunkt für λ = 0 wird dieser Fixpunkt instabil (Hopf Bifurkation) für λ > 0 ist ν = 0 instabil und ν = λ d.h.: x 1 konvergiert gegen λ cos(ϕ 0 + ωt) x 2 konvergiert gegen λ sin(ϕ 0 + ωt) (zeitabhängige Lösung!) Chaos - Nichtlineare Dynamik 20/102
29 Einführung - Grenzzyklen Äg λ < 0 λ > 0 Grenzzyklus (strukturell stabiles Phasenportrait) Chaos - Nichtlineare Dynamik 21/102
30 Einführung - Phasenraum Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 22/102
31 Einführung - Phasenraum Äg Frage: Welche weiteren Phänomene treten neben Fixpunkten (Punkt-Attraktor) und Grenzzyklus (periodischer Attraktor) auf? Beobachtungstrick: niedrigdimensionale Projektionen! Poincaré-Schnitt durch Phasenraum Dynamik der Durchstoßpunkte P i (Dynamik der Minima/Maxima) Chaos - Nichtlineare Dynamik 23/102
32 Einführung - Phasenraum Äg Seien x, y die Koordinaten der Schnitt-Ebene, so kann man diese Dynamik beschreiben mittels: { x n+1 = f (x n, y n ) Rekurrenz /Wiederkehrrelation y n+1 = g(x n, y n ) Beispiel: Grenzzyklus: ein einziger Durchstoßpunkt allgemein: k Durchstoßpunkte: periodischer Attraktor: Zyklus der Ordnung k Chaos - Nichtlineare Dynamik 24/102
33 Einführung - Phasenraum Äg Poincaré-Schnitte: a) Chaotische Bewegung b) Annäherung an einen Fixpunkt c) Einfacher Zyklus d) Zyklus der Periode 2 Chaos - Nichtlineare Dynamik 25/102
34 Einführung - Phasenraum Äg Poincaré-Schnitte: a) Chaotische Bewegung b) Annäherung an einen Fixpunkt c) Einfacher Zyklus d) Zyklus der Periode 2 weiteres Phänomen: Quasiperiodischer Attraktor (invariante Tori) Chaos - Nichtlineare Dynamik 25/102
35 Einführung - Phasenraum Äg 2D-Torus im dreidimensionalen Phasenraum Chaos - Nichtlineare Dynamik 26/102
36 Einführung - Phasenraum Äg Die zweidimensionale Mannigfaltigkeit des Torus in den lokalen Koordinaten ϕ 1 und ϕ 1 auf ein Quadrat umkehrbar eindeutig (bijektiv) abgebildet Chaos - Nichtlineare Dynamik 27/102
37 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 28/102
38 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Verhulst Modell Wachstumsfaktor: µ Anfangspopulation: y 0 y t+1 = µy t (1 y t ) 1845 von Verhulst ( ) eingesetzt zur Modellierung des zyklischen Wachstumsverhaltens einer Population in einem geschlossenen Gebiet. Chaos - Nichtlineare Dynamik 29/102
39 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Herleitung 1. N t+1 = an t, Anzahl der Tiere im Jahr t + 1, (a Wachstumsfaktor) Chaos - Nichtlineare Dynamik 30/102
40 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Herleitung 1. N t+1 = an t, Anzahl der Tiere im Jahr t + 1, (a Wachstumsfaktor) 2. Population kann nicht unbegrenzt wachsen (begrenzte Futtervorräte) Nmax Nt Dies wird duch den Faktor N max berücksichtigt (N max unerreichbarer Maximalwert) ) N t+1 = an t (1 Nt N max Chaos - Nichtlineare Dynamik 30/102
41 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Herleitung 1. N t+1 = an t, Anzahl der Tiere im Jahr t + 1, (a Wachstumsfaktor) 2. Population kann nicht unbegrenzt wachsen (begrenzte Futtervorräte) Nmax Nt Dies wird duch den Faktor N max berücksichtigt (N max unerreichbarer Maximalwert) ) N t+1 = an t (1 Nt N max 3. Einführung dimensionsloser Größen, da für das Verhalten des Systems die absoluten Zahlen N t und N max nicht relevant sind. Wichtig ist das Verhältnis y t = Nt N max Chaos - Nichtlineare Dynamik 30/102
42 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Herleitung 1. N t+1 = an t, Anzahl der Tiere im Jahr t + 1, (a Wachstumsfaktor) 2. Population kann nicht unbegrenzt wachsen (begrenzte Futtervorräte) Nmax Nt Dies wird duch den Faktor N max berücksichtigt (N max unerreichbarer Maximalwert) ) N t+1 = an t (1 Nt N max 3. Einführung dimensionsloser Größen, da für das Verhalten des Systems die absoluten Zahlen N t und N max nicht relevant sind. Wichtig ist das Verhältnis y t = Nt N max 4. Zur Bestimmung des Anteils teile durch N max und erhalte y t+1 = µy t (1 y t ) Chaos - Nichtlineare Dynamik 30/102
43 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Iteration y t+1 = µy t (1 y t ) Verhulst y t+1 = f (y t ) Abbildung mit 0 < y < 1 y t+1 = f µ (y t ) 1. Iterierte f (f (y k )) = y k+2 = f 2 (y k ) 2. Iterierte allgemein: f p (y k ) p-te Iterierte Chaos - Nichtlineare Dynamik 31/102
44 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Iteration y t+1 = µy t (1 y t ) Verhulst y t+1 = f (y t ) Abbildung mit 0 < y < 1 y t+1 = f µ (y t ) 1. Iterierte f (f (y k )) = y k+2 = f 2 (y k ) 2. Iterierte allgemein: f p (y k ) p-te Iterierte Fragen Konvergenz? (abh. von µ) Stabilität der Bahn? (abhängig von y 0 ) Chaos - Nichtlineare Dynamik 31/102
45 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Mathematische Iteration für µ = 2.8 und y 0 = Iteration: f (y 0 ) = (1 0.02) = = y 1 2. Iteration: f (y 1 ) = Iteration: f (y 2 ) = Iteration: f (y 9 ) = Iteration: f (y 14 ) = Iteration: f (y 19 ) = Fixpunkt bei 0.64 Chaos - Nichtlineare Dynamik 32/102
46 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Zeitreihendiagramm für y t+1 = µy t (1 y t ) t max = 40; y 0 = 0.11; µ = 2.8 Chaos - Nichtlineare Dynamik 33/102
47 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Graphische Iteration für µ = 2.8 und y 0 = 0.1 blaue Iterationslinie: Trajektorie Chaos - Nichtlineare Dynamik 34/102
48 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Graphische Iteration für µ = 2.8 und y 0 = 0.24 Chaos - Nichtlineare Dynamik 35/102
49 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Graphische Iteration für µ = 2.8 und y 0 = 0.24 bzw. y 0 = 0.89 Chaos - Nichtlineare Dynamik 36/102
50 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Ein stabiler Fixpunkt y fokussiert die Bahnen (hier: y ) (Fixpunkt-Attraktor). Für µ = 2.8 strebt die Folge immer auf y zu (unabhängig von y 0 ]0; 1[ ) (Bassin) Auch y 0 = 0 ist Fixpunkt, jedoch nur für y 0 = 0 (Repulsor) Chaos - Nichtlineare Dynamik 37/102
51 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Ein stabiler Fixpunkt y fokussiert die Bahnen (hier: y ) (Fixpunkt-Attraktor). Für µ = 2.8 strebt die Folge immer auf y zu (unabhängig von y 0 ]0; 1[ ) (Bassin) Auch y 0 = 0 ist Fixpunkt, jedoch nur für y 0 = 0 (Repulsor) Kriterium für stabilen Fixpunkt: Ein Fixpunkt y ist (lokal) stabil, wenn d dy f (y ) < 1 Chaos - Nichtlineare Dynamik 37/102
52 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Attraktor Ein Punkt, (der auch eine Menge von Punkten sein kann,) der sämtliche Trajektorien anzieht. Chaos - Nichtlineare Dynamik 38/102
53 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Attraktor Ein Punkt, (der auch eine Menge von Punkten sein kann,) der sämtliche Trajektorien anzieht. Bassin Teil des Phasenraumes bzw. Bereich von Startwerten y 0, aus dem alle Trajektoren in einen Attraktor münden. Chaos - Nichtlineare Dynamik 38/102
54 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Attraktor Ein Punkt, (der auch eine Menge von Punkten sein kann,) der sämtliche Trajektorien anzieht. Bassin Teil des Phasenraumes bzw. Bereich von Startwerten y 0, aus dem alle Trajektoren in einen Attraktor münden. Repulsor Ein Fixpunkt, der nur von wenigen Startwerten aus erreicht wird und von dem sich ansonsten alle Trajektorien entfernen. Chaos - Nichtlineare Dynamik 38/102
55 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Attraktor Ein Punkt, (der auch eine Menge von Punkten sein kann,) der sämtliche Trajektorien anzieht. Bassin Teil des Phasenraumes bzw. Bereich von Startwerten y 0, aus dem alle Trajektoren in einen Attraktor münden. Repulsor Ein Fixpunkt, der nur von wenigen Startwerten aus erreicht wird und von dem sich ansonsten alle Trajektorien entfernen. Repellor Das Gegenteil eines Attraktors. Chaos - Nichtlineare Dynamik 38/102
56 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Bisher: Betrachtung der Funktion y t+1 = 2.8y t (1 y t ) Frage: Wie sieht der Attraktor für anderes bzw. größeres µ aus? Wie sieht der Attraktor aus für d dy f (y ) 1? Chaos - Nichtlineare Dynamik 39/102
57 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Bisher: Betrachtung der Funktion y t+1 = 2.8y t (1 y t ) Frage: Wie sieht der Attraktor für anderes bzw. größeres µ aus? Wie sieht der Attraktor aus für d dy f (y ) 1? Es folgt: Betrachtung der Funktion y t+1 = µy t (1 y t ) mit µ = 3.1 Chaos - Nichtlineare Dynamik 39/102
58 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Zeitreihendiagramm für y t+1 = µy t (1 y t ) t max = 40; y 0 = 0.1; µ = 3.1 Chaos - Nichtlineare Dynamik 40/102
59 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Graphische Iteration für µ = 3.1 und y 0 = 0.16 Chaos - Nichtlineare Dynamik 41/102
60 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Trajektorie geht in Zyklus der Periode 2 über (Spaltung des Fixpunktes) Fixpunkte liegen bei y und y Grenzzyklus Chaos - Nichtlineare Dynamik 42/102
61 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Trajektorie geht in Zyklus der Periode 2 über (Spaltung des Fixpunktes) Fixpunkte liegen bei y und y Grenzzyklus Bifurkation Die Spaltung des Fixpunktes bzw. der Fixpunkte. Chaos - Nichtlineare Dynamik 42/102
62 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Frage: Was passiert bei einer weitereren Erhöhung von µ? Chaos - Nichtlineare Dynamik 43/102
63 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Frage: Was passiert bei einer weitereren Erhöhung von µ? Es folgt: Betrachtung der Funktion y t+1 = µy t (1 y t ) mit µ = 3.48 Chaos - Nichtlineare Dynamik 43/102
64 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Zeitreihendiagramm für y t+1 = µy t (1 y t ) t max = 40; y 0 = 0.1; mit µ = 3.48 Chaos - Nichtlineare Dynamik 44/102
65 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Graphische Iteration bis y 100 für µ = 3.48 und y 0 = 0.15 Chaos - Nichtlineare Dynamik 45/102
66 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Erneut Bifurkation der Fixpunkte x1 und x 2 System konvergiert auf einem Zyklus der Periode 4. Chaos - Nichtlineare Dynamik 46/102
67 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Erneut Bifurkation der Fixpunkte x1 und x 2 System konvergiert auf einem Zyklus der Periode 4. Für µ = Bifurkation dieser 4 Fixpunkte... 8 Fixpunkte Periodenverdopplung Chaos - Nichtlineare Dynamik 46/102
68 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Zusammenfassung µ < 1 ein stabiler Fixpunkt bei y = 0; alle Bahnen enden dort. 1 < µ < 3 zwei Fixpunkte: 1. stabiler bei y = 0 2. instabiler µ = 3+ zweiter Fixpunkt wird instabil (Bifurkation) f 2 (y k ) bekommt zwei neue stabile Fixpunkte (Grenzzyklus mit Periode 2 wird stabil) µ = Kaskade von Bifurkationen Chaos - Nichtlineare Dynamik 47/102
69 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Erhöhung von µ führt zur Periodenverdopplung Grenzzyklus der Periode 2 geht über in Grenzzyklus der Periode 4 2 1, 2 2, 2 3,...,2 n Grenzfall n : Periode 2 bei µ = (weiterführende Literatur: [Schuster, 1994]) Chaos - Nichtlineare Dynamik 48/102
70 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Erhöhung von µ führt zur Periodenverdopplung Grenzzyklus der Periode 2 geht über in Grenzzyklus der Periode 4 2 1, 2 2, 2 3,...,2 n Grenzfall n : Periode 2 bei µ = (weiterführende Literatur: [Schuster, 1994]) µ > µ : Chaos deterministisches Chaos irreguläres (a periodisches) Verhalten (scheinbar stochastisch) Chaos - Nichtlineare Dynamik 48/102
71 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Zeitreihendiagramm für y t+1 = µy t (1 y t ) t max = 80; y 0 = 0.12; µ = 3.9 Chaos - Nichtlineare Dynamik 49/102
72 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Graphische Iteration bis y 100 für µ < µ = 3.9 Chaos - Nichtlineare Dynamik 50/102
73 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg Trajektorie verläuft scheinbar zufällig in begrenztem Gebiet mit steigendem µ wird das Gebiet immer größer für µ=4 werden alle Werte zwischen 0 und 1 erfasst Bezeichnung des Gebiets: seltsamer Attraktor Chaos - Nichtlineare Dynamik 51/102
74 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg seltsamer Attraktor beschränkt: alle Trajektorien verlaufen in einem bestimmten Gebiet nicht-periodisch: das Gebiet stellt keinen Zyklus oder definierbaren Bereich dar (seltsam) Chaos - Nichtlineare Dynamik 52/102
75 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg seltsamer Attraktor beschränkt: alle Trajektorien verlaufen in einem bestimmten Gebiet nicht-periodisch: das Gebiet stellt keinen Zyklus oder definierbaren Bereich dar (seltsam) deterministisches Chaos Funktion ist deterministisch jeder Wert der Gleichung läßt sich berechnen Chaos - Nichtlineare Dynamik 52/102
76 Bifurkation und Feigenbaumdiagramme - Die logistische Wachstumsfunktion Äg siehe Tageslicht-Folien 1 und 2 Chaos - Nichtlineare Dynamik 53/102
77 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 54/102
78 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Feigenbaumdiagramm benannt nach dem amerikanischen Physiker Mitchell J. Feigenbaum (*1945) Entdeckung Mitte der siebziger Jahre Wird verwendet zur Darstellung des globalen Verhaltens eines Systems Dient zur Veranschaulichung des Übergangs Ordnung Chaos Abszisse: µ-werte Ordinate: die zugehörigen y-werte des (Fixpunkt-, zyklischen-, oder seltsamen-) Attraktors Chaos - Nichtlineare Dynamik 55/102
79 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Feigenbaumdiagramm für y t+1 = µy t (1 y t ) Chaos - Nichtlineare Dynamik 56/102
80 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Feigenbaumdiagramm für y t+1 = µy t (1 y t ) Chaos - Nichtlineare Dynamik 57/102
81 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Feigenbaumdiagramm für y t+1 = µy t (1 y t ) Chaos - Nichtlineare Dynamik 58/102
82 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Universalität des Feigenbaums : pitchfork bifurcation Für n >> 1 gilt: 1. µ n = µ const δ n 2. d n d n+1 = α Chaos - Nichtlineare Dynamik 59/102
83 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Universalität des Feigenbaums : pitchfork bifurcation Für n >> 1 gilt: 1. µ n = µ const δ n 2. d n d n+1 = α Die Feigenbaumkonstanten δ und α haben die Werte: δ = und α = Chaos - Nichtlineare Dynamik 59/102
84 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Die Feigenbaumkonstanten δ und α δ = und α = sind universell und rational treten in einer Vielzahl (deterministisch-)chaotischer Systeme auf finden sich in physikalischen Experimenten (elektronische Schaltungen, Turbulenz,...) von ähnlich großer Bedeutung (für die Chaostheorie) wie die der Zahlen π und die eulersche Zahl e für die Mathematik Chaos - Nichtlineare Dynamik 60/102
85 Bifurkation und Feigenbaumdiagramme - Das Feigenbaumdiagramm Äg Übergang zum Chaos: universell z.b. über Periodenverdopplung für alle quadratischen Abbildungen für alle Modelle mit folgenden Eigenschaften: Abbildung des Einheitsintervalls auf sich selbst x [0, 1] unimodal (ein Maximum bei x = 0.5) monoton für 0 x 1 2 und 1 2 x 1 ( f f ) 2 < 0 für 0 x 1 Sf = d 2 dx [f (x)] 1 2 = f 2 f 3 2 Schwarz sche Ableitung (dann auch alle Sf n < 0) Chaos - Nichtlineare Dynamik 61/102
86 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 62/102
87 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg Ljapunov-Exponent λ benannt nach dem russischen Mathematiker Ljapunov ( ) Größe zur quantitativen Charaktierisierung chaotischer Bewegungen Maß für den mittleren Verlust an Information (über die Position eines Punktes im Intervall [0, 1]) nach einer Iteration Maß für Vorhersagbarkeit Chaos - Nichtlineare Dynamik 63/102
88 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg Ljapunov-Exponent λ benannt nach dem russischen Mathematiker Ljapunov ( ) Größe zur quantitativen Charaktierisierung chaotischer Bewegungen Maß für den mittleren Verlust an Information (über die Position eines Punktes im Intervall [0, 1]) nach einer Iteration Maß für Vorhersagbarkeit x 0 ε x 0 + ε N Iterationen = f N (x 0 ) εenλ(x 0 ) f N (x 0 + ε) = εe Nλ(x 0) = f N (x 0 + ε) f N (x 0 ) Chaos - Nichtlineare Dynamik 63/102
89 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg εe Nλ(x0) = f N (x 0 + ε) f N (x 0 ) Für ε 0 und N : λ(x 0 ) = lim lim 1 N ε 0N log f N (x 0 + ε) f N (x 0 ) ε (12) 1 = lim N N log d f N (x 0 ) dx 0 (13) 1 N 1 = lim N N log f (x i ) (14) = lim N 1 N N 1 i=0 i=0 log f (x i ) (15) Chaos - Nichtlineare Dynamik 64/102
90 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg Bleibt noch zu zeigen: 1 lim N N log d dx 0 f N (x 0 ) = lim N log N 1 f (x i ) 1 N i=0 Chaos - Nichtlineare Dynamik 65/102
91 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg Bleibt noch zu zeigen: 1 lim N N log d dx 0 f N (x 0 ) = lim N log N 1 f (x i ) 1 N i=0 Beweis mit Hilfe der Kettenregel: d dx f 2 (x) = d x0 dx f [f (x)] (16) x0 = f [f (x 0 )] f (x 0 ) (17) = f (x 1 )f (x 0 ) mit x 1 f (x 0 ) (18) = d dx 0 f N (x 0 ) = N 1 f (x i ) i=0 Chaos - Nichtlineare Dynamik 65/102
92 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg Zusammenfassung λ < 0: Kontraktion asymptotisches Aussterben der Störung λ > 0: Divergenz Störung wird angefacht λ 1 λ 2 λ 3 Phänomen Fokus 0 Grenzzyklus 0 0 Torus + 0 Seltsamer Attraktor (eigentl. kein Chaos, sondern komplexe Ordnung!) Chaos - Nichtlineare Dynamik 66/102
93 Seltsame Attraktoren und ihre Klassifikation - Der Ljapunov-Exponent Äg siehe Tageslicht-Folie 3 Chaos - Nichtlineare Dynamik 67/102
94 Seltsame Attraktoren und ihre Klassifikation - Das Klimamodell von Edward N. Lorenz Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 68/102
95 Seltsame Attraktoren und ihre Klassifikation - Das Klimamodell von Edward N. Lorenz Äg Klimamodell von Lorenz Der Lorenzattraktor ist durch ein System 3 gekoppelter nichtlinearer Differentialgleichungen gegeben: ẋ = σx + σy ẏ = rx y xz σ, r, b sind Modellparameter ż = xy bz Chaos - Nichtlineare Dynamik 69/102
96 Seltsame Attraktoren und ihre Klassifikation - Das Klimamodell von Edward N. Lorenz Äg Klimamodell von Lorenz Der Lorenzattraktor ist durch ein System 3 gekoppelter nichtlinearer Differentialgleichungen gegeben: ẋ = σx + σy ẏ = rx y xz σ, r, b sind Modellparameter ż = xy bz σ σ 0 Die Jacobi-Matrix lautet: r 1 x y x b Für die Ljapunov-Exponenten erhalten wir: λ 1 = 0.9, λ 2 = 0.0 und λ 3 = 12.8 also handelt es sich um einen seltsamen Attraktor Chaos - Nichtlineare Dynamik 69/102
97 Seltsame Attraktoren und ihre Klassifikation - Das Klimamodell von Edward N. Lorenz Äg Der Lorenz-Attraktor Chaos - Nichtlineare Dynamik 70/102
98 Seltsame Attraktoren und ihre Klassifikation - Das Klimamodell von Edward N. Lorenz Äg Der Lorenz-Attraktor Lorenz-Attraktor Chaos - Nichtlineare Dynamik 71/102
99 Seltsame Attraktoren und ihre Klassifikation - Das Klimamodell von Edward N. Lorenz Äg Diskrete Abbildung der relativen maximalen M-Werte (Lorenz, 1963) Chaos - Nichtlineare Dynamik 72/102
100 Fraktale und fraktale Dimension - Fraktale Dimension Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 73/102
101 Fraktale und fraktale Dimension - Fraktale Dimension Äg Dimension dient zur Charakterisierung geometrischer Objekte in der euklidischen Geometrie: Dimension ganzzahlig Objekt Dimension Punkt 0 Linie 1 Fläche 2 Kubus 3 Chaos - Nichtlineare Dynamik 74/102
102 Fraktale und fraktale Dimension - Fraktale Dimension Äg Wie lang ist die Küstenlinie von Großbritannien? die Längenmessung der Küste hängt vom verwendeten Maßstab ab 1. grobe Karte: erste Annährung 2. genaueres Kartenmaterial (mehr Buchten, Landzungen): genauere Annäherung 3. Umwanderung der Insel mit Meßlatte Chaos - Nichtlineare Dynamik 75/102
103 Fraktale und fraktale Dimension - Fraktale Dimension Äg Wie lang ist die Küstenlinie von Großbritannien? die Längenmessung der Küste hängt vom verwendeten Maßstab ab 1. grobe Karte: erste Annährung 2. genaueres Kartenmaterial (mehr Buchten, Landzungen): genauere Annäherung 3. Umwanderung der Insel mit Meßlatte die Küste umschließt eine endliche Fläche, aber mit wachsender Meßgenauigkeit wächst die Umfangslinie ins Unendliche Chaos - Nichtlineare Dynamik 75/102
104 Fraktale und fraktale Dimension - Fraktale Dimension Äg Wie lang ist die Küstenlinie von Großbritannien? die Längenmessung der Küste hängt vom verwendeten Maßstab ab 1. grobe Karte: erste Annährung 2. genaueres Kartenmaterial (mehr Buchten, Landzungen): genauere Annäherung 3. Umwanderung der Insel mit Meßlatte die Küste umschließt eine endliche Fläche, aber mit wachsender Meßgenauigkeit wächst die Umfangslinie ins Unendliche Lösung: Küste ist ein Mittelding zwischen Linie und Fläche von nichtganzzahliger Dimension (Mandelbrot) Chaos - Nichtlineare Dynamik 75/102
105 Fraktale und fraktale Dimension - Fraktale Dimension Äg Wieviele Käfer passen auf ein Blatt? Erwartete Anzahl von Käfern bei einer Blattoberfläche mit der Dimension D = 2 Körperlänge L l l 2 l 3 l x Anzahl N c c 2 2 = c 4 c 3 2 = c 9 c x 2 Chaos - Nichtlineare Dynamik 76/102
106 Fraktale und fraktale Dimension - Fraktale Dimension Äg erwartet: N L 2, gemessen N L 2.78 z.b. für x = 10: erwartet: 100 = x 2, gemessen: 600 = x 2.78 Chaos - Nichtlineare Dynamik 77/102
107 Fraktale und fraktale Dimension - Fraktale Dimension Äg Hausdorff-Besicovitch-Dimension Gegeben: Objekt im d-dimensionalen Raum Vorschrift: Überdecke Objekt mit d-dimensionale Kugeln mit Durchmesser λ Ermittle die minimale Anzahl N(λ) von Kugeln, die zur Überdeckung notwendig sind N(λ) log D = lim λ 0 λ 0 λ D [ N(λ) N(λ ) log [ λ λ ] ] Chaos - Nichtlineare Dynamik 78/102
108 Fraktale und fraktale Dimension - Fraktale Dimension Äg Beispiel: Hausdorff-Dimension einer Linie λ = 1 N = 1 λ = 1 3 N = 3 λ = 1 9 N = 9 λ: Durchmesser; N: Anzahl Chaos - Nichtlineare Dynamik 79/102
109 Fraktale und fraktale Dimension - Fraktale Dimension Äg Beispiel: Hausdorff-Dimension einer Linie λ = 1 N = 1 λ = 1 3 N = 3 λ = 1 9 N = 9 λ: Durchmesser; N: Anzahl D = lim [ ] log N(λ) N(λ ) λ 0 log[ λ λ ] hier: D = log( 1 ( 3) ) = 1 log Chaos - Nichtlineare Dynamik 79/102
110 Fraktale und fraktale Dimension - Fraktale Dimension Äg Beispiel: Dimension der Cantor-Menge λ = 1 N = 1 λ = 1 3 N = 2 λ = 1 9 N = 4 Chaos - Nichtlineare Dynamik 80/102
111 Fraktale und fraktale Dimension - Fraktale Dimension Äg Beispiel: Dimension der Cantor-Menge D = log( 1 ( 2) log λ = 1 N = 1 λ = 1 3 N = 2 λ = 1 9 N = 4 ) = log 2 log 3 = ) [ = λ L = λ ( [ ( )] = λ = 0! ν=0 ] ( 2 ) ν 3 Chaos - Nichtlineare Dynamik 80/102
112 Fraktale und fraktale Dimension - Fraktale Dimension Äg Fraktal Benoit Mandelbrot (*1924) aus dem lateinischen, fractum: Bruchstück ist irregulär fraktale Dimension ist größer als die topologische Dimension weist Selbstähnlichkeit auf besitzt keine Glatte, sondern eine zerklüftete Form Chaos - Nichtlineare Dynamik 81/102
113 Fraktale und fraktale Dimension - Lineare Fraktale Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 82/102
114 Fraktale und fraktale Dimension - Lineare Fraktale Äg Koch-Kurve (um 1904) Gegeben: Linienstück der Länge 1 Iteration: unterteile jedes Linienstück in drei gleichlange Stücke errichte gleichseitiges Dreieck auf dem mittleren Stück entferne die Basis dieses Dreickecks Chaos - Nichtlineare Dynamik 83/102
115 Fraktale und fraktale Dimension - Lineare Fraktale Äg Koch-Kurve (um 1904) Gegeben: Linienstück der Länge 1 Iteration: unterteile jedes Linienstück in drei gleichlange Stücke errichte gleichseitiges Dreieck auf dem mittleren Stück entferne die Basis dieses Dreickecks Länge: unendlich; Fläche: begrenzt Dimension D = Kurve ist weder Linie noch Fläche Chaos - Nichtlineare Dynamik 83/102
116 Fraktale und fraktale Dimension - Lineare Fraktale Äg Konstruktion der Kochschen Schneeflockenkurve Kochsche Schneeflockenkurve Chaos - Nichtlineare Dynamik 84/102
117 Fraktale und fraktale Dimension - Lineare Fraktale Äg Das Sierpinski-Dreieick Konstruktionsvorschrift: Gegeben: ein gefülltes Dreieck Iteration: Verbinde die Mittelpunkte seiner drei Seiten Erhalte so 4 kongruente Dreiecke entferne das im Zentrum liegende Dreieck Chaos - Nichtlineare Dynamik 85/102
118 Fraktale und fraktale Dimension - Lineare Fraktale Äg Konstruktion des Sierpinski-Dreiecks Sierpinski-Dreieck Chaos - Nichtlineare Dynamik 86/102
119 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Einführung Strukturelle Stabilität Grenzzyklen Phasenraum Bifurkation und Feigenbaumdiagramme Die logistische Wachstumsfunktion Das Feigenbaumdiagramm Seltsame Attraktoren und ihre Klassifikation Der Ljapunov-Exponent Das Klimamodell von Edward N. Lorenz Fraktale und fraktale Dimension Fraktale Dimension Lineare Fraktale Nichtlineare Fraktale Chaos - Nichtlineare Dynamik 87/102
120 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge z k+1 = z 2 k c (19) Sei c gegeben, z.b. c = i = f c (z k ) mit z, c C (20)? Wertebereich für z 0 Attraktor (Bassin) z.b. z = 11erZyklus, z =? Grenze zwischen zwei Bassins { } J c = Grenze von z lim f k n c (z) Attraktor Julia-Menge: zusammenhängend nicht zusammenhängend Chaos - Nichtlineare Dynamik 88/102
121 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = i Jordan-Kurve Chaos - Nichtlineare Dynamik 89/102
122 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = i zusammenhängend, inneres Bassin: Zykel der Periode 11 Chaos - Nichtlineare Dynamik 90/102
123 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = i Dendrit Chaos - Nichtlineare Dynamik 91/102
124 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = i Cantor-Menge Chaos - Nichtlineare Dynamik 92/102
125 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = i zusammenhängend, kurz vor dem Zerfall in eine Cantor-Menge Chaos - Nichtlineare Dynamik 93/102
126 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = i Cantor-Menge, entstanden nach geringer Variation des Parameters c Chaos - Nichtlineare Dynamik 94/102
127 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Julia-Menge J c der Abbildung f c (z) = z 2 + c für c = 1.25 Chaos - Nichtlineare Dynamik 95/102
128 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Mandelbrot-Menge Sei z 0 gegeben, z.b. z 0 = 0 z k+1 = z 2 k c (21) = f c (z k ) mit z, c C (22)? Bereich der Parameterwerte c, für die J c zusammenhängend ist { } M = c lim f k n c (0) Mandelbrot-Menge: zusammenhängend, fraktale Struktur Chaos - Nichtlineare Dynamik 96/102
129 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Mandelbrot-Menge (Apfelmännchen) Chaos - Nichtlineare Dynamik 97/102
130 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Mandelbrot-Menge (Ausschnittsvergrößerung) Chaos - Nichtlineare Dynamik 98/102
131 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Zusammenhang zwischen Mandelbrot-Menge und der Periodenverdopplungskaskade der logistischen Abbildung Chaos - Nichtlineare Dynamik 99/102
132 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Zusammenhang zwischen Mandelbrot-Menge und der Periodenverdopplungskaskade der logistischen Abbildung Chaos - Nichtlineare Dynamik 100/102
133 Fraktale und fraktale Dimension - Nichtlineare Fraktale Äg Chaos - Nichtlineare Dynamik 101/102
134 Literatur Äg Argyris, J., Faust, G., and Haase, M. (1994). Die Erforschung des Chaos: eine Einführung für Physiker, Ingenieure und Naturwissenschaftler. Vieweg, Braunschweig/Wiesbaden. ISBN Peitgen, H.-O., Jürgens, H., and Saupe, D. (1992). Bausteine des Chaos: Fraktale. Springer-Verlag, Berlin. ISBN Schuster, H. G. (1994). Deterministisches Chaos. Eine Einführung. VDH, Weinheim. ISBN Chaos - Nichtlineare Dynamik 102/102
Deterministisches Chaos
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
8. Deterministisches Chaos
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Nichtlineare Dynamik Einführung
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
1 Nicht-lineare dynamische Systeme
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Fraktale und Beispiele aus der Physik
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Jan Henrik Sylvester. 10. Februar 2003
Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Seltsame Attraktoren
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
FC3 - Duffing Oszillator
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Lyapunov-Exponenten. Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems:
Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Nichtlinearität in der klassischen Physik
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Vortragsthemen. Reelle Dynamik
Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
Abbildung 1: Feigenbaum-Diagramm
Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
Deterministisches Chaos
Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Chaos Seminar Wetter und Klima. Dominik Fröschl
Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Spezielle Kinetik MC 1.3. Prof. Dr. B. Dietzek. Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie. Wintersemester 2016/2017
Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
Fraktale und Julia-Mengen
Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Der Duffing-Oszillator
11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
Stabile periodische Bewegungen (Grenzzyklen)
Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Die Chaostheorie und Fraktale in der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Markov-Paritionen und geometrische Modelle von Attraktoren
Markov-Paritionen und geometrische Modelle von Attraktoren Jan Christoph Kinne 15. Februar 2003 1 Was sind Markov-Partitionen? Hat man ein diskretes dynamisches System f : M M gegeben, so will man M in
Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos. Wintersemester 2018/ M. Zaks
Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos Wintersemester 2018/19 22.01.2019 M. Zaks hintergrund Kontext: Wettervorhersage. Entstehung von Luftbewegungen infolge der thermischen
Newton-Verfahren und komplexe Dynamik. Jonathan Clausing
Newton-Verfahren und komplexe Dynamik Jonathan Clausing Newton-Verfahren und komplexe Dynamik Von nutzloser und nützlicher Mathematik Iteration komplexer Polynome Die gefüllte Julia-Menge Die Mandelbrotmenge
Ökologische Gleichungen für zwei Spezies
Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Phasenraum. Zeitreihe. Phasenraum. Ort (x) Zeit. Geschwindigkeit (v)
Phasenraum Ort (x) Zeitreihe Zeit Geschwindigkeit (v) v Phasenraum x Phasenraum - geometrische Darstellung der Dynamik im kartesischen Raum - Repräsentation von parametrischen Systemzuständen zu festen
Seminar Populations- und Epidemiemodelle. Die Lorenz-Gleichungen.
Seminar Populations- und Epidemiemodelle. Die Lorenz-Gleichungen. Christian Rose 30. Juni 2013 1 1 Motivation In den sechziger Jahren des 20. Jahrhunderts fragte sich ein Meteorologe namens Lorenz, wie
Dynamik hüpfender Bälle
1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
Chaotische Systeme. ViLab. Marian Panten
Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Feigenbaum, Chaos und die RG
Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
HARMONIK ZWISCHEN ORDNUNG UND CHAOS
HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik?
Juliamengen und Mandelbrotmenge
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Parameterdef. an nichtl. Zweipolkennl.
Parameterdef. an nichtl. Zweipolkennl. nichtlin. Zweipole Typen von Approximationsfunktionen KENNLINIENAPPROXIMATION Rektifikationsmethode y 5α 4α FUNKTION β < β > y = αx β β = 3α 2α α β < β =.5.5 2 2.5
Serie 13: Online Test
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
x= f(x) p= U (x). (b) Zeigen Sie, dass auf jeder auf einem Intervall existierenden Lösung t x(t) die Energie E(t) := 1 2 p(t)2 + U(x(t)) x 1
Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
REFERAT FÜR INNOVATIVE ARCHIKETUREN
REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
Flüsse, Fixpunkte, Stabilität
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Experimente, Ideen und Entwicklung der Chaostheorie
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
2.3 Chaos und Lyapunov-Exponent. d dx f(x) λ = lim n n . (1) Programm. k=0. PROGRAM lyapunov ...
2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
Abbildung 5.1: stabile und instabile Ruhelagen
Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK. K. Taubert Universität Hamburg SS08
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
Nachklausur zur Analysis 2, SoSe 2017
BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
Diskrete Populationsmodelle für Einzelspezies
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Differenzen/Differentialgleichungen Gegenüberstellung und Analogien sneaky, Mai 2007
Differenzengleichung Differentialgleichung 1. Ordnung (konstante Koeff.) Gestalt x n+1 =ax n +b allgemeine Lösung x n = a n x 0 +b((a n -1)/(a-1)) für a 1 oder x n = x 0 +b n für a=1 partikuläre Lösung
Theoretische Physik 2 (Theoretische Mechanik)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Herbert Zeitler Wolfgang Neidhardt. Fraktale und Chaos. Eine Einführung. Wissenschaftliche Buchgesellschaft Darmstadt
Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
BERÜHMTE KURVEN Logarithmische Spirale. Die Logarithmische Spirale wird durch eine Gleichung in Polarkoordinaten angegeben: r(φ)=a*e k φ
BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
Nichtlineare Prozesse in der Elektrochemie II
Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Poincaré-Schnitte. Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert
Poincaré-Schnitte Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert Themen 1. Was sind Poincaré-Schnitte?. Anwendung: Poincaré-Schnitte Mathematica-Beispiel: Attraktor
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Systemanalyse und Modellbildung
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Nichtlineare Gleichungssysteme
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
PROBEPRÜFUNG MATHEMATIK I UND II
PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
Dynamische Systeme eine Einführung
Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Wie lang ist die Küste Großbritanniens?
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Seminar Fraktale. Kapitel 13 Dynamical Systems. Von Dirk Simon
Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
MATHE-BRIEF. Juni 2017 Nr. 80. Die Mandelbrotmenge
MATHE-BRIEF Juni 2017 Nr. 80 Herausgegeben von der Österreichischen Mathematischen Gesellschaft http: // www.oemg.ac.at / Mathe Brief mathe brief@oemg.ac.at Die Mandelbrotmenge Komplexe Zahlen werden im
Merkwürdige und chaotische Attraktoren und deren Stabilität
Merkwürdige und chaotische Attraktoren und deren Stabilität Ann-Kristin Baum Seminar Dynamische Systeme SS 06 1 Inhaltsverzeichnis 2 1 Einführung Reale Vorgänge in den Natur- oder Gesellschaftswissenschaften,
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
AUFGABEN ZUR FUNKTIONENTHEORIE. von. Prof. Dr. H.-W. Burmann
AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
Stabilitätsfragen bei autonomen Systemen
1 Stabilitätsfragen bei autonomen Systemen M. Schuster 09.08.2006 Inhaltsverzeichnis 1 Allgemeines über autonome Systeme 1 1.1 Oft übliche Bezeichnungen mit Übersetzung.......................... 1 2 Stabilität
Lösungen zu Mathematik I/II
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
GRUNDLEGENDE MODELLE. Caroline Herbek
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
tun, sondern nur mit der Reaktion auf verschiedene Anfangswerte.
2.3 Stabilität Eine wichtige Rolle spielt das Stabilitätsverhalten dynamischer Systeme. Wie üblich sei Φ die Fundamentalmatrix des linearen Systems ẋ = A(t)x + u. Im weiteren sei t fixiert, später wird
Einführung. Ablesen von einander zugeordneten Werten
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
1.3 Zweidimensionale Systeme
132 KAPITEL IV. QUALITATIVE THEORIE UND DYNAMISCHE SYSTEME Im Fall a 3 > 0 ist das Gleichgewicht asymptotisch stabil. Für a 2 3 > 4a 1a 2 haben wir < < 0 und es liegt ein stabiler Knoten vor (siehe den
Das Hénon-Heiles Potential Beispiel für Weiches Chaos und die Anwendung des KAM-Theorems
Das Hénon-Heiles Potential Beispiel für Weiches Chaos und die Anwendung des KAM-Theorems Jonathan Wider 16.November 2018 Zusammenfassung Dieses Handout soll die wesentlichen Inhalte des am 16.11.2018 gehaltenen
Hörsaalübung 6 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
Fachbereich Mathematik der Universität Hamburg WiSe 28/29 Dr. Hanna Peywand Kiani Hörsaalübung 6 Differentialgleichungen I für Studierende der Ingenieurwissenschaften Autonome Systeme, Stabilität Die ins
Chaos & Quantenchaos SS 2009
Chaos & Quantenchaos SS 2009 H. J. Korsch FB Physik Technische Universität Kaiserslautern Einleitung Mathematisches Vorspiel : Hamiltonsche Systeme alternativ Dissipative Systeme Wege ins Chaos Quantenchaos
Fibonacci Zahlen: 3. Hamiltonsche Systeme. 3.1 Hamilton Dynamik. Teilverhältnis beim `goldenen Schnitt : definiert als. mit
Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Kapitel 5.6: Nichtlineare Rekursionen. Algorithmen und Datenstrukturen WS 2012/13. Prof. Dr. Sándor Fekete
Kapitel 5.6: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 5.4.3 Master-Theorem: Lineare Rekursionen 5.6 Nichtlineare Rekursionen 5.6.1 Logistische Rekursion
Zu einigen Grundlagen der Stabilitätstheorie dynamischer Systeme
Seminar Zu einigen Grundlagen der Stabilitätstheorie dynamischer Systeme 15.4.201 2 Inhaltsverzeichnis 1 Existenz und Eindeutigkeit 7 1.1 Lineare Systeme.................................... 7 1.2 Der Begriff
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale?
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
2. Fraktale Geometrie
2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
Fixpunkte und Stabilitätsanalyse
Fixpunkte und Stabilitätsanalyse 1 Themenüberblick Motivation 1D-Probleme Bifurkationen 2D-Probleme Fixpunkttypen Lotka-Volterra-Modelle 2 Motivation Bisher: Lineare Dynamik Jetzt: Nichtlineare Systeme
Die komplexe Halbebene faktorisiert nach einer Fuchsschen Gruppe
Die komplexe Halbebene faktorisiert nach einer Fuchsschen Gruppe Matthias Nagel Riemannsche Flächen Stets sei X eine 2-dimensionale Mannigfaltigkeit (Fläche). Definition. ) Eine komplexe Karte auf X ist
Newton-Verfahren und Komplexe Dynamik I
Johannes Gutenberg-Universität Mainz Institut für Mathematik, FB08 Hauptseminar: Eine Einladung in die Mathematik Newton-Verfahren und Komplexe Dynamik I Paul Klimek betreut von Prof. Dr. Mária Lukácová-Medvidová
Übungen zur Vorlesung MATHEMATIK II
Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Analysis und Lineare Algebra mit MuPAD
Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Stochastik I. Vorlesungsmitschrift
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
3 Gewöhnliche Differentialgleichungen 23.4.
3 Gewöhnliche Differentialgleichungen 23.4. 3.1 Differentialgleichungen erster Ordnung 3.1.1 Fundamentalsätze Definition 3.1. Es sei Ω R d eine offene Menge und V : Ω R d eine Vektorfunktion. Eine Kurve
Hauptseminar Fraktale: Andere Begriffe der Dimension
Hauptseminar Fraktale: Andere Begriffe der Dimension 21. November 2006 Überblick 1 Einleitung 2 Fraktale Dimension Begriffsklärung Gewünschte Eigenschaften Beispiel: Teilerdimension 3 Boxdimension Definition
fraktal kommt von f : C C : x x 3.
Kapitel 4 Fraktale und Dimension 4.1 Selbstähnlichkeit Was sind Fraktale? Das Wort fraktal kommt von zerbrochen und steht für die nicht-ganzzahlige Dimension. Wir betrachten also Objekte deren Dimension
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Chaos im getriebenen nicht-linearen Pendel
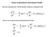Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger. Lösung - Serie 26. ẋ 1 = x 1 + 2x ẋ 2 = 2x 1 + x 2
D-MAVT/D-MATL Analysis II FS 07 Dr. Andreas Steiger Lösung - Serie 6. Es ist das folgende autonome System ẋ = x + x + 3 ẋ = x + x von linearen Differenzialgleichungen. Ordung gegeben. Welche der folgenden
2.2. Lineare Systeme. a) A ist diagonalisierbar, oder b) A ist nicht diagonalisierbar.
.. Lineare Systeme deta < 0 = 0 > 0 SpA Abbildung.9.: Gebiete mit unterschiedlicher Dynamik eines zweidimensionalen linearen dynamischen Systems entsprechend dem Vorzeichen der Diskriminante. a) A ist
Floquet-Theorie IV. 1 Hills Gleichung
Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 08.11.2011 Tobias Roidl Dieser Vortrag befasst sich mit der Hills Gleichung und gibt eine Einführung in die Periodischen Orbits von linearen Systemen.
1,2,3,4,5,... Dabei ist die Reihenfolge wichtig, jede Zahl hat also ihre feste Position. Die Folge 2,1,4,3,... ist eine andere als 1,2,3,4,...
9 Folgen Eine (unendliche) Folge im herkömmlichen Sinn entsteht durch Hintereinanderschreiben von Zahlen, z.b.: 1,2,3,4,5,... Dabei ist die Reihenfolge wichtig, jede Zahl hat also ihre feste Position.