Röntgendiffraktometrie
|
|
|
- Britta Stefanie Dressler
- vor 8 Jahren
- Abrufe
Transkript
1 Röntgendiffraktometrie Name: Matthias Jasch Matrikelnummer: 077 Mitarbeiter: Mirjam und Rahel Eisele Gruppennummer: 7 Versuchsdatum: 9. Mai 009 Betreuer: Verena Schendel 1 Einleitung Bei der Röntgendiffraktometrie wird eine Kristallprobe mit Röntgenstrahlen beschossen und aus dem Interferrenzbild der reflektierten Strahlung die Orientierung der Gitterebenen bestimmt. Aufgabenstellung Es sollte ein Diffraktogramm von je einem Siliziumeinkristall und einem Lithiumfluoridkristall erstellt und daraus die Orientierung der Netzebenen bestimmt werden. Als Röntgenstrahlenquelle diente eine Molybdänröhre, die bei zwei Messungen mit einem Zirkoniumfilter versehen wurde. Eine Messung an Lithiumfluorid sollte ohne Filter durchgeführt und mit der Messung mit Filter verglichen werden. Aus der Messung ohne Filter sollte das Wellenlängenverhältnis der K α - und K β -Linie berechnet werden. 3 Theorie 3.1 Röntgenstrahlen Röntgenstrahlen werden produziert, indem Elektronen aus einem glühenden Wolframdraht über ein E-Feld beschleunigt und auf eine Anode geschossen werden. Die Elektronen treffen auf die Anode und schlagen Elektronen der innersten Schale aus dem Atom. Das zurückbleibende Loch wird aufgefüllt, indem Elektronen aus einer höheren Schale in eine tiefere fallen. Dabei emmitieren sie Photonen mit einer Wellenlänge zwischen 10 8 m und 10 1 m - die Röntgenstrahlung. Röntgenstrahlung setzt sich zusammen aus Bremsstrahlung, die dadurch entsteht, wenn die Elektronen an der Anode gebremst werden, und der charakteristischen Röntgenstrahlung, die von den Elektronenübergängen im Anodenmaterial herrührt. Im Diffraktogramm treten verschiedene Linien, die K α - und K β -Linien, auf. Deren Unterschied liegt in ihrer Entstehung. K α -Linien entstehen, wenn Elektronen von der L- in die K-Schale springen. Springt ein Elektron von der M- in die K-Schale, wird ein Photon einer anderen Wellenlänge emmitiert - die K β -Linie. Für die Diffraktometrie benötigt man monochromatische Röntgenstrahlung, also Strahlung gleicher Wellenlänge. Man filtert die Strahlung deshalb oft mittels eines Filters, der die K β -Linie absorbiert. 3. Braggsche Gleichung Röntgenstrahlen wechselwirken mit den Elektronen der Gitteratome. Trifft Röntegenstrahlung unter dem Winkel ϑ auf eine Gitterebene, wird sie reflektiert und tritt unter dem selben Winkel wieder aus. Diese reflektierten Sekundärstrahlen interferieren miteinander. Für eine konstruktive Interferrenz muss ihr Gangunterschied δ (cf. Abbildung 1) ein ganzzahliges Vielfaches der verwendeten Röntgenstrahlwellenlänge betragen. Ist dies der Fall, gilt die Bragg-Gleichung Abbildung 1: Zur Herleitung der Bragg-Gleichung []. nλ = d hkl sin θ (1) n: Beugungsordnung n N λ: Wellenlänge d hkl : Gitterebenenabstand θ: Winkel 1
2 3.3 Intensität von Röntgenstrahlen Die Intensität einer elektromagnetischen Welle ist proportional zum Betragsquadrat ihrer Schwingungsamplitude. Sie lässt sich näherungsweise beschreiben als: Wobei F hkl den Strukturfaktor bezeichnet. I hkl F hkl () F hkl = j b j f j e πi(hxj+kyj+lzj) T j (3) b j : Besetzungsfaktor f j : Atomformfaktor T j : temperaturabhängiger Faktor, der Atomschwingung berücksichtigt x j, y j, z j : Position des j-ten Atoms h, k, l: Lauesche Indizes Mit dem Strukturfaktor kann berechnet werden, an welchen Netzebene sich Reflexe ergeben, falls die Elementarzelle des Einkristalls bekannt ist. Versuchsbeschreibung Die Proben wurden in das Diffraktometer eingelegt und die nötigen Einstellungen am Gerät vorgenommen (cf. Tabelle 1). Die eigentliche Messung erfolgte dann vollautomatisch und das Diffraktogramm konnte sofort am Computerbildschirm betrachtet werden. Aus der Lage der Peaks konnte dann die Kristallstruktur berechnet werden. Tabelle 1: Messungen. Messung Probe Filter verwendet ϑ min ϑ max Beschleunigungsspannung Scanspeed 1 Si ja kv 8 Sekunden LiF ja kv 9 Sekunden 3 LiF nein kv 9 Sekunden 5 Messwerte und Auswertung Zur Messung wurde eine Molybdänröhre verwendet. Ihre K α -Linie liegt bei λ = 0,709 Å. 5.1 Silizium mit Zirkoniumfilter Gitterkonstante: a = 5,31 Å Es wurden Peaks bei Winkeln von 6, 19,5 6,6 und 3,9 gemessen. Vermutung: Reflexion an der 111-Ebene Berechnung der Reflexe Es liegt ein kubisches Gitter vor, deshalb gilt folgender Zusammenhang zwischen Millerschen Indizes hkl, Gitterkostante a und Netzebenenabstand d hkl : a d hkl = () h + k + l Mit Gleichung (1) folgt für die Winkel ϑ, bei denen ein Reflex auftritt: ( nλ ) h ϑ n = arcsin + k + l a (5) ( nλ ) ( h ϑ 1 = arcsin + k + l 1 0, 709Å 1 ) = arcsin , 5 a 5.31Å
3 Abbildung : Diffraktogramm von Silizium. Tabelle : Berechnete Reflexe von Silizium. Reflexordnung n Winkel ϑ in 1 6,5 13,1 3 19,8 6,9 5 3, 6,7 5. Lithiumfluorid mit Zirkoniumfilter Gitterkonstante: a =,07 Å Abbildung 3: Diffraktogramm von Lithiumfluorid mit Zirkoniumfilter. Es wurden Peaks bei Winkeln von 9, 19,8 31,1 und 3,9 gemessen. Vermutung: Reflexion an der 100-Ebene. 3
4 5..1 Berechnung der Reflexe Es liegt ebenfalls ein kubisches Gitter vor. Mit Gleichung (5) ergeben sich folgende Reflexe: Tabelle 3: Berechnete Reflexe von Lithiumfluorid mit Zirkoniumfilter. Reflexordnung n Winkel ϑ in 1 5,1 10,1 3 15,3 0,6 5 6,1 6 31,9 7 38,0 8,8 5.3 Lithiumfluorid ohne Zirkoniumfilter Gitterkonstante: a =,07 Å Abbildung : Diffraktogramm von Lithiumfluorid ohne Zirkoniumfilter. Es wurden Peaks bei Winkeln von 8,1 9,5 17,3 19,8 7,3 31, und, gemessen. Vermutung: Reflexion an der 100-Ebene. Da kein Filter mehr benutzt wurde, muss jetzt auch die Wellenlänge K β - Linie des Molybdäns und deren Reflexe berücksichtigt werden. Die Wellenlänge der K β - Linie beträgt λ = 0,63 Å
5 5.3.1 Berechnung der Reflexe Es liegt ebenfalls ein kubisches Gitter vor. Mit Gleichung (5) ergeben sich folgende Reflexe: Tabelle : Berechnete Reflexe von Lithiumfluorid mit Zirkoniumfilter. Reflexordnung n Winkel ϑ Kα in Winkel ϑ Kβ in 1 5,1,5 10,1 9,0 3 15,3 13,6 0,6 18,3 5 6,1 3,1 6 31,9 8,1 7 38,0 33,3 8,8 38,9 9 5,,9 6 Diskussion der Ergebnisse 6.1 Siliziumeinkristall mit Zirkoniumfilter Tabelle 5: Berechnete und gemessene Reflexe von Silizium mit Zirkoniumfilter. Reflexordnung n Gemessene Winkel in 6, - 19,5 6,6-3,9 Berechnete Winkel in 6,5 13,1 19,8 6,9 3,,7 Die gemessenen Winkel sind tendenziell etwas kleiner als die theoretisch berechneten. Dies könnte auf ein ungenaues Justieren des Diffraktometers zurückgeführt werden. Die Reflexe zweiter und fünfter Ordnung, die theoretisch auftreten sollten, sind praktisch nicht zu messen, da sich hier die gestreuten Strahlen auslöschen. Bedingung für die Auslöschung ist, dass der Strukturfaktor gleich Null sein muss Strukturfaktor von Silizium Die Faktoren T j und b j von Gleichung (3) können gleich eins gesetzt werden, da der Siliziumkristall nur aus Atomen eines einzigen Elements besteht. Silizium kristallisiert in Diamantstruktur (cf. Abbildung 5). Daraus ergeben sich folgende Atomgitterplätze in der Elementarzelle: (0, 0, 0), 1 ), 0, 0, 1 ), 1, 1 ), 3, 3 ) ( 3, 3, 1 ) ( 3, 1, 3 ) ( 0, 1, 1 ) Abbildung 5: Elementarzelle von Silizium [5]. 5
6 Für den Reflex n-ter Ordnung der 111-Ebene berechnet sich der Strukturfaktor wie folgt: F nnn = j f j exp (πin (x j + y j + z j )) = f exp (πin ( )) + f exp (πin (0, 5 + 0, 5 + 0)) + f exp (πin (0, 5 + 0, 5 + 0, 5)) + f exp (πin (0, , , 5)) + f exp (πin (0 + 0, 5 + 0, 5)) + f exp (πin (0, , 5)) + f exp (πin (0, 5 + 0, , 75)) + f exp (πin (0, , 5 + 0, 75)) F nnn = f (1 + 3 exp (πin) + exp (1, 5πin) + 3 exp (3, 5πin)) = f (1 + 3 cos (πn) + 3i sin (πn) + cos (1, 5πn) + i sin (1, 5πn) + 3 cos (3, 5πn) + 3i sin (3, 5πn)) = f ( cos (1, 5πn) + i sin (1, 5πn)) = f ( + cos (1, 5πn) + i sin (1, 5πn)) Für den Reflex erster Ordnung, also die Steuerung an der 111-Ebene ist der Strukturfaktor F 111 = f ( i) also ungleich Null. Hier findet keine Auslöschung statt, der Reflex ist als Peak im Diffraktogramm sichtbar. Die Strukturfaktoren der höheren Ordnungen sind in Tabelle 6 aufgelistet. Tabelle 6: Strukturfaktoren der höheren Reflexordnungen. Reflexordnung n Netzebene () (333) () (555) (666) Strukturfaktor 0 f( + i) f(8) f( - i) 0 Intensität der Streuung 0 f( + i) f(8) f( - i) 0 Peak vorhanden nein ja ja ja nein Der Reflex zweiter Ordnung ist nicht zu sehen, da hier der Strukturfaktor gleich Null ist. Die Reflexe der dritten und vierten Ordnung sind wieder im Diffraktogramm zu erkennen, der Reflex fünfter Ordnung fehlt allerdings, obwohl hier der Strukturfaktor nicht Null ist. Die Intensität der Strahlung ist hier wohl so klein, dass der Peak sich kaum von der Untergrundstrahlung unterscheidet. Dass die Intensität der Strahlung mit steigender Ordnung abnimmt, liegt an der Winkelabhängigkeit des Formfaktors f j. Er wird für größere Winkel immer kleiner, was den Strukturfaktor und somit sich die Intensität, die ja proportional zum Selbigen ist, verkleinert. Beim Reflex sechter Ordnung wurde ein Stück der Untergrundstrahlung irrtümlich als Peak erkannt, hier ist der Strukturfaktor nämlich wieder gleich Null. Zur Auslöschung kommt es also immer, wenn die Ordnung n = k - mit k N beträgt. 6
7 6. Lithiumfluorideinkristall mit Zirkoniumfilter Tabelle 7: Berechnete und gemessene Reflexe von Lithiumfluorid mit Zirkoniumfilter. Reflexordnung n Gemessene Winkel in - 9, - 19,8-31,1-3,9 - Berechnete Winkel in 5,1 10,1 15,3 0,6 6,1 31,9 38,0,8 5, Die gemessenen Winkel sind auch hier tendenziell etwas kleiner als die theoretisch berechneten. Die Reflexe erster, dritter, fünfter, siebter und neunter Ordnung, die theoretisch auftreten sollten, sind praktisch nicht zu messen, da sich hier die gestreuten Strahlen wieder auslöschen. Bedingung für die Auslöschung ist hier ebenfalls, dass der Strukturfaktor gleich Null sein muss Strukturfaktor von Lithiumfluorid Die Faktoren T j und b j von Gleichung (3) können gleich eins gesetzt werden, da Lithium und Fluorid wegen der Elektrostatik auf festgelegten Plätzen sitzen müssen. Lithiumfluorid kristallisiert in der NaCl-Struktur (cf. Abbildung 6). Daraus ergibt sich, dass sich Lithium (grau) auf folgenden Gitterplätzen befinden muss: (0, 0, 0), 0, 1 ), 1 ), 0 ( 0, 1, 1 ) Fluorid (blau) muss sich entsprechend auf folgenden Plätzen befinden: ( ) ( 1, 0, 0 0, 0, 1 ), 1, 1 ) (0, 1 ), 0 Für den Reflex n-ter Ordnung der 100-Ebene berechnet sich der Strukturfaktor wie folgt: Abbildung 6: Elementarzelle von Lithiumfluorid [6]. F n00 = j f j exp (πi nx j ) = f Li exp (πin 0) + f Li exp (πin 0, 5) + f Li exp (πin 0, 5) + f Li exp (πin 0) +f F exp (πin 0, 5) + f F exp (πin 0) + f F exp (πin 0, 5) + f F exp (πin 0) = (f Li + f F ) ( + exp (πin)) = (f Li + f F ) ( + ( 1) n ) Setzt man nun beispielsweise n = 1, wird der Strukturfaktor gleich Null, womit das Nichtauftreten des Peaks beim Reflex erster Ordnung zu erklären ist. Die Strukturfaktoren der höheren Ordnungen sind in Tabelle 8 aufgelistet. Mit diesen Strukturfaktoren Tabelle 8: Strukturfaktoren der höheren Reflexordnungen. Reflexordnung n Netzebene Strukturfaktor Intensität der Streuung Peak vorhanden (00) (f Li + f F ) (f Li + f F ) ja 3 (300) 0 0 nein (00) (f Li + f F ) (f Li + f F ) ja 5 (500) 0 0 nein 6 (600) (f Li + f F ) (f Li + f F ) ja 7 (700) 0 0 nein 8 (800) (f Li + f F ) (f Li + f F ) ja 9 (900) 0 0 nein lassen sich die auftretenden und nicht auftretenden Peaks erklären. Reflexe treten nur bei gerader Ordnung auf. Es wurden alle Peaks, die auftraten, als solche erkannt. 7
8 6.3 Lithiumfluorideinkristall ohne Zirkoniumfilter Tabelle 9: Berechnete und gemessene Reflexe von Lithiumfluorid ohne Zirkoniumfilter. Reflexordnung n Gemessene Winkel bei ϑ Kα in - 9, - 19,8-31,1-3,9 - Berechnete Winkel bei ϑ Kα in 5,1 10,1 15,3 0,6 6,1 31,9 38,0,8 5, Gemessene Winkel bei ϑ Kβ in - 8,1-17,3-7, Berechnete Winkel bei ϑ Kβ in,5 9,0 13,6 18,3 3,1 8,1 33,3 38,9,9 Die gemessenen Winkel sind hier auch wieder tendenziell etwas kleiner als die theoretisch berechneten. Die Reflexe erster, dritter, fünfter, siebter und neunter Ordnung, die theoretisch auftreten sollten, sind auch hier wieder nicht zu messen, da der Strukturfaktor hier null ist, sich die Strahlen also auslöschen. Die Strukturfaktoren aus Tabelle 8 gelten auch für die K β -Linien. Die Intensität des Reflexes achter Ordnung ist wieder zu schwach, um einen deutlichen Peak sehen zu können. Reflexe treten nur bei gerade Ordnung auf. 6. Berechnung des Wellenlängenverhältnisses der K α - und K β -Linien Aus und nλ α = d hkl sin ϑ α (6) nλ β = d hkl sin ϑ β (7) ergibt sich folgende Gleichung, aus der das Wellenlängenverhältnis berechnet werden kann: λ α λ β = sin ϑ α sin ϑ β Wellenlängenverhältnis bei zweiter Ordnung. λ α = sin ϑ α sin 9, 5 = 1, 1 λ β sin ϑ β sin 8, 1 Wellenlängenverhältnis bei vierter Ordnung. λ α = sin ϑ α sin 19, 8 = 1, 1 λ β sin ϑ β sin 17, 3 Wellenlängenverhältnis bei sechster Ordnung. λ α = sin ϑ α sin 31, = 1, 13 λ β sin ϑ β sin 7, 3 Berechnet man das Wellenlängenverhältnis aus den gegebenen Wellenlängen 0,709 Åund 0,63 Å, erhält man ebenfalls einen Wert von ca. 1,1, die gemessenen Werte stimmen also gut mit dem theoretischen Wert überein. Auch dass das Verhältnis mit steigender Reflexordnung etwas zunimmt lässt sich gut erklären. Die relative Lage der Linien zueinander folgt einer Tangensabhängigkeit: d λ λ = d sin ϑ sin ϑ = cos ϑ d ϑ = d ϑ sin ϑ tan ϑ d ϑ = tan ϑ d λ λ Zwischen Null und 90 steigt der Tangens eines Winkels mit steigendem Winkel. Daher wird der Abstand der Linien mit steigender Ordnung größer. 8
9 7 Fehlerbetrachtung Folgende Umstände können zu Fehlern bei der Messung führen: Ungenaues Justieren des Diffraktometers Fehler beim Ablesen der Peak Nicht ganz eindeutige Peaks aufgrund hoher Untergrundstrahlung Keine perfekte Lage der Probe im Diffraktometer Literatur [1] G. Gottstein, Physikalische Grundlagen der Materialkunde, 3. Auflage, Springer-Verlag [] Praktikumsskript, Diffraktometrie (DF) [3] W. Gust, Skript zur Vorlesung Einführung in die Metallkunde WS 1999/000 [] Wikipedia, Bragg.svg.png, letzter Zugriff: 5. Juni 009, Uhr [5] Wikipedia, letzter Zugriff: 5. Juni 009, 1.30 Uhr [6] Chemgapedia, letzter Zugriff: 6. Juni 009, 17.0 Uhr 9
Röntgenkristallstrukturanalyse : Debye-Scherrer
 16.04.2009 Gliederung Bragg-Bedingung Bragg-Bedingung Bragg-Bedingung: 2d m m m h k l sin(ϑ) = nλ für kubisches Gitter: 2sin(ϑ) = λ h 2 + k 2 + l 2 a d m m m h k l...netzebenenabstand ϑ...braggwinkel n...
16.04.2009 Gliederung Bragg-Bedingung Bragg-Bedingung Bragg-Bedingung: 2d m m m h k l sin(ϑ) = nλ für kubisches Gitter: 2sin(ϑ) = λ h 2 + k 2 + l 2 a d m m m h k l...netzebenenabstand ϑ...braggwinkel n...
Übungen zur Physik des Lichts
 ) Monochromatisches Licht (λ = 500 nm) wird an einem optischen Gitter (000 Striche pro cm) gebeugt. a) Berechnen Sie die Beugungswinkel der Intensitätsmaxima bis zur 5. Ordnung. b) Jeder einzelne Gitterstrich
) Monochromatisches Licht (λ = 500 nm) wird an einem optischen Gitter (000 Striche pro cm) gebeugt. a) Berechnen Sie die Beugungswinkel der Intensitätsmaxima bis zur 5. Ordnung. b) Jeder einzelne Gitterstrich
TEP Strukturbestimmung von NaCl-Einkristallen verschiedener Orientierungen
 Strukturbestimmung von NaCl-Einkristallen TEP Verwandte Begriffe Charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Reziproke Gitter, Millersche- Indizes, Atomfaktor, Strukturfaktor,
Strukturbestimmung von NaCl-Einkristallen TEP Verwandte Begriffe Charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Reziproke Gitter, Millersche- Indizes, Atomfaktor, Strukturfaktor,
Zentralabitur 2012 Physik Schülermaterial Aufgabe I ga Bearbeitungszeit: 220 min
 Thema: Wellen und Quanten Interferenzphänomene werden an unterschiedlichen Strukturen untersucht. In Aufgabe 1 wird zuerst der Spurabstand einer CD bestimmt. Thema der Aufgabe 2 ist eine Strukturuntersuchung
Thema: Wellen und Quanten Interferenzphänomene werden an unterschiedlichen Strukturen untersucht. In Aufgabe 1 wird zuerst der Spurabstand einer CD bestimmt. Thema der Aufgabe 2 ist eine Strukturuntersuchung
TEP Monochromatisierung von charakteristischer Molybdän-Röntgenstrahlung
 Monochromatisierung von charakteristischer TEP Verwandte Begriffe Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Absorption von Röntgenstrahlung, Absorptionskanten, Interferenz, Bragg-Streuung.
Monochromatisierung von charakteristischer TEP Verwandte Begriffe Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Absorption von Röntgenstrahlung, Absorptionskanten, Interferenz, Bragg-Streuung.
Röntgenstrahlen (RÖN)
 TUM Anfängerpraktikum für Physiker II Wintersemester 2006/2007 Röntgenstrahlen (RÖN) Inhaltsverzeichnis 07.11.2006 1.Einleitung...2 2.Photonenemission...2 2.1.Bremsstrahlung...2 2.2.Charakteristische Röntgenstrahlung...2
TUM Anfängerpraktikum für Physiker II Wintersemester 2006/2007 Röntgenstrahlen (RÖN) Inhaltsverzeichnis 07.11.2006 1.Einleitung...2 2.Photonenemission...2 2.1.Bremsstrahlung...2 2.2.Charakteristische Röntgenstrahlung...2
Physikalisches Praktikum für Fortgeschrittene im II. Physikalischen Institut. Versuch Nr. 24: Röntgenographische Methoden
 Physikalisches Praktikum für Fortgeschrittene im II. Physikalischen Institut Versuch Nr. 24: Röntgenographische Methoden Betreuer: M. Cwik, Tel.: 470 3574, E-mail: [email protected] November 2004 Im
Physikalisches Praktikum für Fortgeschrittene im II. Physikalischen Institut Versuch Nr. 24: Röntgenographische Methoden Betreuer: M. Cwik, Tel.: 470 3574, E-mail: [email protected] November 2004 Im
 Die Lage der Emissionsbanden der charakteristischen Röntgenstrahlung (anderer Name: Eigenstrahlung) wird bestimmt durch durch das Material der Kathode durch das Material der Anode die Größe der Anodenspannung
Die Lage der Emissionsbanden der charakteristischen Röntgenstrahlung (anderer Name: Eigenstrahlung) wird bestimmt durch durch das Material der Kathode durch das Material der Anode die Größe der Anodenspannung
Charakteristische Röntgenstrahlung von Wolfram
 Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Aufgabenstellung: Bestimmen Sie die AVOGADRO-Konstante mittels Röntgenbeugung. Führen Sie eine Größtfehlerberechnung durch.
 Aufgabenstellung: Bestimmen Sie die AVOGADRO-Konstante mittels Röntgenbeugung. Führen Sie eine Größtfehlerberechnung durch. Stichworte zur Vorbereitung: AVOGADRO-Konstante, Röntgenstrahlung, Röntgenröhre,
Aufgabenstellung: Bestimmen Sie die AVOGADRO-Konstante mittels Röntgenbeugung. Führen Sie eine Größtfehlerberechnung durch. Stichworte zur Vorbereitung: AVOGADRO-Konstante, Röntgenstrahlung, Röntgenröhre,
Protokoll zum Versuch Debye - Scherrer - Verfahren. Tina Clauß, Jan Steinhoff Betreuer: Dr. Uschmann
 Protokoll zum Versuch Debye - Scherrer - Verfahren Tina Clauß, Jan Steinhoff Betreuer: Dr. Uschmann 6. März 2005 3 Inhaltsverzeichnis 1 Aufgabenstellung 4 2 Theoretische Grundlagen 4 2.1 Röntgenstrahlung.................................
Protokoll zum Versuch Debye - Scherrer - Verfahren Tina Clauß, Jan Steinhoff Betreuer: Dr. Uschmann 6. März 2005 3 Inhaltsverzeichnis 1 Aufgabenstellung 4 2 Theoretische Grundlagen 4 2.1 Röntgenstrahlung.................................
Physikalisches Grundpraktikum Technische Universität Chemnitz
 Physikalisches Grundpraktikum Technische Universität Chemnitz Protokoll «A10 - AVOGADRO-Konstante» Martin Wolf Betreuer: Herr Decker Mitarbeiter: Martin Helfrich Datum:
Physikalisches Grundpraktikum Technische Universität Chemnitz Protokoll «A10 - AVOGADRO-Konstante» Martin Wolf Betreuer: Herr Decker Mitarbeiter: Martin Helfrich Datum:
ISP-Methodenkurs. Pulverdiffraktometrie. Prof. Dr. Michael Fröba, AC Raum 114, Tel: 040 /
 ISP-Methodenkurs Pulverdiffraktometrie Prof. Dr. Michael Fröba, AC Raum 4, Tel: 4 / 4838-337 www.chemie.uni-hamburg.de/ac/froeba/ Röntgenstrahlung (I) Wilhelm Conrad Röntgen (845-93) 879-888 Professor
ISP-Methodenkurs Pulverdiffraktometrie Prof. Dr. Michael Fröba, AC Raum 4, Tel: 4 / 4838-337 www.chemie.uni-hamburg.de/ac/froeba/ Röntgenstrahlung (I) Wilhelm Conrad Röntgen (845-93) 879-888 Professor
Ferienkurs Experimentalphysik 3
 Ferienkurs Experimentalphysik 3 Wintersemester 2014/2015 Thomas Maier, Alexander Wolf Lösung 3 Beugung und Interferenz Aufgabe 1: Seifenblasen a) Erklären Sie, warum Seifenblasen in bunten Farben schillern.
Ferienkurs Experimentalphysik 3 Wintersemester 2014/2015 Thomas Maier, Alexander Wolf Lösung 3 Beugung und Interferenz Aufgabe 1: Seifenblasen a) Erklären Sie, warum Seifenblasen in bunten Farben schillern.
1 Aufgabenstellung 2. 2 Theoretische Grundlagen Das Röntgenspektrum Analyse mit Einkristallen... 4
 Röntgenstrahlung Fachrichtung Physik Physikalisches Grundpraktikum Erstellt: Jakob Krämer Aktualisiert: am 12. 04. 2013 Röntgenstrahlung Inhaltsverzeichnis 1 Aufgabenstellung 2 2 Theoretische Grundlagen
Röntgenstrahlung Fachrichtung Physik Physikalisches Grundpraktikum Erstellt: Jakob Krämer Aktualisiert: am 12. 04. 2013 Röntgenstrahlung Inhaltsverzeichnis 1 Aufgabenstellung 2 2 Theoretische Grundlagen
Charakteristische Röntgenstrahlung von Kupfer
 Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Charakteristische Röntgenstrahlung von Molybdän
 Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Versuch A05: Bestimmung des Planck'schen Wirkungsquantums
 Versuch A05: Bestimmung des Planck'schen Wirkungsquantums 25. April 2016 I Lernziele Entstehung des Röntgen-Bremskontinuums und der charakteristischen Röntgenstrahlung Zusammenhang zwischen Energie, Frequenz
Versuch A05: Bestimmung des Planck'schen Wirkungsquantums 25. April 2016 I Lernziele Entstehung des Röntgen-Bremskontinuums und der charakteristischen Röntgenstrahlung Zusammenhang zwischen Energie, Frequenz
A10 - AVOGADRO - Konstante
 A10 - AVOGADRO - Konstante Aufgabenstellung: Bestimmen Sie die AVOGADRO-Konstante mittels Röntgenbeugung. Führen Sie eine Größtfehlerberechnung durch. Stichworte zur Vorbereitung: AVOGADRO-Konstante, Röntgenstrahlung,
A10 - AVOGADRO - Konstante Aufgabenstellung: Bestimmen Sie die AVOGADRO-Konstante mittels Röntgenbeugung. Führen Sie eine Größtfehlerberechnung durch. Stichworte zur Vorbereitung: AVOGADRO-Konstante, Röntgenstrahlung,
1. Ermitteln Sie die Gitterkonstante eines LiF-Kristalls aus der Messung des -2 -Spektrums unter Verwendung einer Wolframkathode.
 Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum O 21 Röntgenstrahlung Aufgaben 1. Ermitteln Sie die Gitterkonstante eines LiF-Kristalls aus der Messung des -2-Spektrums unter Verwendung
Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum O 21 Röntgenstrahlung Aufgaben 1. Ermitteln Sie die Gitterkonstante eines LiF-Kristalls aus der Messung des -2-Spektrums unter Verwendung
Charakteristische Röntgenstrahlung von Eisen
 Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
Charakteristische Röntgenstrahlung TEP Verwandte Begriffe Röntgenröhren, Bremsstrahlung, charakteristische Röntgenstrahlung, Energieniveaus, Kristallstrukturen, Gitterkonstante, Absorption von Röntgenstrahlung,
FK Experimentalphysik 3, Lösung 3
 1 Transmissionsgitter FK Experimentalphysik 3, Lösung 3 1 Transmissionsgitter Ein Spalt, der von einer Lichtquelle beleuchtet wird, befindet sich im Abstand von 10 cm vor einem Beugungsgitter (Strichzahl
1 Transmissionsgitter FK Experimentalphysik 3, Lösung 3 1 Transmissionsgitter Ein Spalt, der von einer Lichtquelle beleuchtet wird, befindet sich im Abstand von 10 cm vor einem Beugungsgitter (Strichzahl
Klausur -Informationen
 Klausur -Informationen Datum: 4.2.2009 Uhrzeit und Ort : 11 25 im großen Physikhörsaal (Tiermediziner) 12 25 ibidem Empore links (Nachzügler Tiermedizin, bitte bei Aufsichtsperson Ankunft melden) 11 25
Klausur -Informationen Datum: 4.2.2009 Uhrzeit und Ort : 11 25 im großen Physikhörsaal (Tiermediziner) 12 25 ibidem Empore links (Nachzügler Tiermedizin, bitte bei Aufsichtsperson Ankunft melden) 11 25
Röntgenstrahlung ist eine elektromagnetische Strahlung, wie z.b. Licht sie ist für Menschen nicht sichtbar Röntgenstrahlung besitzt
 Röntgenstrahlung ist eine elektromagnetische Strahlung, wie z.b. Licht sie ist für Menschen nicht sichtbar Röntgenstrahlung besitzt Welleneigenschaften, ionisiert Gase, regt manche Stoffe zum Leuchten
Röntgenstrahlung ist eine elektromagnetische Strahlung, wie z.b. Licht sie ist für Menschen nicht sichtbar Röntgenstrahlung besitzt Welleneigenschaften, ionisiert Gase, regt manche Stoffe zum Leuchten
Grundlagen der Röntgenpulverdiffraktometrie. Seminar zur Vorlesung Anorganische Chemie I und II
 David Enseling und Thomas Jüstel Seminar zur Vorlesung Anorganische Chemie I und II Folie 1 Entdeckung + erste Anwendung der X-Strahlen Wilhelm Roentgen, December of 1895. The X-ray of Mrs. Roentgen's
David Enseling und Thomas Jüstel Seminar zur Vorlesung Anorganische Chemie I und II Folie 1 Entdeckung + erste Anwendung der X-Strahlen Wilhelm Roentgen, December of 1895. The X-ray of Mrs. Roentgen's
Masterstudiengang Chemie Vorlesung Struktur und Funktion (WS 2014/15) Struktur und Funktion: (Kap. 2)
 Masterstudiengang Chemie Vorlesung Struktur und Funktion (WS 2014/15) Übersicht 2 Beugung von Röntgenstrahlen an Kristallen 2.1 Erzeugung von Röntgenstrahlen 2.2 Streuung an Elektronen 2.3 Streuung an
Masterstudiengang Chemie Vorlesung Struktur und Funktion (WS 2014/15) Übersicht 2 Beugung von Röntgenstrahlen an Kristallen 2.1 Erzeugung von Röntgenstrahlen 2.2 Streuung an Elektronen 2.3 Streuung an
Materialkundliches Praktikum Phasenanalytik und Röntgendiffraktometrie Verantwortlicher Mitarbeiter: Dr. Matthias Müller
 Materialkundliches Praktikum Phasenanalytik und Röntgendiffraktometrie Verantwortlicher Mitarbeiter: Dr. Matthias Müller Inhalt: 1. Physikalische Grundlagen der Röntgenbeugung. Struktur von Festkörpern,
Materialkundliches Praktikum Phasenanalytik und Röntgendiffraktometrie Verantwortlicher Mitarbeiter: Dr. Matthias Müller Inhalt: 1. Physikalische Grundlagen der Röntgenbeugung. Struktur von Festkörpern,
Typisch metallische Eigenschaften:
 Typisch metallische Eigenschaften: hohe elektrische Leitfähigkeit hohe thermische Leitfähigkeit bei Energiezufuhr (Wärme, elektromagnetische Strahlung) können Elektronen emittiert werden metallischer Glanz
Typisch metallische Eigenschaften: hohe elektrische Leitfähigkeit hohe thermische Leitfähigkeit bei Energiezufuhr (Wärme, elektromagnetische Strahlung) können Elektronen emittiert werden metallischer Glanz
Zugversuch. Der Zugversuch gehört zu den bedeutendsten Versuchen, um die wichtigsten mechanischen Eigenschaften von Werkstoffen zu ermitteln.
 Name: Matthias Jasch Matrikelnummer: 2402774 Mitarbeiter: Mirjam und Rahel Eisele Gruppennummer: 7 Versuchsdatum: 26. Mai 2009 Betreuer: Vera Barucha Zugversuch 1 Einleitung Der Zugversuch gehört zu den
Name: Matthias Jasch Matrikelnummer: 2402774 Mitarbeiter: Mirjam und Rahel Eisele Gruppennummer: 7 Versuchsdatum: 26. Mai 2009 Betreuer: Vera Barucha Zugversuch 1 Einleitung Der Zugversuch gehört zu den
Praktikum GI Gitterspektren
 Praktikum GI Gitterspektren Florian Jessen, Hanno Rein betreut durch Christoph von Cube 9. Januar 2004 Vorwort Oft lassen sich optische Effekte mit der geometrischen Optik beschreiben. Dringt man allerdings
Praktikum GI Gitterspektren Florian Jessen, Hanno Rein betreut durch Christoph von Cube 9. Januar 2004 Vorwort Oft lassen sich optische Effekte mit der geometrischen Optik beschreiben. Dringt man allerdings
Die Bragg sche Beugungsbedingung. θ θ θ θ Ebene hkl
 Die Bragg sche Beugungsbedingung Eintr effender Strahl Austretender Str ahl Gebeugter Strahl θ θ θ θ Ebene hkl d hkl x x Ebene hkl Wegdifferenz: 2 x = 2 d hkl sin θ Konstruktive Interferenz: n λ = 2 d
Die Bragg sche Beugungsbedingung Eintr effender Strahl Austretender Str ahl Gebeugter Strahl θ θ θ θ Ebene hkl d hkl x x Ebene hkl Wegdifferenz: 2 x = 2 d hkl sin θ Konstruktive Interferenz: n λ = 2 d
Versuchsanleitung Laue-Experiment. F1-Praktikum, Versuch R2
 Versuchsanleitung Laue-Experiment F1-Praktikum, Versuch R2 Inhaltsverzeichnis 1. Einleitung...3 2. Physikalischer Hintergrund...3 3. Versuchsaufbau...4 3.1 Die Laue-Apparatur...5 3.2 Das Kühlsystem...5
Versuchsanleitung Laue-Experiment F1-Praktikum, Versuch R2 Inhaltsverzeichnis 1. Einleitung...3 2. Physikalischer Hintergrund...3 3. Versuchsaufbau...4 3.1 Die Laue-Apparatur...5 3.2 Das Kühlsystem...5
NG Brechzahl von Glas
 NG Brechzahl von Glas Blockpraktikum Frühjahr 2007 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Geometrische Optik und Wellenoptik.......... 2 2.2 Linear polarisiertes
NG Brechzahl von Glas Blockpraktikum Frühjahr 2007 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Geometrische Optik und Wellenoptik.......... 2 2.2 Linear polarisiertes
Aufgaben zu Röntgenstrahlen LK Physik 13/1 Sporenberg Roentgen_September_2011 Datum:
 Aufgaben zu Röntgenstrahlen LK Physik 13/1 Sporenberg Roentgen_September_2011 Datum: 08.09.2011 1.Aufgabe: In einem Röntgengerät fällt monochromatische Strahlung ( λ = 71 pm) auf die Oberfläche eines LiF-Kristalls.
Aufgaben zu Röntgenstrahlen LK Physik 13/1 Sporenberg Roentgen_September_2011 Datum: 08.09.2011 1.Aufgabe: In einem Röntgengerät fällt monochromatische Strahlung ( λ = 71 pm) auf die Oberfläche eines LiF-Kristalls.
1 Versuchsbeschreibung Versuchsvorbereitung Versuch: Wellennatur des Elektrons... 3
 Versuch: EB Fachrichtung Physik Physikalisches Grundpraktikum Erstellt: M. Kreller i.a. Dr. Escher Bearbeitet: A. Otto Aktualisiert: am 24. 02. 2011 Elektronenbeugung Inhaltsverzeichnis 1 Versuchsbeschreibung
Versuch: EB Fachrichtung Physik Physikalisches Grundpraktikum Erstellt: M. Kreller i.a. Dr. Escher Bearbeitet: A. Otto Aktualisiert: am 24. 02. 2011 Elektronenbeugung Inhaltsverzeichnis 1 Versuchsbeschreibung
Protokoll in Physik. Datum:
 Protokoll in Physik Datum: 04.11.2010 Protokollantin: Alrun-M. Seuwen Fachlehrer: Herr Heidinger Inhalt: h) Die Bragg-Reflexion 1) Die Wellenlänge des Röntgenlichts 2) Das Bragg-Kristall 3) Inteferenz
Protokoll in Physik Datum: 04.11.2010 Protokollantin: Alrun-M. Seuwen Fachlehrer: Herr Heidinger Inhalt: h) Die Bragg-Reflexion 1) Die Wellenlänge des Röntgenlichts 2) Das Bragg-Kristall 3) Inteferenz
Spektralanalyse. Olaf Merkert (Manuel Sitter) 18. Dezember 2005
 Spektralanalyse Olaf Merkert (Manuel Sitter) 18. Dezember 2005 Zusammenfassung Dieses Praktikums-Protokoll behandelt die Untersuchung des Spektrums einer Energiesparlampe mit Hilfe eines Gitters. Außerdem
Spektralanalyse Olaf Merkert (Manuel Sitter) 18. Dezember 2005 Zusammenfassung Dieses Praktikums-Protokoll behandelt die Untersuchung des Spektrums einer Energiesparlampe mit Hilfe eines Gitters. Außerdem
Klausurinformation. Sie dürfen nicht verwenden: Handy, Palm, Laptop u.ae. Weisses Papier, Stifte etc. Proviant, aber keine heiße Suppe u.dgl.
 Klausurinformation Zeit: Mittwoch, 3.Februar, 12:00, Dauer :90 Minuten Ort: Veterinärmediziner: Großer Phys. Hörsaal ( = Hörsaal der Vorlesung) Geowissenschaftler u.a.: Raum A140, Hauptgebäude 1. Stock,
Klausurinformation Zeit: Mittwoch, 3.Februar, 12:00, Dauer :90 Minuten Ort: Veterinärmediziner: Großer Phys. Hörsaal ( = Hörsaal der Vorlesung) Geowissenschaftler u.a.: Raum A140, Hauptgebäude 1. Stock,
31. Lektion. Röntgenstrahlen. 40. Röntgenstrahlen und Laser
 31. Lektion Röntgenstrahlen 40. Röntgenstrahlen und Laser Lerhnziel: Röntgenstrahlen entstehen durch Beschleunigung von Elektronen oder durch die Ionisation von inneren Elektronenschalen Begriffe Begriffe:
31. Lektion Röntgenstrahlen 40. Röntgenstrahlen und Laser Lerhnziel: Röntgenstrahlen entstehen durch Beschleunigung von Elektronen oder durch die Ionisation von inneren Elektronenschalen Begriffe Begriffe:
Röntgendiffraktometrie
 Kapitel 3.4. Röntgendiffraktometrie Lothar Schwabe, Freie Universität Berlin 1. Einleitung Die Eigenschaft der Röntgenstrahlen, unterschiedliche Materialien zu durchdringen und dabei mehr oder weniger
Kapitel 3.4. Röntgendiffraktometrie Lothar Schwabe, Freie Universität Berlin 1. Einleitung Die Eigenschaft der Röntgenstrahlen, unterschiedliche Materialien zu durchdringen und dabei mehr oder weniger
Fortgeschrittenenpraktikum: Ausarbeitung - Versuch 14 Optische Absorption Durchgeführt am 13. Juni 2002
 Fortgeschrittenenpraktikum: Ausarbeitung - Versuch 14 Optische Absorption Durchgeführt am 13. Juni 2002 30. Juli 2002 Gruppe 17 Christoph Moder 2234849 Michael Wack 2234088 Sebastian Mühlbauer 2218723
Fortgeschrittenenpraktikum: Ausarbeitung - Versuch 14 Optische Absorption Durchgeführt am 13. Juni 2002 30. Juli 2002 Gruppe 17 Christoph Moder 2234849 Michael Wack 2234088 Sebastian Mühlbauer 2218723
TEP Strukturbestimmung von Einkristallen mit Hilfe der Laue-Methode
 Strukturbestimmung von Einkristallen TEP Verwandte Themen Charakteristische Röntgenstrahlung, Bravais-Gitter, Reziproke Gitter, Millersche-Indizes, Atomfaktor, Strukturfaktor, Bragg- Streuung. Prinzip
Strukturbestimmung von Einkristallen TEP Verwandte Themen Charakteristische Röntgenstrahlung, Bravais-Gitter, Reziproke Gitter, Millersche-Indizes, Atomfaktor, Strukturfaktor, Bragg- Streuung. Prinzip
UNIVERSITÄT BIELEFELD. Optik. GV Interferenz und Beugung. Durchgeführt am
 UNIVERSITÄT BIELEFELD Optik GV Interferenz und Beugung Durchgeführt am 10.05.06 Dozent: Praktikanten (Gruppe 1): Dr. Udo Werner Marcus Boettiger Daniel Fetting Marius Schirmer Inhaltsverzeichnis 1 Ziel
UNIVERSITÄT BIELEFELD Optik GV Interferenz und Beugung Durchgeführt am 10.05.06 Dozent: Praktikanten (Gruppe 1): Dr. Udo Werner Marcus Boettiger Daniel Fetting Marius Schirmer Inhaltsverzeichnis 1 Ziel
= 6,63 10 J s 8. (die Plancksche Konstante):
 35 Photonen und Materiefelder 35.1 Das Photon: Teilchen des Lichts Die Quantenphysik: viele Größen treten nur in ganzzahligen Vielfachen von bestimmten kleinsten Beträgen (elementaren Einheiten) auf: diese
35 Photonen und Materiefelder 35.1 Das Photon: Teilchen des Lichts Die Quantenphysik: viele Größen treten nur in ganzzahligen Vielfachen von bestimmten kleinsten Beträgen (elementaren Einheiten) auf: diese
Übungsblatt 1 zur Vorlesung Atom- und Molekülphysik
 Übungsblatt 1 zur Vorlesung Atom- und Molekülphysik Kapitel 1 bis inklusive 2.3 1. Zu Kapitel 1 Wie viele Atome enthält eine Kupfermünze mit einer Masse von 3,4g benutzen Sie eine Masse von 63,5 atomaren
Übungsblatt 1 zur Vorlesung Atom- und Molekülphysik Kapitel 1 bis inklusive 2.3 1. Zu Kapitel 1 Wie viele Atome enthält eine Kupfermünze mit einer Masse von 3,4g benutzen Sie eine Masse von 63,5 atomaren
Versuch 20: Charakteristische Röntgenstrahlung
 Versuch 20: Charakteristische Röntgenstrahlung 1. Einordung in den Kernlehrplan für den Grundkurs Kompetenzen gemäß KLP: Die Schülerinnen und Schüler erläutern die Bedeutung [ ] der charakteristischen
Versuch 20: Charakteristische Röntgenstrahlung 1. Einordung in den Kernlehrplan für den Grundkurs Kompetenzen gemäß KLP: Die Schülerinnen und Schüler erläutern die Bedeutung [ ] der charakteristischen
Vorlesung 2: Größe der Atome Massenspektroskopie Atomstruktur aus Rutherfordstreuung
 Vorlesung 2: Roter Faden: Größe der Atome Massenspektroskopie Atomstruktur aus Rutherfordstreuung Skripte und Folien auf dem Web: http://www-ekp.physik.uni-karlsruhe.de/~deboer/ April 14, 2005 Atomphysik
Vorlesung 2: Roter Faden: Größe der Atome Massenspektroskopie Atomstruktur aus Rutherfordstreuung Skripte und Folien auf dem Web: http://www-ekp.physik.uni-karlsruhe.de/~deboer/ April 14, 2005 Atomphysik
Physik für Mediziner und Zahnmediziner
 Physik für Mediziner und Zahnmediziner Vorlesung 19 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1 PET: Positronen-Emissions-Tomographie Kernphysik PET Atomphysik Röntgen
Physik für Mediziner und Zahnmediziner Vorlesung 19 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1 PET: Positronen-Emissions-Tomographie Kernphysik PET Atomphysik Röntgen
27. Vorlesung EP V. STRAHLUNG, ATOME, KERNE
 27. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 28. Atomphysik, Röntgenstrahlung (Fortsetzung: Röntgenröhre, Röntgenabsorption) 29. Atomkerne, Radioaktivität (Nuklidkarte, α-, β-, γ-aktivität, Dosimetrie)
27. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 28. Atomphysik, Röntgenstrahlung (Fortsetzung: Röntgenröhre, Röntgenabsorption) 29. Atomkerne, Radioaktivität (Nuklidkarte, α-, β-, γ-aktivität, Dosimetrie)
Physik 2 (GPh2) am
 Name: Matrikelnummer: Studienfach: Physik 2 (GPh2) am 17.09.2013 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel zu dieser Klausur: Beiblätter
Name: Matrikelnummer: Studienfach: Physik 2 (GPh2) am 17.09.2013 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel zu dieser Klausur: Beiblätter
UNIVERSITÄT BIELEFELD
 UNIVERSITÄT BIELEFELD 5. Schwingungen und Wellen 5.6 - Beugung von Ultraschall Durchgeführt am 3.0.06 Dozent: Praktikanten (Gruppe ): Dr. Udo Werner Marcus Boettiger Daniel Fetting Marius Schirmer E3-463
UNIVERSITÄT BIELEFELD 5. Schwingungen und Wellen 5.6 - Beugung von Ultraschall Durchgeführt am 3.0.06 Dozent: Praktikanten (Gruppe ): Dr. Udo Werner Marcus Boettiger Daniel Fetting Marius Schirmer E3-463
Symmetrie in Kristallen Anleitung für das F-Praktikum
 Symmetrie in Kristallen Anleitung für das F-Praktikum Sommersemester 2015 Fachbereich Physik Physikalisches Institut Goethe-Universität Frankfurt Betreuer: Kristin Kliemt [email protected]
Symmetrie in Kristallen Anleitung für das F-Praktikum Sommersemester 2015 Fachbereich Physik Physikalisches Institut Goethe-Universität Frankfurt Betreuer: Kristin Kliemt [email protected]
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 12 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 12 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick [email protected] Röntgenbeugung an Pulvern
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 12 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick [email protected] Röntgenbeugung an Pulvern
Verwandte Themen Charakteristische Röntgenstrahlung, Energieniveaus, Auswahlregeln für Röntgenstrahlung, Termsymbole, Bragg-Gleichung.
 Trennung der charakteristischen TEP Verwandte Themen Charakteristische Röntgenstrahlung, Energieniveaus, Auswahlregeln für Röntgenstrahlung, Termsymbole, Bragg-Gleichung. Prinzip Die von einer Röntgenröhre
Trennung der charakteristischen TEP Verwandte Themen Charakteristische Röntgenstrahlung, Energieniveaus, Auswahlregeln für Röntgenstrahlung, Termsymbole, Bragg-Gleichung. Prinzip Die von einer Röntgenröhre
Beugung am Spalt und Gitter
 Demonstrationspraktikum für Lehramtskandidaten Versuch O1 Beugung am Spalt und Gitter Sommersemester 2006 Name: Daniel Scholz Mitarbeiter: Steffen Ravekes EMail: [email protected] Gruppe: 4 Durchgeführt
Demonstrationspraktikum für Lehramtskandidaten Versuch O1 Beugung am Spalt und Gitter Sommersemester 2006 Name: Daniel Scholz Mitarbeiter: Steffen Ravekes EMail: [email protected] Gruppe: 4 Durchgeführt
Es sollen jedoch mehratomige Kristalle betrachtet werden, NaCl und CsCl.
 1. Einleitung In diesem Versuch werden die Gittertypen und Gitterkonstanten von NaCl und CsCl mit Hile des Debye-Scherrer-Verahrens überprüt bzw. bestimmt. 2. Theoretische Grundlagen 2.1 Kristallgittertypen
1. Einleitung In diesem Versuch werden die Gittertypen und Gitterkonstanten von NaCl und CsCl mit Hile des Debye-Scherrer-Verahrens überprüt bzw. bestimmt. 2. Theoretische Grundlagen 2.1 Kristallgittertypen
Lk Physik in 13/1 1. Klausur Nachholklausur Blatt 1 (von 2)
 Blatt 1 (von 2) 1. Elektronenausbeute beim Photoeekt Eine als punktförmig aufzufassende Spektrallampe L strahlt eine Gesamt-Lichtleistung von P ges = 40 W der Wellenlänge λ = 490 nm aus. Im Abstand r =
Blatt 1 (von 2) 1. Elektronenausbeute beim Photoeekt Eine als punktförmig aufzufassende Spektrallampe L strahlt eine Gesamt-Lichtleistung von P ges = 40 W der Wellenlänge λ = 490 nm aus. Im Abstand r =
Röntgenstrukturanalyse nach Debye-Scherrer
 Röntgenstrukturanalyse nach Debye-Scherrer Ilja Homm und Thorsten Bitsch Betreuer: Haiko Didzoleit 02.05.2012 Fortgeschrittenen-Praktikum Abteilung B Inhalt 1 Einführung 2 1.1 Kristallstrukturen und Grundlagen
Röntgenstrukturanalyse nach Debye-Scherrer Ilja Homm und Thorsten Bitsch Betreuer: Haiko Didzoleit 02.05.2012 Fortgeschrittenen-Praktikum Abteilung B Inhalt 1 Einführung 2 1.1 Kristallstrukturen und Grundlagen
Praktikum II PO: Doppelbrechung und eliptisch polatisiertes Licht
 Praktikum II PO: Doppelbrechung und eliptisch polatisiertes Licht Betreuer: Norbert Lages Hanno Rein [email protected] Florian Jessen [email protected] 26. April 2004 Made
Praktikum II PO: Doppelbrechung und eliptisch polatisiertes Licht Betreuer: Norbert Lages Hanno Rein [email protected] Florian Jessen [email protected] 26. April 2004 Made
Physikalisches Praktikum
 Physikalisches Praktikum MI2AB Prof. Ruckelshausen Versuch 3.2: Wellenlängenbestimmung mit dem Gitter- und Prismenspektrometer Inhaltsverzeichnis 1. Theorie Seite 1 2. Versuchsdurchführung Seite 2 2.1
Physikalisches Praktikum MI2AB Prof. Ruckelshausen Versuch 3.2: Wellenlängenbestimmung mit dem Gitter- und Prismenspektrometer Inhaltsverzeichnis 1. Theorie Seite 1 2. Versuchsdurchführung Seite 2 2.1
Materialanalytik. Praktikum
 Materialanalytik Praktikum Röntgenbeugung B503 Stand: 15.04.2015 Ziel: Anhand von Röntgenbeugungsuntersuchungen sollen folgende Bestimmungen durchgeführt werden: Identifikation zweier unbekannter Reinelemente
Materialanalytik Praktikum Röntgenbeugung B503 Stand: 15.04.2015 Ziel: Anhand von Röntgenbeugungsuntersuchungen sollen folgende Bestimmungen durchgeführt werden: Identifikation zweier unbekannter Reinelemente
Physik IV Einführung in die Atomistik und die Struktur der Materie
 Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 2011 Vorlesung 21 30.06.2011 Physik IV - Einführung in die Atomistik Vorlesung 21 Prof. Thorsten Kröll 30.06.2011 1 H 2
Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 2011 Vorlesung 21 30.06.2011 Physik IV - Einführung in die Atomistik Vorlesung 21 Prof. Thorsten Kröll 30.06.2011 1 H 2
Zentralabitur 2011 Physik Schülermaterial Aufgabe I ga Bearbeitungszeit: 220 min
 Thema: Eigenschaften von Licht Gegenstand der Aufgabe 1 ist die Untersuchung von Licht nach Durchlaufen von Luft bzw. Wasser mit Hilfe eines optischen Gitters. Während in der Aufgabe 2 der äußere lichtelektrische
Thema: Eigenschaften von Licht Gegenstand der Aufgabe 1 ist die Untersuchung von Licht nach Durchlaufen von Luft bzw. Wasser mit Hilfe eines optischen Gitters. Während in der Aufgabe 2 der äußere lichtelektrische
Berechnung eines Röntgen-Pulverdiffraktogramms aus Einkristallstrukturdaten ausgehend von einer RES-Datei. n λ = 2 d sinθ
 Versuch Nr. 2 Berechnung eines Röntgen-Pulverdiffraktogramms aus Einkristallstrukturdaten ausgehend von einer RES-Datei Einleitung: Die Pulverbeugung ist eine der wichtigsten Methoden zur Charakterisierung
Versuch Nr. 2 Berechnung eines Röntgen-Pulverdiffraktogramms aus Einkristallstrukturdaten ausgehend von einer RES-Datei Einleitung: Die Pulverbeugung ist eine der wichtigsten Methoden zur Charakterisierung
Physik 4, Übung 2, Prof. Förster
 Physik 4, Übung, Prof. Förster Christoph Hansen Emailkontakt 4. April 03 Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Ich erhebe keinen Anspruch auf Vollständigkeit oder Richtigkeit.
Physik 4, Übung, Prof. Förster Christoph Hansen Emailkontakt 4. April 03 Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Ich erhebe keinen Anspruch auf Vollständigkeit oder Richtigkeit.
Klausur 2 Kurs 13Ph3g Physik
 2010-12-02 Klausur 2 Kurs 13Ph3g Physik Lösung 1 Verbrennt in einer an sich farblosen Gasflamme Salz (NaClNatriumchlorid), so wird die Flamme gelb gefärbt. Lässt man Natriumlicht auf diese Flamme fallen,
2010-12-02 Klausur 2 Kurs 13Ph3g Physik Lösung 1 Verbrennt in einer an sich farblosen Gasflamme Salz (NaClNatriumchlorid), so wird die Flamme gelb gefärbt. Lässt man Natriumlicht auf diese Flamme fallen,
Klausur 2 Kurs 12Ph1e Physik
 2011-12-07 Klausur 2 Kurs 12Ph1e Physik Lösung 1 In nebenstehendem Termschema eines fiktiven Elements My sind einige Übergänge eingezeichnet. Zu 2 Übergängen sind die zugehörigen Wellenlängen notiert.
2011-12-07 Klausur 2 Kurs 12Ph1e Physik Lösung 1 In nebenstehendem Termschema eines fiktiven Elements My sind einige Übergänge eingezeichnet. Zu 2 Übergängen sind die zugehörigen Wellenlängen notiert.
Physik 4 Praktikum Auswertung Hall-Effekt
 Physik 4 Praktikum Auswertung Hall-Effekt Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Elektrischer Strom in Halbleitern..... 2 2.2. Hall-Effekt......... 3 3. Durchführung.........
Physik 4 Praktikum Auswertung Hall-Effekt Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Elektrischer Strom in Halbleitern..... 2 2.2. Hall-Effekt......... 3 3. Durchführung.........
A5 - COMPTON - Effekt
 A5 - COMPTON - Effekt Aufgabenstellung: 1. Nehmen Sie die Energiespektren der an einem Streukörper unter verschiedenen Winkeln gestreuten Röntgenstrahlung auf. Führen Sie eine Energiekalibrierung durch.
A5 - COMPTON - Effekt Aufgabenstellung: 1. Nehmen Sie die Energiespektren der an einem Streukörper unter verschiedenen Winkeln gestreuten Röntgenstrahlung auf. Führen Sie eine Energiekalibrierung durch.
Interferenz und Beugung
 Interferenz und Beugung In diesem Kapitel werden die Eigenschaften von elektromagnetischen Wellen behandelt, die aus der Wellennatur des Lichtes resultieren. Bei der Überlagerung zweier Wellen ergeben
Interferenz und Beugung In diesem Kapitel werden die Eigenschaften von elektromagnetischen Wellen behandelt, die aus der Wellennatur des Lichtes resultieren. Bei der Überlagerung zweier Wellen ergeben
502 Kristalluntersuchungen mit Hilfe von Debye-Scherrer-Aufnahmen
 502 Kristalluntersuchungen mit Hilfe von Debye-Scherrer-Aufnahmen Versuchsprotokoll zum F-Praktikum an der Ruhr-Universität Bochum 07.08.2009 Version
502 Kristalluntersuchungen mit Hilfe von Debye-Scherrer-Aufnahmen Versuchsprotokoll zum F-Praktikum an der Ruhr-Universität Bochum 07.08.2009 Version
Praktikumsversuch B2.1 Zwei röntgenografische Verfahren der Festkörperphysik
 Praktikumsversuch B2.1 Zwei röntgenografische Verfahren der Festkörperphysik Alexander Komarek, Sebastian Bleikamp, Martin Valldor Raum 326 im II. Physikalischen Institut der Universität zu Köln 1 Einleitung
Praktikumsversuch B2.1 Zwei röntgenografische Verfahren der Festkörperphysik Alexander Komarek, Sebastian Bleikamp, Martin Valldor Raum 326 im II. Physikalischen Institut der Universität zu Köln 1 Einleitung
Aufgabe I. 1.1 Betrachten Sie die Bewegung des Federpendels vor dem Eindringen des Geschosses.
 Schriftliche Abiturprüfung 2005 Seite 1 Hinweise: Zugelassene Hilfsmittel: Taschenrechner Die Aufgaben umfassen 5 Seiten. Die Zahlenwerte benötigter Konstanten sind nach der Aufgabe III zusammengefasst.
Schriftliche Abiturprüfung 2005 Seite 1 Hinweise: Zugelassene Hilfsmittel: Taschenrechner Die Aufgaben umfassen 5 Seiten. Die Zahlenwerte benötigter Konstanten sind nach der Aufgabe III zusammengefasst.
Röntgenstrahlung für Nichtmediziner
 1 Röntgenstrahlung für Nichtmediziner Vorbereitung: Erzeugung von Röntgenstrahlen, Funktionsweise einer Röntgenröhre, spektrale Zusammensetzung von Röntgenstrahlung, Eigenschaften von Röntgenstrahlung,
1 Röntgenstrahlung für Nichtmediziner Vorbereitung: Erzeugung von Röntgenstrahlen, Funktionsweise einer Röntgenröhre, spektrale Zusammensetzung von Röntgenstrahlung, Eigenschaften von Röntgenstrahlung,
Kontrollaufgaben zur Optik
 Kontrollaufgaben zur Optik 1. Wie schnell bewegt sich Licht im Vakuum? 2. Warum hat die Lichtgeschwindigkeit gemäss moderner Physik eine spezielle Bedeutung? 3. Wie nennt man die elektromagnetische Strahlung,
Kontrollaufgaben zur Optik 1. Wie schnell bewegt sich Licht im Vakuum? 2. Warum hat die Lichtgeschwindigkeit gemäss moderner Physik eine spezielle Bedeutung? 3. Wie nennt man die elektromagnetische Strahlung,
Röntgenaufnahme der Hand seiner Frau; Ganzkörperröntgenbild eines Menschen
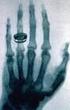 Röntgenstrahlung Historisches F 1.1 1845 Geburt von Wilhelm Conrad Röntgen in Lennep (Bergisches Land/Rheinprovinz) 1888 Professor der Experimentalphysik an der Julius-Maximilian-Universität Würzburg 1895
Röntgenstrahlung Historisches F 1.1 1845 Geburt von Wilhelm Conrad Röntgen in Lennep (Bergisches Land/Rheinprovinz) 1888 Professor der Experimentalphysik an der Julius-Maximilian-Universität Würzburg 1895
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Versuch K 226: Röntgenbeugung an Kristallen
 Fortgeschrittenen Praktikum Teil II Sommersemester 2003 Protokoll zu Versuch K 226: Röntgenbeugung an Kristallen Von Jan Stillings, Kathrin Valerius Semesterzahl: 8 Gruppe α 12 Assistent: Christoph Bommas
Fortgeschrittenen Praktikum Teil II Sommersemester 2003 Protokoll zu Versuch K 226: Röntgenbeugung an Kristallen Von Jan Stillings, Kathrin Valerius Semesterzahl: 8 Gruppe α 12 Assistent: Christoph Bommas
F CT1 Verschiedene Abtastverfahren in der Computertomographie
 F CT1 Verschiedene Abtastverfahren in der Computertomographie AB CT1 Prinzip der Computertomographie AB CT1 Prinzip der Computertomographie - Musterlösung Kollimatoren blenden ein etwa bleistiftdickes
F CT1 Verschiedene Abtastverfahren in der Computertomographie AB CT1 Prinzip der Computertomographie AB CT1 Prinzip der Computertomographie - Musterlösung Kollimatoren blenden ein etwa bleistiftdickes
Lösungen der Übungsaufgaben zum Experimentalphysik III Ferienkurs
 1 Lösungen der Übungsaufgaben zum Experimentalphysik III Ferienkurs Max v. Vopelius, Matthias Brasse 25.02.2009 Aufgabe 1: Dreifachspalt Abbildung 1: Spalt Gegeben ist ein Dreifachspalt 1. Alle Spaltbreiten
1 Lösungen der Übungsaufgaben zum Experimentalphysik III Ferienkurs Max v. Vopelius, Matthias Brasse 25.02.2009 Aufgabe 1: Dreifachspalt Abbildung 1: Spalt Gegeben ist ein Dreifachspalt 1. Alle Spaltbreiten
VL Physik für Mediziner 2009/10. Röntgenstrahlung
 VL Physik für Mediziner 2009/10 Röntgenstrahlung Peter-Alexander Kovermann Institut für Neurophysiologie Medizinische Hochschule Hannover [email protected] Was ist Röntgenstrahlung und. wer
VL Physik für Mediziner 2009/10 Röntgenstrahlung Peter-Alexander Kovermann Institut für Neurophysiologie Medizinische Hochschule Hannover [email protected] Was ist Röntgenstrahlung und. wer
Abiturprüfung Physik, Grundkurs. Aufgabe 1: Kräfte auf bewegte Ladungen in Leitern im Magnetfeld
 Seite 1 von 10 Abiturprüfung 2009 Physik, Grundkurs Aufgabenstellung: Aufgabe 1: Kräfte auf bewegte Ladungen in Leitern im Magnetfeld Eine bewegte elektrische Ladung erfährt in Magnetfeldern bei geeigneten
Seite 1 von 10 Abiturprüfung 2009 Physik, Grundkurs Aufgabenstellung: Aufgabe 1: Kräfte auf bewegte Ladungen in Leitern im Magnetfeld Eine bewegte elektrische Ladung erfährt in Magnetfeldern bei geeigneten
Grundbausteine des Mikrokosmos (7) Wellen? Teilchen? Beides?
 Grundbausteine des Mikrokosmos (7) Wellen? Teilchen? Beides? Experimentelle Überprüfung der Energieniveaus im Bohr schen Atommodell Absorbierte und emittierte Photonen hν = E m E n Stationäre Elektronenbahnen
Grundbausteine des Mikrokosmos (7) Wellen? Teilchen? Beides? Experimentelle Überprüfung der Energieniveaus im Bohr schen Atommodell Absorbierte und emittierte Photonen hν = E m E n Stationäre Elektronenbahnen
5. Oberflächen-und Dünnschichtanalytik. Prof. Dr. Paul Seidel VL Vakuum- und Dünnschichtphysik WS 2014/15
 5. Oberflächen-und Dünnschichtanalytik 1 5.1 Übersicht Schichtanalytik - Schichtmorphologie: - Oberflächeneigenschaften - Lichtmikroskop - Rasterelektronenmikroskop - Transmissionselektronenmikroskop -(STM,
5. Oberflächen-und Dünnschichtanalytik 1 5.1 Übersicht Schichtanalytik - Schichtmorphologie: - Oberflächeneigenschaften - Lichtmikroskop - Rasterelektronenmikroskop - Transmissionselektronenmikroskop -(STM,
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 200/20 8. Übungsblatt - 3.Dezember 200 Musterlösung Franziska Konitzer ([email protected]) Aufgabe ( ) (7 Punkte) Gegeben sei
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 200/20 8. Übungsblatt - 3.Dezember 200 Musterlösung Franziska Konitzer ([email protected]) Aufgabe ( ) (7 Punkte) Gegeben sei
Auswertung P2-10 Auflösungsvermögen
 Auswertung P2-10 Auflösungsvermögen Michael Prim & Tobias Volkenandt 22 Mai 2006 Aufgabe 11 Bestimmung des Auflösungsvermögens des Auges In diesem Versuch sollten wir experimentell das Auflösungsvermögen
Auswertung P2-10 Auflösungsvermögen Michael Prim & Tobias Volkenandt 22 Mai 2006 Aufgabe 11 Bestimmung des Auflösungsvermögens des Auges In diesem Versuch sollten wir experimentell das Auflösungsvermögen
2 Blatt - Festkörperphysik 2-2D Gitter
 Heiko Dumlich April 9, Bltt - Festkörperphysik - D Gitter. (Oberflächen kubisch rumzentrierter Kristlle) ) In Abbildung () befinden sich die drei Drufsichten der (), () und () Ebenen des kubisch-rumzentrierten
Heiko Dumlich April 9, Bltt - Festkörperphysik - D Gitter. (Oberflächen kubisch rumzentrierter Kristlle) ) In Abbildung () befinden sich die drei Drufsichten der (), () und () Ebenen des kubisch-rumzentrierten
Stundenprotokoll vom : Compton Effekt
 Stundenprotokoll vom 9.12.2011: Compton Effekt Zunächst beschäftigten wir uns mit den einzelnen Graphen des Photoeffekts (grün), des Compton-Effekts (gelb) und mit der Paarbildung (blau). Anschließend
Stundenprotokoll vom 9.12.2011: Compton Effekt Zunächst beschäftigten wir uns mit den einzelnen Graphen des Photoeffekts (grün), des Compton-Effekts (gelb) und mit der Paarbildung (blau). Anschließend
Versuch Q1. Äußerer Photoeffekt. Sommersemester Daniel Scholz
 Demonstrationspraktikum für Lehramtskandidaten Versuch Q1 Äußerer Photoeffekt Sommersemester 2006 Name: Daniel Scholz Mitarbeiter: Steffen Ravekes EMail: [email protected] Gruppe: 4 Durchgeführt am:
Demonstrationspraktikum für Lehramtskandidaten Versuch Q1 Äußerer Photoeffekt Sommersemester 2006 Name: Daniel Scholz Mitarbeiter: Steffen Ravekes EMail: [email protected] Gruppe: 4 Durchgeführt am:
Äußerer lichtelektrischer Effekt Übungsaufgaben
 Aufgabe: LB S.66/9 Durch eine Natriumdampflampe wird Licht der Wellenlänge 589 nm (gelbe Natriumlinien) mit einer Leistung von 75 mw ausgesendet. a) Berechnen Sie die Energie der betreffenden Photonen!
Aufgabe: LB S.66/9 Durch eine Natriumdampflampe wird Licht der Wellenlänge 589 nm (gelbe Natriumlinien) mit einer Leistung von 75 mw ausgesendet. a) Berechnen Sie die Energie der betreffenden Photonen!
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Inhalt Stöße Fallunterscheidung Stöße
 Inhalt.. Stöße Fallunterscheidung Stöße Physik, WS 05/06 Literatur M. Alonso, E. J. Finn: Physik; dritte Auflage, Oldenbourg Verlag, 000. Paul A. Tipler: Physik für Wissenschaftler und Ingenieure; sechste
Inhalt.. Stöße Fallunterscheidung Stöße Physik, WS 05/06 Literatur M. Alonso, E. J. Finn: Physik; dritte Auflage, Oldenbourg Verlag, 000. Paul A. Tipler: Physik für Wissenschaftler und Ingenieure; sechste
Festkörperphysik. Bragg-Reflexion: Bestimmung der Gitterkonstanten von Einkristallen. LD Handblätter Physik P Ste
 Festkörperphysik Kristalleigenschaften Röntgenstrukturanalyse LD Handblätter Physik P7.1.2.1 Bragg-Reflexion: Bestimmung der Gitterkonstanten von Einkristallen Versuchsziele Untersuchung und Vergleich
Festkörperphysik Kristalleigenschaften Röntgenstrukturanalyse LD Handblätter Physik P7.1.2.1 Bragg-Reflexion: Bestimmung der Gitterkonstanten von Einkristallen Versuchsziele Untersuchung und Vergleich
Physik für Maschinenbau. Prof. Dr. Stefan Schael RWTH Aachen
 Physik für Maschinenbau Prof. Dr. Stefan Schael RWTH Aachen Vorlesung 11 Brechung b α a 1 d 1 x α b x β d 2 a 2 β Totalreflexion Glasfaserkabel sin 1 n 2 sin 2 n 1 c arcsin n 2 n 1 1.0 arcsin
Physik für Maschinenbau Prof. Dr. Stefan Schael RWTH Aachen Vorlesung 11 Brechung b α a 1 d 1 x α b x β d 2 a 2 β Totalreflexion Glasfaserkabel sin 1 n 2 sin 2 n 1 c arcsin n 2 n 1 1.0 arcsin
Festkörperchemie SYNTHESE. Shake and bake Methode: Sol-Gel-Methode. Am Beispiel :
 Festkörperchemie SYNTHESE Shake and bake Methode: Am Beispiel : Man zerkleinert die Salze mechanisch, damit eine möglichst große Grenzfläche zwischen den beiden Komponenten entsteht und vermischt das ganze.
Festkörperchemie SYNTHESE Shake and bake Methode: Am Beispiel : Man zerkleinert die Salze mechanisch, damit eine möglichst große Grenzfläche zwischen den beiden Komponenten entsteht und vermischt das ganze.
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 10. Übungsblatt - 10. Januar 2011 Musterlösung Franziska Konitzer ([email protected]) Aufgabe 1 ( ) (6 Punkte) a)
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 10. Übungsblatt - 10. Januar 2011 Musterlösung Franziska Konitzer ([email protected]) Aufgabe 1 ( ) (6 Punkte) a)
