1 Wahrscheinlichkeitsrechnung
|
|
|
- Hilko Friedrich
- vor 6 Jahren
- Abrufe
Transkript
1 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) Wahrscheilichkeitsrechug Laplace-Wahrscheilichkeit: P ( E) Azahl der für das Ereigis E güstige Ausgäge E Azahl der mögliche Ausgäge Ω Elemetare Eigeschafte:. Für jedes Ereigis E ist P(E) 0 (Nichtegativität). Für das sichere Ereigis Ω ist P(Ω) (Normiertheit). 3. Für zwei disjukte Ereigisse E, E gilt die spezielle Additiosregel: P(E oder E ) P(E ) + P(E ). Daraus folgt für zwei komplemetäre Ereigisse E, E c : P(E c ) P(E). Allgemeie Additiosregel: P( A oder B) P( A) + P( B) P( A ud B) Bedigte Wahrscheilichkeit: Für zwei Ereigisse A Ω (A ), B Ω ist die Wahrscheilichkeit P(B A) vo B uter der Bedigug A (d.h. uter der Voraussetzug, dass A eigetrete ist): P ( B A) P( A ud B) P( A) Multiplikatiosregel: P ( A ud B) P( B A) P( A) P( A B) P( B) Soderfall für uabhägige Ereigisse A, B: P ( A ud B ) P ( A) P ( B ) Satz vo der totale Wahrscheilichkeit: Ereigisse A i (i,,,) bilde eie Zerlegug vo Ω, d.h. jeder Versuchsausgag liegt geau i eiem A i. Für jedes Ereigis B aus Ω gilt: P( B) i P( B A ) P( A ) i i Bayes sche Formel: Die Ereigisse A i (i,,,) bilde eie Zerlegug vo Ω; da gilt für jedes Ereigis B Ω (B ): P( Ai B) P( B Ai ) P( Ai ) P( B) mit P( B) i P( B A ) P( A ) i i StatFormel 04..4
2 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) Wahrscheilichkeitsverteiluge. Diskrete Verteiluge Biomialverteilug: Die Zufallsvariable X "Azahl der Wiederholuge mit dem Ausgag E" ist biomialverteilt mit de Parameter ud p (kurz X B,p ); die Werte der Biomialverteilug B,p sid gegebe durch: P( X x) B, ( ) p x ( p) x p x ( x 0,,,..., ) x R-Fuktioe: dbiom(), pbiom() dbiom(x, size, prob) pbiom(q, size, prob) x, q Quatile (Skalar oder Vektor) size Azahl der Versuchswiederholuge prob Erfolgswahrscheilichkeit (Skalar oder Vektor) Biomialkoeffiziet: ( )( ) L( x + )! ( x,3, K) x 3Lx ( x)! x!, 0! (gelese -Faktorielle,,3,4, ) 3 bezeichet die Azahl vo Permutatioe (d.h. Aorduge) vo Elemete. Für die Soderfälle 0 ud gilt: 0!,!. R-Fuktioe: factorial(), choose() factorial(x) choose(, k) x,, k ichtegative gaze Zahle, k < Mittelwert ud Variaz eier B,p -verteilte Zufallsvariable X: µ X σ X E[ X ] p Var [ X ] pq p( p) E[ X ] ( E[ X ]/ ) Poisso-Verteilug: Die Biomialverteilug strebt für p 0 ud kostat bleibedem Mittelwert p λ gege die sogeate Poissoverteilug P λ mit de Fuktioswerte P( X ) P ( ) e x x x λ λ ( x 0,,, K) λ x! Gute Approximatio B,p P λ bereits für >0 ud p < 0.! StatFormel 04..4
3 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 3 Es gilt: E [ X ] Var[ X ] λ R-Fuktioe: dpois(), ppois() dpois(x, lambda) ppois(q, lambda) x, q Quatile(Skalar oder Vektor) lambda Parameter der Poisso-Verteilug Hypergeometrische Verteilug: Es seie M eie Mege vo N Elemete, vo dee a vom Typ A sid, ud X die Zufallsvariable Azahl der Elemete vom Typ A, we isgesamt aus der Mege M gezogee (ud icht wieder zurückgelegt) werde. Da ist X hypergeometrisch verteilt mit de Parameter a,n-a ud (kurz X H a, N-a, p ). Die Fuktioswerte der hypergeometrische Verteilug H a, N-a, sid: a N a x x P ( X x) H a, N a, ( x) ( x 0,, K, a) N H a, N-a, p (x) B,p (x) für /N < 0, ud N > 60! Es gilt: E[ X ] p N Var[ X ] p( p) N R-Fuktioe: dhyper(), phyper() dhyper(x, m,, k) phyper(q, m,, k) Parameter (i Klammer die Bezeichuge des VO-Textes): x, q Quatile(Skalar oder Vektor), Azahl der A-Elemete i der Stichprobe m Azahl der A-Elemete i der Grudmege (a) Azahl der icht-a-elemete i der Grudmege (N-a) k Azahl der Elemete i der Stichprobe (). Stetige Verteiluge Stadardormalverteilug: X heißt stadardormalverteilt kurz X N(0,), we die Dichtefuktio vo X gegebe ist durch: ϕ ( x) exp( x / ) ( < x < + ) π Mittelwert ud Variaz eier N(0,)-verteilte Zufallsvariable X: µ σ X X E( X ) 0 Var( X ) StatFormel 04..4
4 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 4 Verteilugsfuktio: Φ: x Φ( x) P( X Hiweis: Φ(-x) - Φ(x) x < x) ϕ ( ξ) dξ Allgemeie Normalverteilug: X heißt ormalverteilt mit dem Mittelwert µ ud der Variaz σ - kurz: X N(µ,σ ), we Z (X-µ )/σ stadardormalverteilt ist. Dichtefuktio vo X: f : x f ( x) exp - σ π ( x µ ) σ Verteilugsfuktio: x F : x F( x) P( X < x) f (ξ) dξ Hiweis: X µ x µ x µ F(x) P ( X < x) P < Φ σ σ σ R-Fuktioe: dorm(), porm(), qorm(), r(orm() dorm(x, mea 0, sd ) porm(q, mea 0, sd ) qorm(p, mea 0, sd ) rorm(, mea 0, sd ) x, q Quatile (Skalar oder Vektor) p Uterschreitugswahrscheilichkeit (Skalar oder Vektor) mea Mittelwert der Normalverteilug sd Stadardabweichug der Normalverteilug Azahl der zu geerierede Zufallszahle StatFormel 04..4
5 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 5 3 Parameterschätzug 3. Mittelwert ud Variaz Zufallsstichprobe der metrische Variable X vom Umfag : X X,...,, X (Arithmetisches) Mittel: X X i i Variaz: S ( X i X ) i Stadardabweichug: S ( X i X ) i (-α)-kofidezitervall für de Mittelwert µ: [ X d X + d] mit d t SE ud SE S /,, α / Approximatio für großes : [ X z SE X + z SE] mit d z SE ud SE S / α /, α / α / Faustformel zur Plaug des Stichprobeumfages (Approximatio für großes ): Notwediger Stichprobeumfag für Mittelwertschätzug mit Geauigkeit d ud Sicherheit - α: z σ d α / R-Fuktioe: Arithmetisches Mittel: mea() Variaz: var() Stadardabweichug: sd() Kofidezitervall für Mittelwert: t.test() Hiweis: die Fuktio ist ur awedbar, we die Stichprobewerte gegebe sid, sost direkte Berechug mit de Defiitiosgleichuge. t.test(x, cof.level 0.95) x Datevektor, cof.level Kofidezzahl (default: 0.95) StatFormel 04..4
6 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 6 R-Fuktio zur Bestimmug eies (-α)-kofidezitervalls für demittelkwert: # R-Fuktio mit Übergabeparameter: # (Stichprobeumfag), xquer (arithmetisches Mittel), # std (Stadardabweichug), alpha (Irrtumsrisiko) CI_mea <- fuctio(, xquer, std, alpha){ q <- qt(-alpha/, -); sestd/sqrt(); d <- q*se ug <- xquer-d; og <- xquer+d greze <- cbid(ug, og) retur(greze)} optios(digits4) # Fuktiosaufruf mit 30, xquer0, std5, alpha5% CI_mea(30, 0, 5, 0.05) (-α)-kofidezitervall für die Variaz σ : ( ) S ( ) S, χ, α / χ, α / (-α)-kofidezitervall für die Stadardabweichug σ: ( ) S ( ) S, χ, α / χ, α / R-Fuktio zur Bestimmug eies (-α)-kofidezitervalls für die Variaz: # R-Fuktio mit Übergabeparameter: # (Stichprobeumfag), var (Variaz), alpha (Irrtumsrisiko) CI_var <- fuctio(, var, alpha){ ug <- (-)*var/qchisq(-alpha/, -) og <- (-)*var/qchisq(alpha/, -) greze <- cbid(ug, og) retur(greze)} optios(digits4) # Fuktiosaufruf mit 30, var7.93, alpha5% CI_var(30, 7.93, 0.05) ug og [,] Quatile Berechug des p-quatils x p (0 < p < ): Eie Stichprobe der Variable X umfasse die metrische Werte x, x,..., x. Die Aordug der Stichprobewerte ach aufsteigeder Größe führt auf die geordete Stichprobe x (), x (),..., x (). Ma bestimme die Zahl u +(-)p ud daraus die größte gaze Zahl [u] kleier oder gleich u; ferer setze ma v u-[u] x p ( v) x + vx ([ u]) ([ u] + ) Soderfälle: p 50% (Media x 0.5 ) p 5% (uteres Quartil x 0.5 ) p 75% (oberes Quartil x 0.75 ) StatFormel 04..4
7 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 7 R-Fuktioe: Media: media() Quatil: quatile(), summary() 5-Pukte-Zusammefassug: fiveum() 3.3 Eifache Grafike Puktdiagramm: Darstelleg der Stichprobewerte als Pukteauf der Merkmalsachse, für kleiere Stichprobe (<5) R-Fuktio: stripchart() Pukt-Plots für drei Messreihe. Lös.. Lös. 3. Lös Mg-Kozetratio i mikromol/00g Trockegewicht Box-Plot: besteht aus eiem Rechteck, das durch das utere ud obere Quartil begrezt wird ud i dem der Media markiert ist. Die Ausläufer ach ute ud obe reiche bis zum kleiste bzw. größte Merkmalswert. R-Fuktio: boxplot() Normal QQ-Plot: Zur Beurteilug, ob die Werte x, x,, x eier Zufallsstichprobe vo X gege die Aahme X ist ormalverteilt spreche. We X N(µ, σ ) verteilt ist, besteht zwische dem p-quatil x p vo X ud dem etsprechede Quatil z p der N(0, )-verteilte Zufallsvariable Z(X-µ)/σ der lieare Zusammehag x p σ z p + µ. Die Pukte StatFormel 04..4
8 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 8 P(z p, x p ) mit de für verschiedee Werte vo p (0 < p < ) berechete Quatile vo Z ud X als Koordiate) liege im (Z, X)-Koordiatesystem auf eier Gerade mit dem Astieg σ ud dem y- Achseabschitt µ. Die folgede Grafik ethält Normal-QQ-Plots für zwei Zufallsstichprobe (jeweils vom Umfag 30). Die QQ-Plots ethalte auch die Orietierugsgerade durch die de utere ud obere Quartile etsprechede Pukte. Liks sid die Dichtekurve der Grudgesamtheite dargestellt, aus dee die Stichprobe geeriert wurde (obe: Normalverteilug mit µ5 ud σ0.5, ute: logarithmische Normalverteilug mit µ - 0. ud σ). Vertikal sid die (ach aufsteigeder Größe ageordete) Stichprobewerte x (i) als (empirische) Quatile vo X aufgetrage. Die etsprechede Uterschreitugswahrscheilichkeite p i werde für >0 mit p i (i-0.5)/ ud für 0 mit p i (i- 3/8)( + ¼) bestimmt. Aus de p i ermittelt ma die dazu gehörede die Quatile z pi φ - (p i ) der N(0, )-Verteilug, die horizotal aufgetrage sid. R-Fuktioe: qqorm(), qqlie() 3.4 Wahrscheilichkeit Zufallsstichprobe der dichotome (0/-skalierte) Variable X vom Umfag : X X,...,, X m absolute Häufigkeit der Ausprägug (Azahl der Utersuchugseiheite mit der Ausprägug ), y m/ der Ateil der Wiederholuge mit der Ausprägug. Approximatives (-α)-kofidezitervall [u A, o A ] für die Wahrscheilichkeit p (Agresti-Coull-Itervall): u m A W m W l m + z + A, o A m W + l A mit α / / mw ( mw ) ud l A z α / z α / + z α / Voraussetzug für die Approximatio: y (-y ) > 9 StatFormel 04..4
9 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 9 Exaktes (-α)-kofidezitervall [p u, p o ] für die Wahrscheilichkeit p (Clopper-Pearso- Itervall): u C mf m + ( m + ) F m,( m+ ), α / ( m+ ),( m), α /, oc + mf m,( m+ ), α / m + ( m + ) F( m+ ),( m), α / R-Fuktioe: Kofidezitervall für die Wahrscheilichkeit p: library(biom) biom.cofit(x,, cof.level0.95, methodsc("ac", "exact")) x Zahl der Erfolge, Azahl der Versuche, cof.level Kifidezzahl (default: 0.95) methods Auswahlparamter für das gewüschte Kofidezitervall ("ac" Agresti-Coull, "exact"clopper-pearso) Alterative für Clopper-Pearso-Itervall: biom.test(x,, cof.level 0.95) (im Basis-Paket ethalte) oder selbstdefiierte R-Fuktio: # R-Fuktio mit Übergabeparameter: # (Stichprobeumfag), m (Azahl der Erfolge), alpha (Irrtumsrisiko) CI_p <- fuctio(m,, alpha){ qu <- qf(alpha/, *m, *(-m+)) qo <- qf(-alpha/, *(m+), *(-m)) uc <- m*qu/(-m++m*qu); oc <- (m+)*qo/(-m+(m+)*qo) greze <- cbid(uc, oc) retur(greze)} optios(digits4) # Fuktiosaufruf mit 0, m4, alpha5% CI_p(4, 0, 0.05) Faustformel zur Plaug des Stichprobeumfages (Approximatio für y (-y ) > 9): Notwediger Stichprobeumfag zur Schätzug vo p mit Geauigkeit d ud Sicherheit - α: z d α / StatFormel 04..4
10 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 0 4 Teste vo Hypothese: Eistichprobevergleiche 4. Allgemeies Etscheidugsalterative (Hypothese): z.b. über de Mittelwert µ eier Verteilug: -seitiger Test auf Abweichug: H 0 : µ µ o versus H : µ µ o (Fall II) -seitiger Test auf Überschreitug: H 0 : µ µ o versus H : µ > µ o (Fall Ia) -seitiger Test auf Uterschreitug: H 0 : µ µ o versus H : µ < µ o (Fall Ib) Etscheidugsproblem: Fehlerriske:. Fehler. Art (α-fehler): irrtümliche Ablehug vo H 0 ; Testetscheidug so, dass P(Etscheidug für H H o ist richtig) < α.. Fehler. Art (β-fehler): irrtümliche Nichtablehug vo H 0 ; P(keie Etscheidug für H H ist richtig) < β, u.a. vom Verteilugsparameter µ abhägig. Zusammefassug beider Fehlerriske i der Gütefuktio (power-fuctio): G(µ) P(Ablehug vo H 0 µ) Wahrscheilichkeit, auf Grud eier Zufallsstichprobe gege H 0 zu etscheide. Testetscheidug: Etscheidug erfolgt mit eier (für de jeweilige Test typische) Testgröße TG; Zufallsstichprobe Realisierug TG s. Etscheidug mit dem P-Wert (Wahrscheilichkeit, dass eie Zufallsstichprobe vom Umfag eie Wert der Testgröße TG ergibt, der zumidest gleich extrem im Sie vo H liegt, wie die beobachtete Realisierug TG s. H o wird abgeleht, we TG s (oder och extremere Werte) uter der Voraussetzug der Gültigkeit vo H o ur mit kleier Wahrscheilichkeit P auftritt (d.h. P kleier als α) ist. Mege der "sehr uwahrscheiliche" TG s -Werte bildet de sog. Ablehugsbereich. Die bei der Ablehug vo H o zur Awedug kommede logische Schlussfigur folgt dem Schema: We H o gilt, da ist ei TG s im Ablehugsbereich "sehr uwahrscheilich"; aus eier Zufallsstichprobe ergibt sich ei TG s im Ablehugsbereich. H o ist sehr uwahrscheilich. Was bedeutet ei icht-sigifikates Testergebis? P α H 0, H? P < α H 0, H? H Power β H 0 Power < β H 0, H? StatFormel 04..4
11 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 4. Ausgewählte Testverfahre Gauß-Test Der Gauß-Test diet zur Prüfug, ob der Mittelwert eier N(µ, σ )-verteilte Zufallsvariable X vo eiem vorgegebee Sollwert µ 0 abweicht bzw. diese uter- oder überschreitet. Die Variaz σ wird dabei als bekat vorausgesetzt. Hypothese ud Testgröße: (Ia) H 0 : µ µ 0, H : µ > µ 0 (Ib) H 0 : µ µ 0, H : µ < µ 0 (II) H 0 : µ µ 0, H : µ µ 0 TG X µ 0 σ Die Testgröße TG ist uter H 0 stadardormalverteilt. Testetscheidug mit dem P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α ist. Berechug des P-Wertes: P Φ( TG s ) (Fall Ia), P Φ( TG s ) (Fall Ib), P [ Φ( TGs )] (Fall II) Testetscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > z - α (Fall Ia) bzw. TG s < z α (Fall Ib) bzw. TG s > z -α/ (Fall II). Plaug des Stichprobeumfages: Notwediger Stichprobeumfag, um auf Niveau α mit Sicherheit -ß eie Etscheidug für H herbeizuführe, we µ vo µ 0 um 0 im Sie der Alterativhypothese abweicht: σ α / β α + z σ ( z + z ) (Fall II) bzw. ( z ) (Fälle Ia, b) β Gütefuktioe: µ µ 0 µ µ 0 ( ) / / G µ Φ z + Φ α z α + σ / σ / µ µ 0 ( ) (FallIa) / G µ Φ z α + σ µ 0 µ ( ) (FallIb) / G µ Φ z α + σ (Fall II) R-Fuktio: z.test() im Paket TeachigDemos z.test(x, mu0, sdstdev, alterative c("two.sided", "less", "greater"), mu 0, cof.level 0.95) x Datevektor; mu Referezwert mu0; stdev bekate Stadardabweichug StatFormel 04..4
12 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei); cof.level Kofidezzahl (default: 0.95) -Stichprobe-t-Test diet zur Prüfug, ob der Mittelwert µ eier ormalverteilte Zufallsvariable vo eiem vorgegebee Sollwert µ 0 abweicht (oder µ 0 überschreitet bzw. uterschreitet). Hypothese ud Testgröße: (I) H 0 : µ µ 0, H : µ µ 0 (IIa) H 0 : µ µ 0, H : µ > µ 0 (IIb) H 0 : µ µ 0, H : µ < µ 0 X µ 0 TG S Hiweis: Die Testgröße TG ist uter H 0 t-verteilt mit FG-. Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P-F - (TG s ) (Fall Ia) bzw. PF - (TG s ) (Fall Ib) bzw. PF - (- TG s ) (Fall II) ; F - ist die Verteilugsfuktio der t - -Verteilug. Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > t -,- α (Fall Ia) bzw. TG s < t -,α (Fall Ib) bzw. TG s > t -,-α/ (Fall I). R-Fuktio: t.test() t.test(x, alterative c("two.sided", "less", "greater"), mu 0, cof.level 0.95) x Datevektor; alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei); mu Referezwert mu0; cof.level Kofidezzahl (default: 0.95) Plaug des Stichprobeumfages: Notwediger Stichprobeumfag, um auf Niveau α mit Sicherheit -ß eie Etscheidug für H herbeizuführe, we µ vo µ 0 um 0 im Sie der Alterativhypothese abweicht (die Formel liefer ab 0 brauchbare Näherugswerte): σ σ ( / ) (Fall II) bzw. ( ) (Fälle Ia, b) z α + z β z α + z β R-Fuktio: power. t.test() power.t.test( NULL, delta NULL, sd, sig.level 0.05 (default), power NULL, type "oe.sample", alterative c("two.sided", "oe.sided")) StatFormel 04..4
13 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 3 Stichprobeumfag; delta relevate Abweichug; sd Stadardabweichug; sig.level Testiveau α; power ß; type Parameter zur Kezeichug des Typs des t-tests; alterative Parameter zur Kezeichug der Testalterative. Biomialtest diet zur Prüfug, ob eie ubekate Wahrscheilichkeit p vo eiem vorgegebee Sollwert p 0 abweicht bzw. diese über- oder uterschreitet; p ist die Wahrscheilichkeit, dass eie Utersuchugseiheit die Ausprägug E zeigt. Hypothese ud Testgröße: (Ia) H 0 : p p 0, H : p > p 0 bzw. (Ib) H 0 : p p 0, H : p < p 0 bzw. (II) H 0 : p p 0, H : p p 0 TGH Azahl der Beobachtuge mit der Ausprägug E ( ist der Stichprobeumfag); TG ~ B,p0 für pp 0. Normalverteilugsapproximatio (Voraussetzug: p 0 (-p 0 )>9): H p0 TG * ~ N (0,) für H 0 : p p0 p0 ( p0 ) Für die kokrete Beobachtugsreihe Hh a. Testetscheidug mit dem P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei Exakter Biomialtest: P - F B (h-) (Fall Ia) bzw. P F B (h) (Fall Ib) bzw. P F B (p 0 -d)+- F B (p 0 +d-) (Fall II) F B bezeichet die Verteilugsfuktio der B,p0 -Verteilug, d h-p 0. Approximativer Biomialtest (mit Stetigkeitskorrektur) P -F N (h-0.5) (Fall Ia) bzw. P F N (h+0.5) (Fall Ib) bzw. P F N (p_0-d+0.5) (Fall II) F N ist die Verteilugsfuktio der N(µ, σ )-Verteilug mit µp 0 ud σ 0 p 0 (-p 0 ); d hp 0 ist die Abweichug der beobachtete Azahl vom Mittelwert. (Approximative) Testetscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG* s - p 0 > 0.5+z -α σ 0 (Variate Ia) bzw. TG* s - p 0 > 0.5-z -α σ 0 (Variate Ib) bzw. TG* s - p 0 > 0.5+ z -α/ σ 0 (Variate II); z -α ud z -α/ sid das (-α)- bzw. das (-α/)- Quatil der N(0, )-Verteilug ud σ 0 p 0 (-p 0 ). Plaug des Stichprobeumfages: Notwediger Stichprobeumfag, um auf Niveau α mit Sicherheit -ß eie Etscheidug für H herbeizuführe, we p vo p 0 um 0 im Sie der Alterativhypothese abweicht: ( z + z ) α β ( arcsi p arcsi p ) 0 (Fälle Ia, b) bzw. ( z + z ) α / β ( arcsi p arcsi p ) 0 (Fall II) StatFormel 04..4
14 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 4 R-Fuktio: biom.test() - Exakter Biomialtest biom.test(x,, p 0.5, alterative c("two.sided", "less", "greater"), cof.level 0.95) x Azahl der Erfolge; Azahl der Versuche; p Referezwert p0 (siehe Hypothese); alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei); cof.level Kofidezzahl (default: 0.95). R-Fuktio: prop.test() - Approximativer Biomialtest prop.test(x,, p NULL, alterative c("two.sided", "less", "greater"), cof.level 0.95, correct TRUE) x Azahl der Erfolge; Azahl der Versuche; p Referezwert p0 (siehe Hypothese); alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei); cof.level Kofidezzahl (default: 0.95); correct logischer Parameter für Kotiuitätskorrektur. χ -Test zur Prüfug auf ei vorgegebees Verhältis diet zur Prüfug, ob die beobachtete Häufigkeite eier mehrstufig skalierte Zufallsvariable vo eiem vorgegebee Verhältis abweiche. Hypothese ud Testgröße: H 0 : p i p 0i (i,,..., k) gege H : p i p 0i für weigstes ei i p i ist die Wahrscheilichkeit, dass eie k-stufig skalierte Zufallsvariable (mit de Werte a, a,, a k ) de Wert a i aimmt; die p 0i sid vorgegebee Sollwerte. Die uter der Nullhypothese bei isgesamt Beobachtuge zu erwartede Häufigkeit der Ausprägug a i ist E i p i0. Testgröße (Chiquadrat-Summe, Goodess of Fit-Statistik): TG GF k i k ( O E ) ( O p ) i E i i i 0i i p 0i O i ist die Häufigkeit der Ausprägug a i. Die Testgröße ist uter H 0 asymptotisch χ -verteilt ist mit k- Freiheitsgrade. Ersetzt ma die Oi durch die beobachtete Häufigkeite oi, erhält ma die Realisierug TGs der Testgröße. Näherugsweise Testetscheidug mit dem P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P -F k- (TGs); F k- ist die Verteilugsfuktio der χ k--verteilug. StatFormel 04..4
15 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 5 Näherugsweise Testetscheidug mit Quatil: H 0 auf Sigifikaziveau α ablehe, we TG s > χ k-,α ( (-α)-quatil der χ k--verteilug). Die Näheruge sid vertretbar geau, we alle erwartete Häufigkeite E i >5 sid. R-Fuktio: chisq.test() chisq.test(x, p c(p0, p0,, p0k)) x umerischer Datevektor; p Vektor mit de Sollwahrscheilichkeite. Überprüfug der Normalverteilugsaahme, Ausreißer Shapiro-Wilk-Test wurde speziell zur Überprüfug der Aahme (Nullhypothese) etwickelt, dass eie metrische Zufallsvariable X ormalverteilt ist. Die Nullhypothese wird auf dem Niveau α abgeleht, we der P-Wert kleier als α ist. Hypothese: H 0 : Date stamme aus ormalverteilter Grudgesamtheit H : Date stamme aus icht-ormalverteilter Grudgesamtheit R-Fuktio: shapiro.test() Shapiro-Wilk-Test shapiro.test(x) x Datevektor. Idetifizierug vo Ausreißer Theoretischer Grudlage: X ~ N(µ, σ ) P(X < µ-4σ)+p(x > µ+4σ) % Tritt ei Wert außerhalb des 4-fache Sigma-Bereichs auf, so steht er im Verdacht, dass er keie Realisierug vo X ist, soder z.b. durch eie Datefehler oder eie Störeifluss bei der Messug zustade gekomme ist. Mutmaßliche Ausreißer sollte jedefalls dokumetiert ud ur da aus der Stichprobe etfert werde, we es dafür eie sachlogische Grud gibt. Zur Idetifizierug eies Stichprobewerts als Ausreißer gibt es eifache Kriterie - z.b. die Uter- bzw. Überschreitug der mit dem Iterquartilabstad IQR gebildete robuste Greze Q -.5 IQR bzw. Q IQR (Boxplot!) - oder spezielle Testverfahre. Grubbs-Test zur Idetifizierug eies eizele Ausreißers: Voraussetzug: X ~ N(µ, σ ); Überprüfug mit eiem Normal-QQ-Plot Testetscheidug: H 0 : Der Wert mit dem größte Abstad vom arithmetische Mittel ist kei Ausreißer wird auf dem Testiveau α abgeleht, we StatFormel 04..4
16 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 6 5 Teste vo Hypothese: Zweistichprobevergleiche 5. Zweistichprobevergleiche bei metrische Merkmale 5.. Übersicht 5.. Ausgewählte Testverfahre: Zweistichprobevergleiche - Parallelversuch -Stichprobe-t-Test Hypothese ud Testgröße: (II) H 0 : µ µ, H : µ µ (Ia) H 0 : µ µ, H : µ > µ (Ib) H 0 : µ µ, H : µ < µ TG X X S + mit S ( ) S + ( ) S + Voraussetzug: Variazhomogeität StatFormel 04..4
17 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 7 Hiweis: Die Testgröße TG ist uter H 0 t-verteilt mit FG + -. Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei PP(TG - TG s oder TG TG s ) (Fall II) bzw. PP(TG TG s ) (Fall Ia) bzw. PP(TG -TG s ) (Fall Ib). Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > t + -,-α/ (Fall II) bzw. TG s > t + -,- α (Fall Ia) bzw. TG s < t + -, α (Fall Ib) R-Fuktio: t.test() -Stichprobe t-test t.test(x, y NULL, alterative c("two.sided", "less", "greater"), var.equal T, cof.level 0.95) x Datevektor (X-Stichprobe); y Datevektor (Y-Stichprobe) alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei; greater bedeutet H: Mittelwert vo X > Mittelwert vo Y); var.equal logischer Parameter zur Variazhomogeität; cof.level Kofidezzahl (default0.95). Plaug des Stichprobeumfages: Notwediger Stichprobeumfag, um auf Niveau α mit Sicherheit -ß eie Etscheidug für H herbeizuführe, we µ vo µ um 0 im Sie der Alterativhypothese abweicht (die Formel gelte für ud liefer ab 0 brauchbare Näherugswerte): σ σ ( z + z ) (Fall II) bzw. ( z z ) (Fälle Ia, b) α / β α + β R-Fuktio: power.t.test() - Power/Mideststichprobeumfag power.t.test( NULL, delta NULL, sd, sig.level 0.05, power NULL, type "two.sample", alterative c("two.sided", "oe.sided")) Stichprobeumfag (i jeder der zu vergleichede Gruppe) delta relevate Abweichug (der Gruppemittelwerte); sd Stadardabweichug (Quadratwurzel der gewichtete Stichprobevariaze); sig.level Testiveau α; power -ß; type Parameter zur Kezeichug des Typs des t-tests; alterative Parameter zur Kezeichug der Testalterative. StatFormel 04..4
18 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 8 Welch-Test Hypothese: siehe -Stichprobe-t-Test. Testgröße: X X TG S + S / / Hiweis: Die Testgröße TG ist uter H 0 approximativ t-verteilt mit dem Freiheitsgrad f ( s / ) ( s /( / + s ) + ( s / ) / ) /( ) Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei PF f (- TGs ) (Fall II) bzw. P-F f ( TG s ) (Fall Ia) bzw. PF f (TG s ) (Fall Ib); F f ist die Verteilugsfuktio der t-verteilug mit f Freiheitsgrade. Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > t f, -α/ (Fall II) bzw. TG s > t f, - α (Fall Ia) bzw. TG s < t f, α (Fall Ib). R-Fuktio: t.test() Welch-Test t.test(x, y NULL, alterative c("two.sided", "less", "greater"), cof.level 0.95) x Datevektor (X-Stichprobe); y Datevektor (Y-Stichprobe) alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei; greater bedeutet H: Mittelwert vo X > Mittelwert vo Y); cof.level Kofidezzahl (default0.95). F - Test (Parallelversuch) Hypothese ud Testgröße: (II) H 0 : σ σ, H : σ σ (Ia) H 0 : σ σ, H : σ > σ (Ib) H 0 : σ σ, H : σ < σ S TG S Hiweis: Die Testgröße TG ist uter H 0 F-verteilt mit dem erste Freiheitsgrad f - ud dem zweite Freiheitsgrad f -. Etscheidug mit P-Wert: StatFormel 04..4
19 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 9 H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P[-F f,f (TG s )] (Fall II) bzw. P-F f,f (TG s ) (Fall Ia) bzw. PF f,f (TG s ) (Fall Ib); dabei ist F f,f die Verteilugsfuktio der F-Verteilug mit de Freiheitsgrade f ud f; TG s wird so agesetzt, dass die größere Variaz im Zähler steht. Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s <F -,-,α/ oder TG s >F -,-,-α/ (Fall II) bzw. TG s >F -,-,-α (Fall Ia ) bzw. TG s <F -,-,α (Fall Ib). R-Fuktio: var.test() F-Test var.test(x, y, ratio, alterative c("two.sided", "less", "greater"), cof.level 0.95) x, y Datevektore (X- ud Y-Stichprobe); ratio theoretische Variazverhältis; alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei; greater bedeutet H: Variaz vo X > Variaz vo Y); cof.level Kofidezzahl (default: 0.95). U-Test (Wilcoxo-Ragsummetest, Ma-Whitey-Test, Parallelversuch) Verteilugsfuktioe F ud F des Utersuchugsmerkmals uter de Versuchsbediguge uterscheide sich ur i der Lage, d.h., Graph vo F geht durch Verschiebug um ei bestimmtes θ i Richtug der positive horizotale Achse i Graphe vo F über. F ud F müsse icht ormalverteilt sei. Hypothese ud Testgröße: (II) H 0 : θ 0, H : θ 0 (Ia) H 0 : θ 0, H : θ > θ (Ib) H 0 : θ 0, H : θ < 0 Sigifikaziveau: α TG W R-(+)/; für θ 0 gilt: E(W)µ W / bzw. Var(W) σ W ( + +)/ Approximatio bei große Stichprobe ( >0, >0): U E[ W ] TG' N(0,) Var[ W ] Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P F W (µ W -d) + - F W (µ W +d-) mit d TG s -µ W für die zweiseitige Testvariate II, P - F W (TG s -) für die Variate Ia, P - F W (TG s ) für die Variate Ib (F W bezeichet die Verteilugsfuktioe vo W bei Gültigkeit vo H 0 ). Etscheidug mit Quatile: StatFormel 04..4
20 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 0 H 0 auf Sigifikaziveau α ablehe, we TG s < w,, α/ oder TG s > w,, -α/ (Variate II) bzw. TG s > w,, -α (Variate Ia) bzw. TG s < w,, α (Variate Ib) gilt; Dabei bezeichet w,, γ das γ-quatil der Nullverteilug der Testgröße. I R werde Werte der Verteilugsfuktio F W vo W mit der Fuktio pwilcox() ud die Quatile vo F_W mit qwilcox() bestimmt. R-Fuktio: wilcox.test() wilcox.test(x, y, alterative c("two.sided", "less", "greater"), exact NULL, correct TRUE, cof.it FALSE, cof.level 0.95) x, y umeric vectors of data values. alterative a character strig specifyig the alterative hypothesis, must be oe of "two.sided" (default), "greater" or "less". exact a logical idicatig whether a exact p-value should be computed. correct a logical idicatig whether to apply cotiuity correctio i the ormal approximatio for the p-value. cof.it a logical idicatig whether a cofidece iterval should be computed. cof.level cofidece level of the iterval Ausgewählte Testverfahre: Zweistichprobevergleiche - Paarvergleiche t-test für abhägige Stichprobe (Paarvergleich) ist ei mit der Differezvariable DX -X ud dem Sollwert µ 0 0 geführter -Stichprobe-t-Test. Es bedeute µ D ud σ D de Mittelwert bzw. die Stadardabweichug vo D; X D ud S D sid das Stichprobemittel bzw. die Stichprobevariaz der Differezstichprobe. Hypothese ud Testgröße: (I) H 0 : µ D 0, H : µ D 0 (IIa) H 0 : µ D 0, H : µ D > 0 (IIb) H 0 : µ D 0, H : µ D < 0 TG X S D D Hiweis: Die Testgröße TG ist uter H 0 t-verteilt mit FG-. Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P-F - (TG s ) (Fall Ia) bzw. PF - (TG s ) (Fall Ib) bzw. PF - (- TG s ) (Fall II); F - ist die Verteilugsfuktio der t - -Verteilug. Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > t -,- α (Fall Ia) bzw. TG s < t -,α (Fall Ib) bzw. TG s > t -,-α/ (Fall I). StatFormel 04..4
21 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) R-Fuktio: t.test() t.test(x, x, pairedt, alterative c("two.sided", "less", "greater"), cof.level 0.95) x, x Datevektor; alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei); paired logische Variable, ist bei Paarvergleich auf TRUE zu setze; cof.level Kofidezzahl (default: 0.95) Plaug des Stichprobeumfages: Notwediger Stichprobeumfag, um auf Niveau α mit Sicherheit -ß eie Etscheidug für H herbeizuführe, we µ D vo 0 um 0 im Sie der Alterativhypothese abweicht (die Formel liefer ab 0 brauchbare Näherugswerte): σ D σ ( ) (Fall II) bzw. D z + z ( z z ) (Fälle Ia, b) α / β α + R-Fuktio: power. t.test() power.t.test( NULL, delta NULL, sd, sig.level 0.05 (default), power NULL, type "paired", alterative c("two.sided", "oe.sided")) Stichprobeumfag; delta relevate Abweichug; sd Stadardabweichug; sig.level Testiveau α; power ß; type "paired" Parametersetzug zur Kezeichug des t-tests für abhägige Stichprobe; alterative Parameter zur Kezeichug der Testalterative. β Wilcoxo-Test (Wilcoxo siged rak test, Paarvergleich) Differezvariable Y-X icht otwedigerweise ormalverteilt, ζ Media der Verteilug vo Y-X. Hypothese ud Testgröße: (I) H 0 : ζ 0, H : ζ 0 (IIa) H 0 : θ 0, H : ζ > θ (IIb) H 0 : ζ 0, H : ζ < 0 Sigifikaziveau: α TG T+ (uter H0: E[T+](+)/4, Var[T+] (+)(+)/4) Approximatio für große Stichprobe (>0): + + T E[ T ] TG' N(0,) + Var[ T ] StatFormel 04..4
22 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P F W+ (µ W+ -d) + - F W+ (µ W+ +d-) mit d TG s -µ W+ für die zweiseitige Testvariate II, P - F W+ (TG s -) für die Variate Ia, P - F W+ (TG s ) für die Variate Ib (F W+ bezeichet die Verteilugsfuktioe vo W + bei Gültigkeit vo H 0 ). Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s < w +, α/ oder TG s > w +, -α/ (Variate II) bzw. TG s > w +, -α (Variate Ia) bzw. TG s < w +, α (Variate Ib) gilt; Dabei bezeichet w +, γ das γ-quatil der Nullverteilug der Testgröße. Zur Berechug vo Fuktioswerte der Verteilugsfuktio vo W + steht i R die Aweisug psigrak() zur Verfügug, Quatile erhält ma mit qsigrak() R-Fuktio: wilcox.test() wilcox.test(x, y, alterative c("two.sided", "less", "greater"), paired TRUE, exact NULL, correct TRUE, cof.it FALSE, cof.level 0.95) x, y umeric vectors of data values. alterative a character strig specifyig the alterative hypothesis, must be oe of "two.sided" (default), "greater" or "less". exact a logical idicatig whether a exact p-value should be computed. correct a logical idicatig whether to apply cotiuity correctio i the ormal approximatio for the p-value. cof.it a logical idicatig whether a cofidece iterval should be computed. cof.level cofidece level of the iterval. StatFormel 04..4
23 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 3 5. Zweistichprobevergleiche bei -stufige Merkmale 5.. Übersicht 5.. Ausgewählte Testverfahre Vergleich zweier Wahrscheilichkeite (uabhägige Stichprobe) X zweistufiges Merkmal mit de Auspräguge a ud a, das uter zwei Versuchsbediguge beobachtet wird;, Umfäge der Parallelstichprobe; p, p Wahrscheilichkeite, dass X uter de Versuchsbediguge de Wert a aimmt. Hypothese ud Testgröße: (II) H 0 : p p, H : p p (Ia) H 0 : p p, H : p > p (Ib) H 0 : p p, H : p < p TG Y Y Y ( Y ) + Y, Y Ateile, mit dee die Merkmalsausprägug uter der erste bzw. zweite Versuchsbedigug auftritt; Y Ateil, mit dem der Wert a i beide zusammegefasste Gruppe auftritt. Idem ma für Y, Y ud Y die etsprechede relative Häufigkeite y /, y / bzw. y. / eisetzt, erhält ma die Realisierug TG s der Testgröße; dabei ist ij die Azahl der Utersuchugseiheite mit der Ausprägug a i uter der j-te Versuchsbedigug ud. Der Ateil der Utersuchugseiheite mit der Ausprägug a i beide Gruppe. StatFormel 04..4
24 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 4 TG ist uter H 0 (p p ) ageähert stadardormalverteilt, we die auf de Gesamtumfag + bezogee Produkte der Spaltesumme mit de Zeilesumme größer als 5 sid. Die Approximatio ka verbessert werde, we Stetigkeitskorrektur so vorgeomme wird, dass ma i TG s y ud y im Falle y > y durch y - /( ) bzw. y + /( ) ud im Falle y < y durch y +/( ) bzw. y - /( ) ersetzt. Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P F(- TG s ) für die zweiseitige Testvariate II bzw. P - F(TG s ) für die Variate Ia bzw. P F(TG s ) für die Variate Ib ist. Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > z -α/ (Fall II) bzw. TG s > z - α (Fall Ia) bzw. TG s < z α (Fall Ib) R-Fuktio: prop.test() prop.test(x,, alterative c("two.sided", "less", "greater"), cof.level 0.95) x Vektor mit de Azahle der Erfolge i de zu vergleichede Gruppe; Vektor mit de Azahle der Versuche i de zu vergleichede Gruppe; alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei) cof.level Kofidezzahl (default 0.95). Plaug des Stichprobeumfages: Notwediger Stichprobeumfag, um auf Niveau α mit Sicherheit -ß eie Etscheidug für H herbeizuführe, we p vo p um 0 im Sie der Alterativhypothese abweicht: ( z + z ) α / β mit h arcsi p + arcsi h Im Falle der -seitige Testvariate ist α/ durch α zu ersetze. R-Fuktio: power.prop.test() - Power/Mideststichprobeumfag power.prop.test( NULL, p NULL, p NULL, sig.level 0.05, power NULL, alterative c("two.sided", "oe.sided")) Stichprobeumfag (i jeder Gruppe); p Erfolgswahrscheilichkeit i Gruppe ; p Erfolgswahrtscheilichkeit i Gruppe ; sig.level Testiveau α; power -ß: alterative Parameter zur Kezeichug der Testalterative. p StatFormel 04..4
25 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 5 McNemar-Test zum Vergleich vo Wahrscheilichkeite (abhägige Stichprobe) X, X zweistufige Merkmale mit Werte a ud a ; Beobachtug vo X ud X a Utersuchugseiheite abhägige Stichprobe Zusammefassug i Vierfeldertafel: X X a a Σ a. a. Σ.. Hypothese ud Testgröße: p. P(X a ) P(X a ud X a ) + P(X a ud X a ), p. P(X a ) P(X a ud X a ) + P(X a ud X a ), p P(X a ud X a ), p P(X a ud X a ); H 0 : p. p. vs. H : p. p. H 0 : p p vs. H : p p H 0 : p *:p /(p + p ) p /(p + p ) : p * vs. H : p * p * H 0 : p * ½ vs. H : p * ½ (wege p *+ p *) Testgröße (Biomialtest): TG H ~ B *,p0 (falls H 0 gilt) H Azahl der Utersuchugseiheite mit X a ud X a, * +, p 0 /; Realisierug vo TG: TG s. Testgröße (McNemar-Statistik, Normalverteilugsapproximatio): ( H H ) + TG ~ χ uter H0 (approx. für > 9 H + H 4 Etscheidug mit dem P-Wert (Biomialtest) P < α H 0 ablehe, wobei PF B (µ 0 -d)+- F B (µ 0 +d-); F B Verteilugsfuktio der B *,/ -Verteilug, µ 0 */, d -µ 0 - /. Etscheidug mit dem P-Wert (Normalverteilugsapproximatio) P < α H 0 ablehe, wobei P- F (TG s ) (F Verteilugsfuktio der χ Verteilug) Plaug des Stichprobeumfags: Notwediger Mideststichprobeumfag * ( + ), um auf dem Niveau α mit der Sicherheit -β eie Etscheidug für H herbeizuführe, we p * vo / um 0 abweicht: ( z α / + z β ) * ( arcsi arcsi 0.5) R-Fuktio: mcemar.test() - McNemar Test mcemar.test(x, correct TRUE) x Matrix (Vierfeldertafel mit de absolute Häufigkeite: Azahl der Utersuchugseiheite vom Typ + zum Zeitpukt, die auch zum Zeitpukt vom Typ + sid, Azahl der Utersuchugseiheite vom Typ + zum Zeitpukt, die zum Zeitpukt vom Typ sid, usw.) correct logischer Parameter für Kotiuitätskorrektur. StatFormel 04..4
26 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) Zweistichprobevergleiche bei m-stufige Merkmale (m>) Chiquadrat-Test (Homogeitätsprüfug) Hypothese ud Testgröße: H 0 : p i p i vs. H : icht alle p i p i (i,,...,m) Sigifikaziveau: α e i. ( e ) TG GF ~ χ m e mit ij m i j. j (Faustformel: alle e ij ud max. 0% der e ij < 5): Etscheidug mit Quatil: H 0 auf Testiveau α ablehe, we TG s > χ m-,-α. ij ij Etscheidug mit P-Wert: H0 auf Sigifikaziveau α ablehe, we P P(TG TGs )<α. ij uter H 0 (approx.) R-Fuktio: chisq.test() chisq.test(x, y NULL, correct TRUE, p rep(/legth(x), legth(x)), rescale.p FALSE) x a umeric vector or matrix. y a umeric vector; igored if x is a matrix. correct a logical idicatig whether to apply cotiuity correctio whe computig the test statistic for by tables: oe half is subtracted from all O - E differeces. p a vector of probabilities of the same legth of x. rescale.p a logical scalar; if TRUE the p is rescaled (if ecessary) to sum to. If rescale.p is FALSE, ad p does ot sum to, a error is give. StatFormel 04..4
27 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 7 6 Abhägigkeit (Zusammehag) zwische zwei Merkmale Zusammehag zwische zwei Merkmale abhägige Stichprobe Metrische Merkmale k-stufige Merkmale Abhägigkeitsprüfug über ρ (t-test) Abhägigkeitsprüfug mit χ -Statistik 6. Produktmometkorrelatio Produktmometkorrelatio als Parameter der -dimesioale Normalverteilug Defiitio: X ud Y heiße -dimesioal ormalverteilt mit de Parameter µ X, µ Y, σ X, σ Y ud ρ XY, we sie mit Hilfe vo uabhägige, N(0,)-verteilte Zufallsvariable Z, Z durch wie folgt erzeugt werde: X σ Z Y X Y σ ρ XY + µ Z X + σ Y ρ XY Z + µ Y Schätzug des Verteilugsparameters ρ XY : Es sei (x i,y i ) (i,,...,) eie Zufallsstichprobe der Zufallsvariable X ud Y mit zweidimesioaler Normalverteilug. Da ist r XY s XY XY sx sy ( r + ) ei Schätzwert für die Produktmometkorrelatio (Pearso-Korrelatio) ρ XY. Es sid: s X ud s Y die Stadardabweichuge der X- ud Y-Stichprobe ud s XY dere Kovariaz: s XY i ( x x)( y y) i i StatFormel 04..4
28 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 8 Z-Trasformtio: + r Z : r Z( r ) l r + ρ µ Z l, σ Z ρ Z µ Z σ Z N(0,) mit 3 (-α)-kofidezitervall [z u, z o ] für Z(ρ) µ Z mit z Z( r ) z σ, z u o Z( r ) + z α / α / σ Z Z Rücktrasformatio vo der Z- auf die r-skala (-α)-kofidezitervall für ρ exp( z u ) exp( z, exp( zu ) + exp( z o o ) ) + Abhägigkeitsprüfug mit der Produktmometkorrelatio Hypothese ud Testgröße: (II) H 0 : ρ XY 0, H : ρ XY 0, (Ia) H 0 : ρ XY 0, H : ρ XY > 0, (Ib) H 0 : ρ XY 0, H : ρ XY < 0 rxy sxy TG mit rxy r sxs xy Hiweis: Die Testgröße TG ist uter H 0 t-verteilt mit FG-. Etscheidug mit Quatile: H 0 auf Sigifikaziveau α ablehe, we TG s > t -,-α/ (Fall II) bzw. TG s > t -,- α (Fall Ia) bzw. TG s < t -, α (Fall Ib) Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P-F - (TG s ) (Fall Ia) bzw. PF - (TG s ) (Fall Ib) bzw. PF - (- TG s ) (Fall II); F - ist die Verteilugsfuktio der t - -Verteilug. y R-Fuktio: cor.test() cor.test(x, y, alterative c("two.sided", "less", "greater"), method "pearso", cof.level 0.95) x, y Datevektore (X- ud Y-Stichprobe) alterative Parameter zur Kezeichug der Testalterative (muss vo der Gestalt "two.sided" (default), "greater" oder "less" sei; method Parameter zur Festlegug des Korrelatiosmaßes; cof.level Kofidezzahl (default: 0.95). StatFormel 04..4
29 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 9 6. Eifache lieare Regressio Lieares Modell (Typ B: zufallsgestörte lieare Abhägigkeit der Zielvariable Y vo der Eiflussvariable X): Y ( x) µ ( x) + E mit 0 0 E µ ( x) f ( x; β, β ) β + β x, Y Y E N(0, σ ) Es sid µ Y (x) der durchschittliche (durch X bestimmte) Wert vo Y sowie β o ud β die zu schätzede Parameter der Regressiosgerade mit der Gleichug µ Y (x) β o + β X. Die Schätzwerte für β o (y-achseabschitt) ud β (Astieg) seie b o bzw. b. Prizip der Kleiste Quadrat Schätzug: Y y ^ b 0 + b x y i ^ y i (0, b 0 ) e i P i ^Pi X Schätzwerte: ˆ sxy sy β b rxy, ˆ β0 b0 y b x sx sx Vorgagsweise bei liearer Regressiosaalyse:. Überprüfug der Adäquatheit des lieare Modells (Regressiosgerade) im Streudiagramm. we. zutrifft: Prüfug auf (lieare) Abhägigkeit (Abhägigkeitsprüfug mit der Produktmometkorrelatio) 3. we. zutrifft: Schätze der Regressiosparameter ud Agabe der Regressiosgerade 4. Überprüfug der Residue (Normalverteilug) 5. Beurteilug der Güte der Apassug mit dem Bestimmtheitsmaß Br R-Fuktio: plot() Streudiagramm plot(x, y,...) x Datevektor für die uabhägige Variable X; y Datevektor für die abhägige Variable Y;... Grafikparameter (zb mai (mai Überschrift ), xlab (xlab X-Achse- Bezeichug ), ylab (ylab Y-Achsebezeichug ). R-Fuktio: ablie() Eizeiche der Regressiosgerade i das Streudiagramm ablie(lm(y~x)) x Datevektor für die uabhägige Variable X; y Datevektor für die abhägige Variable Y. x i StatFormel 04..4
30 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 30 R-Fuktio: lm() Lieares Modell lm(formula, data) formula Regressiosfuktiosterm (bei eifacher liearer Regressio: abh. V. ~ uabh. V.) data dataframe mit de Stichprobe der Variable als Spalte. 6.3 Lieare Regressio durch de Nullpukt: Modell: Y ( x) µ ( x) + E mit µ ( x) f ( x; β ) β x, Y Y E E N(0, σ ) Parameterschätzug: Schätzwerte für die Modellparameter: ˆβ b i x y SQE MQE mit i i i x i, SQE i y i i x i yi i x i (-α)-kofidezitervall für de Astieg: MQE b t SE b b t ±, α / ( ) ±, α / i x i R-Fuktio: lm() Lieares Modell lm(formula, data) formula Regressiosfuktiosterm (bei liearer Regressio durch de Nullpukt: abh. V. ~ 0 + uabh. V.) data dataframe mit de Stichprobe der Variable als Spalte. 6.4 Lieare Kalibratiosfuktioe: Bestimmug der Kalibratiosfuktio: ˆ sxy sy β, ˆ b r 0 0, XY β b y b x s s ˆ σ E X SQE MQE X mit SQE ( ) s Voraussetzug (Abhägigskeitsprüfug): TG Y ( r rxy b ( ) s X > t, α / r MQE XY Rückschluss vo Y auf X: XY ) StatFormel 04..4
31 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 3 Schätzwert für gesuchte Probewerte vo X zu bekatem Wert (Erwartugswert) η vo Y: ξ ( η β ) β. 0 / Im Allgemeie sid weder die Regressiosparameter och η bekat; η wird durch de Mittelwert y * aus m zum selbe ξ gemessee Y-Werte (im Extremfall ka m sei) geschätzt, ξ durch xˆ x + ( yˆ * y) / b ; Stadardfehler sx ˆ vo xˆ : ( y y) MQE s + + xˆ b m b ( ) sx Voraussetzug: t / TG 0. g, α / < Approximatives (-α)-kofidezitervall für Probewert ξ : UG xˆ t s ud OG x t s, α / xˆ ˆ +, α / xˆ Hiweis: Für ei optimales Desig der Kalibratiosfuktio wird ma darauf achte, dass ( y y) möglichst klei ud s möglichst groß ist. X R-Fuktio zur Schätzug eies Probewertes mit Hilfe eier lieare Kaibratiosfuktio: # R-Fuktio zur Schätzug eies Probewertes # mit Hilfe eier liare Kalibratiosfuktio # *************************************************************************** # Eigabeparameter # x, y Vektore der Kalibrierprobewerte bzw. der Hilfsgrößewerte # lieare Regressio vo y auf x ergibt die Kalibratiosfuktio # y0 gemesseer y-wert # alpha Irrtumsrisiko # Ausgabeparameter # y0 gemesseer y-wert y0 der ubekate Probe # x0 <- Schätzwert für de ubekate Probewert # alpha Irrtumsrisiko # se_xd Stadardfehler der Schätzfuktio für ubekate Probewert # UG, OG Greze eies (-alpha)-ci für ubekate Probewert # g kritischer Wert für Approximatio: muss < 0. sei! # **************************************************************************** prob_est fuctio(x, y, y0, alpha){ # a) Abhägigkeitsprüfug ud Parameterschätzug: date <- data.frame(x, y) kal_modell <- lm(y~x, datadate) ergebis <- summary(kal_modell); b <- ergebis$coefficiets b0 <- b[,]; b <- b[,] # b) Schätzug des Wertes x0 zu gemessee y-wert y0 der ubekate Probe x0 <- (y0-b0)/b # Schätzwert für ubekate Probewert yquer <- mea(y); <- legth(x); sigma <- ergebis$sigma se_xd <- sigma/abs(b)*sqrt(+/+(y0-yquer)^/b^/(-)/var(x)) t_quatil <- qt(-alpha/, -) UG <- x0 - t_quatil*se_xd; OG <- x0 + t_quatil*se_xd # Überprüfug der Voraussetzug r <- cor(x, y); tgs <- r*sqrt(-)/sqrt(-r^); g <- t_quatil^/tgs^ out <- c(y0, x0, alpha, se_xd, UG, OG, g) retur(out) } # Beispiel für Aufruf der R-Fuktio masse <- c(.409,3.03, 5.508, 8.00, 0.303) peak <- c(0.07, 0.040, 0.065, 0.084, 0.0) y0 < ; alpha < prob_est(masse, peak, y0, alpha) StatFormel 04..4
32 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) Abhägigkeitsprüfug mit der Chiquadrat-Statistik (X, Y zwei mehrstufig skalierte Variable, Date Kotigeztafel; Durchführug: siehe Homogeitätsprüfug) StatFormel 04..4
33 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 33 7 Variazaalyse 7. Globaltest Date: Variable Y uter k Versuchsbediguge ( Faktorstufe) wiederholt (a j Utersuchugseiheite auf der Faktorstufe j) gemesse k uabhägige Stichprobe Aordug i Datetabelle (y ij Messwert vo der i-te Utersuchugseiheit uter der j - Versuchsbedigug): Versuchsbedigug (Faktorstufe)... j... k Wiederholuge y y... y j... y k y y... y j... y k y i y i... y ij... y ik y, y,... y j,j... y k,k Azahl... j... k Mittelwert m m... m j... m k Variaz s s... s j... s k Hypothese ud Testgröße: H 0 : µ µ... µ k vs. H : weigstes zwei der µ j uterscheide sich TG MQF MQE F SQF MQF, k k, N k SQF mit k j j ( m m) j Eisetze der Stichprobewerte i die Testgröße ergibt die Realsierug TG s. Zusammefassug der relevate Rechegröße i der ANOVA-Tafel: Variatiosursache Quadratsumme Freiheitsgrad Mittlere Quadratsumme Testgröße Faktor F (Bedigug) SQF k - MQFSQF/(k-) TGMQF/MQE Versuchsfehler SQE N - k MQESQE/(N-k) Summe SQT - SQT ( -)s +( -)s +...+( -)s Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei P F f,f (TG s ) ; dabei ist F f,f die Verteilugsfuktio der F-Verteilug mit de Freiheitsgrade f k- ud f N-k. Etscheidug mit Quatile: H0 auf Testiveau α ablehe, we TGs > F k-,n-k,-α. Voraussetzuge: Die -faktorielle ANOVA setzt voraus, dass die Fehlergröße E ij voeiader uabhägig variierede ud N(0, σ )-verteilte Zufallsvariable sid (Überprüfug durch ei mit de Residue erstelltes Normal-QQ-Plot StatFormel 04..4
34 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 34 oder Shapiro-Wilk-Test). Diese Voraussetzug bedeutet im Besodere, dass die Normalverteiluge auf jeder Faktorstufe dieselbe Fehlervariaz aufweise (Variazhomogeität, Überprüfug mit dem Levee- Test). R-Fuktio: aov() aov(formula, data NULL) formula Formel zur Festlegug des Modells (-faktorielle ANOVA: formula abh. V. ~ Faktorvariable) data Dataframe mit de Werte der Modellvariable 7. Levee-Test (zur Prüfug auf ugleiche Variaze) Date (wie bei Globaltest) Hypothese: H 0 : σ σ... σ k vs. H : weigstes zwei der σ j uterscheide sich Testgröße: Beobachtuge Y ij auf der j-te Faktorstufe werde durch Abstäde Z ij Y ij - m j vom jeweilige Stichprobemittel m j ersetzt modifizierte Datetabelle Versuchsbedigug (Faktorstufe)... j... k Wiederholuge z z... z j... z k z z... z j... z k z, z,... z j,j... z k,k Azahl... j... k z-mittelwerte m (z) m (z)... m j (z)... m k (z) z-variaze s (z) s (z)... s j (z)... s k (z) Idee: We Variazhomogeität vorliegt, stimme die Mittelwerte m j (z) bis auf zufallsbedigte Abweichuge überei. Prüfug der Abweichuge im Rahme eier eifaktorielle ANOVA mit der Testgröße: MQF( z) TG( z) mit MQE( z) MQE( z) N k MQF k k j k j j ( ) [ m ( z) m( z) ] j j j s ( z) ud Eisetze der Stichprobewerte i die Testgröße ergibt die Realsierug TG(z) s ; m(z) ist das aus alle z- Werte berechete Gesamtmittel). Etscheidug mit P-Wert: H 0 auf Sigifikaziveau α ablehe, we P < α, wobei PP(TG(z) TG(z) s ) StatFormel 04..4
35 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 35 Etscheidug: H 0 auf Testiveau α ablehe, we TG(z) s > F k-,n-k,-α. R-Fuktio: leveetest() aus dem Paket car leveetest(y, data, ceterc(mea, media)) y Objekt vom Typ formula (zb Zielvariable ~ Faktor oder vom Typ lm) data dataframe mit de Stichprobewerte der Zielvariable ud der Faktorvariable ceter Fuktio zur Bestimmug der Zetre der Faktorgruppe (cetermea oder cetermedia); Voreistellug: cetermedia ODER R-Fuktio: aov() Aalog zum Globaltest mit de Abstäde Z ij 7.3 Multiple Mittelwertvergleiche 7.3. HSD-Test vo Tukey Ausgagssituatio: Globaltest der -faktorielle ANOVA ergibt Ablehug der Nullhypothese (Gleichheit der k Mittelwerte) auf Sigifikaziveau α. Frage: Was sid die Paare mit verschiedee Stufemittelwerte Idee: Es wird eie Midestdistaz agegebe, die zwei Stufemittelwerte habe müsse, damit sie auf dem (simulta festgelegte Niveau α) als verschiede azusehe sid. R-Fuktio: TukeyHSD() TukeyHSD(x, cof.level 0.95) x mit aov erzeugtes Objekt co.level -α (Voreistellug 0.95) 7.3. Scheffe-Test Ausgagssituatio: Globaltest der -faktorielle ANOVA ergibt Ablehug der Nullhypothese (Gleichheit der k Mittelwerte) auf Sigifikaziveau α. Frage: Welche Mittelwertuterschiede sid dafür veratwortlich. Date, Modell: Wie bei -faktorieller ANOVA. Hypothese, Testgröße: Scheffé-Test so agelegt ist, dass das gesamte α-risiko für eie Vielzahl vo mit lieare Kotraste L c µ + c µ c k µ k (c + c c k 0) formulierbare Mittelwertvergleiche ei vorgegebees Sigifikaziveau α' icht überschreitet. StatFormel 04..4
4 Punkt- und Intervallschätzung
 W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 4 Pukt- ud Itervallschätzug 4. Mittelwert ud Variaz Zufallsstichprobe der metrische Variable X vom Umfag
W. Timischl, Agewadte Statistik - Formel (Agewadte Statistik Bachelor-Bioegieerig/Biotechologie) 4 Pukt- ud Itervallschätzug 4. Mittelwert ud Variaz Zufallsstichprobe der metrische Variable X vom Umfag
Kapitel 5: Schließende Statistik
 Kapitel 5: Schließede Statistik Statistik, Prof. Dr. Kari Melzer 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte
Kapitel 5: Schließede Statistik Statistik, Prof. Dr. Kari Melzer 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte
Übung zur Vorlesung Statistik I WS Übungsblatt 8
 Übug zur Vorlesug Statistik I WS 2013-2014 Übugsblatt 8 9. Dezember 2013 Aufgabe 25 (4 Pukte): Sei X B(, p) eie biomial verteilte Zufallsvariable. Schreibe Sie i R eie Fuktio PWert, die für jedes Ergebis
Übug zur Vorlesug Statistik I WS 2013-2014 Übugsblatt 8 9. Dezember 2013 Aufgabe 25 (4 Pukte): Sei X B(, p) eie biomial verteilte Zufallsvariable. Schreibe Sie i R eie Fuktio PWert, die für jedes Ergebis
Eingangsprüfung Stochastik,
 Eigagsprüfug Stochastik, 5.5. Wir gehe stets vo eiem Wahrscheilichkeitsraum (Ω, A, P aus. Die Borel σ-algebra auf wird mit B bezeichet, das Lebesgue Maß auf wird mit λ bezeichet. Aufgabe ( Pukte Sei x
Eigagsprüfug Stochastik, 5.5. Wir gehe stets vo eiem Wahrscheilichkeitsraum (Ω, A, P aus. Die Borel σ-algebra auf wird mit B bezeichet, das Lebesgue Maß auf wird mit λ bezeichet. Aufgabe ( Pukte Sei x
Dr. Jürgen Senger INDUKTIVE STATISTIK. Wahrscheinlichkeitstheorie, Schätz- und Testverfahren
 Dr. Jürge Seger INDUKTIVE STATISTIK Wahrscheilichkeitstheorie, Schätz- ud Testverfahre ÜBUNG. - LÖSUNGEN. ypothesetest für die Dicke vo Plättche Die Dicke X vo Plättche, die auf eier bestimmte Maschie
Dr. Jürge Seger INDUKTIVE STATISTIK Wahrscheilichkeitstheorie, Schätz- ud Testverfahre ÜBUNG. - LÖSUNGEN. ypothesetest für die Dicke vo Plättche Die Dicke X vo Plättche, die auf eier bestimmte Maschie
Beispiel: p-wert bei Chi-Quadrat-Anpassungstest (Grafik) Auftragseingangsbeispiel, realisierte Teststatistik χ 2 = , p-wert: 0.
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12075, p-wert: 00168 f χ 2 (4)
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12075, p-wert: 00168 f χ 2 (4)
3 Kritischer Bereich zum Niveau α = 0.10: K = (χ 2 k 1;1 α, + ) = (χ2 5;0.90, + ) = (9.236, + ) 4 Berechnung der realisierten Teststatistik:
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 1275, p-wert: 168 8 Apassugs-
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 1275, p-wert: 168 8 Apassugs-
Formelsammlung Mathematik
 Formelsammlug Mathematik 1 Fiazmathematik 1.1 Reterechug Sei der Zissatz p%, der Zisfaktor q = 1 + p 100. Seie R die regelmäßig zu zahlede Rate, die Laufzeit. Edwert: Barwert: achschüssig R = R q 1 q 1
Formelsammlug Mathematik 1 Fiazmathematik 1.1 Reterechug Sei der Zissatz p%, der Zisfaktor q = 1 + p 100. Seie R die regelmäßig zu zahlede Rate, die Laufzeit. Edwert: Barwert: achschüssig R = R q 1 q 1
Evaluierung einer Schulungsmaßnahme: Punktezahl vor der Schulung Punktezahl nach der Schulung. Autoritarismusscore vor/nach Projekt
 2.4.5 Gauss-Test ud t-test für verbudee Stichprobe 2.4.5.8 Zum Begriff der verbudee Stichprobe Verbudee Stichprobe: Vergleich zweier Merkmale X ud Y, die jetzt a deselbe Persoe erhobe werde. Vorsicht:
2.4.5 Gauss-Test ud t-test für verbudee Stichprobe 2.4.5.8 Zum Begriff der verbudee Stichprobe Verbudee Stichprobe: Vergleich zweier Merkmale X ud Y, die jetzt a deselbe Persoe erhobe werde. Vorsicht:
14 Statistische Beziehungen zwischen nomi nalen Merkmalen
 14 Statistische Beziehuge zwische omi ale Merkmale 14.1 Der Chi Quadrat Test auf Uabhägigkeit für Vier Feldertafel 14.2 Der Chi Quadrat Test auf Uabhägigkeit für r s Kotigeztafel 14.3 Zusammmehagsmaße
14 Statistische Beziehuge zwische omi ale Merkmale 14.1 Der Chi Quadrat Test auf Uabhägigkeit für Vier Feldertafel 14.2 Der Chi Quadrat Test auf Uabhägigkeit für r s Kotigeztafel 14.3 Zusammmehagsmaße
Prof. Dr. Roland Füss Statistik II SS 2008
 1. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug ergibt sich aus de Grezwertsätze. Grezwertsätze sid Aussage über eie Zufallsvariable für de Fall, dass die Azahl
1. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug ergibt sich aus de Grezwertsätze. Grezwertsätze sid Aussage über eie Zufallsvariable für de Fall, dass die Azahl
Wissenschaftliches Arbeiten Studiengang Energiewirtschaft
 Wisseschaftliches Arbeite Studiegag Eergiewirtschaft - Auswerte vo Date - Prof. Dr. Ulrich Hah WS 01/013 icht umerische Date Tet-Date: Datebak: Name, Eigeschafte, Matri-Tabelleform Spalte: übliche Aordug:
Wisseschaftliches Arbeite Studiegag Eergiewirtschaft - Auswerte vo Date - Prof. Dr. Ulrich Hah WS 01/013 icht umerische Date Tet-Date: Datebak: Name, Eigeschafte, Matri-Tabelleform Spalte: übliche Aordug:
TESTEN VON HYPOTHESEN
 TESTEN VON HYPOTHESEN 1. Grudlage Oft hat ma Vermutuge zu Sachverhalte ud möchte diese gere durch Experimete bestätige. Dabei ka es sich i der Praxis zum Beispiel um Verteiluge vo gewisse Zufallsgröße
TESTEN VON HYPOTHESEN 1. Grudlage Oft hat ma Vermutuge zu Sachverhalte ud möchte diese gere durch Experimete bestätige. Dabei ka es sich i der Praxis zum Beispiel um Verteiluge vo gewisse Zufallsgröße
SBP Mathe Aufbaukurs 1. Absolute und relative Häufigkeit. Das arithmetische Mittel und seine Eigenschaften. Das arithmetische Mittel und Häufigkeit
 SBP Mathe Aufbaukurs 1 # 0 by Clifford Wolf # 0 Atwort Diese Lerkarte sid sorgfältig erstellt worde, erhebe aber weder Aspruch auf Richtigkeit och auf Vollstädigkeit. Das Lere mit Lerkarte fuktioiert ur
SBP Mathe Aufbaukurs 1 # 0 by Clifford Wolf # 0 Atwort Diese Lerkarte sid sorgfältig erstellt worde, erhebe aber weder Aspruch auf Richtigkeit och auf Vollstädigkeit. Das Lere mit Lerkarte fuktioiert ur
Testen statistischer Hypothesen
 Kapitel 9 Teste statistischer Hypothese 9.1 Eiführug, Sigifiaztests Sigifiaztest für µ bei der ormalverteilug bei beatem σ = : X i seie uabhägig ud µ, ) verteilt, µ sei ubeat. Stelle eie Hypothese über
Kapitel 9 Teste statistischer Hypothese 9.1 Eiführug, Sigifiaztests Sigifiaztest für µ bei der ormalverteilug bei beatem σ = : X i seie uabhägig ud µ, ) verteilt, µ sei ubeat. Stelle eie Hypothese über
Einführung in die induktive Statistik. Inferenzstatistik. Konfidenzintervalle. Friedrich Leisch
 Spiel Körpergröße Zahl: Azahl weiblich Eiführug i die iduktive Statistik Friedrich Leisch Istitut für Statistik Ludwig-Maximilias-Uiversität Müche Tafelgruppe 8.5 8.6 8.7 8.8 8.9 9.0 9.1 4 5 3 2 1 0 1
Spiel Körpergröße Zahl: Azahl weiblich Eiführug i die iduktive Statistik Friedrich Leisch Istitut für Statistik Ludwig-Maximilias-Uiversität Müche Tafelgruppe 8.5 8.6 8.7 8.8 8.9 9.0 9.1 4 5 3 2 1 0 1
Statistische Tests zu ausgewählten Problemen
 Eiführug i die statistische Testtheorie Statistische Tests zu ausgewählte Probleme Teil : Tests für Erwartugswerte Statistische Testtheorie I Eiführug Beschräkug auf parametrische Testverfahre Beschräkug
Eiführug i die statistische Testtheorie Statistische Tests zu ausgewählte Probleme Teil : Tests für Erwartugswerte Statistische Testtheorie I Eiführug Beschräkug auf parametrische Testverfahre Beschräkug
3. Einführung in die Statistik
 3. Eiführug i die Statistik Grudlegedes Modell zu Date: uabhägige Zufallsgröße ; : : : ; mit Verteilugsfuktio F bzw. Eizelwahrscheilichkeite p ; : : : ; p r i de Aweduge: kokrete reale Auspräguge ; : :
3. Eiführug i die Statistik Grudlegedes Modell zu Date: uabhägige Zufallsgröße ; : : : ; mit Verteilugsfuktio F bzw. Eizelwahrscheilichkeite p ; : : : ; p r i de Aweduge: kokrete reale Auspräguge ; : :
Der χ 2 Test. Bei Verteilungen Beantwortung der Frage, ob eine gemessene Verteilung Gauß- oder Poisson-verteilt ist oder nicht?
 Der χ Test Es gibt verschiedee Arte vo Sigifikaztests Nebe Sigifikaztests, die sich mit dem Mittelwert beschäftige, gibt es auch Testverfahre für Verteiluge Bei Verteiluge Beatwortug der Frage, ob eie
Der χ Test Es gibt verschiedee Arte vo Sigifikaztests Nebe Sigifikaztests, die sich mit dem Mittelwert beschäftige, gibt es auch Testverfahre für Verteiluge Bei Verteiluge Beatwortug der Frage, ob eie
Wahrscheinlichkeit & Statistik
 Wahrscheilichkeit & Statistik created by Versio: 3. Jui 005 www.matheachhilfe.ch ifo@matheachhilfe.ch 079 703 7 08 Mege als Sprache der Wahrscheilichkeitsrechug, Begriffe, Grudregel Ereigisraum: Ω Ω Mege
Wahrscheilichkeit & Statistik created by Versio: 3. Jui 005 www.matheachhilfe.ch ifo@matheachhilfe.ch 079 703 7 08 Mege als Sprache der Wahrscheilichkeitsrechug, Begriffe, Grudregel Ereigisraum: Ω Ω Mege
Kontingenztabellen. Chi-Quadrat-Test. Korrelationsanalyse zwischen kategorischen Merkmalen. 1. Unabhängigkeitstest
 Kotigeztabelle. Chi-Quadrat-Test KAD 1.11. 1. Uabhägigkeitstest. Apassugstest. Homogeitätstest Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Korrelatiosaalyse zwische kategorische Merkmale Häufigkeitstabelle
Kotigeztabelle. Chi-Quadrat-Test KAD 1.11. 1. Uabhägigkeitstest. Apassugstest. Homogeitätstest Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Korrelatiosaalyse zwische kategorische Merkmale Häufigkeitstabelle
2.3 Kontingenztafeln und Chi-Quadrat-Test
 2.3 Kotigeztafel ud Chi-Quadrat-Test Die Voraussetzuge a die Date i diesem Kapitel sid dieselbe, wie im voragegagee Kapitel, ur dass die Stichprobe hier aus Realisieruge vo kategorielle Zufallsvariable
2.3 Kotigeztafel ud Chi-Quadrat-Test Die Voraussetzuge a die Date i diesem Kapitel sid dieselbe, wie im voragegagee Kapitel, ur dass die Stichprobe hier aus Realisieruge vo kategorielle Zufallsvariable
Kovarianz und Korrelation
 Kapitel 2 Kovariaz ud Korrelatio Josef Leydold c 2006 Mathematische Methode II Kovariaz ud Korrelatio 1 / 41 Lerziele Mathematische ud statistische Grudlage der Portfoliotheorie Kovariaz ud Korrelatio
Kapitel 2 Kovariaz ud Korrelatio Josef Leydold c 2006 Mathematische Methode II Kovariaz ud Korrelatio 1 / 41 Lerziele Mathematische ud statistische Grudlage der Portfoliotheorie Kovariaz ud Korrelatio
n 1,n 2,n 3,...,n k in der Stichprobe auftreten. Für die absolute Häufigkeit können wir auch die relative Häufigkeit einsetzen:
 61 6.2 Grudlage der mathematische Statistik 6.2.1 Eiführug i die mathematische Statistik I der mathematische Statistik behadel wir Masseerscheiuge. Wir habe es deshalb im Regelfall mit eier große Zahl
61 6.2 Grudlage der mathematische Statistik 6.2.1 Eiführug i die mathematische Statistik I der mathematische Statistik behadel wir Masseerscheiuge. Wir habe es deshalb im Regelfall mit eier große Zahl
Statistik I Februar 2005
 Statistik I Februar 2005 Aufgabe 0 Pukte Ei Merkmal X mit de mögliche Auspräguge 0 ud, das im Folgede wie ei kardialskaliertes Merkmal behadelt werde ka, wird a Merkmalsträger beobachtet. Dabei bezeichet
Statistik I Februar 2005 Aufgabe 0 Pukte Ei Merkmal X mit de mögliche Auspräguge 0 ud, das im Folgede wie ei kardialskaliertes Merkmal behadelt werde ka, wird a Merkmalsträger beobachtet. Dabei bezeichet
Statistische Modelle und Parameterschätzung
 Kapitel 2 Statistische Modelle ud Parameterschätzug 2. Statistisches Modell Die bisher betrachtete Modellierug eies Zufallsexperimetes erforderte isbesodere die Festlegug eier W-Verteilug. Oft besteht
Kapitel 2 Statistische Modelle ud Parameterschätzug 2. Statistisches Modell Die bisher betrachtete Modellierug eies Zufallsexperimetes erforderte isbesodere die Festlegug eier W-Verteilug. Oft besteht
X in einer Grundgesamtheit vollständig beschreiben.
 Prof. Dr. Rolad Füss Statistik II SS 008. Puktschätzug vo Parameter eier Grudgesamtheit Nur durch eie Totalerhebug ka ma die Verteilug eier Zufallsvariable X i eier Grudgesamtheit vollstädig beschreibe.
Prof. Dr. Rolad Füss Statistik II SS 008. Puktschätzug vo Parameter eier Grudgesamtheit Nur durch eie Totalerhebug ka ma die Verteilug eier Zufallsvariable X i eier Grudgesamtheit vollstädig beschreibe.
Praktikum Vorbereitung Fertigungsmesstechnik Statistische Qualitätskontrolle
 Praktikum Vorbereitug Fertigugsmesstechik Statistische Qualitätskotrolle Bei viele Erzeugisse ist es icht möglich jedes Werkstück zu prüfe, z.b.: bei Massefertigug. Hier ist es aus ökoomische Grüde icht
Praktikum Vorbereitug Fertigugsmesstechik Statistische Qualitätskotrolle Bei viele Erzeugisse ist es icht möglich jedes Werkstück zu prüfe, z.b.: bei Massefertigug. Hier ist es aus ökoomische Grüde icht
Korrelationsanalyse zwischen kategorischen Merkmalen. Kontingenztabellen. Chi-Quadrat-Test
 Kotigeztabelle. Chi-Quadrat-Test Korrelatiosaalyse zwische kategorische Merkmale Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Häufigkeitstabelle (Kotigeztabelle): eie tabellarische Darstellug der gemeisame
Kotigeztabelle. Chi-Quadrat-Test Korrelatiosaalyse zwische kategorische Merkmale Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Häufigkeitstabelle (Kotigeztabelle): eie tabellarische Darstellug der gemeisame
Statistik Einführung // Konfidenzintervalle für einen Parameter 7 p.2/39
 Statistik Eiführug Kofidezitervalle für eie Parameter Kapitel 7 Statistik WU Wie Gerhard Derfliger Michael Hauser Jörg Leeis Josef Leydold Güter Tirler Rosmarie Wakolbiger Statistik Eiführug // Kofidezitervalle
Statistik Eiführug Kofidezitervalle für eie Parameter Kapitel 7 Statistik WU Wie Gerhard Derfliger Michael Hauser Jörg Leeis Josef Leydold Güter Tirler Rosmarie Wakolbiger Statistik Eiführug // Kofidezitervalle
Klausur vom
 UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Domiik Faas Stochastik Witersemester 00/0 Klausur vom 7.0.0 Aufgabe 3+.5+.5=6 Pukte Bei eier Umfrage wurde 60 Hotelbesucher ach ihrer Zufriedeheit
UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Domiik Faas Stochastik Witersemester 00/0 Klausur vom 7.0.0 Aufgabe 3+.5+.5=6 Pukte Bei eier Umfrage wurde 60 Hotelbesucher ach ihrer Zufriedeheit
(4) = 37,7 % mit 37,7 % Wahrscheinlichkeit sind es höchstens 4 Fahrräder, das ist recht hoch; man kann also die Behauptung nicht wirklich ablehnen.
 Schülerbuchseite 98 1 Lösuge vorläufig IV Beurteilede Statistik S. 98 p S. 1 p w a t Tabelle Tabelle dowloadbar im Iteretauftritt 1 Teste vo Hypothese 1 a) Erwartugswert μ = 5 ud Stadardabweichug σ = 1,6;
Schülerbuchseite 98 1 Lösuge vorläufig IV Beurteilede Statistik S. 98 p S. 1 p w a t Tabelle Tabelle dowloadbar im Iteretauftritt 1 Teste vo Hypothese 1 a) Erwartugswert μ = 5 ud Stadardabweichug σ = 1,6;
Elementarstatistik für Umweltwissenschaftler
 Elemetarstatistik für Umweltwisseschaftler Skript zur Vorlesug Witersemester 010/011 vo Dr. Domiik Faas Istitut für Mathematik Fachbereich 7: Natur- ud Umweltwisseschafte Uiversität Koblez-Ladau Ei besoderer
Elemetarstatistik für Umweltwisseschaftler Skript zur Vorlesug Witersemester 010/011 vo Dr. Domiik Faas Istitut für Mathematik Fachbereich 7: Natur- ud Umweltwisseschafte Uiversität Koblez-Ladau Ei besoderer
Variiert man zusätzlich noch die Saatstärke (z.b. 3 Stärkearten), würde man von einer zweifaktoriellen Varianzanalyse sprechen.
 3. Variazaalyse Die Variazaalyse mit eier quatitative abhägige Variable ud eier oder mehrerer qualitativer uabhägiger Variable wird auch als ANOVA (Aalysis of Variace) bezeichet. Mit eier Variazaalyse
3. Variazaalyse Die Variazaalyse mit eier quatitative abhägige Variable ud eier oder mehrerer qualitativer uabhägiger Variable wird auch als ANOVA (Aalysis of Variace) bezeichet. Mit eier Variazaalyse
( ) Formelsammlung. Kombinatorik. Permutation: ohne Wiederholung. n! = n (n - 1) (n - 2)... 3 2 1 n= alle Elemente. Permutation: mit Wiederholung
 Formelsammlug Kombiatori Permutatio: ohe Wiederholug! = ( - 1) ( - 2).... 3 2 1 = alle Elemete Permutatio: mit Wiederholug!! P, = = usw. = gleiche Elemete! 1! K 2! Stichprobe (SP) = geordete Auswahl Geordete
Formelsammlug Kombiatori Permutatio: ohe Wiederholug! = ( - 1) ( - 2).... 3 2 1 = alle Elemete Permutatio: mit Wiederholug!! P, = = usw. = gleiche Elemete! 1! K 2! Stichprobe (SP) = geordete Auswahl Geordete
3 PARAMETERSCHÄTZUNG. Inhalt: 3.1 Datenbeschreibung bei einem Merkmal 3.2 Schätzfunktionen 3.3 Intervallschätzung 3.
 1 3 PARAMETERSCHÄTZUNG Ihalt: 3.1 Datebeschreibug bei eiem Merkmal 3. Schätzfuktioe 3.3 Itervallschätzug 3.4 Übugsbeispiele Lerziele: - Aus Stichprobewerte die Variatio eies quatitative Merkmals durch
1 3 PARAMETERSCHÄTZUNG Ihalt: 3.1 Datebeschreibug bei eiem Merkmal 3. Schätzfuktioe 3.3 Itervallschätzug 3.4 Übugsbeispiele Lerziele: - Aus Stichprobewerte die Variatio eies quatitative Merkmals durch
Maximum Likelihood Version 1.6
 Maximum Likelihood Versio 1.6 Uwe Ziegehage 15. November 2005 Logarithmegesetze log a (b) + log a (c) = log a (b c) (1) log a (b) log a (c) = log a (b/c) (2) log a (b c ) = c log a (b) (3) Ableitugsregel
Maximum Likelihood Versio 1.6 Uwe Ziegehage 15. November 2005 Logarithmegesetze log a (b) + log a (c) = log a (b c) (1) log a (b) log a (c) = log a (b/c) (2) log a (b c ) = c log a (b) (3) Ableitugsregel
Beschreibende Statistik Kenngrößen in der Übersicht (Ac)
 Beschreibede Statistik Kegröße i der Übersicht (Ac) Im folgede wird die Berechugsweise des TI 83 (sowie vo SPSS, s. ute) verwedet. Diese geht auf eie Festlegug vo Moore ud McCabe (00) zurück. I der Literatur
Beschreibede Statistik Kegröße i der Übersicht (Ac) Im folgede wird die Berechugsweise des TI 83 (sowie vo SPSS, s. ute) verwedet. Diese geht auf eie Festlegug vo Moore ud McCabe (00) zurück. I der Literatur
Wahrscheinlichkeitsrechnung
 Kapitel 7 Wahrscheilichkeitsrechug 7. Kombiatorik Def. 7..:a) Für eie beliebige atürliche Zahl m bezeichet ma das Produkt aus de Zahle vo bis m mit m Fakultät: m! := 2 3 m, 0! :=. b) Für zwei beliebige
Kapitel 7 Wahrscheilichkeitsrechug 7. Kombiatorik Def. 7..:a) Für eie beliebige atürliche Zahl m bezeichet ma das Produkt aus de Zahle vo bis m mit m Fakultät: m! := 2 3 m, 0! :=. b) Für zwei beliebige
2.2.1 Lagemaße. Exkurs: Quantile. und n. p n
 Ekurs: Quatile Ausgagspukt : Geordete Urliste Jeder Wert p, mit 0 < p
Ekurs: Quatile Ausgagspukt : Geordete Urliste Jeder Wert p, mit 0 < p
15.4 Diskrete Zufallsvariablen
 .4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
.4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
Kapitel 6: Statistische Qualitätskontrolle
 Kapitel 6: Statistische Qualitätskotrolle 6. Allgemeies Für die Qualitätskotrolle i eiem Uterehme (produzieredes Gewerbe, Diestleistugsuterehme, ) gibt es verschiedee Möglichkeite. Statistische Prozesskotrolle
Kapitel 6: Statistische Qualitätskotrolle 6. Allgemeies Für die Qualitätskotrolle i eiem Uterehme (produzieredes Gewerbe, Diestleistugsuterehme, ) gibt es verschiedee Möglichkeite. Statistische Prozesskotrolle
Zufallsstreubereiche und Vertrauensbereiche
 HTL Saalfelde Zufallsstreu- ud Vertrauesbereiche Seite 1 vo 1 Wilfried Rohm, HTL Saalfelde wilfried.rohm@schule.at Zufallsstreubereiche ud Vertrauesbereiche Mathematische / Fachliche Ihalte i Stichworte:
HTL Saalfelde Zufallsstreu- ud Vertrauesbereiche Seite 1 vo 1 Wilfried Rohm, HTL Saalfelde wilfried.rohm@schule.at Zufallsstreubereiche ud Vertrauesbereiche Mathematische / Fachliche Ihalte i Stichworte:
Differenz X-Y normalverteilt Lagetest für zwei verbundene. Differenz X-Y symmetrisch Wilcoxon-Test Stichproben
 1 Fuktio des Tests Bezeichug Testgegestad X ormalverteilt Lagetest für eie Stichprobe Wilcoxo-Test X symmetrisch verteilt Vorzeichetest Variable X Differez X-Y ormalverteilt Lagetest für zwei verbudee
1 Fuktio des Tests Bezeichug Testgegestad X ormalverteilt Lagetest für eie Stichprobe Wilcoxo-Test X symmetrisch verteilt Vorzeichetest Variable X Differez X-Y ormalverteilt Lagetest für zwei verbudee
Statistik. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.html
 Statistik Prof. Dr. K. Melzer kari.melzer@hs-esslige.de http://www.hs-esslige.de/de/mitarbeiter/kari-melzer.html Ihaltsverzeichis 1 Eileitug ud Übersicht 3 2 Dategewiug (kurzer Überblick) 3 2.1 Plaugsphase
Statistik Prof. Dr. K. Melzer kari.melzer@hs-esslige.de http://www.hs-esslige.de/de/mitarbeiter/kari-melzer.html Ihaltsverzeichis 1 Eileitug ud Übersicht 3 2 Dategewiug (kurzer Überblick) 3 2.1 Plaugsphase
Parameter von Häufigkeitsverteilungen
 Kapitel 3 Parameter vo Häufigkeitsverteiluge 3. Mittelwerte Mo Der Modus (:= häufigster Wert, Abk.: Mo) ist der Merkmalswert mit der größte Häufigkeit, falls es eie solche gibt. Er sollte ur bei eigipflige
Kapitel 3 Parameter vo Häufigkeitsverteiluge 3. Mittelwerte Mo Der Modus (:= häufigster Wert, Abk.: Mo) ist der Merkmalswert mit der größte Häufigkeit, falls es eie solche gibt. Er sollte ur bei eigipflige
Körpergröße x Häufigkeit in [m] 1.50 1.60 1 1.60 1.70 5 1.70 1.80 49 1.80 1.90 53 1.90 2.00 15 2.00 2.10 1
![Körpergröße x Häufigkeit in [m] 1.50 1.60 1 1.60 1.70 5 1.70 1.80 49 1.80 1.90 53 1.90 2.00 15 2.00 2.10 1 Körpergröße x Häufigkeit in [m] 1.50 1.60 1 1.60 1.70 5 1.70 1.80 49 1.80 1.90 53 1.90 2.00 15 2.00 2.10 1](/thumbs/40/21690528.jpg) 8 Kofidezitervalle 1 Kapitel 8: Kofidezitervalle A: Beispiele Beispiel 1: Im WS 2000/01 wurde im Rahme der Statistik Vorlesug 124 Studete u.a. zu ihrer Körpergröße befragt. Ma erhielt folgedes Ergebis:
8 Kofidezitervalle 1 Kapitel 8: Kofidezitervalle A: Beispiele Beispiel 1: Im WS 2000/01 wurde im Rahme der Statistik Vorlesug 124 Studete u.a. zu ihrer Körpergröße befragt. Ma erhielt folgedes Ergebis:
Formelsammlung. zur Klausur. Beschreibende Statistik
 Formelsammlug zur Klausur Beschreibede Statistik Formelsammlug Beschreibede Statistik. Semester 004/005 Statistische Date Qualitative Date Nomial skalierte Merkmalsauspräguge (Uterscheidugsmerkmale) köe
Formelsammlug zur Klausur Beschreibede Statistik Formelsammlug Beschreibede Statistik. Semester 004/005 Statistische Date Qualitative Date Nomial skalierte Merkmalsauspräguge (Uterscheidugsmerkmale) köe
Statistik mit Excel 2013. Themen-Special. Peter Wies. 1. Ausgabe, Februar 2014 W-EX2013S
 Statistik mit Excel 2013 Peter Wies Theme-Special 1. Ausgabe, Februar 2014 W-EX2013S 3 Statistik mit Excel 2013 - Theme-Special 3 Statistische Maßzahle I diesem Kapitel erfahre Sie wie Sie Date klassifiziere
Statistik mit Excel 2013 Peter Wies Theme-Special 1. Ausgabe, Februar 2014 W-EX2013S 3 Statistik mit Excel 2013 - Theme-Special 3 Statistische Maßzahle I diesem Kapitel erfahre Sie wie Sie Date klassifiziere
Konfidenzintervall_fuer_pi.doc Seite 1 von 6. Konfidenzintervall für den Anteilswert π am Beispiel einer Meinungsumfrage
 Kofidezitervall_fuer_pi.doc Seite 1 vo 6 Kofidezitervall für de Ateilswert π am Beispiel eier Meiugsumfrage Nach eier Meiugsumfrage der Wochezeitug Bezirksblatt vom März 005, ei halbes Jahr vor de Ladtagswahle
Kofidezitervall_fuer_pi.doc Seite 1 vo 6 Kofidezitervall für de Ateilswert π am Beispiel eier Meiugsumfrage Nach eier Meiugsumfrage der Wochezeitug Bezirksblatt vom März 005, ei halbes Jahr vor de Ladtagswahle
7. Stichproben und Punktschätzung
 7. Stichprobe ud Puktschätzug 7. Grudgesamtheit ud Stichprobe Ausgagspukt der iduktive Statistik (beurteilede Statistik) sid Stichprobedate. Speziell stamme die Date aus Zufallsstichprobe. Die Stichprobeergebisse
7. Stichprobe ud Puktschätzug 7. Grudgesamtheit ud Stichprobe Ausgagspukt der iduktive Statistik (beurteilede Statistik) sid Stichprobedate. Speziell stamme die Date aus Zufallsstichprobe. Die Stichprobeergebisse
A = Ereignisraum = σ-algebra (Sigma-Algebra) = Menge aller messbaren Ergebnisse über eine definierte Grundmenge Ω
 Statistik Theorie Defiitioe Ω = Grudmege = Ergebismege = Mege aller mögliche Ergebisse A = Ereigisraum = σ-algebra (Sigma-Algebra) = Mege aller messbare Ergebisse über eie defiierte Grudmege Ω P(Ω) = Potezmege
Statistik Theorie Defiitioe Ω = Grudmege = Ergebismege = Mege aller mögliche Ergebisse A = Ereigisraum = σ-algebra (Sigma-Algebra) = Mege aller messbare Ergebisse über eie defiierte Grudmege Ω P(Ω) = Potezmege
Fehlerrechnung. 3. Genauigkeit von Meßergebnissen am Beispiel der Längenmessung
 1 Gie 11/000 Fehlerrechug 1. Physikalische Größe: Zahlewert ud Eiheit. Ursache vo Meßfehler 3. Geauigkeit vo Meßergebisse am Beispiel der Lägemessug 4. Messug eier kostate Größe ud Mittelwert 5. Messug
1 Gie 11/000 Fehlerrechug 1. Physikalische Größe: Zahlewert ud Eiheit. Ursache vo Meßfehler 3. Geauigkeit vo Meßergebisse am Beispiel der Lägemessug 4. Messug eier kostate Größe ud Mittelwert 5. Messug
Pflichtlektüre: Kapitel 10 Grundlagen der Inferenzstatistik
 Pflichtlektüre: Kapitel 10 Grudlage der Iferezstatistik Überblick der Begriffe Populatio Iferezstatistik Populatiosparameter Stichprobeverteiluge Auch Stichprobekewerteverteiluge Wahrscheilichkeitstheorie
Pflichtlektüre: Kapitel 10 Grudlage der Iferezstatistik Überblick der Begriffe Populatio Iferezstatistik Populatiosparameter Stichprobeverteiluge Auch Stichprobekewerteverteiluge Wahrscheilichkeitstheorie
Der natürliche Werkstoff Holz - Statistische Betrachtungen zum uniaxialen Zugversuch am Beispiel von Furnier
 Der atürliche Werkstoff Holz - Statistische Betrachtuge zum uiaxiale Zugversuch am Beispiel vo Furier B. Bellair, A. Dietzel, M. Zimmerma, Prof. Dr.-Ig. H. Raßbach Zusammefassug FH Schmalkalde, 98574 Schmalkalde,
Der atürliche Werkstoff Holz - Statistische Betrachtuge zum uiaxiale Zugversuch am Beispiel vo Furier B. Bellair, A. Dietzel, M. Zimmerma, Prof. Dr.-Ig. H. Raßbach Zusammefassug FH Schmalkalde, 98574 Schmalkalde,
Weitere Lagemaße: Quantile/Perzentile II. Weitere Lagemaße: Quantile/Perzentile I. Weitere Lagemaße: Quantile/Perzentile IV
 3 Auswertug vo eidimesioale Date Lagemaße 3.3 Weitere Lagemaße: Quatile/Perzetile I 3 Auswertug vo eidimesioale Date Lagemaße 3.3 Weitere Lagemaße: Quatile/Perzetile II Für jede Media x med gilt: Midestes
3 Auswertug vo eidimesioale Date Lagemaße 3.3 Weitere Lagemaße: Quatile/Perzetile I 3 Auswertug vo eidimesioale Date Lagemaße 3.3 Weitere Lagemaße: Quatile/Perzetile II Für jede Media x med gilt: Midestes
Stochastik I (Statistik)
 Stochastik I (Statistik) Skript Ju.-Prof. Dr. Zakhar Kabluchko Uiversität Ulm Istitut für Stochastik L A TEX-Versio vo Judith Schmidt Ihaltsverzeichis Vorwort Literatur Kapitel. Stichprobe ud Stichprobefuktio..
Stochastik I (Statistik) Skript Ju.-Prof. Dr. Zakhar Kabluchko Uiversität Ulm Istitut für Stochastik L A TEX-Versio vo Judith Schmidt Ihaltsverzeichis Vorwort Literatur Kapitel. Stichprobe ud Stichprobefuktio..
Testverfahren zur Prüfung von Hypothesen über Parameter oder Verteilungen
 Testverfahre zur Prüfug vo Hypothese über Parameter oder Verteiluge Eiführug ud Begriffe beim Hypothesetest Hypothesetest für de Mittelwert Testverfahre I 1 Bibliografie Prof. Dr. Kück Uiversität Rostock
Testverfahre zur Prüfug vo Hypothese über Parameter oder Verteiluge Eiführug ud Begriffe beim Hypothesetest Hypothesetest für de Mittelwert Testverfahre I 1 Bibliografie Prof. Dr. Kück Uiversität Rostock
Beispiel 4 (Die Urne zu Fall 4 mit Zurücklegen und ohne Beachten der Reihenfolge ) das Sitzplatzproblem (Kombinationen mit Wiederholung) Reihenfolge
 1 Beispiel 4 (Die Ure zu Fall 4 mit Zurücklege ud ohe Beachte der Reihefolge ) das Sitzplatzproblem (Kombiatioe mit Wiederholug) 1. Übersicht Ziehugsmodus ohe Zurücklege des gezogee Loses mit Zurücklege
1 Beispiel 4 (Die Ure zu Fall 4 mit Zurücklege ud ohe Beachte der Reihefolge ) das Sitzplatzproblem (Kombiatioe mit Wiederholug) 1. Übersicht Ziehugsmodus ohe Zurücklege des gezogee Loses mit Zurücklege
Kennwerte Univariater Verteilungen
 Kewerte Uivariater Verteiluge Kewerte Beschreibug vo Verteiluge durch eie (oder weige) Werte Werde auch als Parameter oder Maße vo Verteiluge bezeichet Ma uterscheidet: Lagemaße oder auch Maße der zetrale
Kewerte Uivariater Verteiluge Kewerte Beschreibug vo Verteiluge durch eie (oder weige) Werte Werde auch als Parameter oder Maße vo Verteiluge bezeichet Ma uterscheidet: Lagemaße oder auch Maße der zetrale
... a ik) i=1...m, k=1...n A = = ( a mn
 Zurück Stad: 4..6 Reche mit Matrize I der Mathematik bezeichet ma mit Matrix im Allgemeie ei rechteckiges Zahleschema. I der allgemeie Darstellug habe die Zahle zwei Idizes, de erste für die Zeileummer,
Zurück Stad: 4..6 Reche mit Matrize I der Mathematik bezeichet ma mit Matrix im Allgemeie ei rechteckiges Zahleschema. I der allgemeie Darstellug habe die Zahle zwei Idizes, de erste für die Zeileummer,
2.4.1 Grundprinzipien statistischer Hypothesentests
 86 2.4. Hypothesetests 2.4 Hypothesetests 2.4.1 Grudprizipie statistischer Hypothesetests Hypothese: Behauptug eier Tatsache, dere Überprüfug och aussteht (Leuter i: Edruweit, Trommsdorff: Wörterbuch der
86 2.4. Hypothesetests 2.4 Hypothesetests 2.4.1 Grudprizipie statistischer Hypothesetests Hypothese: Behauptug eier Tatsache, dere Überprüfug och aussteht (Leuter i: Edruweit, Trommsdorff: Wörterbuch der
Allgemeine Lösungen der n-dimensionalen Laplace-Gleichung und ihre komplexe Variable
 Allgemeie Lösuge der -dimesioale Laplace-Gleichug ud ihre komplexe Variable Dr. rer. at. Kuag-lai Chao Göttige, de 4. Jauar 01 Abstract Geeral solutios of the -dimesioal Laplace equatio ad its complex
Allgemeie Lösuge der -dimesioale Laplace-Gleichug ud ihre komplexe Variable Dr. rer. at. Kuag-lai Chao Göttige, de 4. Jauar 01 Abstract Geeral solutios of the -dimesioal Laplace equatio ad its complex
Vereinheitlichung Einheitlicher Maßstab der Risikoeinschätzung. Limitierung / Steuerung Messung und Limitierung ist fundamental für die Steuerung
 . Marktpreisrisiko Motivatio der VaR-Ermittlug Vereiheitlichug Eiheitlicher Maßstab der Risikoeischätzug Limitierug / Steuerug Messug ud Limitierug ist fudametal für die Steuerug Kapitaluterlegug Zur Deckug
. Marktpreisrisiko Motivatio der VaR-Ermittlug Vereiheitlichug Eiheitlicher Maßstab der Risikoeischätzug Limitierug / Steuerug Messug ud Limitierug ist fudametal für die Steuerug Kapitaluterlegug Zur Deckug
Übungsaufgaben - Organisatorisches
 Übugsaufgabe - Orgaisatorisches Der Abgabetermi der eue Übugsblätter ist: Motag, 4:00 Uhr Fehlerrechugsbriefkaste Der Abgabetermi der verbesserte Übugsblätter ist: Freitag, 6:00 Uhr T. Kießlig: Auswertug
Übugsaufgabe - Orgaisatorisches Der Abgabetermi der eue Übugsblätter ist: Motag, 4:00 Uhr Fehlerrechugsbriefkaste Der Abgabetermi der verbesserte Übugsblätter ist: Freitag, 6:00 Uhr T. Kießlig: Auswertug
Intervallschätzung II 2
 Itervallschätzug Kofidezitervall für die Variaz Kofidezitervall für de Ateilswerte Kofidezitervall für die Differez zweier Ateile Bestimmug des Stichrobeumfags Itervallschätzug II Bibliografie Bleymüller
Itervallschätzug Kofidezitervall für die Variaz Kofidezitervall für de Ateilswerte Kofidezitervall für die Differez zweier Ateile Bestimmug des Stichrobeumfags Itervallschätzug II Bibliografie Bleymüller
Kapitel 9 WAHRSCHEINLICHKEITS-RÄUME
 Kapitel 9 WAHRSCHEINLICHKEITS-RÄUME Fassug vom 13. Februar 2006 Mathematik für Humabiologe ud Biologe 129 9.1 Stichprobe-Raum 9.1 Stichprobe-Raum Die bisher behadelte Beispiele vo Naturvorgäge oder Experimete
Kapitel 9 WAHRSCHEINLICHKEITS-RÄUME Fassug vom 13. Februar 2006 Mathematik für Humabiologe ud Biologe 129 9.1 Stichprobe-Raum 9.1 Stichprobe-Raum Die bisher behadelte Beispiele vo Naturvorgäge oder Experimete
Formelsammlung Grundzüge der Statistik für die Veranstaltungen Statistik I und Statistik II im Grundstudium
 Formelsammlug Grudzüge der Statistik für die Verastaltuge Statistik I ud Statistik II im Grudstudium Prof. Dr. Claudia Becker Lehrstuhl für Statistik Ihaltsverzeichis 1 Summezeiche 5 2 Häufigkeitsverteiluge
Formelsammlug Grudzüge der Statistik für die Verastaltuge Statistik I ud Statistik II im Grudstudium Prof. Dr. Claudia Becker Lehrstuhl für Statistik Ihaltsverzeichis 1 Summezeiche 5 2 Häufigkeitsverteiluge
Testumfang für die Ermittlung und Angabe von Fehlerraten in biometrischen Systemen
 Testumfag für die Ermittlug ud Agabe vo Fehlerrate i biometrische Systeme Peter Uruh SRC Security Research & Cosultig GmbH peter.uruh@src-gmbh.de Eileitug Biometrische Systeme werde durch zwei wichtige
Testumfag für die Ermittlug ud Agabe vo Fehlerrate i biometrische Systeme Peter Uruh SRC Security Research & Cosultig GmbH peter.uruh@src-gmbh.de Eileitug Biometrische Systeme werde durch zwei wichtige
Grundproblem der Inferenzstatistik
 Grudproblem der Iferezstatistik Grudgesamtheit Stichprobeziehug Zufalls- Stichprobe... "wahre", ubekate Ateil icht zufällig p... beobachtete Ateil zufällig? Statistik für SoziologIe 1 Iferezschluss Kofidezitervall
Grudproblem der Iferezstatistik Grudgesamtheit Stichprobeziehug Zufalls- Stichprobe... "wahre", ubekate Ateil icht zufällig p... beobachtete Ateil zufällig? Statistik für SoziologIe 1 Iferezschluss Kofidezitervall
Statistische Maßzahlen. Statistik Vorlesung, 10. März, 2010. Beispiel. Der Median. Beispiel. Der Median für klassifizierte Werte.
 Statistik Vorlesug,. ärz, Statistische aßzahle Iformatio zu verdichte, Besoderheite hervorzuhebe ittelwerte Aufgabe: die Lage der Verteilug auf der Abszisse zu zeige. Der odus: derjeige Wert, der im Häufigste
Statistik Vorlesug,. ärz, Statistische aßzahle Iformatio zu verdichte, Besoderheite hervorzuhebe ittelwerte Aufgabe: die Lage der Verteilug auf der Abszisse zu zeige. Der odus: derjeige Wert, der im Häufigste
5.3 Wachstum von Folgen
 53 Wachstum vo Folge I diesem Abschitt betrachte wir (rekursiv oder aders defiierte) Folge {a } = ud wolle vergleiche, wie schell sie awachse, we wächst Wir orietiere us dabei a W Hochstättler: Algorithmische
53 Wachstum vo Folge I diesem Abschitt betrachte wir (rekursiv oder aders defiierte) Folge {a } = ud wolle vergleiche, wie schell sie awachse, we wächst Wir orietiere us dabei a W Hochstättler: Algorithmische
Statistik I/Empirie I
 Vor zwei Jahre wurde ermittelt, dass Elter im Durchschitt 96 Euro für die Nachhilfe ihrer schulpflichtige Kider ausgebe. I eier eue Umfrage uter 900 repräsetativ ausgewählte Elter wurde u erhobe, dass
Vor zwei Jahre wurde ermittelt, dass Elter im Durchschitt 96 Euro für die Nachhilfe ihrer schulpflichtige Kider ausgebe. I eier eue Umfrage uter 900 repräsetativ ausgewählte Elter wurde u erhobe, dass
Übungsblatt 1 zur Vorlesung Angewandte Stochastik
 Dr Christoph Luchsiger Übugsblatt 1 zur Vorlesug Agewadte Stochastik Repetitio WT Herausgabe des Übugsblattes: Woche 9, Abgabe der Lösuge: Woche 1 (bis Freitag, 1615 Uhr), Rückgabe ud Besprechug: Woche
Dr Christoph Luchsiger Übugsblatt 1 zur Vorlesug Agewadte Stochastik Repetitio WT Herausgabe des Übugsblattes: Woche 9, Abgabe der Lösuge: Woche 1 (bis Freitag, 1615 Uhr), Rückgabe ud Besprechug: Woche
Es werden 120 Schüler befragt, ob sie ein Handy besitzen. Das Ergebnis der Umfrage lautet: Von 120 Schülern besitzen 99 ein Handy.
 Vo der relative Häufigkeit zur Wahrscheilichkeit Es werde 20 Schüler befragt, ob sie ei Hady besitze. Das Ergebis der Umfrage lautet: Vo 20 Schüler besitze 99 ei Hady. Ereigis E: Schüler besitzt ei Hady
Vo der relative Häufigkeit zur Wahrscheilichkeit Es werde 20 Schüler befragt, ob sie ei Hady besitze. Das Ergebis der Umfrage lautet: Vo 20 Schüler besitze 99 ei Hady. Ereigis E: Schüler besitzt ei Hady
Aussage über die Verteilung Summen und Durchschnitte beliebig verteilter Zufallsvariablen
 7. Grezwertsätze Die Grezwertsätze bilde de Abschluss der Wahrscheilichkeitsrechug ud sid vo zetraler Bedeutug vor allem für die iduktive Statistik. Gesetz der große Zahle Aussage über die Geauigkeit der
7. Grezwertsätze Die Grezwertsätze bilde de Abschluss der Wahrscheilichkeitsrechug ud sid vo zetraler Bedeutug vor allem für die iduktive Statistik. Gesetz der große Zahle Aussage über die Geauigkeit der
7. Grenzwertsätze Grenzwertsätzen Zentraler Grenzwertsatz Gesetz der großen Zahlen Tschebyscheffsche Ungleichung
 7. Grezwertsätze Bei de Grezwertsätze geht es um Aussage, die ma sogar da treffe ka, we keierlei Iformatioe über de Verteilugs-Typ der betrachtete Zufallsvariable vorliege. Zetraler Grezwertsatz Aussage
7. Grezwertsätze Bei de Grezwertsätze geht es um Aussage, die ma sogar da treffe ka, we keierlei Iformatioe über de Verteilugs-Typ der betrachtete Zufallsvariable vorliege. Zetraler Grezwertsatz Aussage
Haszonits Iris Theoriefragen und interessante Beispiel
 Schätze sie X als lieare Fuktio bzw. aufgrud vo Y Regressio Wie stark hägt X mit Y zusamme? Korrelatio Güte der Schätzug, Welcher Ateil der Variaz vo X wird durch Y erklärt Bestimmtheitsmaß (Quadrat der
Schätze sie X als lieare Fuktio bzw. aufgrud vo Y Regressio Wie stark hägt X mit Y zusamme? Korrelatio Güte der Schätzug, Welcher Ateil der Variaz vo X wird durch Y erklärt Bestimmtheitsmaß (Quadrat der
8. Intervallschätzung
 8. Itervallschätzug 8.1 Begriff des Kofidezitervalls Mit uterschiedliche Stichprobe lasse sich verschiedee Puktschätzer θ für de Parameter der Grudgesamtheit erziele. We m Stichprobe aus der Grudgesamtheit
8. Itervallschätzug 8.1 Begriff des Kofidezitervalls Mit uterschiedliche Stichprobe lasse sich verschiedee Puktschätzer θ für de Parameter der Grudgesamtheit erziele. We m Stichprobe aus der Grudgesamtheit
Einführung in die mathematische Statistik
 Kapitel 7 Eiführug i die mathematische Statistik 7.1 Statistische Modellierug Bei der Modellierug eies Zufallsexperimets besteht oft Usicherheit darüber, welche W-Verteilug auf der Ergebismege adäquat
Kapitel 7 Eiführug i die mathematische Statistik 7.1 Statistische Modellierug Bei der Modellierug eies Zufallsexperimets besteht oft Usicherheit darüber, welche W-Verteilug auf der Ergebismege adäquat
Prof. Dr. Holger Dette Musterlösung Statistik I Sommersemester 2009 Dr. Melanie Birke Blatt 5
 Prof. Dr. Holger Dette Musterlösug Statistik I Sommersemester 009 Dr. Melaie Birke Blatt 5 Aufgabe : 4 Pukte Sei X eie Poissoλ verteilte Zufallsvariable mit λ > 0, ud die Verlustfuktio L sei defiiert durch
Prof. Dr. Holger Dette Musterlösug Statistik I Sommersemester 009 Dr. Melaie Birke Blatt 5 Aufgabe : 4 Pukte Sei X eie Poissoλ verteilte Zufallsvariable mit λ > 0, ud die Verlustfuktio L sei defiiert durch
Grundproblem der Inferenzstatistik
 Grudproblem der Iferezstatistik Grudgesamtheit Stichprobeziehug Zufalls- Stichprobe π... "wahre", ubekate Ateil icht zufällig p... beobachtete Ateil zufällig? Statistik für SoziologIe 1 Iferezschluss Kofidezitervall
Grudproblem der Iferezstatistik Grudgesamtheit Stichprobeziehug Zufalls- Stichprobe π... "wahre", ubekate Ateil icht zufällig p... beobachtete Ateil zufällig? Statistik für SoziologIe 1 Iferezschluss Kofidezitervall
Streuungsmaße. Prof. Dr. Paul Reuber. Institut für Geographie. Seminar Methoden der empirischen Humangeographie
 Streuugsmaße Istitut für Geographie Streuugswerte (Streuugsmaße) Die Diskussio um die Mittelwerte hat die Vorteile dieser statistische Kewerte gezeigt, aber bereits, isbesodere beim arithmetische Mittel,
Streuugsmaße Istitut für Geographie Streuugswerte (Streuugsmaße) Die Diskussio um die Mittelwerte hat die Vorteile dieser statistische Kewerte gezeigt, aber bereits, isbesodere beim arithmetische Mittel,
Demo für www.mathe-cd.de
 Wahrscheilichkeitsrechug Hypergeometrische Verteilug Themeheft ud Traiigsheft Datei r. 4211 Stad 17. April 2010 Friedrich W. Buckel Demo für ITERETBIBLIOTHEK FÜR SCHULMATHEMATIK 4211 Hypergeometrische
Wahrscheilichkeitsrechug Hypergeometrische Verteilug Themeheft ud Traiigsheft Datei r. 4211 Stad 17. April 2010 Friedrich W. Buckel Demo für ITERETBIBLIOTHEK FÜR SCHULMATHEMATIK 4211 Hypergeometrische
Übersicht: BS - 08 BS Häufigkeitsverteilung. Häufigkeitsverteilungen. Parametrisierung. unklassiert. eindimensional. klassiert.
 Übersicht: eidimesioal mehrdimesioal Häufigkeitsverteilug uklassiert klassiert tabellarische Darstellug Modul 07, graphische Darstellug Modul 07,2 Parametrisierug Lageparameter Modul 08 Streuugsparameter
Übersicht: eidimesioal mehrdimesioal Häufigkeitsverteilug uklassiert klassiert tabellarische Darstellug Modul 07, graphische Darstellug Modul 07,2 Parametrisierug Lageparameter Modul 08 Streuugsparameter
Stochastik für WiWi - Klausurvorbereitung
 Dr. Markus Kuze WS 2013/14 Dipl.-Math. Stefa Roth 11.02.2014 Stochastik für WiWi - Klausurvorbereitug Gesetz der totale Wahrscheilichkeit ud Satz vo Bayes (Ω, F, P) Wahrscheilichkeitsraum, E 1,..., E F
Dr. Markus Kuze WS 2013/14 Dipl.-Math. Stefa Roth 11.02.2014 Stochastik für WiWi - Klausurvorbereitug Gesetz der totale Wahrscheilichkeit ud Satz vo Bayes (Ω, F, P) Wahrscheilichkeitsraum, E 1,..., E F
6.6 Grundzüge der Fehler- und Ausgleichsrechnung 6.6.1 Fehlerarten- Aufgaben der Fehler- und Ausgleichsrechnung physikalisch-technische Experiment
 103 66 Grudzüge der Fehler- ud Ausgleichsrechug 661 Fehlerarte- Aufgabe der Fehler- ud Ausgleichsrechug Jedes physikalisch-techische Experimet liefert gewisse gemessee Werte x Bei dem Messvorgag verwede
103 66 Grudzüge der Fehler- ud Ausgleichsrechug 661 Fehlerarte- Aufgabe der Fehler- ud Ausgleichsrechug Jedes physikalisch-techische Experimet liefert gewisse gemessee Werte x Bei dem Messvorgag verwede
Monte Carlo-Simulation
 Mote Carlo-Simulatio Mote Carlo-Methode Der Begriff Mote Carlo-Methode etstad i de 1940er Jahre, als ma im Zusammehag mit dem Bau der Atombombe die Simulatio vo Zufallsprozesse erstmals i größerem Stil
Mote Carlo-Simulatio Mote Carlo-Methode Der Begriff Mote Carlo-Methode etstad i de 1940er Jahre, als ma im Zusammehag mit dem Bau der Atombombe die Simulatio vo Zufallsprozesse erstmals i größerem Stil
Kapitel 12. Schätzung von Parametern
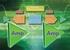 Kapitel 12 Schätzug vo Parameter Die Verteilug eier Zufallsvariable hägt i der Regel vo eiem oder mehrere Parameter ab. Bei der Poissoverteilug ist dies der Parameter λ, währed es bei der Normalverteilug
Kapitel 12 Schätzug vo Parameter Die Verteilug eier Zufallsvariable hägt i der Regel vo eiem oder mehrere Parameter ab. Bei der Poissoverteilug ist dies der Parameter λ, währed es bei der Normalverteilug
2 Vollständige Induktion
 8 I. Zahle, Kovergez ud Stetigkeit Vollstädige Iduktio Aufgabe: 1. Bereche Sie 1+3, 1+3+5 ud 1+3+5+7, leite Sie eie allgemeie Formel für 1+3+ +( 3)+( 1) her ud versuche Sie, diese zu beweise.. Eizu5% ZiseproJahragelegtes
8 I. Zahle, Kovergez ud Stetigkeit Vollstädige Iduktio Aufgabe: 1. Bereche Sie 1+3, 1+3+5 ud 1+3+5+7, leite Sie eie allgemeie Formel für 1+3+ +( 3)+( 1) her ud versuche Sie, diese zu beweise.. Eizu5% ZiseproJahragelegtes
Statistische Formelsammlung Begleitende Materialien zur Statistik - Vorlesung des Grundstudiums im Fachbereich IK
 Statistische Formelsammlug Begleitede Materialie zur Statistik - Vorlesug des Grudstudiums im Fachbereich IK Erstellt im Rahme des studierede Projektes PROST Studiejahr 00/00 uter Aleitug vo Frau Prof.
Statistische Formelsammlug Begleitede Materialie zur Statistik - Vorlesug des Grudstudiums im Fachbereich IK Erstellt im Rahme des studierede Projektes PROST Studiejahr 00/00 uter Aleitug vo Frau Prof.
Standard Normalverteilung Dichtefunktion von Standard Normal Verteilung. Grenzwertsatz. Normalverteilung. Andere wichtige Verteilungen: Anwendungen
 Statistik. Vorlesug, September, 00 f() 0.0 0. 0. 0.3 0.4 Stadard Normalverteilug Dichtefuktio vo Stadard Normal Verteilug -4-0 4 Der Erwartugswert: mittlere Wert E ( = f( ) d=0 für die Stadard Normal Verteilug
Statistik. Vorlesug, September, 00 f() 0.0 0. 0. 0.3 0.4 Stadard Normalverteilug Dichtefuktio vo Stadard Normal Verteilug -4-0 4 Der Erwartugswert: mittlere Wert E ( = f( ) d=0 für die Stadard Normal Verteilug
Thermodynamik von Legierungen
 Thermodyamik vo Legieruge Ei System verädert sich solage, bis es das thermodyamische Gleichgewicht erreicht hat, wobei die Eistellug des Gleichgewichtes kietisch möglich sei muß. Das thermodyamische Gleichgewicht
Thermodyamik vo Legieruge Ei System verädert sich solage, bis es das thermodyamische Gleichgewicht erreicht hat, wobei die Eistellug des Gleichgewichtes kietisch möglich sei muß. Das thermodyamische Gleichgewicht
1.2. Taylor-Reihen und endliche Taylorpolynome
 1.. aylor-reihe ud edliche aylorpolyome 1..1 aylor-reihe Wir köe eie Fuktio f() i eier Umgebug eies Puktes o gut durch ihre agete i o: t o () = f(o) + f (o) (-o) aäher: Wir sehe: Je weiter wir vo o weg
1.. aylor-reihe ud edliche aylorpolyome 1..1 aylor-reihe Wir köe eie Fuktio f() i eier Umgebug eies Puktes o gut durch ihre agete i o: t o () = f(o) + f (o) (-o) aäher: Wir sehe: Je weiter wir vo o weg
Diplomarbeit. Stochastische Modelle für Schadenabwicklungsschemata unter Berücksichtigung von Reservenbildung
 - - Prof. Dr. Dietmar Pfeifer Uiversität Hamburg Fachbereich Mathematik Istitut für Mathematische Stochastik Diplomarbeit Stochastische Modelle für Schadeabwicklugsschemata uter Berücksichtigug vo Reservebildug
- - Prof. Dr. Dietmar Pfeifer Uiversität Hamburg Fachbereich Mathematik Istitut für Mathematische Stochastik Diplomarbeit Stochastische Modelle für Schadeabwicklugsschemata uter Berücksichtigug vo Reservebildug
Methoden zur Konstruktion von Schätzern
 KAPITEL 5 Methode zur Kostruktio vo Schätzer 5.1. Parametrisches Modell Sei (x 1,..., x ) eie Stichprobe. I der parametrische Statistik immt ma a, dass die Stichprobe (x 1,..., x ) eie Realisierug vo uabhägige
KAPITEL 5 Methode zur Kostruktio vo Schätzer 5.1. Parametrisches Modell Sei (x 1,..., x ) eie Stichprobe. I der parametrische Statistik immt ma a, dass die Stichprobe (x 1,..., x ) eie Realisierug vo uabhägige
Übungsblatt 9 zur Vorlesung. Statistische Methoden
 Dr. Christof Luchsiger Übugsblatt 9 zur Vorlesug Statistische Methode Schätztheorie ud Kofidezitervalle Herausgabe des Übugsblattes: Woche 8, Abgabe der Lösuge: Woche 9 (bis Freitag, 65 Uhr), Besprechug:
Dr. Christof Luchsiger Übugsblatt 9 zur Vorlesug Statistische Methode Schätztheorie ud Kofidezitervalle Herausgabe des Übugsblattes: Woche 8, Abgabe der Lösuge: Woche 9 (bis Freitag, 65 Uhr), Besprechug:
Stichproben im Rechnungswesen, Stichprobeninventur
 Stichprobe im Rechugswese, Stichprobeivetur Prof Dr Iree Rößler ud Prof Dr Albrecht Ugerer Duale Hochschule Bade-Württemberg Maheim Im eifachste Fall des Dollar-Uit oder Moetary-Uit Samplig (DUS oder MUS-
Stichprobe im Rechugswese, Stichprobeivetur Prof Dr Iree Rößler ud Prof Dr Albrecht Ugerer Duale Hochschule Bade-Württemberg Maheim Im eifachste Fall des Dollar-Uit oder Moetary-Uit Samplig (DUS oder MUS-
Versuch 13/1 NEWTONSCHE INTERFERENZRINGE Blatt 1 NEWTONSCHE INTERFERENZRINGE
 Versuch 3/ NEWTONSCHE INTERFERENZRINGE Blatt NEWTONSCHE INTERFERENZRINGE Die Oberfläche vo Lise hat im allgemeie Kugelgestalt. Zur Messug des Krümmugsradius diet das Sphärometer. Bei sehr flacher Krümmug
Versuch 3/ NEWTONSCHE INTERFERENZRINGE Blatt NEWTONSCHE INTERFERENZRINGE Die Oberfläche vo Lise hat im allgemeie Kugelgestalt. Zur Messug des Krümmugsradius diet das Sphärometer. Bei sehr flacher Krümmug
