Klausur Technische Mechanik 2
|
|
|
- Joseph Hofmeister
- vor 7 Jahren
- Abrufe
Transkript
1 y HTWG Konstanz ) ( Punkte) Am Riemen des Schaufelradbaggers wirkt der Haftreibungskoeffizient µ = ln(5 1/π ). Der Ausleger mit der Schaufel hat den dargestellten Querschnitt (tanα = 0.75, tanγ = 7/24). a.) Bestimmen Sie im Ausleger die inneren Kräfte und Momente. Runden Sie auf ganze Zahlen. b.) Wie groß ist am Ort der betragsmäßig größten Querkraft das H/2 s z H H 1872F Verhältnis zwischen maximaler und mittlerer Schubspannung. Skizzieren Sie den Schubspannungsverlauf qualitativ über dem Querschnitt. c.) Wie groß ist der Abstand AB, wenn sich das über die Rolle B laufende Seil um /2 dehnt. Das Seil hat die Zugsteifigkeit EA Seil = 57600F. d.) Der waagrechte Abstand vom Schaufelmittelpunkt zum Gegengewicht 2496F beträgt 14. Die äußeren Kettenräder haben den gleichen Abstand zum mittleren. Wie groß ist der waagrechte Abstand des Schaufelmittelpunktes zum mittleren Kettenrad, wenn alle drei Radaufstandskräfte gleich sind? 2 α 4 γ 2 A B F β 3 2.) (7+2+2 Punkte) Die Gesamtschwerkraft beträgt 1000G. Der Oberschenkelknochen ist an beiden Enden gelenkig gelagert. Der Gesäßmuskel und der Hüftstrecker sind durch Seile vereinfacht. Der Hüftstrecker verläuft parallel zum Oberschenkelknochen, der Gesäßmuskel ist senkrecht zum Knochen angebunden. Das Kniegelenk ist genau oberhalb der Tretachse. Am Pedal wirkt nur eine senkrecht Kraft. Das vordere Kettenrad hat den Radius, das hintere /2 (sinα = 0.1, tanβ = 7/24, σr m s/g = 3456/π). 3 2 a.) Bestimmen Sie die Pedalkraft und die inneren Kräfte und Momente im Oberschenkelknochen. α b.) Wie ist das Verhältnis /R m, wenn der Betrag der maximalen Normalspannung im kreisrunden dünnwandigen Oberschenkelknochen σ beträgt? c.) Der Radabstand beträgt 8. Der Gesamtschwerpunkt liegt in der Mitte zwischen den Rädern 6 oberhalb des Bodens. Wie groß ist der maximal mögliche Steigungswinkel α, wenn am Hinterrad der Haftreibungskoeffizient µ = 0.5 gilt? 3.) (4 Punkte) Beim skizzierten 4-Punkt-Biegeversuch hat der Balken eine Höhe von H = 20mm und eine änge von 6 = 600mm. Das Material hat einen E-Modul von x F z 2 2
2 E = 5000N/mm² und erlaubt eine maximale Spannung σ max = 60N/mm². Wirkt die mittige Kraft F = 100N, so senkt sich die Mitte des Balkens um w = 20mm ab. a.) Bei welcher Kraft wird die Maximalspannung σ max erreicht? 2 4.) (5+4 Punkte) Das Antriebssegment einer Förderanlage soll untersucht werden. Der Riemen wird innen durch ein Zahnrad angetrieben. Die weiteren Riemenrollen sind frei drehend. Das Paket hat bei D und E zwei Auflagepunkte. Alle Zahnräder haben den gleichen Radius, zwischen den Zahnrädern werden nur Kräfte in Umfangsrichtung übertragen. M A B C D z x 2 1.5F E y F a.) Bestimmen Sie die inneren Kräfte und Moment in der Welle ABCD, die an den Punkten B und C gelagert ist. b.) Die kreisrunde Hohlwelle hat das Volumen V = 9π mm². σ V ist die Vergleichsspannung nach Mises. Für sie gilt F/σ V = 15π/wurzel(44) mm³. Wie groß ist der Außenradius R a der Welle? 5.) (8+2+3 Punkte) Schneidet man den Fahrer frei, wirken bis auf die Radkräfte die eingezeichneten Kräfte am Tretauto. Bis auf die Tretkurbel ist dieses symmetrisch zur xz-ebene, ebenso die Radkräfte. Die Räder haben den Radius 2. a.) Bestimmen Sie die Radkräfte und 24F 8/3 die inneren Momente im Balken CD. 45F b.) Bestimmen Sie die maximale /2 Vergleichspannung nach Mises infolge der Momente im Balken CD. 16/3 Der Balken hat ein dünnwandiges 2 quadratisches Profil mit der Kantenlänge H und der Wandstärke s (F/(H²s) = 1N/mm²). c.) Die Breite des Querschnittes soll zu ch modifiziert werden. Wie ist der Faktor c zu wählen, damit an beiden Punkten C und D die gleiche maximale Normalspannung wirkt? z x y C F Cx 45F D 2 F Cx
3
4
5
6
7
8
Wiederholklausur Technische Mechanik WIM
 1.) (2+6+2 Punkte) Eine Spätzlepresse, an der nur senkrechte Kräfte wirken, soll untersucht werden. Der Zylinder in welchem sich der Teig befindet hat eine Grundfläche von A = ²/2. A B R a.) Welche Kraft
1.) (2+6+2 Punkte) Eine Spätzlepresse, an der nur senkrechte Kräfte wirken, soll untersucht werden. Der Zylinder in welchem sich der Teig befindet hat eine Grundfläche von A = ²/2. A B R a.) Welche Kraft
Klausur Technische Mechanik 2
 1.) (3+6+3 Punkte) Auf den dargestellten smmetrischen Spindelrasenmäher mit der Gewichtskraft G und der Spurweite 4L wirken die dargestellten Kräfte. Keine Kräfte in x-richtung sind u berücksichtigen Die
1.) (3+6+3 Punkte) Auf den dargestellten smmetrischen Spindelrasenmäher mit der Gewichtskraft G und der Spurweite 4L wirken die dargestellten Kräfte. Keine Kräfte in x-richtung sind u berücksichtigen Die
HTWG Konstanz, Fakultät Maschinenbau, Studiengang WIM 1 Übungen Technische Mechanik F 2 = 20KN P 2 (9;-3) F A (1,3;-5) F 4. x y z
 HTWG Konstan, akultät Maschinenbau, Studiengang WIM 1 ufgabe 1: Berechnen sie die Kraftkomponenten, und und den Betrag der Kraft, falls dieser nicht gegeben ist. Berechnen Sie die Summen der Kräfte 1 und
HTWG Konstan, akultät Maschinenbau, Studiengang WIM 1 ufgabe 1: Berechnen sie die Kraftkomponenten, und und den Betrag der Kraft, falls dieser nicht gegeben ist. Berechnen Sie die Summen der Kräfte 1 und
Rheinische Fachhochschule Köln
 Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello e-mail: Semester Klausur Datum Fach Urteil BM K8 März 4 Kinetik+Kinematik Genehmigte Hilfsmittel: Ergebnis: Punkte Taschenrechner Literatur
Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello e-mail: Semester Klausur Datum Fach Urteil BM K8 März 4 Kinetik+Kinematik Genehmigte Hilfsmittel: Ergebnis: Punkte Taschenrechner Literatur
HTWG Konstanz, Fakultät Maschinenbau, Studiengang MEP 1 Übungen Technische Mechanik 2
 HTWG Konstan, akultät Maschinenbau, Studiengang MEP 1 ufgabe 1: Wo muss (Position ) die Masse m mit der Gewichtskraft 2.4kN montiert werden, wenn die npresskraft wischen den Rollen N = 10kN betragen soll?
HTWG Konstan, akultät Maschinenbau, Studiengang MEP 1 ufgabe 1: Wo muss (Position ) die Masse m mit der Gewichtskraft 2.4kN montiert werden, wenn die npresskraft wischen den Rollen N = 10kN betragen soll?
Übung zu Mechanik 3 Seite 36
 Übung zu Mechanik 3 Seite 36 Aufgabe 61 Ein Faden, an dem eine Masse m C hängt, wird über eine Rolle mit der Masse m B geführt und auf eine Scheibe A (Masse m A, Radius R A ) gewickelt. Diese Scheibe rollt
Übung zu Mechanik 3 Seite 36 Aufgabe 61 Ein Faden, an dem eine Masse m C hängt, wird über eine Rolle mit der Masse m B geführt und auf eine Scheibe A (Masse m A, Radius R A ) gewickelt. Diese Scheibe rollt
Übung zu Mechanik 2 Seite 62
 Übung zu Mechanik 2 Seite 62 Aufgabe 104 Bestimmen Sie die gegenseitige Verdrehung der Stäbe V 2 und U 1 des skizzierten Fachwerksystems unter der gegebenen Belastung! l l F, l alle Stäbe: EA Übung zu
Übung zu Mechanik 2 Seite 62 Aufgabe 104 Bestimmen Sie die gegenseitige Verdrehung der Stäbe V 2 und U 1 des skizzierten Fachwerksystems unter der gegebenen Belastung! l l F, l alle Stäbe: EA Übung zu
Prüfung - Technische Mechanik II
 Prüfung - Technische Mechanik II SoSe 2013 2. August 2013 FB 13, Festkörpermechanik Prof. Dr.-Ing. F. Gruttmann Name: Matr.-Nr.: Studiengang: Platznummer Raumnummer Die Aufgaben sind nicht nach ihrem Schwierigkeitsgrad
Prüfung - Technische Mechanik II SoSe 2013 2. August 2013 FB 13, Festkörpermechanik Prof. Dr.-Ing. F. Gruttmann Name: Matr.-Nr.: Studiengang: Platznummer Raumnummer Die Aufgaben sind nicht nach ihrem Schwierigkeitsgrad
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 S 1. Seilkräfte ufgaben zur Statik 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn m Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. S 2: Zentrales
S 1. Seilkräfte ufgaben zur Statik 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn m Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. S 2: Zentrales
Statische und dynamische Analyse eines Schildersystems. Esslingen
 Statische und dynamische Analyse eines Schildersystems für Gebrüder Hohl GmbH Esslingen Dipl.-Ing. Torsten Wehner Lerchenstraße 23 72649 Wolfschlugen [email protected] 3. Dezember 2002 Inhaltsverzeichnis
Statische und dynamische Analyse eines Schildersystems für Gebrüder Hohl GmbH Esslingen Dipl.-Ing. Torsten Wehner Lerchenstraße 23 72649 Wolfschlugen [email protected] 3. Dezember 2002 Inhaltsverzeichnis
Hauptdiplomprüfung Statik und Dynamik Pflichtfach
 UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. S. Staudacher Hauptdiplomprüfung Statik und Dynamik Pflichtfach Herbst 2011 Aufgabenteil
UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. S. Staudacher Hauptdiplomprüfung Statik und Dynamik Pflichtfach Herbst 2011 Aufgabenteil
Übung zu Mechanik 1 Seite 50
 Übung zu Mechanik 1 Seite 50 Aufgabe 83 Eine quadratische Platte mit dem Gewicht G und der Kantenlänge a liegt wie skizziert auf drei Böcken, so daß nur Druckkräfte übertragen werden können. Welches Gewicht
Übung zu Mechanik 1 Seite 50 Aufgabe 83 Eine quadratische Platte mit dem Gewicht G und der Kantenlänge a liegt wie skizziert auf drei Böcken, so daß nur Druckkräfte übertragen werden können. Welches Gewicht
2.4.2 Ebene Biegung. 140 Kap. 2.4 Biegung
 140 Kap. 2.4 Biegung Aufgabe 2 Ein exzentrischer Kreisring hat die Halbmesser R = 20 cm, r = 10 cm und die Exzentrizität e = 5 cm. Man suche die Hauptträgheitsmomente in Bezug auf seinen Schwerpunkt. 2.4.2
140 Kap. 2.4 Biegung Aufgabe 2 Ein exzentrischer Kreisring hat die Halbmesser R = 20 cm, r = 10 cm und die Exzentrizität e = 5 cm. Man suche die Hauptträgheitsmomente in Bezug auf seinen Schwerpunkt. 2.4.2
2. Definieren Sie die 2 Arten von Verzerrungen. Vorzeichenregeln.
 FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
Übung zu Mechanik 2 Seite 16
 Übung zu Mechanik 2 Seite 16 Aufgabe 27 Ein Stab wird wie skizziert entlang der Stabachse durch eine konstante Streckenlast n beansprucht. Bestimmen Sie den Verlauf der Normalspannungen σ 11 (X 1 ) und
Übung zu Mechanik 2 Seite 16 Aufgabe 27 Ein Stab wird wie skizziert entlang der Stabachse durch eine konstante Streckenlast n beansprucht. Bestimmen Sie den Verlauf der Normalspannungen σ 11 (X 1 ) und
Herbst 2010 Seite 1/14. Gottfried Wilhelm Leibniz Universität Hannover Klausur Technische Mechanik II für Maschinenbau. Musterlösungen (ohne Gewähr)
 Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Musterlösungen (ohne Gewähr)
 Herbst 010 Seite 1/0 rage 1 ( Punkte) Ein masseloser Balken der Länge l stützt sich wie skizziert über einen masselosen Stab auf dem Mittelpunkt P einer Rolle ab. Ein horizontal verlaufendes Seil verbindet
Herbst 010 Seite 1/0 rage 1 ( Punkte) Ein masseloser Balken der Länge l stützt sich wie skizziert über einen masselosen Stab auf dem Mittelpunkt P einer Rolle ab. Ein horizontal verlaufendes Seil verbindet
2. Der ebene Spannungszustand
 2. Der ebene Spannungszustand 2.1 Schubspannung 2.2 Dünnwandiger Kessel 2.3 Ebener Spannungszustand 2.4 Spannungstransformation 2.5 Hauptspannungen 2.6 Dehnungen 2.7 Elastizitätsgesetz Prof. Dr. Wandinger
2. Der ebene Spannungszustand 2.1 Schubspannung 2.2 Dünnwandiger Kessel 2.3 Ebener Spannungszustand 2.4 Spannungstransformation 2.5 Hauptspannungen 2.6 Dehnungen 2.7 Elastizitätsgesetz Prof. Dr. Wandinger
Vorlesungs-Beispiel Kragträger, Vergleich Schalen- und Balkentheorie. r a
 Vorlesungs-Beispiel Kragträger, Vergleich Schalen- und Balkentheorie Skizze der Aufgabenstellung: L F L F r a p Dr. Hellmann Geg.: L 3 mm, L 5mm, r a mm, F 4 N, E.* 5 MPa, ν.3, σ zul 45MPa Ges.:. Dimensionierung
Vorlesungs-Beispiel Kragträger, Vergleich Schalen- und Balkentheorie Skizze der Aufgabenstellung: L F L F r a p Dr. Hellmann Geg.: L 3 mm, L 5mm, r a mm, F 4 N, E.* 5 MPa, ν.3, σ zul 45MPa Ges.:. Dimensionierung
Übung zu Mechanik 1 Seite 65
 Übung zu Mechanik 1 Seite 65 Aufgabe 109 Gegeben ist das skizzierte System. a) Bis zu welcher Größe kann F gesteigert werden, ohne daß Rutschen eintritt? b) Welches Teil rutscht, wenn F darüber hinaus
Übung zu Mechanik 1 Seite 65 Aufgabe 109 Gegeben ist das skizzierte System. a) Bis zu welcher Größe kann F gesteigert werden, ohne daß Rutschen eintritt? b) Welches Teil rutscht, wenn F darüber hinaus
Kraftwinder S = a = a
 Prof. Dr.-ng. Prof. E.h. P. Eberhard A Kraftwinder Der skizzierte Eckpfosten eines Gartenzaunes ist bei A fest im Boden verankert. Er wird in B durch die Kräfte, und belastet. Die Punkte B und C sind durch
Prof. Dr.-ng. Prof. E.h. P. Eberhard A Kraftwinder Der skizzierte Eckpfosten eines Gartenzaunes ist bei A fest im Boden verankert. Er wird in B durch die Kräfte, und belastet. Die Punkte B und C sind durch
Aufgaben zur Festigkeit
 Aufgaben zur estigkeit : Maimale Länge eines Drahtes l Wie lang darf ein Stahldraht mit R m =40 N/mm maimal sein, damit er nicht abreißt? Dichte von Stahl ρ=7850 kg/m 3 Lösung: = G A R m G = A l g l= G
Aufgaben zur estigkeit : Maimale Länge eines Drahtes l Wie lang darf ein Stahldraht mit R m =40 N/mm maimal sein, damit er nicht abreißt? Dichte von Stahl ρ=7850 kg/m 3 Lösung: = G A R m G = A l g l= G
ZUGELASSENE HILFSMITTEL:
 ZUGELASSENE HILFSMITTEL: Täuschungsversuche führen zum Ausschluss und werden als Fehlversuch gewertet. Mobiltelefone und andere elektronische Geräte sowie nicht zugelassene Unterlagen bitte vom Tisch räumen.
ZUGELASSENE HILFSMITTEL: Täuschungsversuche führen zum Ausschluss und werden als Fehlversuch gewertet. Mobiltelefone und andere elektronische Geräte sowie nicht zugelassene Unterlagen bitte vom Tisch räumen.
2. Zentrale Kraftsysteme
 2. Zentrale Kraftsysteme Definition: Ein Kraftsystem, bei dem sich die Wirkungslinien aller Kräfte in einem Punkt schneiden, wird als zentrales Kraftsystem bezeichnet. Die Kräfte dürfen entlang ihrer Wirkungslinie
2. Zentrale Kraftsysteme Definition: Ein Kraftsystem, bei dem sich die Wirkungslinien aller Kräfte in einem Punkt schneiden, wird als zentrales Kraftsystem bezeichnet. Die Kräfte dürfen entlang ihrer Wirkungslinie
Spannungen mit griechischen Kleinbuchstaben
 B. Wietek, Faserbeton, DOI 10.1007/978-3-658-07764-8_2, Springer Fachmedien Wiesbaden 2015 2.2 Zeichen 15 Spannungen mit griechischen Kleinbuchstaben E c... Elastizitätsmodul von Beton [N/mm 2 ] E s...
B. Wietek, Faserbeton, DOI 10.1007/978-3-658-07764-8_2, Springer Fachmedien Wiesbaden 2015 2.2 Zeichen 15 Spannungen mit griechischen Kleinbuchstaben E c... Elastizitätsmodul von Beton [N/mm 2 ] E s...
Technische Mechanik I
 Technische Mechanik I [email protected] Wintersemester 2003/2004 Lehrveranstaltung Zeit Hörsaal Beginn Technische Mechanik I V 3 Mi 14:00 15:30 LB 104 15.10.2003 r 08:15 09:45 LB 104 17.10.2003 14tägig
Technische Mechanik I [email protected] Wintersemester 2003/2004 Lehrveranstaltung Zeit Hörsaal Beginn Technische Mechanik I V 3 Mi 14:00 15:30 LB 104 15.10.2003 r 08:15 09:45 LB 104 17.10.2003 14tägig
Übungsaufgaben Mathematik - Aufgaben (Studiengang Wirtschaftsingenieurwesen)
 40 cm Übungsaufgaben Mathematik - Aufgaben (Studiengang Wirtschaftsingenieurwesen) 1. Zahlenarten und Rechnen b) ( ) 5 ( 2 8 ) ( 1,25) 25 1,8 5,2 ( ) Wie viel sind 20% von? 2. Kenntnisse der Elementargeometrie
40 cm Übungsaufgaben Mathematik - Aufgaben (Studiengang Wirtschaftsingenieurwesen) 1. Zahlenarten und Rechnen b) ( ) 5 ( 2 8 ) ( 1,25) 25 1,8 5,2 ( ) Wie viel sind 20% von? 2. Kenntnisse der Elementargeometrie
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Biegung
 2. Biegung Wie die Normalkraft resultiert auch das Biegemoment aus einer Normalspannung. Das Koordinatensystem des Balkens wird so gewählt, dass die Flächenschwerpunkte der Querschnitte auf der x-achse
2. Biegung Wie die Normalkraft resultiert auch das Biegemoment aus einer Normalspannung. Das Koordinatensystem des Balkens wird so gewählt, dass die Flächenschwerpunkte der Querschnitte auf der x-achse
2. Momentanpol. Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: y A ), v Py. =v Ay
 ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
KREISFUNKTIONEN. Allgemeines
 KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
Verzerrungsenergie. Transformation auf beliebige Achsen x,y,z liefert nach Einsetzen von. Mechanik IA
 Verzerrungsenergie Zieht man ein Volumselement mit der Kantenlänge a in Richtung der Spannungshauptachse in die Länge, so wird folgende Arbeit W verrichtet: W = Fds mit F = λσ a und ds = dλε a. λ entspricht
Verzerrungsenergie Zieht man ein Volumselement mit der Kantenlänge a in Richtung der Spannungshauptachse in die Länge, so wird folgende Arbeit W verrichtet: W = Fds mit F = λσ a und ds = dλε a. λ entspricht
3. Allgemeine Kraftsysteme
 3. Allgemeine Kraftsysteme 3.1 Parallele Kräfte 3.2 Kräftepaar und Moment 3.3 Gleichgewicht in der Ebene Prof. Dr. Wandinger 1. Statik TM 1.3-1 3.1 Parallele Kräfte Bei parallelen Kräften in der Ebene
3. Allgemeine Kraftsysteme 3.1 Parallele Kräfte 3.2 Kräftepaar und Moment 3.3 Gleichgewicht in der Ebene Prof. Dr. Wandinger 1. Statik TM 1.3-1 3.1 Parallele Kräfte Bei parallelen Kräften in der Ebene
Aufgabe 1 (3 Punkte) m m 2. Prüfungsklausur Technische Mechanik I. Techn. Mechanik & Fahrzeugdynamik
 Techn. Mechanik & Fahrzeugdynamik TM I Prof. Dr.-Ing. habil. Hon. Prof. (NUST) D. Bestle 1. März 016 Prüfungsklausur Technische Mechanik I Familienname, Vorname Matrikel-Nummer Fachrichtung Aufgabe 1 (3
Techn. Mechanik & Fahrzeugdynamik TM I Prof. Dr.-Ing. habil. Hon. Prof. (NUST) D. Bestle 1. März 016 Prüfungsklausur Technische Mechanik I Familienname, Vorname Matrikel-Nummer Fachrichtung Aufgabe 1 (3
K5_15-09_L.Docx Seite 1 von 17
 K5 Technische Mechanik Täuschungsversuche führen zum Ausschluss und werden als Fehlversuch gewertet. Elektronische Geräte sowie nicht zugelassene Unterlagen bitte vom Tisch räumen. Mit Annahme der Klausur
K5 Technische Mechanik Täuschungsversuche führen zum Ausschluss und werden als Fehlversuch gewertet. Elektronische Geräte sowie nicht zugelassene Unterlagen bitte vom Tisch räumen. Mit Annahme der Klausur
Berechnungen am Dreieck
 1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
Der Satz von Ceva & Satz von Menelaus
 Der Satz von Ceva & Satz von Menelaus Fast Viktor 21. November 2007 Inhaltsverzeichnis Sätze und ihre Beweise Satz von Menelaus Satz von Ceva Winkelhalbierendenschnittpunkt Höhneschnittpunkt Winkelhalbierendenschnittpunkt
Der Satz von Ceva & Satz von Menelaus Fast Viktor 21. November 2007 Inhaltsverzeichnis Sätze und ihre Beweise Satz von Menelaus Satz von Ceva Winkelhalbierendenschnittpunkt Höhneschnittpunkt Winkelhalbierendenschnittpunkt
1.Kräfte, Fachwerk. 14,7 kn. Bestimmen Sie mit Hilfe des Sinussatzes die Stabkraft F1. 20 kn
 1.Kräfte, Fachwerk # Aufgaben Antw. P. Ein Wandkran wird durch eine Masse m mit F G über eine feste Rolle belastet. 1 Die beiden Stäbe sind Rohre mit einem Durchmesser-Verhältnis d/d = λ = 0,8. Die zulässige
1.Kräfte, Fachwerk # Aufgaben Antw. P. Ein Wandkran wird durch eine Masse m mit F G über eine feste Rolle belastet. 1 Die beiden Stäbe sind Rohre mit einem Durchmesser-Verhältnis d/d = λ = 0,8. Die zulässige
Kommt ein Vektor zur Drogenberatung: "Hilfe ich bin linear abhängig."
 Stephan Peter Wirtschaftsingenieurwesen WS 15/16 Mathematik Serie 8 Vektorrechnung Kommt ein Vektor zur Drogenberatung: "Hilfe ich bin linear abhängig." Aufgabe 1 Gegeben sind die Vektoren a = b = 1 graphisch
Stephan Peter Wirtschaftsingenieurwesen WS 15/16 Mathematik Serie 8 Vektorrechnung Kommt ein Vektor zur Drogenberatung: "Hilfe ich bin linear abhängig." Aufgabe 1 Gegeben sind die Vektoren a = b = 1 graphisch
1.Fachwerke. F1 = 4,5 kn, F2 = 3,4 kn,
 1.Fachwerke # Frage Antw. P. F1 = 4,5 kn, F =,4 kn, 1 a Prüfen Sie das Fachwerk auf statische Bestimmtheit k=s+ ist hier 5 = 7 +, stimmt. Also ist das FW statisch bestimmt. 4 b Bestimmen Sie die Auflagerkraft
1.Fachwerke # Frage Antw. P. F1 = 4,5 kn, F =,4 kn, 1 a Prüfen Sie das Fachwerk auf statische Bestimmtheit k=s+ ist hier 5 = 7 +, stimmt. Also ist das FW statisch bestimmt. 4 b Bestimmen Sie die Auflagerkraft
Übung zur Vorlesung Grundlagen der Fahrzeugtechnik. Übung
 Institut für Fahrzeugsystemtechnik Lehrstuhl für Fahrzeugtechnik Leiter: Prof. Dr. rer. nat. Frank Gauterin Fritz-Erler-Str. 1-3 76133 Karlsruhe Übung zur Vorlesung Grundlagen der Fahrzeugtechnik Übung
Institut für Fahrzeugsystemtechnik Lehrstuhl für Fahrzeugtechnik Leiter: Prof. Dr. rer. nat. Frank Gauterin Fritz-Erler-Str. 1-3 76133 Karlsruhe Übung zur Vorlesung Grundlagen der Fahrzeugtechnik Übung
Mathematischer Vorkurs Lösungen zum Übungsblatt 5
 Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 [email protected] Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 [email protected] Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Übung zu Mechanik 3 Seite 7
 Übung zu Mechanik 3 Seite 7 Aufgabe 7 Gegeben ist der skizzierte Brückenträger aus geschweißten Flachstählen. Er wird im ungünstigsten Lastfall durch die Schnittgrößen max N 1, max Q 3 und max M 2 beansprucht.
Übung zu Mechanik 3 Seite 7 Aufgabe 7 Gegeben ist der skizzierte Brückenträger aus geschweißten Flachstählen. Er wird im ungünstigsten Lastfall durch die Schnittgrößen max N 1, max Q 3 und max M 2 beansprucht.
Probe-Klausur Technische Mechanik B
 Haburg, den 8.. Prof. Dr.-Ing. habil. Thoas Kletschkowski Hochschule für Angewandte Wissenschaften Haburg Fakultät Technik und Inforatik Departent Fahreugtechnik und Flugeugbau Berliner Tor 9 99 Haburg
Haburg, den 8.. Prof. Dr.-Ing. habil. Thoas Kletschkowski Hochschule für Angewandte Wissenschaften Haburg Fakultät Technik und Inforatik Departent Fahreugtechnik und Flugeugbau Berliner Tor 9 99 Haburg
Goldbasispreis: 38 / Platinbasispreis: 32 / Palladiumbasispreis: 24 (Preis/g) Wandstärke: 1.3 mm Breite: 3 mm
 Profile 01 49/01130 49/01130 49/01135 49/01135 333 Gold, Gelb 163 178 333 Gold, Gelb 184 200 333 Gold, Weiss 202 221 333 Gold, Weiss 228 250 585 Gold, Gelb 282 311 585 Gold, Gelb 322 356 585 Gold, Weiss
Profile 01 49/01130 49/01130 49/01135 49/01135 333 Gold, Gelb 163 178 333 Gold, Gelb 184 200 333 Gold, Weiss 202 221 333 Gold, Weiss 228 250 585 Gold, Gelb 282 311 585 Gold, Gelb 322 356 585 Gold, Weiss
τ 30 N/mm bekannt. N mm N mm Aufgabe 1 (7 Punkte)
 Institut für Technische und Num. Mechanik Technische Mechanik IIIII Profs. P. Eberhard, M. Hanss WS 114 P 1. Februar 14 Bachelor-Prüfung in Technischer Mechanik IIIII Nachname, Vorname Matr.-Nummer Fachrichtung
Institut für Technische und Num. Mechanik Technische Mechanik IIIII Profs. P. Eberhard, M. Hanss WS 114 P 1. Februar 14 Bachelor-Prüfung in Technischer Mechanik IIIII Nachname, Vorname Matr.-Nummer Fachrichtung
2. Flächenträgheitsmomente
 . Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
. Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
2. Flächenträgheitsmomente
 . Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
. Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
Sekundarschulabschluss für Erwachsene. Geometrie A 2012
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2012 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2012 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Name. Vorname. Legi-Nr. Ermüdungsfestigkeit Welle-Nabe-Verbindung L/2
 Dimensionieren Prof. Dr. K. Wegener ame Vorname Legi-r. Zusatzübung 1: Passfederverbindung Voraussetzungen F F Flächenpressung zwischen Bauteilen M Last Ermüdungsfestigkeit Welle-abe-Verbindung F/ L/ F/
Dimensionieren Prof. Dr. K. Wegener ame Vorname Legi-r. Zusatzübung 1: Passfederverbindung Voraussetzungen F F Flächenpressung zwischen Bauteilen M Last Ermüdungsfestigkeit Welle-abe-Verbindung F/ L/ F/
Modulprüfung in Technischer Mechanik am 16. August Festigkeitslehre. Aufgaben
 Modulrüfung in Technischer Mechanik am 6. August 206 Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutlich lesbar. Zeichnungen müssen sauber und übersichtlich sein. Die
Modulrüfung in Technischer Mechanik am 6. August 206 Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutlich lesbar. Zeichnungen müssen sauber und übersichtlich sein. Die
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 19. März AUFGABE 1 (16 Punkte)
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
1. Zug und Druck in Stäben
 1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
σ, σ Institut für Technische und Num. Mechanik Technische Mechanik II/III Profs. P. Eberhard / M. Hanss SS 2016 P II Aufgabe 1 (8 Punkte)
 Institut für Technische und Num. Mechanik Technische Mechanik II/III Profs. P. Eberhard / M. Hanss SS 206 P II 2. August 206 Bachelorprüfung in Technische Mechanik II/III Nachname, Vorname E-Mail-Adresse
Institut für Technische und Num. Mechanik Technische Mechanik II/III Profs. P. Eberhard / M. Hanss SS 206 P II 2. August 206 Bachelorprüfung in Technische Mechanik II/III Nachname, Vorname E-Mail-Adresse
tgt HP 1993/94-1: Getriebewelle
 tgt HP 1993/94-1: Getriebewelle l 1 45 mm l 2 35 mm l 3 60 mm l 4 210 mm F 1 700 N F 2 850 N F 3 1300 N An der unmaßstäblich skizzierten Getriebewelle aus E295 sind folgende Teilaufgaben zu lösen: Teilaufgaben:
tgt HP 1993/94-1: Getriebewelle l 1 45 mm l 2 35 mm l 3 60 mm l 4 210 mm F 1 700 N F 2 850 N F 3 1300 N An der unmaßstäblich skizzierten Getriebewelle aus E295 sind folgende Teilaufgaben zu lösen: Teilaufgaben:
TM 2 Übung, Aufgaben an der Tafel , Prof. Gerling, SS 2013
 TM Übung, Aufgaben an der Tafel 9.4.3, Prof. Gerling, SS 03 Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Wir erheben keinen Anspruch auf Vollständigkeit oder Richtigkeit. Falls
TM Übung, Aufgaben an der Tafel 9.4.3, Prof. Gerling, SS 03 Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Wir erheben keinen Anspruch auf Vollständigkeit oder Richtigkeit. Falls
Rheinische Fachhochschule Köln
 Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello Semester Klausur Datum BP I, S K5 Genehmigte Hilfsmittel: Fach Urteil Technische Mechanik Ergebnis: Punkte Taschenrechner Literatur
Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello Semester Klausur Datum BP I, S K5 Genehmigte Hilfsmittel: Fach Urteil Technische Mechanik Ergebnis: Punkte Taschenrechner Literatur
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 17. März 2012 Die Bearbeitungszeit für alle drei Aufgaben beträgt 90 Minuten.
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik. SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am
 Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik Name: Vorname(n): Matrikelnummer: Bitte... SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am 16.03.018 Arbeitszeit: 150 min Aufgabe
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik Name: Vorname(n): Matrikelnummer: Bitte... SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am 16.03.018 Arbeitszeit: 150 min Aufgabe
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Schwerpunktfach Physik und Anwendungen der Mathematik
 Schriftliche Maturitätsprüfung 2014 Kantonsschule Reussbühl Luzern Schwerpunktfach Physik und Anwendungen der Mathematik Prüfende Lehrpersonen Klasse Hannes Ernst ([email protected]) Luigi Brovelli
Schriftliche Maturitätsprüfung 2014 Kantonsschule Reussbühl Luzern Schwerpunktfach Physik und Anwendungen der Mathematik Prüfende Lehrpersonen Klasse Hannes Ernst ([email protected]) Luigi Brovelli
tgt HP 1993/94-1: Getriebewelle
 tgt HP 1993/94-1: Getriebewelle l 1 45 mm l 2 35 mm l 3 60 mm l 4 210 mm F 1 700 N F 2 850 N F 3 1300 N An der unmaßstäblich skizzierten Getriebewelle aus E295 sind folgende Teilaufgaben zu lösen: Teilaufgaben:
tgt HP 1993/94-1: Getriebewelle l 1 45 mm l 2 35 mm l 3 60 mm l 4 210 mm F 1 700 N F 2 850 N F 3 1300 N An der unmaßstäblich skizzierten Getriebewelle aus E295 sind folgende Teilaufgaben zu lösen: Teilaufgaben:
TECHNISCHE MECHANIK. Übungen zur Elastostatik. Prof. Dr.-Ing. Andreas Ettemeyer Prof. Dr.-Ing. Oskar Wallrapp Dr. Bernd Schäfer
 TECHNISCHE MECHANIK Übungen zur Elastostatik Prof. Dr.-Ing. Andreas Ettemeyer Prof. Dr.-Ing. Oskar Wallrapp Dr. Bernd Schäfer Fachhochschule München Fachbereich 06 - Feinwerk- und Mikrotechnik Technische
TECHNISCHE MECHANIK Übungen zur Elastostatik Prof. Dr.-Ing. Andreas Ettemeyer Prof. Dr.-Ing. Oskar Wallrapp Dr. Bernd Schäfer Fachhochschule München Fachbereich 06 - Feinwerk- und Mikrotechnik Technische
Sekundarschulabschluss für Erwachsene. Geometrie A b) Strecken Sie das Dreieck ABC (Streckfaktor: -1/ Streckzentrum Z) (3 Punkte)
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Lehrstuhl für Maschinenelemente Prof. Dr.-Ing. B.-R. Höhn WS 2009/2010
 Lehrstuhl für Maschinenelemente TU München Prof. Dr.-Ing. B.-R. Höhn WS 2009/2010 Übung 1b: Festigkeitsrechnung Nachrechnung einer Getriebewelle Bild 1: Schematische Getriebedarstellung Bild 1 zeigt das
Lehrstuhl für Maschinenelemente TU München Prof. Dr.-Ing. B.-R. Höhn WS 2009/2010 Übung 1b: Festigkeitsrechnung Nachrechnung einer Getriebewelle Bild 1: Schematische Getriebedarstellung Bild 1 zeigt das
tgt HP 2007/08-5: Krabbenkutter
 tgt HP 2007/08-5: Krabbenkutter Zum Fang von Krabben werden die Ausleger in die Waagrechte gebracht. Die Fanggeschirre werden zum Meeresboden abgesenkt. Nach Beendigung des Fanges werden die Ausleger in
tgt HP 2007/08-5: Krabbenkutter Zum Fang von Krabben werden die Ausleger in die Waagrechte gebracht. Die Fanggeschirre werden zum Meeresboden abgesenkt. Nach Beendigung des Fanges werden die Ausleger in
Konstruktion des isoperimetrischen Punktes
 Konstruktion des isoperimetrischen Punktes C. und M. Reinsch Dreieck in der komplexen Ebene Ecken: A, B, C. Seiten: a = B C, b = C A, c = A B. Kreise: A(u) um A mit Radius u, B(v) um B mit Radius v, C(w)
Konstruktion des isoperimetrischen Punktes C. und M. Reinsch Dreieck in der komplexen Ebene Ecken: A, B, C. Seiten: a = B C, b = C A, c = A B. Kreise: A(u) um A mit Radius u, B(v) um B mit Radius v, C(w)
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
tgt HP 2011/12-5: Klappbrücke
 tgt HP 2011/12-5: Klappbrücke Klappbrücken werden an Kanälen eingesetzt um Schiffe mit höheren Aufbauten die Durchfahrt zu ermöglichen. Das Hochklappen des Brückenbodens erfolgt durch eine Zahnstange und
tgt HP 2011/12-5: Klappbrücke Klappbrücken werden an Kanälen eingesetzt um Schiffe mit höheren Aufbauten die Durchfahrt zu ermöglichen. Das Hochklappen des Brückenbodens erfolgt durch eine Zahnstange und
Raumgeometrie - gerade Pyramide
 1.0 Das Quadrat ABCD mit der Seitenlänge 7 cm ist Grundfläche einer geraden Pyramide ABCDS mit der Höhe h = 8 cm. S ist die Pyramidenspitze. 1.1 Fertige ein Schrägbild der Pyramide ABCDS an. 1.2 Berechne
1.0 Das Quadrat ABCD mit der Seitenlänge 7 cm ist Grundfläche einer geraden Pyramide ABCDS mit der Höhe h = 8 cm. S ist die Pyramidenspitze. 1.1 Fertige ein Schrägbild der Pyramide ABCDS an. 1.2 Berechne
Rheinische Fachhochschule Köln
 Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello e-mail: Semester Klausur Datum Fach Urteil BM I, S 3 K8 Juli 13 Kinetik+Kinematik Genehmigte Hilfsmittel: Ergebnis: Punkte Taschenrechner
Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello e-mail: Semester Klausur Datum Fach Urteil BM I, S 3 K8 Juli 13 Kinetik+Kinematik Genehmigte Hilfsmittel: Ergebnis: Punkte Taschenrechner
Aufgabe 1 Bremse (25 P)
 Name, Vorname: Matrikel-Nr.: Unterschrift: Aufgabe 1 Bremse (5 P) Eine Trommel mit dem Massenträgheitsmoment J Tr soll zum Stillstand gebracht werden. Die Anfangswinkelgeschwindigkeit, mit der sich die
Name, Vorname: Matrikel-Nr.: Unterschrift: Aufgabe 1 Bremse (5 P) Eine Trommel mit dem Massenträgheitsmoment J Tr soll zum Stillstand gebracht werden. Die Anfangswinkelgeschwindigkeit, mit der sich die
3. Erhaltungsgrößen und die Newton schen Axiome
 Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray [email protected] 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray [email protected] 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 6: Drehimpuls, Verformung Dr. Daniel Bick 18. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 18. November 2016 1 / 27 Stoß auf Luftkissenschiene
Physik für Biologen und Zahnmediziner Kapitel 6: Drehimpuls, Verformung Dr. Daniel Bick 18. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 18. November 2016 1 / 27 Stoß auf Luftkissenschiene
( und ) Sommer Samstag, 22. August 2015, Uhr, HIL G 15. Name, Vorname: Studenten-Nr.:
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2015 Samstag, 22. August 2015, 09.00 12.00 Uhr, HIL G 15 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2015 Samstag, 22. August 2015, 09.00 12.00 Uhr, HIL G 15 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis
 Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
2.2 Arbeit und Energie. Aufgaben
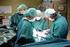 Technische Mechanik 3 2.2-1 Prof. Dr. Wandinger Aufgabe 1 Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt.
Technische Mechanik 3 2.2-1 Prof. Dr. Wandinger Aufgabe 1 Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt.
= -15 MPa. Zeichnen Sie den Mohrschen Spannungskreis und bestimmen Sie
 Webinar: Elastostatik Thema: Mohrscher Spannungskreis Aufgabe: Mohrscher Spannungskreis Gegeben seien die folgenden Spannungen: σ x = -40 MPa, σ y = 60 MPa und τ xy = -15 MPa. Zeichnen Sie den Mohrschen
Webinar: Elastostatik Thema: Mohrscher Spannungskreis Aufgabe: Mohrscher Spannungskreis Gegeben seien die folgenden Spannungen: σ x = -40 MPa, σ y = 60 MPa und τ xy = -15 MPa. Zeichnen Sie den Mohrschen
5 Festigkeitslehre. Inneres Kräftesystem und Beanspruchungsarten
 116 5 Festigkeitslehre Inneres Kräftesystem und Beanspruchungsarten 651 Ein Drehmeißel ist nach Skizze eingespannt und durch die Schnittkraft F s = 12 kn belastet. Die Abmessungen betragen l = 40 mm, b
116 5 Festigkeitslehre Inneres Kräftesystem und Beanspruchungsarten 651 Ein Drehmeißel ist nach Skizze eingespannt und durch die Schnittkraft F s = 12 kn belastet. Die Abmessungen betragen l = 40 mm, b
Elektromagnetische Felder und Wellen
 Elektromagnetische Felder und Wellen Name: Vorname: Matrikelnummer: Aufgabe 1: Aufgabe 2: Aufgabe 3: Aufgabe 4: Aufgabe 5: Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: Aufgabe 10: Aufgabe 11: Aufgabe 12:
Elektromagnetische Felder und Wellen Name: Vorname: Matrikelnummer: Aufgabe 1: Aufgabe 2: Aufgabe 3: Aufgabe 4: Aufgabe 5: Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: Aufgabe 10: Aufgabe 11: Aufgabe 12:
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 6: Drehimpuls, Verformung Dr. Daniel Bick 24. November 2017 Daniel Bick Physik für Biologen und Zahnmediziner 24. November 2017 1 / 28 Versuch: Newton Pendel
Physik für Biologen und Zahnmediziner Kapitel 6: Drehimpuls, Verformung Dr. Daniel Bick 24. November 2017 Daniel Bick Physik für Biologen und Zahnmediziner 24. November 2017 1 / 28 Versuch: Newton Pendel
tgt HP 1992/93-1: Mountainbike
 tgt HP 199/93-1: Mountainbike Eine Radfahrerin fährt mit angezogener Vorderradbremse eine Gefällstrecke hinunter. Ihre Gewichtskraft F G1 greift im Schwerpunkt S 1, die Gewichtskraft des Fahrrades F G
tgt HP 199/93-1: Mountainbike Eine Radfahrerin fährt mit angezogener Vorderradbremse eine Gefällstrecke hinunter. Ihre Gewichtskraft F G1 greift im Schwerpunkt S 1, die Gewichtskraft des Fahrrades F G
TECHNISCHE MECHANIK A (STATIK)
 Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
F DZ F AX F AZ. 11. Übungsblatt Flächenträgheitsmoment, Biegespannung WS 2009/2010. Tutoriumsaufgaben 1/13
 Univ. Prof. Dr. rer nat. olfgang H. Müller Materialtheorie - LKM, Sekr. MS Einsteinufer 5, 0587 Berlin. Übungsblatt Flächenträgheitsmoment, Biegespannung S 009/00 Tutoriumsaufgaben ) Das abgebildete Maschinenteil
Univ. Prof. Dr. rer nat. olfgang H. Müller Materialtheorie - LKM, Sekr. MS Einsteinufer 5, 0587 Berlin. Übungsblatt Flächenträgheitsmoment, Biegespannung S 009/00 Tutoriumsaufgaben ) Das abgebildete Maschinenteil
Probematura Jänner/Februar 2016 Seite 1 / 7
 Probematura Jänner/Februar 2016 Seite 1 / 7 1. Im Casino (20 Punkte) (a) Bei einem Glücksrad beträgt die Gewinnwahrscheinlichkeit 0,3. (3 P) i. Geben Sie eine Formel an, mit der man die Wahrscheinlichkeit
Probematura Jänner/Februar 2016 Seite 1 / 7 1. Im Casino (20 Punkte) (a) Bei einem Glücksrad beträgt die Gewinnwahrscheinlichkeit 0,3. (3 P) i. Geben Sie eine Formel an, mit der man die Wahrscheinlichkeit
Informationen für Lehrpersonen und Lernende GLF-Prüfung Mathematik TALS Juli 2017 (inkl. Nachtermin)
 Informationen für Lehrpersonen und Lernende GLF-Prüfung Mathematik TALS Juli 017 (inkl. Nachtermin) Für die Note 6 müssen nicht alle Aufgaben gelöst werden. Der Notenschlüssel wird nach der Prüfung festgelegt.
Informationen für Lehrpersonen und Lernende GLF-Prüfung Mathematik TALS Juli 017 (inkl. Nachtermin) Für die Note 6 müssen nicht alle Aufgaben gelöst werden. Der Notenschlüssel wird nach der Prüfung festgelegt.
Montageschienen MM-C. Technische Daten für Schienen-Profile MM (verzinkt)
 Montageschienen MM-C Technische Daten für Schienen-Profile MM (verzinkt) Achsendefinition Technische Daten für Schienen-Profile MM (max. Spannweite/Durchbiegung bei Einzellast) Wandstärke t 1,0 1,0 1.75
Montageschienen MM-C Technische Daten für Schienen-Profile MM (verzinkt) Achsendefinition Technische Daten für Schienen-Profile MM (max. Spannweite/Durchbiegung bei Einzellast) Wandstärke t 1,0 1,0 1.75
Rheinische Fachhochschule Köln
 Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello e-mail: Semester Klausur Datum BM II, S K 01. 07. 13 Genehmigte Hilfsmittel: Fach Urteil Statik u. Festigkeit Ergebnis: Punkte Taschenrechner
Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello e-mail: Semester Klausur Datum BM II, S K 01. 07. 13 Genehmigte Hilfsmittel: Fach Urteil Statik u. Festigkeit Ergebnis: Punkte Taschenrechner
Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler"
 Aufgaben 5 Rotations-Mechanik Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler" Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen, dass sich die Wirkung einer Kraft nicht
Aufgaben 5 Rotations-Mechanik Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler" Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen, dass sich die Wirkung einer Kraft nicht
Prof. Dr. G. Knauer Dipl.-Ing. W. Wieser
 Fachhochschule München Fachbereich 03 Maschinenbau Prof. Dr. G. Knauer Dipl.-Ing. W. Wieser Teil II: Berechnungen Die Skizze zeigt eine Seiltrommel. 1 Die Seiltrommel (2) wird über das Zahnrad (1) angetrieben.
Fachhochschule München Fachbereich 03 Maschinenbau Prof. Dr. G. Knauer Dipl.-Ing. W. Wieser Teil II: Berechnungen Die Skizze zeigt eine Seiltrommel. 1 Die Seiltrommel (2) wird über das Zahnrad (1) angetrieben.
Passerelle Mathematik Frühling 2005 bis Herbst 2006
 Passerelle Mathematik Frühling 2005 bis Herbst 2006 www.mathenachhilfe.ch [email protected] 079 703 72 08 Inhaltsverzeichnis 1 Algebra 3 1.1 Termumformungen..................................... 3
Passerelle Mathematik Frühling 2005 bis Herbst 2006 www.mathenachhilfe.ch [email protected] 079 703 72 08 Inhaltsverzeichnis 1 Algebra 3 1.1 Termumformungen..................................... 3
0,6 m. 0,4m. Gegeben seien die obigen drei auf den Balken wirkenden Kräfte mit:
 Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Zweidimensionale Vektorrechnung:
 Zweidimensionale Vektorrechnung: Gib jeweils den Vektor AB und seine Länge an! (a A(, B(6 5 (b A(, B( 4 (c A(, B( 0 (d A(0 0, B(4 (e A(0, B( 0 (f A(, B( Gib jeweils die Summe a + b und die Differenz a
Zweidimensionale Vektorrechnung: Gib jeweils den Vektor AB und seine Länge an! (a A(, B(6 5 (b A(, B( 4 (c A(, B( 0 (d A(0 0, B(4 (e A(0, B( 0 (f A(, B( Gib jeweils die Summe a + b und die Differenz a
Grundlagen der Physik 1 Lösung zu Übungsblatt 8
 Grundlagen der Physik 1 Lösung zu Übungsblatt 8 Daniel Weiss 1. Dezember 29 Inhaltsverzeichnis Aufgabe 1 - inhomogener hängender Balken 1 a) Seilkräfte...................................... 1 b) Schwerpunkt....................................
Grundlagen der Physik 1 Lösung zu Übungsblatt 8 Daniel Weiss 1. Dezember 29 Inhaltsverzeichnis Aufgabe 1 - inhomogener hängender Balken 1 a) Seilkräfte...................................... 1 b) Schwerpunkt....................................
Konstruktion - Methoden und Getriebe -
 Seite 1 WS 92/93 8 Punkte Die skizzierte Arbeitsmaschine wird von einem Elektromotor A angetrieben, der mit der konstanten Drehzahl n A =750U/min läuft. Die Arbeitsmaschine B wird jeweils aus dem Ruhezustand
Seite 1 WS 92/93 8 Punkte Die skizzierte Arbeitsmaschine wird von einem Elektromotor A angetrieben, der mit der konstanten Drehzahl n A =750U/min läuft. Die Arbeitsmaschine B wird jeweils aus dem Ruhezustand
Institut für Maschinenelemente und Konstruktionstechnik Klausur KT1 (alt KT2) SS 2011 Dr.-Ing. S. Umbach I
 Klausur KT1 (alt KT) SS 011 Dr.-Ing. S. Umbach I 30.08.011 Name, Vorname: Unterschrift: Matrikel- Nr.: Klausurbedingungen: Zugelassene Hilfsmittel sind dokumentenechtes Schreibzeug und Taschenrechner.
Klausur KT1 (alt KT) SS 011 Dr.-Ing. S. Umbach I 30.08.011 Name, Vorname: Unterschrift: Matrikel- Nr.: Klausurbedingungen: Zugelassene Hilfsmittel sind dokumentenechtes Schreibzeug und Taschenrechner.




