Analysis: Klausur Analysis
|
|
|
- Gerhard Schräder
- vor 7 Jahren
- Abrufe
Transkript
1 Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz Januar 1 1
2 Pflichtteil - ohne Hilfsmittel Aufgabe P1: ( VP) Gib eine Stammfunktion an: a) f() = + cos(,5) b) g() = ( ) c) Gib die Stammfunktion H() der Funktion h() = 1+ an, für die H() = ist. Aufgabe P: ( + VP) Gegeben ist die Funktion f durch f() =,5, a) Skizziere das Schaubild K von f. Die -Achse, K und die Gerade = begrenzen im Bereich eine Fläche. Berechne den Inhalt dieser Fläche. b) Bestimme die Gleichung der Tangente t an den Graphen von f im Punkt B(/). Der Graph von f, seine Tangente in B(/) und die y-achse begrenzen eine Fläche. Berechne ihren Inhalt. Aufgabe P: ( VP) Gegeben ist die Funktion f mit f() =, >. Der Graph G von f, die -Achse und die Gerade = 1 begrenzen eine ins Unendlich reichende Fläche. Untersuche, ob ihr Inhalt einen Grenzwert hat. Aufgabe P: ( VP) Die Abbildung zeigt das Schaubild einer ganzrationalen Funktion f. Begründe, welche der folgenden Aussagen über die Funktion F() = f(t)dt wahr und welche falsch sind. (1) F() < () Der Graph von F ist für -1 < < 1 eine Linkskurve. () F(-) ist positiv. () F (1) ist Null
3 Wahlteil - mit GTR und Formelsammlung Aufgabe W1: ( + VP) Ein Staubecken wird zur Zeit der Schneeschmelze gefüllt. Da die Schneeschmelze temperaturabhängig ist, kann die momentane Zuflussrate des Wassers durch die Funktion w mit w(t) =,5 t t + t+ 5, t 1 beschrieben werden (t in Stunden seit Beobachtungsbeginn, w(t) in m h ). m a) In welchem Zeitraum ist die momentane Zuflussrate größer als 1 h? Zu welchem Zeitpunkt nimmt die momentane Zuflussrate am stärksten ab? Welche mittlere momentane Zuflussrate erhält man für die ersten 1 Stunden seit Beobachtungsbeginn? b) Zu Beobachtungsbeginn enthält das Staubecken 5 m³ Wasser. Wie viel Wasser enthält es nach 1 Stunden? Zeige (ohne GTR), dass die Funktion f mit 1 f(t) = t t + 18 t + 5 t+ 5 ; t 1 1 (t in Stunden seit Beobachtungsbeginn, f(t) in m³ ) die zum Zeitpunkt t im Staubecken enthaltene Wassermenge angibt. Nach welcher Zeit sind 5 m³ Wasser im Becken? Aufgabe W: ( + VP) Gegeben ist die Funktion f durch f() = ; + 1 Der Graph von f, die -Achse und die Geraden = und = schließen eine Fläche ein. Diese rotiert um die -Achse. Der dabei entstehende Rotationskörper stellt die Designstudie einer Flasche dar (Koordinatenangaben in cm). a) Welches Volumen hat die Flasche? b) Solche Flaschen sollen später gefüllt und in einem zylinderförmigen Karton verkauft werden. Dabei steht eine Flasche so in einem cm hohen Zylinder, dass sie an ihrer breitesten Stelle 1 cm Abstand vom Zylindermantel hat. Der die Flasche umgebende Hohlraum ist mit Holzwolle gefüllt. Welches Volumen hat der Hohlraum?
4 Lösungen Aufgabe P1: 1 1 1,5 1 1,5 a) f() = + cos(,5) F() = + sin(,5) = + sin(,5) 1,5,5 b) f() = ( ) F() = ( ) = ( ) = 1 1 c) Es ist H() = + + C 1 Es gilt H() = : = + + C C= 1 1 Die Stammfunktion lautet H() = + 1 Aufgabe P: a) Die Skizze der nach unten geöffneten Parabel wird mit Hilfe einer Wertetabelle durchgeführt. 1 5 y 1,5 1,5 -,5 - Es ist 1 1 f()d = (1 ) = = Da die Fläche unterhalb der -Achse liegt, ist das Ergebnis des Integrals negativ. 1 Die gesuchte Fläche beträgt A= Flächeneinheiten. Tangentengleichung im Punkt B(/): Die allgemeine Tangentenformel lautet y= f (u) ( u) + f(u) Die Berührung erfolgt an der Stelle u = : y= f () ( ) + f() Mit f () = folgt f () =. Außerdem ist f() =. Tangentengleichung in B: y= ( ) + und vereinfacht y= + 8
5 Der gesuchte grau markierte Flächeninhalt beträgt 1 A = ( + 8 (,5 ))d = ( + 8+,5 )d= + 8+ = + + = Flächeneinheiten Aufgabe P: Da die Fläche nach rechts offen ist, wird als obere Grenze die Variable = z gewählt. z z z z z d= d= = = + Für z + strebt + z Die nach rechts offene Fläche hat den Grenzwert A =. Aufgabe P: (1) Es ist F() = f(t)dt Die Fläche zwischen f(t) und der -Achse im Intervall von bis ist größer als. Die Aussage ist falsch. () Der Graph von F ist eine Linkskurve, wenn F () > ist. Da F () = f () ist, muss somit f () > sein. Im Intervall -1 < 1 ist das Schaubild von f() streng monoton wachsend, somit sind Steigungen der Tangenten an f() positiv und die Aussage ist wahr. () F( ) = f(t)dt liefert einen negativen Wert, da die Fläche zwar oberhalb der t-achse liegt, aber von rechts nach links integriert wird und daher das Integral negativ wird. Die Aussage ist falsch. 5
6 () F (1) = f (1) = ist wahr, da bei = 1 das Schaubild von f() einen Hochpunkt besitzt und damit auch eine waagrechte Tangente. Aufgabe W1: a) Zeitraum, in dem die Zuflussrate größer als 1 m³/h ist: Ansatz: w(t) > 1 Die beiden Schaubilder schneiden sich bei t = sowie bei t =,17. Die Zuflussrate ist größer als 1 m³/h im Zeitraum < t<,17. stärkste Abnahme der momentanen Zuflussrate: Die Zuflussrate nimmt am stärksten ab, wenn w(t) minimal wird. Die Zuflussrate wird nach t = 8 Stunden minimal. Mittlere momentane Zuflussrate = w(t)dt = 1= 8 1 m³/h (GTR). 1 b) Wassermenge nach 1 Stunden = 5+ w(t)dt = 5+ 95= 55 m³ 1 Die Stammfunktion f von w(t) mit f() = 5 beschreibt die zum Zeitpunkt t enthaltene Wassermenge., 5 Stammfunktion von w(t): f(t) = t t + t + 5t+ C 1 und vereinfacht f(t) = t t + 18t + 5t+ C 1 Aus f() = 5 folgt C = 5. 1 Damit lautet die gesuchte Stammfunktion f(t) = t t + 18t + 5t+ 5 und diese 1 stimmt mit der dargestellten Funktion überein.
7 Zeit, nach der 5 m³ im Becken sind: f(t) = 5 Lösung mit GTR: Nach t = 5,1 Stunden sind 5 m³ im Becken. Aufgabe W: a) Volumen der Flasche = π f() d 781, cm³ b) Die breiteste Stelle der Flasche entspricht dem Hochpunkt des Schaubildes. Mit dem GTR ergibt sich als Hochpunkt H(/5). Der Radius der Flasche an der breitesten Stelle beträgt daher r = 5 cm. Aufgrund des vorgegebenen Abstandes muss der Zylinder einen Radius von cm haben. Die Zylinderhöhe beträgt cm. V =π r h=π 9 cm³ Zylinder Der Hohlraum beträgt VHohlraum = 9 781, = 11, cm³. 7
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Pflichtteilaufgaben zur Integralrechnung
 Testklausur K Integralrechnung# Pflichtteilaufgaben zur Integralrechnung Aufgabe : Gib jeweils eine Stammfunktion an: a) f () = ² + f () = Aufgabe : Ermittle eine Stammfunktion für a) f() = n Für welche
Testklausur K Integralrechnung# Pflichtteilaufgaben zur Integralrechnung Aufgabe : Gib jeweils eine Stammfunktion an: a) f () = ² + f () = Aufgabe : Ermittle eine Stammfunktion für a) f() = n Für welche
Analysis: Exponentialfunktionen Analysis
 www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
Die Funktion ist gegeben durch ; 0. a) Die Tangente an den Graphen von im Punkt verläuft durch 0 0,5. Bestimmen Sie die Koordinaten von.
 Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.
 1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
1.2 Berechne den Inhalt der Fläche, die das Schaubild von mit 5P der -Achse einschließt.
 Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg Wahlteil Analysis A1 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 2017 1 Aufgabe
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg Wahlteil Analysis A1 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 2017 1 Aufgabe
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Analysis: Klausur Analysis
 Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 2018 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 08 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 08 Aufgabe A. Der
Hauptprüfung Abiturprüfung 08 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 08 Aufgabe A. Der
Lösung Pflichtteilaufgaben zur Integralrechnung
 Testklausur K Integralrechnung# Lösung Pflichtteilaufgaben ur Integralrechnung Aufgabe : a) F) + b) f) F) Aufgabe : n+ n+ a) f) F) n + Für n kann keine Stammfunktion angegeben werden. Hinweis: Für die
Testklausur K Integralrechnung# Lösung Pflichtteilaufgaben ur Integralrechnung Aufgabe : a) F) + b) f) F) Aufgabe : n+ n+ a) f) F) n + Für n kann keine Stammfunktion angegeben werden. Hinweis: Für die
Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR.
 Lösung A1.1 Lösungslogik GTR-Einstellungen: Y1=6000, Y2= 1 Y3=4000 Y4= 1 Y5=5000 Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR. Zeitraum Änderungsrate
Lösung A1.1 Lösungslogik GTR-Einstellungen: Y1=6000, Y2= 1 Y3=4000 Y4= 1 Y5=5000 Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR. Zeitraum Änderungsrate
Mathematik - Oberstufe
 Mathematik - Oberstufe Pflicht- /Wahlteilaufgaben und Musterlösungen ur Integralrechnung Zielgruppe: Oberstufe Gymnasium Schwerpunkt: Stammfunktion, Flächenberechnung, Rotationsvolumen Aleander Schwar
Mathematik - Oberstufe Pflicht- /Wahlteilaufgaben und Musterlösungen ur Integralrechnung Zielgruppe: Oberstufe Gymnasium Schwerpunkt: Stammfunktion, Flächenberechnung, Rotationsvolumen Aleander Schwar
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Analysis. Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente. Gymnasium Klasse 10
 Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Klausur Nr. 2. Produkt- und Kettenregel, Rotationskörper. keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt.
 Klausur Nr. 2 Produkt- und Kettenregel, Rotationskörper Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche
Klausur Nr. 2 Produkt- und Kettenregel, Rotationskörper Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche
 Abiturprüfung Mathematik 2010 Baden-Württemberg (ohne CAS) Wahlteil - Aufgaben Analysis I 3 Aufgabe I 3: m Ein Segelboot gleitet mit der konstanten Geschwindigkeit 160 min an einem ruhenden Motorboot vorbei.
Abiturprüfung Mathematik 2010 Baden-Württemberg (ohne CAS) Wahlteil - Aufgaben Analysis I 3 Aufgabe I 3: m Ein Segelboot gleitet mit der konstanten Geschwindigkeit 160 min an einem ruhenden Motorboot vorbei.
Hauptprüfung Abiturprüfung 2018 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 018 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 018 1 Aufgabe A.1
Hauptprüfung Abiturprüfung 018 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 018 1 Aufgabe A.1
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Abiturprüfung Mathematik 2008 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Abiturprüfung Mathematik 2013 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen
 1 Abiturprüfung Mathematik 2013 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1 Ein zunächst leerer Wassertank
1 Abiturprüfung Mathematik 2013 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1 Ein zunächst leerer Wassertank
Diverse Aufgaben zur Abi-Vorbereitung - Entwurf -
 Abiturvorbereitung Abi-Aufgaben S. von 5 Basis-Aufgaben Analysis Diverse Aufgaben zur Abi-Vorbereitung - Entwurf - Aufgabe "Allgemeines" a) Bestimme eine Stammfunktion F(x) von f ( x)= 4 sin (x) mit F
Abiturvorbereitung Abi-Aufgaben S. von 5 Basis-Aufgaben Analysis Diverse Aufgaben zur Abi-Vorbereitung - Entwurf - Aufgabe "Allgemeines" a) Bestimme eine Stammfunktion F(x) von f ( x)= 4 sin (x) mit F
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
1.2 Weisen Sie rechnerisch nach, dass das Schaubild der Funktion mit 4P! bei 1 einen Sattelpunkt aufweist.
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Klausur Nr. 2. Produkt- und Kettenregel, Rotationskörper. keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt.
 Klausur Nr. 2 Produkt- und Kettenregel, Rotationskörper Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche
Klausur Nr. 2 Produkt- und Kettenregel, Rotationskörper Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com April 2016 1 Aufgabe
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com April 2016 1 Aufgabe
Pflichtteilaufgaben zu Funktionenkompetenz. Baden-Württemberg
 Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
. Ihr Schaubild sei &. a) Geben Sie die Asymptoten von & an. b) Bestimmen Sie den Schnittpunkt der Tangente an & im Punkt 1 1 mit der Achse.
 Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 1 Lösungen der Aufgaben A 1.1 und A 1.
 1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 1 Lösungen der Aufgaben A 1.1 und A 1.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 1.1
1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 1 Lösungen der Aufgaben A 1.1 und A 1.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 1.1
Aufgabe A2 1.1 Die Funktion ist gegeben durch 3P 21 mit Berechne die Gleichung der Tangente an das Schaubild von im Schnittpunkt mit der -Achse. 1.2 E
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
Hauptprüfung 2006 Aufgabe 1
 Hauptprüfung 6 Aufgabe. Geben Sie eine Funktion h an, deren Schaubild mit der folgenden Kurve übereinstimmt. (6 Punkte). Gegeben ist die Funktion f mit f(x) = x + x, x Ihr Schaubild ist K. Berechnen Sie
Hauptprüfung 6 Aufgabe. Geben Sie eine Funktion h an, deren Schaubild mit der folgenden Kurve übereinstimmt. (6 Punkte). Gegeben ist die Funktion f mit f(x) = x + x, x Ihr Schaubild ist K. Berechnen Sie
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
M I N I S T E R I U M F Ü R K U L T U S, J U G E N D U N D S P O R T. Berufsoberschule (BOS) SO/TO/WO. 2 2x
 Mathematik (43) Musteraufgabe Gruppe I: Analysis ohne Hilfsmittel ab 07 Seite /3 Gegeben ist die Funktion f mit 4 3 f(x) x x 3x 4x ; xir. 6 Bestimmen Sie den Bereich, in dem das Schaubild von f rechtsgekrümmt
Mathematik (43) Musteraufgabe Gruppe I: Analysis ohne Hilfsmittel ab 07 Seite /3 Gegeben ist die Funktion f mit 4 3 f(x) x x 3x 4x ; xir. 6 Bestimmen Sie den Bereich, in dem das Schaubild von f rechtsgekrümmt
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Übungsklausur Analysis & Geometrie Stausee & Personenaufzug Pflichtteil (ohne Hilfsmittel)
 Pflichtteil (ohne Hilfsmittel) ) Berechne die. Ableitung. a) f(x) 3x sin( x ) b) f(x) 3x sin( x ) (VP) 3 ) Berechne und vereinfache x 3) Bestimme die Lösungsmenge der Gleichung sin( x) dx. (3VP) cos(x)
Pflichtteil (ohne Hilfsmittel) ) Berechne die. Ableitung. a) f(x) 3x sin( x ) b) f(x) 3x sin( x ) (VP) 3 ) Berechne und vereinfache x 3) Bestimme die Lösungsmenge der Gleichung sin( x) dx. (3VP) cos(x)
1.4 Schaubild von Schaubild von Schaubild von 1., /
 Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Hauptprüfung Fachhochschulreife Baden-Württemberg
 Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Analysis: Trigonometr. Funktionen Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben
 Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abschlussprûfung Berufskolleg. (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg. Analysis 2 Ganzrationale Funktionen.
 Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Analysis 2 Ganzrationale Funktionen zusammen mit Exponentialfunktionen Jahrgänge 2009 bis 2016 Text Nr. 74302 Stand
Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Analysis 2 Ganzrationale Funktionen zusammen mit Exponentialfunktionen Jahrgänge 2009 bis 2016 Text Nr. 74302 Stand
 Abiturprüfung Mathematik 004 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f() = + 3 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 004 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f() = + 3 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Trigonometrische Funktionen
 Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Exponentialfunktionen. Nur Kurvendiskussionen und Integralrechnung. für die wichtigsten e-funktionen. Lösungen ohne CAS und GTR
 Eponentialfunktionen Nur Kurvendiskussionen und Integralrechnung für die wichtigsten e-funktionen Lösungen ohne CAS und GTR Alle Methoden ganz ausführlich Datei Nr. 45 Stand 5. Oktober 6 FRIEDRICH W. BUCKEL
Eponentialfunktionen Nur Kurvendiskussionen und Integralrechnung für die wichtigsten e-funktionen Lösungen ohne CAS und GTR Alle Methoden ganz ausführlich Datei Nr. 45 Stand 5. Oktober 6 FRIEDRICH W. BUCKEL
Analysis: Ableitung, Änderungsrate,Tangente 2 Analysis Ableitung, Änderungsrate, Tangente Teil 2 Gymnasium Klasse 10
 www.mathe-aufgaben.com Analysis: Ableitung, Änderungsrate,Tangente Analysis Ableitung, Änderungsrate, Tangente Teil Gymnasium Klasse 0 Aleander Schwarz www.mathe-aufgaben.com Oktober 06 www.mathe-aufgaben.com
www.mathe-aufgaben.com Analysis: Ableitung, Änderungsrate,Tangente Analysis Ableitung, Änderungsrate, Tangente Teil Gymnasium Klasse 0 Aleander Schwarz www.mathe-aufgaben.com Oktober 06 www.mathe-aufgaben.com
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
 Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( 3x + ) Aufgabe : ( VP) 9 Berechnen Sie das Integral 4 x dx Aufgabe 3: (3 VP) x. Lösen Sie die Gleichung
Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( 3x + ) Aufgabe : ( VP) 9 Berechnen Sie das Integral 4 x dx Aufgabe 3: (3 VP) x. Lösen Sie die Gleichung
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
K2 MATHEMATIK KLAUSUR. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 4.02.204 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 28 5 5 2 60 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 2 4 5 3 3 4 3 Punkte WT Ana A.a b A2.a b Summe P. (max
K2 MATHEMATIK KLAUSUR 4.02.204 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 28 5 5 2 60 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 2 4 5 3 3 4 3 Punkte WT Ana A.a b A2.a b Summe P. (max
3.* Klausur Pflichtteil
 EI M5 2010-11 MATHEMATIK 3.* Klausur Pflichtteil In diesem Teil sind weder GTR noch die Formelsammlung erlaubt. Um den Wahlteil zu erhalten, gib bitte diesen Pflichtteil bearbeitet ab. 1. Aufgabe light
EI M5 2010-11 MATHEMATIK 3.* Klausur Pflichtteil In diesem Teil sind weder GTR noch die Formelsammlung erlaubt. Um den Wahlteil zu erhalten, gib bitte diesen Pflichtteil bearbeitet ab. 1. Aufgabe light
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
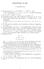 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Einführung des Integrals Stammfunktionen Hauptsatz Flächen Mittelwerte Rotationsvolumen
 14 Integralrechnung Einführung des Integrals Stammfunktionen Hauptsatz Flächen Mittelwerte Rotationsvolumen E-Mail: klaus_messner@web.de, Internet: www.elearning-freiburg.de Einführung des Integrals 15
14 Integralrechnung Einführung des Integrals Stammfunktionen Hauptsatz Flächen Mittelwerte Rotationsvolumen E-Mail: klaus_messner@web.de, Internet: www.elearning-freiburg.de Einführung des Integrals 15
I 1. Ermittle von den folgenden Funktionen jeweils Stammfunktionen: (d) 4cosxdx (e) 3e x dx (f) ( e x + x 2) dx
 Integralrechnung: I. Ermittle von den folgenden Funktionen jeweils Stammfunktionen: (a) y =,5 (b) y = + (c) y = 5 (d) y = 3 (e) y = (f) y = (g) y = 3 (h) y = (i) y = 3 4 4 (j) y = 6 + 3 (k) y = 3 + 4 (l)
Integralrechnung: I. Ermittle von den folgenden Funktionen jeweils Stammfunktionen: (a) y =,5 (b) y = + (c) y = 5 (d) y = 3 (e) y = (f) y = (g) y = 3 (h) y = (i) y = 3 4 4 (j) y = 6 + 3 (k) y = 3 + 4 (l)
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation
 5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Kursarbeit Nr.1 LK Mathematik NAME :
 Kursarbeit Nr.1 LK Mathematik 7. 10. 2004 1. Bestimmen Sie eine Stammfunktion F zur angegebenen Funktion f! a) f :R R, f x =1 1 x 100 b) f :R R, f x =sin 2 x 5 x c) f :R R, f x = x 5 x 3 2 2 x 2 2. Berechnen
Kursarbeit Nr.1 LK Mathematik 7. 10. 2004 1. Bestimmen Sie eine Stammfunktion F zur angegebenen Funktion f! a) f :R R, f x =1 1 x 100 b) f :R R, f x =sin 2 x 5 x c) f :R R, f x = x 5 x 3 2 2 x 2 2. Berechnen
Analysis: Trigonometr. Funktionen Analysis Trigonometrische Funktion Wahlteilaufgaben Gymnasium Oberstufe J1 oder J2
 Analysis Trigonometrische Funktion Wahlteilaufgaben Gymnasium Oberstufe J1 oder J2 Alexander Schwarz www.mathe-aufgaben.com Januar 2015 1 In einem Küstenort kann der Pegelstand im Hafenbecken durch die
Analysis Trigonometrische Funktion Wahlteilaufgaben Gymnasium Oberstufe J1 oder J2 Alexander Schwarz www.mathe-aufgaben.com Januar 2015 1 In einem Küstenort kann der Pegelstand im Hafenbecken durch die
Abiturprüfung an den allgemein bildenden Gymnasien
 MINISTERIUM FÜR KULTUS, JUGEND UND SPORT Hinweise für die Abiturientinnen und Abiturienten Abiturprüfung an den allgemein bildenden Gymnasien Haupttermin 017 Prüfungsfach: Bearbeitungszeit: Hilfsmittel:
MINISTERIUM FÜR KULTUS, JUGEND UND SPORT Hinweise für die Abiturientinnen und Abiturienten Abiturprüfung an den allgemein bildenden Gymnasien Haupttermin 017 Prüfungsfach: Bearbeitungszeit: Hilfsmittel:
8 5 9 : 8 5 ; 0 85<8. 8 : 8 0 > 1 Der Schnittpunkt mit der x-achse ist? 1 0.
 Aufgabe M04A1 Gegeben ist die Funktion mit. Ein Teil des Graphen ist abgebildet. a) Geben Sie die maximale Definitionsmenge von und Gleichungen der Asymptoten von an. besitzt einen Schnittpunkt mit der
Aufgabe M04A1 Gegeben ist die Funktion mit. Ein Teil des Graphen ist abgebildet. a) Geben Sie die maximale Definitionsmenge von und Gleichungen der Asymptoten von an. besitzt einen Schnittpunkt mit der
3 Differenzialrechnung
 Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Pflichtteilaufgaben zu Elemente der Kurvendiskussion. Baden-Württemberg
 Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
 Pflichtteil Aufgaben Aufgabe : ( VP) x Gegeben ist die Funktion f mit f(x) =. x 3 Bilden Sie die Ableitung von f und fassen Sie diese so weit wie möglich zusammen. Aufgabe : ( VP) G ist eine Stammfunktion
Pflichtteil Aufgaben Aufgabe : ( VP) x Gegeben ist die Funktion f mit f(x) =. x 3 Bilden Sie die Ableitung von f und fassen Sie diese so weit wie möglich zusammen. Aufgabe : ( VP) G ist eine Stammfunktion
Abitur 2012 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Göttge-Piller, Höger
 VP b) Das Schaubild von hat für 3 6 genau zwei Wendepunkte. c) Es gilt 4. 3. Gegeben ist die Funktionenschar mit ²² für 0. Für welchen Wert von t schließt das Schaubild der entsprechenden Funktion mit
VP b) Das Schaubild von hat für 3 6 genau zwei Wendepunkte. c) Es gilt 4. 3. Gegeben ist die Funktionenschar mit ²² für 0. Für welchen Wert von t schließt das Schaubild der entsprechenden Funktion mit
Inhalt der Lösungen zur Prüfung 2011:
 Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Übungsbeispiele Differential- und Integralrechnung
 Übungsbeispiele Differential- und Integralrechnung A) Gegeben ist die Funktion: y = 2x 3 9x 2 + 12x. a) Skizzieren Sie die Funktion im Intervall [ 0,5; 3] b) Diskutieren Sie die Funktion (Nullstellen,
Übungsbeispiele Differential- und Integralrechnung A) Gegeben ist die Funktion: y = 2x 3 9x 2 + 12x. a) Skizzieren Sie die Funktion im Intervall [ 0,5; 3] b) Diskutieren Sie die Funktion (Nullstellen,
stellt eine fallende Gerade dar mit Nullstelle bei x = 5/3. 1/3
 Aufgabe 4) Gegeben sind die Funktionen f mit f (x)= 4 x2 + 2 x+ 4 und g mit 3 g ( x)= 4 x2 + 5 2 x 3 4. a) Weisen Sie rechnerisch nach, dass der Graph Gf folgende Eigenschaften besitzt: Der Scheitelpunkt
Aufgabe 4) Gegeben sind die Funktionen f mit f (x)= 4 x2 + 2 x+ 4 und g mit 3 g ( x)= 4 x2 + 5 2 x 3 4. a) Weisen Sie rechnerisch nach, dass der Graph Gf folgende Eigenschaften besitzt: Der Scheitelpunkt
Hauptprüfung 2007 Aufgabe 3
 Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
K2 MATHEMATIK KLAUSUR 4. Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen
 ZK M A (mit CAS) Seite von 5 Nr. Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen Punkte a Nullstellen von f: f ( = 0 x = x = x = + Lokale Extrempunkte:,7
ZK M A (mit CAS) Seite von 5 Nr. Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen Punkte a Nullstellen von f: f ( = 0 x = x = x = + Lokale Extrempunkte:,7
Demo: Mathe-CD. Integration Flächenberechnungen. Sammlung von Trainingsaufgaben. Friedrich Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
 Integration Flächenberechnungen Tet noch nicht fertig Vorabversion! Weitere Aufgaben folgen! Sammlung von Trainingsaufgaben Lösungen in 486 Datei Nr. 48 5 Stand 8. Dezember 008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Integration Flächenberechnungen Tet noch nicht fertig Vorabversion! Weitere Aufgaben folgen! Sammlung von Trainingsaufgaben Lösungen in 486 Datei Nr. 48 5 Stand 8. Dezember 008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
b) Kettenregel anwenden 1 8x + 3sin(x) f '(x) = ( 8x 3( sin(x) )) 2 4x 3cos(x) 2 4x 3cos(x) b) [2P]
![b) Kettenregel anwenden 1 8x + 3sin(x) f '(x) = ( 8x 3( sin(x) )) 2 4x 3cos(x) 2 4x 3cos(x) b) [2P] b) Kettenregel anwenden 1 8x + 3sin(x) f '(x) = ( 8x 3( sin(x) )) 2 4x 3cos(x) 2 4x 3cos(x) b) [2P]](/thumbs/77/74547694.jpg) Mathematik Name: Lösungen Nr. K Punkte: /3 Note: Schnitt: 7..3 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die
Mathematik Name: Lösungen Nr. K Punkte: /3 Note: Schnitt: 7..3 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 27.11.2014 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl (max) 28 15 15 2 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 4 5 5 3 2 1 WT Ana A.1a) b) c) Summe P. (max) 6 4 5 15
K2 MATHEMATIK KLAUSUR 2 27.11.2014 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl (max) 28 15 15 2 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 4 5 5 3 2 1 WT Ana A.1a) b) c) Summe P. (max) 6 4 5 15
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Wahlteil - Aufgaben Analysis I Aufgabe I : Gegeben sind die Funktionen f und g durch f(x) cos( π x) und g(x) ( x) f(x) ; x Ihre Schaubilder sind K
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Wahlteil - Aufgaben Analysis I Aufgabe I : Gegeben sind die Funktionen f und g durch f(x) cos( π x) und g(x) ( x) f(x) ; x Ihre Schaubilder sind K
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Mathematik im Berufskolleg II
 Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Ausführliche Lösungen
 Bohner Ihlenburg Ott Deusch Mathematik für berufliche Gmnasien Jahrgangsstufen und Analsis und Stochastik Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 5. Auflage 05 ISBN 978--80-8- Das
Bohner Ihlenburg Ott Deusch Mathematik für berufliche Gmnasien Jahrgangsstufen und Analsis und Stochastik Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 5. Auflage 05 ISBN 978--80-8- Das
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
a) Begründen Sie, dass der Graph von f symmetrisch zum Punkt S 0 2 f) Ermitteln Sie eine Gleichung der Tangente im Punkt B
 I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x
![b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x](/thumbs/58/42387852.jpg) K1 Punkte: / Note: Schnitt:.10.1 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
K1 Punkte: / Note: Schnitt:.10.1 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
c) Das Schaubild von verläuft im Schnittpunkt mit der y-achse steiler als die erste Winkelhalbierende.
 VP b) Das Schaubild von hat für 36 genau zwei Wendepunkte. c) Das Schaubild von verläuft im Schnittpunkt mit der y-achse steiler als die erste Winkelhalbierende. 3. Gegeben ist die Funktionenschar mit
VP b) Das Schaubild von hat für 36 genau zwei Wendepunkte. c) Das Schaubild von verläuft im Schnittpunkt mit der y-achse steiler als die erste Winkelhalbierende. 3. Gegeben ist die Funktionenschar mit
Pflichtteil Aufgabe 5 Funktionenkompetenz
 Pflichtteil Aufgabe 5 Funktionenkompetenz 2016 (5VP) Die Abbildung zeigt den Graphen einer Stammfunktion F einer Funktion f. Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Begru nden Sie
Pflichtteil Aufgabe 5 Funktionenkompetenz 2016 (5VP) Die Abbildung zeigt den Graphen einer Stammfunktion F einer Funktion f. Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Begru nden Sie
 Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() 3 e =. Bestimmen Sie eine Stammfunktion der Funktion f mit Aufgabe 3: (3 VP) 5 3 Lösen
Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() 3 e =. Bestimmen Sie eine Stammfunktion der Funktion f mit Aufgabe 3: (3 VP) 5 3 Lösen
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 016 (ohne CAS) Baden-Württemberg Wahlteil Analysis 1 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com April 016 1 Aufgabe
Hauptprüfung Abiturprüfung 016 (ohne CAS) Baden-Württemberg Wahlteil Analysis 1 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com April 016 1 Aufgabe
