Ist Mathematik die Sprache der Natur?
|
|
|
- Pamela Abel
- vor 8 Jahren
- Abrufe
Transkript
1 Ist Mathematik die Sprache der Natur? Ehrhard Behrends Sonderdruck aus: MITTEILUNGEN DER MATHEMATISCHEN GESELLSCHAFT IN HAMBURG BAND XXIX 2010 IM AUFTRAG DER GESELLSCHAFT HERAUSGEGEBEN VON T. ANDREAE W. BENZ H. KARZEL A. KREUZER G. OPFER G. TISCHEL H. WEFELSCHEID SCHRIFTLEITUNG H. KIECHLE G. TISCHEL
2
3 Mitt. Math. Ges. Hamburg 29 (2010), Ist Mathematik die Sprache der Natur? Von Ehrhard Behrends Ziel des Vortrags sind Informationen und Kommentare rund um das folgende berühmte Galilei-Zitat aus dem Buch Il Saggiatore : Die Philosophie steht in diesem großen Buch geschrieben, das unserem Blick ständig offen liegt. Aber das Buch ist nicht zu verstehen, wenn man nicht zuvor die Sprache erlernt und sich mit den Buchstaben vertraut gemacht hat, in denen es geschrieben ist. Es ist in der Sprache der Mathematik geschrieben, und deren Buchstaben sind Kreise, Dreiecke und andere geometrische Figuren, ohne die es dem Menschen unmöglich ist, ein einziges Bild davon zu verstehen; ohne diese irrt man in einem dunklen Labyrinth herum. 1 Beschreibung der Welt in der Antike 1.1 Pythagoras Pythagoras, geboren um 570 v. Chr. auf der Insel Samos, verließ wegen politischer Schwierigkeiten seine Heimat und wanderte nach Unteritalien aus. In Kroton (heute Crotone, vgl. Bild 2) gründete er eine philosophische Schule und lebte mit seinen Anhängern dort zusammen. Bild 1 Büste des Pythagoras. Bild 2 Crotone (roter Pfeil). Die Pythagoreer stellten die Mathematik in den Mittelpunkt ihrer Philosophie. Die auf mathematische Experimente mit schwingenden Saiten unterschiedlicher Von G. Tischel bearbeitete Fassung des Vortrages auf der Herbsttagung der Mathematischen Gesellschaft in Hamburg am 6. November
4 Ehrhard Behrends Länge gestützte Entdeckung, dass sich die Intervalle innerhalb der Tonleiter als Verhältnis ganzer Zahlen ausdrücken lassen, machte großen Eindruck auf die Pythagoreer und veranlasste sie zu kühnen Verallgemeinerungen. Nach der pythagoreischen Lehre ist die mathematische Ordnung der Urgrund aller Dinge. Alles Seiende ist Zahl. Die ganze Welt ist geordnet und regelhaft, und der Mensch kann durch mathematisches Denken diese Ordnung verstehen. Zusammengefasst in einem Motto lautet die pythagoreische Lehre: Alles ist Zahl. Für die Mathematik der Pythagoreer ist es charakteristisch, dass sie rein theoretischen Charakter hat. Ihre zahlentheoretischen Überlegungen liefern keine Rechenanweisungen oder technische Anwendungen. Für die Pythagoreer war jede Zahl ein Vielfaches der Eins. Wenn die Dinge Zahlen sind, dann bestehen die Dinge letzten Endes aus Vielfachen von Einheiten. Die Entdeckung von Hippasos von Metapont in der Mitte des 5. Jahrhunderts v. Chr., dass die Diagonale und die Seite eines regelmäßigen 5-Ecks kein gemeinsames Maß haben, erschütterte das spekulative Weltbild der Pythagoreer erheblich. Die Weltbeschreibung der Pythagoreer kann als erster Versuch angesehen werden, die Welt mathematisch zu beschreiben. Vieles war allerdings Spekulation, die Jahre überdauert haben nur die Zahlenmystik und die pythagoräische Tonleiter. 1.2 Platon Platon wurde 427 oder 428 v. Chr. geboren, lebte also rund 100 Jahre später als Pythagoras. Auch seine Weltbeschreibung ist rein spekulativ und stützt sich auf die Mathematik, aber nicht auf Zahlentheorie, sondern auf Geometrie. Seine Kosmologie legte er in dem Dialog Timaios dar. Nach Platon bestehen die Dinge aus den Elementen Feuer, Wasser, Erde und Luft und aus einem fünften Element, aus dem der Himmel gebildet ist. Die Teilchen dieser Elemente entsprechen den Formen der sogenannten Platonischen Körper (Bild 3). Bild 3 Die 5 platonischen Körper. Die einzelnen Zuordnungen bei Platon sind: Erde Würfel, Wasser Ikosaeder, Luft Oktaeder, Feuer Tetraeder. 54
5 Ist Mathematik die Sprache der Natur? Das Dodekaeder bleibt dem Weltganzen vorbehalten. Die Gesamtheit der Körper bilden die Kugel des Kosmos, der um seine Achse rotiert. Die Platonischen Körper sind aber noch nicht die letzten Strukturelemente, da sie von Flächen begrenzt sind, die ihrerseits wieder in Dreiecke zerlegt werden können. Diese Dreiecke gelten als die elementaren Formen. Es handelt sich um zwei Arten von Dreiecken, nämlich das rechtwinklige gleichschenklige Dreieck mit den Seitenverhältnissen 1:1: 2 und das Dreieck mit den Winkeln 30 o, 30 o, 90 o, das die Seitenverhältnisse 1: 2: 3 hat. Diese Dreiecke ergeben sich, wenn man eine Würfelfläche durch ihre Diagonale teilt bzw. eine Fläche des Tetraeders oder Oktaeders oder Ikosaeders durch die Höhe teilt (Bild 4). Das Besondere dieser beiden Arten von Dreiecken ist, dass ihre weitere Teilung durch die Höhe immer wieder ähnliche Dreiecke ergibt. Platon nennt diese Dreiecke daher die schönsten Dreiecke. Bild 4 Platons Spekulationen über den Aufbau der materiellen Dinge können heute nicht mehr ernst genommen werden. Doch immerhin verdient der Gedanke auch heute noch Beachtung, dass sich die Dinge nur durch formale Strukturen erklären lassen. 2 Die kopernikanische Revolution Schon im 3. Jahrhundert v. Chr. hatte Aristarch von Samos die Vermutung, dass die Erde sich mit den anderen Planeten um ein Zentralfeuer als Mittelpunkt des Alls bewegt. Doch seine Auffasung konnte sich nicht durchsetzen. Das geozentrische Weltbild wurde durch Claudius Ptolemäus im 2. Jahrhundert n. Chr. gefestigt. In seinem Großen astronomischen System hat er die in der Antike herrschenden Lehren zusammengefaßt. Seine Lehren entsprachen dem von der Kirche gelehrten Weltbild. Die Abkehr vom geozentrischen Weltbild begann in der frühen Neuzeit mit den Anfängen der Naturwissenschaft. Bild 5 Kopernikus. 55
6 Ehrhard Behrends Den entscheidenden Schritt zum heliozentrischen System vollzog Nikolaus Kopernikus (geb in Thorn, gest in Frauenburg). Kopernikus hatte sich intensiv mit astronomischen Fragen beschäftigt. Dabei wurde ihm klar, dass sich die Plantenbewegungen viel einfacher vom heliozentrischen Standpunkt aus beschreiben ließen. Vermutlich war er bereits 1510 überzeugt vom heliozentrischen Weltbild und versuchte es möglichst gut zu begründen. Er hatte aber nur sehr ungenaue Meßergebnisse, denn es gab noch kein Fernrohr. Er zögerte die Veröffentlichung seiner Theorie fast bis zu seinem Tode hinaus. Erst auf dem Sterbebett erreichte ihn das erste Exemplar seines Buches mit dem Titel De revolutionibus orbium coelestium. Das von Kopernikus vertretene heliozentrische Weltbild war im Rahmen der damals bekannten Physik, in der es noch keine Gravitationskräfte gab, sehr widersprüchlich. Einwände waren u. a. die nicht sichtbare Sternenparallaxe, der fehlende Gegenwind und die nicht vorhandenen Rotationskräfte. Kopernikus übernahm noch Teile des alten Weltbildes, indem er annahm, dass das All eine begrenzte Kugel sei, an dessen Sphäre die Fixsterne befestigt seien. Diese Vorstellung eines begrenzten kugelförmig abgeschlossenen Universums wurde von Giodano Bruno ( ) abgelehnt. Er folgte damit der Auffassung, die Nikolaus von Cusanus ( ) schon früher vertreten hatte. Bruno war wie Nikolaus von Cusanus davon überzeugt, dass die Welt grenzenlos ist und dass die Fixsterne Gestirne von der Art der Sonne sind, deren Bewegung wir nicht wahrnehmen können, da sie sehr weit weg von der Erde sind. Bruno versuchte die Lehre von der Unendlichkeit der Welt durch philosophische und metaphysische Überlegungen zu begründen. Doch seine Auffassungen blieben im Wesentlichen spekulativ, da er die Bedeutung der Mathematik als Sprache, in der die Naturgesetze zu formulieren sind, nicht erkannte. Sein Schicksal ist bekannt: die Verbrennung als Ketzer in Rom. 2.1 Tycho Brahe und Johannes Kepler Bild 6 Tycho Brahe. Bild 7 Johannes Kepler. Tycho Brahe ( ), ein dänischer Adliger, interessierte sich schon in sei- 56
7 Ist Mathematik die Sprache der Natur? ner Jugend für die Astronomie und wurde einer der bedeutendsten Astronomen seiner Zeit. Er befasste sich insbesondere mit der Beobachtung und Messung der Positionen der Himmelskörper. Hierzu baute er eigene Messinstrumente, zum Beispiel einen großen Mauerquadranten mit einem Radius von 2 Metern. Er erreichte damit bei denn Höhenmessungen eine Genauigkeit von wenigen Bogenminuten, und das ohne Fernrohr! Brahe wirkte zuerst in seiner dänischen Heimat, gefördert von dem dänischen König Friedrich II. Nach dessem Tode zog er für kurze Zeit nach Wandsbek bei Hamburg wechselte er nach Prag, wo man ihm die Stelle als Hofmathematiker am Kaiserhof angeboten hatte. Brahe entwickelte sein eigenes Weltsystem, das heliozentrische und geozentrische Aspekte vereint: Im Zentrum steht die Erde und um sie kreisen der Mond und die Sonne. Die Sphäre mit den Fixsternen bewegt sich in 24 Stunden einmal um die Erde. Alle anderen Himmelskörper bewegen sich um die Sonne (Bild 8). Bild 8 Brahes Weltsystem. Bild 9 Keplers Planetenmodell. Brahe war vor allem ein beobachtender Astronom, seine mathematischen Fähigkeiten waren eher gering. Er war beeindruckt von Keplers 1596 erschienenen Erstlingswerk Mysterium Cosmographicum und lud Kepler 1660 nach Prag ein, obwohl Kepler das heliozentrische Weltbild vertrat. Kepler war überzeugt von der Harmonie des Weltalls. Die Existenz von fünf Planeten und fünf platonichen Körpern konnte kein Zufall sein. In seinem Werk Myterium Cosmographicum versuchte er daher, die Bahnen der Planeten Merkur, Venus, Mars, Jupiter und Saturn auf ein- und umbeschriebenen Kugeln der platonischen Körper anzuordnen (Bild 9). Brahe hoffte, von Keplers Gedankenreichtum und mathematischen Fähigkeiten profitieren zu können. Kepler wurde Brahes Assistent, doch die Zusammenarbeit gestaltete sich schwierig und war nur kurz, da Brahe 1601 verstarb. Nach Brahes Tod wurde Kepler sein Nachfolger als Hofmathematiker am Kaiserhof in Prag. Er erbte damit auch das sehr umfangreiche und genaue Beobachtungsmaterial, das Brahe angehäuft hatte. Dieser Beobachtungsschatz ermöglichte Kepler das Auffinden mathematisch einfacher Zusammenhänge bei der Beschreibung der Planetenbahnen. Kepler verwarf auf Grund der genauen Daten 57
8 Ehrhard Behrends Brahes seine früheren Theorien. Er entwickelte ein System, das Ellipsenbahnen benutzte veröffentlichte er die Astronomia nova, die das erste und zweite Keplersche Gesetz enthielt. Nach weiteren intensiven Studien der Daten zur Umlaufbahn des Mars fand er 1618 das dritte Keplersche Gesetz, nach dem d 3 /T 3 für alle Planeten konstant ist. Hierbei bezeichnen d die Länge der großen Halbachse der Bahnellipse und T die Umlaufzeit des Planeten. Er veröffentlichte dieses Gesetz 1619 in dem Werk Harmonices Mundi libri V und nannte es ein harmonisches Gesetz. Kepler gilt als einer der Begründer der modernen Naturwissenschaften. Sein Leben war aber auch von tiefem Gottesglauben geprägt. Er glaubte, dass sich in den Gesetzen zur Planetenbewegung eine himmlische Harmonie enthülle, die der Schöpfer im Sonnensystem verewige. 2.2 Von Galilei zu Newton Galileo Galilei ( ) war Physiker, Mathematiker und Astronom. Er wurde 1589 Lektor für Mathematik an der Universität in Pisa und wurde 1592 auf den Lehrstuhl für Mathematik in Padua berufen.der Großherzog der Toskana ernannte ihn 1610 zum Hofmathematiker in Florenz. Bild 10 Galilei Galileo. Galilei arbeitete auf mehreren Gebieten der Naturwissenschaften und machte bedeutende Entdeckungen. Es war im Wesentlichen Galilei, der den Weg zu einer physikalischen Umwälzung der Natuwissenschaften ebnete. Einige Leistungen in der Astronomie seien hier kurz erwähnt: Er baute das 1609 in Holland von Jan Lippershey erfundene Fernrohr nach und nutzte es für Himmelsbeobachtungen. Dabei bemerkte er u. a.: Die Oberfläche des Mondes ist nicht glatt, sondern rau. Der Jupiter hat vier Monde. Die Milchstraße ist kein Nebel, sondern besteht aus unzähligen Sternen. Die Venus hat Phasen wie der Mond. Es gibt dunkle Flecken auf der Sonne. 58
9 Ist Mathematik die Sprache der Natur? Gestützt auf seine Beobachtungen, vertrat Galilei das heliozentrische Weltbild des Kopernikus mit Kreisbahnen. Keplers Ellipsenbahnen lehnte er ab. Papst Urban erlaubte Galilei, über das kopernikanische System zu publizieren, machte aber zur Auflage, dies als Hypothese zu behandeln erschien Galileis Dialog über die zwei wichtigsten Weltsysteme, das Ptolemäische und das Kopernikanische. Durch den Dialogo geriet Galilei in Konflikt mit der Kirche, und es kam zu einem Inquisitionsprozeß. Galilei entging der Hinrichtung auf dem Scheiterhaufen nur durch den Widerruf seiner Ansichten, von denen er überzeugt war. (Die Widerstände, gegen die Galilei zu kämpfen hatte, sind im Theaterstück Das Leben des Galilei von Bertolt Brecht sehr gut dargestellt.) Das 17. Jahrhundert war von kaum zu überschätzender Bedeutung für die Entwicklung der modernen Wissenschaft. Ausgehend von Erkenntnissen von Galilei und Kepler bemühten sich die fähigsten Köpfe dieser Zeit um das Herausarbeiten der wichtigsten Grundbegriffe und Zusammenhänge: Was ist Geschwindigkeit, was Beschleunigung, was Kraft, was Impuls,...? Beteiligt an der weiteren Entwicklung der mathematichen Sprache waren unter anderm Huygens, Leibniz, Newton, Hooke, Halley. Zu nennen ist auch Descartes ( ), der ein eher qualitatives Weltsystem in Le Monde entwickelte. Descartes beeinflusste die wissenschaftliche Methodik wesentlich durch sein 1637 veröffentlichtes Werk Abhandlung über die Methode, seine Vernunft zu gebrauchen und die Wahrheit in den Wissenschaften zu suchen. Er fordert hierin, nur das als richtig zu akzeptieren, was durch eigene schrittweise Analyse und logische Reflexion als plausibel verifiziert wird. Bild 11 Isaac Newton. Bild 12 René Descartes. Isaac Newton ( ) war Physiker, Mathematiker, Astronom und Philosoph. Er gilt als einer der größten Wissenschaftler aller Zeiten. In seinem Werk Philosophiae Naturalis Principia betont Newton, dass sich Naturgesetze nur auf Grund von Erfahrungen erkennen ließen. Sie sind nicht evidente Gesetze, 59
10 Ehrhard Behrends sondern Hypothesen, die ausgehend von Beobachtungen durch Verallgemeinerung zustande kommen. Newton war der Erste, der Bewegungsgesetze formulierte, die sowohl auf der Erde als auch am Himmel gültig sind. Er führte die drei Keplerschen Gesetze auf die allgemeine Gravitation und die Trägheit zurück. Er zeigte, dass nicht nur Ellipsen, sondern sämtliche Kegelschnitte als Bahnen von Himmelskörpern möglich sind. Newton hat damit die Arbeiten von Kopernikus, Kepler und Galilei bestätigt und vollendet. 2.3 Die Welt als Uhrwerk Die moderne Wissenschaft machte auf allen Gebieten unbeschreibliche Fortschritte. Die Erkenntnisse nahmen im 18. Jahrhundert explosionsartig zu. Es kristallisierte sich ein rein mechanisches Bild der Welt heraus: Die Welt wurde wie ein großes, überaus präzises Uhrwerk betrachtet. Bei genauer Kenntnis des jetzigen Zustands der Welt sollten genaue Aussagen über vergangene und zukünftige Ereignisse möglich sein. Es reicht, die entsprechenden mathematischen Gleichungen zu lösen. 3 Die weitere Mathematisierung der Welt Im 19. und 20. Jahrhundert stellte sich allerdings heraus, dass die Beschränkung auf eine Beschreibung durch Funktionen zu kurz griff. Das mechanische Uhrwerk- Modell konnte spätestens im 19. Jahrhundert nicht mehr aufrecht erhalten werden. Aber nur deswegen, weil es durch kompliziertere mathematische Konzepte ergänzt werden musste. Bild 13 Albert Einstein. Bild 14 Werner Heisenberg. Newtons Auffassung vom absoluten Raum und absoluter Zeit beherrschte lange Zeit das philosophische und naturwissenschaftliche Denken. Einsteins Relati- 60
11 Ist Mathematik die Sprache der Natur? vitätstheorie und die Heisenbergsche Unschärferelation beendeten diese Auffassung Newtons und das Uhrwerk-Modell der Welt. Heute haben mathematische Modelle die ganze Welt erobert, vom Mikrokosmos hier regiert der Zufall bis zum Makrokosmos, in dem man zur genauen Beschreibung nichteuklidische Geometrien braucht. Heute sind ein Fülle mathematischer Begriffe und Methoden im Einsatz, um das Wissen angemessen in Theorien ausdrücken zu können: Wahrscheinlichkeitstheorie, hochdimensionale Räume, unendlich Kleines und unendlich Großes, gekrümmte Räume,... Kurz: Am besten redet man über die Natur in der Sprache der Mathematik. 3.1 Ist das Buch der Natur in der Sprache der Mathematik geschrieben? Inwieweit hatte Galilei Recht, dass das Buch der Natur in der Sprache der Mathematik geschrieben ist? Es folgt eine kleine und sicher unvollständige Sammlung von Tatsachen und Meinungen. Die mathematische Struktur der Welt ist das Werk des Schöpfers. Uns ist vergönnt, einige Aspekte dieser Schöpfung zu erkennen, und in diesem Sinn ist Naturwissenschaft eine Art Gottesdienst. So sahen es zum Beispiel Kepler und Newton. Die mathematische Struktur ist eine Vereinbarung zwischen Menschen, um Ordnung in die chaotische Fülle der Erscheinungen zu bringen. Wir können uns die geeigneten Modelle in weiten Grenzen aussuchen. So können wir uns etwa darauf verständigen, dass die Sonne im Mittelpunkt steht. Das ist der Standpunkt des Konventionalismus. Nur weil die Welt nach kausalen und nicht zu chaotischen Prinzipien aufgebaut ist, konnte sich überhaupt Leben entwickeln und intelligente Wesen hervorbringen. Also: Weil es uns gibt, ist es kein Wunder, dass die Welt nach logischen Gesetzen funktionieren muss. Das ist der anthropozentrische Standpunkt. Heute sind die Naturwissenschaftler fest davon überzeugt, dass das Buch der Natur in der Sprache der Mathematik geschrieben ist. Diese Sprache ist allerdings viel komplizierter, als Galilei es sich gedacht hat. 61
12 4 Die Ausstellung mathema Ehrhard Behrends Im Jahr der Mathematik 2008 gab es im Deutschen Technikmuseum in Berlin die Ausstellung Die Ausstellung wurde von Mitarbeitern des Technikmuseums und dem Referenten vorbereitet, wesentliche finanzielle Unterstützung kam von der Telekomstiftung.. Bild 15 Gruppenbild: Förderer und Organisatoren von mathema bei der Ausstellungseröffnung. Das Thema dieser Ausstellung war die Frage Ist Mathematik die Sprache der Natur? Die Ausstellung sollte dazu einladen, dieser Frage nachzugehen und die Bedeutung der Mathematik in Natur, Technik und Alltag zu erforschen. Doch wie kann man so ein abstraktes Thema einem allgemeinen Publikum auf 1000 Quadratmetern nahebringen? Am Anfang im Eingangsraum steht natürlich das ausführliche Galileizitat. Und dann wird in fünf Themenräumen Mathematik in der Lebenswirklichkeit der Besucher gesucht: Zahl Raum Bewegung Zufall Grenzen der Mathematik. Die Themenräume veranschaulichen die Entwicklung mathematischer Kenntnisse in unterschiedlichen Zeiten und Kulturen und ermöglichen es, 62
13 Ist Mathematik die Sprache der Natur? mathematische Phänomene spielend zu verstehen. Hierzu sind interaktive Stationen aufgebaut, an denen die Besucher mathematische Erfahrungen zu den einzelnen Themen machen können. Von dem breitem Angebot der Ausstellung soll anhand einiger Beispiele berichtet werden. 4.1 Themenraum Zahl Hier wird gezeigt, wie und warum die Zahlen in die Welt kamen. Die Besucher können die Vielfalt der Zahlensysteme und Rechenmethoden auf 5000 Jahre alten sumerischen Tontafeln, auf den Linien der mittelalterlichen Rechenmeister und im dualen Zahlensystem unserer heutigen Computer entdecken. Sie werden aufgefordert, Zahlenverhältnisse in Kunst und Natur zu erforschen. Bild 16 Verwaltungstafel der Sumerer. Bild 17 Sternfrucht. Beim Schneiden der Sternfrucht in Scheiben senkrecht zur Längsachse entstehen regelmäßige fünfzackige Sterne. Bei ihnen teilt eine innere Ecke den Abstand von einer zur anderen Spitze im Goldenen Schnitt. Dieses Teilungsverhältnis gilt als besonders harmonisch und kommt oft in der Kunst vor. Die goldene Schnittzahl hat den ungefähren Wert ist 1,618. Zahlen können Buchstaben verschlüsseln: Hieran erinnert die Enigma. Bild 18 Die Chiffriermaschine Enigma (ca.1938). 63
14 4.2 Themenraum Geometrie Ehrhard Behrends In diesem Themenraum wird die Entwicklung der Geometrie als Weltvermessung von den Anfängen bis zur Gegenwart aufgezeigt. Die Besucher können selbst Winkel, Strecken und Flächen mit modernsten Vermessungsinstrumenten bestimmen und herausfinden, wie die Navigation mit dem GPS-System funktioniert. Auch das Thema Symmetrie wird durch Exponate den Besuchern nahe gebracht. Um ca. 200 v.chr. hat Erathostenes den Erdumfang mit den Mitteln der Geometrie bestimmt. Bild 19 Bestimmung des Erdumfanges. Er ging davon aus, dass Syene (heute Assuan) und Alexandria auf demselben Meridian liegen und wusste, dass zur Zeit der Sonnenwende die Sonne in Assuan im Zenit steht, in Alexandria aber nicht. Dort warf ein Stab einen Schatten. Er bestimmte den Winkel, unter dem in Alexandria die Sonnenstrahlen auf die Erde trafen. Aus dem gemessenen Winkel und der ihm bekannten Entfernung zwischen Syene und Alexandria berechnete er den Umfang der Erde. Bild 20 Navigation mit dem gps-system. Bild 21 Theodolit um
15 Ist Mathematik die Sprache der Natur? Eine perfekte Spiegelung ohne Bruchkanten gibt es nur bei Winkeln, die durch geradzahlige Teiler von 360 entstehen (Bild 22, links). Das fantastische Bild (Bild 22, rechts), das man durch ein Kaleidoskop sehen kann, entsteht durch Spiegelungen von Spiegelbildern. Bild 22 Spiegelungen. 4.3 Themenraum Funktionen Die moderne Mathematik beginnt im 17. Jahrhundert mit der erfolgreichen Erfassung der Bewegung als Funktion. Heute durchdringt der Funktionsbegriff alle Teile der Mathematik. Funktionen sind der mathematische Ausdruck für dynamische Prozesse der Realität, aber auch für statische Zustände. Beim Funktionenlauf können die Besucher selbst eine Funktion laufen und nachvollziehen, welcher Zusammenhang zwischen Strecke, Geschwindigkeit und Zeit besteht und wie diese Beziehungen grafisch dargestellt werden (Bild 23). Beim Flug über Wien mit umgeschnallten Flügeln zur Steuerung können die Besucher erfahren, wie ihre Bewegungen in einen virtuellen Flug umgewandelt werden (Bild 24). (Diese Station bietet mathematisch nicht viel, war aber ein wirklicher Publikumsrenner!) Bild 23 Funktionenlauf. Bild 24 Flug über Wien Simulation. 65
16 Ehrhard Behrends Die Brachystochrone (Bild 25) ist eine bemerkenswerte Kurve: Auf ihr rollt eine Kugel schneller ans Ziel als auf einer kürzeren Geraden. Bild 25 Brachystochrone. Im Themenraum Funktionen gibt es weiterhin Mathematik zum Hören mit den Fragestellungen: Welche Funktionen treten auf, wenn man Klavier spielt oder wenn man selber spricht? Aus welchen einfachen Bausteinen sind Schwingungen zusammengesetzt? 4.4 Themenraum Zufall Hier werden u. a. angeboten: Mathematik und Glücksspiel (insbesondere Lotto), das bekannte Geburtstagsparadoxon, das Roulette und das Galtonbrett, Zufallskompositionen. Der populärste mathematische Zufallsgenerator ist das Roulette (Bild 26). Weniger bekannt, aber mathematisch interessanter ist das Galtonbrett (Bild 27), das von Francis Galton im 19. Jahrhundert erfunden wurde. Mit kleinen Kugeln wird eine Folge von Zufallsereignissen in Gang gesetzt, bei denen sich jeweils eines von zwei Resultaten (Weg nach links oder rechts) ergibt. Die Besucher können beide Zufallsgeräte ausprobieren. Bild 26 Roulette. Bild 27 Galtonbrett. 66
17 Ist Mathematik die Sprache der Natur? Das besondere Interesse vieler Menschen gilt dem Lotto in der Hoffnung auf das große Glück. Die Gewinnchancen beim Lotto werden durch ein anschauliches Beispiel verdeutlicht: Die Wahrscheinlichkeit für 6 Richtige entspricht der Wahrscheinlichkeit auf einer fast 140 km langen Strecke mit einem blind aus dem Autofenster geworfenen Centstück einen wahllos an der Strecke aufgestellten schmalen Stab von 1 cm Breite zu treffen. Für einen Gewinn mit Superzahl ist die Strecke sogar 1400 km lang! Darüber hinaus geht es in diesem Themenraum auch um die Interpretation statistischer Aussagen, um den Vergleich von Versicherungspolicen und um die Beurteilung des Risikos bei Börsen-Transaktionen. 4.5 Themenraum Grenzen Mit Hilfe der Mathematik können wir die Grenzen zu vielen Bereichen überschreiten, die unserer direkten Vorstellung nicht zugänglich sind. Deshalb wird Mathematik manchmal auch als zusätzlicher Sinn des Menschen bezeichnet. Ein Film zur Reiskornparabel macht begreiflich, wie begrenzt unsere Vorstellungskraft vom exponentiellen Wachstum ist. Bild 28 Berlin versinkt unter einem Reisberg. Nach einer alten Legende soll der Erfinder des Schachspiels für seine Erfindung folgenden Lohn gefordert haben: Für das erste. Feld 1 Reiskorn und für jedes weitere Feld doppelt soviel Körner wie für das vorangehende Feld. Was zunächst ein geringe Forderung zu sein scheint, erweist sich als unerfüllbar. Für das 64. Feld wären es Reiskörner und für alle Felder zusammen doppelt so viele. Nimmt man an, dass 40 Körner zusammen 1 g wiegen, so bekäme der Erfinder mehr als 460 Milliarden Tonnen Reis. Die Weltjahresproduktion beträgt aber kaum mehr als 600 Millionen Tonnen. Exponate zu mathematischen Rekorden lassen die Besucher staunen: Das Primzahlbuch enthält nur die Ziffern einer einzigen Primzahl. Der Schwarzsche Stiefel, ausgedacht vom Mathematiker Hermann Schwarz, hat einen endlichen Inhalt, aber eine unendliche Oberfläche. Er entsteht dadurch, dass der Mantel des zylindrischen Körpers in immer kleinere Dreiecke aufgeteilt wird. Ihre Gesamtfläche wächst dabei über jede beliebige Schranke. 67
18 Ehrhard Behrends Bild 29 Das Primzahlbuch. Bild 30 Modell zum Schwarzschen Stiefel. Zwei Exponate (Bilder 31 und 32) zeigen die Gleichung 1 + e πi = 0, die von den Mathematikern zur schönste Formel der Welt gekürt wurde. Die Collage in Bild 31 lehnt sich an ein bekanntes Bild von Rembrandt an. Sie hat die Bildlegende: Seit 1748 verblüfft die schönste Formel 0 = 1 + e πi Fachleute und Laien. Bild e iπ = 0. Bild 32 Collage. Mathematik ist nur dann grenzenlos, wenn sie alle intelligenten Lebewesen des Universums verstehen. Wissenschaftler haben sich mehrmals mit mathematischen Botschaften an Außerirdische gewandt (Bilder 33 und 34). Die beiden Voyager-Raumsonden, die die NASA 1977 startete, führen Schallplatten aus vergoldetem Kupfer mit (Bild 33), die Bilder, Musik, Reden und Geräusche enthalten. Das Cover beschreibt mit Dualzahlen das Abspielen der Platte und die Position der Erde im All. Die Arecibo-Botschaft ist eine Botschaft von der Erde an mögliche Außerirdische in Form eines Radiowellen-Signals. Sie wurde einmalig 1974 ausgehend vom Arecibo-Observatorium in Puerto Rico gesendet. Die Nachricht besteht aus insgesamt Bit. Ein Empfänger müsste diese Zahl in ihre Primfaktoren, 23 und 73, zerlegen und die Folge von Bits anschließend in einer 23 x 73-Matrix als Schwarzweißbild anordnen. Die Botschaft (Bild 34) enthält binär codierte Informationen über die Biologie und Anatomie des Menschen, sowie über die menschliche Population und die Herkunft des Signals. 68
19 Ist Mathematik die Sprache der Natur? Die Arecibo-Botschaft ist in Bild 34 farbig hervorgehoben. Die Besucher können die Funksignale der Botschaft hören. Bild 33 Schallplatte. Bild 34 Botschaft. 4.6 Kunstausstellung Einen Sonderbereich der Ausstellung bildet die angegliederte Kunstausstellung. Auch wenn dieser Bereich nicht direkt zum Thema der Ausstellung Ist Mathematik die Sprache der Natur? passt, so belegt die Kunstausstellung doch die These Mathematik ist überall. Wer eine Fuge hört oder ein Bild von Escher betrachtet, der erkennt den gegenseitigen Einfluss von Mathematik und Kunst. Für die mathema sind speziell solche Kunstwerke und Installationen zusammengestellt, die sich mit dem Thema Kodierung befassen. Dadurch bleibt die Kunst zunächst auch für den Betrachter verschlüsselt. Einen Zugang findet nur, wer die Erklärungen liest. Es werden Werke namhafter Künstler gezeigt, die dieses Thema aus ganz unterschiedlichen Perspektiven aufgreifen. 69
20 Ehrhard Behrends Josef Linschinger färbt den Warencode ein, Karsten Panzer den Gencode. Bild 35 Joseph Linschinger. Bild 36 Karsten Panzer. A. R. Penck erfindet und übernimmt einen persönlichen Symbolvorrat für sein Kunstwerk. Waltraut Cooper nutzt den Dualcode für eine interaktive Neoninstallation, in der Besucher das Verschlüsseln eines Datums auslösen und verfolgen können. Bild 37 A. R. Penck. Bild 38 Waltraut Cooper. Bildrechte der Bilder aus der mathema-ausstellung Inhaber der Rechte Bildnummern c Clemens Kirchner, Deutsches Technikmuseum Berlin: 17, 18, 21, 22, 29, 31 c Ralf K. Wegt, Mathematikum Gießen: 23, 25, 27. c Olaf M. Teßmer, SMB-Vorderasiatisches Museum: 16. c Elke Behrens, Berlin: 28, 32. c Ehrhard Behrens, Berlin: 26. c Modellbau Michael Grosch, Berlin: 30. c NASA: 33. Eingegangen am Adresse: Ehrhard Behrends, Fachbereich Mathematik und Informatik, FU Berlin, Arnimallee 2-6, D Berlin 70
21
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Und was uns betrifft, da erfinden wir uns einfach gegenseitig.
 Freier Fall 1 Der einzige Mensch Der einzige Mensch bin ich Der einzige Mensch bin ich an deem ich versuchen kann zu beobachten wie es geht wenn man sich in ihn hineinversetzt. Ich bin der einzige Mensch
Freier Fall 1 Der einzige Mensch Der einzige Mensch bin ich Der einzige Mensch bin ich an deem ich versuchen kann zu beobachten wie es geht wenn man sich in ihn hineinversetzt. Ich bin der einzige Mensch
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Zahlenwinkel: Forscherkarte 1. alleine. Zahlenwinkel: Forschertipp 1
 Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Kulturelle Evolution 12
 3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
3.2 Spiegelungen an zwei Spiegeln
 3 Die Theorie des Spiegelbuches 45 sehen, wenn die Person uns direkt gegenüber steht. Denn dann hat sie eine Drehung um die senkrechte Achse gemacht und dabei links und rechts vertauscht. 3.2 Spiegelungen
3 Die Theorie des Spiegelbuches 45 sehen, wenn die Person uns direkt gegenüber steht. Denn dann hat sie eine Drehung um die senkrechte Achse gemacht und dabei links und rechts vertauscht. 3.2 Spiegelungen
PD Dr. habil. Werner Becker Max-Planck Institut für extraterr. Physik Email: web@mpe.mpg.de
 PD Dr. habil. Werner Becker Max-Planck Institut für extraterr. Physik Email: web@mpe.mpg.de Worüber wir heute sprechen wollen: Warum interessieren sich die Menschen für die Sterne? Sternbilder und ihre
PD Dr. habil. Werner Becker Max-Planck Institut für extraterr. Physik Email: web@mpe.mpg.de Worüber wir heute sprechen wollen: Warum interessieren sich die Menschen für die Sterne? Sternbilder und ihre
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
infach Geld FBV Ihr Weg zum finanzellen Erfolg Florian Mock
 infach Ihr Weg zum finanzellen Erfolg Geld Florian Mock FBV Die Grundlagen für finanziellen Erfolg Denn Sie müssten anschließend wieder vom Gehaltskonto Rückzahlungen in Höhe der Entnahmen vornehmen, um
infach Ihr Weg zum finanzellen Erfolg Geld Florian Mock FBV Die Grundlagen für finanziellen Erfolg Denn Sie müssten anschließend wieder vom Gehaltskonto Rückzahlungen in Höhe der Entnahmen vornehmen, um
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Messung der Astronomischen Einheit nach Aristarch
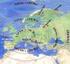 Astronomisches Praktikum Aufgaben für eine Schlechtwetter-Astronomie U. Backhaus, Universität Duisburg-Essen Messung der Astronomischen Einheit nach Aristarch 1 Einleitung Bis ins 17. Jahrhundert war die
Astronomisches Praktikum Aufgaben für eine Schlechtwetter-Astronomie U. Backhaus, Universität Duisburg-Essen Messung der Astronomischen Einheit nach Aristarch 1 Einleitung Bis ins 17. Jahrhundert war die
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
predigt am 5.1. 2014, zu römer 16,25-27
 predigt am 5.1. 2014, zu römer 16,25-27 25 ehre aber sei ihm, der euch zu stärken vermag im sinne meines evangeliums und der botschaft von jesus christus. so entspricht es der offenbarung des geheimnisses,
predigt am 5.1. 2014, zu römer 16,25-27 25 ehre aber sei ihm, der euch zu stärken vermag im sinne meines evangeliums und der botschaft von jesus christus. so entspricht es der offenbarung des geheimnisses,
Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut wird, dass sie für sich selbst sprechen können Von Susanne Göbel und Josef Ströbl
 Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut Von Susanne Göbel und Josef Ströbl Die Ideen der Persönlichen Zukunftsplanung stammen aus Nordamerika. Dort werden Zukunftsplanungen schon
Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut Von Susanne Göbel und Josef Ströbl Die Ideen der Persönlichen Zukunftsplanung stammen aus Nordamerika. Dort werden Zukunftsplanungen schon
40-Tage-Wunder- Kurs. Umarme, was Du nicht ändern kannst.
 40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
Einstein-Wellen-Mobil
 Arbeitsvorschlag für interaktive Station Relativistische Fahrradfahrt Bebachten Sie die Szenerie beim Anfahren und Beschleunigen. Bewegen Sie sich tatsächlich zunächst rückwärts? Wie können Sie das feststellen?
Arbeitsvorschlag für interaktive Station Relativistische Fahrradfahrt Bebachten Sie die Szenerie beim Anfahren und Beschleunigen. Bewegen Sie sich tatsächlich zunächst rückwärts? Wie können Sie das feststellen?
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009)
 Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Computermuseum Hoyerswerda. Zu Besuch bei der Ausstellung zur Geschichte der Rechentechnik
 Computermuseum Hoyerswerda Zu Besuch bei der Ausstellung zur Geschichte der Rechentechnik Ausstellungsverlauf Die Einleitung beginnt mit einem Videofilm unter der Leitung von Herrn Dipl.-Ing. Jens-Uwe
Computermuseum Hoyerswerda Zu Besuch bei der Ausstellung zur Geschichte der Rechentechnik Ausstellungsverlauf Die Einleitung beginnt mit einem Videofilm unter der Leitung von Herrn Dipl.-Ing. Jens-Uwe
Evangelisieren warum eigentlich?
 Predigtreihe zum Jahresthema 1/12 Evangelisieren warum eigentlich? Ich evangelisiere aus Überzeugung Gründe, warum wir nicht evangelisieren - Festes Bild von Evangelisation - Negative Erfahrungen von und
Predigtreihe zum Jahresthema 1/12 Evangelisieren warum eigentlich? Ich evangelisiere aus Überzeugung Gründe, warum wir nicht evangelisieren - Festes Bild von Evangelisation - Negative Erfahrungen von und
Praktikum Schau Geometrie
 Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Evangelisch-Lutherisches Pfarramt St. Christophorus Siegen Dienst am Wort. vor zwei Wochen habe ich euch schon gepredigt, dass das
 Evangelisch-Lutherisches Pfarramt St. Christophorus Siegen Dienst am Wort Johannes 14,23-27 Wer mich liebt, der wird mein Wort halten. Liebe Gemeinde, 24. Mai 2015 Fest der Ausgießung des Heiligen Geistes
Evangelisch-Lutherisches Pfarramt St. Christophorus Siegen Dienst am Wort Johannes 14,23-27 Wer mich liebt, der wird mein Wort halten. Liebe Gemeinde, 24. Mai 2015 Fest der Ausgießung des Heiligen Geistes
Wie löst man Mathematikaufgaben?
 Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Das Leitbild vom Verein WIR
 Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Binnendifferenzierte Aufgaben: Subtrahieren von negativen Zahlen
 Binnendifferenzierte Subtrahieren von negativen Zahlen Mit Hilfe der von uns erstellten Arbeitsblätter sollen die Schülerinnen und Schüler selbstständig erarbeiten, wie man negative Zahlen subtrahiert.
Binnendifferenzierte Subtrahieren von negativen Zahlen Mit Hilfe der von uns erstellten Arbeitsblätter sollen die Schülerinnen und Schüler selbstständig erarbeiten, wie man negative Zahlen subtrahiert.
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Diese 36 Fragen reichen, um sich zu verlieben
 Diese 36 Fragen reichen, um sich zu verlieben Wie verliebt er oder sie sich bloß in mich? Während Singles diese Frage wieder und wieder bei gemeinsamen Rotweinabenden zu ergründen versuchen, haben Wissenschaftler
Diese 36 Fragen reichen, um sich zu verlieben Wie verliebt er oder sie sich bloß in mich? Während Singles diese Frage wieder und wieder bei gemeinsamen Rotweinabenden zu ergründen versuchen, haben Wissenschaftler
FAQ Spielvorbereitung Startspieler: Wer ist Startspieler?
 FAQ Spielvorbereitung Startspieler: Wer ist Startspieler? In der gedruckten Version der Spielregeln steht: der Startspieler ist der Spieler, dessen Arena unmittelbar links neben dem Kaiser steht [im Uhrzeigersinn].
FAQ Spielvorbereitung Startspieler: Wer ist Startspieler? In der gedruckten Version der Spielregeln steht: der Startspieler ist der Spieler, dessen Arena unmittelbar links neben dem Kaiser steht [im Uhrzeigersinn].
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Pflegende Angehörige Online Ihre Plattform im Internet
 Pflegende Angehörige Online Ihre Plattform im Internet Wissen Wichtiges Wissen rund um Pflege Unterstützung Professionelle Beratung Austausch und Kontakt Erfahrungen & Rat mit anderen Angehörigen austauschen
Pflegende Angehörige Online Ihre Plattform im Internet Wissen Wichtiges Wissen rund um Pflege Unterstützung Professionelle Beratung Austausch und Kontakt Erfahrungen & Rat mit anderen Angehörigen austauschen
Die neue Aufgabe von der Monitoring-Stelle. Das ist die Monitoring-Stelle:
 Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Vergleichsarbeiten in 3. Grundschulklassen. Mathematik. Aufgabenheft 1
 Vergleichsarbeiten in 3. Grundschulklassen Mathematik Aufgabenheft 1 Name: Klasse: Herausgeber: Projekt VERA (Vergleichsarbeiten in 3. Grundschulklassen) Universität Koblenz-Landau Campus Landau Fortstraße
Vergleichsarbeiten in 3. Grundschulklassen Mathematik Aufgabenheft 1 Name: Klasse: Herausgeber: Projekt VERA (Vergleichsarbeiten in 3. Grundschulklassen) Universität Koblenz-Landau Campus Landau Fortstraße
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Durch Wissen Millionär WerDen... Wer hat zuerst die Million erreicht? spielanleitung Zahl der spieler: alter: redaktion / autor: inhalt:
 Spielanleitung Durch Wissen Millionär werden... Diesen Traum kann man sich in diesem beliebten Quiz-Spiel erfüllen. Ob allein oder in der geselligen Runde dieses Quiz enthält 330 Fragen und 1.320 Multiple-Choice-Antworten.
Spielanleitung Durch Wissen Millionär werden... Diesen Traum kann man sich in diesem beliebten Quiz-Spiel erfüllen. Ob allein oder in der geselligen Runde dieses Quiz enthält 330 Fragen und 1.320 Multiple-Choice-Antworten.
Projekt 2HEA 2005/06 Formelzettel Elektrotechnik
 Projekt 2HEA 2005/06 Formelzettel Elektrotechnik Teilübung: Kondensator im Wechselspannunskreis Gruppenteilnehmer: Jakic, Topka Abgabedatum: 24.02.2006 Jakic, Topka Inhaltsverzeichnis 2HEA INHALTSVERZEICHNIS
Projekt 2HEA 2005/06 Formelzettel Elektrotechnik Teilübung: Kondensator im Wechselspannunskreis Gruppenteilnehmer: Jakic, Topka Abgabedatum: 24.02.2006 Jakic, Topka Inhaltsverzeichnis 2HEA INHALTSVERZEICHNIS
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Alle gehören dazu. Vorwort
 Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Falten regelmäßiger Vielecke
 Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
1: 9. Hamburger Gründerpreis - Kategorie Existenzgründer - 08.09.2010 19:00 Uhr
 1: 9. Hamburger Gründerpreis - Kategorie Existenzgründer - Sehr geehrter Herr Bürgermeister, sehr geehrter Herr Dr. Vogelsang, sehr geehrter Herr Strunz, und meine sehr geehrte Damen und Herren, meine
1: 9. Hamburger Gründerpreis - Kategorie Existenzgründer - Sehr geehrter Herr Bürgermeister, sehr geehrter Herr Dr. Vogelsang, sehr geehrter Herr Strunz, und meine sehr geehrte Damen und Herren, meine
Örtliche Angebots- und Teilhabeplanung im Landkreis Weilheim-Schongau
 Örtliche Angebots- und Teilhabeplanung im Landkreis Weilheim-Schongau Zusammenfassung der Ergebnisse in Leichter Sprache Timo Wissel Albrecht Rohrmann Timo Wissel / Albrecht Rohrmann: Örtliche Angebots-
Örtliche Angebots- und Teilhabeplanung im Landkreis Weilheim-Schongau Zusammenfassung der Ergebnisse in Leichter Sprache Timo Wissel Albrecht Rohrmann Timo Wissel / Albrecht Rohrmann: Örtliche Angebots-
Elma van Vliet. Mama, erzähl mal!
 Elma van Vliet Mama, erzähl mal! Elma van Vliet Mama, erzähl mal! Das Erinnerungsalbum deines Lebens Aus dem Niederländischen von Ilka Heinemann und Matthias Kuhlemann KNAUR Von mir für dich weil du
Elma van Vliet Mama, erzähl mal! Elma van Vliet Mama, erzähl mal! Das Erinnerungsalbum deines Lebens Aus dem Niederländischen von Ilka Heinemann und Matthias Kuhlemann KNAUR Von mir für dich weil du
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Kurzanleitung für eine erfüllte Partnerschaft
 Kurzanleitung für eine erfüllte Partnerschaft 10 Schritte die deine Beziehungen zum Erblühen bringen Oft ist weniger mehr und es sind nicht immer nur die großen Worte, die dann Veränderungen bewirken.
Kurzanleitung für eine erfüllte Partnerschaft 10 Schritte die deine Beziehungen zum Erblühen bringen Oft ist weniger mehr und es sind nicht immer nur die großen Worte, die dann Veränderungen bewirken.
Welche Gedanken wir uns für die Erstellung einer Präsentation machen, sollen Ihnen die folgende Folien zeigen.
 Wir wollen mit Ihnen Ihren Auftritt gestalten Steil-Vorlage ist ein österreichisches Start-up mit mehr als zehn Jahren Erfahrung in IT und Kommunikation. Unser Ziel ist, dass jede einzelne Mitarbeiterin
Wir wollen mit Ihnen Ihren Auftritt gestalten Steil-Vorlage ist ein österreichisches Start-up mit mehr als zehn Jahren Erfahrung in IT und Kommunikation. Unser Ziel ist, dass jede einzelne Mitarbeiterin
Wichtig ist die Originalsatzung. Nur was in der Originalsatzung steht, gilt. Denn nur die Originalsatzung wurde vom Gericht geprüft.
 Das ist ein Text in leichter Sprache. Hier finden Sie die wichtigsten Regeln für den Verein zur Förderung der Autonomie Behinderter e. V.. Das hier ist die Übersetzung der Originalsatzung. Es wurden nur
Das ist ein Text in leichter Sprache. Hier finden Sie die wichtigsten Regeln für den Verein zur Förderung der Autonomie Behinderter e. V.. Das hier ist die Übersetzung der Originalsatzung. Es wurden nur
Qualitätsbedingungen schulischer Inklusion für Kinder und Jugendliche mit dem Förderschwerpunkt Körperliche und motorische Entwicklung
 Forschungsprojekt: Qualitätsbedingungen schulischer Inklusion für Kinder und Jugendliche mit dem Förderschwerpunkt Körperliche und motorische Entwicklung Leichte Sprache Autoren: Reinhard Lelgemann Jelena
Forschungsprojekt: Qualitätsbedingungen schulischer Inklusion für Kinder und Jugendliche mit dem Förderschwerpunkt Körperliche und motorische Entwicklung Leichte Sprache Autoren: Reinhard Lelgemann Jelena
Wichtige Forderungen für ein Bundes-Teilhabe-Gesetz
 Wichtige Forderungen für ein Bundes-Teilhabe-Gesetz Die Parteien CDU, die SPD und die CSU haben versprochen: Es wird ein Bundes-Teilhabe-Gesetz geben. Bis jetzt gibt es das Gesetz noch nicht. Das dauert
Wichtige Forderungen für ein Bundes-Teilhabe-Gesetz Die Parteien CDU, die SPD und die CSU haben versprochen: Es wird ein Bundes-Teilhabe-Gesetz geben. Bis jetzt gibt es das Gesetz noch nicht. Das dauert
Leitbild. für Jedermensch in leicht verständlicher Sprache
 Leitbild für Jedermensch in leicht verständlicher Sprache Unser Leitbild Was wir erreichen wollen und was uns dabei wichtig ist! Einleitung Was ist ein Leitbild? Jede Firma hat ein Leitbild. Im Leitbild
Leitbild für Jedermensch in leicht verständlicher Sprache Unser Leitbild Was wir erreichen wollen und was uns dabei wichtig ist! Einleitung Was ist ein Leitbild? Jede Firma hat ein Leitbild. Im Leitbild
Physik & Musik. Stimmgabeln. 1 Auftrag
 Physik & Musik 5 Stimmgabeln 1 Auftrag Physik & Musik Stimmgabeln Seite 1 Stimmgabeln Bearbeitungszeit: 30 Minuten Sozialform: Einzel- oder Partnerarbeit Voraussetzung: Posten 1: "Wie funktioniert ein
Physik & Musik 5 Stimmgabeln 1 Auftrag Physik & Musik Stimmgabeln Seite 1 Stimmgabeln Bearbeitungszeit: 30 Minuten Sozialform: Einzel- oder Partnerarbeit Voraussetzung: Posten 1: "Wie funktioniert ein
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Nicaragua. Wo die Menschen leben Mehr als die Hälfte der Menschen lebt in Städten. Denn auf dem Land gibt es wenig Arbeit.
 Nicaragua Nicaragua ist ein Land in Mittel-Amerika. Mittel-Amerika liegt zwischen Nord-Amerika und Süd-Amerika. Die Haupt-Stadt von Nicaragua heißt Managua. In Nicaragua leben ungefähr 6 Millionen Menschen.
Nicaragua Nicaragua ist ein Land in Mittel-Amerika. Mittel-Amerika liegt zwischen Nord-Amerika und Süd-Amerika. Die Haupt-Stadt von Nicaragua heißt Managua. In Nicaragua leben ungefähr 6 Millionen Menschen.
Impulse Inklusion 2015. Selbst-bestimmtes Wohnen und Nachbarschaft
 Impulse Inklusion 2015 Selbst-bestimmtes Wohnen und Nachbarschaft Impulse sind Ideen und Vorschläge. Inklusion bedeutet: Alle Menschen können selbst-bestimmt und gleich-berechtigt am Leben teilnehmen.
Impulse Inklusion 2015 Selbst-bestimmtes Wohnen und Nachbarschaft Impulse sind Ideen und Vorschläge. Inklusion bedeutet: Alle Menschen können selbst-bestimmt und gleich-berechtigt am Leben teilnehmen.
Nicht kopieren. Der neue Report von: Stefan Ploberger. 1. Ausgabe 2003
 Nicht kopieren Der neue Report von: Stefan Ploberger 1. Ausgabe 2003 Herausgeber: Verlag Ploberger & Partner 2003 by: Stefan Ploberger Verlag Ploberger & Partner, Postfach 11 46, D-82065 Baierbrunn Tel.
Nicht kopieren Der neue Report von: Stefan Ploberger 1. Ausgabe 2003 Herausgeber: Verlag Ploberger & Partner 2003 by: Stefan Ploberger Verlag Ploberger & Partner, Postfach 11 46, D-82065 Baierbrunn Tel.
Die Magnetkraft wirkt nur auf bestimmt Stoffe, nämlich Eisen, Nickel und Cobalt. Auf welche Stoffe wirkt die Magnetkraft?
 Auf welche Stoffe wirkt die Magnetkraft? Die Magnetkraft wirkt nur auf bestimmt Stoffe, nämlich Eisen, Nickel und Cobalt. Wie nennt man den Bereich, in dem die Magnetkraft wirkt? Der Bereich in dem die
Auf welche Stoffe wirkt die Magnetkraft? Die Magnetkraft wirkt nur auf bestimmt Stoffe, nämlich Eisen, Nickel und Cobalt. Wie nennt man den Bereich, in dem die Magnetkraft wirkt? Der Bereich in dem die
Es gilt das gesprochene Wort. Anrede
 Sperrfrist: 28. November 2007, 13.00 Uhr Es gilt das gesprochene Wort Statement des Staatssekretärs im Bayerischen Staatsministerium für Unterricht und Kultus, Karl Freller, anlässlich des Pressegesprächs
Sperrfrist: 28. November 2007, 13.00 Uhr Es gilt das gesprochene Wort Statement des Staatssekretärs im Bayerischen Staatsministerium für Unterricht und Kultus, Karl Freller, anlässlich des Pressegesprächs
Die Ringe des Kentauren Chariklo
 Die Ringe des Kentauren Chariklo Die Entdeckung der Ringe Chariklo ist ein Kleinplanet der Gruppe der Kentauren, die zwischen Saturn und Neptun ihre Bahn ziehen. Als im Rahmen einer Routinearbeit auf La
Die Ringe des Kentauren Chariklo Die Entdeckung der Ringe Chariklo ist ein Kleinplanet der Gruppe der Kentauren, die zwischen Saturn und Neptun ihre Bahn ziehen. Als im Rahmen einer Routinearbeit auf La
Modul: Soziale Kompetenz. Vier Ohren. Zeitl. Rahmen: ~ 45 min. Ort: drinnen
 Modul: Soziale Kompetenz Vier Ohren Zeitl. Rahmen: ~ 45 min. Ort: drinnen Teilnehmer: 3-20 Personen (Die Übung kann mit einer Gruppe von 3-6 Personen oder bis zu max. vier Gruppen realisiert werden) Material:
Modul: Soziale Kompetenz Vier Ohren Zeitl. Rahmen: ~ 45 min. Ort: drinnen Teilnehmer: 3-20 Personen (Die Übung kann mit einer Gruppe von 3-6 Personen oder bis zu max. vier Gruppen realisiert werden) Material:
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Papa - was ist American Dream?
 Papa - was ist American Dream? Das heißt Amerikanischer Traum. Ja, das weiß ich, aber was heißt das? Der [wpseo]amerikanische Traum[/wpseo] heißt, dass jeder Mensch allein durch harte Arbeit und Willenskraft
Papa - was ist American Dream? Das heißt Amerikanischer Traum. Ja, das weiß ich, aber was heißt das? Der [wpseo]amerikanische Traum[/wpseo] heißt, dass jeder Mensch allein durch harte Arbeit und Willenskraft
Programme für Mathematik, Physik und Astronomie 22 Kleines Planetarium
 Programme für Mathematik, Physik und Astronomie 22 Kleines Planetarium Allgemeines, der Lauf der 1) Geben Sie folgendes Datum ein: 12.12.2000. Geografische Breite für Altdorf (47 ). Es ist Mitternacht.
Programme für Mathematik, Physik und Astronomie 22 Kleines Planetarium Allgemeines, der Lauf der 1) Geben Sie folgendes Datum ein: 12.12.2000. Geografische Breite für Altdorf (47 ). Es ist Mitternacht.
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Pädagogik. Melanie Schewtschenko. Eingewöhnung und Übergang in die Kinderkrippe. Warum ist die Beteiligung der Eltern so wichtig?
 Pädagogik Melanie Schewtschenko Eingewöhnung und Übergang in die Kinderkrippe Warum ist die Beteiligung der Eltern so wichtig? Studienarbeit Inhaltsverzeichnis 1. Einleitung.2 2. Warum ist Eingewöhnung
Pädagogik Melanie Schewtschenko Eingewöhnung und Übergang in die Kinderkrippe Warum ist die Beteiligung der Eltern so wichtig? Studienarbeit Inhaltsverzeichnis 1. Einleitung.2 2. Warum ist Eingewöhnung
Was sind Soziale Netzwerke? Stelle dazu selbstständig Überlegungen an!
 Erkundungsbogen Datenspionage Klassenstufen 7-9 Spionage gibt es nicht nur in Film und Fernsehen, sondern hat über viele Jahrhunderte auch unser Leben sehr beeinflusst! Mit den neuen, digitalen Medien
Erkundungsbogen Datenspionage Klassenstufen 7-9 Spionage gibt es nicht nur in Film und Fernsehen, sondern hat über viele Jahrhunderte auch unser Leben sehr beeinflusst! Mit den neuen, digitalen Medien
Lösungsmethoden gewöhnlicher Differentialgleichungen (Dgl.)
 Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
 Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Vibono Coaching Brief -No. 39
 Gemüse hat doch auch Kohlenhydrate! Wieso kann man mit Gemüse also überhaupt abnehmen? Vibono GmbH 2011-2012, www.vibono.de Kann man mit Gemüse abnehmen, wenn es doch auch Kohlenhydrate hat? Diese Frage
Gemüse hat doch auch Kohlenhydrate! Wieso kann man mit Gemüse also überhaupt abnehmen? Vibono GmbH 2011-2012, www.vibono.de Kann man mit Gemüse abnehmen, wenn es doch auch Kohlenhydrate hat? Diese Frage
Schriftliche Abschlussprüfung Physik Realschulbildungsgang
 Sächsisches Staatsministerium für Kultus Schuljahr 1992/93 Geltungsbereich: für Klassen 10 an - Mittelschulen - Förderschulen - Abendmittelschulen Schriftliche Abschlussprüfung Physik Realschulbildungsgang
Sächsisches Staatsministerium für Kultus Schuljahr 1992/93 Geltungsbereich: für Klassen 10 an - Mittelschulen - Förderschulen - Abendmittelschulen Schriftliche Abschlussprüfung Physik Realschulbildungsgang
Anleitung zur Daten zur Datensicherung und Datenrücksicherung. Datensicherung
 Anleitung zur Daten zur Datensicherung und Datenrücksicherung Datensicherung Es gibt drei Möglichkeiten der Datensicherung. Zwei davon sind in Ges eingebaut, die dritte ist eine manuelle Möglichkeit. In
Anleitung zur Daten zur Datensicherung und Datenrücksicherung Datensicherung Es gibt drei Möglichkeiten der Datensicherung. Zwei davon sind in Ges eingebaut, die dritte ist eine manuelle Möglichkeit. In
Schritte 4. Lesetexte 13. Kosten für ein Girokonto vergleichen. 1. Was passt? Ordnen Sie zu.
 Kosten für ein Girokonto vergleichen 1. Was passt? Ordnen Sie zu. a. die Buchung, -en b. die Auszahlung, -en c. der Dauerauftrag, - e d. die Überweisung, -en e. die Filiale, -n f. der Kontoauszug, - e
Kosten für ein Girokonto vergleichen 1. Was passt? Ordnen Sie zu. a. die Buchung, -en b. die Auszahlung, -en c. der Dauerauftrag, - e d. die Überweisung, -en e. die Filiale, -n f. der Kontoauszug, - e
Kolumbus fuhr noch dreimal zur See. Aber er fand keinen Seeweg nach Indien. Seine Träume erfüllten sich nicht und er starb 1506 in Spanien.
 Christopher Kolumbus war ein berühmter Seefahrer. Er wurde 1451 in Genua in Italien geboren. Vor über 500 Jahren wollte er mit seiner Mannschaft von Spanien aus nach Indien segeln. Zu dieser Zeit war Indien
Christopher Kolumbus war ein berühmter Seefahrer. Er wurde 1451 in Genua in Italien geboren. Vor über 500 Jahren wollte er mit seiner Mannschaft von Spanien aus nach Indien segeln. Zu dieser Zeit war Indien
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lernwerkstatt für die Klassen 7 bis 9: Linsen und optische Geräte
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernwerkstatt für die Klassen 7 bis 9: Linsen und optische Geräte Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernwerkstatt für die Klassen 7 bis 9: Linsen und optische Geräte Das komplette Material finden Sie hier: Download bei School-Scout.de
Praktikum Physik. Protokoll zum Versuch: Geometrische Optik. Durchgeführt am 24.11.2011
 Praktikum Physik Protokoll zum Versuch: Geometrische Optik Durchgeführt am 24.11.2011 Gruppe X Name1 und Name 2 (abc.xyz@uni-ulm.de) (abc.xyz@uni-ulm.de) Betreuerin: Wir bestätigen hiermit, dass wir das
Praktikum Physik Protokoll zum Versuch: Geometrische Optik Durchgeführt am 24.11.2011 Gruppe X Name1 und Name 2 (abc.xyz@uni-ulm.de) (abc.xyz@uni-ulm.de) Betreuerin: Wir bestätigen hiermit, dass wir das
So funktioniert Ihr Selbstmanagement noch besser
 So funktioniert Ihr Selbstmanagement noch besser HANS-FISCHER FISCHER-SEMINARE SEMINARE St. Wendelinsstrasse 9 86932 Pürgen-Lengenfeld Telefon 08196 99 82 10 Fax 08196 99 82 10 www.fischerseminare.de hans.fischer@fischerseminare.de
So funktioniert Ihr Selbstmanagement noch besser HANS-FISCHER FISCHER-SEMINARE SEMINARE St. Wendelinsstrasse 9 86932 Pürgen-Lengenfeld Telefon 08196 99 82 10 Fax 08196 99 82 10 www.fischerseminare.de hans.fischer@fischerseminare.de
Egal, ob Sie neu bauen oder renovieren mit DATALIGHT bekommen Sie ein zukunftssicheres Strom- und Datennetz in einem. Und das bedeutet grenzenlose
 FREIHEIT ERLEBEN EINFACH LEBEN Grenzenlos, frei und unabhängig: Leben Sie das Leben, wie Sie es wollen. Warum sollten Sie sich Gedanken darüber machen, ob Ihr Datennetzwerk für die neuesten Technologien
FREIHEIT ERLEBEN EINFACH LEBEN Grenzenlos, frei und unabhängig: Leben Sie das Leben, wie Sie es wollen. Warum sollten Sie sich Gedanken darüber machen, ob Ihr Datennetzwerk für die neuesten Technologien
10.1 Auflösung, Drucken und Scannen
 Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird.
 Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Ein und dieselbe Taufe
 1 Ein und dieselbe Taufe Eph. 4,5 Nach V. 3 geht es um die Einheit des Geistes. In diesem Zusammenhang nennt Paulus sieben Aspekte der geistlichen Einheit: Ein [geistlicher] Leib Ein Geist Eine Hoffnung
1 Ein und dieselbe Taufe Eph. 4,5 Nach V. 3 geht es um die Einheit des Geistes. In diesem Zusammenhang nennt Paulus sieben Aspekte der geistlichen Einheit: Ein [geistlicher] Leib Ein Geist Eine Hoffnung
DER SELBST-CHECK FÜR IHR PROJEKT
 DER SELBST-CHECK FÜR IHR PROJEKT In 30 Fragen und 5 Tipps zum erfolgreichen Projekt! Beantworten Sie die wichtigsten Fragen rund um Ihr Projekt für Ihren Erfolg und für Ihre Unterstützer. IHR LEITFADEN
DER SELBST-CHECK FÜR IHR PROJEKT In 30 Fragen und 5 Tipps zum erfolgreichen Projekt! Beantworten Sie die wichtigsten Fragen rund um Ihr Projekt für Ihren Erfolg und für Ihre Unterstützer. IHR LEITFADEN
Er musste so eingerichtet werden, dass das D-Laufwerk auf das E-Laufwerk gespiegelt
 Inhaltsverzeichnis Aufgabe... 1 Allgemein... 1 Active Directory... 1 Konfiguration... 2 Benutzer erstellen... 3 Eigenes Verzeichnis erstellen... 3 Benutzerkonto erstellen... 3 Profil einrichten... 5 Berechtigungen
Inhaltsverzeichnis Aufgabe... 1 Allgemein... 1 Active Directory... 1 Konfiguration... 2 Benutzer erstellen... 3 Eigenes Verzeichnis erstellen... 3 Benutzerkonto erstellen... 3 Profil einrichten... 5 Berechtigungen
Wir machen uns stark! Parlament der Ausgegrenzten 20.-22.9.2013
 Wir machen uns stark! Parlament der Ausgegrenzten 20.-22.9.2013 Die Armutskonferenz Einladung zum Parlament der Ausgegrenzten 20.-22. September 2013 Was ist das Parlament der Ausgegrenzten? Das Parlament
Wir machen uns stark! Parlament der Ausgegrenzten 20.-22.9.2013 Die Armutskonferenz Einladung zum Parlament der Ausgegrenzten 20.-22. September 2013 Was ist das Parlament der Ausgegrenzten? Das Parlament
Tag der Schulverpflegung 2014
 Tag der Schulverpflegung 2014 (Bundesministerium für Ernährung und Landwirtschaft des Landes Rheinland Pfalz) Thema: Lebensmittelverschwendung Erschreckend!!! Jeder von uns wirf durchschnittlich pro Jahr
Tag der Schulverpflegung 2014 (Bundesministerium für Ernährung und Landwirtschaft des Landes Rheinland Pfalz) Thema: Lebensmittelverschwendung Erschreckend!!! Jeder von uns wirf durchschnittlich pro Jahr
Steinmikado I. Steinmikado II. Steinzielwerfen. Steinwerfen in Dosen
 Steinmikado I Steinmikado II : ab 4 : ab 4 : 20 Steine : 20 Steine Spielregel : M 10-01 In der Mitte des Raumes schichten wir einen Steinberg auf. Die Aufgabe besteht darin, vom Fuße des Berges jeweils
Steinmikado I Steinmikado II : ab 4 : ab 4 : 20 Steine : 20 Steine Spielregel : M 10-01 In der Mitte des Raumes schichten wir einen Steinberg auf. Die Aufgabe besteht darin, vom Fuße des Berges jeweils
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit
 Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
1.1 Bitte geben Sie an, wie wichtig Ihnen die im Folgenden genannten Merkmale unabhängig von Ihrem Arbeitsplatz sind!
 I Allgemeine Einschätzungen und Merkmale Ihrer Tätigkeit 1.1 Bitte geben Sie an, wie wichtig Ihnen die im Folgenden genannten Merkmale unabhängig von Ihrem Arbeitsplatz sind! Wie wichtig ist Ihnen, dass
I Allgemeine Einschätzungen und Merkmale Ihrer Tätigkeit 1.1 Bitte geben Sie an, wie wichtig Ihnen die im Folgenden genannten Merkmale unabhängig von Ihrem Arbeitsplatz sind! Wie wichtig ist Ihnen, dass
DAS PARETO PRINZIP DER SCHLÜSSEL ZUM ERFOLG
 DAS PARETO PRINZIP DER SCHLÜSSEL ZUM ERFOLG von Urs Schaffer Copyright by Urs Schaffer Schaffer Consulting GmbH Basel www.schaffer-consulting.ch Info@schaffer-consulting.ch Haben Sie gewusst dass... >
DAS PARETO PRINZIP DER SCHLÜSSEL ZUM ERFOLG von Urs Schaffer Copyright by Urs Schaffer Schaffer Consulting GmbH Basel www.schaffer-consulting.ch Info@schaffer-consulting.ch Haben Sie gewusst dass... >
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
