T1 Organisatorisches - Anmeldung Projektaufgaben
|
|
|
- Jobst Reinhardt Hafner
- vor 6 Jahren
- Abrufe
Transkript
1 Praktikum ASP Blatt 6 1 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung Arbeitsblatt 6 Am ist Dies Academicus. Alle Lehrveranstaltungen entfallen. Bitte verteilen Sie sich möglichst gleichmäßig auf andere Tutorgruppen. T1 Organisatorisches - Anmeldung Projektaufgaben Sehr geehrte PraktikumsteilnehmerInnen, in der 2. Dezemberwoche werden wir die Projektaufgaben an Sie verteilen. Von Ihnen zwei Schritte notwendig: 1. Melden Sie sich bis zum (Freitag) für eine Projektgruppe an (s. unten) 2. Melden Sie sich rechtzeitig (bis zum ) für die Prüfung in TUMonline an Das Verpassen einer von beiden Terminen reicht, um das Praktikum nicht erfolgreich abschließen zu können. Anmeldung zu den Projektaufgaben Wie angekündigt, werden Sie die Projektaufgaben in 3er-Gruppen bearbeiten. Sie haben die Wahl zwischen: Anmeldung zur Projektaufgabe als 3er-Gruppe Anmeldung zur Projektaufgabe als 2er-Gruppe (drittes Gruppenmitglied wird zugewiesen) Anmeldung zur Projektaufgabe alleine (Gruppe wird zugewiesen) Bei Anmeldungen als 3er-Gruppe ist die Zuteilung als solche garantiert. Bei Anmeldungen als 2er-Gruppe versuchen wir die Teilnehmer so weit wie möglich in einer Projektgruppe zuzuordnen, können dies aber nicht garantieren. Melden Sie sich bis zum bei einem Tutor in einer der Übungen oder per . (Eine Anmeldung pro Gruppe!) Die Informationen, die von Ihrem Tutor zur erfolgreichen Anmeldung notwendig sind: Vor- und Nachname der Mitglieder adressen der entsprechenden GitLab-Accounts (
2 Praktikum ASP Blatt 6 2 Bei allen Teilnehmern, die diesen Termin nicht einhalten, gehen wir davon aus, dass Sie nicht weiter am Praktikum teilnehmen. Mit freundlichen Grüßen, Die Übungsleitung
3 Praktikum ASP Blatt 6 3 T2 Der Spieler im Casino (Anwendung) Wir werden in dieser Einheit Spieltheorie mit Statistik kombinieren, um ein Modell für ein bestimmtes Szenario beim Roulette-Spiel zu bilden. Anschließend werden wir das Modell verwenden, um numerisch einige Erkenntnisse zu erlangen zur Berechnung verwenden wir das Raspberry Pi 3. T2.1 Aufgabenstellung Ein Spieler betritt ein Casino mit 4000 Euro. Er setzt stets genau 1000 Euro beim (Französischen) Roulette auf Schwarz (Gewinn zu Einsatz = 2 : 1), unabhängig davon, ob er in der Runde zuvor gewonnen oder verloren hat. Allerdings ist der Spieler ein Fanatiker, weswegen er das Casino erst verlassen wird, wenn er entweder 7000 Euro besitzt, oder aber alles Geld verspielt hat. Mit welcher Wahrscheinlichkeit wird der Spieler als Gewinner aus dem Abend hervorgehen? T2.2 Modellbildung 1. Das obige Szenario modelliert man typischer Weise mithilfe einer Markovkette. Man kann diese darstellen als einen endlichen Automaten, mit den aktuellen Geldbeträgen als Zuständen und den Gewinnwahrscheinlichkeiten als Übergangswahrscheinlichkeiten zwischen den Zuständen. Eine einfache Markovkette für eine beliebig lange Kette an (fairen) Münzwürfen ließe sich beispielsweise so darstellen: Kopf Zahl Erstellen Sie nun eine Markovkette für den Spieler im Casino! Achten Sie darauf, dass die Wahrscheinlichkeiten an den ausgehenden Pfeilen jedes Zustands in Summe stets 1 ergeben! 2. Bilden Sie nun aus der Markovkette die Matrix der Übergangswahrscheinlichkeiten M: { p ij wenn p ij > 0 M = m ij = p ij = 0 sonst p ij bezeichne dabei die Wahrscheinlichkeit, in einem Schritt von Zustand i in Zustand j überzugehen. Offensichtlich gelten mit n als Zahl der Zustände außerdem die folgenden beiden Gleichungen:
4 Praktikum ASP Blatt 6 4 n p ij = 1 j=0 n n p ij = n. i=0 j=0 Überprüfen Sie diese Gleichungen bei Ihrem Lösungsvorschlag auf Gültigkeit! 3. Die Matrix der Übergangswahrscheinlichkeiten kann nun einfach verwendet werden, um die Wahrscheinlichkeiten nach einer beliebigen Zahl von Schritten m zu berechnen. Es gilt für die Matrix der Übergangswahrscheinlichkeiten nach m Schritten M m : M m = M m Der Eintrag (M m ) ij beträgt dann genau die Wahrscheinlichkeit vom Zustand i ausgehend nach m Schritten im Zustand j zu landen. Welcher Eintrag der Matrix M m ist in der Aufgabenstellung gesucht? 4. Der oben beschriebene Umstand ermöglicht es uns, das Ergebnis numerisch zu bestimmen: Wählen wir m nur hoch genug, können wir das System im eingeschwungenen Zustand betrachten. Im Anwendungsfall entspricht dies genau dem Verhalten des Spielers, der unendlich lange spielt, bis er entweder verloren hat, oder aber 7000 Euro besitzt. T2.3 Implementierung 1. Gegeben ist das folgende Rahmenprogramm: 1 # include < s t d i o. h> 2 # include < s t r i n g. h> 3 4 # define MATRIXSIZE 8 5 i n t main ( i n t argc, char argv ) { 6 7 f l o a t matrix [MATRIXSIZE ] [ MATRIXSIZE] = 8 { 9 / I h r e Matrix a l s 2 dimensionales C Array / 10 } ; f l o a t r e s u l t M a t r i x [MATRIXSIZE ] [ MATRIXSIZE ] ; 13 i n t i, j = 0 ; f o r ( i = 0 ; i < 8 ; i ++) { 16 _asm_matrquad(& matrix [ 0 ] [ 0 ], &r e s u l t M a t r i x [ 0 ] [ 0 ] ) ; 17 memcpy( matrix, resultmatrix, s i z e o f ( matrix ) ) ; 18 } p r i n t f ( " r e s u l t M a t r i x [%d][%d ] = \n{\n", MATRIXSIZE, MATRIXSIZE) ; 21 f o r ( i = 0 ; i < MATRIXSIZE ; i ++) { 22 p r i n t f ( " { " ) ; 23 f o r ( j = 0 ; j < MATRIXSIZE ; j ++) { 24 p r i n t f ( " %.1 f ", r e s u l t M a t r i x [ i ] [ j ] ) ;
5 Praktikum ASP Blatt ( j < MATRIXSIZE 1)? p r i n t f ( ", " ) : p r i n t f ( " " ) ; 26 } 27 ( i < MATRIXSIZE 1)? p r i n t f ( " },\n" ) : p r i n t f ( " }\n" ) ; 28 } 29 p r i n t f ( " }\n" ) ; 30 return 0 ; 31 } Listing 1: Matrix-Vorlage Diskretisieren Sie Ihre in der vorangegangenen Teilaufgabe gefundene Matrix der Übergangswahrscheinlichkeiten auf drei Nachkommastellen und fügen Sie sie anstelle des Kommentars in Zeile 8 ein. 2. Wie in T1 gezeigt, wollen wir M m für einen großen Wert m bestimmen. Nach der bekannten Formel für die Multiplikation zweier Matrizen A (m n-matrix) und B (n p-matrix) gilt für die Ergebnismatrix C (m p-matrix): C = A B n c ij = a ik b kj k=1 Wie leicht zu erkennen ist, benötigt man für jedes Element der Ergebnismatrix (c i,j ) die einzelnen Elemente in der Spalte i der Matrix b. Da ein spaltenweiser Zugriff auf den Speicher mit mehr Implementierungsaufwand verbunden ist, kann man die Formel durch das Verwenden der Transponierten Matrix T vereinfachen. Dies vereinfacht Speicherzugriffe im Assemblercode, da die Rechenvorschrift zum Multiplizieren zweier Matrizen sequentiell sowohl ganze Reihen als auch Spalten der Matrix benötigt. Frischen Sie Ihre elementaren Kenntnisse über die Multiplikation zweier Matrizen auf und berechnen Sie das folgende Beispiel. Machen Sie sich dabei klar, welche Zahlen miteinander auf welche Weise verrechnet werden Wie speichert C zweidimensionale Arrays ab? Warum stellt das Transponieren der Matrix in diesem Kontext eine Erleichterung beim Speicherzugriff dar, wenn die Matrix selbst quadriert werden soll? 4. Nutzen Sie Ihr Wissen über die Matrixmultiplikation nun, um einen Algorithmus zu entwerfen, welcher mithilfe der Transponierten das Quadrat einer gegebenen Matrix berechnet. Verwenden Sie eine Pseudo-Code-Notation Ihrer Wahl. 5. Schreiben Sie eine Funktion void _asm_matrtransp(float *input, float *result);
6 Praktikum ASP Blatt 6 6 in eine eigene Assemblerdatei, welche eine Matrix input sowie einen Zeiger auf einen entsprechend großen Speicherbereich übergeben bekommt und in result die Transponierte von input speichert. Rufen Sie Ihre Funktion vom obigen Testprogramm aus auf und überprüfen Sie die Ausgabe auf Richtigkeit! 6. Nutzen Sie nun die NEON-Befehle, um eine Assemblerfunktion void _asm_matrquad(float *input, float *result); zu schreiben, welche eine Matrix input übergeben bekommt und das Quadrat der Matrix in result zurückgibt. Der Speicherbereich für result kann im Rahmenprogramm entweder statisch oder dynamisch allokiert werden. Verwenden Sie die ARM-Dokumentation, um die passenden Befehle nachzuschlagen. Wie lautet das Ergebnis? Wie ist es im Kontext der Anwendungsaufgabe zu interpretieren? 7. Berechnen Sie den eingeschwungenen Zustand des Systems nach m = 2 8 = 256 Schritten (= Spielen!), indem Sie die Funktion _asm_matrquad entsprechend oft aufrufen und das Ergebnis result nach jedem Aufruf wieder in den Speicherbereich input kopiert. Beantworten Sie sodann mithilfe der errechneten Matrix die ursprüngliche Frage aus der Aufgabenstellung. Sind auch weitere Einträge der Matrix im Anwendungszusammenhang deutbar? Sind diese plausibel? H1 Hausaufgabe Implementieren Sie die verbleibenden Punkte aus der Tutorübung! Es besteht keine Verpflichtung, diese Hausaufgaben abzugeben. Sie dienen lediglich der Übung und werden in der folgenden Tutorstunde besprochen. Wir raten Ihnen dringend, anhand der Aufgabe auf diesem Blatt zu überprüfen, ob Sie den bisherigen Inhalt des Praktikums verstanden haben. Wir können durchaus von Ihnen erwarten, dass Sie Aufgaben wie die vorangegangene Anwendung des Spielers im Casino selbstständig als Projektaufgabe bearbeiten können. Fragen zu den bisher behandelten Themen, dem Raspberry Pi 3 und dem Ausführen von Projekten sollten mit diesem Blatt abschließend geklärt sein.
Übungspaket 23 Mehrdimensionale Arrays
 Übungspaket 23 Mehrdimensionale Arrays Übungsziele: Skript: Deklaration und Verwendung mehrdimensionaler Arrays Kapitel: 49 Semester: Wintersemester 2016/17 Betreuer: Kevin, Matthias, Thomas und Ralf Synopsis:
Übungspaket 23 Mehrdimensionale Arrays Übungsziele: Skript: Deklaration und Verwendung mehrdimensionaler Arrays Kapitel: 49 Semester: Wintersemester 2016/17 Betreuer: Kevin, Matthias, Thomas und Ralf Synopsis:
Praktikum ASP Blatt 2 6. LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung
 Praktikum ASP Blatt 2 6 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung T1 Organisatorisches T1.1 Handhabung der Boards 26.10.2015-30.10.2015
Praktikum ASP Blatt 2 6 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung T1 Organisatorisches T1.1 Handhabung der Boards 26.10.2015-30.10.2015
Übungspaket 23 Mehrdimensionale Arrays
 Übungspaket 23 Mehrdimensionale Arrays Übungsziele: Skript: Deklaration und Verwendung mehrdimensionaler Arrays Kapitel: 49 Semester: Wintersemester 2016/17 Betreuer: Kevin, Matthias, Thomas und Ralf Synopsis:
Übungspaket 23 Mehrdimensionale Arrays Übungsziele: Skript: Deklaration und Verwendung mehrdimensionaler Arrays Kapitel: 49 Semester: Wintersemester 2016/17 Betreuer: Kevin, Matthias, Thomas und Ralf Synopsis:
Blockmatrizen. Beispiel 1 Wir berechnen das Produkt von A R 4 6 mit B R 6 4 :
 Blockmatrizen Beispiel 1 Wir berechnen das Produkt von A R 4 6 mit B R 6 4 : 2 1 3 1 1 0 1 0 1 0 0 2 1 1 11 1 1 4 0 1 0 1 0 1 4 1 0 2 1 0 1 0 1 0 3 1 2 1 = 2 4 3 5 11 1 1 4 0 1 0 1 0 1 5 1 2 1 2 4 3 5
Blockmatrizen Beispiel 1 Wir berechnen das Produkt von A R 4 6 mit B R 6 4 : 2 1 3 1 1 0 1 0 1 0 0 2 1 1 11 1 1 4 0 1 0 1 0 1 4 1 0 2 1 0 1 0 1 0 3 1 2 1 = 2 4 3 5 11 1 1 4 0 1 0 1 0 1 5 1 2 1 2 4 3 5
Programmierstarthilfe SS 2008 Fakultät für Ingenieurwissenschaften und Informatik 5. Blatt Für den 26. und
 Programmierstarthilfe SS 2008 Fakultät für Ingenieurwissenschaften und Informatik 5. Blatt Für den 26. und 27.5.2008 Organisatorisches Um auf die Mailingliste aufgenommen zu werden schicke einfach eine
Programmierstarthilfe SS 2008 Fakultät für Ingenieurwissenschaften und Informatik 5. Blatt Für den 26. und 27.5.2008 Organisatorisches Um auf die Mailingliste aufgenommen zu werden schicke einfach eine
Am Dienstag, den 16. Dezember, ist Eulenfest. 1/45
 Am Dienstag, den 16. Dezember, ist Eulenfest. 1/45 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009
Am Dienstag, den 16. Dezember, ist Eulenfest. 1/45 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009
Ein kleiner Blick auf die generische Programmierung
 TgZero Technik.Blosbasis.net June 3, 2013 1 Inhaltsverzeichnis 1 Vorwort 3 2 Ein kleines Beispiel 3 3 Templates 3 4 Verschiedene Datentypen 4 5 Variadic Templates 5 6 Unterschied zwischen den Programmiersprachen
TgZero Technik.Blosbasis.net June 3, 2013 1 Inhaltsverzeichnis 1 Vorwort 3 2 Ein kleines Beispiel 3 3 Templates 3 4 Verschiedene Datentypen 4 5 Variadic Templates 5 6 Unterschied zwischen den Programmiersprachen
a 11 a 12 a 1(m 1) a 1m a n1 a n2 a n(m 1) a nm Matrizen Betrachten wir das nachfolgende Rechteckschema:
 Matrizen Betrachten wir das nachfolgende Rechteckschema: a 12 a 1(m 1 a 1m a n1 a n2 a n(m 1 a nm Ein solches Schema nennt man (n m-matrix, da es aus n Zeilen und m Spalten besteht Jeder einzelne Eintrag
Matrizen Betrachten wir das nachfolgende Rechteckschema: a 12 a 1(m 1 a 1m a n1 a n2 a n(m 1 a nm Ein solches Schema nennt man (n m-matrix, da es aus n Zeilen und m Spalten besteht Jeder einzelne Eintrag
Am Dienstag, den 16. Dezember, ist Eulenfest. 1/48
 Am Dienstag, den 16. Dezember, ist Eulenfest. 1/48 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009
Am Dienstag, den 16. Dezember, ist Eulenfest. 1/48 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009
Primzahlen und Programmieren
 Primzahlen Wir wollen heute gemeinsam einen (sehr grundlegenden) Zusammenhang zwischen Programmieren und Mathematik herstellen. Die Zeiten in denen Mathematiker nur mit Zettel und Stift (oder Tafel und
Primzahlen Wir wollen heute gemeinsam einen (sehr grundlegenden) Zusammenhang zwischen Programmieren und Mathematik herstellen. Die Zeiten in denen Mathematiker nur mit Zettel und Stift (oder Tafel und
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Spezielle Matrizen. Invertierbarkeit.
 Spezielle Matrizen. Invertierbarkeit. Lineare Algebra I Kapitel 4 2. Mai 2012 Logistik Dozent: Olga Holtz, MA 378, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/ holtz Email: holtz@math.tu-berlin.de
Spezielle Matrizen. Invertierbarkeit. Lineare Algebra I Kapitel 4 2. Mai 2012 Logistik Dozent: Olga Holtz, MA 378, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/ holtz Email: holtz@math.tu-berlin.de
WiMa-Praktikum 1. Woche 8
 WiMa-Praktikum 1 Universität Ulm, Sommersemester 2017 Woche 8 Lernziele In diesem Praktikum sollen Sie üben und lernen: Besonderheiten der For-Schleife in Matlab Wiederholung des Umgangs mit Matrizen und
WiMa-Praktikum 1 Universität Ulm, Sommersemester 2017 Woche 8 Lernziele In diesem Praktikum sollen Sie üben und lernen: Besonderheiten der For-Schleife in Matlab Wiederholung des Umgangs mit Matrizen und
37 Gauß-Algorithmus und lineare Gleichungssysteme
 37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
Mathematik IT 2 (Lineare Algebra)
 Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof Dr L Cromme Mathematik IT (Lineare Algebra für die Studiengänge Informatik, IMT und ebusiness im Sommersemester 3 Lineare Gleichungssysteme
Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof Dr L Cromme Mathematik IT (Lineare Algebra für die Studiengänge Informatik, IMT und ebusiness im Sommersemester 3 Lineare Gleichungssysteme
Felder, Rückblick Mehrdimensionale Felder. Programmieren in C
 Übersicht Felder, Rückblick Mehrdimensionale Felder Rückblick Vereinbarung von Feldern: typ name [anzahl]; typ name = {e1, e2, e3,..., en} Die Adressierung von Feldelementen beginnt bei 0 Die korrekte
Übersicht Felder, Rückblick Mehrdimensionale Felder Rückblick Vereinbarung von Feldern: typ name [anzahl]; typ name = {e1, e2, e3,..., en} Die Adressierung von Feldelementen beginnt bei 0 Die korrekte
Kapitel 5. LU Zerlegung. 5.1 L- und U-Matrizen
 Kapitel 5 LU Zerlegung In vielen Fällen interessiert uns die inverse Matrix A 1 gar nicht. Stattdessen suchen wir die Lösung der Matrixgleichung Ax = b bzw. x = A 1 b 5.1) für einen oder wenige Vektoren
Kapitel 5 LU Zerlegung In vielen Fällen interessiert uns die inverse Matrix A 1 gar nicht. Stattdessen suchen wir die Lösung der Matrixgleichung Ax = b bzw. x = A 1 b 5.1) für einen oder wenige Vektoren
T1 Setup und erste Schritte
 Praktikum ASP Blatt 1 1 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung 23.10.2017-29.10.2017 Arbeitsblatt 1 Nach der Bearbeitung dieses
Praktikum ASP Blatt 1 1 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung 23.10.2017-29.10.2017 Arbeitsblatt 1 Nach der Bearbeitung dieses
Teil 5: Zeiger, Felder, Zeichenketten Gliederung
 Teil 5: Zeiger, Felder, Zeichenketten Gliederung Zeiger und Adressen Felder (Arrays) Zeichenketten (Strings) Zeigerarithmetik Mehrdimensionale Felder Zeiger und Adressen Felder Zeichenketten Zeigerarithmetik
Teil 5: Zeiger, Felder, Zeichenketten Gliederung Zeiger und Adressen Felder (Arrays) Zeichenketten (Strings) Zeigerarithmetik Mehrdimensionale Felder Zeiger und Adressen Felder Zeichenketten Zeigerarithmetik
Programmierpraktikum
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Praktikum: Grundlagen der Programmierung Programmierpraktikum Woche 05 (24.11.2016) Stefan Berktold s.berktold@tum.de PRÄSENZAUFGABEN Heutige Übersicht
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Praktikum: Grundlagen der Programmierung Programmierpraktikum Woche 05 (24.11.2016) Stefan Berktold s.berktold@tum.de PRÄSENZAUFGABEN Heutige Übersicht
Invertierbarkeit von Matrizen
 Invertierbarkeit von Matrizen Lineare Algebra I Kapitel 4 24. April 2013 Logistik Dozent: Olga Holtz, MA 417, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/ holtz Email: holtz@math.tu-berlin.de
Invertierbarkeit von Matrizen Lineare Algebra I Kapitel 4 24. April 2013 Logistik Dozent: Olga Holtz, MA 417, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/ holtz Email: holtz@math.tu-berlin.de
Übungsaufgaben Lösungen
 Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Folie zur Vorlesung Wahrscheinlichkeitsrechnung und Stoch. Prozesse
 Folie zur Vorlesung Wahrscheinlichkeitsrechnung und Stoch. Prozesse Zu Markov-Prozessen: Bemerkungen: 17.01.2013 Wir betrachten im Folgenden eine Markovkette (X n ) n N0, wobei jedes X n Werte in Z = {0,1,2,...,s}
Folie zur Vorlesung Wahrscheinlichkeitsrechnung und Stoch. Prozesse Zu Markov-Prozessen: Bemerkungen: 17.01.2013 Wir betrachten im Folgenden eine Markovkette (X n ) n N0, wobei jedes X n Werte in Z = {0,1,2,...,s}
W-Rechnung und Statistik für Ingenieure Übung 11
 W-Rechnung und Statistik für Ingenieure Übung 11 Aufgabe 1 Ein Fahrzeugpark enthält 6 Fahrzeuge. Jedes Fahrzeug hat die Wahrscheinlichkeit p = 0.1 (bzw. p = 0.3), dass es kaputt geht. Pro Tag kann nur
W-Rechnung und Statistik für Ingenieure Übung 11 Aufgabe 1 Ein Fahrzeugpark enthält 6 Fahrzeuge. Jedes Fahrzeug hat die Wahrscheinlichkeit p = 0.1 (bzw. p = 0.3), dass es kaputt geht. Pro Tag kann nur
TECHNISCHE UNIVERSITÄT MÜNCHEN. Einführung in die Matrizenrechnung
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra WS 006/07 en Blatt 3.0.006 Einführung in die Matrizenrechnung Zentralübungsaufgaben
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra WS 006/07 en Blatt 3.0.006 Einführung in die Matrizenrechnung Zentralübungsaufgaben
Konzepte der Programmiersprachen
 Konzepte der Programmiersprachen Sommersemester 2010 4. Übungsblatt Besprechung am 9. Juli 2010 http://www.iste.uni-stuttgart.de/ps/lehre/ss2010/v_konzepte/ Aufgabe 4.1: Klassen in C ++ Das folgende C
Konzepte der Programmiersprachen Sommersemester 2010 4. Übungsblatt Besprechung am 9. Juli 2010 http://www.iste.uni-stuttgart.de/ps/lehre/ss2010/v_konzepte/ Aufgabe 4.1: Klassen in C ++ Das folgende C
Universität Stuttgart Physik und ihre Didaktik PD Dr. Holger Cartarius. Matrizen. a 1,1 a 1,2 a 1,n a 2,1 a 2,2 a 2,n A = a m,1 a m,2 a m,n
 Universität Stuttgart Physik und ihre Didaktik PD Dr Holger Cartarius Matrizen Matrizen: Ein rechteckiges Zahlenschema der Form a 1,1 a 1,2 a 1,n a 2,1 a 2,2 a 2,n A a m,1 a m,2 a m,n (a) nennt man eine
Universität Stuttgart Physik und ihre Didaktik PD Dr Holger Cartarius Matrizen Matrizen: Ein rechteckiges Zahlenschema der Form a 1,1 a 1,2 a 1,n a 2,1 a 2,2 a 2,n A a m,1 a m,2 a m,n (a) nennt man eine
Lineare Algebra und Numerische Mathematik für D-BAUG
 P. Grohs T. Welti F. Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 5 Aufgabe 5.1 Kommutierende Matrizen In der Vorlesung und vergangenen
P. Grohs T. Welti F. Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 5 Aufgabe 5.1 Kommutierende Matrizen In der Vorlesung und vergangenen
Musterlösung zur 6. Übung
 Universität des Saarlandes FR 6.2 Informatik Prof. Dr. Hans-Peter Lenhof Dipl. Inform. Andreas Hildebrandt Programmierung II, SS 2003 Musterlösung zur 6. Übung Aufgabe 1: Faire Münzen (10 Punkte) Offensichtlich
Universität des Saarlandes FR 6.2 Informatik Prof. Dr. Hans-Peter Lenhof Dipl. Inform. Andreas Hildebrandt Programmierung II, SS 2003 Musterlösung zur 6. Übung Aufgabe 1: Faire Münzen (10 Punkte) Offensichtlich
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 9 20. Mai 2010 Kapitel 9. Matrizen und Determinanten Der Begriff der Matrix Die transponierte Matrix Definition 84. Unter einer (reellen) m n-matrix
Mathematik für Naturwissenschaftler II SS 2010 Lektion 9 20. Mai 2010 Kapitel 9. Matrizen und Determinanten Der Begriff der Matrix Die transponierte Matrix Definition 84. Unter einer (reellen) m n-matrix
Lineare Algebra und Numerische Mathematik für D-BAUG. Serie 6
 R. Hiptmair S. Pintarelli E. Spindler Herbstsemester 2014 Lineare Algebra und Numerische Mathematik für D-BAUG Serie 6 ETH Zürich D-MATH Einleitung. Diese Serie behandelt nochmals das Rechnen mit Vektoren
R. Hiptmair S. Pintarelli E. Spindler Herbstsemester 2014 Lineare Algebra und Numerische Mathematik für D-BAUG Serie 6 ETH Zürich D-MATH Einleitung. Diese Serie behandelt nochmals das Rechnen mit Vektoren
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Nur Matrizen gleicher Dimension können addiert oder subtrahiert werden. Zur Berechnung werden zwei Matrizen A und B in den Matrix-Editor eingegeben.
 R. Brinkmann http://brinkmann-du.de Seite 1 14.02.2014 Casio fx-cg20 Operationen mit Matrizen Bei nachfolgend beschriebenen Matrizenoperationen wird davon ausgegangen, dass die Eingabe von Matrizen in
R. Brinkmann http://brinkmann-du.de Seite 1 14.02.2014 Casio fx-cg20 Operationen mit Matrizen Bei nachfolgend beschriebenen Matrizenoperationen wird davon ausgegangen, dass die Eingabe von Matrizen in
Analytische Geometrie
 Der fx-991 DE X im Mathematik- Unterricht Analytische Geometrie Station 1 Schnittgerade zweier Ebenen Da der Taschenrechner nur eindeutige Lösungen eines Gleichungssystems liefert, kann er nur Schnittpunkte
Der fx-991 DE X im Mathematik- Unterricht Analytische Geometrie Station 1 Schnittgerade zweier Ebenen Da der Taschenrechner nur eindeutige Lösungen eines Gleichungssystems liefert, kann er nur Schnittpunkte
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Zentralübung zur Vorlesung Diskrete Strukturen
 WS 2010/11 Zentralübung zur Vorlesung Diskrete Strukturen Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2010ws/ds/uebung/ 1. Dezember 2010 ZÜ DS ZÜ VI Übersicht: 1.
WS 2010/11 Zentralübung zur Vorlesung Diskrete Strukturen Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2010ws/ds/uebung/ 1. Dezember 2010 ZÜ DS ZÜ VI Übersicht: 1.
Matrix: Eine rechteckige Anordnung reeller Zahlen a ij (i = 1,..., n i ; j = 1,..., m) in Zeilen und Spalten. Die a ij heiÿen Elemente von A.
 Matrizenrechnung Matrix: Eine rechteckige Anordnung reeller Zahlen a ij i = 1,..., n i ; j = 1,..., m in Zeilen und Spalten. Die a ij heiÿen Elemente von A. a 11 a 12... a ij... a 1m a 21 a 22.........
Matrizenrechnung Matrix: Eine rechteckige Anordnung reeller Zahlen a ij i = 1,..., n i ; j = 1,..., m in Zeilen und Spalten. Die a ij heiÿen Elemente von A. a 11 a 12... a ij... a 1m a 21 a 22.........
MLAN1 1 MATRIZEN 1 0 = A T =
 MLAN1 1 MATRIZEN 1 1 Matrizen Eine m n Matrix ein rechteckiges Zahlenschema a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n a m1 a m2 a m3 amn mit m Zeilen und n Spalten bestehend aus m n Zahlen Die Matrixelemente
MLAN1 1 MATRIZEN 1 1 Matrizen Eine m n Matrix ein rechteckiges Zahlenschema a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n a m1 a m2 a m3 amn mit m Zeilen und n Spalten bestehend aus m n Zahlen Die Matrixelemente
Effiziente Algorithmen und Datenstrukturen I. Kapitel 10: Lineare Algebra
 Effiziente Algorithmen und Datenstrukturen I Kapitel 10: Lineare Algebra Christian Scheideler WS 2008 19.02.2009 Kapitel 10 1 Überblick Notation Arithmetik auf großen Zahlen (Addition und Multiplikation)
Effiziente Algorithmen und Datenstrukturen I Kapitel 10: Lineare Algebra Christian Scheideler WS 2008 19.02.2009 Kapitel 10 1 Überblick Notation Arithmetik auf großen Zahlen (Addition und Multiplikation)
Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 12
 Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 12 Die Lösungshinweise dienen
Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 12 Die Lösungshinweise dienen
36 2 Lineare Algebra
 6 Lineare Algebra Quadratische Matrizen a a n sei jetzt n m, A, a ij R, i, j,, n a n a nn Definition Eine quadratische Matrix A heißt invertierbar genau dann, wenn es eine quadratische Matrix B gibt, so
6 Lineare Algebra Quadratische Matrizen a a n sei jetzt n m, A, a ij R, i, j,, n a n a nn Definition Eine quadratische Matrix A heißt invertierbar genau dann, wenn es eine quadratische Matrix B gibt, so
Übungen zur Vorlesung EidP (WS 2015/16) Blatt 6
 Andre Droschinsky Ingo Schulz Dortmund, den 0. Dezember 2015 Übungen zur Vorlesung EidP (WS 2015/16) Blatt 6 Block rot Es können 4 + 1 Punkte erreicht werden. Abgabedatum: 10. Dezember 2015 2:59 Uhr Hinweise
Andre Droschinsky Ingo Schulz Dortmund, den 0. Dezember 2015 Übungen zur Vorlesung EidP (WS 2015/16) Blatt 6 Block rot Es können 4 + 1 Punkte erreicht werden. Abgabedatum: 10. Dezember 2015 2:59 Uhr Hinweise
Vorbereitungskurs Mathematik zum Sommersemester 2011 Tag 7
 Vorbereitungskurs Mathematik zum Sommersemester 2011 Tag 7 Timo Stöcker Erstsemestereinführung Informatik TU Dortmund 22. März 2011 Heute Themen Lineare Gleichungssysteme Matrizen Timo Stöcker https://fsinfo.cs.tu-dortmund.de/studis/ese/vorkurse/mathe
Vorbereitungskurs Mathematik zum Sommersemester 2011 Tag 7 Timo Stöcker Erstsemestereinführung Informatik TU Dortmund 22. März 2011 Heute Themen Lineare Gleichungssysteme Matrizen Timo Stöcker https://fsinfo.cs.tu-dortmund.de/studis/ese/vorkurse/mathe
3. Übungsblatt zur Lineare Algebra I für Physiker
 Fachbereich Mathematik Prof. Dr. Mirjam Dür Dipl. Math. Stefan Bundfuss. Übungsblatt zur Lineare Algebra I für Physiker WS 5/6 6. Dezember 5 Gruppenübung Aufgabe G (Basis und Erzeugendensystem) Betrachte
Fachbereich Mathematik Prof. Dr. Mirjam Dür Dipl. Math. Stefan Bundfuss. Übungsblatt zur Lineare Algebra I für Physiker WS 5/6 6. Dezember 5 Gruppenübung Aufgabe G (Basis und Erzeugendensystem) Betrachte
Tutorium: Diskrete Mathematik. Matrizen
 Tutorium: Diskrete Mathematik Matrizen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de Definition I Eine Matrix ist eine rechteckige Anordnung (Tabelle) von Elementen, mit denen man in bestimmter
Tutorium: Diskrete Mathematik Matrizen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de Definition I Eine Matrix ist eine rechteckige Anordnung (Tabelle) von Elementen, mit denen man in bestimmter
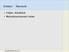
Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P.
![Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P. Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P.](/thumbs/64/51976840.jpg) 2.2 Berechnung von Übergangswahrscheinlichkeiten Wir beschreiben die Situation zum Zeitpunkt t durch einen Zustandsvektor q t (den wir als Zeilenvektor schreiben). Die i-te Komponente (q t ) i bezeichnet
2.2 Berechnung von Übergangswahrscheinlichkeiten Wir beschreiben die Situation zum Zeitpunkt t durch einen Zustandsvektor q t (den wir als Zeilenvektor schreiben). Die i-te Komponente (q t ) i bezeichnet
Matrizen. Lineare Algebra I. Kapitel April 2011
 Matrizen Lineare Algebra I Kapitel 2 26. April 2011 Logistik Dozent: Olga Holtz, MA 378, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/~holtz Email: holtz@math.tu-berlin.de Assistent: Sadegh
Matrizen Lineare Algebra I Kapitel 2 26. April 2011 Logistik Dozent: Olga Holtz, MA 378, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/~holtz Email: holtz@math.tu-berlin.de Assistent: Sadegh
Ingenieurinformatik Diplom-FA (Teil 2, C-Programmierung)
 Hochschule München, FK 03 SS 2014 Ingenieurinformatik Diplom-FA (Teil 2, C-Programmierung) Zulassung geprüft: (Grundlagenteil) Die Prüfung ist nur dann gültig, wenn Sie die erforderliche Zulassungsvoraussetzung
Hochschule München, FK 03 SS 2014 Ingenieurinformatik Diplom-FA (Teil 2, C-Programmierung) Zulassung geprüft: (Grundlagenteil) Die Prüfung ist nur dann gültig, wenn Sie die erforderliche Zulassungsvoraussetzung
Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza)
 SS 2013 Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ss/dwt/uebung/ 10. Mai 2013
SS 2013 Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ss/dwt/uebung/ 10. Mai 2013
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 24-6. Sitzung Marcus Georgi tutorium@marcusgeorgi.de 04.12.2009 1 Repräsentation von Graphen im Rechner Adjazenzlisten Adjazenzmatrizen Wegematrizen 2 Erreichbarkeitsrelationen
Grundbegriffe der Informatik Tutorium 24-6. Sitzung Marcus Georgi tutorium@marcusgeorgi.de 04.12.2009 1 Repräsentation von Graphen im Rechner Adjazenzlisten Adjazenzmatrizen Wegematrizen 2 Erreichbarkeitsrelationen
8.2 Invertierbare Matrizen
 38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Übungspaket 29 Dynamische Speicherverwaltung: malloc() und free()
 Übungspaket 29 Dynamische Speicherverwaltung malloc() und free() Übungsziele Skript In diesem Übungspaket üben wir das dynamische Alloziieren 1. und Freigeben von Speicherbereichen 2. von Zeichenketten
Übungspaket 29 Dynamische Speicherverwaltung malloc() und free() Übungsziele Skript In diesem Übungspaket üben wir das dynamische Alloziieren 1. und Freigeben von Speicherbereichen 2. von Zeichenketten
Parallele und funktionale Programmierung Wintersemester 2016/ Übung Abgabe bis , 16:00 Uhr
 4. Übung Abgabe bis 25.11.2016, 16:00 Uhr Aufgabe 4.1: Verklemmungsbedingungen a) Welche drei Bedingungen müssen gelten, damit es zu einer Verklemmung in einem parallelen System kommen kann? b) Nach welcher
4. Übung Abgabe bis 25.11.2016, 16:00 Uhr Aufgabe 4.1: Verklemmungsbedingungen a) Welche drei Bedingungen müssen gelten, damit es zu einer Verklemmung in einem parallelen System kommen kann? b) Nach welcher
Einführung in die Programmierung (EPR)
 Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Dossier: Rechnungen und Lieferscheine in Word
 www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
Institut für Informatik
 Technische Universität München Institut für Informatik Lehrstuhl für Computer Graphik & Visualisierung WS 2010 Praktikum: Grundlagen der Programmierung Aufgabenblatt 4 Prof. R. Westermann, A. Lehmann,
Technische Universität München Institut für Informatik Lehrstuhl für Computer Graphik & Visualisierung WS 2010 Praktikum: Grundlagen der Programmierung Aufgabenblatt 4 Prof. R. Westermann, A. Lehmann,
Lineare Gleichungssysteme und Matrizen
 Kapitel 11 Lineare Gleichungssysteme und Matrizen Ein lineares Gleichungssystem (lgs) mit m linearen Gleichungen in den n Unbekannten x 1, x 2,..., x n hat die Gestalt: Mit a 11 x 1 + a 12 x 2 + a 13 x
Kapitel 11 Lineare Gleichungssysteme und Matrizen Ein lineares Gleichungssystem (lgs) mit m linearen Gleichungen in den n Unbekannten x 1, x 2,..., x n hat die Gestalt: Mit a 11 x 1 + a 12 x 2 + a 13 x
Tag 4 Repetitorium Informatik (Java)
 Tag 4 Repetitorium Informatik (Java) Dozent: Patrick Kreutzer Lehrstuhl für Informatik 2 (Programmiersysteme) Friedrich-Alexander-Universität Erlangen-Nürnberg Wintersemester 2016/2017 Willkommen zum Informatik-Repetitorium!
Tag 4 Repetitorium Informatik (Java) Dozent: Patrick Kreutzer Lehrstuhl für Informatik 2 (Programmiersysteme) Friedrich-Alexander-Universität Erlangen-Nürnberg Wintersemester 2016/2017 Willkommen zum Informatik-Repetitorium!
3.4 Der Gaußsche Algorithmus
 94 34 Der Gaußsche Algorithmus Wir kommen jetzt zur expliziten numerischen Lösung des eingangs als eine Motivierung für die Lineare Algebra angegebenen linearen Gleichungssystems 341 n 1 a ik x k = b i,
94 34 Der Gaußsche Algorithmus Wir kommen jetzt zur expliziten numerischen Lösung des eingangs als eine Motivierung für die Lineare Algebra angegebenen linearen Gleichungssystems 341 n 1 a ik x k = b i,
Klausur Einführung in die Informatik I für Elektrotechniker 16. Juli 2003
 Fakultät Elektrotechnik/Informatik Klausur Einführung in die Informatik I für Elektrotechniker Name:...................... Matr.-Nr....................... Bearbeitungszeit: 120 Minuten Bewertung (bitte
Fakultät Elektrotechnik/Informatik Klausur Einführung in die Informatik I für Elektrotechniker Name:...................... Matr.-Nr....................... Bearbeitungszeit: 120 Minuten Bewertung (bitte
Übung Augmented Reality
 Ludwig-Maximilians-Universität München LFE Medieninformatik Prof. Dr. Andreas Butz Fabian Hennecke Sommersemester 2009 Übungsblatt 1 28. April 2009 Übung Augmented Reality Abgabetermin: Die Lösung zu diesem
Ludwig-Maximilians-Universität München LFE Medieninformatik Prof. Dr. Andreas Butz Fabian Hennecke Sommersemester 2009 Übungsblatt 1 28. April 2009 Übung Augmented Reality Abgabetermin: Die Lösung zu diesem
Schriftlicher Test (120 Minuten) VU Einführung ins Programmieren für TM. 25. Jänner 2016
 Familienname: Vorname: Matrikelnummer: Aufgabe 1 (3 Punkte): Aufgabe 2 (4 Punkte): Aufgabe 3 (2 Punkte): Aufgabe 4 (2 Punkte): Aufgabe 5 (2 Punkte): Aufgabe 6 (1 Punkte): Aufgabe 7 (3 Punkte): Aufgabe
Familienname: Vorname: Matrikelnummer: Aufgabe 1 (3 Punkte): Aufgabe 2 (4 Punkte): Aufgabe 3 (2 Punkte): Aufgabe 4 (2 Punkte): Aufgabe 5 (2 Punkte): Aufgabe 6 (1 Punkte): Aufgabe 7 (3 Punkte): Aufgabe
Angewandte Stochastik
 Angewandte Stochastik Dr. C.J. Luchsinger 13 Allgemeine Theorie zu Markov-Prozessen (stetige Zeit, diskreter Zustandsraum) Literatur Kapitel 13 * Grimmett & Stirzaker: Kapitel 6.9 Wie am Schluss von Kapitel
Angewandte Stochastik Dr. C.J. Luchsinger 13 Allgemeine Theorie zu Markov-Prozessen (stetige Zeit, diskreter Zustandsraum) Literatur Kapitel 13 * Grimmett & Stirzaker: Kapitel 6.9 Wie am Schluss von Kapitel
Numerische Lineare Algebra - Matlab-Blatt 2
 Prof. Dr. Stefan Funken Universität Ulm M.Sc. Andreas Bantle Institut für Numerische Mathematik Dipl.-Math. oec. Klaus Stolle Wintersemester 014/015 Numerische Lineare Algebra - Matlab-Blatt Lösung (Besprechung
Prof. Dr. Stefan Funken Universität Ulm M.Sc. Andreas Bantle Institut für Numerische Mathematik Dipl.-Math. oec. Klaus Stolle Wintersemester 014/015 Numerische Lineare Algebra - Matlab-Blatt Lösung (Besprechung
FH Ravensburg-Weingarten Schriftlich Prüfung Programmieren
 FH Ravensburg-Weingarten Schriftlich Prüfung Programmieren Prof. Dr. M. Zeller Datum, Zeit Aufgabenblätter erreichbare Punktzahl zugelassene Hilfsmittel, 0800 1000 Uhr (120 min) 16 Seiten (einschl. Deckblatt)
FH Ravensburg-Weingarten Schriftlich Prüfung Programmieren Prof. Dr. M. Zeller Datum, Zeit Aufgabenblätter erreichbare Punktzahl zugelassene Hilfsmittel, 0800 1000 Uhr (120 min) 16 Seiten (einschl. Deckblatt)
A.5.1 Die Matrix und elementare wirtschaftsrelevante Anwendungen
 A.5.1 Die Matrix und elementare wirtschaftsrelevante Anwendungen Eine Matrix vom Typ M mxn (oder eine (m x n)-matrix) ist ein rechteckiges Zahlenschema mit m Zeilen und n Spalten. Im folgenden Beispiel
A.5.1 Die Matrix und elementare wirtschaftsrelevante Anwendungen Eine Matrix vom Typ M mxn (oder eine (m x n)-matrix) ist ein rechteckiges Zahlenschema mit m Zeilen und n Spalten. Im folgenden Beispiel
Numerisches Programmieren, Übungen
 Technische Universität München SoSe 3 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Jürgen Bräckle Numerisches Programmieren, Übungen Musterlösung 3. Übungsblatt:
Technische Universität München SoSe 3 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Jürgen Bräckle Numerisches Programmieren, Übungen Musterlösung 3. Übungsblatt:
C- Kurs 07 Höhere Datentypen
 C- Kurs 07 Höhere Datentypen Dipl.- Inf. Jörn Hoffmann jhoffmann@informa?k.uni- leipzig.de Universität Leipzig Ins?tut für Informa?k Technische Informa?k Höhere Datentypen Überblick Höhere Datentypen Werden
C- Kurs 07 Höhere Datentypen Dipl.- Inf. Jörn Hoffmann jhoffmann@informa?k.uni- leipzig.de Universität Leipzig Ins?tut für Informa?k Technische Informa?k Höhere Datentypen Überblick Höhere Datentypen Werden
3 Matrizenrechnung. 3. November
 3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
Beispiele 1. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix (A
 133 e 1. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 2. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 Schritte des
133 e 1. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 2. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 Schritte des
Chuck a Luck Zielstellung Diese Aufgabe soll weniger dem Erlernen neuer Inhalte dienen, sondern ist als Anwendungs bzw.
 Chuck a Luck Zielstellung Diese Aufgabe soll weniger dem Erlernen neuer Inhalte dienen, sondern ist als Anwendungs bzw. Projektaufgabe gedacht. Material Aufgabenstellung, Lösungsvorschlag und BlueJ Projekte
Chuck a Luck Zielstellung Diese Aufgabe soll weniger dem Erlernen neuer Inhalte dienen, sondern ist als Anwendungs bzw. Projektaufgabe gedacht. Material Aufgabenstellung, Lösungsvorschlag und BlueJ Projekte
Grundlagen: Algorithmen und Datenstrukturen
 Technische Universität München Fakultät für Informatik Lehrstuhl für Effiziente Algorithmen Dr. Hanjo Täubig Tobias Lieber Sommersemester 011 Übungsblatt 30. Mai 011 Grundlagen: Algorithmen und Datenstrukturen
Technische Universität München Fakultät für Informatik Lehrstuhl für Effiziente Algorithmen Dr. Hanjo Täubig Tobias Lieber Sommersemester 011 Übungsblatt 30. Mai 011 Grundlagen: Algorithmen und Datenstrukturen
Algebraische und arithmetische Algorithmen
 Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
(1) In dieser Aufgabe kreuzen Sie bitte nur die Antworten an, die Sie für richtig halten. Eine Begründung wird nicht verlangt.
 () In dieser Aufgabe kreuzen Sie bitte nur die Antworten an, die Sie für richtig halten. Eine Begründung wird nicht verlangt. a) Es seien A und B beliebige n n-matrizen mit Einträgen in einem Körper K.
() In dieser Aufgabe kreuzen Sie bitte nur die Antworten an, die Sie für richtig halten. Eine Begründung wird nicht verlangt. a) Es seien A und B beliebige n n-matrizen mit Einträgen in einem Körper K.
Beginn der Vorlesung zur Numerik I (Wintersemester 2010/2011)
 M. Sc. Frank Gimbel Beginn der Vorlesung zur Numerik I (Wintersemester 2010/2011) 1 Motivation Ziel ist es, ein gegebenes lineares Gleichungssystem der Form Ax = b (1) mit x, b R n und A R n n zu lösen.
M. Sc. Frank Gimbel Beginn der Vorlesung zur Numerik I (Wintersemester 2010/2011) 1 Motivation Ziel ist es, ein gegebenes lineares Gleichungssystem der Form Ax = b (1) mit x, b R n und A R n n zu lösen.
Algorithmische Methoden zur Netzwerkanalyse
 Algorithmische Methoden zur Netzwerkanalyse Juniorprof. Dr. Henning Meyerhenke Institut für Theoretische Informatik 1 KIT Henning Universität desmeyerhenke, Landes Baden-Württemberg Institutund für Theoretische
Algorithmische Methoden zur Netzwerkanalyse Juniorprof. Dr. Henning Meyerhenke Institut für Theoretische Informatik 1 KIT Henning Universität desmeyerhenke, Landes Baden-Württemberg Institutund für Theoretische
Übungen zur Linearen Algebra, Kap. 1 bis Kap. 3
 Übungen zur Linearen Algebra, Kap. bis Kap. 3. Gegeben seien die beiden Matrizen Berechnen Sie Lösungen zu Übung 6 3 4, B = ( 3 5 4 A B, B A, (A B, (B A Dies ist fast eine reine Rechenaufgabe. Wir wollen
Übungen zur Linearen Algebra, Kap. bis Kap. 3. Gegeben seien die beiden Matrizen Berechnen Sie Lösungen zu Übung 6 3 4, B = ( 3 5 4 A B, B A, (A B, (B A Dies ist fast eine reine Rechenaufgabe. Wir wollen
B =(b1,1. + b 1,2. + b 1,3 1,3. + b 2,4 + b 3,1. + b 2,2. + b 2,3. + b 3,2. + b 3,3
 Matrizen Matrizen sind zunächst einmal einfach eine rechteckige Anordnung von Zahlen, Elementen oder mathematischen Operationen, die lineare Zusammenhänge zwischen verschiedenen Größen übersichtlich darstellen.
Matrizen Matrizen sind zunächst einmal einfach eine rechteckige Anordnung von Zahlen, Elementen oder mathematischen Operationen, die lineare Zusammenhänge zwischen verschiedenen Größen übersichtlich darstellen.
3 Elementare Umformung von linearen Gleichungssystemen und Matrizen
 3 Elementare Umformung von linearen Gleichungssystemen und Matrizen Beispiel 1: Betrachte das Gleichungssystem x 1 + x 2 + x 3 = 2 2x 1 + 4x 2 + 3x 3 = 1 3x 1 x 2 + 4x 3 = 7 Wir formen das GLS so lange
3 Elementare Umformung von linearen Gleichungssystemen und Matrizen Beispiel 1: Betrachte das Gleichungssystem x 1 + x 2 + x 3 = 2 2x 1 + 4x 2 + 3x 3 = 1 3x 1 x 2 + 4x 3 = 7 Wir formen das GLS so lange
Informationen zur Klausur
 Einführung in die Rechnerarchitektur Informationen zur Klausur Tilman Küstner Marcel Meyer Arndt Bode, Michael Gerndt, Einführung in die Rechnerarchitektur Lehrstuhl für Rechnertechnik und Rechnerorganisation
Einführung in die Rechnerarchitektur Informationen zur Klausur Tilman Küstner Marcel Meyer Arndt Bode, Michael Gerndt, Einführung in die Rechnerarchitektur Lehrstuhl für Rechnertechnik und Rechnerorganisation
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 5/.. Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 4. Übungsblatt Aufgabe
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 5/.. Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 4. Übungsblatt Aufgabe
Arrays. Einleitung. Deklarieren einer Array Variablen
 Arrays Einleitung bisher jede Variable einzeln deklariert: 12 3 14 12 32 32 3 32 5 3 double sum; int count; ÿ Sie können Zweck und Aufbau von Array-Datentypen erklären ÿ Sie können einen Array korrekt
Arrays Einleitung bisher jede Variable einzeln deklariert: 12 3 14 12 32 32 3 32 5 3 double sum; int count; ÿ Sie können Zweck und Aufbau von Array-Datentypen erklären ÿ Sie können einen Array korrekt
9.2 Invertierbare Matrizen
 34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
T1 Setup und erste Schritte
 Praktikum ASP Blatt 1 1 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung T1 Setup und erste Schritte 19.10.2015-23.10.2015 Arbeitsblatt
Praktikum ASP Blatt 1 1 LEHRSTUHL FÜR RECHNERTECHNIK UND RECHNERORGANISATION Aspekte der systemnahen Programmierung bei der Spieleentwicklung T1 Setup und erste Schritte 19.10.2015-23.10.2015 Arbeitsblatt
In der Computersprache C ist die Standardmethode zur Behandlung von Matrizen durch
 Kapitel Matrizen in C++ In der Computersprache C ist die Standardmethode zur Behandlung von Matrizen durch 1 const int n=10; 3 double a[n][n]; gegeben. Allerdings gibt es bei dieser Methode eine Reihe
Kapitel Matrizen in C++ In der Computersprache C ist die Standardmethode zur Behandlung von Matrizen durch 1 const int n=10; 3 double a[n][n]; gegeben. Allerdings gibt es bei dieser Methode eine Reihe
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 10. Aufgabe ETH Zürich D-MATH. Herbstsemester Dr. V. Gradinaru D.
 Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
3 Determinanten, Eigenwerte, Normalformen
 Determinanten, Eigenwerte, Normalformen.1 Determinanten Beispiel. Betrachte folgendes Parallelogramm in der Ebene R 2 : y (a + c, b + d) (c, d) (a, b) x Man rechnet leicht nach, dass die Fläche F dieses
Determinanten, Eigenwerte, Normalformen.1 Determinanten Beispiel. Betrachte folgendes Parallelogramm in der Ebene R 2 : y (a + c, b + d) (c, d) (a, b) x Man rechnet leicht nach, dass die Fläche F dieses
U4-1 Aufgabe 3: einfache malloc-implementierung
 U4 3. Übung U4 3. Übung Besprechung der Aufgabe 2: wsort Aufgabe 3: malloc-implementierung Ziele der Aufgabe Zusammenhang zwischen "nacktem Speicher" und typisierten bereichen verstehen Funktion aus der
U4 3. Übung U4 3. Übung Besprechung der Aufgabe 2: wsort Aufgabe 3: malloc-implementierung Ziele der Aufgabe Zusammenhang zwischen "nacktem Speicher" und typisierten bereichen verstehen Funktion aus der
Lesen Sie alle Aufgabenstellungen sorgfältig durch, bevor Sie mit der Bearbeitung der ersten Aufgabe beginnen.
 INE1 Musteraufgaben für die Semesterendprüfung Hilfsmittel Vier Seiten selbst verfasste Zusammenfassung keine weiteren Hilfsmittel keine elektronischen Hilfsmittel Abgabe Füllen Sie das erste Aufgabenblatt
INE1 Musteraufgaben für die Semesterendprüfung Hilfsmittel Vier Seiten selbst verfasste Zusammenfassung keine weiteren Hilfsmittel keine elektronischen Hilfsmittel Abgabe Füllen Sie das erste Aufgabenblatt
Mehrdimensionale Arrays
 Informatik Studiengang Chemische Technologie Michael Roth michael.roth@h-da.de Hochschule Darmstadt -Fachbereich Informatik- WS 2012/2013 Inhalt Teil X Michael Roth (h_da) Informatik (CT) WS 2012/2013
Informatik Studiengang Chemische Technologie Michael Roth michael.roth@h-da.de Hochschule Darmstadt -Fachbereich Informatik- WS 2012/2013 Inhalt Teil X Michael Roth (h_da) Informatik (CT) WS 2012/2013
Kapitel 2: Matrizen. 2.1 Matrizen 2.2 Determinanten 2.3 Inverse 2.4 Lineare Gleichungssysteme 2.5 Eigenwerte 2.6 Diagonalisierung
 Kapitel 2: Matrizen 2.1 Matrizen 2.2 Determinanten 2.3 Inverse 2.4 Lineare Gleichungssysteme 2.5 Eigenwerte 2.6 Diagonalisierung 2.1 Matrizen M = n = 3 m = 3 n = m quadratisch M ij : Eintrag von M in i-ter
Kapitel 2: Matrizen 2.1 Matrizen 2.2 Determinanten 2.3 Inverse 2.4 Lineare Gleichungssysteme 2.5 Eigenwerte 2.6 Diagonalisierung 2.1 Matrizen M = n = 3 m = 3 n = m quadratisch M ij : Eintrag von M in i-ter
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Matrizen, Determinanten, lineare Gleichungssysteme
 Matrizen, Determinanten, lineare Gleichungssysteme 1 Matrizen Definition 1. Eine Matrix A vom Typ m n (oder eine m n Matrix, A R m n oder A C m n ) ist ein rechteckiges Zahlenschema mit m Zeilen und n
Matrizen, Determinanten, lineare Gleichungssysteme 1 Matrizen Definition 1. Eine Matrix A vom Typ m n (oder eine m n Matrix, A R m n oder A C m n ) ist ein rechteckiges Zahlenschema mit m Zeilen und n
Züchtungslehre - Einführung in Lineare Algebra Peter von Rohr
 Züchtungslehre - Einführung in Lineare Algebra Peter von Rohr 04-09-2016 Einführung in Lineare Algebra Aus der linearen Algebra brauchen wir für diese Vorlesung nur das Rechnen mit Vektoren und Matrizen.
Züchtungslehre - Einführung in Lineare Algebra Peter von Rohr 04-09-2016 Einführung in Lineare Algebra Aus der linearen Algebra brauchen wir für diese Vorlesung nur das Rechnen mit Vektoren und Matrizen.
Lineare Algebra 1. Roger Burkhardt
 Lineare Algebra 1 Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft HS 2010/11 3 und lineare Gleichungssysteme und
Lineare Algebra 1 Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft HS 2010/11 3 und lineare Gleichungssysteme und
LR Zerlegung. Michael Sagraloff
 LR Zerlegung Michael Sagraloff Beispiel eines linearen Gleichungssystems in der Ökonomie (Input-Output Analyse Wir nehmen an, dass es 3 Güter G, G, und G 3 gibt Dann entspricht der Eintrag a i,j der sogenannten
LR Zerlegung Michael Sagraloff Beispiel eines linearen Gleichungssystems in der Ökonomie (Input-Output Analyse Wir nehmen an, dass es 3 Güter G, G, und G 3 gibt Dann entspricht der Eintrag a i,j der sogenannten
Grundlagen der Programmiersprache C für Studierende der Naturwissenschaften
 Grundlagen der Programmiersprache C für Studierende der Naturwissenschaften Teil 7: Matrizen, Vektoren und dynamische Speicherverwaltung Martin Nolte Abteilung für Angewandte Mathematik Universität Freiburg
Grundlagen der Programmiersprache C für Studierende der Naturwissenschaften Teil 7: Matrizen, Vektoren und dynamische Speicherverwaltung Martin Nolte Abteilung für Angewandte Mathematik Universität Freiburg
Lösung Übungsblatt 7
 M4 Numerik für Physiker Lösung Übungsblatt 7 SoSe 008 Lösung Übungsblatt 7 Aufgabe 1: Lineare Ausgleichsrechnung Ein mehrdimensionales, lineares Ausgleichungsproblem lässt sich folgendermaßen darstellen:
M4 Numerik für Physiker Lösung Übungsblatt 7 SoSe 008 Lösung Übungsblatt 7 Aufgabe 1: Lineare Ausgleichsrechnung Ein mehrdimensionales, lineares Ausgleichungsproblem lässt sich folgendermaßen darstellen:
Korrelationsmatrix. Statistische Bindungen zwischen den N Zufallsgrößen werden durch die Korrelationsmatrix vollständig beschrieben:
 Korrelationsmatrix Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit N Dimensionen bietet sich zweckmäßiger Weise
Korrelationsmatrix Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit N Dimensionen bietet sich zweckmäßiger Weise
