Ein Karussell mit chaotischen Möglichkeiten
|
|
|
- Justus Kästner
- vor 6 Jahren
- Abrufe
Transkript
1 Praxis der Naturwissenschaften- Physik 36/8 (1987) Ein Karussell mit chaotischen Möglichkeiten Von U. Backhaus und H. J. Schlichting 1 Was ist Chaos? Der Erfolg der klassischen Physik liegt vor allem darin begründet, daß sie die zukünftige Entwicklung eines Systems, dessen Anfangsbedingungen und Dynamik (Bewegungsgleichung) bekannt sind, voraussagen kann. Dies gilt insbesondere für die Bestimmung zukünftiger Planetenbewegungen, Mondfinsternisse und ähnlicher Phänomene. Möchte man jedoch das Verhalten von Gasmolekülen oder von turbulenten Flüssigkeitsströmen vorhersagen, so kommt man über Wahrscheinlichkeitsaussagen nicht hinaus, obwohl auch dort die physikalischen Gesetze gelten. Bis vor nicht allzu langer Zeit war man überzeugt, daß unser unvollständiges Wissen über derart komplexe Systeme die Ursache dafür sei und eine immer genauere Voraussagbarkeit mit Hilfe wachsender Datenmengen und mit Computern möglich sei. Diese Überzeugung wurde inzwischen stark erschüttert. Man hat nämlich entdeckt, daß selbst einfache deterministische Systeme sich zufällig verhalten können. Diese Zufälligkeit ist in einer Weise fundamental, daß sie auch durch noch so umfangreiche Informationen nicht beseitigt werden kann. Man spricht daher von chaotischem Verhalten oder kurz von Chaos. Wie kommt es dazu, daß manche Systeme sich ordentlich oder regulär, andere aber chaotisch oder unvorhersehbar verhalten? Lange Zeit herrschte die Meinung vor [1], chaotisches Verhalten sei vor allem durch die Komplexität des Systems bedingt. Selbst als Lorenz im Jahre 1963 ein dreidimensionales Modellsystem mit chaotischem Verhalten vorstellte [2], um meteorologische Erscheinungen zu erklären, dauerte es noch fast ein Jahrzehnt, bis sich auch in der physikalischen Fachwelt die Einsicht durchzusetzen begann: Auch einfache Systeme können sich chaotisch verhalten. Jetzt erinnerte man sich wieder an eine längst vergessene Arbeit von Poincaré, der bereits 1892 beim Studium des 3- Körperproblems entdeckte, daß selbst die so stabil erscheinende Himmelsmechanik Probleme heraufbeschwört, die wir heute als chaotisch bezeichnen würden [3]. Er gab auch schon den Hinweis auf eine mögliche Erklärung: Eine kleine Ursache, die unserer Aufmerksamkeit entgeht, ruft eine beträchtliche Wirkung hervor, die wir nicht übersehen können" [4]. Man denke etwa an die labile Gleichgewichtslage eines auf dem Kopf stehenden Pendels. Kleinste Einflüsse, die wir nicht im Griff haben, können zu völlig verschiedenen Wirkungen führen, nämlich das Pendel nach links oder rechts kippen zu lassen. Während ein einfaches Pendel jedoch nur eine derart sensible Stelle besitzt, ist ein chaotisches Abb. 1 Ein "Billardspiel" (aus [5]) System an jedem Punkt seiner Bewegung so sensibel: Jeder noch so kleine Einfluß verändert das System in unvorhersehbarer Weise. Das kann man sich im Anschluß an Sexl an einer Art Billiardspiel klarmachen [5]. Man verlangt, daß der Ball in Abb. 1 nacheinander die festgehaltenen Bälle 1, 2... n treffen soll. Eine kleine Rechnung zeigt dann, daß bei Vernachlässigung der Reibung bereits die 9te Reflexion indeterministisch ist, wenn man nur die prinzipiell vorhandene Unschärfe aufgrund des Planckschen Wirkungsquantums zugrundelegt. Wegen der gekrümmten Oberfläche der zusammenstoßenden Kugeln wächst nämlich die Unschärfe exponentiell an und läßt den Reflexionswinkel nach dem 9ten Stoß beliebig groß werden. Nichtchaotische Systeme unterscheiden sich so gesehen nur dadurch von chaotischen, daß ein prinzipiell vorhandener Fehler langsamer wächst und daher innerhalb menschlicher Beobachtungszeiten nicht virulent wird. Oder aber die Dämpfung des Systems ist so groß, daß die Veränderungen bereits zum Erliegen gekommen sind, bevor ein größerer Fehler bemerkt werden kann. Die Beschränkung auf solche nichtchaotischen Systeme hat es erlaubt, so lange die Fiktion vom Determinismus in der Physik aufrechtzuerhalten, obwohl sie in der Realität kaum vorkommen. Trotzdem beruht unser physikalisches Verständnis von der Natur weitgehend auf ihnen. Die daraus resultie- 1
2 renden Defizite der physikalischen Weltbeschreibung machen sich aber allenthalben bemerkbar. Chaotische Systeme sind demnach solche Systeme, in denen wegen des exponentiellen Anwachsen des Fehlers bereits innerhalb kürzester Zeiträume jede Voraussage bedeutungslos wird. Vor diesem Hintergrund erscheint die von Poincaré in Frage gestellte Stabilität unseres Planetensystems in einem, anderen Licht. Max Born schlägt in diesem Zusammenhang vor, die Zeitskalen in der Astronomie und in der Atomphysik zu vergleichen: Das Alter der Welt wird auf einige 10 9 Jahre, d. h. Perioden des Erdumlaufs, geschätzt. Die Zahl der Perioden im Grundzustande des Wasserstoffatoms aber ist von der Größenordnung pro Sekunde. Gemessen in den jeweilig natürlichen Einheiten der Zeit, ist also die Sachlage gerade umgekehrt wie die naive Meinung: Die Sternenwelt ist kurzlebig, die Atomwelt äußerst langlebig. Ist es nicht gewagt, aus Erfahrungen in der kurzlebigen Welt Schlüsse zu ziehen, die auch für die langlebige gelten sollen?" [61 E- benso umwälzend wie die Erkenntnis, daß deterministische Systeme chaotisch werden können, ist die Art und Weise eines solchen Übergangs. Es zeigt sich nämlich, das der Weg ins Chaos sehr regelmäßig sein kann. Das System kündigt gewissermaßen den bevorstehenden Zusammenbruch deterministischen Verhaltens an. Es versteht sich von selbst, daß dies von außerordentlichem praktischen Interesse ist: Beispielsweise interessiert man sich in der Medizin dafür, inwieweit sich lebensbedrohende chaotische Herzrhythmen im EKG in einem erkennbaren, also regelmäßigen Muster ankündigen [7]. Mit einem solchen regelmäßigen Weg ins Chaos wollen wir uns im folgenden befassen: Unser Chaospendel durchläuft nämlich eine Sequenz von Frequenzverdopplungen, die schließlich im Chaos endet. Dieses sog. Feigenbaumszenario beobachtet man auch in ganz anderen Systemen, so daß man daraus wie auch aus anderen ähnlich regelmäßigen Szenarien den weitreichenden Schluß ziehen darf: Das Chaos ist in vielen Fällen in universeller Weise organisiert. Ordnung und Chaos scheinen stärker ineinander verwoben zu sein, als man es dem üblichen Verständnis nach anzunehmen geneigt ist. Damit wird - was bislang für ausgeschlossen gehalten wurde - das Chaos wenigstens in einem eingeschränkten Sinne der physikalischen Untersuchung zugänglich. 2 Behandlung des Chaos im Unterricht Unter obiger Perspektive kann das unvorhersagbare, chaotische Geschehen als das Normale angesehen werden, durch das das Vorhersagbare, Geordnete als vorübergehende Erscheinung hervor und schließlich auch wieder zum Verschwinden gebracht wird. Der die Ordnung bedrohende Aspekt des Chaos bedingt das Interesse, herauszufinden, - wie sich Chaos ankündigt, bzw. wie weit ein physikalisches System vom Chaos entfernt ist und - wie weit Chaos mit physikalischen Mitteln erfaßbar ist. Auf den ersten Blick erscheint es hoffnungslos, chaotische Erscheinungen in der Schule zu behandeln. Es zeigt sich jedoch, daß ein kompliziertes Systemverhalten wie Chaos nicht notwendig an komplexe Systeme gebunden ist (siehe oben), sondern als Konsequenz nichtlinearer Wechselwirkungen einfacher Systeme auftreten kann. Auf diese Weise lassen sich die wesentlichen Merkmale chaotischen Verhaltens an einfachen mechanischen Modellsystemen erarbeiten und auf einem angemessenen Niveau beschreiben. Das Pohlsche Rad und gekoppelte Pendel sind beliebte Beispiele für eine Einführung ins Chaos (siehe z. B. [8]). Eine ähnliche Möglichkeit der Komplexitätsreduktion ohne wesentliche Einbußen besteht übrigens auch für die in Vielteilchensystemen auftretenden Phasenübergänge. Sie lassen sich ebenfalls anhand einfacher nichtlinearer mechanischer Systeme diskutieren und für den Physikunterricht fruchtbar machen (siehe z. B. [9]). Daß darüber hinaus der Ü- bergang von Ordnung zu Chaos seinerseits eine A- nalogie zu Phasenübergängen zeigt, weist auf eine erst im Umrissen gesehene Universalität hin [10]. 3 Das Chaoskarussell Wir untersuchen im folgenden ein System, das im wesentlichen aus einem ebenen Pendel besteht, dessen Aufhängepunkt im Abstand r mit der Winkelgeschwindigkeit w um eine senkrechte Achse rotiert (Abb. 2). Man kann es sich als das Modell der Gondel eines Kettenkarussells vorstellen. Allerdings ist die Bewegung des Pendels durch Fixierung der Achse in der Aufhängung auf die Ebene beschränkt, die durch Rotationsachse und Ausleger aufgespannt wird. Im mitrotierenden Bezugssystem wirken längs der Bahn zwei Kräfte auf den Pendelkörper (Abb. 3): die Tangentialkomponenten der Schwerkraft F, und der Zentrifugalkraft F, Daraus ergibt sich leicht die Bewegungsgleichung: 2 l!! δ = gsinδ + ω r+ lsinδ cosδ ( )!! g r δ = ω sin 0 δ + ω ( α + sin δ) mit ω, 0 = α = l l Dieser entnimmt man durch die Multiplikation mit δ und einmalige Integration einen Ausdruck für ein sog. effektives Potential U. 2
3 ( sin ) 1 d d δ! + ω cos δ Ω ω α dt dt 2 δ sin δ oder ( 1 cos ) 2 U = ω0 δ ω ω0 α sin Ω + δ sin δ Ω = 2 ω0 = 0 und eine Bestimmungsgleichung für den Gleichgewichtswinkel δ 0 : ( ) sinδ =Ω α + sinδ cosδ und Ω 2, die wir an anderer Stelle [11] beschrieben haben. Um die Anzahl der freien Parameter klein zu halten, beschränken wir uns hier auf den Fall der Aufhängung in der Rotationsachse (α = 0), der sich auch leicht experimentell realisieren läßt (z. B. mit einem Metallbaukasten). In diesem Fall liegt die Gleichgewichtslage bei δ 0 = 0 0, solange die Winkelgeschwindigkeit klein ist. Erst ab einer Grenze (Ω 2 = 1) wächst sie schnell zu größeren Werten an. Dieses Verhalten zeigt sich deutlich in der Verformung des Potentials U (Abb. 4), das für Ω 2 1 nur ein Minimum bei δ = 0 0 hat, aus dem dann zwei symmetrisch liegende Minima herauswachsen. Wird das Pendel also bei genügend schneller Umdrehung des Karussells (Ω 2 > 1) einmal angestoßen, so schwingt es unsymmetrisch um eine dieser Gleichgewichtslagen herum, bzw. bei genügender Anfangsauslenkung um beide. Um realistischer zu sein, berücksichtigen wir die Reibung in der Aufhängung des Pendels. Um trotz dem stationäre Schwingungen erwarten zu können, muß dann zusätzlich ein Antrieb eingebaut werden, den wir der Einfachheit halber als harmonisch ansetzen. Damit nimmt die zu untersuchende Bewegungsgleichung folgende Gestalt an: Abb. 3 Zur Ableitung der Bewegungsgleichung!! δ = ρδ! ω sin sin cos f sin 0 δ +Ω ω0 δ δ + ω a t Wir integrieren diese explizit zeitabhängige Bewegungsgleichung, indem wir sie in ein System dreier Differentialgleichungen erster Ordnung umformen: Abb. 2 Das Chaoskarussell a Prinzipskizze, b Experimentelle Realisation zur Untersuchung der Gleichgewichtslage: mit dem kleinen Motor kann während der Drehung die Länge des Auslegers variiert werden. Die Gleichgewichtslage zeigt eine phasenübergangsartige Abhängigkeit von den Parametern α x : = δ x! = y y : = δ! y! = ρy ω sin x +Ω ω sin xcos x + f sin z z : = ω t z! = ω a a Wir lösen dieses System mit dem Runge-Kutta- Verfahren 4. Ordnung. Dabei hat sich in den meis- 3
4 ten Fällen eine Integrationsschrittweite von 50 Schritt pro Anregungsperiode als ausreichend erwiesen. Die in den weiteren Abschnitten beschriebenen Ergebnisse haben wir mit folgenden mehr oder weniger zufällig ausgewählten Parametern erhalten: ω0 = 1 s, ω = 1s. 1 1 a Die Behandlung des Problems wurde auf einem ATARI 520 ST+ in Pascal programmiert. Die Diagramme wurden als Hardcopies des Bildschirms erhalten. Beziehungen zu beschreiben und zu untersuchen [12]. Lenkt man beispielsweise bei unserem Chaoskarussell eine Gondel aus, so kommt sie nach einer gewissen Zeit wieder in ihrer jeweiligen Gleichgewichtslage zur Ruhe. Die Bahn im Phasenraum zieht sich auf einen Punkt zusammen (Abb. 5). Dieser Fixpunkt ist der Attraktor. Hält man die Gondel durch einen (z. B. harmonischen) Antrieb in Schwingung, so beobachtet man ein anderes Grenzverhalten. Die Phasenraumbahn läuft nach einer gewissen Einschwingzeit in sich selbst zurück. Der 4 Das Konzept des Attraktors Im Mittelpunkt der folgenden Überlegungen steht Abb. 5 Punktattraktor: Ohne Antrieb kommt das Pendel bei der Gleichgewichtslage zur Ruhe: Die Bahnkurve im Phasenraum wird vom Punkt (δ = 66.4 / <δ - 0) "angezogen 4 Abb. 4 Das effektive Potential des armlosen Pendels (α = 0) als Funktion des Auslenkungswinkels δ für verschiedene Winkelgeschwindigkeiten das oben beschriebene Chaoskarussell. Es handelt sich thermodynamisch gesehen um ein einfaches dissipatives System (siehe unten). Die dem System per Antrieb zugeführte Energie wird im zeitlichen Mittel als Wärme wieder an die Umgebung abgegeben. Zwar ist chaotisches ebenso wie reguläres Verhalten nicht an dissipative Systeme gebunden. Diese sind aber insofern von besonderer Bedeutung, als alle realen Systeme als dissipativ anzusehen sind. Für dissipative Systeme ist das Konzept des Attraktors fundamental. Der Attraktor ist anschaulich gesprochen etwas, das das Systemverhalten im Laufe der Zeit zustrebt, bzw. das Systemverhalten "anzieht" Es ist zwar im abstrakten Orts- Geschwindigkeitsraum (Phasenraum) definiert, erlaubt aber letztlich, Chaos mit Hilfe geometrischer Attraktor ist nunmehr ein sogenannter Grenzzyklus (Abb. 6 rechts). (Ein Grenzzyklus ist übrigens charakteristisch für das reguläre Endverhalten sich selbst organisierender dissipativer Systeme [131). Abb. 6 Grenzzyklus: Solange die Anregungsamplitude f nicht zu groß ist (f < 0.745), schwingt das Pendel nach kurzer Einschwingzeit mit konstanter Amplitude unsymmetrisch um eine der beiden Gleichgewichtslagen: Das Systemverhalten wird von einem der beiden Grenzzyklen angezogen 4
5 Abb. 7 Chaotischer Attraktor: Übersteigt die Anregungsamplitude f einen gewissen Grenzwert (f 0.783), dann antwortet das Pendel mit ständig wechselnden Amplituden. Für geringfügig unterschiedliche Anfangszustände (a. und c. δ 0 = 0, b. und d. δ 0 = 1 ) ist das Grenzverhalten im Großen identisch (a. und b.). Die Details sind jedoch völlig verschieden (c. und d. zeigen den Bereich 90 δ 100 ). Die Bilder zeigen die Reaktion des Pendels auf die ersten 300 Anregungsperioden. Das Karussell besitzt noch weitere Grenzzyklen. Geht man nämlich von anderen Anfangsbedingungen aus, so gelangt man gegebenenfalls zu einem ganz anderen Grenzzyklus (Abb. 6 links). Die Anfangsbedingungen (Punktmengen im Phasenraum), die sich zu einem bestimmten Attraktor entwickeln, nennt man den Einzugsbereich oder das Bassin des Attraktors. Neben Punkt- und Grenzzykel- gibt es bei mehrdimensionalen Systemen den Torus-Attraktor, bei dem sich die Bahnkurve um einen Torus herumwindet. Er kommt durch eine Überlagerung mehrerer unabhängiger Schwingungen zustande. Bis zur Entdeckung des ersten chaotischen Attraktors durch Lorenz im Jahre 1963 [21 war der Torus in höherdimensionalen Räumen das Komplizierteste, das man kannte. Der chaotische Attraktor reflektiert das chaotische Systemverhalten auf geometrischer Ebene: Dem exponentiellen Anwachsen von Unschärfen entspricht eine exponentiell wachsende Auseinanderentwicklung ursprünglich benachbarter Bahnen. Dieser Attraktor wird auch seltsamer Attraktor genannt. Seine Seltsamkeit kommt darin zum Ausdruck, daß er global eine stabile, lokal a- ber eine instabile Struktur besitzt. Betrachtet man beispielsweise für einen gegebenen Satz von Anfangsbedingungen im chaotischen Bereich, die in einem Parameter geringfügig voneinander abweichen die zugehörigen (chaotischen) Attraktoren, so sind sie in der äußeren Form kaum zu unterscheiden (Abb. 7a u. b). Betrachtet man jedoch die Vergrößerung eines lokalen Ausschnitts, so stellt man einen großen Unterschied in den Bildern fest (Abb. 7c u. d). Das bedeutet, daß sich die von nahezu gleichen Anfangsbedingungen ausgehenden (sozusagen benachbarten) Bahnkurven bald beliebig weit voneinander entfernt haben und völlig verschiedene Spuren ziehen. Das Seltsame des chaotischen Attraktors rührt schließlich auch noch daher, daß er zwar wie ein Grenzzyklus das "stationäre" Endverhalten des Systems charakterisiert, dabei jedoch die Bahnkurve niemals in sich selbst zurückläuft. 5
6 5 Simulationen Im folgenden soll anhand einiger typischer Darstellungen für ausgewählte Parameterbereiche das chaotische Systemverhalten und vor allem der Ü- bergang vom regulären zum chaotischen Verhalten demonstriert werden. Die Zahl der Parameter bietet dazu eine Vielzahl von Möglichkeiten. Wir mußten daher eine Auswahl treffen. Dazu bot sich die Anregungsamplitude f als in der Praxis am leichtesten zu variierende Größe an. Um zu zeigen, daß auch aufgrund der Variation anderer Parameter Übergänge vom regulären zum chaotischen Verhalten induziert werden können, haben wir darüber hinaus den Dämpfungsparameter ρ variiert. Alle anderen Parameterwerte wurden festgehalten. Abb. 8 Empfindlichkeit des Pendels im chaotischen Bereich gegen winzige Störungen: Ein kleiner Unterschied in den Anfangsbedingungen (a. und c. δ 0 = 0, b. und d. δ 0 = 0.01 ) macht sich in den ersten 10 Perioden (a. und b.) nicht bemerkbar, führt aber bereits nach 40 Perioden (c. und d.) zu völlig verschiedenem Systemverhalten Abb.. 9 Übergang des Pendels ins Chaos bei wachsender Anregungsamplitude f, dargestellt als a Ort-Zeit-Diagramm, b kleine Anzahl der "Meßwerte" (100 Perioden) zurückzuführen) f = 0,7 6
7 Abb. 10 Übergang des Pendels ins Chaos bei wachsender Anregungsamplitude f, dargestellt als a Ort-Zeit-Diagramm, b kleine Anzahl der "Meßwerte" (100 Perioden) zurückzuführen) f = Abb. 11 Übergang des Pendels ins Chaos bei wachsender Anregungsamplitude f, dargestellt als a Ort-Zeit-Diagramm, b kleine Anzahl der "Meßwerte" (100 Perioden) zurückzuführen) f Abb. 12 Übergang des Pendels ins Chaos bei wachsender Anregungsamplitude f, dargestellt als a Ort-Zeit-Diagramm, b kleine Anzahl der "Meßwerte" (100 Perioden) zurückzuführen) f = Einschwingverhalten Wie man es von erzwungenen Schwingungen kennt, muß eine gewisse Einschwingzeit abgewartet werden, um zum stationären Endverhalten des Systems zu gelangen. Da das Einschwingverhalten La. irregulär ist, kann es vom chaotischen Endverhalten nur schwer unterschieden werden. Deshalb muß im letzteren Fall hinreichend lange gewartet werden, um sicher sein zu können, daß das System nicht doch noch regulär wird. 5.2 Exponentielles Wachstum von Fehlern Während für den regulären Schwingungsbereich geringfügige Unterschiede in den Anfangsbedingungen das Einschwingverhalten ebenfalls nur geringfügig beeinflussen und im stationären Endverhalten sogar vollständig aufgehoben sind (die Anfangsbedingungen werden vergessen), schaukeln sie sich im chaotischen Bereich sehr schnell so weit auf, daß ein völlig andersartiges Verhalten resultiert. Letzeres entnimmt man der Abb.8. Die Anfangsauslenkung unterscheidet sich in beiden Fällen um 1/100 Grad. Zwar ist in den ersten zehn Schwingungen von diesem Unterschied noch nichts zu merken (Abb. 8a u. b). Jedoch sind bereits die Schwingungen 40 bis 50 völlig verschieden voneinander (Abb. 8c u. d). 5.3 Darstellungsarten In den Abb.9 bis 14 wird reguläres und chaotisches Endverhalten des Chaospendels auf drei verschiedene Weisen dargestellt. Die Vorteile der einen Darstellungsart vor der anderen erweisen sich vor allem bei der Untersuchung der Übergänge ins Chaos (siehe unten), wo es häufig schwierig ist, 7
8 verbleibende Regelmäßigkeiten zu erkennen. Im vorliegenden Fall ist die Sachlage eindeutig: Das reguläre Endverhalten, wie es sich insbesondere in dem einfachen Grenzzyklus und dem deutlichen Peak im Frequenzspektrum manifestiert, beinhaltet ein Höchstmaß an Ordnung (Abb. 9b und c). Dem chaotischen Attraktor und dem unregelmäßigen Frequenzspektrum hingegen ist kaum Ordnung mehr anzusehen (Abb. 14b und c). sich bei f = 0,7718 erneut aufspalten und zu einer weiteren Frequenzverdopplung, insgesamt also zu einer Frequenzvervierfachung, Anlaß geben (Abb. 11a). Der zugehörige Attraktor hat dementsprechend vier Umlaufbahnen (Abb. 11b) und das Frequenzspektrum vier Peaks (Abb. 11c). Die Verdopplung wiederholt sich bei weiterer Vergrößerung von f in immer kürzer werdenden Abständen, so daß es schwierig wird, sie weiter zu verfolgen. Abb. 13 Übergang des Pendels ins Chaos bei wachsender Anregungsamplitude f, dargestellt als a Ort-Zeit-Diagramm, b kleine Anzahl der Meßwerte (100 Perioden) zurückzuführen) f = (Hier zeigt c. statt des Fourierspektrums eine Vergrößerung des Attraktors im Bereich -7 δ 0 ) Abb. 14 Übergang des Pendels ins Chaos bei wachsender Anregungsamplitude f, dargestellt als a Ort-Zeit-Diagramm, b kleine Anzahl der Meßwerte (100 Perioden) zurückzuführen) 5.4 Verdopplungssequenzen Bei niedrigen Anregungsamplituden f zeigt das Chaoskarussell für die vorliegende Parameterfestlegung stets ein reguläres Endverhalten. Vergrößert man f über den Wert von hinaus, so beobachtet man, daß sich im Orts-Zeit-Diagramm plötzlich zwei verschiedene Amplituden abwechseln. Der stationäre Endzustand ist nunmehr durch zwei Frequenzen gekennzeichnet. Man spricht von Frequenzverdopplung. Das System pendelt gewissermaßen zwischen zwei Endzuständen hin und her (Abb. 10a). Dem entspricht im Phasenraum eine einfache Aufspaltung des Grenzzyklus (Abb. 10b). Im Frequenzspektrum tritt neben der Anregungsfrequenz ω a die halbe Anregungsfrequenz auf (Abb. 10c). Bei weiterer Vergrößerung von f wachsen die beiden Amplituden immer weiter auseinander bis sie Sie endet schließlich im Chaos, dem im Phasenraum ein chaotischer Attraktor entspricht (Abb. 14). In den Abb. 12 und 13 sind noch die 8- und 16-fache Aufspaltung dargestellt. Eine Ausschnittsvergrößerung zeigt, daß die Attraktoren der vorangegangenen Verdopplungssequenzen noch als Überstruktur zu erkennen sind (Abb. 13c). Darin deutet sich bereits die sogenannte fraktale Struktur [14] des im Grenzfall einer unendlich fortgesetzten Verdopplungssequenz entstehenden chaotischen Attraktors an: Jede Ausschnittsvergrößerung zeigt wieder dieselbe Verdopplungsstruktur (Selbstähnlichkeit). 5.5 Feigenbaumszenario Einen Überblick über die gesamte Verdopplungssequenz erhält man, wenn man die Schwingungsminima im stationären Endverhalten gegen den variierten Parameter f aufträgt (Abb. 15). Das so er- 8
9 zeugte sogenannte Feigenbaumdiagramm ist weit über das hier betrachtete spezielle System hinaus von universeller Bedeutung. Wie Feigenbaum zeigen konnte, ist es typisch für den "geordneten" Ü- bergang ins Chaos bei einer ganzen Klasse unterschiedlicher chaotischer Systeme [15]. Ob man nun die logistische Gleichung betrachtet, die das Wachstum von Lebewesenpopulationen beschreibt [16], oder eine Bewegungsgleichung, die die Dynamik eines Prellballs [17], eines chaotischen Schwingkreises [18] oder unseres Chaoskarussells beinhaltet, immer erhält man für geeignet gewählte Parameter den obigen Feigenbaum. Dabei stimmen die Feigenbäume nicht nur qualitativ überein. Die Verhältnisse der Abstände zwischen Abb. 15 Der Übergang ins Chaos als Feigenbaum-Diagramm: Die Anregungsamplitude wurde von f = 0.74 bis f = in etwa 550 Schritten vergrößert. Für jeden Wert von f wurden nach 50 Einschwingperioden die Schwingungsminima von 100 weiteren Perioden markiert. Für die Ausschnittsvergrößerung im Bereich f wurden jeweils nach 200 Einschwingperioden die Minima von weiteren 200 Perioden berechnet. Die Rechenzeit betrug trotz des schnellen Prozessors jeweils mehr als zwei Tage aufeinanderfolgenden Verzweigungspunkten streben stets dem selben Grenzwert, der universellen Konstante ( λn+ 1 λn) ( λ λ ) δ = lim = 4, n n+ 2 n+ 1 zu. Da diese Folge sehr schnell konvergiert, können wir bereits aufgrund der von uns ausgemessenen Verzweigungen das δ zu 4,23, also mit 9 % Genauigkeit bestimmen, indem wir λ durch f ersetzen, wobei n die Verzweigungen durchzählt. Auch die Verhältnisse der Stärke der Aufspaltungen (in unserem Fall die Differenz zwischen den Amplituden bei der jeweils nächsten Aufspaltung) streben einer universellen Konstante α = 2, zu, die wir durch unsere Ergebnisse ebenfalls bereits aufgrund der ersten vier Bifurkationen zu 2.59, also mit 3 % Genauigkeit reproduzieren können. Einen gleichen Feigenbaum erhalten wir bei Variation der Dämpfungskonstante ρ. Allerdings erscheint er umgekehrt: Die Verzweigungssequenz tritt mit abnehmendem ρ auf. Mit dem hier beschriebenen chaotischen Verhalten haben wir nur einen kleinen Ausschnitt aus der Fülle der Möglichkeiten erfaßt. Er entspricht im Bilde des Potentials (Abb. 4) der Beschränkung der Schwingung auf eine Potentialmulde, wobei die Minima der Schwingung in der Gegend des relativen Maximums bei 0 0 auftreten, das die beiden Mulden voneinander trennt. Bei weiterer Vergrößerung des Anregungsparameters f schwappt die Schwingung bis in die jeweils andere Mulde hinein (Abb. 16). In der Folge tritt nach einem breiten chaotischen Band plötzlich in einem weiten Bereich ein reguläres Übergangsverhalten in Form eines 3er Zyklus auf. Diesem 3er Zyklus schließen sich weitere chaotische und reguläre Bereiche an, bis sich schließlich Chaos allmählich wieder auf sehr geordnete Weise über einen inversen Feigenbaum zu einem völlig regulären Verhalten zurückentwickelt. Dies entspricht wiederum im Bilde des Potentials (Abb. 4) einer Schwingung über beide Mulden hinweg derart, daß das Pendel vom dazwischenliegenden relativen Maximum gleichsam nichts mehr "merkt". Gelangt das Pendel schließlich bei weiterer Vergrößerung von f in den Bereich des Überschlags, dann ist erneut ein Übergang zu chaotischem Verhalten zu beobachten. 5.6 Ordnung im Chaos Aber nicht nur der Weg ins Chaos erfolgt auf geordnete Weise. Das Chaos selbst besitzt darüber hinaus eine Struktur wie man Abb. 15 entnimmt. Zum einen scheinen sich die Verzweigungsäste im chaotischen Bereich fortzusetzen. Dem chaotischen Rauschen ist eine entsprechende Überstruktur aufgeprägt. Zum anderen gibt es im chaotischen Bereich Fenster, in denen nur die Fortsetzungen der Verzweigungsäste auftreten. Dementsprechend be- 9
10 obachtet man in diesen Bereichen wieder entsprechende Zyklen, wie beispielsweise den im Bereich f = 0,7938 auftretenden 5er Zyklus. Jeder der fünf Zweige ist übrigens wieder Ausgangspunkt für einen neuen Feigenbaum, wie die Ausschnittsvergrößerung in Abb. 15 auf eindrucksvolle Weise zeigt. Dieser Tochterfeigenbaum stimmt mit dem Mutterfeigenbaum bis ins kleinste Detail überein, insbesondere darin, daß er wiederum ein Fenster mit fünf Abb. 16 Obersicht über das Verhalten des Pendels in einem großen Parameterbereich. Der in Abb. 15 sichtbare Ausschnitt ist umrahmt. Zweigen besitzt, die ihrerseits Ausgangspunkt von Enkelfeigenbäumen sind usw. ad infinitum. Diese an die Ineinanderschachtelung russischer Puppen erinnernde Selbstähnlichkeit bringt die bereits oben erwähnte fraktale Struktur der chaotischen Attraktionen auch auf der Ebene der Feigenbaumdarstellung zum Ausdruck [14]. Literatur [1] L.D. Landau, E.M. Lifschitz: Hydrodynamik. Berlin: Akademie-Verlag 1970 [2] E. N. Lorenz: Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130 (1963) [3] J. Moser: Is the solar system stable? Math. Intelligencer 1,65 (1978) [4] H. Poincaré: Les methodes nouvelles de la mechanique celeste. Paris: Gauthier-Villars 1892 [5] R. Sexl: Irreversible Prozesse. Physik und Didaktik 8/1, 1 (1980) [6] M. Born: Ist die klassische Physik tatsächlich deterministisch? Phys. Bl. 11, 49 (1955) [7] L. Glass, A. Shrier, J. Betair: Chaotic cardiac rhythms. In: A. V. Holden (Ed.): Chaos. Manchester: UP 1986 [8] K. Luchner R. Worg: Chaotische Schwingungen. PdN-Ph. 35/4, 9 (1986) [9] R Rodewald, H. J Schlichting: Prinzipien der Synergetik erarbeitet an Spielzeugen. PdN-Ph. 35/4, 33 (1986). B. Rodewald, H. J Schlichting: Ein Spielzeug zur Veranschaulichung von Katastrophen in Ökosystemen. NiU-P/C, 8, 294 (1984). Ders.: A catastrophic toy. Am. J. Phys. 53/12 (1985). H. J Schlichting, B. Rodewald: Zum kritischen Verhalten eines invertierten Pendels. Physik und Didaktik 1511 (1987) [10] R. Lipowsky: Die Renormierung in der statistischen Physik. Phys. Bl. 39/12, 387 (1983) [11] P Farwig, U. Backhaus: Mathematisches Pendel und Kettenkarussell. In: A. Scharmann (Hrsg.): Vorträge auf der Frühjahrstagung der DPG, Gießen 1983, S. 61. U. Backhaus: Phasenübergänge 1. und 2. Ordnung an einem einfachen mechanischen System. In: W. Kuhn (Hrsg.): Vorträge Physikertagung Gießen 1986, S. 189 [12] R. H. Abraham und C. D. Shaw nutzten solche geometrischen Darstellungen aus, um chaotisches Verhalten zu veranschaulichen. In: Dynamics - The geometry of behavior, part 2: Chaotic Behavior. Santa Cruz: University of California 1984 [13] H. J Schlichting, B. Rodewald: Physikalische Phänomene am Dampf-Jet-Boot. Erscheint in PdN-Ph. [14] siehe z. B. H. 0. Peitgen, P H. Richter: Fraktale und die Theorie der Phasenübergänge. Phys. Bl. 42/1, 9 (1986) [15] M. Feigenbaum: Universal Behavior in Nonlinear Systems. Los Alamos Science 1, 4 (1981) [16] D. R. Hofstadter: Seltsame Attraktoren in der Grauzone zwischen Ordnung und Chaos. Spektrum der Wiss. 1, 7 (1982) [17] N. B. Tufillaro, A. M. Albano: Chaotic dynamics of a bouncing ball. Am. J. Phys.-4/10, 993 (1986) [18] W. Lauterborn, W. Meyer-Ilse: Chaos. Physik in unserer Zeit 17/6, 177 (1986). Weitere allgemeinverständliche deutschsprachige Einführungen: [19] U. Deker, H. Thomas: Die Chaos Theorie. Bild der Wissenschaft 1, 62 (1983) [20] J P Crutchfield, J D. Farmer N. H. Packard, R. S. Shaw: Chaos. Spektrum der Wissenschaften 2, 78 (1987) [21] R. Graham: Ein Stück unberechenbarer Natur: Die Turbulenz. Bild der Wissenschaft 4, 68 (1982) 10
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Jan Henrik Sylvester. 10. Februar 2003
 Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Chaos im getriebenen nicht-linearen Pendel
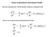 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Die Darstellung nichtlinearer Bewegungsabläufe
 Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Auf der Suche nach Ordnung im Chaos. von
 Auf der Suche nach Ordnung im Chaos von Dr. Udo Backhaus und Prof. Dr. H. Joachim Schlichting (aus: MNU 43/8, 456 466 (199)) Der Zugang zur Chaosphysik wird vor allem durch die Vielzahl neuer und auf den
Auf der Suche nach Ordnung im Chaos von Dr. Udo Backhaus und Prof. Dr. H. Joachim Schlichting (aus: MNU 43/8, 456 466 (199)) Der Zugang zur Chaosphysik wird vor allem durch die Vielzahl neuer und auf den
Untersuchungen am magnetischen Doppelpendel - Spaceball
 Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
Lyapunov-Exponenten. Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems:
 Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Chaotische Systeme. ViLab. Marian Panten
 Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
SINIS Simulation nichtlinearer Systeme
 In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
2. Physikalisches Pendel
 2. Physikalisches Pendel Ein physikalisches Pendel besteht aus einem starren Körper, der um eine Achse drehbar gelagert ist. A L S φ S z G Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.2-1 2.1 Bewegungsgleichung
2. Physikalisches Pendel Ein physikalisches Pendel besteht aus einem starren Körper, der um eine Achse drehbar gelagert ist. A L S φ S z G Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.2-1 2.1 Bewegungsgleichung
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Lösung der harmonischen Oszillator-Gleichung
 Lösung der harmonischen Oszillator-Gleichung Lucas Kunz 8. Dezember 016 Inhaltsverzeichnis 1 Physikalische Herleitung 1.1 Gravitation................................... 1. Reibung.....................................
Lösung der harmonischen Oszillator-Gleichung Lucas Kunz 8. Dezember 016 Inhaltsverzeichnis 1 Physikalische Herleitung 1.1 Gravitation................................... 1. Reibung.....................................
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Feigenbaum, Chaos und die RG
 Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Erzwungene Schwingungen
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Diskrete Populationsmodelle für Einzelspezies
 Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
zum Thema Lissajous-Figuren
 Ratsgymnasium Rotenburg Gerberstraße 14 27356 Rotenburg Wümme Facharbeit im Leistungskurs Physik zum Thema Lissajous-Figuren Verfasser: Christoph Siemsen Fachlehrer: Herr Konrad Abgabetermin: 24.05.04
Ratsgymnasium Rotenburg Gerberstraße 14 27356 Rotenburg Wümme Facharbeit im Leistungskurs Physik zum Thema Lissajous-Figuren Verfasser: Christoph Siemsen Fachlehrer: Herr Konrad Abgabetermin: 24.05.04
Hamilton-Systeme. J. Struckmeier
 Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Gewöhnliche Differentialgleichungen: Einleitung
 Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
F R. = Dx. M a = Dx. Ungedämpfte freie Schwingungen Beispiel Federpendel (a) in Ruhe (b) gespannt: Auslenkung x Rückstellkraft der Feder
 6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
2.9 Gedämpfter Harmonischer Oszillator
 72 KAPITEL 2. DYNAMIK EINES MASSENPUNKTES 2.9 Gedämpfter Harmonischer Oszillator In diesem Abschnitt wollen wir die Bewegung eines Massenpunktes betrachten, der sich in einer Raumrichtung x in einer Harmonischen
72 KAPITEL 2. DYNAMIK EINES MASSENPUNKTES 2.9 Gedämpfter Harmonischer Oszillator In diesem Abschnitt wollen wir die Bewegung eines Massenpunktes betrachten, der sich in einer Raumrichtung x in einer Harmonischen
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Chaos am invertierten Pendel
 Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
Synchronisation in Natur und Technik
 Am Beispiel des Kuramoto-Modells Jan Baumbach Christoph Schöler Christian Barthel 2 Inhalt 1. Einleitung 2. Kuramoto-Modell 3. Simulation und Ergebnisse 3 Die Motivation Das Phänomen Synchronisation tritt
Am Beispiel des Kuramoto-Modells Jan Baumbach Christoph Schöler Christian Barthel 2 Inhalt 1. Einleitung 2. Kuramoto-Modell 3. Simulation und Ergebnisse 3 Die Motivation Das Phänomen Synchronisation tritt
2.4 Stoßprozesse. entweder nicht interessiert o- der keine Möglichkeit hat, sie zu untersuchen oder zu beeinflussen.
 - 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
- 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Dynamik hüpfender Bälle
 1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen.
 10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
M13. Gekoppeltes Pendel
 M3 Gekoppeltes Pendel In diesem Versuch werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken werden die Schwingungsdauern
M3 Gekoppeltes Pendel In diesem Versuch werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken werden die Schwingungsdauern
Wie lang ist die Küste Großbritanniens?
 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Auswertung P1-22 Schwingungen & Resonanz
 Auswertung P- Schwingungen & Resonanz Michael Prim & Tobias Volkenandt 4. November 5 Aufgabe Drehpendel/Pohlsches Rad und freie Schwingungen Mit dem Messwerterfassungssystem CASSY nahmen wir die Auslenkung
Auswertung P- Schwingungen & Resonanz Michael Prim & Tobias Volkenandt 4. November 5 Aufgabe Drehpendel/Pohlsches Rad und freie Schwingungen Mit dem Messwerterfassungssystem CASSY nahmen wir die Auslenkung
11.4. Lineare Differentialgleichungen höherer Ordnung
 4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
Übungen zu Lagrange-Formalismus und kleinen Schwingungen
 Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
8. Periodische Bewegungen
 8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
5.3 Drehimpuls und Drehmoment im Experiment
 5.3. DREHIMPULS UND DREHMOMENT IM EXPERIMENT 197 5.3 Drehimpuls und Drehmoment im Experiment Wir besprechen nun einige Experimente zum Thema Drehimpuls und Drehmoment. Wir betrachten ein System von N Massenpunkten,
5.3. DREHIMPULS UND DREHMOMENT IM EXPERIMENT 197 5.3 Drehimpuls und Drehmoment im Experiment Wir besprechen nun einige Experimente zum Thema Drehimpuls und Drehmoment. Wir betrachten ein System von N Massenpunkten,
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
5. Kritische Drehzahl
 Aufgabenstellung: 5. Kritische Drehzahl y y Ω c/4 c/4 m c/4 e z O O S c/4 x Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.5-1 Der starre Körper mit der Masse m dreht sich mit der konstanten Winkelgeschwindigkeit
Aufgabenstellung: 5. Kritische Drehzahl y y Ω c/4 c/4 m c/4 e z O O S c/4 x Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.5-1 Der starre Körper mit der Masse m dreht sich mit der konstanten Winkelgeschwindigkeit
X.4 Elektromagnetische Wellen im Vakuum
 X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N
 Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Schwingwagen ******
 5.3.0 ****** Motivation Ein kleiner Wagen und zwei Stahlfedern bilden ein schwingungsfähiges System. Ein Elektromotor mit Exzenter lenkt diesen Wagen periodisch aus seiner Ruhestellung aus. Die Antriebsfrequenz
5.3.0 ****** Motivation Ein kleiner Wagen und zwei Stahlfedern bilden ein schwingungsfähiges System. Ein Elektromotor mit Exzenter lenkt diesen Wagen periodisch aus seiner Ruhestellung aus. Die Antriebsfrequenz
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
 3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
7.4 Gekoppelte Schwingungen
 7.4. GEKOPPELTE SCHWINGUNGEN 333 7.4 Gekoppelte Schwingungen Als Beispiel für 2 gekoppelte Schwingungen betrachten wir das Doppelpendel, das in Abb. 7.19 dargestellt ist. Zunächst vernachlässigen wir die
7.4. GEKOPPELTE SCHWINGUNGEN 333 7.4 Gekoppelte Schwingungen Als Beispiel für 2 gekoppelte Schwingungen betrachten wir das Doppelpendel, das in Abb. 7.19 dargestellt ist. Zunächst vernachlässigen wir die
5. Mechanische Schwingungen und Wellen. 5.1 Mechanische Schwingungen
 5. Mechanische Schwingungen und Wellen Der Themenbereich mechanische Schwingungen und Wellen ist ein Teilbereich der klassischen Mechanik, der sich mit den physikalischen Eigenschaften von Wellen und den
5. Mechanische Schwingungen und Wellen Der Themenbereich mechanische Schwingungen und Wellen ist ein Teilbereich der klassischen Mechanik, der sich mit den physikalischen Eigenschaften von Wellen und den
Stabile periodische Bewegungen (Grenzzyklen)
 Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
2. Anfangswertprobleme 2. Ordnung
 2. Anfangswertprobleme 2. Ordnung 2.1 Grundlagen 2.2 Mathematisches Pendel 2.3 Selbstzentrierung Prof. Dr. Wandinger 7. Numerische Methoden Dynamik 2 7.2-1 2.1 Grundlagen Für ein Anfangswertproblem 2.
2. Anfangswertprobleme 2. Ordnung 2.1 Grundlagen 2.2 Mathematisches Pendel 2.3 Selbstzentrierung Prof. Dr. Wandinger 7. Numerische Methoden Dynamik 2 7.2-1 2.1 Grundlagen Für ein Anfangswertproblem 2.
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
1.2 Schwingungen von gekoppelten Pendeln
 0 1. Schwingungen von gekoppelten Pendeln Aufgaben In diesem Experiment werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken
0 1. Schwingungen von gekoppelten Pendeln Aufgaben In diesem Experiment werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken
4.5 Gekoppelte LC-Schwingkreise
 4.5. GEKOPPELTE LC-SCHWINGKEISE 27 4.5 Gekoppelte LC-Schwingkreise 4.5. Versuchsbeschreibung Ein elektrischer Schwingkreis kann induktiv mit einem zweiten erregten Schwingkreis 2 koppeln. Der Kreis wird
4.5. GEKOPPELTE LC-SCHWINGKEISE 27 4.5 Gekoppelte LC-Schwingkreise 4.5. Versuchsbeschreibung Ein elektrischer Schwingkreis kann induktiv mit einem zweiten erregten Schwingkreis 2 koppeln. Der Kreis wird
1. Bestimmen Sie die Phasengeschwindigkeit von Ultraschallwellen in Wasser durch Messung der Wellenlänge und Frequenz stehender Wellen.
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 10/015 M Schallwellen Am Beispiel von Ultraschallwellen in Wasser werden Eigenschaften von Longitudinalwellen betrachtet. Im ersten
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 10/015 M Schallwellen Am Beispiel von Ultraschallwellen in Wasser werden Eigenschaften von Longitudinalwellen betrachtet. Im ersten
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze
 Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
120 Gekoppelte Pendel
 120 Gekoppelte Pendel 1. Aufgaben 1.1 Messen Sie die Schwingungsdauer zweier gekoppelter Pendel bei gleichsinniger und gegensinniger Schwingung. 1.2 Messen Sie die Schwingungs- und Schwebungsdauer bei
120 Gekoppelte Pendel 1. Aufgaben 1.1 Messen Sie die Schwingungsdauer zweier gekoppelter Pendel bei gleichsinniger und gegensinniger Schwingung. 1.2 Messen Sie die Schwingungs- und Schwebungsdauer bei
1. Vorwort zum Versuch Ziel des Versuchs Aufgabenstellung Aufgaben zur Vorbereitung Versuchsdurchführung...
 Albert-Ludwigs-Universität Freiburg Fakultät für Physik Fortgeschrittenenpraktikum I FP I Deterministisches Chaos Inhalt A. Versuchsanleitung: Seite 1. Vorwort zum Versuch... 2 2. Ziel des Versuchs...
Albert-Ludwigs-Universität Freiburg Fakultät für Physik Fortgeschrittenenpraktikum I FP I Deterministisches Chaos Inhalt A. Versuchsanleitung: Seite 1. Vorwort zum Versuch... 2 2. Ziel des Versuchs...
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: , Abgabe am )
 Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
 Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Zugänge zur nichtlinearen Dynamik. W. Oehme, Universität Leipzig
 Zugänge zur nichtlinearen Dynamik W. Oehme, Universität Leipzig einfache physikalische Experimente Wirtschaft Wetter historische Bezüge Nichtlineare Dynamik Chaos und Ordnung Verkehrsstau Populationsdynamik
Zugänge zur nichtlinearen Dynamik W. Oehme, Universität Leipzig einfache physikalische Experimente Wirtschaft Wetter historische Bezüge Nichtlineare Dynamik Chaos und Ordnung Verkehrsstau Populationsdynamik
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
M 10 Resonanz und Phasenverschiebung bei der mechanischen Schwingung
 Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum M 1 esonanz und Phasenverschiebung bei der mechanischen Schwingung Aufgaben 1. Bestimmen Sie die Frequenz der freien gedämpften Schwingung
Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum M 1 esonanz und Phasenverschiebung bei der mechanischen Schwingung Aufgaben 1. Bestimmen Sie die Frequenz der freien gedämpften Schwingung
9. Vorlesung Wintersemester
 9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
Bifurkationstheorie. 1. Verzweigungen stationärer Zustände
 Bifurkationstheorie 1. Verzweigungen stationärer Zustände Die Lage, Anzahl und Stabilität der stationären Zustände von nichtlinearen Systemen hängt in der Regel noch von bestimmten Systemparametern ab.
Bifurkationstheorie 1. Verzweigungen stationärer Zustände Die Lage, Anzahl und Stabilität der stationären Zustände von nichtlinearen Systemen hängt in der Regel noch von bestimmten Systemparametern ab.
Theoretische Biophysik - Statistische Physik
 Theoretische Biophysik - Statistische Physik 10. Vorlesung Pawel Romanczuk Wintersemester 2018 http://lab.romanczuk.de/teaching/ 1 Brownsche Bewegung Zusammenfassung letzte VL Formulierung über Newtonsche
Theoretische Biophysik - Statistische Physik 10. Vorlesung Pawel Romanczuk Wintersemester 2018 http://lab.romanczuk.de/teaching/ 1 Brownsche Bewegung Zusammenfassung letzte VL Formulierung über Newtonsche
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Gewöhnliche Differentialgleichungen. Teil II: Lineare DGLs mit konstanten Koeffizienten
 - 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
- 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
1 Die logistische Gleichung X t+1 = λx t (1 X t )
 1 Die logistische Gleichung X t+1 = X t (1 X t ) Bisher haben wir Rekursionen mit mehr oder weniger einfachem Verhalten betrachtet; wir konnten entweder eine explizite Lösungsformel aufstellen oder ohne
1 Die logistische Gleichung X t+1 = X t (1 X t ) Bisher haben wir Rekursionen mit mehr oder weniger einfachem Verhalten betrachtet; wir konnten entweder eine explizite Lösungsformel aufstellen oder ohne
Kapitel 7. Differenzengleichungen
 apitel 7 Differenzengleichungen I n h a ltsverze ichnis DIFFERENZENGLEICHUNGEN... 3 EINFÜHRUNG UND BEISPIELE... 3 DIFFERENZENGLEICHUNG 1. ORDNUNG... 3 ELEMENTARE DIFFERENTIALGLEICHUNGEN... 4 GEWÖHNLICHE
apitel 7 Differenzengleichungen I n h a ltsverze ichnis DIFFERENZENGLEICHUNGEN... 3 EINFÜHRUNG UND BEISPIELE... 3 DIFFERENZENGLEICHUNG 1. ORDNUNG... 3 ELEMENTARE DIFFERENTIALGLEICHUNGEN... 4 GEWÖHNLICHE
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 8 1 d Alembertsches Prinzip und Lagrangegleichungen 1. Art Teil II 2 Das d Alembertsche Prinzip für N-Teilchensysteme
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 8 1 d Alembertsches Prinzip und Lagrangegleichungen 1. Art Teil II 2 Das d Alembertsche Prinzip für N-Teilchensysteme
M1 Maxwellsches Rad. 1. Grundlagen
 M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
 Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 008 Theoretische Mechanik 4. Übung Lösungen 4. Spezielle Kraftgesetze Lösen Sie die
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 008 Theoretische Mechanik 4. Übung Lösungen 4. Spezielle Kraftgesetze Lösen Sie die
Modellbildung und Simulation, Kap (S ) 10 Zwei-Spezies-Modelle
 Erratum zu Modellbildung und Simulation, Kap. 1.3 (S. 256 261) 1 Zwei-Spezies-Modelle Interessanter als einzelne Populationen sind Modelle mit mehreren Arten, die miteinander in Wechselwirkung stehen,
Erratum zu Modellbildung und Simulation, Kap. 1.3 (S. 256 261) 1 Zwei-Spezies-Modelle Interessanter als einzelne Populationen sind Modelle mit mehreren Arten, die miteinander in Wechselwirkung stehen,
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester Physik-Institut der Universität Zürich
 Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
 Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
P1-12,22 AUSWERTUNG VERSUCH RESONANZ
 P1-12,22 AUSWERTUNG VERSUCH RESONANZ GRUPPE 19 - SASKIA MEIßNER, ARNOLD SEILER 0.1. Drehpendel - Harmonischer Oszillator. Bei dem Drehpendel handelt es sich um einen harmonischen Oszillator. Das Trägheitsmoment,
P1-12,22 AUSWERTUNG VERSUCH RESONANZ GRUPPE 19 - SASKIA MEIßNER, ARNOLD SEILER 0.1. Drehpendel - Harmonischer Oszillator. Bei dem Drehpendel handelt es sich um einen harmonischen Oszillator. Das Trägheitsmoment,
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
Physik LK 11, 3. Klausur Schwingungen und Wellen Lösung
 Die Rechnungen bitte vollständig angeben und die Einheiten mitrechnen. Antwortsätze schreiben. Die Reibung ist bei allen Aufgaben zu vernachlässigen, wenn nicht explizit anders verlangt. Besondere Näherungen
Die Rechnungen bitte vollständig angeben und die Einheiten mitrechnen. Antwortsätze schreiben. Die Reibung ist bei allen Aufgaben zu vernachlässigen, wenn nicht explizit anders verlangt. Besondere Näherungen
Schwingungen. Harmonische Schwingungen. t Anharmonische Schwingungen. S. Alexandrova FDIBA TU Sofia 1
 Schwingungen Harmonische Schwingungen x t Anharmonische Schwingungen x x t S. Alexandrova FDIBA TU Sofia 1 t ANHARMONISCHE SCHWINGUNGEN EHB : Kraft F = -k(x-x o ) Potentielle Energie: E p E p Parabel mit
Schwingungen Harmonische Schwingungen x t Anharmonische Schwingungen x x t S. Alexandrova FDIBA TU Sofia 1 t ANHARMONISCHE SCHWINGUNGEN EHB : Kraft F = -k(x-x o ) Potentielle Energie: E p E p Parabel mit
6. Erzwungene Schwingungen
 6. Erzwungene Schwingungen Ein durch zeitveränderliche äußere Einwirkung zum Schwingen angeregtes (gezwungenes) System führt erzwungene Schwingungen durch. Bedeutsam sind vor allem periodische Erregungen
6. Erzwungene Schwingungen Ein durch zeitveränderliche äußere Einwirkung zum Schwingen angeregtes (gezwungenes) System führt erzwungene Schwingungen durch. Bedeutsam sind vor allem periodische Erregungen
Experimente, Ideen und Entwicklung der Chaostheorie
 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
Deterministisches Chaos
 Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Die Entwicklung des Erde-Mond-Systems
 THEORETISCHE AUFGABE Nr. 1 Die Entwicklung des Erde-Mond-Systems Wissenschaftler können den Abstand Erde-Mond mit großer Genauigkeit bestimmen. Sie erreichen dies, indem sie einen Laserstrahl an einem
THEORETISCHE AUFGABE Nr. 1 Die Entwicklung des Erde-Mond-Systems Wissenschaftler können den Abstand Erde-Mond mit großer Genauigkeit bestimmen. Sie erreichen dies, indem sie einen Laserstrahl an einem
Ferienkurs Experimentalphysik 1
 Ferienkurs Experimentalphysik 1 Julian Seyfried Wintersemester 2014/2015 1 Seite 2 Inhaltsverzeichnis 3 Energie, Arbeit und Leistung 3 3.1 Energie.................................. 3 3.2 Arbeit...................................
Ferienkurs Experimentalphysik 1 Julian Seyfried Wintersemester 2014/2015 1 Seite 2 Inhaltsverzeichnis 3 Energie, Arbeit und Leistung 3 3.1 Energie.................................. 3 3.2 Arbeit...................................
