Experimente, Ideen und Entwicklung der Chaostheorie
|
|
|
- Bettina Huber
- vor 7 Jahren
- Abrufe
Transkript
1 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück
2 Ursprünge der Chaostheorie Edward Lorenz ( ) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment x'= a (y - x) y'=x (b - z) - y z'=x y - c z PHYSIK AM SAMSTAG MÄRZ 2009
3 kausalität Eindeutige Beziehung von Ursache und Wirkung starke Kausalität schwache Kausalität U W U W ähnliche Ursachen ähnliche Wirkung ähnliche Ursachen sehr verschiedene Wirkung
4 kausalität Eindeutige Beziehung von Ursache und Wirkung starke Kausalität schwache Kausalität U W Grundlage der Erkenntnisgewinnung durch ähnliche Experimente Ursachen ähnliche Wirkung U W Determinismus bleibt erhalten! kein ähnliche völliges Ursachen Chaos sehr verschiedene Wirkung
5 Phasenraum / Trajektorie Phasenraum: Das Verhalten (Dynamik) eines physikalischen Systems wird durch zeitlich veränderliche Größen beschrieben. Der Phasenraum eines Systems besteht aus allen Punkten eines Satzes von Größen, der ausreicht, um das System zu beschreiben. Pendel: Winkel und seine Geschwindigkeit: φ(t) und ω(t) Trajektorie: Die Entwicklungslinie, die sich aus den im Laufe der Zeit angenommenen Werten der Phasenraumvariablen ergibt, nennt man Trajektorie.
6 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder.
7 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder. Mögliche Attraktoren: Grundregel: Trajektorien dürfen sich nicht schneiden!
8 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder. Mögliche Attraktoren: Fixpunkt (mind. 1-dim)
9 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder. Mögliche Attraktoren: Fixpunkt (mind. 1-dim) Grenzzyklus (mind. 2-dim)
10 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder. Mögliche Attraktoren: Fixpunkt (mind. 1-dim) Grenzzyklus (mind. 2-dim) Torus (mind. 3-dim)
11 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder. Mögliche Attraktoren: Fixpunkt (mind. 1-dim) Grenzzyklus (mind. 2-dim) Torus (mind. 3-dim)
12 Attraktor Ein Attraktor ist dasjenige Gebiet in einem Phasenraum, auf die sich die Trajektorien eines (dynamisches) Systems im Laufe der Zeit zubewegt. Ein Attraktor gibt das Langzeitverhalten des Systems wieder. Mögliche Attraktoren: Fixpunkt (mind. 1-dim) Grenzzyklus (mind. 2-dim) Torus (mind. 3-dim) seltsamer Attraktor (mind. 3-dim)
13 Wann ist chaotische Dynamik möglich??? schwache Kausalität auseindander laufende Trajektorien zurückfalten mindestens 3 Dimensionen & Streck-Falt-Mechanismus
14 Der Rössler - Attraktor Zusammengebautes Chaos Otto E. Rössler (geb. 1940) An Equation for Continuous Chaos (1976) inspiriert durch Betrachtung einer Knetmaschine Toffeemasse wird immer wieder gestreckt und gefaltet
15 Chaotische Pendel 1. Doppelpendel Idee: Phasenraum erweitern expansive Trajektorien durch wiederholte Annäherung an Instabilitätslage 4 Dimensionen (jedes Pendel 2)
16 Chaotische Pendel 2. Ebenes Federpendel Idee: Phasenraum erweitern Nichtlinearität in Rückstellkraft der Feder durch S. v. Pythagoras aufgrund senkrechter Koordinaten F = D! ( x 2 + y 2 - l)
17 Chaotische Pendel 2. Ebenes Federpendel Idee: Phasenraum erweitern Nichtlinearität in Rückstellkraft der Feder durch S. v. Pythagoras aufgrund senkrechter Koordinaten wieder 4 Dimensionen geht es auch mit 3?
18 Chaotische Pendel 3. Pohlsches Rad mit Zusatzmasse angetriebenes nichtlineares Drehpendel
19 Weitere Beispiel-Systeme mit Chaotischer Dynamik Karussellpendel, Federstabpendel, Magnetpendel Chaotischer Prellball tropfender Wasserhahn elektronische nichtlineare Oszillatoren Billardsysteme mit Rundungen Drei-(und mehr-)körperproblem (Astronomie)
20 Der Shinriki-Oszillator Selbstschwingender nichtlinearer Schwingkreis Frequenz: f 0 = 1 2 LC! 890Hz! PHYSIK AM SAMSTAG MÄRZ 2009
21 Shinriki - Ergebnisse Landkarte der verschiedenen Zustände
22 Shinriki - Ergebnisse Bifurkationsdiagramm
23 Magnetpendel Variante eines sphärischen Pendels Das Gewicht am Ende des leichten Stabes ist magnetisch. Auf dem Boden sind mehrere Magnete angebracht. Trajektorienverläufe: von oben betrachtet Farbe des einfangenden Magneten
24 Magnetpendel Attraktor-Einzugsbereiche - Bassins
25 Magnetpendel Attraktor-Einzugsbereiche - Bassins
26 Magnetpendel Attraktor-Einzugsbereiche - Bassins
27 Magnetpendel Attraktor-Einzugsbereiche - Bassins
28 Blick in die Forschung Anwendungen der nichtlinearen Dynamik in Physik komplexer Systeme, Astronomie, Chemie (Reaktionskinetik), Medizin (Herz, Gehirn, Epillepsie...), Geologie (Erdbebenvorhersage), Wirtschaftswissenschaften (Börsenkurse) Zeitserienanalyse Chaos- Kontrolle Grundsätzliche Fragestellungen
29 Beispiel aus Medizin - Herz Unteruchung an Langzeit-Elektrokardiogrammen (EKGs) PHYSIK AM SAMSTAG MÄRZ 2009 G.E. Morfill et al. (1994) MPI Garching
30 Erdbebendaten Manshour, Saberi, Muhammad Sahimi, Peinke, Amalio, Pacheco, and Tabar - PRL 102, (2009)
31 Erdbebendaten Manshour, Saberi, Muhammad Sahimi, Peinke, Amalio, Pacheco, and Tabar - PRL 102, (2009)
32 Zeitserienanalyse R. Friedrich, S. Siegert, J. Peinke, St. Lück, M. Siefert, M. Lindemann, J. Raethjen, G. Deuschl und G. Pfister - Physics Letters A, 271, (2000) PHYSIK AM SAMSTAG MÄRZ 2009
33 Chaos- Kontrolle normaler Regelkreis y soll! yist "y Regler Lineares System y ist Methode I (OGY) Methode II (Pyragas) xn+1 xn y(t!#)! y(t) "y(t) K F(t) Chaotisches System y(t) stabile Mannigfaltigkeit xfp!xfp xn+1" instabile Mannigfaltigkeit # Verzögerungsleitung PHYSIK AM SAMSTAG MÄRZ 2009
34 Chaos- Kontrolle normaler Regelkreis y soll! yist "y Regler Lineares System y ist F. Lange, T. Letz, K. Pyragas, A. Kittel - Stabilization of the output power of intracavity frequency-doubled lasers (2003) PHYSIK AM SAMSTAG MÄRZ 2009
35 Wo steht die nichtlineare Dynamik? «Bei der Chaosforschung handelt es sich lediglich um eine neue Betrachtung 'alter Hüte', die zwar viel Verwirrung produziert, aber nichts Neues hervor bringt.» «Die Entdeckung des deterministischen Chaos hat eine Revolution im wissenschaftlichen Denken geliefert, die in etwa mit der bei der Quantenmechanik vergleichbar ist.»
36 Wo steht die nichtlineare Dynamik? Einfache Systeme starke Kausalität (Linearisierung) periodische, wiederholbare Echt komplexe Systeme schwache Kausalität & hochdim. Turbulenz, stochastische Systeme PHYSIK AM SAMSTAG MÄRZ 2009
37 Wo steht die nichtlineare Dynamik? stark kausales / berechenbares Verhalten Ziel: komplexes Verhalten der Natur beschreiben
38 Das war s Vielen Dank für Ihre Aufmerksamkeit! Informationen und Materialien demnächst auf folgender Website: PHYSIK AM SAMSTAG MÄRZ 2009
Chaotische Systeme. ViLab. Marian Panten
Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Deterministisches Chaos
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Nichtlineare Dynamik Einführung
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Die Darstellung nichtlinearer Bewegungsabläufe
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Lyapunov-Exponenten. Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems:
Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Seltsame Attraktoren
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Erzwungene Schwingungen
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Prozessorientierte und embodimentorientierte Psychotherapieforschung (d)
Prozessorientierte und embodimentorientierte Psychotherapieforschung (d) Dynamische Invarianten, Attraktoren Wolfgang Tschacher, Vorlesung 2015 tschacher@spk.unibe.ch http://www.embodiment.ch/ dynamische
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
8. Deterministisches Chaos
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Zugänge zur nichtlinearen Dynamik. W. Oehme, Universität Leipzig
Zugänge zur nichtlinearen Dynamik W. Oehme, Universität Leipzig einfache physikalische Experimente Wirtschaft Wetter historische Bezüge Nichtlineare Dynamik Chaos und Ordnung Verkehrsstau Populationsdynamik
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Chaos im getriebenen nicht-linearen Pendel
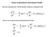Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos. Wintersemester 2018/ M. Zaks
Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos Wintersemester 2018/19 22.01.2019 M. Zaks hintergrund Kontext: Wettervorhersage. Entstehung von Luftbewegungen infolge der thermischen
Fraktale und Beispiele aus der Physik
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Ausarbeitung Pohlsches Rad / Chaos Autoren: Simone Lingitz, Sebastian Jakob
Ausarbeitung Pohlsches Rad / Chaos Autoren: Simone Lingitz, Sebastian Jakob 1. Vorarbeiten zu Hause 1.1 Erzwungene Schwingung einer Feder mit Dämpfung Bewegungsgleichung: m & x + b x& + k x m g = F cos(
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Nichtlinearität in der klassischen Physik
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Phasenraum. Zeitreihe. Phasenraum. Ort (x) Zeit. Geschwindigkeit (v)
Phasenraum Ort (x) Zeitreihe Zeit Geschwindigkeit (v) v Phasenraum x Phasenraum - geometrische Darstellung der Dynamik im kartesischen Raum - Repräsentation von parametrischen Systemzuständen zu festen
Stabile periodische Bewegungen (Grenzzyklen)
Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Chaos - Nichtlineare Dynamik
Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Kausalität: Verhältnis von Ursache und Wirkung
Kausalität: Verhältnis von Ursache und Wirkung Einleitung Wenn jemand einen Ball fallen lässt wisst ihr sicherlich jedesmal ungefähr, wohin der Ball fällt. Wisst ihr das auch, wenn ein Blatt Papier fallengelassen
1 Nicht-lineare dynamische Systeme
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Wie lang ist die Küste Großbritanniens?
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Seminar Fraktale. Kapitel 13 Dynamical Systems. Von Dirk Simon
Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
SINIS Simulation nichtlinearer Systeme
In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
Der Duffing-Oszillator
11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
nichtlineare dynamische Systeme
nichtlineare dynamische Systeme dynamische Systeme: - Systeme mit Krafteinwirkung (δυναµιο = Kraft) - zeitabhängige Systemzustände - Zustandsänderung abhängig vom momentanen Zustand deterministisch gleiche
Pendel. Versuch: P Vorbereitung - Inhaltsverzeichnis. Physikalisches Anfängerpraktikum 1 Wintersemester 2005/06 Julian Merkert ( )
Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 005/06 Julian Merkert (1999) Versuch: P1-0 Pendel - Vorbereitung - Vorbemerkung Das einfachste Modell, um einen Pendelversuch zu beschreiben,
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Chaos Oder Mandelbrot und Peitsche
Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Algorithmen für Chaos und Fraktale
Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Deterministisches Chaos
Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Hartes Chaos am Beispiel des anisotropen Keplerproblems
Hartes Chaos am Beispiel des anisotropen Keplerproblems M. C. Gutzwiller Mechanik Seminar WiSe 17/18 Robert Klassert Institut für Theoretische Physik, Universität Heidelberg Hartes Chaos am Beispiel des
Spezielle Kinetik MC 1.3. Prof. Dr. B. Dietzek. Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie. Wintersemester 2016/2017
Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
FC3 - Duffing Oszillator
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Physikalisches Anfaengerpraktikum. Pohlsches Rad
Physikalisches Anfaengerpraktikum Pohlsches Rad Ausarbeitung von Marcel Engelhardt & David Weisgerber (Gruppe 37) Mittwoch, 6. März 25 email: Marcel.Engelhardt@mytum.de Weisgerber@mytum.de ()Einführung
3 Zweidimensionale dynamische Systeme Oszillationen
3 Zweidimensionale dynamische Systeme Oszillationen Lineare Systeme Ein Beispiel für ein zweidimensionales dynamisches System ist die Gleichung ẍ + ω 2 sin x = 0 für ebene Schwingungen eines reibungsfreien
Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Big Data Science in und außerhalb der Physik
Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Ausarbeitung zum Vortrag im Rahmen des Hauptseminars Big Data Science in und außerhalb der Physik an der Fakultät für Physik am Karlsruher Institut
8. Periodische Bewegungen
8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
+ + Personalmanagement Stuff-Turnover. Simulation im Excel. Organizational Headcount. Turnover. Recruitment
Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
Probestudium der Physik 2011/12
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Neuronale Netzwerke: Feed-forward versus recurrent (d.h. feed-back )
Neuronale Netzwerke: Feed-forward versus recurrent (d.h. feed-back ) A: Schrittweise vorwärts-gerichtete Abbildung: Eingangssignal (Input) r in Ausgansgsignal (Output) r out Überwachtes Lernen (wie z.b.
Dynamik hüpfender Bälle
1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
Einführung in die Physik I. Schwingungen und Wellen 1
Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Zu einigen Grundlagen der Stabilitätstheorie dynamischer Systeme
Seminar Zu einigen Grundlagen der Stabilitätstheorie dynamischer Systeme 15.4.201 2 Inhaltsverzeichnis 1 Existenz und Eindeutigkeit 7 1.1 Lineare Systeme.................................... 7 1.2 Der Begriff
Nichtlineare Prozesse in der Elektrochemie II
Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Inhalt der Vorlesung A1
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
Zusatzmaterialien zu Übung 5 zur Vorlesung Informatik II für Verkehrsingenieurwesen: Systemeigenschaften und Gewichtsfunktion/folge
Fakultät Informatik Institut für Angewandte Informatik, Professur für Technische Informationssysteme Zusatzmaterialien zu Übung 5 zur Vorlesung Informatik II für Verkehrsingenieurwesen: Systemeigenschaften
Ein Idealer Generator - Variante
Ein Idealer Generator - Variante Dein Freund Luis möchte bei einem schulischen Wettbewerb mit folgender genialer antreten: Er hat einen Wechselspannungsgenerator entworfen, der, einmal angeworfen, für
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Nichtlineare Zeitreihenanalyse
Studentenseminar "Statistische Methoden in der Physik" 27 Gliederung 1 2 Kritik an Methoder der 3 Gliederung 1 2 Kritik an Methoder der 3 Charakterisierung (Deterministisches) dynamisches System gegeben
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Kapitel 5.5: Nichtlineare Rekursionen. Algorithmen und Datenstrukturen WS 2017/18. Pro f. Dr. Sán do r Fe k e te
Kapitel 5.5: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 e H! e t u 2 Ankreuzliste für Übungsgruppen 1 4 3 7 5 5 6 6 9 10 8 2 2 10 3 5.3.3 Master-Theorem:
2. Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
Poincaré-Schnitte. Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert
Poincaré-Schnitte Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert Themen 1. Was sind Poincaré-Schnitte?. Anwendung: Poincaré-Schnitte Mathematica-Beispiel: Attraktor
Feigenbaum, Chaos und die RG
Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
Fibonacci Zahlen: 3. Hamiltonsche Systeme. 3.1 Hamilton Dynamik. Teilverhältnis beim `goldenen Schnitt : definiert als. mit
Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Chaotische Systeme Der Weg ins Chaos Kontrollmethoden Probleme bei großen Systemen Zusammenfassung Quellen. Chaotische Systeme
Der Weg ins Chaos und zurück Otto-von-Guericke- Fakultät für Informatik Institut für Simulation und Grafik Das virtuelle Labor 20.12.2007 Wo treffen wir auf chaotische Systeme Herzschlag Populationsentwicklungen
Aufgabe 1: Laplace-Transformation
Aufgabe 1: Laplace-Transformation (15 Punkte) Ein technisches System sei gegeben durch folgende Differentialgleichung 3.Ordnung: y (t)+6ÿ(t)+12ẏ(t)+8y(t) =2ü(t)+1 u(t)+8u(t). Dieses System wird eingangsseitig
Das Hénon-Heiles Potential Beispiel für Weiches Chaos und die Anwendung des KAM-Theorems
Das Hénon-Heiles Potential Beispiel für Weiches Chaos und die Anwendung des KAM-Theorems Jonathan Wider 16.November 2018 Zusammenfassung Dieses Handout soll die wesentlichen Inhalte des am 16.11.2018 gehaltenen
x=r cos y=r sin } r2 =x 2 y 2
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
7.3 Anwendungsbeispiele aus Physik und Technik
262 7. Differenzialrechnung 7.3 7.3 Anwendungsbeispiele aus Physik und Technik 7.3.1 Kinematik Bewegungsabläufe lassen sich durch das Weg-Zeit-Gesetz s = s (t) beschreiben. Die Momentangeschwindigkeit
Die Chaostheorie und Fraktale in der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Chaos Seminar Wetter und Klima. Dominik Fröschl
Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Bedeutende Theorien des 20. Jahrhunderts
Bedeutende Theorien des 20. Jahrhunderts Ein Vorstoß zu den Grenzen von Berechenbarkeit und Erkenntnis Quantenmechanik - Relativitätstheorie - Gravitation - Kosmologie - Chaostheorie - Prädikatenlogik
Theoretische Physik 1
Florian Scheck Theoretische Physik 1 Mechanik Von den Newtonschen Gesetzen zum deterministischen Chaos Sechste Auflage mit 172 Abbildungen, 11 praktischen Übungen und 118 Aufgaben mit vollständigen Lösungen
2.7 Nichtlineare Dynamik Determinismus vs. Chaos. 2 Analytische Mechanik
Die Generatoren M i, i = x,y,z, bilden eine (Lie)- Algebra mit folgenden Eigenschaften Mi,M j M i M j M j M i = εijm k k k Wir können auch zeigen (Übung) dass ebenfalls Li,L j = ε k ij Ł k gilt. Wir überprüfen
Kapitel 5.6: Nichtlineare Rekursionen. Algorithmen und Datenstrukturen WS 2012/13. Prof. Dr. Sándor Fekete
Kapitel 5.6: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 5.4.3 Master-Theorem: Lineare Rekursionen 5.6 Nichtlineare Rekursionen 5.6.1 Logistische Rekursion
tun, sondern nur mit der Reaktion auf verschiedene Anfangswerte.
2.3 Stabilität Eine wichtige Rolle spielt das Stabilitätsverhalten dynamischer Systeme. Wie üblich sei Φ die Fundamentalmatrix des linearen Systems ẋ = A(t)x + u. Im weiteren sei t fixiert, später wird
PP Physikalisches Pendel
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Chaos am invertierten Pendel
Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
4.3 Schwingende Systeme
Dieter Suter - 217 - Physik B3 4.3 Schwingende Systeme Schwingungen erhält man immer dann, wenn die Kraft der Auslenkung entgegengerichtet ist. Ist sie außerdem proportional zur Kraft, so erhält man eine
GP Getriebenes Pendel
GP Getriebenes Pendel Blockpraktikum Frühjahr 7 (Gruppe ) 5. April 7 Inhaltsverzeichnis 1 Einführung Theoretische Grundlagen 3 Versuchsdurchführung 3 4 Messergebnisse und Auswertung 3 4.1 Abhängigkeit
Theoretische Physik 2 (Theoretische Mechanik)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Motivation. Motivation 2
Grenzzyklen 1 Motivation Grenzzyklen modellieren von selbst oszillierende Systeme Stabile Grenzzyklen kleine Abweichungen in den Anfangsbedingungen gehen in Grenzzyklus über Beispiele: Van-der-Pol Schwingkreis
Systemisches Schulmanagement Führungsherausforderung in komplexen dynamischen Systemen
Systemisches Schulmanagement Führungsherausforderung in komplexen dynamischen Systemen Workshop Dr. email@hanjahansen.ch www.hanjahansen.ch Systemisches Organisationsverständnis Organisationen sind soziale
2.2. Lineare Systeme. a) A ist diagonalisierbar, oder b) A ist nicht diagonalisierbar.
.. Lineare Systeme deta < 0 = 0 > 0 SpA Abbildung.9.: Gebiete mit unterschiedlicher Dynamik eines zweidimensionalen linearen dynamischen Systems entsprechend dem Vorzeichen der Diskriminante. a) A ist
Physik 1 für Chemiker und Biologen 11. Vorlesung
Physik 1 für Chemiker und Biologen 11. Vorlesung 22.01.2018 Wiederholungs-/Einstiegsfrage: Abstimmen unter pingo.upb.de, #282978 http://xkcd.com/1161/ Heute: - Wiederholung: Schwingungen - Resonanz - Wellen
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Systemanalyse und Modellbildung
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung
Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Schriftliche Prüfung aus Automatisierungstechnik 1 Vorlesung, am 03. Juli 017 Name: Vorname(n): Matr.Nr.: SKZ:
Untersuchungen am magnetischen Doppelpendel - Spaceball
Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik. SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am 8.7.211 Arbeitszeit: 12 min Name: Vorname(n): Matrikelnummer: Note: Aufgabe
Differentialgleichungen 2. Differentialgleichungen und Dynamische Systeme. Peter Szmolyan
Differentialgleichungen 2 Differentialgleichungen und Dynamische Systeme Peter Szmolyan Institut für Analysis und Scientific Computing TU-Wien 1 The theory of dynamical systems is one of the domains of
Flüsse, Fixpunkte, Stabilität
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Institut für Elektrotechnik und Informationstechnik. Aufgabensammlung zur. Regelungstechnik B. Prof. Dr. techn. F. Gausch Dipl.-Ing. C.
Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Regelungstechnik B Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski 10.03.2011 Übungsaufgaben zur Regelungstechnik B Aufgabe 0
durch Ratengleichungen der Form t t = F 2 N 1 t, N 2 t d N 1 t
5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
Psychopathologische Prozesse und psychologische Intervention (C)
Psychopathologische Prozesse und psychologische Intervention (C) Dynamische Invarianten, Attraktoren Prof. Dr. Wolfgang Tschacher Universität Bern 2 dynamische Invarianten in der Psychopathologie was ist
Harmonische Schwingungen
Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
Chaoskontrolle nach Pyragas: Delayed Feedback Control
Chaoskontrolle nach Pyragas: Delayed Feedback Control Diplomarbeit von Thomas Bernard Institut für Festkörperphysik TH Darmstadt September 1995 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 4 2