2.7 Nichtlineare Dynamik Determinismus vs. Chaos. 2 Analytische Mechanik
|
|
|
- Jonas Melsbach
- vor 6 Jahren
- Abrufe
Transkript
1 Die Generatoren M i, i = x,y,z, bilden eine (Lie)- Algebra mit folgenden Eigenschaften Mi,M j M i M j M j M i = εijm k k k Wir können auch zeigen (Übung) dass ebenfalls Li,L j = ε k ij Ł k gilt. Wir überprüfen diese an Hand von L x,l y L x = yp z zp y L y = zp x xp z Lx L y {L x,l y } = L x L y k=x,y,z x k p k p k x k = ( p y ( x) yp x )=L z exemplarisch nach. 2.7 Nichtlineare Dynamik Determinismus vs. Chaos Wenn wir die Bewewgungsgleichungen eines Systems kennen, können wir grundsätzlich voraussagen, wie es sich in Zukunft verhalten wird: das System ist deterministisch. Bei den meisten bisher diskutierten Systemen bedeutet dies auch, dass sich für zwei Anfangszustände, die sich nur wenig unterscheiden, das Verhalten in der Zukunft nicht wesentlich unterscheidet. Diese Beobachtung führt nicht nur in der Physik zu großen philosophischen Debatten. So schrieb z.b. Laplace 1814 in seinem Essai philosophique sur les probabilités: Nous devons envisager l état présent de l univers comme l effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d ailleurs elle était assez vaste pour soumettre ces données à l analyse, embrasserait dans la même formule les mouvements des plus grands corps de l univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l avenir, comme le passé, serait présent à ses yeux. Pierre- Simon Laplace, Essai philosophique sur les probabilités (1814). Vom physkalischen Standpunkt aus muss diese Aussage in 2 Punkten revidiert werden: Bei Systemen, die sich quantenmechanisch verhalten, erhält man aus der Lösung der Bewegungsgleichungen im Allgemeinen nur Aussagen über die Wahrscheinlichkeiten bei zukünftigen Messungen, also nur über die Statistik der Messungen, und keine Aussagen über den Ausgang von einzelnen Messungen. Dieser Punkt wird im vierten Semester, im Rahmen der Quantenmechanik, genauer diskutiert werden. Hier soll der zweite Punkte genauer betrachtet werden: Es gibt viele Systeme, bei denen fast identische Anfangsbedingungen völlig verschiedene Lösungen haben. Da man den Zustand eines Systems (also die Anfangsbedingung) immer nur mit endlicher Präzision kennt (u.a. auf Grund der quantenmechanischen Unschärfe), kann deshalb nur über einen beschränkten Zeitraum eine Voraussage gemacht werden. Das gleiche gilt für die Vergangenheit: Die Zahl der Anfangszustände, welche zum heute bekannten Zustand geführt haben können, ist sehr groß. Des gleichen können sehr kleine äußere Störungen sehr großen Einfluss haben. Solche Systeme werden häufig als chaotisch bezeichnet. Abb zeigt dies schematisch. Ein typisches Beispiel ist das Billardspiel: bei jedem Stoß führt die Abweichung vom zentralen Stoß zu einer Vergrößerung des Winkels und damit zu einer größeren Abweichung beim nächsten Stoß. Dies gilt allgemein für Stöße zwischen harten Kugeln, die auch als gutes Modell für die Dynamik von Molekülen verwendet werden können. 61
2 Endzustand 1 benachbarte Anfangsbedingungen Endzustand 2 Abbildung 2.27: Benachbarte Anfangsbedingungen können zu qualitativ unterschiedlichem Verhalten führen. Weitere Beispiele von Systemen, bei denen benachbarte Anfangsbedingungen zu sehr unterschiedlichem Verhalten führen, sind gekoppelte nichtlineare Oszillatoren, Doppelpendel, Federpendel oder Dreikörpersysteme. Dieses Verhalten ist im Allgemeinen nicht global, sondern es gilt nur für bestimmte Parameterbereiche und für bestimmte Bereiche von Anfangsbedingungen. Eines der einfachsten Beispiele ist das einer Kugel auf einem Sattelpunkt: je nach Anfangsbedingungen rollt sie auf die eine oder andere Seite hinunter oder bleibt dort liegen. Ein sehr wichtiges Beispiel ist auch die Dynamik des Sonnensystems: Die Keplerschen Gesetze legen es nahe, zu glauben, die Bahnen der Planeten um die Sonne seien stabil und leicht zu berechnen. Dies gilt allerdings nur in der einfachsten Näherung, bei der ein einzelner Planet in großem Abstand um die Sonne kreist. Berücksichtigt man die Wechselwirkung zwischen mehreren Himmelskörpern, so erhält man schnell chaotische Trajektorien: Einzelne Körper können aus dem Sonnensystem herausgeschleudert werden, wobei der Zeitpunkt praktisch nicht vorhergesagt werden kann. Wann chaotisches Verhalten auftritt ist im Allgemeinen nicht vorhersagbar. Es gibt jedoch Kriterien, die einem erlauben, vorherzusagen, dass chaotisches Verhalten nicht auftritt. Einige Beispiele sind Die Bewegungsgleichungen haben analytische Lösungen. Die Bewegungsgleichungen eines Systems sind nicht explizit zeitabhängig und bestehen aus einer einzigen Differentialgleichung (maximal) zweiter Ordnung. Die Lösung der Bewegungsgleichungen kann auf eindimensionale Integrale zurückgeführt werden. Wenn eine dieser Bedigungen erfüllt ist, so tritt kein chaotisches Verhalten auf. Ende des 19. Jahrhunderts gewann Henri Poincaré einen Preis mit dem Lösungsansatz für die Frage, ob das Sonnensystem stabil ist. Er konnte zeigen, dass dieses nicht der Fall ist und die Reihen zur Divergenz neigen, die durch interne Resonanzen bedingt sind. Manche Quellen geben dies als die Geburtsstunde der Chaosforschung an, es dauerte jedoch bis in die Mitte des 2.Jahrhunderts bis der Lösungsansatz von Poincaré mit Hilfe von Computern brauchbar umgesetzt werden konnte Superpositionsprinzip Bisher haben wir hauptsächlich lineare Bewegungsgleichungen betrachtet, also Gleichungen der Art ẋ = ax. Für die Lösungen solcher Gleichungen gilt allgemein das Superpositionsprinzip: Sind x 1 (t) und x 2 (t) Lösungen der Bewegungsgleichung, so ist auch die Linearkombination c 1 x 1 (t)+c 2 x 2 (t) (mit beliebigen Koeffizienten c 1,c 2 ) eine Lösung. Der Beweis erfolgt einfach durch Einsetzen. Das einfachste Beispiel ist der harmonische Oszillator: Hier kann man z.b. beliebige Lösungen als Linearkombination von x 1 (t)=cos(ωt) und x 2 (t)=sin(ωt) darstellen. Offensichtlich ist in einem solchen System die Vorhersagbarkeit sehr gut; benachbarte Anfangsbedingungen bleiben auch in der weiteren Zeitentwicklung benachbart. Das Superpositionsprinzip ist auch sehr wichtig in der Quantenmechanik, da dort die relevante Bewegungsgleichung (die Schrödingergleichung) linear ist. 62
3 Das Superpositionsprinzip gilt nicht mehr wenn die Bewegungsgleichungen nichtlinear werden. Ein wichtiges Beispiel hatten wir in Kapitel gesehen: Dort veränderte sich die Frequenz mit der Amplitude, d.h. sie war abhängig von den Anfangsbedingungen. Wir betrachten hier einen ähnlichen Fall. α π Mathematisches Pendel Während man beim physikalischen Pendel ( harmonischer Oszillator) annimmt, dass die Periode unabhängig von der Auslenkung ist, findet man in Wirklichkeit, dass die Periode mit der Auslenkung zunimmt. Abbildung 2.28: Exp. 1 Ebenes Pendel. Berechnung der Periode : siehe Übungen 2 Abbildung 2.3: Phasenraumtrajektorien für das mathematische Pendel. Abbildung 2.3 zeigt die Bewegung des mathematischen Pendels im Phasenraum: die geschlossenen Kurven stellen die eigentliche Pendelbewegung dar. Bei geringer Amplitude sind es Ellipsen, sie sich bei zunehmender Amplitude antlang der horizontalen (α ) Achse verlängern und bei α = π Spitzen bilden. Bei den horizontal verlaufenden Kurven ist die Geschwindigkeit groß genug, dass das Pendel rotiert, also die Bewegungsrichtung konstant ist. Zwischen den beiden Bereichen verläuft die Separatrix. Befindet sich das System auf dieser Kurve, so ist es nicht stabil. Immer wenn es den Punkt α = π erreicht, also senkrecht nach oben steht, gibt es zwei mögliche Richtung, in die es sich weiter bewegen kann. Die Annäherung an diesen kritischen Punkt benötigt jedoch unendlich lange, da α geht. Periode T / T /2 Amplitude Abbildung 2.29: Periodendauer des mathematischen Pendels als Funktion der Amplitude in Einheiten der Periode des physikalischen Pendels, T = 2π /g. Die Periodendauer geht gegen undendlich wenn Fixpunkte und Trajektorien Wenn wir ein System mit n Freiheitsgraden mit Hilfe von n Bewegungsgleichungen zweiter Ordnung diskutieren, ist es natürlich, die Lösung in einem n-dimensionalen Raum zu betrachten. Wie wir oben gesehen haben, ist es aber auch nützlich, die n Bewegungsgleichungen zweiter Ordnung in 2n Bewegungsgleichungen erster Ordnung umzuwandeln. Dann ist es auch sinnvoll, die Lösungen als Funktion dieser 2n Parameter (also z.b. n Ortskoordinaten und n Impulse) zu diskutieren. Ein Vorteil dieser Phasenraum-Darstellung ist z.b. dass zu jedem Punkt auch die Ableitung, also die Bewegungsrichtung vorgegeben ist. 63
4 Für einen Freiheitsgrad, also eine Ortskoordinate und zugehörigen Impuls, ergibt eine Differentialgleichung erster Ordnung, ẋ = ax + b. eine Gerade. Das System bewegt sich auf dieser Gerade immer in einer Richtung (Determinismus). Ist die Steigung a =, so schneidet die Gerade die x- Achse. Abbildung 2.32: Harmonischer Oszillator im Phasenraum. Fixpunkt Abbildung 2.31: Fixpunkt in einem linearen System erster Ordnung. An dieser Stelle ist die Geschwindigkeit ẋ =, d.h. das System kommt zur Ruhe. Es handelt sich somit um einen Fixpunkt. Die Nullstelle x = b/a ist stabil, wenn die Steigung a < : Für Werte x < x ist dann ẋ >, d.h. das System bewegt sich nach rechts, nähert sich also der Nullstelle. Für x > x ist ẋ <, d.h. das System bewegt sich nach links, nähert sich ebenfalls der Nullstelle. In der Abbildung ist eine instabile Situation dargestellt (a > ): Am Punkt x + δx hat die Ableitung ẋ(x + δx)=aδx das gleiche Vorzeichen wie δx. Somit wächst die Abweichung. Sind die Bewegungsgleichungen nicht linear, so sind die Trajektorien keine Geraden mehr. Im Falle des harmonischen Oszillators, z.b., sind die Trajektorien geschlossen, x ẋ = a cos(ωt + ϕ) Ω a sin(ωtϕ). Dies entspricht einer Ellipse. Unterschiedliche Anfangsbedingungen führen zu unterschiedlichen Ellipsen. So lange das System deterministisch bleibt, können sich die unterschiedlichen Trajektorien nicht schneiden: an einem gegebenen Punkt im Phasenraum ist die zeitliche Entwicklung bestimmt und damit die Richtung, in die sich das System weiter bewegt. Dies gilt allerdings nur, solange wir den vollständigen Phasenraum betrachten. Besitzt das System mehr Freiheitsgrade als der Unterraum, den wir betrachten, in den wir somit projizieren, können Überschneidungen auftreten Duffing Oszillator Als nächstes betrachten wir einen harmonischen Oszillator, bei dem wir zusätzlich zum quadratischen Potenzial einen Term vierter Ordnung berücksichtigen: mẍ +Cẋ + Dx + Ex 3 = F cosωt. Dieses System wird als Duffing Oszillator bezeichnet. Der Term Cẋ beschreibt eine Dämpfung, die rechte Seite eine periodische externe Kraft. Das System liefert Beispiele für reguläre, wie auch chaotische Dynamik. Für dieses System existiert keine allgemeine analytische Lösung, lediglich verschiedene Näherungsmethoden. Über eine Fourier-Reihe kann man die Bewegungsgleichung beliebig genau annähern. Für kleine Werte von E kann man das System als gestörten harmonischen Oszillator behandeln. 64
5 Die Frobenius-Methode liefert eine komplizierte aber brauchbare Lösung. Numerische Methoden. Für den Spezialfall der verschwindenden Dämpfung (C ) und verschwindender externer Kraft (F ) erhält man eine Lösung mit Hilfe elliptischer Funktionen. Wir betrachten zunächst das System ohne Dämpfung: mẍ + Dx + Ex 3 = F cosωt. Für bestimmte Werte der Parameter und Anfangsbedingungen erhält man wie beim harmonischen Oszillator eine stationäre Lösung. Ein Näherung dafür erhalten wir z.b., mit dem Ansatz x(t)=x 1 cos(ωt). Einsetzen ergibt mx 1 Ω 2 + Dx 1 + Ex 3 1 = F, wobei wir Terme höherer Ordnung, wie z.b. x 3 1 cos3 (Ωt) nicht berücksichtigt haben. In dieser Näherung gibt es drei stationäre Lösungen mit β + 27E 2 F 1/3 x 1,1 = 32 1/3 21/3 D mω 2 E (β + 27E 2 F ) 1/3 1 i 3 β + 27E 2 1/3 F x 1,2 = 62 1/3 E 1 + i 3 D mω /3 (β + 27E 2 F ) 1/3 1 + i 3 β + 27E 2 1/3 F x 1,3 = 62 1/3 E 1 i 3 D mω /3 (β + 27E 2 F ) 1/3 β = 729E 4 F E3 (D mω 2 ) 3. Diese fallen zusammen oberhab einer kritischen Frequenz ω k = 1 D /3 m 4 3 EF2. Für Ω < ω k existieren 3 Äste, sofern D > 9 2 1/3 4 3 EF2. Amplitude x Frequenz Abbildung 2.33: Stationäre Amplituden des Duffing-Oszillators für die Parameter F =.1,E = 1 3,m = 1,D = 1. Eine genauere Betrachtung zeigt, dass die beiden Lösungen x 1,2 und x 1,3 nicht stabil sind: Es handelt sich um instabile Fixpunkte. Für Amplituden oberhalb dieser Werte läuft das System auseinander, d.h. das Potenzial nimmt ab Spezialfälle Freier Oszillator ohne Dämpfung Wir betrachten den Fall ohne Dämpfung und ohne äußere Kraft mẍ + Dx + Ex 3 =. Wir können das auch schreiben als ẍ + ω 2 x + 2βx 3 =, d.h. als gestörten harmonischen Oszillator mit D ω = m 2β = E m. Multiplikation mit ẋ gibt ẍẋ + ω 2 xẋ + 2βx 3 ẋ =. Dies können wir schreiben als d 1 2ẋ2 + 1 dt 2 ω2 x βx4 =. 65
6 Somit ist die Größe h = ẋ 2 + ω 2 x 2 + βx 4 eine Erhaltungsgröße. Doppelminimumpotenzial Eine andere interessante Situation erhalten wir, wenn wir D < und E > wählen: der quadratische Term ist abstoßend, der Term vierter Ordnung anziehend. Abbildung 2.35: Doppelminimum Potenzial in Abhängigkeit von der Stärke D des quadratischen Terms. Im Ursprung ist D =, hinten >, vorne < Abbildung 2.34: Doppelminimum Potenzial für D = 1, E = 1. Das resultierede System besitzt am Ursprung ein Maximum und bei D x = ± 2E zwei Minima Zeitabhängigkeit Wir schreiben diese Bewegungsgleichung dritter Ordnung als ein System von Differentialgleichungen erster Ordnung indem wir als Variablen den Ort x, den Impuls p = mẋ und eine modifizierte Zeit τ = Ωt verwenden: x Diese Gleichungen können z.b. numerisch integriert werden. In Abb sind Trajektorien dargestellt, welche zu unterschiedlichen Afangsbedingungen gehören: bei niedriger Amplitude und Geschwindigkeit schwingt es um eines der beiden Minima. Bei hoher Anfangsgeschwindigkeit oder Auslenkung oszilliert das System über beide Minima. Dazwischen liegt die Separatrix, welche durch den Ursprung des Phasenraums bei x =,ẋ = läuft. Abbildung 2.37 zeigt ein Beispiel für den allgemeinen Fall. Das System beginnt mit der Amplitude x() =25. Damit schwingt es über dem Zwischenmaximum. Mit abnehmender Amplitude (auf Grund der Dämpfung) erreicht es den kritischen Punkt, an dem es dieses Maximum nicht mehr überqueren kann. Je nach Anfangsbedinungungen landet es im linken oder rechten Minimum. Dies ist ein sehr einfaches Modell für spontane Symmetriebrechnung : Damit bezeichnet man z.b. das spontane Auftreten eines magnetischen Momentes, wenn ein Ferromagnet beim Durchqueren der Curie-Temperatur magnetisch wird. ẋ = p m ṗ = C m p Dx Ex3 + F cosτ τ = Ω. (2.42) Übergang zum Chaos Der Duffing Oszillator kann auch in einem Parameterbereich betrieben werden, in dem er chaotisch 66
7 ẋ Time history: Omega = Phase plane plot 15 2 x Abbildung 2.36: Phasenraum-Trajektorien für den Duffing Oszillator mit D = 1 und E =.2, wobei Dämpfung c = und äußere Kraft F = zu Null gesetzt wurden. wird. In Abb ist ein Beispiel gezeigt. Hier wird das System resonant getrieben. Für F =.1, also relativ schwache externe Kraft, schwingt das System in der Nähe eines Potenzialminimums. Um welches Minimum es sich handelt hängt von den Anfangsbedingungen ab. Wird die externe Kraft soweit erhöht, dass die Schwingungsamplitude den Wert des lokalen Maximums erreicht, so kann es in das andere Minimum hinüber wechseln. Je nach Phasenlage wird es daran manchmal reflektiert, manchmal kann es das Maximum überqueren. Unter den hier gewählten Bedingungen wird das System chaotisch. Wird die Amplitude weiter erhöht, so erreicht wird die Auslenkung groß genug, dass es nicht mehr reflektiert wird. Die Bewegung wird dann wieder regulär. Wie an diesem Beispiel gezeigt, können Bewegungsgleichungen normalerweise relativ problemlos numerisch integriert werden. Allerdings gibt es hierbei eine Reihe von Einschränkungen: Die Integration muss für jede Anfangsbedingung separat durchgeführt werden. Damit ist es sehr schwierig, Aussagen über globale Eigenschaften des Systems, wie z.b. Stabilität zu erhalten. Bei chaotischen Problemen laufen die Trajektorien exponentiell auseinander. Auf Grund der endlichen Präzision der Rechnung und der Abbildung 2.37: Links: Zeitabhängigkeit der Oszillatoramplitude. Rechts: Trajektorie im Phasenraum. In welchem Minimum das System landet, hängt empfindlich von den Parametern und von den Anfangsbedingungen ab. Kenntnisse der Anfangsbedingungen nimmt die Voraussagbarkeit damit exponentiall mit der Zeit ab. 2.8 Stabilität und Chaos Wie bereits erwähnt ist es nicht einfach, allgemeine Kriterien auzustellen, wann ein System eine reguläre Dynamik zeigt und wann es sich chaotisch verhält. Insbesondere hängt dies sowohl von den Systemparameters wie auch von den Anfangsbedingungen ab. Hier werden zunächst einige Möglichkeiten diskutiert, wie man die Stabilität von Fixpunkten beurteilen kann Stabilität von Fixpunkten in linearen Systemen Die Frage, ob ein Fixpunkt stabil ist oder nicht, kann zunächst an linearen Systemen betrachtet werden. Wir verwenden für die Beschreibung der Dynamik 67
4.2 Der Harmonische Oszillator
 Dieter Suter - 208 - Physik B3, SS03 4.2 Der Harmonische Oszillator 4.2.1 Harmonische Schwingungen Die Zeitabhängigkeit einer allgemeinen Schwingung ist beliebig, abgesehen von der Periodizität. Die mathematische
Dieter Suter - 208 - Physik B3, SS03 4.2 Der Harmonische Oszillator 4.2.1 Harmonische Schwingungen Die Zeitabhängigkeit einer allgemeinen Schwingung ist beliebig, abgesehen von der Periodizität. Die mathematische
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
 Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Ferienkurs Theoretische Mechanik 2009 Hamilton Formalismus und gekoppelte Systeme
 Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
2. Physikalisches Pendel
 2. Physikalisches Pendel Ein physikalisches Pendel besteht aus einem starren Körper, der um eine Achse drehbar gelagert ist. A L S φ S z G Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.2-1 2.1 Bewegungsgleichung
2. Physikalisches Pendel Ein physikalisches Pendel besteht aus einem starren Körper, der um eine Achse drehbar gelagert ist. A L S φ S z G Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.2-1 2.1 Bewegungsgleichung
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
F R. = Dx. M a = Dx. Ungedämpfte freie Schwingungen Beispiel Federpendel (a) in Ruhe (b) gespannt: Auslenkung x Rückstellkraft der Feder
 6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
6 Der Harmonische Oszillator
 6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
Serie 13. Analysis D-BAUG Dr. Cornelia Busch FS 2016
 Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
ẋ = v 0 (t t 1 ). x(t) = x 1 + v 0 (t t 1 ). t 1 t 2 (x 2 x 1 ) 2 (t 2 t 1 ) 2. m (x 2 x 1 ) 2. dtl = = m x 2 x 1
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 1 Prof Dr Alexander Shnirman Blatt 7 Dr Boris Narozhny, Dr Holger Schmi 25521 1 Die
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 1 Prof Dr Alexander Shnirman Blatt 7 Dr Boris Narozhny, Dr Holger Schmi 25521 1 Die
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Hochschule Düsseldorf University of Applied Sciences. 22. Dezember 2016 HSD. Physik. Schwingungen
 Physik Schwingungen Zusammenfassung Mechanik Physik Mathe Einheiten Bewegung Bewegung 3d Newtons Gesetze Energie Gravitation Rotation Impuls Ableitung, Integration Vektoren Skalarprodukt Gradient Kreuzprodukt
Physik Schwingungen Zusammenfassung Mechanik Physik Mathe Einheiten Bewegung Bewegung 3d Newtons Gesetze Energie Gravitation Rotation Impuls Ableitung, Integration Vektoren Skalarprodukt Gradient Kreuzprodukt
Poisson-Klammern. Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und Zeit abhängen: Def: "Poisson-Klammer von F und G":
 Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p, q,
Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p, q,
Das mathematische Pendel
 1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
Klassische Theoretische Physik I WS 2013/ Nicht so schnell (10 Punkte) Ein kleiner
 Karlsruher Institut für Technologie www.tkm.kit.edu/lehre/ Klassische Theoretische Physik I WS 23/24 Prof. Dr. J. Schmalian Blatt, Punkte Dr. P. P. Orth Abgabe und Besprechung 24..24. Nicht so schnell
Karlsruher Institut für Technologie www.tkm.kit.edu/lehre/ Klassische Theoretische Physik I WS 23/24 Prof. Dr. J. Schmalian Blatt, Punkte Dr. P. P. Orth Abgabe und Besprechung 24..24. Nicht so schnell
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
9. Vorlesung Wintersemester
 9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen:
 Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
 3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen:
 Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Bewegung auf Paraboloid 2
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 8 vom 17.06.13 Abgabe: 24.06. Aufgabe 34 4 Punkte Bewegung auf Paraboloid 2 Ein Teilchen der Masse m bewege sich reibungsfrei unter
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 8 vom 17.06.13 Abgabe: 24.06. Aufgabe 34 4 Punkte Bewegung auf Paraboloid 2 Ein Teilchen der Masse m bewege sich reibungsfrei unter
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Abbildung 5.1: stabile und instabile Ruhelagen
 Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
Exkurs: Method of multiple scales (Mehrskalen Methode)
 Exkurs: Method of multiple scales (Mehrskalen Methode) dr. karin mora* Im folgenden betrachten wir nichtlineare dynamische Systeme (NDS) mit sogenannten kleinen nichtlinearen Termen. Viele mathematische
Exkurs: Method of multiple scales (Mehrskalen Methode) dr. karin mora* Im folgenden betrachten wir nichtlineare dynamische Systeme (NDS) mit sogenannten kleinen nichtlinearen Termen. Viele mathematische
1 Lagrange-Formalismus
 Lagrange-Formalismus SS 4 In der gestrigen Vorlesung haben wir die Beschreibung eines physikalischen Systems mit Hilfe der Newton schen Axiome kennen gelernt. Oft ist es aber nicht so einfach die Kraftbilanz
Lagrange-Formalismus SS 4 In der gestrigen Vorlesung haben wir die Beschreibung eines physikalischen Systems mit Hilfe der Newton schen Axiome kennen gelernt. Oft ist es aber nicht so einfach die Kraftbilanz
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Theoretische Physik I: Lösungen Blatt Michael Czopnik
 Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Einführung in die Physik
 Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Harmonische Schwingungen
 Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
X.4 Elektromagnetische Wellen im Vakuum
 X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
Experimentalphysik E1
 Experimentalphysik E1 Gedämpfte & erzwungene Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 16. Dez. 16 Harmonische Schwingungen Auslenkung
Experimentalphysik E1 Gedämpfte & erzwungene Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 16. Dez. 16 Harmonische Schwingungen Auslenkung
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators
 Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
11.4. Lineare Differentialgleichungen höherer Ordnung
 4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
Übungsaufgaben zur Hamilton-Mechanik
 Übungsaufgaben zur Hamilton-Mechanik Simon Filser 24.9.09 1 Parabelförmiger Draht Auf einem parabelförmig gebogenen Draht (z = ar² = a(x² + y²), a = const), der mit konstanter Winkelgeschwindigkeit ω 0
Übungsaufgaben zur Hamilton-Mechanik Simon Filser 24.9.09 1 Parabelförmiger Draht Auf einem parabelförmig gebogenen Draht (z = ar² = a(x² + y²), a = const), der mit konstanter Winkelgeschwindigkeit ω 0
Hochschule Düsseldorf University of Applied Sciences. 12. Januar 2017 HSD. Physik. Schwingungen III
 Physik Schwingungen III Wiederholung Komplexe Zahlen Harmonischer Oszillator DGL Getrieben Gedämpft Komplexe Zahlen Eulersche Formel e i' = cos ' + i sin ' Komplexe Schwingung e i!t = cos!t + i sin!t Schwingung
Physik Schwingungen III Wiederholung Komplexe Zahlen Harmonischer Oszillator DGL Getrieben Gedämpft Komplexe Zahlen Eulersche Formel e i' = cos ' + i sin ' Komplexe Schwingung e i!t = cos!t + i sin!t Schwingung
Der Duffing-Oszillator
 11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
7 Die Hamilton-Jacobi-Theorie
 7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
Gewöhnliche Differentialgleichungen. Teil II: Lineare DGLs mit konstanten Koeffizienten
 - 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
- 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Wiederholung der zweiten Schularbeit Mathematik Klasse 7D WIKU am
 Wiederholung der zweiten Schularbeit Mathematik Klasse 7D WIKU am 22.12.2014 SCHÜLERNAME: Punkte im ersten Teil: Punkte im zweiten Teil: Davon Kompensationspunkte: Note: Notenschlüssel: Falls die Summe
Wiederholung der zweiten Schularbeit Mathematik Klasse 7D WIKU am 22.12.2014 SCHÜLERNAME: Punkte im ersten Teil: Punkte im zweiten Teil: Davon Kompensationspunkte: Note: Notenschlüssel: Falls die Summe
Fibonacci Zahlen: 3. Hamiltonsche Systeme. 3.1 Hamilton Dynamik. Teilverhältnis beim `goldenen Schnitt : definiert als. mit
 Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Experimentalphysik E1
 Experimentalphysik E1 Erzwungene & gekoppelte Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 10. Jan. 016 Gedämpfte Schwingungen m d x dt +
Experimentalphysik E1 Erzwungene & gekoppelte Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 10. Jan. 016 Gedämpfte Schwingungen m d x dt +
Eine DG ist eine Gleichung, die Ableitungen der gesuchten Funktion enthält.
 C7 Differentgleichungen (DG) (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel C7 weicht ab vom Altland-Delft-Text] C7.1 Was ist eine DG, wozu wird sie gebraucht?
C7 Differentgleichungen (DG) (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel C7 weicht ab vom Altland-Delft-Text] C7.1 Was ist eine DG, wozu wird sie gebraucht?
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
 Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
2.4 Stoßprozesse. entweder nicht interessiert o- der keine Möglichkeit hat, sie zu untersuchen oder zu beeinflussen.
 - 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
- 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
Das Unschärfeprodukt x p in der klassischen Mechanik Seminar zur Theorie der Atome, Kerne und kondensierten Materie. Jonas Lübke
 Das Unschärfeprodukt x p in der klassischen Mechanik Seminar zur Theorie der Atome, Kerne und kondensierten Materie Jonas Lübke 7. November 013 Inhaltsverzeichnis 1 Einführung 1 Beziehung zwischen klassischer
Das Unschärfeprodukt x p in der klassischen Mechanik Seminar zur Theorie der Atome, Kerne und kondensierten Materie Jonas Lübke 7. November 013 Inhaltsverzeichnis 1 Einführung 1 Beziehung zwischen klassischer
Hochschule Düsseldorf University of Applied Sciences. 05. Januar 2017 HSD. Physik. Schwingungen II
 Physik Schwingungen II Ort, Geschwindigkeit, Beschleunigung x(t) = cos! 0 t v(t) =ẋ(t) =! 0 sin! 0 t t a(t) =ẍ(t) =! 2 0 cos! 0 t Energie In einem mechanischen System ist die Gesamtenergie immer gleich
Physik Schwingungen II Ort, Geschwindigkeit, Beschleunigung x(t) = cos! 0 t v(t) =ẋ(t) =! 0 sin! 0 t t a(t) =ẍ(t) =! 2 0 cos! 0 t Energie In einem mechanischen System ist die Gesamtenergie immer gleich
Chaos im getriebenen nicht-linearen Pendel
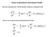 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Motivation. Motivation 2
 Grenzzyklen 1 Motivation Grenzzyklen modellieren von selbst oszillierende Systeme Stabile Grenzzyklen kleine Abweichungen in den Anfangsbedingungen gehen in Grenzzyklus über Beispiele: Van-der-Pol Schwingkreis
Grenzzyklen 1 Motivation Grenzzyklen modellieren von selbst oszillierende Systeme Stabile Grenzzyklen kleine Abweichungen in den Anfangsbedingungen gehen in Grenzzyklus über Beispiele: Van-der-Pol Schwingkreis
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie
 Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: , Abgabe am )
 Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
(a) Transformation auf die generalisierten Koordinaten (= Kugelkoordinaten): ẏ = l cos(θ) θ sin(ϕ) + l sin(θ) cos(ϕ) ϕ.
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Blatt 1. Kinematik- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Vorlesung Physik für Pharmazeuten und Biologen
 Vorlesung Physik für Pharmazeuten und Biologen Schwingungen Mechanische Wellen Akustik Freier harmonischer Oszillator Beispiel: Das mathematische Pendel Bewegungsgleichung : d s mg sinϕ = m dt Näherung
Vorlesung Physik für Pharmazeuten und Biologen Schwingungen Mechanische Wellen Akustik Freier harmonischer Oszillator Beispiel: Das mathematische Pendel Bewegungsgleichung : d s mg sinϕ = m dt Näherung
Vorbereitung. (1) bzw. diskreten Wellenzahlen. λ n = 2L n. k n = nπ L
 Physikalisches Fortgeschrittenenpraktikum Gitterschwingungen Vorbereitung Armin Burgmeier Robert Schittny 1 Theoretische Grundlagen Im Versuch Gitterschwingungen werden die Schwingungen von Atomen in einem
Physikalisches Fortgeschrittenenpraktikum Gitterschwingungen Vorbereitung Armin Burgmeier Robert Schittny 1 Theoretische Grundlagen Im Versuch Gitterschwingungen werden die Schwingungen von Atomen in einem
Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
6. Erzwungene Schwingungen
 6. Erzwungene Schwingungen Ein durch zeitveränderliche äußere Einwirkung zum Schwingen angeregtes (gezwungenes) System führt erzwungene Schwingungen durch. Bedeutsam sind vor allem periodische Erregungen
6. Erzwungene Schwingungen Ein durch zeitveränderliche äußere Einwirkung zum Schwingen angeregtes (gezwungenes) System führt erzwungene Schwingungen durch. Bedeutsam sind vor allem periodische Erregungen
Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten
 http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 7 vom Abgabe:
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
Kapitel 1:»Rechnen« c 3 c 4 c) b 5 c 4. c 2 ) d) (2x + 3) 2 e) (2x + 0,01)(2x 0,01) f) (19,87) 2
 Kapitel :»Rechnen«Übung.: Multiplizieren Sie die Terme so weit wie möglich aus. a /5 a 5 Versuchen Sie, vorteilhaft zu rechnen. Übung.2: Berechnen Sie 9% von 2573. c 3 c 4 b 5 c 4 ( b 2 c 2 ) (2x + 3)
Kapitel :»Rechnen«Übung.: Multiplizieren Sie die Terme so weit wie möglich aus. a /5 a 5 Versuchen Sie, vorteilhaft zu rechnen. Übung.2: Berechnen Sie 9% von 2573. c 3 c 4 b 5 c 4 ( b 2 c 2 ) (2x + 3)
Blatt 10. Hamilton-Formalismus- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik T) im SoSe 20 Blatt 0. Hamilton-Formalismus- Lösungsvorschlag Aufgabe 0.. Hamilton-Formalismus
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik T) im SoSe 20 Blatt 0. Hamilton-Formalismus- Lösungsvorschlag Aufgabe 0.. Hamilton-Formalismus
Anwendung: Gedämpfter, getriebener harmonischer Oszillator Unendlich viele Anwendungen in der Physik, auch außerhalb der Mechanik!
 Anwendung: Gedämpfter, getriebener harmonischer Oszillator Unendlich viele Anwendungen in der Physik, auch außerhalb der Mechanik! Bewegungsgleichung: Dämpfungsrate: Einheit: Kreisfrequenz des Oszillators:
Anwendung: Gedämpfter, getriebener harmonischer Oszillator Unendlich viele Anwendungen in der Physik, auch außerhalb der Mechanik! Bewegungsgleichung: Dämpfungsrate: Einheit: Kreisfrequenz des Oszillators:
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Hinweis: Geben Sie für den Winkel α keinen konkreten Wert, sondern nur für sin α und/oder cos α an.
 1. Geschwindigkeiten (8 Punkte) Ein Schwimmer, der sich mit konstanter Geschwindigkeit v s = 1.25 m/s im Wasser vorwärts bewegen kann, möchte einen mit Geschwindigkeit v f = 0.75 m/s fließenden Fluß der
1. Geschwindigkeiten (8 Punkte) Ein Schwimmer, der sich mit konstanter Geschwindigkeit v s = 1.25 m/s im Wasser vorwärts bewegen kann, möchte einen mit Geschwindigkeit v f = 0.75 m/s fließenden Fluß der
BASISPRÜFUNG MATHEMATIK I UND II
 ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder
 DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
2ml2 folgt die Form der Phasenraumtrajektorien zu
 PDDr.S.Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt WS 8/9 3..9. Phasenraumportrait eines Fadenpendels. Eine Masse m sei an einer masselosen Stange der Länge l aufgehängt,
PDDr.S.Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt WS 8/9 3..9. Phasenraumportrait eines Fadenpendels. Eine Masse m sei an einer masselosen Stange der Länge l aufgehängt,
3. Berechnen Sie auch die Beschleunigung a als Funktion der Zeit t. 4. Erstellen Sie ein SIMULINK Modell, das x(t) numerisch berechnet.
 unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
Schwingungen. Harmonische Schwingungen. t Anharmonische Schwingungen. S. Alexandrova FDIBA TU Sofia 1
 Schwingungen Harmonische Schwingungen x t Anharmonische Schwingungen x x t S. Alexandrova FDIBA TU Sofia 1 t ANHARMONISCHE SCHWINGUNGEN EHB : Kraft F = -k(x-x o ) Potentielle Energie: E p E p Parabel mit
Schwingungen Harmonische Schwingungen x t Anharmonische Schwingungen x x t S. Alexandrova FDIBA TU Sofia 1 t ANHARMONISCHE SCHWINGUNGEN EHB : Kraft F = -k(x-x o ) Potentielle Energie: E p E p Parabel mit
5. Zustandsgleichung des starren Körpers
 5. Zustandsgleichung des starren Körpers 5.1 Zustandsgleichung 5.2 Körper im Schwerefeld 5.3 Stabilität freier Rotationen 2.5-1 5.1 Zustandsgleichung Zustand: Der Zustand eines starren Körpers ist durch
5. Zustandsgleichung des starren Körpers 5.1 Zustandsgleichung 5.2 Körper im Schwerefeld 5.3 Stabilität freier Rotationen 2.5-1 5.1 Zustandsgleichung Zustand: Der Zustand eines starren Körpers ist durch
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester Physik-Institut der Universität Zürich
 Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Übungen zu: Theoretische Physik I klassische Mechanik W 13 Tobias Spranger - Prof. Tom Kirchner WS 005/06 http://www.pt.tu-clausthal.de/qd/teaching.html. Dezember 005 Übungsblatt 7 Lösungsvorschlag 4 Aufgaben,
Übungen zu: Theoretische Physik I klassische Mechanik W 13 Tobias Spranger - Prof. Tom Kirchner WS 005/06 http://www.pt.tu-clausthal.de/qd/teaching.html. Dezember 005 Übungsblatt 7 Lösungsvorschlag 4 Aufgaben,
Klausur zur T1 (Klassische Mechanik)
 Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Zeitentwicklung von Observablen und Zuständen in der klassischen Mechanik
 Zeitentwicklung von Observablen und Zuständen in der klassischen Mechanik Martin Vojta 05.01.2012 1 Hamiltonsche Mechanik Die Hamiltonsche Mechanik befasst sich mit der Bewegung im Phasenraum. Dabei kann
Zeitentwicklung von Observablen und Zuständen in der klassischen Mechanik Martin Vojta 05.01.2012 1 Hamiltonsche Mechanik Die Hamiltonsche Mechanik befasst sich mit der Bewegung im Phasenraum. Dabei kann
tun, sondern nur mit der Reaktion auf verschiedene Anfangswerte.
 2.3 Stabilität Eine wichtige Rolle spielt das Stabilitätsverhalten dynamischer Systeme. Wie üblich sei Φ die Fundamentalmatrix des linearen Systems ẋ = A(t)x + u. Im weiteren sei t fixiert, später wird
2.3 Stabilität Eine wichtige Rolle spielt das Stabilitätsverhalten dynamischer Systeme. Wie üblich sei Φ die Fundamentalmatrix des linearen Systems ẋ = A(t)x + u. Im weiteren sei t fixiert, später wird
18.2 Implizit definierte Funktionen
 18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
7. Übungsblatt Physik I für MWWT Komplexe Zahlen, gewöhnliche Differentialgleichungen
 Prof. Dr. Walter Arnold Lehrstuhl für Materialsimulation Universität des Saarlandes 5. Januar 2016 7. Übungsblatt Physik I für MWWT Komplexe Zahlen, gewöhnliche Differentialgleichungen Abgabe des Übungsblattes
Prof. Dr. Walter Arnold Lehrstuhl für Materialsimulation Universität des Saarlandes 5. Januar 2016 7. Übungsblatt Physik I für MWWT Komplexe Zahlen, gewöhnliche Differentialgleichungen Abgabe des Übungsblattes
Partielle Differentialgleichungen
 http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Formelsammlung: Physik I für Naturwissenschaftler
 Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 13. Dezember 212 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m]
Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 13. Dezember 212 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m]
) (1 BE) 1 2 ln 2. und somit
 1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
Fragen zu Kapitel III Seite 1 III
 Fragen zu Kapitel III Seite 1 III Grundbegriffe der klassischen Mechanik Fragen 3.1 bis 3.8 Zur Beantwortung der Fragen benötigen Sie folgende Daten Masse der Erde 5,974 10 4 kg Erdradius 6371 km Erdbeschleunigung
Fragen zu Kapitel III Seite 1 III Grundbegriffe der klassischen Mechanik Fragen 3.1 bis 3.8 Zur Beantwortung der Fragen benötigen Sie folgende Daten Masse der Erde 5,974 10 4 kg Erdradius 6371 km Erdbeschleunigung
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Ferienkurs Theoretische Mechanik Sommer 2010 Newton/Koordinaten/Dgl s
 Fakultät für Physik Friedrich Wulschner Technische Universität München Vorlesung Montag Ferienkurs Theoretische Mechanik Sommer 2010 Newton/Koordinaten/Dgl s Inhaltsverzeichnis 1 Newtons 3 Axiome 2 2 Lösungsverfahren
Fakultät für Physik Friedrich Wulschner Technische Universität München Vorlesung Montag Ferienkurs Theoretische Mechanik Sommer 2010 Newton/Koordinaten/Dgl s Inhaltsverzeichnis 1 Newtons 3 Axiome 2 2 Lösungsverfahren
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
4.3 Schwingende Systeme
 Dieter Suter - 217 - Physik B3 4.3 Schwingende Systeme Schwingungen erhält man immer dann, wenn die Kraft der Auslenkung entgegengerichtet ist. Ist sie außerdem proportional zur Kraft, so erhält man eine
Dieter Suter - 217 - Physik B3 4.3 Schwingende Systeme Schwingungen erhält man immer dann, wenn die Kraft der Auslenkung entgegengerichtet ist. Ist sie außerdem proportional zur Kraft, so erhält man eine
