Zugänge zur nichtlinearen Dynamik. W. Oehme, Universität Leipzig
|
|
|
- Tobias Daniel Giese
- vor 6 Jahren
- Abrufe
Transkript
1 Zugänge zur nichtlinearen Dynamik W. Oehme, Universität Leipzig
2 einfache physikalische Experimente Wirtschaft Wetter historische Bezüge Nichtlineare Dynamik Chaos und Ordnung Verkehrsstau Populationsdynamik Fraktale Soziophysik oszillierende chemische Reaktionen Medizin Astronomie
3 Siebenschläfer Das Wetter zum Siebenschläfer-Tag sieben Wochen bleiben mag. 27. Juni 2005: ein sonniger Tag Er ist nicht schuld! aber: verregneter Sommer 2005 Bei großzügiger Interpretation: Trefferquote 70%
4 Chaos und Kosmos Hesiod aber sagt: Chaos entstand vor allem zuerst; es wurde dann Gaea mit weitem Gefild, Eros zugleich, der weit vor allen Unsterblichen vorglänzt. Quelle: Aristoteles Metaphysik Hesiodes ca. 700 v. Chr. Gaia ( Erde ) Zeichnung am Pergamon Zeus Altar Chaos (griech.): ungeordneter und ungeformter Zustand der Dinge; mystischer Urzustand; leerer Raum Kosmos (griech.): Welt als geordnete Einheit
5 Die Welt als Uhrwerk (klassischer Determinismus) Pierre Simon Laplace ( ) Pierre Laplace (1812): Eine Intelligenz, welche für einen gegebenen Augenblick alle in der Natur wirkenden Kräfte sowie die gegenseitige Lage der sie zusammensetzenden Elemente kennt...; nichts würde ihr ungewiss sein und Zukunft und Vergangenheit würden ihr offen vor Augen liegen.
6 Kausalität Henry Poincaré ( ) schwache Kausalität: Gleiche Ursachen haben gleiche Wirkungen. starke Kausalität: Ähnliche Ursachen haben ähnliche Wirkungen. Henry Poincaré, 1903, nach theoretischen Untersuchungen zur Stabilität des Planetensystems: Eine sehr kleine Ursache, die wir nicht bemerken, bewirkt einen beachtlichen Effekt, den wir nicht übersehen können, und dann sagen wir, der Effekt sei zufällig. Vorhersagen werden damit unmöglich. Verletzung der starken Kausalität deterministisches Chaos
7 Buckelpiste und Magnetpendel Potentialmulden Einzugsgebiete Wohin rollt die Kugel? Wohin geht das Magnetpendel?
8 Berechnungen zum Magnetpendel Potentialmulden Pendelbewegung Sensitivität Einzugsgebiete
9 Verhulst-Dynamik und logistische Gleichung X n = A X a ( 1 X ) a Pierre Francois Verhulst ( ) Populationsmodell N a N n = c*n a aktuelle Tierzahl nächste Generation c Reproduktionsfaktor c>1 => Überbevölkerung c<1 => Aussterben Dämpfungsfaktor (N max N a )/N max N max maximal ernährbare Tierzahl
10 Berechnungen mit der logistischen Gleichung Einschwingverhalten Selbstähnlichkeit 1. und 2. Bifurkation Feigenbaumdiagramm
11 Räuber-Beute-Systeme Quelle: Universität Bonn Hudson Bay Company: Buchführung über die aufgekauften Felle von Luchsen und Schneeschuhhasen zwischen 1845 und 1935
12 Räuber-Beute-Systeme x y = ax (1 cx = by (1 dy + ey) fx) Beute x Räuber y Beute
13 Pohlsches Drehpendel mit Unwucht Drehmomente Potentiale Feder Zusatzmasse Summe Feder Zusatzmasse Summe 0 2 cos 2 1 sin U r g m D U r g m D M + + = + = α α α α Feder Zusatzmasse Drehschwinger mit Zusatzmasse Feder Antrieb Wirbelstromdämpfung
14 Experimente ohne Unwucht Variation der Anregung ohne Antrieb mit Antrieb
15 Experimente mit Unwucht Variation der Dämpfung starke Dämpfung Chaos 1. 2 Bifurkation schwache Dämpfung
16 Feder Reibung Antrieb Zusatzmasse
17 Berechnungen zum Drehpendel
18 Linearer elektrischer Schwingkreis u(t) Experiment u L u R u C L Q+ ul + ur + uc = u(t) R Q+ 1 Q C = Usin( ω t) Simulation UC Zeitverhalten Phasendiagramm Resonanzkurve
19 Nichtlinearer elektrischer Schwingkreis u(t) u L u R Experiment ul + ur + ud = u(t) u D Simulation LQ+ Q RQ+ U0 (exp( ) 1) = Usin( ω t) C U o o
20 Diode als Plattenkondensator A C= ε 0 εr d =d(u ) d CU ( ) = α U+ U C0 U CU ( ) = U+ U U D Q = U0 (exp( ) 1) C U 0 0 d ( U+ U ) ~ 0 C=C(U) U 0 = α 0 α=c0 U0 U0 C ( 0) = C dq C= du Durchbruchsspannung
21 Berechnungen zum nichtlinearen elektrischen Schwingkreis Zeitdiagramm Phasendiagramm
22 Wettervorhersage Lorenz-Modell = α ( Y X ) X = β X Y Z = γ Z + X Z Y X Y Benard-Zellen Quelle: Uni Fankfurt ebene Konvektion Lorenz-Attraktor
23 Sierpinski-Dreieck P3 S1 S4 S3 S2 Startpunkt P1 P2 Spielregeln: zufällige Ziele P1, P2 und P3; halber Weg zum Zielpunkt
24 Fraktale Lorenz-Attraktor Farn Mandelbrots Apfelmännchen Attraktor des Drehpendels Sierpinski-Dreieck
25 Oszillierende chemische Reaktionen Belousov-Zhabotinsky-Reaktion Bromierung der Malonsäure Br Prozess A + BrO3 + 2 Br + 3CH 2( COOH ) 2 + 3H 3O 3BrCH ( COOH ) 2 + 6H 2O Prozess B BrO3 + Ce + CH2( COOH) 2 + 5H3O Ce + BrCH( COOH) 2 + 8H 2O Ce + BrCH ( COOH ) 2 + 7H 2O 4Ce + HCOOH + 2CO2 + 5H 3O + Br
26 Belousov-Zhabotinsky-Reaktion Z B k X A k Z Z k B f Y X k Y A k Y X k X A k Y X k Y A k X c c = + = + = Z=[Ce 4+ ] Oregonator-Modell
27 einfache physikalische Experimente Wirtschaft Wetter historische Bezüge Nichtlineare Dynamik Chaos und Ordnung Verkehrsstau Populationsdynamik Fraktale Soziophysik oszillierende chemische Reaktionen Medizin Astronomie
28 Quellenangabe: Titelseite, Satellitenbild, Deutscher Wetterdienst, Offenbach (DWD) Folie 5, Prager Uhr, Wikipedia.org User Maros Folie 7, Buckelpiste, Wikipedia.org User Art-top Folie 12, Frosch, Wikipedia.org User Fabelfroh; Storch Wikipedia.org User SirEx Folie 22, Altocummulus, Wikipedia.org User Fir0002
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
 Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Wie lang ist die Küste Großbritanniens?
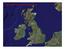 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
SINIS Simulation nichtlinearer Systeme
 In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Experimente, Ideen und Entwicklung der Chaostheorie
 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Die Chaostheorie und Fraktale in der Natur
 Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Algorithmen für Chaos und Fraktale
 Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Kapitel 5.5: Nichtlineare Rekursionen. Algorithmen und Datenstrukturen WS 2017/18. Pro f. Dr. Sán do r Fe k e te
 Kapitel 5.5: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 e H! e t u 2 Ankreuzliste für Übungsgruppen 1 4 3 7 5 5 6 6 9 10 8 2 2 10 3 5.3.3 Master-Theorem:
Kapitel 5.5: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 e H! e t u 2 Ankreuzliste für Übungsgruppen 1 4 3 7 5 5 6 6 9 10 8 2 2 10 3 5.3.3 Master-Theorem:
Achtung Nebel! Ein Komplexitäts-Crashkurs für Projektmanager*innen
 complexity-research.com Achtung Nebel! Ein Komplexitäts-Crashkurs für Projektmanager*innen Priv.-Doz. Dr. Dr. Dipl.-Psych. Guido Strunk guido.strunk@complexity-research.com www.complexity-research.com
complexity-research.com Achtung Nebel! Ein Komplexitäts-Crashkurs für Projektmanager*innen Priv.-Doz. Dr. Dr. Dipl.-Psych. Guido Strunk guido.strunk@complexity-research.com www.complexity-research.com
Kapitel 5.6: Nichtlineare Rekursionen. Algorithmen und Datenstrukturen WS 2012/13. Prof. Dr. Sándor Fekete
 Kapitel 5.6: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 5.4.3 Master-Theorem: Lineare Rekursionen 5.6 Nichtlineare Rekursionen 5.6.1 Logistische Rekursion
Kapitel 5.6: Nichtlineare Rekursionen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 5.4.3 Master-Theorem: Lineare Rekursionen 5.6 Nichtlineare Rekursionen 5.6.1 Logistische Rekursion
Versuch 6 - Nichtlineares Pendel
 UNIVERSITÄT REGENSBURG Naturwissenschaftliche Fakultät II - Physik Anleitung zum Anfängerpraktikum A1 Versuch 6 - Nichtlineares Pendel 23. überarbeitete Auflage 2009 Dr. Stephan Giglberger Prof. Dr. Christian
UNIVERSITÄT REGENSBURG Naturwissenschaftliche Fakultät II - Physik Anleitung zum Anfängerpraktikum A1 Versuch 6 - Nichtlineares Pendel 23. überarbeitete Auflage 2009 Dr. Stephan Giglberger Prof. Dr. Christian
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Chaos Oder Mandelbrot und Peitsche
 Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Nichtlineare Phänomene und Selbstorganisation
 Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
P1-12,22 AUSWERTUNG VERSUCH RESONANZ
 P1-12,22 AUSWERTUNG VERSUCH RESONANZ GRUPPE 19 - SASKIA MEIßNER, ARNOLD SEILER 0.1. Drehpendel - Harmonischer Oszillator. Bei dem Drehpendel handelt es sich um einen harmonischen Oszillator. Das Trägheitsmoment,
P1-12,22 AUSWERTUNG VERSUCH RESONANZ GRUPPE 19 - SASKIA MEIßNER, ARNOLD SEILER 0.1. Drehpendel - Harmonischer Oszillator. Bei dem Drehpendel handelt es sich um einen harmonischen Oszillator. Das Trägheitsmoment,
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Thema 10 Gewöhnliche Differentialgleichungen
 Thema 10 Gewöhnliche Differentialgleichungen Viele Naturgesetze stellen eine Beziehung zwischen einer physikalischen Größe und ihren Ableitungen (etwa als Funktion der Zeit dar: 1. ẍ = g (freier Fall;
Thema 10 Gewöhnliche Differentialgleichungen Viele Naturgesetze stellen eine Beziehung zwischen einer physikalischen Größe und ihren Ableitungen (etwa als Funktion der Zeit dar: 1. ẍ = g (freier Fall;
6 chaotische Vorgänge
 6 chaotische Vorgänge Kausalität und Determinismus ( S. 125) sind wesentliche Grundlagen der klassischen Physik: Keine Wirkung tritt ohne Ursache auf, und jede Ursache hat eine Wirkung. Ist der Zustand
6 chaotische Vorgänge Kausalität und Determinismus ( S. 125) sind wesentliche Grundlagen der klassischen Physik: Keine Wirkung tritt ohne Ursache auf, und jede Ursache hat eine Wirkung. Ist der Zustand
Aufgabe 1: Elektro-mechanischer Oszillator
 37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
Modellbildung, Simulation und Populationsdynamik
 ΔN Bild: Reg Mckenna, UK ΔN Bild: Wikipedia.org User StefanGe Modellbildung, Simulation und Populationsdynamik W. Oehme, Uniersität Leipzig Bild: Wikipedia.org User Barbarossa Bild: Wikipedia.org User
ΔN Bild: Reg Mckenna, UK ΔN Bild: Wikipedia.org User StefanGe Modellbildung, Simulation und Populationsdynamik W. Oehme, Uniersität Leipzig Bild: Wikipedia.org User Barbarossa Bild: Wikipedia.org User
Ausarbeitung Pohlsches Rad / Chaos Autoren: Simone Lingitz, Sebastian Jakob
 Ausarbeitung Pohlsches Rad / Chaos Autoren: Simone Lingitz, Sebastian Jakob 1. Vorarbeiten zu Hause 1.1 Erzwungene Schwingung einer Feder mit Dämpfung Bewegungsgleichung: m & x + b x& + k x m g = F cos(
Ausarbeitung Pohlsches Rad / Chaos Autoren: Simone Lingitz, Sebastian Jakob 1. Vorarbeiten zu Hause 1.1 Erzwungene Schwingung einer Feder mit Dämpfung Bewegungsgleichung: m & x + b x& + k x m g = F cos(
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Chaos im getriebenen nicht-linearen Pendel
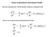 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
+ + Personalmanagement Stuff-Turnover. Simulation im Excel. Organizational Headcount. Turnover. Recruitment
 Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
Belousov-Zhabotinskii Oszillierende Reaktionen
 Belousov-Zhabotinskii Oszillierende Reaktionen Aline Brost 08. Januar 2013 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Gliederung 1 Die Belousov-Reaktion und
Belousov-Zhabotinskii Oszillierende Reaktionen Aline Brost 08. Januar 2013 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Gliederung 1 Die Belousov-Reaktion und
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Chaos - Nichtlineare Dynamik
 Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Einfache Modelle der Neurodynamik.
 Vorlesung Einfache Modelle der Neurodynamik. Anregbarkeit und canards. Wintersemester 2015/16 12.01.2016 M. Zaks Aufbau eines Neurons: Gesamtbild 2 / 16 neuron Aufbau eines Neurons: Axon und Dendriten
Vorlesung Einfache Modelle der Neurodynamik. Anregbarkeit und canards. Wintersemester 2015/16 12.01.2016 M. Zaks Aufbau eines Neurons: Gesamtbild 2 / 16 neuron Aufbau eines Neurons: Axon und Dendriten
Einfache Modelle der Populationsdynamik
 Vorlesung 4. Einfache Modelle der Populationsdynamik Wintersemester 215/16 1.11.215 M. Zaks allgemeine vorbemerkungen In kleinen Populationen schwanken die Bevolkerungszahlen stochastisch: Geburt/Tod von
Vorlesung 4. Einfache Modelle der Populationsdynamik Wintersemester 215/16 1.11.215 M. Zaks allgemeine vorbemerkungen In kleinen Populationen schwanken die Bevolkerungszahlen stochastisch: Geburt/Tod von
Serie 13. Analysis D-BAUG Dr. Cornelia Busch FS 2016
 Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Klausur zur Vorlesung Physikalische Chemie V Elektrochemie 6. bzw. 8. Fachsemester am , 10:00 bis 12:00 Uhr
 Universität Regensburg Institut für Physikalische und Theoretische Chemie Prof. Dr. G. Schmeer 18. Juli 27 Bitte füllen Sie zuerst dieses Deckblatt aus, das mit Ihren Lösungen abgegeben werden muss....
Universität Regensburg Institut für Physikalische und Theoretische Chemie Prof. Dr. G. Schmeer 18. Juli 27 Bitte füllen Sie zuerst dieses Deckblatt aus, das mit Ihren Lösungen abgegeben werden muss....
Die Wettervorhersage und ihre Tücken
 Lehrerfortbildung 11. Juni 2008 Die Wettervorhersage und ihre Tücken M. Kunz Institut für Meteorologie und Klimaforschung Universität / Forschungszentrum Karlsruhe die Realität Orkantief Lothar am 26.12.1999
Lehrerfortbildung 11. Juni 2008 Die Wettervorhersage und ihre Tücken M. Kunz Institut für Meteorologie und Klimaforschung Universität / Forschungszentrum Karlsruhe die Realität Orkantief Lothar am 26.12.1999
Chaos Seminar Wetter und Klima. Dominik Fröschl
 Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Vorlesung Modelle in Biophysik/Biochemie 4. Fraktale
 Vorlesung Modelle in Biophysik/Biochemie 4. Fraktale c Priv.-Doz. Dr. Adelhard Köhler May 19, 2005 1 Gebrochene (fraktale) Dimension Fraktale haben eine gebrochene Dimension. Unterschiedliche Dimensionsbegriffe
Vorlesung Modelle in Biophysik/Biochemie 4. Fraktale c Priv.-Doz. Dr. Adelhard Köhler May 19, 2005 1 Gebrochene (fraktale) Dimension Fraktale haben eine gebrochene Dimension. Unterschiedliche Dimensionsbegriffe
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Wir betrachten hier den Polarisationszustand einer Normalmode
 Kapitel 5 Die Polarisation elektromagnetischer Wellen 5.1 Einführung Der zeitliche Verlauf des reellen elektrischen Feldvektors E r r,t) bestimmt den Polarisationszustand des Feldes. Wir betrachten hier
Kapitel 5 Die Polarisation elektromagnetischer Wellen 5.1 Einführung Der zeitliche Verlauf des reellen elektrischen Feldvektors E r r,t) bestimmt den Polarisationszustand des Feldes. Wir betrachten hier
Die Darstellung nichtlinearer Bewegungsabläufe
 Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
1 Aufwärmen nach den Ferien
 Physikalische Chemie II Lösung 23. September 206 Aufwärmen nach den Ferien. Ermitteln Sie die folgenden Integrale. Partielle Integration mit der Anwendung der generellen Regel f g = fg fg (in diesem Fall
Physikalische Chemie II Lösung 23. September 206 Aufwärmen nach den Ferien. Ermitteln Sie die folgenden Integrale. Partielle Integration mit der Anwendung der generellen Regel f g = fg fg (in diesem Fall
Eine kleine Reise durch die Welt der zellulären Automaten
 Eine kleine Reise durch die Welt der zellulären Automaten Wolfgang Oehme, Universität Leipzig 1. Einleitung 2. Zelluläre Automaten 2.1. Game of Life als klassischer zellulärer Automat 2.2. Populationsdynamik
Eine kleine Reise durch die Welt der zellulären Automaten Wolfgang Oehme, Universität Leipzig 1. Einleitung 2. Zelluläre Automaten 2.1. Game of Life als klassischer zellulärer Automat 2.2. Populationsdynamik
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Nichtlineare Dynamik in biologischen Systemen
 Universität Leipzig Fakultät für Physik und Geowissenschaften Bereich Didaktik der Physik 29. August 2006 11 Nichtlineare Dynamik in biologischen Systemen Erster Gutachter: Prof. Dr. Wolfgang Oehme, Universität
Universität Leipzig Fakultät für Physik und Geowissenschaften Bereich Didaktik der Physik 29. August 2006 11 Nichtlineare Dynamik in biologischen Systemen Erster Gutachter: Prof. Dr. Wolfgang Oehme, Universität
Biologische Oszillatoren und Schalter - Teil 1
 Biologische Oszillatoren und Schalter - Teil 1 Elena Süs 11.12.2012 Literatur: J.D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Gliederung 1 Motivation 2 Historische Entwicklung
Biologische Oszillatoren und Schalter - Teil 1 Elena Süs 11.12.2012 Literatur: J.D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Gliederung 1 Motivation 2 Historische Entwicklung
Fakultät Grundlagen. Februar 2016
 Schwingungsdifferenzialgleichung Fakultät Grundlagen Hochschule Esslingen Februar 016 Fakultät Grundlagen Schwingungsdifferenzialgleichung Übersicht 1 Schwingungsdifferenzialgleichung Fakultät Grundlagen
Schwingungsdifferenzialgleichung Fakultät Grundlagen Hochschule Esslingen Februar 016 Fakultät Grundlagen Schwingungsdifferenzialgleichung Übersicht 1 Schwingungsdifferenzialgleichung Fakultät Grundlagen
Strömungssimulation in Li-Dualinsertationszellen
 Strömungssimulation in Li-Dualinsertationszellen Julius Sewing, Nikolaus Krause, Dennis Dieterle j.sewing@gmx.net nikokrause@gmx.de dennis.dieterle@uni-muenster.de 22. Juni 2010 Sewing, Krause, Dieterle
Strömungssimulation in Li-Dualinsertationszellen Julius Sewing, Nikolaus Krause, Dennis Dieterle j.sewing@gmx.net nikokrause@gmx.de dennis.dieterle@uni-muenster.de 22. Juni 2010 Sewing, Krause, Dieterle
Übungen zu Oberflächenintegralen Lösungen zu Übung 17
 Übungen zu Oberflächenintegralen Lösungen zu Übung 17 17.1 Sei die Oberfläche der Einheitskugel : {(x, y, z) IR 3 : x + y + z 1.} Berechnen Sie für f(x, y, z) : a, a IR, a const. das Oberflächenintegral
Übungen zu Oberflächenintegralen Lösungen zu Übung 17 17.1 Sei die Oberfläche der Einheitskugel : {(x, y, z) IR 3 : x + y + z 1.} Berechnen Sie für f(x, y, z) : a, a IR, a const. das Oberflächenintegral
AUSWERTUNG: SCHWINGUNGEN, RESONANZVERHALTEN 1. AUFGABE 1
 AUSWERTUNG: SCHWINGUNGEN, RESONANZVERHALTEN TOBIAS FREY & FREYA GNAM, GRUPPE 6, DONNERSTAG 1. AUFGABE 1 An das Winkel-Zeit-Diagramm (Abb. 1) haben wir eine einhüllende e-funktion der Form e = Ae βt angelegt.
AUSWERTUNG: SCHWINGUNGEN, RESONANZVERHALTEN TOBIAS FREY & FREYA GNAM, GRUPPE 6, DONNERSTAG 1. AUFGABE 1 An das Winkel-Zeit-Diagramm (Abb. 1) haben wir eine einhüllende e-funktion der Form e = Ae βt angelegt.
Versuch dp : Drehpendel
 U N I V E R S I T Ä T R E G E N S B U R G Naturwissenschaftliche Fakultät II - Physik Anleitung zum Physikpraktikum für Chemiker Versuch dp : Drehpendel Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung
U N I V E R S I T Ä T R E G E N S B U R G Naturwissenschaftliche Fakultät II - Physik Anleitung zum Physikpraktikum für Chemiker Versuch dp : Drehpendel Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung
Einführung in einige Teilbereiche der Wirtschaftsmathematik für Studierende des Wirtschaftsingenieurwesens
 in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2013 Hochschule Augsburg : Gliederung 1 Finanzmathematik 2 Lineare Programme 3 Differentialgleichungen 4 Statistik:
in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2013 Hochschule Augsburg : Gliederung 1 Finanzmathematik 2 Lineare Programme 3 Differentialgleichungen 4 Statistik:
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Chaos Fraktale Strukturen oder Von den Schwierigkeiten die nichtlineare Dynamik zu den Schülern zu bringen
 1 Chaos Fraktale Strukturen oder Von den Schwierigkeiten die nichtlineare Dynamik zu den Schülern zu bringen Friederike Korneck, Institut für Didaktik der Physik, J.W.-Goethe-Universität Frankfurt Seit
1 Chaos Fraktale Strukturen oder Von den Schwierigkeiten die nichtlineare Dynamik zu den Schülern zu bringen Friederike Korneck, Institut für Didaktik der Physik, J.W.-Goethe-Universität Frankfurt Seit
Schwingungen. Kurt Magnus Karl Popp Walter Sextro
 Kurt Magnus Karl Popp Walter Sextro Schwingungen Eine Einfuhrung in die physikalischen Grundlagen und die theoretische Behandlung von Schwingungsproblemen 8., uberarbeitete Auflage Mit 211 Abbildungen
Kurt Magnus Karl Popp Walter Sextro Schwingungen Eine Einfuhrung in die physikalischen Grundlagen und die theoretische Behandlung von Schwingungsproblemen 8., uberarbeitete Auflage Mit 211 Abbildungen
Fragen zum Versuch12 Oszillierende Reaktionen:
 Fragen zum Versuch12 Oszillierende Reaktionen: 1. Oszillierende Reaktionen sind Reaktionen: a. Bei denen nach gewisser Zeit einen Gleichgewichtszustand erreicht wird b. Die nur in einer Richtung ablaufen
Fragen zum Versuch12 Oszillierende Reaktionen: 1. Oszillierende Reaktionen sind Reaktionen: a. Bei denen nach gewisser Zeit einen Gleichgewichtszustand erreicht wird b. Die nur in einer Richtung ablaufen
Vorbereitung. Resonanz. Carsten Röttele. 17. Januar Drehpendel, freie Schwingungen 3. 2 Drehpendel, freie gedämpfte Schwingungen 3
 Vorbereitung Resonanz Carsten Röttele 17. Januar 01 Inhaltsverzeichnis 1 Drehpendel, freie Schwingungen 3 Drehpendel, freie gedämpfte Schwingungen 3 3 Messung der Winkelrichtgröße D 4 4 Drehpendel, erzwungene
Vorbereitung Resonanz Carsten Röttele 17. Januar 01 Inhaltsverzeichnis 1 Drehpendel, freie Schwingungen 3 Drehpendel, freie gedämpfte Schwingungen 3 3 Messung der Winkelrichtgröße D 4 4 Drehpendel, erzwungene
Die Modellierung einer Lithium-Batterie Zwischenpräsentation zum Praktikum Nichtlineare Modellierung in den Naturwissenschaften
 MÜNSTER Die Modellierung einer Lithium-Batterie Zwischenpräsentation zum Praktikum Nichtlineare Modellierung in den Naturwissenschaften Christoph Fricke, Natascha von Aspern, Carla Tameling 12.06.2012
MÜNSTER Die Modellierung einer Lithium-Batterie Zwischenpräsentation zum Praktikum Nichtlineare Modellierung in den Naturwissenschaften Christoph Fricke, Natascha von Aspern, Carla Tameling 12.06.2012
Was hat Schönheit mit Chaos zu tun?
 Physik in der Schule 31/2, 71 (1993) Was hat Schönheit mit Chaos zu tun? Vergleich der Mandelbrot-Iteration mit einem chaotischen Drehpendel Udo Backhaus (Universität Osnabrück), H.- Joachim Schlichting,
Physik in der Schule 31/2, 71 (1993) Was hat Schönheit mit Chaos zu tun? Vergleich der Mandelbrot-Iteration mit einem chaotischen Drehpendel Udo Backhaus (Universität Osnabrück), H.- Joachim Schlichting,
Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator
 Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators
 Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Gewöhnliche Differentialgleichungen: Einleitung
 Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Institut für Elektrotechnik und Informationstechnik. Aufgabensammlung zur. Systemtheorie
 Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Systemtheorie Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski Dipl.-Ing. R. Besrat 05.04.2013 Übungsaufgaben zur Systemtheorie
Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Systemtheorie Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski Dipl.-Ing. R. Besrat 05.04.2013 Übungsaufgaben zur Systemtheorie
11.4. Lineare Differentialgleichungen höherer Ordnung
 4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
Thermochemie. Arbeit ist das Produkt aus wirkender Kraft F und Weglänge s. w = F s 1 J = 1 Nm = 1 kgm 2 /s 2
 Thermochemie Energie ist die Fähigkeit, Arbeit zu leisten. E pot = m g h E kin = ½ m v 2 Arbeit ist das Produkt aus wirkender Kraft F und Weglänge s. w = F s 1 J = 1 Nm = 1 kgm 2 /s 2 Eine wirkende Kraft
Thermochemie Energie ist die Fähigkeit, Arbeit zu leisten. E pot = m g h E kin = ½ m v 2 Arbeit ist das Produkt aus wirkender Kraft F und Weglänge s. w = F s 1 J = 1 Nm = 1 kgm 2 /s 2 Eine wirkende Kraft
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Partielle Differentialgleichungen
 http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
in natürlichen und technischen Systemen Dr. rer. nat. Michael Schanz Universität Stuttgart 8. November 2004
 Universität Stuttgart 8. November 2004 in natürlichen und technischen Systemen Page 1 Dr. rer. nat. Michael Schanz Was ist Selbstorganisation 1. Selbstorganisation ist Page 2 Was ist Selbstorganisation
Universität Stuttgart 8. November 2004 in natürlichen und technischen Systemen Page 1 Dr. rer. nat. Michael Schanz Was ist Selbstorganisation 1. Selbstorganisation ist Page 2 Was ist Selbstorganisation
1. Schularbeit - Gruppe A M 0 1(1) 6C A
 . Schularbeit - Gruppe A M 0 () 6C 3 0 97 A. Ergänze folgende Tabelle: Potenz Bruch / Wurzel numerischer Wert 3-5 n -5 8 0,00 3 5 4 x 3 8 7. Berechne: a) ( x y) ( x + y) 0 = b) 9x 6ax : = 5 4a 3 3. Rechne
. Schularbeit - Gruppe A M 0 () 6C 3 0 97 A. Ergänze folgende Tabelle: Potenz Bruch / Wurzel numerischer Wert 3-5 n -5 8 0,00 3 5 4 x 3 8 7. Berechne: a) ( x y) ( x + y) 0 = b) 9x 6ax : = 5 4a 3 3. Rechne
Differenzengleichungen
 Universität Basel Wirtschaftswissenschaftliches Zentrum Differenzengleichungen Dr. Thomas Zehrt Inhalt: 1. Einführungsbeispiele 2. Definition 3. Lineare Differenzengleichungen 1. Ordnung (Wiederholung)
Universität Basel Wirtschaftswissenschaftliches Zentrum Differenzengleichungen Dr. Thomas Zehrt Inhalt: 1. Einführungsbeispiele 2. Definition 3. Lineare Differenzengleichungen 1. Ordnung (Wiederholung)
5. Kritische Drehzahl
 Aufgabenstellung: 5. Kritische Drehzahl y y Ω c/4 c/4 m c/4 e z O O S c/4 x Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.5-1 Der starre Körper mit der Masse m dreht sich mit der konstanten Winkelgeschwindigkeit
Aufgabenstellung: 5. Kritische Drehzahl y y Ω c/4 c/4 m c/4 e z O O S c/4 x Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.5-1 Der starre Körper mit der Masse m dreht sich mit der konstanten Winkelgeschwindigkeit
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme
 7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
Medizinische Physik: Physikalische Grundlagen der Analyse biomedizinischer Signale
 Medizinische Physik: Physikalische Grundlagen der Analyse biomedizinischer Signale Physics in Medicine: Physical Fundamentals of Analyzing Biomedical Signals (D/E) Klaus Lehnertz Winter Term 2003 / 2004
Medizinische Physik: Physikalische Grundlagen der Analyse biomedizinischer Signale Physics in Medicine: Physical Fundamentals of Analyzing Biomedical Signals (D/E) Klaus Lehnertz Winter Term 2003 / 2004
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
Synergetik. Hermann Haken. Eine Einführung. Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie
 Hermann Haken Synergetik Eine Einführung Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie Übersetzt von A. Wunderlin Dritte, erweiterte Auflage Mit 168 Abbildungen
Hermann Haken Synergetik Eine Einführung Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie Übersetzt von A. Wunderlin Dritte, erweiterte Auflage Mit 168 Abbildungen
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Experimentelle Physik I
 Veranstaltung 4010011 https://campus.studium.kit.edu/event/h7ke2nevdu6ociwvcuiqyw 29. Vorlesung: 6.3 Schwingungen und Wellen (6): Licht und Materie, Nicht-lineare Systeme 9. Februar 2017 Experimentelle
Veranstaltung 4010011 https://campus.studium.kit.edu/event/h7ke2nevdu6ociwvcuiqyw 29. Vorlesung: 6.3 Schwingungen und Wellen (6): Licht und Materie, Nicht-lineare Systeme 9. Februar 2017 Experimentelle
Seminar Fraktale. Kapitel 13 Dynamical Systems. Von Dirk Simon
 Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Praktikum. Versuch SIM-1 Numerische Integrationsverfahren zur Lösung von Simulationsaufgaben
 Praktikum Versuch SIM-1 Numerische Integrationsverfahren zur Lösung von Simulationsaufgaben Verantwortlicher Hochschullehrer: Prof. Dr. Ing. habil. P. Li Versuchsverantwortlicher: Dr. Ing. S. Hopfgarten
Praktikum Versuch SIM-1 Numerische Integrationsverfahren zur Lösung von Simulationsaufgaben Verantwortlicher Hochschullehrer: Prof. Dr. Ing. habil. P. Li Versuchsverantwortlicher: Dr. Ing. S. Hopfgarten
Dämpfung. . Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung. Elastodynamik 2 SS
 Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
b) Fertige eine Skizze an und kontrolliere deine Skizze mit jener auf dem ersten Lösungsblatt.
 Ein Flugzeug startet von einem Punkt A der Startbahn aus, fährt am Kontrollpunkt des Flugplatzes vorbei und beginnt von einem Punkt B aus ohne Richtungsänderung zu steigen. Von dem h = 20m hohen Kontrollturm
Ein Flugzeug startet von einem Punkt A der Startbahn aus, fährt am Kontrollpunkt des Flugplatzes vorbei und beginnt von einem Punkt B aus ohne Richtungsänderung zu steigen. Von dem h = 20m hohen Kontrollturm
120 Gekoppelte Pendel
 120 Gekoppelte Pendel 1. Aufgaben 1.1 Messen Sie die Schwingungsdauer zweier gekoppelter Pendel bei gleichsinniger und gegensinniger Schwingung. 1.2 Messen Sie die Schwingungs- und Schwebungsdauer bei
120 Gekoppelte Pendel 1. Aufgaben 1.1 Messen Sie die Schwingungsdauer zweier gekoppelter Pendel bei gleichsinniger und gegensinniger Schwingung. 1.2 Messen Sie die Schwingungs- und Schwebungsdauer bei
Formelsammlung Elektrotechnik von Sascha Spors V1.3 /
 Formelsammlung Elektrotechnik von Sascha Spors V.3 /..96 Mathematische Formeln : arctan( b a Z a + jb Y arg(z ; arctan( b a arctan( b < a für a >, b +π für a π für a
Formelsammlung Elektrotechnik von Sascha Spors V.3 /..96 Mathematische Formeln : arctan( b a Z a + jb Y arg(z ; arctan( b a arctan( b < a für a >, b +π für a π für a
Elemente der Mathematik - Sommer 2016
 Elemente der Mathematik - Sommer 06 Prof. Dr. Matthias Lesch, Regula Krapf Übungsblatt 8 Aufgabe 7 (8 Punkte). Ein Parallelogramm ist ein Rechteck ABCD mit Seiten a, b, c, d wie unten dargestellt, mit
Elemente der Mathematik - Sommer 06 Prof. Dr. Matthias Lesch, Regula Krapf Übungsblatt 8 Aufgabe 7 (8 Punkte). Ein Parallelogramm ist ein Rechteck ABCD mit Seiten a, b, c, d wie unten dargestellt, mit
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - harmonische Schwingungen - Prof. Dr. Ulrich Hahn WS 216/17 kinematische Beschreibung Auslenkungs Zeit Verlauf: ( t) ˆ cost Projektion einer gleichförmigen Kreisbewegung
Physik III im Studiengang Elektrotechnik - harmonische Schwingungen - Prof. Dr. Ulrich Hahn WS 216/17 kinematische Beschreibung Auslenkungs Zeit Verlauf: ( t) ˆ cost Projektion einer gleichförmigen Kreisbewegung
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
Physikalisches Anfaengerpraktikum. Pohlsches Rad
 Physikalisches Anfaengerpraktikum Pohlsches Rad Ausarbeitung von Marcel Engelhardt & David Weisgerber (Gruppe 37) Mittwoch, 6. März 25 email: Marcel.Engelhardt@mytum.de Weisgerber@mytum.de ()Einführung
Physikalisches Anfaengerpraktikum Pohlsches Rad Ausarbeitung von Marcel Engelhardt & David Weisgerber (Gruppe 37) Mittwoch, 6. März 25 email: Marcel.Engelhardt@mytum.de Weisgerber@mytum.de ()Einführung
Grundwissen. 8. Jahrgangsstufe. Mathematik
 Grundwissen 8. Jahrgangsstufe Mathematik Grundwissen Mathematik 8. Jahrgangsstufe Seite 1 1 Proportionalität 1.1 Direkte Proportionalität Eigenschaften: y Quotientengleichheit Bei kommt immer das Gleiche
Grundwissen 8. Jahrgangsstufe Mathematik Grundwissen Mathematik 8. Jahrgangsstufe Seite 1 1 Proportionalität 1.1 Direkte Proportionalität Eigenschaften: y Quotientengleichheit Bei kommt immer das Gleiche
CHAOS. 1.2 Was ist deterministisches Chaos? 1.1 Einführung. 1. Deterministisches Chaos - allgemeine Vorbemerkungen. 1.1 Einführung
 CHAOS 1. Deterministisches Chaos - allgemeine Vorbemerkungen 1.1 Einführung 1.2 Was ist deterministisches Chaos? 1.3 Prinzipielle "Unschärfen" 1.4 Chaotische Experimente 2. Das Magnetpendel 2.1 Versuchsaufbau
CHAOS 1. Deterministisches Chaos - allgemeine Vorbemerkungen 1.1 Einführung 1.2 Was ist deterministisches Chaos? 1.3 Prinzipielle "Unschärfen" 1.4 Chaotische Experimente 2. Das Magnetpendel 2.1 Versuchsaufbau
F R. = Dx. M a = Dx. Ungedämpfte freie Schwingungen Beispiel Federpendel (a) in Ruhe (b) gespannt: Auslenkung x Rückstellkraft der Feder
 6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Rudolf Jürgler. Maschinendynamik. Dritte, neu bearbeitete Auflage. Mit 550 Abbildungen. Springer
 Rudolf Jürgler Maschinendynamik Dritte, neu bearbeitete Auflage Mit 550 Abbildungen Springer VII Inhaltsverzeichnis 1 Einleitung 1 2 Schwingungstechnische Grundbegriffe 3 2.1 Definition der Schwingung
Rudolf Jürgler Maschinendynamik Dritte, neu bearbeitete Auflage Mit 550 Abbildungen Springer VII Inhaltsverzeichnis 1 Einleitung 1 2 Schwingungstechnische Grundbegriffe 3 2.1 Definition der Schwingung
Deterministisches Chaos
 Platen-Gymnasium Ansbach Kollegstufe 001/003 FACHARBEIT aus dem Fach Physik Thema: Deterministisches Chaos Verfasser: Jörg Stadlinger Leistungskurs: Physik Inhaltsverzeichnis 1. Einführung in die Chaostheorie
Platen-Gymnasium Ansbach Kollegstufe 001/003 FACHARBEIT aus dem Fach Physik Thema: Deterministisches Chaos Verfasser: Jörg Stadlinger Leistungskurs: Physik Inhaltsverzeichnis 1. Einführung in die Chaostheorie
Prüfung. Prüfung: mündl min, Termin nach Absprache ( )
 Prüfung Prüfung: mündl. 20-30 min, Termin nach Absprache (Email) (Ergänzte/Geordnete) Unterlagen zur Vorlesung werden ab dem 22.7. am LTI verkauft (3 ) XIV: Nichtlineare Optik - Maxwell-Gleichungen und
Prüfung Prüfung: mündl. 20-30 min, Termin nach Absprache (Email) (Ergänzte/Geordnete) Unterlagen zur Vorlesung werden ab dem 22.7. am LTI verkauft (3 ) XIV: Nichtlineare Optik - Maxwell-Gleichungen und
Übungen zu Partielle Differentialgleichungen, WS 2016
 Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Gedämpfte harmonische Schwingung
 Gedämpfte harmonische Schwingung Die Differentialgleichung u + 2ru + ω 2 0u = c cos(ωt) mit r > 0 modelliert sowohl eine elastische Feder als auch einen elektrischen Schwingkreis. Gedämpfte harmonische
Gedämpfte harmonische Schwingung Die Differentialgleichung u + 2ru + ω 2 0u = c cos(ωt) mit r > 0 modelliert sowohl eine elastische Feder als auch einen elektrischen Schwingkreis. Gedämpfte harmonische
Vorwissen Lineare Modelle zweier Bevölkerungen
 Reiser Stephan 1 Ablauf Vorwissen Lineare Modelle zweier Bevölkerungen Das Konkurrenzmodell von Volterra Ein allgemeineres Konkurrenzmodell Periodische Bahnen für die allgemeine Volterra-Lotka- Gleichung
Reiser Stephan 1 Ablauf Vorwissen Lineare Modelle zweier Bevölkerungen Das Konkurrenzmodell von Volterra Ein allgemeineres Konkurrenzmodell Periodische Bahnen für die allgemeine Volterra-Lotka- Gleichung
π und die Quadratur des Kreises
 π und die Quadratur des Kreises Schnupper-Uni für SchülerInnen 8. Februar 2006 Dr. Michael Welter http://www.math.uni-bonn.de/people/welter 1 Konstruktionen mit Zirkel und Lineal Gegeben sei eine Menge
π und die Quadratur des Kreises Schnupper-Uni für SchülerInnen 8. Februar 2006 Dr. Michael Welter http://www.math.uni-bonn.de/people/welter 1 Konstruktionen mit Zirkel und Lineal Gegeben sei eine Menge
